1 Introduction

Fractional order systems (FOSs) are general with respect to integer order systems (IOSs) which are a special case of FOSs [1,2,3]. On the other hand, many physical systems or processes can be described better by fractional derivatives and integrals such as the viscoelasticity of polymer materials [4], the fractional order electrical circuit systems [5], and signal processing [6]. Therefore, in the past several decades, FOSs have attracted great attention from the control field. The stability analysis of FOSs was first investigated [7,8,9,10,11,12]. A stability criterion for the FOSs was provided [7] by examining the locations of the system matrix eigenvalues. Some stability conditions were further given [8] by solving the LMIs with complex variables, and the approaches to transforming the complex variables to the real variables were developed [9, 10] for ease of solution. To this end, some brief theorems without LMIs were further established [11, 12] that simplify the stability analysis significantly. On the other hand, the observer and controller designs were carried out [13,14,15,16,17,18,19,20]. A non-fragile observer was constructed [13]; some output-feedback controllers based on the iterative algorithms were designed [14, 15]. To simplify the design and computational complexity, the LMI tool [16]- [20] or the singular value decomposition technique [16] was skillfully adopted. For nonlinear FOSs, the Takagi-Sugeno (T-S) fuzzy model was employed in the control design [17,18,19]. And in the presence of model uncertainties, the sliding mode control method was applied to the T-S fuzzy singular FOSs [20]. To further enhance the robustness of the control systems, the \(H_\infty\) control method was applied to the FOSs successfully [21,22,23].

It should be noted that the above-mentioned results are established in the fault-free case. With the fast development of modern industry and information technology, many control systems are increasingly complex. As a result, the system is more likely to meet faults. Faults lead to unfavorable effects on the performance and/or stability of the control system, and even cause disastrous consequences. Therefore, the control system with tolerance to unexpected faults, especially to the actuator faults that change the control action straightforward, is of great significance. For this purpose, a variety of fault-tolerant control (FTC) approaches were proposed in the literature. In general, an observer is designed to estimate the faults for compensation. For example, under the assumption of known fault bounds, a sliding mode observer was constructed [24]. To avoid the difficulty in solving the bilinear matrix inequalities, the fault observer and the controller were designed separately [25, 26]. However, the comparative result between the integrated and separate designs [27] reveals that the former achieves better estimation and control performance. On the other hand, when the full system state is available, some FTC schemes were developed [28, 29] with respect to the energy-bounded faults. Further, an output-feedback FTC strategy was proposed [30]. To the FTC problem for FOSs, some solutions were also reported in recent years [31,32,33,34]. The model uncertainty was taken into consideration [31, 32], yielding some robust FTC laws. Under the assumption that the actuator faults are n-order differentiable, an augmented fault observer was developed [33]. The \(H_\infty\) control method and the dynamic output-feedback control design method were combined to deal with the actuator faults [34].

Motivated by the above observation, this paper presents a novel output-feedback FTC strategy for a class of FOSs with actuator faults. Its advantages are as follows.

  1. (1)

    The stability domain of the faulty FOS is extended by our approach. In the existing literature on FTC of FOSs [32], the control design and analysis are based mainly on the indirect Lyapunov theory, that is, the designers follow the FTC method for IOSs. This yields the system stability domain covering only the left half of the plane. Instead of the indirect Lyapunov theory, the D-stability-based analysis approach in which the nonconvex property of the FOS is taken into account fully [8, 10], is adopted in this paper. In this way, the system stability domain is extended significantly.

  2. (2)

    The proposed approach of fault estimation and FTC is robust against the measurement noise and external disturbances which however are not considered in the existing FTC designs for FOSs [31, 32]. The robustness is achieved by adopting the \(H_\infty\) control method. Moreover, we evade the calculation of complex matrix inequalities [21]- [23], and the controller parameters are determined by solving real LMIs. This reduces the design complexity of the fault observer and the controller.

  3. (3)

    In addition, the proposed output-feedback control design for FOSs is less restrictive than the existing ones. The output matrix is required to be of full row rank or same [13, 16] and [28]; certain matrices in the intermediate steps of the control design need to be in the block diagonal form [13]. However, this paper is without the above requirements.

Notations: In this paper, \(\mathbb{R},\) \(\mathbb{R}^n,\) \(\mathbb{R}^{n\times m}\) and \(\mathbb{C}^{n\times m}\) denote the real number field, n-dimensional Euclidean space, the set of all \(n\times m\) real matrices, and the set of all \(n\times m\) complex matrices, respectively. Re(P) and Im(P) mean the real and image parts of complex matrix P,  respectively. j is an imaginary unit. \(X>0~(<0)\) demonstrates that X is a positive (negative) definite matrix. \(X^T\) and \(X^{-1}\) stand for the transpose and the inverse of X,  respectively. The symbols \(\mathrm{sym}\{Y\}\) and \(\star\) represent \(Y+Y^T\) and the transpose in the symmetric positions of a matrix, respectively. \(I_n\) stands for an identity matrix with n dimensions. For brevity, denote \(a=\mathrm{sin}(\frac{\alpha \pi }{2})\) and \(b=\mathrm{cos}(\frac{\alpha \pi }{2})\) in the sequel. A matrix is assumed to have appropriate dimensions to be compatible for algebraic calculus without specially statement.

2 System Description and Preliminaries

2.1 System Description

Different from the classical T-S fuzzy model [17,18,19,20, 35, 36], the type-2 fuzzy model is an effective way to describe the system with model uncertainties [37,38,39,40]. In an integer order type-2 fuzzy model, its ith fuzzy rule is:

Plant rule i: IF \(h_{1}(x(t))\) is \(H_{i1}~ \mathrm{and}~\cdots ~ \mathrm{and}~ h_{p}(x(t))\) is \(H_{ip}\), THEN

$$\begin{aligned} \begin{aligned} \dot{x}(t)&=A_ix(t)+B_iu(t)+\tilde{G}_{i}\omega _1(t),\\ y(t)&=C_{i}x(t)+\tilde{D}_{i}\omega _2(t), \end{aligned}\end{aligned}$$
(1)

for \(i=1,2,\ldots ,r\) with r the number of the IF-THEN rules, where \(H_{ig}\) and \(h_{g}(x(t))\) stand for the fuzzy set and the premise variable, respectively, \(g=1,~2, \ldots , p;\) \(x(t)\in \mathbb{R}^{n}\), \(u(t)\in \mathbb{R}^{m},\) \(\omega _1(t)\in \mathbb{R}^{n}\) and \(\omega _2(t)\in \mathbb{R}^{s}\) are the state, control input, external disturbance and measurement uncertainty, respectively; \(y(t)\in \mathbb{R}^{s}\) is the measured output; \(A_i,~ B_i,~\tilde{G}_{ i},~ C_i\) and \(\tilde{D}_i\) are the system matrices. Accordingly, the overall fuzzy system is

$$\begin{aligned} \begin{aligned} \dot{x}(t)&=\sum ^{r}_{i=1}\theta _i(x (t))(A_{i}x(t)+B_iu(t)+\tilde{G}_{ i}\omega _1(t)),\\ y(t)&=\sum ^{r}_{i=1}\theta _i(x (t))(C_{i}x(t)+\tilde{D}_i\omega _2(t)), \end{aligned}\end{aligned}$$
(2)

where \(\theta _i(x (t))\) are the grades of membership:

$$\begin{aligned} \theta _i(x (t))=\underline{\lambda }_i(x(t))\underline{\theta }_i (x (t)) +\overline{\lambda }_i(x(t))\overline{\theta }_i (x (t)), \end{aligned}$$
(3)

where \(\underline{\lambda }_i(x(t))\) and \(\overline{\lambda }_i(x(t))\) are adjustable nonlinear functions according to the change of uncertain parameters, which meet

$$\begin{aligned} 0\le \underline{\lambda }_i(x(t))&\le 1,\\ 0\le \overline{\lambda }_i(x(t))&\le 1,\\ \underline{\lambda }_i(x(t))+\overline{\lambda }_i(x(t))&=1,~i=1,\cdots ,r. \end{aligned}$$

And \(\underline{\theta }_i (x (t))\) and \(\overline{\theta }_i (x (t))\) are the lower and upper bounds of the membership functions of the ith rule, respectively, with

$$\begin{aligned}&\underline{\theta }_i(x(t))=\prod \limits ^p_{g=1}\underline{\mu }_{H_{ig}}(h_g(x(t))), \\&\overline{\theta }_i(x(t))=\prod \limits ^p_{g=1}\overline{\mu }_{H_{ig}}(h_g(x(t))), \end{aligned}$$

where \(\underline{\mu }_{H_{ig}}(h_g(x(t)))\) and \(\overline{\mu }_{H_{ig}}(h_g(x(t)))\) denote the lower and upper membership of \(h_g(x(t))\) in \(H_{ig}\), respectively, meeting

$$\begin{aligned} \overline{\mu }_{H_{ig}}(h_s(x(t))) \ge \underline{\mu }_{H_{ig}}(h_s(x(t)))&\ge 0, i=1,2,\cdots ,r.\\ \overline{\theta }_i (x (t)))\ge \underline{\theta }_i (x (t))&\ge 0. \end{aligned}$$

For simplification of notation, let \(\theta _i=\theta _i(x(t))\) and \(\eta _i=\eta _i(x(t))\). Define

$$\begin{aligned} A(\theta )&=\sum ^{r}_{i=1}\theta _iA_{i},~~B(\theta )=\sum ^{r}_{i=1}\theta _iB_{i},~~\tilde{G}(\theta )=\sum ^{r}_{i=1}\theta _i\tilde{G}_{ i},\\ C(\theta )&=\sum ^{r}_{i=1}\theta _iC_{i},~~\tilde{D}(\theta )=\sum ^{r}_{i=1}\theta _i\tilde{D}_{i}. \end{aligned}$$

Then, (2) becomes

$$\begin{aligned} \begin{aligned} \dot{x}(t)&=A(\theta )x(t)+B(\theta )u(t)+\tilde{G}(\theta )\omega _1(t),\\ y(t)&=C(\theta )x(t)+\tilde{D}(\theta )\omega _2(t). \end{aligned}\end{aligned}$$
(4)

Now we consider a fractional order type-2 fuzzy model. Usually, the Caputo definition is adopted to describe the FOSs.

Definition 1

The \(\alpha\) order Caputo derivative of the function g(t) is defined as [2]

$$\begin{aligned} \mathscr {D}^{\alpha }g(t)=\frac{1}{\Gamma (m-\alpha )}\int ^{t}_{0}\frac{g^{(m)}(\tau )}{(t-\tau )^{\alpha +1-m}}d\tau , \end{aligned}$$

with \(m-1<\alpha <m\) for an integer m,  and

$$\begin{aligned} \Gamma (s)=\int ^{\infty }_0t^{s-1}e^{-t}dt. \end{aligned}$$

Following (1), the type-2 fuzzy fractional order model is written as:

Plant rule i: IF \(h_{1}(x(t))\) is \(H_{i1}~ \mathrm{and}~\cdots ~ \mathrm{and}~ h_{p}(x(t))\) is \(H_{ip}\), THEN

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha {x}(t)&=A_ix(t)+B_iu(t))+\tilde{G}_{i}\omega _1(t),\\ y(t)&=C_{i}x(t)+\tilde{D}_{i}\omega _2(t). \end{aligned}\end{aligned}$$
(5)

As usual, we discuss the fixed order \(\alpha\) with \(0<\alpha <1\) [9,10,11,12,13,14]. The overall fuzzy FOS is

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha x(t)&=\sum ^{r}_{i=1}\theta _i(x (t))(A_{i}x(t)+B_iu(t)+\tilde{G}_{ i}\omega _1(t)),\\ y(t)&=\sum ^{r}_{i=1}\theta _i(x (t))(C_{i}x(t)+\tilde{D}_i\omega _2(t)). \end{aligned}\end{aligned}$$
(6)

The possible actuator faults are taken into account: \(u_f(t)=u(t)+f(t)\). The faulty system is thus:

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha x(t)&=\sum ^{r}_{i=1}\theta _i(x (t))(A_{i}x(t)+B_iu_f(t)+\tilde{G}_{ i}\omega _1(t)),\\ y(t)&=\sum ^{r}_{i=1}\theta _i(x (t))(C_{i}x(t)+\tilde{D}_i\omega _2(t)). \end{aligned}\end{aligned}$$
(7)

Assumption 1

\(\dot{f}(t)\) belongs to \(L_2 [0,~ \infty )\) [30].

Remark 1

Besides Assumption 1, it is usually assumed in the related works on fault estimation that \(f(t) \in L_2 [0, \infty )\) [41] or that the fault bound is known [24]. In this paper, these requirements are not involved.

For ease of exposition, rewrite (7) in the following form:

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha x(t)&=\sum ^{r}_{i=1}\theta _i(x (t))(A_{i}x(t)+B_iu_f(t)+G_{ i}\omega (t)),\\ y(t)&=\sum ^{r}_{i=1}\theta _i(x (t))(C_{i}x(t)+D_i\omega (t)), \end{aligned}\end{aligned}$$
(8)

where \(\omega (t)=\left[ \begin{array}{c} \omega _1(t)\\ \omega _2(t)\\ \end{array} \right] ,~G_{ i}=\tilde{G}_{ i}\left[ \begin{array}{cc} I&{}0\\ \end{array} \right]\) and \(\tilde{D}_{ i}\left[ \begin{array}{cc} 0&{}I\\ \end{array} \right] .\)

The control objective for the system in (8) is stabilization, even in the presence of actuator faults.

2.2 Preliminaries

Consider the following FOS with \(0<\alpha <1,\)

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha x(t)&=Ax(t)+G\omega (t),\\ y(t)&=Cx(t)+D\omega (t). \end{aligned}\end{aligned}$$
(9)

In the classical \(H_\infty\) control designs for (9) [21, 22], the following lemma is usually applied to solving the linear complex matrix inequalities.

Lemma 1

The FOS in (9) meets \(\Vert y(t)\Vert _2<\gamma \Vert \omega (t)\Vert _2\) if there exists a complex matrix P such that

$$\begin{aligned} P=X+Yj&>0,\end{aligned}$$
(10)
$$\begin{aligned} \left[ \begin{array}{ccc} \mathrm{sym}\{A(aX-bY)\}&{} \star &{} \star \\ C(aX-bY)&{}-\gamma I_p&{} \star \\ G^T&{}D^T&{}-\gamma I_q\\ \end{array} \right]&<0.\end{aligned}$$
(11)

Lemma 1 yields complex solutions. In general, it is nontrivial to solve complex matrix inequalities; for example, the complex matrix inequality is unsolvable by the widely used mathematical tool MATLAB. This is because the complex matrix should be mapped to a real matrix for calculation. Motivated by this, a new lemma is established in this paper, presented as follows.

Lemma 2

The FOS in (9) meets \(\Vert y(t)\Vert _2<\gamma \Vert \omega (t)\Vert _2\) if there exist a symmetric matrix X and a skew-symmetric matrix Y such that

$$\begin{aligned} \left[ \begin{array}{cc} X&{} Y\\ -Y&{}X\\ \end{array} \right]&>0,\end{aligned}$$
(12)
$$\begin{aligned} \left[ \begin{array}{ccc} \mathrm{sym}\{A^T(aX-bY)\}&{} \star &{} \star \\ G^T(aX-bY)&{}-\gamma I_p&{} \star \\ C&{}D&{}-\gamma I_q\\ \end{array} \right]&<0.\end{aligned}$$
(13)

Proof

Note that \(\Vert G_{wz}(s)\Vert =\Vert C(s^\alpha I-A)^{-1}G+D\Vert <\gamma\) is equivalent to \(\Vert G^T_{wz}(s)\Vert =\Vert G^T(s^\alpha I-A^T)^{-1}C^T+D^T\Vert <\gamma .\) This yields (13), straightforward. Next, we show that \(P=X+Yj>0\) if

$$\begin{aligned} \left[ \begin{array}{cc} \mathrm{Re}(P)&{}\mathrm{Im}(P)\\ -\mathrm{Im}(P)&{}\mathrm{Re}(P)\\ \end{array} \right] >0. \end{aligned}$$
(14)

Under (14), there is \(\mathrm{Im}(P)^T=-\mathrm{Im}(P).\) For any \(x,~y\in \mathbb{R}^n,\) there thus hold \(x^T\mathrm{Im}(P)x= 0\) and \(y^T\mathrm{Im}(P)y= 0.\) Calculating the real part of

$$\begin{aligned} \varSigma =(x^T-y^Tj)(\mathrm{Re}(P)+ \mathrm{Im}(P)j)(x+yj), \end{aligned}$$

one has

$$\begin{aligned}&\mathrm{Re}((x^T-y^Tj)(\mathrm{Re}(P) +\mathrm{Im}(P)j)(x+yj))\\ =&x^T\mathrm{Re}(P)x+ y^T\mathrm{Re}(P)y-x^T\mathrm{Im}(P)y+y^T\mathrm{Im}(P)x\\ =&\left[ \begin{array}{cc} x^T &{}y^T \\ \end{array} \right] \left[ \begin{array}{cc} \mathrm{Re}(P) &{} -\mathrm{Im}(P) \\ \mathrm{Im}(P)&{} \mathrm{Re}(P) \\ \end{array} \right] \left[ \begin{array}{c} x \\ y\\ \end{array} \right] . \end{aligned}$$

From (14), we have \(\mathrm{Re}(\varSigma )>0.\) Calculating the imaginary part of \(\varSigma\), we have

$$\begin{aligned}&\mathrm{Im}((x^T-y^Tj)(\mathrm{Re}(P) +\mathrm{Im}(P)j)(x+yj))\\ = \, &x^T\mathrm{Re}(P)y-y^T\mathrm{Re}(P)x+x^T\mathrm{Im}(P)x+y^T\mathrm{Im}(P)y=0. \end{aligned}$$

Due to \(\varSigma =\mathrm{Re} (\varSigma )+\mathrm{Im}(\varSigma )j=\mathrm{Re}(\varSigma )>0,\) \(P>0\) holds. This completes the proof. \(\square\)

As seen, Lemma 2 gives a straightforward way to solve real matrix inequalities, yielding real solutions. Therefore, it significantly reduces the computation complexity, simplifying the \(H_\infty\) control design for FOSs.

In addition, two lemmas [42] are given as follows.

Lemma 3

For any constant matrices \(S_1\), \(S_2\) and \(S_3\) with \(S_1^T=S_1\) and \(S_3^T=S_3>0\), there is \(S_1+S_2S_3^{-1}S_2^T<0\) if and only if

$$\begin{aligned} \left[ \begin{array}{cc} S_1 &{} S_2 \\ S_2^T &{} -S_3 \\ \end{array} \right] <0.\end{aligned}$$

Lemma 4

For any T, H,  E and \(F^T(\sigma )F(\sigma )\le I\), there holds

$$\begin{aligned} T+HF(\sigma )E + E^TF^T(\sigma )H^T< 0, \end{aligned}$$

if and only if there exists an \(\varepsilon >0\) such that

$$\begin{aligned}T+\varepsilon HH^T+\varepsilon ^{-1}E^TE<0,\end{aligned}$$

where \(\sigma \in \varTheta \subset \mathbb{R}.\)

3 Control Design

To achieve the control objective, an output-feedback FTC scheme based on a non-fragile observer is developed in this section.

3.1 Observer Design

To detect and estimate the actuator faults, the following non-fragile fault observer is constructed.

Observer rule i: IF \(h_{1}(x(t))\) is \(H_{i1}~ \mathrm{and}~\cdots ~ \mathrm{and}~ h_{p}(x(t))\) is \(H_{ip}\), THEN

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha {\hat{x}}(t)=&{A}_i\hat{x}(t)+{B}_i(u(t)+\hat{f}(t))+(L_i+\varDelta L_i)(y(t)-\hat{y}(t)),\\ \hat{y}(t)=&C_i\hat{x}(t),\\ \mathscr {D}^\alpha {\hat{f}}(t)=&(F_i+\varDelta F_i)(y(t)-\hat{y}(t)), \end{aligned}\end{aligned}$$
(15)

where \(\hat{x}(t),~\hat{y}(t)\) and \(\hat{f}(t)\) are the estimates of x(t),  y(t) and f(t),  respectively; \(L_i,~F_i,~ \varDelta L_i\) and \(\varDelta F_i\) constitute the observer gains, with

$$\begin{aligned}&\left[ \begin{array}{cc} \varDelta L_i&{}\varDelta F_i\\ \end{array} \right] =\left[ \begin{array}{cc} U_{Li}F(\sigma )V_{Li}&{}U_{Fi}F(\sigma )V_{Fi}\\ \end{array} \right] ,\end{aligned}$$
(16)

where \(L_i, F_i, U_{Li}, V_{Li}, U_{Fi}\) and \(V_{Fi}\) are fixed, and \(F(\sigma )\) is variable but should meet

$$\begin{aligned} F^T(\sigma )F(\sigma )<I. \end{aligned}$$
(17)

Then the overall fault observer is

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha {\hat{x}}(t)=&{A}(\theta )\hat{x}(t)+{B}(\theta )(u(t)+\hat{f}(t))+(L(\theta )+\varDelta L(\theta ))(y(t)-\hat{y}(t)),\\ \hat{y}(t)=&C(\theta )\hat{x}(t),\\ \mathscr {D}^\alpha {\hat{f}}(t)=&(F(\theta )+\varDelta F(\theta ))(y(t)-\hat{y}(t)), \end{aligned}\end{aligned}$$
(18)

where

$$\begin{aligned} L(\theta )=&\sum ^{r}_{i=1}\theta _iL_{i},~F(\theta )=\sum ^{r}_{i=1}\theta _iF_{i},\\ \varDelta L(\theta )=&\sum _{i=1}^r\theta _i\varDelta L_i=\sum _{i=1}^r\theta _iU_{Li}F(\sigma )V_{Li},\\ \varDelta F(\theta )=&\sum _{i=1}^r\theta _i\varDelta F_i=\sum _{i=1}^r\theta _iU_{Fi}F(\sigma )V_{Fi}. \end{aligned}$$

Remark 2

The non-fragile observer is used to estimate the state and the actuator faults simultaneously. The observer gains are comprised of the fixed and variable gains such that the non-fragile observer is still effective when tiny bias or disturbances occur in the observer gains.

Next, we determine the observer parameters \(L_i\) and \(F_i\) in (15). It begins with analyzing the error systems. Let \(e_x(t)=x(t)-\hat{x}(t),\) \(e_f(t)=f(t)-\hat{f}(t),\) \(e_y(t)=y(t)-\hat{y}(t).\) From (8) and (18), the error systems are described by

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha {e}_x(t)=&(A(\theta )-(L(\theta )+\varDelta L(\theta ))C(\theta ))e_x(t)+B(\theta )e_f(t)\\&+(F(\theta )-(L(\theta )+\varDelta L(\theta ))D(\theta ))\omega (t),\\ \mathscr {D}^\alpha {e}_f(t)=&-(F(\theta )+\varDelta F(\theta ))C(\theta )e_x(t)-(F(\theta )+\varDelta F(\theta ))D(\theta )\omega (t)+\mathscr {D}^\alpha {f}(t),\\ e_y(t)=&C(\theta )e_x(t)+D(\theta )\omega (t). \end{aligned} \end{aligned}$$
(19)

By Definition 1, Assumption 1 implies that \(\mathscr {D}^\alpha {f}(t)\) belongs to \(L_2 [0,~ \infty ).\) Let

$$\begin{aligned} e(t)&=\left[ \begin{array}{c} e_x(t)\\ e_f(t)\\ \end{array} \right] ,~~\xi (t)=\left[ \begin{array}{c} \omega (t)\\ \mathscr {D}^\alpha f(t)\\ \end{array} \right] ,~~\hat{A}(\theta )=\left[ \begin{array}{cc} A(\theta )&{}B(\theta )\\ 0 &{} 0\\ \end{array} \right] ,~~\hat{L}(\theta )=\left[ \begin{array}{c} L(\theta )\\ F(\theta )\\ \end{array} \right] ,\\ \hat{C}(\theta )&=\left[ \begin{array}{cc} C(\theta )&{}0\\ \end{array} \right] ,~~\hat{D}(\theta )=\left[ \begin{array}{cc} {D}(\theta )&{}0\\ \end{array} \right] ,~~\hat{G}(\theta )=\left[ \begin{array}{cc} {G}(\theta )&{}0\\ 0&{}I\\ \end{array} \right] ,\\ \varDelta \hat{L}(\theta )&=\left[ \begin{array}{c} \varDelta L(\theta )\\ \varDelta F(\theta )\\ \end{array} \right] =\sum _{i=1}^r\theta _i\varDelta \hat{L}_i=\sum _{i=1}^r\theta _i\hat{U}_i\hat{F}(\sigma )\hat{V}_i,\\ \varDelta \hat{L}_i&= \hat{U}_{i} \hat{F}(\sigma ) \hat{V}_{i},~~\hat{U}_i=\left[ \begin{array}{cc} U_{Li}&{}0\\ 0&{}U_{Fi}\\ \end{array} \right] ,~~\hat{F}(\sigma )=\left[ \begin{array}{cc} F(\sigma )&{}0\\ 0&{}F(\sigma )\\ \end{array} \right] ,~~\hat{V}_i= \left[ \begin{array}{c} V_{Li}\\ V_{Fi}\\ \end{array} \right] . \end{aligned}$$

The overall error system is

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha {e}(t)=&(\hat{A}(\theta )-(\hat{L}(\theta )+\varDelta \hat{L}(\theta ))\hat{C}(\theta ))e(t)\\&+(\hat{G}(\theta )-(\hat{L}(\theta )+\varDelta \hat{L}(\theta ))\hat{D}(\theta ))\xi (t),\\ e_y(t)=&\hat{C}(\theta )e(t)+\hat{D}(\theta )\xi (t). \end{aligned}\end{aligned}$$
(20)

Choose a symmetric matrix \(X_o,\) a skew-symmetric matrix \(Y_o,\) and a bank of matrices with the appropriate dimensions, \(W_k, k=1,2,\cdots ,r,\) together with a set of positive scalars \(\varepsilon _{ik},\) \(i,~k=1,~2,~\cdots ,~r,\) such that

$$\begin{aligned} \left[ \begin{array}{cc} X_o&{} Y_o\\ -Y_o&{}X_o\\ \end{array} \right]&>0,\end{aligned}$$
(21)
$$\begin{aligned} Q_{ii}&<0,\end{aligned}$$
(22)
$$\begin{aligned} Q_{ik}+Q_{ki}&<0,~i<k, \end{aligned}$$
(23)

where

$$\begin{aligned} Q_{ik}&=\left[ \begin{array}{cccc} \varPi _{11ik}&{}\star &{}\star &{}\star \\ \varPi _{21ik}&{}\varPi _{22ik}&{}\star &{}\star \\ \hat{I}&{}0&{}-\gamma _o I&{}\star \\ \hat{U}^T_k(aX_o-bY_o)&{}0&{}0&{}-\varepsilon _{ik} I\\ \end{array} \right] ,\\ \varPi _{11ik}&=\mathrm{sym}\{\hat{A}^T_i(aX_o-bY_o)-\hat{C}^T_iW_k\}+\varepsilon _{ik} \hat{C}^T_i\hat{V}^T_k\hat{V}_k\hat{C}_i,\\ \varPi _{21ik}&=\hat{G}^T_i(aX_o-bY_o)-\hat{D}^T_iW_k+\varepsilon _{ik}\hat{D}^T_i\hat{V}^T_k\hat{V}_k\hat{C}_i,\\ \varPi _{22ik}&=-\gamma _o I+\varepsilon _{ik}\hat{D}^T_i\hat{V}^T_k\hat{V}_k\hat{D}_i\\ \hat{I}&=\left[ \begin{array}{cc} 0&{}I_s\\ \end{array} \right] . \end{aligned}$$

Accordingly, the observer gain is set to be

$$\begin{aligned} \hat{L}_i=(aX_o-bY_o)^{-T}W^T_i, i=1,2,\cdots ,r. \end{aligned}$$
(24)

3.2 Controller Design

With the fault estimates, we design a dynamic output feedback fault-tolerant controller to stabilize the system in (8).

Controller rule k: IF \(f_{1}(x(t))\) is \(F_{k1}~ \mathrm{and}~\cdots ~ \mathrm{and}~ f_{p}(x(t))\) is \(F_{kp}\), THEN

$$\begin{aligned} \begin{aligned} u(t)&={C}_{ck}\psi (t)-\hat{f}(t),\\ \mathscr {D}^\alpha {\psi }(t)&={A}_{ck}\psi (t)+{B}_{ck}y(t), \end{aligned}\end{aligned}$$
(25)

where \(F_{kg}\) stands for the kth fuzzy set of the function \(f_g (x (t)), k= 1, 2,\cdots ,r, g =1, 2,\cdots ,p,\) and p is the number of the premise variables. \(A_{ck} , B_{ck},\) and \(C_{ck}\) are the controller gains to be determined. Let

$$\begin{aligned} {A}_{ck}=\sum ^{r}_{i=1}\theta _iA_{cik}, \end{aligned}$$

and

$$\begin{aligned} {A}_{c}(\theta ,\eta )&=\sum ^{r}_{i=1}\sum ^r_{k=1}\theta _i\eta _kA_{cik},~~{B}_{c}(\eta )=\sum ^{r}_{k=1}\eta _kB_{ck},~~ {C}_{c}(\eta )=\sum ^{r}_{k=1}\eta _kC_{ck}. \end{aligned}$$

The overall output feedback controller is

$$\begin{aligned} \begin{aligned} u(t)&={C}_{c}(\eta )\psi (t)-\hat{f}(t),\\ \mathscr {D}^\alpha {\psi }(t)&={A}_{c}(\theta ,\eta )\psi (t)+{B}_{c}(\eta )y(t), \end{aligned}\end{aligned}$$
(26)

where

$$\begin{aligned} \eta _k(x(t))=\underline{m}_k(x(t))\underline{\eta }_k (x(t)) +\overline{m}_k(x(t))\overline{\eta }_k (x(t))\ge 0, \end{aligned}$$
(27)

and \(\underline{m}_k(x(t))\) and \(\overline{m}_k(x(t))\) are the predefined functions that meet

$$\begin{aligned} 0\le \underline{m}_k(x(t))\le 1,\\ 0\le \overline{m}_k(x(t))\le 1,\\ \underline{m}_k(x(t))+\overline{m}_k(x(t))=1. \end{aligned}$$

In (27), \(\underline{\eta }_k (x (t))\) and \(\overline{\eta }_k (x (t))\) are the lower and upper bounds of the membership functions of the kth rule, respectively, with

$$\begin{aligned} \underline{\eta }_k(x(t))=&\prod \limits ^p_{g=1}\underline{\mu }_{F_{kg}}(f_g(x(t))),\\ \overline{\eta }_k(x(t))=&\prod \limits ^p_{g=1}\overline{\mu }_{F_{kg}}(f_g(x(t))), \end{aligned}$$

where \(\underline{\mu }_{F_{kg}}(f_g(x(t)))\) and \(\overline{\mu }_{F_{kg}}(f_g(x(t)))\) denote the lower and upper memberships of \(f_g(x(t))\) in \(F_{kg}\), respectively, meeting

$$\begin{aligned} \overline{\mu }_{F_{kg}}(f_s(x(t))) \ge \underline{\mu }_{F_{kg}}(f_s(x(t)))&\ge 0, i=1,2,\cdots ,r.\\ \overline{\eta }_k (x (t)))\ge \underline{\eta }_k (x (t))&\ge 0. \end{aligned}$$

Substituting (26) into (8) gives the dynamic equation of the closed-loop system:

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha {\varphi }(t)&=\bar{A}(\theta ,\eta )\varphi (t)+\bar{G}(\theta ,\eta )\nu (t),\\ y(t)&=\hat{C}(\theta )\varphi (t)+\hat{D}(\theta )\nu (t), \end{aligned}\end{aligned}$$
(28)

where

$$\begin{aligned} \varphi (t)&=\left[ \begin{array}{c} x(t)\\ \psi (t) \\ \end{array} \right] ,~\nu (t)=\left[ \begin{array}{c} \omega (t)\\ e_f(t) \\ \end{array} \right] ,\\ \bar{A}(\theta ,\eta )&=\left[ \begin{array}{cc} A(\theta )&{}B(\theta )C_{c}(\eta )\\ B_{c}(\eta )C (\theta )&{}A_{c} (\theta ,\eta )\\ \end{array} \right] ,~\bar{G}(\theta ,\eta )=\left[ \begin{array}{cc} G(\theta )&{}B(\theta )\\ B_{c}(\eta )D(\theta ) &{}0 \\ \end{array} \right] .\end{aligned}$$

A principle for the selection of the controller gains is given as follows. Choose two symmetric matrices \(X_{c1}\) and \(X_{c2},\) a skew-symmetric matrix \(Y_{c1},\) and two banks of matrices with appropriate dimensions, \(\varPhi _i\) and \(\varPsi _i,~i=1,~2,~\cdots ,~r\) such that

$$\begin{aligned} \left[ \begin{array}{cccc} X_{c1} &{} Y_{c1} &{}I&{}0\\ -Y_{c1} &{} X_{c1}&{}0&{}I\\ I&{}0&{}X_{c2} &{} 0\\ 0&{}I&{} 0&{} X_{c2}\\ \end{array} \right]&>0, \end{aligned}$$
(29)
$$\begin{aligned} \varXi _{ik}-\varDelta _i&<0, \end{aligned}$$
(30)
$$\begin{aligned} \varrho _i\varXi _{ii}+(1-\varrho _i)\varDelta _i&<0, \end{aligned}$$
(31)
$$\begin{aligned} \varrho _k\varXi _{ik}+(1-\varrho _k)\varDelta _i+ \varrho _i\varXi _{ki}+(1-\varrho _i)\varDelta _k&<0,i<k, \end{aligned}$$
(32)

where

Accordingly, the controller gain matrices are set to be

$$\begin{aligned} \begin{aligned} A_{cik} =&-(a(X^{-1}_{c2}-X_{c1})+bY_{c1})^{-T}({a}A^T_iX^{-1}_{c2}\\&+(aX_{c1}-bY_{c1})^T(B_i\varPsi _k X^{-1}_{c2}+A_i)+\varPhi _k C_i),\\ B_{ci} =&(a(X^{-1}_{c2}-X_{c1})+bY_{c1})^{-T}\varPhi _i,\\ C_{ci} =&\varPsi _i X^{-1}_{c2}. \end{aligned}\end{aligned}$$
(33)

4 Performance Analysis

We first show the effectiveness of the designed observer by the following theorem.

Theorem 1

Under Assumption 1, applying the observer in (18) with (24) to the system in (20) ensures \(\Vert e_f(t)\Vert _2<\gamma _o\Vert \xi (t)\Vert _2.\)

Proof

Substituting (24) into (20) gives

$$\begin{aligned} \begin{aligned} \mathscr {D}^\alpha {e}(t)=&(\hat{A}(\theta )-((aX_o-bY_o)^{-T}W^T(\theta )+\varDelta \hat{L}(\theta ))\hat{C}(\theta ))e(t)\\&+(\hat{G}(\theta )-((aX_o-bY_o)^{-T}W^T(\theta )+\varDelta \hat{L}(\theta ))\hat{D}(\theta ))\xi (t), \end{aligned}\end{aligned}$$
(34)

where \(W^T(\theta )=\sum _{i=1}^r \theta _i W^T_i.\) Note that

$$\begin{aligned} {e}_f(t)=\hat{I}e(t), \end{aligned}$$
(35)

with \(\hat{I}=\left[ \begin{array}{cccc} 0&{}I_s\\ \end{array} \right] .\) Applying Lemma 3, it is obtained that (22) is equivalent to

$$\begin{aligned}&\left[ \begin{array}{ccc} \varPi _{11ii}&{}\star &{}\star \\ \varPi _{21ii}&{}-\gamma _o I+\varepsilon _{ii}\hat{D}^T_i\hat{V}^T_i\hat{V}_i\hat{D}_i&{}\star \\ \hat{I}&{}0&{}-\gamma _o I\\ \end{array} \right] \nonumber \\&+\frac{1}{\varepsilon _{ii}}\left[ \begin{array}{c} (aX_o-bY_o)^T\hat{U}_i\\ 0\\ 0\\ \end{array} \right] \left[ \begin{array}{c} (aX_o-bY_o)^T\hat{U}_i\\ 0\\ 0\\ \end{array} \right] ^T\nonumber \\ =&\left[ \begin{array}{ccc} \mathrm{sym}\{\hat{A}^T_i(aX-bY)-\hat{C}^T_iW_i\}&{}\star &{}\star \\ \hat{G}^T_{i }(aX-bY)-\hat{D}^T_iW_i&{}-\gamma _o I&{}\star \\ \hat{I}&{}0&{}-\gamma _o I\\ \end{array} \right] \nonumber \\&+\varepsilon _{ii}\left[ \begin{array}{c} -\hat{C}^T_i\hat{V}^T_i\\ -\hat{D}^T_i\hat{V}^T_i\\ 0\\ \end{array} \right] \left[ \begin{array}{c} -\hat{C}^T_i\hat{V}^T_i\\ -\hat{D}^T_i\hat{V}^T_i\\ 0\\ \end{array} \right] ^T\nonumber \\&+\frac{1}{\varepsilon _{ii}}\left[ \begin{array}{c} (aX-bY)^T\hat{U}_i\\ 0\\ 0\\ \end{array} \right] \left[ \begin{array}{c} (aX-bY)^T\hat{U}_i\\ 0\\ 0\\ \end{array} \right] ^T <0. \end{aligned}$$
(36)

From (17), we have

$$\begin{aligned}&\hat{F}^T(\sigma )\hat{F}(\sigma )=\left[ \begin{array}{cc} F(\sigma )&{}0\\ 0&{}F(\sigma )\\ \end{array} \right] ^T\left[ \begin{array}{cc} F(\sigma )&{}0\\ 0&{}F(\sigma )\\ \end{array} \right] =\left[ \begin{array}{cc} F^T(\sigma )F(\sigma )&{}0\\ 0&{}F^T(\sigma )F(\sigma )\\ \end{array} \right] <I.\end{aligned}$$
(37)

By Lemma 4, combining (36) and (37) yields

$$\begin{aligned}&\left[ \begin{array}{ccc} \mathrm{sym}\{\hat{A}^T_i(aX_o-bY_o)-\hat{C}^T_iW_i\}&{}\star &{}\star \\ \hat{G}^T_{ i}(aX_o-bY_o)-\hat{D}^T_iW_i&{}-\gamma _o I&{}\star \\ \hat{I}&{}0&{}-\gamma _o I\\ \end{array} \right] \nonumber \\&+\mathrm{sym}\{\left[ \begin{array}{c} -\hat{C}^T_i\hat{V}^T_i\\ -\hat{D}^T_i\hat{V}^T_i\\ 0\\ \end{array} \right] \hat{F}^T(\sigma ) \left[ \begin{array}{c} (aX_o-bY_o)^T\hat{U}_i\\ 0\\ 0\\ \end{array} \right] ^T\} <0. \end{aligned}$$
(38)

Noting that

$$\begin{aligned} \varDelta \hat{L}_i= \hat{U}_{i} \hat{F}(\sigma ) \hat{V}_{i}, \end{aligned}$$

(38) is rewritten as

$$\begin{aligned}&\left[ \begin{array}{ccc} \mathrm{sym}\{\hat{A}^T_i(aX_o-bY_o)-\hat{C}^T_iW_i\}&{}\star &{}\star \\ \hat{G}^T_{ i}(aX_o-bY_o)-\hat{D}^T_iW_i&{}-\gamma _o I&{}\star \\ \hat{I}&{}0&{}-\gamma _o I\\ \end{array} \right] \nonumber \\&+\mathrm{sym}\{\left[ \begin{array}{c} -\hat{C}^T_i\\ -\hat{D}^T_i\\ 0\\ \end{array} \right] \varDelta \hat{L}^T_i \left[ \begin{array}{c} (aX_o-bY_o)^T\\ 0\\ 0\\ \end{array} \right] ^T\} <0. \end{aligned}$$
(39)

From (39), it follows that

$$\begin{aligned} T_{ii}<0. \end{aligned}$$
(40)

Similarly, from (23), we have

$$\begin{aligned} T_{ik}+T_{ki}<0, ~~~~i<k, \end{aligned}$$
(41)

where

$$\begin{aligned} T_{ik}=\!\left[ \! \begin{array}{ccc} \mathrm{sym}\{(\hat{A}_i-\varDelta \hat{L}_k\hat{C}_i)^T(aX_o-bY_o)-\hat{C}_i^TW_i\}&{}\star &{}\star \\ (\hat{G}_{ i}-\varDelta \hat{L}_k\hat{D}_i)^T(aX_o-bY_o)-\hat{D}_i^TW_i&{}-\gamma _o I&{}\star \\ \hat{I}&{}0&{}-\gamma _o I\\ \end{array} \!\right] \!. \end{aligned}$$
(42)

According to

$$\begin{aligned} \sum \limits _{i=1}^r\sum \limits _{k=1}^r\theta _i\theta _kT_{ik}=\sum \limits _{i=1}^{r}\theta ^2_iT_{ii}+\sum \limits _{i=1}^{r-1}\sum \limits _{k=i+1}^{r}\theta _i\theta _k(T_{ik}+T_{ki}), \end{aligned}$$

it is straightforward to see by the combination of (40) and (41) that

$$\begin{aligned} \left[ \begin{array}{ccc} \varPi _{11}&{}\star &{}\star \\ \varPi _{21}&{}-\gamma _o I&{}\star \\ \hat{I}&{}0&{}-\gamma _o I\\ \end{array} \right]&<0, \end{aligned}$$
(43)

where

$$\begin{aligned}&\varPi _{11}=\mathrm{sym}\{(\hat{A}(\theta )-\varDelta \hat{L}(\theta )\hat{C}(\theta ))^T(aX_o-bY_o)-\hat{C}^T(\theta )W(\theta )\},\\&\varPi _{21}=(\hat{G}(\theta )-\varDelta \hat{L}(\theta )\hat{D}(\theta ))^T(aX_o-bY_o)-\hat{D}^T(\theta )W(\theta ). \end{aligned}$$

Following Lemma 1, we have \(\Vert e_f(t)\Vert _2<\gamma _o\Vert \xi (t)\Vert _2.\) This ends the proof. \(\square\)

It is noted that the minimum \(H_\infty\) attenuation level of Theorem 1 can be obtained by solving the programming problem: minimize \(\gamma _o\) subject to (21)–(23).

Next, we show the effectiveness of the designed controller by the following theorem.

Theorem 2

Apply the controller in (26) with (33) to the system in (8). Under Assumption 1 and \(\eta _k-\varrho _k\theta _k\ge 0,0<\varrho _k<1,~i,~k=1,2,\cdots ,r\), the resulting control system in (28) is robustly stable and meets \(\Vert y(t)\Vert _2<\gamma _c\Vert \nu (t)\Vert _2.\)

Proof

Eq. (29) shows

$$\begin{aligned}&\left[ \begin{array}{cc} X_{c1} &{} Y_{c1} \\ -Y_{c1} &{} X_{c1}\\ \end{array} \right]>0,~~ \left[ \begin{array}{cc} X_{c2} &{} 0\\ 0&{} X_{c2}\\ \end{array} \right] >0,\end{aligned}$$
(44)

and

$$\begin{aligned} \left[ \begin{array}{cc} X_{c1} &{} Y_{c1}\\ -Y_{c1}&{} X_{c1}\\ \end{array} \right] -\left[ \begin{array}{cc} X_{c2} &{} 0\\ 0&{} X_{c2}\\ \end{array} \right] ^{-1}=\left[ \begin{array}{cc} X_{c1} -X^{-1}_{c2}&{} Y_{c1}\\ -Y_{c1}&{} X_{c1}-X^{-1}_{c2}\\ \end{array} \right] >0. \end{aligned}$$
(45)

Let

$$\begin{aligned} X_c&= \left[ \begin{array}{cc} X_{c1} &{} X^{-1}_{c2}-X_{c1}\\ X^{-1}_{c2}-X_{c1}&{} -X^{-1}_{c2}+X_{c1}\\ \end{array} \right] ,\end{aligned}$$
(46)
$$\begin{aligned} Y_c&= \left[ \begin{array}{cc} Y_{c1}&{} -Y_{c1}\\ -Y_{c1}&{} Y_{c1}\\ \end{array} \right] , \end{aligned}$$
(47)

and then construct the following matrix in the form of (12):

(48)

Let \(Z=\left[ \begin{array}{cccc} I &{} 0&{}0 &{} 0\\ 0&{} 0&{}I&{} 0\\ 0&{} I&{}0 &{} 0\\ 0 &{} 0&{} 0&{} I\\ \end{array} \right] .\) Then, there is

$$\begin{aligned} Z\left[ \begin{array}{cc} X_c &{} Y_c\\ -Y_c&{} X_c\ \end{array} \right] Z^T \!=\!\!\left[ \! \begin{array}{cccc} X_{c1} &{}Y_{c1} &{} X^{-1}_{c2}-X_{c1}&{} -Y_{c1}\\ -Y_{c1} &{} X_{c1} &{}Y_{c1}&{} X^{-1}_{c2}-X_{c1} \\ X^{-1}_{c2}-X_{c1}&{} -Y_{c1} &{}-X^{-1}_{c2}+X_{c1}&{}Y_{c1}\\ Y_{c1} &{} X^{-1}_{c2}-X_{c1}&{} -Y_{c1}&{} -X^{-1}_{c2}+X_{c1}\\ \end{array} \!\right] \!.\end{aligned}$$
(49)

From (44), we have

$$\begin{aligned}&\left[ \begin{array}{cc} X_{c1} &{}Y_{c1} \\ -Y_{c1} &{} X_{c1} \\ \end{array} \right] -\left[ \begin{array}{cc} X^{-1}_{c2}-X_{c1}&{} -Y_{c1}\\ Y_{c1}&{} X^{-1}_{c2}-X_{c1} \\ \end{array} \right] \nonumber \\&\times \left[ \begin{array}{cc} -X^{-1}_{c2}+X_{c1}&{}Y_{c1}\\ -Y_{c1}&{} -X^{-1}_{c2}+X_{c1}\\ \end{array} \right] ^{-1} \left[ \begin{array}{cc} X^{-1}_{c2}-X_{c1}&{} -Y_{c1} \\ Y_{c1} &{} X^{-1}_{c2}-X_{c1}\\ \end{array} \right] \nonumber \\ &\left[ \begin{array}{cc} X_{c2} &{} 0\\ 0&{} X_{c2}\\ \end{array} \right] ^{-1}>0, \end{aligned}$$
(50)

which meets the condition of Lemma 3. Therefore, by Lemma 3, we further have

$$\begin{aligned} Z\left[ \begin{array}{cc} X_c &{} Y_c\\ -Y_c&{} X_c\\ \end{array} \right] Z^T>0, \end{aligned}$$
(51)

which in turn means that

$$\begin{aligned} \left[ \begin{array}{cc} X_c &{} Y_c\\ -Y_c&{} X_c\\ \end{array} \right] >0. \end{aligned}$$
(52)

Combining (46) and (47) yields

$$\begin{aligned} aX_c-bY_c = \left[ \begin{array}{cc} aX_{c1}-bY_{c1} &{} a(X^{-1}_{c2}-X_{c1})+bY_{c1}\\ a(X^{-1}_{c2}-X_{c1})+bY_{c1} &{}-a(X^{-1}_{c2}-X_{c1})-bY_{c1}\\ \end{array} \right] . \end{aligned}$$
(53)

Let

(54)

Due to \(\sum \limits _{i=1}^r\sum \limits _{k=1}^r\theta _i(\theta _k-\eta _k)\varDelta _i=0,\) where \(\varDelta _i=\varDelta ^T_i\) is introduced only for analysis, (54) becomes

$$\begin{aligned} \varXi =&\sum _{i=1}^r\sum _{k=1}^r\theta _i\eta _k\varXi _{ik}\nonumber \\ =&\sum _{i=1}^r\sum _{k=1}^r\theta _i\eta _k\varXi _{ik}+\sum _{i=1}^r\sum _{k=1}^r\theta _i(\theta _k-\eta _k)\varDelta _i\nonumber \\ =&\sum _{i=1}^r\sum _{k=1}^r\theta _i(\eta _k+\varrho _k\theta _k-\varrho _k\theta _k)\varXi _{ik}+\sum _{i=1}^r\sum _{k=1}^r\theta _i(\theta _k-\eta _k+\varrho _k\theta _k-\varrho _k\theta _k)\varDelta _i\nonumber \\ =&\sum _{i=1}^r\sum _{k=1}^r\theta _i\theta _k(\varrho _k\varXi _{ik}+(1-\varrho _k)\varDelta _i) +\sum _{i=1}^r\sum _{k=1}^r\theta _i(\eta _k-\varrho _k\theta _k)(\varXi _{ik}-\varDelta _i). \end{aligned}$$
(55)

Under \(\eta _k-\varrho _k\theta _k\ge 0\), from (30), we further have

$$\begin{aligned} \varXi<&\sum _{i=1}^r\sum _{k=1}^r\theta _i\theta _k(\varrho _k\varXi _{ik}+(1-\varrho _k)\varDelta _i)\nonumber \\ =&\sum _{i=1}^r\theta ^2_i(\varrho _i\varXi _{ii}+(1-\varrho _i)\varDelta _i)+\sum _{k=1}^r\sum _{i<k}\theta _i\theta _k(\varrho _k\varXi _{ik}+(1-\varrho _k)\varDelta _i\nonumber \\&+\varrho _i\varXi _{ki}+(1-\varrho _i)\varDelta _k). \end{aligned}$$
(56)

Note that \(\sum \limits _{i=1}^r\sum \limits _{k=1}^r\theta _i\theta _k=\sum \limits _{i=1}^r\theta _i=1,\) and recall (30)–(32). Then, (56) further meets

$$\begin{aligned} \varXi <0. \end{aligned}$$
(57)

By Lemma 3, (57) is equivalent to

$$\begin{aligned}&\sum \limits _{i=1}^r\sum _{k=1}^r\theta _i\eta _k\left[ \begin{array}{cc} \Gamma _{11ik} &{} \star \\ 0&{} \Gamma _{22ik}\\ \end{array} \right] +\frac{1}{\gamma _c}(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} C^T_i\\ X_{c2}C^T_i\\ \end{array} \right] )( \sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} C^T_i\\ X_{c2}C^T_i\\ \end{array} \right] )^T\nonumber \\&+ (\sum \limits _{i=1}^r\sum _{k=1}^r\theta _i\eta _k\left[ \begin{array}{cc} \Gamma _{31ik}&{} \Gamma _{32i}\\ \Gamma _{41i}&{} \Gamma _{42i} \end{array} \right] ^T+\frac{1}{\gamma _c}(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} C^T_i\\ X_{c2}C^T_i\\ \end{array}\right] )(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} D^T_i\\ 0\\ \end{array}\right] )^T)\nonumber \\&(\gamma _c I+(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} D^T_i\\ 0\\ \end{array}\right] )(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} D^T_i\\ 0\\ \end{array}\right] )^T)^{-1}( \sum \limits _{i=1}^r\sum _{k=1}^r\theta _i\eta _k\left[ \begin{array}{cc} \Gamma _{31ik}&{} \Gamma _{32i}\\ \Gamma _{41i}&{} \Gamma _{42i} \end{array} \right] \nonumber \\&+\frac{1}{\gamma _c}(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} C^T_i\\ X_{c2}C^T_i\\ \end{array}\right] )(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} D^T_i\\ 0\\ \end{array}\right] )^T)^T<0. \end{aligned}$$
(58)

Then, after algebraic manipulations, we get

$$\begin{aligned} & \Lambda^{T} \mathrm{sym}\{\bar{A}^{T}(\theta ,\eta )(aX_c-bY_c)\}\Lambda \nonumber \\ =&\sum _{i=1}^r \sum _{k=1}^r\theta _i\eta _k \Lambda ^T\mathrm{sym}\{\left[ \begin{array}{cc} A_i &{} B_iC_{ck}\\ B_{ck}C_i&{} A_{cik}\\ \end{array} \right] ^T\nonumber \\&\left[ \begin{array}{cc} aX_{c1}-bY_{c1} &{} a(X^{-1}_{c2}-X_{c1})+bY_{c1}\\ a(X^{-1}_{c2}-X_{c1})+bY_{c1}&{}-a(X^{-1}_{c2}-X_{c1})-bY_{c1}\\ \end{array} \right] \}\Lambda \nonumber \\ =&\sum _{i=1}^r\sum _{k=1}^r\theta _i\eta _k (\left[ \begin{array}{cc} \Gamma _{11ik} &{}\star \\ 0&{}\Gamma _{22ik}\\ \end{array} \right] ), \end{aligned}$$
(59)

where

$$\begin{aligned} \varLambda =\left[ \begin{array}{cc} I &{} X_{c2}\\ 0&{} X_{c2}\\ \end{array} \right] , \end{aligned}$$

and

$$\begin{aligned} \varPhi _k&=(a(X^{-1}_{c2}-X_{c1})+bY_{c1})^{T}B_{ck},\\ \varPsi _k&=C_{ck}X_{c2}. \end{aligned}$$

Accordingly, there hold

$$\begin{aligned}&\varLambda ^T( (aX_c-bY_c)^T\bar{G}(\theta ,\eta )+\frac{1}{\gamma _c} \hat{C}^T(\theta )\hat{D}(\theta ))(\gamma _c I-\frac{1}{\gamma _c} \hat{D}^T(\theta )\hat{D}(\theta ))^{-1}\nonumber \\&\times (\bar{G}^T(\theta ,\eta )(aX_c-bY_c)+\frac{1}{\gamma _c} \hat{D}^T(\theta )\hat{C}(\theta ))\varLambda \nonumber \\ =&\left[ \begin{array}{cc} \Gamma _{31}(\theta ,\eta ) &{} \Gamma _{32}(\theta )\\ \Gamma _{41}(\theta )&{} \Gamma _{42}(\theta )\\ \end{array} \right] ^T\left[ \begin{array}{cc} \gamma _c I-\frac{1}{\gamma _c} D^T(\theta )D(\theta ) &{} 0\\ 0&{} \gamma _c I\\ \end{array} \right] ^{-1}\left[ \begin{array}{cc} \Gamma _{31} (\theta ,\eta )&{} \Gamma _{32}(\theta )\\ \Gamma _{41}(\theta )&{} \Gamma _{42}(\theta )\\ \end{array} \right] \nonumber \\ =&(\sum \limits _{i=1}^r\sum _{k=1}^r\theta _i\eta _k \left[ \begin{array}{cc} \Gamma _{31ik}&{} \Gamma _{32i}\\ \Gamma _{41i}&{} \Gamma _{42i} \end{array} \right] ^T+\frac{1}{\gamma _c}(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} C^T_i\\ X_{c2}C^T_i\\ \end{array}\right] )(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} D^T_i\\ 0\\ \end{array}\right] )^T)\nonumber \\&(\gamma _c I+(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} D^T_i\\ 0\\ \end{array}\right] )(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} D^T_i\\ 0\\ \end{array}\right] )^T)^{-1}(\sum \limits _{i=1}^r\sum \limits _{k=1}^r\theta _i\eta _k \left[ \begin{array}{cc} \Gamma _{31ik}&{} \Gamma _{32i}\\ \Gamma _{41i}&{} \Gamma _{42i} \end{array} \right] \nonumber \\&+\frac{1}{\gamma _c}(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} C^T_i\\ X_{c2}C^T_i\\ \end{array}\right] )(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} D^T_i\\ 0\\ \end{array}\right] )^T)^T, \end{aligned}$$
(60)

and

$$\begin{aligned}&\frac{1}{\gamma _c} \varLambda ^T \hat{C}^T(\theta )\ \hat{C}(\theta )\varLambda \nonumber \\ =&\frac{1}{\gamma _c} \left[ \begin{array}{cc} C(\theta )&{} C(\theta )X_{c2}\\ \end{array} \right] ^T\left[ \begin{array}{cc} C(\theta ) &{} C(\theta )X_{c2}\\ \end{array} \right] \nonumber \\ =&\frac{1}{\gamma _c}(\sum \limits _{i=1}^r\theta _i\left[ \begin{array}{c} C^T_i\\ X_{c2}C^T_i\\ \end{array} \right] )(\sum \limits _{i=1}^r\theta _i \left[ \begin{array}{c} C^T_i\\ X_{c2}C^T_i\\ \end{array} \right] )^T. \end{aligned}$$
(61)

Now, we combine (58)–(61), and obtain

$$\begin{aligned}&\varLambda ^T( \mathrm{sym}\{\bar{A}^T(\theta ,\eta )(aX_c-bY_c)\}+\frac{1}{\gamma _c} \hat{C}^T(\theta )\hat{C}(\theta )\nonumber \\&+ ( (aX_c-bY_c)^T\bar{G}(\theta ,\eta )+\frac{1}{\gamma _c} \hat{C}^T(\theta )\hat{D}(\theta )) (\gamma _c I-\frac{1}{\gamma _c} \hat{D}^T(\theta )\hat{D}(\theta ))^{-1}\nonumber \\&\times (\bar{G}^T(\theta ,\eta )(aX_c-bY_c)+\frac{1}{\gamma _c} \hat{D}^T(\theta )\hat{C}(\theta )))\varLambda <0, \end{aligned}$$
(62)

which means

$$\begin{aligned}&\mathrm{sym}\{\bar{A}^T(\theta ,\eta )(aX_c-bY_c)\}+\frac{1}{\gamma _c} \hat{C}^T(\theta )\hat{C}(\theta )\nonumber \\&+ ( (aX_c-bY_c)^T\bar{G}(\theta ,\theta )+\frac{1}{\gamma _c} \hat{C}^T(\theta )\hat{D}(\theta ))(\gamma _c I-\frac{1}{\gamma _c} \hat{D}^T(\theta )\hat{D}(\theta ))^{-1}\nonumber \\&\times (\bar{G}^T(\theta ,\eta )(aX_c-bY_c)+\frac{1}{\gamma _c} \hat{D}^T(\theta )\hat{C}(\theta )) <0. \end{aligned}$$
(63)

According to Lemma 3, (63) is equivalent to

$$\begin{aligned} \left[ \begin{array}{ccc} \mathrm{sym}\{\bar{A}^T(\theta ,\eta )(aX_c-bY_c)\}&{} \star &{} \star \\ \bar{G}^T(\theta ,\theta )(aX_c-bY_c)&{}-\gamma _c I&{} \star \\ \hat{C}(\theta )&{}\hat{D}(\theta )&{}-\gamma _c I\\ \end{array} \right] <0. \end{aligned}$$
(64)

This means that the closed-loop system in (28) is robustly stable and meets the \(H_\infty\) performance index \(\Vert y(t)\Vert _2<\gamma \Vert \nu (t)\Vert _2.\) This completes the proof. \(\square\)

It is also noted that the minimum \(H_\infty\) attenuation level of Theorem 2 can be obtained by solving the programming problem: minimize \(\gamma _c\) subject to (29)–(32).

5 Simulation Examples

In this section, two simulation examples are given to illustrate the effectiveness of the control strategy proposed in this paper and the performance of the resulting control system.

5.1 Electrical Circuit System

Consider an electrical circuit system shown in Fig. 1 with the inductor L,  the capacitance C,  the resistance R,  and the source voltage \(u_s\). Let \(i_L\) and \(i_C\) denote the currents passing through the inductor L,  and the capacitance C, respectively; let \(u_L\) and \(u_C\) denote the voltage on the inductor L and on the capacitance C,  respectively. As described [3],

$$\begin{aligned} u_L(t) = \, &L\frac{d^\alpha i_L(t)}{dt^\alpha }, \\ i_C(t) =&C\frac{d^\alpha u_C(t)}{dt^\alpha }, ~0< \alpha < 1. \end{aligned}$$

Further, according to the Kirchhoffs law, we have

$$\begin{aligned} u_s= \, &Ri_L+L\frac{d^\alpha i_L}{dt^\alpha }+u_C,\\ i_L=&C\frac{d^\alpha u_C}{dt^\alpha }.\end{aligned}$$

Therefore, the electrical circuit system is described by

$$\begin{aligned} \frac{d^\alpha }{dt^\alpha } \left[ \begin{array}{c} u_C\\ i_L\\ \end{array} \right] = \, \left[ \begin{array}{cc} 0&{}\frac{1}{C} \\ -\frac{1}{L}&{}-\frac{R}{L}\\ \end{array} \right] \left[ \begin{array}{c} u_C\\ i_L\\ \end{array} \right] +\left[ \begin{array}{c} 0 \\ \frac{1}{L} \\ \end{array} \right] u_s. \end{aligned}$$

Let \(u_f(t)=u(t)+f(t),\) where

$$\begin{aligned} f(t)&=\left\{ \begin{array}{ll} 0,&{}0<t<30,\\ 5(1-e^{30-t}),&{}\mathrm{else},\\ \end{array} \right. \end{aligned}$$

simulates the actuator fault. Moreover, to test the robustness of our observer, referring to Ref. [3], consider the measurement output as

$$\begin{aligned} y(t)=\sum ^{r}_{i=1}\theta _i(x (t))(C_{i}x(t)+\tilde{D}_i\omega _2(t)), \end{aligned}$$

with

$$\begin{aligned} \omega _2(t)&= 1/(t+10), \end{aligned}$$

and take the external disturbance into account:

$$\begin{aligned} \omega _1(t)&=0.1\mathrm{sin}(5t). \end{aligned}$$

In the simulation, let \(\alpha =0.9,L=2,C=1,R=4+2\mathrm{sin}(t)\) and \(u_s=1.\) The matrices in the fuzzy system in (8) are selected as

$$\begin{aligned} A_1=&\left[ \begin{array}{cc} 0&{} 1\\ -0.5&{}\mathrm{max}\{-\frac{R}{L}\}\\ \end{array} \right] =\left[ \begin{array}{cc} 0&{} 1\\ -0.5&{}-1\\ \end{array} \right] ,\\ A_2=&\left[ \begin{array}{cc} 0&{} 1\\ -0.5&{}\mathrm{min}\{-\frac{R}{L}\}\\ \end{array} \right] =\left[ \begin{array}{cc} 0&{} 1\\ -0.5&{}-3\\ \end{array} \right] ,\\ B=&\left[ \begin{array}{c} 0\\ 0.5\\ \end{array} \right] ,~ \tilde{G}=\left[ \begin{array}{c} 0.1\\ 0.2\\ \end{array} \right] ,~ C_1=\left[ \begin{array}{cc} 1&{} -3\\ \end{array} \right] ,\\ \tilde{D}_1=&0.1,~ C_2=\left[ \begin{array}{cc} 1&{} -2\\ \end{array} \right] ,~ \tilde{D}_2= -0.2.\end{aligned}$$

The corresponding membership functions are chosen as \(\theta _1=(1-0.5\mathrm{sin}(t))/2\) and \(\theta _2=1-\theta _1.\) Note that the above system is input-to-state stable. Thus, it is mainly used to verify the effectiveness of our fault observer. Following Theorem 1, we design an non-fragile observer for the above system. The variable gains in the observer in (18) are determined by

$$\begin{aligned} U_{L1}&=\left[ \begin{array}{c} -0.1 \\ 0.2 \\ \end{array} \right] ,~~U_{L2}=\left[ \begin{array}{c} -0.1 \\ -0.2 \\ \end{array} \right] ,~~V_{L1}= 0.2,~~V_{L2}=0.3,\\ U_{F1}&= 0.1,~~V_{F1}=-0.2,~~ U_{F2}= 0.5,~~V_{F2}= 0.2,~~F(\sigma )=\mathrm{cos}(0.2\sigma ). \end{aligned}$$

Set the \(H_\infty\) performance index to be \(\gamma _o=0.5.\) Then, the constant observer gains are obtained by solving the LMIs in (21)–(23):

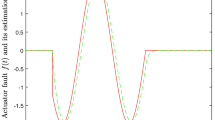
$$\begin{aligned} \hat{L}_1&=\left[ \begin{array}{c} 32.5392\\ 8.0845\\ 51.7311\\ \end{array} \right] ,~ \hat{L}_2=\left[ \begin{array}{c} 42.1103\\ 11.5032\\ 68.6017\\ \end{array} \right] .\end{aligned}$$

Applying the designed fault observer to the electrical circuit system, the simulation results are exhibited in Figs. 2, 3 and 4. It is observed that the fault estimation is achieved by our observer, despite the presence of measurement uncertainties and external disturbances. This thus illustrates the effectiveness of the proposed approach for the observer design.

Fig. 1
figure 1

Electrical circuit system

Full size image
Fig. 2
figure 2

The actuator fault and its estimate

Full size image
Fig. 3
figure 3

The system state and its estimate

Full size image
Fig. 4
figure 4

The estimation errors

Full size image

5.2 Numerical Example

Now, we adopt a general example to show the effectiveness of our control approach. Consider an FOS with \(\alpha =0.8\) and with three state variables and one input,

$$\begin{aligned} D^{0.8} x(t)=&\left[ \begin{array}{ccc} 2&{} 2&{} -1\\ 2&{} -2&{} 1\\ 4 &{}3&{} 2z(t)\\ \end{array} \right] x(t)+\left[ \begin{array}{c} 1\\ 2\\ -z(t)\\ \end{array} \right] u(t)+\tilde{G}\omega _1(t),\nonumber \\ y(t)=&Cx(t)+\tilde{D}\omega _2(t), \end{aligned}$$
(65)

where \(z(t)=\mathrm{sin}(x_1(t))+M,\) and \(M\in [-1,0]\) is a uncertain parameter. It is described by (8) with the following rules.

Plant rule 1: IF \(x_1(t)\) is \(\theta _{1}(x_1(t)),\) THEN

$$\begin{aligned} A_1=\left[ \begin{array}{ccc} 2&{} 2&{} -1\\ 2&{} -2&{} 1\\ 4 &{}3&{} 2\\ \end{array} \right] ,~B_1=\left[ \begin{array}{c} 1\\ 2\\ -1\\ \end{array} \right] ,~ \tilde{G}_{ 1}=\left[ \begin{array}{ccc} 0.01\\ 0\\ 0.01 \\ \end{array} \right] ,~ C_1=\left[ \begin{array}{ccc} 1&{} -1&{} 3\\ 2&{}2&{}0\\ \end{array} \right] ,~ \tilde{D}_1=\left[ \begin{array}{c} 0.001\\ 0.002 \\ \end{array} \right] ,\end{aligned}$$

Plant rule 2: IF \(x_1(t)\) is \(\theta _{2}(x_1(t)),\) THEN

$$\begin{aligned} A_2=\left[ \begin{array}{ccc} 2 &{}2&{} -1\\ 2 &{}-2&{} 1\\ 4&{} 3&{} 2\\ \end{array} \right] ,~B_2=\left[ \begin{array}{c} 1\\ 2\\ 1\\ \end{array} \right] ,~ \tilde{G}_{ 2}=\left[ \begin{array}{ccc} 0.01\\ 0\\ 0.01 \\ \end{array} \right] ,~ C_2=\left[ \begin{array}{ccc} 1&{} -1&{} 3\\ 2&{}2&{}0\\ \end{array} \right] ,~ \tilde{D}_2=\left[ \begin{array}{c} 0.001\\ 0.002 \\ \end{array} \right] .\end{aligned}$$

To test the fault tolerance and robustness of our approach, the following actuator fault is taken into account in the simulation:

$$\begin{aligned} f(t)&=\left\{ \begin{array}{ll} 0,&{}0<t<10,\\ 10\mathrm{sin}(t-10),&{}\mathrm{else}.\\ \end{array} \right. \end{aligned}$$

The external disturbance and measurement uncertainty are the same as those in last simulation example.

Following Theorems 1 and 2, we design an FTC scheme for the above system. We first construct a non-fragile observer for fault estimation. The variable gains in the observer in (18) are determined by

$$\begin{aligned} U_{L1}&=\left[ \begin{array}{c} -0.1 \\ 0.2 \\ 0.3\\ \end{array} \right] ,~~U_{L2}=\left[ \begin{array}{c} -0.1 \\ -0.2 \\ 0.1\\ \end{array} \right] ,\\ V_{L1}&=\left[ \begin{array}{cc} 0.2&{}0.2\\ \end{array} \right] ,~~V_{L2}=\left[ \begin{array}{cc} 0.3&{}0.1\\ \end{array} \right] ,\\ U_{F1}&= 0.1 ,~~ U_{F2}= 0.5 ,~~ F(\sigma )=\mathrm{sin}(0.2\sigma )\\ V_{F1}&=\left[ \begin{array}{cc} -0.2&{}0.1\\ \end{array} \right] ,~~V_{F2}=\left[ \begin{array}{cc} 0.2&{}0.2\\ \end{array} \right] . \end{aligned}$$

The lower and upper membership functions of the type-2 fuzzy model are listed in Table 1. Then, set the corresponding weights as \(\overline{\lambda }_i =\underline{\lambda }_i = 0.5,~i = 1,~ 2.\) By (3), the membership functions of the type-2 fuzzy model can be obtained. The lower and upper membership functions of the type-2 fuzzy controller are listed in Table 2. Then, set the corresponding weights as \(\overline{m}_k =\underline{m}_k = 0.5,~k= 1,~ 2.\) By (27), the membership functions of the type-2 controller can be obtained.

Table 1 Membership functions of the system
Full size table
Table 2 Membership functions of the controller
Full size table

Set the \(H_\infty\) performance index as \(\gamma _o=0.1,\) and then solve the LMIs in (21)–(23). The resulting observer gain matrices are

$$\begin{aligned} L_1&=\left[ \begin{array}{cc} -0.0298 &{} 1.3845\\ 0.7548 &{} 1.3437\\ 1.1579 &{} 2.1611\\ \end{array} \right] ,&L_2=\left[ \begin{array}{cc} 0.0756 &{} 1.4599\\ 0.9650 &{} 1.2055\\ -0.0210 &{} 3.1254\\ \end{array} \right] ,\\ E_1&=\left[ \begin{array}{ccc} -158.3659 &{} 359.6916\\ \end{array} \right] ,&E_2=\left[ \begin{array}{ccc} -11.9519 &{} 199.3545\\ \end{array} \right] . \end{aligned}$$

Next, we design an output feedback controller in the form of (26). Set \(\gamma _c=2.5,~\varrho _1=\varrho _2=0.2,~\varrho _3=0.3,\) and calculate the LMIs in (29)–(32). The resulting controller gain matrices are

$$\begin{aligned} A_{c11}&=\left[ \begin{array}{ccc} -299.9633 &{}-188.8278&{} -172.5259\\ -556.1612 &{}-348.2801 &{}-326.0795\\ -176.6531 &{} -51.5066 &{}-188.6263\\ \end{array} \right] ,~~A_{c12}=\left[ \begin{array}{ccc} -302.6856&{} -187.4891&{} -178.6757\\ -561.1038 &{}-345.9107 &{}-337.1585\\ -178.3161 &{}-50.7541&{} -192.2446\\ \end{array} \right] ,\\ A_{c21}&=\left[ \begin{array}{ccc} -364.4329&{} -215.8316 &{}-242.3319\\ -680.7257 &{}-400.2992 &{}-461.2425\\ -290.0705&{} -98.8483 &{}-311.7352\\ \end{array} \right] , ~~A_{c22}=\left[ \begin{array}{ccc} -367.3040 &{}-214.5241 &{}-248.7640\\ -685.9513 &{}-397.9893 &{}-472.8587\\ -291.9908 &{} -98.1497 &{}-315.8415\\ \end{array} \right] ,\\ B_{c1}&=\left[ \begin{array}{cc} 50.1776 &{}117.5344\\ 95.2037 &{} 214.6950\\ 67.2869 &{} 65.0342\\ \end{array} \right] ,~~B_{c2}=\left[ \begin{array}{cc} 52.1758 &{} 117.8556\\ 98.7979&{} 215.2911\\ 68.4974 &{} 65.2640\\ \end{array} \right] ,\\ C_{c1}&=\left[ \begin{array}{ccc} -16.3667 &{} -6.8745 &{} -15.6860\\ \end{array} \right] ,~~ C_{c2}=\left[ \begin{array}{ccc} -16.4050 &{} -6.8826 &{} -15.7587\\ \end{array} \right] . \end{aligned}$$

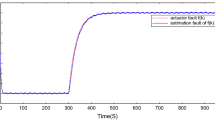
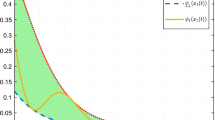
Applying the above controller to the system under consideration, the simulation results are displayed in Figs. 5, 6, 7 and 8. Figure 5 shows that the stabilization of the FOS is achieved, in spite of the measurement uncertainty, the persistent disturbance, and the persistent fault. Specifically, Fig. 6 clearly presents that the system output meets the prescribed \(H_\infty\) performance index. Besides, Figs. 7 and 8 indicate the effectiveness of the designed observer and the boundedness of the computed control signal and the actuator output, respectively. Therefore, the simulation results clarify and verify the theoretical findings established above.

Fig. 5
figure 5

The system state

Full size image
Fig. 6
figure 6

The \(H_\infty\) performance with \(\gamma =2.5.\)

Full size image
Fig. 7
figure 7

The estimation errors

Full size image
Fig. 8
figure 8

The control signal and actuator output

Full size image

For comparison, a non-fragile control design approach [17] for fractional order fuzzy systems is adopted. Apply it to the system in (65) under the same simulation condition. The result is displayed in Fig. 9, which shows that the state convergence is lost when \(t\ge 10\)s, due to the actuator faults. This in turn illustrates the superiority of our control approach in enhancing the fault tolerance of the control system.

Fig. 9
figure 9

The state response obtained by the comparative approach [17]

Full size image

6 Conclusion

This paper presents an output feedback robust fault-tolerant control strategy for a class of interval type-2 fuzzy fractional order systems subject to the possible actuator faults. Its superiority over the existing approaches lies in three aspects. First, the stability domain of the faulty FOS is extended significantly. This is attributed to the introduction of the concept of D-stability to the control design and stability analysis, instead of the conventional indirect Lyapunov theory. Second, the resulting control system is robust against the measurement noise and external disturbances that, however, are not taken into account in the existing FTC designs for FOSs. This is achieved by adopting the \(H_\infty\) control method in a new way, in which the controller parameters are determined by solving real LMIs rather than complex matrix inequalities. As a byproduct, the FTC design is simplified. Third, our design approach is less restrictive than the existing ones: certain requirements for the system output matrix or the structure of the control gain matrices are eliminated. The simulation results on an electrical circuit system and a numeral example both illustrate the effectiveness of the proposed approach.