A novel approach for solving rough multi-objective transportation problem: development and prospects

Abstract

Transportation problem is the prominent class of mathematical programming problems that has a significant role in many practical transportation fields. Naturally, the transportation parameters inherently involve uncertainty in real life caused by lacking of information, imprecision in judgment, environmental factors, and etc. Therefore, it is very valuable to handle transportation problem under uncertainty aspect. The aim of this paper is to study the solution of the rough multi-objective transportation problem by supposing that the decision makers realize the transportation cost, availability and demand of the product as rough interval coefficients. The proposed approach exploits the merits of the weighted sum method to find the non-inferior solutions and it has two distinguishing features. Firstly, the proposed approach characterizes the surely Pareto optimal solution through converting the lower interval into two crisp transportation problems. Secondly, the proposed approach characterizes the possibly Pareto optimal solution through decomposing the upper interval into two crisp transportation problems. Furthermore, the expected nondominated value is applied to obtain the optimal compromise solutions of multi-objective transportation problem in rough environment. The presented approach is showed with rough multi-objective optimization problem as numerical illustration, where a wide set of the expected compromise solution ranged from 15.75 to 25.8 can be obtained. Furthermore, the investigation on the rough multi-objective transportation problem is conducted a real thought-provoking case study, where the optimal rough interval of transportation cost ranged from 97 to 314 can be achieved. With the adoption of rough environment modeling, a wide variate of optimal solutions can be achieved that can help the decision maker to extract the best compromise alternative according to practical situations. This represents a novel contribution to the decision making field and profit satisfaction models.

1 Introduction

The classical transportation problem (TP) was originally developed by Hitchcock (1941). The central concept is to transport the required goods from the supply points to the demand points so as to minimize the total transportation costs with fixed parameters. The basic model of a traditional TP consists of an objective function and two kinds of constraints, namely, source constraint and destination constraint in the single objective. In this sense, Ezekiel and Edeki (2018) proposed a modified Vogel’s approximation method to deal with the TP. Dantzig and Thapa (2006) presented the Simplex method to the transportation problem as the primal Simplex transportation method.

In some realistic transportation problems, the complexity of the social and economic environment requires the explicit consideration of multiple objective functions other than single objective function. This is denoted as a multi-objective programming problem. The complexity of this problem is being in its incommensurate and conflict nature with one another. In multi-objective transportation problems, the concept of optimal solution gives place to the concept of non-dominated solution or the non-inferior solution (any solution satisfies the constraints, such that the improvement in any objective function is attained without sacrificing on at least one of the other objective functions).

Many authors have carried out investigations on multi-objective transportation problems (MOTPs). Aneja and Nair (1979) described a method for solving the bicriteria TP. Isermann (1979) introduced a new algorithm for solving the linear MOTP in which all the non-dominated solutions are identified. Ringuest and Rinks (1987) introduced two interactive algorithms to solve the linear MOTPs. Bit et al. (1992) proposed a new algorithm using fuzzy programming technique for the solution of linear MOTPs. Amaliah et al. (2020) proposed a novel heuristic method to find the initial basic feasible solution (IBFS) while solving the TP. The introduced method aims to improve the accuracy of existing methods and save the computational time of finding the optimal solution of the TP. Karagul and Sahin (2020) developed a new approximation method, named Karagul–Sahin Approximation Method (KSAM), to achieve an efficient IBFS while handling the TP. The KSAM is faster than the Vogel’s Approximation method and the Northwest Corner method.

Naturally, MOTPs involve many parameters include transportation cost, availability, and demand of the product, whose possible values may be assigned by the experts (Bera et al. 2018). In conventional MOTPs, such parameters are fixed at some values in an experimental and/or subjective manner through the experts’ understanding of the nature of the parameters. However, in the real-world applications, the coefficients of the transportation problems may not be known precisely. It is due to the fact that some of the relevant data nearly always made on the basis of information which, at least in part, is vague or imprecise data in nature (Akilbasha et al. 2018)‏. In this regard, researchers have been tried to consider the uncertainty aspects with the TP (Majumder et al. 2019; Roy and Midya 2019; Biswas and Pal 2019; Bagheri et al. 2020a; Ebrahimnejad 2016).

Apart from the previously existed deterministic aspect-based TP, many attentions have been presented in the literature to address the uncertainty aspect-based TP with aim to handle the practical situations in which the lack of information about the parameters is occurred; for example, multi-objective non-linear fixed charge TP using multi-mode transport has been solved through the crisp aspect and interval environments-based uncertainty aspect (Biswas et al. 2019). Pratihar et al. (2020) studied TP using the interval type 2 fuzzy set regarding the transportation cost, supply, and demand. Mahajan and Gupta (2019) formulated the MOTP based on the fully intuitionistic fuzzy (FIF), where membership function is presented in different forms including linear, exponential and hyperbolic aspects. In this sense, the problem is transformed to a crisp MOTP using accuracy function and then the solution is obtained using the proposed algorithm. Mishra and Kumar (2020) proposed a new method to convert an unbalanced FIF transportation problems (FIFTPs) to a balanced FIFTP. Srinivasan et al. (2020) presented a new algorithm to deal with the fully fuzzy TP (FFTP) through assuming that the decision maker (DM) is uncertain about the precise values regarding the demand, supply and transportation costs that are represented through the triangular fuzzy numbers. Uddin et al. (2021) solved the uncertain MOTP based on fuzzy linear membership function using goal programming tactic. Bagheri et al. (2020a, b) addressed the uncertain MOTP with fuzzy costs, where the fuzzy arithmetic data envelopment analysis (FADEA) approach is conducted to solve the problem under hand. Adhami and Ahmad (2020) suggested a novel Pythagorean hesitant fuzzy programming approach (PHFPA) to solve the MOTP under uncertain cost, supply and demand parameters. Rizk-Allah et al. (2018) developed a novel neutrosophic compromise programming approach (NCPA) that is inspired by neutrosophic set terminology along with Zimmermann’s fuzzy programming for solving the MOTP. The NCPA is characterized by the truth membership, indeterminacy membership and falsity membership that are adopted to simulate the uncertainty aspect regarding each objective function.

Although, the suggested approaches in the literature to deal with the uncertain frameworks of the MOTP, a continuous effort is being made to explore other uncertainty-related MOTP. In this sense, the vagueness occurrence can be represented as roughness framework that is occurred due to vague information or approximate information about the parameters of MOTP. Thus by motivating these facts, the present work proposes a novel approach to solve MOTP under roughness tactic that represents all opinions of experts through the rough intervals environment. In this sense, the supply, demand and transportation costs of MOTP are specified imprecisely using rough intervals scenario, thus the proposed study is developed to handle the MOTP under roughness tactic for the first time. The proposed study can serve as a fruitful tool to address the realistic decisions through including the intersection and union of the experts’ knowledge to represent the roughness tactic, where the intersection aspect realizes the consensus of all experts’ knowledge, while union aspect realizes the respecting any of the experts’ knowledge.

Recently, Rough set theory (RST) was proposed by Pawlak (1982) as a novel mathematical tool to handle imprecise, vague and uncertain data (Hassanien et al. 2018; Wei and Liang 2019). In RST, any concept, a subset of the universe, is characterized based on defining the lower and upper approximations. Using the lower and upper approximations, the knowledge concealed in information systems can be expressed in the form of rules. The basic advantage of RST in information analysis is that no need any preliminary or additional information about data (Pengfei et al. 2021). The ability to deal with the vagueness and imprecision in real world problems has attracted many researchers to use RST in many fields including feature selection (Jie et al. 2020), knowledge reduction (Li et al. 2013), rule extraction (Apolloni et al. 2006), uncertainty reasoning (Düntsch and Gediga 1998), granular computing (Liang and Qian 2006; José et al. 2020) and others (Niroomand et al. 2020; Li et al. 2016; Rizk-Allah 2016; Sarra and Inès 2020; Sharma et al. 2020; Stankovic et al. 2019, Ebrahimnejad 2019, Ebrahimnejad and Verdegay 2018). On the other hand, there are some approaches in the literature of TP using rough set techniques, for example Kundu (2015) proposed TP under uncertain environments, where different uncertainty manipulation mechanisms such as fuzzy types and rough variable are introduced to solve this problem, while Tao and Xu (2012) proposed a new approach based on hybridizing the rough set theory with genetic algorithm to solve the solid TP, where the rough set is adopted to make the process of the decision-making more flexible, then the genetic algorithm is implemented to obtain the optimal solution.

The aim of this paper is to study the solution of the rough multi-objective transportation problem (RMOTP) under the rough interval scenario (RIS) regarding the transportation cost, availability and demand. The RIS is inspired from the intersection of the experts’ knowledge (consensus opinion) and the union of the experts’ knowledge (respecting opinion) to represent the lower and upper approximation intervals, respectively. In this sense, the RMOTP is decomposed into two sub-interval models, namely, lower interval model (LIM) and upper interval model (UIM). The proposed approach exploits the merits of the weighted sum method to find the non-inferior solution and it has two distinguishing features. Firstly, the proposed approach characterizes the surely Pareto optimal solution through converting the LIM into two crisp sub-transportation problem using the borders of this interval. Secondly, the proposed approach characterizes the possibly Pareto optimal solution through decomposing the UIM into two crisp sub-transportation problem using the borders of this interval. Furthermore, an expected rule is presented to obtain the best compromise solution of the RMOTP. The presented approach is showed with rough multi-objective optimization problem (RMOOP) as numerical illustration and then applied on RMOTP a real thought-provoking case study to illustrate its feasibility and robustness. This methodology represents a novel contribution to the decision making field and profit satisfaction situations.

The novelty of the presented methodology is contained in developing a new formulation for the MOTPs on the basis of rough set theory (RST) through reformulating the MOTPs’ parameters with rough interval form which is denoted as RMOTP. This representation unlike the literature formulations, and thus this makes our work more challenging and novel.

The contributions of the presented methodology are as follows:

• 1. A new formulation for the MOTPs with RICs named RMOTP is introduced and solved.

• 2. The RMOTP is presented on the basis of the RST to simulate the impreciseness and uncertainties.

• 3. The solution methodology operates by constructing two sub-model, lower interval model (LIM) that simulates the consenting of all DMs’ information and upper interval model (UIM) that means the respecting any of the DMs’ information, where each interval sub-model is decomposed into two crisp sub-transportation problem using the borders of this interval.

• 4. The proposed methodology is investigated and validated using an illustrative example as well as the application on RMOTP.

• 5. The developed framework can serve as a great tool for DMs to address the real-life situations that include consenting and opposing knowledge.

The frame of this paper is outlined as follows. In Sect. 2, we describe the preliminaries and deductions regarding rough set concepts. The proposed approach for rough multi-objective transportation problem (RMOTP) is explained in detail in Sect. 3. Section 4 provides an illustrative numerical example and the real case study of RMOTP to demonstrate the proposed approach. Finally, the conclusion and future work are declared in Sect. 5.

2 Preliminaries

In this section, we give some definitions regarding the basics of real intervals, rough set theory and rough intervals (Hamzehee et al. 2014; Luhandjula and Rangoaga 2014). Furthermore, the nomenclature that summarizes the main characteristics of the presented work is given in Table 1.

Table 1 Model nomenclature and list of abbreviations

2.1 Real intervals (RI)

We denote by RI the family of all compact intervals in R (the set of all real numbers), i.e., $RI = \{ [a,b]\,|\,a,b \in \,R\,\,{\text{and}}\;\,a \le b\}$.

For $A \in RI$, we write $A = [a,b]$, where a and b are the lower and the upper bounds of A, respectively (Hamzehee et al. 2014).

The operations on $RI$ used in this paper can be defined as follows: Let $A = [a,\,b]\,\,$ and $B = [c,\,d]\,\,$ be two RIs. Then, we have:

• 1. Addition: $A + B = [a + c,\,\,b + d]\,,$

• 2. Negation: $- A = [ - b, - a]$,

• 3. Subtraction: $A - B = [\min (a - c,\,b - d)\,,\,\,\max \,(a - c,\,b - d)\,]$.

• 4. Multiplication: $kA = [ka,kb],k \ge 0,\,\,kA = [kb,ka],k < 0.$

The order relation (≤) is defined as follows: $A \le B$ if and only if $a \le c\,\,{\text{and}}\,\,b \le d$.

2.2 Some properties of interval-valued function

Let $X \subset \,R^{n}$, then the interval-valued function F can be defined as $F:\,X \subset \,R^{n} \to \,RI$, i.e.,$F(x) = [\,f^{l} (x)\,,\,f^{u} (x)\,]$.

2.2.1 Convexity

Definition 1

(Luhandjula and Rangoaga 2014) Let $F(x)$ be an interval-valued function defined on a convex set $X \subset \,R^{n}$. Then, $F(x)$ is said to be convex on X if $F(\lambda x^{1} + (1 - \lambda )x^{2} ) \le \lambda F(x^{1} ) + (1 - \lambda )F(x^{2} ),$ for all $0 \le \lambda \le 1$ and $x^{1} ,x^{2} \in X$.

Proposition 1

(Luhandjula and Rangoaga 2014) Let $F(x)$ be an interval-valued function defined on a convex set $X \subset \,R^{n}$. Then,

• $F(x)$ is convex on X if and only if $f^{l} (x)$ and $f^{u} (x)$ are convex real-valued function on X.

• $F(x)$ is convex on X if and only if $\alpha f^{l} (x) + (1 - \alpha )f^{u} (x)$ is convex on X for all $0 \le \alpha \le 1\,$.

The proof of Proposition 2.1 and details may be found in Luhandjula and Rangoaga (2014).

2.3 Rough set theory

Rough set theory and its extensions have been flourished in many fields (Sami et al. 2020; Majid et al. 2020; Masoud 2020). It was proposed by Pawlak (1982) as a novel mathematical tool to handle roughness, vague and uncertain data without any prior knowledge about the data. Assume that we deal only with the available information provided by the data to generate conclusion. Let U is a non-empty finite set of objects we are interested in, and let $\Re$ be an equivalence relation on U and $\Re (x)$ be the equivalence class of the relation which contains $x \in U$. The equivalence relation $\Re$ shall be referred as indiscernibility relation. For any concept $X \in U$, the lower and upper approximations of X by $\Re$ are described as follows:

$$ \underline{\Re } X = \left\{ {x \in U\,|\,\Re (x) \subseteq \,X} \right\}\,, $$

(1)

$$ \overline{\Re }X = \left\{ {x \in U\,|\,\Re (x) \cap \,X \ne \phi } \right\}. $$

(2)

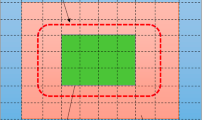
Clearly, the lower approximation $\underline{\Re } X$ is the biggest definable set contained in X, and the upper approximation $\overline{\Re }X$ is the smallest definable set containing X. The boundary region of rough set X is defined as

$$ BN_{\Re } (X) = \overline{\Re }X - \underline{\Re } X. $$

(3)

The boundary region represents the area which cannot be classified, neither to X nor to its complement $U - X$. The boundary region becomes an empty set when the upper approximation and lower approximation of the definable set are equal. The graphical representation of rough set is depicted in Fig. 1.

Fig. 1

Schematic definitions of the rough set theory

2.4 Rough interval

A Rough interval can be considered as a qualitative value from vague concept defined on a variable X in R, which is abstracted in the following definition.

Definition 2.

The qualitative value ${X}^{\mathbb{R}}$ is called a rough interval when one can assign two closed intervals ($X^{l}$ and $X^{u}$) on R, such that $X^{l} \subseteq X^{u}$. Moreover,

• 1. If $x \in X^{l}$ then $X^{{\mathbb{R}}}$ surely takes x (denoted by $x \in X^{{\mathbb{R}}}$).

• 2. If $x \in X^{u}$ then $X^{{\mathbb{R}}}$ possibly contains x.

• 3. If $x \notin X^{u}$ then $X^{{\mathbb{R}}}$ surely not takes x (denoted by $x \notin X^{{\mathbb{R}}}$).

where $X^{l}$ and $X^{u}$ are called lower and upper approximations intervals of $X^{{\mathbb{R}}}$_, respectively. Further $X^{{\mathbb{R}}}$ is denoted by $X^{{\mathbb{R}}} = (X^{l} ,X^{u} )$. Here $X^{l}$ and $X^{u}$ are conventional intervals, and $X^{l} \in X^{u}$. When $X^{l} = X^{u}$,$X^{{\mathbb{R}}}$ becomes a conventional interval, i.e., $X^{{\mathbb{R}}} = X^{l} = X^{u}$. Superscript ${\mathbb{R}}$ indicates that the corresponding parameters/decision variables show rough-interval feature.

Definition 3

(Luhandjula and Rangoaga 2014) For a rough interval $X^{{\mathbb{R}}}$_, we have,

• $X^{{\mathbb{R}}} \ge 0,\; {\text{iff}}\;X^{u} \ge 0\;\;{\text{and}}\;\;X^{l} \ge 0.$

• $X^{{\mathbb{R}}} \le 0,\;\;{\text{iff}}\;X^{u} \le 0\;\;{\text{and}}\;\;X^{l} \le 0.$

For example, consider a firm wants to plan the scheduling of products through use the opinions of three experts for production time due to the uncertainty of parameters. Each expert gives approximate production time of the product as follows: Expert 1: $A = [3,\,4]$_, Expert 2: $B = [2.5,\,3.5]$; Expert 3: $C = [3,\,5]$. Therefore, the intersection of the experts’ opinions (consensus opinion) represents the lower interval,$X^{l}$ (i.e., assume that the intersection of the experts' opinions has is an nonempty set), while the union of the experts’ opinions (respect opinion) represents the upper interval, $X^{u}$, which lead to the rough interval $X^{{\mathbb{R}}}$ that be formulated as follows $X^{{\mathbb{R}}} = \left( {\left[ {3,3.5\left] , \right[2.5,5} \right]} \right)$_.

The operations on rough intervals can be defined as follows:

Let $A^{{\mathbb{R}}} = \left( {A^{l} ,A^{u} } \right) = \left( {\left[ {\underline{a}^{l} ,\underline{a}^{u} \left] , \right[\overline{a}^{l} ,\overline{a}^{u} } \right]} \right)$ and $B^{{\mathbb{R}}} = \left( {B^{l} ,B^{u} } \right) = \left( {\left[ {\underline{b}^{l} ,\underline{b}^{u} \left] , \right[\overline{b}^{l} ,\overline{b}^{u} } \right]} \right)$ be two rough intervals. Then, we have:

• 1. Addition: $A^{{\mathbb{R}}} + B^{{\mathbb{R}}} = \left( {A^{l} + B^{l} ,A^{u} + B^{u} } \right) = \left( {\left[ {\underline{a}^{l} + \underline{b}^{l} ,\underline{a}^{u} + \underline{b}^{u} \left] , \right[\overline{a}^{l} + \overline{b}^{l} ,\overline{a}^{u} + \overline{b}^{u} } \right]} \right)$.

• 2. Negation: $- A^{{\mathbb{R}}} = \left( { - A^{u} , - A^{l} } \right) = \left( {\left[ { - \underline{a}^{u} , - \underline{a}^{l} \left] , \right[ - \overline{a}^{u} , - \overline{a}^{l} } \right]} \right)$.

• 3. Subtraction: $A^{{\mathbb{R}}} - B^{{\mathbb{R}}} = \left( {A^{l} - B^{l} ,A^{u} - B^{u} } \right) = \left( {\left[ {\underline{a}^{l} - \underline{b}^{u} ,\underline{a}^{u} - \underline{b}^{l} \left] , \right[\overline{a}^{l} - \overline{b}^{u} ,\overline{a}^{u} - \overline{b}^{l} } \right]} \right)$.

• 4. Intersection: $A^{{\mathbb{R}}} \cap B^{{\mathbb{R}}} = ([\max \{ \underline{a}^{l} ,\underline{b}^{l} \} ,\min \{ \underline{a}^{u} ,\underline{b}^{u} \} \left] , \right[\max \{ \overline{a}^{l} ,\overline{b}^{l} \} ,\min \{ \overline{a}^{u} ,\overline{b}^{u} \} ])$.

• 5. Union: $A^{{\mathbb{R}}} \cup B^{{\mathbb{R}}} = ([\min \{ \underline{a}^{l} ,\underline{b}^{l} \} ,\max \{ \underline{a}^{u} ,\underline{b}^{u} \} \left] , \right[\min \{ \overline{a}^{l} ,\overline{b}^{l} \} ,\max \{ \overline{a}^{u} ,\overline{b}^{u} \} ])$..

• 6. Multiplication:

  • $kA^{{\mathbb{R}}} = \left( {\left[ {k\underline{a}^{l} ,k\underline{a}^{u} } \right],\left[ {k\overline{a}^{l} ,k\overline{a}^{u} } \right]} \right),k > 0,$

  • $kA^{{\mathbb{R}}} = \left( {\left[ {k\underline{a}^{u} ,k\underline{a}^{l} \left] , \right[k\overline{a}^{u} ,k\overline{a}^{l} } \right]} \right),\;k < 0,$

  • $\begin{aligned} A^{{\mathbb{R}}} \times B^{{\mathbb{R}}} & = ([\min \{ \underline{a}^{l} \underline{b}^{l} ,\underline{a}^{l} \underline{b}^{u} ,\underline{a}^{u} \underline{b}^{l} ,\underline{a}^{u} \underline{b}^{u} \} ,\max \{ \underline{a}^{l} \underline{b}^{l} ,\underline{a}^{l} \underline{b}^{u} ,\underline{a}^{u} \underline{b}^{l} ,\underline{a}^{u} \underline{b}^{u} \} ], \\ & \quad [\min \{ \overline{a}^{l} \overline{b}^{l} ,\overline{a}^{l} \overline{b}^{u} ,\overline{a}^{u} \overline{b}^{l} ,\overline{a}^{u} \overline{b}^{u} \} ,\max \{ \overline{a}^{l} \overline{b}^{l} ,\overline{a}^{l} \overline{b}^{u} ,\overline{a}^{u} \overline{b}^{l} ,\overline{a}^{u} \overline{b}^{u} \} ]). \\ \end{aligned}$

3 The proposed rough multi-objective transportation problem

In this section, the MOTP formulation in crisp and rough (RMOTP) environments are presented. In the RMOTP, the parameters are considered as rough intervals for the supply and demand.

3.1 MOTP in crisp environment

The Linear MOTP can be formulated mathematically as

$$ \begin{aligned} P_{1} & :\,{\text{Min}}\;Z^{k} \left( {\varvec{x}} \right) = \mathop \sum \limits_{i = 1}^{m} c_{ij}^{k} x_{ij} ,\quad k = 1,2, \ldots ,K, \\ & \;\;{\text{subject to}} \\ & \quad \mathop \sum \limits_{j = 1}^{n} x_{ij} = a_{i} , \quad i = 1,2, \ldots ,m, \\ & \quad \mathop \sum \limits_{i = 1}^{m} x_{ij} = b_{j} ,\quad j = 1,2, \ldots ,n, \\ & \quad x_{ij} \ge 0 \forall i,j. \\ \end{aligned} $$

(4)

where $Z = \left\{ {Z^{1} \left( {\varvec{x}} \right),Z^{2} \left( {\varvec{x}} \right), \ldots ,Z^{K} \left( {\varvec{x}} \right) } \right\}$ denotes the vector of the K objective functions, and $x_{ij}$ defines the product amount to be shipped from ith source to jth destination. Here, $c_{ij}^{k}$ defines the penalty or the cost for a unit of the product during the transporting from ith source to jth destination at the kth criterion, and $a_{i}$ and $b_{j}$ define the availability at ith source and the demand at jth destination, respectively. It is assumed that $a_{i} > 0 \forall i,$ $b_{j} > 0 \forall j$ and $c_{ij}^{k}$ $\forall i,j$ and $\sum\nolimits_{i = 1}^{m} {a_{i} } = \sum\nolimits_{j = 1}^{n} {b_{j} }$.

3.2 MOTP in rough environment (RMOTP)

In this section, the formulation of the MOTP under the rough environment (RMOTP) is presented. In this sense, the parameters of the cost (penalty), availability and demand are represented by rough interval scenario (RIS). The RIS is inspired from the intersection of the experts’ knowledge (consensus opinion) and the union of the experts’ knowledge (respecting opinion) to represent the lower and upper approximation intervals, respectively. In this sense, the RMOTP is decomposed into two sub-interval models, namely, lower interval model (LIM) and upper interval model (UIM). Afterwards the LIM is decomposed into two crisp sub-transportation problem using the borders of this interval to characterize the surely Pareto optimal solution and also the UIM is decomposed into two crisp sub-transportation problem using the borders of this interval to characterize the possibly Pareto optimal solution. By this way, rough Pareto optimal solution can be obtained.

Thus, $P_{1}$ in rough environment can be formulated by $P_{2}$ as follows:

$$ \begin{aligned} & P_{2} :Min Z^{{k{\mathbb{R}}}} \left( {\varvec{x}} \right) = \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} ([\underline{c}_{ij}^{lk} ,\underline{c}_{ij}^{uk} \left] , \right[\overline{c}_{ij}^{lk} ,\overline{c}_{ij}^{uk} ])x_{ij}^{{\mathbb{R}}} ,\quad k = 1,2, \ldots ,K, \\ & \quad \;\;{\text{subject to}} \\ & \quad \quad \mathop \sum \limits_{j = 1}^{n} x_{ij}^{{\mathbb{R}}} = (\left[ {\underline{a}_{i}^{l} ,\underline{a}_{i}^{u} \left] , \right[\overline{a}_{i}^{l} ,\overline{a}_{i}^{u} } \right]),\;\;i = 1,2, \ldots ,m, \\ & \quad \quad \mathop \sum \limits_{i = 1}^{m} x_{ij}^{{\mathbb{R}}} = \left( {\left[ {\underline{b}_{j}^{l} ,\underline{b}_{j}^{u} \left] , \right[\overline{b}_{j}^{l} ,\overline{b}_{j}^{u} } \right]} \right),\;\;j = 1,2, \ldots ,n, \\ & \quad \quad x_{ij}^{{\mathbb{R}}} \ge 0,\;\;i = 1,2, \ldots ,m,\;\;j = 1,2, \ldots ,n, \\ & {\text{with}} \\ &\mathop \sum \limits_{i = 1}^{m} \left( {\left[ {\underline{a}_{i}^{l} ,\underline{a}_{i}^{u} \left] , \right[\overline{a}_{i}^{l} ,\overline{a}_{i}^{u} } \right]} \right) = \mathop \sum \limits_{j = 1}^{n} \left( {\left[ {\underline{b}_{j}^{l} ,\underline{b}_{j}^{u} \left] , \right[\overline{b}_{j}^{l} ,\overline{b}_{j}^{u} } \right]} \right), \\ \end{aligned} $$

(5)

where RMOTP is the problem of minimizing K interval valued objective functions and $([\underline {c}_{\,ij}^{lk} \,,\underline {c}_{\,ij}^{uk} ],\,[\overline{c}_{ij}^{lk} \,,\overline{c}_{ij}^{uk} ]\,)$ is the uncertain cost for the transportation problem in rough interval representation that can represent delivery time, quantity of goods delivered, etc. $([\underline {a}_{\,i}^{l} \,,\underline {a}_{\,i}^{u} ],\,[\overline{a}_{i}^{l} \,,\overline{a}_{i}^{u} ])$ and $([\underline {b}_{j}^{l} \,,\underline {b}_{j}^{u} ],\,[\overline{b}_{j}^{l} \,,\overline{b}_{j}^{u} ])$ are rough intervals representing the source and destination parameters, respectively.

Remark 1.

From the properties of rough intervals given in Sect. 2, we have,

• 1. $[\underline{c}_{\,ij}^{l} \,,\underline{c}_{\,ij}^{u} ] \subseteq \,\,[\overline{c}_{ij}^{l} \,,\overline{c}_{ij}^{u} ]\, \Leftrightarrow \overline{c}_{ij}^{l} \le \underline{c}_{ij}^{l} \, \le \underline{c}_{ij}^{u} \le \overline{c}_{ij}^{u} ,$

• 2. $[\underline{a}_{i}^{l} \,,\underline{a}_{i}^{u} ]\, \subseteq \,[\overline{a}_{i}^{l} \,,\overline{a}_{i}^{u} ]\, \Leftrightarrow \overline{a}_{i}^{l} \le \underline{a}_{i}^{l} \, \le \underline{a}_{i}^{u} \le \overline{a}_{i}^{u} ,$

• 3. $[\underline{b}_{j}^{l} \,,\underline{b}_{j}^{u} ] \subseteq \,\,[\overline{b}_{j}^{l} \,,\overline{b}_{j}^{u} ]\, \Leftrightarrow \overline{b}_{j}^{l} \le \,\underline{b}_{j}^{l} \, \le \underline{b}_{j}^{u} \le \overline{b}_{j}^{u} .$

for all $k = 1,2,...,K,\,\,i = 1,2,...,m\,$ and $j = 1,2,...,n$.

Definition 4

${\varvec{x}}^{*} \in X^{{\mathbb{R}}}$ is said to be rough Pareto optimal solution (RPOS) of $P_{1}$ if there is no ${\varvec{x}} \in X^{{\mathbb{R}}}$, such that $Z^{{k{\mathbb{R}}}} \left( {\varvec{x}} \right) \le Z^{{k{\mathbb{R}}}} \left( {{\varvec{x}}^{*} } \right)$ for all $k = 1,2, \ldots ,K$ with at least one $k \in \{ 1,2, \ldots ,K\}$, such that $Z^{{k{\mathbb{R}}}} \left( {\varvec{x}} \right) < Z^{{k{\mathbb{R}}}} \left( {{\varvec{x}}^{*} } \right)$.

For characterizing the RPOS of $P_{2}$, let us consider the following weighted problem (Tao and Xu 2012; Hamzehee et al. 2014):

$$ \begin{aligned} P_{3} & :\;\;{\text{Min}}\;\,Z^{{\mathbb{R}}} \left( w \right) = \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} w_{k} ([\underline{c}_{ij}^{lk} ,\underline{c}_{ij}^{uk} \left] , \right[\overline{c}_{ij}^{lk} ,\overline{c}_{ij}^{uk} ])x_{ij}^{{\mathbb{R}}} , \\ & \quad {\text{subject}}\;{\text{to}} \\ & \quad \quad {\varvec{x}} \in \Omega^{{\mathbb{R}}} \quad {\text{and}}\;{\text{for}}\;{\text{any}}\;\;w \in W = \left\{ {w \in R^{K} \left| {\sum\limits_{k = 1}^{K} {w_{k} = 1,} \;w_{k} \ge 0} \right.} \right\} \\ \end{aligned} $$

(6)

The rough set of all feasible solutions of the transportation problem will be denoted by ${\Omega }^{\mathbb{R}}$ asollows:

$$ \Omega^{{\mathbb{R}}} = \left\{ {\begin{array}{*{20}l} {\mathop \sum \limits_{j = 1}^{n} x_{ij}^{{\mathbb{R}}} = (\left[ {\underline{a}_{i}^{l} ,\underline{a}_{i}^{u} \left] , \right[\underline{a}_{i}^{l} ,\underline{a}_{i}^{u} } \right]),\quad i = 1,2, \ldots ,m,} \hfill \\ {\mathop \sum \limits_{i = 1}^{m} x_{ij}^{{\mathbb{R}}} = \left( {\left[ {\underline{b}_{j}^{l} ,\underline{b}_{j}^{u} \left] , \right[\underline{b}_{j}^{l} ,\underline{b}_{j}^{u} } \right]} \right),\quad j = 1,2, \ldots ,n,} \hfill \\ {x_{ij}^{{\mathbb{R}}} \ge 0,\quad i = 1,2, \ldots ,m,\quad j = 1,2, \ldots ,n,} \hfill \\ {\mathop \sum \limits_{i = 1}^{m} \left( {\left[ {\underline{a}_{i}^{l} ,\underline{a}_{i}^{u} \left] , \right[\underline{a}_{i}^{l} ,\underline{a}_{i}^{u} } \right]} \right) = \mathop \sum \limits_{j = 1}^{n} \left( {\left[ {\underline{b}_{j}^{l} ,\underline{b}_{j}^{u} \left] , \right[\underline{b}_{j}^{l} ,\underline{b}_{j}^{u} } \right]} \right)} \hfill \\ \end{array} } \right\} $$

(7)

Definition 5

For given $w^{*} \in W$, the solution ${\varvec{x}} \in X^{{\mathbb{R}}}$ _{is said} to be a rough feasible solution, if it satisfies the feasible region ${ }\Omega^{{\mathbb{R}}}$.

Definition 6

For given $w^{*} \in W$, the a rough feasible solution ${\varvec{x}}^{*} \in X^{{\mathbb{R}}}$, is said to be a rough optimal solution of the problem $P_{2}$ if the following rule is satisfied:

$$ \begin{aligned} & \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} w_{k} \left( {\left[ {\underline{c}_{ij}^{lk} ,\underline{c}_{ij}^{uk} } \right],\left[ {\underline{c}_{ij}^{lk} ,\underline{c}_{ij}^{uk} } \right]} \right)x_{ij}^{{*{\mathbb{R}}}} \\ & \quad \le \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} w_{k} \left( {\left[ {\underline{c}_{ij}^{lk} ,\underline{c}_{ij}^{uk} } \right],\left[ {\underline{c}_{ij}^{lk} ,\underline{c}_{ij}^{uk} } \right]} \right)x_{ij}^{\mathbb{R}} \quad \forall i = 1,2, \ldots ,m,\;\;j = 1,2, \ldots ,n. \\ \end{aligned} $$

Theorem 1

The rough optimal solution of the problem $P_{3}$ can be characterized by finding the solutions of the following two sub-model, lower interval model (LIM) named Model 1 and upper interval model (UIM) Model 2.

• Model 1: LIM

  The LIM model is characterized by taking the lower interval of the problem $P_{3}$ that is defined as $P_{4}$:

  $$ \begin{aligned} & P_{4} :\;\;{\text{Min}}\;Z^{l} \left( w \right) = \mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} w_{k} ([\underline{c}_{ij}^{lk} ,\underline{c}_{ij}^{uk} ])x_{ij}^{l} \\ & \quad \quad {\text{subject}}\;{\text{to}} \\ & \quad \quad \quad \mathop \sum \limits_{j = 1}^{n} x_{ij}^{l} = (\left[ {\underline{a}_{i}^{l} ,\underline{a}_{i}^{u} } \right]),\;\;i = 1,2, \ldots ,m, \\ & \quad \quad \mathop \sum \limits_{i = 1}^{m} x_{ij}^{l} = \left( {\left[ {\underline{b}_{j}^{l} ,\underline{b}_{j}^{u} } \right]} \right),\;\;j = 1,2, \ldots ,n, \\ & \quad \quad x_{ij}^{l} \ge 0,\;\;i = 1,2, \ldots ,m,\;\;j = 1,2, \ldots ,n, \\ & \quad \quad \sum\limits_{i = 1}^{m} {([\underline{a}_{\,i}^{l} \,,\underline{a}_{\,i}^{u} ]} ) = \sum\limits_{j = 1}^{n} {([\underline{b}_{j}^{l} \,,\underline{b}_{j}^{u} ])} , \\ & {\text{and}}\;{\text{for}}\;{\text{any}}\;\;w \in W = \left\{ {w \in R^{K} \left| {\sum\limits_{k = 1}^{K} {w_{k} = 1,\,} w_{k} \ge 0} \right.} \right\}. \\ \end{aligned} $$

  (9)

  Theorem 2

  Consider the constraints of LIM model ($P_{4}$), where $x_{ij}^{{}} \ge 0,\,\,i = 1,2, \ldots ,m,$ $j = 1,2, \ldots ,n$. Then, $\sum\nolimits_{j = 1}^{n} {x_{ij}^{{}} = \underline {a}_{{{\kern 1pt} i}}^{l} }$; $\sum\nolimits_{i = 1}^{m} {x_{ij}^{{}} = \underline {b}_{j}^{l} }$ and $\sum\nolimits_{j = 1}^{n} {x_{ij}^{{}} = \underline {a}_{{{\kern 1pt} i}}^{u} } ;\;\;\sum\nolimits_{i = 1}^{m} {x_{ij}^{{}} = \underline {b}_{j}^{u} }$ are lower and upper approximations of the feasible range, respectively.

  Theorem 3

  Consider LIM model ($P_{4}$). Then, for any given feasible solution $x_{ij}^{{}} \ge 0,\,\,i = 1,2,...,m,$ $j = 1,2,...,n$, we have,

  $$ \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {w_{k} (\underline {c}_{\,ij}^{lk} } \,)x_{ij}^{{}} } } < \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {w_{k} (\underline {c}_{\,ij}^{uk} } )x_{ij}^{{}} } } $$

  (10)

  Proof

  The proof is trivial by the fact that $x_{ij}^{{}} \ge 0,$ for all $i = 1,2,...,m,$ and $j = 1,2, \ldots ,n$_.

  Definition 7

  For a given feasible solution ${\mathbf{x}} \in X^{l}$ of LIM model ($P_{4}$), the value $\sum\nolimits_{k = 1}^{K} {\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {w_{k} (\underline {c}_{{{\kern 1pt} ij}}^{lk} } {\mkern 1mu} )x_{ij}^{l} } }$ is called the most favorable value, while $\sum\nolimits_{k = 1}^{K} {\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {w_{k} (\underline {c}_{{{\kern 1pt} ij}}^{uk} } )x_{ij}^{l} } }$ is the least favorable value of the cost function.

  Theorems 2, 3 and Definition 4 allow obtaining the best and worst optimal solutions of the LIM model. In fact, it is done by transforming the original LIM model into two classical TPs. We call them TP lower for the lower interval (${\text{TP}}_{{{\text{LL}}}}$) and TP upper for the lower interval (${\text{TP}}_{{{\text{UL}}}}$), where the best optimal solution $\underline{{\mathbf{x}}}^{l}$ of the lower interval solution $X^{l}$ is found by solving the following form:

  $$ \begin{aligned} {\text{TP}}_{{{\text{LL}}}} & :\;\;{\text{Min}}\;\;\underline{z}_{{}}^{l} (w) = \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {w_{k} \left( {\underline{c}_{\,ij}^{lk} } \right)} x_{ij}^{l} } } , \\ & \quad {\text{subject}}\,{\text{to}}\, \\ & \quad \quad \sum\limits_{j = 1}^{n} {x_{ij}^{{}} = \underline{a}_{\,i}^{l} } ,\;\;i = 1,2, \ldots ,m,\,\,\,\sum\limits_{i = 1}^{m} {x_{ij}^{{}} = \underline{b}_{j}^{l} } ,\;\;j = 1,2, \ldots ,n, \\ & \quad \quad x_{ij}^{l} \ge 0,\;\;i = 1,2, \ldots ,m,\,\,\,j = 1,2, \ldots ,n, \\ \end{aligned} $$

  (11)
  
  

  with

  $$ \sum\limits_{i = 1}^{m} {\underline{a}_{\,i}^{l} \,} = \sum\limits_{j = 1}^{n} {\underline{b}_{j}^{l} } \quad {\text{and}}\;{\text{for}}\;{\text{any}}\quad w \in W = \left\{ {w \in R^{K} \left| {\sum\limits_{k = 1}^{K} {w_{k} = 1,\,} w_{k} \ge 0} \right.} \right\}. $$

  In addition, the worst optimal solution ${\overline{\mathbf{x}}}^{l}$ of the lower interval solution $X^{l}$ is found by solving the following form:

  $$ \begin{aligned} {\text{TP}}_{{{\text{UL}}}} & :\;\;{\text{Min}}\;\;\overline{z}_{{}}^{l} (w) = \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {w_{k} \left( {\underline{c}_{\,ij}^{uk} } \right)} x_{ij}^{{}} } } , \\ & \quad {\text{subject}}\,{\text{to}} \\ & \quad \quad \sum\limits_{j = 1}^{n} {x_{ij}^{{}} = \underline {a}_{\,i}^{u} } ,\,\,i = 1,2, \ldots ,m,\,\,\,\sum\limits_{i = 1}^{m} {x_{ij}^{{}} = \underline {b}_{j}^{u} } ,\,\,j = 1,2, \ldots ,n, \\ & \quad \quad x_{ij}^{l} \ge 0,\,\,i = 1,2, \ldots ,m,\,\,\,j = 1,2, \ldots ,n, \\ \end{aligned} $$

  (12)
  
  

  with

  $$ \sum\limits_{i = 1}^{m} {\underline {a}_{\,i}^{u} } = \sum\limits_{j = 1}^{n} {\underline {b}_{j}^{u} } \quad {\text{and}}\;{\text{for}}\;{\text{any}}\;w \in W = \left\{ {w \in R^{K} \,\left| {\sum\limits_{k = 1}^{K} {w_{k} = 1,} \;w_{k} \ge 0} \right.} \right\}. $$

  Indeed, ${\text{TP}}_{{{\text{LL}}}}$ (${\text{TP}}_{{{\text{UL}}}}$) uses the least (most) favorable value of the lower interval cost value.

  ($Z^{l} (w) = [\underline {z}_{{}}^{l} (w),\,\underline {z}_{{}}^{u} (w)]$) and lower interval solution $X^{l}$ is obtained as $X^{l} = [{\mathbf{\underline {x} }}^{l} ,\,{\overline{\mathbf{x}}}^{l} ]$ that is named surely Pareto optimal range.

• Model 2: UIM The UIM model is characterized by taking the upper interval of the problem $P_{3}$ that is defined as $P_{5}$:

  $$ \begin{aligned} & {\text{P}}_{{5}} :\;\;{\text{Min}}\;\;Z^{u} (w) = \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {w_{k} } \left( {[\overline{c}_{ij}^{lk} \,,\overline{c}_{ij}^{uk} ]} \right)x_{ij}^{u} } } ,\,\, \\ & \quad \quad {\text{subject}}\,{\text{to}}\, \\ & \quad \quad \quad \sum\limits_{j = 1}^{n} {x_{ij}^{u} = (\,[\overline{a}_{i}^{l} \,,\overline{a}_{i}^{u} ]\,} ),\,\,i = 1,2, \ldots ,m, \\ & \quad \quad \quad \sum\limits_{i = 1}^{m} {x_{ij}^{u} = \left( {\,[\overline{b}_{j}^{l} \,,\overline{b}_{j}^{u} ]} \right)} ,\;\;j = 1,2, \ldots ,n, \\ & \quad \quad \quad x_{ij}^{u} \ge 0,\,\,i = 1,2, \ldots ,m,\;\;j = 1,2, \ldots ,n, \\ & {\text{with}} \\ & \sum\limits_{i = 1}^{m} {([\overline{a}_{i}^{l} \,,\overline{a}_{i}^{u} ]} ) = \sum\limits_{j = 1}^{n} {(\,[\overline{b}_{j}^{l} \,,\overline{b}_{j}^{u} ])}\\ & \quad {\text{and}}\;{\text{for}}\;{\text{any}}\;\;w \in W = \left\{ {w \in R^{K} \,\left| {\sum\limits_{k = 1}^{K} {w_{k} = 1,} \;w_{k} \ge 0} \right.} \right\}. \\ \end{aligned} $$

  (13)

  By implementing Theorems 2, 3 and Definition 4 in UIM model, the best and worst optimal solutions of the UIM model can be computed. In fact, it is done by transforming the original UIM model into two classical TPs, where we call them TP lower for the upper interval (${\text{TP}}_{{{\text{LU}}}}$) and TP upper for the lower interval (${\text{TP}}_{{{\text{UU}}}}$₎.

  where the best optimal solution $\underline{{\mathbf{x}}}^{u}$ of the upper interval solution $X^{u}$ is found by solving the following aspect:

  $$ \begin{aligned} & {\text{TP}}_{{{\text{LU}}}} :{\text{Min}}\;\underline{z}_{{}}^{u} (w) = \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {w_{k} (\overline{c}_{ij}^{lk} } )x_{ij}^{u} } } , \\ & \;\;\quad \quad {\text{subject}}\,{\text{to}}\, \\ & \quad \quad \quad \;\sum\limits_{j = 1}^{n} {x_{ij}^{{}} = \overline{a}_{i}^{l} } \,,\,\,i = 1,2, \ldots ,m,\quad \sum\limits_{i = 1}^{m} {x_{ij}^{{}} = \overline{b}_{j}^{l} } ,\;\;j = 1,2, \ldots ,n, \\ & \quad \quad \;x_{ij}^{l} \ge 0\,\,\,,\,\,i = 1,2, \ldots ,m,\quad j = 1,2, \ldots ,n, \\ & {\text{with}} \\ & \sum\limits_{i = 1}^{m} {\overline{a}_{i}^{l} } = \sum\limits_{j = 1}^{n} {\overline{a}_{i}^{l} } \quad {\text{and}}\;{\text{for}}\;{\text{any}}\;w \in W = \left\{ {w \in R^{K} \left| {\sum\limits_{k = 1}^{K} {w_{k} = 1,} \;w_{k} \ge 0} \right.} \right\}. \\ \end{aligned} $$

  (14)

  In addition, the worst optimal solution ${\overline{\mathbf{x}}}^{u}$ of the lower interval solution $X^{u}$ is found by solving the following form:

  $$ \begin{aligned} & {\text{TP}}_{{{\text{UU}}}} :\;\;{\text{Min}}\,\,\overline{z}_{{}}^{l} (w) = \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {w_{k} (\overline{c}_{ij}^{uk} } \,)x_{ij}^{{}} } } , \\ & \quad \quad \quad {\text{subject}}\,{\text{to}} \\ & \quad \quad \quad \quad \sum\limits_{j = 1}^{n} {x_{ij}^{{}} = \overline{a}_{i}^{u} } ,\quad i = 1,2, \ldots ,m,\quad \sum\limits_{i = 1}^{m} {x_{ij}^{{}} = \overline{b}_{j}^{u} } ,\quad j = 1,2, \ldots ,n, \\ & \quad \quad \quad \quad x_{ij}^{l} \ge 0,\quad i = 1,2, \ldots ,m,\quad j = 1,2, \ldots ,n, \\ & {\text{with}} \\ & \sum\limits_{i = 1}^{m} {\overline{a}_{i}^{u} } = \sum\limits_{j = 1}^{n} {\overline{b}_{j}^{u} } \quad {\text{and}}\;{\text{for}}\;{\text{any}}\;w \in W = \left\{ {w \in R^{K} \,\left| {\sum\limits_{k = 1}^{K} {w_{k} = 1,} \;w_{k} \ge 0} \right.} \right\}. \\ \end{aligned} $$

  (15)

  Indeed, ${\text{TP}}_{{{\text{LU}}}}$ (${\text{TP}}_{{{\text{UU}}}}$) uses the least (most) favorable value of the upper interval cost value ($Z^{u} (w) = [\overline{z}_{{}}^{l} (w),\,\overline{z}_{{}}^{u} (w)]$) and upper interval solution $X^{u}$ is obtained as $X^{u} = [{\mathbf{\underline {x} }}^{u} ,\,{\overline{\mathbf{x}}}^{u} ]$ that is named possibly Pareto optimal range.

  As discussed in Sect. 2, let $Z^{l} (w) = [\underline{z}_{{}}^{l} (w),\,\underline{z}_{{}}^{u} (w)]$ ($Z^{u} (w) = [\overline{z}_{{}}^{l} (w),\,\overline{z}_{{}}^{u} (w)]$). Then, for some $w \in W$ the expected non-dominated value, $E(z^{*} (w))$, for ${\text{P}}_{{2}}$ is obtained from the following relation (Dash and Mohanty 2013):

  $$ E(z^{*} (w)) = \frac{1}{4}[\underline{z}_{{}}^{l} (w) + \underline{z}_{{}}^{u} (w) + \overline{z}_{{}}^{l} (w) + \overline{z}_{{}}^{u} (w)]. $$

  (16)

  Definition 8

  • 1. If $E(z^{*} (w)) \in [\underline {z}_{{}}^{l} (w),\,\underline {z}_{{}}^{u} (w)]$, then $E(z^{*} (w))$ is surely non-dominated solution of $P_{3}$.

  • 2. If $E(z^{*} (w)) \in [\overline{z}_{{}}^{l} (w),\,\overline{z}_{{}}^{u} (w)] - [\underline {z}_{{}}^{l} (w),\,\underline {z}_{{}}^{u} (w)]$, then $E(z^{*} (w))$ is possibly non-dominated solution of $P_{3}$.

  • 3. If $E(z^{*} (w)) \notin [\overline{z}_{{}}^{l} (w),\,\overline{z}_{{}}^{u} (w)]$, then $E(z^{*} (w))$ is surely dominated solution of $P_{3}$.

  Following the above discussion, the algorithm for the proposed approach, in this paper, for solving RMOTP is given in Algorithm 1.

  

4 Simulation results

In this section, the proposed methodology is investigated and validated by introducing a counter example for rough multi-objective optimization problem (RMOOP) and followed by the case study, rough multi-objective transportation problem (RMOTP).

4.1 Numerical illustration

The proposed methodology is illustrated via the numerical RMOOP as follows:

$$ \begin{aligned} & {\text{Max}}\;Z_{1} ({\mathbf{x}}) = ([1\,,3],\,[0\,,5]\,)x_{1} \, + ([1\,,2],\,[1\,,3]\,)x_{2} \\ & {\text{Max}}\;Z_{2} ({\mathbf{x}}) = ([3\,,5],\,[2\,,6]\,)x_{1} \, + ([2\,,6],\,[1\,,7]\,)x_{2} \\ & {\text{Subject}}\,{\text{to}}: \\ & \quad ([2\,,3],\,[1\,,3]\,)x_{1} \, + ([2\,,4],\,[1\,,5]\,)x_{2} \le ([7\,,9],\,[5\,,10]\,) \\ & \quad ([2,3],\,[1\,,5]\,)x_{1} \, + ([1\,,2],\,[0\,,6]\,)x_{2} \le ([5,8],\,[3\,,9]\,) \\ & \quad x_{1} ,x_{2} \ge 0. \\ \end{aligned} $$

First, the rough multi-objective optimization problem (RMOOP) is decompose into four classical linear programming problems according LIM and UIM models as in Table 2, then each problem of the RMOOP is combined into single objective problem (SOP) through the weighted sum method. Different weights of objective functions are imposed and the corresponding Pareto optimal solutions in the decision space are obtained, as shown in Table 3.

Table 2 Decomposition of the RMOOP

Table 3 _{Pareto optimal value and Pareto optimal solution for each sub-problem (ND: non-dominated; POS: Pareto optimal solution)}

Table 3 shows that, the non-dominated solutions (i.e., $\underline{z}_{{}}^{l} (w),\underline{z}_{{}}^{u} (w),\overline{z}^{l} (w),\overline{z}^{u} (w)$) for the four problems ${\text{P}}_{{{\text{LL}}}}$,${\text{P}}_{{{\text{UL}}}}$,${\text{TP}}_{{{\text{LU}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ with the corresponding Pareto set of solutions for different weights. Table 4 demonstrates that the Pareto optimal rough intervals, where for problems ${\text{P}}_{{{\text{LL}}}}$,${\text{P}}_{{{\text{UL}}}}$, we can achieve the surely Pareto optimal range for taking different weights for the objective functions, while the possibly Pareto optimal range for problems ${\text{TP}}_{{{\text{LU}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ is determined by taking different weights for the objective functions. In addition, Table 4 provides the surely, possibly as rough optimal ranges. Additionally, to help the decision maker to extract the “preferred’’ solution from the surely and possibly Pareto optimal ranges, expected non-dominated solution is introduced, as shown in Table 4, where the first four expected values lie in the surely range, while the remain values lie the possibly range.

Table 4 Surely, possibly and rough optimal ranges

Furthermore, the bounds of the surely and possibly Pareto optimal range is depicted in Fig. 2 and denoted by $\underline{z}_{{}}^{l}$ (lower for the lower objective) and $\underline{z}_{{}}^{u}$ (upper for the lower objective), respectively. In addition, the bounds of the possibly Pareto optimal range is depicted in Fig. 2 and denoted by $\overline{z}^{l}$(lower for the upper objective) and $\overline{z}^{u}$(upper for the upper objective), respectively.

Fig. 2

Rough non-dominated solutions with different weights

4.2 Case study: RMOTP

This section is introduced to validate the proposed approach for solving RMOTP, where the cost functions' coefficients $C^{{k,{\mathbb{R}}}}$, the source parameters $a^{{\mathbb{R}}}$, and destination parameters $b^{{\mathbb{R}}}$ are represented as rough interval form. The RMOTP can be formulated as follows:

$$ \begin{aligned} & {\text{Min}}\;Z_{1}^{{\mathbb{R}}} \left( x \right) = \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} C_{1}^{{\mathbb{R}}} x_{ij}^{{\mathbb{R}}} \\ & {\text{Min}}\;Z_{2}^{{\mathbb{R}}} \left( x \right) = \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} C_{2}^{{\mathbb{R}}} x_{ij}^{{\mathbb{R}}} \\ & \mathop \sum \limits_{j = 1}^{n} x_{ij}^{{\mathbb{R}}} = a_{i}^{{\mathbb{R}}} ,i = 1,2, \ldots ,m, \\ & \mathop \sum \limits_{i = 1}^{m} x_{ij}^{{\mathbb{R}}} = b_{i}^{{\mathbb{R}}} ,j = 1,2, \ldots ,n, \\ & \mathop \sum \limits_{j = 1}^{n} a_{i}^{{\mathbb{R}}} = \mathop \sum \limits_{i = 1}^{m} b_{i}^{{\mathbb{R}}} ,\;x_{ij}^{{\mathbb{R}}} \ge 0,\;i = 1,2, \ldots ,m,\;j = 1,2, \ldots ,n. \\ \end{aligned} $$

Rough interval coefficients $C_{1}^{{\mathbb{R}}}$ and $C_{2}^{{{\mathbb{R}} }}$ for both objectives are defined as follows:

$$ C_{1}^{{\mathbb{R}}} = \left( {\begin{array}{*{20}l} {\left( {\left[ {1,2\left] , \right[0,3} \right]} \right)} \hfill & {\left( {\left[ {1,3\left] , \right[0,4} \right]} \right)} \hfill & {\left( {\left[ {5,9\left] , \right[4,10} \right]} \right)} \hfill & {\left( {\left[ {4,8\left] , \right[3,9} \right]} \right)} \hfill \\ {\left( {\left[ {1,2\left] , \right[0,3} \right]} \right)} \hfill & {\left( {\left[ {7,10\left] , \right[6,11} \right]} \right)} \hfill & {\left( {\left[ {2,6\left] , \right[1,7} \right]} \right)} \hfill & {\left( {\left[ {3,5\left] , \right[2,6} \right]} \right)} \hfill \\ {\left( {\left[ {7,9\left] , \right[6,10} \right]} \right)} \hfill & {\left( {\left[ {7,11\left] , \right[6,12} \right]} \right)} \hfill & {\left( {\left[ {3,5\left] , \right[2,6} \right]} \right)} \hfill & {\left( {\left[ {5,7\left] , \right[4,8} \right]} \right)} \hfill \\ \end{array} } \right), $$

$$ C_{2}^{{\mathbb{R}}} = \left( {\begin{array}{*{20}c} {\left( {\left[ {3,4\left] , \right[2,5} \right]} \right)} & {\left( {\left[ {3,5\left] , \right[2,6} \right]} \right)} & {\left( {\left[ {7,11\left] , \right[6,12} \right]} \right)} & {\left( {\left[ {6,10\left] , \right[5,11} \right]} \right)} \\ {\left( {\left[ {3,4\left] , \right[2,5} \right]} \right)} & {\left( {\left[ {9,12\left] , \right[8,13} \right]} \right)} & {\left( {\left[ {4,8\left] , \right[3,9} \right]} \right)} & {\left( {\left[ {5,7\left] , \right[4,8} \right]} \right)} \\ {\left( {\left[ {9,11\left] , \right[8,12} \right]} \right)} & {\left( {\left[ {9,13\left] , \right[8,14} \right]} \right)} & {\left( {\left[ {5,7\left] , \right[4,8} \right]} \right)} & {\left( {\left[ {7,9\left] , \right[6,10} \right]} \right)} \\ \end{array} } \right). $$

In addition, the rough source parameters $a^{{\mathbb{R}}}$, and rough destination parameters $b^{{\mathbb{R}}}$ are defined as follows:

$$ \begin{aligned} a_{1}^{{\mathbb{R}}} & = \left( {\left[ {7,9\left] , \right[6,10} \right]} \right),a_{2}^{{\mathbb{R}}} = \left( {\left[ {17,21\left] , \right[16,22} \right]} \right),a_{3}^{{\mathbb{R}}} = \left( {\left[ {16,18\left] , \right[15,19} \right]} \right) \\ b_{1}^{{\mathbb{R}}} & = \left( {\left[ {10,12\left] , \right[9,13} \right]} \right),b_{2}^{{\mathbb{R}}} = \left( {\left[ {2,4\left] , \right[1,5} \right]} \right),b_{3}^{{\mathbb{R}}} = \left( {\left[ {13,15\left] , \right[12,16} \right]} \right), \\ b_{4}^{{\mathbb{R}}} &= \left( {\left[ {15,17\left] , \right[15,17} \right]} \right). \\ \end{aligned} $$

First, we formulate the weighted sum problem to combine the two costs into single cost function as follows:

$$ C^{{\mathbb{R}}} = w_{1} C_{1}^{{\mathbb{R}}} + w_{2} C_{2}^{{\mathbb{R}}} . $$

Let $(w_{1} ,w_{2} ) = (0.5,0.5)$, we obtain $C^{{\mathbb{R}}}$ as

$$ C^{\mathbb{R}} = \left( {\begin{array}{*{20}c} {\left( {\left[ {2,3\left] , \right[1,4} \right]} \right)} & {\left( {\left[ {2,4\left] , \right[1,5} \right]} \right)} & {\left( {\left[ {6,10\left] , \right[5,11} \right]} \right)} & {\left( {\left[ {5,9\left] , \right[4,10} \right]} \right)} \\ {\left( {\left[ {2,3\left] , \right[1,4} \right]} \right)} & {\left( {\left[ {8,11\left] , \right[7,12} \right]} \right)} & {\left( {\left[ {3,7\left] , \right[2,8} \right]} \right)} & {\left( {\left[ {4,6\left] , \right[3,7} \right]} \right)} \\ {\left( {\left[ {8,10\left] , \right[7,11} \right]} \right)} & {\left( {\left[ {8,12\left] , \right[7,13} \right]} \right)} & {\left( {\left[ {4,6\left] , \right[3,7} \right]} \right)} & {\left( {\left[ {6,8\left] , \right[5,9} \right]} \right)} \\ \end{array} } \right). $$

Now, we are going to formulate LIM and UIM for the RMOTP. Then the LIM is spited into two crisp TPs, where the coefficients, source and destination parameters for ${\text{TP}}_{{{\text{LL}}}}$ and ${\text{TP}}_{{{\text{UL}}}}$ are illustrated in Table 5 as follows:

Table 5 Coefficients, source and destination parameters for${\text{TP}}_{{{\text{LL}}}}$ and ${\text{TP}}_{{{\text{UL}}}}$

The ${\text{TP}}_{{{\text{LL}}}}$ model is formulated as follows.

$$ \begin{aligned} & {\text{Min}}\;Z = 2x_{11} + 2x_{12} + 6x_{13} + 5x_{14} \, + \,2x_{21} + 8x_{22} + 3x_{23} + 4x_{24} \\ & \quad \quad \quad \;\; + 8x_{31} + 8x_{32} + 4x_{33} + 6x_{34} \\ & {\text{Subject}}\;{\text{to}}: \\ & \quad x_{11} + x_{12} + x_{13} + x_{14} = 7 \\ & \quad x_{21} + x_{22} + x_{23} + x_{24} = 17 \\ & \quad x_{31} + x_{32} + x_{33} + x_{34} = 16 \\ & \quad x_{11} + x_{21} + x_{31} = 10 \\ & \quad x_{12} + x_{22} + x_{32} = 2 \\ & \quad x_{13} + x_{23} + x_{33} = 13 \\ & \quad x_{14} + x_{24} + x_{34} = 15 \\ & \quad x_{ij} \ge 0\quad \forall i,j. \\ \end{aligned} $$

Apply the simplex method to solve ${\text{TP}}_{{{\text{LL}}}}$ model. The solution for ${\text{TP}}_{{{\text{LL}}}}$ is obtained as $x_{ij}^{LL} = \left\{ {5,\,2,\,0,\,0;5,\,0,\,0,\,12;0,\,0,\,13,\,3} \right\}$ and the corresponding objective (cost) function value for ${\text{TP}}_{{{\text{LL}}}}$ is obtained as $\underline {z}_{{}}^{l} (w) = 142$.

In addition, the ${\text{TP}}_{{{\text{UL}}}}$ model is formulated as follows:

$$ \begin{aligned} & {\text{Min}}\,\,Z = 3x_{11} + 4x_{12} + 10x_{13} + 9x_{14} \, + \,3x_{21} + 11x_{22} + 7x_{23} + 6x_{24} \\ & \quad \quad \quad \;\; + 10x_{31} + 12x_{32} + 6x_{33} + 8x_{34} \\ & {\text{Subject}}\;{\text{to}}: \\ & \quad x_{11} + x_{12} + x_{13} + x_{14} = 9 \\ & \quad x_{21} + x_{22} + x_{23} + x_{24} = 21 \\ & \quad x_{31} + x_{32} + x_{33} + x_{34} = 18 \\ & \quad x_{11} + x_{21} + x_{31} = 12 \\ & \quad x_{12} + x_{22} + x_{32} = 4 \\ & \quad x_{13} + x_{23} + x_{33} = 15 \\ & \quad x_{14} + x_{24} + x_{34} = 17 \\ & \quad x_{ij} \ge 0\quad \forall i,j. \\ \end{aligned} $$

In addition, the simplex is implemented for the ${\text{TP}}_{{{\text{UL}}}}$ problem and the solution for the ${\text{TP}}_{{{\text{UL}}}}$ is given by $x_{ij}^{UL} = \left\{ {5,\,4,\,0,\,0;7,\,0,\,0,\,14;0,\,0,\,15,\,3} \right\}$, where the objective (cost) function value for ${\text{TP}}_{{{\text{UL}}}}$ becomes $\underline {z}_{{}}^{u} (w) = 250$.

Similarly, the UIM is spited into two crisp TPs, where the coefficients, source and destination parameters for ${\text{TP}}_{{{\text{LU}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ are illustrated in Table 6 and the models for ${\text{TP}}_{{{\text{LU}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ is formulated as ${\text{TP}}_{{{\text{LL}}}}$ and ${\text{TP}}_{{{\text{UL}}}}$ models.

Table 6 Coefficients, source and destination parameters for${\text{TP}}_{{{\text{LU}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$

We solve the ${\text{TP}}_{{{\text{LU}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ problems with the simplex and the optimal solution for the ${\text{TP}}_{{{\text{LU}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ problems are as follows: $x_{ij}^{UL} = \left\{ {5,\,1,\,0,\,0;4,\,0,\,0,\,12;0,\,0,\,12,\,3} \right\}$ and $x_{ij}^{UU} = \left\{ {5,5,\,0,\,0;8,\,0,\,0,\,14;0,\,0,\,16,\,3} \right\}$, where the cost functions for ${\text{TP}}_{{{\text{UL}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ are $\overline{z}_{{}}^{l} (w) = 97$ and $\overline{z}_{{}}^{u} (w) = 314$, respectively.

The rough Pareto optimal transported amount for the RMOTP is illustrated in Table 7. Furthermore, by solving the rough model of transportation problem, we obtain a rough interval cost ($Z^{{\mathbb{R}}} = \left( {\left[ {142,250\left] , \right[97,314} \right]} \right)$). But in real applications the decision maker shall prefer one set of solution rather being confused with a rough interval cost. In this section, we proposed one solution as a compromise solution by calculating the expected value for the decision makers, that is obtained by Eq. (16) as $E(z^{*} (w)) = 200.75$.

Table 7 Rough Pareto optimal transported amount

4.3 Discussion

The proposed approach is implemented on rough multi-objective optimization problem as numerical illustration, where different weights are presented to exhibit the rough Pareto optimal range that comprises the surely Pareto optimal range as the lower approximation interval and the possibly Pareto optimal range as the upper approximation interval. In this context, a wide set of the expected compromise solution ranged from 15.75 to 25.8 can be obtained. It is evident that in view of profit and workers satisfaction, the proposed model is more fruitful for the decision maker (DM) as it provide different optimal suits and thus can facilities the choice’ mission for the DM. Furthermore, the investigation on the RMOTP is conducted a real thought-provoking case study, where the unit transportation cost, the supply, and destination are represented by rough interval form. The RMOTP is decomposed through two sub-model, namely, LIM and UIM. Firstly, the parameters of the LIM are illustrated in Table 5 then the optimal results for these models are obtained. In this context, the LIM is decomposed to ${\text{TP}}_{{{\text{LL}}}}$ and ${\text{TP}}_{{{\text{UL}}}}$, where the solution for ${\text{TP}}_{{{\text{LL}}}}$ is obtained as $x_{ij}^{LL} = \left\{ {5,\,2,\,0,\,0;5,\,0,\,0,\,12;0,\,0,\,13,\,3} \right\}$ with the corresponding objective (cost) function value as $\underline{z}_{{}}^{l} (w) = 142$, while the solution for the ${\text{TP}}_{{{\text{UL}}}}$ is obtained as $x_{ij}^{UL} = \left\{ {5,\,4,\,0,\,0;7,\,0,\,0,\,14;0,\,0,\,15,\,3} \right\}$ with the objective (cost) function value as $\underline{z}_{{}}^{u} (w) = 250$. It is observed that the surely Pareto optimal range of the cost has been obtained between $142$ and $250$. Secondly, the parameters for the UIM are illustrated in Table 6, and then the results for UIM model are obtained by solving the ${\text{TP}}_{{{\text{LU}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ problems, where the solutions are obtained as $x_{ij}^{UL} = \left\{ {5,\,1,\,0,\,0;4,\,0,\,0,\,12;0,\,0,\,12,\,3} \right\}$ with corresponding cost $\overline{z}_{{}}^{l} (w) = 97$ for ${\text{TP}}_{{{\text{LU}}}}$ problem and $x_{ij}^{UU} = \left\{ {5,5,\,0,\,0;8,\,0,\,0,\,14;0,\,0,\,16,\,3} \right\}$ with the corresponding cost function $\overline{z}_{{}}^{u} (w) = 314$ for ${\text{TP}}_{{{\text{UU}}}}$ problem. Thus the possibly Pareto optimal range of the transportation cost has been obtained between 97 and 314. Therefore, theses intervals can represent the rough Pareto optimum value ($Z^{{\mathbb{R}}} = \left( {\left[ {142,250} \right],\left[ {97,314} \right]} \right)$. In addition, the transported amount from the sources to destination as a rough Pareto optimal solution is shown in Table 7. In addition, rough Pareto optimal solution for each model is depicted for ${\text{TP}}_{{{\text{LL}}}}$,${\text{TP}}_{{{\text{UL}}}}$,${\text{TP}}_{{{\text{UL}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ models to demonstrate the rough interval for the proposed models. In addition, the optimal transported amounts for the RMOTP models are depicted in Fig. 3. In this sense, the decompose visualization of ${\text{TP}}_{{{\text{LL}}}}$,${\text{TP}}_{{{\text{UL}}}}$,${\text{TP}}_{{{\text{UL}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$ models can assist the decision maker to decide the adequate transported amount for candidate situation. Furthermore, the expected value is obtained as a compromise solution. Finally, the proposed algorithm has been demonstrated its robustness in handling impreciseness of the mathematical modeling (occurring due to environmental fluctuations or due to instabilities in the global market and the rapid fluctuations of prices) and has been empirically approved its facility to the decision makers who are handling cost, availability and demand are in rough interval parameters.

Fig. 3

Optimal transported amount for the RMOTP models

5 Conclusion

The present paper proposes an algorithm for rough multiobjective transportation problem (RMOTP) in which the cost of transportation, the source and destination parameters have been considered as rough interval parameters. The systematic procedure of the proposed incorporates the weighted sum method to find the non-inferior solution. Then two models are introduced, namely, LIM and UIM. The LIM characterizes the surely Pareto optimal solution through converting the lower interval into two deterministic transportation problems. The UIM characterizes the possibly Pareto optimal solution through decomposing the upper interval into two deterministic transportation problems. Furthermore, expected non-dominated value is applied to derive optimal compromise solutions of multi-objective transportation problem in rough environment. The main benefits of the proposed methodology can be observed as follows:

• 1. It has practicality vision by incorporating the classical multiobjective transportation problem under the rough interval concept to cope with the impreciseness and vagueness aspects.

• 2. It can decompose the RMOTP into four crisp sub-model,${\text{TP}}_{{{\text{LL}}}}$, ${\text{TP}}_{{{\text{UL}}}}$, ${\text{TP}}_{{{\text{UL}}}}$ and ${\text{TP}}_{{{\text{UU}}}}$.

• 3. It can asset the hesitant decision maker to make a right decision by introducing expected value measure to obtain the best compromise solution.

• 4. The results of the RMOTP model have a practical meaningful and demonstrate the validity of the proposed approach.

• 5. A wide operational domain can be achieved by integrating different values for weights interactively.

• 6. It can exhibit a new insight for rough multiobjective transportation problem.

• 7. It can present adequate way to build an optimization models for real-world situations in which uncertainty are imposed by considering both of the intersection of the experts’ information (consensus opinion) and the union of the experts’ information (respect opinion).

The main advantage of the proposed study lies behind the possibility of considering the different and multiple sources of uncertainty that engaged from different experts. In the context, the consensus of all experts’ knowledge, and respecting any of the experts’ knowledge are represented as a rough interval fashion. In this context, the rough MOTP is formulated and solved under the concepts of Pareto optimal solution through decomposing the original problem into four sub-problem. In this sense, a relaxed solution space is visualized that is fruitful for decision maker to decide the more realistic solution among the obtained solution space. However, the proposed framework needs to be investigated in multiple cases, especially for high-dimensional problems to prove its scalability. In addition, the fully rough MOTP that having all parameters and the variables as a rough interval fashion should be investigated in the area of transportation sectors. Future work can focus on extending the proposed approach in different optimization natures such as assignment problems, bi-level programming, geometric programming and fractional programming under the rough set theory aspects.