On solving fully rough multi-objective fractional transportation problem: development and prospects

Abstract

In these days, rough set theory has emerged as an invaluable tool for expressing uncertainty in various optimization problems as it takes into account both the consistency and the expertise of all the involved experts and thus leads to more realistic decisions. In view of this characteristic of the rough set theory, in this study, a fractional transportation problem in rough environment is investigated which is of great benefit because of being able to study the relative efficiency in various fields such as transportation, resource allocation, information theory, education, administration, etc. In particular, for many real-life transportation problems the objective may be interpreted as the ratio of physical and economic values, such as profit/cost, delivery speed/wastage, actual cost/standard cost, actual time/standard time, etc. A new methodology has been developed to solve the multi-objective fractional transportation problem with rough parameters in which, firstly, the problem is decomposed into two sub-models namely, the upper interval model and the lower interval model. Then the upper interval model is decomposed into two crisp fractional transportation problems to characterize the possibly Pareto-optimal solution and the lower interval model is decomposed into two crisp fractional transportation problems to characterize the surely Pareto-optimal solution, respectively. The proposed methodology incorporates the variable transformation method to address the non-linearity of the objective functions. Thereafter, the Pareto-optimal solution of the linearized model is obtained by using the weighted-sum method. The proposed approach provides a wide range for the obtained optimal compromise solution and allows the decision-maker to choose the best one as per the practical uses. At last, a case study is solved to demonstrate the applicability of the proposed methodology.

1 Introduction

The transportation problem is a special kind of linear programming problem which was invented by Hitchcock (1941) in 1941 to minimize the transportation cost of items between sources and destinations. The basic model of classical transportation problem includes the objective function and two types of constraints viz., the supply constraints and the demand constraints. To solve the classical transportation problem many strategies (Dantzig and Thapa 2006; Ahmed et al. 2016; Amaliah et al. 2022a, b; Karagul and Sahin 2020) have been developed in the literature. Sometimes, in a real-life transportation system, the decision-maker needs to optimize the ratio of two objective functions. These kinds of problems lie in the category of fractional transportation problem (FTP), which was developed by Swarup (1966) in 1966. In FTP, the objective function is considered in the ratio of two linear functions. The interpretation of FTP in the ratio of physical and economical values represents the efficiency of any system. Many researchers have carried out work on FTP such as Joshi and Gupta (2011) investigated FTP by varying the demand and the supply quantities. A novel algorithm was proposed by Khurana and Arora (2006) to address the linear plus linear fractional transportation problems. Gupta et al. (1993) presented a paradox in linear FTP with mixed constraints. But all these problems investigated by the researchers are single objective problems.

However, in practical situations, decision-maker may need to simultaneously optimize multiple objectives. For instance, in the transportation system, the fundamental goal of the decision-maker is to reduce the total cost of transportation. The problem becomes a multi-objective transportation problem if, in the meantime, the decision-maker wants to minimize the transport time of the item, the rate of breakability, the amount of carbon emitted from the transport system, etc. In a multi-objective transportation problem, the concept of the optimal solution is replaced by the concept of the Pareto-optimal solution or optimal compromise solution. Numerous researchers (Gupta et al. 2020; Bagheri et al. 2020; Roy et al. 2019; Ghosh and Roy 2021; Giri and Roy 2022; Ghosh et al. 2022; Mardanya et al. 2022) have given their investigations on multi-objective transportation problem. When the FTP addresses multiple objectives, then it is referred to as a multi-objective fractional transportation problem (MOFTP). Javaid et al. (2017) studied MOFTP with uncertain parameters and used fuzzy goal programming approach to solve it. Mardanya and Roy (2022) investigated time-variant multi-objective FTP with interval-valued parameters. Sadia et al. (2016) solved multi-objective capacitated FTP with mixed constraints by using fuzzy programming technique with linear as well as non-linear membership functions. In this investigation, researchers considered crisp parameters.

However, in real-life problems, it is almost impossible for the decision-maker to exactly define the parameters of the transportation problems due to the instability of the financial market, lack of information, or many other uncontrollable factors. To handle this situation, Zadeh (1965) established the idea of fuzzy set, which is very helpful when dealing with imprecise data. In a fuzzy set, the degree of membership $\in [0, 1]$ represents the uncertainty of the parameters. Following the development of fuzzy set, Atanassov (1986) proposed the idea of an intuitionistic fuzzy set, in which the uncertainty of the parameters was defined by both the membership and the non-membership degree. Since then, numerous researchers (Sharma et al. 2021; Garg et al. 2021; Khalifa et al. 2021; Anukokila and Radhakrishnan 2019; El Sayed and Abo-Sinna 2021; Bhatia et al. 2022; Saini et al. 2022) have investigated FTP in fuzzy/intuitionistic fuzzy environment. The two-stage fractional transshipment problem, in which all of the parameters are defined by fuzzy numbers, was studied by Garg et al. (2021). Khalifa et al. (2021) applied fuzzy programming approach to obtain the Pareto-optimal solution of the two-stage FTP under a fuzzy environment. In these studies, the researchers found a crisp solution to the fuzzy problem, but the solution evaluated in the form of fuzzy numbers is more instructive. Therefore, Anukokila and Radhakrishnan (2019) formulated the model of fully fuzzy FTP and solved it using the goal programming approach. El Sayed and Abo-Sinna (2021) developed the model of fully intuitionistic fuzzy MOFTP and used the intuitionistic fuzzy programming approach to solve it. Bharati (2019) proposed a solution methodology for the intuitionistic fuzzy FTP in which uncertainty of the parameters is represented by trapezoidal intuitionistic fuzzy numbers. Midya et al. (2021) solved multi-objective fixed-charge FTP using two different kinds of uncertainty.

Moreover, for assessing the ambiguity or uncertainty in optimization problems, the rough set theory proposed by Pawlak (1982) plays a significant role. Rough set theory is free from any extra data-related information such as probability distribution in statistics, degree of membership, or degree of possibility and necessity in fuzzy set theory. Therefore, the optimization process will become more flexible and practical if we employ the rough set theory to address the ambiguity in optimization problems. The rough set has the limitation that it can only be applied to discrete data problems and cannot be utilized to solve continuous variable problems. To solve this shortcoming in rough set theory, Rebolledo (2006) invented the concept of rough interval, which is a specific instance of the rough set. Rough interval can describe continuous variables and also satisfy the characteristics and essential notions of the rough set. Rough interval also has the ability to handle parameters that are ill-defined or partially unknown. Several investigators have paid their attention towards rough set theory to deal with imprecision and vagueness such as Velazquez Rodriguez et al. (2020) in granular computing, Arabani (2006) in civil engineering problems, and Bouzayane and Saad (2020), Sharma et al. (2020), Stankovic et al. (2019), Naouali et al. (2020) and Zhao et al. (2020) have used the concept of rough set theory in different fields. Few researchers have also used the rough set theory to tackle the uncertainty of transportation problems. Garg and Rizk-Allah (2021) suggested an innovative strategy to solve the rough interval multi-objective transportation problems. Bera and Mondal (2020) introduced the rough and bi-rough variables to tackle the uncertainty of two-stage multi-objective transportation problems. The multi-objective fixed-charge transportation problem with rough parameters is solved by Midya and Roy (2020) with three different approaches. Profit-maximizing four-dimensional transportation problem with multi-item is investigated by Bera et al. (2018) in the rough interval context.

But as per our knowledge, no one has used the rough set theory to represent the uncertainty of FTP. Therefore, in the present study, the model of MOFTP is developed in which all the parameters and decision variables are rough intervals and the problem is called as fully rough multi-objective fractional transportation problem (FRMOFTP). The rough intervals which are derived from the intersection and union of the experts knowledge are used to depict the lower and upper approximation intervals. In this way, the FRMOFTP is divided into two sub-interval models: the upper interval model (UIM) and the lower interval model (LIM). The proposed solution methodology has two distinctive characteristics, firstly, the suggested approach divides the UIM into two crisp FTPs using the boundaries of its interval in order to describe the probably Pareto-optimal solution. Furthermore, the suggested method identifies the surely Pareto-optimal solution by splitting the LIM into two crisp FTPs utilizing the boundaries of its interval. To discover the non-dominated solution, the proposed approach utilizes the advantages of the weighted-sum method (WSM). The formulation of the MOFTP in rough interval environment and getting the solution in the same environment is the novelty of the proposed methodology.

1.1 Motivation for the proposed research work

• Garg and Rizk-Allah (2021) suggested an innovative approach to solve the rough interval multi-objective linear transportation problems. But, the approach is not applicable on FTP. As a result, the methodology proposed by the authors has been extended in the present study to solve the MOFTP.

• Sadia et al. (2016) and Veeramani et al. (2021) have solved the FTP in which the value of the parameters is considered as crisp numbers. But, as we know the crisp data may not represent the real-life factors precisely. Hence, the method proposed by the authors lacks practical implications.

• Many authors (Anukokila and Radhakrishnan 2019; Agrawal and Ganesh 2020; El Sayed and Abo-Sinna 2021) have addressed the uncertainty aspect of FTP using stochastic, fuzzy, intuitionistic fuzzy set theory, etc. However, no one has examined the FTP with rough parameters by analyzing the benefits of the rough set theory over the existing theories.

• Liu (2016) and Mahmoodirad et al. (2019) have solved the FTP but the said techniques can not be applied to the problem with multiple objectives. Whereas, the solution methodology proposed in the present study effectively addresses the uncertainty-based FTP with multiple objectives.

• A method for MOFTP that is based on the ranking function of intuitionistic fuzzy number is proposed by El Sayed and Abo-Sinna (2021). But, while applying the various ranking techniques, there is a risk of hesitancy or ambiguity and hence such a technique may not provide the best solution for the uncertain problem.

1.2 Contribution of the proposed study

• The model of FRMOFTP is composed on the basis of rough set theory.

• A new method is proposed to find the rough Pareto-optimal solution of FRMOFTP which operates by decomposing the problem into two sub-models namely, the UIM and the LIM, where each sub-model is decomposed into two crisp FTPs by using the boundaries of this interval.

• To deal with fractional objectives, the variable transformation method (VTM) is embedded in the proposed approach.

• The WSM is utilized for scaling down the multi-objective problem to single objective problem.

• The validation of the proposed methodology is done on a case study.

The remainder of the paper is structured as follows: Sect. 2 presents the basic definitions and theorems related to the rough set theory. Section 3 depicts the crisp model of MOFTP and the VTM to linearise the fractional problem. The mathematical model of the proposed FRMOFTP and the stepwise procedure to solve it, is presented in Sect. 4. The advantages and some limitations of the proposed solution methodology are mentioned in Sect. 5. A case study is solved in Sect. 6 to show the applicability of the proposed solution strategy. Section 7 gives results and discussion. Conclusions and scope of the future research are given in Sect. 8.

2 Preliminaries

The fundamental definitions and theorems related to the rough set theory are presented in this section.

2.1 Rough space and the rough set

Definition 1

(Liu 2009) Let $\Delta$ be a non-empty set, $\Upsilon$ be $\sigma$ algebra of subset of $\Delta$, $\Lambda$ be an element in $\Upsilon$ and $\tau$ be an additive set function with positive, real-valued coefficient. Then, $(\Delta , \Lambda , \Upsilon , \tau )$ is referred to as a rough space.

Definition 2

(Tao and Xu 2012) Let ${\mathscr {U}}$ be the non-empty universe, ${\mathscr {R}}$ be an equivalence relation on ${\mathscr {U}}$ and ${\mathscr {R}}(\pi )$ be an equivalence class of the relation that includes $\pi \in {\mathscr {U}}$. Then for any $\Pi \subseteq {\mathscr {U}},$ the lower and upper approximations of $\Pi$ are given as follows:

$$\begin{aligned}{} & {} \underline{{\mathscr {R}}}(\Pi )=\underset{\pi \in \Pi }{\bigcup }\{{\mathscr {R}}(\pi ):{{\mathscr {R}}(\pi )\subseteq \Pi }\}\\{} & {} \overline{{\mathscr {R}}}(\Pi )=\underset{\pi \in \Pi }{\bigcup }\{{\mathscr {R}}(\pi ):{{\mathscr {R}}(\pi )\cap \Pi \ne \phi }\} \end{aligned}$$

Clearly, the lower approximation $\underline{{\mathscr {R}}}(\Pi )$ represents the set of all objects that can be categorize as $\Pi$ with respect to ${\mathscr {R}}$ with surety, whereas the upper approximation $\overline{{\mathscr {R}}}(\Pi )$ represents the set of all objects that can be categorize as $\Pi$ with respect to ${\mathscr {R}}$ with possibility. The boundary region $bn_{{\mathscr {R}}}(\Pi )$ of the rough set $\Pi$ is defined as

$$\begin{aligned} bn_{{\mathscr {R}}}(\Pi )=\overline{{\mathscr {R}}}(\Pi )-\underline{{\mathscr {R}}}(\Pi ) \end{aligned}$$

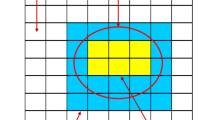
The area described as the boundary is that which cannot be classified as belonging to either $\Pi$ or its complement ${\mathscr {U}}-\Pi$. The boundary region transform into an empty set when both the upper and lower approximations of the defined set are equal. In Fig. 1, the rough set is depicted graphically.

Fig. 1

Graphical representation of rough set

2.2 Rough interval

Rebolledo developed the concept of rough interval in his work (Rebolledo 2006) as an example of the rough set that keeps all of the essential and defining characteristics of the rough set, including the lower and upper approximation intervals. These are specified in the following definitions:

Definition 3

(Xu and Tao 2011) A rough interval is defined as $\widetilde{T}^{RI}=[\omega ^{LL}, \omega ^{UL}][\omega ^{LU}, \omega ^{UU}]$ where $\omega ^{LL},$ $\omega ^{UL},$ $\omega ^{LU},$ $\omega ^{UU}$ are all real numbers and $\omega ^{LU}\le \omega ^{LL}\le \omega ^{UL}\le \omega ^{UU}$. The interval ${[}\omega ^{LL}, \omega ^{UL}]$ is called lower approximation interval and ${[}\omega ^{LU}, \omega ^{UU}]$ is called upper approximation interval such that

• If $\pi \in [\omega ^{LL}, \omega ^{UL}],$ then ${\widetilde{T}}^{RI}$ definitely takes $\pi .$

• If $\pi \in [\omega ^{LU}, \omega ^{UU}],$ then ${\widetilde{T}}^{RI}$ probably takes $\pi$.

• If $\pi \notin [\omega ^{LU}, \omega ^{UU}],$ then ${\widetilde{T}}^{RI}$ definitely does not takes $\pi$.

An upper approximation interval $[\omega ^{LU}, \omega ^{UU}]$ and a lower approximation interval $[\omega ^{LL}, \omega ^{UL}]$ are the two parts of the rough interval. It means that the variable takes values in lower approximation in normal cases and takes values in upper approximation in rare cases, i.e., the variable does not accept any values outside of the upper approximation range. If $\omega ^{LL}= \omega ^{LU}$ and $\omega ^{UL}= \omega ^{UU}$, i.e., no exceptional cases happen, the rough interval ${\widetilde{T}}^{RI}$ degenerates into a crisp interval.

Remark 1: The rough interval ${\widetilde{T}}^{RI}=[0, 0][0, 0]$ is referred as a zero rough interval.

Example 1 Let $\gamma$ stand for the “waste generation rate” in a city, which normally ranges from 800 to 820 ton/day. The rate of waste generation varies between 780 and 840 ton/day during holidays, festivals, and other special occasions. The following rough interval: $\gamma = ({\underline{\gamma }}, {\overline{\gamma }}) = [800, 820][780, 840]$ can be used to represent this “waste generation rate”. It implies, the waste generation rate in a city is surely between [800, 820] ton/day and probably between [780, 840] ton/day.

Definition 4

A rough interval ${\widetilde{T}}^{RI}=[\omega ^{LL}, \omega ^{UL}][\omega ^{LU}, \omega ^{UU}]$ is said to be non-negative iff $\omega ^{LU}\ge 0$.

Definition 5

Let ${\widetilde{T}}^{RI}=[\omega ^{LL}, \omega ^{UL}][\omega ^{LU}, \omega ^{UU}]$ and ${\widetilde{S}}^{RI}=[\sigma ^{LL}, \sigma ^{UL}][\sigma ^{LU}, \sigma ^{UU}]$ be two positive rough intervals. Then

• ${\widetilde{T}}^{RI}\oplus {\widetilde{S}}^{RI}=[\omega ^{LL}+\sigma ^{LL}, \omega ^{UL}+\sigma ^{UL}]{[}\omega ^{LU}+\sigma ^{LU}, \omega ^{UU}+\sigma ^{UU}],$

• ${\widetilde{T}}^{RI}\ominus {\widetilde{S}}^{RI}= [\omega ^{LL}-\sigma ^{UL}, \omega ^{UL}-\sigma ^{LL}]{[}\omega ^{LU}-\sigma ^{UU}, \omega ^{UU}-\sigma ^{LU}],$

• $k{\widetilde{Q}}^{RI}={\left\{ \begin{array}{ll} {[}k\omega ^{LL}, k\omega ^{UL}][k\omega ^{LU}, k\omega ^{UU}] , \text { if } k\ge 0\\ {[}k\omega ^{UL}, k\omega ^{LL}][k\omega ^{UU}, k\omega ^{LU}] , \text { if } k< 0, \end{array}\right. }$

• ${\widetilde{T}}^{RI}\otimes {\widetilde{S}}^{RI}=[\omega ^{LL}\sigma ^{LL}, \omega ^{UL}\sigma ^{UL}] {[}\omega ^{LU}\sigma ^{LU}, \omega ^{UU}\sigma ^{UU}],$

• ${\widetilde{T}}^{RI}\oslash {\widetilde{S}}^{RI}=[\omega ^{LL}/\sigma ^{UL}, \omega ^{UL}/\sigma ^{LL}]{[}\omega ^{LU}/\sigma ^{UU}, \omega ^{UU}/\sigma ^{LU}].$

Example 2 Let ${\widetilde{T}}^{RI}=[6, 8][5, 10]$ and ${\widetilde{S}}^{RI}=[3, 6][2, 8]$ be two rough intervals. Then ${\widetilde{T}}^{RI}+{\widetilde{S}}^{RI}=[9, 14][7, 18],$ ${\widetilde{T}}^{RI}-{\widetilde{S}}^{RI}=[0, 5][-3, 8],$ ${\widetilde{T}}^{RI}*{\widetilde{S}}^{RI}=[18, 48][10, 80],$ ${\widetilde{T}}^{RI}/{\widetilde{S}}^{RI}=[1, 8/3][5/8, 5],$ $4{\widetilde{T}}^{RI}=[24, 32][20, 40],$ and $-4{\widetilde{T}}^{RI}=[-32, -24][-40, -20].$

Definition 6

Let ${\widetilde{T}}^{RI}=[\omega ^{LL}, \omega ^{UL}][\omega ^{LU}, \omega ^{UU}]$ and ${\widetilde{S}}^{RI}=[\sigma ^{LL}, \sigma ^{UL}][\sigma ^{LU}, \sigma ^{UU}]$ be two rough intervals, then ${\widetilde{T}}^{RI}={\widetilde{S}}^{RI}$ if and only if $\omega ^{LL}=\sigma ^{LL}, \omega ^{UL}=\sigma ^{UL}, \omega ^{LU}=\sigma ^{LU}, \omega ^{UU}=\sigma ^{UU}.$

2.3 Expected value of rough interval

Definition 7

(Xu and Tao 2011) Let $\Pi$ be an event defined by $\{\pi |\sigma (\pi )\in \Pi \},$ where $\sigma$ is a function from the universe ${\mathscr {U}}$ to real line ${\mathfrak {R}},$ if $T\subseteq {\mathfrak {R}},$ and $\Pi$ be approximated by $({{\underline{\Pi }}}, {\overline{\Pi }})$ in accordance with the similarity relation ${\mathscr {R}}$. The lower expected value of $\Pi$ is therefore defined as

$$\begin{aligned}{} & {} {\underline{E}}[\sigma ]=\int _{0}^{\infty } {\underline{Appr}}\{\sigma \ge r\}dr-\int _{-\infty }^{0}{\underline{Appr}}\{\sigma \le r\}dr\\{} & {} \text {where} \hspace{.5cm}{\underline{Appr}}=\frac{|\Pi \cap {{\underline{\Pi }}}|}{{{\underline{\Pi }}}}~ \text {and}~ |\Pi \cap {{\underline{\Pi }}}| ~\text {represents the cardinality of}~ \Pi \cap {{\underline{\Pi }}}. \end{aligned}$$

and the upper expected value of $\Pi$ is defined by

$$\begin{aligned}{} & {} {\overline{E}}[\sigma ]=\int _{0}^{\infty } {\overline{Appr}}\{\sigma \ge r\}dr-\int _{-\infty }^{0}{\overline{Appr}}\{\sigma \le r\}dr\\{} & {} \text {where} \hspace{.5cm}{\overline{Appr}}=\frac{|\Pi |}{{{\overline{\Pi }}}}~ \text {and}~ |\Pi | ~\text {represents the cardinality of}~ \Pi . \end{aligned}$$

Hence, the expected value of $\Pi$ is defined as

$$\begin{aligned}{} & {} {E}[\Pi ]=\int _{0}^{\infty } {Appr}\{\sigma \ge r\}dr-\int _{-\infty }^{0}{Appr}\{\sigma \le r\}dr \end{aligned}$$

Theorem 1

(Xu and Tao 2011) Let ${\widetilde{T}}^{RI}= [\omega ^{LL}, \omega ^{UL}][\omega ^{LU}, \omega ^{UU}]$ be a rough interval. Then, the expected-value of ${\widetilde{T}}^{RI}$ is denoted by $E({\widetilde{T}}^{RI})$ and is defined as

$$\begin{aligned} E({\widetilde{T}}^{RI})=\frac{1}{2}\big [\delta (\omega ^{LL}+\omega ^{UL})+(1-\delta )(\omega ^{LU}+\omega ^{UU})\big ],~\text { where}~ \delta \in [0, 1]~\text { is a parameter}. \end{aligned}$$

Remark 2: If $\delta =0.5,$ then expected-value of ${\widetilde{T}}^{RI}$ is calculated as $E({\widetilde{T}}^{RI})=\frac{1}{4}\big (\omega ^{LL}+\omega ^{UL}+\omega ^{LU}+\omega ^{UU}\big ).$

Theorem 2

(Xu and Tao 2011) Let ${\widetilde{T}}^{RI}=[\omega ^{LL}, \omega ^{UL}][\omega ^{LU}, \omega ^{UU}]$ and ${\widetilde{S}}^{RI}=[\sigma ^{LL}, \sigma ^{UL}]$$[\sigma ^{LU}, \sigma ^{UU}]$ be two rough intervals. Then $E[\eta {\widetilde{T}}^{RI}+\phi {\widetilde{S}}^{RI}]=\eta E[{\widetilde{T}}^{RI}]+\phi E[{\widetilde{S}}^{RI}]$ for any two positive real numbers $\eta ,$ $\phi .$

Proof: Let ${\widetilde{T}}^{RI}=[\omega ^{LL}, \omega ^{UL}][\omega ^{LU}, \omega ^{UU}]$ and ${\widetilde{S}}^{RI}=[\sigma ^{LL}, \sigma ^{UL}][\sigma ^{LU}, \sigma ^{UU}]$ are two rough intervals and $\eta ,$ $\phi$ be any two positive real numbers. Then using the arithmetic operations on rough intervals

$$\begin{aligned}{} & {} \eta {\widetilde{T}}^{RI}+\phi {\widetilde{S}}^{RI}=[\eta \omega ^{LL}+\phi \sigma ^{LL}, \eta \omega ^{UL}+\phi \sigma ^{UL}][\eta \omega ^{LU}+\phi \sigma ^{LU}, \eta \omega ^{UU}+\phi \sigma ^{UU}] \\{} & {} \text { is also a rough interval}. \end{aligned}$$

From Theorem 1, the expected value of rough interval $\eta {\widetilde{T}}^{RI}+\phi {\widetilde{S}}^{RI}$ is given as

$$\begin{aligned} E\big [\eta {\widetilde{T}}^{RI}+\phi {\widetilde{S}}^{RI}\big ]{} & {} =\frac{1}{2}\big [\delta (\eta \omega ^{LL}+\phi \sigma ^{LL}+\eta \omega ^{UL}+\phi \sigma ^{UL})\\{} & {} \quad +(1-\delta )(\eta \omega ^{LU}+\phi \sigma ^{LU}+\eta \omega ^{UU}+\phi \sigma ^{UU})\big ]\\{} & {} =\frac{\eta }{2}\big [\delta (\omega ^{LL}+\omega ^{UL})+(1-\delta )(\omega ^{LU}+\omega ^{UU})\big ]\\{} & {} \quad +\frac{\phi }{2}\big [\delta (\sigma ^{LL}+\sigma ^{UL})+(1-\delta )(\sigma ^{LU}+\sigma ^{UU})\big ]\\{} & {} =\eta E[{\widetilde{T}}^{RI}]+\phi E[{\widetilde{S}}^{RI}] \end{aligned}$$

This completes the proof of theorem.

3 Multi-objective fractional transportation problem (MOFTP) in crisp environment

The crisp model of MOFTP in which each parameter is taken into account as a crisp number is presented in this section. Also, the linearization process of the fractional problem using the VTM is described here.

3.1 MOFTP in crisp environment

The general MOFTP mathematically can be defined as:

$$\begin{aligned} {({} P_{1})}{} & {} \text {Max}\hspace{.1cm}O_{k}(x)=\frac{N_{k}(x)}{D_{k}(x)}=\frac{\sum _{l=1}^{p}\sum _{m=1}^{q}p_{lm}^{k}x_{lm} +\mu ^{k}}{\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{k}x_{lm}+\nu ^{k}},\hspace{.3cm}k=1, 2, \ldots , K \end{aligned}$$

(3.1)

$$\begin{aligned}{} & {} \text {subject to}\nonumber \\{} & {} \sum _{m=1}^{q}x_{lm}= a_{l},\hspace{.3cm} l=1, 2, \ldots , p \end{aligned}$$

(3.2)

$$\begin{aligned}{} & {} \sum _{l=1}^{p}x_{lm}=b_{m},\hspace{.3cm} m=1, 2, \ldots , q \end{aligned}$$

(3.3)

$$\begin{aligned}{} & {} x_{lm}\ge 0,\hspace{.3cm} l=1, 2, \ldots , p;\hspace{.2cm} m=1, 2, \ldots , q. \end{aligned}$$

(3.4)

where $O=\{O_{1}(x), O_{2}(x), \ldots , O_{K}(x)\}$ is the set of K objective functions. The coefficients of the kth objective function are denoted by $p_{lm}^{k}$ and $c_{lm}^{k}$ respectively, in the numerator $N_{k}(x)$ and denominator $D_{k}(x).$ The relative constant values for the numerator and denominator of the kth objective function are indicated by $\mu ^{k}$ and $\nu ^{k},$ respectively. The product is shipped from $p(l=1, 2,\ldots , p)$ sources to $q(m = 1, 2, \ldots , q)$ destinations and $x_{lm}$ denotes the units of the product transported from lth source to mth destination. The supply capacity of lth source and demand of mth destination are depicted by $a_{l}$ and $b_{m}$ respectively. We assumes that $D_{k}(x)>0,\hspace{.1cm} N_{k}(x)\ge 0,\hspace{.1cm} \mu ^{k}\ge 0,\hspace{.1cm} \nu ^{k}\ge 0 \hspace{.3cm}\forall \hspace{.1cm} k=1, 2, \ldots , K$ and $\sum _{l=1}^{p}a_{l}=\sum _{m=1}^{q}b_{m}.$

Definition 8

A feasible solution $x^{*}=\{x_{lm}^{*}:l=1, 2, \ldots , p;~ m=1, 2, \ldots q\}$ of problem $(P_1)$ is said to be a Pareto-optimal (optimal-compromise) solution if there exist no other feasible solution $x=\{x_{lm}:l=1, 2, \ldots , p;~ m=1, 2, \ldots q\}$ such that $O_{k}(x)\ge O_{k}(x^{*})~\forall$ $k=1, 2, \ldots , K$ and $O_{k}(x)>O_{k}(x^{*})$ for at least one k.

3.2 Variable transformation method (VTM)

Charnes and Cooper (1962) proposed the VTM to transform the single objective fractional programming problem into a linear programming problem. Later on, Arya et al. (2020); El Sayed and Abo-Sinna (2021) used Charnes–Cooper transformation technique to transform the multi-objective fractional programming problem into multi-objective linear programming problem by introducing a new variable $z_{lm}=x_{lm}*t;\hspace{.1cm} t>0.$ Since $D_{k}(x)>0,\hspace{.1cm}N_{k}(x)\ge 0,\hspace{.1cm} \mu ^{k}\ge 0,\hspace{.1cm} \nu ^{k}\ge 0 \hspace{.2cm}\forall ~k=1, 2, \ldots K$ and $x_{lm}\ge 0$. In this circumstance, we take the least value of $\frac{1}{D_{k}(x)}=t,$ i.e.,

$$\begin{aligned} \bigcap \frac{1}{\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{k}x_{lm}+\nu ^{k}}=t;\hspace{.3cm} k=1, 2, \ldots , K. \end{aligned}$$

(3.5)

In general, it can also be written as:

$$\begin{aligned} \frac{1}{\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{k}x_{lm}+\nu ^{k}}\ge t;\hspace{.3cm} k=1, 2, \ldots , K. \end{aligned}$$

(3.6)

Using the transformation $z_{lm}=x_{lm}*t;\hspace{.1cm} t>0$ and equation (3.6), problem $(P_1)$ is converted into an equivalent multi-objective linear transportation problem as shown below:

$$\begin{aligned} ({} P_{2}){} & {} \text{ Max }\hspace{.1cm} O_{k}(z, t)=tN_{k}\bigg (\frac{z_{lm}}{t}\bigg ), \hspace{.3cm}\forall \hspace{.1cm}l,~m;\hspace{.2cm} k=1, 2, \ldots , K \end{aligned}$$

(3.7)

$$\begin{aligned}{} & {} \text {subject to}\nonumber \\{} & {} tD_{k}\bigg (\frac{z_{lm}}{t}\bigg )\le 1,\hspace{.3cm}\forall \hspace{.1cm}l,~m;\hspace{.2cm} k=1, 2, \ldots , K \end{aligned}$$

(3.8)

$$\begin{aligned}{} & {} \sum _{m=1}^{q}\bigg (\frac{z_{lm}}{t}\bigg )=a_{l}, \hspace{.3cm}l=1, 2, \ldots , p \end{aligned}$$

(3.9)

$$\begin{aligned}{} & {} \sum _{l=1}^{p}\bigg (\frac{z_{lm}}{t}\bigg )=b_{m}, \hspace{.3cm}m=1, 2, \ldots , q \end{aligned}$$

(3.10)

$$\begin{aligned}{} & {} z_{lm}\ge 0,\hspace{.1cm} t>0,\hspace{.1cm} l=1, 2, \ldots , p;\hspace{.1cm} m=1, 2, \ldots , q. \end{aligned}$$

(3.11)

Theorem 3

(El Sayed and Abo-Sinna 2021) The solution $x_{lm}^{*}$ is a Pareto-optimal solution of problem $(P_1)$ iff the solution $(z_{lm}^{*},~ t^{*})$ is a Pareto-optimal solution of problem $(P_2)$.

Proof: Contrarily, suppose that $\{x_{lm}^{*}=\frac{z_{lm}^{*}}{t^{*}}\}$ is a Pareto-optimal solution of $(P_1)$, but the solution $(z_{lm}^{*},~ t^{*})$ is not a Pareto-optimal solution of problem $(P_2)$. Therefore, there exist a feasible solution $\{z_{lm}\}\in F^{'},$ where $F^{'}$ is the set of feasible solutions of problem $(P_2)$, such that

$$\begin{aligned} t^{*}N_{k}\bigg (\frac{z_{lm}^{*}}{t^{*}}\bigg )\le tN_{k}\bigg (\frac{z_{lm}}{t}\bigg ),\hspace{.3cm}\forall \hspace{.1cm}k=1, 2, \ldots , K\\ \text {and}\hspace{.3cm} t^{*}N_{k}\bigg (\frac{z_{lm}^{*}}{t^{*}}\bigg )< tN_{k}\bigg (\frac{z_{lm}}{t}\bigg ),\hspace{.3cm} \text {for at least one}\hspace{.1cm} k. \end{aligned}$$

Using the transformation technique of Chakraborty and Gupta (2002) and Arya et al. (2020), we infer:

$$\begin{aligned} t^{*}N_{k}\big (x_{lm}^{*}\big )\le tN_{k}\bigg (\frac{z_{lm}}{t}\bigg ),\hspace{.3cm} \forall \hspace{.1cm} k=1, 2, \ldots , K\\ \text {and}\hspace{.3cm} t^{*}N_{k}\big (x_{lm}^{*}\big )< tN_{k}\bigg (\frac{z_{lm}}{t}\bigg ), \hspace{.3cm}\text {for at least one}\hspace{.1cm} k. \end{aligned}$$

This implies that

$$\begin{aligned} \frac{N_{k}(x_{lm}^{*})}{D_{k}(x_{lm}^{*})}\le \frac{N_{k}(x_{lm})}{D_{k}(x_{lm})}, \hspace{.3cm}\forall \hspace{.1cm}k=1,2, \ldots , K\\ \text {and}\hspace{.3cm} \frac{N_{k}(x_{lm}^{*})}{D_{k}(x_{lm}^{*})}< \frac{N_{k}(x_{lm})}{D_{k}(x_{lm})},\hspace{.3cm} \text {for at least one}\hspace{.1cm} k. \end{aligned}$$

This demonstrates that $\{x_{lm}^{*}\}$ is not a Pareto-optimal solution of problem $(P_1)$, which is the contradiction of our supposition. Therefore, concludes that solution $(z_{lm}^{*},~ t^{*})$ is a Pareto-optimal solution of problem $(P_2).$

Conversely, let $(z_{lm}^{*},~ t^{*})$ is a Pareto-optimal solution to problem $(P_2)$, but $\{x_{lm}^{*}\}$ is not a Pareto-optimal solution to problem $(P_1)$. Then, there must exist a feasible solution $\{x_{lm}\}\in F,$ where F is the set of feasible solutions of problem $(P_1)$, such that

$$\begin{aligned} \frac{N_{k}(x_{lm}^{*})}{D_{k}(x_{lm}^{*})}\le \frac{N_{k}(x_{lm})}{D_{k}(x_{lm})}, \hspace{.3cm}\forall \hspace{.1cm}k=1,2, \ldots , K\\ \hspace{-.7cm} \text {and}\hspace{.3cm} \frac{N_{k}(x_{lm}^{*})}{D_{k}(x_{lm}^{*})}< \frac{N_{k}(x_{lm})}{D_{k}(x_{lm})},\hspace{.3cm} \text {for at least one}\hspace{.1cm} k \end{aligned}$$

Now by using the transformation $z_{lm}^{*}=x_{lm}^{*}*t^{*}$ we infer that:

$$\begin{aligned} t^{*}N_{k}\bigg (\frac{z_{lm}^{*}}{t^{*}}\bigg )\le \frac{N_{k}(x_{lm})}{D_{k}(x_{lm})},\hspace{.3cm}\forall \hspace{.1cm}k=1, 2, \ldots , K\\ \text {and}\hspace{.3cm} t^{*}N_{k} \bigg (\frac{z_{lm}^{*}}{t^{*}}\bigg )< \frac{N_{k}(x_{lm})}{D_{k}(x_{lm})},\hspace{.3cm} \text {for at least one}\hspace{.1cm} k \end{aligned}$$

This shows that $(z_{lm}^{*},~ t^{*})$ is not a Pareto-optimal solution to problem $(P_2)$ , which is the contradiction to our supposition. Therefore, $\{x_{lm}^{*}\}$ is a Pareto-optimal solution to problem $(P_1).$

Hence, proved the theorem.

3.3 Weighted-sum method (WSM)

The WSM proposed by Zadeh (1963) is an effective method to solve the multi-objective optimization problems. This approach is based on the idea of combining the set of objectives into a single objective by assigning weights to each objective. Based on the importance of a particular objective, the decision-maker determines/decides its weight. The sum of the weights assigned to the objectives should be equal to one. For the multi-objective problem $(P_2),$ the following single-objective problem $(P_3)$ is obtained by applying the WSM:

$$\begin{aligned} {({} P_{3})}{} & {} \text{ Max }\hspace{.1cm} O(z, t)=w_{1}O_{1}(z,t)+w_{2}O_{2}(z,t)+ \cdots +w_{K}O_{K}(z,t)\\{} & {} \text {subject to constraints from (3.8) to (3.11)}\\{} & {} \text {and}\hspace{.2cm} \sum _{k=1}^{K}w_{k}=1,\hspace{.2cm} w_{k}\ge 0, \end{aligned}$$

where $w_{k}$ represents the weights assigned to the kth objectives.

Theorem 4

If $(z^{*},~t^{*})=\{(z_{lm}^{*},~ t^{*}): l=1,2, \ldots ,p;~ m=1,2, \ldots ,q\}$ is an optimal solution of $(P_3)$, then it is also a Pareto-optimal solution of $(P_2)$.

Proof: This theorem is proved by contradiction. Assume that $(z^{*},~ t^{*})$ is not a Pareto-optimal solution of $(P_2)$. Therefore, by Definition 8, there exist at least one solution (z,  t) such that

$$\begin{aligned}{} & {} O_{k}(z,~ t)\ge O_{k}(z^{*},~ t^{*})\hspace{.2cm} \text {for}\hspace{.1cm} k=1,2, \ldots ,K \hspace{.2cm}\text {and}\\{} & {} O_{k}(z,~ t)> O_{k}(z^{*},~ t^{*}) \hspace{.2cm} \text {for at least one} \hspace{.1cm}k. \end{aligned}$$

As $w_{k}>0$ for $k=1, 2, \ldots , K$. Therefore,

$$\begin{aligned}{} & {} w_{k}O_{k}(z,~ t)\ge w_{k}O_{k}(z^{*},~ t^{*})\hspace{.2cm} \text {for}\hspace{.1cm} k=1,2, \ldots , K \hspace{.2cm}\text {and} \end{aligned}$$

(3.12)

$$\begin{aligned}{} & {} w_{k}O_{k}(z,~ t)> w_{k}O_{k}(z^{*},~ t^{*}) \hspace{.2cm} \text {for at least one} \hspace{.1cm}k. \end{aligned}$$

(3.13)

From (3.12) and (3.13), we get

$$\begin{aligned} \sum _{k=1}^{K}w_{k}O_{k}(z,~ t)>\sum _{k=1}^{K}w_{k}O_{k}(z^{*},~ t^{*}) \end{aligned}$$

which is a contradiction to the fact that $(z^{*},~ t^{*})$ is an optimal solution of $(P_3)$. Thus, $(z^{*},~ t^{*})$ is a Pareto-optimal solution of $(P_2)$.

4 Mathematical formulation and solution methodology for fully rough multi-objective fractional transportation problem (FRMOFTP)

In this section, the model of FTP has been formulated with $K(k=1, 2, \ldots , K)$ objective functions which may represent the ratio of total profit to total transportation cost, total delivery speed to total wastage along the shipping route, total actual transportation time to total standard transportation time, etc. The assumption made in the suggested model is that the product is transported from $p(l = 1, 2, \ldots , p)$ sources to $q(m = 1, 2, \ldots , q)$ destinations. The aim of this model formulation is to evaluate the amount of product transported from lth source to mth destination in a way that gives the decision-maker the best value for each objective function with in the given constraints. All of the parameters and decision variables have been treated as rough intervals due to the incomplete information. To formulate the proposed mathematical model of FRMOFTP, the following notations and assumptions are utilized :

Notations:

p : number of sources $(l = 1, 2, \ldots , p),$

q : number of destinations $(m = 1, 2, \ldots , q),$

${\widetilde{N}}_{k}^{RI}$ : coefficient vector for the numerator of the kth objective , 

${\widetilde{D}}_{k}^{RI}$ : coefficient vector for the denominator of the kth objective , 

${\widetilde{p}}_{lm}^{(k)RI}$ : rough interval elements of the set ${\widetilde{N}}_{k}^{RI}$ for the kth objective , 

${\widetilde{c}}_{lm}^{(k)RI}$ : rough interval elements of the set ${\widetilde{D}}_{k}^{RI}$ for the kth objective , 

${\widetilde{a}}_{l}^{RI} :$ rough interval availability of the product at lth source, 

${\widetilde{b}}_{m}^{RI} :$ rough interval demand of the product at mth destination.

${\widetilde{x}}_{lm}^{RI} :$ rough interval amount of the product shipped from lth source to mth destination , 

Assumptions:

• The problem is assumed as a balanced problem. The proposed methodology is not directly applicable for obtaining a rough optimal solution to an unbalanced FRMOFTP. To solve the unbalanced FRMOFTP with proposed methodology, one first requires to convert it into a balanced problem either by introducing a dummy source or dummy destination (Shivani et al. 2022).

• In proposed FRMOFTP, the relative constant value for the numerator and denominator of the kth objective function is assumed to be zero rough interval, i.e., [0, 0][0, 0].

• ${\widetilde{p}}_{lm}^{(k)RI}=[p_{lm}^{(k)LL}, p_{lm}^{(k)UL}][p_{lm}^{(k)LU}, p_{lm}^{(k)UU}],$      $(k=1, 2, 3, \ldots , K)$

• ${\widetilde{c}}_{lm}^{(k)RI}=[c_{lm}^{(k)LL}, c_{lm}^{(k)UL}][c_{lm}^{(k)LU}, c_{lm}^{(k)UU}],$        $(k=1, 2, 3, \ldots , K)$

• ${\widetilde{a}}_{l}^{RI}=[a_{l}^{LL}, a_{l}^{UL}][a_{l}^{LU}, a_{l}^{UU}],$ ${\widetilde{b}}_{m}^{RI}=[b_{m}^{LL}, b_{m}^{UL}][b_{m}^{LU}, b_{m}^{UU}]$,

• ${\widetilde{x}}_{lm}^{RI}=[x_{lm}^{LL}, x_{lm}^{UL}][x_{lm}^{LU}, x_{lm}^{UU}],$

• ${\widetilde{D}}_{k}^{RI}>0,$ ${\widetilde{N}}_{k}^{RI}\ge 0.$

The proposed model of FRMOFTP mathematically can be formulated as below:

$$\begin{aligned}{} & {} ({} P_{4})~~\text {Max}~ {\widetilde{O}}_{k}^{RI}(x)=\frac{{\widetilde{N}}_{k}^{RI}(x)}{{\widetilde{D}}_{k}^{RI}(x)}\nonumber \\{} & {} \quad =\frac{\sum _{l=1}^{p}\sum _{m=1}^{q}[p_{lm}^{(k)LL}, p_{lm}^{(k)UL}][p_{lm}^{(k)LU}, p_{lm}^{(k)UU}]\otimes [x_{lm}^{LL}, x_{lm}^{UL}][x_{lm}^{LU}, x_{lm}^{UU}]}{\sum _{l=1}^{p}\sum _{m=1}^{q}[c_{lm}^{(k)LL}, c_{lm}^{(k)UL}][c_{lm}^{(k)LU}, c_{lm}^{(k)UU}]\otimes {[}x_{lm}^{LL}, x_{lm}^{UL}][x_{lm}^{LU}, x_{lm}^{UU}] }, (k=1, 2, \ldots , K)\nonumber \\{} & {} \hspace{11cm} \end{aligned}$$

(4.1)

$$\begin{aligned}{} & {} \text {subject to}\nonumber \\{} & {} \sum _{m=1}^{q}[x_{lm}^{LL}, x_{lm}^{UL}][x_{lm}^{LU}, x_{lm}^{UU}]=[a_{l}^{LL}, a_{l}^{UL}][a_{l}^{LU}, a_{l}^{UU}], ~~~~ l=1, 2, \ldots , p \text { (supply constraints)} \end{aligned}$$

(4.2)

$$\begin{aligned}{} & {} \sum _{l=1}^{p} [x_{lm}^{LL}, x_{lm}^{UL}][x_{lm}^{LU}, x_{lm}^{UU}]=[b_{m}^{LL}, b_{m}^{UL}][b_{m}^{LU}, b_{m}^{UU}], ~~~~ m=1, 2, \ldots , q \text { (demand constraints)} \end{aligned}$$

(4.3)

$$\begin{aligned}{} & {} \sum _{l=1}^{p}[a_{l}^{LL}, a_{l}^{UL}][a_{l}^{LU}, a_{l}^{UU}]=\sum _{m=1}^{q}[b_{m}^{LL}, b_{m}^{UL}][b_{m}^{LU}, b_{m}^{UU}] \end{aligned}$$

(4.4)

$$\begin{aligned}{} & {} {[}x_{lm}^{LL}, x_{lm}^{UL}][x_{lm}^{LU}, x_{lm}^{UU}]\ge 0\hspace{.3cm} \forall \hspace{.1cm} l,~m. \end{aligned}$$

(4.5)

The lower and upper approximation intervals are represented by the rough intervals, which takes its inspiration from the intersection of expert knowledge and the union of expert knowledge. In this way, the FRMOFTP (P$_4$) is divided into two sub-interval models: UIM and LIM. The UIM is defined by using the upper interval of the problem (P$_4$), which is defined as (P$_5$), and the LIM is defined by using the lower interval of the problem (P$_4$), which is defined as (P$_6$). These definitions are presented below:

$$\begin{aligned} {\textbf {UIM:}}\\ ({} P_{5}){} & {} \text {Max}~ O_{k}^{U}(x)=\frac{\sum _{l=1}^{p}\sum _{m=1}^{q}[p_{lm}^{(k)LU}, p_{lm}^{(k)UU}]\otimes [x_{lm}^{LU}, x_{lm}^{UU}]}{\sum _{l=1}^{p}\sum _{m=1}^{q}[c_{lm}^{(k)LU}, c_{lm}^{(k)UU}]\otimes [x_{lm}^{LU}, x_{lm}^{UU}]},\hspace{.5cm}(k=1, 2, \ldots , K)\\{} & {} \text {subject to}\\{} & {} \sum _{m=1}^{q}[x_{lm}^{LU}, x_{lm}^{UU}]=[a_{l}^{LU}, a_{l}^{UU}], ~~~~ l=1, 2, \ldots , p \\{} & {} \sum _{l=1}^{p} [x_{lm}^{LU}, x_{lm}^{UU}]=[b_{m}^{LU}, b_{m}^{UU}], ~~~~ m=1, 2, \ldots , q \\{} & {} \sum _{l=1}^{p}[a_{l}^{LU}, a_{l}^{UU}]=\sum _{m=1}^{q}[b_{m}^{LU}, b_{m}^{UU}]\\{} & {} {[}x_{lm}^{LU}, x_{lm}^{UU}]\ge 0\hspace{.3cm} \forall \hspace{.1cm} l,~m. \\ {\textbf {LIM:}}\\ {({} P_{6})}{} & {} \text {Max}~ O_{k}^{L}(x)=\frac{\sum _{l=1}^{p}\sum _{m=1}^{q}[p_{lm}^{(k)LL}, p_{lm}^{(k)UL}]\otimes [x_{lm}^{LL}, x_{lm}^{UL}]}{\sum _{l=1}^{p}\sum _{m=1}^{q}[c_{lm}^{(k)LL}, c_{lm}^{(k)UL}]\otimes {[}x_{lm}^{LL}, x_{lm}^{UL}] },\hspace{.5cm}(k=1, 2, \ldots , K)\\{} & {} \text {subject to}\\{} & {} \sum _{m=1}^{q}[x_{lm}^{LL}, x_{lm}^{UL}]=[a_{l}^{LL}, a_{l}^{UL}], ~~~~ l=1, 2, \ldots , p \\{} & {} \sum _{l=1}^{p} [x_{lm}^{LL}, x_{lm}^{UL}]=[b_{m}^{LL}, b_{m}^{UL}], ~~~~ m=1, 2, \ldots , q \\{} & {} \sum _{l=1}^{p}[a_{l}^{LL}, a_{l}^{UL}]=\sum _{m=1}^{q}[b_{m}^{LL}, b_{m}^{UL}] \\{} & {} {[}x_{lm}^{LL}, x_{lm}^{UL}]\ge 0\hspace{.3cm} \forall \hspace{.1cm} l,~m. \end{aligned}$$

From the models UIM and LIM, four crisp fractional transportation problems named as Upper Upper fractional transportation problem $(TP^{UU}),$ Upper Lower fractional transportation problem $(TP^{UL}),$ Lower Lower fractional transportation problem $(TP^{LL})$ and Lower Upper fractional transportation problem $(TP^{LU})$ have been constructed. The models $(TP^{UU}),$ $(TP^{LU})$ represent the possibly Pareto-optimal solution by using the boundary of UIM and the models $(TP^{LL}),$ $(TP^{UL})$ represent the surely Pareto-optimal solution by using the boundary of LIM, as follows:

$$\begin{aligned} \begin{aligned} (TP^{UU}):\hspace{.2cm}&\text {Max}~O_{k}^{UU}=\frac{\sum _{l=1}^{p}\sum _{m=1}^{q}p_{lm}^{(k)UU}\otimes x_{lm}^{UU}}{\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{(k)LU}\otimes x_{lm}^{LU}}\\&\hspace{2cm}(k=1, 2, \ldots , K)\\&\text {subject to}\\&\sum _{m=1}^{q}x_{lm}^{UU}= a_{l}^{UU},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}x_{lm}^{UU}=b_{m}^{UU},\hspace{.3cm} m=1, 2, \ldots , q,\\&\sum _{m=1}^{q}x_{lm}^{LU}= a_{l}^{LU},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}x_{lm}^{LU}=b_{m}^{LU},\hspace{.3cm} m=1, 2, \ldots , q,\\&x_{lm}^{LU},\hspace{.1cm} x_{lm}^{UU}\ge 0\hspace{.2cm}\forall \hspace{.1cm} l,~m. \end{aligned}\hspace{.5cm} \begin{aligned} (TP^{UL}):\hspace{.2cm}&\text {Max}~O_{k}^{UL}=\frac{\sum _{l=1}^{p}\sum _{m=1}^{q}p_{lm}^{(k)UL}\otimes x_{lm}^{UL}}{\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{(k)LL}\otimes x_{lm}^{LL}}\\&\hspace{2cm}(k=1, 2, \ldots , K)\\&\text {subject to}\\&\sum _{m=1}^{q}x_{lm}^{UL}= a_{l}^{UL},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}x_{lm}^{UL}=b_{m}^{UL},\hspace{.3cm} m=1, 2, \ldots , q,\\&\sum _{m=1}^{q}x_{lm}^{LL}= a_{l}^{LL},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}x_{lm}^{LL}=b_{m}^{LL},\hspace{.3cm} m=1, 2, \ldots , q,\\&x_{lm}^{LL},\hspace{.1cm} x_{lm}^{UL}\ge 0\hspace{.2cm}\forall \hspace{.1cm} l,~m. \end{aligned}\\ \begin{aligned} (TP^{LL}):\hspace{.2cm}&\text {Max}~O_{k}^{LL}=\frac{\sum _{l=1}^{p}\sum _{m=1}^{q}p_{lm}^{(k)LL}\otimes x_{lm}^{LL}}{\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{(k)UL}\otimes x_{lm}^{UL}}\\&\hspace{2cm}(k=1, 2, \ldots , K)\\&\text {subject to}\\&\sum _{m=1}^{q}x_{lm}^{LL}= a_{l}^{LL},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}x_{lm}^{LL}=b_{m}^{LL},\hspace{.3cm} m=1, 2, \ldots , q,\\&\sum _{m=1}^{q}x_{lm}^{UL}= a_{l}^{UL},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}x_{lm}^{UL}=b_{m}^{UL},\hspace{.3cm} m=1, 2, \ldots , q,\\&x_{lm}^{LL},\hspace{.1cm} x_{lm}^{UL}\ge 0\hspace{.2cm} \forall \hspace{.5cm} l,~m. \end{aligned}\hspace{.5cm} \begin{aligned} (TP^{LU}):\hspace{.2cm}&\text {Max}~O_{k}^{LU}=\frac{\sum _{l=1}^{p}\sum _{m=1}^{q}p_{lm}^{(k)LU}\otimes x_{lm}^{LU}}{\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{(k)UU}\otimes x_{lm}^{UU}}\\&\hspace{2cm}(k=1, 2, \ldots , K)\\&\text {subject to}\\&\sum _{m=1}^{q}x_{lm}^{LU}= a_{l}^{LU},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}x_{lm}^{LU}=b_{m}^{LU},\hspace{.3cm} m=1, 2, \ldots , q,\\&\sum _{m=1}^{q}x_{lm}^{UU}= a_{l}^{UU},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}x_{lm}^{UU}=b_{m}^{UU},\hspace{.3cm} m=1, 2, \ldots , q,\\&x_{lm}^{LU},\hspace{.1cm} x_{lm}^{UU}\ge 0\hspace{.2cm} \forall \hspace{.1cm} l,~m.\\ \end{aligned} \end{aligned}$$

Theorem 5

If $x^{UU*},$ $x^{UL*},$ $x^{LL*},$ and $x^{LU*}$ be a Pareto-optimal solution of $(TP^{UU}),$ $(TP^{UL}),$ $(TP^{LL}),$ and $(TP^{LU}),$ respectively, then ${\widetilde{x}}^{RI}=[{x^{LL}}^{*}, x^{UL*}][x^{LU*}, x^{UU*}]$ is a Pareto-optimal solution of problem $(P_4)$.

Proof: Let ${\widetilde{y}}^{RI}=[y^{LL*}, y^{UL*}][y^{LU*}, y^{UU*}]$ be a feasible solution of the problem $(P_4).$ Therefore, $y^{UU*},$ $y^{UL*},$ $y^{LL*},$ and $y^{LU*}$ are feasible solution to the problem $(TP^{UU}),$ $(TP^{UL}),$ $(TP^{LL}),$ and $(TP^{LU}),$ respectively. Now, since $x^{UU*},$ $x^{UL*},$ $x^{LL*},$ and $x^{LU*}$ are Pareto-optimal solution of $(TP^{UU}),$ $(TP^{UL}),$ $(TP^{LL}),$ and $(TP^{LU})$ respectively, then $O_{k}^{UU}(x^{UU*})\ge O_{k}^{UU}(y^{UU})$

$O_{k}^{UL}(x^{UL*})\ge O_{k}^{UL}(y^{UL})$

$O_{k}^{LL}(x^{LL*})\ge O_{k}^{LL}(y^{LL})$

$O_{k}^{LU}(x^{LU*})\ge O_{k}^{LU}(y^{LU})$ $\hspace{ .2cm}\forall \hspace{ .2cm}k=1, 2, \ldots , K$

and $O_{k}^{UU}(x^{UU*})> O_{k}^{UU}(y^{UU})$

$O_{k}^{UL}(x^{UL*})> O_{k}^{UL}(y^{UL})$

$O_{k}^{LL}(x^{LL*})> O_{k}^{LL}(y^{LL})$

$O_{k}^{LU}(x^{LU*})> O_{k}^{LU}(y^{LU})$ for at least one k.

Therefore, $O_{k}({\widetilde{x}}^{RI})\ge O_{k}({\widetilde{y}}^{RI})\hspace{ .2cm}\forall \hspace{ .2cm} k=1, 2, \ldots , K$ and $O_{k}({\widetilde{x}}^{RI})> O_{k}({\widetilde{y}}^{RI})$ for at least one k. Therefore, ${\widetilde{x}}^{RI}=[{x^{LL}}^{*}, x^{UL*}][x^{LU*}, x^{UU*}]$ is a Pareto-optimal solution of problem $(P_4)$.

Hence, the theorem is proved $\square$.

For the fractional models $(TP^{UU}),$ $(TP^{UL}),$ $(TP^{LL}),$ and $(TP^{LU}),$ equivalent linear models can be written by applying the VTM discussed in Sect. 3.2. For model $(TP^{UU}),$ considering $x_{lm}^{LU}=x_{lm}^{UU}-\psi _{lm}^{UU}$ and substituting $z_{lm}^{UU}= x_{lm}^{UU}*t^{LU},~\chi _{lm}^{UU}= \psi _{lm}^{UU}*t^{LU};\hspace{.2cm} t^{LU}>0,$ the equivalent linear model $TP^{UU'}$ is presented below. Similarly for model $TP^{UL},$ the equivalent model $TP^{UL'}$ is written by taking $x_{lm}^{LL}=x_{lm}^{UL}-\psi _{lm}^{UL}$ and substituting $z_{lm}^{UL}= x_{lm}^{UL}*t^{LL},~\chi _{lm}^{UL}= \psi _{lm}^{UL}*t^{LL};\hspace{.2cm} t^{LL}>0.$ Similar models have been written for $(TP^{LL}),$ and $(TP^{LU}).$

$$\begin{aligned}&\begin{aligned} (TP^{UU'}):~&\text {Max}~O_{k}^{UU'}=\sum _{l=1}^{p}\sum _{m=1}^{q}p_{lm}^{(k)UU}\otimes z_{lm}^{UU}\\&\hspace{2cm}(k=1, 2, \ldots , K)\\&\text {subject to}\\&\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{(k)LU}\otimes (z_{lm}^{UU}-\chi _{lm}^{UU})\le 1\\&\sum _{m=1}^{q}z_{lm}^{UU}= a_{l}^{UU}\otimes t^{LU},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}z_{lm}^{UU}=b_{m}^{UU} \otimes t^{LU},\hspace{.3cm} m=1, 2, \ldots , q,\\&\sum _{m=1}^{q}(z_{lm}^{UU}-\chi _{lm}^{UU})= a_{l}^{LU}\otimes t^{LU},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}(z_{lm}^{UU}-\chi _{lm}^{UU})=b_{m}^{LU}\otimes t^{LU},\hspace{.3cm} m=1, 2, \ldots , q,\\&z_{lm}^{UU},~z_{lm}^{UU}\ge \chi _{lm}^{UU}\hspace{.2cm}\forall ~l,~m. \end{aligned}\hspace{-.2cm} \begin{aligned} (TP^{UL'}):\hspace{.2cm}&\text {Max}~O_{k}^{UL'}=\sum _{l=1}^{p}\sum _{m=1}^{q}p_{lm}^{(k)UL}\otimes z_{lm}^{UL}\\&\hspace{2cm}(k=1, 2, \ldots , K)\\&\text {subject to}\\&\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{(k)LL}\otimes (z_{lm}^{UL}-\chi _{lm}^{UL})\le 1\\&\sum _{m=1}^{q}z_{lm}^{UL}= a_{l}^{UL}\otimes t^{LL},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}z_{lm}^{UL}=b_{m}^{UL}\otimes t^{LL},\hspace{.3cm} m=1, 2, \ldots , q,\\&\sum _{m=1}^{q}(z_{lm}^{UL}-\chi _{lm}^{UL})= a_{l}^{LL}\otimes t^{LL},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}(z_{lm}^{UL}-\chi _{lm}^{UL})=b_{m}^{LL}\otimes t^{LL},\hspace{.3cm} m=1, 2, \ldots , q,\\&z_{lm}^{UL}\ge 0,~z_{lm}^{UL}\ge \chi _{lm}^{UL}\hspace{.2cm}\forall ~ l,~m. \end{aligned}\\&\begin{aligned} (TP^{LL'}):~&\text {Max}~O_{k}^{LL'}=\sum _{l=1}^{p}\sum _{m=1}^{q}p_{lm}^{(k)LL}\otimes z_{lm}^{LL}\\&\hspace{2cm}(k=1, 2, \ldots , K)\\&\text {subject to}\\&\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{(k)UL}\otimes (z_{lm}^{LL}+\chi _{lm}^{LL})\le 1\\&\sum _{m=1}^{q}z_{lm}^{LL}= a_{l}^{LL}\otimes t^{UL},\hspace{.3cm} l=1, 2, \ldots , p,\\ \end{aligned}\hspace{.8cm} \begin{aligned}(TP^{LU'}):\hspace{.2cm}&\text {Max}~O_{k}^{LU'}=\sum _{l=1}^{p}\sum _{m=1}^{q}p_{lm}^{(k)LU}\otimes z_{lm}^{LU}\\&\hspace{2cm}(k=1, 2, \ldots , K)\\&\text {subject to}\\&\sum _{l=1}^{p}\sum _{m=1}^{q}c_{lm}^{(k)UU}\otimes (z_{lm}^{LU}+\chi _{lm}^{LU})\le 1\\&\sum _{m=1}^{q}z_{lm}^{LU}= a_{l}^{LU}\otimes t^{UU},\hspace{.3cm} l=1, 2, \ldots , p,\\ \end{aligned}\\&\hspace{1.1cm}\begin{aligned}&\sum _{l=1}^{p}z_{lm}^{LL}=b_{m}^{LL}\otimes t^{UL},\hspace{.3cm} m=1, 2, \ldots , q,\\&\sum _{m=1}^{q}(z_{lm}^{LL}+\chi _{lm}^{LL})= a_{l}^{UL}\otimes t^{UL},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}(z_{lm}^{LL}+\chi _{lm}^{LL})=b_{m}^{UL}\otimes t^{UL},\hspace{.3cm} m=1, 2, \ldots , q,\\&z_{lm}^{LL}\ge 0,~z_{lm}^{LL}+\chi _{lm}^{LL}\ge 0\hspace{.2cm}\forall ~ l,~m. \end{aligned}\hspace{1.1cm} \begin{aligned}&\sum _{l=1}^{p}z_{lm}^{LU}=b_{m}^{LU}\otimes t^{UU},\hspace{.3cm} m=1, 2, \ldots , q,\\&\sum _{m=1}^{q}(z_{lm}^{LU}+\chi _{lm}^{LU})= a_{l}^{UU}\otimes t^{UU},\hspace{.3cm} l=1, 2, \ldots , p,\\&\sum _{l=1}^{p}(z_{lm}^{LU}+\chi _{lm}^{LU})=b_{m}^{UU}\otimes t^{UU},\hspace{.3cm} m=1, 2, \ldots , q,\\&z_{lm}^{LU},~z_{lm}^{LU}+\chi _{lm}^{LU}\ge 0 \hspace{.2cm}\forall ~l,~m. \end{aligned} \end{aligned}$$

Remark 1: In model $TP^{LL}$ there are two variables $x_{lm}^{LL}$ and $x_{lm}^{UL}~~(x_{lm}^{UL}>x_{lm}^{LL})$. In the proposed methodology, these variables are associated by defining the relation $x_{lm}^{UL}= x_{lm}^{LL}+\psi _{lm}^{LL}.$ After that by substituting $z_{lm}^{LL}=x_{lm}^{LL}*t^{UL},~~\chi _{lm}^{LL}=\psi _{lm}^{LL}*t^{UL};~~ t^{UL}>0,$ the fractional problem $TP^{LL}$ is transformed into a linear programming problem $TP^{LL'}.$ Similar procedure is applied to transform the fractional problem $TP^{LU}$ to $TP^{LU'}$.

With all of the aforementioned factors taken into consideration, the step-by-step process of the proposed methodology for solving the FRMOFTP is as follows:

Step 1: Formulate the considered FRMOFTP as model $(P_{4}).$

Step 2: Decompose the model $(P_4)$ into two sub-models as UIM $(P_{5})$ and LIM $(P_{6})$.

Step 3: From the UIM and the LIM, construct four crisp fractional transportation problems, namely, Upper Upper fractional transportation problem $(TP^{UU})$, Upper Lower fractional transportation problem $(TP^{UL})$, Lower Lower fractional transportation problem $(TP^{LL})$, and Lower Upper fractional transportation problem $(TP^{LU})$.

Step 4: Linearize the fractional problems $(TP^{UU}),$ $(TP^{UL}),$ $(TP^{LL})$ and $(TP^{LU})$ as explained above and get the linear models $(TP^{UU'}),$ $(TP^{UL'}),$ $(TP^{LL'})$, and $(TP^{LU'})$, respectively.

Step 5: Solve the multi-objective linearized model $(TP^{UU'})$ using the WSM discussed in Sect. 3.3 to find the efficient solution $\{z_{lm}^{UU*},~\chi _{lm}^{UU*},~t^{LU*}\}$ with objective functions value ${O_{k}^{UU'}}^{*}$.

Step 6: To maintain the feasibility condition of the proposed model $(P_{4})$, solve the linearized model $(TP^{UL'})$ with additional constraints $\big (\frac{z_{lm}^{UL}}{t^{LL}}\big )\le \big (\frac{z_{lm}^{UU*}}{t^{LU*}}\big ),~ \big (\frac{z_{lm}^{UL}-\chi _{lm}^{UL})}{t^{LL}}\big )\ge \big ( \frac{z_{lm}^{UU*}-\chi _{lm}^{UU*}}{t^{LU*}}\big )~\forall ~ l,~m,$ to find the efficient solution $\{z_{lm}^{UL*},~\chi _{lm}^{UL*},~t^{LL*}\}$ with objective functions value ${O_{k}^{UL'}}^{*}.$

Step 7: Solve the linearized model $(TP^{LL'})$ by substituting the solution from Step 6 as $\big (\frac{z_{lm}^{LL}}{t^{UL}}\big )=\big (\frac{z_{lm}^{UL*}-\chi _{lm}^{UL*}}{t^{LL*}}\big )$ to find the efficient solution $\{z_{lm}^{LL*}, ~\chi _{lm}^{LL*},~t^{UL*}\}.$

Step 8: Solve the linearized model $(TP^{LU'})$ by substituting the solution from Step 5 as $\big (\frac{z_{lm}^{LU}}{t^{UU}}\big )=\big (\frac{z_{lm}^{UU*}-\chi _{lm}^{UU*}}{t^{LU*}}\big )$ to find the efficient solution $\{z_{lm}^{LU*},~ \chi _{lm}^{LU*},~t^{UU*}\}.$

Step 9: Find the values of the original parameters from the obtained solutions by using the substitutions $x_{lm}^{UU*}=\frac{z_{lm}^{UU*}}{t^{LU*}},~$ $x_{lm}^{UL*}=\frac{z_{lm}^{UL*}}{t^{LL*}},~$ $x_{lm}^{LL*}=\frac{z_{lm}^{LL*}}{t^{UL*}},~$ $x_{lm}^{LU*}=\frac{z_{lm}^{LU*}}{t^{UU*}}.$

Step 10: The set of rough interval $\{{\widetilde{x}}_{lm}^{RI*}\}=\big \{[x_{lm}^{LL*}, x_{lm}^{UL*}][x_{lm}^{LU*}, x_{lm}^{UU*}]\big \}$ is a Pareto-optimal solution to the given FRMOFTP with the objectives value $({\widetilde{O}}_{k}^{RI*})=[O_{k}^{LL*}, O_{k}^{UL*}]$$[O_{k}^{LU*}, O_{k}^{UU*}].$

Remark 2: In the proposed problem, the solution variables are rough intervals, i.e., ${\widetilde{x}}_{lm}^{RI}= [x_{lm}^{LL}, x_{lm}^{UL} [x_{lm}^{LU}, x_{lm}^{UU}]$ and each model $TP^{UU}, TP^{UL}, TP^{LL},$ and $TP^{LU}$ has two variables one in numerator and other in denominator. Using appropriate substitution, these models are converted into a single variable problem. For instance, in model $TP^{LL},$ $x_{lm}^{UL}$ is considered as $x_{lm}^{UL}=x_{lm}^{LL}+\psi _{lm}^{LL}$ and then using the VTM this fractional model is converted into linear transportation model $TP^{LL'}$ by substituting $z_{lm}^{LL}=x_{lm}^{LL}*t^{UL},~\chi _{lm}^{LL}=\psi _{lm}^{LL}*t^{UL};~~ t^{UL}> 0.$ A similar justification can be done for the model $TP^{UU}, TP^{UL}$ and $TP^{LU}$. In the proposed methodology, to obtain the Pareto-optimal solution of the considered problem, model $TP^{UU'}$ is solved and the obtained solution is used to solve model $TP^{UL'}$. To evaluate the objective function value of models $TP^{LL'}$ and $TP^{LU'}$, the previously obtained solutions from $TP^{UU'}$ and $TP^{UL'}$ are used. To evaluate the objective function value of models $TP^{LL'}$ and $TP^{LU'}$, the previously obtained solutions from $TP^{UU'}$ and $TP^{UL'}$ are used.

The flowchart representation of the proposed solution algorithm is depicted in Fig. 2.

Fig. 2

Flow chart of the proposed algorithm

5 Advantages and limitations of the proposed methodology

In this section, the advantages and limitations of the proposed model and solution procedure are mentioned.

5.1 Advantages

• The proposed technique is applicable for solving the FTP with rough intervals, and the rough set theory is more capable of dealing with the ambiguity and imprecision of real-world problems. As a result, the modeling of the problem is realistic.

• The proposed method does not include any ranking function for the rough intervals and hence it is free from any ambiguity that may arise from using different ranking functions.

• The proposed method provides the rough interval solution of the rough problem, i.e., the Pareto-optimal solution is obtained in the same environment, which gives the decision-maker a wide range and a better understanding of the solutions.

• The FTP is a further extension of the linear transportation problem which plays a vital role to reduce cost and improve service in logistics and supply management. The solution methodology suggested in the present study successfully solves the proposed model of FTP.

• Unlike, the method given by Liu (2016) and Mahmoodirad et al. (2019), the proposed technique is applicable to problems with multiple objectives.

5.2 Limitations

• The proposed method is not applicable for unbalanced FRMOFTP.

• The proposed approach cannot be used for the non-linear FRMOFTP as in this approach VTM is employed to handle fractional objectives with linear decision variables. But if the decision variables are non-linear in nature, then VTM could not be applied and the proposed approach will become inapplicable.

6 A case study-FRMOFTP

A case study has been solved in this section to demonstrate the applicability of the proposed technique. Two objective functions are considered in this problem: the ratio of total profit to total transportation costs and the ratio of total delivery speed to total waste along the transportation route. The products are supplied to four destinations from the three source locations. Due to the lack of precise information, all the data including profit, transportation costs, delivery speed, total wastage along the shipping route, supply capacity of sources, and demand of destinations have been represented as rough intervals and are shown in Tables 1 and 2.

Table 1 Profit $({\widetilde{p}}_{lm}^{RI})$ and the transportation cost $( {\widetilde{c}}_{lm}^{RI})$

Table 2 Delivery speed $({\widetilde{s}}_{lm}^{RI})$ and the wastage of product $({\widetilde{w}}_{lm}^{RI})$ during transportation

To obtain the rough interval Pareto-optimal solution, the problem is solved by using the proposed methodology. As per Step 2 of the solution algorithm, the UIM and the LIM for the proposed problem are formulated as follows

UIM:

$$\begin{aligned}{} & {} \text {Max}~O_{1}^{U}(x)= \\{} & {} \quad \frac{\begin{matrix}\otimes [x_{11}^{LU}, x_{11}^{UU}]+[13, 16]\otimes [x_{12}^{LU}, ]x_{12}^{UU}]+[6, 10]\otimes [x_{13}^{LU}, x_{13}^{UU}]+[10, 15]\otimes [x_{14}^{LU}, x_{14}^{UU}]&{}\\ +[7, 9]\otimes [x_{21}^{LU}, x_{21}^{UU}]+[9, 15]\otimes [x_{22}^{LU}, x_{22}^{UU}]+[10, 17]\otimes [x_{23}^{LU}, x_{23}^{UU}]+[6, 11]\otimes [x_{24}^{LU}, x_{24}^{UU}]&{}\\ +[7, 11]\otimes [x_{31}^{LU}, x_{31}^{UU}]+[4, 9]\otimes [x_{32}^{LU}, x_{32}^{UU}]+[12, 17]\otimes [x_{33}^{LU}, x_{33}^{UU}]+[7, 10]\otimes [x_{34}^{LU}, x_{34}^{UU}]\end{matrix}}{\begin{matrix}\otimes [x_{11}^{LU}, x_{11}^{UU}]+[11, 13]\otimes [x_{12}^{LU}, x_{12}^{UU}]+[14, 19]\otimes [x_{13}^{LU}, x_{13}^{UU}]+[5, 11]\otimes [x_{14}^{LU}, x_{14}^{UU}]&{}\\ +[8, 12]\otimes [x_{21}^{LU}, x_{21}^{UU}]+[5, 7]\otimes [x_{22}^{LU}, x_{22}^{UU}]+[10, 17]\otimes [x_{23}^{LU}, x_{23}^{UU}]+[9, 15]\otimes [x_{24}^{LU}, x_{24}^{UU}]&{}\\ +[10, 15]\otimes [x_{31}^{LU}, x_{31}^{UU}]+[13, 17]\otimes [x_{32}^{LU}, x_{32}^{UU}]+[9, 16]\otimes [x_{33}^{LU}, x_{33}^{UU}]+[7, 14]\otimes [x_{34}^{LU}, x_{34}^{UU}]\end{matrix}} \\{} & {} \text {Max}~O_{2}^{U}(x)\\{} & {} \quad = \frac{\begin{matrix}\otimes [x_{11}^{LU}, x_{11}^{UU}]+[3, 10]\otimes [x_{12}^{LU}, ]x_{12}^{UU}]+[2, 9]\otimes [x_{13}^{LU}, x_{13}^{UU}]+[0, 4]\otimes [x_{14}^{LU}, x_{14}^{UU}]&{}\\ +[1, 4]\otimes [x_{21}^{LU}, x_{21}^{UU}]+[3, 6]\otimes [x_{22}^{LU}, x_{22}^{UU}]+[0, 2]\otimes [x_{23}^{LU}, x_{23}^{UU}]+[2, 6]\otimes [x_{24}^{LU}, x_{24}^{UU}]&{}\\ +[1, 4]\otimes [x_{31}^{LU}, x_{31}^{UU}]+[0, 3]\otimes [x_{32}^{LU}, x_{32}^{UU}]+[2, 7]\otimes [x_{33}^{LU}, x_{33}^{UU}]+[2, 4]\otimes [x_{34}^{LU}, x_{34}^{UU}]\end{matrix}}{\begin{matrix}\otimes [x_{11}^{LU}, x_{11}^{UU}]+[1, 6]\otimes [x_{12}^{LU}, x_{12}^{UU}]+[1, 8]\otimes [x_{13}^{LU}, x_{13}^{UU}]+[5, 7]\otimes [x_{14}^{LU}, x_{14}^{UU}]&{}\\ +[2, 5]\otimes [x_{21}^{LU}, x_{21}^{UU}]+[1, 6]\otimes [x_{22}^{LU}, x_{22}^{UU}]+[4, 8]\otimes [x_{23}^{LU}, x_{23}^{UU}]+[0, 4]\otimes [x_{24}^{LU}, x_{24}^{UU}]&{}\\ +[3, 7]\otimes [x_{31}^{LU}, x_{31}^{UU}]+[1, 4]\otimes [x_{32}^{LU}, x_{32}^{UU}]+[2, 5]\otimes [x_{33}^{LU}, x_{33}^{UU}]+[1, 3]\otimes [x_{34}^{LU}, x_{34}^{UU}]\end{matrix}}\\{} & {} \text {subject to}\\{} & {} {[}x_{11}^{LU}, x_{11}^{UU}]+[x_{12}^{LU}, x_{12}^{UU}]+[x_{13}^{LU}, x_{13}^{UU}]+[x_{14}^{LU}, x_{14}^{UU}]=[6, 10]\\{} & {} {[}x_{21}^{LU}, x_{21}^{UU}]+[x_{22}^{LU}, x_{22}^{UU}]+[x_{23}^{LU}, x_{23}^{UU}]+[x_{24}^{LU}, x_{24}^{UU}]=[16, 22]\\{} & {} {[}x_{31}^{LU}, x_{31}^{UU}]+[x_{32}^{LU}, x_{32}^{UU}]+[x_{33}^{LU}, x_{33}^{UU}]+[x_{34}^{LU}, x_{34}^{UU}]=[15, 19]\\{} & {} {[}x_{11}^{LU}, x_{11}^{UU}]+[x_{21}^{LU}, x_{21}^{UU}]+[x_{31}^{LU}, x_{31}^{UU}]=[9, 13]\\{} & {} {[}x_{12}^{LU}, x_{12}^{UU}]+[x_{22}^{LU}, x_{22}^{UU}]+[x_{32}^{LU}, x_{32}^{UU}]=[1, 5]\\{} & {} {[}x_{13}^{LU}, x_{13}^{UU}]+[x_{23}^{LU}, x_{23}^{UU}]+[x_{33}^{LU}, x_{33}^{UU}]=[12, 16]\\{} & {} {[}x_{14}^{LU}, x_{14}^{UU}]+[x_{24}^{LU}, x_{24}^{UU}]+[x_{34}^{LU}, x_{34}^{UU}]=[15, 17] \end{aligned}$$

LIM:

$$\begin{aligned}{} & {} \text {Max}~O_{1}^{L}(x)\\{} & {} \quad = \frac{\begin{matrix}\otimes [x_{11}^{LL}, x_{11}^{UL}]+[13, 14]\otimes [x_{12}^{LL}, ]x_{12}^{UL}]+[7, 9]\otimes [x_{13}^{LL}, x_{13}^{UL}]+[10, 13]\otimes [x_{14}^{LL}, x_{14}^{UL}]&{}\\ +[8, 8]\otimes [x_{21}^{LL}, x_{21}^{UL}]+[11, 13]\otimes [x_{22}^{LL}, x_{22}^{UL}]+[13, 16]\otimes [x_{23}^{LL}, x_{23}^{UL}]+[6, 9]\otimes [x_{24}^{LL}, x_{24}^{UL}]&{}\\ +[8, 10]\otimes [x_{31}^{LL}, x_{31}^{UL}]+[5, 6]\otimes [x_{32}^{LL}, x_{32}^{UL}]+[15, 16]\otimes [x_{33}^{LL}, x_{33}^{UL}]+[9, 10]\otimes [x_{34}^{LL}, x_{34}^{UL}]\end{matrix}}{\begin{matrix}\otimes [x_{11}^{LL}, x_{11}^{UL}]+[11, 13]\otimes [x_{12}^{LL}, x_{12}^{UL}]+[14, 17]\otimes [x_{13}^{LL}, x_{13}^{UL}]+[7, 9]\otimes [x_{14}^{LL}, x_{14}^{UL}]&{}\\ +[9, 11]\otimes [x_{21}^{LL}, x_{21}^{UL}]+[5, 7]\otimes [x_{22}^{LL}, x_{22}^{UL}]+[11, 14]\otimes [x_{23}^{LL}, x_{23}^{UL}]+[11, 13]\otimes [x_{24}^{LL}, x_{24}^{UL}]&{}\\ +[13, 14]\otimes [x_{31}^{LL}, x_{31}^{UL}]+[14, 16]\otimes [x_{32}^{LL}, x_{32}^{UL}]+[11, 12]\otimes [x_{33}^{LL}, x_{33}^{UL}]+[8, 11]\otimes [x_{34}^{LL}, x_{34}^{UL}]\end{matrix}}\\{} & {} \text {Max}~O_{2}^{L}(x)\\{} & {} \quad = \frac{\begin{matrix}\otimes [x_{11}^{LL}, x_{11}^{UL}]+[5, 8]\otimes [x_{12}^{LL}, ]x_{12}^{UL}]+[3, 6]\otimes [x_{13}^{LL}, x_{13}^{UL}]+[1, 3]\otimes [x_{14}^{LL}, x_{14}^{UL}]&{}\\ +[1, 2]\otimes [x_{21}^{LL}, x_{21}^{UL}]+[5, 6]\otimes [x_{22}^{LL}, x_{22}^{UL}]+[0, 2]\otimes [x_{23}^{LL}, x_{23}^{UL}]+[3, 5]\otimes [x_{24}^{LL}, x_{24}^{UL}]&{}\\ +[1, 2]\otimes [x_{31}^{LL}, x_{31}^{UL}]+[0, 1]\otimes [x_{32}^{LL}, x_{32}^{UL}]+[2, 5]\otimes [x_{33}^{LL}, x_{33}^{UL}]+[2, 4]\otimes [x_{34}^{LL}, x_{34}^{UL}]\end{matrix}}{\begin{matrix}\otimes [x_{11}^{LL}, x_{11}^{UL}]+[2, 3]\otimes [x_{12}^{LL}, x_{12}^{UL}]+[2, 5]\otimes [x_{13}^{LL}, x_{13}^{UL}]+[5, 7]\otimes [x_{14}^{LL}, x_{14}^{UL}]&{}\\ +[4, 5]\otimes [x_{21}^{LL}, x_{21}^{UL}]+[2, 3]\otimes [x_{22}^{LL}, x_{22}^{UL}]+[4, 7]\otimes [x_{23}^{LL}, x_{23}^{UL}]+[1, 3]\otimes [x_{24}^{LL}, x_{24}^{UL}]&{}\\ +[4, 6]\otimes [x_{31}^{LL}, x_{31}^{UL}]+[3, 4]\otimes [x_{32}^{LL}, x_{32}^{UL}]+[2, 3]\otimes [x_{33}^{LL}, x_{33}^{UL}]+[2, 2]\otimes [x_{34}^{LL}, x_{34}^{UL}]\end{matrix}}\\{} & {} \text {subject to}\\{} & {} {[}x_{11}^{LL}, x_{11}^{UL}]+[x_{12}^{LL}, x_{12}^{UL}]+[x_{13}^{LL}, x_{13}^{UL}]+[x_{14}^{LL}, x_{14}^{UL}]=[7, 9]\\{} & {} {[}x_{21}^{LL}, x_{21}^{UL}]+[x_{22}^{LL}, x_{22}^{UL}]+[x_{23}^{LL}, x_{23}^{UL}]+[x_{24}^{LL}, x_{24}^{UL}]=[17, 21]\\{} & {} {[}x_{31}^{LL}, x_{31}^{UL}]+[x_{32}^{LL}, x_{32}^{UL}]+[x_{33}^{LL}, x_{33}^{UL}]+[x_{34}^{LL}, x_{34}^{UL}]=[16, 18]\\{} & {} {[}x_{11}^{LL}, x_{11}^{UL}]+[x_{21}^{LL}, x_{21}^{UL}]+[x_{31}^{LL}, x_{31}^{UL}]=[10, 12]\\{} & {} {[}x_{12}^{LL}, x_{12}^{UL}]+[x_{22}^{LL}, x_{22}^{UL}]+[x_{32}^{LL}, x_{32}^{UL}]=[2, 4]\\{} & {} {[}x_{13}^{LL}, x_{13}^{UL}]+[x_{23}^{LL}, x_{23}^{UL}]+[x_{33}^{LL}, x_{33}^{UL}]=[13, 15]\\{} & {} {[}x_{14}^{LL}, x_{14}^{UL}]+[x_{24}^{LL}, x_{24}^{UL}]+[x_{34}^{LL}, x_{34}^{UL}]=[15, 17] \end{aligned}$$

Then as per Step 3 of the solution algorithm, from UIM and LIM four crisp multi-objective fractional transportation problems have been constructed, which are given below:

$(TP^{UU}):$

$$\begin{aligned}{} & {} \text {Max}~O_{1}^{UU}\\{} & {} \quad = \frac{11x_{11}^{UU}{+}16x_{12}^{UU}{+}10x_{13}^{UU}{+}15x_{14}^{UU}{+}9x_{21}^{UU}{+}15x_{22}^{UU}{+}17x_{23}^{UU}{+}11x_{24}^{UU}{+}11x_{31}^{UU}{+}9x_{32}^{UU}{+}17x_{33}^{UU}{+}10x_{34}^{UU}}{12x_{11}^{LU}+11x_{12}^{LU}+14x_{13}^{LU}+5x_{14}^{LU}+8x_{21}^{LU}+5x_{22}^{LU}+10x_{23}^{LU}+9x_{24}^{LU}+10x_{31}^{LU}+13x_{32}^{LU}+9x_{33}^{LU}+7x_{34}^{LU}} \\{} & {} \text {Max}~O_{2}^{UU}\\{} & {} \quad =\frac{6x_{11}^{UU}+10x_{12}^{UU}+9x_{13}^{UU}+4x_{14}^{UU}+4x_{21}^{UU}+6x_{22}^{UU}+2x_{23}^{UU}+6x_{24}^{UU}+4x_{31}^{UU}+3x_{32}^{UU}+7x_{33}^{UU}+4x_{34}^{UU}}{0x_{11}^{LU}+x_{12}^{LU}+x_{13}^{LU}+5x_{14}^{LU}+2x_{21}^{LU}+x_{22}^{LU}+4x_{23}^{LU}+0x_{24}^{LU}+3x_{31}^{LU}+x_{32}^{LU}+2x_{33}^{LU}+x_{34}^{LU}}\\{} & {} \text {subject to}\\{} & {} x_{11}^{UU}+x_{12}^{UU}+x_{13}^{UU}+x_{14}^{UU}= 10,~ x_{21}^{UU}+x_{22}^{UU}+x_{23}^{UU}+x_{24}^{UU}= 22,~ x_{31}^{UU}+x_{32}^{UU}+x_{33}^{UU}+x_{34}^{UU}= 19,\\{} & {} x_{11}^{UU}+x_{21}^{UU}+x_{31}^{UU}= 13,~ x_{12}^{UU}+x_{22}^{UU}+x_{32}^{UU}= 5,~ x_{13}^{UU}+x_{23}^{UU}+x_{33}^{UU}= 16,~ x_{14}^{UU}+x_{24}^{UU}+x_{34}^{UU}= 17,\\{} & {} x_{11}^{LU}+x_{12}^{LU}+x_{13}^{LU}+x_{14}^{LU}= 6,~ x_{21}^{LU}+x_{22}^{LU}+x_{23}^{LU}+x_{24}^{LU}= 16,~ x_{31}^{LU}+x_{32}^{LU}+x_{33}^{LU}+x_{34}^{LU}= 15,\\{} & {} x_{11}^{LU}+x_{21}^{LU}+x_{31}^{LU}= 9,~ x_{12}^{LU}+x_{22}^{LU}+x_{32}^{LU}= 1,~ x_{13}^{LU}+x_{23}^{LU}+x_{33}^{LU}= 12,~ x_{14}^{LU}+x_{24}^{UL}+x_{34}^{LU}= 15,\\{} & {} x_{lm}^{UU},~ x_{lm}^{LU}\ge 0\hspace{.2cm}\forall \hspace{.2cm} l=1, 2, 3;\hspace{.2cm} m=1, 2, 3, 4 \end{aligned}$$

$(TP^{UL}):$

$$\begin{aligned}{} & {} \text {Max}~O_{1}^{UL}\\{} & {} \quad =\frac{10x_{11}^{UL}+14x_{12}^{UL}+9x_{13}^{UL}+13x_{14}^{UL}+8x_{21}^{UL}+13x_{22}^{UL}+16x_{23}^{UL}+9x_{24}^{UL}+10x_{31}^{UL}+6x_{32}^{UL}+16x_{33}^{UL}+10x_{34}^{UL}}{14x_{11}^{LL}+11x_{12}^{LL}+14x_{13}^{LL}+7x_{14}^{LL}+9x_{21}^{LL}+5x_{22}^{LL}+11x_{23}^{LL}+11x_{24}^{LL}+13x_{31}^{LL}+14x_{32}^{LL}+11x_{33}^{LL}+8x_{34}^{LL}}\\{} & {} \text {Max}~O_{2}^{UL}\\{} & {} \quad =\frac{5x_{11}^{UL}+8x_{12}^{UL}+6x_{13}^{UL}+3x_{14}^{UL}+2x_{21}^{UL}+6x_{22}^{UL}+2x_{23}^{UL}+5x_{24}^{UL}+2x_{31}^{UL}+x_{32}^{UL}+5x_{33}^{UL}+4x_{34}^{UL}}{x_{11}^{LL}+2x_{12}^{LL}+2x_{13}^{LL}+5x_{14}^{LL}+4x_{21}^{LL}+2x_{22}^{LL}+4x_{23}^{LL}+x_{24}^{LL}+4x_{31}^{LL}+3x_{32}^{LL}+2x_{33}^{LL}+2x_{34}^{LL}}\\{} & {} \text {subject to}\\{} & {} x_{11}^{UL}+x_{12}^{UL}+x_{13}^{UL}+x_{14}^{UL}= 9,~ x_{21}^{UL}+x_{22}^{UL}+x_{23}^{UL}+x_{24}^{UL}= 21,~ x_{31}^{UL}+x_{32}^{UL}+x_{33}^{UL}+x_{34}^{UL}= 18,\\{} & {} x_{11}^{UL}+x_{21}^{UL}+x_{31}^{UL}= 12,~ x_{12}^{UL}+x_{22}^{UL}+x_{32}^{UL}= 4,~ x_{13}^{UL}+x_{23}^{UL}+x_{33}^{UL}= 15,~ x_{14}^{UL}+x_{24}^{UL}+x_{34}^{UL}= 17,\\{} & {} x_{11}^{LL}+x_{12}^{LL}+x_{13}^{LL}+x_{14}^{LL}= 7,~ x_{21}^{LL}+x_{22}^{LL}+x_{23}^{LL}+x_{24}^{LL}= 17,~ x_{31}^{LL}+x_{32}^{LL}+x_{33}^{LL}+x_{34}^{LL}= 16,\\{} & {} x_{11}^{LL}+x_{21}^{LL}+x_{31}^{LL}= 10,~ x_{12}^{LL}+x_{22}^{LL}+x_{32}^{LL}= 2,~ x_{13}^{LL}+x_{23}^{LL}+x_{33}^{LL}= 13,~ x_{14}^{LL}+x_{24}^{LL}+x_{34}^{LL}= 15,\\{} & {} x_{lm}^{LL},~x_{lm}^{UL}\ge 0 \hspace{.2cm}\forall \hspace{.2cm} l=1, 2, 3;\hspace{.2cm} m=1, 2, 3, 4 \end{aligned}$$

$(TP^{LL}):$

$$\begin{aligned}{} & {} \text {Max}~O_{1}^{LL}\\{} & {} \quad =\frac{10x_{11}^{LL}+13x_{12}^{LL}+7x_{13}^{LL}+10x_{14}^{LL}+8x_{21}^{LL}+11x_{22}^{LL}+13x_{23}^{LL}+6x_{24}^{LL}+8x_{31}^{LL}+5x_{32}^{LL}+15x_{33}^{LL}+9x_{34}^{LL}}{17x_{11}^{UL}+13x_{12}^{UL}+17x_{13}^{UL}+9x_{14}^{UL}+11x_{21}^{UL}+7x_{22}^{UL}+14x_{23}^{UL}+13x_{24}^{UL}+14x_{31}^{UL}+16x_{32}^{UL}+12x_{33}^{UL}+11x_{34}^{UL}}\\{} & {} \text {Max}~O_{2}^{LL}\\{} & {} \quad =\frac{3x_{11}^{LL}+5x_{12}^{LL}+3x_{13}^{LL}+x_{14}^{LL}+x_{21}^{LL}+5x_{22}^{LL}+0x_{23}^{LL}+3x_{24}^{LL}+x_{31}^{LL}+0x_{32}^{LL}+2x_{33}^{LL}+2x_{34}^{LL}}{x_{11}^{UL}+3x_{12}^{UL}+5x_{13}^{UL}+7x_{14}^{UL}+5x_{21}^{UL}+3x_{22}^{UL}+7x_{23}^{UL}+3x_{24}^{UL}+6x_{31}^{UL}+4x_{32}^{UL}+3x_{33}^{UL}+2x_{34}^{UL}}\\{} & {} \text {subject to}\\{} & {} x_{11}^{LL}+x_{12}^{LL}+x_{13}^{LL}+x_{14}^{LL}= 7,~ x_{21}^{LL}+x_{22}^{LL}+x_{23}^{LL}+x_{24}^{LL}= 17,~ x_{31}^{LL}+x_{32}^{LL}+x_{33}^{LL}+x_{34}^{LL}= 16,\\{} & {} x_{11}^{LL}+x_{21}^{LL}+x_{31}^{LL}= 10,~ x_{12}^{LL}+x_{22}^{LL}+x_{32}^{LL}= 2,~ x_{13}^{LL}+x_{23}^{LL}+x_{33}^{LL}= 13,~ x_{14}^{LL}+x_{24}^{LL}+x_{34}^{LL}= 15,\\{} & {} x_{11}^{UL}+x_{12}^{UL}+x_{13}^{UL}+x_{14}^{UL}= 9,~ x_{21}^{UL}+x_{22}^{UL}+x_{23}^{UL}+x_{24}^{UL}= 21,~ x_{31}^{UL}+x_{32}^{UL}+x_{33}^{UL}+x_{34}^{UL}= 18,\\{} & {} x_{11}^{UL}+x_{21}^{UL}+x_{31}^{UL}= 12,~ x_{12}^{UL}+x_{22}^{UL}+x_{32}^{UL}= 4,~ x_{13}^{UL}+x_{23}^{UL}+x_{33}^{UL}= 15,~ x_{14}^{UL}+x_{24}^{UL}+x_{34}^{UL}= 17,\\{} & {} x_{lm}^{LL},~x_{lm}^{UL}\ge 0\hspace{.2cm}\forall \hspace{.2cm} l=1, 2, 3;\hspace{.2cm} m=1, 2, 3, 4 \end{aligned}$$

$(TP^{LU}):$

$$\begin{aligned}{} & {} \text {Max}~O_{1}^{LU}\\{} & {} \quad =\frac{9x_{11}^{LU}+13x_{12}^{LU}+6x_{13}^{LU}+10x_{14}^{LU}+7x_{21}^{LU}+9x_{22}^{LU}+10x_{23}^{LU}+6x_{24}^{LU}+7x_{31}^{LU}+4x_{32}^{LU}+12x_{33}^{LU}+7x_{34}^{LU}}{17x_{11}^{UU}+13x_{12}^{UU}+17x_{13}^{UU}+9x_{14}^{UU}+11x_{21}^{UU}+7x_{22}^{UU}+14x_{23}^{UU}+13x_{24}^{UU}+14x_{31}^{UU}+16x_{32}^{UU}+12x_{33}^{UU}+11x_{34}^{UU}}\\{} & {} \text {Max}~O_{2}^{LU}\\{} & {} \quad =\frac{2x_{11}^{LU}+3x_{12}^{LU}+2x_{13}^{LL}+0x_{14}^{LU}+x_{21}^{LU}+3x_{22}^{LU}+0x_{23}^{LU}+2x_{24}^{LU}+x_{31}^{LU}+0x_{32}^{LU}+2x_{33}^{LU}+2x_{34}^{LU}}{2x_{11}^{UU}+6x_{12}^{UU}+8x_{13}^{UU}+7x_{14}^{UU}+5x_{21}^{UU}+6x_{22}^{UU}+8x_{23}^{UU}+4x_{24}^{UU}+7x_{31}^{UU}+4x_{32}^{UU}+5x_{33}^{UU}+3x_{34}^{UU}}\\{} & {} \text {subject to}\\{} & {} x_{11}^{LU}+x_{12}^{LU}+x_{13}^{LU}+x_{14}^{LU}= 6,~ x_{21}^{LU}+x_{22}^{LU}+x_{23}^{LU}+x_{24}^{LU}= 16,~ x_{31}^{LU}+x_{32}^{LU}+x_{33}^{LU}+x_{34}^{LU}= 15,\\{} & {} x_{11}^{LU}+x_{21}^{LU}+x_{31}^{LU}= 9,~ x_{12}^{LU}+x_{22}^{LU}+x_{32}^{LU}= 1, x_{13}^{LU}+x_{23}^{LU}+x_{33}^{LU}= 12,~ x_{14}^{LU}+x_{24}^{LU}+x_{34}^{LU}= 15,\\{} & {} x_{11}^{UU}+x_{12}^{UU}+x_{13}^{UU}+x_{14}^{UU}= 10,~ x_{21}^{UU}+x_{22}^{UU}+x_{23}^{UU}+x_{24}^{UU}= 22,~ x_{31}^{UU}+x_{32}^{UU}+x_{33}^{UU}+x_{34}^{UU}= 19,\\{} & {} x_{11}^{UU}+x_{21}^{UU}+x_{31}^{UU}= 13,~ x_{12}^{UU}+x_{22}^{UU}+x_{32}^{UU}= 5, x_{13}^{UU}+x_{23}^{UU}+x_{33}^{UU}= 16,~ x_{14}^{UU}+x_{24}^{UU}+x_{34}^{UU}= 17,\\{} & {} x_{lm}^{LU},~x_{lm}^{UU}\ge 0\hspace{.2cm}\forall \hspace{.2cm} l=1, 2, 3;\hspace{.2cm} m=1, 2, 3, 4 \end{aligned}$$

7 Results and discussion

The models $(TP^{UU}),$ $(TP^{UL}),$ $(TP^{LL}),$ and $(TP^{LU})$ are completely deterministic in nature. By utilizing Step 4 to Step 9 of the proposed solution algorithm defined in Sect. 4, the Pareto-optimal solution of the case study is obtained at different weight sets by using LINGO 18.0 optimization solver, which is shown in Table 3.

Table 3 Pareto-optimal solution for different weight sets

The weights for the objective functions may be assigned by the decision-maker according to their priority or it may be computed using methods like AHP, TOPSIS, etc. In addition, the proposed methodology gives the fully rough solution to the given problem, i.e., the transported amount of product have also been obtained in terms of the rough intervals which is presented in Table 4 and shown graphically in Fig. 3. In this way, the models $(TP^{UU}),$ $(TP^{UL}),$ $(TP^{LL}),$ and $(TP^{LU})$ can help the decision-maker in determining the appropriate transported amount for the customers. Moreover, the best compromise solution is obtained by calculating the expected value of objective functions.

Table 4 Optimal transported amount for different weight sets

Fig. 3

Graphical representation of optimal transported amount for different weight sets

7.1 Discussion

The proposed method gives the rough interval optimal compromise solution of the FRMOFTP. A set of compromise solutions has been obtained by altering the weights with respect to the objective functions. The obtained results are in accordance with the trends, i.e., when more weightage is given to the first objective then ${\widetilde{O}}_{1}^{RI}$ gives a better solution, and lesser weightage to the second objective, decreases the value of ${\widetilde{O}}_{2}^{RI}.$

For instance, when maximum weightage is given to ${\widetilde{O}}_{1}^{RI},$ i.e., $w_{1}=1,$ $w_{2}=0,$ the solution obtained is ${\widetilde{O}}_{1}^{RI}=[0.7831, 1.6049][0.4705, 2.4084]$ with expected value 1.3167,  and ${\widetilde{O}}_{2}^{RI}=[0.2478, 1.1969]$ [0.1419, 2.3404] with expected value 0.9817. Similarly, $w_{1}=0$ and $w_{2}=1$ gives ${\widetilde{O}}_{1}^{RI}=[0.7687, 1.4987][0.4764, 2.3310]$ with expected value 1.2687,  and ${\widetilde{O}}_{2}^{RI}=[0.4021, 1.7768][0.2093, 3.8684]$ with expected value 1.5641. The solutions for different weight sets have been given in Table 4 and are graphically represented in Fig. 3. The decision-maker may choose a solution depending upon his/her weightage to the different objectives and as per his/her satisfaction. In the obtained rough interval solution, the lower interval represents the possible Pareto-optimal solution range and the upper interval represents the range of surely Pareto-optimal solution. Expected value has been used to get the practically working solution out of this range.

8 Conclusions and scope of the future research

The parameters of the real-life transportation problems may be uncertain in nature. Therefore, numerous researchers have studied transportation problems under various uncertain environments such as interval, stochastic, fuzzy, type-2 fuzzy environment, etc. But the rough set theory has higher practical implications than other theories since it takes into consideration the opinion of all involved experts (intersection) and respects their knowledge (union) by lower and upper approximation intervals, respectively In order to examine this benefit, an algorithm has been proposed in the present study to solve the fully rough multi-objective fractional transportation problems. The systematic procedure of the proposed approach operates by decomposing the problem into two sub-models: the upper interval model and the lower interval model. Then to solve these two sub-models, four crisp multi-objective fractional transportation problems are constructed which are then linearized by using the variable transformation method. Finally, using the weighted-sum method for different weight sets, the rough interval solution of the objective functions is obtained. The reformulation of the fractional transportation problem in terms of the rough set theory and extending the solution technique adds to the novelty of the proposed work. In contrast to existing approaches that provide crisp solutions to rough problems, the suggested algorithm obtains the solution in the same environment, which is a significant advantage. This algorithm, therefore, extends the scope of the obtained solutions and manages indeterminacy and imprecision in a better way. The practical visualization of the obtained solutions validates the proposed algorithm.

The extension of the fractional transportation problem in rough set theory exhibits a new insight for the transportation sector as the obtained results have practical meanings. The expected value helps the hesitant decision-maker to make better decisions towards choosing the compromise solution. In the future, interested investigators may extend the proposed approach for an unbalanced or non-linear fractional transportation problem. The investigation of the proposed approach for proving the scalability for higher dimensional problems will also be an interesting research direction.