Solving nonlinear systems of fractional-order partial differential equations using an optimization technique based on generalized polynomials

Abstract

This paper addresses the application of generalized polynomials for solving nonlinear systems of fractional-order partial differential equations with initial conditions. First, the solutions are expanded by means of generalized polynomials through an operational matrix. The unknown free coefficients and control parameters of the expansion with generalized polynomials are evaluated by means of an optimization process relating the nonlinear systems of fractional-order partial differential equations with the initial conditions. Then, the Lagrange multipliers are adopted for converting the problem into a system of algebraic equations. The convergence of the proposed method is analyzed. Several prototype problems show the applicability of the algorithm. The approximations obtained by other techniques are also tested confirming the high accuracy and computational efficiency of the proposed approach.

1 Introduction

Fractional calculus generalizes the differentiation and integration to non-integer orders (Podlubny 1999). In recent years, fractional differential equations attracted the attention of researchers in many branches of science such as mathematics, physics, engineering, and biosciences (Miller and Ross 1993; Hilfer 2000; Zhou et al. 2015; Hassani et al. 2019, 2020; Riewe 1997; Shekari et al. 2019; Rahimkhani and Ordokhani 2020; Zhao et al. 2019). The modeling of systems with differential equations has been an important research topic. Owolabi et al. (2018) studied the analytical and numerical solutions of a dynamical model comprising three species of systems using the fractional Fourier transform. Alliera and Amster (2018) used the topological degree theory and proved the existence of positive periodic solutions for a system of delay differential equations. Ablinger et al. (2019) developed an algorithm to solve analytically linear systems of differential equations that factorize to first order. Sabermahani et al. (2018) proposed a set of fractional functions based on the Lagrange polynomials to solve a class of fractional differential equations. Sabermahani et al. (2020a) introduced a formulation for fractional-order general Lagrange scaling functions and employed these functions for solving fractional differential equations. Sabermahani et al. (2020b) used hybrid functions of block-pulse and fractional-order Fibonacci polynomials for obtaining the approximate solution of fractional delay differential equations. Sabermahani et al. (2020c) presented a numerical technique based on two-dimensional Müntz–Legendre hybrid functions to solve fractional-order partial differential equations in the sense of the Caputo derivative. Several other studies on systems of differential equations can be found in Schittkowski (1997), Zhou and Casas (2014), Owolabi (2018), Feng et al. (2019), and Jaros and Kusano (2014).

Partial differential equations (PDE) are used to describe different types of phenomena in biosciences (Gupta et al. 2013; Shangerganesh et al. 2019). Recently, Kumar et al. (2018) addressed initial-value boundary problems in hyperbolic PDE in the cryosurgery of lung cancer. The bio-heat transfer during cryosurgery of lung cancer was studied using the Lagrange wavelet Galerkin method to convert the problem into generalized systems of Sylvester equations. Gupta et al. (2010) proposed a mathematical model for describing the process of heat transfer in biological tissues for different coordinate system during thermal therapy. Roohi et al. (2018) found the general form of the space–time-fractional heat conduction equation with locally variable initial condition and time-dependent boundary conditions. Ganesan and Lingeshwaran (2017) proposed a finite-element scheme using the Galerkin finite-element method for computations of the cancer invasion model. Avazzadeh and Hassani (2019) applied transcendental Bernstein series as base functions to solve reaction–diffusion equations with nonlocal boundary conditions. Ravi Kanth and Garg (2020) presented a combination of the Crank–Nicolson and exponential B-spline methods for solving a class of time-fractional reaction–diffusion equation. Yang et al. (2020) considered the Crank–Nicolson orthogonal spline collocation method for the approximate solution of the variable coefficient fractional mobile–immobile equation. Liu and Wang (2019) proposed a unified size-structured PDE model for the growth of metastatic tumors, which extends a well-known coupled PDE dynamical model. Farayola et al. (2020) presented a mathematical model of a radiotherapy cancer treatment process. The model was used to simulate the fractionated treatment process of six patients. Mohammadi and Dehghan (2020) used the meshless method to solve numerically models showing cancer cell invasion of tissue with/without considering the effect of cell–cell and cell–matrix adhesion.

In this study, we apply the generalized polynomials (GP) for solving the following nonlinear systems of fractional-order partial differential equations (NSF-PDE) (Zhao et al. 2017):

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} ^C_0{D_{x}^{\alpha }}u+u_{x}+f_{1}(u,v)=g_{1}(x,t), \\ ^C_0{D_{t}^{\beta }}v+v_{t}+f_{2}(u,v)=g_{2}(x,t), \end{array}\right. \quad (x,t)\in [0,1]\times [0,1],\quad 1<\alpha ,\beta \le 2, \end{aligned}$$

(1)

with the initial conditions:

$$\begin{aligned} u(0,t)=u(x,0)=v(0,t)=v(x,0)=0. \end{aligned}$$

(2)

Here, $^C_0{D_{t}^{\alpha }}$ and $^C_0{D_{t}^{\beta }}$ denote the fractional derivative of the Caputo-type orders with $1<\alpha ,\,\beta \le 2$, respectively.

We proposed an optimization process based on the GP and operational matrices of derivatives together with the help of the Lagrange multipliers method to approximate the solution of the NSF-PDE (1). The algorithm transforms the problem into a system of nonlinear algebraic equations with unknown coefficients, parameters and Lagrange multipliers. The method is illustrated by means of three examples and the numerical approximations compared with the analytical solutions.

The paper is organized as follows. Section 2 presents the fundamental aspects of the fractional calculus. Section 3 introduces the GP and their properties, including function approximation, convergence analysis, and the operational matrix of derivative. Section 4 develops an algorithm for the solution of Eq. (1). Section 5 analyzes three problems that illustrate the applicability and accuracy of the proposed method. Finally, Sect. 6 summarizes the conclusions.

2 Fundamental aspects

In this section, we give the definitions and mathematical concepts that are used in this paper.

Definition 1

(Dahaghin and Hassani 2017a, b; Farooq et al. 2019) A real function $u(t),~t>0$ is said to be in the space $C_{\rho },~\rho \in \mathbb {R}$ if there exists a real number $p>\rho$, such that $u(t)=t^{p}u_{1}(t)$, where $u_{1}(t)\in C[0,\infty )$, and it is said to be in the space $C_{\rho }^{n}$ if $u^{(n)}\in C_{\rho },~n\in \mathbb {N}$.

Definition 2

(Dahaghin and Hassani 2017a, b; Farooq et al. 2019) The fractional derivative of order $\alpha >0$, of the Caputo type, is defined as:

$$\begin{aligned} \left( ^C_0{D_{t}^{\alpha }}u\right) (t)=\left\{ \begin{array}{lll} \displaystyle \frac{1}{\varGamma (n-\alpha )}\int _{0}^{t}{(t-s)^{n-\alpha -1}u^{(n)}(s)\mathrm{{d}}s}, &{}&{} n-1<\alpha < n, \\ \displaystyle \frac{\mathrm{{d}}^{n}u(t)}{\mathrm{{d}}t^{n}}, &{}&{} \alpha =n\in \mathbb {N}, \\ \end{array}\right. \end{aligned}$$

(3)

where n is a natural number, $t>0$, and $u\in C_{1}^{n}$.

From the definitions of the fractional derivatives of the Caputo type, it is straightforward to conclude that:

$$\begin{aligned} ^C_0{D_{t}^{\alpha }}t^{m}= \displaystyle \left\{ \begin{array}{ll} \displaystyle \frac{\varGamma (m+1)}{\varGamma (m-\alpha +1)}\,t^{m-\alpha }, &{} n\le m \in \mathbb {N}, \\ 0, &{} \mathrm{{otherwise}}, \end{array} \right. \end{aligned}$$

(4)

where $n-1<\alpha \le n$.

3 Operational matrices and analysis of the proposed method

This section introduces the GP in the perspective of their application as a class of basis functions. Furthermore, the operational matrices of fractional derivatives of the GP in the Caputo type, function approximation, and the convergence analysis are also presented.

3.1 GP and operational matrices of GP

To solve the NSF-PDE, we introduce the GP class of basis functions. Let us define the GP of degree m as follows:

$$\begin{aligned} \psi _{i}(t)=\left\{ \begin{array}{lll} 1,&{}&{}i=0,\\ t^{i+k_{i}},&{}&{}i=1,2,\ldots , m, \end{array} \right. \end{aligned}$$

(5)

where the symbol $k_{i}$ denotes control parameters. The expansions of given functions u(x, t) and v(x, t) in terms of GP can be represented with the following matrices:

$$\begin{aligned} u(x,t)\simeq & {} \mathscr {D}_{m_{1}}(x)^{T}\,\mathscr {A}\,\mathscr {F}_{m_{2}}(t), \end{aligned}$$

(6)

$$\begin{aligned} v(x,t)\simeq & {} \mathscr {H}_{n_{1}}(x)^{T}\,\mathscr {B}\,\mathscr {Z}_{n_{2}}(t), \end{aligned}$$

(7)

where $\mathscr {A}=[a_{ij}]$ and $\mathscr {B}=[b_{ij}]$ are $(m_{1}+1)\times (m_{2}+1)$ and $(n_{1}+1)\times (n_{2}+1)$ unknown matrices of free coefficients, respectively, which must be computed, and $\mathscr {D}_{m_{1}}(x)$, $\mathscr {F}_{m_{2}}(t)$, $\mathscr {H}_{n_{1}}(x)$, and $\mathscr {Z}_{n_{2}}(t)$ are vectors defined as:

$$\begin{aligned}&\mathscr {D}_{m_{1}}(x)= [d_{0}(x)\,\,\,d_{1}(x)\,\ldots \,d_{m_{1}}(x)]^{T},\quad \mathscr {F}_{m_{2}}(t)= [f_{0}(t)\,\,\,f_{1}(t)\,\ldots \,f_{m_{2}}(t)]^{T},\nonumber \\&\mathscr {H}_{n_{1}}(x)=[h_{0}(x)\,\,\,h_{1}(x)\,\ldots \,h_{n_{1}}(x)]^{T},\quad \mathscr {Z}_{n_{2}}(t)=[z_{0}(t)\,\,\,z_{1}(t)\,\ldots \,z_{n_{2}}(t)]^{T},\nonumber \\&\mathscr {A}= \begin{pmatrix} a_{00}&{} a_{01}&{}\cdots &{} a_{0m_{2}}\\ a_{10}&{} a_{11}&{}\cdots &{} a_{1m_{2}} \\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ a_{m_{1}0} &{} a_{m_{1}1}&{}\cdots &{} a_{m_{1}m_{2}} \\ \end{pmatrix},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathscr {B}= \begin{pmatrix} b_{00}&{} b_{01}&{}\cdots &{} b_{0n_{2}}\\ b_{10}&{} b_{11}&{}\cdots &{} b_{1n_{2}} \\ \vdots &{} \vdots &{}\ddots &{} \vdots \\ b_{n_{1}0} &{} b_{n_{1}1}&{}\cdots &{} b_{n_{1}n_{2}} \\ \end{pmatrix}, \end{aligned}$$

(8)

$$\begin{aligned}&d_{i}(x)=\left\{ \begin{array}{lll} x^{i},&{}&{}i=0,1, \\ x^{i+k_{i}},&{}&{}i=2,3,\ldots ,m_{1}, \end{array} \right. \quad f_{j}(t)=\left\{ \begin{array}{lll} t^{j},&{}&{}j=0,1,\\ t^{j+s_{j}},&{}&{}j=2,3,\ldots ,m_{2}, \end{array} \right. \end{aligned}$$

(9)

$$\begin{aligned}&h_{i}(x)=\left\{ \begin{array}{lll} x^{i},&{}&{}i=0,1,\\ x^{i+r_{i}},&{}&{}i=2,3,\ldots , n_{1}, \end{array} \right. \quad z_{j}(t)=\left\{ \begin{array}{lll} t^{j},&{}&{}j=0,1,\\ t^{j+l_{j}},&{}&{}j=2,3,\ldots , n_{2}, \end{array} \right. \end{aligned}$$

(10)

where $k_{i}$, $s_{j}$, $r_{i}$, and $l_{j}$ are control parameters.

The fractional derivatives of orders $\,1<\alpha ,\,\beta \le 2\,$ of $\,\mathscr {D}_{m_{1}}(x)\,$ and $\,\mathscr {Z}_{n_{2}}(t)\,$ can be written as:

$$\begin{aligned} ^C_0{D_{x}^{\alpha }}\mathscr {D}_{m_{1}}(x)=\mathcal {D}^{(\alpha )}_{x}\mathscr {D}_{m_{1}}(x), \quad ^C_0{D_{t}^{\beta }}\mathscr {Z}_{n_{2}}(t)=\mathcal {D}^{(\beta )}_{t}\mathscr {Z}_{n_{2}}(t), \end{aligned}$$

(11)

where $\,\mathcal {D}^{(\alpha )}_{x}\,$ and $\,\mathcal {D}^{(\beta )}_{t}\,$ denote the $\,(m_{1}+1)\times (m_{1}+1)\,$ and $\,(n_{2}+1)\times (n_{2}+1)\,$ operational matrices of fractional derivatives, respectively, which are defined by:

$$\begin{aligned} \mathcal {D}^{(\alpha )}_{x}=x^{-\alpha } \begin{pmatrix} 0 &{} 0&{}0&{}0&{}\cdots &{} 0\\ 0 &{} 0&{}0&{}0&{}\cdots &{} 0 \\ 0 &{} 0&{}\frac{\varGamma \left( 3+k_{2}\right) }{\varGamma \left( 3-\alpha +k_{2}\right) }&{}0&{}\cdots &{} 0 \\ 0 &{} 0&{}0&{}\frac{\varGamma \left( 4+k_{3}\right) }{\varGamma \left( 4-\alpha +k_{3}\right) }&{}\cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{}\vdots &{}\ddots &{} \vdots \\ 0 &{} 0&{}0&{}0&{}\cdots &{} \frac{\varGamma \left( m_{1}+1+k_{m_{1}}\right) }{\varGamma \left( m_{1}+1-\alpha +k_{m_{1}}\right) } \\ \end{pmatrix}, \end{aligned}$$

(12)

$$\begin{aligned} \mathcal {D}^{(\beta )}_{t}=t^{-\beta } \begin{pmatrix} 0 &{} 0&{}0&{}0&{}\cdots &{} 0\\ 0 &{} 0&{}0&{}0&{}\cdots &{} 0 \\ 0 &{} 0&{}\frac{\varGamma \left( 3+l_{2}\right) }{\varGamma \left( 3-\beta +l_{2}\right) }&{}0&{}\cdots &{} 0 \\ 0 &{} 0&{}0&{}\frac{\varGamma \left( 4+l_{3}\right) }{\varGamma \left( 4-\beta +l_{3}\right) }&{}\cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{}\vdots &{}\ddots &{} \vdots \\ 0 &{} 0&{}0&{}0&{}\cdots &{} \frac{\varGamma \left( n_{2}+1+l_{n_{2}}\right) }{\varGamma \left( n_{2}+1-\beta +l_{n_{2}}\right) } \\ \end{pmatrix}. \end{aligned}$$

(13)

The first-order derivatives of $\,\mathscr {D}_{m_{1}}(x)\,$ and $\,\mathscr {Z}_{n_{2}}(t)\,$ are given by:

$$\begin{aligned} \frac{\mathrm{{d}}\mathscr {D}_{m_{1}}(x)}{\mathrm{{d}}x}=\mathcal {D}^{(1)}_{x}\,\mathscr {D}_{m_{1}}(x),\quad \frac{\mathrm{{d}}\mathscr {Z}_{n_{2}}(t)}{\mathrm{{d}}t}=\mathcal {D}^{(1)}_{t}\,\mathscr {Z}_{n_{2}}(t), \end{aligned}$$

(14)

where $\mathcal {D}^{(1)}_{x}$ and $\mathcal {D}^{(1)}_{t}$ denote the following $\,(m_{1}+1)\times (m_{1}+1)\,$ and $\,(n_{2}+1)\times (n_{2}+1)\,$ operational matrix of derivatives:

$$\begin{aligned} \mathcal {D}^{(1)}_{x}= \begin{pmatrix} 0 &{} 0&{}0&{}\cdots &{} 0\\ 0 &{} \frac{1}{x}&{}0&{}\cdots &{} 0 \\ 0 &{} 0&{}\frac{2+k_{2}}{x}&{}\cdots &{} 0 \\ \vdots &{} \vdots &{}\vdots &{} \ddots &{} \vdots \\ 0 &{} 0&{}0&{}\cdots &{} \frac{m_{1}+k_{m_{1}}}{x} \\ \end{pmatrix},\,\,\,\,\,\,\,\,\,\,\,\mathcal {D}^{(1)}_{t}= \begin{pmatrix} 0 &{} 0&{}0&{}\cdots &{} 0\\ 0 &{} \frac{1}{t}&{}0&{}\cdots &{} 0 \\ 0 &{} 0&{}\frac{2+l_{2}}{t}&{}\cdots &{} 0 \\ \vdots &{} \vdots &{}\vdots &{} \ddots &{} \vdots \\ 0 &{} 0&{}0&{}\cdots &{} \frac{n_{2}+l_{n_{2}}}{t} \\ \end{pmatrix}. \end{aligned}$$

(15)

3.2 Function approximation

Let $X=L^{2}[0,1]\times [0,1]$ and $Y=\left\langle x^{\beta _{i}}t^{\gamma _{j}};\,\ 0\le i\le m_{1},\,\ 0\le j\le m_2\right\rangle$. Then, Y is a finite-dimensional vector subspace of $X\,\left( \mathrm{{dim}} Y \le (m_1+1)(m_2+1)<\infty \right)$ and each $\tilde{v}=\tilde{v}(x,t)\in X$ has a unique best approximation $v_0=v_0(x,t)\in Y$, so that:

$$\begin{aligned} \forall ~\hat{v}\in Y,~~~\parallel \tilde{v}-v_{0}\parallel _2\le \parallel \tilde{v}-\hat{v}\parallel _2. \end{aligned}$$

For more details, see Theorem 6.1-1 of Kreyszig (1978). Since $v_0\in Y$ and Y is a finite-dimensional vector subspace of X, by an elementary argument in linear algebra, there exist unique coefficients $b_{ij} \in \mathbb {R}$, such that the dependent variable $v_0(x,t)$ may be expanded in terms of the GP as:

$$\begin{aligned} v_0(x,t)=\sum _{i=0}^{n_{1}}\sum _{j=0}^{n_{2}}b_{ij}x^{r_{i}}t^{l_{j}}=\mathscr {H}_{n_{1}}(x)^{T}\,\mathscr {B}\,\mathscr {Z}_{n_{2}}(t), \quad r_{i}\ge 0,\,\,l_{j}\ge 0, \end{aligned}$$

where $\mathscr {H}_{n_{1}}(x)$ and $\mathscr {Z}_{n_{2}}(t)$ are defined in Eq. (8).

3.3 Convergence analysis

In the following, we present a theorem that insures the existence of a GP for approximating an arbitrarily continuous function.

Theorem 1

Let $f:[0,1]\times [0,1]\rightarrow \mathbb {R}$ be a continuous function. Then, for every $x,t\in [0,1]$ and $\epsilon >0$, there exists a generalized polynomial $\mathcal{{Q}}_{m_1,m_2}(x,t)$, such that:

$$\begin{aligned} |f(x,t)-\mathcal{{Q}}_{m_1,m_2}(x,t)|<\epsilon . \end{aligned}$$

Proof

Let $\epsilon >0$ be arbitrarily chosen. In view of Weierstrass theorem (Kreyszig 1978), there exists a polynomial $P_{m_1,m_2}(x,t)=\sum ^{m_1}_{i=0}\sum ^{m_2}_{j=0}a_{i,j}x^it^j$, $x,t\in [0,1]$ and $a_{i,j}\in \mathbb {R}$, such that:

$$\begin{aligned} \Vert f-P_{m_1,m_2}\Vert =\sup _{x,t\in [0,1]}|f(x,t)-P_{m_1,m_2}(x,t)|<\frac{\epsilon }{2}. \end{aligned}$$

We construct a GP, $\mathcal{{Q}}_{m_1,m_2}(x,t)$, as follows:

We first notice that for the case of $x=0$ and $t=0$, by setting $k_0=0$, $s_0=0$ and $\mathcal{{Q}}_{m_1,m_2}(x,t)=a_{0,0}$, the conclusion follows immediately. Now, we proceed to the case of $x,t\in (0,1]$. We consider two sequences $\{k_{i,n}\}_{n\in \mathbb {N}}$ and $\{s_{j,n}\}_{n\in \mathbb {N}}$ of real numbers, such that $k_{i,n}\rightarrow 0$ as $n\rightarrow \infty$, and $s_{j,n}\rightarrow 0$ as $n\rightarrow \infty$, for all $i=0,1,2,\ldots ,m_1$ and $j=0,1,2,\ldots ,m_2$. This ensures that $x^{k_{i,n}}\rightarrow 1$ as $n\rightarrow \infty$, and that $t^{s_{j,n}}\rightarrow 1$ as $n\rightarrow \infty$, for $i=0,1,2,\ldots ,m_1$ and $j=0,1,2,\ldots ,m_2$. Hence, for every $\epsilon >0$, there exist the values $N_0,N_1,\ldots ,N_{m_1}$ and $Z_0,Z_1,\ldots ,Z_{m_2}$ in $\mathbb {N}$, such that:

$$\begin{aligned} |1-x^{k_{i,n}}t^{s_{j,n}}|<\frac{\epsilon }{2\max \{|a_{i,j}|:i=0,1,2,\ldots ,m_1, ~j=0,1,2,\ldots ,m_2\}(m_1+1)(m_2+1)}, \end{aligned}$$

for all $i=0,1,2,\ldots ,m_1$ and $j=0,1,2,\ldots ,m_2$. Setting $N=\max \{N_0,N_1,\ldots ,N_{m_1},Z_0,Z_1,\ldots ,Z_{m_2}\}$ and:

$$\begin{aligned} P_{m_1,m_2}(x,t)=\sum ^{m_1}_{i=0}\sum ^{m_2}_{i=0,j=0}a_{i,j}x^{i+{k}_{i,N}}t^{j+{s}_{j,N}}, \end{aligned}$$

we conclude that:

$$\begin{aligned} |P_{m_1,m_2}(x,t)-\mathcal{{Q}}_{m_1,m_2}(x,t)|<\frac{\epsilon }{2}. \end{aligned}$$

This implies that:

$$\begin{aligned} |f(x,t)-\mathcal{{Q}}_{m_1,m_2}(x,t)|&\le |f(x,t)-P_{m_1,m_2}(x,t)|+|P_{m_1,m_2}(x,t)-\mathcal{{Q}}_{m_1,m_2}(x,t)|\nonumber \\&<\frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon . \end{aligned}$$

(16)

This completes the proof. $\square$

3.4 Error analysis

We investigate the error analysis of the system fractional PDEs. Let $C(\varGamma ,\Vert \cdot \Vert )$ denote the Banach space of all continuous functions defined $\varOmega =[0,1]\times [0,1]$ with the norm:

$$\begin{aligned} \Vert u\Vert =\max _{(z,s)\in \varOmega }|u(z,s)|. \end{aligned}$$

We first assume that u(x, t) and v(x, t), and $u^*(x,t)$ and $v^*(x,t)$ are the exact and approximate solutions of the system, respectively. Let the nonlinear terms $f_1$ and $f_2$ be defined in Lipschitz condition, such that:

$$\begin{aligned} \left\{ \begin{array}{ll}|f_1(u,v)-f_1(u^*,v^*)|\le L_1|u-u^*|+L_2|v-v^*|,\\ |f_2(u,v)-f_2(u^*,v^*)|\le M_1|u-u^*|+M_2|v-v^*|. \end{array}\right. \end{aligned}$$

(17)

We assume that $f_1$ and $f_2$ are continuous functions with variables u, v and $u^*$, $v^*$, respectively.

Let $e_1(x,t)=\Vert u(x,t)-u^*(x,t)\Vert$ and $e_2(x,t)=\Vert v(x,t)-v^*(x,t)\Vert$ be the error functions of the system. Then, we consider:

$$\begin{aligned} e_1(x,t)= & {} \Vert u(x,t)-u^*(x,t)\Vert \nonumber \\= & {} \max _{(z,s)\in \varOmega }|I^{\alpha }\{f_1(u(z,s),v(x,t))-f_1(u^*(z,s),v^*(z,s))\}|\nonumber \\\le & {} \frac{1}{\varGamma (1+\alpha )} \max _{(z,s)\in \varOmega }|f_1(u(z,s),v(z,s))-f_1(u^*(z,s),v^*(z,s))|\nonumber \\\le & {} \frac{L_1}{\varGamma (1+\alpha )} \Vert u-u^*\Vert +\frac{L_2}{\varGamma (1+\alpha )} \Vert v-v^*\Vert \end{aligned}$$

(18)

and

$$\begin{aligned} e_2(x,t)= & {} \Vert v(x,t)-v^*(x,t)\Vert \nonumber \\= & {} \max _{(z,s)\in \varOmega }|I^{\beta }\{f_1(u(z,s),v(z,s))-f_1(u^*(z,s),v^*(z,s))\}|\nonumber \\\le & {} \frac{1}{\varGamma (1+\beta )} \max _{(z,s)\in \varOmega }|f_1(u(z,s),v(z,s))-f_1(u^*(z,s),v^*(z,s))|\nonumber \\\le & {} \frac{M_1}{\varGamma (1+\beta )} \Vert u-u^*\Vert +\frac{M_2}{\varGamma (1+\beta )} \Vert v-v^*\Vert , \end{aligned}$$

(19)

where

$$\begin{aligned} (I^{\alpha }f)(t)=\left\{ \begin{array}{ll}\frac{1}{\varGamma (\alpha )}\int ^t_{0}(t-s)^{\alpha -1}f(s)\mathrm{{d}}s, \quad \alpha >0;\\ f(t),\quad \alpha =0. \end{array}\right. \end{aligned}$$

If we transform Eq. (19), then we obtain from $0<\frac{M_2}{\varGamma (1+\beta )}<1$ that:

$$\begin{aligned} e_2(x,t)\le \left\{ \frac{M_1}{\varGamma (1+\beta )}\left( 1-\frac{M_2}{\varGamma (1+\beta )}\right) ^{-1} \right\} e_1(x,t). \end{aligned}$$

(20)

Substituting Eq. (20) into Eq. (18), we are led to:

$$\begin{aligned} e_2(x,t)\le & {} \frac{L_1}{\varGamma (1+\alpha )}e_1(x,t)\nonumber \\&+\frac{L_2}{\varGamma (1+\alpha )}\left[ \frac{M_1}{\varGamma (1+\beta )}\left( 1-\frac{M_2}{\varGamma (1+\beta )}\right) ^{-1} \right] e_1(x,t). \end{aligned}$$

(21)

Setting $\eta _1=\frac{L_1}{\varGamma (1+\alpha )}+\frac{L_2}{\varGamma (1+\alpha )}\left[ \frac{M_1}{\varGamma (1+\beta )}\left( 1-\frac{M_2}{\varGamma (1+\beta )}\right) ^{-1} \right]$, from (21), we conclude that:

$$\begin{aligned} (1-\eta _1)e_1(x,t)\le 0. \end{aligned}$$

(22)

Similarly, from Eq. (18) and $0<\frac{L_1}{\varGamma (1+\alpha )}<1$, it yields:

$$\begin{aligned} e_1(x,t)\le \left\{ \frac{L_2}{\varGamma (1+\alpha )}\left( 1-\frac{L_1}{\varGamma (1+\alpha )}\right) ^{-1} \right\} e_2(x,t). \end{aligned}$$

(23)

Substituting Eq. (23) into Eq. (19), we obtain:

$$\begin{aligned} e_1(x,t)\le & {} \frac{M_1}{\varGamma (1+\beta )}\left[ \frac{L_2}{\varGamma (1+\alpha )}\left( 1-\frac{L_1}{\varGamma (1+\alpha )}\right) ^{-1} \right] e_1(x,t)\nonumber \\&+\frac{M_2}{\varGamma (1+\beta )}e_1(x,t). \end{aligned}$$

(24)

Setting $\eta _2=\frac{M_1}{\varGamma (1+\beta )}\left[ \frac{L_2}{\varGamma (1+\alpha )}\left( 1-\frac{L_1}{\varGamma (1+\alpha )}\right) ^{-1} \right] +\frac{M_2}{\varGamma (1+\beta )}$, from (24), we conclude that:

$$\begin{aligned} (1-\eta _2)e_2(x,t)\le 0. \end{aligned}$$

(25)

Finally, letting $m_1\rightarrow \infty$ and $m_2\rightarrow \infty$ in relation (6), and taking into account (22) and (25), we deduce that $e_1(x,t)\rightarrow 0$ and $e_2(x,t)\rightarrow 0$. This completes the proof.

4 Description of the method

In the follow-up, and using the results obtained in the previous sections, we explain the procedure of the new method for solving Eq. (1) with:

$$\begin{aligned} u(0,t)=u(x,0)=v(0,t)=v(x,0)=0. \end{aligned}$$

(26)

To reduce the problem to a simpler one, we approximate the solutions using the GP as:

$$\begin{aligned} u(x,t)\simeq \mathscr {D}_{m_{1}}(x)^{T}\,\mathscr {A}\,\mathscr {F}_{m_{2}}(t), \end{aligned}$$

(27)

$$\begin{aligned} v(x,t)\simeq \mathscr {H}_{n_{1}}(x)^{T}\,\mathscr {B}\, \mathscr {Z}_{n_{2}}(t), \end{aligned}$$

(28)

where $\mathscr {A}=[a_{ij}]$ and $\mathscr {B}=[b_{ij}]$ are undetermined matrices, and $\mathscr {D}_{m_{1}}(x)$, $\mathscr {F}_{m_{2}}(t)$, $\mathscr {H}_{n_{1}}(x)$, and $\mathscr {Z}_{n_{2}}(t)$ are in accordance with Eq. (8). From Eqs. (11) and (14), we can write:

$$\begin{aligned}&^C_0{D_{x}^{\alpha }}u(x,t)\simeq \left( \mathcal {D}^{(\alpha )}_{x}\mathscr {D}_{m_{1}}(x)\right) ^{T}\,\mathscr {A}\,\mathscr {F}_{m_{2}}(t),\nonumber \\&^C_0{D_{t}^{\beta }}v(x,t)\simeq \mathscr {H}_{n_{1}}(x)^{T}\,\mathscr {B}\, \mathcal {D}^{(\beta )}_{t}\mathscr {Z}_{n_{2}}(t),\nonumber \\&u_{x}(x,t)\simeq \left( \mathcal {D}^{(1)}_{x}\,\mathscr {D}_{m_{1}}(x)\right) ^{T}\,\mathscr {A}\,\mathscr {F}_{m_{2}}(t), \nonumber \\&v_{t}(x,t)\simeq \mathscr {H}_{n_{1}}(x)^{T}\,\mathscr {B}\, \mathcal {D}^{(1)}_{t}\,\mathscr {Z}_{n_{2}}(t). \end{aligned}$$

(29)

Replacing Eqs. (27) and (28) into Eq. (26) yields:

$$\begin{aligned}&\varLambda _{1}(t)\triangleq \mathscr {D}_{m_{1}}(0)^{T}\,\mathscr {A}\,\mathscr {F}_{m_{2}}(t),\nonumber \\&\varLambda _{2}(x)\triangleq \mathscr {D}_{m_{1}}(x)^{T}\,\mathscr {A}\,\mathscr {F}_{m_{2}}(0),\nonumber \\&\varLambda _{3}(t)\triangleq \mathscr {H}_{n_{1}}(0)^{T}\,\mathscr {B}\, \mathscr {Z}_{n_{2}}(t), \nonumber \\&\varLambda _{4}(x)\triangleq \mathscr {H}_{n_{1}}(x)^{T}\,\mathscr {B}\, \mathscr {Z}_{n_{2}}(0). \end{aligned}$$

(30)

Substituting Eqs. (27)–(29) into Eq. (1), we get:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} \displaystyle \mathscr {D}_{m_{1}}(x)^{T}\left( \mathcal {D}^{(\alpha )}_{x}+\mathcal {D}^{(1)}_{x}\right) ^{T}\,\mathscr {A}\,\mathscr {F}_{m_{2}}(t)+f_{1}(u,v)-g_{1}(x,t)\triangleq \mathcal {R}_{1}(x,t)\\ \displaystyle \mathscr {H}_{n_{1}}(x)^{T}\,\mathscr {B}\left( \mathcal {D}^{(\beta )}_{t}+\mathcal {D}^{(1)}_{t}\right) \mathscr {Z}_{n_{2}}(t)+f_{2}(u,v)-g_{2}(x,t)\triangleq \mathcal {R}_{2}(x,t) \end{array}\right. \end{aligned}$$

(31)

and the 2-norm of the residual functions can be expressed as:

$$\begin{aligned} \mathcal {M}(\mathscr {A},\mathscr {B},\mathscr {K},\mathscr {S},\mathscr {R},\mathscr {L})=\int _{0}^{1}\int _{0}^{1}\left( \mathcal {R}_{1}^{2}(x,t)+\mathcal {R}_{2}^{2}(x,t)\right) \mathrm{{d}}x\mathrm{{d}}t. \end{aligned}$$

(32)

Here, $\mathscr {K},\mathscr {S},\mathscr {R}$, and $\mathscr {L}$ represent unknown control vectors for $\mathscr {D}_{m_{1}}(x)$, $\mathscr {F}_{m_{2}}(t)$, $\mathscr {H}_{n_{1}}(x)$, and $\mathscr {Z}_{n_{2}}(t)$, respectively, and may be defined as follows:

$$\begin{aligned}&\mathscr {K}=\left[ k_{2}\,\ k_{3}\,\ldots \,k_{m_{1}}\right] ,~~~\mathscr {S}=\left[ s_{2}\,\ s_{3}\,\ldots \,s_{m_{2}}\right] , \nonumber \\&\mathscr {R}=\left[ r_{2}\,\ r_{3}\,\ldots \, r_{n_{1}}\right] ,~~~~~~\mathscr {L}=\left[ l_{2}\,\ l_{3}\,\ldots \,l_{n_{2}}\right] . \end{aligned}$$

(33)

Since we must evaluate the unknown matrices $\mathscr {A}$ and $\mathscr {B}$ and the control parameters $\mathscr {K},\mathscr {S},\mathscr {R}$ and $\mathscr {L}$, for finding the approximate solution, we consider an optimization problem:

$$\begin{aligned} \min \,\mathcal {M}(\mathscr {A},\mathscr {B},\mathscr {K},\mathscr {S},\mathscr {R},\mathscr {L}), \end{aligned}$$

(34)

subject to:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{lll} \displaystyle \varLambda _{1}\left( \frac{i-1}{m_{1}}\right) =0, &{}&{} i=1,2,\ldots ,m_{1}+1.\\ \displaystyle \varLambda _{2}\left( \frac{i}{m_{2}}\right) =0, &{}&{} i=1,2,\ldots ,m_{2}.\\ \displaystyle \varLambda _{3}\left( \frac{i-1}{n_{1}}\right) =0, &{}&{} i=1,2,\ldots ,n_{1}+1.\\ \displaystyle \varLambda _{4}\left( \frac{i}{n_{2}}\right) =0, &{}&{} i=1,2,\ldots ,n_{2}. \end{array}\right. \end{aligned}$$

(35)

We use the Lagrange multipliers method to solve the minimization problem:

$$\begin{aligned} \mathcal {J}^{*}[\mathscr {A},\mathscr {B},\mathscr {K},\mathscr {S},\mathscr {R},\mathscr {L};\mathscr {\lambda }]=\mathcal {M}(\mathscr {A},\mathscr {B},\mathscr {K},\mathscr {S},\mathscr {R},\mathscr {L})+\mathscr {\lambda } \varLambda , \end{aligned}$$

(36)

where the vector $\lambda$ represents the unknown Lagrange multipliers and $\varLambda$ is a known column vector whose entries are equality constraints expressed in Eq. (35). The necessary conditions for the extremum are given by the following system of nonlinear algebraic equations:

$$\begin{aligned} \begin{array}{lllllll} \displaystyle \frac{\partial \mathcal {J}^{*}}{\partial \mathscr {A}}=0,&\displaystyle \frac{\partial \mathcal {J}^{*}}{\partial \mathscr {B}}=0,&\displaystyle \frac{\partial \mathcal {J}^{*}}{\partial \mathscr {K}}=0,&\displaystyle \frac{\partial \mathcal {J}^{*}}{\partial \mathscr {S}}=0,&\displaystyle \frac{\partial \mathcal {J}^{*}}{\partial \mathscr {R}}=0,&\displaystyle \frac{\partial \mathcal {J}^{*}}{\partial \mathscr {L}}=0,&\displaystyle \frac{\partial \mathcal {J}^{*}}{\partial \lambda }=0. \end{array} \end{aligned}$$

(37)

We can solve the above system of nonlinear algebraic equations using software packages such as MAPLE or MATLAB. Finally, using the unknown free coefficients and control parameters, we can approximately determine the solutions of the problem using Eqs. (27) and (28), respectively. The algorithm is described briefly in the table.

5 Illustrative examples

In this section, we include three examples for different values of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$ to illustrate the applicability and computational efficiency of the proposed method. All numeric calculations are executed by means of MAPLE 17 via 15 decimal digits. The absolute error (AE) functions are obtained by applying the following formulae:

$$\begin{aligned} \left| e_{1}\left( x_{i},t_{i}\right) \right|= & {} \left| \mathscr {D}_{m_{1}}\left( x_{i}\right) ^{T}\,\mathscr {A}\,\mathscr {F}_{m_{2}}\left( t_{i}\right) -u\left( x_{i},t_{i}\right) \right| ,\quad (x_{i},t_{i})\in [0,1]\times [0,1],\\ \left| e_{2}\left( x_{i},t_{i}\right) \right|= & {} \left| \mathscr {H}_{n_{1}}\left( x_{i}\right) ^{T}\,\mathscr {B}\,\mathscr {Z}_{n_{2}}\left( t_{i}\right) -v\left( x_{i},t_{i}\right) \right| ,\quad (x_{i},t_{i})\in [0,1]\times [0,1]. \end{aligned}$$

Example 1

Consider the following NSF-PDE:

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle ^C_0{D_{x}^{1.3}}u(x,t)+u_{x}(x,t)+u(x,t)\,v(x,t)=\frac{\varGamma {\left( 5.6\right) }\,x^{4.6-\alpha }\,t^{3.5}}{\varGamma {\left( 5.6-\alpha \right) }}\\ \quad +4.6\left( x^{3.6}\,t^{3.5}\right) +\left( x^{4.6}\,t^{3.5}\right) \,\left( x^{3.9}\,t^{5.1}\right) , \\ \displaystyle ^C_0{D_{t}^{1.5}}v(x,t)+v_{t}(x,t)-u^{3}(x,t)-v^{3}(x,t)=\frac{\varGamma {\left( 6.1\right) }\,x^{3.9}\,t^{5.1-\beta }}{\varGamma {\left( 6.1-\beta \right) }}\\ \quad +5.1\left( x^{3.9}\,t^{4.1}\right) -\left( x^{4.6}\,t^{3.5}\right) ^{3}-\,\left( x^{3.9}\,t^{5.1}\right) ^{3}, \end{array}\right. \end{aligned}$$

(38)

with the following initial conditions:

$$\begin{aligned} u(0,t)=u(x,0)=v(0,t)=v(x,0)=0. \end{aligned}$$

The required information can be achieved via the analytic solutions $u(x,t)=x^{4.6}\,t^{3.5}$ and $v(x,t)=x^{3.9}\,t^{5.1}$. We implement the proposed scheme for finding the approximate solution when $m_{1}=m_{2}=n_{1}=n_{2}=2$. As described in the previous sections, the solution can be expanded as follows:

$$\begin{aligned} u(x,t)\simeq \mathscr {D}_{2}(x)^{T}\,\mathscr {A}\,\mathscr {F}_{2}(t),\quad v(x,t)\simeq \mathscr {H}_{2}(x)^{T}\,\mathscr {B}\, \mathscr {Z}_{2}(t), \end{aligned}$$

where

$$\begin{aligned}&\mathscr {D}_{2}(x)\triangleq [1\,\,\,\,\,\,x\,\,\,\,\,\,x^{2+k_{2}}]^{T},\quad \mathscr {F}_{2}(t)\triangleq [1\,\,\,\,\,\,t\,\,\,\,\,\,t^{2+s_{2}}]^{T},\\&\mathscr {H}_{2}(x)\triangleq [1\,\,\,\,\,\,x\,\,\,\,\,\,x^{2+r_{2}}]^{T},\quad \mathscr {Z}_{2}(t)\triangleq [1\,\,\,\,\,\,t\,\,\,\,\,\,t^{2+l_{2}}]^{T}, \end{aligned}$$

and $k_{2},\,s_{2},\,r_{2}$ and $l_{2}$ are control parameters. Moreover, the unknown coefficient matrices of $\mathscr {A}$ and $\mathscr {B}$ are given by:

$$\begin{aligned} \mathscr {A}= \begin{pmatrix} a_{00} &{} a_{01} &{} a_{02}\\ a_{10} &{} a_{11} &{} a_{12}\\ a_{20} &{} a_{21} &{} a_{22}\\ \end{pmatrix},\quad \mathscr {B}= \begin{pmatrix} b_{00} &{} b_{01} &{} b_{02}\\ b_{10} &{} b_{11} &{} b_{12}\\ b_{20} &{} b_{21} &{} b_{22}\\ \end{pmatrix}. \end{aligned}$$

The control parameters and free coefficients with $m_{1}=m_{2}=n_{1}=n_{2}=2$ are obtained as follows:

$$\begin{aligned}&k_{2}=2.5999,~~s_{2}=1.4999,~~r_{2}=1.9000,~~l_{2}=3.0999,~~a_{00}=0,~~a_{01}=0,\\&a_{02}=0,~~a_{10}=0,~~a_{11}=0,~~a_{12}=0,~~a_{20}=0,~~a_{21}=0,~~a_{22}=1,~~b_{00}=0,\\&b_{01}=0,~~b_{02}=0,~~b_{10}=0,~~b_{11}=0,~~b_{12}=0,~~b_{20}=0,~~b_{21}=0,~~~b_{22}=1. \end{aligned}$$

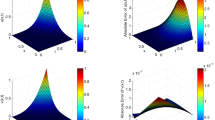
This problem is also solved by the GP method with $m_{1}=3,\,m_{2}=2,\,n_{1}=3$ and $n_{2}=2$. The AE values of the GP method at various points are listed in Table 1. The runtime of the proposed method with different choices of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$ are reported in Table 2. The GP solutions and AE functions are represented in Fig. 1 for $m_{1}=m_{2}=n_{1}=n_{2}=2$. The approximate and exact solutions for different values of x and t are shown in Figs. 2 and 3. Table 1 and Figs. 1, 2, and 3 show the accurate numerical results. As can be seen, using more terms of the GP provides higher accuracy. Also, from Table 2, we conclude that if we choose large values of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$, then we have an higher computational load.

Table 1 The AE values using the GP method at various points in Example 1

Table 2 The runtime (in s) of the proposed method with different choices of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$ for Example 1

Fig. 1

Approximate solution (left) and absolute error function (right) for Example 1 with $m_{1}=m_{2}=n_{1}=n_{2}=2$

Fig. 2

The approximate and exact solutions for u(x, 0.4) (left side) and v(x, 0.4) (right side) with $m_{1}=m_{2}=n_{1}=n_{2}=2$ for Example 1

Fig. 3

The approximate and exact solutions for u(0.4, t) (left side) and v(0.4, t) (right side) with $m_{1}=m_{2}=n_{1}=n_{2}=2$ for Example 1

Example 2

Consider the following system of fractional PDE (Zhao et al. 2017):

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle ^C_0{D_{x}^{\frac{4}{3}}}u(x,t)+u_{x}(x,t)+u(x,t)+v(x,t)=\frac{3\,x^{\frac{2}{3}}\,t}{\varGamma {\left( \frac{2}{3}\right) }}\\ \quad +(2x-1)t+xt(x+t-2),\\ \displaystyle ^C_0{D_{t}^{\frac{3}{2}}}v(x,t)+v_{t}(x,t)+u(x,t)-v(x,t)=\frac{4\,\sqrt{t}\,x}{\sqrt{\pi }}+(2t-1)x\\ \quad +xt(x-t), \end{array}\right. \end{aligned}$$

(39)

with the following initial conditions:

$$\begin{aligned} u(0,t)=u(x,0)=v(0,t)=v(x,0)=0. \end{aligned}$$

The analytical solutions of this system are $u(x,t)=xt(x-1)$ and $v(x,t)=xt(t-1)$. This problem is solved by means of the GP method with $m_{1}=3,\,m_{2}=2,\,n_{1}=2,\,n_{2}=3$ and $m_{1}=m_{2}=n_{1}=n_{2}=3$. The obtained AE in different points of $(x, t)\in [0,1]\times [0,1]$ are listed in Table 3. The runtime of the proposed method with different choices of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$ is reported in Table 4. The approximate solutions and AE functions are depicted in Fig. 4 for $m_{1}=n_{2}=3,\,m_{2}=n_{1}=2$. The charts of the approximate and exact solutions for different values of x and t are depicted in Figs. 5 and 6. We verify that the new method is accurate in all cases and that using more terms of the GP improves the accuracy. Also, from Table 4, we conclude choosing larger values of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$, leads to an increasing computational load.

Zhao et al. (2017) introduced an efficient numerical technique based on the shifted Chebyshev orthogonal polynomials as basis functions for solving the system of fractional PDE (39). If we comparing Table 3 and Fig. 4 with the results obtained in Zhao et al. (2017), then we verify that we achieve a better accuracy.

Table 3 The AE values using the GP method at various points in Example 2

Table 4 The runtime (in s) of the proposed method with different choices of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$ for Example 2

Fig. 4

Approximate solution (left) and absolute error function (right) for Example 2 with $m_{1}=n_{2}=3,\,m_{2}=n_{1}=2$.

Fig. 5

The approximate and exact solutions for u(x, 0.6) (left side) and v(x, 0.6) (right side) with $m_{1}=n_{2}=3,\,m_{2}=n_{1}=2$ for Example 2

Fig. 6

The approximate and exact solutions for u(0.6, t) (left side) and v(0.6, t) (right side) with $m_{1}=n_{2}=3,\,m_{2}=n_{1}=2$ for Example 2

Table 5 The AE values for u(x, t) using the GP method at various points in Example 3

Table 6 The AE values for v(x, t) using the GP method at various points in Example 3

Table 7 The runtime (in s) of the proposed method with different choices of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$ for Example 3

Example 3

Consider the following system of fractional PDE (Zhao et al. 2017):

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle ^C_0{D_{x}^{\frac{3}{2}}}u(x,t)+u_{x}(x,t)+2v(x,t)-u(x,t)=\frac{4\,x^{\frac{3}{2}}\,\sinh (t)}{\sqrt{\pi }}\\ \quad +3x^{2}\sinh (t) +2t^{3}\sinh (x)-x^{3}\sinh (t),\\ \displaystyle ^C_0{D_{t}^{\frac{3}{2}}}v(x,t)+v_{t}(x,t)+v(x,t)+2u(x,t)=\frac{4\,t^{\frac{3}{2}}\,\sinh (x)}{\sqrt{\pi }}\\ \quad +3t^{2}\sinh (x) +2x^{3}\sinh (t)+t^{3}\sinh (x), \end{array}\right. \end{aligned}$$

(40)

with the following initial conditions:

$$\begin{aligned} u(0,t)=u(x,0)=v(0,t)=v(x,0)=0. \end{aligned}$$

The analytical solutions of the system are $u(x,t)=x^{3}\sinh (t)$ and $v(x,t)=t^{3}\sinh (x)$. This problem is also solved by the GP method with different values for $m_{1},\,m_{2},\,n_{1}$ and $n_{2}$. In Zhao et al. (2017), the shifted Chebyshev orthogonal polynomials, as basis functions, are applied to solve the system of fractional PDE (40). The AE of u(x, t) and v(x, t) by the GP method in different points $(x,t)\in [0,1]\times [0,1]$ are collected in Tables 5 and 6, respectively. We verify that they compare well with those reported previously in Zhao et al. (2017). The runtime of the proposed method with different choices of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$ are reported in Table 7. The approximate solutions and AE functions are shown in Fig. 7 for $m_{1}=m_{2}=n_{1}=n_{2}=5$. The approximate and exact solutions for different x and t are depicted in Figs. 8 and 9. From Tables 5 and 6, we conclude that GP method is suitable for this problem, and that by increasing the number of GP, the accuracy is improved. Also, from Table 7, we verify that if we choose larger values of $m_{1}$, $m_{2}$, $n_{1}$, and $n_{2}$, then result in an increasing computational load.

Fig. 7

Approximate solution (left) and absolute error function (right) for Example 3 with $m_{1}=m_{2}=n_{1}=n_{2}=5$

Fig. 8

The approximate and exact solutions for u(x, 0.8) (left side) and v(x, 0.8) (right side) with $m_{1}=m_{2}=n_{1}=n_{2}=5$ for Example 3

Fig. 9

The approximate and exact solutions for u(0.8, t) (left side) and v(0.8, t) (right side) with $m_{1}=m_{2}=n_{1}=n_{2}=5$ for Example 3

6 Conclusion

In this work, the GP and their operational matrices are applied to find a solution to the NSF-PDE. The generated operational matrices and the Lagrange multipliers method were employed to convert the NSF-PDE into a system of nonlinear algebraic equations to obtain an optimal selection of the free coefficients and control parameters. The convergence of the new method was discussed. Also, the method was illustrated by means of three numerical examples. Throughout the convergence analysis and numerical examples, it was verified that the algorithm is precise and efficient and that a small number of basis functions is sufficient to obtain a favorable approximate solution. A comparison between the results by the GP and other schemes confirms the accuracy of the proposed algorithm.