Numerical approach based on fractional-order Lagrange polynomials for solving a class of fractional differential equations

Abstract

In this study, we propose a new set of fractional functions based on the Lagrange polynomials to solve a class of fractional differential equations. Fractional differential equations are the best tools for modelling natural phenomenon that are elaborated by fractional calculus. Therefore, we need an accurate and efficient technique for solving them. The main purpose of this article is to generalize new functions based on Lagrange polynomials to the fractional calculus. At first, we present a new representation of Lagrange polynomials and in continue, we propose a new set of fractional-order functions which are called fractional-order Lagrange polynomials (FLPs). Besides, a general formulation for operational matrices of fractional integration and derivative of FLPs on arbitrary nodal points are extracted. These matrices are obtained using Laplace transform. The initial value problems is reduced to the system of algebraic equations using the operational matrix of fractional integration and collocation method. Also, we find the upper bound of error vector for the fractional integration operational matrix and we indicate convergence of approximations of FLPs. Illustrative examples are included to demonstrate the validity and applicability of the proposed technique.

1 Introduction

FDEs are generalizations of ordinary differential equations to an arbitrary order. A history of the development of fractional differential operators is given in Oldham and Spanier (1974) and Miller and Ross (1993). During the last few decades, fractional calculus has been widely used to describe many phenomena, such as hydrologic (Benson et al. 2013), dynamic viscoelasticity modeling (Larsson et al. 2015), economics (Baillie 1996), temperature and motor control (Bohannan 2008), continuum and statistical mechanics (Mainardi 1997), solid mechanics (Rossikhin and Shitikova 1997), bioengineering (Magin 2004), medicine (Hall and Barrick 2008), earthquake (He 1988) and electromagnetism (Engheta 1996). Although, exploring and studying on new analytical and numerical methods to solve various fractional differential equations has become a valuable topic. Many authors investigated on the existence and uniqueness of solutions to the fractional differential equations, such as Mainardi (1997) and Podlubny (1999).

In recent studies, several methods have been employed to solve fractional differential equations, such as Laplace transforms (Daftardar-Gejji and Jafari 2007), Homotopy analysis method (Dehghan et al. 2010), variational iteration method (Odibat and Momani 2006), finite difference method (Meerschaert and Tadjeran 2006), Legendre wavelets method (Jafari et al. 2011), Haar wavelet (Rehman and Khan 2012), Bernoulli polynomials method (Keshavarz et al. 2014), Fifth-kind orthonormal Chebyshev polynomial (Abd-Elhameed and Youssri 2017), and so on.

On the other hand, Lagrange interpolation is commendable for analytical tools. The Lagrange approximate is in most cases the method of choice for dealing with polynomial interpolation (Burden and Faires 2010). Lagrange interpolation is used to solve integral equations (Rashed 2004; Mustafa and Ghanim 2014; Shahsavaran 2011). Also, Shamsi and Razzaghi (2004), Foroozandeh and Shamsi (2012) solved a class of optimal control problems using the interpolating scaling functions.

Recently, Kazem et al. (2013), proposed the new orthogonal functions based on the Legendre polynomials to obtain a new method to solve FDEs. Bhrawy et al. (2014) defined the fractional-order generalized Laguerre functions based on the generalized Laguerre polynomials. Yuzbasi (2013) introduced fractional Bernstein polynomials for solving the fractional Riccati type differential equations. Moreover, Rahimkhani et al. (2016) proposed the new functions based on Bernoulli wavelet and Krishnasamy and Razzaghi (2016) solved Bagley–Torvik equation with fractional Taylor basis.

In the present paper, our aim is to introduce the fractional-order Lagrange polynomials, which are employed to produce operational matrices of fractional derivative and integration generally, using Laplace transform to solve numerically linear and nonlinear FDEs with initial conditions.

This paper is organized as follows. In the next section, we describe some necessary definitions and required mathematical preliminaries for our subsequent development. In Sect. 3, we introduce a new representation of Lagrange polynomials and fractional-order Lagrange polynomials. In Sect. 4, we achieve the FLPs operational matrices of fractional order integration and derivative using Laplace transform without considering point of interpolation. Section 5 is devoted to the numerical method for solving a class of the initial value differential equations of fractional order and a system of fractional differential equations. In Sect. 6, we prove convergence of approximations of fractional-order Lagrange polynomials and we find an upper bound for error of vector operational matrix of fractional integration. In Sect. 7, we demonstrate the accuracy and effectiveness of the present method by considering some numerical examples.

2 Preliminaries

In this section, we recall some basic definitions and properties of fractional calculus theory.

Definition 1

Let $f: [a, b] \rightarrow R$ be a function, $\nu > 0$ a real number and $n= \lceil \nu \rceil$, the Riemann–Liouville integral of fractional order is defined as (Mashayekhi and Razzaghi 2016)

$$\begin{aligned} I^{\nu }f(x) = \left\{ \begin{array}{ll} \frac{1}{\varGamma ( \nu )} \int _{0}^{x} (x-t)^{ \nu -1}f (t) \mathrm{d}t = \frac{1}{\varGamma (\nu )} x^{ \nu -1} * f(x) &{}\quad \nu >0,\\ f(x) &{} \quad \nu =0, \end{array}\right. \end{aligned}$$

(1)

where $x^{ \nu -1} * f(x)$ is the convolution product of $x^{\nu -1}$ and f(x) and $\lceil \nu \rceil$ denotes the smallest integer greater than or equal to $\alpha$.

Moreover, for the Riemann–Liouville fractional integrals, the following relationships are established (Mashayekhi and Razzaghi 2016)

$$\begin{aligned} I^{\nu } x^{n} = \frac{\varGamma (n+1)}{\varGamma (n+1+ \nu )} x^{\nu + n},\;\;\;n> -1, \end{aligned}$$

(2)

and

$$\begin{aligned} (D^{\nu } I^{\nu } f)(x)= & {} f(x), \end{aligned}$$

(3)

$$\begin{aligned} (I^{\nu }f)(x)= & {} f(x) - \sum _{i=0}^{\lceil \nu \rceil -1} f^{(i)}(0) \frac{x^{i}}{i!}. \end{aligned}$$

(4)

Definition 2

Fractional derivative of order $\nu$ in Caputo sense is defined as (Mashayekhi and Razzaghi 2016)

$$\begin{aligned} D^ \nu f(x) = \frac{1}{\varGamma (m- \nu )}\int _{0}^{x} \frac{f^{(m)}(t)}{(x-t)^{\nu -m+1}} \mathrm{d}t, \end{aligned}$$

(5)

for $m-1 < \nu \le m,\;m \in N$, $x > 0$. For the Caputo derivative, we have (Rahimkhani et al. 2016):

$$\begin{aligned} D^ \nu x^k= & {} \left\{ \begin{array}{ll} 0,&{}\nu \in N_{0},\; k < \nu ,\\ \frac{k!}{\varGamma (k- \nu +1)} x^{k- \nu }, &{} \textit{otherwise} \end{array}\right. \nonumber \\ D^ \nu \lambda= & {} 0, \end{aligned}$$

(6)

where $\lambda$ is constant.

and

$$\begin{aligned} D^{\nu } f(x) + \mu D^{\nu } y(x) \end{aligned}$$

where $\lambda$ and $\mu$ are constants.

Definition 3

(Generalized Taylors formula) Let $D^{k \alpha }f(x) \in C (0,1]$ for $k=0,1,\ldots ,n+1$. Then, we have (Odibat and Shawagfeh 2007)

$$\begin{aligned} f(x) = \sum _{k=0}^{n} \frac{x^{k \alpha }}{\varGamma (k \alpha +1)} D^{k \alpha }f(0^{+}) + \frac{x^{(n+1) \alpha }}{\varGamma ((n+1) \alpha +1)} D^{(n+1) \alpha }f (\xi ), \end{aligned}$$

(7)

with $0 < \xi \le x,\;\forall x \in (0, \;1]$. Moreover, one has (Kazem et al. 2013):

$$\begin{aligned} \vert f(x) - \sum _{k=0}^{n} \frac{x^{k \alpha }}{\varGamma (k \alpha +1)} D^{k \alpha }f(0^{+}) \vert \le M_{\alpha } \frac{x^{(n+1) \alpha }}{\varGamma ((n+1) \alpha +1)} , \end{aligned}$$

(8)

where $M_{\alpha } \ge \sup _{\xi \in (0,\;1]} \vert D^{(n+1) \alpha }f (\xi ) \vert$.

Definition 4

The Laplace transform of a function $u(x,\;t),\;t \ge 0$, is defined by (Javidi and Ahmad 2013)

$$\begin{aligned} L[u(x,\;t)]= \int _{0}^{\infty } e^{-\tau t}u(x,\;t) \,\mathrm{d}t, \end{aligned}$$

(9)

where $\tau$ is the transformed parameter and is assumed to be real and positive.

Also, the Laplace transform of $D^{\nu }f (t)$ can be found as follows:

$$\begin{aligned} L[D^{\nu }f(x)]= & {} L[I^{m- \nu }f^{(m)}(x)] \nonumber \\= & {} L \biggl [ \frac{1}{\varGamma (m- \nu )} \int _{0}^{x} (x- t)^{m- \nu -1} f^{(m)}(t) \mathrm{d} t \biggl ] \nonumber \\= & {} \frac{1}{r^{m- \nu }} L[f^{(m)}(x)] \nonumber \\= & {} \frac{1}{r^{m- \nu }} [ r^{m} L[f(x)]-r^{m-1}f(0)-r^{m-2}f^{'}(0)\nonumber \\&-r^{m-3}f^{''}(0)- \cdots -f^{(m-1)}(0)]. \end{aligned}$$

(10)

3 Fractional-order Lagrange polynomials

In this section, first, we recall the definition of Lagrange polynomials and we present a new representation of Lagrange polynomials. Then we propose the fractional-order Lagrange polynomials and their properties.

3.1 Lagrange polynomials

Lagrange polynomial based on these points can be defined as follows (Stoer and Bulirsch 1996):

$$\begin{aligned} L_{i}(x) := \prod _{\small {\begin{array}{c} j=0 \\ j \ne i \end{array}}}^{n} \frac{(x-x_{j})}{(x_{i} -x_{j})}. \end{aligned}$$

(11)

where, the set of nodes be given by $x_{i} \in [0, 1],\;i=0, 1, \ldots , n$.

Also, Lagrange polynomials satisfy this condition

$$\begin{aligned} L_{i}(x_{l}) = \delta _{il} = \left\{ \begin{array}{ll} 1, &{}\quad i=l, \\ 0, &{} \quad i \ne l\end{array}\right. \end{aligned}$$

(12)

3.1.1 A new representation of Lagrange polynomials

Lemma 1

Let $L_i(x),i=0, 1, \ldots , n$ are Lagrange polynomials on the set of nodes $x_i \in [0, 1]$. Lagrange polynomials in these points are described by

$$\begin{aligned} L_{i}(x)= & {} \frac{1}{\prod _{\tiny {\begin{array}{c} i=0 \\ j \ne i \end{array}}}^{n} (x_{i}-x_{j})} \left( x^{n} -\sum _{\tiny {\begin{array}{c} k_{1}=0 \\ i \ne k_{1} \end{array}}}^{n} x_{k_{1}} x^{n-1} + \sum _{\tiny {\begin{array}{c} k_{2}=k_{1}+1 \\ i \ne k_{1} \ne k_{2} \end{array}}}^{n} \sum _{k_{1}=0}^{n-1} x_{k_{1}}x_{k_{2}} x^{n-2} - \cdots \right. \nonumber \\&\left. + \, (-1)^{n} \sum _{\tiny {\begin{array}{c} k_{n} =k_{n-1}+1 \\ i \ne k_{n} \ne \ k_{n-1} \ne \cdots \ne k_{1} \end{array}}}^{n}\sum _{k_{n-1} = k_{n-2}+1}^{n-1} ... \sum _{k_{1} = 0}^{1}\; \small {\prod _{r=1}^{n}} x_{k_{r}} \right) \end{aligned}$$

(13)

Remark 1

Using Eq. (13), we can rewrite each of $L_{i}(x)$ as follows

$$\begin{aligned} L_{i}(x) = \sum _{s=0}^{n} \alpha _{is} x^{n-s},\;\;\;i=0,\;1,\;\ldots ,\;n. \end{aligned}$$

(14)

where

$$\begin{aligned} \alpha _{i0}= & {} \frac{1}{\prod _{\tiny {\begin{array}{c} i=0 \\ j \ne i \end{array}}}^{n}(x_{i}-x_{j})} \end{aligned}$$

(15)

$$\begin{aligned} \alpha _{is}= & {} \frac{(-1)^{s}}{\prod _{\tiny {\begin{array}{c} i=0 \\ j \ne i \end{array}}}^{n}(x_{i}-x_{j})} \sum _{k_{s}=k_{s-1}+1}^{n} \cdots \sum _{k_{1}=0}^{n-s+1} \prod _{r=1}^{s} x_{k_{r}}, \end{aligned}$$

(16)

and $s=1,\;2,\; \ldots ,\;n,\;\;\;i \ne k_{1} \ne \cdots \ne k_{s}$.

3.2 Fractional-order Lagrange polynomials

We define a new set of fractional functions called fractional-order Lagrange polynomials (FLPs). These polynomials constructed by changing of variable x to $x^{\alpha }$, $(0<\alpha \le 1)$, on the Lagrange polynomials, which are denoted by $L_{i}^{\alpha }(x)$.

Using Eq.  (14), the analytic form of $L_{i}^{\alpha }(x)$, given by:

$$\begin{aligned} L_{i}^{\alpha }(x) = \sum _{s=0}^{n} \alpha _{is} x^{\alpha (n-s)},\;\;i=0,\;1,\;2,\;\ldots ,\;n. \end{aligned}$$

(17)

where

$$\begin{aligned} \alpha _{i0}= & {} \frac{1}{\prod _{\tiny {\begin{array}{c} i=0 \\ j \ne i \end{array}}}^{n}(x_{i}-x_{j})} \end{aligned}$$

(18)

$$\begin{aligned} \alpha _{is}= & {} \frac{(-1)^{s}}{\prod _{\tiny {\begin{array}{c} i=0\\ j \ne i \end{array}}}^{n}(x_{i}-x_{j})} \sum _{k_{s}=k_{s-1}+1}^{n} \cdots \sum _{k_{1}=0}^{n-s+1} \prod _{r=1}^{s} x_{k_{r}}, \end{aligned}$$

(19)

and $s=1, 2, \ldots , n, i \ne k_{1} \ne \cdots \ne k_{s}$.

These fractional functions on arbitrary nodal points are obtained. Then, we can have different choices for Lagrange polynomials. For example, if we consider zeros of shifted Legendre polynomials as these points, we have a set of orthogonal polynomials.

The fractional-order Lagrange functions for $n=2$ and $x_{i} = \frac{i}{n}$ are as:

$$\begin{aligned} L_{0}^{\alpha }(x)= 1-3x^{\alpha }+2x^{2 \alpha },\;\;L_{1}^{\alpha }(x)=4x^{\alpha }-4x^{2 \alpha },\;\;L_{2}^{\alpha }(x)=-x^{\alpha }+2x^{2 \alpha }. \end{aligned}$$

Also, Fig. 1 represents the graphs of FLPs for $n=2$ and various values of $\alpha$.

Fig. 1

Graph of the FLPs with $n=2$ and a $\alpha =1$, b $\alpha =\frac{1}{2}$ and c $\alpha =\frac{1}{4}$

3.3 Function approximation

A function f which is defined over $[0,\;1]$ can be expanded in terms of fractional-order Lagrange polynomials as

$$\begin{aligned} f(x) \simeq \sum _{i=0}^{n} c_{i}L_{i}^{\alpha }(x) = C^{T}L^{\alpha }(x), \end{aligned}$$

(20)

where C and $L^{\alpha }(x)$ are $(n+1) \times 1$ vectors given by:

$$\begin{aligned} C = [c_0, c_1, \ldots , c_n]^{T},\quad L^{\alpha }(x) = [L_0^{\alpha }(x), L_1^{\alpha }(x), \ldots , L_n^{\alpha }(x)]^{T}. \end{aligned}$$

(21)

and T indicates transposition. We suppose that

$$\begin{aligned} f_{j} = \langle f, L_{j}^{\alpha } \rangle = \int _{0}^{1} f(x) L_{j}^{\alpha }(x)x^{\alpha -1} \mathrm{d}x, \end{aligned}$$

(22)

where $\langle , \rangle$ denotes inner product, so we have:

$$\begin{aligned} f_{j} \simeq \sum _{i=0}^{n} c_{i} \int _{0}^{1} L_{i}^{\alpha }(x)L_{j}^{\alpha }(x) x^{\alpha -1} \mathrm{d}x = \sum _{i=0}^{n} c_{i} d_{ij},\quad j=0, 1, \ldots , n, \end{aligned}$$

(23)

that

$$\begin{aligned} d_{ij}= \int _{0}^{1} L_{i}^{\alpha }(x) L_{j}^{\alpha }(x)x^{\alpha -1} \mathrm{d}x,\quad i, j=0, 1, \ldots , n. \end{aligned}$$

(24)

Now, we suppose that

$$\begin{aligned} F=[f_{0}, f_{1}, \ldots ,\;f_{n}]^{T}, D= [d_{ij}], \end{aligned}$$

we get

$$\begin{aligned} F^{T} = C^{T} D, \end{aligned}$$

(25)

then

$$\begin{aligned} C= D^{-1} \langle f, L^{\alpha } \rangle , \end{aligned}$$

(26)

where D is matrix of order $(n+1) \times (n+1)$ as follows

$$\begin{aligned} D= \langle ^{\alpha }(x),L^{\alpha }(x)\rangle = \int _{0}^{1}L^{\alpha }(x) (L^{\alpha }(x))^{T} x^{\alpha -1}\mathrm{d}x. \end{aligned}$$

(27)

4 Operational matrices of fractional integration and derivative

In this section, we derive operational matrix of fractional integration and fractional derivative of FLPs. We achieve these matrices in general, without regarding to the nodes of $x_{i}, i=0, 1, \ldots , n$.

4.1 Fractional integration operational matrix of FLPs

We assume $L^{\alpha }(x)$ be Lagrange polynomials vector defined in Eq. (21), then we have

$$\begin{aligned} I^{\nu }L^{\alpha }(x) \simeq F^{(\nu ,\;\alpha )} L^{\alpha }(x), \end{aligned}$$

(28)

where $F^{(\nu ,\;\alpha )}$ is $(n+1) \times (n+1)$ operational matrix of fractional integration of order $\nu$. Using Eq. (1), we achieve

$$\begin{aligned} I^{\nu }L_{i}^{\alpha }(x) = \frac{1}{\varGamma (\nu )}x^{\nu -1} * \left( \sum _{s=0}^{n} \alpha _{is} x^{ \alpha (n-s)}\right) , \quad i=0, 1,\ldots ,n. \end{aligned}$$

(29)

To obtain $I^{\nu }L^{\alpha }(x)$, we take the Laplace transform from Eq. (29). Then, we have

$$\begin{aligned} L\left[ I^{\nu }L_{i}^{\alpha }(x)\right] = L\left[ \frac{1}{\varGamma (\nu )}x^{\nu -1}\right] L\left[ \sum _{s=0}^{n} \alpha _{is} x^{\alpha (n-s)}\right] =\sum _{s=0}^{n} F_{i}(s,r,\alpha ), i=0, 1, \ldots , n. \end{aligned}$$

(30)

Taking the inverse Laplace transform of Eq. (30), yields

$$\begin{aligned} I^{\nu }L_{i}^{\alpha }(x) = \sum _{s=0}^{n} \tilde{F}_{i}(s,x,\alpha ). \end{aligned}$$

(31)

Now, we can expand $\tilde{F}_{i}(s,x,\alpha )$ in terms of FLPs as

$$\begin{aligned} \tilde{F}_{i}(s,x,\alpha )=\sum \limits _{j= 0}^{n} c_{i,j,s} L_j^{\alpha }(x), i=0, 1,\ldots , n, \end{aligned}$$

(32)

with

$$\begin{aligned} c_{i,j,s}= D^{-1}\left\langle \tilde{F}_{i}(s,x,\alpha ),L_j^{\alpha }(x)\right\rangle \end{aligned}$$

(33)

Therefore, we have

$$\begin{aligned} F^{(\nu , \alpha )}=\left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \sum \nolimits _{s= 0}^{n}c_{0,0,s} &{}\sum \nolimits _{s= 0}^{n} c_{0,1,s} &{}\ldots &{} \sum \nolimits _{s= 0}^{n}c_{0,n,s} \\ \sum \nolimits _{s= 0}^{n}c_{1,0,s} &{} \sum \nolimits _{s= 0}^{n} c_{1,1,s}&{} \ldots &{}\sum \nolimits _{s= 0}^{n} c_{1,n,s}\\ \vdots &{}\vdots &{}\ddots &{} \vdots \\ \sum \nolimits _{s= 0}^{n} c_{n,0,s} &{}\sum \nolimits _{s= 0}^{n}c_{n,1,s} &{}\ldots &{}\sum \nolimits _{s= 0}^{n} c_{n,n,s}\\ \end{array}} \right] . \end{aligned}$$

(34)

For example, we consider the following two cases. In each case, we present the corresponding fractional integration opertional matrix of FLPs.

Case 1 For $n=2,\;x_{i},\;(i=0, 1, \ldots , n)$ are zeros of shifted Legendre polynomials

$$\begin{aligned} F^{(0.5,0.5)}= \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0.139599&{} 0.123229 &{} 0.00577636 \\ -0.0169154&{}0.474041 &{} 0.480693 \\ 0.00448695 &{} -0.0330801 &{} 0.514739 \\ \end{array}} \right] . \end{aligned}$$

Case 2 For $n=2,\;x_{i} = \frac{i}{2}, (i=0, 1, \ldots , n)$

$$\begin{aligned} F^{(0.5,0.5)}= \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0.0752253 &{} 0.0875826&{}-0.101021 \\ -0.150451 &{} 0.510101 &{}0.686347 \\ 0.0752253 &{}-0.0334935 &{} 0.543053 \\ \end{array}} \right] . \end{aligned}$$

4.2 The FLPs operational matrix of the fractional derivative

The derivative of the function vector $L^{\alpha }$ can be approximated as follows

$$\begin{aligned} D^{\nu } L^{\alpha }(x) \simeq D^{(\nu , \alpha )} L^{\alpha }(x), \end{aligned}$$

(35)

$D^{(\nu , \alpha )}$ is called the FLPs operational matrix of derivative in the Caputo sense.

Using Eq. (17), we achieve:

$$\begin{aligned} D^{\nu }L_{i}^{\alpha }(x) = D^{\nu } \biggl (\sum _{s=0}^{n} \alpha _{is} x^{\alpha (n-s)} \biggl ) = \sum _{s=0}^{n} \alpha _{is} D^{\nu } x^{\alpha (n-s)} \end{aligned}$$

(36)

Taking the Laplace transform from Eq. (36), we get

$$\begin{aligned} L\left[ D^{\nu }L_{i}^{\alpha }(x) \right] = \sum _{s=0}^{n} \alpha _{is} L\left[ D^{\nu } x^{\alpha (n-s)}\right] = \sum _{s=0}^{n} \alpha _{is} F_{i}(r) \end{aligned}$$

(37)

where

$$\begin{aligned} F_{i}( r)=\frac{1}{r^{m- \nu }} \left[ r^{m} L[\varOmega _{s} (x)]- r^{m-1} \varOmega _{s} (0) - \cdots - \varOmega _{s}^{(m-1)}(0)\right] ,\quad \varOmega _{s} (x)=x^{\alpha (n-s)}. \end{aligned}$$

(38)

Taking the inverse Laplace transform of $F_{i}( r)$, yields

$$\begin{aligned} D^{\nu }L_{i}^{\alpha }(x) = \sum _{s=0}^{n} \tilde{F_{is}}(x), \end{aligned}$$

(39)

where

$$\begin{aligned} \tilde{F_{is}}(x) = L^{-1}\bigg [ \frac{\alpha _{is}}{r^{m- \nu }} \left[ r^{m} L[\varOmega _{s} (x)]- r^{m-1} \varOmega _{s} (0) - \cdots - \varOmega _{s}^{(m-1)}(0)\right] \bigg ]. \end{aligned}$$

(40)

Now, we can expand $\tilde{F}_{is}(x)$ in terms of FLPs as

$$\begin{aligned} \tilde{F}_{is}(x)=\sum \limits _{j= 0}^{n}\tilde{u}_{i,s,j} L_j^{\alpha }(x) , \end{aligned}$$

(41)

with

$$\begin{aligned} \tilde{u}_{i,s,j}=D^{-1} \left\langle \tilde{F}_{is}(x),L^{\alpha }_j(x)\right\rangle \end{aligned}$$

(42)

Then, we have

$$\begin{aligned} D^{\nu }L_{i}^{\alpha }(x) \simeq \sum \limits _{j= 0}^{n} \sum \limits _{s= 0}^{n} \tilde{u}_{i,s,j}L^{\alpha }_{j}(x), \end{aligned}$$

(43)

and

$$\begin{aligned} D^{\nu } L_i^{\alpha }(x)\simeq \left[ \sum \limits _{s= 0}^{n}\tilde{u}_{i,s,0},\sum \limits _{s= 0}^{ n}\tilde{u}_{i,s,1},\ldots ,\sum \limits _{s= 0}^{n}\tilde{u}_{i,s,n}\right] L^{\alpha }(x),\quad i=0,\;1,\;\ldots ,\;n. \end{aligned}$$

(44)

Hence, we have

$$\begin{aligned} D^{(\nu ,\alpha )}=\left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \sum \nolimits _{s= 0}^{n}\tilde{u}_{0,0,s} &{}\sum \nolimits _{s= 0}^{n} \tilde{u}_{0,1,s} &{}\ldots &{} \sum \nolimits _{s= 0}^{n}\tilde{u}_{0,n,s}\\ \sum \nolimits _{s= 0}^{n}\tilde{u}_{1,0,s} &{} \sum \nolimits _{s= 0}^{n} \tilde{u}_{1,1,s}&{} \ldots &{}\sum \nolimits _{s= 0}^{n}\tilde{u}_{1,n,s}\\ \vdots &{}\vdots &{}\ddots &{} \vdots \\ \sum \nolimits _{s= 0}^{n} \tilde{u}_{n,0,s} &{}\sum \nolimits _{s= 0}^{n}\tilde{u}_{n,1,s} &{}\ldots &{}\sum \limits _{s= 0}^{n} \tilde{u}_{n,n,s}\\ \end{array}} \right] . \end{aligned}$$

(45)

5 Numerical method

The matrices presented in the previous section are generally obtained. Then, we can have different choices for Lagrange polynomials. In this paper, we choose the points of Lagrange polynomials $x_{i}=\frac{i}{n}$.

We consider the following problems:

• (a) The multi-order fractional differential equation

  $$\begin{aligned} \tilde{G}(x, u(x), D^{\nu _{j}}u(x))=0, \quad 0 \le x \le 1, \end{aligned}$$

  (46)

  subject to

  $$\begin{aligned} u^{(k)}(0)=u_{0k}, \quad k=0, 1, \ldots , l-1, \end{aligned}$$

  (47)

  with $l= \lceil \nu _{r} \rceil$, where $\nu _{j}, (\nu _{1}< \nu _{2}< \cdots < \nu _{r} )$ are positive real numbers and $\lceil \nu _{r} \rceil$ denotes the ceiling function.

• (b) System of fractional differential equations

  $$\begin{aligned} D^{\nu _{j}}u_{j}(x) = \tilde{G}_{j} (x, u_{1}(x), \ldots , u_{n}(x)), \quad 0< \nu _{j} \le 1, j=0, 1, \ldots , n, 0\le x \le 1, \end{aligned}$$

  (48)

  with the initial conditions

  $$\begin{aligned} u_{j}(0)=u_{j0}, \quad j=1, 2, \ldots , n. \end{aligned}$$

For problem (a), we expand $D^{\nu _{r}}u(x)$ by FLPs as

$$\begin{aligned} D^{\nu _{r}}u(x) \simeq C^{T}L^{\alpha }(x), \end{aligned}$$

so, we get

$$\begin{aligned} u(x) \simeq C^{T} F^{(\nu _{r},\alpha )} L^{\alpha }(x) +\sum _{k=0}^{l-1} \frac{x^{k}}{k!}u_{0k} \simeq C^{T} F^{(\nu _{r},\alpha )} L^{\alpha }(x) + E^{T} L^{\alpha }(x), \end{aligned}$$

(49)

where

$$\begin{aligned} E(x)=\sum _{k=0}^{l-1} \frac{x^{k}}{k!}u_{0k}. \end{aligned}$$

(50)

From Eqs. (48)–(50), we get

$$\begin{aligned} D^{\nu _{j}}u(x) \simeq C^{T}F^{(\nu _{r}-\nu _{j})} L^{\alpha }(x) + \sum _{k=0}^{l-1} \frac{D^{\nu _{j}}(x^{k})}{k!}u_{0k} \simeq C^{T} F^{(\nu _{r}-\nu _{j}, \alpha )} L^{\alpha }(x)+\tilde{E_{j}}^{T}L^{\alpha }(x), \end{aligned}$$

(51)

where

$$\begin{aligned} \tilde{E_{j}}(x)=\sum _{k=0}^{l-1} \frac{D^{\nu _{j}}(x^{k})}{k!}u_{0k},\;\;j=1, \ldots , r. \end{aligned}$$

(52)

Substituting above relations in Eq. (46), we achieve an algebraic equation. Moreover, we collocate this equation at $x_{i},i=0, 1, 2, \ldots , n$. Therefore, we have a system of algebraic equations, which can be solved for the unknown vector C using Newton’s iterative method.

Similar to problem (a), we expand $D^{\nu _{j}}u_{j}(x), \, j=0, 1, \ldots , n$, by FLPs as

$$\begin{aligned} D^{\nu _{j}}u_{j}(x) \simeq C_{j}^{T} L^{\alpha }(x), \quad j=1, 2, \ldots ,n. \end{aligned}$$

From Eq. (28), we have

$$\begin{aligned} u_{j}(x) \simeq C_{j}^{T} F^{(\nu _{j},\alpha )}+u_{j0}, \quad j=1, 2, \ldots ,n. \end{aligned}$$

Substituting above equations in Eq. (48), we derive a system of algebraic equations. Then, we collocate this system at $x_{i}$. This system can be solved using Newton’s iterative method.

6 Error analysis

A function $f \in L^{2}[0,\;1]$ can be expanded as

$$\begin{aligned} f(x) \simeq \sum _{i=0}^{n}c_{i}L_{i}^{\alpha }(x)=C^{T}L^{\alpha }(x)=f_{n}(x). \end{aligned}$$

We define error function $\widehat{E}(x)$ as follows:

$$\begin{aligned} \widehat{E}(x) = \vert f(x)- f_{n}(x) \vert , x \in [0,\;1] \end{aligned}$$

(53)

Theorem 1

Let $D^{k \alpha }f \!\in \! C (0, 1], k=0,\;1, \ldots ,\;n$ and $Y_{n}^{\alpha } = \{L_{0}^{\alpha }(x),\;L_{1}^{\alpha }(x),\;\ldots ,\;L_{n}^{\alpha }(x) \}$. If $f_{n}(x)$ is the best approximation to f(x) out of $Y_{n}^{\alpha }$, then the error bound of the approximation solution $f_{n}(x)$ using FLPs can be obtained as follows:

$$\begin{aligned} \Vert f-f_{n} \Vert _{2} \le \frac{M_{\alpha }}{\varGamma ((n+1) \alpha +1) \sqrt{(2n+2) \alpha +1}}. \end{aligned}$$

(54)

where $M_{\alpha }=\sup _{x \in [0,1]} \vert D^{(n+1) \alpha }f(x) \vert$.

Proof

We define

$$\begin{aligned} \tilde{f}(x) = \sum _{i=0}^{n} \frac{x^{k \alpha }}{\varGamma (k \alpha +1)}D^{k \alpha }f(0^{+}), \end{aligned}$$

(55)

from the generalized Taylors formula in Definition 3, we have

$$\begin{aligned} \vert f(x) - \tilde{f}(x) \vert \le \frac{x^{(n+1) \alpha }}{\varGamma ((n+1)\alpha +1)} \sup _{x \in [0,1]} \vert D^{(n+1) \alpha }f(x) \vert . \end{aligned}$$

(56)

Utilizing the fact that $\tilde{f}(x) \in Y_{n}^{\alpha }$ is the best approximation of f out of $Y_{n}^{\alpha }$ and using Eq. (56), we get

$$\begin{aligned} \Vert f- f_{n} \Vert _{2}^{2}\le & {} \Vert f-\tilde{f} \Vert _{2}^{2} = \int _{0}^{1} \vert f(x) - \tilde{f}(x) \vert ^{2} \mathrm{d}x \nonumber \\\le & {} \int _{0}^{1} \frac{x^{(2n+2) \alpha }}{\varGamma ((n+1) \alpha +1)^{2}} M_{\alpha }^{2} \nonumber \\= & {} \frac{M_{\alpha }^{2}}{\varGamma ((n+1) \alpha +1)^{2}} \int _{0}^{1} x^{(2n+2) \alpha } \mathrm{d}x \nonumber \\= & {} \frac{M_{\alpha }^{2}}{\varGamma ((n+1) \alpha +1)^{2} ((2n+2) \alpha +1)}, \end{aligned}$$

(57)

The theorem is proved by taking the square roots.

Therefore, FLP’s approximations of f(x) are convergent. $\square$

6.1 Upper bound of error vector for the fractional integration operational matrix

Now, we look for an upper bound for the error vector of $F^{(\nu ,\alpha )}$ and we show that this error tends to zero, by increasing the number of FLPs.

Theorem 2

Let H is a Hilbert space and Y is a close subspace of H such that $dim Y < \infty$ and $y_{1}, y_{2}, \ldots , y_{n}$, is any basis for Y. Let z be an arbitrary element in H and $y^{*}$ be the unique best approximation to z out of Y. Then (Kreyszig 1978)

$$\begin{aligned} \Vert z-y^{*} \Vert _{2}^{2} = \frac{G(z, y_{1}, y_{2}, \ldots , y_{n})}{G(y_{1}, y_{2}, \ldots , y_{n})} \end{aligned}$$

(58)

where

$$\begin{aligned} G( x, y_{1}, y_{2}, \ldots , y_{n}) = \left| \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \langle x , x\rangle &{} \langle x , y_{1}\rangle &{} \cdots &{} \langle x , y_{n}\rangle \\ \langle y_{1} , x\rangle &{} \langle y_{1} , y_{1}\rangle &{} \cdots &{} \langle y_{1} , y_{n}\rangle \\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ \langle y_{n} , x\rangle &{} \langle y_{n} , y_{1}\rangle &{} \cdots &{} \langle y_{n} , y_{n}\rangle \\ \end{array}\right| . \end{aligned}$$

(59)

The error vector $\tilde{E}^{(\nu )}$ of the operational matrix $F^{(\nu ,\alpha )}$ is given by

$$\begin{aligned} \tilde{E}^{(\nu )}= I^{\nu } L^{\alpha }(x) - F^{(\nu ,\alpha )}L^{\alpha }(x),\;\;\;\;\tilde{E}^{(\nu )} = \left[ \begin{array}{cccc} \tilde{e_{0}} \\ \tilde{e_{1}} \\ \vdots \\ \tilde{e_{n}}\\ \end{array}\right] , \end{aligned}$$

(60)

We approximate $\tilde{F}_{i}(s,x,\alpha )$ as follows

$$\begin{aligned} \tilde{F}_{i}(s,x,\alpha ) \simeq \sum _{j=0}^{n} b_{j}L_{j}^{\alpha }(x), \end{aligned}$$

(61)

from Theorem 2, we have:

$$\begin{aligned} \Big \Vert \tilde{F}_{i}(s,x,\alpha ) - \sum _{j=0}^{n} b_{j}L_{j}^{\alpha }(x) \Big \Vert _{2} = \biggl (\frac{G(\tilde{F}_{i}(s,x,\alpha ),\;L_{0}^{\alpha },\;L_{1}^{\alpha },\;\ldots ,\;L_{n}^{\alpha })}{G(L_{0}^{\alpha },\;L_{1}^{\alpha },\;\ldots ,\;L_{n}^{\alpha })} \biggl )^{\frac{1}{2}}. \end{aligned}$$

(62)

Then, using Eqs. (32) and (62), we get

$$\begin{aligned} \Vert \tilde{e_{i}} \Vert _{2}= & {} \Big \Vert I^{\nu }L_{i}^{\alpha }(x) - \sum \limits _{j= 0}^{n} \sum \limits _{s= 0}^{n} c_{i,j,s} L_j^{\alpha }(x) \Big \Vert \nonumber \\\le & {} \Big \Vert \sum _{s=0}^{n}\tilde{F}_{i}(s,x,\alpha ) - \sum \limits _{j= 0}^{n} \sum \limits _{s= 0}^{n} c_{i,j,s} L^{\alpha }_j(t) \Big \Vert \nonumber \\\le & {} \sum \limits _{s= 0}^{n}\biggl (\frac{G\big (\tilde{F}_{i}(s,x,\alpha ), \;L_{0}^{\alpha },\;L_{1}^{\alpha },\;\ldots ,\;L_{n}^{\alpha }\big )}{G\big (L_{0}^{\alpha },\;L_{1}^{\alpha },\;\ldots ,\;L_{n}^{\alpha }\big )} \biggl )^{\frac{1}{2}}. \end{aligned}$$

(63)

By considering the above discussion and Eq.  (54), it can be concluded that by increasing the number of the fractional-Lagrange polynomials, the error vector $\tilde{E}^{(\nu )}$ tend to zero.

7 Illustrative test problems

In this section, we apply our method to solve the following examples.

Example 1

Consider the following fractional differential equation (Lakestani et al. 2012):

$$\begin{aligned} D^{0.5}u(x)+ u(x)= \sqrt{x}+\frac{\sqrt{\pi }}{2}, \end{aligned}$$

(64)

subject to

$$\begin{aligned} u(0)=0, \end{aligned}$$

The exact solution of this problem is $u(x)=\sqrt{x}$.

Applying the present method for $n=1$ and $\alpha = \nu =\frac{1}{2}$, the problem reduces to:

$$\begin{aligned} C^{T}L^{\alpha }(x)+C^{T}F^{(0.5, \alpha )}L^{\alpha }(x) =E^{T}L^{\alpha }(x), \end{aligned}$$

(65)

where $\sqrt{x}+\frac{\sqrt{\pi }}{2} \simeq E^{T}L^{\alpha }(x)$.

Using Eqs. (26), (32), for $\nu =\alpha = \frac{1}{2}$, we have

$$\begin{aligned} F^{\left( \frac{1}{2},\frac{1}{2}\right) }= & {} \left[ \begin{array}{cccc} \frac{\sqrt{\pi }}{12} &{} \frac{2}{ \sqrt{\pi }}-\frac{5 \sqrt{\pi }}{12} \\ \frac{-\sqrt{\pi }}{12} &{} \frac{5 \sqrt{\pi }}{12}\\ \end{array}\right] , \quad \quad \quad E=\left[ \frac{\sqrt{\pi }}{2},\;1+ \frac{\sqrt{\pi }}{2}\right] ^{T}. \nonumber \\ C= & {} \left[ \frac{\sqrt{\pi }}{2},\;\frac{\sqrt{\pi }}{2}\right] ^{T}, \end{aligned}$$

(66)

by substituting these matrices in Eq. (65) and using collocation method in $x_{i}$, the exact solution is obtained, while error of method based on B-spline functions (Lakestani et al. 2012) is presented in Table 1.

Table 1 $L_{\infty }$ and $L_{2}$ errors for u(x) using B-spline functions in Example 1

Example 2

Consider the following linear initial value problem (Bhrawy et al. 2014; Hashim et al. 2009; Saadatmandi and Dehghan 2010; Diethelm et al. 2002)

$$\begin{aligned} D^{\nu }u(x)+u(x)= 0, \quad 0< \nu <2, \end{aligned}$$

(67)

subject to

$$\begin{aligned} u(0)=1, \quad u^{'}(0)=0. \end{aligned}$$

The second initial condition is for $\nu > 1$ only. The exact solution of this problem is as follows (Stoer and Bulirsch 1996):

$$\begin{aligned} u(x) = \sum _{k=0}^{\infty } \frac{(-x^{\nu })^{k}}{\varGamma (k \nu +1)}. \end{aligned}$$

(68)

For $\nu = 1$, the exact solution is $u(x) = e^{-x}$ and the exact solution for $\nu = 2$, is $u(x) = \cos (x)$.

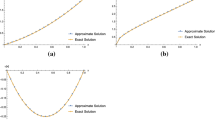
The numerical results for u(x) in $n=4,\;\alpha =1$ and $\nu = 0.65, 0.75, 0.85, 0.95$ and 1 are plotted in Fig. 2 a. Also, we present the results for $\nu > 1$. Fig. 2b shows the approximate solutions obtained for $n=4,\;\alpha =1$ and $\nu = 1.65, 1.75, 1.85, 1.95$, and 2.

Fig. 2

Curves of exact and numerical values of u(x) for various of $\nu$, in Example 2

In these figures, we see that our approximate solutions converge to the exact solutions.

In addition, we solve this problem for $\nu =2,\;\alpha =1$ with $n=4$ and the absolute error which is obtained between the approximation solution and the exact solution for this case is plotted in Fig. 3.

For more investigation, we apply our method for $\alpha =\nu =0.85$. In Table 2, the absolute error obtained between our numerical results and the exact solution for various of x and compared with the results of method in Yuzbasi (2013). Figure 2 and Table 2 demonstrate the validity and effectiveness of our method for this problem.

Fig. 3

Absolute error between the exact and approximation solution, for $\alpha =1,\;\nu =2$, in Example 2

Table 2 Comparison of the absolute error with (Saadatmandi and Dehghan 2010), for $\alpha =\nu =0.85,\;n=8$ in Example 2

Example 3

Consider the following system of fractional differential equations (Rahimkhani et al. 2016)

$$\begin{aligned} \left\{ \begin{array}{ll} D^ {\nu _{1}}u_{1}(x) = u_{1}(x)+u_{2}(x),&{}\quad 0< \nu _{1} \le 1,\;\;0 \le x \le 1, \\ D^{\nu _{2}}u_{2}(x)=-u_{1}(x)+u_{2}(x), &{}\quad 0< \nu _{2} \le 1, \end{array}\right. \end{aligned}$$

(69)

subject to

$$\begin{aligned} u_{1}(0)=0,\;\;u_{2}(0)=1. \end{aligned}$$

The exact solution of this system when, $\alpha =\nu _{1}= \nu _{2} =1$, is $u_{1}(x)=e^{x}sin(x),\;u_{2}(x)=e^{x}cos(x)$. We apply the proposed method to solve this system. Then this system reduces as

$$\begin{aligned}&C_{i}^{T}L^{\alpha }(x)-C_{1}^{T}F^{(\nu _{1},\alpha })L^{\alpha }(x)-C_{2}^{T}F^{(\nu _{2},\alpha )}L^{\alpha }(x)-E^{T}L^{\alpha }(x)=0,\\&C_{2}^{T}L^{\alpha }(x)+C_{1}^{T}F^{(\nu _{1},\alpha )}L^{\alpha }(x)-C_{2}^{T} F^{(\nu _{},\alpha )}L^{\alpha }(x)-E^{T}L^{\alpha }(x)=0, \end{aligned}$$

where $1 \simeq E^{T} L^{\alpha }(x)$.

Fig. 4

Plots of system in Example 3, when $\alpha =\nu _{1} = \nu _{2} = 1$

Fig. 5

Absolute error obtained between the approximate solutions and the exact solution with $n=8$ and $\alpha =\gamma _{1} = \gamma _{2} = 1$ for (a) $u_{1}(x)$ and (b) $u_{2}(x)$ in Example 3

Figure 4 shows the numerical solutions of this system, using our method with $n=8$. Also, Fig. 5 displays the absolute error obtained between the approximate solutions and the exact solution at $\alpha =\nu _{1} = \nu _{2} = 1$ and $n=8$ for $u_{1}(x)$ and $u_{2}(x)$.

Moreover, since the exact solutions for $\nu _{1} \ne 1,\;\nu _{2} \ne 1$ are not exist, then, we measured the reliability using defining the norm of error $(\Vert R_{N}(x) \Vert ^{2})$.

$$\begin{aligned} R_{1N}(x)= & {} C_{i}^{T}L^{\alpha }(x)-C_{1}^{T}F^{(\nu _{1},\alpha })L^{\alpha }(x)-C_{2}^{T}F^{(\nu _{2},\alpha )}L^{\alpha }(x)-E^{T}L^{\alpha }(x),\\ R_{2N}= & {} C_{2}^{T}L^{\alpha }(x)+C_{1}^{T}F^{(\nu _{1},\alpha )}L^{\alpha }(x)-C_{2}^{T} F^{(\nu _{},\alpha )}L^{\alpha }(x)-E^{T}L^{\alpha }(x),\\ \Vert R_{1N} \Vert ^{2}= & {} \int _{0}^{1} R_{1N}^{2}(x) \mathrm{d}x,\;\;\;\Vert R_{2N} \Vert ^{2} = \int _{0}^{1} R_{2N}^{2}(x) \mathrm{d}x,\\ \Vert R_{N} \Vert ^{2}= & {} \max ( \Vert R_{1N} \Vert ^{2},\;\Vert R_{2N} \Vert ^{2}), \end{aligned}$$

Table 3 shows $\Vert R_{N} \Vert ^{2}$ for $\alpha =\nu _{1}=\nu _{2}$ and $n=8$. This table demonstrates that the FLPs are more effective in solving systems of fractional differential equations.

Table 3 The $\Vert \mathrm{Res}_{N} \Vert ^{2}$ with $n=8$ and various values of $\nu _{1}=\nu _{2} = \alpha$ for Example 3

Example 4

We consider the following nonlinear system of fractional differential equations (Rahimkhani et al. 2016)

$$\begin{aligned} \left\{ \begin{array}{ll} D^ {\nu _{1}}u_{1}(x) = \frac{1}{2} u_{1}(x), &{} \quad 0< \nu _{1} \le 1,\;\;0 \le x \le 1, \\ D^{\nu _{2}}u_{2}(x)=u_{2}(x)+u^{2}_{1}(x),&{} \quad 0< \nu _{2} \le 1, \end{array}\right. \end{aligned}$$

(70)

subject to the initial conditions

$$\begin{aligned} u_{1}(0)=1,\quad u_{2}(0)=0. \end{aligned}$$

The exact solution of this system, in $\nu _{1}=\nu _{2}=\alpha =1$, is $u_{1}(x)= e^{\frac{x}{2}},\;u_{2}(x)=xe^{x}$.

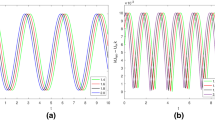
We solve this system using present method for $n=8$. Figure 6 shows the approximate solutions for $\alpha =\nu _{1}=\nu _{2}$ with various values of $\alpha$, and the exact solution. Also, Fig. 7 displays the absolute error obtained between the approximate solutions and the exact solution in $\alpha = \nu _{1} = \nu _{2} = 1$ and $n=8$ for this problem.

Fig. 6

The comparison of approximate solutions for $n=8, \alpha =\nu _{1}=\nu _{2}$ and the exact solution for Example 4

Fig. 7

Absolute error obtained between the approximate solutions and the exact solution with $n=8$ and $\alpha =\nu _{1} = \nu _{2} = 1$ for (a) $u_{1}(x)$ and (b) $u_{2}(x)$ in Example 4

Example 5

In this example, we consider the following nonlinear initial value problem (Kazem et al. 2013)

$$\begin{aligned}&D^{3}u(x)+D^{\frac{5}{2}}u(x)+u^{2}(x)=x^{4},\nonumber \\&\quad u(0)=0,\;u^{'}(0)=0,\;u^{''}(0)=2. \end{aligned}$$

(71)

The exact solution of this problem is $u(x)=x^2$. Applying the technique described in Sect. 5, we obtain exact solution with $n=4$ and $\alpha =1$.

Example 6

Consider the following fractional Riccati equation (Jafari et al. 2011; Keshavarz et al. 2014)

$$\begin{aligned} D^{\nu }u(x) = -u^{2}(x)+1,\quad 0< \nu \le 1, \end{aligned}$$

(72)

subject to initial condition

$$\begin{aligned} u(0)=0. \end{aligned}$$

The exact solution, when $\nu = 1$, is

$$\begin{aligned} u(x)= \frac{e^{2x}-1}{e^{2x}+1}. \end{aligned}$$

(73)

By applying the technique described in Sect. 5, the problem became as

$$\begin{aligned} C^{T}L^{\alpha }(x)=-(C^{T}F^{(\nu ,\alpha )}L^{\alpha }(x))(C^{T}F^{(\nu ,\alpha )}L^{\alpha }(x))^{T}+E^{T}L^{\alpha }(x), \end{aligned}$$

(74)

where

$$\begin{aligned} 1 \simeq E^{T}L^{\alpha }(x). \end{aligned}$$

We apply the FLP approach to solve this problem with $n=5$ and various values of $\nu ,\;\alpha$. The approximation solution for this problem by Legendre wavelet method in $k = 1,\; M = 25,\;\nu =1$ is plotted in Jafari et al. (2011) and absolute difference between exact and approximation solutions obtained by Bernoulli wavelet method for $k = 1,\; M = 5,\; \nu =1$ is plotted in Keshavarz et al. (2014). From these figures and Fig. 8a, we see that we can achieve a reasonable approximation with the exact solution. Moreover, Fig. 8b shows the approximation solutions obtained for $\alpha =1,\;n=5$ and different values of $\nu$ using the FLP scheme. From these results, it is seen that the approximation solutions converge to the exact solution.

The exact solutions for the values of $\nu \ne 1$ do not exist. Therefore, to demonstrate an efficiency of the proposed method for this problem, we define the norm of residual error as follows

$$\begin{aligned} \mathrm{Res}_{n}(x)= & {} C^{T}L^{\alpha }(x)+(C^{T}F^{(\nu ,\alpha )}L^{\alpha }(x))(C^{T}F^{(\nu ,\alpha )}L^{\alpha }(x))^{T} -E^{T}L^{\alpha }(x),\nonumber \\ \Vert \mathrm{Res}_{n} \Vert ^{2}= & {} \int _{0}^{1} \mathrm{Res}_{n}^{2}(x) \mathrm{d}x. \end{aligned}$$

(75)

Table 4 displays $\Vert \mathrm{Res}_{n} \Vert ^{2}$ with some n and various values of $\nu = \alpha$. Table 4 and figures show the advantage of the present technique for solving this nonlinear problem.

Fig. 8

Absolute error between the exact and approximation solutions and comparison of u(x) with various values of $\nu$ and the exact solution, with $n= 5$ and $\alpha =1$ for Example 6

Table 4 The $\Vert \mathrm{Res}_{n} \Vert ^{2}$ with $n=5$ and various values of $\nu = \alpha$ for Example 6

Fig. 9

a Comparing the exact and approximate solutions, b comparison of u(x) with various values of $\nu$ and the exact solution, with $n= 5$ and $\alpha =1$ for Example 7

Example 7

Consider the following fractional Riccati equation (Jafari et al. 2011)

$$\begin{aligned} D^{\nu }u(x)=2u(x)-u^{2}(x)+1,\quad 0< \nu \le 1 \end{aligned}$$

(76)

subject to initial condition $u(0)=0$. The exact solution, when $\nu = 1$, is

$$\begin{aligned} u(x)=1+ \sqrt{2}\tan h \biggl ( \sqrt{2}x+ \frac{1}{2}Log \big (\frac{\sqrt{2}-1}{\sqrt{2}+1}\big ) \biggl ). \end{aligned}$$

By setting $n=5$ and $\alpha = 1$, we obtain fractional-Lagrange polynomial solution for various $\nu$. In Fig. 9c, we show the FLP solutions for $\alpha =1$ and various values of $\nu$. Fig. 5 shows that the FLP solution converges to the exact solution. Also, the approximate solution for this problem by Legendre wavelet method in $k = 1, M = 25$ is plotted in (Jafari et al. 2011). From Fig. 9, it is obvious that we can achieve a good approximation with the exact solution using a small number of bases.

The exact solutions for the values of $\nu \ne 1$ do not exist. Therefore, to show efficiency of the present method for this problem, we define the norm of residual error as follows

$$\begin{aligned} \mathrm{Res}_{n}(x)= & {} C^{T}L^{\alpha }(x)-2(C^{T}F^{(\nu ,\alpha )}L^{\alpha }(x))+ (C^{T}F^{(\nu ,\alpha )}L^{\alpha }(x))(C^{T}F^{(\nu ,\alpha )}L^{\alpha }(x))^{T}\nonumber \\&-E^{T}L^{\alpha }(x),\\&\Vert \mathrm{Res}_{n} \Vert ^{2} = \int _{0}^{1} \mathrm{Res}_{n}^{2}(x) \mathrm{d}x. \end{aligned}$$

Table 5 displays $\Vert \mathrm{Res}_{4} \Vert ^{2}$ with various values of $\nu = \alpha$. From Table 5 and Fig. 9, we can see the advantage of the proposed method for this example.

Table 5 The $\Vert \mathrm{Res}_{4} \Vert ^{2}$ with various values of $\nu = \alpha$ for Example 7

8 Conclusion

In this paper, new functions named fractional-order Lagrange polynomials (FLPs) based on Lagrange polynomials has been constructed to solve the fractional differential equations. In addition, we have used the application of the fractional-order Lagrange polynomials for solving systems of FDEs.

First, we presented a new representation of Lagrange polynomials. Next, we introduce a new set of functions called fractional Lagrange polynomials (FLPs). Also, we obtain operational matrices of the Caputo fractional derivative and Riemann–Liouville fractional integration generally, without considering the nodes of Lagrange polynomials. These matrices are obtained using Laplace transform. The operational matrix of fractional integration together with collocation method have been used to approximate the numerical solution of the FDEs. Our numerical results in comparison with exact solutions and with the solutions obtained by some other numerical methods shows that this method is more accurate.