The bivariate Müntz wavelets composite collocation method for solving space-time-fractional partial differential equations

Abstract

Herein, we consider an effective numerical scheme for numerical evaluation of three classes of space-time-fractional partial differential equations (FPDEs). We are going to solve these problems via composite collocation method. The procedure is based upon the bivariate Müntz–Legendre wavelets (MLWs). The bivariate Müntz–Legendre wavelets are constructed for first time. The bivariate MLWs operational matrix of fractional-order integral is constructed. The proposed scheme transforms FPDEs to the solution of a system of algebraic equations which these systems will be solved using the Newton’s iterative scheme. Also, the error analysis of the suggested procedure is determined. To test the applicability and validity of our technique, we have solved three classes of FPDEs.

1 Introduction

In recent years, fractional equations appear in modeling of various real-life phenomena, for example dynamic viscoelasticity modeling (Larsson et al. 2015), hydrologic (Benson et al. 2013), economics (Baillie 1996), temperature and motor control (Bohannan 2008), solid mechanics (Rossikhin and Shitikova 1997), bioengineering (Magin 2004), medicine (Hall and Barrick 2008), porous media (He 1998), fluid-dynamic traffic model (He 1999), etc. Therefore, there is an increasing demand for numerical and analytical solutions of various types of fractional differential equations such as finite-difference/finite-element technique (Dehghan and Abbaszadeh 2018a, b, 2019), compact difference schemes (Hu and Zhang 2012), homotopy analysis method (Dehghan et al. 2010), homotopy perturbation method (Abdulaziz et al. 2008), dual reciprocity boundary elements method (Dehghan and Safarpoor 2016), fifth-kind orthonormal Chebyshev polynomial method (Abd-Elhameed and Youssri 2018), B-spline functions (Lakestani et al. 2012), fractional-order Bernoulli function method (Rahimkhani et al. 2017), hybrid method (Mashayekhi and Razzaghi 2015), Legendre wavelet method (Heydari et al. 2014), fractional-order Lagrange polynomials (Sabermahani et al. 2018), fractional-order Bernoulli wavelets method (Rahimkhani et al. 2016), Müntz–Legendre wavelet method (Rahimkhani et al. 2018), etc.

Spectral schemes have received noticeable consideration for approximate solutions of various FPDEs, for example fractional diffusion equation (Lin and Xu 2007), fractional modified anomalous sub-diffusion equation (Dehghan et al. 2016), fractional cable equation (Lin et al. 2011), fractional Fokker–Planck equation (Zheng et al. 2015), FPDEs (Bhrawy and Zaky 2015), fractional advection–diffusion equations (Bhrawy and Baleanu 2013), etc.

In mathematical research, wavelets have been applied in different engineering fields for instance, signal analysis, image processing, edge extrapolation, optimal control problems, time–frequency analysis, fast algorithms, multiscale phenomena modeling, and pattern recognition (Chui 1997; Shamsi and Razzaghi 2005; Lakestani et al. 2006; Beylkin et al. 1991).

In recent years, diverse wavelets have been employed for numerical solution of several differential equations, for example Bernoulli wavelet (Rahimkhani et al. 2017), CAS wavelet (Saeedi et al. 2011), Chebyshev wavelet (Li 2010), second-kind Chebyshev wavelet (Zhu and Fan 2013), and Legendre wavelet (Rehman and Rahmat 2011; Heydari et al. 2013).

In this work, we present a computational scheme based on bivariate MLWs basis for solving three classes of FPDEs. First, bivariate MLWs are constructed. Then, we construct the bivariate MLWs’ operation matrix of fractional integral. Finally, this operational is applied to convert the solution of the FPDEs to the solution of algebraic equations. Therefore, there are some questions to be answered:

• How to construct the Riemann–Liouville fractional integral operation matrix of bivariate MLWs.

• How to analyze FPDEs via fractional integration operational matrix of the bivariate MLWs.

• How to choose parameter of fractional-order $(\gamma )$ of bivariate MLWs.

• How to select points of collocation methods.

• How long does CPU time of proposed method.

The current a paper is as follows:

In Sect. 2, we construct the bivariate MLWs and give some their properties. In Sect. 3, we derive the fractional-order integral operational matrix for bivariate MLWs. The problem is expressed in Sect. 4. In Sect. 5, a technique for numerical solution of three classes of FPDEs is presented. In Sect. 6, we give the convergence of approximate solution and the error of our scheme. Numerical findings are reported in Sect. 7. Also, Sect. 8 contains a conclusion.

2 Wavelets and bivariate MLWs

The bivariate MLWs are defined on $[0, 1)\times [0, 1)$ as:

$$\begin{aligned} \psi _{n,m,n',m'}(x,t)= \left\{ \begin{array}{ll} (2\lambda _{m}+1)^{\frac{1}{2}}(2\lambda _{m'}+1)^{\frac{1}{2}} 2^{\frac{k+k'}{2}-1}L_{m}(2^{k-1}x -{\hat{n}})L_{m'}(2^{k'-1}t-{\tilde{n}}), \\ \\ \qquad \qquad \frac{{\hat{n}}}{2^{k-1}} \le x< \frac{{\hat{n}}+1}{2^{k-1}}, \frac{{\tilde{n}}}{2^{k'-1}} \le t < \frac{{\tilde{n}}+1}{2^{k'-1}},\\ \\ 0 , \qquad \qquad \qquad \text {otherwise}, \end{array} \right. \end{aligned}$$

(1)

where

$$\begin{aligned}&\displaystyle {\hat{n}}=n-1, {\tilde{n}}=n'-1, \quad n=1, 2, \ldots , 2^{k-1}; n'=1, 2, \ldots , 2^{k'-1},\\&\displaystyle m=0, 1, 2, \ldots , M-1;\quad m'=0, 1, 2, \ldots , M'-1 ; \end{aligned}$$

and

$$\begin{aligned} {\hat{m}}=2^{k-1}M; \quad {\tilde{m}}=2^{k'-1}M' . \end{aligned}$$

Here, $L_{m}(x)$ and $L_{m'}(t)$ are the Müntz–Legendre functions (MLFs) on [0, 1] as Rahimkhani et al. (2018):

$$\begin{aligned} L_{m}(x) = \sum _{s=0}^{m} c_{s,m}x^{\lambda _{s}},\quad c_{s,m} = \frac{\varPi _{j=0}^{m-1}(\lambda _{s}+\lambda _{j}+1)}{\varPi _{j=0, j\ne s}^{m}(\lambda _{s} - \lambda _{j})},\quad (m \in N_{0}), \end{aligned}$$

(2)

and

$$\begin{aligned} L_{m'}(t) = \sum _{s'=0}^{m'} c'_{s',m'}t^{\lambda _{s'}},\quad c'_{s',m'} = \frac{\varPi _{j=0}^{m'-1}(\lambda _{s'}+\lambda _{j}+1)}{\varPi _{j=0, j\ne s'}^{m'}(\lambda _{s'} - \lambda _{j})},\quad (m' \in N_{0}). \end{aligned}$$

(3)

These functions satisfy the following orthogonality condition: (Rahimkhani et al. 2018):

$$\begin{aligned} \int _{0}^{1} L_{n}(x) L_{m}(x) dx = \frac{\delta _{n,m}}{(2\lambda _{m}+1)},\quad (m> n). \end{aligned}$$

Also, the bivariate MLFs are defined on $[0, T_{1})\times [0, T_{2})$ as:

$$\begin{aligned} L_{m, n}(x,t) =\sum _{s'=0}^{m'} \sum _{s=0}^{m} c_{s,m}c'_{s',m'}\frac{x^{\lambda _{s}}t^{\lambda _{s'}}}{T_{1}^{\lambda _{s}}T_{2}^{\lambda _{s'}}}. \end{aligned}$$

(4)

In this article, we consider $\lambda _{k}= k \gamma ,$ where $\gamma$ is a real constant. Figures 1 and 2 demonstrate plots of 2D-MLWs for $\gamma =1$.

Fig. 1

Plot of 2D-MLWs and its contour with $n=n'=1; m=2, m'=3$ and $\gamma =1$

Fig. 2

Plot of 2D-MLWs and its contour with $n=n'=2; m=3, m'=4$ and $\gamma =1$

Remark 1

We consider order of Müntz–Legendre polynomials fits by paper (Esmaeili et al. 2011).

Let $f \in L^{2}\big ([0, 1) \times [0, 1)\big )$ and the best approximation of f obtained using bivariate MLWs $(P_{M,M'}^{k, k'}f),$ and then:

$$\begin{aligned} f(x, t) \simeq P_{M,M'}^{k, k'}f(x, t)= & {} \sum _{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}\sum _{n'=1}^{2^{k'-1}}\sum _{m'=0}^{M'-1}c_{n,m,n',m'}\psi _{n,m,n',m'}(x, t) \end{aligned}$$

(5)

$$\begin{aligned}= & {} \sum _{i=0}^{({\hat{m}}{\tilde{m}})-1}c_{i}\psi _{i}(x, t)= C^{T}\varPsi (x, t), \end{aligned}$$

(6)

where

$$\begin{aligned} C=\left[ c_{0}, c_{1}, c_{2}, \ldots , c_{({\hat{m}}{\tilde{m}})-1}\right] ^{T}, \end{aligned}$$

(7)

and

$$\begin{aligned} \varPsi (x, t)=\left[ \psi _{0}(x, t), \psi _{1}(x, t), \psi _{2}(x, t), \ldots , \psi _{({\hat{m}}{\tilde{m}})-1}(x, t)\right] ^{T}. \end{aligned}$$

(8)

3 Fractional integral operational matrix of bivariate MLWs

If $\varPsi (x, t)$ is the vector in accordance with relation (8), then:

$$\begin{aligned} _{0}^{R} I_{x}^{\alpha } \varPsi (x, t)=\varLambda (x, \alpha ) \varPsi (x, t)= (P_{{\hat{m}}\times {\hat{m}}}(x, \alpha )\otimes I_{{\tilde{m}} \times {\tilde{m}}}) \varPsi (x, t), \end{aligned}$$

(9)

and

$$\begin{aligned} {}_{0}^{R}I_{t}^{\alpha }\varPsi (x, t)=\varLambda '(t, \beta ) \varPsi (x, t)= (I_{{\hat{m}}\times {\hat{m}}}\otimes P_{{\tilde{m}}\times {\tilde{m}}}'(t, \beta )) \varPsi (x, t); \end{aligned}$$

(10)

here:

• I is matrix of identity,

• $\varLambda (x, \alpha )$ and $\varLambda '(t, \beta )$ are $({\hat{m}}{\tilde{m}})\times ({\hat{m}}{\tilde{m}})$ the 2D-MLWs operational matrices of fractional-order integration,

• $P(x, \alpha )$ and $P'(t, \beta )$ are the 1D-MLWs operational matrices of fractional-order integration obtained on [0, 1) as Rahimkhani et al. (2018):

  $$\begin{aligned} P(x, \alpha ) = \zeta ^{-1}F(x, \alpha ) \zeta , \end{aligned}$$

  (11)

  and

  $$\begin{aligned} P'(t, \beta ) = \zeta ^{-1}F'(t, \beta ) \zeta , \end{aligned}$$

  (12)

• $\zeta ^{-1}$ is the convert matrix of the MLWs to the piecewise fractional-order Taylor functions (PFTFs),

• matrices $F(x, \alpha )$ and $F'(t, \alpha )$ are the PFTFs’ operational matrices of fractional integration that these matrices are obtained in Rahimkhani et al. (2018).

4 Problem statement

In this study, we restrict ourselves on the following space-time FPDEs.

4.1 Problem a

The following FPDEs as:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}u(x, t)= F\left( x, t, u(x, t), {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}u(x, t), {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)\right) ,\quad 0\le x, t < 1, \end{aligned}$$

(13)

with Dirichlet boundary conditions as:

$$\begin{aligned} u(x, 0)= f_{0}(x), \quad u(0, t)=g_{0}(t), \quad u(1, t)=g_{1}(t), \end{aligned}$$

(14)

where $1< \alpha \le 2, 0< \beta , \nu \le 1$ and ${}_{0}^{C}{\mathcal {D}}^{\alpha }$ is Caputo fractional derivative.

4.2 Problem b

The FPDEs in Eq. (13) with boundary conditions as:

$$\begin{aligned} u(x, 0)= f_{0}(x), \quad u(0, t)=h_{1}(t), \quad u_{x}(0, t)=h_{2}(t). \end{aligned}$$

(15)

4.3 Problem c

The FPDEs with proportional delays as:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}u(x, t)= F\left( x, t, u(a_{0}x, b_{0}t), {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}u(a_{1}x, b_{1}t), {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(a_{2}x, b_{2}t)\right) ,\quad 0\le x, t < 1, \end{aligned}$$

(16)

subject to the initial and boundary conditions in Eq. (14).

5 Description of the bivariate Müntz–Legendre wavelets composite collocation method

In this part, we introduced the 2D Müntz–Legendre wavelets composite collocation method. For this purpose, let $x_{m}(m= 0, 1, \ldots , M-1)$ and $t_{m'}, (m'=0, 1, \ldots , M'-1)$ be zeros of the shifted Legendre polynomials $P_{M}(x)$ and $P_{M'}(t).$ Therefore, we define the composite collocation points as:

$$\begin{aligned} x_{nm}= & {} \frac{1}{2^{k-1}}(x_{m}+n-1), \quad n=1, 2, \ldots , 2^{k-1}; m=0, 1, \ldots , M-1, \end{aligned}$$

(17)

$$\begin{aligned} t_{n'm'}= & {} \frac{1}{2^{k'-1}}(t_{m'}+n'-1), \quad n'=1, 2, \ldots , 2^{k'-1}; m'=0, 1, \ldots , M'-1. \end{aligned}$$

(18)

We use the bivariate MLWs’ operational matrix of fractional-order integration, properties of Caputo fractional derivative, and the composite collocation scheme for solving problems (a), (b), and (c).

5.1 Problem a

For numerical solution of problem (a), we expand $\frac{\partial ^{\alpha + \nu }u(x, t)}{\partial x^{\alpha } \partial t^{\nu } }$ by the bivariate MLWs as:

$$\begin{aligned} \frac{\partial ^{\alpha + \nu }u(x, t)}{\partial x^{\alpha } \partial t^{\nu } } \simeq C^{T} \varPsi (x, t). \end{aligned}$$

(19)

Integrating of relation (19) of order $\nu$ with respect to t achieves:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}u(x, t)\simeq & {} {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}P_{M, M'}^{k, k'}u(x, t) = C^{T} \varLambda '(t, \nu ) \varPsi (x, t) + {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}u(x, t) \bigg \vert _{t=0}\nonumber \\= & {} C^{T} \varLambda '(t, \nu ) \varPsi (x, t) + {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}f_{0}(x). \end{aligned}$$

(20)

Also, by fractional integration from Eq. (19) of order $\alpha$ with respect to x,  we get:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t) \simeq C^{T} \varLambda (x, \alpha ) \varPsi (x, t) + {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t) \bigg \vert _{x=0} + x \frac{\partial }{\partial x}\left( {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t) \right) \bigg \vert _{x=0}. \end{aligned}$$

(21)

We put $x=1$ in Eq. (21), and using Eq. (14), we get:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)\simeq & {} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}P_{M, M'}^{k, k'}u(x, t)=C^{T} \varLambda (x, \alpha ) \varPsi (x, t) \nonumber \\&- x C^{T} \varLambda (1, \alpha ) \varPsi (1, t) + (1-x) {}_{0}^{C}{\mathcal {D}}^{\nu }_{t} g_{0}(t)+x{}_{0}^{C}{\mathcal {D}}^{\nu }_{t} g_{1}(t). \end{aligned}$$

(22)

Integrating Eq. (20) of order $\alpha$ with respect to x yields:

$$\begin{aligned} u(x, t) \simeq C^{T} \varLambda '(t, \nu ) \varLambda (x, \alpha ) \varPsi (x, t) + f_{0}(x)-f_{0}(0) -xf'_{0}(0)+g_{0}(t)+x\frac{\partial u(x, t)}{\partial x}\bigg \vert _{x=0}. \end{aligned}$$

(23)

We let $x=1$ in Eq. (23), and considering Eq. (14), then Eq. (23) can be expressed as:

$$\begin{aligned} u(x, t) \simeq P_{M, M'}^{k, k'}u(x, t)= & {} C^{T} \varLambda '(t, \nu ) \varLambda (x, \alpha ) \varPsi (x, t) \nonumber \\&- x C^{T}\varLambda '(t, \nu ) \varLambda (1, \alpha ) \varPsi (1, t) + \omega (x, t), \end{aligned}$$

(24)

where

$$\begin{aligned} \omega (x, t)= g_{0}(t) + f_{0}(x) -f_{0}(0) -xf'_{0}(0)+x\left( g_{1}(t) - g_{0}(t)\right) + x\left( -f_{0}(1) + f_{0}(0)+ f'_{0}(0)\right) . \end{aligned}$$

By derivative of order $\beta$ with respect to x from Eq. (24), we get:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}u(x, t)\simeq & {} {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}P_{M, M'}^{k, k'}u(x, t)= C^{T} \varLambda '(t, \nu ) \varLambda (x, \alpha - \beta ) \varPsi (x, t) \nonumber \\&- \frac{x^{1-\beta }}{\varGamma (2- \beta )}C^{T} \varLambda '(t, \nu ) \varLambda (1, \alpha ) \varPsi (1, t) + {}_{0}^{C}{\mathcal {D}}^{\beta }_{x} \omega (x, t). \end{aligned}$$

(25)

By substituting above approximations into Eq. (13) and replacing $\simeq$ by $=$ and collocating this equation at the composite collocation points given into Eqs. (17) and (18), we achieve:

$$\begin{aligned}&\displaystyle {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}P_{M,M'}^{k, k'}u(x_{n,m}, t_{n',m'})= F(x_{n,m}, t_{n',m'}, P_{M,M'}^{k, k'}u(x_{n,m}, t_{n',m'}), \nonumber \\&\displaystyle \quad {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}P_{M,M'}^{k, k'}u(x_{n,m}, t_{n',m'}), {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}P_{M,M'}^{k, k'}u(x_{n,m}, t_{n',m'})), \nonumber \\&\displaystyle \quad n=1, 2, \ldots , 2^{k-1}, \quad m=0, 1, \ldots , M-1,\nonumber \\&\displaystyle \quad n'=1, 2, \ldots , 2^{k'-1}, \quad m'=0, 1, \ldots , M'-1. \end{aligned}$$

(26)

Equation (26) gives ${\hat{m}}\times {\tilde{m}}$ equations, after solving this system by applying Newton’s iterative scheme (Stoer and Bulirsch 2002), we get unknown vector $C^{T}$.

For example 1, when $k=k'=2, M=M'=2$ and $\gamma =1$, we let: $c_{i}^{(0)}=0,\quad , i=0, \ldots ,15.$

Using Newton’s iterative scheme, we get:

• $c_{0}^{(1)}=c_{0}^{(2)}=\cdots =0.210757,$

• $c_{1}^{(1)}=c_{1}^{(2)}=\cdots =0.144816,$

• $c_{2}^{(1)}=c_{2}^{(2)}=\cdots =1.38863,$

• $c_{3}^{(1)}=c_{3}^{(2)}=\cdots =0.12982,$

• $c_{4}^{(1)}=c_{4}^{(2)}=\cdots =0.101842,$

• $c_{5}^{(1)}=c_{5}^{(2)}=\cdots =0.0710262,$

• $c_{6}^{(1)}=c_{6}^{(2)}=\cdots =0.457712,$

• $c_{7}^{(1)}=c_{7}^{(2)}=\cdots =0.035036,$

• $c_{8}^{(1)}=c_{8}^{(2)}=\cdots =0.106264,$

• $c_{9}^{(1)}=c_{9}^{(2)}=\cdots =0.0621804,$

• $c_{10}^{(1)}=c_{10}^{(2)}=\cdots =0.216712,$

• $c_{11}^{(1)}=c_{11}^{(2)}=\cdots =0.028955,$

• $c_{12}^{(1)}=c_{12}^{(2)}=\cdots =0.0528427,$

• $c_{13}^{(1)}=c_{13}^{(2)}=\cdots =0.0320725,$

• $c_{14}^{(1)}=c_{14}^{(2)}=\cdots =0.157604,$

• $c_{15}^{(1)}=c_{15}^{(2)}=\cdots =0.0320673.$

5.2 Problem b

For solving problem (b), we expand $\frac{\partial ^{3}u(x, t)}{\partial x^{2} \partial t }$ by the bivariate MLWs as:

$$\begin{aligned} \frac{\partial ^{3}u(x, t)}{\partial x^{2} \partial t } \simeq C^{T} \varPsi (x, t). \end{aligned}$$

(27)

Integrating with respect to x of Eq. (27) gives:

$$\begin{aligned} \frac{\partial ^{2}u(x, t)}{\partial x \partial t} \simeq C^{T} \varLambda (x, 1) \varPsi (x, t) + \frac{\partial ^{2}u(x, t)}{\partial x \partial t} \bigg \vert _{x=0} = C^{T} \varLambda (x, 1) \varPsi (x, t) + h'_{2}(t). \end{aligned}$$

(28)

Also, integrating from Eq. (27) with respect to t:

$$\begin{aligned} \frac{\partial ^{2}u(x, t)}{\partial x^{2}} \simeq C^{T} \varLambda '(t, 1) \varPsi (x, t) + \frac{\partial ^{2}u(x, t)}{\partial x^{2}} \bigg \vert _{t=0} = C^{T} \varLambda '(t, 1) \varPsi (x, t) + f''_{0}(x). \end{aligned}$$

(29)

Integrating with respect to x of Eq. (28) gives:

$$\begin{aligned} \frac{\partial u(x, t)}{ \partial t}\simeq & {} C^{T} \varLambda ^{2}(x, 1) \varPsi (x, t) + h'_{2}(t)x+ \frac{\partial u(x, t)}{ \partial t} \bigg \vert _{x=0} \nonumber \\= & {} C^{T} \varLambda ^{2}(x, 1) \varPsi (x, t) + h'_{2}(t)x+h'_{1}(t), \end{aligned}$$

(30)

and

$$\begin{aligned} u(x, t) \simeq C^{T} \varLambda ^{2}(x, 1) \varLambda '(t, 1) \varPsi (x, t) + \varpi (x, t), \end{aligned}$$

(31)

where

$\varpi (x, t) = x(h_{2}(t) - h_{2}(0))+ (h_{1}(t) - h_{1}(0)) + f_{0}(x).$

For $1 < \alpha \le 2$ by integrating from Eq. (29) with respect to x of order $2- \alpha$, we achieve:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}u(x, t)= & {} {} _{0}^{R} I_{x}^{2- \alpha }\bigg (\frac{\partial ^{2}u(x, t)}{\partial x^{2}}\bigg ) \simeq C^{T} \varLambda '(t, 1) \varLambda (x, 2-\alpha ) \varPsi (x, t) + {} _{0}^{R}I_{x}^{2- \alpha } {}_{0}^{C}{\mathcal {D}}^{2}_{x}f_{0}(x) \nonumber \\= & {} C^{T} \varLambda '(t, 1) \varLambda (x, 2-\alpha ) \varPsi (x, t) + {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}f_{0}(x). \end{aligned}$$

(32)

Also, for $0 < \nu \le 1$ by integrating from Eq. (30) with respect to t of order $1- \nu$, we get:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)= & {} {} _{0}^{R}I_{t}^{1- \nu }\bigg (\frac{\partial u(x, t)}{\partial t}\bigg ) \simeq C^{T} \varLambda ^{2}(x, 1) \varLambda '(t, 1-\nu ) \varPsi (x, t) \nonumber \\&+ x {} _{0}^{R}I_{t}^{1- \nu } {}_{0}^{C}\left( \frac{\partial h_{2}(t)}{\partial t}\right) + {} _{0}^{R}I_{t}^{1- \nu } {}_{0}^{C}{\mathcal {D}}_{t}\left( \frac{\partial h_{1}(t)}{\partial t}\right) \nonumber \\= & {} C^{T} \varLambda ^{2}(x, 1) \varLambda '(t, 1-\nu ) \varPsi (x, t) + x {}_{0}^{C}{\mathcal {D}}^{\nu }_{t} h_{2}(t)+ {}_{0}^{C}{\mathcal {D}}^{\nu }_{t} h_{1}(t). \end{aligned}$$

(33)

By derivative from Eq. (31) with respect to x of order $\beta$ yields:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}u(x, t)= & {} \simeq C^{T} \varLambda ^{2}(x, 1-\beta ) \varLambda '(t, 1) \varPsi (x, t)\nonumber \\&\qquad + \frac{x^{1-\beta }}{\varGamma (2 -\beta )}(h_{2}(t) - h_{2}(0))+{}_{0}^{C}{\mathcal {D}}^{\beta }_{x}f_{0}(x). \end{aligned}$$

(34)

We substitute above approximations in relation (13) and collocate obtained equation in composite collocation points $(x_{n,m}, t_{n',m'})$ given in Eqs. (17) and (18). This equation gives ${\hat{m}}{\tilde{m}}$ algebraic equations; after solving this system by applying Newton’s iterative scheme (Stoer and Bulirsch 2002), we achieve unknown vector $C^{T}$.

5.3 Problem c

For solving problem (c), by applying relations (22), (24) and (25), we get:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(a_{2}x, b_{2}t)\simeq & {} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}P^{k, k'}_{M, M'}u(a_{2}x, b_{2}t)= C^{T} \varLambda (a_{2}x, \alpha ) \varPsi (a_{2} x, b_{2}t) \nonumber \\&- a_{2} x C^{T} \varLambda (1, \alpha ) \varPsi (1, b_{2}t) + (1-a_{2}x) {}_{0}^{C}{\mathcal {D}}^{\nu }_{t} g_{0}(b_{2} t)+a_{2}x{}_{0}^{C}{\mathcal {D}}^{\nu }_{t} g_{1}(b_{2}t),\nonumber \\ \end{aligned}$$

(35)

and

$$\begin{aligned} u(a_{0}x, b_{0}t)\simeq & {} P_{M, M'}^{k, k'} u(a_{0}x, b_{0}t)= C^{T} \varLambda '(b_{0}t, \nu ) \varLambda (a_{0}x, \alpha ) \varPsi (a_{0}x, b_{0}t) \nonumber \\&- a_{0}x C^{T}\varLambda '(b_{0}t, \nu ) \varLambda (1, \alpha ) \varPsi (1, b_{0}t) + \omega (a_{0}x, b_{0}t), \end{aligned}$$

(36)

and

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}u(a_{1}x, b_{1}t)\simeq & {} {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}P_{M, M'}^{k, k'}u(a_{1}x, b_{1}t)= C^{T} \varLambda '(b_{1}t, \nu ) \varLambda (a_{1}x, \alpha - \beta ) \varPsi (a_{1}x, b_{1}t) \nonumber \\&- \frac{(a_{1}x)^{1-\beta }}{\varGamma (2- \beta )}C^{T} \varLambda '(b_{1}t, \nu ) \varLambda (1, \alpha ) \varPsi (1, b_{1}t) + {}_{0}^{C}{\mathcal {D}}^{\beta }_{x} \omega (a_{1} x, b_{1}t).\nonumber \\ \end{aligned}$$

(37)

By substituting Eqs. (20) and (35)–(37) into Eq. (16) and taking composite collocation points $(x_{n,m}, t_{n',m'}, n=1, 2, \ldots , 2^{k-1}, m=0, 1, \ldots , M-1, n'=1, 2, \ldots , 2^{k'-1}, m'=0, 1, \ldots , M'-1)$, in the obtained equation, we get:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}P_{M,M'}^{k, k'}u\left( x_{n,m}, t_{n',m'}\right)= & {} F\left( x_{n,m}, t_{n,m}, P_{M,M'}^{k, k'}u\left( a_{0}x_{n,m}, b_{0}t_{n',m'}\right) , \right. \nonumber \\&\left. {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}P_{M,M'}^{k, k'}u\left( a_{1}x_{n,m}, b_{1}t_{n',m'}\right) ,\right. \nonumber \\&\left. {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}P_{M,M'}^{k, k'}u\left( a_{2}x_{n,m}, b_{2}t_{n',m'}\right) \right) . \end{aligned}$$

(38)

This system is solved using Newton iteration scheme (Stoer and Bulirsch 2002) for finding vector C. Therefore, we achieve the approximate solution of the problem (c).

6 Convergence analysis

In this part, we derive the convergence of the approximate solution with respect to the bivariate Müntz–Legendre wavelets basis. Then, we give an error analysis of present method.

6.1 Error bound for the interpolation

We indicate convergence the bivariate MLWs expansion of a function u(x, t). First, we present some necessary symbols as:

$$\begin{aligned}&\left. \left. I_{k, n}= \left[ \frac{n-1}{2^{k-1}}, \frac{n}{2^{k-1}}\right) , \quad I_{k', n'}= \left[ \frac{n'-1}{2^{k'-1}}, \frac{n'}{2^{k'-1}}\right) ,\right. \right. \\&\varLambda = I_{k, n} \times I_{k' ,n'},\quad \varOmega = [0, 1) \times [0, 1),\\&R_{M, M'}^{k, k'}= \mathrm{sup} _{(x, t) \in \varOmega } \left| {}_{0}^{C}{\mathcal {D}}^{M \gamma }_{x} ({}_{0}^{C}{\mathcal {D}}^{M' \gamma }_{t}u(x, t)) \right| ,\\&r_{M, M'}^{k, k'}= \mathrm{sup} _{(x, t) \in \varLambda } \left| {}_{0}^{C}{\mathcal {D}}^{M \gamma }_{x} ({}_{0}^{C}{\mathcal {D}}^{M' \gamma }_{t}u(x, t)) \right| ,\\&L^{2}(\varOmega )= \lbrace \vartheta : \vartheta \hbox { is measurable on } \varOmega \hbox { and }\Vert \vartheta \Vert < \infty \rbrace . \end{aligned}$$

Theorem 1

Let ${}_{0}^{C}{\mathcal {D}}^{i \gamma }_{x} ({}_{0}^{C}{\mathcal {D}}^{j \gamma }_{t}u(x, t)) \in C(\varOmega )$ for $i=0, 1, \ldots , M; j=0, 1, \ldots , M'$ and $\varDelta _{M, M'}^{k, k'}=span \lbrace L_{0, 1}(x, t), L_{0, 2}(x, t), \ldots , L_{0, M'-1}(x, t), L_{1, 0}(x, t) \ldots , L_{M-1, M'-1}(x, t) \rbrace$ . If we show the best approximation solution of function u(x, t) from $\varDelta _{M, M'}^{k, k'}$ on $\varLambda$ by $p_{M, M'}^{k, k'}u(x, t)$, then the error bound of the approximate solution $P_{M, M'}^{k, k'}u(x, t)$ by applying bivariate Müntz–Legendre wavelets series on the interval $\varOmega$ would be obtained as:

$$\begin{aligned} \Vert u(x, t) - P_{M, M'}^{k, k'}u(x, t) \Vert _{L^{2}(\varOmega )} \le \frac{R_{M, M'}^{k, k'}}{\varGamma (M\gamma +1) \varGamma (M' \gamma +1) \sqrt{(2M\gamma +1) (2M'\gamma +1)}}. \end{aligned}$$

(39)

Proof

We define:

$$\begin{aligned} h_{M, M'}^{k, k'}(x, t) = \sum _{i=0}^{M-1} \sum _{j=0}^{M' -1}\frac{x^{i\gamma } t^{j\gamma }}{\varGamma (i \gamma +1) \varGamma (j\gamma +1)} {}_{0}^{C}{\mathcal {D}}^{i \gamma }_{x} ({}_{0}^{C}{\mathcal {D}}^{j \gamma }_{t}u(x, t))\bigg \vert _{(0, 0)}. \end{aligned}$$

(40)

Multi-variable Taylor formula (Hormander 1990) and generalized Taylor’s formula (Odibat and Shawagfeh 2007) yield:

$$\begin{aligned} \vert u(x, t) - h_{M, M'}^{k, k'}(x, t) \vert \le \frac{x^{M\gamma } t^{M' \gamma }}{\varGamma (M\gamma +1) \varGamma (M' \gamma +1)} r_{M, M'}^{k, k'}. \end{aligned}$$

(41)

Since $p_{M, M'}^{k, k'}u(x, t)$ is the best approximation solution of u(x, t) out of $\varDelta _{M, M'}^{k, k'}$ on $\varLambda$, we get:

$$\begin{aligned} \Vert u(x, t) - P_{M, M'}^{k, k'}u(x, t) \Vert _{L^{2}(\varOmega )}^{2}= & {} \Vert u(x, t) - C^{T}\varPsi (x, t) \Vert _{L^{2}(\varOmega )}^{2}\nonumber \\= & {} \sum _{n=1}^{2^{k-1}}\sum _{n'=1}^{2^{k'-1}} \Vert u(x, t) - p_{M, M'}^{k, k'}u(x, t) \Vert _{L^{2}(\varLambda )}^{2}\nonumber \\\le & {} \sum _{n=1}^{2^{k-1}}\sum _{n'=1}^{2^{k'-1}} \Vert u(x, t) - h_{M, M'}^{k, k'}(x, t) \Vert _{L^{2}(\varLambda )}^{2}\nonumber \\\le & {} \sum _{n=1}^{2^{k-1}}\sum _{n'=1}^{2^{k'-1}} \int _{I_{k, n}} \int _{I_{k', n'}} \bigg [ \frac{x^{M\gamma } t^{M' \gamma }}{\varGamma (M\gamma +1) \varGamma (M' \gamma +1)} r_{M, M'}^{k, k'} \bigg ] ^{2}\mathrm{d}t \mathrm{d}x \nonumber \\\le & {} \int _{0}^{1} \int _{0}^{1} \bigg [ \frac{x^{M\gamma } t^{M' \gamma }}{\varGamma (M\gamma +1) \varGamma (M' \gamma +1)}R_{M, M'}^{k, k'} \bigg ] ^{2}\mathrm{d}t \mathrm{d}x\nonumber \\\le & {} \frac{1}{\varGamma (M\gamma +1)^{2} \varGamma (M' \gamma +1)^{2}(2M\gamma +1) (2M'\gamma +1)}(R_{M, M'}^{k, k'})^{2},\nonumber \\ \end{aligned}$$

(42)

as a result of Eq. (42), we get Eq. (39) $\square$

Now, we can express the convergence of the presented scheme, which depends on two parameters $(M, M')$. By increasing $M, M'$, it implies that:

$$\begin{aligned} M, M'\rightarrow \infty , \quad \Vert u(x, t) - P_{M, M'}^{k, k'}u(x, t) \Vert _{L^{2}(\varOmega )}\rightarrow 0. \end{aligned}$$

6.2 Error analysis of present method

Now, we want to obtain error of present method; for this aim, we present following theorems.

Theorem 2

Suppose that $u(x, t), p_{M, M'}^{k, k'}u(x, t)$ and ${}_{0}^{C}{\mathcal {D}}^{i \gamma }_{x} ({}_{0}^{C}{\mathcal {D}}^{j \gamma }_{t}u(x, t))$ satisfy the conditions of Theorem 1. Then:

$$\begin{aligned}&\Vert {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } u(x, t) - {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } P_{M, M'}^{k, k'}u(x, t) \Vert _{L^{2}(\varOmega )}\nonumber \\&\quad \le \frac{1}{\varGamma (M\gamma +1-\alpha ) \varGamma (M' \gamma +1)\sqrt{ (2M\gamma -2\alpha +1) (2M'\gamma +1)}}R_{M, M'}^{k, k'}. \end{aligned}$$

(43)

Proof

According to Eq. (40) and properties of Caputo fractional derivative, we can write:

$$\begin{aligned} \left| {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } u(x, t) - {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } h_{M, M'}^{k, k'}(x, t) \right| \le \frac{x^{M\gamma - \alpha } t^{M' \gamma }}{\varGamma (M\gamma +1- \alpha ) \varGamma (M' \gamma +1)} r_{M, M'}^{k, k'}; \end{aligned}$$

(44)

then:

$$\begin{aligned}&\left\| {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } u(x, t) - {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } P_{M, M'}^{k, k'}u(x, t) \right\| _{L^{2}(\varOmega )}^{2} \nonumber \\&\quad = \sum _{n=1}^{2^{k-1}}\sum _{n'=1}^{2^{k'-1}} \left\| {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } u(x, t) - {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } p_{M, M'}^{k, k'}u(x, t) \right\| _{L^{2}(\varLambda )}^{2}\nonumber \\&\quad \le \sum _{n=1}^{2^{k-1}}\sum _{n'=1}^{2^{k'-1}} \left\| {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } u(x, t) - {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } h_{M, M'}^{k, k'}(x, t) \right\| _{L^{2}(\varLambda )}^{2}\nonumber \\&\quad \le \sum _{n=1}^{2^{k-1}}\sum _{n'=1}^{2^{k'-1}} \int _{I_{k, n}} \int _{I_{k', n'}} \left[ \frac{x^{M\gamma - \alpha } t^{M' \gamma }}{\varGamma (M\gamma +1- \alpha ) \varGamma (M' \gamma +1)} r_{M, M'}^{k, k'} \right] ^{2}\mathrm{d}t \mathrm{d}x \nonumber \\&\quad \le \int _{0}^{1} \int _{0}^{1} \left[ \frac{x^{M\gamma -\alpha } t^{M' \gamma }}{\varGamma (M\gamma +1-\alpha ) \varGamma (M' \gamma +1)}R_{M, M'}^{k, k'} \right] ^{2}\mathrm{d}t \mathrm{d}x\nonumber \\&\quad \le \frac{1}{\varGamma (M\gamma +1-\alpha )^{2} \varGamma (M' \gamma +1)^{2}(2M\gamma -2\alpha +1) (2M'\gamma +1)}(R_{M, M'}^{k, k'})^{2}. \end{aligned}$$

(45)

Therefore, the theorem is proved. $\square$

Corollary 1

According to the assumptions of Theorem 2, it yields:

$$\begin{aligned}&\left\| {}_{0}^{C}{\mathcal {D}}_{x}^{\beta } u(x, t) - {}_{0}^{C}{\mathcal {D}}_{x}^{\beta } P_{M, M'}^{k, k'}u(x, t) \right\| _{L^{2}(\varOmega )}\nonumber \\&\quad \le \frac{1}{\varGamma (M\gamma +1-\beta ) \varGamma (M' \gamma +1) \sqrt{(2M\gamma -2\beta +1) (2M'\gamma +1)}}R_{M, M'}^{k, k'}. \end{aligned}$$

(46)

Proof

It is an immediate consequence of Theorem 2. $\square$

Corollary 2

According to the assumptions of Theorem 2, we have:

$$\begin{aligned}&\left\| {}_{0}^{C}{\mathcal {D}}_{t}^{\nu } u(x, t) - {}_{0}^{C}{\mathcal {D}}_{t}^{\nu } P_{M, M'}^{k, k'}u(x, t) \right\| _{L^{2}(\varOmega )}\nonumber \\&\quad \le \frac{1}{\varGamma (M\gamma +1) \varGamma (M' \gamma +1-\nu ) \sqrt{(2M\gamma +1) (2M'\gamma +1-2\nu )}}R_{M, M'}^{k, k'}. \end{aligned}$$

(47)

Proof

It is an immediate consequence of Theorem 2. $\square$

Theorem 3

According to the assumptions of Theorem 2 and suppose F in Eq. (13) is Lipschitz, with the Lipschitz constants $\eta _{1}, \eta _{2}$ and $\eta _{3}$. The error bound $(E_{M, M'}^{k, k'})$ is given by:

$$\begin{aligned} \Vert E_{M, M'}^{k, k'}(x, t)\Vert _{L^{2}(\varOmega )}\le & {} \frac{R_{M, M'}^{k, k'}}{\varGamma (M\gamma +1-\alpha ) \varGamma (M' \gamma +1) \sqrt{(2M\gamma -2\alpha +1) (2M'\gamma +1)}}\nonumber \\&+ \eta _{1}\frac{R_{M, M'}^{k, k'}}{\varGamma (M\gamma +1) \varGamma (M' \gamma +1)\sqrt{(2M\gamma +1) (2M'\gamma +1)}}\nonumber \\&+ \eta _{2}\frac{R_{M, M'}^{k, k'}}{\varGamma (M\gamma +1-\beta ) \varGamma (M' \gamma +1) \sqrt{(2M\gamma -2\beta +1) (2M'\gamma +1)}}\nonumber \\&+ \eta _{3} \frac{R_{M, M'}^{k, k'}}{\varGamma (M\gamma +1) \varGamma (M' \gamma +1-\nu ) \sqrt{(2M\gamma +1) (2M'\gamma +1-2\nu )}}.\nonumber \\ \end{aligned}$$

(48)

Proof

We know:

$$\begin{aligned} \Vert E_{M, M'}^{k, k'}(x, t)\Vert _{L^{2}(\varOmega )}= & {} \left\| {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}P_{M, M'}^{k, k'}u(x, t)- F(x, t, P_{M, M'}^{k, k'}u(x, t),\right. \nonumber \\&\left. {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}P_{M, M'}^{k, k'}u(x, t), {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}P_{M, M'}^{k, k'}u(x, t)) \right\| _{L^{2}(\varOmega )}. \end{aligned}$$

(49)

By applying relation (13), we obtain:

$$\begin{aligned} \Vert E_{M, M'}^{k, k'}(x, t)\Vert _{L^{2}(\varOmega )}= & {} \left\| {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}u(x, t)- F\left( x, t, u(x, t), {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}u(x, t), {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)\right) \right. \nonumber \\&\left. - {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}P_{M, M'}^{k, k'}u(x, t)+F\left( x, t, P_{M, M'}^{k, k'}u(x, t),\nonumber \right. \right. \\&\left. \left. {}_{0}^{C}{\mathcal {D}}^{\beta }_{x}P_{M, M'}^{k, k'}u(x, t), {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}P_{M, M'}^{k, k'}u(x, t)\right) \right\| _{L^{2}(\varOmega )}, \end{aligned}$$

(50)

since F satisfies a Lipschitz condition with Lipschitz constants $\eta _{1}, \eta _{2}$ and $\eta _{3}$, we have:

$$\begin{aligned} \Vert E_{M, M'}^{k, k'}(x, t)\Vert _{L^{2}(\varOmega )}\le & {} \left\| {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } u(x, t) - {}_{0}^{C}{\mathcal {D}}_{x}^{\alpha } P_{M, M'}^{k, k'}u(x, t) \right\| _{L^{2}(\varOmega )}\nonumber \\&+ \eta _{1} \left\| u(x, t) - P_{M, M'}^{k, k'}u(x, t) \right\| _{L^{2}(\varOmega )}\nonumber \\&+ \eta _{2} \left\| {}_{0}^{C}{\mathcal {D}}_{x}^{\beta }u(x, t) - {}_{0}^{C}{\mathcal {D}}_{x}^{\beta }P_{M, M'}^{k, k'}u(x, t) \right\| _{L^{2}(\varOmega )}\nonumber \\&+ \eta _{3} \left\| {}_{0}^{C}{\mathcal {D}}_{t}^{\nu }u(x, t) - {}_{0}^{C}{\mathcal {D}}_{t}^{\nu }P_{M, M'}^{k, k'}u(x, t) \right\| _{L^{2}(\varOmega )}. \end{aligned}$$

(51)

Using Eqs. (39), (43), (46), and (47), we yield:

$$\begin{aligned}&\Vert E_{M, M'}^{k, k'}(x, t)\Vert _{L^{2}(\varOmega )} \nonumber \\&\quad \le \frac{1}{\varGamma (M\gamma +1-\alpha ) \varGamma (M' \gamma +1) \sqrt{(2M\gamma -2\alpha +1) (2M'\gamma +1)}}R_{M, M'}^{k, k'}\nonumber \\&\qquad + \eta _{1}\frac{1}{\varGamma (M\gamma +1) \varGamma (M' \gamma +1)\sqrt{(2M\gamma +1) (2M'\gamma +1)}}R_{M, M'}^{k, k'}\nonumber \\&\qquad + \eta _{2}\frac{1}{\varGamma (M\gamma +1-\beta ) \varGamma (M' \gamma +1) \sqrt{(2M\gamma -2\beta +1) (2M'\gamma +1)}}R_{M, M'}^{k, k'}\nonumber \\&\qquad + \eta _{3} \frac{1}{\varGamma (M\gamma +1) \varGamma (M' \gamma +1-\nu ) \sqrt{(2M\gamma +1) (2M'\gamma +1-2\nu )}}R_{M, M'}^{k, k'}; \end{aligned}$$

(52)

therefore, the proof is complete. $\square$

Remark 2

Error of method of problems (b) and (c) is similar of problem (a) that we obtain above theorems.

7 Numerical experiments

In this part, we present five examples to show the validity and applicability of the applied technique. The computations were performed on a personal computer, and the codes were written in Mathematica 10.

7.1 Problem a

Example 1

Consider the space-time-fractional Convection–Diffusion equation as: (Wei et al. 2012; Chen et al. 2014)

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)+x^{0.8}u_{x}(x, t)-(\varGamma (2.8)x/2){}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}u(x, t)+x^{1.5}u(x,t)=f(x, t),\quad 0 \le x,t <1, \end{aligned}$$

(53)

where

$$\begin{aligned} f(x, t)=\frac{\varGamma (3)x^{2}(1-x)t^{1.2}}{\varGamma (2.2)}+\left[ 2x^{1.8}-3x^{2.8}-\frac{\varGamma (2.8)\varGamma (3) x^{1.5}}{2\varGamma (1.5)}+\frac{ \varGamma (2.8) \varGamma (4) x^{2.5}}{2\varGamma (2.5)}+x^{3.5}-x^{4.5}\right] t^{2} \end{aligned}$$

and

$$\begin{aligned} u(x, 0) = u(0, t) = u(1, t) =0. \end{aligned}$$

For the above equation, we have the analytical solution $u(x, t)= x^{2}(1-x)t^{2},$ when $\alpha =1.5 , \nu =0.8$.

In Tables 1 and 2 we compare absolute error of proposed scheme for $M=M'=3; k=k'=2; \gamma =1$ with Haar wavelet method (Chen et al. 2014) for $m=n=3$ and Tau method based on fractional-order Legendre functions (Wei et al. 2012) for $m=8$. Also, CPU time of suggested scheme is presented in Tables 1 and 2.

Table 1 Comparison of absolute error for $k=k'=2, \gamma =1$ of Example 1

Table 2 Comparison of absolute error for $k=k'=2, \gamma =1$ of Example 1

Example 2

Consider the following nonlinear fractional heat equation as: Daftardar-Gejji and Bhalekar (2010)

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)= u_{xx}(x, t) + u(x, t)u_{x}(x, t), \quad 0< \nu \le 1, \end{aligned}$$

(54)

subject to

$$\begin{aligned} u(x, 0)=2-x,\quad u(0, t)=\frac{2}{1+t},\quad u(1, t)= \frac{1}{1+t}. \end{aligned}$$

The analytical solution is $u(x, t) = \frac{2-x}{1+t},$ when $\nu =1.$

We solve the above problem by applying the bivariate MLWs with $M=M'=1; k=k'=2; \nu =1$ and every value of $\gamma$. Let:

$$\begin{aligned} \frac{\partial ^{2+\nu }u(x, t)}{\partial x^{2}\partial t^{\nu }}\simeq c_{0}\psi _{0}(x, t) +c_{1}\psi _{1}(x, t) +c_{2}\psi _{2}(x, t) +c_{3}\psi _{3}(x, t)= C^{T}\varPsi (x, t), \end{aligned}$$

(55)

where

$$\begin{aligned} C^{T}=[c_{0}, c_{1}, c_{2}, c_{3}],\quad \varPsi (x, t)= [\psi _{0}(x, t), \psi _{1}(x, t), \psi _{2}(x, t), \psi _{3}(x, t)]^{T}. \end{aligned}$$

Using Eqs. (20), (22), (24), (25), (55), and conditions of problem for $\alpha =2, \beta =1$, achieve:

$$\begin{aligned} u_{xx}(x, t)\simeq & {} C^{T}\varLambda '(t, \nu ) \varPsi (x, t), \end{aligned}$$

(56)

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)\simeq & {} C^{T}\varLambda (x, 2)\varPsi (x, t) -x C^{T}\varLambda (1, 2) \varPsi (1, t)+ \frac{x-2}{(1+t)^{2}}, \end{aligned}$$

(57)

$$\begin{aligned} u(x, t)\simeq & {} C^{T}\varLambda '(t, \nu ) \varLambda (x, 2) \varPsi (x, t) - x C^{T}\varLambda '(t, \nu ) \varLambda (1, 2) \varPsi (1, t)+\frac{2-x}{1+t},\nonumber \\ \end{aligned}$$

(58)

and

$$\begin{aligned} u_{x}(x, t) \simeq C^{T}\varLambda ' (t, \nu ) \varLambda (x, 1) \varPsi (x, t) - C^{T}\varLambda ' (t, \nu ) \varLambda (1, 2)\varPsi (1, t)- \frac{1}{1+t}. \end{aligned}$$

(59)

By substituting Eqs. (56)–(59) into Eq. (54) and collocating this equation in the following composite collocation points:

$$\begin{aligned} x_{1, 0}= t_{1,0}=0.25,\quad x_{1, 1}=t_{1,1}=0.75, \end{aligned}$$

and by solving the obtained system of equations yields:

$$\begin{aligned} c_{0}=c_{1}=c_{2}=c_{3}=0. \end{aligned}$$

Therefore, by employing relation (58), we obtain $u(x, t)=\frac{2-x}{1+t}$ which is the analytical solution of problem.

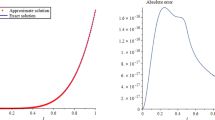
In Fig. 3, we compare our numerical results with a iterative technique in Daftardar-Gejji and Bhalekar (2010), Adomian decomposition technique, and the exact solution for case $\nu =1$ at $t=0.3$. Figure 4a, b shows approximate solutions with Daftardar-Gejji and Bhalekar (2010) and the suggested method, respectively, for $\nu =1.$ Also, the CPU time (in seconds) of this problem is 0.250.

Fig. 3

Comparison of our numerical results at $M=M'=1, k=k'=2$ with other schemes of Example 2

Fig. 4

Comparison of our numerical results at $M=M'=1, k=k'=2$ with iterative scheme of Example 2

7.2 Problem b

Example 3

Consider the space fractional advection-dispersion equation as: Momani and Odibat (2008)

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}u(x, t)=u_{x}(x, t) + u_{t}(x, t) +f(x, t), \quad 1< \alpha \le 2, \end{aligned}$$

(60)

where

$$\begin{aligned} f(x, t) = 2-2t-2x, \end{aligned}$$

subject to:

$$\begin{aligned} u(x, 0)=x^{2},\quad u(0, t)=t^{2},\quad u_{x}(0, t)= 0. \end{aligned}$$

For the above equation, we have the analytical solution $u(x, t) = x^{2}+t^{2}$ when $\alpha =2$.

For solving the above example, we let $k=k'=2, M=M'=2,$ with every value of $0 < \gamma \le 1$. Using approximating $\frac{\partial ^{3}u(x, t)}{\partial x^{2} \partial t}$, we obtain:

$$\begin{aligned} \frac{\partial ^{3}u(x, t)}{\partial x^{2} \partial t} \simeq \sum _{i=0}^{15}c_{i}\psi _{i}(x, t) = C^{T} \varPsi (x, t). \end{aligned}$$

(61)

From Eqs. (32), (30), and (31), we have:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\alpha }_{x}u(x, t)\simeq & {} C^{T}\varLambda '(t, 1) \varLambda (x, 2-\alpha ) \varPsi (x, t) + \frac{2}{\varGamma (3- \alpha )} x^{2-\alpha }, \end{aligned}$$

(62)

$$\begin{aligned} \frac{\partial u(x, t)}{\partial t}\simeq & {} C^{T}\varLambda ^{2}(x, 1) \varPsi (x, t)+ 2t, \end{aligned}$$

(63)

and

$$\begin{aligned} u(x, t) \simeq C^{T}\varLambda ^{2}(x, 1) \varLambda ' (t, 1) \varPsi (x, t) + x^{2} + t^{2}. \end{aligned}$$

(64)

Now, by derivative from Eq. (64) of order 1 with respect to x, achieve:

$$\begin{aligned} \frac{\partial u(x, t)}{\partial x} \simeq C^{T}\varLambda (x, 1) \varLambda ' (t, 1) \varPsi (x, t) + 2x. \end{aligned}$$

(65)

By substituting Eqs. (62)–(65) into Eq. (60) and collocating this equation in the following composite collocation point:

$$\begin{aligned} x_{1,0}= & {} t_{1,0}=0.105662,\quad x_{1,1}=t_{1,1}=0.394338,\\ x_{2,0}= & {} t_{2,0}=0.605662,\quad x_{2,1}=t_{2,1}=0.894338, \end{aligned}$$

and by solving the obtained system of equations yields:

$$\begin{aligned} c_{i}=0, \quad i=0, 1, \ldots , 15. \end{aligned}$$

By applying relation (64), we obtain the exact value u(x, t) for $\alpha =2.$ Also, The CPU time (in seconds) of this problem for this case is 0.625.

We plot the numerical solution of u(0.6, t) and u(x, 0.6) for $\gamma =1$ with different values of $\alpha$ in Fig. 5a, b. Results indicate that when $\alpha$ approaches to 2, the numerical solutions tend to the analytical solution. Figures. 6, 7, 8 represent the graphs of the numerical solutions and contour plot using the proposed method with $\gamma = \frac{1}{3}$ and $M=M'=2; k=k'=2$ for $\alpha = 2, 1.9, 1.8$, respectively.

Fig. 5

Numerical solution of present approach for different values of $\alpha$ with $k=k'=2, M=M'=2, \gamma = 1$ for Example 3

Fig. 6

a Numerical solution and b contour plot with $\alpha =2$ and $\gamma = \frac{1}{3}$ for Example 3

Fig. 7

a Numerical solution and b contour plot with $\alpha =1.9$ and $\gamma = \frac{1}{3}$ for Example 3

Fig. 8

a Numerical solution and b contour plot with $\alpha =1.8$ and $\gamma = \frac{1}{3}$ for Example 3

Example 4

Consider the following time FPDEs as (Chen et al. 2010; Saadatmandi et al. 2012):

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)= - u_{xx}(x, t)-xu_{x}(x, t) +f(x, t), \quad 0 < \nu \le 1, \end{aligned}$$

(66)

where

$$\begin{aligned} f(x, t)=2x^{2}+2t^{\nu }+2, \end{aligned}$$

subject to:

$$\begin{aligned} u(x, 0)= x^{2}, \quad u(0, t) = \frac{2\varGamma (\nu +1)}{\varGamma (2 \nu +1)}t^{2\nu }, \quad u_{x}(0, t) = 0. \end{aligned}$$

For above equation, we have the exact solution $u(x, t) = x^{2}+ \frac{2 \varGamma (\nu +1)}{\varGamma (2\nu +1)}t^{2\nu }$ when $\nu =1.$

For solving the above example, we let $k=k'=2, M=M'=1$ with every value of $0 < \gamma , \nu \le 1.$ By attention Eqs. (33), (29), and (31), yield:

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)\simeq & {} C^{T}\varLambda ^{2}(x, 1) \varLambda '(t, 1-\nu )\varPsi (x, t)+2 t^{\nu }, \end{aligned}$$

(67)

$$\begin{aligned} u_{xx}(x, t)\simeq & {} C^{T} \varLambda '(t, 1) \varPsi (x, t) +2, \end{aligned}$$

(68)

and

$$\begin{aligned} u(x, t) \simeq C^{T}\varLambda ^{2}(x, 1) \varLambda '(t, 1) \varPsi (x, t) + \frac{2 \varGamma (\nu +1)}{\varGamma (2 \nu +1)}t^{2\nu } +x^{2}. \end{aligned}$$

(69)

By derivative from Eq. (69) of order 1 with respect to x, we obtain:

$$\begin{aligned} u_{x}(x, t) \simeq C^{T} \varLambda (x, 1) \varLambda '(t, 1)\varPsi (x, t) +2x. \end{aligned}$$

(70)

By substituting Eqs. (67)–(70) into Eq. (66) and collocating this equation in the composite collocation points given in (17) and (18), we obtain the unknown vector C, and by applying Eq. (69), we achieve the exact solution for every value of $\nu$.

Table 3 establishes the comparison of absolutes error of suggested scheme for $M=M'=1, k=k'=2$ together with the Haar wavelet (Chen et al. 2010) for $m=64$ and Sinc–Legendre collocation technique (Saadatmandi et al. 2012) for $m=25$. The graphs of numerical solution and contour plot are shown in Fig. 9a, b.

Table 3 Comparison of absolute error for $\nu = 0.5, t=0.5, \gamma = \alpha$ of Example 4

Fig. 9

a Numerical solution and b contour plot with $\gamma = \nu =0.5$ of Example 4

7.3 Problem c

Example 5

Consider the time fractional Burgers equation with proportional delay as Singh and Kumar (2017):

$$\begin{aligned} {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t)= u_{xx}(x, t)+ u\left( \frac{x}{2}, \frac{t}{2}\right) u_{x}\left( x, \frac{t}{2}\right) + \frac{1}{2}u(x, t), \quad 0 < \nu \le 1, \end{aligned}$$

(71)

subject to:

$$\begin{aligned} u(x, 0)= x, \quad u(0, t) = 0, \quad u(1, t) = e^{t}. \end{aligned}$$

For above equation, we have the analytical solution $u(x, t) = xe^{t}$ when $\nu =1$.

For numerical solution of this example, we select $k = k'= 2; M = M'= 2$ and $\gamma = \frac{1}{2}.$ From Eqs. (20), (22), (36), (37), and (24) for $\alpha =2$ and $\beta =1$, we have:

$$\begin{aligned}&\displaystyle u_{xx}(x, t) \simeq C^{T} \varLambda '(t, \nu ) \varPsi (x, t), \end{aligned}$$

(72)

$$\begin{aligned}&\displaystyle {}_{0}^{C}{\mathcal {D}}^{\nu }_{t}u(x, t) \simeq C^{T}\varLambda (x, 2) \varPsi (x, t) - x C^{T}\varLambda (1, 2) \varPsi (1, t) + xt^{1- \nu }E_{1, 2-\nu }(t), \end{aligned}$$

(73)

$$\begin{aligned}&\displaystyle u\left( \frac{x}{2}, \frac{t}{2}\right) \simeq C^{T}\varLambda ' \left( \frac{t}{2}, \nu \right) \varLambda \left( \frac{x}{2}, 2\right) \varPsi \left( \frac{x}{2}, \frac{t}{2}\right) - \frac{x}{2} C^{T} \varLambda '\left( \frac{t}{2}, \nu \right) \varLambda (1, 2) \varPsi \left( 1, \frac{t}{2}\right) + \frac{x}{2} e^{\frac{t}{2}}, \end{aligned}$$

(74)

$$\begin{aligned}&\displaystyle u_{x}\left( x, \frac{t}{2}\right) \simeq C^{T}\varLambda '\left( \frac{t}{2}, \nu \right) \varLambda (x, 1) \varPsi \left( x, \frac{t}{2}\right) - C^{T}\varLambda ' \left( \frac{t}{2}, \nu \right) \varLambda (1, 2) \varPsi \left( 1, \frac{t}{2}\right) +e^{\frac{t}{2}}, \end{aligned}$$

(75)

$$\begin{aligned}&\displaystyle u(x, t) \simeq C^{T}\varLambda '(t, \nu ) \varLambda (x, 2) \varPsi (x, t) - xC^{T}\varLambda ' (t, \nu ) \varLambda (1, 2) \varPsi (1, t)+xe^{t}. \end{aligned}$$

(76)

By substituting Eqs. (72)–(76) into Eq. (71) and collocating this equation in the composite collocation points given in (17) and (18), and Newton’s iterative scheme, we achieve the analytical solution for $\nu =1$.

Table 4 displays the absolute error of suggested scheme by choosing $k=k'=2; M=M'=2; \nu =1$ and $\gamma = \frac{1}{2}, 1$ together with homotopy perturbation transform method (Singh and Kumar 2017). In addition, CPU time for $\gamma =\frac{1}{2}$ and $\gamma = 1$ are revealed in Table 4. The plots of the solution with present method and Singh and Kumar (2017) for various values of $\nu = 0.8, 0.9, 1$ are depicted in Fig. 10. Also, the numerical solutions behavior of u(x, t) and contour plots for various values of $\nu = 0.8, 0.9, 1$ are depicted in Figs. 11, 12, and 13.

Table 4 Comparison of absolute error for $k=k'=2, M=M' =2, \gamma =\frac{1}{2}, 1$ for Example 5

Fig. 10

Approximate solutions of (left side): present method with $\gamma =1$ and (right side): Singh and Kumar (2017) with $\nu =0.8, 0.9, 1$ for Example 5

Fig. 11

a Numerical solution and b contour plot with $\nu =1, \gamma =\frac{1}{2}$ for $M=M'=2$ and $k=k'=2$ of Example 5

Fig. 12

a Numerical solution and b contour plot with $\nu =0.9, \gamma =\frac{1}{2}$ at $M=M'=2$ and $k=k'=2$ of Example 5

Fig. 13

a Numerical solution and b contour plot with $\nu =0.8, \gamma =\frac{1}{2}$ for $M=M'=2$ and $k=k'=2$ of Example 5

8 Discussion and future work

The aim of this study was to present an effective numerical algorithm for solving three classes of FPDEs using bivariate MLWs. The MLWs’ operational matrix of fractional integration is derived. This operational matrix and the composite collocation scheme are used to transform FPDEs into systems of nonlinear equations to provide an approximate solution of FPDEs. The obtained results by our technique emphasized that:

• 1. The scheme is very easy to implement and achieves high accurate approximate solutions.

• 2. Few terms of bivariate MLWs are applied to provide effective and accuracy results.

• 3. The bivariate MLWs’ scheme has less CPU time when compared to the other schemes.

• 4. There are three degrees of freedom $(k, M, \gamma )$ for MLWs, but two degrees of freedom (k, M) for other wavelets.

• 5. Stability analysis of the suggested technique for numerical solution of FPDEs is an interesting problem for future work.