Robust $H_{\infty }$ Filters for Uncertain Systems with Finite Frequency Specifications

Abstract

This paper deals with $H_{\infty }$ filtering problem of linear discrete-time uncertain systems with finite frequency input signals. The uncertain parameters are supposed to reside in a polytope. By applying the generalized Kalman–Yakubovich–Popov lemma, polynomially parameter-dependent Lyapunov function and some key matrices to eliminate the product terms between the filter parameters and the Lyapunov matrices, an improved condition is obtained for analyzing the $H_{\infty }$ performance of the filtering error system. Then sufficient condition in terms of linear matrix inequality is established for designing filters with a guaranteed $H_{\infty }$ filtering performance level. Finally, a numerical examples are used to demonstrate the effectiveness of the proposed method.

1 Introduction

Over the past decades, the filtering problem has been widely studied and has found many practical applications in signal processing and communication, particularly for the study of practical electrical circuits systems. The $H_{\infty }$ filtering was introduced for the first time in Elsayed and Grimble (1989), in which external noise signal is assumed to be energy bounded, and the main objective is to minimize the $H_{\infty }$ norm from the process noise to the estimation error. A great number of $H_{\infty }$ filtering results have been reported (Li and Fu 1977; Oliveira et al. 1999; Benzaouia et al. 2016; Boukili et al. 2013), and various approaches, such as the linear matrix inequalities (LMIs) and parameter-dependent Lyapunov function, were adopted in order to reduce the conservatism of the problem. For instance, the polynomial equation approach (Gao and Li 2014; Grimble and El Sayed 1990; El-Kasri et al. 2013; De Souza et al. 2010; Boukili et al. 2016a; Gao et al. 2008; Lacerda et al. 2011), the algebraic Riccati equation approach (Nagpal and Khargonekar 1991; Takaba and Katayama 1996), the reduced order $H_{\infty }$ filtering problem (Geromel and Levin 2006; Boukili et al. 2016b), the mixed $H_{\infty }/H_{2}$ filtering design problem (Li et al. 2016; Rotstein et al. 1996; Qiu et al. 2008; Palhares and Peres 2001), the robust $H_{\infty }$ filtering problem, and the $H_{\infty }$ filtering problem for uncertain discrete-time systems (Duan et al. 2006; Chang et al. 2015; Dong and Yang 2013) are among the results on this topic.

The aforementioned techniques deal with the full frequency domain, however, if the frequency ranges of noises are known beforehand, for these case, designing a filter in the full frequency domain may introduce some unnecessary conservatism. In this view, the generalized Kalman–Yakobovich–Popov (gKYP) lemma (Iwasaki and Hara 2005) may be used to cast a certain frequency domain inequality in a finite frequency range in terms of an LMIs condition, which involves the matrices that composes the system’s transfer function. The results of the literature dealing this problem are given in Gao and Li (2011), Iwasaki et al. (2005, 2011), Wang et al. (2013), Lee (2013), Li and Yang (2014), Romao et al. (2016), Ding and Yang (2009), Li and Gao (2012), Li and Gao (2013), Chen et al. (2010), El-amrani et al. (2016) and reference therein.

The aim of this paper is to cope with the $H_{\infty }$ filtering problem for a class of discrete time systems with finite frequency specifications. We use the gKYP lemma, and the homogeneous polynomially parameter-dependent matrices of arbitrary degree approach. In the case in which a priori information about the noise is known (i.e, their frequency spectrum), the filters designed by the proposed condition have better performance in terms of the $H_{\infty }$ norm than those obtained with full frequency specifications. The theoretical results are given in the form of LMIs, which can be solved by standard numerical software, thus providing a simple methodology. By comparing with the existing full frequency methods (Gao and Li 2014; Lacerda et al. 2011; Lee 2013) and FF approach in Lee (2013), the FF method proposed in this paper receives better results for the cases when frequency ranges of noises are known. Numerical examples are also given to illustrate the effectiveness of the proposed approach.

This paper is organized as follows. In Sect. 2, the system description and the design objectives are presented. In Sect. 3, a sufficient condition guaranteeing robust asymptotic stability with finite frequency and entire frequency $H_{\infty }$ performance for such discrete time systems is derived by means of LMI technique. Using this result, the filter design problem is solved in Sect. 4. Examples are given in Sect. 5, and conclusions are drawn in Sect.  6.

$\mathbf {Notations:}$ The superscript $``T''$ stands for matrix transposition. In symmetric block matrices or long matrix expressions, we use an asterisk $``*''$ to represent a term that is induced by symmetry. The notation $P>0$ means that matrix P is positive semi definite. The symbol I denotes an identity matrix with appropriate dimension. Generally, $sym\{A\}$ denotes $A+A^{T}$, $diag\{..\}$ stands for block diagonal matrix. ${\bar{\sigma }}(G)$ denotes the maximum singular value of the transfer matric G.

2 Problem Formulation and Preliminaries

Consider the following robust asymptotically stable linear time-invariant discrete-time system:

$$\begin{aligned}&x(k+1)=A_{\alpha }x(k)+ B_{\alpha }w{(k)}\nonumber \\&y(k)=C_{\alpha } x(k)+ D_{\alpha }w{(k)}\\&z(k)=L_{\alpha }x(k)+ E_{\alpha }w{(k)}\nonumber \end{aligned}$$

(1)

where $x{(k)}\in {\mathbb {R}}^{n_{x}}$ is the state vector, $y{(k)}\in {\mathbb {R}}^{n_{y}}$ is the measured output, $z{(k)}\in {\mathbb {R}}^{n_{z}}$ is the signal to be estimated, $w{(k)}\in {\mathbb {R}}^{n_{w}}$ is the noise series satisfying $w={w(k)}\in \ell _{2}[0,\infty )$, whose energy is known to reside in one of the following sets frequency of w(k) resides in a known but finite frequency set $\varTheta$ is assumed to be the general LF/MF/HF form defined as

$$\begin{aligned} \Theta= & {} \left\{ \begin{array}{ll} \theta \in {\mathbb {R}}| |\theta |\le \theta _{l},\theta _{l}\ge 0,(LF)\\ \theta \in {\mathbb {R}}| \theta _{1}\le \theta \le \theta _{2}, 0\le \theta _{2}-\theta _{1}\le 2\pi ,(MF)\\ \theta \in {\mathbb {R}}| |\theta |\ge \theta _{h},\theta _{h}\ge 0,(HF) \end{array} \right. \end{aligned}$$

(2)

where LF, MF and HF stand for low-, middle-, and high- frequency ranges, respectively. The system matrices

$$\begin{aligned} \varOmega _{\alpha }= & {} \{A_{\alpha },\; B_{\alpha },\; C_{\alpha } ,\;D_{\alpha },\; L_{\alpha },\;E_{\alpha }\} \end{aligned}$$

(3)

belong to a convex bounded polyhedral domain, described by

$$\begin{aligned} \Gamma= & {} \left\{ \varOmega _{\alpha }|\varOmega _{\alpha }=\sum _{i=1}^{s}\alpha _{i}\varOmega _{i};\; \sum _{i=1}^{s}\alpha _{i}=1,\; \alpha _{i}\ge 0\right\} \end{aligned}$$

(4)

where

$$\begin{aligned} \varOmega _{i}:= & {} (A_{i},\; B_{i},\; C_{i},\; D_{i},\; L_{i},\; E_{i}) \end{aligned}$$

(5)

denotes the ith vertex of the polytope. The dynamic matrix $A_{\alpha }$ is said to be Hurwitz (Schur) stable if the eigenvalues lie in the open left-half plane (inside the unit disk) for all $\alpha \in \Gamma$.

In this paper, we consider the following $H_{\infty }$ filter to estimate z(k)

$$\begin{aligned}&{\hat{x}}(k+1) = A_{f}\hat{x}(k)+B_{f}w(k)\nonumber \\&{\hat{z}}(k) = C_{f}\hat{x}(k)+D_{f}w(k) \end{aligned}$$

(6)

where $\hat{x}(k)\in {\mathbb {R}}^{n_{x}}$ is the filter state vector, $\hat{z}(k)\in {\mathbb {R}}^{n_{z}}$ is the output of the filter. The matrices $A_{f}$, $B_{f}$, $C_{f}$ and $D_{f}$ are the filter matrices to be determined.

Defining $\xi (k)=\left[ \begin{array}{cc} x(k)^{T} &{} \quad \hat{x}(k)^{T}\\ \end{array} \right] ^{T}$ and $e(k)=z(k)- \hat{z}(k)$, the filtering error system is given by

$$\begin{aligned}&\xi (k+1) = {\bar{A}}_{\alpha }\xi (k) + \bar{B}_{\alpha }w(k)\nonumber \\&e(k) = \bar{C}_{\alpha }\xi (k) + {\bar{D}}_{\alpha }w(k) \end{aligned}$$

(7)

where

$$\begin{aligned}&{\bar{A}}_{\alpha }=\left[ \begin{array}{ll} A_{\alpha } &{} \quad 0 \\ B_{f}C_{\alpha } &{} \quad A_{f}\\ \end{array} \right] ;\;\; \bar{B}_{\alpha }=\left[ \begin{array}{c} B_{\alpha }\\ B_{f}D_{\alpha }\\ \end{array} \right] ;\nonumber \\&\bar{C}_{\alpha }=\left[ \begin{array}{cc} L_{\alpha }-D_{f}C_{\alpha } &{} \quad -C_{f} \\ \end{array} \right] ;\; {\bar{D}}_{\alpha }= \begin{array}{c} E_{\alpha }-D_{f}D_{\alpha } \\ \end{array}. \end{aligned}$$

(8)

The transfer function of the filtering error system (7) is then

$$\begin{aligned} G\left( e^{j\theta }\right) =\bar{C}_{\alpha }[Ie^{j\theta }-{\bar{A}}_{\alpha }]^{-1} \bar{B}_{\alpha }+{\bar{D}}_{\alpha }\quad \forall \alpha \in (4). \end{aligned}$$

(9)

Thus, the robust $H_{\infty }$ filtering error problem can be stated as follows:

$\mathbf {Problem\; description}$: The robust $H_{\infty }$ filtering problem for uncertain discrete time systems with finite frequency specifications is formulated as: find an admissible filter in (6) for the system in (1) such that two conditions are satisfied:

• The filtering error system in (7) is robustly asymptotically stable.

• Under zero-initial conditions, the following finite frequency index holds:

  $$\begin{aligned} \bar{\sigma }(G(e^{j\theta }))<\gamma \forall \theta \in (2), \forall \alpha \in (4). \end{aligned}$$

  (10)

Lemma 2.1

(Lacerda et al. 2011) Let $\varDelta \in {\mathbb {R}}^{n}$, $\Sigma \in {\mathbb {R}}^{n\times n}$ and $\varLambda \in {\mathbb {R}}^{m\times n}$ with rank $(\varLambda )=r<n$ and $\varLambda ^{\perp }\in {\mathbb {R}}^{n\times (n-r)}$ be full-column-rank matrix satisfying $\varLambda \varLambda ^{\perp }=0$. Then, the following conditions are equivalent:

• (i) $\varDelta ^{T}\Sigma \varDelta <0, \forall \varDelta \ne 0:\varLambda \varDelta =0$

• (ii) $\varLambda ^{\perp T}\Sigma \varLambda ^{\perp }<0$

• (iii) $\exists \mu \in {\mathbb {R}}: \;\;\;\;\;\;\Sigma -\mu \varLambda ^{T}\varLambda <0$

• (vi) $\exists Z\in {\mathbb {R}}^{n\times m}: \Sigma +Z\varLambda + \varLambda ^{T}Z^{T}<0$

Lemma 2.2

(Iwasaki and Hara 2005) Consider the filtering error system (7), for a given symmetric matrix

$$\begin{aligned} \Pi =\left[ \begin{array}{cc} I &{} \quad 0 \\ 0&{} \quad -\gamma ^{2}I\\ \end{array} \right] \end{aligned}$$

the following statements are equivalent

• 1. The FF inequality

  $$\begin{aligned} \left[ \begin{array}{cc} G(e^{j\theta })&\quad I \end{array} \right] \varPi \left[ \begin{array}{c} G(e^{j\theta })^{T} \\ I \end{array} \right] <\gamma \forall \theta \in (2), \forall \alpha \in (4).\nonumber \\ \end{aligned}$$

  (11)

• 2. There exist Hermitian matrix functions $P_{\alpha }$, $Q_{\alpha }$ satisfying $Q_{\alpha }>0$ such that

  $$\begin{aligned}&\left[ \begin{array}{cc} {\bar{A}}_{\alpha } &{} \quad \bar{B}_{\alpha } \\ I &{} \quad 0 \\ \end{array} \right] ^{T}\varXi \left[ \begin{array}{cc} {\bar{A}}_{\alpha } &{} \quad \bar{B}_{\alpha } \\ I &{} \quad 0 \\ \end{array} \right] \nonumber \\&\quad + \left[ \begin{array}{cc} \bar{C}_{\alpha } &{} \quad {\bar{D}}_{\alpha }\\ 0 &{} \quad I \\ \end{array} \right] ^{T}\varPi \left[ \begin{array}{cc} \bar{C}_{\alpha } &{} \quad {\bar{D}}_{\alpha }\\ 0 &{} \quad I \\ \end{array} \right] <0 \end{aligned}$$

  (12)

  where

  • For the low-frequency range $|\theta |\le \theta _{l}$

    $$\begin{aligned} \varXi _{\alpha }= & {} \left[ \begin{array}{ll} P_{\alpha } &{} \quad Q_{\alpha }\\ Q_{\alpha } &{} \quad -P_{\alpha }-2cos\theta _{l}Q_{\alpha } \\ \end{array} \right] \end{aligned}$$

    (13)

  • For the middle-frequency range $\theta _{1}\le \theta \le \theta _{2}$

    $$\begin{aligned} \varXi _{\alpha }= & {} \left[ \begin{array}{ll} P_{\alpha } &{} \quad e^{j\theta _{c}}Q_{\alpha }\\ e^{-j\theta _{c}}Q_{\alpha } &{}\quad -P_{\alpha }-2cos\theta _{w}Q_{\alpha } \\ \end{array} \right] \end{aligned}$$

    (14)
    $$\begin{aligned} \theta _{c}= & {} \frac{\theta _{2}+\theta _{1}}{2},\quad \theta _{w}=\frac{\theta _{2}-\theta _{1}}{2}. \end{aligned}$$

  • For the high-frequency range $|\theta |\ge \theta _{h}$

    $$\begin{aligned} \varXi _{\alpha }= & {} \left[ \begin{array}{ll} P_{\alpha }&{} \quad -Q_{\alpha } \\ -Q_{\alpha } &{} \quad -P_{\alpha }+2cos\theta _{h}Q_{\alpha } \\ \end{array} \right] \end{aligned}$$

    (15)

Remark 2.3

Condition (12) is the extension of the gKYP lemma for polytopic systems. Note that $P_{\alpha }$ and $Q_{\alpha }$ are chosen to be parameter-dependent to relax the condition, decreasing the conservatism when compared to the case in which P and Q are parameter-independent.

3 $H_{\infty }$ Filtering Analysis

In this section, stable filters with finite frequency performance are designed.

Theorem 3.1

Consider the system in (1). For given $\gamma >0$, a filter of from (6) exists such that the filtering error system in (7) is asymptotically stable with an $H_{\infty }$ performance bound $\gamma$. If there exist Hermitian matrices $P_{\alpha }$, $Q_{\alpha }>0$ and matrices $G_{\alpha }$, $F_{\alpha }$, ${\bar{F}}_{\alpha }$, $\bar{G}_{\alpha }$ and $H_{\alpha }$ and symmetric matrix ${\bar{P}}_{\alpha }>0$, for all $\alpha \in (4)$ satisfying

$$\begin{aligned} \varPhi _{\alpha }= & {} \left[ \begin{array}{llll} \varPhi _{1\alpha } &{} \quad \varPhi _{2\alpha } &{} \quad G_{\alpha }\bar{B}_{\alpha }-H^{T}_{\alpha } &{} \quad 0 \\ * &{} \quad \varPhi _{3\alpha } &{} \quad F_{\alpha }\bar{B}_{\alpha }+{\bar{A}}^{T}_ {\alpha }H^{T}_{\alpha } &{} \quad \bar{C}^{T}_{\alpha } \\ * &{} \quad * &{} \quad -\gamma ^{2}I+H_{\alpha }\bar{B}_{\alpha }+\bar{B}^{T}_{\alpha }H^{T}_ {\alpha } &{} \quad {\bar{D}}^{T}_{\alpha }\\ * &{} \quad * &{} \quad * &{} \quad -I\\ \end{array} \right] <0\nonumber \\ \end{aligned}$$

(16)

where

• For the low-frequency (LF) range $|\theta |\le \theta _{l}$

  $$\begin{aligned} \varPhi _{1\alpha }= & {} P_{\alpha }-G_{\alpha }- G^{T}_{\alpha };\\ \varPhi _{2\alpha }= & {} Q_{\alpha }-F^{T}_{\alpha }+G_{\alpha }{\bar{A}}_{\alpha };\\ \varPhi _{3\alpha }= & {} -P_{\alpha }-2cos\theta _{l}Q_{\alpha }+F_{\alpha }{\bar{A}}_ {\alpha }+{\bar{A}}^{T}_{\alpha }F^{T}_{\alpha }. \end{aligned}$$

• For the middle-frequency range (MF) range $\theta _{1}\le \theta \le \theta _{2}$

  $$\begin{aligned}&\varPhi _{1\alpha }=P_{\alpha }-G_{\alpha }- G^{T}_{\alpha };\\&\varPhi _{2\alpha }= e^{j\theta _{c}}Q_{\alpha }-F^{T}_{\alpha } +G_{\alpha }{\bar{A}}_{\alpha };\\&\varPhi _{3\alpha }=-P_{\alpha }-2cos\theta _{w}Q_{\alpha } +F_{\alpha }{\bar{A}}_{\alpha }+{\bar{A}}^{T}_{\alpha }F^{T}_{\alpha };\\&\theta _{c}=\frac{(\theta _{1}+\theta _{2})}{2}; \theta _{w} =\frac{(\theta _{2}-\theta _{1})}{2}. \end{aligned}$$

• For the high-frequency (HF) range $|\theta |\ge \theta _{h}$

  $$\begin{aligned} \varPhi _{1\alpha }= & {} P_{\alpha }-G_{\alpha }- G^{T}_{\alpha };\\ \varPhi _{2\alpha }= & {} -Q_{\alpha }-F_{\alpha }^{T}+G_{\alpha }{\bar{A}}_{\alpha };\\ \varPhi _{3\alpha }= & {} -P_{\alpha }+2cos\theta _{h}Q_{\alpha }+F_{\alpha }{\bar{A}} _{\alpha }+{\bar{A}}^{T}_{\alpha }F^{T}_{\alpha }. \end{aligned}$$

and

$$\begin{aligned} \varPsi _{\alpha }= & {} \left[ \begin{array}{ll} {\bar{P}}_{\alpha }-{{\bar{F}}}_{\alpha }-{\bar{F}}^{T}_{\alpha } &{} \quad {{\bar{F}}}_{\alpha }{\bar{A}}_{\alpha }-\bar{G}^{T}_{\alpha } \\ * &{} \quad -\bar{P}_{\alpha }+ \bar{G}_{\alpha }{\bar{A}}_{\alpha } +{\bar{A}}^{T}_{\alpha }\bar{G}^{T}_{\alpha } \\ \end{array} \right] <0\nonumber \\ \end{aligned}$$

(17)

Proof 3.2

First, we consider the LF case, we prove that (12–13) is equivalent to (16). Suppose that (16) hold, denote

$$\begin{aligned} \varSigma= & {} \left[ \begin{array}{lll} P_{\alpha } &{} \quad Q_{\alpha } &{}\quad 0 \\ Q_{\alpha } &{} \quad -P_{\alpha }-2cos\theta _{l}Q_{\alpha }+\bar{C}_ {\alpha }^{T}\bar{C}_{\alpha } &{} \quad \bar{C}_{\alpha }^{T}{\bar{D}}_{\alpha }\\ 0 &{} \quad {\bar{D}}_{\alpha }^{T}\bar{C}_{\alpha } &{} \quad -\gamma ^{2}I+{\bar{D}}_{\alpha }^{T} {{\bar{D}}}_{\alpha }\\ \end{array} \right] ;\nonumber \\ Z= & {} \left[ \begin{array}{lll} G_{\alpha }\\ F_{\alpha }\\ H_{\alpha }\\ \end{array} \right] ;\;\;\;\varLambda =\left[ \begin{array}{lll} -I &{}\quad {\bar{A}}_{\alpha } &{}\quad \bar{B}_{\alpha }\\ \end{array} \right] . \end{aligned}$$

(18)

By Shur complement, (16) is equivalent to

$$\begin{aligned} \varSigma +Z\varLambda +\varLambda ^{T}Z^{T}<0 \end{aligned}$$

(19)

under condition (iv) of Lemma 2.1, with

$$\begin{aligned} \varLambda ^{\bot }=\left[ \begin{array}{lll} {\bar{A}}_{\alpha } &{} \quad \bar{B}_{\alpha } \\ I &{} \quad 0\\ 0 &{} \quad I\\ \end{array} \right] \end{aligned}$$

which, using condition (ii) of Lemma 2.1, given (12–13).

In addition, let us construct a Lyapunov function inequality, ${\bar{A}}_{\alpha }$ is stable if and only if there exists $\bar{P}_{\alpha }=\bar{P}_{\alpha }^{T}>0$ such that

$$\begin{aligned} \begin{array}{c} \bar{P}_{\alpha }-{\bar{A}}^{T}_{\alpha }\bar{P}_{\alpha }{\bar{A}}_{\alpha }>0 \end{array} \end{aligned}$$

(20)

which is rewritten in the form

$$\begin{aligned} \left[ \begin{array}{cc} {\bar{A}}_{\alpha }\\ I \end{array} \right] ^{T}\left[ \begin{array}{cc} \bar{P}_{\alpha } &{} \quad 0 \\ 0 &{} \quad -\bar{P}_{\alpha } \\ \end{array} \right] \left[ \begin{array}{cc} {\bar{A}}_{\alpha }\\ I \end{array} \right] <0 \end{aligned}$$

(21)

Define

$$\begin{aligned} \varLambda= & {} \left[ \begin{array}{cc} \bar{P}_{\alpha } &{} \quad 0 \\ 0 &{} \quad -\bar{P}_{\alpha } \\ \end{array} \right] ;\;\; Z=\left[ \begin{array}{cc} {\bar{F}}_{\alpha } \\ \bar{G}_{\alpha } \\ \end{array} \right] ;\nonumber \\ \varLambda= & {} \left[ \begin{array}{cc} -I &{} \quad {\bar{A}}_{\alpha } \\ \end{array} \right] ;\;\; \varLambda ^{\bot }=\left[ \begin{array}{cc} {\bar{A}}_{\alpha }\\ I \end{array} \right] . \end{aligned}$$

(22)

By Lemma 2.1, (21) and (22) are equivalent to

$$\begin{aligned}&\left[ \begin{array}{cc} \bar{P}_{\alpha } &{} \quad 0\\ 0 &{} \quad -\bar{P}_{\alpha } \\ \end{array} \right] +\left[ \begin{array}{cc} {\bar{F}}_{\alpha } \\ \bar{G}_{\alpha } \\ \end{array}\right] \left[ \begin{array}{cc} -I &{} \quad {\bar{A}}_{\alpha } \\ \end{array}\right] +\nonumber \\&\left[ \begin{array}{cc} -I &{} \quad {\bar{A}}_{\alpha } \\ \end{array}\right] ^{T}\left[ \begin{array}{cc} {\bar{F}}_{\alpha } \\ \bar{G}_{\alpha } \\ \end{array}\right] ^{T}<0 \end{aligned}$$

(23)

which is nothing but (17).

Similar to the LF case, the proof for MF and HF cases can be completed. It is omitted for brevity. $\square$

For finite frequency $H_{\infty }$ filtering performance analysis, Theorem 3.1 provides a new condition with the property of matrix decouple. In the sequel, the existence conditions of finite frequency $H_{\infty }$ filters will be investigated based on this developed analysis condition.

4 $H_{\infty }$ Filtering Design

In this section, a methodology is established for designing the finite frequency $H_{\infty }$ filter (6), that is, to determine the filter matrices such that the filtering error system (7) is asymptotically stable with an $H_{\infty }$-norm bounded by $\gamma$ .

4.1 Finite Frequency Case

Based on Theorem 3.1, we select for variables $P_{\alpha }$, $Q_{\alpha }$ and $\bar{P}_{\alpha }$ the following structures

$$\begin{aligned}&P_{\alpha }=\left[ \begin{array}{cc} P_{1\alpha } &{} \quad P_{2\alpha }\\ *&{} \quad P_{3\alpha }\\ \end{array} \right] ;\;\;\; Q_{\alpha }=\left[ \begin{array}{cc} Q_{1\alpha } &{} \quad Q_{2\alpha } \\ *&{} \quad Q_{3\alpha }\\ \end{array} \right] ; \end{aligned}$$

$$\begin{aligned}&\bar{P}_{\alpha }=\left[ \begin{array}{cc} \bar{P}_{1\alpha } &{} \quad \bar{P}_{2\alpha }\\ *&{} \quad \bar{P}_{3\alpha }\\ \end{array} \right] \end{aligned}$$

(24)

Then, let the slack variables $G_{\alpha }$ , $F_{\alpha }$, $H_{\alpha }$, ${\bar{F}}_{\alpha }$ and $\bar{G}_{\alpha }$ take the following structure

$$\begin{aligned} G_{\alpha }= & {} \left[ \begin{array}{cc} G_{1\alpha } &{}\quad V \\ G_{2\alpha } &{}\quad V\\ \end{array} \right] ;\;\;\; F_{\alpha }=\left[ \begin{array}{cc} F_{1\alpha } &{} \quad \lambda _{1}V \\ F_{2\alpha } &{} \quad \lambda _{2}V\\ \end{array} \right] ;\nonumber \\ {\bar{F}}_{\alpha }= & {} \left[ \begin{array}{cc} {\bar{F}}_{1\alpha } &{} \quad V\\ {\bar{F}}_{2\alpha } &{} \quad V\\ \end{array} \right] ;\;\;\; \bar{G}_{\alpha }=\left[ \begin{array}{cc} \bar{G}_{1\alpha } &{} \quad 0\\ \bar{G}_{2\alpha } &{} \quad 0\\ \end{array} \right] ;\nonumber \\ H_{\alpha }= & {} \left[ \begin{array}{cc} H_{1\alpha } &{} \quad \lambda _{3}V \\ \end{array} \right] . \end{aligned}$$

(25)

V is fixed for the entire uncertainty domain and, without loss of generality, invertible; the scalar parameters $\lambda _{1}$, $\lambda _{2}$ and $\lambda _{3}$ will be used as optimization parameters. With a structure of variable matrices, we obtain the following results:

Theorem 4.1

Consider the system (1). For given a constants $\gamma >0$, $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$, a filter of from (6) exists such that the filtering error system in (7) is asymptotically stable with an $H_{\infty }$ performance bound $\gamma$. If there exist Hermitian matrices $P_{\alpha =}\left[ \begin{array}{cc} P_{1\alpha } &{} \quad P_{2\alpha }\\ *&{} \quad P_{3\alpha }\\ \end{array} \right]$, $Q_{\alpha }=\left[ \begin{array}{cc} Q_{1\alpha } &{} \quad Q_{2\alpha }\\ *&{} \quad Q_{3\alpha }\\ \end{array} \right] >0$ and symmetric matrix $\bar{P}_{\alpha }=\left[ \begin{array}{cc} \bar{P}_{1\alpha } &{} \quad \bar{P}_{2\alpha } \\ *&{} \quad \bar{P}_{3\alpha }\\ \end{array} \right] >0$ and matrices ${\hat{A}}_{f}$, ${\hat{B}}_{f}$, $\hat{C}_{f}$, $\hat{D}_{f}$, $G_{1\alpha }$, $G_{2\alpha }$, $\bar{G}_{1\alpha }$, $\bar{G}_{2\alpha }$, $F_{1\alpha }$, $F_{2\alpha }$, ${\bar{F}}_{1\alpha }$, ${\bar{F}}_{2\alpha }$, V and $H_{1\alpha }$, for all $\alpha \in$ (4) such that

$$\begin{aligned} \bar{\varOmega }_{\alpha }+{\bar{\varPhi }}_{\alpha }<0 \end{aligned}$$

(26)

$$\begin{aligned} {\bar{\varPsi }}_{\alpha }<0 \end{aligned}$$

(27)

with

$$\begin{aligned} {\bar{\varPhi }}_{\alpha }= & {} \left[ \begin{array}{llllll} {{\bar{\varPhi }}}_{11\alpha } &{} \quad -V-G_{2\alpha }^{T} &{} \quad {\bar{\varPhi }}_{13\alpha } &{} \quad {{\bar{\varPhi }}}_{14\alpha } &{} \quad {\bar{\varPhi }}_{15\alpha } &{} \quad 0 \\ *&{} \quad -V-V^{T} &{} \quad {\bar{\varPhi }}_{23\alpha } &{} \quad {\bar{\varPhi }}_{24\alpha } &{} \quad {\bar{\varPhi }}_{25\alpha } &{} \quad 0 \\ *&{}\quad *&{} \quad {\bar{\varPhi }}_{33\alpha } &{} \quad {\bar{\varPhi }}_{34\alpha } &{} \quad {\bar{\varPhi }}_{35\alpha } &{} \quad L_{\alpha }^{T}-C_{\alpha }^{T}\hat{D}_{f}^{T} \\ *&{} \quad *&{} \quad *&{} \quad {\bar{\varPhi }}_{44\alpha } &{} \quad {\bar{\varPhi }}_{45\alpha } &{} \quad -{\hat{C}}_{f}^{T}\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad {\bar{\varPhi }}_{55\alpha } &{} \quad E_{\alpha }^{T}-D_{\alpha }^{T}\hat{D}_{f}^{T} \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -I\\ \end{array} \right] \end{aligned}$$

$$\begin{aligned} {\bar{\varPsi }}_{\alpha }= & {} \left[ \begin{array}{llll} \bar{\varPsi }_{11\alpha }&{} \quad \bar{P}_{2\alpha }-V-{\bar{F}}^{T}_{2\alpha } &{} \quad \bar{\varPsi }_{13\alpha }&{} \quad {\hat{A}}_{f}-\bar{G}^{T}_{2\alpha } \\ *&{} \quad \bar{P}_{3\alpha }-V-V^{T} &{} \quad \bar{\varPsi }_{23\alpha } &{} \quad {\hat{A}}_{f} \\ *&{} \quad *&{} \quad \bar{\varPsi }_{33\alpha } &{} \quad -\bar{P}_{2\alpha } +A_{\alpha }^{T}\bar{G}^{T}_{2\alpha }\\ *&{} \quad *&{} \quad *&{} \quad -\bar{P}_{3\alpha } \\ \end{array} \right] \end{aligned}$$

$$\begin{aligned} {\bar{\varPhi }}_{11\alpha }= & {} -G_{1\alpha }-G_{1\alpha }^{T};\\ {\bar{\varPhi }}_{13\alpha }= & {} -F_{1\alpha }^{T}+G_{1\alpha } A_{\alpha }+{\hat{B}}_{f}C_{\alpha };\\ {\bar{\varPhi }}_{14\alpha }= & {} -F_{2\alpha }^{T}+{\hat{A}}_{f};\\ {\bar{\varPhi }}_{15\alpha }= & {} -H_{1\alpha }^{T}+G_{1\alpha }B_{\alpha } +{{\hat{B}}}_{f}D_{\alpha };\\ {\bar{\varPhi }}_{23\alpha }= & {} -\lambda _{1}V^{T}+G_{2\alpha }A_{\alpha } +{{\hat{B}}}_{f}C(\alpha );\\ {\bar{\varPhi }}_{24\alpha }= & {} -\lambda _{2}V^{T}+{\hat{A}}_{f};\\ {\bar{\varPhi }}_{25\alpha }= & {} G_{2\alpha }B_{\alpha }+{{\hat{B}}}_{f}D_{\alpha } -\lambda _{3}V^{T};\\ {\bar{\varPhi }}_{33\alpha }= & {} sym(F_{1\alpha }A_{\alpha }+\lambda _{1} {\hat{B}}_{f}C_{\alpha });\\ {\bar{\varPhi }}_{34\alpha }= & {} \lambda _{1}{\hat{A}}_{f} +A_{\alpha }^{T}F_{2\alpha }^{T}+\lambda _{2}C_{\alpha }^{T}{\hat{B}}_{f}; \\ {\bar{\varPhi }}_{35\alpha }= & {} A_{\alpha }^{T}H_{1\alpha }^{T} +\lambda _{3}C_{\alpha }^{T}{\hat{B}}^{T}_{f}+F_{1\alpha } B_{\alpha }+\lambda _{1}{\hat{B}}_{f}D_{\alpha };\\ {\bar{\varPhi }}_{44\alpha }= & {} \lambda _{2}(A_{f}+A^{T}_{f});\\ {\bar{\varPhi }}_{45\alpha }= & {} \lambda _{3} {\hat{A}}^{T}_{f}+F_{2\alpha }B_{\alpha }+ \lambda _{2}{\hat{B}}_{f}D_{\alpha };\\ {\bar{\varPhi }}_{55\alpha }= & {} -\gamma ^{2} I+sym(H_{1\alpha }B_{\alpha }+\lambda _{3}{\hat{B}}_{f}D_{\alpha });\\ \bar{\varPsi }_{11\alpha }= & {} \bar{P}_{1\alpha }-{\bar{F}}_{1\alpha } -{\bar{F}}^{T}_{1\alpha };\\ \bar{\varPsi }_{13\alpha }= & {} {\bar{F}}_{1\alpha }A_{\alpha }+ {\hat{B}}_{f}C_{\alpha }-\bar{G}^{T}_{1\alpha };\\ \bar{\varPsi }_{23\alpha }= & {} {\bar{F}}_{2\alpha }A_{\alpha }+{\hat{B}}_{f}C_{\alpha };\\ \bar{\varPsi }_{33\alpha }= & {} -\bar{P}_{3\alpha }+sym(\bar{G}_{1\alpha }A_{\alpha }); \end{aligned}$$

Matrix $\bar{\varOmega }_{\alpha }$ is defined as follows:

• For the low-frequency (LF) range $|\theta |\le \theta _{l}$

  $$\begin{aligned} \bar{\varOmega }_{\alpha }= & {} \left[ \begin{array}{llllll} P_{1\alpha } &{} \quad P_{2\alpha } &{} \quad Q_{1\alpha } &{} \quad Q_{2\alpha } &{} \quad 0 &{} \quad 0 \\ *&{} \quad P_{3\alpha } &{} \quad Q_{2\alpha }^{T} &{} \quad Q_{3\alpha } &{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad \bar{\varOmega }_{1\alpha } &{} \quad -P_{2\alpha }-2cos \theta _{l}Q_{2\alpha } &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -P_{3\alpha }-2cos\theta _{l}Q_{3\alpha } &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0\\ \end{array} \right] \end{aligned}$$
  $$\begin{aligned} \bar{\varOmega }_{1\alpha }= & {} -P_{1\alpha }-2cos\theta _{l}Q_{1\alpha }. \end{aligned}$$

• For the middle-frequency (MF) range $\theta _{1}\le \theta \le \theta _{2}$

  $$\begin{aligned} \bar{\varOmega }_{\alpha }= & {} \left[ \begin{array}{llllll} P_{1\alpha } &{} \quad P_{2\alpha } &{} \quad e^{j\theta _{c}}Q_{1\alpha } &{} \quad e^{j\theta _{c}}Q_{2\alpha } &{} \quad 0 &{} \quad 0 \\ *&{} \quad P_{3\alpha } &{} \quad e^{-j\theta _{c}}Q_{2\alpha }^{T} &{} \quad e^{j\theta _{c}}Q_{3\alpha } &{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad \bar{\varOmega }_{1\alpha } &{} \quad -P_{2\alpha }-2cos\theta _{w}Q_{2\alpha } &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -P_{3\alpha }-2cos\theta _{w}Q_{3\alpha } &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0\\ \end{array} \right] \end{aligned}$$
  $$\begin{aligned} \bar{\varOmega }_{1\alpha }= & {} -P_{1\alpha }-2cos\theta _{w}Q_{1\alpha };\\ \theta _{c}= & {} \frac{(\theta _{1}+\theta _{2})}{2};\;\;\;\; \theta _{w}=\frac{(\theta _{2}-\theta _{1})}{2}. \end{aligned}$$

• For the high-frequency (HF) range $|\theta |\ge \theta _{h}$

  $$\begin{aligned} \bar{\varOmega }_{\alpha }= & {} \left[ \begin{array}{llllll} P_{1\alpha } &{} \quad P_{2\alpha } &{} \quad -Q_{1\alpha } &{} \quad -Q_{2\alpha } &{} \quad 0 &{} \quad 0 \\ *&{} \quad P_{3\alpha } &{} \quad -Q_{2\alpha }^{T} &{} \quad -Q_{3\alpha } &{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad \bar{\varOmega }_{1\alpha } &{} \quad -P_{2\alpha }+2cos\theta _{h}Q_{2\alpha } &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad -P_{3\alpha }+2cos\theta _{h}Q_{3\alpha } &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0\\ \end{array} \right] \end{aligned}$$
  $$\begin{aligned} {\bar{\varOmega }}_{1\alpha }= & {} -P_{1\alpha }+2cos\theta _{h}Q_{1\alpha }. \end{aligned}$$

Moreover, if the previous conditions are satisfied, an state-space realization of the $H_{\infty }$ filter is given by

$$\begin{aligned} A_{f}=V^{-1}{\hat{A}}_{f},\; B_{f}=V^{-1}{\hat{B}}_{f},\; C_{f}=\hat{C}_{f},\;D_{f}=\hat{D}_{f} \end{aligned}$$

(28)

4.2 Entire Frequency Case

In this subsection, we discuss the entire frequency (EF) case of Theorem 4.1. For the EF case, $Q_{k\alpha }$ is set as $Q_{k\alpha }=0$, $k=1,2,3$ while $P_{\alpha }$ is set to satisfy $\left[ \begin{array}{cc} P_{1\alpha } &{} P_{2\alpha } \\ *&{} P_{3\alpha }\\ \end{array} \right] >0$ such that stability is also implied by inequality in (26). In summary, Theorem (4.1) is reduced to the following result for EF $H_{\infty }$ filtering.

Corollary 1

Consider the system in (1) . For Given $\gamma >0$, and scalars $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$, a filter of from (5) exists such that the filtering error system in (6) is asymptotically stable with an $H_{\infty }$ performance bound $\gamma$. If there exist symmetric matrix $\bar{P}_{\alpha }=\left[ \begin{array}{cc} \bar{P}_{1\alpha } &{} \bar{P}_{2\alpha }\\ *&{} \bar{P}_{3\alpha }\\ \end{array} \right] >0$ and matrices ${\hat{A}}_{f}$, ${\hat{B}}_{f}$, $\hat{C}_{f}$, $\hat{D}_{f}$, $G_{1\alpha }$, $G_{2\alpha }$, $F_{1\alpha }$, $F_{2\alpha }$, V and $H_{1\alpha }$, for all $\alpha \in$ (4) satisfying

$$\begin{aligned} {\bar{\varXi }}_{\alpha }= & {} \left[ \begin{array}{llllll} {\bar{\varXi }}_{11\alpha } &{} \quad {{\bar{\varXi }}}_{12\alpha } &{} \quad {\bar{\varXi }}_{13\alpha } &{} \quad {\bar{\varXi }}_{14\alpha } &{} \quad {\bar{\varXi }}_{15\alpha } &{} \quad 0 \\ *&{} \quad {{\bar{\varXi }}}_{22\alpha } &{} \quad {\bar{\varXi }}_{23\alpha } &{} \quad {\bar{\varXi }}_{24\alpha } &{} \quad {\bar{\varXi }}_{25\alpha } &{} \quad 0 \\ *&{} \quad *&{} \quad {\bar{\varXi }}_{33\alpha } &{} \quad {\bar{\varXi }}_{34\alpha } &{} \quad {\bar{\varXi }}_{35\alpha } &{} \quad L_{\alpha }^{T}-C_{\alpha }^{T}\hat{D}_{f}^{T} \\ *&{} \quad *&{} \quad *&{} \quad {\bar{\varXi }}_{44\alpha } &{} \quad {\bar{\varXi }}_{45\alpha } &{} \quad -\hat{C}_{f}^{T}\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad {\bar{\varXi }}_{55\alpha } &{} \quad E_{\alpha }^{T}-D_{\alpha }^{T}\hat{D}_{f}^{T} \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -I\\ \end{array} \right] \nonumber \\< & {} 0 \end{aligned}$$

(29)

$$\begin{aligned} {\bar{\varXi }}_{11\alpha }= & {} P_{1\alpha }-G_{1\alpha }-G_{1\alpha }^{T},\\ {\bar{\varXi }}_{12\alpha }= & {} P_{2\alpha }-V-G_{2\alpha }^{T};\\ {\bar{\varXi }}_{13\alpha }= & {} -F_{1\alpha }^{T}+G_{1\alpha }A_{\alpha }+{\hat{B}}_{f}C_{\alpha };\\ {\bar{\varXi }}_{14\alpha }= & {} -F_{2\alpha }^{T}+{\hat{A}}_{f};\\ {\bar{\varXi }}_{15\alpha }= & {} -H_{1\alpha }^{T}+G_{1\alpha }B_{\alpha }+{\hat{B}}_{f}D_{\alpha };\\ {\bar{\varXi }}_{22\alpha }= & {} P_{3}(\alpha )-V-V^{T};\\ {\bar{\varXi }}_{23\alpha }= & {} -\lambda _{1}V^{T}+G_{2\alpha }A_{\alpha }+{\hat{B}}_{f}C_{\alpha };\\ {\bar{\varXi }}_{24\alpha }= & {} -\lambda _{2}V^{T}+{\hat{A}}_{f};\\ {\bar{\varXi }}_{25\alpha }= & {} G_{2\alpha }B_{\alpha }+{\hat{B}}_{f}D_{\alpha }-\lambda _{3}V^{T};\\ {\bar{\varXi }}_{33\alpha }= & {} -P_{1\alpha }+sym(F_{1\alpha }A_{\alpha }+\lambda _{1}{\hat{B}}_{f}C_{\alpha });\\ {\bar{\varXi }}_{34\alpha }= & {} -P_{2\alpha }+\lambda _{1}{\hat{A}}_{f}+A_{\alpha }^{T}F_{2\alpha }^{T}+\lambda _{2}C_{\alpha }^{T}{\hat{B}}_{f};\\ {\bar{\varXi }}_{35\alpha }= & {} A_{\alpha }^{T}H_{1\alpha }^{T}+\lambda _{3}C_{\alpha }^{T}{\hat{B}}^{T}_{f}+F_{1\alpha }B_{\alpha }+\lambda _{1}{\hat{B}}_{f}D_{\alpha };\\ {\bar{\varXi }}_{44\alpha }= & {} -P_{3\alpha }+\lambda _{2}(A_{f}+A^{T}_{f});\\ {\bar{\varXi }}_{45\alpha }= & {} \lambda _{3}{\hat{A}}^{T}_{f}+F_{2\alpha }B_{\alpha }+ \lambda _{2}{\hat{B}}_{f}D_{\alpha };\\ {\bar{\varXi }}_{55\alpha }= & {} -\gamma ^{2}I+sym(H_{1\alpha }B_{\alpha })+\lambda _{3}{\hat{B}}_{f}D_{\alpha }). \end{aligned}$$

Moreover, if (29) are feasible, then a suitable filter can be obtained by (28).

4.3 Solution Using Parameter-Dependent Polynomails

Before presenting the formulation of Theorem 4.1 and Corollary 2 using homogeneous polynomially parameter-dependent matrices, some definitions and preliminaries from Gao et al. (2008) are needed to represent and handle products and sums of homogeneous polynomials. First, we define the homogeneous polynomially parameter-dependent matrices of degree g by

$$\begin{aligned} {\bar{P}}_{1\alpha }=\displaystyle \sum _{j=1}^{J(g)}\alpha _{1}^{k_{1}} \alpha _{2}^{k_{2}}\ldots \alpha _{s}^{k_{N}}\bar{P}_{1k_{j}(g)},\; [k_{1},k_{2}, \ldots ,k_{N}]=K_{j}(g)\nonumber \\ \end{aligned}$$

(30)

Similarly, matrices $\bar{P}_{2\alpha }$, $\bar{P}_{3\alpha }$, $P_{v\alpha }$, $Q_{v\alpha }$, $v=1,2,3$, $F_{t\alpha }$, ${\bar{F}}_{t\alpha }$, $G_{t\alpha }$, $\bar{G}_{t\alpha }$, $t=1,2$ and $H_{1\alpha }$ take the same form.

The notations in the above are explained as follows. Define K(g) as the set of N-tuples obtained as all possible combination of $[k_{1},k_{2}, \ldots ,k_{N}]$, with $k_{i}$ being nonnegative integers, such that $k_{1}+k_{2}+ \cdots +k_{N}=g$. $K_{j}(g)$ is the jth N-tuples of K(g) which is lexically ordered, $j=1, \ldots ,J(g)$. Since the number of vertices in the polytope $\Gamma$ is equal to s, the number of elements in K(g) as given by $J(g)=\frac{(N +g-1)!}{g!(N -1)!}$. These elements define the subscripts $k_{1},k_{2}, \ldots ,k_{N}$ of the constant matrices

$$\begin{aligned} \bar{P}_{v k_{1},k_{2}, \ldots k_{N}}\triangleq & {} \bar{P}_{ v k_{j}(g)};\;\; P_{vk_{1},k_{2}, \ldots k_{N}}\triangleq P_{ vk_{j}(g)};\\ Q_{v k_{1},k_{2}, \ldots k_{N}}\triangleq & {} Q_{ vk_{j}(g)};\;\; F_{t k_{1},k_{2}, \ldots k_{N}}\triangleq F_{t k_{j}(g)};\\ {\bar{F}}_{t k_{1},k_{2}, \ldots k_{N}}\triangleq & {} {\bar{F}}_{ t k_{j}(g)};\;\; G_{t k_{1},k_{2}, \ldots k_{N}}\triangleq G_{t k_{j}(g)};\\ \bar{G}_{t k_{1},k_{2}, \ldots k_{N}}\triangleq & {} \bar{G}_{t k_{j}(g)} ;\;\; H_{1k_{1},k_{2}, \ldots k_{N}}\triangleq H_{1k_{j}(g)}. \end{aligned}$$

(where $v=1,2,3$ and $t=1,2.$), which are used to construct the homogeneous polynomial dependent matrices $\bar{P}_{v\alpha }$, $P_{v\alpha }$, $Q_{v\alpha }$, $F_{t\alpha }$, ${\bar{F}}_{t\alpha }$, $G_{t\alpha }$, $\bar{G}_{t\alpha }$ (where $v=1,2,3$ and $t=1,2$) and $H_{1\alpha }$ in (29).

For each set K(g), define also the set I(g) with elements $I_{j}(g)$ given by subsets of $i,\; i\in \{1,2, \ldots ,N\}$, associated to s-tuples $K_{j}(g)$ whose $k_{i}$’s are nonzero. For each i, i = 1, ...,N, define the s-tuples $K_{j}^{i}(g)$ as being equal to $K_{j}(g)$ but with $k_{i}>0$ replaced by $k_{i}-1$. Note that the s-tuples $K_{j}^{i}(g)$ are defined only in the cases where the corresponding $k_{i}$ is positive. Note also that, when applied to the elements of $K(g+1)$, the s-tuples $K_{j}^{i}(g+1)$ define subscripts $k_{1},k_{2}, \ldots ,k_{N}$ of matrices $\bar{P}_{vk_{1},k_{2}, \ldots k_{N}}$, $P_{vk_{1},k_{2}, \ldots k_{N}}$, $Q_{vk_{1},k_{2}, \ldots k_{N}}$, $F_{ t k_{1},k_{2}, \ldots k_{N}}$, $G_{tk_{1},k_{2}, \ldots k_{N}}$, ${\bar{F}}_{ t k_{1},k_{2}, \ldots k_{N}}$, $\bar{G}_{tk_{1},k_{2}, \ldots k_{N}}$, (where $v=1,2,3$ and $t=1,2$) and $H_{1k_{1},k_{2}, \ldots k_{N}}$, associated with homogeneous polynomial parameter-dependent matrices of degree g.

Finally, define the scalar constant coefficients $\beta _{j}^{i}(g+1)=\frac{g!}{(k_{1}!k_{2}! \ldots k_{N}!)},$ with $[k_{1},k_{2}, \ldots ,k_{N}]\in K_{j}^{i}(g+1)$.

The main result in this section is given by the following Theorem 4.2 and Corollary 2 respectively.

Theorem 4.2

Given a stable system (1). For given a constants $\gamma >0$, $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$, a filter of from (5) exists such that the filtering error system in (6) is asymptotically stable with an $H_{\infty }$ performance bound $\gamma$. If there exist Hermitian matrices $P(k_{j}(g))=\left[ \begin{array}{cc} P_{1k_{j}(g)} &{} P_{2k_{j}(g)} \\ *&{} P_{3k_{j}(g)}\\ \end{array} \right]$, $Q(k_{j}(g))=\left[ \begin{array}{cc} Q_{1k_{j}(g)} &{} Q_{2k_{j}(g)} \\ *&{} Q_{3k_{j}(g)}\\ \end{array} \right] >0$ and symmetric matrix $\bar{P}(k_{j}(g))=\left[ \begin{array}{cc} \bar{P}_{1k_{j}(g)} &{} \bar{P}_{2k_{j}(g)} \\ *&{} \bar{P}_{3k_{j}(g)}\\ \end{array} \right] >0$, matrices ${\hat{A}}_{f}$, ${\hat{B}}_{f}$, $\hat{C}_{f}$, $\hat{D}_{f}$, $G_{tk_{j}(g)}$, $F_{t k_{j}(g)}$ (where $t=1,2$), $H_{1k_{j}(g)}$, V and the real scalars $\lambda _{1}$, $\lambda _{2}$ and $\lambda _{3}$ such that the following LMIs hold for all $K_{l}(g+1)\in K(g+1)$ , $l=1, \ldots ,J(g+1)$:

$$\begin{aligned} \displaystyle \sum _{i\in I_{l}(g+1)}\left[ \bar{\varOmega }_{k}+{\bar{\varPhi }}_{k}\right] <0 \end{aligned}$$

(31)

$$\begin{aligned} \displaystyle \sum _{i\in I_{l}(g+1)}\bar{\varPsi }_{k}<0 \end{aligned}$$

(32)

with

$$\begin{aligned} {\bar{\varPhi }}_{k}= & {} \left[ \begin{array}{llllll} {\bar{\varPhi }}_{11k} &{} \quad {\bar{\varPhi }}_{12k} &{} \quad {\bar{\varPhi }}_{13k} &{} \quad {\bar{\varPhi }}_{14k} &{} \quad {\bar{\varPhi }}_{15k} &{} \quad 0 \\ *&{} \quad {\bar{\varPhi }}_{22k} &{} \quad {\bar{\varPhi }}_{23k} &{} \quad {\bar{\varPhi }}_{24k} &{} \quad {\bar{\varPhi }}_{25k} &{} \quad 0 \\ *&{} \quad *&{} \quad {\bar{\varPhi }}_{33k} &{} \quad {\bar{\varPhi }}_{34k} &{} \quad {\bar{\varPhi }}_{35k} &{} \quad {\bar{\varPhi }}_{36k}\\ *&{} \quad *&{} \quad *&{} \quad {\bar{\varPhi }}_{44k} &{} \quad {\bar{\varPhi }}_{45k} &{} \quad -\beta _{j}^{i}(g+1)\hat{C}_{f}^{T}\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad {\bar{\varPhi }}_{55k} &{} \quad {\bar{\varPhi }}_{56k} \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\beta _{j}^{i}(g+1)I\\ \end{array} \right] \end{aligned}$$

$$\begin{aligned} \bar{\varPsi }_{k}= & {} \left[ \begin{array}{llll} \bar{\varPsi }_{11k} &{} \quad \bar{\varPsi }_{12k} &{} \quad \bar{\varPsi }_{13k} &{} \quad \beta _{j}^{i}(g+1){\hat{A}}_{f}-\bar{G}^{T}_{2k_{j}(g)} \\ *&{} \quad \bar{\varPsi }_{22k} &{} \quad \bar{\varPsi }_{3k} &{} \quad \beta _{j}^{i}(g+1){\hat{A}}_{f} \\ *&{} \quad *&{} \quad \bar{\varPsi }_{4k} &{} \quad -\bar{P}_{2k_{j}(g)} +A^{T}_{i}\bar{G}^{T}_{2k_{j}(g)}\\ *&{} \quad *&{} \quad *&{} \quad -\bar{P}_{3k_{j}(g)} \\ \end{array} \right] \end{aligned}$$

$$\begin{aligned} {\bar{\varPhi }}_{11k}= & {} -G_{1k_{j}(g)}-G_{1k_{j}(g)}^{T};\\ {\bar{\varPhi }}_{12k}= & {} -\beta _{j}^{i}(g+1)V-G_{2k_{j}(g)}^{T};\\ {\bar{\varPhi }}_{13k}= & {} -F_{1k_{j}(g)}^{T}+G_{1k_{j}(g)}A_{i} +\beta _{j}^{i}(g+1){\hat{B}}_{f}C_{i};\\ {\bar{\varPhi }}_{14k}= & {} -F_{2k_{j}(g)}^{T}+\beta _{j}^{i}(g+1){\hat{A}}_{f};\\ {\bar{\varPhi }}_{15k}= & {} -H_{1k_{j}(g)}^{T}+G_{1k_{j}(g)}B_{i} +\beta _{j}^{i}(g+1){\hat{B}}_{f}D_{i};\\ {\bar{\varPhi }}_{23k}= & {} -\lambda _{1}\beta _{j}^{i}(g+1)V^{T} +G_{2k_{j}(g)}A_{i}+\beta _{j}^{i}(g+1){\hat{B}}_{f}C_{i};\\ {\bar{\varPhi }}_{24k}= & {} -\lambda _{2}\beta _{j}^{i}(g+1)V^{T} +\beta _{j}^{i}(g+1){\hat{A}}_{f};\\ {\bar{\varPhi }}_{25k}= & {} G_{2k_{j}(g)}B_{i} +\beta _{j}^{i}(g+1){\hat{B}}_{f}D_{i}-\lambda _{3}\beta _{j}^{i}(g+1)V^{T};\\ {\bar{\varPhi }}_{33k}= & {} sym(F_{1k_{j}(g)}A_{i} +\lambda _{1}\beta _{j}^{i}(g+1){\hat{B}}_{f}C_{i});\\ {\bar{\varPhi }}_{34k}= & {} \lambda _{1}\beta _{j}^{i}(g+1) {\hat{A}}_{f}+A_{i}^{T}F_{2k_{j}(g)}^{T}+\lambda _{2} \beta _{j}^{i}(g+1)C_{i}^{T}{\hat{B}}_{f};\\ {\bar{\varPhi }}_{35k}= & {} A_{i}^{T}H_{1k_{j}(g)}^{T} +\lambda _{3}\beta _{j}^{i}(g+1)C_{i}^{T}{\hat{B}}^{T}_{f}\\&+\, F_{1k_{j}(g)}B_{i}+\lambda _{1}\beta _{j}^{i}(g+1){\hat{B}}_{f}D_{i};\\ {\bar{\varPhi }}_{36k}= & {} \beta _{j}^{i}(g+1)L^{T}_{i} -\beta _{j}^{i}(g+1)C^{T}_{i}\hat{D}_{f}^{T};\\ {\bar{\varPhi }}_{44k}= & {} \lambda _{2}\beta _{j}^{i}(g+1)(A_{f}+A^{T}_{f});\\ {\bar{\varPhi }}_{45k}= & {} \lambda _{3}\beta _{j}^{i} (g+1){\hat{A}}^{T}_{f}+F_{2k_{j}(g)}B_{i}+ \lambda _{2}\beta _{j} ^{i}(g+1){\hat{B}}_{f}D_{i};\\ {\bar{\varPhi }}_{55k}= & {} -\beta _{j}^{i}(g+1)\gamma ^{2}I+sym(H_{1k_{j}(g)}B_{i}\\&+\, \lambda _{3}\beta _{j}^{i}(g+1){\hat{B}}_{f}D_{i});\\ {\bar{\varPhi }}_{56k}= & {} \beta _{j}^{i}(g+1)E^{T}_{i}- \beta _{j}^{i}(g+1)D^{T}_{i}\hat{D}_{f}^{T};\\ \bar{\varPsi }_{11k}= & {} \bar{P}_{1k_{j}(g)}-{\bar{F}}_{1k_{j}(g)}- {\bar{F}}^{T}_{1k_{j}(g)};\\ {\bar{\varPsi }}_{12k}= & {} {\bar{P}}_{2k_{j}(g)}-\beta _{j}^{i}(g+1)V- {\bar{F}}^{T}_{2k_{j}(g)};\\ {\bar{\varPsi }}_{13k}= & {} {\bar{F}}_{1k_{j}(g)}A_{i}+\beta _{j}^{i}(g+1) {\hat{B}}_{f}C_{i}-\bar{G}^{T}_{1k_{j}(g)};\\ {\bar{\varPsi }}_{22k}= & {} {\bar{P}}_{3k_{j}(g)}-\beta _{j}^{i}(g+1)V -\beta _{j}^{i}(g+1)V^{T};\\ {\bar{\varPsi }}_{3k}= & {} {\bar{F}}_{2k_{j}(g)}A_{i}+\beta _{j}^{i}(g+1){\hat{B}}_{f}C_{i};\\ {\bar{\varPsi }}_{4k}= & {} -{\bar{P}}_{3k_{j}(g)}+sym(\bar{G}_{1k_{j}(g)}A_{i}). \end{aligned}$$

Matrix $\bar{\varOmega }_{k}$ is defined as follows:

• For the low-frequency (LF) range $|\theta |\le \theta _{l}$

  $$\begin{aligned} \bar{\varOmega }_{k}= & {} \left[ \begin{array}{llllll} P_{1k_{j}(g)} &{} \quad P_{2k_{j}(g)} &{} \quad Q_{1k_{j}(g)} &{} \quad Q_{2k_{j}(g)} &{} \quad 0 &{} \quad 0 \\ *&{} \quad P_{3k_{j}(g)} &{} \quad Q_{2k_{j}(g)}^{T} &{} \quad Q_{3k_{j}(g)} &{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad \bar{\varOmega }_{1k} &{} \quad \bar{\varOmega }_{2k} &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad \bar{\varOmega }_{3k} &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0\\ \end{array} \right] \end{aligned}$$
  $$\begin{aligned} {\bar{\varOmega }}_{1k}= & {} -P_{1k_{j}(g)}-2cos\theta _{l}Q_{1k_{j}(g)};\\ {\bar{\varOmega }}_{2k}= & {} -P_{2k_{j}(g)}-2cos\theta _{l}Q_{2k_{j}(g)};\\ {\bar{\varOmega }}_{3k}= & {} -P_{3k_{j}(g)}-2cos\theta _{l}Q_{3k_{j}(g)}. \end{aligned}$$

• For the middle-frequency (MF) range $\theta _{1}\le \theta \le \theta _{2}$

  $$\begin{aligned} \bar{\varOmega }_{k}= & {} \left[ \begin{array}{llllll} P_{1k_{j}(g)} &{} \quad P_{2k_{j}(g)} &{} \quad e^{j\theta _{c}}Q_{1k_{j}(g)} &{} \quad Q_{2k_{j}(g)} &{} \quad 0 &{} \quad 0 \\ *&{} \quad P_{3k_{j}(g)} &{} \quad e^{-j\theta _{c}}Q_{2k_{j}(g)}^{T} &{} \quad e^{j\theta _{c}}Q_{3k_{j}(g)} &{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad \bar{\varOmega }_{1k} &{} \quad \bar{\varOmega }_{2k} &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad \bar{\varOmega }_{3k} &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0\\ \end{array} \right] \end{aligned}$$
  $$\begin{aligned} {\bar{\varOmega }}_{1k}= & {} -P_{1k_{j}(g)}-2cos\theta _{w}Q_{1k_{j}(g)};\\ {\bar{\varOmega }}_{2k}= & {} -P_{2k_{j}(g)}-2cos\theta _{w}Q_{2k_{j}(g)};\\ {\bar{\varOmega }}_{3k}= & {} -P_{3k_{j}(g)}-2cos\theta _{w}Q_{3k_{j}(g)};\\ \theta _{c}= & {} \frac{(\theta _{1}+\theta _{2})}{2},\;\;\;\;\theta _{w}=\frac{(\theta _{2}-\theta _{1})}{2}. \end{aligned}$$

• For the high-frequency (HF) range $|\theta |\ge \theta _{h}$

  $$\begin{aligned} {\bar{\varOmega }}_{\alpha }= & {} \left[ \begin{array}{llllll} P_{1k_{j}(g)} &{} \quad P_{2k_{j}(g)} &{} \quad -Q_{1k_{j}(g)} &{} \quad Q_{2k_{j}(g)} &{} \quad 0 &{} \quad 0 \\ *&{} \quad P_{3k_{j}(g)} &{} \quad -Q_{2k_{j}(g)}^{T} &{} \quad -Q_{3k_{j}(g)} &{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad \bar{\varOmega }_{1k} &{} \quad \bar{\varOmega }_{2k} &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad \bar{\varOmega }_{3k} &{} \quad 0 &{} \quad 0\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0 &{} \quad 0 \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad 0\\ \end{array} \right] \end{aligned}$$
  $$\begin{aligned} {\bar{\varOmega }}_{1k}= & {} -P_{1k_{j}(g)}+2cos\theta _{h}Q_{1k_{j}(g)};\\ {\bar{\varOmega }}_{2k}= & {} -P_{2k_{j}(g)}+2cos\theta _{h}Q_{2k_{j}(g)};\\ {\bar{\varOmega }}_{3k}= & {} -P_{3k_{j}(g)}+2cos\theta _{h}Q_{3k_{j}(g)}. \end{aligned}$$

Then the homogeneous polynomially parameter-dependent matrices given by (30) ensure (26) and (27) for all $\alpha \in \Gamma$. Moreover, if the LMIs of (31) and (32) are fulfilled for a given degree $\bar{g}$, then the LMIs corresponding to any degree $g>\bar{g}$ are also satisfied.

Proof 4.3

The proof is similar to that of Theorem 3 in Gao et al. (2008) and is thus omitted. $\square$

Corollary 2

Given a stable system (1). For given a constants $\gamma >0$, $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$, a filter of from (5) exists such that the filtering error system in (6) is asymptotically stable with an $H_{\infty }$ performance bound $\gamma$. If there exist symmetric matrix $P(k_{j}(g))=\left[ \begin{array}{cc} P_{1k_{j}(g)} &{} P_{2k_{j}(g)} \\ *&{} P_{3k_{j}(g)}\\ \end{array} \right] >0$, matrices ${\hat{A}}_{f}$, ${\hat{B}}_{f}$, $\hat{C}_{f}$, $\hat{D}_{f}$, $\bar{G}_{tk_{j}(g)}$, ${\bar{F}}_{tk_{j}(g)}$ (where $t=1,2$), $H_{1k_{j}(g)}$, V and the real scalars $\lambda _{1}$, $\lambda _{2}$ and $\lambda _{3}$ such that the following LMIs hold for all $K_{l}(g+1)\in K(g+1)$ , $l=1, \ldots ,J(g+1)$:

$$\begin{aligned} {\bar{\varXi }}_{k}= & {} \left[ \begin{array}{llllll} {\bar{\varXi }}_{11k} &{} \quad {\bar{\varXi }}_{12k} &{} \quad {\bar{\varXi }}_{13k} &{} \quad {\bar{\varXi }}_{14k} &{} \quad {\bar{\varXi }}_{15k} &{} \quad 0 \\ *&{} \quad {\bar{\varXi }}_{22k} &{} \quad {\bar{\varXi }}_{23k} &{} \quad {\bar{\varXi }}_{24k} &{} \quad {\bar{\varXi }}_{25k} &{} \quad 0 \\ *&{} \quad *&{} \quad {\bar{\varXi }}_{33k} &{} \quad {\bar{\varXi }}_{34k} &{} \quad {\bar{\varXi }}_{35k} &{} \quad {\bar{\varXi }}_{36k} \\ *&{} \quad *&{} \quad *&{} \quad {\bar{\varXi }}_{44k} &{} \quad {\bar{\varXi }}_{45k} &{} \quad -\beta _{j}^{i}(g+1)\hat{C}_{f}^{T}\\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad {\bar{\varXi }}_{55k} &{} \quad {\bar{\varXi }}_{46k} \\ *&{} \quad *&{} \quad *&{} \quad *&{} \quad *&{} \quad -\beta _{j}^{i}(g+1)I\\ \end{array} \right] \nonumber \\< & {} 0 \end{aligned}$$

(33)

with

$$\begin{aligned} {\bar{\varXi }}_{11k}= & {} P_{1k_{j}(g)}-G_{1k_{j}(g)}-G_{1k_{j}(g)}^{T},\\ {\bar{\varXi }}_{12k}= & {} P_{2k_{j}(g)}-\beta _{j}^{i}(g+1)V-G_{2k_{j}(g)}^{T};\\ {\bar{\varXi }}_{13k}= & {} -F_{1k_{j}(g)}^{T}+G_{1k_{j}(g)}A_{i} +\beta _{j}^{i}(g+1){\hat{B}}_{f}C_{i};\\ {\bar{\varXi }}_{14k}= & {} -F_{2k_{j}(g)}^{T}+\beta _{j}^{i}(g+1){\hat{A}}_{f};\\ {\bar{\varXi }}_{15k}= & {} -H_{1k_{j}(g)}^{T}+G_{1k_{j}(g)}B_{i}+\beta _{j}^{i} (g+1){\hat{B}}_{f}D_{i};\\ {\bar{\varXi }}_{22k}= & {} P_{3k_{j}(g)}-\beta _{j}^{i}(g+1)V-\beta _{j}^{i}(g+1)V^{T};\\ {\bar{\varXi }}_{23k}= & {} -\beta _{j}^{i}(g+1)\lambda _{1}V^{T} +G_{2k_{j}(g)}A_{i}+\beta _{j}^{i}(g+1){\hat{B}}_{f}C_{i};\\ {\bar{\varXi }}_{24k}= & {} -\beta _{j}^{i}(g+1)\lambda _{2}V^{T} +\beta _{j}^{i}(g+1){\hat{A}}_{f};\\ {\bar{\varXi }}_{25k}= & {} G_{2k_{j}(g)}B_{i}+\beta _{j}^{i}(g+1) {\hat{B}}_{f}D_{i}-\beta _{j}^{i}(g+1)\lambda _{3}V^{T};\\ {\bar{\varXi }}_{33k}= & {} -P_{1k_{j}(g)} +sym(F_{1k_{j}(g)}A_{i}+\beta _{j}^{i}(g+1)\lambda _{1}{\hat{B}}_{f}C_{i});\\ {\bar{\varXi }}_{34k}= & {} -P_{2k_{j}(g)}+\beta _{j}^{i}(g+1) \lambda _{1}{\hat{A}}_{f}+A_{i}^{T}F_{2k_{j}(g)}^{T}\\&+\, \beta _{j}^{i}(g+1)\lambda _{2}C_{i}^{T}{\hat{B}}_{f};\\ {\bar{\varXi }}_{35k}= & {} A_{i}^{T}H_{1\alpha }^{T} +\beta _{j}^{i}(g+1)\lambda _{3}C_{i}^{T}{\hat{B}}^{T}_{f}+F_{1k_{j}(g)}B_{i}\\&+\, \beta _{j}^{i}(g+1)\lambda _{1}{\hat{B}}_{f}D_{i};\\ {\bar{\varXi }}_{36k}= & {} \beta _{j}^{i}(g+1)L_{i} ^{T}-\beta _{j}^{i}(g+1)C_{i}^{T}\hat{D}_{f}^{T};\\ {\bar{\varXi }}_{44k}= & {} -P_{3k_{j}(g)}+\beta _{j}^{i} (g+1)\lambda _{2}(A_{f}+A^{T}_{f});\\ {\bar{\varXi }}_{45k}= & {} \beta _{j}^{i}(g+1)\lambda _{3} {\hat{A}}^{T}_{f}+F_{2k_{j}(g)}B_{i}+ \beta _{j}^{i}(g+1)\lambda _{2} {\hat{B}}_{f}D_{i};\\ {\bar{\varXi }}_{45k}= & {} \beta _{j}^{i}(g+1)E_{i}^{T}-\beta _{j}^{i} (g+1)D_{i}^{T}\hat{D}_{f}^{T};\\ {\bar{\varXi }}_{55k}= & {} -\beta _{j}^{i}(g+1)\gamma ^{2}I+sym(H_{1k_{j}(g)}B_{i})\\&+\, \beta _{j}^{i}(g+1)\lambda _{3}{\hat{B}}_{f}D_{i}). \end{aligned}$$

Then the homogeneous polynomially parameter-dependent matrices given by (30) ensure (29) for all $\alpha \in \Gamma$. Moreover, if the LMIs of (33)is fulfilled for a given degree $\bar{g}$, then the LMIs corresponding to any degree $g>\bar{g}$ are also satisfied.

Proof 4.4

The proof is parallel to that of Theorem 3 in Gao et al. (2008), using the result in Corollary 2, so it is omitted. $\square$

Remark 4.5

Theorem 4.2 provide sufficient conditions for the FF $H_{\infty }$ filtering for uncertain discrete-time linear systems in different frequency ranges. Numerical examples show that the proposed FF approach has better performances than the existing full frequency ones when the frequency ranges of the noises are known.

Remark 4.6

When the scalars $\lambda _{1}$, $\lambda _{2}$ and $\lambda _{3}$ of Theorems 4.1, 4.2 and Corollaries 1, 2 are fixed to be constants, then (26), (27), (29), (31), (32) and (33) are LMIs which are effectively linear in the variables. To select values for these scalars, optimization can be used to optimize some performance measure (for example $\gamma$ , the disturbance attenuation level).

Remark 4.7

As the degree g of the polynomial increases, the conditions become less conservative since new free variables are added to the LMIs. Although the number of LMIs is also increased, each LMIs becomes easier to be fulfilled due to the extra degrees of freedom provided by the new free variables and smaller values of $H_{\infty }$ guaranteed costs can be obtained.

5 Numerical Examples

In this section, simulation examples are provided to illustrate the effectiveness of the proposed filtering design approach. We compare our work with some elegant results from the literature.

Table 1 Comparison of filtering performance obtained by different methods for example 1

5.1 Numerical Example 1:

Consider a system of from (1) is described by Gao and Li (2014):

$$\begin{aligned}&x{(k+1)}=\left[ \begin{array}{cc} \delta &{} \quad -0.5 \\ 1 &{} \quad 1 \\ \end{array} \right] x{(k)}+ \left[ \begin{array}{cc} -6 &{} \quad 0 \\ 2 &{} \quad 0 \\ \end{array} \right] w{(k)}\nonumber \\&y{(k)}=\left[ \begin{array}{cc} -100 &{} \quad 10 \\ \end{array} \right] x{(k)}+ \left[ \begin{array}{cc} 0 &{} \quad 1 \\ \end{array} \right] w{(k)}\\&z{(k)}=\left[ \begin{array}{cc} 1 &{} \quad 0 \\ \end{array} \right] x{(k)}+ \left[ \begin{array}{cc} 0 &{} \quad 0 \\ \end{array} \right] w{(k)}\nonumber \end{aligned}$$

(34)

The uncertain parameters $\delta$ is now assumed to be $-0.25\le \delta \le 0.25$, so the above system is represented by a two-vertex polytope. Our aim is to design a finite frequency $H_{\infty }$ filter in the form of (6) such that the resulting filtering error system in (7) is asymptotically stable with a guaranteed $H_{\infty }$ disturbance attenuation level.

LMIs (31), (32) and (33) were solved using Yalmip (Lofberg 2004) and SeDuMi (Sturm et al. 1999) in MATLAB 7.6, for increasing values of the degree g. The comparison result with the technique proposed in Algorithm 8 (Gao and Li 2014) in shown in Table 1, which shows the smaller conservativeness of the approach proposed in this paper.

In addition, the $H_{\infty }$ performance improved when the parameters $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$ and $\lambda _{4}$ of Theorem 4.2 and Corollary 2 are searched using simplex algorithm. The role of these scalar parameters in the LMIs conditions is to provide extra degrees and to reduce the conservativeness of the LMIs tests.

The filter parameters are given as follows:

5.1.1 Entire Frequency Case:(Corollary 1)

For degree $g=0$, the obtained disturbance attenuation level is $\gamma =1.0494$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} -0.2093 &{} \quad -0.7442 \\ 0.5058 &{} \quad 1.1290 \\ \end{array}&{} \begin{array}{c} 0.0044 \\ 0.0045 \end{array} \\ \begin{array}{cc} -0.0430 &{} \quad -0.0956 \end{array}&\begin{array}{c} -0.0096 \end{array} \end{array} \right] \end{aligned}$$

(35)

On the other hand, when degree $g=1$, $\gamma =0.2815$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} 0.8046 &{} \quad 0.0069\\ 0.8335 &{} \quad 0.8632 \end{array}&{} \begin{array}{c} 0.0542\\ -0.0151 \end{array} \\ \begin{array}{cc} -0.0134 &{} \quad -0.0012 \end{array}&\begin{array}{c} -0.0096 \end{array} \end{array} \right] \end{aligned}$$

(36)

Finally, when degree $g=2$, $\gamma =0.2558$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} -0.7178 &{} \quad -0.5175\\ 0.5500 &{} \quad 1.0740 \end{array}&{} \begin{array}{c} 0.0114\\ 0.0035 \end{array} \\ \begin{array}{cc} -0.0329 &{} \quad -0.0967 \end{array}&\begin{array}{c} -0.0097 \end{array} \end{array} \right] \end{aligned}$$

(37)

5.1.2 Finite Frequency: (Theorem 4.2)

Low-Frequency (LF) Range $|\theta |\le \frac{\pi }{8}$: For degree $g=0$, $\gamma =0.4579$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} 0.6520 &{} \quad -0.0023\\ 0.9481 &{} \quad 0.8836\\ \end{array}&{} \begin{array}{c} 0.0447\\ -0.0201 \end{array} \\ \begin{array}{cc} -0.0161 &{} \quad -0.0050 \end{array}&\begin{array}{c} -0.0097 \end{array} \end{array} \right] \end{aligned}$$

(38)

In addition, when degree $g=1$, $\gamma =0.1862$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} 0.7468 &{} \quad -0.0034\\ 0.8791 &{} \quad 0.9213\\ \end{array}&{} \begin{array}{c} 0.0356\\ -0.0085 \end{array} \\ \begin{array}{cc} -0.0202 &{} \quad -0.0035 \end{array}&\begin{array}{c} -0.0097 \end{array} \end{array} \right] \end{aligned}$$

(39)

Finally, when $g=2$, $\gamma =0.1688$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} 0.8393 &{} \quad 0.0010\\ 0.7943 &{} \quad 0.8951 \end{array}&{} \begin{array}{c} 0.0377\\ -0.0080 \end{array} \\ \begin{array}{cc} -0.0183 &{} \quad -0.0014\\ \end{array}&\begin{array}{c} -0.0097 \end{array} \end{array} \right] \end{aligned}$$

(40)

Middle-Frequency (MF) Range $\frac{\pi }{8}\le |\theta |\le \frac{\pi }{5}$:

For degree $g=0$, the obtained disturbance attenuation level is $\gamma =0.7626$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} -0.6308 &{} \quad 0.0781\\ 1.2732 &{} \quad 0.7919\\ \end{array}&{} \begin{array}{c} 0.0855\\ -0.0316 \end{array} \\ \begin{array}{cc} -0.0155 &{} \quad -0.0160 \end{array}&\begin{array}{c} -0.0095 \end{array} \end{array} \right] \end{aligned}$$

(41)

On the other hand, when degree $g=1$, $\gamma =0.2389$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} -0.7392 &{} \quad -0.2984\\ 0.5224 &{} \quad 0.9946\\ \end{array}&{} \begin{array}{c} 0.0138\\ 0.0028 \end{array} \\ \begin{array}{cc} -0.0302 &{} \quad -0.0978 \end{array}&\begin{array}{c} -0.0097 \end{array} \end{array} \right] \end{aligned}$$

(42)

In addition, when degree $g=2$, $\gamma =0.2268$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} -0.7566 &{} \quad -0.2896\\ 0.5070 &{} \quad 0.9901 \end{array}&{} \begin{array}{c} 0.0145\\ 0.0027 \end{array} \\ \begin{array}{cc} -0.0310 &{} \quad -0.0984\\ \end{array}&\begin{array}{c} -0.0097 \end{array} \end{array} \right] \end{aligned}$$

(43)

High-Frequency (HF) Range $|\theta |\ge \frac{\pi }{6}$: For degree $g=0$, $\gamma =0.2000$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} 0.9482 &{} \quad 0.0222\\ 0.4485 &{} \quad 0.4018\\ \end{array}&{} \begin{array}{c} 0.0297\\ -0.0255 \end{array} \\ \begin{array}{cc} -0.0262 &{} \quad -0.0010 \end{array}&\begin{array}{c} -0.0098 \end{array} \end{array} \right] \end{aligned}$$

(44)

In addition, when degree $g=1$, $\gamma =0.1453$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} 0.8348 &{} \quad -0.0011\\ 0.8859 &{} \quad 0.8745\\ \end{array}&{} \begin{array}{c} 0.0305\\ -0.0082 \end{array} \\ \begin{array}{cc} -0.0235 &{} \quad -0.0015 \end{array}&\begin{array}{c} -0.0097 \end{array} \end{array} \right] \end{aligned}$$

(45)

Finally, when $g=2$, $\gamma =0.1453$ and the corresponding filter matrices are:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} 0.8166 &{} \quad -0.0089\\ 0.9459 &{} \quad 0.9833 \end{array}&{} \begin{array}{c} 0.0352\\ -0.0028 \end{array} \\ \begin{array}{cc} -0.0200 &{} \quad -0.0013\\ \end{array}&\begin{array}{c} -0.0096 \end{array} \end{array} \right] \end{aligned}$$

(46)

To illustrate the effectiveness of these designed filters, we consider polytopic case (degree $g=1$), by, respectively, connecting (36), (39), (42) and (45) to the systems in (34), the frequency responses of the filtering error systems are depicted in Figs. 1, 2, 3, 4. All the singular values in these figures are lower than the achieved $H_{\infty }$ filtering performance disturbance attenuation level $\gamma$, which demonstrates the effectiveness of our proposed method.

Fig. 1

Frequency response of the filtering error system with filter (36)

Fig. 2

Frequency response of the filtering error system with filter (39)

Fig. 3

Frequency response of the filtering error system with filter (42)

Fig. 4

Frequency response of the filtering error system with filter (45)

Assume that the uncertain parameter $\delta =-0.25$ and degree $g=1$, applying the obtained low-frequency $|\theta |\le \frac{\pi }{8}$, the disturbance input

$$\begin{aligned} w(k)= sin(k) \left[ \begin{array}{cc} \frac{1}{k^{2}+1}&\quad \frac{1}{k^{3}+1} \end{array} \right] ^{T} \end{aligned}$$

(47)

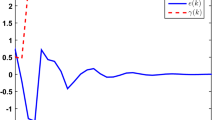
the initial conditions are chosen as $x(0)=[-0.1\;\;0.1]^{T}$ and $\hat{x}(0)=[0\;\;0]^{T}$, the simulation result of the filtering error $e(k)=z(k)-\hat{z(k)}$ with the filtering matrices (35) and (38) is shown in Fig. 5. It is shown that the filtering error e(k) tends to zero, which means that the estimated $\hat{z(k)}$ follows z(k) well. The ratio of $\sqrt{\sum _{k=0}^{\infty }e^{T}(k)e(k)/\sum _{k=0}^{\infty }w^{T}(k)w(k)}$ can show the influence of the disturbance w(k) on the filter error e(k) , and the plot of the ratio is shown in Fig. 6. It can be seen that the ratio tends to a constant value 0.1552, which is less than the prescribed value 0.1862. It can be seen from Fig. 6 that the proposed method has a better noise-attenuation performance over the existing method.

Fig. 5

Estimation error e(k) subject to sinusoidal disturbance

Fig. 6

Value of($\sqrt{\sum _{k=0}^{\infty }e^{T}(k)e(k)/\sum _{k=0}^{\infty }w^{T}(k)w(k)}$) for the system (34) connected with filter (36)

5.2 Numerical Example 2:

Based on the example given in Lee (2013), Lacerda et al. (2011) described by:

$$\begin{aligned}&x{(k+1)}=\left[ \begin{array}{cc} 0&{} \quad -0.5 \\ 1 &{} \quad 1+\beta \\ \end{array} \right] x{(k)}+ \left[ \begin{array}{cc} -6 &{}\quad 0 \\ 1 &{}\quad 0 \\ \end{array} \right] w{(k)}\nonumber \\&y{(k)}=\left[ \begin{array}{cc} -100 &{}\quad 10 \\ \end{array} \right] x{(k)}+ \left[ \begin{array}{cc} 0 &{}\quad 1 \\ \end{array} \right] w{(k)}\\&z{(k)}=\left[ \begin{array}{cc} 1 &{}\quad 0 \\ \end{array} \right] x{(k)}+ \left[ \begin{array}{cc} 0 &{}\; 0 \\ \end{array} \right] w{(k)}\nonumber \end{aligned}$$

(48)

where $\delta$ is uncertain real parameter satisfying $|\beta |\le 0.45$.

Table 2 Comparison of filtering performance obtained in different finite frequency ranges for example 2

By using Theorem 4.2 and Corollary 2, in different frequency ranges. Let $g=1$ (linearly parameter-dependent polynomial), we get the following robust filter’s parameters:

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{}\quad B_{f} \\ C_{f} &{}\quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} -0.2488 &{} \quad -1.4571\\ 0.2415 &{} \quad -0.0248 \end{array}&{} \begin{array}{c} 0.0070\\ 0.0100 \end{array} \\ \begin{array}{cc} -0.0073 &{} \quad -0.0675\\ \end{array}&\begin{array}{c} -0.0079 \end{array} \end{array} \right] \end{aligned}$$

(49)

for EF range, with an $H_{\infty }$ performance index $\gamma =1.6398$.

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{}\quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} -2.0883 &{} \quad -0.5473\\ 9.8404 &{} \quad 2.4640 \end{array}&{} \begin{array}{c} 0.0035\\ -0.0119 \end{array} \\ \begin{array}{cc} -1.9145 &{} \quad -0.3663\\ \end{array}&\begin{array}{c} -0.0063 \end{array} \end{array} \right] \end{aligned}$$

(50)

for LF $|\theta |\le \frac{\pi }{6}$, with an $H_{\infty }$ performance index $\gamma =1.1401$.

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} -0.7519 &{} \quad -0.1214 \\ 1.8593 &{} \quad 0.9560 \end{array}&{} \begin{array}{c} 0.0255 \\ -0.0202 \end{array} \\ \begin{array}{cc} -0.0552 &{} \quad -0.0305\\ \end{array}&\begin{array}{c} -0.0089 \end{array} \end{array} \right] \end{aligned}$$

(51)

for MF $\frac{\pi }{6}\le |\theta |\le \frac{\pi }{4}$, with an $H_{\infty }$ performance index $\gamma =0.7173$.

$$\begin{aligned} \left[ \begin{array}{c|c} A_{f} &{} \quad B_{f} \\ C_{f} &{} \quad D_{f} \end{array} \right]= & {} \left[ \begin{array}{c|c} \begin{array}{cc} -1.0556 &{} \quad -0.0807\\ 0.0394 &{} \quad -0.9452 \end{array}&{} \begin{array}{c} 0.6321\\ 0.4902 \end{array} \\ \begin{array}{cc} -0.0879 &{} \quad -0.1235\\ \end{array}&\begin{array}{c} -0.0093 \end{array} \end{array} \right] \end{aligned}$$

(52)

for HF $|\theta |\ge \frac{5\pi }{6}$ with an $H_{\infty }$ performance index $\gamma =0.1023$.

Table 3 Comparison of filtering performance obtained in different full frequency ranges for example 2

In order to demonstrate the value of our proposed approach, we provide in Table 2 the robust $H_{\infty }$ filtering performance levels obtained by the finite frequency approaches proposed in this work and in Lee (2013).

In addition, Table 3 shows that even in the EF range, our proposed approach outperform some recent results in the literature, which study the full frequency robust $H_{\infty }$ filtering problem.

It is clearly shown that Theorem 4.2 yields less conservative results than the FF method proposed in Lee (2013), as well as the EF methods in Corollary 2, and Lacerda et al. (2011). We consider polytopic case (degree $g=1$), by, respectively, connecting (49), (50), and (52) to the systems in (48), the frequency responses of the filtering error systems are depicted in Figs. 7, 8, 9. From the results, it is clear that the singular values evaluated in a certain frequency domain are always lower than the robust $H_{\infty }$ performance estimated using Corollary 2 and Theorem 4.2. This shows the efficiency of the proposed method.

Fig. 7

Frequency response of the filtering error system with filter (49)

Fig. 8

Frequency response of the filtering error system with filter (50)

Fig. 9

Frequency response of the filtering error system with filter (52)

We assume that $\frac{\pi }{6}\le |\theta |\le \frac{\pi }{4}$, and degree $g=1$, the initial conditions are chosen as $x(0)=[0\;\;0]^{T}$ and $\hat{x}(0)=[0\;\;0]^{T}$. The ratio of $\sqrt{\sum _{k=0}^{\infty }e^{T}(k)e(k)/\sum _{k=0}^{\infty }w^{T}(k)w(k)}$ can show the influence of the disturbance w(k) in (47) on the filter error e(k) , and the plot of the ratio is shown in Fig. 6. It can be seen that the ratio tends to a constant value 0.4896, which is less than the prescribed value 0.7173. It can be seen from Fig. 10 that the proposed method has a better noise-attenuation performance over the existing method.

Fig. 10

Value of ($\sqrt{\sum _{k=0}^{\infty }e^{T}(k)e(k)/\sum _{k=0}^{\infty }w^{T}(k)w(k)}$) for the system (48) connected with filters (51)

6 Conclusions

This paper has investigated the problem of filtering design a finite frequency for the linear time-invariant discrete-time with polytopic uncertainties. The contribution of the paper is to assume that the disturbance has energy limited on LF/MF/HF ranges, and to use the gKYP in order to develop new filter design conditions. Numerical experiments show the advantage of the developed approach in comparison with the existing results.