Stress Concentration in Composite Cantilever Plates—Effect of Stiffeners and Remedy

Abstract

The present study examines a composite cantilever beam containing a plate with two parallel sides stiffened symmetrically. A simplified procedure is used to analyze the flexural behavior of the beam. A numerical example illustrates the simplicity and accuracy of the methodology. When the edges of the cantilever plate are stiffened, the stress concentration is increased. The centerline stresses of the plate at the fixed end are considerably higher. A low aspect ratio (l/w) and a low G/E ratio significantly influence stress concentration. The present study demonstrates that stiffeners with high flexural rigidity could significantly reduce stress concentration along cantilever plate centerlines, allowing them to achieve similar results to those predicted by simple bending theory (SBT). Comparison and verification of the proposed simplified methodology are conducted using existing literature and finite element analysis. The theoretical results are in good agreement with those obtained by the literature and finite element analysis.

Notations

The following symbols are used in this paper:

E, G	=	Young's modulus and shear modulus of the beam
EeIe, EpIp, EsIs	=	Flexural rigidity
h	=	Height of the fiber from the neutral axis
hs	=	Thickness of stiffener
Ip, Is	=	Moment of inertia
k, n	=	Reissner’s parameters
l	=	Span length
M(x), M	=	Bending moment
P, q	=	Loading’s intensity
t, ts	=	The thickness of the plate and width of the stiffener
u (x)	=	Longitudinal displacement
u (z)	=	Vertical displacement
u (x, y)	=	Spanwise sheet displacement
U(x) or U	=	Correction due to shear lag
w	=	The half-width of the plate
x, y, z	=	Coordinates
x1, x2	=	End of the interval of integration
α, β	=	Constants
δ	=	Deflection
δo	=	Maximum deflection in EBT
µ		Poisson’s ratio
$\varepsilon_{x} ,\gamma$	=	Linear and shear strain of the cover sheet
Πl, Πst, Πp, ΠT	=	Potential energy
σ, σx, σ (x, y)	=	Bending stress
σmax		Maximum bending stress (at the fixed end)
σEBT	=	Bending stress in EBT
σo	=	Maximum bending stress in EBT (at the fixed end)

Introduction

In engineering design, cantilever plates are frequently used for variable, discontinuous, concentrated, or eccentric loads. Cantilever walls, projecting floor slabs, projecting piers heads, and gear teeth are examples of cantilever plates [1]. Other thin cantilever plates stiffened by an attached member are box, U-T-, and I-beams with thin cover plates as flanges. Ship hulls, floors, tanks, aircraft, box-girder bridges, and tubular-tall buildings utilize these beams. In these beams, stress distribution across the width is not uniform similar to elementary beam theory (EBT) stresses in narrow beams. These types of beams do not satisfy the assumption of elementary beam theory that the normal stress in the flange does not vary in the direction across the width because of the shear deformability of the flanges [2].

As a result of the bending in the cantilever plate, complex boundary conditions are produced [3,4,5,6,7,8,9]. In particular, the shape of the plate is cylindrical, and two corners are lifted [4, 7, 10,11,12,13]. In the past literature, a plate with different boundary condition has been analyzed by various scholars [14,15,16,17,18,19,20]. The authors analyze the cantilever plate using numerical methods, preferably finite difference method, superposition method, and the generalized variational principle [1,3,3]. However, the stresses do not follow a uniform distribution across the width in very short wide plates. In order to calculate the strength of such a plate, the concept of effective width was introduced [1,2,3, 19,20,21]. In addition, Tenchev [21] reported that Poisson's ratio in calculating the effective width produces a significant error in the plates composed of composite material as the E/G ratio of the plate affects the variation in stress along the width of the plate. It also did not include any provisions for different E/G ratios in the code for fiber composites and sandwich constructions [22].

A thin plate is also used as a flange in a box beam, I-, T-beam, and U-beam, stiffened by another plate called the web. Therefore, stiffening the thin plate in this manner produces a 2D plane stress problem [23,24,25,26,27,28]. Box beam, I-, T-beam, and U-beam cross sections become warped under shear stresses [23,24,25,26,27,28,29,30,31,32,33]. Thus, preventing the free warping of the flange produces stress concentration in the flange. The bending stress distribution across the width becomes unequal, and this phenomenon is called shear lag [2, 23,24,25,26,27,28]. Actual stresses are significant at the junction of the flange and web. A positive shear lag occurs at the flange–web junction when the actual stresses are higher than the other part of the flange [23,24,25,26,27,28]. However, the opposite of this phenomenon is negative shear lag [30,31,32,33], which occurs whenever the actual stresses at the flange–web junction are lowest compared with those at the other part of the flange.

Researchers have examined the effects of stiffening on preventing the free warping of thin plates [34, 35]. The warping displacement of the flange is used to study the stress concentration in terms of shear lag effect. Many researchers have studied and explained the shear lag phenomenon using 2D models [36,37,38,39,40]. In addition to the other notable methods to analyze these structures [24, 41,42,43,44], the energy method is quite versatile as well. The least work method uses the stress compatibility equilibrium equations, and the minimum potential energy method uses the strain compatibility equilibrium equations [2, 23, 28, 30, 45,46,47,48,49,50,51,52,53]. The shape functions of the warping of the flange of the structure are assumed to be polynomials of degrees two, three, four, and five. The assumed shape function shows the stress distribution across the width [27, 54, 55].

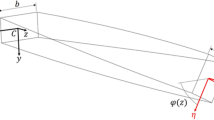
According to the rigorous literature review, stress concentration is a major concern when analyzing the cantilever plate [1, 3, 15]. A part of flanges located far from web–flange junctions does not take their full share of the resisting bending moment in thin plate sections [2, 25,26,27]. Utilizing Poisson's ratio may result in an incorrect stress distribution across the width of composite plates. Therefore, this study aims to analyze a composite cantilever beam composed of a plate symmetrically stiffened along its parallel sides (Fig. 1). Stiffeners provide an additional constraint along the parallel sides of the cantilever to restrain the plate's free warping. The cantilever plate can be stiffened along the parallel sides to prevent it from bending cylindrically and the corners from lifting (Fig. 1a). The entire composite cantilever beam can be considered as a 2D plane stress problem. The composite cantilever beam is discretized using the variation approach [2, 53]. For the entire simulation, the G/E ratio was used instead of Poisson's ratio. The warping displacement function is assumed to follow a second-order polynomial. Because the order of differential equation is higher than in elementary beam theory, additional boundary conditions appear in addition to the governing equations.

Fig. 1

Composite panel composed of cantilever plate stiffened along parallel sides: a single panel, b multiple panels, c geometry and coordinates of the composite cantilever beam/panel

Analytical Formulation

The present study considers a composite cantilever beam with length l. It has a width of 2w and a thickness of t (Fig. 1c). The stiffener has a width of t_s and a thickness of h_s. For shear deformation coupled with normal stress, the corresponding span-wise displacement is assumed to be a polynomial function. Assuming that the span-wise coordinate is x, the coordinates perpendicular to the x-direction are y and z. Coordinate z(x) represents the deflection of the neutral axis of the beam.

Here are the assumptions.

• Parts of the beam are rigidly connected.

• A simple bending theory is followed by the stiffeners.

• Assuming shear deformation coupled with normal stress, the corresponding span-wise displacement of the plate would be:

  $$u\left(x,y\right)=\pm h\left(\frac{dz}{dx}+\frac{{y}^{2}}{{w}^{2}}U\left(x\right)\right)$$

  (1)

  where U(x) is the correction due to shear lag. The stiffened cantilever plate's potential energy may be composed of the elastic potential energy of the load system П_l, the strain energy of the two stiffeners П_st, and the strain energy of the plate П_p.

The elastic potential energy of a load system for a distribution of bending moments M along the length l is given by:

$${\Pi }_{l}=\int M\frac{{d}^{2}z}{d{x}^{2}}dx$$

(2)

The strain energy of the two stiffeners

$$\Pi_{st} = \frac{1}{2}\int E_{s} I_{s} \left( {\frac{{d^{2} z}}{{dx^{2} }}} \right)^{2} dx\quad \left( {{\text{Where}}\;I_{s} = \frac{1}{6}t_{s} h_{s}^{3} } \right)$$

(3)

I_s denotes the principal moment of inertia of the two-sided stiffener. Denoting, E_s and E_p are the modulus of elasticity of the stiffener and the plate, and G_p is the modulus of rigidity of the plate. The strain energy of plate

$$\Pi_{p} = \frac{1}{2}\iiint {\left\{ {E_{p} \varepsilon_{x}^{2} + G_{p} \gamma^{2} } \right\}dxdydh}$$

(4)

The span-wise linear and shear strain in the plate can be calculated from Eq. 1 as follows:

$$\varepsilon _{x} = \pm h\left( {z'' + \left( {\frac{{y^{2} }}{{w^{2} }}} \right)U'} \right);\;\gamma = \pm \frac{{2h}}{w}\frac{y}{w}U$$

(5)

Putting the values of linear and shear strain from Eq. 5 in Eq. 4, the strain energy of the plate

$$\Pi _{p} = \frac{1}{2}\int E_{p} I_{p} \left\{ {\left( {z''} \right)^{2} + \frac{1}{5}\left( {U'} \right)^{2} + \frac{2}{3}z''U' + \frac{{G_{p} }}{{E_{p} }}\frac{4}{{3w^{2} }}U^{2} } \right\}dx\quad {\text{where}}\;\left( {I_{p} = \frac{1}{6}{\text{wt}}^{3} } \right)$$

(6)

After combining Eq. 2, Eq. 3, and Eq. 6, the total potential energy for the system

$$\Pi _{T} = \int \left\{ {\frac{1}{2}E_{e} I_{e} \left( {z''} \right)^{2} + Mz''} \right\}dx + \smallint \frac{1}{2}E_{p} I_{p} \left\{ {\frac{1}{5}\left( {U'} \right)^{2} + \frac{2}{3}z''U' + \frac{4}{{3w^{2} }}\frac{{G_{p} }}{{E_{p} }}U^{2} } \right\}dx,\;{\text{where}}\;E_{e} I_{e} = E_{p} I_{p} + E_{s} I_{s}$$

(7)

The differential equation and boundary condition for z and U can be derived using theorem of minimum potential energy, i.e., $\delta {\Pi }_{T}=0$. Thus, with x₁and x₂ denoting the interval of integration

$$\delta \Pi _{T} = \int \left\{ {\left[ {E_{e} I_{e} z'' + M + \frac{1}{3}E_{p} I_{p} U'} \right]\delta z'' + E_{p} I_{p} \left[ { - \frac{1}{5}U'' - \frac{1}{3}z''' + \frac{4}{{3w^{2} }}\frac{{G_{p} }}{{E_{p} }}U} \right]\delta U} \right\}dx + \left\{ {E_{p} I_{p} \left[ {\frac{1}{5}U' + \frac{1}{3}z''} \right]\delta U} \right\}_{{x_{1} }}^{{x_{2} }} = 0$$

(8)

The following relations can be established.

$$\left[ {z'' + \frac{1}{3}\frac{{E_{p} I_{p} }}{{E_{e} I_{e} }}U' + \frac{M}{{E_{e} I_{e} }}} \right] = 0$$

(9)

$$E_{p} I_{p} \left[ {\frac{1}{5}U'' - \frac{4}{3}\frac{{G_{p} }}{{E_{p} }}\frac{1}{{w^{2} }}U + \frac{1}{3}z^{\prime\prime\prime}} \right] = 0$$

(10)

$${\left\{{E}_{p}{I}_{p}\left[\frac{1}{5}{U}^{^{\prime}}+\frac{1}{3}z"\right]\delta U\right\}}_{{x}_{1}}^{{x}_{2}}=0$$

(11)

From Eqs. 10 and 11, eliminating the U' and U'' and arranging the term

$$z"-\frac{{z}^{IV}}{{k}^{2}}=-\frac{M}{{E}_{e}{I}_{e}}+\frac{n}{{k}^{2}}\frac{M"}{{E}_{e}{I}_{e}}$$

(12)

The two Reissner’s parameters are

$$n = \frac{1}{{1 - \frac{5}{9}\frac{{E_{p} I_{p} }}{{E_{e} I_{e} }}}}\;{\text{and}}\;k = \frac{1}{w}\sqrt {\frac{20}{3}n\frac{{G_{p} }}{{E_{p} }}}$$

(13)

Solutions

The cantilever beam is analyzed by applying uniformly distributed load q throughout the span, point load P at the free end, uniformly varied load with maximum intensity q at the support, and uniformly varied load with maximum intensity q at the free end, respectively. The bending stress distribution in the cantilever is derived, assuming the free end is the origin of the coordinate system. As a result of bending Eqs. 18, 19, 20, and 21, Eq. (12) can be solved in close form accordance with Reissner [2] and Singh et al. [53] for each load case, respectively, as follows.

$${\sigma }_{x}=\pm \frac{q{l}^{2}}{2}\frac{{E}_{p}h}{{E}_{e}{I}_{e}}\left[{\left(\frac{x}{l}\right)}^{2}+\frac{10}{3}\frac{n}{{\left(kl\right)}^{2}}\left\{\frac{1}{3}\frac{{E}_{p}{I}_{p}}{{E}_{e}{I}_{e}}-\frac{{y}^{2}}{{w}^{2}}\right\}\left\{\frac{\mathrm{cosh}\,\left(l-x\right)+kl\,\mathrm{sinh}\,kx}\,{\mathrm{cosh}\,kl}-1\right\}\right]$$

(14)

$${\sigma }_{x}=\pm Pl\frac{{E}_{p}h}{{E}_{e}{I}_{e}}\left[\frac{x}{l}+\frac{5}{3}\frac{n}{kl}\left\{\frac{1}{3}\frac{{E}_{p}{I}_{p}}{{E}_{e}{I}_{e}}-\frac{{y}^{2}}{{w}^{2}}\right\}\left\{\frac{\mathrm{sinh}\,kx}{\mathrm{cosh}\,kl}\right\}\right]$$

(15)

$${\sigma }_{x}=\pm \frac{q{l}^{2}}{6}\frac{{E}_{p}h}{{E}_{e}{I}_{e}}\left[{\left(\frac{x}{l}\right)}^{3}+\frac{10n}{{\left(kl\right)}^{2}}\left\{\frac{1}{3}\frac{{E}_{p}{I}_{p}}{{E}_{e}{I}_{e}}-\frac{{y}^{2}}{{w}^{2}}\right\}\left\{-\frac{x}{l}+\left(\frac{kl}{2}+\frac{1}{kl}\right)\frac{\mathrm{sinh}\,kx}{\mathrm{cosh}\,kl}\right\}\right]$$

(16)

$${\sigma }_{x}=\pm \frac{q{l}^{2}}{3}\frac{{E}_{p}h}{{E}_{e}{I}_{e}}\left[\frac{3}{2}{\left(\frac{x}{l}\right)}^{2}-{\frac{1}{2}\left(\frac{x}{l}\right)}^{3}+\frac{5n}{{\left(kl\right)}^{2}}\left\{\frac{1}{3}\frac{{E}_{p}{I}_{p}}{{E}_{e}{I}_{e}}-\frac{{y}^{2}}{{w}^{2}}\right\}\left\{\frac{x}{l}-1+\mathrm{cosh}\,kx+\left(\frac{kl}{2}-\mathrm{sinh}\,kl-\frac{1}{kl}\right)\frac{\mathrm{sinh}\,kx}{\mathrm{cosh}\,kl}\right\}\right]$$

(17)

Results and Discussion

In the example, a composite cantilever beam of 250 mm length, 2w = 100 mm, t = 20 mm, is obtained by adding stiffeners of 20 mm thickness (h_s) and 6 mm width (t_s) to the plate. Material properties of the beam are as follows: Young's modulus of plate (E_p) = 70 GPa, G_p/E_p ratio = 0.38, Young's modulus of stiffeners (E_s) = 200 GPa. Aspect ratio (l/w) and stiffness ratio (E_pI_p/E_eI_e) of the cantilever are five and 0.75, respectively. Three-dimensional finite-element analysis of the composite beam is carried out using ANSYS version 15 for all load cases considered. The longitudinal and vertical displacements at the end of the beam are restrained by setting u(x) = 0 and u(z) = 0. An additional boundary condition is applied to fulfill the assumption made in the present study by restricting the lateral displacements and rotations at the edges of stiffeners at the free end. A 20-noded 3D homogenous structural solid element, SOLID186, which adopts a higher-order deformation theory, was used as part of the analysis. The model is discretized using a global mess size of 7.5 mm, resulting in 1632 elements (Fig. 2). The stress concentration is expressed as a stress factor (σ/σ^EBT), i.e., the ratio of actual stress to stress calculated by the elementary beam theory. A peak stress factor indicates the greatest stress observed across the width of a beam (σ^max/σ_o).

Fig. 2

Finite element analysis model of the composite cantilever beam

According to Eqs. 18, 19, 20, and 21, the deflection profiles of the composite beam are calculated and compared with those of the FEA and existing literature and presented in Fig. 3. The calculated results are in close agreement with those obtained by the FEA, Reissner's box beam [2], and Euler–Bernoulli's beam. There is a trivial deviation in the deflection profile compared to Euler–Bernoulli's beam due to the additional deflection produced by the shear deformation. In comparison with a cantilever box beam, there is an apparent increase in the maximum deflection of the composite cantilever.

Fig. 3

Comparison of the deflection profile of the composite cantilever beam with the literature and FEA

Further, to verify the accuracy of the present methodology, the stresses in the centerline of the plate along the length of the top fiber are also compared to the FEA results for all loading cases (Fig. 4). There is excellent agreement between the present methodology and FEA results for all loading scenarios. Even though FEA can evaluate stress in various structures, the results at the fixed end of the cantilever cannot be determined directly and precisely due to singularities.

Fig. 4

Comparison of the variation in the stress at the top fiber in the centerline of the of the plate in the cantilever beam

A composite cantilever beam considered in the present study exhibits a negative shear lag effect at the fixed end similar to those obtained by Singh et al. [53]. Applied loads induced higher stresses apart from the plate–stiffeners junction and along the plate's centerline at the support. This can be observed in Fig. 5 for uniformly distributed load q, for point load P at the free end, for uniformly varied load with maximum intensity q at support, and for uniformly varied load with maximum intensity q at the free end. The stress factor is used to calculate the additional stresses produced. Peak stress factors in the centerline of the example beam generated by each load case are 1.12, 1.066, 1.164, and 1.10, respectively. The centerline of the beam at the fixed end exhibits a higher stress factor than the box beam [2] due to reverse shear transmission. There is a positive shear lag effect after a certain distance along the length of the cantilever from the fixed end as shown in Fig. 5. Similar results are observed for negative shear lag along the length of a cantilever box beam [30].

Fig. 5

Stress profile across the plate width in the composite cantilever beam: a for uniformly distributed load; b for point load at free end; c for uniformly varied load with maximum intensity at the support; and d for uniformly varied load with maximum intensity at the free end

If the present study is extended to cantilever beams consisting of a plate and stiffeners of the same material, the stiffness ratio E_pI_p/EI is transformed into I_p/I. As shown in Fig. 5, the variation of the bending stresses in the plate of the composite beam is not uniform, and the maximum stresses are located at the centerline of the fixed end. This method can be applied to estimate the exact stress variation in H-shaped beams, fletched wood beams, ship hulls, composite glass, ceramic, and metallic plates, and composite concrete slabs under varying load conditions. The present study also applies to stiffening the edges of layered composite cantilever plates using Young's modulus and shear modulus for transverse bending. It is practical and economical to design the composite beam using the exact estimation of the stress variations. A precise prediction of the adhesive bond strength and weld length can be made when fabricating this type of composite. As a result of space constraints, the results for different end conditions are not presented in the present study, but they can be easily derived from Kuzmanovic and Graham [56]. In the parametric analysis section, detailed discussions on the various parameters affecting the stress concentration are included. A parametric analysis of stress localization based on stress factors is presented in the following paragraphs.

Effect of Aspect Ratio

The aspect ratio (l/w) is one of the most important parameters affecting the shear lag. In Fig. 6, the peak stress factor developed due to the negative shear lag effect is plotted against the aspect ratio. The variation in peak stress factor follows the pattern of the box beam. The peak stress factor is observed to be greater for lower aspect ratios. The fixed end stress is significantly affected by stiffening the cantilever plate with an aspect ratio below five. Peak stress factors at the fixed end of the cantilever for square plates (aspect ratio 2) are 1.25, 1.17, 1.31, and 1.22 for uniformly distributed load, point load at free end, uniformly varied load at support, and uniformly varied load at free end, respectively. Aspect ratios of 20 or more result in a lower peak stress factor of 1.05 (Fig. 6a).

Fig. 6

a Variation in the peak stress factor at the fixed end with respect to the aspect ratio (l/w); b variation in the peak stress factor at the fixed end with respect to the stiffness ratio (E_pI_p/E_eI_e); c variation in the peak stress factor at the fixed end with respect to the G_p/E_p ratio

Effect of Stiffness Ratio

Variations in the stiffness ratio (E_pI_p/EI) correspond to changes in the relative stiffness of the plate. Figure 6b shows the variation in stress factor to stiffness ratio (E_pI_p/EI) in the composite cantilever beam's plate for the aspect ratio five. Some existing box girder bridges have stiffness ratios ranging from 0.8 to 0.96 [43, 47, 57]. For the cantilever beam, the stiffness ratio is assumed by Reissner [2] to be 0.5. The stiffness ratio of composite beams may be lower [21]. Therefore, the stiffness ratio range is taken as 0.1 to 0.90. Stress concentration in terms of negative shear lag effect is noted to increase with a higher stiffness ratio. Moffatt and Dowling [43] observed a similar phenomenon in box beams for the positive shear lag. The peak stress factor increases as the stiffness ratio of the flange plate increases. Additionally, the combination of the plate and stiffeners may result in a lower stiffness ratio, reducing the stress concentration at the fixed end. According to Fig. 6b, the peak stress factor is reduced by 1.05 or less for stiffness ratios below 0.3. The stress factors are closer to one, which is closer to the results of the SBT.

Effect of Material Property

The present methodology is based on the G_p/E_p ratio instead of the Poison's ratio [55], which results in an inevitable error when analyzing composite beams [21]. Material properties are presented in terms of variations in peak stress factors relative to the G_p/E_p ratio. In this study, the G_p/E_p ratio ranges from 0.18 to 0.64. Figure 6c shows the relation between the G_p/E_p ratio and the stress factor for the aspect ratio five. Significantly higher stress levels are observed in the cantilever beam with lower G_p/E_p ratios of the plate. Lin and Zhao [47] report a similar observation. For a box beam loaded in its nonlinear range of behavior, a higher stress concentration is observed. Therefore, the G_p/E_p ratio is an essential parameter when analyzing composite structures and equally relevant when the beam is loaded in its nonlinear range.

Effect of Stiffeners and Remedy

Although stiffeners are used to prevent the cantilever plate from being bent cylindrically or lifted at the corners, the plate still shows stress concentration at the fixed end, similar to past studies [1, 3, 4, 7]. Accordingly, the present study suggests that minimizing localized stresses at the fixed end of a composite cantilever beam can result in an approximately uniform distribution of stresses across its width. It is possible to minimize stress localization by combining plates and stiffeners in a way that produces a low stiffened ratio. Because the stiffness ratio depends on the stiffness of both the plate and the stiffener, stiffeners with high flexural rigidity will reduce the stiffness ratio of a composite beam made of specific plates (Fig. 7).

Fig. 7

Variation in the peak stress factor at the fixed end with respect to the relative stiffness of the stiffeners and plate for different loadings

The variation of the stress factor for the relative stiffness of the stiffeners and plate (E_sI_s/E_pI_p) is depicted in Fig. 7 for G/E = 0.6 and the aspect ratios in most of the practical range. The stiffeners with higher relative stiffness reduce the stress factor closer to one. However, in a very wide beam, the shear lag effect is higher, and thus the stress concentration. Consequently, the stiffeners even having the relative stiffness two or more are not able to reduce the stress factor significantly in very wide beam/panel (l/w ≤ 1). Partitioning the panels, in this case, can reduce the stress concentration at the fixed end of the plate. Partitioning the panels (Fig. 1b) may result in a higher relative stiffness of the stiffeners along with an increased aspect ratio of the plate. This may reduce stress concentrations along the centerline of the fixed end of the plate.

Conclusions

This paper analyzes a cantilever plate symmetrically stiffened along its parallel sides using the simplified procedure for varying shear loads. A higher stress concentration is observed at the centerline of the fixed end due to a negative shear lag effect. The results are verified by comparing with the result of existing literature and finite element analysis. Additionally, the conclusions of the present study are as follows.

• (a) Adding stiffeners to the sides of a cantilever plate produces stress concentrations in the centerline at the fixed end due to the negative shear lag effect and reduced stress at the plate–stiffener interface. Aspect ratio greatly influences shear lag—a lower aspect ratio results in higher stress concentrations.

• (b) Higher plate stiffness results in a higher negative shear lag effect. Nevertheless, stiffeners with high flexural rigidity may reduce the stress concentration in the centerline at the fixed end of the composite cantilever beam significantly and even more so than the SBT.

• (c) The G/E ratio of the plate significantly affects the negative shear lag in composite cantilever beams. With lower G/E ratios, stress levels are significantly higher. This makes the G/E ratio an essential parameter in analyzing composite structures and equally relevant when the beam is loaded in its nonlinear range.

Thus, the present study recommends using stiffeners with higher flexural rigidities in composite beam construction than stiffeners with lower flexural rigidities. This accomplishes the objective of analyzing the composite cantilever beam.

Appendix 1 Additional Equations

Assuming the coordinate x = 0, x = l at free end fixed end of the beam, respectively, the equations for the bending moment can be written (Eqs. 18–21 for each loading cases, respectively)

$$M=-\frac{q{l}^{2}}{2}{\left(\frac{x}{l}\right)}^{2}$$

(18)

$$M=-Pl\left(\frac{x}{l}\right)$$

(19)

$$M=-\frac{q{l}^{2}}{6}{\left(\frac{x}{l}\right)}^{3}$$

(20)

$$M=-\frac{q{l}^{2}}{3}\left[\frac{3}{2}{\left(\frac{x}{l}\right)}^{2}-\frac{1}{2}{\left(\frac{x}{l}\right)}^{3}\right]$$

(21)

The cantilever's deflection profile for each loading case can be obtained after putting U' and M in Eq. 12 and integrating twice. Making z (l) = z' (l) = 0, the equations for the deflection profile for uniformly distributed load q, point load P at free end, uniformly varied load with maximum intensity q at the support, uniformly varied load with maximum intensity q at the free end can be obtained, respectively, as

$$z\left(x\right)=\frac{q{l}^{4}}{8{E}_{e}{I}_{e}}\left[\frac{1}{3}{\left(\frac{x}{l}\right)}^{4}-\frac{4}{3}\left(\frac{x}{l}\right)+1+\frac{8(n-1)}{{\left(kl\right)}^{2}}\left\{\frac{1}{2}\left(1-{\left(\frac{x}{l}\right)}^{2}\right)+\frac{\mathrm{cosh}\,kx-\mathrm{cosh}\,kl}{{\left(kl\right)}^{2}}-\frac{\mathrm{sinh}\,kx-\mathrm{sinh}\,kl}{{\left(kl\right)}^{2}\mathrm{cosh}\,kl}\left(\mathrm{sinh}\,kl-kl\right)\right\}\right]$$

(22)

$$z\left(x\right)=\frac{P{l}^{3}}{3{E}_{e}{I}_{e}}\left[\frac{1}{2}{\left(\frac{x}{l}\right)}^{3}-\frac{3}{2}\left(\frac{x}{l}\right)+1+\frac{3(n-1)}{{\left(kl\right)}^{2}}\left\{-\frac{x}{l}+\frac{\mathrm{sinh}\,kx}{kl\mathrm{cosh}\,kl}-\frac{\mathrm{tanh}\,kl}{kl}+1\right\}\right]$$

(23)

$$z\left(x\right)=\frac{q{l}^{4}}{30{E}_{e}{I}_{e}}\left[\frac{1}{4}{\left(\frac{x}{l}\right)}^{5}-\frac{5}{4}\left(\frac{x}{l}\right)+1+\frac{30(n-1)}{{\left(kl\right)}^{2}}\left\{\frac{1}{3}\left(1-{\left(\frac{x}{l}\right)}^{3}\right)+\frac{2}{{\left(kl\right)}^{2}}\left(1-\frac{x}{l}\right)+\left(kl+\frac{2}{kl}\right)\frac{\mathrm{sinh}\,kx-\mathrm{sinh}\,kl}{{\left(kl\right)}^{2}\mathrm{cosh}\,kl}\right\}\right]$$

(24)

$$z\left(x\right)=\frac{11q{l}^{4}}{120{E}_{e}{I}_{e}}\left[-\frac{1}{11}{\left(\frac{x}{l}\right)}^{5}+\frac{5}{11}{\left(\frac{x}{l}\right)}^{4}-\frac{15}{11}\frac{x}{l}+1+\frac{120}{11}\frac{(n-1)}{{\left(kl\right)}^{2}}\left\{\frac{1}{6}{\left(\frac{x}{l}\right)}^{3}-\frac{1}{2}{\left(\frac{x}{l}\right)}^{2}+\frac{1}{3}-\frac{1}{{\left(kl\right)}^{2}}\left(1-\frac{x}{l}\right)+\frac{\mathrm{cosh}\,kx-\mathrm{cosh}\,kl}{{\left(kl\right)}^{2}}+\left(\frac{kl}{2}-\frac{1}{kl}-\mathrm{sinh}\,kl\right)\frac{\mathrm{sinh}\,kx-\mathrm{sinh}\,kl}{{\left(kl\right)}^{2}\mathrm{cosh}\,kl}\right\}\right]$$

(25)