Introduction

In modern days, curved panels are often used in various structures of aerospace, civil, marine and mechanical engineering. Singly and doubly curved panels are mostly used in civil engineering as roofing units in order to cover large span areas. The use of curved panels is increasing significantly due to appreciation of community from aesthetic point of view. Owing to its geometry, curved panels are structurally stiffer than flat panels. In practical situations, many times these structures are exposed to various non-uniform loads, such as triangular, point, patch or arbitrary loads at the boundaries due to which non-uniform in-plane stresses are developed. The non-uniform in-plane stress distribution may also be developed due to material and geometrical discontinuities in structures. When a structure is subjected to non-uniform in-plane compressive force, it undergoes large transverse displacements and complex stress distribution occurs in structures. Therefore, the study of buckling characteristics of curved panels under non-uniform in-plane loads is of utmost technical importance so far as the understanding of the behaviour of these systems is concerned.

In the past, several researchers reported the vibration and buckling study of isotropic plates under various in-plane loadings employing different methods. Timoshenko and Gere [1] presented the numerical results on the critical buckling loads for flat plates under various uniform loads and a pair of concentrated loads at mid breadth. Khan and Walker [2] studied the buckling characteristics of plate subjected to localized edge loading by a simple theoretical method and compared the results obtained using finite element solution. Numerical study on vibration and buckling behaviour of plates under in-plane hydrostatic loading was reported by Kielb and Han [3]. The bucking and vibration solutions of rectangular plates under complicated in-plane stress were presented by Kaldas and Dickinson [4] using the Rayleigh–Ritz method. The elastic stability behaviour of rectangular plates under locally distributed edge forces was investigated by Baker and Pavlovic [5] for simply supported boundary condition. Leissa and Ayoub [6] investigated the buckling and vibration behaviour of a rectangular plate for concentrated forces which are directed opposite to each other employing the Ritz and finite element method (FEM). The elastic stability of plates under concentrated and distributed tangential loads was carried out by Brown [7, 8]. Kitipornchai et al. [9] investigated the bucking behaviour of thick skew plates using the Rayleigh–Ritz method. The bucking characteristics of Mindlin plates under normal in-plane forces were investigated by Wang et al. [10] and Liew et al. [11] employing the Rayleigh–Ritz method and Levy type solution method, respectively. Similarly, the buckling analysis of rectangular Mindlin plates under partial in-plane loading was carried out by Liew and Chen [12] employing the radial point interpolation method. The differential quadrature method was also applied to analyse the buckling of rectangular plates by Wang et al. [13]. Bradford and Azhari [14] studied the buckling of plate for various end conditions employing the finite strip method. The vibration, buckling and instability study of plates with an opening positioned in the middle under in-plane loading at the edges (tension and compression) are reported by Prabhakara and Dutta [15]. The buckling and vibration behaviour of simply supported free simply supported free (SS-F-SS-F) rectangular plates subjected to in-plane moments was investigated by Kang and Leissa [16].

Leissa and Kang [17], Kang and Leissa [18] and Wang et al. [19] reported the exact solutions for buckling and vibration of plates of rectangular dimension under linearly varying in-plane stress for different boundary conditions using power series method, method of Frobenius and differential quadrature method, respectively. The buckling behaviour of rectangular Reissner–Mindlin plates with simply supported boundary condition under linearly varying in-plane load was studied by Zhong and Gu [20] using both analytical method and computer software ANSYS. The buckling analysis of rectangular thin plate with varying thickness under biaxial compression was carried out by Eisenberger and Alexandrov [21] employing the extended Kantorovich method. Moreover, the buckling behaviour of plates subjected to various non-uniform in-plane loading was investigated by various researchers [22,23,24] using various methods. Ikhenazen et al. [25] studied the buckling behaviour of linear plates subjected to in-plane patch loading using FEM. Similarly, Wang and Yuan [26] applied the differential quadrature method to analyse the buckling of skew plates under general in-plane loading.

In addition to the study of buckling behaviour of isotropic plates, a number of research works were also reported on the buckling characteristics of composite plates. The buckling analyses of laminated composite plates with various boundary conditions under uniform in-plane loading were carried out by Baharlou and Leissa [27] and Dawe and Wang [28] using Ritz and spline finite strip methods, respectively. Chai et al. [29] and Chai and Kong [30] investigated the optimization of laminated plates of rectangular dimension under linearly varying in-plane loading. Similarly, the buckling analysis of symmetrical composite rectangular plates under linearly varying in-plane load was carried out by Zhong and Gu [31] and Ni et al. [32] for different boundary conditions. The buckling analysis of moderately thick rectangular composite and sandwich plates subjected to partial edge loading was also carried out by Sunderesan et al. [33] and Chakrabarti and Seikh [34], respectively. Shufrin et al. [35] applied a semi-analytical approach to investigate the buckling behaviour of symmetrical laminated rectangular plates under various combinations of in-plane compression for general boundary conditions. Buckling behaviour of composite plates subjected to partial or concentrated in-plane loading was investigated by Daripa and Singha [36] employing FEM. Lopatin and Morozov [37,38,39] and Bourada et al. [40] reported the buckling characteristics of orthotropic rectangular plates subjected to various in-plane loadings for different boundary conditions. Panda and Ramachandra [41] obtained the critical buckling loads of rectangular laminated plates subjected to non-uniform in-plane loading for various boundary conditions using Galerkin’s approximation.

Though there were extensive researches on the buckling behaviour of isotropic and composite plates, few researches were reported on the buckling of shells. Yamada et al. [42] conducted experimental study on the buckling behaviour of shallow spherical shells with clamped boundary condition subjected to external pressure. Featherston and Ruiz [43] also conducted a series of tests to establish the accuracy of the theoretical critical buckling loads of curved panels subjected to combined compression and shear. The buckling behaviour of thick cylindrical shells under axial stress was investigated by Matsunaga [44] using higher-order shell theory. Hilburger et al. [45, 46] studied the buckling characteristics of quasi-isotropic curved panels having a circular cut-out under compression. Matsunaga [47] investigated analytically the stability and vibration of thick shallow shells with simply supported boundary condition under in-plane stresses. The experiments were conducted by Mandal and Calladine [48] on self-weight buckling behaviour of thin cylindrical shells under axial compression. Sahu and Datta [49] studied the buckling and parametric instability behaviour of curved panels under non-uniform harmonic load. Ravi Kumar et al. [50] studied the vibration and buckling behaviour of curved panels with various in-plane tensile in-plane loading using FEM. The same authors [51] also investigated the parametric instability and tensile buckling of curved panels with an opening positioned in the middle exposed to uniaxial in-plane partially distributed tensile load at the edges using the same method. Khelil [52] investigated theoretically and numerically the buckling behaviour of steel shells under non-uniform axial and pressure loading. The buckling behaviour of circular cylindrical shells under axial compression was studied by Edlund [53] and Ullah [54] using various methods.

Further, a number of research works were also carried out on the buckling characteristics of composite shells. The buckling analysis of symmetrical laminated cylindrical curved panels under axial compression was carried out by Jun and Hung [55] with respect to fibre angle and width of the panels employing the nonlinear finite element method. Geier and Rohwer [56] investigated the buckling behaviour of composite plates and shells for comparing different plate/shell theories. The buckling characteristics of composite conical shells subjected to axial compression were studied by Tong and Wang [57] and Shadmehri et al. [58] using various techniques. Greenberg and Stavsky [59] studied the buckling behaviour of orthotropic cylindrical shells under non-uniform axial loading. The buckling behaviour of anisotropic curved panels having variable curvature was investigated by Jaunky et al. [60] using segment approach. The buckling characteristics of composite elliptical cylinders under axial compression were investigated by Sambandam et al. [61] employing FEM. The study of post-buckling and dynamic instability characteristics of cylindrical shell with dynamic partial edge loading and transverse patch loading was performed by Dey and Ramachandra [62]. The same authors [63] also investigated the buckling and post-buckling characteristics of cylindrical sandwich panels subjected to non-uniform in-plane load using analytical method.

Asmolovskiy et al. [64] analysed various methods of numerical buckling load estimation and formulated simulation procedures suitable for commercial software and provided the recommendations with regard to their applications for cylindrical composite shells. Demir et al. [65] investigated the buckling behaviour of simply supported isotropic, laminated composite and functionally graded conical shells using discrete singular convolution method. The post-buckling characteristics of functionally graded cylindrical, spherical, elliptical and hyperbolic curved panels under the uniaxial and biaxial edge loading were investigated by Kar and Panda [66] using nonlinear finite element analysis. Civalek [67] investigated the buckling characteristics of composite conical and cylindrical panels and shells subjected to axial compression using discrete singular convolution method.

From the literature review, it is found that extensive research works have been conducted on the study of buckling behaviour of isotropic and composite plates and shells with uniform loading, concentrated loading and non-uniform loading including patch loading and different types of linearly varying in-plane edge loading. Moreover, several research works are also now being carried out on buckling behaviour of singly and doubly curved panels under various in-plane loading throughout the globe, which shows the research potentiality of this field. However, it is observed that most of the above works have focused on the development of suitable methods/models for obtaining the critical buckling loads with/without parametric study. Hence, the further exhaustive parametric study on the buckling characteristics of curved panels under non-uniform in-plane loading needs to be investigated in order to give a clear understanding to the designers. Moreover, the design charts in non-dimensional forms are yet to be developed to estimate the critical buckling load of the singly and doubly curved panels under any non-uniform in-plane loading. These charts will be of immense help to the designers for determining the buckling loads of these curved panels under any in-plane loading directly from these charts without the use of the complicated models or software at the time of preliminary design.

In order to fill up the above research gap, an exhaustive parametric study for static stability analysis of isotropic singly and doubly curved panels under linearly varying in-plane load, which is a special case of non-uniform in-plane loading and also very common in practical fields, is presented in this paper using FEM to obtain the influences of various parameters, such as type of loading, aspect ratio, curvature, boundary condition and Poisson’s ratio. Further, a comparison of the influences of the various in-plane loads, such as triangular, parabolic, patch and concentrated in-plane loads, on the buckling characteristics of cylindrical, spherical and hyperbolic panels is made. Moreover, various design charts in the non-dimensional form are also developed for the clamped isotropic spherical panels of commonly adopted dimensions using the present FEM code to obtain the buckling loads of various curved panels of any isotropic material under any type of linearly varying in-plane loads, which enhances the novelty of this work further. At the last, the accuracy of the design charts is also established by comparing the values obtained from the design charts with those from the computer code developed in the present investigation.

Theory and Formulations

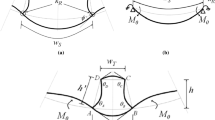
An isotropic rectangular doubly curved panel having length a and width b in plan form and radii of curvature Rx and Ry under linearly varying in-plane loading (Fig. 1) is considered here as the fundamental configuration of the present problem. The purpose behind choosing of the geometry of a doubly curved panel as a fundamental configuration is that the panel configuration (form) depends upon the value of curvature, such as single curved cylindrical panel for Ry/Rx = 0, double curved spherical panel for Ry/Rx = 1 and hyperbolic panel for Ry/Rx = -1 as special cases, which are shown in Fig. 2.

Fig. 1
figure 1

Geometry of a typical doubly curved panel

Full size image
Fig. 2
figure 2

Different forms of curved panels: a cylindrical shell, b elliptic paraboloid shell (special case: spherical shell, Rx = Ry and a = b), c hyperbolic paraboloid shell (special case, Rx = −Ry and a = b)

Full size image

A typical rectangular doubly curved panel with plan dimensions a and b under linearly varying in-plane stresses at two opposite edges (x = 0 and x = a), while the other two opposite edges (y = 0 and y = b) are free from any load, is shown in Fig. 3. The linearly varying load is expressed as:

$$N_{x} = - N_{0} \left( {1 - \gamma \frac{y}{b}} \right)$$
(1)
Fig. 3
figure 3

Plan form of a curved panel under linearly varying in-plane load

Full size image

where Nx denotes the normal force acting per unit length of curved panel at y along x direction. N0 is the force per unit length along x direction at y = 0. The negative sign of N0 indicates that the force is compressive in nature and γ is a numerical load factor. The distributions of stress applied at the edges of the curved panels at x = 0 and x = a are identical. By changing the value of γ, various cases as shown in Fig. 4 can be obtained. It is assumed that the curved panel is thin and of uniform thickness. The material used is homogeneous, linearly elastic and isotropic.

Fig. 4
figure 4

Examples of in-plane loading Nx along the edges x = 0 and x = a

Full size image

Formulation

The governing equation for static stability is written as

$$\left[ {\left[ K \right] - P\left[ {K_{{\text{g}}} } \right]} \right]\left\{ q \right\} = \left\{ 0 \right\}$$
(2)

where [K] and [Kg] are elastic stiffness and geometric stiffness matrices, respectively, and P is the in-plane edge load vector. Equation (2) is an Eigen value problem. The lowest of the Eigen values is the critical buckling load, Pcr, and {q} is the corresponding Eigen vector.

In order to form the Eigen value problem, an eight-nodded curved isoparametric element is used in the present finite element formulation with five degrees of freedom per node, i.e. u, v, w, θx and θy. The shape function of the element is obtained employing the interpolation polynomial as

$$u(\xi ,\eta ) = \alpha_{1} + \alpha_{2} \xi + \alpha_{3} \eta + \alpha_{4} \xi^{2} + \alpha_{5} \xi \eta + \alpha_{6} \eta^{2} + \alpha_{7} \xi^{2} \eta + \alpha_{8} \xi \eta^{2}$$
(3)

The shape functions Ni, derived from Eq. (1), are expressed as

$$\begin{array}{*{20}l} {N_{i} = \, (1 + \xi \xi_{i} ) \, (1 + \eta \eta_{i} ) \, (\xi \, \xi_{i} + \eta \, \eta_{i} - 1)/4 \quad i = \, 1{\text{ to }}4} \hfill \\ \begin{gathered} N_{i} = \, {{\left( {1 - \xi^{2} } \right) \, \left( {1 + \eta \, \eta_{i} } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \xi^{2} } \right) \, \left( {1 + \eta \, \eta_{i} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2} \, \quad i = \, 5, \, 7 \hfill \\ N_{i} = \, {{\left( {1 + \xi \, \xi_{i} } \right) \, \left( {1 - \eta^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \xi \, \xi_{i} } \right) \, \left( {1 - \eta^{2} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\quad i = \, 6, \, 8 \hfill \\ \end{gathered} \hfill \\ \end{array}$$
(4)

where ξ and η are the local natural coordinates and ξi and ηi are the values of ξ and η, respectively, at ith node. The derivations of the shape functions Ni with respect to x and y are expressed in terms of their derivations with respect to ξ and η using the Jacobian matrix.

The first-order shear deformation theory (FSDT) is considered. A shear correction factor of 5/6 is applied to account the nonlinear shear distribution as explained in the literature [49, 50]. The generalized displacement functions are expressed as follows:

$$\begin{gathered} \overline{u} \;\left( {x,\;y,\;z} \right) = u\;\left( {x,\;y} \right) + z\theta_{x} \left( {x,\;y} \right)\; \hfill \\ \overline{v} \;\left( {x,\;y,\;z} \right) = v\;\left( {x,\;y} \right) + z\theta_{y} \left( {x,\;y} \right)\; \hfill \\ \overline{w} \;\left( {x,\;y,\;z} \right) = w\;\left( {x,\;y} \right)\; \hfill \\ \end{gathered}$$
(5)

where \(\overline{u} ,\,\overline{v} \,{\text{and}}\,\overline{w}\) and u, v and w are the linear displacements along x, y and z directions at any arbitrary point and at mid surface, respectively. Similarly, θx, and θy are the rotations along x and y directions, respectively.

In this formulation, the structural analysis has been carried out using Green–Lagrange’s strain displacement relations. Donnell’s shell theory is considered in this study. The linear and nonlinear parts of strain are considered to obtain the elastic and geometric stiffness matrices, respectively, as explained in the literature [49, 50]. The total strain is expressed as

$$\left\{ \varepsilon \right\}\, = \,\,\left\{ {\varepsilon_{l} } \right\}\, + \,\left\{ {\varepsilon_{nl} } \right\}$$
(6)

where ɛl and ɛnl are linear and nonlinear strains.

The linear strain displacement relations are:

$$\begin{gathered} \varepsilon_{xl} = \frac{\partial u}{{\partial x}} + \frac{w}{{R_{x} }} + zk_{x} ,\quad \varepsilon_{yl} = \frac{\partial v}{{\partial y}} + \frac{w}{{R_{y} }} + zk_{y} ,\quad \gamma_{xyl} = \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} + \frac{2w}{{R_{xy} }} + zk_{xy} , \hfill \\ \gamma_{yzl} = \frac{\partial w}{{\partial x}} + \theta_{x} - \frac{u}{{R_{x} }} - \frac{v}{{R_{xy} }},\quad \gamma_{zxl} = \frac{\partial w}{{\partial y}} + \theta_{y} - \frac{v}{{R_{y} }} - \frac{u}{{R_{xy} }}\quad \hfill \\ \end{gathered}$$
(7)

where the bending strains are expressed as

$$k_{x} = \frac{{\partial \theta_{x} }}{\partial x}\quad k_{y} = \frac{{\partial \theta_{y} }}{\partial y}\quad {\text{and}}\quad k_{xy} = \frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}$$
(8)

The nonlinear strain components are as follows:

$$\varepsilon_{xnl} = \frac{1}{2}\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \frac{1}{2}\left( {\frac{\partial v}{{\partial x}}} \right)^{2} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}} - \frac{u}{{R_{x} }}} \right)^{2} + \frac{1}{2}z^{2} \left[ {\left. {\left( {\frac{{\partial \theta_{x} }}{\partial x}} \right.} \right)^{2} + \left( {\frac{{\partial \theta_{y} }}{\partial x}} \right)^{2} } \right]$$
(9)
$$\varepsilon_{ynl} = \frac{1}{2}\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \frac{1}{2}\left( {\frac{\partial v}{{\partial y}}} \right)^{2} + \frac{1}{2}\left( {\frac{\partial w}{{\partial y}} - \frac{v}{{R_{y} }}} \right)^{2} + \frac{1}{2}z^{2} \left[ {\left( {\frac{{\partial \theta_{x} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial \theta_{y} }}{\partial y}} \right)^{2} } \right]$$
(10)
$$\gamma_{xynl} = \frac{\partial u}{{\partial x}}\left( {\frac{\partial u}{{\partial y}}} \right) + \frac{\partial v}{{\partial x}}\left( {\frac{\partial v}{{\partial y}}} \right) + \left( {\frac{\partial w}{{\partial x}} - \frac{u}{{R_{x} }}} \right)\left( {\frac{\partial w}{{\partial y}} - \frac{v}{{R_{y} }}} \right) + z^{2} \left[ {\left( {\frac{{\partial \theta_{x} }}{\partial x}} \right)\left( {\frac{{\partial \theta_{x} }}{\partial y}} \right) + \left( {\frac{{\partial \theta_{y} }}{\partial x}} \right)\left( {\frac{{\partial \theta_{y} }}{\partial y}} \right)} \right]$$
(11)

The constitutive relationship for the shell is expressed as follows:

$$F = \left[ D \right]\left\{ \varepsilon \right\}$$
(12)

where {F} = [N1, N2, N3, M1, M2, M3, Q1, Q2]T, [D] is flexural rigidity matrix and {ɛ} is strain vector, N1, N2, N3 = Normal in-plane force resultants, M1, M2, M3 = Bending moment resultants and Q1, Q2 = shearing stress resultants.

The flexural rigidity matrix [D], as given in the literature [49, 50] is expressed as follows:

$$\left[ D \right] = \left[ {\begin{array}{*{20}c} {\frac{Eh}{{1 - \nu^{2} }}} & {\frac{\nu Eh}{{1 - \nu^{2} }}} & 0 & 0 & 0 & 0 & 0 & 0 \\ {\frac{\nu Eh}{{1 - \nu^{2} }}} & {\frac{Eh}{{1 - \nu^{2} }}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {\frac{Eh}{{2\left( {1 + \nu } \right)}}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}} & {\frac{{\nu Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{{\nu Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}} & {\frac{{Eh^{3} }}{{12\left( {1 - \nu^{2} } \right)}}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{{Eh^{3} }}{{24\left( {1 + \nu } \right)}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\frac{Eh}{{2.4\left( {1 + \nu } \right)}}} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\frac{Eh}{{2.4\left( {1 + \nu } \right)}}} \\ \end{array} } \right]$$
(13)

The element elastic stiffness matrix [K]e can be obtained as follows.

$$\left[ K \right]_{{\text{e}}} = \int\limits_{ - 1}^{1} {\int\limits_{ - 1}^{1} {\left[ B \right]^{T} \left[ D \right]\,\left[ B \right]} } \,\left| J \right|\,{\text{d}}\xi \,{\text{d}}\eta$$
(14)

where [B] is the strain–displacement matrix, which is mentioned in the literature [49, 50] as follows:

$$\left[ {Bi} \right] = \left[ {\begin{array}{*{20}c} {N_{i,x} } & 0 & {N_{i} /R_{x} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ 0 & {N_{i,y} } & {N_{i} /R_{y} } & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {N_{i,y} } & {N_{i,x} } & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ {\begin{array}{*{20}c} {N_{i,x} } \\ {N_{i,y} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {N_{i,x} } \\ 0 \\ {N_{i,y} } \\ {\begin{array}{*{20}c} {N_{i} } \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {N_{i,y} } \\ {N_{i,x} } \\ {\begin{array}{*{20}c} 0 \\ {N_{i} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\quad {\text{for}}\quad i = 1,{\kern 1pt} \;2 \ldots 8$$
(15)

Ni is the shape function, Ni,x and Ni,y are the derivatives of the shape function with respect to x and y, i denotes the node number of the element and [J] is the Jacobian matrix.

The element geometric stiffness matrix [Kg]e is derived due to applied in-plane load by adopting the procedure as explained in the book by Cook et al. [68] using the nonlinear Green’s in-plane strains with radius of curvature. The in-plane stresses are developed due to in-plane edge loading and the geometric stiffness matrix is derived by considering the in-plane stress function. Stress field being non-uniform, the plane stress analysis has been performed by adopting FEM to find out the stresses, which are considered to generate the geometric stiffness matrix.

The strain energy due to initial stress is given by

$$U_{2} = \int {\left[ {\sigma^{0} } \right]}^{T} \left\{ {\varepsilon_{{{\text{nl}}}} } \right\}{\text{d}}v$$
(16)

Using the nonlinear strains, the strain energy can be written as

$$\begin{aligned} U_{2} = & \int\limits_{A} {\frac{h}{2}\left[ \begin{gathered} \sigma_{x}^{0} \left\{ {\left( {\frac{\partial u}{{\partial x}}} \right)^{2} + \left( {\frac{\partial v}{{\partial x}}} \right)^{2} + \left( {\frac{\partial w}{{\partial x}} - \frac{u}{{R_{x} }}} \right)^{2} } \right\} + \sigma_{y}^{0} \left\{ {\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \left( {\frac{\partial v}{{\partial y}}} \right)^{2} + \left( {\frac{\partial w}{{\partial y}} - \frac{v}{{R_{y} }}} \right)^{2} } \right\} \hfill \\ + 2\tau_{xy}^{0} \left\{ {\left( {\frac{\partial u}{{\partial x}}\frac{\partial u}{{\partial y}}} \right) + \left( {\frac{\partial v}{{\partial x}}\frac{\partial v}{{\partial y}}} \right) + \left( {\frac{\partial w}{{\partial x}} - \frac{u}{{R_{x} }}} \right)\left( {\frac{\partial w}{{\partial y}} - \frac{v}{{R_{y} }}} \right)} \right\} \hfill \\ \end{gathered} \right]} {\text{d}}x{\text{d}}y + \\ & \quad \int\limits_{A} {\frac{h3}{{24}}} \left[ {\sigma_{x}^{0} \left\{ {\left( {\frac{{\partial \theta_{x} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial \theta_{y} }}{\partial x}} \right)^{2} } \right\} + \sigma_{y}^{0} \left\{ {\left( {\frac{{\partial \theta_{y} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial \theta_{x} }}{\partial y}} \right)^{2} } \right\}2\tau_{xy}^{0} \left\{ {\left( {\frac{{\partial \theta_{y} }}{\partial x}\frac{{\partial \theta_{y} }}{\partial y}} \right) + \left( {\frac{{\partial \theta_{x} }}{\partial x}\frac{{\partial \theta_{x} }}{\partial y}} \right)} \right\}} \right]{\text{d}}x{\text{d}}y \\ \end{aligned}$$
(17)

This can be expressed as

$$U_{2} = \frac{1}{2}\int\limits_{v} {\left[ f \right]}^{T} \left[ S \right]\left[ f \right]{\text{d}}v$$
(18)

where

$$\left\{ f \right\} = \left[ {\frac{\partial u}{{\partial x}},\frac{\partial u}{{\partial y}},\frac{\partial v}{{\partial x}},\frac{\partial v}{{\partial y}},\left( {\frac{\partial w}{{\partial x}} - \frac{u}{{R_{x} }}} \right),\left( {\frac{\partial w}{{\partial y}} - \frac{v}{{R_{y} }}} \right),\frac{{\partial \theta_{x} }}{\partial x},\frac{{\partial \theta_{x} }}{\partial y},\frac{{\partial \theta_{y} }}{\partial x},\frac{{\partial \theta_{y} }}{\partial y}} \right]^{T}$$
(19)

where [S] is the in-plane stress matrix and expressed as

$$\left[ S \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} s & 0 \\ \end{array} } & 0 & 0 & 0 \\ {\begin{array}{*{20}c} 0 & s \\ \end{array} } & 0 & 0 & 0 \\ {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } & s & 0 & 0 \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} s \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ s \\ \end{array} } \\ \end{array} } \right]$$
(20)

where

$$\left[ s \right] = \left[ {\begin{array}{*{20}c} {\sigma_{x}^{0} } & {\tau_{xy}^{0} } \\ {\tau_{xy}^{0} } & {\sigma_{y}^{0} } \\ \end{array} } \right] = \frac{1}{h}\left[ {\begin{array}{*{20}c} {N_{x}^{0} } & {N_{xy}^{0} } \\ {N_{xy}^{0} } & {N_{y}^{0} } \\ \end{array} } \right]$$
(21)

where Nx0, Ny0 and Nxy0 are the in-plane stress resultants.

Moreover, {f} can be expressed as

$$\left\{ f \right\} = \left[ G \right]\left\{ {\delta_{e} } \right\}$$
(22)

where \(\left\{ {\delta_{e} } \right\} = \left[ {u\quad v\quad w\quad \theta_{x} \quad \theta_{y} } \right]^{T} \;\) and [G] is the strain matrix for geometric stiffness, which is expressed as follows:

$$\left[ G \right] = \left[ {\begin{array}{*{20}c} {N_{i,x} } & 0 & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {N_{i,y} } & 0 & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ 0 & {N_{i,x} } & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ { - N_{i} /R_{x} } \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {N_{i,y} } \\ 0 \\ { - N_{i} /R_{y} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {N_{i,x} } \\ {N_{i,y} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ {\begin{array}{*{20}c} {N_{i,x} } \\ {N_{i,y} } \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ {\begin{array}{*{20}c} 0 \\ 0 \\ {N_{i,x} } \\ {N_{i,y} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(23)

The strain energy U2 becomes

$$U_{2} = \iiint {\frac{1}{2}\left\{ {\delta_{e} } \right\}^{T} \left[ G \right]^{T} \left[ S \right]\left[ G \right]\left\{ {\delta_{e} } \right\}{\text{d}}v = \;\frac{1}{2}\left\{ {\delta_{e} } \right\}^{T} \left[ {K_{g} } \right]\left\{ {\delta_{e} } \right\}}$$
(24)

where [Kg] is the element geometric stiffness matrix and is written as

$$\left[ {K_{{\text{g}}} } \right]_{{\text{e}}} = \int\limits_{ - 1}^{ - 1} {\int\limits_{ - 1}^{1} {\left[ G \right]} }^{T} \left[ S \right]\,\left[ G \right]\left| J \right|{\text{d}}\xi {\text{d}}\eta$$
(25)

The nodal load vector for an element when subjected to linearly varying edge loads (Nx) can be determined by the expression as given below:

$$\left\{ {p_{e} } \right\}\, = \,\int\limits_{ - 1}^{ + 1} {\,\left[ N \right]}^{T} N_{x} \left| J \right|\,{\text{d}}\eta$$
(26)

where {p}e is the nodal load vector of the element, [N] denotes the shape function matrix and |J| represents the determinant of the Jacobian matrix.

A FEM code is developed using FORTAN language to compute the buckling loads of curved panels under linearly varying in-plane loads. To avoid the shear locking, reduced integration technique is employed for obtaining the element matrices. The element matrices are then assembled using skyline technique to get the overall matrices. Equation (1) is solved using subspace iteration process. The solution of Eq. (1) gives the Eigen values for different Eigen vectors, which are the buckling loads of different mode shapes. The lowest value of buckling loads is known as the critical buckling load, Pcr. The boundary conditions are applied constraining the generalized displacements components at various nodal points of the discretized structure.

Numerical Results and Discussions

Convergence and Validation of FEM Code

The convergence study has been conducted for non-dimensional buckling load for curved panels for the load factor (γ = 0.5), and the result so obtained is indicated in Table 1. A mesh size of 10 × 10 indicates good convergence and all further results have been computed with this mesh size.

Table 1 Convergence of λ of SSSS and CCCC curved panels under linearly varying load (γ = 0.5) for a/b = 1, b/h = 100, b/Ry = 0.25, ν = 0.3, E = 2.0 × 1011 N/m2, λ = Pcrb2/D
Full size table

To validate the present FEM code for the buckling of isotropic shells under linearly varying load, two types of problems, i.e. buckling of plates subjected to linearly varying load and buckling of shells under uniform load, are considered in the present paper, as there is no suitable result available in the existing literature on the buckling of isotropic shells subjected to linearly varying in-plane load. In the first type of problem, the simply supported (SSSS) plates under linearly varying load of Kang and Leissa [18] and SCSC plates under linearly varying load of Leissa and Kang [17] and Wang et al. [19] with varying load factor (γ) and aspect ratio (a/b) are considered. To obtain the buckling loads, Leissa and Kang [17] and Kang and Leissa [18] solved the above problems employing the power series method (PSM). Similarly, Wang et al. [19] obtained the buckling characteristics of SCSC plates using the differential quadrature method (DQM). The critical buckling loads in the non-dimensional form of the SSSS and SCSC plates obtained from the present formulation are presented in Table 2 along with those of the above mentioned earlier investigations for a comparison. From Table 2, it is observed that the results obtained from the present study and previous studies are well compared validating the present FEM code for the buckling analysis of the plates under linearly varying in-plane loads.

Table 2 Comparison of λ of SSSS and SCSC rectangular plates with linearly varying in-plane edge loading applied to two opposite simply supported ends of plate for different values of a/b (λ = Pcrb2/D, b/h = 100, ν = 0.3, E = 2 × 1011 N/m2)
Full size table

Further, in the second type of problems, the buckling of generalized doubly curved shells (special cases of plate, elliptic paraboloid, cylindrical and hyperbolic paraboloid shells) under uniform in-plane load of earlier investigations [47, 49, 50] is considered to compare the present results for validating the present FEM code for shell problem. To obtain the critical buckling loads of curved panels, Matsunaga [47] used the power series method (PSM) whereas Sahu and Datta [49] and Ravi Kumar et al. [50] employed FEM. The critical buckling loads of above isotropic shells obtained from the present FEM code are furnished in Table 3 along with the results of the previous works mentioned above. It is seen from Table 3 that the present results are well compared with those of the above earlier researchers. As the present FEM code is validated for isotropic plates under linearly varying in-plane load and isotropic shells under uniform in-plane load, the same would be automatically validated for isotropic shells subjected to linearly varying loads.

Table 3 Comparison of λ for the SSSS curved panel under uniform in-plane load (λ = Pcrb2/D, a/b = 1, E = 2 × 1011 N/m2, ν = 0.3)
Full size table

Parametric Study

Extensive parametric studies are presented on buckling of singly and doubly curved panels under linearly varying in-plane edge loads for six boundary conditions. The boundary conditions are SSSS, CCCC, CFCF, SCSC, SSSF and SFSF. The first, second, third and fourth letters in the nomenclature of the above abbreviations correspond to the boundary conditions at x = 0, y = 0, x = a and y = b, respectively. Similarly, the three letters, i.e. S, C and F, in the nomenclature of boundary conditions correspond to simply supported, clamped and free, respectively, which are described below.

  • Simply supported boundary (S)

    v = w = θy = 0, u ≠ 0 and θx ≠ 0 at x = 0, a and u = w = θx = 0, v ≠ 0 and θy ≠ 0 at y = 0, b

  • Clamped boundary (C)

    u = v = w = θx = θy = 0 at x = 0, a and y = 0, b

  • Free boundary (F)

u = v = w = θx = θy ≠ 0 at x = 0, a and y = 0, b

A typical SSSS boundary condition of shell plan form is shown in Fig. 5 for better understanding.

Fig. 5
figure 5

Typical curved panels with simply supported boundary condition (SSSS)

Full size image

Three types of curved panels, such as cylindrical (CYL), spherical (SPH) and hyperbolic paraboloid (HYP), are considered here to study the non-dimensional buckling load (λ) characteristics for different load factors (γ), aspect ratios (a/b) and boundary conditions. The variations of λ with a/b (value ranging from 0.5 to 3) for these curved panels for three linearly varying in-plane load cases (γ = 0, 0.5 and 1.0) with six boundary conditions, i.e. SSSS, SCSC, SSSF, SFSF, CCCC and CFCF, are presented in Figs. 6, 7,8, 9, 10 and 11, respectively. Thereafter, the effects of Poisson's ratio (ν) on λ for HYP, CYL and SPH panels with SSSS boundary condition under linearly varying in-plane load at two opposite ends (x = 0, x = a) for different values of a/b are obtained and presented in Table 4. The curved panels having non-dimensional parameters b/h = 100, b/Ry = 0.25, ν = 0.3 and E = 2 × 1011 N/m2are considered. The non-dimensional buckling load parameter, λ = Pcrb2/D is used throughout the buckling analysis, where D = Eh3/[12(1 − ν2)]. Moreover, a comparative study of the effects of the various in-plane loads, such as triangular, parabolic, patch and concentrated in-plane loads, on the buckling loads of the above panels is presented. At the end, typical design charts of clamped spherical panels having different non-dimensional parameters like a/b value ranging from 0.5 to 3.0, b/h = 50, 100, 150 and 200, Ry/b = 5, 10, 15, 20, 25 and 30, load factor γ = 0, 0.5 and 1.0 are presented. Using the design charts, the critical buckling load can be found out for clamped spherical panels of any isotropic material, any linear loads (γ = 0.0 to 1.0), any value of a/b ranging from 0.5 to 3, any value of b/h ranging from 50 to 200 and any value of Ry/b ranging from 5 to 30 directly from the charts.

Fig. 6
figure 6

Variation of λ with a/b for SSSS curved panels

Full size image
Fig. 7
figure 7

Variation of λ with a/b for SCSC curved panels

Full size image
Fig. 8
figure 8

Variation of λ with a/b for SSSF curved panels

Full size image
Fig. 9
figure 9

Variation of λ with a/b for SFSF curved panels

Full size image
Fig. 10
figure 10

Variation of λ with a/b for CCCC curved panels

Full size image
Fig. 11
figure 11

Variation of λ with a/b for CFCF curved panels

Full size image

Effect of Load Factor (γ)

The variation of λ with a/b varying from 0.5 to 3.0 for different curved panels under linearly varying in-plane load cases (γ = 0.0, 0.5 and 1.0) with SSSS, SCSC, SSSF, SFSF, CCCC and CFCF boundary conditions is shown in Figs. 6, 7,8, 9, 10 and 11. These figures indicate that for all the parameters considered here, the value of λ is the highest for load factor γ = 1.0 followed by γ = 0.5 and γ = 0. This is because for a fixed N0, the total in-plane force over the width of the panel is the highest for γ = 0 followed by γ = 0.5 with trapezoidal distribution and γ = 1.0 with triangular distribution. The same trend is also reported by earlier investigators [17,18,19] for the case of isotropic plates under linearly varying in-plane loads.

It is worth mentioning that in the cases of SFSF and CFCF boundary conditions (Figs. 9 and 11), the value of λ with respect to a/b for all load factors and curved panels is close to each other, and hence, the impact of load factor is not significant on the values of λ unlike in the cases of SSSS, SCSC, CCCC and SSSF boundary conditions.

Effect of Form of Curved Panels

In the cases of SSSS, SCSC and CCCC boundary conditions (Figs. 6,7 and 10), it is seen that for all loading factors and aspect ratios considered here, the synclastic doubly curved (SPH) panels show the highest value of λ followed by singly curved CYL and anticlastic doubly curved HYP panels. This is because both curvatures in x and y directions for SPH panel, single curvature in y direction and zero curvature along x direction for CYL panel and two opposite curvatures along x and y directions for HYP panel. The HYP panel having both curvatures in opposite directions cancels curvature effects and behaves as a flat panel due to which it has the lowest buckling load as in the case of plate. The above trend is also supported by the earlier investigations of Matsunaga [47], Sahu and Datta [49] and Ravi Kumar et al. [50] for the case of SSSS curved panels under uniform in-plane load. However, in the case of CFCF boundary condition (Fig. 11), the HYP panel shows the best performance with respect to the buckling load followed by SPH and CYL panels, which may be due to the free opposite edges.

In case of SSSF and SFSF boundary conditions (Figs. 8 and 9), it is observed that the performance of curved panel is greatly influenced by aspect ratio (a/b) and loading factors (γ) mentioned above. From Fig. 9, it is seen that for lower range of a/b = 0.5 to 1.0, the value of λ is observed to be the highest for SPH panel followed by HYP and CYL panels. Then with the increase of a/b up to 1.8, superior performance is observed by HYP panel followed by SPH and CYL panels. Thereafter, for higher value of a/b = 2.8–3, the value of λ is observed to be the highest for CYL panel followed by HYP and SPH panels.

It is seen from Fig. 8 that for all values of a/b and load factor γ = 1, the value of λ is observed to be the highest for SPH panel followed by CYL and HYP panels. In the case of load factor γ = 0.5, the value of λ is observed to be the highest for SPH panel followed by CYL and HYP panels for a/b up to 2.4. Thereafter, for a/b = 2.4–2.6, HYP panel shows better performance than CYL and SPH panel. When a/b > 2.6, the value of λ is found to be close to each other and hence significant impact of curvature is not observed on λ. For load factor γ = 0, the value of λ is observed to be the highest for SPH panel followed by CYL and HYP panels for a/b = 0.5–1.2 and 1.8–2.2. The order of superiority changes to SPH panel followed by HYP and CYL panels for a/b = 1.2–1.5. Thereafter, HYP panel shows superior performance followed by CYL and SPH panels with further increase of a/b = 2.5–3.

Effect of Boundary Conditions

It is observed from Figs. 6, 7,8, 9, 10 and 11 that the value of λ is the highest for CCCC boundary condition and the lowest for SFSF boundary condition for all types of curved panels and aspect ratios. However, for SPH and CYL panels, superior performance is observed in CCCC boundary condition followed by SCSC, SSSS, SSSF, CFCF and SFSF, whereas for HYP panel the above order is CCCC, SCSC, CFCF, SSSS, SSSF and SFSF. It is also observed that HYP panel with SSSS, SSSF, SFSF boundary conditions shows fluctuations in buckling load with aspect ratio in the presence of at least two opposite SSSS boundary conditions along loading edges and without any clamped support. However, this fluctuation diminishes when there is addition of at least one clamped support. On the other hand, all curved panels show the worst performance in case of having free boundary condition as expected.

Effect of Aspect Ratio

From Fig. 6, it is seen that for SPH and CYL panels with SSSS boundary condition, the value of λ fluctuates with the increase in aspect ratio from 0.0 to 1.5 beyond which it remains nearly constant. However, for HYP panel with SSSS boundary condition (Fig. 6), it decreases and increases alternatively with the increase in aspect ratio showing the number of half longitudinal waves having maxima at a/b = 0.5,1.5 and 2.5 and minima at a/b = 1.0, 2.0 and 3.0.

It is seen from Fig. 7 that the value ofλ for SCSC boundary condition fluctuates slightly in the lower values of a/b, i.e. from 0.5 to 1.5, for all the curved panels and loading factors, beyond which the value of λ increases marginally up to a/b = 2.8. Thereafter, it decreases marginally up to a/b = 3.0. The same trend is also observed in the earlier work of Kang and Leissa [18] for the case of the SCSC plates under linearly varying in-plane stress.

In CCCC boundary condition (Fig. 10), it is observed that for all curved panels and loading factors the values of λ are the highest for a/b = 0.5, which reduces with the increase in a/b up to 1.5. Thereafter, it remains almost constant with further increase in a/b up to 3. It is worth mentioning that variation of λ with a/b for clamped HYP panel is similar to that of SPH and CYL panels unlike in simply supported one.

In the case of CFCF boundary condition (Fig. 11), it is seen that for all loading factors and aspect ratios, the value of λ decreases exponentially with increase of a/b from 0.5 to 3.0 unlike in other cases discussed earlier. Though superior performance is observed for load factor equal to 1 followed by 0.5 and 0.0 and for HYP panel followed by SPH and CYL panels, it is worth mentioning that the values of λ for different panels and load factors are close to each other without showing any significant effects of curved panels and load factors unlike in other cases.

In case of SSSF and SFSF boundary conditions (Figs. 8, 9), it is seen that the HYP panel with load factor (0.0, 0.5 and 1.0) shows the same trend as in the case of the HYP panel with SSSS boundary condition (Fig. 6). In case of SFSF, the value of λ decreases and increases alternatively having maxima at a/b = 0.5 and 1.4 and minima at a/b = 1.0 and 3.0 and in case of SSSF, the value of λ decreases and increases alternatively having maxima at a/b = 0.5, 1.4 and 2.6, and minima at a/b = 1.0, 2.0 and 3.0. For other curved panels, the value of λ is higher for smaller values of a/b and decreases exponentially with the increase in the value of a/b.

Effect of Poisson’s Ratio

The influence of Poisson's ratio ν on λ for HYP, CYL and SPH panels with SSSS boundary condition under linearly varying in-plane stress at two opposite ends (x = 0, x = a) for different values of a/b is presented in Table 4. It is observed that the HYP panel, λ is not affected by ν for all the load factors. On the other hand, for CYL and SPH panels with all load factors γ, the value of λ decreases considerably as ν increases.

Table 4 Effect of “ν” on λ for a SSSS curved panels under linearly varying in-plane loading at two opposite ends for different values of a/b (λ = Pcrb2/D, b/h = 100, b/Ry = 0.25, E = 2 × 1011 N/m2)
Full size table

Comparison of Influences of Various Non-Uniform In-Plane Loads on Critical Buckling Load

A comparative study on the effects of different types of non-uniform in-plane loads, such as parabolic load (Type I), triangular load (Type II), concentrated load at mid-breadth (Type III), partial load from the end at y = 0 with c/b = 0.2 (Type IV) and partial load at mid-breadth with c/b = 0.5 (Type V), as shown in Fig. 12, on buckling behaviour of curved panels with six commonly used boundary conditions, such as SSSS, CCCC, SCSC, SSSF, SFSF and CFCF, is furnished in this section. Here, c is the length of the partial in-plane load. Three types of curved panels, such as CYL, SPH and HYP panels with radii of curvatures (a/Rx = 0, b/Ry = 0.25), (a/Rx = 0.25, b/Ry = 0.25) and (a/Rx = -0.25, b/Ry = 0.25), respectively, are considered. The curved panels are having b/h = 100, ν = 0.3 and E = 2 × 1011 N/m2. The non-dimensional buckling load parameter is considered as λ = Pcrb2/D for the load types I, II, IV and V. But, for the load type III, it is taken as λ = Pcrb/D. The variations of λ with a/b varying from 0.5 to 3.0 for different curved panels subjected to above load types are shown in Figs. 13, 14, 15, 16, 17 and 18 for SSSS, CCCC, SCSC, SSSF, SFSF and CFCF boundary conditions, respectively.

Fig. 12
figure 12

Curved panels under different types of non-uniform in-plane loads (plan view): a parabolic load-type I, b triangular load-type II, c concentrated load-type III, d partial edge load from the end at y = 0 with c/b = 0.2-type IV, e partial edge load at mid-breadth with c/b = 0.5-type V

Full size image
Fig. 13
figure 13

Variation of λ with a/b for SSSS curved panels under various in-plane loads: a CYL b SPH and c HYP

Full size image
Fig. 14
figure 14

Variation of λ with a/b for CCCC curved panels under various in-plane loads: a CYL b SPH and c HYP

Full size image
Fig. 15
figure 15

Variation of λ with a/b for SCSC curved panels under various in-plane loads: a CYL b SPH and c HYP

Full size image
Fig. 16
figure 16

Variation of λ with a/b for SSSF curved panels under various in-plane loads: a CYL b SPH and c HYP

Full size image
Fig. 17
figure 17

Variation of λ with a/b for SFSF curved panels under various in-plane loads: a CYL b SPH and c HYP

Full size image
Fig. 18
figure 18

Variation of λ with a/b for CFCF curved panels under various in-plane loads: a CYL b SPH and c HYP

Full size image

It is observed from Fig. 13a, b that for CYL and SPH panels with SSSS boundary condition, the value of λ is the highest for triangular load (Type II) followed by parabolic load (Type I), partial load at mid-breadth with c/b = 0.5 (Type V), partial load from the end at y = 0 with c/b = 0.2 (Type IV) and concentrated load (Type III). In these panels with load cases II, IV and V; the value of λ marginally increases/decreases with the increase in the value of a/b up to 3.0. Further, in the case of HYP panel (Fig. 13c), the value of λ is the highest for triangular load (Type II), followed by Parabolic load (Type I), partial edge load from the end at y = 0 with c/b = 0.2 (Type IV), partial load at mid-breadth with c/b = 0.5 (Type V) and concentrated load (Type III). However, the value of λ decreases and increases alternatively with the increase in aspect ratio showing number of half longitudinal waves having maxima near a/b = 0.5, 1.5 and 2.5 and minima near a/b = 1.0, 2.0 and 3.0. It is worth mentioning that the present results of all the three SSSS panels subjected to parabolic load (Type I) show the similar trend with that of the SSSS plates subjected to parabolic load of the earlier work of Panda and Ramachandra [41]. Moreover, in the earlier investigations for the SSSS plates with concentrated load [6] and partial load at mid-breadth [24], the value of λ is higher at a/b = 0.5 and then lower at a/b = 1.0 and again higher at a/b = 2.0. Similar trend is also observed in the present investigation for the SSSS HYP curved panel. This is due to the fact that the HYP panel having both curvatures in opposite directions cancels curvature effects and behaves as a flat panel, which has been discussed in the earlier section. However, the trends of SSSS CYL and SPH panels are different from the above trend due to the introduction of curvatures in the one or both directions, respectively.

For CCCC boundary condition (Fig. 14), it is observed that the trends of variation of λ with a/b for all the curved panels considered here are same unlike these panels with SSSS boundary condition. This may be due to the constraints along all edges by CCCC boundary condition unlike SSSS boundary condition. In this case, for the values of a/b from 0.5 to 1.2, the value of λ is the highest for triangular load (Type II) followed by parabolic load (Type I), partial edge load from the end at y = 0 with c/b = 0.2 (Type IV), partial edge load at mid-breadth with c/b = 0.5 (Type V) and concentrated load (Type III). However, for the values of a/b from 1.2 to 1.8, the order of decreasing of the value of λ is same except the load types IV and V, where the value of λ for load type V is higher than that of load type IV unlike the earlier case. When the value of a/b exceeds 1.8, the above order again changes, i.e. the value of λ for the load type III is higher than that of the load type IV, which has the lowest value of λ among all load types in this range of a/b.

For all CCCC curved panels with the triangular load (Type II), the value of λ is the highest for a/b = 0.5 which decreases with increase in a/b up to 1.5. Thereafter, it remains almost constant with further increase in a/b up to 3 (Fig. 14). Similarly, for all these panels with load Types IV and V, the value of λ decreases with increase in a/b from 0.5 to 1.2. Thereafter, it remains almost constant with further increase in a/b up to 3. The value of λ for the above curved panels with the concentrated load (Type III) decreases marginally with the increase in a/b from 0.5 to 0.6, and thereafter, it increases marginally up to a/b = 3.0. However, for all curved panels with the parabolic load (Type I), the value of λ is high for small value of a/b = 0.5 and the value decreases with increase in a/b up to 1.5. Thereafter, it marginally increases and decreases with the increase in a/b up to 3.0 at which it has higher value. It is worth mentioning that for the CCCC boundary condition, the variation of λ with respect to a/b for HYP panel is similar to those of SPH and CYL panels unlike in the simply supported one due to the constraints along the four edges. The trend of present results of the above panels with parabolic load is also similar to that of plate with parabolic load as reported in the literature [41]. But, the values of λ are significantly higher due to the introduction of curvature in the cases of SPH, CYL and HYP curved panels.

It is observed from Fig. 15a, b, c that for CYL, SPH and HYP panels with SCSC boundary condition, the value of λ is the highest for triangular load (Type II), followed by parabolic load (Type I), partial load from the end at y = 0 with c/b = 0.2 (Type IV), partial load at mid-breadth with c/b = 0.5 (Type V) and concentrated load (Type III). In these panels with all the types of loads, the value of λ marginally increases/decreases with the increase in the value of a/b up to 3.0, i.e. there is very little effect of aspect ratio on the buckling loads. It is worth mentioning that for SCSC boundary condition, the similar trend is observed like CCCC boundary condition, but unlike SSSS boundary condition due to the constraints along the two opposite edges. Moreover, the present results of SPH, CYL and HYP panels with SCSC boundary condition subjected to parabolic load show more or less similar trend with that of Panda and Ramachandra [41] for SCSC plates under the same type load, but having higher values of λ due to introduction of curvature in the present case.

It is observed from Fig. 16a, b that for CYL and SPH panels with SSSF boundary condition, the value of λ is the highest for triangular load (Type II) followed by parabolic load (Type I), partial load at mid-breadth with c/b = 0.5 (Type V), partial load from the end at y = 0 with c/b = 0.2 (Type IV) and concentrated load (Type III) for a/b up to 1.2. Thereafter, the value of λ is the highest for triangular load (Type II) followed by Type IV, I, III and V. It is worth noting that the variation of λ with a/b is insignificant for load type III and V. In case of the load types II, III and V, the value of λ is high for small values of aspect ratio and maintains a constant value with increase of a/b from 0.5 to 1.5 and thereafter the value of λ decreases with further increase of a/b up to 3.0. But in the case of load type I, the value of λ decreases exponentially with increase of a/b up to 3. However, in the case of load type IV, the value of λ remains same with the increase in a/b up to 1.8. Thereafter, it increases suddenly with the increase of a/b up to 2.2 and then decreases/increases marginally with the further increase of a/b up to 3. In the case of HYP panel with SSSF boundary condition (Fig. 16c), the value of λ is the highest for triangular load (Type II) followed by Parabolic load (Type I), partial edge load from the end at y = 0 with c/b = 0.2 (Type IV), partial load at mid-breadth with c/b = 0.5 (Type V) and concentrated load (Type III) unlike the trends observed in the cases of SPH and CYL panels. However, the value of λ decreases and increases alternatively with the increase in aspect ratio showing number of half longitudinal waves having maxima near a/b = 0.5, 1.5 and 2.5 and minima near a/b = 1.0, 2.0 and 3.0 like HYP panel with SSSS boundary condition.

It is observed from Fig. 17a, b that for all the load types with CYL and SPH panels with SFSF boundary condition, the value of λ decreases with increase of a/b from 0.5 to 3. The value of λ is the highest for parabolic load (Type I), followed by triangular load (Type II), partial load at mid-breadth with c/b = 0.5 (Type V), concentrated load (Type III) and the partial load from the end at y = 0 with c/b = 0.2 (Type IV) for small value of a/b up to 1. For a/b value beyond 1, the values of λ for CYL and SPH panels are close to each other without showing any significant effect of load Type (I, II, III and V). In the case of HYP panel with SFSF boundary condition (Fig. 17c), the value of λ is the highest for triangular load (Type II), followed by parabolic load (Type I), partial load at mid-breadth with c/b = 0.5 (Type V), concentrated load (Type III) and partial edge load from the end at y = 0 with c/b = 0.2 (Type IV). However, the value of λ decreases and increases alternatively with the increase in aspect ratio showing the number of half longitudinal waves having maxima near a/b = 0.5 and 1.4 and minima near a/b = 1.0 and 3.0 for all the load types except the partial load from y = 0 (c/b = 0.2).

For CFCF boundary condition (Fig. 18), it is observed that for all curved panels and load cases considered here, the value of λ is high for small values of aspect ratio and decreases exponentially with increase of a/b from 0.5 to 3. This is due to the free support at two opposite ends of the panels. For all the curved panels, the value of λ is the highest for parabolic load (Type I) followed by triangular load (Type II), partial load at mid-breadth with c/b = 0.5 (Type V), concentrated load (Type III) and the partial load from the end at y = 0 with c/b = 0.2 (Type IV). For a/b value beyond 1.0, the values of λ for all the three panels are close to each other without showing any significant effect of load Types I, II, III and V.

From the above discussion, it is found that in the cases of SSSS, CCCC, SCSC and SSSF boundary conditions, all three curved panels under the triangular in-plane load (Type II) show the best performance and these panels under the concentrated load (Type III) show the worst performance among the five load types considered here with respect to their critical buckling loads. Similarly, in the cases of CFCF and SFSF boundary conditions, all three curved panels under the parabolic in-plane load (Type I) show the best performance and these panels with the partial in-plane load from the end at y = 0 with c/b = 0.2 (Type IV) show the worst performance among the five load types considered here with respect to their critical buckling loads. These two boundary conditions show different trends as compared to other boundary conditions due to the presence of two opposite free ends.

Design Charts for Clamped Spherical Panel

With an aim to prepare design charts, clamped spherical panels of various dimensions subjected to in-plane loading (γ = 0.0, 0.5 and 1.0), which are commonly adopted in the practical field applications, are considered to estimate the non-dimensional critical buckling load. Various non-dimensional parameters such as γ values 0, 0.5 and 1.0, a/b values ranging from 0.5 to 3.0, b/h with values of 50,100, 150 and 200 and Ry/b with values of 5, 10, 15, 20, 25 and 30 have been considered here to include the γ value ranges from 0 to 1.0, thickness, span and radius of curvature of curved panel in various ranges. Thereafter, the values of λ of these spherical panels are obtained from the present FEM code with different aspect ratios. The variation of λ with respect to aspect ratio of these panels is presented in Figs. 19, 20 and 21, which are termed as design charts. These charts will be used to obtain buckling loads for different clamped spherical panels under any linear in-plane loading with γ ranging from 0 to 1.0 for various dimensions and any isotropic materials commonly adopted in the practice.

Fig. 19
figure 19

Variation of λ with a/b for CCCC spherical panel: a load factor γ = 0, Ry/b = 5, b load factor γ = 0, Ry/b = 10 c load factor γ = 0, Ry/b = 15 d load factor γ = 0, Ry/b = 20 e load factor γ = 0, Ry/b = 25 f load factor γ = 0, Ry/b = 30

Full size image
Fig. 20
figure 20

Variation of λ with a/b for CCCC spherical panel: a load factor γ = 0.5, Ry/b = 5, b load factor γ = 0.5, Ry/b = 10, c load factor γ = 0.5, Ry/b = 15 d load factor γ = 0.5, Ry/b = 20 e load factor γ = 0.5, Ry/b = 25 f load factor γ = 0.5, Ry/b = 30

Full size image
Fig. 21
figure 21

Variation of λ with a/b for CCCC spherical panel: a load factor γ = 1, Ry/b = 5, b load factor γ = 1, Ry/b = 10, c load factor γ = 1, Ry/b = 15 d load factor γ = 1, Ry/b = 20 e load factor γ = 1, Ry/b = 25 f load factor γ = 1, Ry/b = 30

Full size image

Moreover, ten numbers of practical field examples of clamped spherical panels of various dimensions and materials, such as steel (three examples), aluminium (three examples) and concrete (four examples having different moduli of elasticity and Poisson's ratio), have been selected to establish the validity of these design charts (Figs. 19, 20 and 21). The different parameters such as a, b, h and Ry have been selected from the practical field application point of view and mentioned in Table 5. The dimensional parameters of all these examples considered here are converted to the non-dimensional parameters. With the help of these non-dimensional parameters, the values of λ for these examples are calculated from the design charts (Figs. 19, 20 and 21) by linear interpolation of various non-dimensional parameters such as a/b, b/h, Ry/b and γ. Further, the critical buckling loads, Pcr of these examples are calculated from the corresponding λ values considering actual dimension of these clamped spherical panel, using the expression Pcr = λD/b2 = λ[Eh3/12(1 − ν2)/b2]. Furthermore, the critical buckling loads of these problems are computed directly using the present computer code. The values of Pcr of these examples obtained from both the methods are indicated in Table5 with the percentage of deviation between these values. The above percentage of deviations is within the range of (5%), which is accepted from the engineering point of view. Though these charts (Figs. 19, 20 and 21) are obtained for the steel with Poisson’s ratio 0.3, the critical buckling load of other materials such as concrete having Poisson’s ratios of 0.15 and 0.17 and aluminium having Poison’s ratio of 0.33 has been calculated from the design charts confining the error limit within 5%. Further, though the design charts are obtained for γ = 0, 0.5 and 1.0, the Pcr can be found for any load factor ranging from 0.0 to 1.0. Moreover, it is noteworthy that the design charts are prepared in the form of non-dimensional parameters and hence, Pcr can be found out from these charts for any dimension, material properties and load factor. Thus, Figs. 19, 20 and 21 can be beneficial for the designers to ascertain the critical buckling load, Pcr for clamped spherical panel of any dimension, material and load factor without using complicated computer programme. Similarly, these design charts can also be prepared for spherical shells with other boundary conditions. Further, the design charts can also be prepared for other curved panels such as CYL and HYP by following the above novelty.

Table 5 Critical buckling load (Pcr) of clamped spherical panel obtained from the computer code and design charts
Full size table

Accordingly, the above design charts (Figs. 19, 20 and 21) are suggested as ‘Design aids’ to the designers for obtaining the critical buckling loads of clamped isotropic spherical panels with any type of linearly varying in-plane load at the stage of preliminary design. Hence, these charts are very much useful for the designers to calculate the buckling load without going through the tedious calculation using computer code or using commercially available complicated FEM software.

Conclusion

The buckling characteristics of three curved panels, such as spherical, cylindrical and hyperbolic panels, under linearly varying in-planeload with six boundary conditions and aspect ratio ranging from 0.5 to 3 can be concluded as follows:

  1. (1)

    The critical buckling loads of all three curved panels under linearly varying in-plane load show the best performance with γ = 1 (triangular load) followed by γ = 0.5 (trapezoidal load) and γ = 0 (uniform load) as the total longitudinal force for a fixed N0 is maximum for γ = 0 followed by γ = 0.5 and γ = 1.0.

  2. (2)

    For all load factors and aspect ratios considered in this study, the critical buckling loads are observed to be the highest for synclastic doubly curved spherical (SPH) panel followed by singly curved cylindrical (CYL) panel and anticlastic doubly curved hyperbolic paraboloid (HYP) panel with SSSS, SCSC and CCCC boundary conditions. However, for CFCF boundary conditions, HYP panel shows the best performance in the critical buckling loading followed by SPH and CYL panels. Further, it is worthy to note that the performance of these panels is greatly influenced by the aspect ratios for other two boundary conditions, i.e. SSSF and SFSF.

  3. (3)

    HYP panel for all load factors shows fluctuation of critical buckling load with the aspect ratio in the presence of at least two opposite loading edges simply supported and without any clamped support such as SSSS, SSSF and SFSF. However, this fluctuation is diminished when there is one or more clamped support in the curved panels such as SCSC. The variation of λ with respect to aspect ratio is greatly influenced with load factors and boundary conditions of curved panels.

  4. (4)

    The critical buckling load of a curved panel with linearly varying in-plane edge load is the highest for CCCC boundary condition and the lowest for SFSF boundary condition. SPH and CYL panels show superior performance with CCCC boundary condition followed by SCSC, SSSS, SSSF, CFCF and SFSF with regard to critical buckling load. On the other hand, for HYP panel, the above sequence is CCCC, SCSC, CFCF, SSSS, SSSF and SFSF.

  5. (5)

    The critical buckling load for simply supported HYP panel with all load factors is not affected by Poisson's ratio, whereas the same for simply supported CYL and SPH panels with all load factors decreases considerably as Poisson's ratio increases.

  6. (6)

    When SPH, CYL and HYP panels with six boundary conditions are subjected to five different non-uniform in-plane loads, such as parabolic load, triangular load, concentrated load at mid breadth, partial load from the end at y = 0 with c/b = 0.2 and partial load a mid-breadth with c/b = 0.5, the best and worst performances are observed for the triangular and concentrated in-plane loads, respectively, with respect to the critical buckling load in case of SSSS, CCCC, SCSC and SSSF boundary conditions. But in case of CFCF and SFSF boundary conditions the best and worst performances are observed for the parabolic and partial load from the end at y = 0 with c/b = 0.2, respectively, with respect to the critical buckling load.

  7. (7)

    The suggested design charts (Figs. 19, 20 and 21) will be very much useful for the designers to determine the critical buckling load of any isotropic clamped spherical panel with any dimension and load factor ranging from 0 to 1.0 with minimum error at the time of preliminary design without going through the tedious computations.

From the above study, it is found that the buckling characteristics of the curved panels are greatly influenced by various parameters, and hence, the designers have to be cautious while designing structures under non-uniform in plane edge loading. Moreover, these results can be considered as the benchmarks for the future researchers.