1 Introduction

Flow and heat transfer aspects of various fluids through rectangular channels find wide applications in different industrial and engineering processes. Numerous researchers considered flow through rectangular channel with low aspect ratio (ratio of depth and width of the channel) which reduced the problem to that of flow through large parallel plates, for which analytical solution is admissable. During the last decade, technological shift toward miniaturization attracted the research community to consider flow and heat transfer aspects of fluids through micro-channel which find wide spectrum of applications in the fields of micro-electro-mechanical systems (MEMS), bio-technology, small-scale heat exchangers etc. Some of the important studies are discussed here. Shashikumar et al. [1] investigated effects of different alloy nanoparticles of aluminum and titanium on micro-channel flow with partial slip and convective boundary condition. Menni et al. [2] carried out analysis of turbulent flow and heat transfer in forced convection of pure water, pure ethylene glycol as base fluids, with dispersion of Al2O3 nanosized particles. Effects of different base fluids and shape of the nanoparticle on the flow and heat transfer were analyzed. Chamkha [3] studied laminar flow and heat transfer of a suspension in an electrically conducting fluid through channel and circular pipes, and the effect of the magnetic field, viscosity ratio on the friction coefficient, Nusselt number, particle-phase volume flow rate and liquid-phase flow rate was reported. Mixed convection of pulsating ferro-fluid flow over a backward facing step has been studied by Selimefendigil et al. [4] employing finite element method. Unsteady two-fluid flow and heat transfer of two-viscous fluids in a rectangular channel was studied by Umavathi et al. [5]. Analytical solution has been obtained, and the effect of viscosity ratio, conductivity ratio, Prandtl (Pr) number and the frequency parameter on the velocity and temperature has been analyzed. Chamkha [6] studied mixed convection in a vertical channel with symmetric and asymetric wall heating conditions. Analytical solutions for velocity and temperature have been obtained, and the effects of pertinent parameters on velocity and temperature have been obtained. A comprehensive review on nanofluids applications in micro-channel has been carried out by Chamkha et al. [7]. Oscillatory flow and heat transfer in unsteady condition in a horizontal composite porous medium channel has been examined by Umavathi et al. [8]. Another interesting aspect of channel flow could be the flow in different geometries with flexible walls which have adjustable elasticity, thin size and desirable thermal properties. Some important and interesting studies on flow through cavities with flexible walls can be found in Refs. [9,10,11,12].

The preceding discussion reports the studies on flow of Newtonian fluids through channel, micro-channel and the possibilities of exploring the flow through channels with flexible walls. However, it is well known that several fluids used in the industry do not follow the linear stress–strain rate relation of the Newtonian fluid model and exhibit nonlinear stress–strain rate behavior. For capturing the complex response of such fluids to shear force, several non-Newtonian fluid models such as power law fluid, third grade fluid, viscoelastic fluid, Casson fluid and Sisko fluid have been proposed by the researchers. Viscoelastic model possesses the characteristics of both solid and fluid, and this model has drawn the attention of numerous researchers [13,14,15]. Narain et al. [16] reported how even Newtonian fluids can display the characteristics of viscoelastic fluids. The power law fluid model is another widely adopted non-Newtonian fluid model. Tso et al. [17] investigated flow and heat transfer of a power law fluid through large parallel plates. Exact solutions for the velocity and temperature distribution are obtained, and the effects of the non-Newtonian index and the non-Newtonian parameter on the temperature and heat transfer have been discussed. Electro-magneto-hydrodynamic (EMHD) flow and heat transfer of a third-grade fluid through large parallel plates have been studied by Wang et al. [18], and the ordinary differential equations (ODEs) describing the flow and heat transfer have been solved by the perturbation method and spectral method. Exact analytical solutions of the velocity of a third-grade fluid, for Poiseuille and Couette-Poiseuille flow, flowing between parallel plates have been reported by Danish et al. [19]. The effect of the third-grade fluid parameter on the non-dimensional velocity has been analyzed and an expression for the flow rate is obtained. Akbarzadeh [20] investigated pulsatile magneto-hydro-dynamic blood flow through the porous blood vessel, modeling blood as a third-grade fluid. The equations governing the flow are solved by the perturbation method and also by numerical technique. The effects of the pertinent no-dimensional parameters on the velocity, flow rate and the wall shear stress have been discussed.

The above discussion emphasizes the importance of applications of the non-Newtonian fluids in different fields. One such fluid is the Sisko model which can describe the flow of several fluids in the high shear rate region. Different polymers, polymer melts, rubber melts and slurries are observed to follow the Sisko model. Sisko fluid model is introduced by A. W. Sisko [21], which is a three-parameter model. This model can be adopted to describe the flow of the fluids, mentioned above, for a wider range of shear rate. Some important investigations on Sisko fluid are discussed here. Khan et al. [22] investigated flow and heat transfer of a Sisko fluid in an annular pipe. The equations governing the flow and heat transfer have been solved by employing the homotopy analysis method (HAM) [23]. Chaudhuri and Das [24] investigated forced convection of Sisko fluid in a pipe and semi-analytical solutions, adopting the least square method (LSM) [25, 26] for the velocity and temperature have been obtained. The effects of the Sisko fluid parameter, non-Newtonian index on the velocity, temperature and heat transfer have been analyzed. Taylor’s scrapping problem of a Sisko fluid has been studied by Siddiqui et al. [27]. In a recent study, Khan et al. [28] investigated entropy generation in flow of a Sisko nanofluid employing HAM and the effect of various parameters on the entropy generation rate has been examined. Wire coating analysis by withdrawal from a bath of Sisko fluid has been studied by Sajid and Hayat [29]. Peristaltic flows of a Sisko fluid through an endoscope and through an inclined tube have been investigated by the researchers [30, 31]. Peristaltic flow, with heat and mass transfer effect, in a undulating porous curved channel has been studied by Zeeshan et al. [32].Implicit finite difference (FDM) scheme is employed to solve the highly nonlinear ordinary differential equations. Saheen et al. [33] investigated peristaltic flow of Sisko fluids, under the action of a magnetic field, including the effect of viscous dissipation. The effect of variable thermal conductivity has been included. Flow of Sisko nanofluid over a curved surface has been numerically studied by Ali et al. [34]. The effect of chemical process, radiation, thermophoresis and Lorentz force is considered.

The researches, cited above, indicate that the flow of Sisko fluids in various engineering systems is an important area of study. The flow of Sisko fluid through a rectangular channel, considering the effect of the aspect ratio, has never been investigated, though it finds wide applications in industry involving flow of polymer melt, rubber melt. Most of the investigations on non-Newtonian fluids for rectangular geometry considered the flow through large parallel plates which neglected the effect of the aspect ratio. In most of the real-life situations, however, plates are not very large in the lateral direction and effect of the aspect ratio plays a significant role in the flow and thermal characteristics. In this regard, the investigation by Chaudhuri and Sahoo [35] can be mentioned, which considered the effect of the aspect ratio on the magneto-hydrodynamic (MHD) flow of a third-grade fluid through a rectangular channel. In the present study, the effect of the aspect ratio has been considered for hydro-dynamically fully developed flow of a Sisko fluid through a rectangular channel. Inclusion of the effect of the aspect ratio in the governing equation yields a highly nonlinear partial differential equation (PDE), required to describe the flow. On the contrary, if the flow is considered through large parallel plates (neglecting the effect of the aspect ratio), the equation describing the flow is a nonlinear ordinary differential equation (ODE), relatively simple to obtain the solution. The PDE describing the flow of Sisko fluid through a rectangular channel is reported for the first time in the present study, and numerical solution has been generated adopting the finite difference scheme. The results of numerical solution are compared with that of the exact solution of Sisko fluid flowing through large parallel plates (aspect ratio zero) for a special case of the non-Newtonian index. The comparison of the results exhibits an excellent agreement which validates the results of the present numerical solution. Moreover, an expression of the friction factor has been provided. Non-dimensional velocity distributions and wall shear-stress variation at the lower wall, for three different cases, namely pressure-driven flow, shear-driven flow and combined pressure and shear driven flow, have been presented. The effects of the pertinent non-dimensional parameters such as aspect ratio, Sisko fluid parameter, non-Newtonian index and the non-dimensional pressure gradient on velocity and wall shear are discussed.

2 Mathematical Formulation

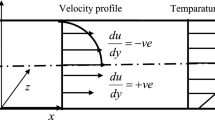
Hydro-dynamically fully developed flow of a Sisko fluid through a rectangular channel is considered. The physical problem addressed here is pictorially sketched in Fig. 1. The reference frame is fixed at the center of the channel as depicted in the figure. The x axis is along the direction of the flow, y axis is chosen along the direction perpendicular to the flow and z axis is chosen along the lateral direction.

Fig. 1
figure 1

Problem geometry

Full size image

The flow is assumed to be steady, laminar and incompressible. The equations governing the flow are derived from the mass and momentum conservation principle which are the basic equations of fluid mechanics [22] and for the sake of brevity, not presented here. The stress tensor for non-Newtonian fluid differs from that of the Newtonian fluid.

The stress tensor equation [22], in general, is given as:

$$ \tilde{T} = - p\tilde{I} + \tilde{S} $$
(1)

where \( \tilde{T},p,\tilde{S},\tilde{I} \) are Cauchy stress tensor, thermodynamic pressure, extra stress tensor and unit stress tensor, respectively. Depending on the behavior of the non-Newtonian fluids, the extra stress tensor introduces various forms of nonlinearity into the equation. The equation of extra stress tensor for the Sisko fluid [22] is given as:

$$ \tilde{S} = \left[ {a + b\left( {\sqrt {0.5{\text{tr}}(A_{1}^{2} )} } \right)^{n - 1} } \right]A_{1} $$
(2)
$$ \tilde{A}_{1} = \tilde{L} + \tilde{L}^{\text{T}} $$
(3)
$$ \tilde{L} = {\text{grad}}\,\vec{V} $$
(4)

A1 is the first Rivlin–Erickson tensor [22], L is the velocity gradient matrix [22], a, b and n are constants which vary for different Sisko fluids. For hydro-dynamically fully developed flow condition, only the axial component of velocity u exists and u is a function of y, z and independent of x. We seek a solution of the following form:

$$ \vec{V} = \left[ {u\left( {y,z} \right),0,0} \right] $$
(5)

where V is the velocity vector, u is the velocity of the fluid in the axial direction x. y and z are the coordinates along the vertical and lateral directions, respectively. The inertia term from the momentum equation vanishes as the flow considered is hydro-dynamically fully developed.

Using Eqs. (5), (1) and (2), the momentum conservation equations in the x, y and z directions are obtained as follows:

$$ \begin{aligned} & a\left[ {\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right] + b\frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} + 2\left( {\frac{n - 1}{2}} \right)b\frac{\partial u}{\partial y}\left[ {\frac{\partial u}{\partial y}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\partial u}{\partial z}\frac{{\partial^{2} u}}{\partial y\partial z}} \right]\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 3}{2}}} \\ & \quad + b\frac{{\partial^{2} u}}{{\partial z^{2} }}\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} + 2\left( {\frac{n - 1}{2}} \right)b\frac{\partial u}{\partial z}\left[ {\frac{\partial u}{\partial y}\frac{{\partial^{2} u}}{\partial y\partial z} + \frac{\partial u}{\partial z}\frac{{\partial^{2} u}}{{\partial z^{2} }}} \right]\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 3}{2}}} = \frac{\partial p}{\partial x} \\ \end{aligned} $$
(6)

From the momentum conservation equations in the other directions, it can be concluded that the pressure gradient along the axial direction is only function of x; the LHS of Eq. (6) indicates that it is a function of y and z only, while the RHS is a function of x only. These two conditions can be satisfied only if

$$ \frac{\partial p}{\partial x} = C $$
(7)

For shear-driven flow, the pressure gradient term is set to be zero, which then describes the PDE for shear-driven flow condition. If u is assumed to be independent of z (large parallel plate case, A = 0), then Eq. (6) [22] reduces to the following:

$$ a\frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} + nb\frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }}\left| {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right|^{n - 1} = \frac{{{\text{d}}p}}{{{\text{d}}x}} $$
(8)

2.1 Pressure-Driven Flow

$$ {\text{At}}\,y = \pm L_{1} ,\quad u = 0 $$
(9.1)
$$ {\text{At}}\,z = \pm L_{2} ,\quad u = 0 $$
(9.2)

2.2 Shear-Driven Flow

$$ {\text{At}}\,y = - L_{1} ,\quad u = 0,\quad {\text{at}}\,y = L_{1} , \, u = U_{\text{p}} $$
(10.1)
$$ {\text{At}}\,z = \pm L_{2} , \, u = 0 $$
(10.2)

2L1 and 2L2 are the depth and width of the rectangular channel, respectively, and Up is the velocity of the upper plate in shear-driven and combined pressure and shear driven flow conditions. For combined pressure and shear driven flow, the boundary conditions are same as the boundary conditions of shear-driven flow.

For reducing Eq. (6) into its non-dimensional form, following non-dimensional variables and parameters are introduced:

$$ y^{*} = \frac{y}{{L_{1} }},z^{*} = \frac{z}{{L_{2} }},u^{*} = \frac{u}{{u_{0} }},A = \frac{{L_{1} }}{{L_{2} }},N = \frac{{{\text{d}}p}}{{{\text{d}}x}}\frac{{L_{1}^{2} }}{{au_{0} }},b^{*} = \frac{b}{a}\left( {\frac{{u_{0} }}{{L_{1} }}} \right)^{n - 1} $$
(11)

where y*, z*, u*, u0, A, N are the non-dimensional coordinates in the vertical and lateral directions, non-dimensional velocity in the axial direction, reference velocity, aspect ratio of the channel and non-dimensional pressure gradient. u0 for shear-driven flow and combined pressure and shear driven flow can be considered as the velocity of the upper plate. For pressure-driven flow condition, u0 is considered as follows:

$$ u_{0} = \frac{1}{N}\left( {\frac{{{\text{d}}p}}{{{\text{d}}x}}} \right)\frac{{L_{1}^{2} }}{a} $$
(12)

It is important to mention that u0, defined in Eq. (12), is not the average velocity through the channel. For a specific value of N only, u0 from Eq. (12) represents the average velocity. In case of Newtonian fluid, this N has got a specific value for average velocity; however, in case of non-Newtonian fluid, the average velocity is not directly proportional to the pressure gradient, rather it is a nonlinear function of the pressure gradient. But to express the average velocity for non-Newtonian fluid in the same form as that of Newtonian fluid case, a factor N can be introduced and u0 can be expressed as given in Eq. (12). The value of N can be fixed once the average velocity is calculated. Higher pressure gradient results in a higher average velocity. This leads to an increase in the factor N. Therefore, N can be considered as a measure of the pressure gradient. N could be considered as unity also as assumed in the study of Danish et al. [19]. But in that case, the effect of the higher pressure gradient cannot be included in the study. Average velocity, however, has to be calculated numerically (analytical solution, even if possible, will be valid for a very small range of parameters, only) which requires the values of the material constants a, b and n, which are not reported in the literature. For this reason, here, N is arbitrarily chosen, for which u0 can be considered as a multiplication of the average velocity and some factor. This factor may be less than unity or greater than unity or even unity (unit value represents the average velocity).

Using the non-dimensional variables and parameters given by Eqs. (11) and (12) and omitting the asterisks for convenience, the non-dimensional forms of the governing equation and the boundary conditions are given below as:

$$ \begin{aligned} & \frac{{\partial^{2} u}}{{\partial y^{2} }} + A^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }} + b\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + A^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} \frac{{\partial^{2} u}}{{\partial y^{2} }} \\ & \quad + (n - 1)b\frac{\partial u}{\partial y}\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + A^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 3}{2}}} \left( {\frac{\partial u}{\partial y}\frac{{\partial^{2} u}}{{\partial y^{2} }} + A^{2} \frac{\partial u}{\partial z}\frac{{\partial^{2} u}}{\partial y\partial z}} \right) \\ & \quad + A^{2} b\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + A^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} \frac{{\partial^{2} u}}{{\partial z^{2} }} \\ & \quad + A^{2} (n - 1)b\frac{\partial u}{\partial z}\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + A^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 3}{2}}} \left( {\frac{\partial u}{\partial y}\frac{{\partial^{2} u}}{\partial y\partial z} + A^{2} \frac{\partial u}{\partial z}\frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) = N \\ \end{aligned} $$
(13)

Boundary conditions in the non-dimensional form for three different cases are given as follows:

2.3 Pressure-Driven Flow

$$ {\text{At}}\,y = \pm 1, \, u = 0 $$
(14.1)
$$ {\text{And}},\,{\text{at}}\,z = \pm 1, \, u = 0 $$
(14.2)

2.4 Shear-Driven Flow

For shear-driven flow and combined pressure and shear driven flow, the velocity is made non-dimensional by taking the velocity of the upper plate Up as the reference velocity. The boundary conditions for shear-driven flow are given below as:

$$ {\text{At}}\,y = - 1, \, u = 0\,{\text{and}}\,{\text{at}}\,y = 1, \, u = 1 $$
(15.1)
$$ {\text{At}}\,z = \pm 1, \, u = 0 $$
(15.2)

Boundary conditions for combined pressure and shear driven flow are same as the boundary conditions of shear-driven flow condition.

2.5 Shear Stress

The expression of the shear stress, in the axial direction, for Sisko fluid is given as follows:

$$ \tau_{xy} = a\frac{\partial u}{\partial y} + b\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} \frac{\partial u}{\partial y} $$
(16)

The shear-stress equation in the lateral direction is as given below:

$$ \tau_{xz} = a\frac{\partial u}{\partial z} + b\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} \frac{\partial u}{\partial z} $$
(17)

Upon substitution of the non-dimensional variables from Eq. (11) into Eqs. (16) and (17), and omitting the asterisks, the non-dimensional forms of the shear-stress equations are as given below:

$$ \tau_{xy} = \frac{\partial u}{\partial y} + b\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + A^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} \frac{\partial u}{\partial y} $$
(18)
$$ \tau_{xz} = A\frac{\partial u}{\partial z} + b\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + A^{2} \left( {\frac{\partial u}{\partial z}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} A\frac{\partial u}{\partial z} $$
(19)

To obtain the wall shear stress in the axial direction at the lower wall, y = − 1 is substituted in Eq. (18). Shear stress along the lateral direction in the wall is zero as u is zero at the wall (no slip) rendering the gradient of u with respect to z is zero at all points. Therefore, from Eq. (16) we obtain that τxz = 0. For flow through large parallel plates, A is negligible and considered to be zero. Substituting A = 0 in Eq. (18), the expression of the shear stress in the axial direction reduces to the following:

$$ \tau_{xy} = \frac{{{\text{d}}u}}{{{\text{d}}y}} + b\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{n} $$
(20)

3 Solution

The non-dimensional governing differential equation (i.e., Eq. 13) is a second-order highly nonlinear PDE involving cross-derivatives which does not have any exact analytical solution. Moreover, getting a solution employing any of the approximate analytical method, too, is a formidable task. Hence, the nonlinear PDE has been solved numerically using finite difference method. The nonlinear momentum equation is first discretized using second-order accurate central difference scheme in order to keep the numerical error within the acceptable limit. The resulting system of algebraic equations is written in an explicit fashion, i.e., the right-hand side of the algebraic equation is calculated based on the known values of the variables from the previous iteration. The iterative solver is executed till the difference between the values of the unknown (here velocity) obtained from two successive iterations attains the required tolerance level. In order to make the results independent of the mesh size, mesh sensitivity test is carried out. The number of grid points both in y and z direction are varied from 10 to 300, and the local velocity as well as the wall shear stress are plotted as a function of number of grids. The grid size is fixed 200 × 200 as no appreciable variation in the local velocity and wall shear stress is observed by reducing grid size further. Uniform and equal grid spacing is considered. The convergence criterion is fixed at error less than 10−6. The error is defined as follows:

$$ {\text{error}}\, = \,\sqrt {\sum\limits_{j = 1}^{M} {\sum\limits_{i = 1}^{M} {\left( {u_{ij}^{k + 1} - u_{ij}^{k} } \right)^{2} } } } $$
(21.1)

where \( u_{ij}^{k} \) is the velocity in the x direction at ij node for the kth iteration. For the calculation of wall shear stress using Eq. 20, the 1st velocity gradient at the wall is calculated by using one-sided three-point second-order difference scheme to keep the result second-order accurate.

3.1 Exact Solution for the Sisko Fluid, for n = 2, Flowing Through Large Parallel Plates (A = 0)

Equation (8), in the non-dimensional form, after omitting the asterisks, is given below as:

$$ \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} + nb\frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }}\left| {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right|^{n - 1} = N $$
(22)

Substituting n = 2 in Eq. (2), we get the following form:

$$ \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} + 2b\frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }}\frac{{{\text{d}}u}}{{{\text{d}}y}} = N $$
(23)

In the ODE, a modulus sign is present in Eq. (23). To get rid of this, Eq. (23) has been solved in the domain of y = − 1 to y = 0. In this domain, u decreases with a decrease in y (at the plate u = 0 and u increase toward the center). Beyond the center (y = 0), u decreases with an increase in y. Therefore, in the domain y = 0 to y = − 1, modulus of the velocity gradient is positive. In the domain y = 0 to y = 1, the velocity will be symmetric. Once the velocity in the domain y = − 1 to y = 0 is obtained, the velocity from y = 0 to y = 1 can be reproduced using the condition of symmetry. Equation (23) is a second-order, nonlinear ODE requiring two boundary conditions for obtaining the solution. The boundary conditions are given below as:

$$ {\text{At}}\,y = - 1, \, u = 0 $$
(24.1)
$$ y = 0,\,\frac{{{\text{d}}u}}{{{\text{d}}y}} = 0 $$
(24.2)

The solution of Eq. (23), using the boundary conditions by Eqs. (24.1)–(24.2), is given below as:

$$ u = - \frac{1}{2b}\left( {1 + y} \right) + \frac{1}{{12b^{2} N}}\left[ {\left( {1 + 4bNy} \right)^{1.5} - \left( {1 - 4bN} \right)^{1.5} } \right] $$
(25)

3.2 Exact Solution for Combined Pressure and Shear Driven Flow of a Sisko Fluid, with n = 2, Through Large Parallel Plates (A = 0)

To obtain the solution for combined pressure and shear driven flow, governing differential equations remain same as given by Eq. (23), but the boundary conditions are different from the previous case. It is a known fact that for combined pressure and shear driven flows, the maximum velocity does not occur always at the upper moving plate. Rather, the maximum velocity is observed to occur at a point away from the plate depending on the magnitude of the pressure gradient. It is important to note that the modulus sign present in the governing equation will produce positive values of the velocity gradient term (du/dy)n−1 for odd values of n. However, for even n, modulus of (du/dy)n−1 will be negative beyond the point where the velocity is maximum. For n = 2, an exact solution can be easily obtained. For combined pressure and shear driven flow, the location of the point where the peak velocity occurs, is unknown a priori. To locate the point, we will assume the distance from the center is being in the positive direction of the coordinate system as shown in Fig. 1. Then the domain is divided in two region \( - 1 \le y \le r \) and the other region is \( r \le y \le 1 \).

The governing differential equations are given below as:

$$ \frac{{{\text{d}}^{2} u_{1} }}{{{\text{d}}y^{2} }} + 2b\frac{{{\text{d}}^{2} u_{1} }}{{{\text{d}}y^{2} }}\frac{{{\text{d}}u_{1} }}{{{\text{d}}y}} = N\quad - 1 \le y \le r $$
(26)
$$ \frac{{{\text{d}}^{2} u_{2} }}{{{\text{d}}y^{2} }} - 2b\frac{{{\text{d}}^{2} u_{2} }}{{{\text{d}}y^{2} }}\frac{{{\text{d}}u_{2} }}{{{\text{d}}y}} = N\quad r \le y \le 1 $$
(27)

The boundary conditions are as follows:

$$ y = - 1,\quad u_{1} = 0 $$
(28.1)
$$ y = r,\quad u_{1} = u_{2} $$
(28.2)
$$ y = r,\quad \frac{{{\text{d}}u_{1} }}{{{\text{d}}y}} = \frac{{{\text{d}}u_{2} }}{{{\text{d}}y}} $$
(28.3)
$$ y = 1,\;u_{2} = 1 $$
(28.4)

Solutions of Eqs. (26) and (27) are given below as:

$$ u_{1} = \frac{1}{2b}\left[ { - y + \frac{{\left\{ {1 + 4b\left( {Ny + k_{1} } \right)} \right\}^{1.5} }}{6bN}} \right] + k_{2} $$
(29)
$$ u_{2} = - \frac{1}{2b}\left[ { - y - \frac{{\left\{ {1 - 4b\left( {Ny + k_{3} } \right)} \right\}^{1.5} }}{6bN}} \right] + k_{4} $$
(30)

where k1, k2, k3 and k4 are constants. Utilizing the boundary conditions given by Eqs. (28.1)–(28.4), four algebraic equations are obtained; the solution of which provides the values of unknowns k1, k2, k3, and k4. The equations are as given below:

$$ \frac{1}{2b}\left[ {1 - \frac{{\left\{ {1 + 4b\left( { - N + k_{1} } \right)} \right\}^{1.5} }}{6bN}} \right] + k_{2} = 0 $$
(31.1)
$$ \frac{1}{2b}\left[ { - r - \frac{{\left\{ {1 + 4b\left( {Nr + k_{1} } \right)} \right\}^{1.5} }}{6bN}} \right] + k_{2} = \frac{ - 1}{2b}\left[ { - r - \frac{{\left\{ {1 - 4b\left( {Nr + k_{3} } \right)} \right\}^{1.5} }}{6bN}} \right] + k_{4} $$
(31.2)
$$ \frac{1}{2b}\left[ { - 1 + \sqrt {1 + 4b\left( {Nr + k_{1} } \right)} } \right] = - \frac{1}{2b}\left[ { - 1 - \sqrt {1 - 4b\left( {Nr + k_{3} } \right)} } \right] $$
(31.3)
$$ \frac{ - 1}{2b}\left[ { - 1 - \frac{{\left\{ {1 - 4b\left( {N + k_{3} } \right)} \right\}^{1.5} }}{6bN}} \right] + k_{4} = 1 $$
(31.4)

Equations (31.1)–(31.4) are coupled, nonlinear algebraic equations. For a fixed value of r, the unknowns k1, k2, k3 and k4 can be determined by solving the coupled equations. As the equations are nonlinear, multiple roots are possible. Physically realistic values are chosen such that velocity field is positive. The value of r, where the non-dimensional velocity attains the peak value, depends on the factors like the non-dimensional pressure gradient N and the Sisko fluid parameter b. Hence, r is an unknown which needs to be fixed. In order to determine the value of r, we again fix the coordinate system at the bottom surface. The governing equations remain the same as given by Eqs. (26) and (27), but the boundary conditions get modified as follows:

$$ y = - 1,\;u_{1} = 0 $$
(32.1)
$$ y = 0.5 + r,u_{1} = u_{2} $$
(32.2)
$$ y = 0.5 + r,\;\frac{{{\text{d}}u_{1} }}{{{\text{d}}y}} = \frac{{{\text{d}}u_{2} }}{{{\text{d}}y}} $$
(32.3)
$$ y = 1,u_{2} = 1 $$
(32.4)

The no-slip boundary conditions remain same as the previous case. But the point, where the peak velocity occurs, now has the coordinate of 0.5 + r. Therefore, in Eq. (32.2) and in Eq. (32.3) r will be replaced by 0.5 + r and the two sets of equation will be solved. The value of r has to be guessed and the solutions of the two sets are obtained. The velocity profiles will coincide for the correct value of the r. Therefore, by hit and trial process, that r has to be fixed for which the velocity profiles, obtained from the solution of Eqs. (26) and (27) using the boundary conditions given by Eqs. (31.1)–(31.4) and Eqs. (32.1)–(32.4), are the same.

3.3 Shear-Driven Flow

For shear-driven flow, the governing equation (with A = 0) is given below as:

$$ \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} + nb\frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }}\left| {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right|^{n - 1} = 0 $$
(33)

The solution, using the boundary conditions of Eqs. (15.1) and (15.2), is given below as:

$$ u = \frac{1 + y}{2} $$
(34)

3.4 Evaluation of Friction Factor

Friction factor is an important parameter in determining the pressure drop in the channel for pressure-driven and combined pressure and shear driven flow conditions. The expression of the friction factors for flow of Sisko fluid can be yielded by modifying the available relation of the friction factor in case of Newtonian fluid. For flow of a Newtonian fluid through a circular pipe, the friction factor is given by the well-known relation:

For flow of non-Newtonian fluids, a modified Reynolds number is defined which is based on the apparent viscosity or effective viscosity of the fluids. In the present study, for the flow of a Sisko fluid, the apparent viscosity has to be identified first. For flow of a Sisko fluid through large parallel plates, the expression of the shear stress, in the axial direction, can be obtained from Eq. (16) upon substitution which gives the required equation as follows:

$$ \frac{{\partial {\text{u}}}}{{\partial {\text{z}}}} = 0\quad \tau_{xy} = a\frac{{{\text{d}}u}}{{{\text{d}}y}} + b\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{n - 1} $$
(35)

The effective viscosity can be obtained from Eq. (35) as follows:

$$ \mu_{\text{e}} = a + b\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{n - 1} $$
(36)

Equation (36) can be modified to the following as mentioned by Gupta [36]:

$$ \mu_{\text{e}} = a + b\left( {\frac{{8u_{0} }}{{D_{e} }}} \right)^{n - 1} $$
(37)

where De is the hydraulic diameter [36] of the rectangular channel, as given below:

$$ D_{e} = \frac{{4L_{1} L_{2} }}{{L_{1} + L_{2} }} $$
(38)
$$ \text{Re}_{\text{m}} = \frac{1}{{\frac{1}{{\text{Re}_{\text{N}} \left( {\frac{1}{1 + A}} \right)}} + \frac{1}{{\text{Re}_{\text{p}} \left( {\frac{1}{{\left( {1 + A} \right)^{n} }}} \right)}}}} $$
(39)
$$ \text{Re}_{\text{N}} = \frac{{\rho u_{0} 4L_{1} }}{a}\quad \text{Re}_{\text{p}} = \frac{{\rho u_{0}^{2 - n} \left( {4L_{1} } \right)^{n} }}{{8^{n - 1} b}} $$
(40)

ReN and Rep can be considered as the Reynolds numbers of the Newtonian (a represents the dynamic viscosity of the fluid when b = 0) and power law fluid (when a = 0, b is used to define the modified Reynolds number for power law fluid), respectively. Therefore, the friction factor for the pressure-driven flow of a Sisko fluid through a rectangular channel is given below as:

$$ f = \frac{16}{{\text{Re}_{\text{m}} }} $$
(41)

4 Results and Discussion

4.1 Validation

Before proceeding further with the study of the effect of parametric variation in the velocity distribution, first, a comparison of the results obtained from the numerical solution for the limiting case of A = 0, and the exact solution obtained for large parallel plate flow problem (A = 0) for n = 2, has been made in Fig. 2a–d for pressure-driven and combined pressure and shear driven flow conditions. Figure 2a and c presents the comparison for N = − 6, and for different values of the Sisko fluid parameter b for pressure-driven flow and combined pressure and shear driven flow. In Fig. 2b and d, comparison between the velocity distributions is made for N = − 8 and different values of b for pressure-driven and combined pressure and shear driven flow conditions. In both the cases, the results of the numerical solution are observed to overlap with the exact solution which demonstrates the validity of the present numerical scheme. Then, the physically permissible values of the non-dimensional parameters have to be fixed, before carrying out the study of parametric variation. Sisko fluid parameter b, in the previous studies [10], has been varied in the range of 0.1 to 0.9. Therefore, in the present study, b has been varied in the same range. The value of N is considered in between − 6 and − 8. n has been varied in the range of 1.1 to 2.5 for shear-thickening fluids and for shear-thinning fluids, n has been varied in between 0.7 and 0.9.

Fig. 2
figure 2

Comparison of the velocity distributions (pressure-driven flow) obtained from the numerical solution and the exact solution aA = 0 and n = 2 for N = − 6; bA = 0, n = 2 and N = − 8; c velocity distributions (combined pressure and shear driven flow) when A = 0, n = 2, N = − 6; dA = 0, n = 2, N = − 8

Full size image

4.2 Pressure-Driven Flow

Effect of the aspect ratio on non-dimensional velocity distribution, for shear-thickening and shear-thinning fluids, is displayed in Fig. 3a and b, respectively. It is evident from the figures, that both for shear-thickening and shear-thinning fluids, the non-dimensional velocity decreases with an increase in the aspect ratio. With an increase in the aspect ratio, the resistance offered by the side walls on the flow increases. Therefore, the effect of wall friction on the velocity increases resulting in a decrease in the velocity. Figure 3c and d depicts effect of the aspect ratio on the wall shear-stress variation along the lateral direction, both for shear-thickening and shear-thinning fluids. The results indicate that the wall shear stress increases with a decrease in the aspect ratio. A decrease in the aspect ratio indicates an increase in the distance between the side walls. Therefore, the resistance offered by the side walls decreases which, finally, leads to the higher velocity resulting in an increase in the wall shear stress. Wall shear stress reaches maximum at the central plane, as the velocity is maximum and then it gradually reduces toward the side walls. It is interesting to note that for A = 0.1, Fig. 3c displays a different trend compared to other graphs. The reason is discussed as follows.

Fig. 3
figure 3

a Non-dimensional velocity distribution at z = 0, for different A, when N = − 6, b = 0.5 and n = 1.5, b Non-dimensional velocity distribution at z = 0, for different A, when N = − 6, b = 0.5 and n = 0.8, c Non-dimensional wall shear-stress variation with z for different A, when N = − 6, b = 0.5, n = 1.5, d Non-dimensional wall shear-stress variation with z for different A when N = − 6, b = 0.5 and n = 0.8

Full size image

Lower values of the aspect ratio A indicates a higher length along the lateral direction of the channel. This means when A reaches a certain value, the effect of the side walls on the central part of the channel is insignificant indicating flow through parallel plates. It can be mentioned here that for flow through parallel plates, it is assumed that the results are independent of the lateral coordinate (z). Practically, it means that the results of parallel plates case are valid only in the central portion of the channel. In Fig. 3c, the graph for A = 0.1 displays a flatter portion near the central portion of the channel, which is in sharp contrast to the other curves for A = 0.75, 0.5 and 0.25. The flat portion means that the shear stress is invariant along the lateral direction (or independent of z). The graph for A = 0.1 shows that when aspect ratio is 0.1 or lower, the shear-stress distribution is independent of z for a significant portion along the central region indicating resemblance with flow through parallel plates. Figure 3d indicates a different when A = 0.1.

Figure 3c displays the result for n = 1.5 (shear-thickening fluids, n > 1), and Fig. 3d displays the results for n = 0.8 (shear-thinning fluids, n < 1). With a decrease in the aspect ratio A, the effect of the wall on the results diminishes and when A reaches a certain value, the variation with z is insignificant for a large portion of the channel. Figure 3 d displays that when aspect ratio A reaches 0.1, for n = 0.8 the results are independent of z resembling the flow through the parallel plate case.

Effect of Sisko fluid parameter on the non-dimensional velocity, for shear-thickening and shear-thinning fluids, is presented in Fig. 4a and b, respectively. It is evident from the figures that the velocity decreases with an increase in the Sisko fluid parameter both for shear-thickening and shear-thinning fluids. An increase in b implies an increase in the viscosity effect, which indicates higher resistance for pressure-driven flow. Therefore, both for shear-thinning and shear-thickening fluids, velocity decreases. Similar trends have been reported for the flow of a Sisko fluid through annular pipe studied by Khan et al. [10]. It is interesting to note, in Fig. 4a, that an increase in b from 0.1 to 0.3 results in a drastic reduction in the velocity. Whereas the decrease in velocity caused by a change in b from 0.3 to 0.5 is marginal. In this case, the value of the non-Newtonian index n is 1.8; n = 1 signifies the case for Newtonian fluid; n = 1.8 indicates a strong deviation from a Newtonian fluid. Therefore, when b changes from 0.1 to 0.3, the effect is drastic. On the contrary, when n = 0.8, the decrease in the velocity caused by an increase in b from 0.1 to 0.3 is relatively less. For n = 0.8, the non-Newtonian effect is not so strong; as a result a change in b for 0.1 to 0.3 causes less effect in the velocity. The velocity in case of shear-thinning fluid is higher compared to the velocity in shear-thickening fluids in all the cases.

Fig. 4
figure 4

a Non-dimensional velocity distribution at z = 0, for different values of b, when A = 0.8, N = − 8, n = 1.8, b non-dimensional velocity distribution at z = 0, for different values of b, when A = 0.8, N = − 8 and n = 0.8, c non-dimensional wall shear-stress variation with z, for different b, when A = 0.8, N = − 8, n = 1.8, d non-dimensional wall shear-stress variation with z for different b, when A = 0.8, N = − 8 and n = 0.8

Full size image

Figure 4c and d presents the effect of b on the wall shear-stress variation along the lateral direction of shear-thickening and shear-thinning fluids. It is evident from the figures that wall shear stress is higher for lower values of b as the velocity is higher resulting in a higher velocity gradient. As expected, the wall shear stress is a maximum at the center plane as the velocity is a maximum.

Non-dimensional velocity distribution at z = 0, considering n as a parameter, for both shear-thickening and shear-thinning fluids is presented in Fig. 5a and b, respectively. The results clearly indicate that an increase in the non-Newtonian index n causes a decrease in the velocity both for shear-thickening and shear-thinning fluids. However, the rate of decrease in velocity due to increase in n is lower in case of shear-thinning fluid compared to shear-thickening fluid. It is evident from Fig. 5a and b that, for other parameters remaining the same, for n < 1 (shear-thinning fluids), the velocity is higher than the velocity of the fluid for n > 1 (shear-thickening fluids). Figure 5a reveals that the velocity profile is almost uniform for n = 2 and for higher values of n for shear-thickening fluids. It is important to note that for n = 2.5, a different trend is displayed in Fig. 5a. With increase in the non-Newtonian index n, the resistance toward the flow increases. As a result, velocity decreases. For n = 2.5, velocity remains unchanged along y meaning that velocity is nearly constant along the depth of the channel.

Fig. 5
figure 5

a Non-dimensional velocity distribution at z = 0 for different n, when N = − 8, A = 0.8, b = 0.5, b non-dimensional velocity distribution at z = 0 for different n, when N = − 8, A = 0.8, b = 0.5, c non-dimensional wall shear-stress variation with z for different n when A = 0.8, N = − 8 and b = 0.5, d non-dimensional wall shear-stress variation with z for different n when A = 0.8, N = − 8 and b = 0.5

Full size image

Non-dimensional wall shear-stress variation with z for different values of n is presented in Fig. 5c and d. It is evident from the figure that an increase in n leads to a decrease in the wall shear stress for both shear-thickening and shear-thinning fluids. An increase results in an increase in the viscosity effect, which results in a decrease in flow velocity. Consequently, the wall shear stress is reduced.

4.3 Shear-Driven Flow

For shear-driven flow, the effect of various parameters on the non-dimensional velocity and wall shear stress is graphically presented in this section. Figure 6a and b depicts the effect of the aspect ratio on the non-dimensional velocity both for shear-thickening and shear-thinning fluids, respectively. The results indicate that with an increase in the aspect ratio A, the velocity decreases significantly. An increase in the aspect ratio (A) indicates higher resistance toward the flow, resulting in a decrease in the velocity. In Fig. 6a, the graph for A = 0.1 represents the case when effect of the aspect ratio is marginal and the velocity profile nearly follows a straight line starting from zero at the lower plate and reaching the velocity of the upper plate linearly. Even the velocity profile for A = 0.25 also displays a linear pattern as depicted in Fig. 6a. The effect of the aspect ratio is clearly indicated by the nonlinear nature of the velocity profile starting from A = 0.5. The linear profiles of the velocity up to A = 0.25 reveal that for values of the parameters b = 0.5, n = 1.5, N = − 8, up to the aspect ratio 0.25, the flow can very well be considered as flow through large parallel plates and relatively simple ODE can be solved to obtain the velocity field. Beyond A = 0.5, for given values of the other parameters, the effect of the aspect ratio is dominant and must be considered. For shear-thinning fluids also, Fig. 6b reveals that up to aspect ratio A = 0.25, the velocity profiles follow a linear pattern and the flow can very well be considered as flow through large parallel plates.

Fig. 6
figure 6

a Non-dimensional velocity distribution at z = 0 for different A, when b = 0.5, n = 1.5, b non-dimensional velocity distribution at z = 0 for different A, when b = 0.5, n = 0.8, c non-dimensional wall shear-stress variation with z for different A when b = 0.5, n = 1.5, d non-dimensional wall shear-stress variation with z for different A, when b = 0.5, n = 0.8

Full size image

Effect of the aspect ratio on the non-dimensional wall shear-stress variation along z is depicted in Fig. 6c and d for shear-thickening and shear-thinning fluids, respectively. The results indicate that for A = 0.1, both for n = 1.5 and n = 0.8, the wall shear stress is invariant along z in almost entire portion of the channel except near the walls. For A = 0.25, the deviation from a constant wall shear stress is large and the effect of the aspect ratio starts dominating.

Effect of the Sisko fluid parameter b on non-dimensional velocity, for shear-thickening fluids, is depicted in Fig. 7a. The results indicate that with an increase in b, the velocity decreases. When b changes from 0.1 to 0.3, the decrease in velocity is significant. For other values of b, the change in velocity is relatively marginal. For shear-thinning fluids, it is interesting to note that for n = 0.8, velocity remains more or less unaffected by any increase in b. Effect of the Sisko fluid parameter on variation of the wall shear stress is depicted in Fig. 7c and d both for shear-thickening and shear-thinning fluids respectively. It is evident from the figure that with an increase in b, the wall shear stress decreases significantly. For n = 0.8, the wall shear stress is higher as displayed in the figures. For n = 0.8 (n < 1), the fluid exhibits shear-thinning behavior, resulting in a higher velocity compared to n > 1 case. Aspect ratio A in both the cases is chosen to be 0.8. Therefore, the velocity profile does not indicate any constant value of wall shear stress over any portion of the channel wall.

Fig. 7
figure 7

a Non-dimensional velocity distribution at z = 0 for different b, when n = 1.8, A = 0.8, b non-dimensional velocity distribution at z = 0 for different b, when n = 0.8, A = 0.8, c non-dimensional wall shear-stress variation with z for different b when n = 1.8, A = 0.8, d non-dimensional wall shear-stress variation with z for different b, when n = 0.8, A = 0.8

Full size image

The effect of non-Newtonian index n on the non-dimensional velocity distribution at z = 0, both for shear-thickening and shear-thinning fluids is depicted in Fig. 8a and b respectively. With an increase in n, the velocity is observed to decrease. A higher value of n indicates an increase in the resistance toward the flow, thus causing a decrease in the velocity. The variation of wall shear stress with n is presented in Fig. 8c and d for shear-thickening and shear-thinning fluids, respectively. Wall shear stress decreases with an increase in n both of shear-thickening and shear-thinning fluids. However, in case of shear-thinning fluids, the effect is marginal.

Fig. 8
figure 8

a Non-dimensional velocity distribution at z = 0 for different n (shear thickening), when b = 0.5, A = 0.8, b non-dimensional velocity distribution at z = 0 for different n (for shear thinning), when b = 0.5, A = 0.8, c non-dimensional wall shear-stress variation with z for different n (shear thickening), when b = 0.5, A = 0.8, d non-dimensional wall shear-stress variation with z for different n (shear thinning), when b = 0.5, A = 0.8

Full size image

4.4 Combined Pressure and Shear Driven Flow

Figure 9a and b presents effect of the aspect ratio on non-dimensional velocity distribution at z = 0, both for shear-thickening and shear-thinning fluids, respectively, for combined pressure and shear driven flow conditions. It is evident from the figures that effect of the aspect ratio A is significant on the velocity distribution both for shear-thickening and shear-thinning fluids. It is important to note that for a change in A from 0.1 to 0.25, decrease in velocity is not very high, but a change in A from 0.25 to 0.5 causes a drastic reduction in velocity both for shear-thickening and shear-thinning fluids. For shear-thinning fluid, the velocity is higher than the velocity of shear-thickening fluid for other parameters remaining the same.

Fig. 9
figure 9

a Non-dimensional velocity distribution at z = 0 for different A, when N = − 6, b = 0.5 and n = 1.5, b non-dimensional velocity distribution at z = 0 for different A, when N = − 6, b = 0.5 and n = 0.8, c non-dimensional wall shear-stress variation with z considering A as a parameter, when N = − 6, b = 0.5 and n = 1.5, d non-dimensional wall shear-stress variation with z considering A as a parameter, when N = − 6, b = 0.5 and n = 0.8

Full size image

Effect of the aspect ratio A, on the non-dimensional wall shear-stress variation on the lower wall, is depicted in Fig. 9c and d, for shear-thickening and shear-thinning fluid, respectively. For n = 1.8, it is observed from Fig. 9c that wall shear stress exhibits a flat portion, indicating an invariant shear stress along the lateral direction. This invariance along the lateral direction implies that for nearly 75% of the channel in the central core, the flow is dominated by the characteristics of flow through large parallel plates for the chosen values of the parameters.

Effect of b on the non-dimensional velocity distribution at z = 0, for shear-thickening and shear-thinning fluid, is presented in Fig. 10a and b, respectively. The results indicate that velocity decreases drastically with an increase in b, when b is small. Figure 10a depicts that for b = 0.1, the velocity profile exhibits mainly the characteristics of pressure-driven flow. But as b increases from 0.1 to 0.3, the characteristic of pressure-driven flow is suppressed and the characteristics of shear-driven flow dominate. With a further increase in b, the velocity remains significantly lower than the velocity of the moving plate, up to a major portion of the channel. Velocity again increases and finally reaches the velocity of the moving plate only after reaching region very close to the plate.

Fig. 10
figure 10

a Non-dimensional velocity distribution at z = 0 for different values of b when N = − 6, A = 0.8 and n = 1.8, b non-dimensional velocity distribution at z = 0 for different values of b when N = − 6, A = 0.8 and n = 0.8, c non-dimensional wall shear stress at z = 0 for different values of b when N = − 6, A = 0.8 and n = 1.8, d non-dimensional wall shear stress at z = 0 for different values of b when N = − 6, A = 0.8 and n = 0.8

Full size image

Figure 10a displays the velocity distribution for combined pressure and shear driven flow. It is evident that for b = 0.1, the nature of the graph is different from the other graph. The non-Newtonian parameter b is a measure of the viscosity of the fluid. For lower values of b, the resistance toward the flow is less (contribution of the pressure-driven flow is present) and fluid velocity increases in nearly all parts of the channel. But near the upper plate as the plate itself moves, the fluid velocity reaches that of the plate (no slip condition). Thus, velocity shows an increasing pattern up to a certain depth and then it decreases the plate velocity. But with increase in b, the resistance toward the flow increases and velocity in the entire section decreases. Near the upper plate, due to the movement of the plate, velocity increases and reach that of the plate. Therefore, for higher values of b, velocity in lower and central part is less and then near the upper wall it shows an increasing trend ad reaches the plate velocity. Therefore, the graph for b = 0.1 shows an opposite trend.

For shear-thinning fluids, Fig. 10b indicates an increase in the velocity for all the corresponding values of the parameters. It is evident from the figure that when b changes from 0.7 to 0.9, velocity decreases drastically and the decrease in velocity, when b changes from 0.1 to 0.7, is gradual. For higher values of the non-Newtonian parameter b, the resistance toward the flow increases. Therefore, with increase in b, velocity decreases. For b = 0.9, velocity decreases significantly indicating that beyond this value of b (for the other values of the parameters as given) velocity is significantly lower in the entire channel.

Wall shear stress, at the lower wall, along z for different values of b is presented in Fig. 10c and d. Figure 10d displays nearly unaffected behavior with a change in b. With an increase in b, velocity decreases due to increase in flow resistance. However, this decrease in velocity is marginal when the velocity is already lower for higher values of b.

Figure 11a and b depicts the effect of n on the non-dimensional velocity distribution both for shear-thickening and shear-thinning fluids. An increase in n causes a significant decrease in the velocity both for shear-thickening and shear-thinning fluids. However, for shear-thickening fluid, velocity is higher as expected. For n = 2, in case of shear-thickening fluid, the velocity decreases at a very lower value and then again it increases near the plate. It is interesting to note that velocity profile displays a different trend for with changes in n. Higher values of the non-Newtonian index n result in higher values of apparent viscosity of the fluids at any shear rate. Therefore, with an increase in n, for combined pressure and shear driven flow, for a given N (non-dimensional pressure gradient) the resistance toward the flow increases which results in a decrease in the velocity. From the figure, it is clear that for N = − 6 and n = 1.1 the maximum velocity achieved is higher than that of the plate velocity. That means the shearing of the plate is retarding flow induced by the pressure gradient. For n = 1.5, velocity decreases compared to the case of n = 1.1 as shown in Fig. 11a. With further increase in n, for n = 2, there is a significant decrease in the velocity in the central zone below that of the plate velocity. This may be attributed to the adverse effect of increased viscosity on the driving force due to the pressure gradient. However, near the upper plate (near y = 1), velocity shows an increasing trend due to the influence of the moving upper plate. At y = 1 (in the upper plate), velocity reaches the same velocity as of the plate. n = 1 implies the case of Newtonian fluid; therefore, n = 1.1 indicates that the deviation from the Newtonian fluid behavior is marginal. For this case, velocity is relatively higher and then near the upper plate, it reaches the plate velocity. The graph for this case (n = 1.1) first shows an increasing trend with the depth followed by a decrease near the upper plate. In contrast, the velocity for n = 2 displays in increase with depth, but rate of increase is marginal. Near the plate, there is a significant increase in the velocity due to the moving plate. Therefore, the nature of these graphs differs in their pattern.

Fig. 11
figure 11

a Non-dimensional velocity distribution at z = 0, for different n when N = − 6, A = 0.8 and b = 0.5, b non-dimensional velocity distribution at z = 0, for different n when N = − 6, A = 0.8 and b = 0.5, c non-dimensional wall shear-stress variation in lower wall along z, for different n when N = − 6, A = 0.8 and b = 0.5, d non-dimensional wall shear-stress variation in lower wall along z for different n when N = − 6, A = 0.8 and b = 0.5

Full size image

An increase in n, results in a significant variation in the lower wall shear stress as depicted in Fig. 11c and d.

Figure 12a and b presents the variation of non-dimensional velocity with A for different values of b, for shear-thickening and shear-thinning fluids, respectively, in case of pressure-driven flow. It is important to note that even for A in the range of 0.1 to 0.2, the change in the maximum velocity, for n = 1.8, is higher in case of pressure-driven flow condition, indicating a significant effect of the aspect ratio on the velocity. It is evident from Fig. 12a that the maximum velocity decreases with an increase in A. This rate of decrease of umax with A is lower for higher values of b when A is greater than 0.5. For higher values of A, the velocity is lower. Any further increase in b, causes a marginal decrease in the velocity as revealed by Fig. 12a. Figure 12b reveals that for shear-thinning fluid when n = 0.8, the influence of aspect ratio A on the maximum velocity is insignificant when A lies in the range 0.1 to 0.2. For b = 0.9, the effect of A on umax is less even for A = 0.4. For higher values of b, the velocity is lower; with any increase in A, then, the rate of decrease in velocity is lower rendering umax insensitive toward A even for A = 0.4. For combined pressure and shear driven flow, the effect of A on umax is depicted in Fig. 12c and d for shear-thickening and shear-thinning fluid, respectively. It is interesting to note from Fig. 12c that umax is unaffected by A for A > 0.5, when b = 0.9. When b = 0.7, umax is unaffected when A lies in the range 0.8 to 1. The results indicate that max is nearly unaffected by A on the higher side, for higher values of b. Higher values of b imply higher flow resistance, nullifying the effect of pressure gradient in case of combined pressure and shear driven flow, rendering the maximum non-dimensional velocity to be unity (same as upper plate velocity). It is interesting to note that effect of change in the parameter b diminishes as the parameter A increases. Increase in b implies increase in the viscosity and thus higher resistance to the flow causing lower velocity. Similarly, higher values of the aspect ratio A means higher resistance offered by the wall friction resulting in lower velocity. It is evident from the figure that for A = 0.75 and above and for b = 0.3 and above, velocity is low. For this range of A, with an increase in b, the rate of decrease in the velocity is marginal. As the velocity is relatively low, any further increase in b affects the velocity marginally. However, for b = 0.1 to b = 0.3, the decrease in velocity with a decrease in b is significant even for higher values of A (A = 0.75 and above) as depicted by Fig. 12c.

Fig. 12
figure 12

a Variation of maximum non-dimensional velocity with A, for pressure-driven flow, considering b as a parameter when N = − 8 and n = 1.8, b variation of maximum non-dimensional velocity with A, for pressure-driven flow, considering b as a parameter when N = − 8 and n = 0.8, c variation of maximum non-dimensional velocity with A, for pressure- and shear-driven flow, considering b as parameter when N = − 8 and n = 1.8, d variation of maximum non-dimensional velocity with A, for combined pressure and shear driven flow, considering b as parameter when N = − 8 and n = 0.8

Full size image

Due to the combined effect of increase in b and A, velocity decreases significantly and any further change in b or even in A cannot affect the velocity significantly which is displayed by the graph for b = 0.7.

For n = 0.8, as presented in Fig. 12d, it is observed that the effect of A on umax is less for higher values of b even for A up to 0.5. Beyond A = 0.5, the effect of A on umax is significant for all values of b.

5 Conclusion

The pressure-driven, shear-driven and combined pressure and shear driven flow of Sisko fluid through rectangular channels has been investigated. Effect of the aspect ratio for flow of Sisko fluid has never been considered, and PDE, governing the flow, is reported for the first time. The governing PDE is strongly nonlinear in nature, and obtaining a closed-form solution or approximate analytical or semi-analytical solution is a formidable task. Explicit finite difference scheme with an iterative solver is used to generate the numerical solution of the equation, and the variation of velocity and wall shear stress has been studied. The important conclusions made from the study are given below:

  • For pressure-driven flow, for A up to 0.1, effect of the aspect ratio in a rectangular channel can be neglected.

  • The wall shear-stress variation along the lateral direction remains nearly unaltered for around 60% of the channel indicating the characteristics of flow through large parallel plates.

  • In case of shear-driven flow and combined pressure and shear driven flow also, the characteristics of flow through large parallel plates are observed in nearly 50% of the channel for A = 0.1 or less. This implies for up to 50% of the channel, near the core, the l assumption of large parallel plate generates reasonably accurate results, beyond which the effect of the aspect ratio is significant on several occasions.

  • An increase in the aspect ratio in case of both shear-driven and combined pressure and shear driven flow, from 0.1 to 1, drastically decreases the velocity in a large portion of the channel. Whereas the linear velocity profiles, obtained in case of large parallel plate assumptions, for shear-driven flow, are observed for up to A = 0.25 and less, for both shear-thickening and shear-thinning fluids.

  • The velocity of shear-thinning fluid is higher than the velocity of shear-thickening fluid in all cases.

  • The effect of n on velocity and wall shear stress is very strong both for shear-thickening and shear-thinning fluids.

  • With an increase in n, velocity and shear stress decreases significantly.

  • The effect of b in presence of the aspect ratio effect is interesting. An increase in b from 0.1 to 0.3, when deviation of n from 1 is large, results in a drastic decrease in the velocity for pressure-driven, shear-driven and combined pressure and shear driven flows. This feature is depicted for the shear-thickening fluid case shown for n = 1.8. However, when n is close to unity, the effect of b on the velocity is gradual over a relatively wide range for all the cases.

In the present study, only the momentum conservation equation is solved and the results may be useful for study of forced convection heat transfer of Sisko fluid through rectangular channels, where the velocity field is required to solve the energy conservation equation. For further investigation, flow and heat transfer aspect through channel with flexible walls can be considered; the advantages of flexible walls are already discussed. Forced convection and mixed convection can be considered with temperature-dependent properties, which will produce a coupled set of momentum and energy conservation equation, requiring more computational effort. It is important to mention that no experimental results on the flow of Sisko fluids through channel for pressure-driven, shear-driven and combined pressure and shear driven flow are reported in the open literature. Therefore, the results of the present study cannot be compared with any experimental data. In future, experimental study can also be conducted and the results of the present study can be compared.