Effect of the aspect ratio on the flow characteristics of magnetohydrodynamic (MHD) third grade fluid flow through a rectangular channel

Abstract

The magnetohydrodynamic (MHD) flow of a third grade fluid through a rectangular channel, considering the effect of aspect ratio, has been investigated. The flow considered is steady, laminar, incompressible and hydro-dynamically fully developed. The equation, describing the flow, is a highly non-linear partial differential equation (PDE) with remote possibility of having an exact solution and even numerical solution also is very difficult to obtain. A combination of the homotopy perturbation method (HPM) and integral method (IM) has been employed to solve the non-linear PDE which is scarce in open literature. The results of the present study are compared with the results obtained by the least square method (LSM) of the MHD third grade fluid flow through a rectangular channel, without the effect of aspect ratio and are found to be in close agreement. The results indicate that the flow field is significantly affected by the aspect ratio which should be considered for practical applications. In all the available literatures of the third grade fluid flow, the aspect ratio effect is neglected and this simplifying assumption reduces the highly complicated non-linear PDE to a non-linear ordinary differential equation (ODE). The novelty of the subject work lies in the inclusion of the effects of aspect ratio in the governing equation describing the flow of a third grade fluid through a channel and solving this by a combined analytical method (HPM and IM). Further, the effects of the Hartmann number and non-Newtonian third grade fluid parameter on the flow filed are discussed.

1 Introduction

Pressure-driven flow of both Newtonian and non-Newtonian fluid through rectangular channels is of great practical importance due to its wide spread applications in liquid metal flow, polymer melt flow, small size heat exchangers and many more. In hydro-dynamically fully developed condition, for Newtonian fluid, the solution of the governing equation is too simple if the aspect ratio is neglected. However, if the aspect ratio is considered, then the governing equation is a linear 2^nd order partial differential equation (PDE) which can be solved analytically. In [1], the authors studied the flow of Newtonian fluid through a rectangular channel considering the effect of aspect ratio by employing integral methods and put forward some approximate solutions, which are easier to use for obtaining the temperature by solving the energy equation. It is well known that many of the fluids used in the industry do not follow the Newtonian fluid model and depending on their rheological behavior, several non-Newtonian fluid models such as power fluid model, Casson fluid model, Ellis fluid model, third grade fluid, Sisko model, etc. have been proposed. Flow and heat transfer of various non-Newtonian fluids through rectangular channel have been studied by numerous researchers. Flow and heat transfer of a power law fluid flowing through parallel plates, considering the effect of viscous dissipation, has been investigated in [2]. Exact analytical solutions for the velocity and temperature have been provided and the effects of non-Newtonian index and Brinkman number on velocity, temperature and Nusselt number have been discussed. Couette flow, Poiseuille flow and combined Couette-Poiseuille flow through parallel plates with constant wall temperature condition has been studied in [3]. Analytical solutions for the velocity and temperature have been obtained by employing HPM. In [4], the exact analytical solution for the Poiseuille and Couette-Poiseuille flow of a third grade fluid through parallel plate has been reported and the results were compared with the results presented in [3].

MHD flow has drawn the attention of the researchers due to its immense practical importance for various engineering and medical applications. MHD is the study of the interaction between the conducting fluid and the external magnetic field imposed on it. The Lorentz force, stemming from the interaction of these two, is the key factor in MHD which serves as a non-intrusive means for having a better control over the flow, which helps in polymer melt flow, targeted drug delivery for treatment of the tumors, in small scale heat exchangers and many more. Over the last decade, electromagnetohydrodynamic (EMHD) flow has been an active area of research due to its wide spread applications in the field of micro fluidics. Naturally, MHD and EMHD flow and heat transfer of different Newtonian and non-Newtonian fluids have been investigated by numerous researchers. Mixed convection flow of a second grade visco-elastic fluid past a wedge with porous suction and injection has been investigated in [5]. The authors of [6] investigated MHD flow and heat transfer in a visco-elastic fluid over a stretching sheet considering the effect of radiation. In [7], MHD flow and heat transfer in a power law fluid in a stretching sheet has been studied. EMHD flow and heat transfer in a third grade fluid flowing through micro-parallel plates, considering the effect of viscous dissipation, is studied by the authors of [8]. The non-linear momentum and energy conservation equations have been solved by the traditional perturbation method and spectral method and the effects of various parameters on the velocity, temperature and Nusselt number have been reported.

The aforementioned discussion clearly indicates that non-Newtonian third grade fluid has been widely explored by the researchers as various polymers, liquid metals, suspensions are observed to follow this model. Though many research works have been carried out on flow and heat transfer of third grade fluids through parallel plates (equivalent to flow through a channel for very small aspect ratio), flow through a rectangular channel, considering the aspect ratio effect, has never been included in the study. But the aspect ratio effect is a very important factor which significantly affects the flow and thus heat transfer characteristics. In the present study, MHD flow of a third grade fluid through a rectangular channel has been investigated, considering the effect of the aspect ratio, which has never been included in the previous studies. The partial differential equation describing the flow phenomena is highly non-linear. For solving the equations, a combination of HPM and IM has been employed. HPM is an analytical technique, introduced by He, which is a coupling of the homotopy theory and the traditional perturbation method and some important studies by He can be found in [9, 10]. HPM does not require the presence of any small or large parameter in the problem and can take the full advantages of the traditional perturbation method. These advantages of the HPM have attracted numerous researchers who have applied this in various problems of engineering and industrial applications. Some important studies by the researchers can be found in [11,12,13,14]. Integral method is another powerful technique which has been employed by the authors [1]. The present study provides a solution for the highly nonlinear PDE highlighting the influence of the aspect ratio on the velocity. The results are compared with the LSM results for corresponding flow of a third grade fluid without the effect of aspect ratio and are found to be in close agreement. Further, the effects of the third grade fluid parameter and Hartmann number on the velocity and flow rate have been discussed.

2 Problem formulation

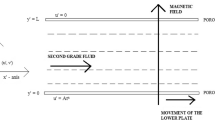
The flow of a third grade fluid through a rectangular channel, under the influence of magnetic field has been pictorially sketched in figure 1. The flow is steady, laminar, incompressible and hydro-dynamically fully developed. The coordinates are selected as shown in figure 1. The effect of the imposed magnetic field has been shown by the vector B.

Figure 1

MHD Flow of a third grade fluid through the rectangular channel.

For steady, incompressible flow, the mass conservation equation is given as follows:

$$ \nabla .V^{*} = 0 $$

(1)

where, V^* is the velocity vector. The Lorentz force, generated as a result of the interaction between the conducting fluid (an overall neutral fluid where the electrons are responsible for the current) and the magnetic field, will contribute to the body force vector in the momentum conservation equation; however, it is to be noted that this force can not cause the fluid flow by itself, but it will affect the flow characteristics significantly. This force, stemming from the interaction of the magnetic field and the moving conducting fluid, acts in the opposite direction of flow and can play a role of non-intrusive means to have a control over the flow.

Neglecting the force due to gravity, the momentum conservation equation will be of the following form:

$$ \rho \frac{dV}{dt}^{*} = \nabla .\tau + f $$

(2)

where, ρ is the density of the fluid, τ is the stress tensor and f is the body force per unit volume and t is the time. The body force per unit volume is given as

$$ f = J \times B $$

(3)

f is the body force here, comprising of Lorentz force. B and J are the applied magnetic field and the current density respectively. In the influence of magnetic field, the current density is related to B as follows:

$$ J = \sigma (V^{*} \times B) $$

(4)

where, σ is the electrical conductivity of the fluid. The stress tensor in the momentum conservation equation is split into isotropic and deviatoric stress tensors, which for Newtonian fluid provides a linear stress and strain-rate relation. But in case of non-Newtonian fluids, depending on the rheological behavior, the deviatoric part captures the physics of the complex flow phenomena by incurring different forms of non-linearity into the governing equation. For third grade fluid also, these complexities are captured in the equation through the inclusion of the extra stress tensor rendering a highly non-linear stress and strain-rate relation as given below.

$$ \tau = - p^{*} I + \mu A_{1} + \alpha_{1} A_{2} + \alpha_{2} A_{1}^{2} + \beta_{1} A_{3} + \beta_{2} (A_{1} A_{2} + A_{2} A_{1} ) + \beta_{3} (trA_{1}^{2} )A_{1} $$

(5)

where, p^* is the static pressure, μ is the dynamic viscosity the fluid, I is unit matrix, α₁,α₂, β₁, β_2, β₃ are the material constants of the third grade fluid and A₁, A₂, and A₃ are kinematic tensors expressed as follows:

$$ A_{1} = (gradV^{*} ) + (gradV^{*} )^{Transpose} $$

(6)

$$ A_{n} = \frac{{dA_{n - 1} }}{dt} + A_{n - 1} (gradV^{*} ) + (gradV^{*} )^{Transpose} A_{n - 1} ,n = 1,2,3 $$

(7)

The equations given by Eqs. (1)–(5) have been used by the authors of [8] to study the EMHD flow and heat transfer of third grade fluid through parallel plates. According to the assumption of hydro-dynamically fully developed flow condition, only the axial velocity component u^*(y^*, z^*) is present and v^* and w^* are zero. Therefore, we seek a solution of the form

$$ V^{*} = [u^{*} (y^{*} ,z^{*} ),0,0] $$

(8)

Using Eq. (5), Eq. (6) and Eq. (7) we get the x^*, y^* and z^* momentum equations as follows:

$$ \mu \left( {\frac{{\partial^{2} u^{*} }}{{\partial y^{*2} }} + \frac{{\partial^{2} u^{*} }}{{\partial z^{*2} }}} \right) + 2\beta_{2} \frac{\partial }{{\partial y^{*} }}\left[ {\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}} \right)^{3} + \frac{{\partial u^{*} }}{{\partial y^{*} }}\left( {\frac{{\partial u^{*} }}{{\partial z^{*} }}} \right)^{2} } \right] + 2\beta_{2} \frac{\partial }{{\partial z^{*} }}\left[ {\left( {\frac{{\partial u^{*} }}{{\partial z^{*} }}} \right)^{3} + \frac{{\partial u^{*} }}{{\partial z^{*} }}\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}} \right)^{2} } \right] - \sigma B^{2} u^{*} = \frac{{\partial p^{*} }}{{\partial x^{*} }} $$

(9.1)

$$ (2\alpha_{1} + \alpha_{2} )\frac{\partial }{{\partial y^{*} }}\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}} \right)^{2} + (2\alpha_{1} + \alpha_{2} )\frac{\partial }{{\partial z^{*} }}\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}\frac{{\partial u^{*} }}{{\partial z^{*} }}} \right) = \frac{{\partial p^{*} }}{{\partial y^{*} }} $$

(9.2)

$$ (2\alpha_{1} + \alpha_{2} )\frac{\partial }{{\partial z^{*} }}\left( {\frac{{\partial u^{*} }}{{\partial z^{*} }}} \right)^{2} + (2\alpha_{1} + \alpha_{2} )\frac{\partial }{{\partial y^{*} }}\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}\frac{{\partial u^{*} }}{{\partial z^{*} }}} \right) = \frac{{\partial p^{*} }}{{\partial z^{*} }} $$

(9.3)

u^* is a function of y^*and z^*. Therefore, from Eq. (9.2) and Eq. (9.3), it can be concluded that the pressure may be expressed as follows after carrying out the integration:

$$ p^{*} = F(y^{*} ,z^{*} ) + G(x^{*} ) $$

(10)

The right hand side of Eq. (9.1), that is the pressure gradient in the axial direction is a function of x^* alone and the left hand side of Eq. (9.1) is a function of y^*, z^*. This is only possible when both the sides are separately equal to a constant. Therefore we can write the x^*momentum equation as follows:

$$ \mu \left( {\frac{{\partial^{2} u^{*} }}{{\partial y^{*2} }} + \frac{{\partial^{2} u^{*} }}{{\partial z^{*2} }}} \right) + 2\beta_{2} \frac{\partial }{{\partial y^{*} }}\left[ {\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}} \right)^{3} + \frac{{\partial u^{*} }}{{\partial y^{*} }}\left( {\frac{{\partial u^{*} }}{{\partial z^{*} }}} \right)^{2} } \right] + 2\beta_{2} \frac{\partial }{{\partial z^{*} }}\left[ {\left( {\frac{{\partial u^{*} }}{{\partial z^{*} }}} \right)^{3} + \frac{{\partial u^{*} }}{{\partial z^{*} }}\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}} \right)^{2} } \right] - \sigma B^{2} u^{*} = \frac{{\partial p^{*} }}{{\partial x^{*} }} = C $$

(11)

where, C is a constant.

Following non-dimensional variables and parameters are introduced to convert Eq. (11) into its non-dimensional form:

$$ y = \frac{{y^{*} }}{{L_{1} }},z = \frac{{z^{*} }}{{L_{2} }},u = \frac{{u^{*} }}{U},U = \frac{{Q^{*} }}{{L_{1} L_{2} }},Ha = \sqrt {\frac{\sigma }{\mu }} BL_{1} ,N = \frac{C}{\mu U}L_{1}^{2} ,As = \frac{{L_{1} }}{{L_{2} }},A = \frac{{\beta_{2} U^{2} }}{{\mu L_{1}^{2} }} $$

(12)

where, y, z are the non-dimensional coordinates, Ha is the Hartmann number, N is the non-dimensional pressure gradient, As is the aspect ratio of the channel, A is the third grade fluid parameter, U is the average velocity through the channel, Q^* is the dimensional flow rate, L₁ is the half depth and L₂ is the half width of the channel.

Utilizing the non-dimensional variables given in Eq. (12) the non-dimensional form of the x^* momentum equation reduces to the following:

$$ \frac{{\partial^{2} u}}{{\partial y^{2} }} + As^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }} + 6A\left( {\frac{\partial u}{\partial y}} \right)^{2} \left( {\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + 2AAs^{4} \frac{{\partial^{2} u}}{{\partial y^{2} }}\left( {\frac{\partial u}{\partial z}} \right)^{2} + 8AAs^{2} \frac{\partial u}{\partial y}\frac{\partial u}{\partial z}\frac{{\partial^{2} u}}{\partial y\partial z} + 6AAs^{4} \left( {\frac{\partial u}{\partial z}} \right)^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }} + 2AAs^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }} - \left( {Ha} \right)^{2} u = N $$

(13)

2.1 Boundary conditions

The non-dimensional boundary conditions to be satisfied by the velocity are the no slip at the walls which are given as follows:

$$ u\left( { - 1,z} \right) = u(1,z) = u(y, - 1) = u(y,1) = 0 $$

(14)

3 Solution

Equation (13) is a non-linear PDE and no established method is available to solve this. A combination of HPM and IM is proposed to solve the equation in this study. At first, a homotopy has been constructed as follows:

$$ \left( {\frac{{\partial^{2} u}}{{\partial y^{2} }} + As^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }} - \left( {Ha} \right)^{2} u - N} \right) + q\left( \begin{aligned} 2AAs^{4} \frac{{\partial^{2} u}}{{\partial y^{2} }}\left( {\frac{\partial u}{\partial z}} \right)^{2} + 8AAs^{2} \frac{\partial u}{\partial y}\frac{\partial u}{\partial z}\frac{{\partial^{2} u}}{\partial y\partial z} \hfill \\ + 6AAs^{4} \left( {\frac{\partial u}{\partial z}} \right)^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }} + 2AAs^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }} \hfill \\ \end{aligned} \right) = 0 $$

(15)

Here, q is an embedding parameter. q = 0 denotes a simplified equation of Newtonian fluid flow problem under the influence of magnetic field considering the effect of aspect ratio. Whereas q = 1 gives the actual equation to be solved. For solving Eq. (15), the velocity u is expanded with respect to the embedding parameter q up to 1^st order as follows:

$$ u(y,z)=u_{0}(y,z)+qu_{1}(y,z)+\ldots$$

(16)

where, u₀ and u₁ are the 0^th order and the 1^st order solutions, respectively. It is important to mention here that the series solution for velocity, given by Eq.(16), has been truncated to 1^st order term only, which means that the results given is valid for weakly non-linear behavior of the non-Newtonian third grade fluid.

Now substituting Eq. (16) in to Eq. (15) and collecting the coefficients of q⁰ and q¹ and equating these terms to zero, 0^th oder and 1^st order equations are obtained. The 0^th order equation and boundary conditions are given below:

3.1 0^th order equation

The 0^th order equation is given as follows

$$ \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + As^{2} \frac{{\partial^{2} u_{0} }}{{\partial z^{2} }} - (Ha)^{2} u_{0} - N = 0. $$

(17.1)

3.1a Boundary conditins: Boundary conditions are the no slip at the walls given below as

$$ u_{0} \left( { - 1,z} \right) = u_{0} (1,z) = u_{0} (y, - 1) = u_{0} (y,1) = 0 $$

(17.2)

3.2 1^st order equation

1^st order equation is given as follows

$$ \frac{{\partial^{2} u_{1} }}{{\partial y^{2} }} + As^{2} \frac{{\partial^{2} u_{1} }}{{\partial z^{2} }} + 6A\left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} \left( {\frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}} \right) + 2AAs^{4} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}\left( {\frac{{\partial u_{0} }}{\partial z}} \right)^{2} + 8AAs^{2} \frac{{\partial u_{0} }}{\partial y}\frac{{\partial u_{0} }}{\partial z}\frac{{\partial^{2} u_{0} }}{\partial y\partial z} + 6AAs^{4} \left( {\frac{{\partial u_{0} }}{\partial z}} \right)^{2} \frac{{\partial^{2} u_{0} }}{{\partial z^{2} }} + 2AAs^{2} \left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} \frac{{\partial^{2} u_{0} }}{{\partial z^{2} }} = 0 $$

(18.1)

3.2a Boundary conditions: Boundary conditions to be satisfied by the 1^st order velocity are no slip at the walls given as

$$ u_{1} \left( { - 1,z} \right) = u_{1} (1,z) = u_{1} (y, - 1) = u_{1} (y,1) = 0 $$

(18.2)

3.3 Solution of the 0^th order equation

Equation (17.1) is solved by IM for which the velocity field is approximated by the following function [1]:

$$ u_{0} = (1 - y^{2} )(1 - z^{2} )(a_{0} + a_{1} y^{2} ) $$

(19)

Equation (19) satisfies the boundary conditions given by Eq. (17.2). In this context, it is important to note that the chosen functional form for the 0^th order velocity, given by Eq. (19), satisfies the appropriate boundary conditions, but the MHD term, present in the governing equation, will affect the solution of velocity and will lead to the exponential decay of velocity by introducing the Hartmann number in the solution. This factor limits the results of the present investigation to be valid for small Hartmann numbers. The same is true about the selection of the functional form for the solution of the 1^st order velocity given by Eq. (23). Equation (19) is substituted in Eq. (17.1) and integrated over the cross-sectional area of the channel to get the integral equation as follows:

$$ \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left( {\frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} + As^{2} \frac{{\partial^{2} u_{0} }}{{\partial z^{2} }} - (Ha)^{2} u_{0} } \right)dydz} } = \int\limits_{0}^{1} {\int\limits_{0}^{1} {Ndydz} } $$

(20)

Equation (20) provides one condition involving two unknowns. The second equation is obtained from the following condition:

$$ \left| {\frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}} \right|_{y = 0,z = 0} + As^{2} \left| {\frac{{\partial^{2} u_{0} }}{{\partial z^{2} }}} \right|_{y = 0.z = 0} - (Ha)^{2} \left| {u_{0} } \right|_{y = 0} = N $$

(21)

For application of the IM, the study by Kundu et al [1] can be referred.

Solving Eq. (20) and Eq. (21) the unknown constants are determined to be

$$ a_{0} = \frac{N}{{2\left[ {\left\{ { - \frac{4}{3}\left( {1 + As^{2} } \right) - \frac{4}{9}(Ha)^{2} } \right\} + \frac{{(Ha)^{2} + 2 + 2As^{2} }}{2}\left\{ { - \frac{12}{9} - \frac{4}{15}As^{2} - (Ha)^{2} \frac{4}{15}} \right\}} \right]}} $$

(22.1)

$$ a_{1} = \frac{{N + \left[ {(Ha)^{2} + 2 + 2As^{2} } \right]}}{2} $$

(22.2)

3.4 Solution of the 1^st order equation

For solving the 1^st order equation, the approximate function is chosen which satisfies the boundary conditions given by Eq. (18.2) and are given below:

$$ u_{1} = (1 - y^{2} )(1 - z^{2} )(b_{0} + b_{1} y^{2} ) $$

(23)

The two unknowns b₀ and b₁ of the velocity u₁ is obtained by solving the following two equations:

$$ \begin{aligned} & \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left( {\frac{{\partial^{2} u_{1} }}{{\partial y^{2} }} + As^{2} \frac{{\partial^{2} u_{1} }}{{\partial z^{2} }}} \right)dydz} } + \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left( {6A\left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} \left( {\frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}} \right)} \right)dydz} } \\ & \quad + \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left( {2AAs^{4} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}\left( {\frac{{\partial u_{0} }}{\partial z}} \right)^{2} } \right)dydz} } + \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left( {8AAs^{2} \frac{{\partial u_{0} }}{\partial y}\frac{{\partial u_{0} }}{\partial z}\frac{{\partial^{2} u_{0} }}{\partial y\partial z}} \right)dydz} } \\ & \quad + \int\limits_{0}^{1} {\int\limits_{0}^{1} {6AAs^{4} \left( {\frac{{\partial^{2} u_{0} }}{{\partial z^{2} }}\left( {\frac{{\partial u_{0} }}{\partial z}} \right)^{2} } \right)dydz} } + \int\limits_{0}^{1} {\int\limits_{0}^{1} {\left( {\frac{{\partial^{2} u_{0} }}{{\partial z^{2} }}\left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} } \right)dydz} } = 0 \\ \end{aligned} $$

(24)

$$ \begin{aligned} \hfill \\ \left| {\frac{{\partial^{2} u_{1} }}{{\partial y^{2} }} + As^{2} \frac{{\partial^{2} u_{1} }}{{\partial z^{2} }}} \right|_{y = 0,z = 0} + \left| \begin{aligned} &6A\left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} \left( {\frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}} \right) + 2AAs^{4} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}\left( {\frac{{\partial u_{0} }}{\partial z}} \right)^{2} \hfill \\ &+ 8AAs^{2} \frac{{\partial u_{0} }}{\partial y}\frac{{\partial u_{0} }}{\partial z}\frac{{\partial^{2} u_{0} }}{\partial y\partial z} \hfill \\ \end{aligned} \right|_{y = 0,z = 0} + \left| {6AAs^{4} \left( {\frac{{\partial u_{0} }}{\partial z}} \right)^{2} \frac{{\partial^{2} u_{0} }}{{\partial z^{2} }} + 2AAs^{2} \left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} \frac{{\partial^{2} u_{0} }}{{\partial z^{2} }}} \right|_{y = 0,z = 0} = 0 \hfill \\ \end{aligned} $$

(25)

Solving Eq. (24) and Eq. (25) the values of unknowns are obtained as follows:

$$ b_{0} = \frac{{b_{1} }}{{1 + As^{2} }} $$

(26.1)

$$ b_{1} = - \left( {\frac{1}{{\frac{16}{3} - \frac{4}{15}As^{2} }}} \right)\left( {I_{1} + I_{2} + I_{3} + I_{4} + I_{5} } \right) $$

(26.2)

$$ \begin{aligned} I_{1} = \int\limits_{0}^{1} {\int\limits_{0}^{1} {6A\left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}dydz} } ,I_{2} = \int\limits_{0}^{1} {\int\limits_{0}^{1} {2AAs^{4} \left( {\frac{{\partial u_{0} }}{\partial z}} \right)^{2} \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}dydz} } , \hfill \\ I_{3} = \int\limits_{0}^{1} {\int\limits_{0}^{1} {8AAs^{2} \frac{{\partial u_{0} }}{\partial y}\frac{{\partial u_{0} }}{\partial z}\frac{{\partial^{2} u_{0} }}{{\partial y\partial z^{{}} }}dydz,} } I_{4} = \int\limits_{0}^{1} {\int\limits_{0}^{1} {6AAs^{4} \left( {\frac{{\partial u_{0} }}{\partial z}} \right)^{2} \frac{{\partial^{2} u_{0} }}{{\partial z^{2} }}dydz} } , \hfill \\ I_{5} = \int\limits_{0}^{1} {\int\limits_{0}^{1} {2AAs^{2} \frac{{\partial^{2} u_{0} }}{{\partial z^{2} }}\left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} dydz} } \hfill \\ \end{aligned} $$

(26.3)

Solving for b₀ and b₁ we get the final solution for u from Eq. (16) by substituting q = 1, given below as:

$$ \begin{aligned} & u(y,z) = (1 - y^{2} )(1 - z^{2} )(a_{0} + a_{1} y^{2} ) + (1 - y^{2} )(1 - z^{2} )(b_{0} + b_{1} y^{2} ) \\ & = (1 - y^{2} )(1 - z^{2} )\left[ {a_{0} + b_{0} + (a_{1} + b_{1} )y^{2} } \right] \\ \end{aligned} $$

(27)

For As = 0.2, N = − 1.2, Ha = 2 and A = 0.3 the values are a₀ = 0.2522, a₁ = 0.1667, b₀ = − 0.05565 and b₁ = − 0.05788.

The flow rate through the channel is given as follows:

$$ Q^{*} = 4\int\limits_{0}^{1} {\int\limits_{0}^{1} {u^{*} dy^{*} dz^{*} } } $$

(28)

The non-dimensional flow rate is expressed as:

$$ Q = 4\int\limits_{0}^{1} {\int\limits_{0}^{1} {udydz} } = 4\int\limits_{0}^{1} {\int\limits_{0}^{1} {(1 - y^{2} )(1 - z^{2} )\left[ {\left( {a_{0} + b_{0} } \right) + (a_{1} + b_{1} )y^{2} } \right]dydz} } = \frac{16}{9}\left( {a_{0} + b_{0} } \right) + \left( {a_{1} + b_{1} } \right)\frac{16}{15} $$

(29)

$$ Q = \frac{{Q^{*} }}{{Q_{0} }},Q_{0} = 4UL_{1} L_{2} $$

(30)

where, Q is the non-dimensional flow rate, Q₀ is the average flow rate.

The results of the present study are validated by comparing with the solution of MHD third grade fluid flow solved by LSM without the effect of aspect ratio. LSM is a very powerful semi-analytical method introduced by Ozisik and later on has been applied for solving different problems of engineering interest; some of which are cited in [15, 16]. Neglecting the aspect ratio, the governing equation describing the fluid flow is obtained by substituting As = 0 in Eq. (18.1) which is given as follows:

$$ \frac{{d^{2} u}}{{dy^{2} }} + 6A\frac{{d^{2} u}}{{dy^{2} }}\left( {\frac{du}{dy}} \right)^{2} - (Ha)^{2} u = N $$

(31)

Boundary conditions are

$$ u( - 1) = u(1) = 0 $$

(32)

For solving Eq. (31), along with boundary conditions given by Eq. (32), by LSM, an approximate solution for the velocity of the following form is chosen:

$$ u = c_{1} (1 - y^{2} ) + c_{2} (1 - y^{4} ) $$

(33)

where, c₁ and c₂ are the constants to be determined. The base functions (1 − y²) and (1 − y⁴) are chosen such that they satisfy the boundary conditions given by Eq. (32). If Eq. (33) is substituted in Eq. (31), a residual R will be generated. The notion of the LSM is to minimize the square of the residuals over the entire domain. Substituting Eq. (33) in Eq. (31) we get the residual R as follows:

$$ R(y) = - 2c_{1} - 12c_{2} y^{2} + 6A( - 2c_{1} - 12c_{2} y^{2} )(4c_{1}^{2} y^{2} + 16c_{2}^{2} y^{6} + 16c_{1} c_{2} y^{6} ) - (Ha)^{2} \left[ {c_{1} \left( {1 - y^{2} } \right) + c_{2} \left( {1 - y^{4} } \right)} \right] $$

(34)

The total residual square over the domain has to be minimized with respect to the unknowns c₁ and c₂ to get the equations as follows:

$$ \int\limits_{ - 1}^{1} {2R(y)\frac{\partial R(y)}{{\partial c_{1} }}} = 0,\int\limits_{ - 1}^{1} {2R(y)\frac{\partial R(y)}{{\partial c_{2} }}} = 0 $$

(35)

Solving Eq. (35) for two unknowns c₁ and c₂ for different values of A, N and Ha velocity of the fluid can be obtained. For example, when A = 0.3, Ha = 3 and N = − 3, the values are c₁ = 0.1799 and c₂ = 0.1183.

4 Results and discussions

Before proceeding further with the discussion of the effects of various parameters on the flow field, the results of the present study have to be validated first. In this regard, it is expected that the results of the present investigation, where the axial velocity u is a function of both y and z, should be compared with the results of the numerical or experimental investigation on the same flow situation. But due to the lack of availability of any result of these types in the literature, error analysis by a comparison between the results of the two methods is not possible and the validation is carried out by an alternative option. For validation, MHD flow of a third grade fluid through a channel neglecting the effect of aspect ratio has been considered. Equation (31) describes the MHD flow of a third grade fluid through a channel, very large in the lateral direction rendering the aspect ratio to be zero. Equation (31) is a highly non-linear ODE for which exact solution is difficult to obtain. LSM has been applied to get the solution for the velocity and the results are compared with that of the present study. Though LSM is an approximate semi-analytical method, it produces accurate results for a wide class of non-linear equations especially for ODEs. Therefore, for validation purpose, the results of the LSM can be used as a reliable source. The results of the present study are compared with the LSM results (without the aspect ratio effect) by substituting the aspect ratio to be zero in Eq. (18.1). Figure 2 shows the comparison of the velocity profiles obtained by using combined HPM and IM from the present study by considering As = 0 and the LSM results. The maximum difference between the results occur at y = 0.7 for both figures 2(a) and figure 2(b); the magnitudes of the differences are 0.01384 and 0.01147. The corresponding relative errors are 17.8% and 14.8%. For figure 2(a), when y < 0.46 and y > 0.85, the difference between the results is less than 0.01 and in between 0.47 < y < 0.44, the difference gradually increases from 0.01 to a maximum value of 0.001384. For figure 2(b), when y < 0.58 and y > 0.79, the difference between the results is less than 0.01 and in between 0.59 < y < 0.78; the magnitude of the difference increases from 0.01 to a maximum value of 0.01184. If higher order terms are considered, instead of truncating the series of velocity after 1^st order terms, then the accuracy will be improved, but the level of complexity will increase a lot. Considering this factor, higher order terms have not been considered and solution up to the 1^st order term only has been presented.

Figure 2

(a) Comparison of the velocity profiles from the present study and the flow of a third grade fluid through channel without the effect of aspect ratio when N = − 1.2, Ha = 2.5 and A = 0.3. (b) N = − 1.2, Ha = 2.5 and A = 0.4.

Now, the physically permissible values of the different parameters are to be fixed before discussion of their effects. In [7], the maximum value of Hartmann number considered is 3, which has also been followed in the present study. The authors of [17] considered the Sisko fluid parameter maximum up to 0.8; the governing equation for third grade fluid bears similarity in form with Sisko fluid for index three which indicates similarity in their properties too. In the present study third grade fluid parameter has been varied in the range of 0.05–0.5. Aspect ratio has been varied in the range of 0–1.

Velocity profiles at z = 0 plane for different aspect ratios have been depicted in figure 3. It is evident from the figure that the velocity decreases with an increase in the aspect ratio. Increase in the aspect ratio, offers more resistance towards the flow due to the influence of the side walls of the channel. For a channel which is very large in the lateral direction, the effects of the side walls are very less. As the aspect ratio increases, the presence of the solid surface offers more flow resistance and reduces the velocity. The central flat portion in the velocity profile is the result of the opposing force of the magnetic field. As the opposing force is directly proportional to the square of the velocity, its magnitude is large near the central part compared to the velocity near the walls. Therefore, near the central core, the velocity is relatively smaller rendering the velocity profile flatter near this region.

Figure 3

Velocity profiles in the z = 0 plane for different aspect ratios when N = − 1.2, A = 0.3 and Ha = 3.

The effects of the Hartmann number Ha on the velocity profiles are pictorially sketched in figure 4(a). It is evident from the figure that Ha significantly affects the velocity. For lower values of Ha velocity profile does not display any flat region, but for higher values of Ha velocity profiles become flatter which has already been explained. Figure 4(b) depicts the influence of non-Newtonian third grade fluid parameter on the velocity. Increase in the third grade fluid parameter A signifies an increase in the effective viscosity which increases the flow resistance for the pressure driven flow. Therefore, increase in A results in a decrease in the velocity.

Figure 4

(a) Velocity profiles at z = 0 plane for different Ha when As = 0.4, A = 0.3 and N = − 1.2. (b) Velocity profiles for different A when As = 0.4, Ha = 3.

Figure 5(a) shows the non-dimensional flow rate variation with As. The flow rate decreases with an increase in the aspect ratio As. As discussed earlier, the velocity decreases with an increase in As which results in a decrease in the flow rate. Variation of the non-dimensional flow rate with A is presented in figure 5(b) which shows a decrease in flow rate with an increase in the third grade fluid parameter A. Increase in A causes reduced velocity resulting in a lower flow rate.

Figure 5

(a) Variation of the flow rate with aspect ratio for N = − 1.2, A = 0.3. (b) Variation of the flow rate with the third grade fluid parameter when As = 0.3.

Figures 6(a) and 6(b) present contour plots of the velocity for different values of Ha. The contour plots clearly display how the velocity is reduced for increase in Ha. For both the figures, the central core velocity, indicated by the red region, is higher compared to the region near the walls, displayed in blue.

Figure 6

(a) Contour plot of velocity when N = − 1.2, Ha = 2, As = 0.5 and A = 0.3. (b) Contour plot of velocity when N = − 1.2, Ha = 3, As = 0.5 and A = 0.3.

5 Conclusions

The present study highlights the effects of the aspect ratio on the velocity for flow of a third grade fluid through a rectangular channel under the influence of magnetic field. The equation governing the flow is highly non-linear, which is difficult to solve even numerically. A combination of HPM and IM has been proposed to get analytical solution for the velocity field and the effects of the aspect ratio, third grade fluid parameter and the magnetic field on the velocity and flow are discussed. Following important conclusions are drawn from the study: A change in aspect ratio from 0.2 to 1 causes a reduction in the central plane velocity almost by 50%, which is quite significant. When Ha = 2, the flow rate decreases by nearly 80% due to increase in As from zero to unity. However, an increase in Ha decreases the rate of flow reduction caused by an increase in As. For Ha = 2, an increase in third grade fluid parameter A from 0.1 to 0.5 results in the flow reduction by nearly 35%. The increase in Ha, causes a decrease in the rate of flow reduction.