MHD natural convection of Cu–Al₂O₃ water hybrid nanofluids in a cavity equally divided into two parts by a vertical flexible partition membrane

Abstract

The aim of the present study is to investigate the effects of a hybrid nanofluid in a square cavity that is divided into two equal parts by a vertical flexible partition in the presence of a magnetic field. A numerical method called the Galerkin finite element method is utilized to solve the governing equations. The effects of different parameters, namely the Rayleigh number (10⁶ ≤ Ra ≤ 10⁸) and the Hartmann number (0.0 ≤ Ha ≤ 200) as well as the effects of nanoparticles concentration (0.0 ≤ φ ≤ 0.02) and magnetic field orientation (0 ≤ γ ≤ π), on the flow and heat transfer fields for the cases of pure fluid, nanofluid and hybrid nanofluid are investigated. The results indicate that the streamline patterns change remarkably and the convective heat transfer augments with increasing values of the Rayleigh number. Additionally, the maximum stress imposed on the flexible partition resulting from the interaction of the partition and pure fluid is more than those caused by the nanofluid and the hybrid nanofluid. Furthermore, the increase in the magnetic field strength decreases the fluid velocity in the cavity, which declines the fluid thermal mixing and heat transfer effects.

Introduction

When it comes to enclosures, natural convection is the most important mean of heat transfer. Enclosures have a variety of applications in engineering such as boilers, energy storage and conservation systems, solar collectors–receivers, nuclear reactor systems, food and metallurgical industries, fire control and chemical, etc. Comprehensive studies have been done in recent years in this field [1,2,3,4,5]. Although, in many industrial applications, natural convection is considered as a beneficial phenomenon, the phenomenon becomes undesirable in some cases. One of the ways to control that is by applying an external magnetic field for magneto hydro dynamic (MHD) flows [6,7,8,9,10,11]. Results obtained by Sathiyamoorthy and Chamkha [7] indicated that the magnetic field with inclined angle affected the flow field and heat transfer rates. Sheikholeslami and Ganji investigated [12] natural convection heat transfer of ferrofluid Fe₃O₄–water nanofluid with a point source external magnetic field. Their results indicated the reduction in heat transfer caused by the magnetic field.

Additionally, the flow inside cavities could be controlled by inserting dividers [13, 14]. By using dividers inside cavities, the flow field, and correspondingly the heat transfer rate, can be controlled. The cavities with partitions can be classified in three groups: (a) partially divided cavities [15,16,17], (b) cavities with inclined partitions [18, 19] and (c) cavities fully divided horizontally or vertically with partition/partitions [20,21,22]. Jamesahar et al. [21] and Mehryan et al. [22] conducted a numerical study on the heat transfer in a divided square cavity using a flexible membrane. Jamesahar et al. [21] reported that the presence of a flexible diagonal partition could enhance the heat transfer, while the deflection of the flexible partition could also affect the heat and flow patterns. It was reported by Mehryan et al. [23] that there was an optimum value of magnetic inclination angle to maximize the heat transfer in the partitioned cavity. Additionally, they [23] reported that the dimensionless average temperature could be increased by applying the magnetic field when the Rayleigh number was in a moderate range (Ra = 10⁶–10⁷), especially under a magnetic field (Hartmann number Ha ≥ 50). Xu et al. [24] studied the transient natural convection inside a differentially heated cavity, which was filled with water and separated by a solid partition without any deflection. Three categorized natural convection main stages were found, including an initial stage, a transitional stage and a steady-state stage.

Fully divided cavities with an impermeable divider have many interesting applications. For instance, thermal conductive partitions are used to divide a box containing electronic units, and a conductive metallic cover can be installed to separate a sensitive electronic equipment from the surrounding. Chemical species, in many cases, should be segregated from each other in a chemical reactor, but heat can be transferred between the species through partitions. These practical applications of fully divided cavities have motivated researchers to investigate the effect of dividers and partitions on convective heat and mass transfer phenomena in cavity enclosures. An experimental study has been done by Nishimura et al. [25] considering the effects of N multiple vertical partitions on natural convection in a rectangular enclosure. It was found that the Nusselt number decreased with the increase in the partition numbers.

The natural convection phenomena in a partitioned cavity were investigated by Oztop et al. [26]. On each sub-cavity, combinations of water and air were considered. Additionally, the effects of the presence of a vertical partition on the flow and heat inside in an enclosure were investigated by Kahveci [27], with the partition heated by uniform heat flux. It was shown that the vertical partition had a considerable effect on natural convection when the two parts of the enclosure were filled with the same fluid.

Dispersion of nanometer-sized particles in base fluids is now known as nanofluids, which are now widely used in a variety of thermal systems to enhance the heat transfer characteristics [28,29,30,31,32,33]. Even for a small volume fraction of nanoparticles, nanofluids have shown an extreme increase in their thermal conductivities. Fluids such as water, ethylene glycol, bio-fluids, polymer solutions, oils and other lubricants are usually considered as base fluids. Different types of nanoparticles including metallic particles (Cu, Al, Fe, Au, and Ag) and non-metallic particles (Al₂O₃, CuO, Fe₃O₄, TiO₂, and SiC) have been utilized in experimental and numerical studies. The non-metallic particles such as Al₂O₃ are known for their excellent stability and chemical inertness. Unfortunately, non-metallic particles show lower thermal conductivity compared to the metallic nanoparticles. Kahveci [34] investigated five types of nanoparticles inside a differentially heated, tilted enclosure, and showed that the average heat transfer rate of metallic nanoparticles was higher than those of non-metallic nanoparticles. On the other hand, metallic nanoparticles, for instance, copper (Cu) or aluminum (Al) have much higher thermal conductivities, but their poor stability and tendency to chemical reactions prevented researchers to utilize them widely.

Most of the earlier investigations have addressed the effect of using a single type of metallic or non-metallic nanoparticles on the heat transfer performance of nanofluids. However, combination of non-metallic nanoparticles with a small amount of metal nanoparticles can enhance the thermal properties of the base fluid significantly. Jena et al. [35] have successfully synthesized a homogeneous mixture of well-dispersed CuO and Al₂O₃ composite briquette by using hydrogen reduction technique. Suresh et al. [36] have investigated the thermos-physical properties of Alumina–Copper hybrid nanofluids. The outcomes demonstrated that the presence of hybrid nanoparticles significantly enhanced the thermal conductivity and dynamic viscosity of hybrid nanofluids. In an experimental study by Suresh et al. [37], it was reported that the Nusselt number can be increased up to 13.56% by using Al₂O₃–Cu hybrid nanofluids. Mahian et al. [38, 39] performed an excellent review on modeling and simulation of nanofluid flows. More studies on the hybrid nanofluid can be observed in [40,41,42,43,44,45].

The membranes are in important parts of fuel cells, filters and separators. Therefore, any approach capable of modeling or analysis of the membranes is of great importance. As mentioned, in very recent studies, Jamesahar et al. [21] and Mehryan et al. [23] have studied the heat transfer of a pure fluid in a square cavity divided into two sub-cavities by a flexible partition. Following [21] and [23], the present study aims to analyze the effects of Cu–Al₂O₃/water hybrid nanofluid and magnetic field on the natural convection inside a fully divided cavity. The motivation of the present study is to answer the following questions:

• 1. What is the effect of magnetic field inclination on the heat and flow patterns of hybrid nanofluids?

• 2. Does the presence of nanoparticles enhances the heat transfer in the divided cavity? Is there any significant difference between heat transfer enhancement of Al₂O₃ nanoparticles and Cu–Al₂O₃ hybrid nanoparticles?

• 3. How the presence of nanoparticles could change the shape of the flexible partition and the heat transfer rate?

• 4. Which types of nanoparticles (Al₂O₃ or Cu–Al₂O₃) are better for heat transfer enhancement in the presence of a magnetic field?

Description of the work

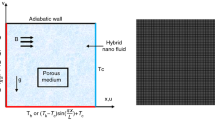
A view of the considered problem geometry is shown schematically in Fig. 1 which is utilized to derive the governing equations and boundary conditions. The dimensions of the enclosure in x^*, y^* coordinates are so much higher than that in z^* one. Accordingly, a two-dimensional mathematical domain is considered. It is defined that the left surface with the temperature of $T_{\text{h}}^{*}$ is hotter than the right surface with the temperature of $T_{\text{c}}^{*}$ ($T_{\text{h}}^{*}$ > $T_{\text{c}}^{*}$). The lower and upper bounds of the enclosure are thermally impervious. Moreover, it is assumed that all the solid boundaries are made of electrically non-conducting material. A vertical thin flexible partition breaks up the square cavity into two equal parts. $t_{\text{p}}^{*}$ represents the thickness of the flexible partition. The flexible partition material is isotropic and nonmagnetic. Both parts are glutted with the Newtonian electromagnetic Cu–Al₂O₃/water hybrid nanofluid or Al₂O₃/water nanofluid. A hybrid nanofluid contains a base fluid and two or more types of nanoparticles. In this study, solid particles of the hybrid nanofluid are the nanoparticles of Al₂O₃ and Cu. The thermophysical properties of the forming components of hybrid/regular nanofluid are represented in Table 1. Both the types of nanoparticles are always suspended and stable. This means that the nanoparticles do not agglomerate and become collective. There is a thermal and dynamic equilibrium between the suspended nanocomposite particles and the host fluid. The fluid flow is laminar and steady state. The buoyancy effects are modeled using Boussinesq approximation. Since the flexible partition is thin and with low thermal resistance, the gradient of temperature in it is zero. Additionally, all the solid surfaces are impervious to the mass flow. The flow domain is exposed a tilted magnetic field with the amplitude and angle of B₀ and γ, respectively. It is supposed that the convection and diffusion values of the energy balance are so much higher than viscous dissipation and Joule heating. The densities of the hybrid nanofluid and the flexible partition are the same. The partition behaves as a hyper-elastic material reacting nonlinearly against applied loads.

Fig. 1

The schematic view of the physical model and boundary conditions

Table 1 The thermophysical properties of the hybrid nanofluid components [46]

The Lorentz force is one that is applied to the flow domain due to the existence of the magnetic field vector B with the density of electrical current J

$${\mathbf{LF}} = {\mathbf{J}} \times {\mathbf{B}}$$

(1a)

where J is defined by Ohm’s law:

$${\mathbf{J}} = \chi_{\text{hnf}} ( - \nabla \phi + {\mathbf{u}}^{*} \times {\mathbf{B}})$$

(1b)

where $\upchi_{\text{hnf}}$ represents the electrical conductivity of the fluid. ${\mathbf{u}}^{*} \left( {u^{*} ,v^{*} } \right)$ is the velocity vector of the fluid in the cavity. The bounds of the enclosure are electrically impervious, so, according to the Maxwell theory, $\nabla \phi = 0$. Therefore, we have

$${\mathbf{LF}} = \chi_{\text{hnf}} ({\mathbf{u}}^{*} \times {\mathbf{B}}) \times {\mathbf{B}}$$

(1c)

Description of the reciprocal effects of the fluid and deformable solid material is performed by the known technique of the Arbitrary Lagrangian–Eulerian (ALE). The fluid flow within the enclosure is portrayed by the incompressible mass conservation and the linear momentum equations for the pressure and velocity fields [21, 23, 47]:

$$\nabla^{*} \cdot {\mathbf{u}}^{*} = 0$$

(2)

$$\frac{{\partial {\mathbf{u}}^{*} }}{\partial t} + \left( {{\mathbf{u}}^{*} - {\mathbf{w}}^{*} } \right) \cdot \nabla^{*} {\mathbf{u}}^{*} = - \frac{1}{{\rho_{\text{hnf}} }}\nabla^{*} P^{*} + \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}\nabla^{*2} {\mathbf{u}}^{*} + \frac{{\chi_{\text{hnf}} }}{{\rho_{\text{hnf}} }}({\mathbf{u}}^{*} \times {\mathbf{B}}) \times {\mathbf{B}} + \beta_{\text{hnf}} {\mathbf{g}}\left( {T^{*} - T_{\text{c}}^{*} } \right)$$

(3)

$$\frac{{\partial T^{*} }}{\partial t} + \left( {{\mathbf{u}}^{*} - {\mathbf{w}}^{*} } \right).\nabla^{*} T^{*} = \alpha_{\text{hnf}} \nabla^{*2} T^{*}$$

(4)

The structural deformations of the flexible partition can be achieved by the following nonlinear geometric and elastic formulation:

$$\rho_{\text{s}} \frac{{{\text{d}}^{2} {\mathbf{d}}_{\text{s}}^{*} }}{{{\text{d}}t^{2} }} - \nabla^{*} {\varvec{\upsigma}}^{*} = {\mathbf{F}}_{\text{v}}^{*}$$

(5)

${\mathbf{F}}_{\text{v}}^{*}$ of the above-written equation is the applied volume forces on the deformable partition, σ^* is the solid stress tensor, d ^*_s the displacement vector of moving coordinate system so that dd ^*_s /dt = w^* and $\rho_{\text{s}}$ is the density of the partition.

In this study, the stress tensor σ^* is computed using a Neo-Hookean model to characterize the stress–strain nonlinear behavior of a hyper-elastic material with large deformations. The hyper-elastic theory is used more for modeling of rubbery behavior of a polymeric material and polymeric foams that can have large deformations. The model can be written as follows:

$${\varvec{\upsigma}}^{*} = J^{ - 1} FSF^{\text{T}}$$

(6)

where

$$F = \left( {I + \nabla^{*} {\mathbf{d}}_{\text{s}}^{*} } \right) , { }J = { \det }\left( F \right)\,{\text{and}}\,S = \, \partial W_{\text{s}} /\partial \varepsilon$$

(7)

are the deformation gradient, determinant of the matrix F and the partial differential of the density function of strain energy, respectively. Also, the density function of the strain energy W_s and strain ε is defined through the equations below:

$$W_{\text{s}} = \frac{1}{2}\mu_{\text{l}} \left( {J^{ - 1} I_{ 1} - 3} \right) - \mu_{\text{l}} \ln \left( J \right) + \frac{1}{2}\lambda \left( {\ln \left( J \right)} \right)^{2}$$

(8)

$$\varepsilon = \frac{1}{2}\left( {\nabla^{*} {\mathbf{d}}_{\text{s}}^{*} + \nabla^{*} {\mathbf{d}}_{s}^{{*{\text{T}}}} + \nabla^{*} {\mathbf{d}}_{\text{s}}^{{*{\text{T}}}} \nabla^{*} {\mathbf{d}}_{\text{s}}^{*} } \right)$$

(9)

where

$$\lambda = E\nu /\left( {\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)} \right) , { }\mu_{\text{l}} = E/\left( {2\left( {1 + \nu } \right)} \right)$$

(10)

λ and $\mu_{\text{l}}$ of the above equations, known as Lame’s first and second constants, respectively. I₁ is called the first constant of the deformation tensor.

All the bounds of the enclosure are motionless ($u^{*} = v^{*} = 0$). The lower and topper bounds of the both sub-cavities are thermally insulated (${{\partial T^{*} } \mathord{\left/ {\vphantom {{\partial T^{*} } {\partial y^{*} }}} \right. \kern-0pt} {\partial y^{*} }} = 0$). The right hand wall is at the low temperature of $T^{*} = T_{\text{c}}^{*}$, while the temperature of the opposite wall is higher (i.e. $T^{*} = T_{\text{h}}^{*}$).

Along the fluid–solid interface, continuity of the dynamic motion and kinematic forces are the boundary conditions utilized to model the fluid and deformable divider interaction. These conditions can be represented as:

$$\frac{{\partial {\mathbf{d}}_{\text{s}}^{*} }}{\partial t} = {\mathbf{u}}^{*} \quad {\text{and}}\quad {\varvec{\upsigma}}^{*} .n = - P^{*} + \mu_{\text{f}} {\nabla }^{*} {\mathbf{u}}^{*}$$

(11)

Applying the conservation of energy on the flexible divider along with the previous assumptions results in the equation below:

$$\frac{\partial T}{\partial n}^{* + } = \frac{\partial T}{\partial n}^{* - } {\text{ and }}T^{* + } = T^{* - }$$

(12)

In this equation, the plus and minus marks denote the right and left sides of the deformable divider, respectively. Also, the boundary condition for both eyelets can be represented as follows:

$$\left[ { - P^{*} + \mu_{\text{hnf}} \nabla {\mathbf{u}}^{*} } \right].n = 0$$

(13)

To provide with dimensions, non-dimensional parameters are introduced below;

$$\begin{aligned} {\mathbf{d}}_{\text{s}} & = \frac{{{\mathbf{d}}_{s}^{*} }}{L}, \, {\varvec{\upsigma}} = \frac{{{\varvec{\upsigma}}^{*} }}{E}, \, \tau = \frac{{t\alpha_{\text{f}} }}{{L^{2} }}, \, \left( {x,y} \right) = \frac{{\left( {x^{*} ,y^{*} } \right)}}{L} , { }{\mathbf{u}} = \frac{{{\mathbf{u}}^{*} L}}{{\alpha_{\text{f}} }} , { }{\mathbf{w}} = \frac{{{\mathbf{w}}^{*} L}}{{\alpha_{\text{f}} }} \\ P & = \frac{{L^{2} }}{{\rho_{\text{f}} \alpha_{\text{f}}^{2} }}P^{*} , { }T = \frac{{T^{*} - T_{\text{c}}^{*} }}{{T_{\text{h}}^{*} - T_{\text{c}}^{*} }}, \, \nabla = \frac{{\nabla^{*} }}{{{1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0pt} L}}}, \, \nabla^{2} = \frac{{\nabla^{*2} }}{{{1 \mathord{\left/ {\vphantom {1 {L^{2} }}} \right. \kern-0pt} {L^{2} }}}}, \, t_{\text{p}} = \frac{{t_{\text{p}}^{*} }}{L} \\ \end{aligned}$$

(14)

To dimensionalize the equations, the above parameters are substituted for the Eqs. (1)–(4). Therefore, we then have,

$$\frac{1}{{\rho_{\text{R}} }}\frac{{{\text{d}}^{2} {\mathbf{d}}_{\text{s}} }}{{{\text{d}}\tau^{2} }} - E_{\uptau} \nabla {\varvec{\upsigma}} = E_{\uptau} {\mathbf{F}}_{\text{v}}$$

(15)

$$\nabla .{\mathbf{u}}\text{ = 0}$$

(16)

$$\begin{aligned} \frac{{\partial {\mathbf{u}}}}{\partial \tau } + \left( {{\mathbf{u}} - {\mathbf{w}}} \right) \cdot \nabla {\mathbf{u}} & = - \frac{{\rho_{\text{f}} }}{{\rho_{\text{hnf}} }}\nabla P + \left( {\frac{{\rho_{\text{f}} }}{{\rho_{\text{hnf}} }}} \right)\left( {\frac{{\mu_{\text{hnf}} }}{{\mu_{\text{f}} }}} \right)Pr\nabla^{2} {\mathbf{u}} + \frac{{\left( {\rho \beta } \right)_{\text{hnf}} }}{{\rho_{\text{hnf}} \beta_{\text{f}} }}PrRaT \\ & \quad + \left( {\frac{{\rho_{\text{f}} }}{{\rho_{\text{hnf}} }}} \right)\left( {\frac{{\chi_{\text{hnf}} }}{{\chi_{\text{f}} }}} \right)Pr({\mathbf{u}} \times {\mathbf{Ha}}) \times {\mathbf{Ha}} \\ \end{aligned}$$

(17)

$$\frac{\partial T}{\partial \tau } + \left( {{\mathbf{u}} - {\mathbf{w}}} \right).\nabla T = \frac{{\alpha_{\text{hnf}} }}{{\alpha_{\text{f}} }}\nabla^{2} T$$

(18)

In Eq. (15), $\rho_{\text{R}}$ is the density ratio, E_τ is the dimensionless elasticity modulus and F_v is dimensionless volume force vector.

$$\rho_{\text{R}} = \frac{{\rho_{\text{hnf}} }}{{\rho_{\text{s}} }}, \, E_{\uptau} = \frac{{EL^{2} }}{{\rho_{\text{hnf}} \alpha_{\text{f}}^{2} }}, \, {\mathbf{F}}_{\text{v}} = \frac{{\left( {\rho_{\text{hnf}} - \rho_{\text{s}} } \right)L{\mathbf{g}}}}{E}$$

(19)

In Eq. (17), the dimensionless numbers are defined as the following:

$$Pr\text{ = }\frac{{\upsilon_{\text{f}} }}{{\alpha_{\text{f}} }}\text{,} \, Ra = \frac{{\text{g}\beta \left( {T_{\text{h}} - T_{\text{c}} } \right)L^{3} }}{{\upsilon_{\text{f}} \alpha_{\text{f}} }}, \, {\mathbf{Ha}} = L{\mathbf{B}}\sqrt {\frac{{\chi_{\text{f}} }}{{\mu_{\text{f}} }}}$$

(20)

The non-dimensional parameter of Hartmann number is a vector with two components along the x- (Ha sin (γ)) and the y-axes (Ha cos (γ)). The volume force expression rising from the magnetic field, known as Lorentz force, is rewritten as follows:

In the x-direction:

$$\left( {\frac{{\rho_{\text{f}} }}{{\rho_{\text{hnf}} }}} \right)\left( {\frac{{\chi_{\text{hnf}} }}{{\chi_{\text{f}} }}} \right)PrHa^{2} (v\text{ sin}\gamma \cos \gamma - u \, \text{sin}^{2} \gamma )$$

(21)

In the y-direction:

$$\left( {\frac{{\rho_{\text{f}} }}{{\rho_{\text{hnf}} }}} \right)\left( {\frac{{\chi_{\text{hnf}} }}{{\chi_{\text{f}} }}} \right)PrHa^{2} (u\text{ sin}\gamma \cos \gamma - v{ \cos }^{2} \gamma )$$

(22)

where

$$\rho_{\text{hnf}} = \rho_{\text{f}} \left( {1 - \varphi_{\text{hnp}} } \right) + \rho_{{{\text{Al}}_{2} {\text{O}}_{3} }} \varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \rho_{\text{Cu}} \varphi_{\text{Cu}}$$

(23)

$$(\rho \beta )_{\text{hnf}} = (1 - \varphi_{\text{hnp}} )(\rho \beta )_{\text{f}} + \varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }} (\rho \beta )_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \varphi_{\text{Cu}} (\rho \beta )_{\text{Cu}}$$

(24)

$$\chi_{\text{hnf}} = \chi_{\text{f}} \left( {1 + \frac{{3\left( {\frac{{\chi_{\text{hnp}} }}{{\chi_{\text{f}} }} - 1} \right)\varphi_{\text{hnp}} }}{{\left( {\frac{{\chi_{\text{hnp}} }}{{\chi_{\text{f}} }} + 2} \right) - \left( {\frac{{\chi_{\text{hnp}} }}{{\chi_{\text{f}} }} - 1} \right)\varphi_{\text{hnp}} }}} \right) \,$$

(25)

$$\begin{aligned} \varphi_{\text{hnp}} & = \varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \varphi_{\text{Cu}} \\ \sigma_{\text{hnp}} \varphi_{\text{hnp}} & = \sigma_{{{\text{Al}}_{2} {\text{O}}_{3} }} \varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \sigma_{\text{Cu}} \varphi_{\text{Cu}} \\ \end{aligned}$$

(26)

In all the above-mentioned relations, φ represents the nanoparticles concentration. here ρ_s = ρ_hnf, therefore the volume force of F_v is zero. Noticing the thermophysical properties represented in Table 1, the electrical conductivity orders of Al₂O₃ and Cu nanoparticles are O (10⁻¹⁰) and O (10⁷), respectively. Hence, compared to the nanoparticles of Cu, the electrical conductivity of Al₂O₃ nanoparticles is very close to zero. Therefore, the electrical conductivity of the hybrid nanoparticles can be rewritten as follows:

$$\chi_{\text{hnp}} = \left( {\frac{{\varphi_{\text{Cu}} }}{{\varphi_{\text{hnp}} }}} \right)\chi_{\text{Cu}}$$

(27)

The heat capacity of the hybrid nanofluid is calculated from the following equation:

$$\left( {\rho c_{\text{p}} } \right)_{\text{hnf}} = \left( {1 - \varphi_{\text{hnp}} } \right)\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }} \left( {\rho c_{\text{p}} } \right)_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \varphi_{\text{Cu}} \left( {\rho c_{\text{p}} } \right)_{\text{Cu}}$$

(28)

In addition, by employing the classical Maxwell [48] and Bruggeman [49] models, we then have:

The classical Maxwell model Maxwell [48]:

$$\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }} = \frac{{k_{\text{hnp}} + 2k_{\text{f}} - 2\varphi_{\text{hnp}} \left( {k_{\text{f}} - k_{\text{hnp}} } \right)}}{{k_{\text{hnp}} + 2k_{\text{f}} + \varphi_{\text{hnp}} \left( {k_{\text{f}} - k_{\text{hnp}} } \right)}}$$

(29)

The classical Bruggeman model [49]:

$$k_{\text{hnf}} = \frac{1}{4}\left[ {(3\varphi_{\text{hnp}} - 1)k_{\text{hnp}} + (2 - 3\varphi_{\text{hnp}} )k_{\text{f}} } \right] + \frac{{k_{\text{f}} }}{4}\sqrt \varXi$$

(30)

$$\varXi = \left[ {(3\varphi_{\text{hnp}} - 1)^{2} \left( {\frac{{k_{\text{hnp}} }}{{k_{\text{f}} }}} \right) + (2 - 3\varphi_{\text{hnp}} )^{2} + 2\left( {2 + 9\varphi_{\text{hnp}} - 9\varphi_{\text{hnp}}^{2} } \right)\left( {\frac{{k_{\text{hnp}} }}{{k_{\text{f}} }}} \right)} \right]$$

(31)

where in both of the above relations k_hnp is defined as:

$$k_{\text{hnp}} \varphi_{\text{hnp}} = k_{{{\text{Al}}_{2} {\text{O}}_{3} }} \varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + k_{\text{Cu}} \varphi_{\text{Cu}}$$

(32)

In order to check the validity of these relations for Cu–Al₂O₃/water hybrid nanofluid, the values of the thermal conductivity obtained from both of the above relations for the hybrid nanofluid are calculated for different volume concentrations. Then, these values have been evaluated using the experimental data as shown in Fig. 2a. This comparison clearly depicts that the Maxwell and Bruggeman relations cannot estimate the real values of the thermal conductivity of the Cu-Al₂O₃/water hybrid nanofluid. Therefore, the remaining calculations are done based on the experimental thermal conductivity. Also, a comparison is done between the theoretical models and the experimental results to study the potential of the classical models to estimate the viscosity of the hybrid nanofluid. Three theoretical models are as follows:

Fig. 2

a Thermal conductivity and b dynamic viscosity obtained by the classical models

Einstein model [50]:

$$\frac{{\mu_{\text{hnf}} }}{{\mu_{\text{f}} }} = 1 + k_{{\upmu1}} \varphi_{\text{hnp}}$$

(33)

Brinkman model [51]:

$$\frac{{\mu_{\text{hnf}} }}{{\mu_{\text{f}} }} = \frac{1}{{\left( {1 - \varphi_{\text{hnp}} } \right)^{2.5} }}$$

(34)

Batchelor model [52]:

$$\frac{{\mu_{\text{hnf}} }}{{\mu_{\text{f}} }} = 1 + k_{{\upmu1}} \varphi_{\text{hnp}} + k_{{\upmu2}} \varphi_{\text{hnp}}^{2}$$

(35)

As this comparison shows in Fig. 2b, the classical models significantly underpredict the viscosity. For this reason, the experimental results are employed to continue the computations. The experimental thermal conductivity and dynamic viscosity of Al₂O₃/water nanofluid and Cu–Al₂O₃/water hybrid nanofluid are given in Table 2. Table 2 also shows the volume fractions of both the nanoparticles Cu and Al₂O₃ suspended in the basefluid.

Table 2 The thermal conductivity and dynamic viscosity obtained by experiment [36]

The dimensionless forms of the boundary conditions are:

$${\text{For\;all\;the\;out\;bounds}}\;u = v = 0$$

$${\text{For\;the\;adiabatic\;walls\;at\;the\;top\;and\;bottom}}\;\frac{\partial T}{\partial y} = 0$$

(36a)

$${\text{For\;the\;left\;bound}}\;T = 1$$

$${\text{For\;the\;right\;bound}}\;T = 0$$

(36b)

$${\text{For\;the\;partition}}\;\frac{\partial T}{\partial n}^{ + } = \frac{\partial T}{\partial n}^{ - } \;{\text{and}}\;T^{ + } = T^{ - }$$

(36c)

$${\text{On}}\,{\text{the}}\,{\text{solid{-}fluid\;interface:}}\;\frac{{\partial {\mathbf{d}}_{\text{s}} }}{\partial \tau } = {\mathbf{u}}\;{\text{and}}\;E_{\uptau} {\varvec{\upsigma}}.n = - P + \left( {\frac{{\mu_{\text{hnf}} }}{{\mu_{\text{f}} }}} \right)Pr\nabla {\mathbf{u}}$$

(37)

For the eyelets:

$$\left[ { - P + \left( {\frac{{\mu_{\text{hnf}} }}{{\mu_{\text{f}} }}} \right)Pr\nabla {\mathbf{u}}} \right].n = 0$$

(38)

The local heat transfer rate is defined by the following relation:

$$Nu_{\text{local}} = - \frac{{k_{\text{hnf}} }}{{k_{\text{f}} }}\frac{\partial T}{\partial x}$$

(39)

Integrating the above relation leads to the mean Nusselt number:

$$Nu_{\text{avg}} = \int\limits_{0}^{1} {Nu_{\text{local}} } {\text{d}}y$$

(40)

Another important parameter is the mean temperature of the whole domain:

$$T_{\text{avg}} = \frac{{\int_{A} {T_{\text{local}} } {\text{d}}A}}{{\int_{A} {{\text{d}}A} }}$$

(41)

Solution procedure, grid evaluation and verification

Since the system of the governing Eqs. (15)–(18) as well as the boundary conditions (36)–(38) are coupled and nonlinear, it is necessary to use a numerical method to solve them. To do this, the numerical Galerkin finite element approach is applied to do the weak form of the equations in the deformable grid system of ALE. The details of the Galerkin finite element approach have been explained in [44]. Fluid and solid are two regions of the computational domain. Both the regions are discretized to small structural elements. Before starting calculations, to evaluate the solution sensitivity to the element numbers, the grid independence test is done. The gird used is non-uniform structural quadrilateral grid. This test is performed for the case Ra = 10⁸, Ha = 0, φ_hnp = 0 and E_τ = 10¹⁴. The results of the examination are presented in Fig. 3 and Table 3. The figure and table are made based on Nu_local and ψ_max, respectively. ψ is the stream function. Figure 3 shows that the variations of Nu_local are so slight when the number of elements is more than 50 × 50. However, as it is shown in Table 3, the relative error is 15.40% for this grid. So, it is necessary to evaluate the grids with the more number of elements. The elements rising process continues until the relative error becomes < 1% (exactly 0.58%) in the grid 130 × 130. Therefore, the grid 130 × 130 is considered very appropriate and is chosen.

Fig. 3

Grid independence test in Ra = 10⁸, φ_hnp = 0 and Ha = 0

Table 3 The grid independence test based on the maximum values of streamlines

In the current investigation, several comparisons are performed to confirm the correctness and precision of the used numerical approach. The first validation consists of the case investigated in [34]. This comparison is shown in Fig. 4. The very high accordance between the results published by Kahveci [34] and those obtained by the present study vouches the correctness and precision of the numerical approach.

Fig. 4

Variations of Nu_avg according to the nanoparticles concentration φ at the various values of Ra resulted from [34] and the present study

In the second validation (shown in Fig. 5), the curvature of the lower bound in the lid-driven cavity modeled by the present study and Küttler and Wall [53] are compared. The deformation curves simulated in this study and literature [53] are in a good agreement. Therefore, we can claim that the numerical procedure used is absolutely true.

Fig. 5

The deformation curves of the deformable lower bound of the lid-driven enclosure examined by Küttler and Wall [53] and the present study at t = 7.5 s

The third validation is presented in Fig. 6 and shows the isotherms contours simulated in the current investigation and Sathiyamoorthy and Chamkha [7]. The good agreement between the outcomes of this investigation and those of Sathiyamoorthy and Chamkha [7] states that the employed solution method can correctly simulate a cavity under an external volume force.

Fig. 6

The isotherms of this study (solid lines) and those obtained by Sathiyamoorthy and Chamkha [7] (points) for the case of a simple cavity when Ha = 10, Ra = 10⁵, Pr = 0.054 and γ = 0

As shown in Fig. 7, there exists an excellent compatibility for the numerical results rising from the current survey, experimental data of literature [25] and Churchill’s equation [54]. Therefore, the used code is trusty. N is the number of vertical partitions dividing the enclosure. AR is the ratio of the height to width of the enclosure.

Fig. 7

The comparison of the results obtained by the present study with experimental data [25] and Churchill’s relation [54] at AR=4 and Pr = 6

In the last validation, the precision and correctness of our data have been measured with those of Xu et al. [24]. These authors have studied the transient natural convection in a partitioned cavity subject to temperature difference at the side walls. Considering a very rigid partition and assuming zero fraction of nanoparticles, the results of the present study can be compared with the results reported in [24]. Figure 8 depicts a comparison between the results of the present study and [24] for the transient non-dimensional temperature profile. The non-dimensional temperature profile of Fig. 8 corresponds to a specified point with the coordinate of (0.0083, 0.375) which is located next to the partition. It is worth noticing that Xu et al. [24] have used τ = tαRa^1/2/L² as the non-dimensional time variable.

Fig. 8

Comparison of the dimensionless temperature reported by Xu et al. [24] and this study at the certain point (0.0083, 0.375)

The definition of the dimensionless time in the present investigation and Xu et al. [24] is different. The dimensionless time and Rayleigh number are defined as $\tau = {{t\alpha_{\text{f}} Ra^{2} } \mathord{\left/ {\vphantom {{t\alpha_{\text{f}} Ra^{2} } {L^{2} }}} \right. \kern-0pt} {L^{2} }}$ and $Ra = {{g\beta \left( {T_{\text{h}}^{*} - T_{\text{c}}^{*} } \right)L^{3} } \mathord{\left/ {\vphantom {{g\beta \left( {T_{\text{h}}^{*} - T_{\text{c}}^{*} } \right)L^{3} } {\upsilon_{\text{f}} \alpha_{\text{f}} }}} \right. \kern-0pt} {\upsilon_{\text{f}} \alpha_{\text{f}} }}$ in the study of Xu et al. [24]. As can be seen from Fig. 8, there is an excellent agreement between the outcomes of this work and those reported in [24]. This validation verifies the sufficiency of the present formulation and solution to simulate the transient natural convection in the fluid domain and the partition.

Results and discussion

This section deals with the results acquired from the problem simulation. Here, the impacts of the dimensionless parameters like the Rayleigh number (10⁶ ≤ Ra ≤ 10⁸), nanoparticles concentration (0.0 ≤ φ ≤ 0.02), Hartmann number (0.0 ≤ Ha ≤ 200) and the angle of magnetic field vector (0 ≤ γ ≤ π) on the flow and temperature fields are investigated. Additionally, the effects of these parameters on the stresses of the flexible partition are studied. The values of E_τ = 10¹⁴ and Pr = 6.2 are kept constant. As previously mentioned, the densities of the hybrid nanofluid and the flexible partition are the same. Therefore, ρ_R and F_v have the value of 1 and 0, respectively. The angles rang of the magnetic field vector has been selected from 0 to π because the Lorentz force is a periodic one with the period of π.

Figure 9 depicts the streamlines for different values of nanoparticles concentration at low Rayleigh number 10⁶ and high Rayleigh number 10⁸. Here, Ha is 50 and γ is 2π/3. Solid and dashed lines have been defined for the pure fluid and nanofluid, respectively. For both low and high Rayleigh numbers 10⁶ and 10⁸, the results illustrate that the presence of the Al₂O₃ nanoparticles enhances the strength of fluid flow while the simultaneous presence of Cu and Al₂O₃ nanoparticles reduces the flow strength. Moreover, it is observed that the governing streamlines patterns do not change by the presence of Cu–Al₂O₃ and Al₂O₃ nanoparticles; however, the nanoparticles can change the initial location of the streamlines.

Fig. 9

The streamlines contours of a Cu-Al₂O₃/water hybrid nanofluid (dashed line) and b Al₂O₃/water nanofluid (dashed line) for the various values of φ when IRa = 10⁶ and IIRa = 10⁸ for the fixed values of γ = 2π/3 and Ha = 50

Figure 10 illustrates the corresponding isotherms contours of the streamlines shown in Fig. 9 for both nanofluid and hybrid nanofluid. As Fig. 10(I) and (II)-(a) show, adding Al₂O₃ nanoparticles to the host fluid does not affect the temperature field. Dispersing the nanoparticles of Cu–Al₂O₃ changes the location of the isotherms when Ra = 10⁶ and φ_hnf = 0.01 and 0.02.

Fig. 10

The isotherms contours of a Cu-Al₂O₃/water hybrid nanofluid (dashed lines) and b Al₂O₃/water nanofluid (dashed lines) for the various values of φ when IRa = 10⁶ and IIRa = 10⁸ for the fixed values of γ = 2π/3 and Ha = 50

The impacts of Rayleigh and Hartmann numbers on the stream patterns are displayed in Fig. 11 for the picked values of γ = π/6 and φ_nf = φ_hnf = 0.02. As it is observed, increasing Ra significantly changes the stream patterns. The streamlines are horizontally stretched inside the cold sub-cavity with an increase in Ra. In addition, an increase in fluid flow strength due to the increase in Ra augments the flexible partition displacement. In some cases, the streamlines continue to stretch with increasing Ra until the vortices inside the cold sub-cavity break up into two vortices.

Fig. 11

The streamline contours of the hybrid nanofluid (dashed lines) and the nanofluid with Al₂O₃ nanoparticles (solid lines) for various values of Ra when aHa = 0, bHa = 50 and cHa = 200 for γ = π/6 and φ_hnf = $\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ = 2%

The strength of the vortices created in both the sub-cavities decreases with increasing Ha. The Lorentz force coming from the magnetic field is a drag force acting against the fluid movement. In fact, the magnetic field behaves as an opposite factor to the buoyancy force. Thus, it is justified that the fluid flow strength declines with an increase in Ha. Furthermore, it can be seen that the magnetic field has no effect on the flexible partition deformation at the steady state. In the cases with two or three vortices, an increase in the Hartmann number causes the vortices to approach to each other so that a unique vortex is finally formed. The center of the vortices in the left and right sub-enclosures swing toward down and up, respectively. The results state that in the similar conditions, the fluid flow strength for the single nanofluid (Al₂O₃/water nanofluid) is more than that of the hybrid nanofluid. Apparently, the reduction in the hybrid nanofluid flow strength is due to the intense increase in the hybrid nanofluid viscosity as a result of the simultaneous presence of Cu and Al₂O₃ nanoparticles.

Figure 12 shows the isotherms contours relating to the streamlines shown in Fig. 11. These results illustrate that the dominant mechanism of heat transfer varies with the change of Rayleigh number and Hartmann number. The isotherms incline to possess a stratification pattern as Ra augments. In fact, these stratification patterns are formed as a result of the increase in the fluid flow strength. The patterns demonstrate the thermal mixing of fluid. On the other hand, the lines of isotherms contours tend to be parallel to the vertical bounds when Ha increases. In other words, as the magnetic field strength augments, the conduction and advection contributions at heat transfer process increases and decreases, respectively. The isotherms of Ha = 200 and Ra = 10⁶ clearly illustrate that the conduction mode is dominant.

Fig. 12

The isotherms contours of the hybrid nanofluid (blue lines) and the nanofluid with Al₂O₃ nanoparticles (red lines) for the various values of Ra when aHa = 0, bHa = 50 and cHa = 200 for γ = π/6 and φ_hnf = $\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ = 2%. (Color figure online)

Figure 13 depicts the effects of the parameters of magnetic field on the streamlines of the hybrid and single nanofluids. The values of Ra and φ are 10⁷ and 0.02, respectively. Obviously, the strength of circulation augments as the angle of the magnetic field inclination, γ, grows by π/2. After that, the mobility of the fluid flow continuously begins to diminish when γ varies from π/2 to π. In fact, the vertical component of Lorentz force, which acts as a resistant one against buoyancy term, is reduced as γ increases from π/2 to π. This component of Lorentz force is exactly zero when γ = π/2. Therefore, it is expected that the buoyancy force has the maximum effects when the magnetic field vector is perpendicular with respect to the horizontal axis. In addition, the variations of inclination angle γ affect the governing patterns. The sub-figures shown in Fig. 13 depict that the created secondary vortices in the center of the sub-cavities unify with increasing Ha for all the inclination angles expect γ = π/2. This phenomenon is due to that the drag force of Lorentz has the least impact when it is applied perpendicularly. Furthermore, it can be seen that the results are the same for γ = 0 and π. As previously mentioned, the Lorentz force is a periodic one with the period of π.

Fig. 13

The streamlines contours of the hybrid nanofluid (dashed lines) and the nanofluid with Al₂O₃ nanoparticles (solid lines) for different values of Ha in aγ = 0, bγ = 45, cγ = 90, dγ = 135 and eγ = 180 for Ra = 10⁷ and φ_hnf = $\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ = 2%

The effect of γ and Ha on the isotherms is displayed in Fig. 14 for Ra = 10⁷ and φ_hnf = $\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ = 2%. When the magnetic field is applied to the flow domain, the fluid thermal mixing is reduced. When Ra = 10⁷ and φ_hnf = $\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ = 2%, it is not observed noticeable differences among the isotherms patterns. However, it is worth mentioning that the isotherms of γ = π/2 differ from those of the other values of γ.

Fig. 14

The isotherms contours of the hybrid nanofluid (dashed lines) and the nanofluid with Al₂O₃ nanoparticles (solid lines) for different values of Ha in aγ = 0, bγ = 45, cγ = 90, dγ = 135 and eγ = 180 for Ra = 10⁷ and φ_hnf = $\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ = 2%

Figure 15a, b shows the variations trend of Nu_avg according to γ for different values of Ha. The other parameters are constant so that Ra = 10⁸ and φ = 2%. Nu_avg increases as γ increases by γ = π/2. After that, it begins to reduce by γ = π. In other words, the maximum value of Nu_avg is at γ = π/2. This result arises from the fact that the fluid flow strength is maximum when γ = π/2. In addition, Nu_avg decreases with the increment of Ha. As said earlier, the mobility of the fluid flow exposed the magnetic field is reduced. Thus, this can justify that an increase in Ha causes a decrease in Nu_avg. Finally, the results depict that dispersing Al₂O₃ nanoparticles in the host fluid augments the rate of heat transfer, while Cu–Al₂O₃ nanoparticles decline the rate.

Fig. 15

The effects of Ha and γ on Nu_avg for a the nanofluid with $\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ = 2% and b the hybrid nanofluid with $\varphi_{\text{hnf}}$ = 2% for Ra = 10⁸

Figure 16a, b illustrates the variations trend of the mean temperature according to γ for different values of Ha. Here, φ and Ra are 0.02% and 10⁸, respectively. The results indicate that T_avg reduces as γ augments. The T_avg variation according to γ is a quasi-sinusoidal function. Furthermore, the amplitude of these quasi-sinusoidal functions increases with the increment of Ha. Figure 16a clearly indicates that the volume fraction 0.02 for  Al₂O₃/water nanofluid causes increases in T_avg at all γ and Ha values. However, for Cu-Al₂O₃/water hybrid nanofluid adn Ha = 200, when 0 ≤ γ < 120 and 165 < γ ≤ 180, the simultaneous presence of Cu and Al₂O₃ raises T_avg. On the other hand, if 120 < γ < 165, the presence of these nanoparticles decreases the mean temperature. Apparently, for all types of fluids, when Ha = 100 or 200, the maximum and minimum values of T_avg occurs at 50° and 140°, respectively.

Fig. 16

The effects of Ha and γ on the average temperature T_avg for a the nanofluid with $\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ = 2% and b the hybrid nanofluid with $\varphi_{\text{hnf}}$ = 2% for Ra = 10⁸

Figure 17 illustrates that σ_max increases with an increase in Ha for all types of fluids. It is observed that at the beginning, σ_max decreases as γ increases by 30°. After that for Ha ≤ 100, the maximum stress increases until γ reaches 105°, while for Ha = 200, the maximum stress occurs around γ = 90°. Then, it can be seen that σ_max continuously decreases as γ grows. Figure 17a, b expresses that the maximum stress imposed on the flexible partition due to the interaction of the pure fluid and the partition is more than that caused via the interaction of the nanofluid/hybrid nanofluid and the solid.

Fig. 17

The effects of Ha and γ on the maximum stress imposed on the partition for a the nanofluid with $\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ = 2% and b the hybrid nanofluid with $\varphi_{\text{hnf}}$ = 2% for Ra = 10⁸

The effects of Ha and φ_hnf/$\varphi_{{{\text{Al}}_{2} {\text{O}}_{3} }}$ on Nu_avg and T_avg at the fixed values of Ra = 10⁷ and γ = 2π/3 are presented in Fig. 18a, b. The examined values for the volume fractions are 1 and 2%. It is obvious that an increase in Ha increases and decreases the average temperature and Nusselt number, respectively. As previously mentioned, the magnetic field acts as a drag force against the fluid flow. Accordingly, increasing the value of Ha means augmentation in the drag force acting against the advection mechanism. In general, it can be said that for a specific volume fraction, the reduction in Nu_avg or augmentation of T_avg with increasing values of Ha for Al₂O₃/water nanofluid is more than that for Cu-Al₂O₃/water hybrid nanofluid. From Fig 18a, increasing the volume fraction of the single and hybrid nanofluids increases and decreases Nu_avg, respectively. In order to justify this outcome, it can be said that the increase in the hybrid nanofluid viscosity due to the simultaneous presence of Cu and Al₂O₃ nanoparticles is extremely larger than the increase in the other thermophysical properties especially the thermal conduction. Therefore, as previously seen, the intense reduction in the mobility of the hybrid nanofluid flow due to the intense increase in viscosity can be the reason of decreasing Nu_avg. Also, from Fig. 18b, it is concluded that the presence of Al₂O₃ and Cu–Al₂O₃ nanoparticles at Ra = 10⁷ and γ = 2π/3 increases and decreases the average temperature of the fluid, respectively.

Fig. 18

The effects of Ha and φ on a the Nusselt number b the average temperature in Ra = 10⁷, γ = 2π/3

Figure 19 illustrates that for all types of fluids an increase in Ha increases σ_max when Ra = 10⁷ and γ = 2π/3. On the other hand, the use of Al₂O₃ and Cu–Al₂O₃ nanoparticles decreases σ_max. Nevertheless, it cannot be said with certainty that which type of nanofluids reduce σ_max more. Generally, when Ha ≥ 100 and for different values of φ, σ_max for the single and hybrid nanofluids are the same.

Fig. 19

The effects of Ha and φ on the maximum stress imposed on the partition at Ra = 10⁷ and γ = 2π/3

Comparison of Nu_avg of the single and hybrid nanofluids for different values of Ra and φ is presented in Table 4. The other parameters are selected constant so that Ha = 50 and γ = π/3. The data presented in Table 4 indicates that for all Ra values and both types of nanofluids, the Nu_av is decreased when φ = 0.1. Moreover, increasing the volume fraction of Al₂O₃ and Cu-Al₂O₃ nanoparticles enhances and declines the Nu_avg, respectively. The data also indicate that an increase in Ra extremely augments the heat transfer rate (Table 4).

Table 4 Comparison of Nu_avg of the single and hybrid nanofluids for various values of Ra and φ when Ha = 50 and γ = π/3

The data presented in Table 5 give information on the mean temperature variations with Ra and φ when Ha = 50 and γ = π/3. Clearly, dispersing the single and hybrid nanoparticles in the host fluid increase T_avg. Moreover, the results demonstrate that the increase in T_avg due to adding the hybrid nanoparticles is more than that for the single nanoparticles. Also, an increase in Ra extremely reduces T_avg.

Table 5 Comparison of the average temperature between Al₂O₃/water nanofluid and Al₂O₃–Cu/water hybrid nanofluid for different values of Ra and φ

The results given in Table 6 explain that at Ha = 50 and γ = π/3, the maximum stress in the flexible partition increases when Ra increases. In contrast, increasing the volume fraction of single and hybrid nanoparticles decreases the induced maximum stress. In fact, an increase in Ra makes an increase in the mobility of the fluid flow, consequently, increases the interaction between the fluid and solid. Also, comparison of the results shows that the maximum stress at the flexible partition of cavity filled with the hybrid nanofluid is more than that of cavity occupied using the single nanofluid.

Table 6 Comparison of the maximum value of stress in flexible partition between Al₂O₃/water nanofluid and Al₂O₃–Cu/water hybrid nanofluid for various values of Ra and φ when Ha = 50 and γ = π/3

Conclusions

Unsteady natural convection within an enclosure equally divided by a flexible partition is numerically investigated utilizing the Galerkin finite element method. The enclosure occupied by the hybrid nanofluid is under the influence of a uniform magnetic field. The effects of different parameters including the Hartmann number Ha, the Rayleigh number Ra, the nanoparticles concentration φ and the angle of the magnetic field vector γ on the flow strength, the rate of heat transfer and the stress of flexible partition are studied. The main findings of the current work are summarized as follows:

• 1. The strength of the hybrid and regular nanofluids circulation augments as the magnetic field vector angle γ increases until γ reaches π/2. Then, the mobility of fluid begins to vanish when γ varies from π/2 to π. The impact of magnetic field on the mean Nusselt number Nu_avg is the maximum at γ = π/2.

• 2. Compared to the base fluid, the presence of 2% volume fraction of Al₂O₃ nanoparticles increases Nu_avg, the same volume faction of Cu–Al₂O₃ nanoparticles decreases the average Nusselt number. Moreover, the presence of Al₂O₃ nanoparticles enhances the fluid flow strength while the combination of Cu and Al₂O₃ nanoparticles (hybrid nanoparticles) results in the reduction in circulation strength. The reduction in Nu_avg is mainly due to the significant increase in the dynamic viscosity of hybrid nanofluids.

• 3. The maximum stress imposed on the flexible partition coming from the pure fluid and the partition interaction is larger than that of the solid and regular/hybrid nanofluid interaction. The presence of nanoparticles would cause smaller partition deflection compared to the case of pure fluid.

• 4. The vortices-strength inside both the sub-cavities decreases with the increase of  Ha. However, the fluid flow strength rises as Ra increases. Moreover, the dominant mechanism of heat transfer changes with Ra and Ha values. The presence of hybrid nanoparticles in the host fluid (water) results in a fluid with higher dynamic viscosity and thermal conductivity. The increase in the thermal conductivity tends to enhance the natural convective heat transfer; in contrast, the augmentation of the dynamic viscosity tends to decrease the heat transfer. The overall effect of dispersing hybrid nanoparticles in the host fluid is the reduction in Nu_avg. However, the presence of the same amount of single Al₂O₃ nanoparticles would enhance Nu_avg.