Optimal Coordination of Overcurrent Relays Using Improved Leadership-Based Grey Wolf Optimizer

Abstract

Coordination of overcurrent relays is a nonlinear and highly constrained optimization problem in a large distribution system where the operating time of all relays is to be minimized. Proper coordination of protective devices is a very crucial task for appropriate functioning of the electrical power system with distributed power generating stations. In order to solve this problem, various unconventional optimization techniques have been proposed. Random Walk Grey Wolf Optimizer (RW-GWO) is a recently developed algorithm based on improving the search ability of the leading wolves in classical GWO algorithm to overcome the issues of stagnation to local optima and premature convergence while solving nonlinear and complex optimization problems. Therefore, in the present work, RW-GWO algorithm is employed to find the optimal setting for directional overcurrent relay problem which is a highly complex problem. In the present paper, the results are also reported for classical GWO and the comparison is performed with several other optimization methods. The comparison of results demonstrates the strength of the RW-GWO in obtaining the optimal setting for the proper coordination of overcurrent relays as compared to other optimization methods.

1 Introduction

In power systems, various generating stations run in parallel to feed a high voltage network. Many equipments are connected via these networks. The fault that occurs in power system may be very harmful. Therefore, securing network from these faults, protective relays are integrated into power systems and these protective relays detach the non-functioning components from a system by tripping the circuit. Overcurrent relays which are widely used protection devices [1] can sense the flow of current only in one direction. Directional overcurrent relay should operate for a fault which occurs in its zone for the functioning of the power system properly. Primary relays operate on the appearance of a fault and are backed up by secondary relays, and the secondary or backup relays operate when primary relay fails. Proper coordination of direction overcurrent relays is very crucial for the better performance of the power systems and to escape from the problem of equipment damages, and this relay coordination is very time-consuming and a tedious task. The protection of directional overcurrent relays consists of two types of settings—TS (Time Dial Setting) and PS (Plug Setting)—and by determining these optimal settings, an efficient coordination for overcurrent relays can be achieved. Earlier this has been done manually which was very tedious. The use of computer helps engineers with laborious efforts. Generally, there are two approaches that are used for directional overcurrent relay.

In conventional techniques, first the fault analysis is conducted and after that meshed networks are broken into radial form, then relay at far end is set, and in the last, setup of back relays is established and this process is repeated for all the relays. Final Time Dial Setting and Plug Setting depend on the selection of the initial relays which are known as breakpoints [2]. These breakpoints are selected by using graph theory. The number of iterations here depends on the selection of breakpoints. It has been observed that the values of Time Dial Setting and Plug Setting determined by conventional techniques are not optimal [3]. Coordination of overcurrent relays in a large distribution network with multi-source and multi-looped network by using deterministic optimization becomes infeasible [3]. Therefore, the unconventional parameter optimization techniques that are designed, especially for highly nonlinear or non-differentiable problems, are more effective for these types of problems. These techniques are called as nature-inspired optimization techniques or meta-heuristic techniques. These techniques are designed from the inspiration of nature.

In 1988 [4], first time the optimization theory has been utilized to deal coordination of directional overcurrent relay. The practical importance of these problems inspires to apply different optimization strategies to solve this type of problems. In [5], linear programming is also used to find the optimal setting of parameters in overcurrent relay.

In the literature, various nature-inspired optimization techniques are used to solve the relay coordination problem. For example, in [6,7,8,9,10], Genetic Algorithm (GA) and its modified variants are used to determine the optimal setting for the proper coordination of overcurrent relays. In [10,11,12,13,14], Differential Evolution (DE) and its modified variants are employed on the coordination of overcurrent relay problem to find the optimal setting of decision parameters called TS and PS. In [15, 16], mixed-integer nonlinear programming formulation is used and the relay coordination problem is solved using Particle Swarm Optimization (PSO). In [17,18,19], modified variants of PSO are introduced to solve relay coordination problem. In [20], Random Search Technique is applied to solve the coordination problem. Seeker Algorithm is applied in [21] with step length and adaptive search direction to find the decision parameters so that the operating time of all relays can be minimized.

Grey Wolf Optimizer Algorithm [22] is a recently developed optimization approach and is very efficient to approximate the optima of the optimization problem. This algorithm is designed from the inspiration of grey wolf pack where the dominant leadership behaviour can be observed which helps in the search process of prey. In [22], it has been suggested that GWO algorithm performs better than some state-of-the-art algorithms like Particle Swarm Optimization (PSO) [23], Gravitational Search Algorithm (GSA) [24], Fast Evolutionary Process (FEP) [25] and is very competitive as compared to the Differential Evolution (DE) [26]. However, similar to the other meta-heuristic search algorithms, GWO also faces the problem of getting trapped in sub-optimal solutions and premature convergence in some cases.

In the literature, various efforts have been made to improve the search accuracy of classical GWO. Mittal et al. [27] have modified the parameters of GWO to maintain an appropriate balance between the operators’ exploration and exploitation. Malik et al. [28] have proposed a weighted position update mechanism to update the search agents. In [29], Levy flight search strategy is employed to enhance the search efficiency of wolf pack. In [30], evolutionary population dynamics (EPD) is applied to discard the worst fitted wolf from the pack and introduce a new wolf with the help of EPD. In [31], the crossover and mutation operators are introduced into classical GWO to enhance its performance. In [32], the GWO and PSO are hybridized to maintain an appropriate balance between exploitation and exploration in GWO. In [33, 34], the concept of opposition-based learning is introduced to avoid the problem of stagnation at local optima. In order to accelerate the convergence rate, chaos theory has been integrated in GWO [35, 36]. In [37], an adaptive bridging mechanism based on β-chaotic sequence is introduced to balance exploitation and exploration in the classical GWO. In [38, 39], random walk strategy based on Cauchy distribution is applied to the leading hunters of the grey wolf pack to reduce the problem of getting trapped in sub-optimal solutions and to enhance the search accuracy of classical GWO. In [40], exploration of search agents in GWO has been enhanced by proposing a new position update mechanism. In [41], a weighted grey wolf optimizer is introduced to enhance the performance of classical GWO and enhance the search around the best search agents. A brief literature review on GWO can be found in [42].

In the present work, the Random Walk Grey Wolf Optimizer (RW-GWO) [38, 39] is used to find the optimal setting of directional overcurrent relay problem which is nonlinear, highly complex, and highly constrained in nature. The experimental analysis conducted in the paper also verifies the ability of RW-GWO to avoid the stagnation problem of wolf pack in local optimums as compared to the classical GWO.

The rest of the paper is organized as follows: in Sect. 2, the problem of coordination of directional overcurrent relays is described briefly. Section 3 presents a framework of an efficient swarm intelligence-based optimization approach called Grey Wolf Optimizer (GWO). In Sect. 4, mechanism of RW-GWO algorithm is described briefly. In Sect. 5, experimental setup and obtained results on IEEE 4-bus system are presented. Finally, Sect. 6 concludes the work and suggests some future research directions.

2 Problem Description

The coordination problem of directional overcurrent relays is to minimize the sum of operating time of all relays corresponding to the maximum fault current [17, 43, 44]. A mathematical form of the problem can be stated as

$${\text{Min}}\,T = \sum\limits_{{i = 1}}^{N} {t_{{i,{\text{op}}}} }$$

(1)

$${\text{s}} . {\text{t}} .\quad t_{{j,{\text{ob}} }} - t_{{i,{\text{op}}}} \ge {\text{CTI}}$$

(2)

$${\text{TS}}_{{i,{{\rm min} }}} \le {\text{TS}}_{i} \le {\text{TS}}_{{i,{{\rm max} }}}$$

(3)

$${\text{PS}}_{{i,{{\rm min} }}} \le {\text{PS}}_{i} \le {\text{PS}}_{{i,{{\rm max} }}}$$

(4)

$$t_{i,{\rm min} } \le t_{{i,{{\rm op}}}} \le t_{i,{\rm max} }$$

(5)

where T is the objective function, $t_{{i,{\text{op}}}}$ is the operating time of the ith relay, and N is the number of relays within the system. In Eq. (2), $t_{{j,{\text{ob }}}}$ and $t_{{i,{\text{op}}}}$ are the operating time of ith primary relay and its jth backup relay. In Eq. (3), ${\text{TS}}_{{i,{ \hbox{min} }}}$ and ${\text{TS}}_{{i,{ \hbox{max} }}}$ are the lower and upper limits for the decision variable TS. In Eq. (4), ${\text{PS}}_{{i,{ \hbox{min} }}}$ and ${\text{PS}}_{{i,{ \hbox{max} }}}$ are the lower and upper limits for the decision variable PS. In Eq. (5), $t_{i,\hbox{min} }$ and $t_{i,\hbox{max} }$ are the lower and upper limits on the operating time of ith relay.

The operating time of any relay can be obtained from its characteristic curve and is defined by IEEE/IEC as follows [45]:

$$t_{{i,{\text{op}}}} = \frac{{\mu \times {\text{TS}}_{i} }}{{\left( {\frac{{I_{{{\text{f}},i}} }}{{{\text{PS}}_{i} }}} \right)^{\alpha } - 1}} + L$$

(6)

where $\mu , \alpha$, and L are the characteristic constants of the relays and $I_{{{\text{f}},i}}$ is the fault current through ith relay. TS and PS are the decision parameters which are to be optimized. For standard inverse definite minimum time relays, $\mu = 0.14, \alpha = 0.02$, and $L = 0$ [45].

From the objective function defined in Eq. (1), it is clear that the operative time of primary relay is minimized without any restrictions on operating time of its backup relays. Therefore, in [46, 47], a new objective function is introduced which minimizes the operating time of primary and backup relays simultaneously. Mathematically, the objective function is defined as follows:

$${\text{Min}}\quad F = \beta_{1} \mathop \sum \limits_{i = 1}^{N} t_{{i,{\text{op}}}}^{2} + \beta_{2} \mathop \sum \limits_{i = 1}^{M} \left( {t_{{j,{\text{ob}} }} - {\text{CTI}}} \right)^{2}$$

(7)

$${\text{s}} . {\text{t}} .\quad (2) - (5)$$

(8)

where M is total number of relay pairs. $\beta_{1}$ and $\beta_{2}$ are the positive weights corresponding to primary and backup relays, and $\beta_{1} + \beta_{2} = 1$. The values of weighting factors $\beta_{1}$ and $\beta_{2}$ provide a conciliation between the operating times of backup and primary relays [46]. In the present work, the value of CTI is fixed as 0.2. The minimum and maximum limits on the operating times of primary relays are fixed in the range [0.1, 4]. The values of TS have been considered in the range [0.1, 1.1]. In the present paper, the values of $\beta_{1}$ and $\beta_{2}$ are taken as 0.73 and 0.27, respectively. This parameter selection is adopted from [47]. The description of the Grey Wolf Optimizer (GWO) along with their working steps is describes as follows:

3 Classical Grey Wolf Optimizer Algorithm

Grey Wolf Optimizer [22] is designed from the inspiration of leadership and social behaviour present in a pack or group of grey wolves. Grey wolves are considered as apex predators, and they are on the top of food chain. Their pack is about 5–11 wolves, and within the pack, discipline and leadership behaviour are maintained by dividing pack into 4 types of wolf—alpha (the dominant wolf of the pack which is responsible for all the important and major decisions regarding the various activities of wolves within pack), beta (these are the subordinate wolf to the alpha and act as a leading wolf if the alpha wolf passes away), delta (the sentinels, caretakers, and elder wolves belong to this category), and omega (all the remaining wolves of the pack that are allowed to eat in the end). The wolf alpha, beta, and delta are known as leading wolves of the pack, and the hunting process of prey is totally depending on these wolves. According to Muro et al. [48], grey wolves perform their hunting process in 3 steps that can be expressed as:

• 1. Tracking and pursuing of prey,

• 2. Encircling of prey, and

• 3. The attack on prey to complete the hunting process.

All these characteristics of grey wolves are modelled in mathematical form by Mirjalili et al. [22] to find their food (prey). Briefly, the mathematical model can be summarized as:

3.1 Mathematical Modelling of GWO

In this section, mathematical equations that are designed from the simulation of grey wolves’ activities, while searching prey, are presented to demonstrate the ability of wolf pack. The stepwise description of hunting strategies that grey wolves follow is described as follows:

3.1.1 Leadership Hierarchy

In a wolf pack, wolves are divided into several categories based on their leadership characteristics. To simulate this, the top three fittest solutions to the problem are elected as dominant hunters for the pack. These leading solutions are called as alpha, beta, and delta. The rest of the solutions are called omega solutions to the problem. These omega solutions update their position according to the position of leading hunters based on exploitation and exploration operators.

3.1.2 Encircling Prey

It is obvious that the prey is hunted by wolves when it stops moving, and to hunt the prey first wolves encircle the prey in a group. The encircling mathematical equations that are designed from the inspiration of encircling behaviour of grey wolves are given as follows:

$$y_{t + 1} = y_{p,t} - a \cdot d$$

(9)

$$d = \left| {c \cdot y_{p,t} - y_{t} } \right|$$

(10)

$$a = 2 \cdot b \cdot r_{1} - b$$

(11)

$$c = 2 \cdot r_{2}$$

(12)

where $y_{t} , y_{t + 1 }$ are the states of the grey wolf at tth and $(t + 1){\text{th}}$ iteration, respectively; $y_{p,t}$ represents the state of prey at tth iteration. d represents the difference vector, a and c are coefficient vectors, and b is a vector that decreases linearly over the course of iterations and can be formulated as:

$$b = 2 - 2 \cdot \left( {\frac{t}{{{\text{maximum}}\,{\text{no}} .\,{\text{of}}\,{\text{iterations}}}}} \right)$$

(13)

and $r_{1} ,r_{2}$ are random vectors whose components are generated within the interval (0, 1) and are uniformly distributed.

3.1.3 Hunting

Grey wolves have the ability to recognize the position of prey and encircle them. Generally, the hunting procedure is guided by alpha wolves, but occasionally, beta and delta wolves also participate in hunting process with the assumption that they have enough information about the prey. Therefore, these leading wolves are gathered in each iteration of algorithm and updated when the better location is achieved. Having the useful information about prey, these leading wolves of pack help to estimate the prey location with the help of the following mathematical equations:

$$d_{\alpha } = \left| {c_{\alpha } \cdot y_{\alpha ,t} - y_{t} } \right|$$

(14)

$$d_{\beta } = \left| {c_{\beta } \cdot y_{\beta ,t} - y_{t} } \right|$$

(15)

$$d_{\delta } = \left| {c_{\delta } \cdot y_{\delta ,t} - y_{t} } \right|$$

(16)

where $y_{\alpha ,t}$, $y_{\beta ,t}$, and $y_{\delta ,t}$ are the locations of leading wolves (alpha, beta, and delta) at tth iteration, respectively. $c_{\alpha } , c_{\beta }$, and $c_{\delta }$ are the random vectors as defined in Eq. (9). With the help of difference vectors $d_{\alpha } , d_{\beta }$ and $d_{\delta }$, the states of wolves for $(t + 1){\text{th}}$ iteration can be updated as:

$$y_{1} = y_{\alpha ,t} - a_{\alpha } \cdot d_{\alpha }$$

(17)

$$y_{2} = y_{\beta ,t} - a_{\beta } \cdot d_{\beta }$$

(18)

$$y_{3} = y_{\delta ,t} - a_{\delta } \cdot d_{\delta }$$

(19)

$$y_{t + 1} = \left( {y_{1} + y_{2} + y_{3} } \right)/3$$

(20)

Therefore, the leading wolves alpha, beta, and delta estimate the state of prey and omega wolves update their states around the prey. In this way, on repeating the process of encircling and hunting activity of grey wolves in mathematical form the optima can be found for any optimization problem.

3.1.4 Exploration (Search for Prey) and Exploitation (Attack on Prey) in GWO

In GWO algorithm, the search process of prey stops when wolf pack chases the prey and prey stops moving. In order to simulate the behaviour of chasing the prey, the value of b is linearly decreased as the iteration proceeds. In the algorithm, the exploration of a search space by grey wolves is controlled by vectors A and C. When $\left| A \right| > 1$ or $\left| C \right| > 1$, the new search regions are discovered by wolves in order to explore the unvisited regions of search space that helps in preventing the pack from stagnation in local optima and this situation refers the process of searching prey within search space.

When $\left| A \right| < 1$ or $\left| C \right| < 1$, the search spaces are exploited locally by grey wolves in order to discover the better positions around the explored regions and this situation demonstrates the attacking behaviour by wolves on prey.

As the iterations increase, the value of b decreases, and therefore, the value of A decreases, and when $t \to {\text{maximum}} \,{\text{no}}. \,{\text{of}}\,{\text{iterations}}$, the value of $A \to 0$, and therefore, the vector C is accountable for the exploration of search space at this state.

4 Random Walk Grey Wolf Optimizer

This algorithm was proposed by the authors [38, 39] for unconstraint and constraint optimization problem to enhance the search ability of leading wolves alpha, beta, and delta of the pack. It has been observed experimentally that the classical GWO faces the problem of premature convergence in local optimum as the algorithm is completely dependent on the leading guidance of alpha, beta, and delta wolves, and if they trapped in sub-optimal solutions, then the whole wolf pack trapped in local optima due to the absence of optimum leading guidance. Another reason of proposing this modified GWO (RW-GWO) is to update the states of leading hunters, alpha, beta and delta of the pack. Because, in the classical GWO, it has been observed that these leading wolves were updating their states with the guidance of low fitted wolf. For example, alpha wolf was updating with the guidance of beta and delta. Similarly, beta wolf was updating with the help of delta wolf. Therefore, a proper optimum guidance should be there so that the leaders can improve their states to find prey. With the motivation of improvement in leaders with optimum direction, authors proposed a novel search strategy for leading wolves based on the Cauchy random walk.

4.1 Cauchy Random Walk Search Strategy for Leading Wolves

The random walk [48] is a random search process in which search proceeds with consecutive random steps. Mathematically the random walk can be defined as:

$$w_{T} = \mathop \sum \limits_{t = 1}^{T} s_{t}$$

(21)

where $s_{t}$ is a step length that can follow any random distribution. Mathematically a relation can be established between any two successive random walks as:

$$\begin{aligned} w_{T} & = s_{1} + s_{2} + \cdots + s_{T - 1} + s_{T} \\ & = \mathop \sum \limits_{t = 1}^{T} s_{t} = \mathop \sum \limits_{t = 1}^{T - 1} s_{t} + s_{t + 1} \\ \end{aligned}$$

(22)

From this relation, it can be observed that next position depends only on current state and selected step length from current state to next state. In a random walk, the step can be fixed or can be varied. For our algorithm, assume that the current state of the wolf is $y_{0}$ and the final state after N steps by a random walk is $y_{N}$, i.e.

$$y_{N} = y_{0} + a_{1} y_{1} + \cdots + a_{N} y_{N} = y_{0} + \mathop \sum \limits_{j = 1}^{N} a_{j} y_{j}$$

(23)

where $a_{j}$ is a parameter used to control the step length. In our proposed algorithm Random Walk GWO, random steps $y_{j}$ follow the Cauchy distribution. The reason behind choosing Cauchy distribution is the variance of Cauchy distribution which is infinite and which helps the leaders to explore the search space with the exploitation of search regions which are already explored as the parameter $y_{j}$ sometimes takes a higher value which helps in taking a long jump when the leaders are trapped in local solution, and the small value of $y_{j}$ that is obtained from distribution helps in discovering the optimum states in a neighbourhood of already explored states. Thus, the Cauchy-distributed random steps help in local as well as a global search of search space. In this strategy, parameter $a_{j}$ is considered as a vector that is decreased linearly from 2 to 0 as the iterations proceed to converge the wolf pack (population of solutions). The framework of the algorithm Random Walk Grey Wolf Optimizer is presented in Algorithm 1.

4.2 Computational Complexity of Random Walk Grey Wolf Optimizer

Since the algorithm complexity plays an important role to analyse the complexity of algorithms, the user always prefers less complex algorithm. Therefore, in the present section, the worst time complexity of classical GWO and the RW-GWO algorithms has been calculated in terms of big O notation. The pseudocode of the algorithms presented in Algorithm 1 can be used to evaluate the complexity. Therefore, the complexity of algorithm for classical GWO and Random Walk Grey Wolf Optimizer is calculated as:

$$\begin{aligned} O\left( {\text{GWO}} \right) & = O\left( {{\text{position}}\,{\text{update}}} \right) + O\left( {{\text{selection}}\,{\text{of}}\,{\text{leaders}}} \right) \\ & = O\left( {T \times \left( {N \times D} \right)} \right) + O\left( N \right) \\ & = O(T \times N \times D) \\ \end{aligned}$$

Similarly, for RW-GWO,

$$O({\text{Random}}\,{\text{Walk}}\,{\text{Grey}}\,{\text{Wolf}}\,{\text{Optimizer}}) = O\left( {T \times N \times D} \right)$$

where T is the total number of iterations and N is the size of wolf pack and D represents the dimension of the problem under consideration. Hence, it can be concluded that in terms of computational complexity, both the algorithms classical GWO and the RW-GWO are same.

4.3 Constraint Handling

A majority of the meta-heuristic algorithms are designed initially to obtain an efficient result of unconstraint optimization problems. However, in real life, most of the problems are constrained optimization problem. In the present study, the considered coordination of overcurrent relay problem is highly complex and highly constrained. Therefore, to deal with the constraints a static penalty approach [49] is used to obtain a solution of the problem in which the objective function is defined as

$${\text{obj}} = \left\{ {\begin{array}{*{20}l} {f(x) } \hfill & {\quad {\text{if}}\,{\text{the}}\,{\text{solution}}\,x\,{\text{is}}\,{\text{feasible}}} \hfill \\ {f\left( x \right) + \mathop \sum \limits_{j = 1}^{m} c_{j} \times \left[ {\hbox{max} \left( {0,g_{j} \left( x \right)} \right)} \right]^{\alpha } } \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right.$$

(24)

where the value of $\alpha$ can be 1 or 2 and $c_{j}$$\left( {j = 1,2, \ldots ,m} \right)$ are the penalty parameters. The equality constraint $h$ can be transformed easily into inequality constraint by the simple transformation

$$g\left( x \right) = \left| {h\left( x \right)} \right| - \in$$

(25)

where $\in$ is predefined tolerance parameter and $h\left( x \right)$ is the equality constraint.

5 Experimental Setup and Results

In the present work, Random Walk Grey Wolf Optimizer is applied to solve the complex nonlinear coordination overcurrent relay problem. The population size is a very crucial parameter for any meta-heuristic algorithm. As very small size of the population fails to explore the search space of the problem, very large population size may fail to determine an efficient solution. Therefore, a suitable population size for algorithm should be chosen. In the present study, the population size is fixed as 30 for each algorithm, and the 30 runs of each algorithm are executed on each case of bus system to analyse the search efficiency of applied algorithms. In order to compare the performance of the RW-GWO algorithm, the recent optimization methods such as classical GWO [22], improved Grey Wolf Optimizer (mGWO) [27], Exploration Enhanced Grey Wolf Optimizer (EEGWO) [40], Weighted Grey Wolf Optimizer (wGWO) [41], Salp Swarm Algorithm (SSA) [50], Chaotic Salp Swarm Algorithm (cSSA) [51], and Sine Cosine Algorithm (SCA) [52] are used. For fair comparison, the maximum number of iterations are fixed as 100 for each algorithm. Since each search agent is evaluated once in an iteration of each algorithm, the total number of function evaluations which are utilized to solve the problem is 3 × 10³. The 4-bus system which is used to evaluate the search efficiency of RW-GWO algorithm is described as follows:

5.1 Test Model

To evaluate the performance of the RW-GWO algorithm, a 4-bus distribution network (DN) with distributed energy resources (DERs) is considered which is shown in Fig. 1. The DN consists of three DERs such as synchronous-based DER (SBDER) and inverter-based DERs (IBDERs) connected at buses B₂, B₃, and B_4, respectively. The capacity of SBDER and IBDER is 3MVA and 2 MW, respectively. The current transformer (CT) ratio is calculated based on maximum load current (I_Lmax) flowing through each relay and is given in Table 1. Three phase-to-ground faults (F₁–F₃) are considered at midpoint of all three feeders to determine fault currents flowing through primary and backup relays. The DN with DERs fault logic is developed using real-time digital simulator (RTDS) [53]. The three phase-to-ground fault and line-to-line fault are considered as maximum and minimum faults, respectively.

Fig. 1

4-Bus system

Table 1 Current transformer (CT) ratio for relays

The RW-GWO algorithm is tested for three different operating modes (cases) of 4-bus DN with DERs and is given as:

• 1. Grid-connected mode (GCM).

• 2. Islanded mode (IM).

• 3. Disconnection of DERs (DCDERs).

5.1.1 Grid-Connected Mode (GCM) of Operation

The DN is operated in grid-connected mode when switches S₁, S₂, S₃, and S₄ are closed as shown in Fig. 1. In this mode of operation, whenever fault occurs, the fault current is contributed by both main grid and DERs connected to the DN. The maximum load current, minimum fault current, and maximum fault current flowing through all the relays (R₁–R₆) are provided in Table 2. The fault current flowing through all primary and backup relays is shown in Table 3. The obtained setting of decision variables TS and PS by RW-GWO and classical GWO algorithms is shown in Table 4. The value of the obtained relay operating time is also presented in Table 11. In the same tables, the results are also compared with several optimization methods such as improved Grey Wolf Optimizer (mGWO) [27], Exploration Enhanced Grey Wolf Optimizer (EEGWO) [40], Weighted Grey Wolf Optimizer (wGWO) [41], Salp Swarm Algorithm (SSA) [50], Chaotic Salp Swarm Algorithm (cSSA) [51], and Sine Cosine Algorithm (SCA) [52].

Table 2 Load current, fault current, and CT ratio for case 1 of 4-bus system

Table 3 Primary-backup relay pairs and the corresponding fault currents for case 1 of 4-bus system

Table 4 Comparison of result for case 1 of 4-bus system

5.1.2 Islanded Mode (IM) of Operation

The DN is operated in islanded mode when switches S₂, S₃, and S₄ are closed as shown in Fig. 1. In this mode of operation, whenever fault occurs, the fault current is contributed by only DERs connected to the DN. The maximum load current, minimum fault current, and maximum fault current flowing through all the relays are provided in Table 5. The fault current flowing through all primary and backup relays is shown in Table 6. The obtained value of decision variables TS and PS by RW-GWO and classical GWO algorithms is shown in Table 7. The value of the obtained relay operating time is also presented in Table 11. In the same tables, the results are also compared with several optimization methods as similar to case 1.

Table 5 Load current, fault current, and CT ratio for case 2 of 4-bus system

Table 6 Primary-backup relay pairs and the corresponding fault currents for case 2 of 4-bus system

Table 7 Comparison of result for case 2 of 4-bus system

5.1.3 Disconnection of DERs (DCDERs)

The DN is operated in disconnection of DERs mode when only the switch S₁ is closed as shown in Fig. 1. In this mode of operation, whenever fault occurs, the fault current is contributed by only main grid. The maximum load current, minimum fault current, and maximum fault current flowing through all the relays are provided in Table 8. The fault current flowing through all primary and backup relays is shown in Table 9. The obtained value of decision variables TS and PS by RW-GWO and classical GWO algorithms is shown in Table 10. The value of the obtained relay operating time is also presented in Table 11. In the same tables, the results are also compared with several optimization methods as similar to cases 1 and 2.

Table 8 Load current, fault current, and CT ratio for case 3 of 4-bus system

Table 9 Primary-backup relay pairs and the corresponding fault currents for case 3 of 4-bus system

Table 10 Comparison of result for case 3 of 4-bus system

Table 11 Comparison of results on different cases of 4-bus system with various state-of-the-art algorithms

From Table 11, where the operating time for each case of 4-bus system is presented, it can be observed that the RW-GWO algorithm determines the minimum operative time and optimal setting for overcurrent relays as compared to the other comparative algorithms.

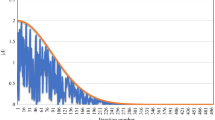
The diversity plot in terms of average distance between the solutions in each generation is plotted in Fig. 2. The Euclidean distance ||.|| between two solutions $X = \left( {x_{1} , x_{2} , \ldots ,x_{d} } \right)$ and $Y = \left( {y_{1} , y_{2} , \ldots ,y_{d} } \right)$ is calculated as follows:

$$\left| {\left| {X - Y} \right|} \right|_{2} = \sqrt {\mathop \sum \limits_{j = 1}^{d} \left( {x_{j} - y_{j} } \right)^{2} }$$

(26)

From the diversity curves, it can be analysed that the average distance between the search agents in RW-GWO is less as compared to classical GWO which shows the better balance between the exploration and exploitation in RW-GWO. From these curves, it can be also observed that the leading hunters which are improved through random walk provide a better guidance as compared to classical GWO because RW-GWO provides better solution to the problem and the average distance between the search agents is less as compared to classical GWO.

Fig. 2

Diversity plot 4-bus system

6 Conclusion and Future Scope

Coordination of directional overcurrent relays is a very trending and complex nonlinear problem in the field of electrical engineering. The problem consists of a large number of constraints which makes the problem more difficult to solve compared to unconstrained problems. In the present work, to find the optimal setting for overcurrent relays, a Novel Random Walk Grey Wolf Optimizer is employed. In the paper, three cases of 4-bus system are used. The performance comparison of RW-GWO algorithm is conducted with classical GWO, improved Grey Wolf Optimizer (mGWO), Exploration Enhanced Grey Wolf Optimizer (EEGWO), Weighted Grey Wolf Optimizer (wGWO), Salp Swarm Algorithm (SSA), Chaotic Salp Swarm Algorithm (cSSA), and Sine Cosine Algorithm (SCA). The experimental analysis and performance comparison with algorithms indicate the better quality of solution accuracy of RW-GWO algorithm to solve the coordination problem. Analysing the comparative performance, it can be recommended to use Random Walk Grey Wolf Optimizer to find the efficient optimal setting for the coordination of overcurrent relays.

In future, another complex bus model can be considered for the evaluation of search ability of Grey wolf optimizer and Random Walk Grey Wolf Optimizer. The other constraint-handling mechanisms can also be integrated in the RW-GWO to develop a constrained RW-GWO.