Nonlinear radiative heat flux in Oldroyd-B nanofluid flow with Soret and Dufour effects

Abstract

Present paper investigates the flow of Oldroyd-B nanofluid due to stretching cylinder. Heat transfer aspects are expressed by nonlinear radiation and non-uniform heat source/sink. Analysis of Soret and Dufour effects are emphasized. Brownian movement and thermophoresis phenomena are retained. Characteristics of mass transfer subject to first-order chemical reaction is examined. Consideration of suitable transformations yields ordinary differential systems. Relevant problem is solved by Optimal homotopic approach. The concept of minimization is employed by defining the average squared residual errors. Behavior of various physical variables on dimensionless velocity, temperature and concentration fields are determined. In addition, the rates of heat and mass transfer are studied through graphs. Here, we noticed a growth in velocity, temperature and concentration for larger values of curvature parameter.

Introduction

Nanofluids containing nanomaterials such as metallic oxides, copper, silver and carbides have greater thermal conductivity to that of conventional base fluid. Water, engine oil and ethylene glycol are commonly used heat transfer fluids. Nanofluid can effectively be used for a wide range of mechanical industrial processes such as glass fiber innovation, melt spinning, microprocessors, chillers and hybrid power engine. Choi (1995) introduced nanofluid containing nanoparticles in base fluid to enhance their thermal properties. Then, Buongiorno (2006) developed the mathematical model for convective transport of nanofluids. The present model contains two elements, namely Brownian motion and thermophoresis parameter which are very important in nanofluids. Brownian motion is random motion of particles in a fluid due to their collision with molecules of water. Nanofluid flow over a stretching sheet with thermophoresis and Brownian motion effects has been discussed by Babu and Sandeep (2016). Reddy et al. (2017) studied the flow of Williamson nanofluid due to stretching sheet with variable thickness. Recent developments about nanofluid are cited in Khan et al. (2017), Munyalo and Zhang (2018), Madavan et al. (2018), Minakov et al. (2018), Hayat et al. (2018a), Khan et al. (2018) and Irfan and Khan (2019).

Most of the researches are limited to fluids which obey Newtonian postulate and cannot predict the elastic characteristics. Many industrial and geophysical processes such as petroleum drilling, pulps, polymers, slurries, pastes and complex mixtures involve viscoelastic fluids which examine both viscosity and elasticity. Viscoelastic fluids are subclasses of non-Newtonain fluids. Oldroyd-B fluid model is a significant rate type viscoelastic fluid which can simultaneously specify the features of relaxation and retardation. The rate type viscoelastic fluids carry one or more time derivatives in extra stress tensors. Bhatnagar et al. (1995) presented the flow of an Oldroyd-B fluid model. Heat transfer in the flow of an Oldroyd-B fluid due to stretching surface of decreasing index has been studied by Hayat et al. (2017). Rasheed and Anwar (2018) worked on fractional nonlinear viscoelastic fluid flow. Relaxation–retardation characteristics of Oldroyd-B fluid with viscous dissipation and chemical reaction are given by Zhang et al. (2018). Farooq et al. (2018) discussed three-dimensional Oldroyd-B fluid with Soret and Dufour effects. Chemical reacting species in a fractional viscoelastic fluid flow has been developed by Rasheed and Anwar (2019).

Nowadays, much attention has been focused on fluid flows caused by stretching cylinder with Soret and Dufour effects. When the phenomena of heat and mass transport occur simultaneously in liquid motion, then relations between driving potentials and enthalpy and mass fluxes are highly complicated. It is worth mentioning that not only does the temperature gradient produce heat flux, but also it is caused by the concentration gradient as well. Dufour effects describe the diffusion of heat transport via the concentration gradient, while Soret effects describe the temperature gradient that can cause mass flux. In many cases, these effects were often neglected due to their smaller magnitude in comparison with effects indicated by Fourier’s and Fick’s laws. Significant applications of Soret and Dufour effects in hydrology and petrology include solidification of binary alloys, isotope separation, groundwater pollutant migration, chemical reactors and geosciences multi-component melts. Nishimura et al. (1998) proposed a model of combined horizontal temperature and concentration gradients in a rectangular enclosure. The impact of non-uniform heated plate on double-diffusive natural convection of micropolar fluid in a square cavity with Soret and Dufour effects is given by Muthtamilselvan et al. (2018). Mudhaf et al. (2018) worked on the flow of natural convection in porous trapezoidal enclosures with Soret and Dufour effects. Oldroyd-B nanofluid flow due to stretching cylinder was investigated by Khan et al. (2019).

The main objective of the present article is to discuss the chemically reactive flow of Oldroyd-B nanofluid with heat and mass transfer mechanisms. The consequences of Brownian motion and thermophoresis diffusion in viscoelastic nanofluid due to stretching cylinder were examined. The influence of nonlinear radiative heat flux, internal heat generation/absorption and Soret and Dufour effects were also incorporated in detail. Reduced coupled nonlinear ordinary differential system was solved by OHAM (Awais et al. 2016; Anwar and Rasheed 2017; Gupta et al. 2018; Anwar and Rasheed 2018; Awais et al. 2018; Hayat et al. 2018b, c; Abel et al. 2012; Megahed 2013). The best optimal values of convergence control parameters are awarded in terms of numerical and graphical illustrations to study the emerging physical variables.

Modeling

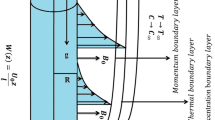
Here, two-dimensional axisymmetric flow of viscoelastic fluid obeying Oldroyd-B model due to stretching cylindrical sheet is examined. The contributions due to Brownian movement and thermophoresis phenomena are also explored. Soret and Dufour effects are accounted in a given flow configuration. The aspects of nonlinear radiation, first-order chemical reaction and non-uniform heat source/sink are imposed. Cylindrical coordinates $\left( {r,\,z} \right)$ are used to model the relevant equations. Flow is initiated due to a stretching cylinder with velocity $w_{\text{w}} = w_{0} \left( {\tfrac{z}{L}} \right)$ in the axial direction. Coordinate systems and geometry of the problem are shown in Fig. 1.

Fig. 1

Geometry of the problem

The relevant flow problem satisfies (Irfan et al. 2018; Alshomrani et al. 2018):

$$\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0,$$

(1)

$$\begin{aligned} u\frac{\partial w}{\partial r} + w\frac{\partial w}{\partial z} + \lambda_{1} \left[ {w^{2} \frac{{\partial^{2} w}}{{\partial z^{2} }} + u^{2} \frac{{\partial^{2} w}}{{\partial r^{2} }} + 2uw\frac{{\partial^{2} w}}{\partial r\partial z}} \right] = \nu \left[ {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{\partial r}} \right] \hfill \\ \;\;\; + \nu \lambda_{2} \left[ {\frac{u}{{r^{2} }}\frac{\partial w}{\partial r} - \frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial z} - \frac{2}{r}\frac{\partial u}{\partial r}\frac{\partial w}{\partial r} + \frac{w}{r}\frac{{\partial^{2} w}}{\partial r\partial z} - \frac{\partial w}{\partial r}\frac{{\partial^{2} w}}{\partial r\partial z} - 2\frac{\partial w}{\partial r}\frac{{\partial^{2} u}}{{\partial r^{2} }}} \right. \hfill \\ \;\;\;\left. { + \frac{u}{r}\frac{{\partial^{2} w}}{{\partial r^{2} }} - \frac{\partial w}{\partial z}\frac{{\partial^{2} w}}{{\partial r^{2} }} - w\frac{{\partial^{3} w}}{{\partial r^{2} \partial z}} + u\frac{{\partial^{3} w}}{{\partial r^{3} }}} \right], \hfill \\ \end{aligned}$$

(2)

$$\begin{aligned} u\frac{\partial T}{\partial r} + w\frac{\partial T}{\partial z} & = \alpha_{1} \left[ {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r}} \right] + \tau \left[ {D_{\text{B}} \frac{\partial C}{\partial r}\frac{\partial T}{\partial r} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial r}} \right)^{2} } \right] \\ & \;\;\; - \frac{1}{{\left( {\rho C_{\text{p}} } \right)}}\frac{1}{r}\frac{\partial }{\partial r}\left( {rq} \right) + \frac{{D_{\text{B}} K_{\text{T}} }}{{\mu C_{\text{p}} C_{\text{s}} }}\left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{\partial r}} \right) + \frac{1}{{\left( {\rho C_{\text{p}} } \right)}}Q^{\prime\prime\prime}, \\ \end{aligned}$$

(3)

$$\begin{aligned} u\frac{\partial C}{\partial r} + w\frac{\partial C}{\partial z} \, = \, & D_{\text{B}} \left[ {\left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{\partial r}} \right)} \right] + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left[ {\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r}} \right)} \right]\, \\ & + \, \frac{{D_{\text{B}} K_{\text{T}} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r}} \right) - K_{\text{c}} \left( {C - C_{\infty } } \right), \\ \end{aligned}$$

(4)

where $\left( {w,\,u} \right)$ are the components of velocity in $z$ and $r$ directions, respectively, $\lambda_{1}$ is the relaxation time, $\lambda_{2}$ is the retardation time, $\nu$ is the kinematic viscosity, $\alpha_{1} = \tfrac{k}{{\left( {\rho C_{\text{p}} } \right)}}$ is the thermal diffusivity, $T$ is the temperature, $\tau = \tfrac{{\left( {\rho C_{\text{p}} } \right)}}{{\left( {\rho C_{\text{f}} } \right)}}$ is the heat capacity ratio, $D_{\text{B}}$ is the Brownian diffusion coefficient, $D_{\text{T}}$ is the thermophoresis diffusion coefficient, $C$ is the nanoparticle volume fraction, $\mu$ is the dynamic viscosity, $\rho$ is the fluid density, $C_{\text{p}}$ is the specific heat, $C_{\text{s}}$ is the concentration susceptibility and $K_{\text{c}}$ is the chemical reaction rate. The nonlinear radiative heat flux is given by

$$q = - \frac{{4\sigma^{ * } \partial T^{4} }}{{3k^{ * } \partial r}} = - \frac{{16\sigma^{ * } }}{{3k^{ * } }}T^{3} \frac{\partial T}{\partial r},$$

(5)

where $\sigma^{ * }$ and $k^{ * }$ are the Stefan–Boltzmann and Rosseland mean absorption coefficient, respectively. Utilizing Eqs. (5) in (3) we have

$$\begin{aligned} u\frac{\partial T}{\partial r} + w\frac{\partial T}{\partial z} \,= \, & \alpha_{1} \left[ {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r}} \right] + \tau \left[ {D_{\text{B}} \frac{\partial C}{\partial r}\frac{\partial T}{\partial r} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial r}} \right)^{2} } \right]\, \\ & \;\; + \frac{1}{{\left( {\rho C_{\text{p}} } \right)_{\text{f}} }}\frac{{16\sigma^{ * } }}{{3k^{ * } }}\frac{1}{r}\frac{\partial }{\partial r}\left( {rT^{3} \frac{\partial T}{\partial r}} \right) + \frac{1}{{\left( {\rho C_{\text{p}} } \right)}}Q^{\prime\prime\prime}. \\ \end{aligned}$$

(6)

The non-uniform heat source/sink is modeled as:

$$Q^{\prime\prime\prime} = \left( {\frac{{kw_{\text{w}} }}{z\nu }} \right)\,\left[ {A^{ * } \left( {T_{\text{w}} - T_{\infty } } \right)\,f^{\prime} + \left( {T - T_{\infty } } \right)\,B^{ * } } \right],$$

(7)

where $A^{ * }$ and $B^{ * }$ are parameters of the space-dependent and temperature-dependent internal heat generation/absorption, respectively. The case corresponds to internal heat generation when $\left( {A^{ * } > 0} \right)$ and $\left( {B^{ * } > 0} \right)$, and correspond to internal heat absorption when $\left( {A^{ * } < 0} \right)$ and $\left( {B^{ * } < 0} \right)$.

The associated boundary conditions are

$$\begin{aligned} u = 0,\, & \, v = 0,\, \, w = w_{w} = \frac{{zw_{0} }}{L},\, \, T = T_{\text{w}} ,\, \, C = C_{w} ,\,{\text{ at }}r = R_1, \\ & \;\;w \to w_{\infty } ,\, \, T \to T_{\infty } ,\, \, C \to C_{\infty } ,\,{\text{ as }}r \to \infty . \\ \end{aligned}$$

(8)

Selecting

$$\begin{aligned} u & = - \frac{R_1}{r}\sqrt {\frac{{\nu w_{0} }}{L}} f\left( \xi \right),\, \, w = \frac{{zw_{0} }}{L}f^{\prime}\left( \xi \right),\, \, \theta \left( \xi \right) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}, \\ \, \phi (\xi ) & = \frac{{C - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }},\, \, \xi = \frac{{r^{2} - R_1^{2} }}{2R_1}\sqrt {\frac{{w_{0} }}{L\nu }} . \\ \end{aligned}$$

(9)

Equations (2), (3) and (6) take the form

$$\begin{aligned} (1 + 2\alpha \xi )f^{\prime\prime\prime} & + 2\xi f^{\prime\prime} + ff^{\prime\prime} - f^{\prime 2} + 2\beta_{1} ff^{\prime}f^{\prime\prime} - \beta_{1} f^{2} f^{\prime\prime\prime} - \frac{{\xi \beta_{1} }}{(1 + 2\xi \eta )}f^{2} f^{\prime\prime} \\ & + (1 + 2\alpha \eta )\beta_{2} (f^{\prime \prime 2} - ff^{iv} ) - 4\alpha \beta_{2} ff^{\prime\prime\prime} = 0, \\ \end{aligned}$$

(10)

$$\begin{aligned} \frac{1}{Pr} & \left[ {\left( {1 + R\left( {\theta \left( {\theta_{\text{w}} - 1} \right) + 1} \right)^{3} } \right)\,\left( {\left( {1 + 2\alpha \xi } \right)\,\theta^{\prime\prime} + 2\alpha \theta^{\prime}} \right)} \right] \\ & \;\; + \frac{3R}{Pr}\left[ {\left( {\theta \left( {\theta_{\text{w}} - 1} \right) + 1} \right)^{2} \left( {\theta_{w} - 1} \right)\,\left( {1 + 2\alpha \xi } \right)\,\theta^{\prime 2} } \right] + f\theta^{\prime} + (1 + 2\alpha \eta )Nb\theta^{\prime}\phi^{\prime} \\ & \;\; + \left( {1 + 2\alpha \eta } \right)Nt\theta^{\prime 2} + \left( {q_{1} f^{\prime} + q_{2} \theta } \right) + D_{f} \left( {\left( {1 + 2\alpha \xi } \right)\,\phi^{\prime\prime} + 2\alpha \phi^{\prime}} \right) = 0, \\ \end{aligned}$$

(11)

$$\begin{aligned} \left( {1 + 2\alpha \eta } \right)\phi^{\prime\prime} & + 2\alpha \phi^{\prime} + Sc \, f \, \phi^{\prime} \\ & \;\; + \left( {\frac{Nt}{Nb} + S_{\text{r}} S_{\text{c}} } \right)\,\left( {\left( {1 + 2\alpha \xi } \right)\,\theta^{\prime\prime} + 2\alpha \theta^{\prime}} \right) - ScC_{r} \phi = 0, \\ \end{aligned}$$

(12)

$$f(0) = 0,\, \, f^{\prime}(0) = 1,\, \, \theta (0) = 1,\, \, \phi (0) = 1,$$

(13)

$$f^{\prime}(\infty ) = 0,\, \, \theta (\infty ) = 0,\, \, \phi (\infty ) = 0,$$

(14)

where $\beta_{1} = \tfrac{{w_{0} \lambda_{1} }}{L}$ is the Deborah number with respect to relaxation time, $\beta_{2} = \tfrac{{w_{0} \lambda_{2} }}{L}$ the Deborah number with respect to retardation time, $Pr = \tfrac{{\left( {\mu C_{\text{p}} } \right)}}{k}$ the Prandtl number, $R = \tfrac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } k}}$ the radiation parameter, $Nb = \tfrac{{\tau \left( {C_{\text{w}} - C_{\infty } } \right)\,D_{\text{B}} }}{\nu }$ the Brownian motion parameter, $Nt = \tfrac{{\tau \left( {T_{w} - T_{\infty } } \right)\,D_{\text{T}} }}{{T_{\infty } \nu }}$ the thermophoresis parameter, $S_{\text{r}} = \tfrac{{D_{\text{B}} K_{\text{T}} \left( {T_{\text{w}} - T_{\infty } } \right)}}{{\left( {C_{\text{w}} - C_{\infty } } \right)\,\nu T_{\infty } }}$ the Soret number, $D_{\text{f}} = \tfrac{{D_{\text{B}} K_{\text{T}} \left( {C_{\text{w}} - C_{\infty } } \right)}}{{\left( {T_{\text{w}} - T_{\infty } } \right)\,C_{\text{p}} C_{\text{s}} }}$ the Dufour number, $C_{\text{r}} = \tfrac{{LK_{\text{c}} }}{{w_{0} }}$ the chemical reaction parameter, $Sc = \tfrac{\nu }{{D_{\text{B}} }}$ the Schmidt number, and the curvature parameter $\alpha = \sqrt {\tfrac{L\nu }{{w_{0} R_1^{2} }}}$. It is worth pointing here that governing problem reduces to the Maxwell fluid case when $\beta_{2} = 0.$ Moreover, the analysis for the Newtonian model can be retrieved by selecting $\beta_{1} = 0.$

Quantities of interest

Nusselt number

Mathematically,

$$Nu = \frac{{zq_{\text{w}} }}{{k\left( {T_{\text{w}} - T_{\infty } } \right)}},$$

(15)

where wall heat flux is

$$q_{\text{w}} = -k{\left( {\frac{\partial T}{\partial r}} \right)}_{r = R_1} + \frac{{16\sigma^{ * } T^{3} }}{{3k^{ * } }}{\left( {\frac{\partial T}{\partial r}} \right)}_{r = R_1},$$

(16)

and dimensionless expression of $Nu$ is

$$Re_{z}^{ - 1/2} Nu = - \left[ {1 + R\left( {\theta_{\text{w}} } \right)^{3} } \right]\,\theta^{\prime}(0).$$

(17)

Sherwood number

$$Sh = \frac{{j_{\text{w}} }}{{D_{\text{B}} \left( {C_{\text{w}} - C_{\infty } } \right)}},$$

(18)

where the wall mass flux is

$$j_{\text{w}} = - D_{\text{B}} \left( {\frac{\partial C}{\partial r}} \right)_{r = R_1} ,$$

(19)

and the dimensionless expression of $Sh$ is

$$Re{\kern 1pt}_{z}^{ - 1/2} Sh = - \phi^{\prime}(0),$$

(20)

in which the local Reynolds number is $Re_{z} = zw_{w} \left( z \right)/\nu .$

Solution methodology

With the aim of computing the solutions, the best optimal values are determined using optimal (OHAM). We define the initial guess for both $\left( {f_{0} ,\, \, \theta_{0} ,\, \, \phi_{0} } \right)$ and $\left( {{\mathcal{L}}_{f} ,\, \, {\mathcal{L}}_{\theta } ,\, \, {\mathcal{L}}_{\phi } } \right)$ as

$$f_{0} (\xi ) = 1 - \exp ( - \xi ),\, \, \theta_{0} (\xi ) = \exp ( - \xi ),\, \, \phi_{0} (\xi ) = \exp ( - \xi ),$$

(21)

with

$${\mathcal{L}}_{f} = f^{\prime\prime\prime} - f^{\prime},\, \, {\mathcal{L}}_{\theta } = \theta^{\prime\prime} - \theta ,\, \, {\mathcal{L}}_{\phi } = \phi^{\prime\prime} - \phi ,$$

(22)

and

$$\begin{aligned} {\mathcal{L}}_{f} \left[ {\mathop C\limits^{ \circ }_{1} + \mathop C\limits^{ \circ }_{2} \exp ( - \xi ) + \mathop C\limits^{ \circ }_{3} \exp (\xi )} \right] = & \, 0,\, \\ {\mathcal{L}}_{\theta } \left[ {\mathop C\limits^{ \circ }_{4} \exp \left( \xi \right) + \mathop C\limits^{ \circ }_{5} \exp \left( { - \xi } \right)} \right] = & \, 0,\, \\ {\mathcal{L}}_{\phi } \left[ {\mathop C\limits^{ \circ }_{6} \exp \left( \xi \right) + \mathop C\limits^{ \circ }_{7} \exp \left( { - \xi } \right)} \right] = \, & 0,\, \\ \end{aligned}$$

(23)

where the arbitrary constants are $\mathop C\limits^{ \circ }$ ($i = 1 - 7$).

Optimal convergence control variables

Non-zero auxiliary parameters $\hbar_{f} ,$ $\hbar_{\theta }$ and $\hbar_{\phi }$ define the convergence region of the homotopy series solutions. Minimization concept is applied for obtaining the best optimal data of $\hbar_{f} ,$ $\hbar_{\theta }$ and $\hbar_{\phi }$ by taking averaged squared residual errors as deliberated by

$${\varrho }_{m}^{f} = \frac{1}{k + 1}\mathop \sum \limits_{l = 0}^{k} \left[ {{\mathcal{N}}_{f} \left( {\mathop \sum \limits_{i = 0}^{m} f\left( \xi \right),\,\mathop \sum \limits_{i = 0}^{m} \theta \left( \xi \right)} \right)_{\xi = l\delta \xi } } \right]^{2} ,$$

(24)

$${\varrho }_{m}^{\theta } = \frac{1}{k + 1}\mathop \sum \limits_{l = 0}^{k} \left[ {{\mathcal{N}}_{\theta } \left( {\mathop \sum \limits_{i = 0}^{m} f\left( \xi \right),\,\mathop \sum \limits_{i = 0}^{m} \theta \left( \xi \right),\,\mathop \sum \limits_{i = 0}^{m} \phi \left( \xi \right)} \right)_{\xi = l\delta \xi } } \right]^{2} ,$$

(25)

$${\varrho }_{m}^{\phi } = \frac{1}{k + 1}\mathop \sum \limits_{l = 0}^{k} \left[ {{\mathcal{N}}_{\phi } \left( {\mathop \sum \limits_{i = 0}^{m} f\left( \xi \right),\,\mathop \sum \limits_{i = 0}^{m} \theta \left( \xi \right),\,\mathop \sum \limits_{i = 0}^{m} \phi \left( \xi \right)} \right)_{\xi = l\delta \xi } } \right]^{2} ,$$

(26)

$${\varrho }_{m}^{t} = {\varrho }_{m}^{f} + {\varrho }_{m}^{\theta } + {\varrho }_{m}^{\phi } ,$$

(27)

where ${\varrho }_{m}^{t} = 0.0515078$ represents the total squared residual error, $\delta \xi = 0.5$ and $k = 20.$ The best optimal values of convergence control variables are $\hbar_{f} = - 1.21023,$ $\hbar_{\theta } = - 1.19268$ and $\hbar_{\phi } = - 1.47231$. Table 1 highlights the averaged residual errors with optimal values. A decline is observed for higher order of approximations. Plot for residual error is sketched in Fig. 2.

Fig. 2

Total error for Oldroyd-B fluid

Table 1 Optimal convergence control parameters and total averaged squared residual errors using BVPh 2.0

Discussion

This section provides the graphical outlook on the effects of significant flow variables on velocity, temperature, concentration, Nusselt number $\left( {Re_{z}^{{\tfrac{ - 1}{2}}} Nu} \right)$ and Sherwood number $\left( {Re_{z}^{{\tfrac{ - 1}{2}}} Sh} \right)$. The optimal homotopy technique is implemented. Table 2 is prepared to give a comparison of $\left( { - f^{\prime\prime}(0)} \right)$ in limiting cases with those of Hayat et al. (2018b) and Abel et al. (2012).

Table 2 Comparison of $- f^{\prime\prime}(0)$ in limiting sense for different values of $\beta_{1}$ when $\alpha = \beta_{2} = 0$

Velocity

Figure 3 is sketched to examine the the influence of Deborah number $\left( {\beta_{1} = 0.1,\,0.4,\,0.8,\,1.2} \right)$ on velocity. Here, we have noticed that the velocity of the fluid reduces gradually for higher $\left( {\beta_{1} } \right).$ Physically, Deborah number $\left( {\beta_{1} } \right)$ is the ratio of the timescale of the material response to observation timescale. We can judge the polymeric behavior of a material from three different cases. When $\left( {\beta_{1} < < 1} \right)$ the material is purely viscous, when $\left( {\beta_{1} > > 1} \right)$ the material is elastic like, and when $\left( {\beta_{1} = 1} \right)$ the material is viscoelastic. For higher values of $\left( {\beta_{1} } \right)$, stress relaxation is less in comparison to the characteristic timescale. Hence, the fluid behavior is closely similar to that of especially solid material. The role of retardation time parameter $\left( {\beta_{2} = 1.5,\,1.6,\,1.7,\,1.8} \right)$ on fluid velocity is plotted in Fig. 4. As expected, that motion of fluid increases for larger $\left( {\beta_{2} } \right)$. Basically, retardation time refers to time required for the buildup of shear stress in a fluid. Thus, it can show the timescale observation that is not explained by relaxation time. It is clear that flow parallel to the sheet accelerates with an enhancement in fluid retardation time. Figure 5 highlights the behavior of the curvature parameter $\left( {\alpha = 0,\,1,\,2,\,3} \right)$ for velocity. $f^{\prime}\left( \eta \right)$ is directly proportional to $\left( \alpha \right)$, due to the fact that the radius of the cylinder decreases when $\left( \alpha \right)$ amplifies. Therefore, fluid motion get experiences with minimum resistance and thus the velocity increases.

Fig. 3

Impact of β₁ on $f^{\prime}(\xi )$

Fig. 4

Impact of β₂ on $f^{\prime}(\xi )$

Fig. 5

Impact of α on $f^{\prime}(\xi )$

Temperature

Figure 6 shows the behavior of Brownian motion parameter $\left( {Nb = 0.1,\,0.4,\,0.7,\,1.1} \right)$ on temperature $\theta (\xi )$. It is observed that the temperature is a decreasing function of $\left( {Nb} \right).$ For multiple values of $\left( {Nt = 0.1,\,0.15,\,0.2,\,0.3} \right),$ the temperature field is depicted in Fig. 7 Physically for higher values of $\left( {Nt} \right)$, an enhancement in thermophoresis force develops which tends to move the nanoparticles from the hot to cold regions. Hence, the temperature rises. Figure 8 shows the influence of temperature ratio parameter $\left( {\theta_{\text{w}} = 1.1,\,1.3,\,1.5,\,1.7} \right)$ on temperature. It is obvious that an increase in $\left( {\theta_{\text{w}} } \right)$ enhances the temperature. Higher wall temperature in comparison with the ambient temperature of the fluid is observed due to larger $\left( {\theta_{\text{w}} } \right)$. Due to this, the temperature of the fluid increases gradually. Figure 9 provides the analysis for variation of the radiation parameter $\left( {R = 0.0,\,0.4,\,0.8,\,1.2} \right)$ on temperature. A rise in temperature curves is observed when $\left( R \right)$ is increased. Physically for higher values of $\left( R \right)$, the mean absorption coefficient decreases. The existence of a temperature difference is due to diffusion flux. This is a cause of temperature $\theta (\xi )$ enhancement. The temperature profile for different values of Dufour number $\left( {D_{\text{f}} = 0.2,\,0.6,\,1.0,\,1.4} \right)$ is analyzed in Fig. 10. It depicts that larger values of $\left( {D_{\text{f}} } \right)$ enhance the temperature field. Figure 11 shows the influence of Prandtl number $\left( {Pr = 0.5,\,1.0,1.5,\,2.0} \right)$ on temperature. For larger values of $\left( {Pr} \right)$, the temperature of the fluid decays. Prandtl number has an inverse relation to thermal diffusivity. Higher Pr creates a weaker thermal diffusivity which causes of reduction of temperature field. Figure 12 shows the influence of curvature parameter $\left( {\alpha = 0,\,1,\,2,\,3} \right)$ on temperature $\theta (\xi ).$ It is noted that when $\left( \alpha \right)$ increases, the temperature field is enhanced. Physically, the radius of curvature decreases, which reduces the interaction region of the cylinder with the liquid. Hence, the temperature profile increases.

Fig. 6

Impact of Nb on $\theta \left( \xi \right)$

Fig. 7

Impact of Nt on $\theta \left( \xi \right)$

Fig. 8

Impact of θ_w on $\theta \left( \xi \right)$

Fig. 9

Impact of R on $\theta \left( \xi \right)$

Fig. 10

Impact of D_f  on $\theta \left( \xi \right)$

Fig. 11

Impact of Pr on $\theta \left( \xi \right)$

Fig. 12

Impact of α on $\theta \left( \xi \right)$

Concentration

The physical aspects for increasing values of Brownian motion $\left( {Nb = 0.1,\,0.4,\,0.7,\,1.1} \right)$ and thermophoresis $\left( {Nt = 0.1,\,0.15,\,0.2,\,0.3} \right)$ are displayed in Figs. 13 and 14. We noted that $Nb$ and $Nt$ have conflicting impact on concentration $\phi \left( \xi \right).$ To examine the aspect of Soret number $\left( {S_{\text{r}} = 0.1,\,0.4,\,0.8,\,1.2} \right)$ on concentration $\phi \left( \xi \right),$ Fig. 15 has been prepared. There is an enhancement in the concentration profile for larger values of $Sr.$ Figure 16 shows the impact of the curvature parameter $\left( {\alpha = 0,\,0.1,\,0.2,\,0.3} \right)$ on concentration $\phi \left( \xi \right).$ It was reported that the concentration $\phi \left( \xi \right)$ increased with higher $\alpha$. Furthermore, in the case of a flat surface, the concentration boundary layer is dominant when associated with a stretching cylinder. The behavior of the chemical reaction parameter $(C_{\text{r}} = 0,\,0.3,\,0.6,\,0.9)$ on concentration $\phi \left( \xi \right)$ is plotted in Fig. 17. The concentration $\phi \left( \xi \right)$ declines for growing values of $C_{\text{r}}$. This happens because the species rate decays when $C_{\text{r}}$ intensifies. Hence, the concentration field $\phi \left( \xi \right)$ declines. Figure 18 illustrates that the concentration $\phi \left( \xi \right)$ declines for higher Schmidt number $\left( {Sc = 0.5,\,1.0,\,1.5,\,2.0} \right)$. Physically, smaller mass diffusivity causes a reduction in $\phi \left( \xi \right)$ when $Sc$ increases.

Fig. 13

Impact of Nb on $\phi \left( \xi \right)$

Fig. 14

Impact of Nt on $\phi \left( \xi \right)$

Fig. 15

Impact of S_r on $\phi \left( \xi \right)$

Fig. 16

Impact of α on $\phi \left( \xi \right)$

Fig. 17

Impact of C_r on $\phi \left( \xi \right)$

Fig. 18

Impact of Sc on $\phi \left( \xi \right)$

Heat transfer rate

The influences of Brownian motion $\left( {Nb} \right)$, thermophoresis parameter $\left( {Nt} \right),$ Dufour number $\left( {D_{\text{f}} } \right)$ and radiation parameter $\left( R \right)$ on Nusselt number $\left( {Nu} \right)$ are depicted in Figs. (19, 20, 21 and 22). The heat transfer quantity for higher values of $Nb,$ $Nt,$ $D_{\text{f}}$ and $R$ declines as shown in these plots.

Fig. 19

Impact of Nb on Nu

Fig. 20

Impact of Nt on Nu

Fig. 21

Impact of D_f on Nu

Fig. 22

Impact of R on Nu

Mass transfer rate

The behavior of Sherwood number $\left( {Sh} \right)$ for higher values of thermophoresis parameter $\left( {Nt} \right)$ and Soret number $\left( {S_{\text{r}} } \right)$ indicates a decline in the mass transfer quantity as shown in Figs. (23 and 24).

Fig. 23

Impact of Nt on Sh

Fig. 24

Impact of S_r on Sh

Major findings

Here, the impact of Soret and Dufour and nonlinear thermal radiation in Oldroyd-B nanofluid is reported by utilizing the optimal homotopic approach. The aspects of non-uniform heat sink/source and chemical reaction have been considered. This study indicated that the Deborah numbers $(\beta_{1}$ and $\beta_{2} )$ display opposite behavior for the velocity field. The temperature field increased Brownian motion $\left( {Nb} \right)$, thermophoresis $\left( {Nt} \right)$ and curvature $\left( \alpha \right)$ parameters. The impacts of Soret number $\left( {S_{\text{r}} } \right)$ and chemical reaction parameter $\left( {C_{\text{r}} } \right)$ are totally opposite on the concentration profile. For higher values of Schmidt number, the concentration of the nanofluid decreases. The local Nusselt number decreased for higher radiation parameter $\left( R \right)$ and Dufour number $\left( {D_{\text{f}} } \right)$. An enhancement in thermophoresis $\left( {Nt} \right)$ and Soret number $\left( {S_{\text{r}} } \right)$ caused the reduction of Sherwood number.