Thermal and solutal stratifications in flow of Oldroyd-B nanofluid with variable conductivity

Abstract

This article reports the heat transfer enhancement on magnetohydrodynamic (MHD) flow of Oldroyd-B nanofluid influenced by stretching cylinder. The aspects of mixed convection and heat sink/source are considered. The model used for nanofluid incorporate the properties of Brownian motion and thermophoresis. The temperature-dependent thermal conductivity with the influence of thermal and mass stratifications is adopted. The nonlinear PDEs are condensed into ODEs via apposite conversions. The analytically homotopic approach has been adopted to elucidate the nonlinear ODEs. The stimulus of essential concerns on velocity, temperature, concentration, Nusselt number and Sherwood number is depicted. This analysis reported that the liquid velocity has a conflicting tendency for larger magnetic and mixed convection parameter. Furthermore, the liquid temperature decays for the higher thermal stratification parameter, whereas analogous influence is being noticed for mass stratification parameter on concentration field. For the confirmation of these outcomes an assessment table with former effort is also established.

1 Introduction

The breakdown of non-Newtonian materials is that, it does not establish postulation of a linear correlation between the stress and the strain rate and, therefore, these are termed as non-Newtonian liquids (Refs. [1,2,3,4,5,6,7,8,9,10]). Countless experts and scientists are quite enthused to find ground-breaking features of nonlinear materials owing to their broad assortment in industrial and trade applications such as die swelling and yield stress. Numerous liquids such as greasing lubricants, penetrating sludge, organic liquids and liquid sparklers, which have viscoelastic behavior, and rheologically difficult liquids cannot be defined simply as Newtonian liquids. Oldroyd-B liquid is one of an ordinary subclass of non-Newtonian liquids where the convective derivative is switched by the time derivative and is solitary of an viscoelastic non-Newtonian liquid model that establishes the structures of both the relaxation and retardation time. In that instance, Hashmi et al. [11] scrutinized analytical elucidation of MHD mixed convective reactive flow of an Oldroyd-B liquid between isothermal stretching disks. They described that with the rise of Prandtl number and Eckert number, the liquid temperature intensifies; thus, the heat transfer amount becomes slower from lesser disk, whereas reverse trend is noted at upper disk. The flow between two unbounded equivalent rigid plates of a generalized Oldroyd-B liquid was considered by Feng et al. [12]. Khan et al. [13] explored the rotating flow of an Oldroyd-B liquid by utilizing the features of developed heat transfer and mass dispersion relations. They established that the thermal and concentration relaxation time parameters decay the temperature and concentration of Oldroyd-B liquid. Nourazar et al. [14] analyzed the thermal flow consideration of nanoliquid with the properties of magnetic field in porous stretching cylinder.

Recently, a breakthrough happened in the field of heat transfer at Argonne National Lab (ANL) by Choi [15], established on the incorporation of numerous nanomaterials (<100 nm) with diverse magnitude and shapes into conventional liquids. Over the years, countless diverse nanomaterials such as metals and ceramic nitride, carbon nanotubes (CNTs), oxide and carbide have been pooled with conventional liquids to produce remarkable heat conductors. These nanoliquids are exaggerated by numerous influences comprising agglomeration, stability, interfacial nanomaterial layering, Brownian motion and nanomaterial size. The strategic benefits of the nanoliquids are that they can be made to function to preferably attain particular purposes, such as reduction of friction, greater storing capacity thermal energy and coefficients of heat transfer. For instance, numerous studies have established that the growth of nanoparticles will expand the thermal resources of conventional base liquids such as thermal conductivity of base liquids (Refs.  [16,17,18,19,20,21,22]). Hayat et al. [23] reported the chemical species and variable thickness on nanofluid towards rotating disk. They initiated that the higher thickness coefficient decline the rate of surface shear stress while it enhance for silver-based nanoparticles of volume fraction. The stagnation point flow of unsteady 3D Al–Cu water nanoliquid is inspected by Nithyadavi et al. [24]. They detected that when unsteadiness parameter declines, the Nusselt number increases and the velocity gradient ratio intensifies in the nodal point area. Irfan et al. [25] scrutinized numerically the impact of temperature-dependent thermal conductivity and heat sink/source of unsteady 3D flow of Carreau nanoliquid. Two-phase flow by utilizing AgH$_{2}$O and CuH$_{2}$O nanomaterials with impact of radiation was studied by Hayat et al. [26]. Using non-integer Caputo time derivatives on fractional rate type nanomaterial was investigated by Anwar and Rasheed [27]. They noted that in lower and upper disks, conflicting performance is being established for Eckert number. The behavior of uniform Lorentz force on Fe3O4–water nanoliquid was reported by Sheikholeslami and Shehzad [28].

Stratification is a mechanism which has strategic impact on industries and natural advances. The temperature and concentration discrepancies or liquids having diverse densities are liable for the generation of stratification mechanisms. Instantaneously, occurrence of both heat and mass allocation provides double stratification. The attention concerning doubly stratified flows has implication in fabrication of sheet material, thermal energy storing structures analogous to solar ponds, assortments of heterogeneous in atmosphere, and dismissal of environmental heat such as oceans and canals and copper cords thinning. Waqas et al. [29] described the consequences of double stratification with the influence of heat generation on Oldroyd-B nanofluid. Numerically, the MHD nanoliquid stratified flow with viscous and Joule heating was reported by Daniel et al. [30]. They remarked that the thermal and mass stratifications clue to a decline in nanoparticle temperature and concentration. Mahantesh et al. [31] scrutinized the stimulus of an improved heat conduction relation and UMC nanoliquid with the phenomena of double stratification.

In the vision of overhead scrutiny, the purpose of this thoughtfulness is to highlighting the aspects of MHD mixed convection stratified flow of Oldroyd-B nanofluid. Additionally, temperature-dependent thermal conductivity and heat sink/source [32, 33] are presented for heat transfer mechanism. The convergent series elucidation of nonlinear ODEs is established via homotopic approach [34,35,36,37]. The influence of intricate parameters is conferred through graphs and tables.

2 Mathematical formulation

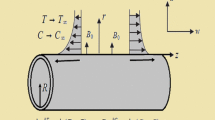
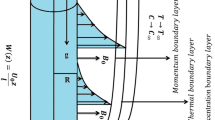
We scrutinize steady 2D axisymmetric mixed convection flow of magneto-Oldroyd-B nanofluid subject to double stratification towards stretching cylinder of radius R with velocity $\frac{U_{0}z}{l},$ along z-direction, where $(U_{0},l)$ is the reference velocity and specific length, respectively. The heat and mass transport phenomena are manifest subject to temperature-dependent thermal conductivity and heat source/sink. The impact of Brownian and thermophoresis is considered. Let the cylindrical polar coordinates (z, r) be considered in such a way that z-axis goes close to the axis of the cylinder and r-axis is restrained near the radial direction. Additionally, a uniform magnetic field of length $B_{0}$ is applied (as depicted in Fig. 1). Due to lower magnetic Reynolds number, the electric and induced magnetic fields are neglected. The equations of Oldroyd-B nanofluid under the assessment of overhead consideration are specified as follows:

$$\begin{aligned} \frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(1)

$$\begin{aligned}&u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}+\lambda _{1} \left[ w^{2}\frac{\partial ^{2}w}{\partial z^{2}}+u^{2}\frac{\partial ^{2}w}{ \partial r^{2}}+2uw\frac{\partial ^{2}w}{\partial r\partial z}\right] =v \left[ \frac{\partial ^{2}w}{\partial r^{2}}+\frac{1}{r}\frac{\partial w}{ \partial r}\right] \nonumber \\&+v\lambda _{2}\left[ \begin{array}{c} \frac{u}{r^{2}}\frac{\partial w}{\partial r}-\frac{1}{r}\frac{\partial w}{ \partial r}\frac{\partial w}{\partial z}-\frac{2}{r}\frac{\partial u}{ \partial r}\frac{\partial w}{\partial r}+\frac{w}{r}\frac{\partial ^{2}w}{ \partial r\partial z}-\frac{\partial w}{\partial r}\frac{\partial ^{2}w}{ \partial r\partial z}-2\frac{\partial w}{\partial r}\frac{\partial ^{2}u}{ \partial r^{2}} \\ +\frac{u}{r}\frac{\partial ^{2}w}{\partial r^{2}}-\frac{\partial w}{\partial z}\frac{\partial ^{2}w}{\partial r^{2}}+w\frac{\partial ^{3}w}{\partial r^{2}\partial z}+u\frac{\partial ^{3}w}{\partial r^{3}} \end{array} \right] \nonumber \\&+\frac{\sigma B_{0}^{2}}{\rho _{f}}\left( -w-\lambda _{1}u\frac{\partial w }{\partial r}\right) +g[\beta _{T}(T-T_{\infty })+\beta _{C}(C-C_{\infty })], \end{aligned}$$

(2)

$$\begin{aligned}&u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}=\frac{1}{ \left( \rho c\right) _{f}}\frac{1}{r}\frac{\partial }{\partial r}\left[ K(T)\left( r\frac{\partial T}{\partial r}\right) \right] \nonumber \\&+\tau \left[ D_{B}\frac{\partial C}{\partial r}\frac{\partial T}{\partial r} +\frac{D_{T}}{T_{\infty }}\left( \frac{\partial T}{\partial r}\right) ^{2} \right] +\frac{Q_{0}(T-T_{\infty })}{(\rho c)_{f}}, \end{aligned}$$

(3)

$$\begin{aligned} u\frac{\partial C}{\partial r}+w\frac{\partial C}{\partial z}=D_{B}\frac{1}{r }\frac{\partial }{\partial r}\left( r\frac{\partial C}{\partial r}\right) + \frac{D_{T}}{T_{\infty }}\frac{1}{r}\frac{\partial }{\partial r}\left( r \frac{\partial T}{\partial r}\right) , \end{aligned}$$

(4)

with boundary conditions

$$\begin{aligned} w(z,r)&= W(z)=\frac{U_{0}z}{l},\,\, u(z,r)=0,\,\, T=T_{w}=T_{0}+d_{1}z, \nonumber \\ C&= C_{w}=C_{0}+e_{1}z\,\text {at}\,r=R,\end{aligned}$$

(5)

$$\begin{aligned} w\rightarrow & {} 0,\,\,T\rightarrow T_{\infty }=T_{0}+d_{2}z,\,\,\,C\rightarrow C_{\infty }=C_{w}=C_{0}+e_{2}z\,\,\text {as } r\rightarrow \infty \text {,} \end{aligned}$$

(6)

where (w,  u) are the components of velocity in z- and r-directions respectively, $\nu$ is the kinematic viscosity, $\lambda _{i}$ and $(i=1,2)$ are the relaxation and retardation times, respectively, $\sigma$ is the electrical conductivity of nanoliquid, g is the gravitational acceleration, $(\beta _{T}$ and $\beta _{C})$ are the thermal and concentration expansion coefficients, respectively, $(\rho _{f}$ and $c_{f})$ are the liquid density and specific heat of the liquid, respectively, and k is the thermal conductivity of nanoliquid, $\tau$ is the ratio of effective heat capacity of the nanoparticle material to the heat capacity of the base liquid, $Q_{0}$ is the heat sink/source coefficient, (T,  C) are the nanoliquid temperature and concentration, respectively, $(T_{w}$ and $C_{w})$ are the wall temperature and concentration, respectively, $(D_{B\text { }}$ and $D_{T})$ are the Brownian and thermophoresis diffusion coefficients, respectively, $(T_{0}$ and $C_{0})$ are the reference temperature and concentration, respectively, $(d_{1},d_{2},e_{1},e_{2})$ are the dimensional constants and K(T) is the temperature-dependent thermal conductivity which is given by the following expression:

$$\begin{aligned} K(T)=k_{\infty }\left[ 1+\varepsilon \left( \frac{T-T_{\infty }}{\Delta T} \right) \right] , \end{aligned}$$

(7)

where $\left( k_{\infty },\varepsilon \right)$ are the nanoliquid thermal conductivity far away from the stretched surface and the thermal conductivity parameter, respectively, and $\Delta T=T_w-T_0.$

Fig. 1

Flow configuration

Utilizing the following conversions

$$\begin{aligned} u= & {} -\frac{R}{r}\sqrt{\frac{U_{0}\nu }{l}}f(\eta ),\,\, w=\frac{ U_{0}z}{l}f^{\prime }(\eta ),\,\,\theta (\eta )=\frac{T-T_{\infty }}{ T_{w}-T_{0}}, \nonumber \\ \phi (\eta )= & {} \frac{C-C_{\infty }}{C_{w}-C_{0}},\, \, \eta =\sqrt{ \frac{U_{0}}{\nu l}}\left( \frac{r^{2}-R^{2}}{2R}\right) . \end{aligned}$$

(8)

By means of the overhead conversions, the Eq. (1) is satisfied automatically and Eqs. (2)–(6) yield

$$\begin{aligned}&(1+2\alpha \eta )f^{\prime \prime \prime }+2\alpha f^{\prime \prime }+ff^{\prime \prime }-f^{\prime 2}+2\beta _{1}ff^{\prime }f^{\prime \prime }-\beta _{1}f^{2}f^{\prime \prime \prime }-\frac{\alpha \beta _{1}}{ (1+2\alpha \eta )}f^{2}f^{\prime \prime }+\nonumber \\&(1+2\alpha \eta )\beta _{2}(f^{\prime \prime 2}-ff^{iv})-4\alpha \beta _{2}ff^{\prime \prime \prime }-M^{2}(f^{\prime }-\beta _{1}ff^{\prime \prime })+\lambda (\theta +N\phi )=0, \end{aligned}$$

(9)

$$\begin{aligned}&(1+2\alpha \eta )(\theta \theta ^{\prime \prime }+\theta ^{\prime 2})\epsilon +2\alpha \epsilon \theta \theta ^{\prime }+(1+2\alpha \eta )\theta ^{\prime \prime }+2\alpha \theta ^{\prime }+\Pr f\theta ^{\prime }-\Pr f^{\prime }\theta \nonumber \\&+(1+2\alpha \eta )\Pr N_{b}\theta ^{\prime }\phi ^{\prime }+(1+2\alpha \eta )\Pr N_{t}\theta ^{\prime 2}-\Pr S_{1}f^{\prime }+\Pr \delta \theta =0, \end{aligned}$$

(10)

$$\begin{aligned} (1+2\alpha \eta )\phi ^{\prime \prime }+2\alpha \phi ^{\prime }- & {} Le\Pr f^{\prime }\phi +Le\Pr f\phi ^{\prime }+(1+2\alpha \eta )\left( \frac{N_{t}}{ N_{b}}\right) \theta ^{\prime \prime }\nonumber \\+ & {} 2\alpha \left( \frac{N_{t}}{N_{b}}\right) \theta ^{\prime }-Le\Pr S_{2}f^{\prime }=0, \end{aligned}$$

(11)

$$\begin{aligned} f(0)= & {} 0,\,\,f\text { }^{\prime }(0)=1,\,\,\theta \left( 0\right) =1-S_{1},\ \ \ \phi \left( 0\right) =1-S_{2}, \end{aligned}$$

(12)

$$\begin{aligned} f^{\prime }(\infty )= & {} 0,\,\,\theta (\infty )=0,\,\,\phi (\infty )=0, \end{aligned}$$

(13)

where $\alpha \left( =\frac{1}{R}\sqrt{\frac{\nu l}{U_{0}}}\right)$ is the curvature parameter,  $\beta _{i}\left( =\frac{\lambda _{i}U_{0}}{l}\right)$ $i=1,2$ the Deborah numbers, $M\left( =\sqrt{\frac{\sigma lB_{0}^{2}}{ U_{0}\rho _{f}}}\right)$ the magnetic parameter, $\lambda \left( =\frac{ g\beta _{T}l^2(T_{w}-T_{0 })}{U_0^{2}z}\right) ,$ the mixed convection parameter, $N\left( =\frac{\beta _{c}(C_{w}-C_{0 })}{\beta _{T}(T_{w}-T_{0})}\right) \$ the Buoyancy ratio parameter, $\Pr \left( =\frac{\nu }{\alpha _{1}}\right)$ the Prandtl number, $N_{b}\left( =\frac{ \tau D_{B}(C_{w}-C_{0 })}{\upsilon }\right)$ the Brownian motion parameter, $N_{t}\left( =\frac{\tau D_{T}(T_{w}-T_{0 })}{\upsilon T_{w }}\right)$ the thermophoresis parameter, $\delta \left( =\frac{ lQ_{0}}{U_{0}(\rho c)_{f}}\right)$ the heat sink/source parameter,$\ Le\left( =\frac{\alpha _{1}}{D_{B}}\right)$ the Lewis number, $S_{1}(=\frac{ d_{2}}{d_{1}})$ the thermal stratification and $S_{2}(=\frac{e_{2}}{e_{1}})$ the mass stratification parameters.

2.1 Physical quantities of interest

The quantities of interest, the local Nusselt number $\left( Nu_{z}\right)$ and local Sherwood number $\left( Sh_{z}\right)$, are

$$\begin{aligned} Nu_{z}=\frac{zq_{m}}{k(T_{w}-T_{\infty })},\,\,Sh_{z}=\frac{zj_{m}}{ D_{B}(C_{w}-C_{\infty })}, \end{aligned}$$

(14)

where $q_{m}$ and $\ j_{m}$ are the heat and mass flux, respectively

$$\begin{aligned} q_{m}=-k\left( \frac{\partial T}{\partial r}\right) _{r=R}, \,\,j_{m}=-D_{B}\left( \frac{\partial C}{\partial r}\right) _{r=R}. \end{aligned}$$

(15)

The dimensionless form of the above expression is given by

$$\begin{aligned} Nu_{z}\mathop {Re_z}^{-\frac{1}{2}}=-\left( \frac{1}{1-S_{1}}\right) \theta ^{\prime }(0),\,\,Sh_{z}\mathop {Re_z}^{-\frac{1}{2}}=-\left( \frac{1 }{1-S_{2}}\right) \phi ^{\prime }\left( 0\right) , \end{aligned}$$

(16)

where ${Re}_{z}=\frac{W(z)z}{\nu }$ is local Reynolds number.

2.2 Convergence of the homotopy solutions

The supporting $\hslash _{f}$, $\hslash _{\theta }$ and $\hslash _{\phi }$ are very enthusiastic to adjust the convergence of the series solutions via homotopic approach. The related value of these auxiliary parameters is anticipated by seeing least square error which is given by

$$\begin{aligned} F_{f,m}=\frac{1}{N+1}\sum \limits _{j=0}^{N}\left[ N_{f}\sum \limits _{i=0}^{m}F_{j}\left( i\Delta \eta \right) \right] ^{2}. \end{aligned}$$

(17)

Table 1 validates the convergence of the series solution which displays that convergent solution for the velocity is attained at 18th order of estimation while such a convergence for temperature and concentration is also achieved at 21st order of estimation.

Table 1 Convergence of homotopy solutions when $\alpha =\beta _{1}=\beta _{2}=\lambda =N=\delta =N_{t}=0.1,$ $S_{1}=S_{2}=$ $\epsilon =N_{b}=0.2,$ $\ M=0.3,$ Pr $=2.0$ and $Le=1.0$ are fixed.

3 Analysis of results

This crucial intention here is to disclose the graphical depiction of essential somatic parameters of Oldroyd-B nanoliquid influenced by a stretching surface on velocity, temperature and concentration fields via homotopic approach. Furthermore, properties of magnetic field, mixed convection, temperature-dependent thermal conductivity, stratifications and heat sink/source are incorporated.

3.1 Impact of M and $\lambda$ on $f^{\prime }(\eta )$

Figure 2a, b visualizes the performance of magnetic parameter M and mixed convection parameter $\lambda$ on velocity component. From these scheme it is remarkable to note that the liquid velocity decline via enormous values of M which diminishes the thickness of boundary layer while the impact of $\lambda$ is entirely conflicting for velocity component. Infect augmentations in the Lorentz force reason much resistance in the liquid flow which retards liquid velocity.

Fig. 2

a, b Variation of M and $\lambda$ on$\ f^{\prime }(\eta )$

3.2 Impact of M and $\beta _{2}$ on $\theta (\eta )$

The characteristics of magnetic parameter M and Deborah number $\beta _{2}$ on nanoliquid temperature of Oldroyd-B fluid for amassed values of these parameters is reported in Fig. 3a, b. Strengthening in the values of M enhances the liquid temperature and its allied thickness of the boundary layer. For higher values of M the Lorentz force augments which produce additional heat that outcomes the temperature field growths. Instead, the nanoliquid temperature spectacles the reverse tendency for progressive values of $\beta _{2}$. As $\beta _{2}$ comprises retardation time, which resembles a lesser temperature for greater retardation time. Hence, we establish a consequence that augmented values of M reason advances in temperature, but larger $\beta _{2}$ portrays lesser in nanoliquid temperature of Oldroyd-B liquid.

Fig. 3

a, b Variation of M and $\beta _{2}$ on $\theta (\eta )$

3.3 Impact of $(\delta <0)$ and $(\delta>0)$ on $\theta (\eta )$

Aspects of heat sink $(\delta <0)$ and source $(\delta>0)$ parameter in temperature field are depicted in Fig. 4a, b. From these designs we can notice that the heat sink parameter is declining function of temperature for progressive values of heat sink parameter via larger heat source parameter heightened both the temperature and allied thickness of the boundary layer. In fact, considerable heat is transferred to the liquid which reasons the magnification in the nanoliquid temperature of Oldroyd-B fluid. Therefore, finally we govern that the influence of heat sink/source is moderately antithesis on temperature field.

Fig. 4

a, b Variation $\delta <0$ and $\delta>0$ on $\theta (\eta )$

3.4 Impact of $N_{t}$ and $N_{b}$ on $\theta (\eta )$

The characteristics of thermophoretic parameter $N_{t}$ and Brownian motion $N_{b}$ on nanoliquid temperature are shown in Fig. 5a, b which spectacle an energetic measure in heat transfer. From these schemes, rise in $N_{t}$ and $N_{b}$ results in the heightening of temperature and its allied thickness of the boundary layer. Physically, when we rise $N_{t}$ and $N_{b}$ the thermal conductivity of liquid increases. Such existence of nanoparticles exaggerates the liquid thermal conductivity which forms an increasing behavior in the liquid temperature. Additionally, the Brownian motion parameter $N_{b}$ increases the particle collision which delivers additional heat that is liable for the boost of temperature field.

Fig. 5

a, b Variation $N_{t}$ and $N_{b}$ on $\theta (\eta )$

3.5 Impact of $\epsilon$ and $S_{1}$ on $\theta (\eta )$

Figure 6a, b shows the stimulus of deviation in thermal conductivity $\epsilon$ and thermal stratification parameter $S_{1}$ on temperature distribution. The temperature of Oldroyd-B liquid enriched for amassed values of $\epsilon$ as exposed in Fig. 6a. The thermal conductivity of nanoliquid enhanced the heat transfer proficiency which aims to increase the liquid temperature. Instead, the behavior of $S_{1}$ is reasonably differing to the thermal conductivity and boost in $S_{1}$ decays the liquid temperature. In detail, when we augment $S_{1}$ then the consistency between the heated surface temperature and away from the surface decays. Consequently, the liquid temperature is noticed to be declining.

Fig. 6

a, b Variation of $\epsilon$ and $S_{1}$ on $\theta (\eta )$

3.6 Impact of $N_{t}$ and $N_{b}$ on $\phi (\eta )$

The interpretation of $N_{t}$ and $N_{b}$ on nanoparticle volume fraction on the Oldroyd-B liquid is portrayed in Fig. 7a, b. It fits out from these drafts that with the magnification of $N_{t}$ and $N_{b}$ the nanoparticle volume fraction of the liquid intensifies for $N_{t}$ while it diminishe for $N_{b}$. Actually, with intensification in $N_{t}$ the thermophoresis force increase, which tends to transport nanoparticles from hot to cold regions and, therefore, the magnitude of nanoparticle volume fraction fields grows. Thus, the concentration of Oldroyd-B liquid boosts. Moreover, the macroscopic particle collision of the liquid augments when we enhance $N_{b},$ because Brownian motion $N_{b}$ is the unsystematic association of nanomaterials which decline the concentration field as presented in scheme 7(b).

Fig. 7

a, b Variation of $N_{t}$ and $N_{b}$ on $\phi (\eta )$

3.7 Impact of $S_{2}$ and Le on $\phi (\eta )$

To scrutinize the properties of mass stratification parameter $S_{2}$ and Lewis number Le on concentration field Fig. 8a, b is depicted. These drafts explore that $S_{2}$ and Le are retreating functions of concentration profile. Physically, it is notable that when we enhance $S_{2}$ the volumetric fraction between surface and reference nanomaterials decays. Hence, the nanoliquid concentration field declines. Thus, these consequences specify that the analogous impact of both parameters is identified in nanoliquid concentration field.

Fig. 8

a, b Variation of $S_{2}$ and Le on $\phi (\eta )$

3.8 Local Nusselt number $-\theta ^{\prime }(0)$ and local Sherwood number $-\phi (0)$

The graphical portrayal of different values of $\alpha$, $S_{1}$, $\epsilon ,$ Pr, $N_{t}$ and $N_{b}$ on wall temperature gradient $-\theta ^{\prime }(0)$ and $S_{2},$ Le on Sherwood number is discussed in Figs. 9a, b, 10a, b 11a, b and 12a, b. These depictions show that the Nusselt number $-\theta ^{\prime }(0)$ enhanced when we increase the values of $\alpha$ and Pr whereas it reduced for $S_{1}$, $\epsilon ,$ $N_{t}$ and $N_{b}$ as displayed in Figs. 9a, b, 10, and 11a, b. Moreover, Fig. 12a, b displays the variation of $S_{2}$ and Le on $-\phi (0)$. From these plans, we remarked that the impact of both the parameters is quite conflicting on $-\phi (0).$ Additionally, Table 2 is the assessment table of $-f^{\prime \prime }(0)$ of the present outcomes with existing text and displays a brilliant agreement.

Fig. 9

a, b Variation $\alpha$ and $S_{1}$ on $-\theta ^{\prime }(0)$

Fig. 10

a, b Variation of $\epsilon$ and Pr on $-\theta ^{\prime }(0)$

Fig. 11

a, b Variation of $N_{t}$ and $N_{b}$ on $-\theta ^{\prime }(0)$

Fig. 12

a, b Variation of $S_{2}$ and Le on $-\phi ^{\prime }(0)$

Table 2 Comparison values of $-f^{\prime \prime }(0)$ for numerous values of $\ \beta _{1}$ in limiting cases when $\alpha =\beta _{2}=M=\lambda =N=0$.

4 Main points

This article scrutinized the impact of mixed convection and magnetic field with the influence of thermal and mass stratification on Oldroyd-B nanofluid towards stretching cylinder. The phenomena of heat transport is deliberated subject to temperature-dependent thermal conductivity and heat sink/source. The core facts of overhead scrutiny are declared as follows:

• The magnetic parameter M decayed the liquid velocity as well as the temperature of Oldroyd-B nanofluid although it enhanced for mixed convection parameter $\lambda$.

• An augmented value of thermal stratification parameter $S_{1}$ declined the temperature while similar drift were being identified for mass stratification parameter $S_{2}$ on concentration field.

• Quite analogous depiction were noted in temperature distribution for increasing values of thermophoretic parameter $N_{t}$, Brownian motion $N_{b}$ and variable conductivity parameter $\epsilon .$

• Impacts of Deborah number $\beta _{2}$ on temperature and Lewis number Le on concentration of Oldroyd-B nanofluid are same.

• The local Nusselt number enhanced for Prandtl number Pr while it decayed for thermophoretic parameter $N_{t}$ and Brownian motion $N_{b}.$