Chemically reactive and nonlinear radiative heat flux in mixed convection flow of Oldroyd-B nanofluid

Abstract

This paper investigates the aspects of magnetic field and chemical reaction in Oldroyd-B nanofluid influenced by a stretching cylinder. The properties of mixed convection, nonlinear radiation and heat sink/source are incorporated. By means of noteworthy conversions, the nonlinear PDEs are altered into nonlinear ODEs and elucidated via homotopic approach. The influence of countless variables for velocity, temperature and concentration fields in addition to local Nusselt and Sherwood numbers are portrayed and conferred. These upshots portray that the liquid velocity enhances for intensifying value of mixed convection parameter whereas, it diminish for magnetic parameter. Moreover, the Brownian motion parameter and radiation parameter enhances the liquid temperature of Oldroyd-B nanofluid. For the endorsement of current upshots an assessment values in restrictive circumstances is also presented.

Introduction

At present, the thoughtfulness of nanomaterial’s has increased noteworthy reputation from the researchers and scientists. Limited thermal aspects of established liquids confine their suitability for up-to-date utilizations demanding a high level enactment, while retaining compact size of the thermal structures. For instance, micro-electromechanical systems and make cold of chips in computer mainframes and to acquire fast transient systems in warming structures. Nanoliquids are diluted deferral of nano-scale elements in disreputable liquids which exaggerates the heat transfer of the elucidation and intensify the storage propensity. Nanofluids have engrossing thermo-physical aspects and heat transfer enactment with energetic probable uses owing to which these are deliberated as next generation heat transport liquids. The hybrid-powered procedures, solar accumulators, engine and energy cells, pharmacological development and atomic uses are specimens of developing nanotechnologies. The notion to intensifying the thermal conductivity of disreputable liquids was presented by Choi (1995). Later on, numerous theoretical and experimental exertions are established to scrutinize the diverse aspects of nanofluids see (Mustafa et al. 2015; Mahanthesh et al. 2016, 2017a, b; Hayat et al. 2017a, b; Anwar and Rasheed 2017; Haq et al. 2017; Khan et al. 2017). Numerically a reviewed model for MHD flow of Carreau nanomaterial was considered by Waqas et al. (2017a). Their study established that radiation parameter and Biot number enhanced the liquid temperature of Carreau nanofluid. By exploiting the approach of CVFEM, Sheikholeslami and Oztop (2017) reported the aspect of MHD in ${\text{Fe}}_{3} {\text{O}}_{4}$-water nanoliquid in a cavity with sinusoidal outside cylinder. Aspects of chemical reaction and MHD in 3D radiative flow of nanofluid were considered by Hayat et al. (2018). They noted that the nanoparticles volume fraction and magnetic parameter rises the skin friction coefficient. The properties of the heat sink/source and convective heat transport in Maxwell nanomaterial was explored by Irfan et al. (2018). They acquired that the liquid velocity decays for magnetic parameter and intensified the temperature and concentration fields. Recently, Ellahi (2018) disclosed the modern advances of nanoliquids. He reported that nanofluid technology can benefit to improve superior emollients and oils for real-world solicitations. Haq et al. (2019) reported the behavior of thermal management of carbon nanotubes in partially heated triangular cavity. Sheikholeslami et al. (2019) studied the aspect of heat transport by heat storage unit utilizing nanoparticles.

No doubt the behavior of chemical reaction spectacles enthusiastic parts with the intention to scrutinize the aspects of heat and mass transport in built-up regions. Utilizations of a chemical reaction can initiate in diverse industrial and built-up uses for that instance, solar antenna, the strategy of chemical dispensation apparatus, rubbery isolation, dispersion of prescription in lifeblood, effluence, humidity over gardening pitches and fissionable discarded depositories etc. Furthermore, the first order chemical reaction is directly correlated to the concentration and numerous studies on chemical reaction with diverse geometries can be comprehended in Anjalidevi and Kandasamy (1999), Zhang et al. (2015), Hayat et al. (2017c), Kumar et al. (2017). Sreedevi et al. (2017) presented chemically radiated nanofluid in porous media by functioning numerical Galerkin (FEM) approach. Hayat et al. (2017c) studied the performance of chemical reaction and nonlinear thermal radiation in magneto Jeffrey liquid considering Newtonian heating. Their analysis established conflicted behavior for destructive and generative chemical reaction parameter on concentration field. Alshomrani et al. (2018) scrutinized the combined aspects of stratifications and convective phenomena in chemically reactive Oldroyd-B fluid. The thermal radiation and MHD impacts were also presented. Their assessment reported that the reaction parameter and mass Biot number decline the concentration field. Aspects of chemical reaction and non-Fourier heat flux theory in Carreau nanoliquid with wedge and cone geometries have been reported by Kumar et al. (2018). They established that the features of flow and transfer were controlled when nanoparticle volume fraction varies. The characteristics of chemical reaction in radiated flow of Maxwell nanofluid caused by rotating disk were examined by Ahmed et al. (2019).

Here our strategic concern is to scrutinize the aspects of MHD mixed convection in nonlinear radiative Oldroyd-B fluid. The impact of heat sink/source and chemical reaction are also considered. Elucidations are established through homotopic scheme (Rehman et al. 2017; Irfan et al. 2019a, b; Rashid et al. 2019). To confer the somatic performance of emerging variables graphs are portrayed. Endorsement of the current analytical process is made by associating the outcomes of $- f^{{\prime \prime }} (0)$ with presented studies and such assessment seems to be worthy in agreement.

Development of mathematical model

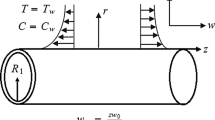
Here we analyze steady (2D) MHD flow of Oldroyd-B fluid caused by stretching cylinder of radius R with velocity $\tfrac{{U_{0} z}}{l}$ along z-directions, where (U₀, l) represents reference velocity and specific length, respectively. Furthermore, the aspects of mixed convection, nonlinear radiation, heat sink/source and chemical reaction are reported. Consider the cylindrical polar coordinates (z, r) in such scheme that z-axis goes close to the axis of the cylinder and r-axis is restrained near the radial direction. We consider electrically conducting fluid where applied magnetic field acts transversely to the flow. The influence of induced magnetic field on Oldroyd-B fluid is neglected because of small Reynolds number. Additionally, the flow field is effected by magnetic strength B₀ (see Fig. 1).

Fig. 1

Flow configuration and coordinates system

The equations of Oldroyd-B nanofluid under these norms can be written as (Irfan et al. 2019a, b):

$$\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0,$$

(1)

$$\begin{aligned} & u\frac{\partial w}{\partial r} + w\frac{\partial w}{\partial z} + \lambda_{1} \left[ {w^{2} \frac{{\partial^{2} w}}{{\partial z^{2} }} + u^{2} \frac{{\partial^{2} w}}{{\partial r^{2} }} + 2uw\frac{{\partial^{2} w}}{\partial r\partial z}} \right] = \upsilon \left[ {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{\partial r}} \right] \\ & \quad + \upsilon \lambda_{2} \left[ {\frac{u}{{r^{2} }}\frac{\partial w}{\partial r} - \frac{1}{r}\frac{\partial w}{\partial r}\frac{\partial w}{\partial z} - \frac{2}{r}\frac{\partial u}{\partial r}\frac{\partial w}{\partial r} + \frac{w}{r}\frac{{\partial^{2} w}}{\partial r\partial z} - \frac{\partial w}{\partial r}\frac{{\partial^{2} w}}{\partial r\partial z} - 2\frac{\partial w}{\partial r}\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{u}{r}\frac{{\partial^{2} w}}{{\partial r^{2} }} - \frac{\partial w}{\partial z}\frac{{\partial^{2} w}}{{\partial r^{2} }} - w\frac{{\partial^{3} w}}{{\partial r^{2} \partial z}} + u\frac{{\partial^{3} w}}{{\partial r^{3} }}} \right] \\ & \quad - \frac{{\sigma B_{0}^{2} }}{{\rho_{f} }}(w + \lambda_{1} u\frac{\partial w}{\partial r}) + g[\beta_{T} (T - T_{\infty } ) + \beta_{C} (C - C_{\infty } )], \\ \end{aligned}$$

(2)

$$\begin{aligned} & u\frac{\partial T}{\partial r} + w\frac{\partial T}{\partial z} = \alpha_{1} \left[ {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r}} \right] \\ & \quad + \tau \left[ {D_{B} \frac{\partial C}{\partial r}\frac{\partial T}{\partial r} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial r}} \right)^{2} } \right] - \frac{1}{{(\rho c)_{f} }}\frac{1}{r}\frac{{\partial \left( {rq_{r} } \right)}}{\partial r} - \frac{{Q_{0} (T - T_{\infty } )}}{{(\rho c)_{f} }}, \\ \end{aligned}$$

(3)

$$u\frac{\partial C}{\partial r} + w\frac{\partial C}{\partial z} = D_{B} \frac{1}{r}\frac{\partial }{\partial r}\left[ {\left( {r\frac{\partial C}{\partial r}} \right)} \right] + \frac{{D_{T} }}{{T_{\infty } }}\frac{1}{r}\frac{\partial }{\partial r}\left[ {\left( {r\frac{\partial T}{\partial r}} \right)} \right] - k_{c} (C - C_{\infty } ),$$

(4)

with boundary conditions

$$w(r,z) = W(z) = \frac{{U_{0} z}}{l},\quad \, u(r,z) = 0,\quad T = T_{w} ,\quad C = C_{w} ,\quad {\text{at}}\quad r = R,$$

(5)

$$w \to 0,\quad T \to T_{\infty } ,\quad C \to C_{\infty } \quad {\text{at}}\quad r \to \infty .$$

(6)

Here (u, w) signify the velocity components in r- and z-directions, respectively, $\lambda_{i \, } (i = 1,\,2)$ the relaxation–retardation times, respectively, ν the kinematic viscosity, σ the nanofluid electrically conductivity, g the gravitational acceleration, (β_T, β_C) are the thermal and concentration expansion coefficients, respectively, α₁ the thermal diffusivity of nanoliquid, (ρ_f, c_f) the liquid density and specific heat, respectively, (T, C) the temperature and concentration of nanoliquid, respectively, τ the ratio of effective heat capacity of nanomaterial to the heat capacity of the base liquid, (D_B, D_T) the Brownian and thermophoresis diffusion coefficients, respectively, (T_∞, C_∞) the temperature and concentration of nanoliquid far-off from the stretched surface, Q₀ the heat sink/source coefficient and k_c the reaction rate. Furthermore, via Rossland’s approximation the nonlinear radiative heat flux q_r is given as

$$q_{r} = - \frac{{4\sigma^{ * } }}{{3k^{ * } }}\frac{{\partial T^{4} }}{\partial r} = - \frac{{16\sigma^{ * } }}{{3k^{ * } }}T^{3} \frac{\partial T}{\partial r},$$

(7)

where (σ*, k*) are the Stefan Boltzmann constant and the mean absorption coefficient, respectively.

Appropriate transformations

Let us consider

$$\begin{aligned} & u = - \frac{R}{r}\sqrt {\frac{{U_{0} \nu }}{l}} f(\eta ),\quad w = \frac{{U_{0} z}}{l}f^{{\prime }} (\eta ),\quad \eta = \sqrt {\frac{{U_{0} }}{\upsilon l}} \left( {\frac{{r^{2} - R^{2} }}{2R}} \right), \\ & \quad \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\quad \varphi (\eta ) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}. \\ \end{aligned}$$

(8)

Using Eqs. (7) and (8), then Eqs. (1)–(6) reduced to

$$\begin{aligned} & (1 + 2\alpha \eta )f^{\prime\prime\prime} + 2\alpha f^{\prime\prime} + ff^{\prime\prime} - f^{\prime 2} + 2\beta_{1} ff^{\prime}f^{\prime\prime} - \beta_{1} f^{2} f^{\prime\prime\prime} - \frac{{\alpha \beta_{1} }}{(1 + 2\alpha \eta )}f^{2} f^{\prime\prime} \\ & \quad + (1 + 2\alpha \eta )\beta_{2} (f^{\prime \prime 2} - ff^{iv} ) - 4\alpha \beta_{2} ff^{\prime\prime\prime} - M^{2} (f^{\prime} - \beta_{1} ff^{\prime\prime}) + \lambda (\theta + N \varphi ) = 0, \\ \end{aligned}$$

(9)

$$\begin{aligned} & [\{ 1 + R_{d} (1 + (\theta_{w} - 1)\theta )^{3} \} (1 + 2\alpha \eta )\theta^{\prime}]^{\prime} + \mathop {Pr}\limits f\theta^{\prime} \\ & \quad + (1 + 2\alpha \eta )\mathop {\Pr }\limits N_{b} \theta^{\prime}\varphi^{\prime} + (1 + 2\alpha \eta )\mathop {Pr}\limits N_{t} \theta^{\prime 2} + \mathop {Pr}\limits \delta \theta = 0, \\ \end{aligned}$$

(10)

$$\begin{aligned} & (1 + 2\alpha \eta )\varphi^{\prime\prime} + 2\alpha \varphi^{\prime} + LePr \, f \, \varphi^{\prime} \\ & \quad + (1 + 2\alpha \eta )\left( {\frac{{N_{t} }}{{N_{b} }}} \right)\,\theta^{\prime\prime} + 2\alpha \left( {\frac{{N_{t} }}{{N_{b} }}} \right)\,\theta^{\prime} - Le\mathop {Pr}\limits C_{r} \varphi = 0, \\ \end{aligned}$$

(11)

$$f(0) = 0,\quad \, f^{\prime}(0) = 1,\quad \theta (0) = 1,\quad \, \varphi (0) = 1,$$

(12)

$$f^{\prime}(\infty ) = 0,\quad \theta (\infty ) = 0,\quad \varphi (\infty ) = 0.$$

(13)

Here $\alpha = \left( {\tfrac{1}{R}\sqrt {\tfrac{\nu l}{{U_{0} }}} } \right)$ the curvature parameter, $\beta_{i} = \left( {\tfrac{{\lambda_{i} U_{0} }}{l}} \right)\,(i = 1,2)$ Deborah numbers, $M = \left( {\sqrt {\tfrac{{\sigma lB_{0}^{2} }}{{U_{0} \rho_{f} }}} } \right)$ magnetic parameter, $\lambda = \left( {\tfrac{{g\beta_{T} (T_{w} - T_{\infty } )}}{{U_{0}^{2} z}}} \right)$ mixed convection parameter, $N = \left( {\tfrac{{\beta_{C} (C_w - C_{\infty } )}}{{\beta_{T} (T_{w} - T_{\infty } )}}} \right)$ buoyancy parameter, $R_{d} = \left( {\tfrac{{16\sigma^{ * } T_{\infty }^{3} }}{{3kk^{ * } }}} \right)$ Radiation parameter, $\theta_{w} = \left( {\tfrac{{T_{w} }}{{T_{\infty } }}} \right)$ temperature ratio parameter, $Pr = \left( {\tfrac{\nu }{{\alpha_{1} }}} \right)$ Prandtl number, $N_{b} = \left( {\tfrac{{\tau D_{B} (C_{w} - C_{\infty } )}}{\nu }} \right)$ Brownian motion parameter, $N_{t} = \left( {\tfrac{{\tau D_{T} (T_{w} - T_{\infty } )}}{{\nu T_{\infty } }}} \right)$ thermophoresis parameter, $Le = \left( {\tfrac{{\alpha_{1} }}{{D_{B} }}} \right)$ Lewis number and $C_{r} = \left( {\tfrac{{k_{c} l}}{{U_{0} }}} \right)$ chemical reaction parameter.

Physical quantities of notable interest

The industrial point of vision the quantities of physical interest are the local Nusselt and local Sherwood numbers, respectively.

The local Nusselt and Sherwood numbers

The local Nusselt and Sherwood numbers are defined by

$$Nu_{z} = \frac{{zq_{m} }}{{k(T_{w} - T_{\infty } )}},\quad Sh_{z} = \frac{{zj_{m} }}{{D_{B} (C_{w} - C_{\infty } )}},$$

(14)

where q_m the heat flux and j_m the mass flux, respectively, and defined as

$$q_{w} = - k\left( {\frac{\partial T}{\partial r}} \right)_{r = R} - \frac{{16\sigma^{ * } T^{3} }}{{3k^{ * } }}\left( {\frac{\partial T}{\partial r}} \right)_{r = R} ,\quad \, j_{m} = - D_{B} \left( {\frac{\partial C}{\partial r}} \right)_{r = R} ,$$

(15)

The dimensionless quantities are

$$Nu_{z} Re_{z}^{{ - \tfrac{1}{2}}} = - \left( {1 + \frac{4}{3}R_{d} \left( {1 + \left( {\theta_{w} - 1} \right)\,\theta \left( 0 \right)} \right)} \right)^{3} \theta^{\prime}\left( 0 \right),\quad Sh_{z} Re_{z}^{{ - \tfrac{1}{2}}} = - \varphi^{\prime}\left( 0 \right).$$

(16)

where $Re_{z} = \tfrac{W(z)z}{\nu }$ signifies the local Reynolds number.

Solution methodology

Homotopy analysis solutions (HAM)

The nonlinear ODEs (9)–(11) with boundary conditions (12) and (13) are elucidated via homotopic algorithm (HAM). The initial guesses (f₀, θ₀, φ₀) and auxiliary linear operators (L_f, L_θ, L_φ) are defined as:

$$f_{0} \left( \eta \right) = 1 - \exp \left( { - \eta } \right),\quad \theta_{0} \left( \eta \right) = \exp \left( { - \eta } \right),\quad \varphi_{0} \left( \eta \right) = \exp \left( { - \eta } \right),$$

(17)

$$L_{f} = \frac{{{\text{d}}^{3} f}}{{{\text{d}}\eta^{3} }} - \frac{{{\text{d}}f}}{{{\text{d}}\eta }},\quad L_{\theta } = \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }} - \theta ,\quad L_{\varphi } = \frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}\eta^{2} }} - \varphi ,$$

(18)

The overhead operators satisfied the following properties

$$\begin{aligned} & L_{f} \left[ {C_{1}^{ * } + C_{2}^{ * } \exp \left( \eta \right) + C_{3}^{ * } \exp \left( { - \eta } \right)} \right] = 0, \\ & L_{\theta } \left[ {C_{4}^{ * } \exp \left( \eta \right) + C_{5}^{ * } \exp \left( { - \eta } \right)} \right] = 0, \\ & L_{\varphi } \left[ {C_{6}^{ * } \exp \left( \eta \right) + C_{7}^{ * } \exp \left( { - \eta } \right)} \right] = 0, \\ \end{aligned}$$

(19)

here C ^*_i (i = 1–7) are the arbitrary constants.

Analysis

The aspects of influential parameters on velocity f′(η), temperature θ(η), concentration φ(η) and Nusselt number $Nu_{z} Re_{z}^{{ - \tfrac{1}{2}}}$ are highlighted in this section. The homotopic methodology has been utilized. The executed values of influential parameters throughout the computations are β₁ = β₂ = N = λ = N_t = C_r = 0.2, α = N_b = δ = 0.3, M = 0.4, R_d = 0.5, Pr = θ_w = 1.2 and Le = 1 except particular pointed out in the graphs. Additionally, the assessment of −f″(0) for different values of β₁ with former attainable studies are reported in Table 1. An admirable settlement is being established from this table which satisfies us that our outcomes are accurate.

Table 1 A comparison of β₁ for −f″(0) in limiting sense when $\beta_{2} = M = \lambda = N = 0$

Velocity f′(η)

On velocity field f′(η) the aspects of magnetic parameter (M) and mixed convection parameter (λ) are plotted which are exposed in Fig. 2a, b. The velocity field decline for M; however, rise for λ when the values of these parameter enhanced. The Lorentz force intensifies, when we heighten M, which formed more struggle to the fluid motion. Therefore, velocity of Oldroyd-B fluid falloffs. Moreover, physically buoyancy force goes as boosting pressure gradient, so stronger buoyancy force helps the flow in the growing direction which enhance f′(η) when λ enlarged.

Fig. 2

Impact of a M and b λ on f′(η)

Temperature θ(η)

The aspects of curvature parameter (α) and Deborah number (β₂) on temperature field θ(η) are established in Fig. 3a, b. The higher value of α enhances the temperature of Oldroyd-B fluid; however, conflicting behavior is being noted for β₂. The increasing values of α decline the heat transfer quantity, which enhances the temperature field. Moreover, physically, β₂ involves retardation time, which causes a reduced in temperature for larger retardation time and hence, the temperature field decreases. The Brownian (N_b) and thermophoretic (N_t) nanoparticles impact on temperature field θ(η) is reported in Fig. 4a, b. The temperature field decline for higher N_b and similar enactment is being remarked for N_t. As, Brownian motion is an unsystematic exertion of liquid particles, which molded much heat to the liquid and enhances the temperature field. Similar portrayal for larger N_t is true on temperature field which intensifies the temperature of Oldroyd-B fluid. Figure 5a, b discussed the physical aspects of thermal radiation (R_d) and magnetic parameter (M) on temperature field. Both the parameters are intensifying function of temperature field, when R_d and M enlarged. As we increase R_d the mean absorption coefficient declines and thermal thickness of the layer uninterruptedly intensifies. Hence, temperature field for R_d escalates. Furthermore, the higher M spectacles identical performance on temperature field. The Lorentz force is a resistive force and M is related to Lorentz force. The enhancing in M transport extra effort which exaggerates temperature field. The temperature field of Oldroyd-B nanofluid for heat sink/source parameter (δ) is plotted in Fig. 6a, b. These strategies recognize conflicting enactment on temperature field. The huge quantity of heat is fascinated for (δ < 0) and enormous amount of heat is provided (δ > 0), respectively, to the fluid when we intensified these parameters. This reason causes the decay of temperature field for (δ < 0); however, conflicting enactment is acknowledge for (δ > 0).

Fig. 3

Impact of a α and b β₂ on θ(η)

Fig. 4

Impact of a N_b and b N_t on θ(η)

Fig. 5

Impact of a R_d and b M on θ(η)

Fig. 6

Impact of a δ < 0 and b δ > 0 on θ(η)

Concentration field φ(η)

To establish the properties of reaction parameter (C_r) and Lewis number (Le) on the concentration field Fig. 7a, b is depicted. These diagrams exhibit analogous enactment and decline the concentration field. For larger value of C_r exaggerates the quantity of chemical reaction and liquid species more proficiently, which decays concentration field. Moreover, same trend is noted for Le on concentration field for augmented values of Le. In conclusion, we reported that both C_r and Le have identical impact on Oldroyd-B concentration field.

Fig. 7

Impact of a C_r and b Le on φ(η)

Local Nusselt number $Nu_{z} Re_{z}^{{ - \tfrac{1}{2}}}$

Figures 8a, b and 9a, b are acknowledged to plot the aspects of influential parameters on Nusselt number for the fluctuating values of N_b, N_t, R_d and Pr. These depictions reported that the heat transport amount decays for the higher values of these parameters.

Fig. 8

Impact of a N_b and b N_t on $Nu_{z} Re_{z}^{{ - \tfrac{1}{2}}}$

Fig. 9

Impact of a R_d and b Pr on $Nu_{z} Re_{z}^{{ - \tfrac{1}{2}}}$

Closing remarks

The nonlinear aspects of thermal radiation subject to chemical reaction in flow of an Oldroyd-B nanofluid with magnetic and mixed convection properties were studied. The heat sink/source features were also incorporated. The essential conclusions of this study itemized below:

• The higher values of M declined the velocity field; however, for λ the velocity of Oldroyd-B fluid enhanced.

• Opposed behavior were noted for larger α and β₂ on θ(η).

• The intensifying values of N_b and N_t boosted the temperature of Oldroyd-B fluid, while conflicted performance were reported for δ < 0 and δ > 0 on θ(η).

• The concentration of Oldroyd-B nanoliquid diminished for enhancing values of C_r and Le.

• The local Nusselt number $(Nu_{z} Re_{z}^{{ - \tfrac{1}{2}}} )$ decayed for higher estimations of N_b and N_t.