1 Introduction

Real life problems such as production planning, water resource management etc., involve multiple conflicting objectives subject to constraints. The optimization problem with two or greater than two objective functions which are conflicting in nature is called multi-objective optimization problem. Thus the model under these multiple objective is called multi-objective programming model. The concept of multi-objective decision making problems was adopted and modified by different researchers namely; Zimmermann (1978); Yeger (1979); Henan (1979); Rommelfanger (1989); Chakraborty and Gupta (2002) and etc.

A quadratic programming (QP) problem is a optimization problem in which a quadratic function must be maximized or minimized subject to linear constraints (Rout et al. 2019). Unlike the linear programming problem the solutions procedure for QP problem is slightly complex. Some economic and business problems can be expressed mathematically and are directly applicable to the QP. Several algorithms have been devised to solve QP problems, including Powell (1985); Lawson and Hanson (1995); Goldfarb and Idnani (1983), and others. A QP problem involving two or more than two objectives functions are termed as multi-objective quadratic programming (MOQP) problem. The uncertainties in the parameters of a programming problems are due to fuzziness or randomness. The one arising from randomness can be incorporated through a probability distribution and other from fuzziness can be characterized by fuzzy numbers. A MOQP problem with all or some of its input parameters are assumed to be fuzzy number is called multi-objective fuzzy quadratic programming problem. Authors, like Sert et al. (2015); Yue et al. (2019) and Yang et al. (2020) suggested MOQP problem under the environment of fuzziness. Most of the time fuzziness of the mathematical programming problem is due to fuzziness appearing in different parts of a programming problem for example the right hand side part, constraint coefficient or the objective function coefficients or involved as decision variables. Taghi-Nezhad and Taleshian (2018) suggested a solution approach for solving fuzzy QP problem where the cost coefficients, the matrix of the quadratic form, constraints coefficients, and the righthand sides are all fuzzy numbers. Mansoori et al. (2018) introduced fuzzy QP problem with fuzzy parameters coefficients. Fathy (2019) introduced multi-objective and multi-level integer fuzzy QP problems, where all the parameters and decision variables of the programming problem are fuzzy number. Nasseri et al. (2019) suggested a fuzzy multi-objective quadratic model with variable constraints for optimal water resource allocation among different water-user sectors. Mussafi and Ismail (2021) exploited the QP problem to get the best risk level for risk-adjusted Islamic portfolios recently.

In majority of the literatures, authors assumed the decision parameters as fuzzy numbers while the decision variables as crisp ones. Since the variables are crisp, the solution obtained as the crisp, which is a real number. The solution is exact value in the fuzzy programming problems with fuzzy parameters. The fuzzy aspect of the decision is partly lost in this case so, it is reasonable and important to consider fuzzy mathematical programming problem with fuzzy decision variables. A fully fuzzy multi-objective quadratic programming (FFMOQP) problem is proposed in this paper where all the input parameters and decision variables of the programming problems are assumed to be triangular fuzzy number and triangular fuzzy decision variables respectively.

One of the many mathematical programming techniques that can be utilized to handle the problem of multi-objective optimization is called goal programming (GP) method. More importantly, fuzzy goal programming (FGP), has been shown to be an effective method for handling future aspirations for decision makers even when those making the decisions do not have precise knowledge about the future goals. In other word FGP is an extension of conventional GP used to solving multi-objective decision problems with imprecisely defined model parameters. FGP approach is used by a number of researchers to solve multi objective optimization problem. Narasimhan (1980); Ignizio (1982) and Aouni et al. (2009) are researchers who took initiative on solving problems employing FGP method. Lachhwani (2012) suggested a FGP procedure for fuzzy multi-objective quadratic programming problem. Pramanik and Dey (2011) proposed a priority based FGP approach to multi-objective quadratic programming problem. Some the recent work on this aspects are Dalman and Bayram (2017); Ambad and Kulkarni (2017); Hossain and Hossain (2018); Ali et al. (2019); Kundu and Islam (2019); Rivaz et al. (2020); Rani et al. (2021), etc.

The different FGP formulations can be classified as: weighted FGP, lexicographic FGP, fuzzy MIN-MAX Goal Programming and interactive FGP. Weighted FGP is used in this paper. Generally, the decision makers appreciation of the positive and the negative deviations from the fuzzy goals can be different according to the relative importance of the objective, which can be revealed through the weights of each objective under considerations.

In this paper computation between two fuzzy numbers and variables, is done by using fuzzy arithmetic operations and we have used ranking function and property of fuzzy inequality for fuzzy objective functions and fuzzy constraints respectively to remove fuzziness. Weighted FGP (WFGP) approximation is used to obtain efficient solutions of crisp multi-objective programming problem.

The rest of the work is categorized as follows: basic preliminary is discussed in Sect. 2, after the introduction section. The mathematical model and the the solution procedures respectively are defined in Sect. 3 and in Sect. 4. Numerical example is provided for illustration of the methodology in Sect. 5. Result and discussion are included in Sect. 6. The paper is concluded in Sect. 7 followed by supportive references.

2 Basic preliminaries

Definition 2.1

For \((a^{(p)},a,a^{(o)})\) \(\in \) \(\mathrm{I\!R}\), the membership function \(\mu _{\widetilde{a}}(x)\) of triangular fuzzy(TF) number \((a^{(p)},a,a^{(o)})=\widetilde{a}\) is defined as: \(\mu _{\tilde{a}}(x)=\left\{ \begin{array}{ll} 0, &{} x\le a^{(p)}\\ \frac{x-a^{(p)}}{a-a^{(p)}}, &{} a^{(p)}\le x\le a \\ \frac{a^{(o)}-x}{a^{(o)}-a}, &{} a\le x\le a^{(o)} \\ 0, &{} \mathrm otherwise \\ \end{array} \right. \)

Definition 2.2

For two TF numbers \((a^{(p)},a,a^{(o)})\approx \widetilde{a}\) and \((b^{(p)},b,b^{(o)})\approx \widetilde{b}\), the following fuzzy operations between two fuzzy numbers hold true:

  1. (i)

    \((a^{(p)},a,a^{(o)})\oplus (b^{(p)},b,b^{(o)})\approx (a^{(p)}+b^{(p)},a+b,a^{(o)}+b^{(o)})\)

  2. (ii)

    \((a^{(p)},a,a^{(o)})\ominus (b^{(p)},b,b^{(o)})\approx (a^{(p)}-b^{(o)},a-b,a^{(o)}-b^{(p)})\)

  3. (iii)

    \(k(a^{(p)},a,a^{(o)})\approx (ka^{(p)},ka,ka^{(o)})\), \(k\ge 0\)

  4. (iv)

    \(k(a^{(p)},a,a^{(o)})\approx (ka^o,ka,ka^p)\), \(k\le 0\)

  5. (v)

    \((a^{(p)},a,a^{(o)})\otimes (b^{(p)},b,b^{(o)})\approx (a^{(p)}b^{(p)},ab,a^{(o)}b^{(o)}\), if \(a^{(p)}\ge 0~and~~ b^{(p)}\ge 0\)

  6. (vi)

    \((a^{(p)},a,a^{(o)})\otimes (b^{(p)},b,b^{(o)})\approx (a^{(p)}b^{(o)},ab,a^{(o)}b^{(o)})\), if \(a^{(p)}<0,a^{(o)}\ge 0, b^{(p)}\ge 0 \)

  7. (vii)

    \((a^{(p)},a,a^{(o)})\otimes (b^{(p)},b,b^{(o)})\approx (a^{(p)}b^{(o)},ab,a^{(p)}b^{(o)})\), if \(a^{(o)}\le 0~ and ~b^{(p)}\ge 0 \)

Definition 2.3

For two TF numbers \(\widetilde{a}\approx (a^{(p)},a,a^{(o)} )\) and  \(\widetilde{b}\approx (b^{(p)},b,b^{(o)})\), the following properties are true

  1. (i)

    \(\widetilde{a}\approx \tilde{b}\) iff \(a^{(p)}\approx b^{(p)}\), \(a\approx b\) and  \(a^{(o)}\approx b^{(o)}\)

  2. (ii)

    \(\tilde{a}\approx (a^{(p)},a,a^{(o)})\ge 0 \) iff \( a^{(p)} \ge 0 \)

Definition 2.4

A ranking function is a function \(\mathbb {R}\):\(F(R)\rightarrow R\) that maps each fuzzy number into the real line. F(R) is a set of fuzzy numbers defined on set of real numbers. Let \((a^{(p)},a,a^{(o)})\approx \widetilde{a}\)   be a TF number, then \(\mathbb {R}(\tilde{a})\approx \frac{a^{(p)}+2a+a^{(o)}}{4}\)

Definition 2.5

[Pareto-optimal solution (Abebaw Gessesse et al. 2020)]: For a multi-objective programming problem, a feasible solution \(x^*\) is said to be pareto-optimal or optimal compromise solution if and only if there does not exist any other feasible solution x such that \(Z^{k_{1}}(x)\le Z^{k_{1}}(x^*)\) for \(\forall k_{1} \epsilon 1,2 ,...,K\) and \(Z^{k_{2}}(x)< Z^{k_{2}}(x^*)\) for \(\forall k_{2} \epsilon 1,2,...,K\). The collection of all the Pareto optimal solutions in the decision space is called the Pareto optimal set (PS), and the projection of PS in the objective space is called the Pareto optimal front (PF).

Definition 2.6

[Multi-objective optimization problem (Abebaw Gessesse et al. 2020)]: Many real-world optimization problems involve multiple conflicting objectives, known as multi-objective optimization problems, which can be mathematically formulated as follows:

$$\begin{aligned} \min : Z(x)=(Z^1(x),Z^2(x),...,Z^k(x)) \end{aligned}$$

subject to

$$\begin{aligned} x\epsilon X, \end{aligned}$$

where X is the search space of decision variable with \(X={x_1,x_2,..x_k}\)  denoting the  decision vector.

Definition 2.7

When each of the objectives is given an imprecise aspiration level, these objectives are referred to be fuzzy goals. The fuzzy goals are now defined in the area of fuzzy programming by their related membership functions. According to Gupta and Chakraborty (1997) the membership function for the \(i \mathrm{th}\) fuzzy goal can be defined as:

$$\begin{aligned} \mu _{i}(d_{i}(x))= \left\{ \begin{array}{lr} 0,&{} \text {for}\,\, d_{i} \ge p \\ \frac{p-d_{i}(x)}{p} ,&{} \text {for}\,\, 0 \le d_{i}(x) \le p \\ 1,&{} \text {for}\,\, d_{i}(x) \le 0, \end{array} \right\} \end{aligned}$$

where the distance function: \(d_{i}(x)\)= \(|\overline{Z_{i}}-Z_{i}(x)|\),  i =1, 2, 3,...,k. This distance depends up on x. At x=\(\overline{x}\) (ideal point in x-space) \(d_{i}\)=0 and at \(x=\underline{x}\) implies \(Z_i(x)=\underline{Z_{i}}\). The maximum value of \({d}_i(x)\) can be calculated as  \(\overline{d_i}=|\overline{Z_i}-Z_i|\) for \(p= sup\{\overline{d_i}\}\)

3 Mathematical model

FFMOQP problem with fuzzy decision variables is of the form:

$$\begin{aligned} \max :\widetilde{Z}_{k}\approx \sum _{j=1}^{n} \widetilde{c_j}^{(k)}\otimes \widetilde{x_j} \oplus \frac{1}{2}\sum _{i=1}^{n}\sum _{j=1}^{n}\widetilde{q_{ij}}^{(k)} \widetilde{x}_{i} \widetilde{x_j}, (k=1,2...,K) \end{aligned}$$
(3.1)

Subject to

$$\begin{aligned} \sum _{j=1}^{n} \widetilde{a_{ij}} \widetilde{x}_{j}\preceq \widetilde{b_i}, i\in \{1,2,...,m\} \end{aligned}$$
(3.2)
$$\begin{aligned} \widetilde{x}_{j}\succeq 0, j\in [1,2,...n] \end{aligned}$$
(3.3)

where \(\widetilde{q}_{ij}\) = \(({q}^p_{ij},{q}_{ij},{q}^o_{ij})\) is constant symmetric matrix assumed to be triangular fuzzy number,

\(\widetilde{c_j}\) = \((c^{p}_j,c_j,c^{o}_j)\) is cost coefficient assumed to be triangular fuzzy number,

\((a^{p}_{ij},a_{ij},a^{o}_{ij})\) = \(\widetilde{a}\) and \((b^{p}_i,b_i,b^{o}_i)\) = \(\widetilde{b}_i\) are triangular fuzzy constraint coefficients and

\(\widetilde{x_1}\) = \((x^{p}_1,x_1,x^{o}_1)\) = \((x_1, x_2, x_3)\) and \(\widetilde{x_2}\) = \((x^{p}_2,x_2,x^{o}_2)\) = \((x_4, x_5, x_6)\) are triangular fuzzy decision variables and their representations.

3.1 Fuzzy goal programming formulation

From the defined membership function 2.7 above, the flexible goals with aspired level 1 is defined, thus the fuzzy goal programming(FGP) problem becomes: Lachhwani (2012)

$$\begin{aligned} \frac{p-d_{i}}{p} + D^{-}_{i}-D^{+}_{i}=1,\; i=1,2,... \end{aligned}$$
(3.4)

(or)

$$\begin{aligned} -\overline{Z_{i}} +Z_{i}(x) + pD^{-}_{i} + pD^{+}_{i}=0, ~~\forall i=1,2,... \end{aligned}$$
(3.5)

The \(i \mathrm th\) membership goal with aspired level 1 can presented as:

$$\begin{aligned} C_ix +x^{T}H_ix-\overline{Z_i} + pD^-_i-pD^+=0 \end{aligned}$$
(3.6)

where  \(D^{-}_{i}(\ge 0)\) and \(D^{+}_{i}(\ge 0)\) with \(D^{-}_{i} D^{+}_{i}=0\) represent under or over deviational variables respectively form the aspired levels.

3.2 Weighted fuzzy goal programming formulation

In conventional GP, the under and/or over deviational variables are included in the achievement function for minimizing them and that depends upon the type of the objective functions to be optimized. In this work, only the under deviational variables \(D^{-}\) is required to be minimized to achieve the aspired levels of the fuzzy goals. It may be noted that when a membership goal is fully achieved, the we get \(D^{-}\)= 0 and \(D^{+}\) = 1. The weighted WFGP approach becomes, find x so as to minimize:

$$\begin{aligned} \sum _{i=1}^{K} \omega _{i}D^{-}_i \end{aligned}$$
(3.7)

Subject to

$$\begin{aligned} C_ix +x^{T}H_ix-\overline{Z_i} + pD^-_i-pD^+=0 \end{aligned}$$
(3.8)
$$\begin{aligned} x\in S=\bigl \{x\in R^n : Ax \le b,x\ge 0 \bigr \}, \end{aligned}$$
(3.9)

In the above model \(C_i\),\(H_i\) are are row vectors with n-components and x and b are column vectors with n and m-components. \(x^{T}H_ix \)is a strictly concave quadratic function on the convex set S of all its possible solutions, with a global unique maximum of Zi(x) for every i = 1,2,...,k over S. The relative importance of obtaining the sought level of the different fuzzy objectives subject to the constraint established in the decision-making situation is represented by the \(\omega _i\ge 0\) (i = 1, 2,...).

4 Solution procedures

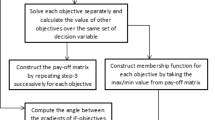
This section presents an approach for solving a multi-objective fully fuzzy QP problem (Table 1).

The solution methodologies are discussed in depth as follows:

  1. Step 1.

    Ranking function method is applied on Eq. (3.1) and to handle fuzzy QP programming problem and moreover, the property of inequality between two fuzzy numbers are used for defuzzification of fuzzy constraints, (3.2)–(3.3). Thus the programming problem becomes:

    $$\begin{aligned} \max :{Z}_{k}=\frac{1}{4}\sum _{j=1}^{n} (({q}^{k}_{ij})^{p}{x}^p_{j}+2q^{k}_{ij}x_{j}+({q}^{k}_{j})^{o}{x}^{o}_{j})+\frac{1}{8}\sum _{i=1}^{n}\sum _{j=1}^{n} (({q}^{k}_{ij})^{p}{x}^p_{i}{x}^p_{j} \end{aligned}$$
    $$\begin{aligned} +2q^{k}_{ij}x_{i}x_{j}+({q}^{k}_{ij})^{o}{x}^{o}_{i}{x}^{o}_{j}), k\in \{ 1,2.....K\} \end{aligned}$$
    (4.1)

    Subject to

    $$\begin{aligned}&\sum _{j=1}^{n}a^p_{ij} {x}^p_{j}\le b^p_i, i\in \{1,2,...,m\} \end{aligned}$$
    (4.2)
    $$\begin{aligned}&\sum _{j=1}^{n}a_{ij} {x}_{j}\le b_i, i\in \{1,2,...,m\} \end{aligned}$$
    (4.3)
    $$\begin{aligned}&\sum _{j=1}^{n}a^o_{ij} {x}^o_{j}\le b^o_i, i\in \{1,2,...,m\} \end{aligned}$$
    (4.4)
    $$\begin{aligned}&{x}^o_{j}-{x}_{j}\ge 0, j\in \{1,2,...,n\} \end{aligned}$$
    (4.5)
    $$\begin{aligned}&{x}_{j}-{x}^p_{j}\ge 0, j\in \{1,2,...,n\} \end{aligned}$$
    (4.6)
    $$\begin{aligned}&{x}^p_{j}\ge 0, j\in \{1,2,...,n\} \end{aligned}$$
    (4.7)
  2. Step 2

    Use any commercially available optimization packages such as LINDO, LINGO, CPLEX and etc. to solve the defined problem in step 1 individually to obtain the ideal solutions.

  3. Step 3.

    Create payoff matrix.

  4. Step 4.

    Find the upper (\(\overline{Z_i}\)) and lower(\(\underline{Z_i}\)) bound of each objective function at each ideal solution resulted from optimizing single objective.

  5. Step 5.

    Compute the distance \(\overline{d_i}\)=\(|\overline{Z_i}-\underline{Z_i}|\).

  6. Step 6.

    Find p= \(sup\{\overline{d}\}\)

  7. Step 7.

    For each objective function, define a membership function in light of definition 2.7.

  8. Step 8.

    Formulate the WFGP from all the above steps.

  9. Step 9.

    Solve the WFGP model with the purpose of minimizing the weighted sum of deviations from the goal.

  10. Step 10.

    The resultant crisp non-linear mathematical model is solved by LINGO software and fuzzy optimal solution \(\tilde{x}_{i}\)=\((x_1,x_2,x_3)\) is obtained.

Note: \((a^p,a,a^o)\approx \widetilde{a}\) and \((b^p,b,b^o)\approx \widetilde{b}\) and \((x^p,x,x^o)\approx \widetilde{x}\approx (x_1,x_2,x_3)\)

The general solution procedure of FFMOQP problem is depicted by the following flowchart (Fig. 1):

Fig. 1
figure 1

Flowchart on general solution procedures of multi-objective fuzzy QP problem

Full size image

5 Numerical example

$$\begin{aligned}&\max :\tilde{Z}_1\approx (10,14,18)\otimes \tilde{x}_{1}\oplus (4,10,14)\otimes \tilde{ x}_{2}\ominus (0,2,3)\otimes \tilde{ x}^2_{1}\ominus (1,3,5)\otimes \tilde{ x}^2_{2} \end{aligned}$$
(5.1)
$$\begin{aligned}&\max :\tilde{Z}_2\approx (5,15,25)\otimes \tilde{ x}_{1}\oplus (5,15,25)\otimes \tilde{x}_{2}\ominus (0.5,1,1.5)\otimes \tilde{ x}^2_{1}\ominus (0.5,1,1.5)\otimes \tilde{ x}^2_{2} \end{aligned}$$
(5.2)
$$\begin{aligned}&\max :\tilde{Z}_3 \approx (8,24,40)\otimes \tilde{ x}_{1}\oplus (5,15,25)\otimes \tilde{ x}_{2}\ominus (0.5,1,1.5)\otimes \tilde{ x}^2_{1}\ominus (0.5,1,1.5)\otimes \tilde{ x}^2_{2} \end{aligned}$$
(5.3)

Subject to

$$\begin{aligned}&(0.5,1,1.5)\tilde{ x}_{1}\oplus (0.5,1,1.5)\tilde{ x}_{2}\preceq (1,3,5) \end{aligned}$$
(5.4)
$$\begin{aligned}&(2,4,6)\tilde{ x}_{1}\oplus (0.5,1,1.5)\tilde{ x}_{2}\preceq (6,7,8) \end{aligned}$$
(5.5)
$$\begin{aligned}&\tilde{ x}_{i}\succeq 0,~~ i=1, 2 \end{aligned}$$
(5.6)

Using ranking function for the defuzzification of fuzzy objective function and the property of inequality between fuzzy numbers for defuzzification of fuzzy constraints, we get the following crisp multi-objective QP problem:

$$\begin{aligned}&\max : {Z}_1=\frac{10{x}_{1}+4{x}_{4}-3{x}^2_{3}-5{x}^2_{6}+28{x}_{2}+20{x}_{5}-4{x}^2_{2}-6{x}^2_{5}+18{x}_{3}+14{x}_{6}-{x}^2_{4}}{4} \end{aligned}$$
(5.7)
$$\begin{aligned}&\max :{Z}_2=\frac{15{x}_{1}+5{x}_{4}-1.5{x}^2_{3}-1.5{x}^2_{6}+30{x}_{2}+30{x}_{5}-2{x}^2_{2}-2{x}^2_{5}+25{x}_{3}+25{x}_{6}-0.5{x}^2_{1}-0.5{x}^2_{4}}{4} \end{aligned}$$
(5.8)
$$\begin{aligned}&\max :{Z}_3=\frac{8{x}_{1}+4{x}_{4}-1.5{x}^2_{3}-1.5{x}^2_{6}+24{x}_{2}+30{x}_{5}-2{x}^2_{2}-2{x}^2_{5}+40{x}_{3}+25{x}_{6}-0.5{x}^2_{1}-0.5{x}^2_{4}}{4} \end{aligned}$$
(5.9)

Subject to

$$\begin{aligned}&0.5{x}{1}+0.5{x}{4}\le 1 \end{aligned}$$
(5.10)
$$\begin{aligned}&{x}_{2}+{x}_{5}\le 3 \end{aligned}$$
(5.11)
$$\begin{aligned}&1.5{x}_{4}+1.5{x}_{6}\le 5 \end{aligned}$$
(5.12)
$$\begin{aligned}&2{x}_{1}+0.5{x}_{4}\le 6 \end{aligned}$$
(5.13)
$$\begin{aligned}&4{x}_{2}+{x}_{5}\le 7 \end{aligned}$$
(5.14)
$$\begin{aligned}&6{x}_{3}+6{x}_{6}\le 8 \end{aligned}$$
(5.15)
$$\begin{aligned}&0\le x_{1}\le x_{2} \le x_{3} \end{aligned}$$
(5.16)
$$\begin{aligned}&0\le x_{4}\le x_{5} \le x_{6} \end{aligned}$$
(5.17)

The following steps are taken to formulate fuzzy membership function:

  1. i.

    Each objective function is separately maximized with respect to the given constraints.

  2. ii.

    Then payoff matrix is formulated.

  3. iii.

    Lower and Upper bound of the objective functions are identified at all the ideal solutions resulted from step 1.

Table 1 Payoff matrix
Full size table

From the payoff matrix 1, above we can calculate \(\bar{d}_1= |{Z}^U_1- {Z}^l_1 |=|19.599-7.465|=12.134\), \({\bar{d}}_{2}= |{Z}^U_2- {Z}^l_2 |=|39.542-22.499|=17.043\) \(\bar{d}_3= |{Z}^U_3- {Z}^l_3 |=|41.147-32.499|=9.096\). Then p=\(sup\{ \bar{d}_i\}=17.043\) for i = 1, 2, 3. The formulation of equivalent WFGP is give as follows:

$$\begin{aligned} \min : \omega _1D^-_1+\omega _2D^-_2+\omega _3D^-_3 \end{aligned}$$
(5.18)

Subject to

$$\begin{aligned}&\frac{10{x}_{1}+4{x}_{4}-3{x}^2_{3}- 5{x}^2_{6}+28{x}_{2}+20{x}_{5}-4{x}^2_{2}-6{x}^2_{5} +18{x}_{3}+14{x}_{6}-{x}^2_{4}}{4}\nonumber \\&\quad -19.599+17.043D^{-}_1-17.043D^{+}_1 =0 \frac{15{x}_{1}+5{x}_{4}-1.5{x}^2_{3}- 1.5{x}^2_{6}+30{x}_{2}+30{x}_{5}-2{x}^2_{2}-2{x}^2_{5}+25{x}_{3}+25{x}_{6}-0.5{x}^2_{1}-0.5{x}^2_{4}}{4}\end{aligned}$$
(5.19)
$$\begin{aligned}&-39.542+17.043D^{-}_2-17.043D^{+}_2=0\nonumber \\&\frac{8{x}_{1}+4{x}_{4}-1.5{x}^2_{3}-1.5{x}^2_{6}+24{x}_{2}+30{x}_{5}-2{x}^2_{2}-2{x}^2_{5}+40{x}_{3}+25{x}_{6}-0.5{x}^2_{1}-0.5{x}^2_{4}}{4} \end{aligned}$$
(5.20)
$$\begin{aligned}&-41.147+17.043D^-_3-17.043D^+_3=0 \end{aligned}$$
(5.21)
$$\begin{aligned}&0.5{x}_{1}+0.5{x}_{4}\le 1 \end{aligned}$$
(5.22)
$$\begin{aligned}&{x}_{2}+{x}_{5}\le 3 \end{aligned}$$
(5.23)
$$\begin{aligned}&1.5{x}_{4}+1.5{x}_{6}\le 5 \end{aligned}$$
(5.24)
$$\begin{aligned}&2{x}_{1}+0.5{x}_{4}\le 6 \end{aligned}$$
(5.25)
$$\begin{aligned}&4{x}_{2}+{x}_{5}\le 7 \end{aligned}$$
(5.26)
$$\begin{aligned}&6{x}_{3}+6{x}_{6}\le 8 \end{aligned}$$
(5.27)
$$\begin{aligned}&0\le x_{1}\le x_{2} \le x_{3} \end{aligned}$$
(5.28)
$$\begin{aligned} 0\le x_{4}\le x_{5} \le x_{6} \end{aligned}$$
(5.29)

The crisp nonlinear-programming model from 5.18 to 5.29 is solved in light of three cases shown as below. Case 1: \(\omega _1\)=0.5, \(\omega _2\)=0.3, \(\omega _3\)=0.2

Case 2: \(\omega _1\)=0.5, \(\omega _2\)=0.2, \(\omega _3\)=0.3

Case 3: \(\omega _1\)=0.3, \(\omega _2\)=0.5, \(\omega _3\)=0.2

The following Tables 2 and 3 recapitulate all the results of solved model from 5.18 to 5.29

Table 2 Fuzzy PO solutions of WFGP model
Full size table
Table 3 Fuzzy optimal values of the three objective functions and the membership values achieved
Full size table

6 Result and discussion

Average of the three cases (1, 2 and 3) of each fuzzy optimal value of objective function is taken and discussed as follows:

From the results illustrated in the Tables 2 and 3 it is found that the maximized fuzzy values of objective functions \(\widetilde{Z}_1\), \(\widetilde{Z}_2\) and \(\widetilde{Z}_3\) respectively are (-9.5513, 17.4120, 41.4340), (2.8355, 36.6541, 62.6566) and (5.4192, 36.0772, 78.9210). It is observed that amount of highest membership value achieved by fuzzy objective function, \(\widetilde{Z}_3\) is 0.8960. The least amount of membership values achieved by fuzzy objective function, \(\widetilde{Z}_1\) is 0.8299. In general WFGP approach is powerful method to handle multi-objective problems where the aspiration levels are not known certainly.

7 Conclusion

A solution procedure of FFMOQP problem is proposed in this study. All the input parameters and decision variables are considered to be triangular fuzzy number and triangular fuzzy decision variables. Moreover triangular fuzzy number is used as decision solutions. Initially, the fuzzy objective functions are defuzzified by applying the ranking function for triangular fuzzy number on each individual objective function. The inequality constraints involved in the multi-objective QP model with fuzzy parameters and fuzzy decision variables are converted to their crisp equivalent by using the property of inequality among the fuzzy numbers. Finally WFGP approach is applied to handle the crisp multi-objective QP problem. The transformed model is solved by the existing software(LINGO). The numerical example’s result has been found to be superior.

The proposed methods employed in this work are very important; to find the crisp equivalent of the fully fuzzy mathematical programming problems and finally to solve the equivalent crisp model accordingly. The study be applied to fully fuzzy real-world decision-making situations including fuzzy supply chain management, portfolio management, and so forth.