A neural network to solve quadratic programming problems with fuzzy parameters

Abstract

In this paper, a representation of a recurrent neural network to solve quadratic programming problems with fuzzy parameters (FQP) is given. The motivation of the paper is to design a new effective one-layer structure neural network model for solving the FQP. As far as we know, there is not a study for the neural network on the FQP. Here, we change the FQP to a bi-objective problem. Furthermore, the bi-objective problem is reduced to a weighting problem and then the Lagrangian dual is constructed. In addition, we consider a neural network model to solve the FQP. Finally, some illustrative examples are given to show the effectiveness of our proposed approach.

1 Introduction

In this paper, we study the following FQP (quadratic programming problems with fuzzy parameters):

$$\begin{aligned} \min \quad&{\tilde{f}}(x)={\tilde{c}}^Tx+\frac{1}{2}x^T{\tilde{H}}x,\\s.t.\quad&{\tilde{A}}x\le {\tilde{b}},\nonumber \\&x\ge 0, \end{aligned}$$

(1)

where ${\tilde{H}}$ is a fuzzy positive semi-definite and symmetric matrix (see Definition 3.1) of order $n\times n, {\tilde{A}}, {\tilde{c}}$, and ${\tilde{b}}$ are matrices of order $m\times n, n\times 1$, and $m\times 1$, respectively. Recently, many mathematical programming topics extended in a fuzzy way. Wu (2003) presented the fuzzy-valued Lagrangian function of fuzzy optimization problem via the concept of fuzzy scalar (inner) product. Also, Wu (2004b) introduced a solution concept of fuzzy optimization problems, which is essentially similar to the notion of Pareto optimal solution (non-dominated solution) in multi-objective programming problems, by imposing a partial ordering on the set of all fuzzy numbers.

Some real world problems and many interesting applications are classified as quadratic programming problem such as inventory management (Abdel-Malek and Areeractch 2007), portfolio selection (Ammar and Khalifa 2003; Wu and Liu 2012), engineering design (Petersen and Bodson 2006), etc. These real problems have uncertain and vague data that can be dealt with using fuzzy logic. Thus, the development of methods for solving quadratic programming problem under fuzzy environment emerges as a way of solving these kinds of problems. Some studies have been developed to solve the FQP (see Ammar and Khalifa 2003; Liu 2009; Silva et al. 2013; Cruz et al. 2011). For solving the FQP, Ammar and Khalifa (2003) described a method where all decision variables are non negative and the linear term in the objective function does not exist. They converted the original problem into the lower bound and the upper bound problems. The two quadratic programs can be solved by using the Karush–Kuhn–Tucker optimality conditions for each $\alpha$-cut (Ammar and Khalifa 2003). The optimal solution of the original problem, is inside of the interval formed for the optimal solutions obtained by the lower bound and the upper bound problems. Also, Liu (2009) transformed the FQP to a two-level mathematical programming problem for finding the bounds of the fuzzy objective values. Then, he described how to transform the two-level mathematical program into the conventional one-level quadratic program. Beside, Liu (2009) converted the problem (1) into the lower bound and the upper bound problems as well. However, the upper bound problem is a non-linear program. Here, we reformulate the problem (1) into the bi-objective problem. Moreover, the bi-objective problem is reduced to a weighting problem and after that the Lagrangian dual is constructed. In addition, the dual program and then the fuzzy form of Dorn’s dual quadratic program are provided. Then, we show that the solution of the problem is equal to the solution of a dynamical system. We call this dynamical system as a neural network model and apply to solve the FQP (1).

Neural networks concepts were found in 1985 by Hopfield and Tank (1985). There exist some neural network models for solving the quadratic optimization problem (Chen and Fang 2000; Effati and Ranjbar 2011; Effati et al. 2015; Eshaghnezhad et al. 2016. Chen and Fang (2000) presented a neural network computational scheme with time-delay consideration for solving convex quadratic programming problems. Effati and Ranjbar (2011) proposed a neural network for solving quadratic programming problems. In 2011, Effati et al. established the first fuzzy neural network. They presented a new neural network model for solving the linear programming problem. In fact, their model solved the fuzzy shortest path and the fuzzy maximum flow problems. Also, Mansoori et al. (2016) proposed a recurrent neural network to solve the non-linear optimization problem with fuzzy parameters.

The motivation of this paper is to design a new effective one-layer structure neural network model for solving the FQP defined in (1). As mentioned above, there are several neural network models to solve crisp mathematical programming problems. This methodology is going to study the possibility of extending the existing neural network model to solve the FQP. Additionally, for showing the stability of the proposed neural network model, we give a Lyapunov function for dynamical system. Also, we compare our results with two other crisp neural network (Effati et al. 2015; Xia and Wang 2000), for $\alpha =1$, i. e., when the fuzziness goes to zero.

The rest of the paper is organized as follows. Section 2 contains preliminaries. In Sect. 3, the FQP is established. We present the neural network model in Sect. 4. In Sect. 5, the stability condition and global convergence for the proposed neural network are discussed. Illustrative examples are given in Sect. 6 to show the validity and applicability of our method. Finally, Sect. 7 states a brief description about some issues for the proposed method and findings of the paper.

2 Preliminaries

In this section, we give some preliminaries of fuzzy set theory and optimization.

2.1 Fuzzy set theory

Here, our requirements from the fuzzy set theory are presented.

Definition 2.1

(Friedman et al. 1999) A fuzzy number is a fuzzy set ${\tilde{u}}: {\mathbb {R}}\rightarrow [0, 1]$ with the following properties:

• 1. ${\tilde{u}}$ is upper semi-continuous function.

• 2. ${\tilde{u}}$ is normal, i. e., there exists an $x_0\in {\mathbb {R}}$, with ${\tilde{u}}(x_0) = 1$.

• 3. ${\tilde{u}}$ is fuzzy convex, i. e., ${\tilde{u}}((1-\lambda )x+\lambda y) \ge \min \{{\tilde{u}}(x), {\tilde{u}}(y)\}$ whenever $x, y \in {\mathbb {R}}$ and $\lambda \in [0, 1]$.

• 4. $cl (supp\ {\tilde{u}}) = cl\{x\in {\mathbb {R}} : {\tilde{u}}(x) > 0\}$ is a compact set.

The collection of all fuzzy numbers is denoted by $E^1$. Also, the $\alpha$-cut sets of a fuzzy number ${\tilde{u}}\in E^1$ is denoted by $[{\underline{u}}(\alpha ), {\overline{u}}(\alpha )]$, that is defined by,

$$\begin{aligned} {\tilde{u}}[\alpha ]=[u]^\alpha =[{\underline{u}}(\alpha ), {\overline{u}}(\alpha )]={\left\{ \begin{array}{ll} \{x\in {\mathbb {R}} : {u}(x) \ge \alpha \},&{}\quad { if}\ 0<\alpha \le 1 \\ cl (supp\ {\tilde{u}}), &{}\quad { if}\ \alpha =0. \end{array}\right. } \end{aligned}$$

Definition 2.2

(Friedman et al. 1999) A fuzzy number ${\tilde{u}}$ is completely determined by any pair ${\tilde{u}}=({\underline{u}}, {\overline{u}})$ of functions ${\underline{u}}(\alpha ),{\overline{u}}(\alpha ):[0,1]\rightarrow {\mathbb {R}}$, defining the endpoints of the $\alpha$-cuts, satisfying the three conditions:

• 1. ${\underline{u}}(\alpha )$ is a bounded monotonic increasing (non-decreasing) left-continuous function for all $\alpha \in (0, 1]$ and right-continuous for $\alpha = 0$.

• 2. ${\overline{u}}(\alpha )$ is a bounded monotonic decreasing (non-increasing) left-continuous function for all $\alpha \in (0, 1]$ and right-continuous for $\alpha = 0$.

• 3. For all $\alpha \in (0,1]$ we have, ${\underline{u}}(\alpha )\le {\overline{u}}(\alpha )$.

From Definition 2.2, a fuzzy number ${\tilde{u}}\in E^1$ is determined by the endpoints of the interval $[{\underline{u}}(\alpha ),{\overline{u}}(\alpha )]$. Thus, we can identify a fuzzy number ${\tilde{u}}$ with the parameterized triple:

$$\begin{aligned} \{({\underline{u}}(\alpha ),{\overline{u}}(\alpha ),\alpha ): \alpha \in [0,1]\}. \end{aligned}$$

Let ${\tilde{A}}$ be an $m\times n$ fuzzy matrix, then according to the above notations, ${\tilde{A}}=({\tilde{a}}_{ij})_{m\times n}$, can be shown in the following form:

$$\begin{aligned} {\tilde{A}}=(\{(\underline{a_{ij}}(\alpha ),\overline{a_{ij}}(\alpha ), \alpha ):\alpha \in [0,1]\})_{m\times n}. \end{aligned}$$

Throughout the paper, we denote ${\tilde{A}}$ by $({\underline{A}}(\alpha ),{\overline{A}}(\alpha ))$ where,

$$\begin{aligned} {\underline{A}}(\alpha )=(\underline{a_{ij}}(\alpha ))_{m\times n},\quad {\overline{A}}(\alpha )=(\overline{a_{ij}}(\alpha ))_{m\times n}. \end{aligned}$$

Definition 2.3

(Wu 2004a) Let $A=[{\underline{a}},{\overline{a}}]$ and $B=[{\underline{b}},{\overline{b}}]$ be two closed interval in ${\mathbb {R}}$. We note $A\preceq B$, if and only if, ${\underline{a}}\le {\underline{b}}$ and ${\overline{a}}\le {\overline{b}}$. Also, we write $A\prec B$, if and only if, $A\preceq B$ and $A\ne B$. Equivalently, we observe that $A\prec B$, if and only if,

$$\begin{aligned} {\left\{ \begin{array}{ll} {\underline{a}}<{\underline{b}},\\ {\overline{a}}<{\overline{b}}, \end{array}\right. } {or}\quad {\left\{ \begin{array}{ll} {\underline{a}}\le {\underline{b}},\\ {\overline{a}}<{\overline{b}}, \end{array}\right. } {or}\quad {\left\{ \begin{array}{ll} {\underline{a}}<{\underline{b}},\\ {\overline{a}}\le {\overline{b}}. \end{array}\right. } \end{aligned}$$

Definition 2.4

(Friedman et al. 1999) A subset S of $E^1$ is bounded from above, if there exists a fuzzy number ${\tilde{v}}\in E^1$, called an upper bound of S, such that ${\tilde{u}}\le {\tilde{v}}$ for any ${\tilde{u}} \in E^1$. ${\tilde{v}}_0\in E^1$ is called the supremum of S if ${\tilde{v}}_0$ is an upper bound of S and satisfies ${\tilde{v}}_0\le v$ for any upper bound ${\tilde{v}}$ of S, and we denote it as ${\tilde{v}}_0=\sup _{{\tilde{u}}\in A} {\tilde{u}}$. A lower bound and the infimum of S are defined similarly. S is said to be order bounded if it is both bounded from above and bounded from below.

Definition 2.5

(Wu 2004a) A triangular fuzzy number is denoted by ${\tilde{u}} = (a, b, c)$, and its $\alpha$-cuts is denoted by ${\tilde{u}}[\alpha ] = [a+\alpha (b - a),c-\alpha (c-b)]$.

Definition 2.6

(Lupulescu 2009) For arbitrary fuzzy numbers ${\tilde{u}}=[{\underline{u}}, {\overline{u}}], {\tilde{v}}=[{\underline{v}}, {\overline{v}}]$, the distance between ${\tilde{u}}$ and ${\tilde{v}}$ is defined as follows,

$$\begin{aligned} d({\tilde{u}},{\tilde{v}})=\sup \limits _{\alpha \in [0,1]} d_H([u]^\alpha , [v]^\alpha ), \end{aligned}$$

(2)

where $d_H$ is the Hausdorff distance.

Definition 2.7

(Lupulescu 2009) The opposite of a fuzzy number ${\tilde{u}}$ to be the fuzzy number $-{\tilde{u}}$. If ${\tilde{u}}[\alpha ]=[{\underline{u}}(\alpha ), {\overline{u}}(\alpha )]$, then $-{\tilde{u}}[\alpha ]=[-{\overline{u}}(\alpha ),-{\underline{u}}(\alpha )]$. Also,

• 1. $(k{\tilde{u}})[\alpha ]=[\min \{k{\underline{u}}(\alpha ), k{\overline{u}}(\alpha )\}, \max \{k{\overline{u}}(\alpha ), k{\underline{u}}(\alpha )\}], \quad \forall k\in {\mathbb {R}}^+$.

• 2. $({\tilde{u}}+{\tilde{v}})[\alpha ]=[{\underline{u}}(\alpha )+{\underline{v}}(\alpha ), {\overline{u}}(\alpha )+{\overline{v}}(\alpha )]$.

• 3. $({\tilde{u}}-{\tilde{v}})[\alpha ]=[{\underline{u}}(\alpha )-{\overline{v}}(\alpha ), {\overline{u}}(\alpha )-{\underline{v}}(\alpha )]$.

• 4. $({\tilde{u}}{\tilde{v}})[\alpha ]=[({\underline{uv}})(\alpha ), ({\overline{uv}})(\alpha )]$, where:

  $$\begin{aligned} ({\underline{uv}})(\alpha )&=\min \{{\overline{u}}(\alpha ){\underline{v}}(\alpha ),{\overline{u}}(\alpha ){\overline{v}}(\alpha ) , {\underline{u}}(\alpha ){\underline{v}}(\alpha ), {\underline{u}}(\alpha ){\overline{v}}(\alpha ) \},\\({\overline{uv}})(\alpha )&= \max \{ {\overline{u}}(\alpha ){\underline{v}}(\alpha ),{\overline{u}}(\alpha ){\overline{v}}(\alpha ) , {\underline{u}}(\alpha ){\underline{v}}(\alpha ), {\underline{u}}(\alpha ){\overline{v}}(\alpha ) \}. \end{aligned}$$

  (3)

Any $m\in {\mathbb {R}}$ can be considered as a fuzzy number ${\tilde{m}}$ in the following form:

$$\begin{aligned} {\tilde{m}}(r)={\left\{ \begin{array}{ll} 1, &{}\quad { if}\ \ r=m\\ 0, &{}\quad { if}\ \ r\ne m, \end{array}\right. } \end{aligned}$$

(4)

and note that from Definition 2.2, we can write ${\tilde{m}}=(m,m)$. Particularly, the fuzzy number ${\tilde{0}}$ is defined as ${\tilde{0}}(r)=1$, if $r = 0$ and ${\tilde{0}}(r)=0$ otherwise.

${\tilde{A}}$ is said to be an n-dimensional fuzzy vector, if the components of ${\tilde{A}}$ are composed by n fuzzy numbers, denoted by ${\tilde{A}}= ({\tilde{x}}_1,{\tilde{x}}_2,\ldots ,{\tilde{x}}_n)^T$.

A $\alpha$-level vector of fuzzy vector ${\tilde{A}}=({\tilde{x}}_1,{\tilde{x}}_2,\ldots ,{\tilde{x}}_n)^T$ is defined as,

$$\begin{aligned} {\tilde{A}}[\alpha ]= ({\tilde{x}}_1[\alpha ],{\tilde{x}}_2[\alpha ],\ldots ,{\tilde{x}}_n[\alpha ]), \end{aligned}$$

and,

$$\begin{aligned} {\underline{A}}[\alpha ]= (\underline{x_1}[\alpha ], \underline{x_2}[\alpha ],\ldots , \underline{x_n}[\alpha ]),\qquad {\overline{A}}[\alpha ]= (\overline{x_1}[\alpha ], \overline{x_2}[\alpha ],\ldots , \overline{x_n}[\alpha ]). \end{aligned}$$

Also, for ${\tilde{A}}=({\tilde{x}}_1,{\tilde{x}}_2,\ldots ,{\tilde{x}}_n)^T$ and ${\tilde{B}}=({\tilde{y}}_1,{\tilde{y}}_2,\ldots ,{\tilde{y}}_n)^T$, we have:

$$\begin{aligned} {\tilde{A}}+{\tilde{B}}=({\tilde{x}}_1+{\tilde{y}}_1,{\tilde{x}}_2+{\tilde{y}}_2,\ldots ,{\tilde{x}}_n+{\tilde{y}}_n)^T,\quad k{\tilde{A}}= (k{\tilde{x}}_1,k{\tilde{x}}_2,\ldots ,k{\tilde{x}}_n)^T,\ (k\in {\mathbb {R}}). \end{aligned}$$

2.2 Fuzzy calculus

Here, our requirements from the fuzzy calculus are stated.

Definition 2.8

(Panigrahi et al. 2008) Let ${\tilde{f}}:{\varOmega }\subseteq {\mathbb {R}}^n\rightarrow E^1$ be a fuzzy mapping where ${\varOmega }$ is an open subset of ${\mathbb {R}}^n$. We denote the $\alpha$-cut of ${\tilde{f}}$ at $t\in {\varOmega }$ with ${\tilde{f}}(t)[\alpha ]=[{\underline{f}}(t,\alpha ),{\overline{f}}(t,\alpha )]$ which is a closed and bounded interval. Here, ${\underline{f}}(t,\alpha )$ and ${\overline{f}}(t,\alpha )$ are real valued functions, where ${\underline{f}}(t,\alpha )$ is a bounded increasing function of $\alpha$ and ${\overline{f}}(t,\alpha )$ is a bounded decreasing function of $\alpha$. Also, for each $\alpha \in [0,1], {\underline{f}}(t,\alpha )\le {\overline{f}}(t,\alpha )$.

Definition 2.9

(Panigrahi et al. 2008) Let d be the metric defined in Definition 2.6. A fuzzy function ${\tilde{f}}{:}\,(a,b)\rightarrow E^1$ is differentiable at ${\hat{t}}\in (a,b)$, if there exists $\tilde{f'}({\hat{t}})\in E^1$, such that the limits:

$$\begin{aligned} d\left( \lim \limits _{h\rightarrow 0^+}\frac{{\tilde{f}}({\hat{t}}+h)-{\tilde{f}}({\hat{t}})}{h}, \tilde{f'}({\hat{t}})\right) ,\quad d\left( \lim \limits _{h\rightarrow 0^+}\frac{{\tilde{f}}({\hat{t}})-{\tilde{f}}({\hat{t}}-h)}{h}, \tilde{f'}({\hat{t}})\right) , \end{aligned}$$

(5)

exist and both equal to 0.Then $\tilde{f'}({\hat{t}})$ is called the derivative of ${\tilde{f}}$ at ${\hat{t}}$ (Lupulescu 2009).

Theorem 2.10

(Panigrahi et al. 2008) Suppose ${\tilde{f}}$ is a fuzzy function with ${\tilde{f}}(t)[\alpha ]=[{\underline{f}}(t,\alpha ),{\overline{f}}(t,\alpha )]$ where $0\le \alpha \le 1$, and ${\tilde{f}}$ is differentiable according to Definition 2.9, then ${\underline{f}}(t,\alpha )$ and ${\overline{f}}(t,\alpha )$ are differentiable functions and we have:

$$\begin{aligned} \tilde{f'}(t)[\alpha ]=[\underline{f'}(t,\alpha ),\overline{f'}(t,\alpha )]. \end{aligned}$$

Definition 2.11

(Panigrahi et al. 2008) Let ${\tilde{f}}:{\varOmega }\subseteq {\mathbb {R}}^n\rightarrow E^1$ be a fuzzy mapping, where ${\varOmega }$ is an open subset of ${\mathbb {R}}^n$. Let $(x_1, x_2 ,\ldots , x_n)^T\in {\varOmega }$ and $\frac{\partial }{\partial x_i}, i=1,2,\ldots ,n$ stands for the partial differentiation with respect to the i-th variable $x_i$. Assume that for all $\alpha \in [0,1], {\overline{f}}(x,\alpha )$ and ${\underline{f}}(x,\alpha )$ (the $\alpha$-cuts of ${\tilde{f}}$) have continuous partial derivatives, such that $\frac{\partial {\underline{f}}(x,\alpha )}{\partial x_i}$ and $\frac{\partial {\overline{f}}(x,\alpha )}{\partial x_i}$ are continuous. Define,

$$\begin{aligned} \frac{{\tilde{\partial }}{\tilde{f}}(x)}{\partial x_i}[\alpha ]=\left[ \frac{\partial {\underline{f}}(x,\alpha )}{\partial x_i}, \frac{\partial {\overline{f}}(x,\alpha )}{\partial x_i}\right] ,\quad i=1,2,\ldots , n,\quad \alpha \in [0,1]. \end{aligned}$$

(6)

If for each $i=1,2,\ldots , n$ (6) defines the $\alpha$-cuts of a fuzzy number, then we will say that ${\tilde{f}}$ is differentiable at x, and we write:

$$\begin{aligned} {\tilde{\nabla }}{\tilde{f}}(x)=\left( \frac{{\tilde{\partial }}{\tilde{f}}(x)}{\partial x_1},\frac{{\tilde{\partial }}{\tilde{f}}(x)}{\partial x_2},\ldots , \frac{{\tilde{\partial }}{\tilde{f}}(x)}{\partial x_n}\right) . \end{aligned}$$

(7)

We call ${\tilde{\nabla }}{\tilde{f}}(x)$ the gradient of the fuzzy function ${\tilde{f}}$ at x (here ${\tilde{\nabla }}$ stands for fuzzy gradient of fuzzy function ${\tilde{f}}$).

A subset C of ${\varOmega }$ is said to be convex, if $(1-\lambda )x+\lambda y\in C$ whenever $x\in C$, $y\in C$, and $0< \lambda < 1$.

Theorem 2.12

(Wang and Wu 2003) A fuzzy mapping ${\tilde{f}}:C\rightarrow E^1$ defined on a convex subset C in ${\varOmega }$ is convex, if and only if,

$$\begin{aligned} {\tilde{f}}((1-\lambda )x+\lambda y)\le (1-\lambda ){\tilde{f}}(x)+\lambda {\tilde{f}}(y),\quad \lambda \in [0, 1], \end{aligned}$$

for every x and y in C.

A fuzzy mapping ${\tilde{f}}:C\rightarrow E^1$ defined on a convex subset C in ${\varOmega }$ is called strictly convex if,

$$\begin{aligned} {\tilde{f}}((1-\lambda )x+\lambda y)<(1-\lambda ){\tilde{f}}(x)+\lambda {\tilde{f}}(y),\quad \forall x,y\in C,\ x\ne y, \quad \lambda \in (0, 1). \end{aligned}$$

According to the parametric representation of fuzzy number, a fuzzy mapping ${\tilde{f}}(x)$ can be written as follows:

$$\begin{aligned} {\tilde{f}}(x)=\{(\underline{f(x)}(\alpha ),\overline{f(x)}(\alpha ),\alpha ): \alpha \in [0,1]\}. \end{aligned}$$

Theorem 2.13

(Wang and Wu 2003) Let C be a convex subset in ${\varOmega }$ and ${\tilde{f}}:C\rightarrow E^1$ be a fuzzy mapping, then ${\tilde{f}}$ is convex, if and only if, both of $\underline{f(x)}(\alpha )$ and $\overline{f(x)}(\alpha )$ are convex functions at x for any fixed $\alpha \in [0, 1]$.

Theorem 2.14

(Wang and Wu 2003) If ${\tilde{f}}_1, {\tilde{f}}_2$,..., ${\tilde{f}}_m$ are convex fuzzy mappings defined on $C\subseteq {\varOmega }, \lambda _i\ge 0$ ($i=1,\ldots , m)$, then $\lambda _1{\tilde{f}}_1+\lambda _2{\tilde{f}}_2+\ldots +\lambda _m{\tilde{f}}_m$ is a convex fuzzy mappings on C.

2.3 Fuzzy optimization

Here, our requirements from the fuzzy optimization are investigated.

Definition 2.15

(Wu 2004a) Let $f(x)=[{\underline{f}}(x), {\overline{f}}(x)]$ be an interval-valued function on ${\varOmega }\subseteq {\mathbb {R}}^n$. We consider the following minimized problem with the interval-valued objective function:

$$\begin{aligned} \min \quad&{f}(x)=[{\underline{f}}(x), {\overline{f}}(x)],\\s.t. \quad&x\in {\varOmega }, \end{aligned}$$

(8)

where the feasible set ${\varOmega }$ is assumed as a convex subset on ${\mathbb {R}}^n$.

Definition 2.16

(Miettinen 1999) A decision vector $x^*\in {\varOmega }$ is a Pareto optimal, if there does not exist another decision vector $x\in {\varOmega }$, such that $f_i(x)\le f_i(x^*)$ for all $i=1,\ldots ,k$ and $f_j(x)<f_j(x^*)$ for at least one index j.

Definition 2.17

(Wu 2004a) A feasible point $x^*\in {\varOmega }$ is said to be an efficient solution for (8), if there exists no feasible point ${\bar{x}}\in {\varOmega }$, such that $f({\bar{x}})\prec f(x^*)$.

Consider the following weighting problem:

$$\begin{aligned} \min \quad&\sum _{i=1}^kw_if_i(x),\\s.t. \quad&x\in {\varOmega }, \end{aligned}$$

(9)

where $w_i\ge 0$ for all $i=1,\ldots , k$ and $\sum \limits _{i=1}^kw_i=1$.

Theorem 2.18

(Miettinen 1999) The unique solution of weighting problem (9) is a Pareto optimal, if the weighting coefficients are positive.

Theorem 2.19

(Miettinen 1999) Let the multi-objective optimization problem be convex. If $x^*\in {\varOmega }$ is a Pareto optimal, then there exists a weighting vector w, such that $x^*$ is a solution of weighting problem (9).

Corollary 2.20

(Miettinen 1999) A point to be a properly Pareto optimal solution of a multi-objective optimization problem, if and only if, that point is a solution of a weighting problem with all the weighting coefficient being positive.

Consider the following bi-objective optimization problem:

$$\begin{aligned} \min \quad&({\underline{f}}(x), {\overline{f}}(x)),\\s.t. \quad&x\in {\varOmega }. \end{aligned}$$

(10)

Also, consider the weighting problem of (10) defined by:

$$\begin{aligned} \min \quad&w_1{\underline{f}}(x)+w_2{\overline{f}}(x),\\s.t. \quad&x\in {\varOmega }, \end{aligned}$$

(11)

where $w_1$ and $w_2$ are positive real numbers and $w_1+w_2=1$. Based on Corollary 2.20, if $x^*$ is an optimal solution of problem (11), then $x^*$ is a Pareto optimal solution of problem (10) and according to Definition 2.17, $x^*$ is an efficient solution of problem (8).

3 Fuzzy quadratic programming problem

In this section, the FQP is presented.

Definition 3.1

(Positive semi-definite and symmetric fuzzy matrix) An $n\times n$ fuzzy matrix ${\tilde{A}}= (\{(\underline{a_{ij}}(\alpha ), \overline{a_{ij}}(\alpha ), \alpha ):\alpha \in [0,1]\})_{n\times n}$ is said to be positive semi-definite and symmetric, if for any $\alpha \in [0,1], {\underline{A}}(\alpha )=(\underline{a_{ij}}(\alpha ))_{n\times n}$ and ${\overline{A}}(\alpha )=(\overline{a_{ij}}(\alpha ))_{n\times n}$ are $n\times n$ positive semi-definite and symmetric.

Theorem 3.2

Let ${\bar{x}}\in {\mathbb {R}}^n_+$ is a local optimal solution to the problem (1), then ${\bar{x}}$ is a global optimal solution of (1). Also, if ${\tilde{f}}$ is strictly convex, then ${\bar{x}}$ is the unique global optimal solution of (1).

Proof

See “Appendix 3”. $\square$

Consider the FQP in (1). We can rewrite this problem as,

$$\begin{aligned} \min \quad&{\tilde{f}}(x)={\tilde{c}}^Tx+\frac{1}{2}x^T{\tilde{H}}x,\\s.t.\quad&\tilde{A'}x\le \tilde{b'}, \end{aligned}$$

(12)

where $\tilde{A'}=\begin{bmatrix} {\tilde{A}} \\ -I \end{bmatrix}, \tilde{A'}(\alpha )=\begin{bmatrix} {\underline{A}}(\alpha ) \\ {\overline{A}}(\alpha )\\ -I \end{bmatrix}$ and $\tilde{b'}=\begin{bmatrix} {\tilde{b}}\\ 0 \end{bmatrix}, \tilde{b'}(\alpha )=\begin{bmatrix} {\underline{b}}(\alpha ) \\ {\overline{b}}(\alpha ) \\ -I \end{bmatrix}$. Based on Definition 2.15, we can write (12) as an interval program:

$$\begin{aligned} \min \quad&[{\underline{f}}(x)(\alpha ), {\overline{f}}(x)(\alpha )]\\s.t.\quad&[\underline{A'}(\alpha ), \overline{A'}(\alpha )]x\le [\underline{b'}(\alpha ), \overline{b'}(\alpha )],\nonumber \\&0\le \alpha \le 1, \end{aligned}$$

(13)

or it can be written as a bi-objective problem:

$$\begin{aligned} \min \quad&({\underline{f}}(x)(\alpha ),{\overline{f}}(x)(\alpha ))\\s.t.\quad&\underline{A'}(\alpha )x \le \underline{b'}(\alpha ),\nonumber \\&\overline{A'}(\alpha )x\le \overline{b'}(\alpha ),\\&0\le \alpha \le 1, \end{aligned}$$

(14)

where ${\underline{f}}(x)(\alpha )={\underline{c}}(\alpha )^Tx+\frac{1}{2}x^T{\underline{H}}(\alpha )x$ and ${\overline{f}}(x)(\alpha )={\overline{c}}(\alpha )^Tx+\frac{1}{2}x^T{\overline{H}}(\alpha )x$. According to Corollary 2.20, by reformulating (14) into a weighting problem as in (11), we have:

$$\begin{aligned} \min \quad&w_1{\underline{f}}(x)(\alpha )+w_2{\overline{f}}(x)(\alpha )\\s.t.\quad&\underline{A'}(\alpha )x \le \underline{b'}(\alpha ),\nonumber \\&\overline{A'}(\alpha )x\le \overline{b'}(\alpha ),\\&0\le \alpha \le 1, \end{aligned}$$

(15)

where $w_1+w_2=1$. The Lagrangian of (15) is derived as:

$$\begin{aligned} {L}(x,u_1,u_2)= & {} w_1{\underline{f}}(x)(\alpha )+w_2{\overline{f}}(x)(\alpha )+u_1^T(\underline{A'}(\alpha )x -\underline{b'}(\alpha ))\\&+\,u_2^T(\overline{A'}(\alpha )x- \overline{b'}(\alpha )),\quad u_1,u_2\ge 0,\quad 0\le \alpha \le 1. \end{aligned}$$

The Lagrangian dual of (15) is given by:

$$\begin{aligned} \max \limits _{u_1,u_2\ge 0}\ \min \limits _{x\ge 0} {L}(x,u_1,u_2)= & {} \max \limits _{u_1,u_2\ge 0}\ \min \limits _{x\ge 0} \big \{w_1{\underline{f}}(x)(\alpha )+w_2{\overline{f}}(x)(\alpha )\nonumber \\&+\,u_1^T(\underline{A'}(\alpha )x -\underline{b'}(\alpha ))+u_2^T(\overline{A'}(\alpha )x- \overline{b'}(\alpha ))\big \}.\qquad \end{aligned}$$

(16)

The Lagrangian dual in (16) can be written another form as (Bazaraa et al. 1979):

$$\begin{aligned} \max \quad&w_1{\underline{f}}(x)(\alpha )+w_2{\overline{f}}(x)(\alpha )+u_1^T(\underline{A'}(\alpha )x -\underline{b'}(\alpha ))+u_2^T(\overline{A'}(\alpha )x- \overline{b'}(\alpha )),\nonumber \\ s.t.\quad&w_1({\underline{c}}(\alpha )+{\underline{H}}(\alpha )x)+w_2({\overline{c}}(\alpha )+{\overline{H}}(\alpha )x)+\underline{A'}(\alpha )^Tu_1+\overline{A'}(\alpha )^Tu_2={0},\nonumber \\&u_1,u_2\ge 0,\quad 0\le \alpha \le 1. \end{aligned}$$

(17)

Thus, (17) can be as follow:

$$\begin{aligned} \max \quad&w_1\left[ {\underline{c}}(\alpha )^Tx+\frac{1}{2}x^T{\underline{H}}(\alpha )x\right] +w_2\left[ {\overline{c}}(\alpha )^Tx+\frac{1}{2}x^T{\overline{H}}(\alpha )x\right] \nonumber \\&+u_1^T(\underline{A'}(\alpha )x -\underline{b'}(\alpha ))+u_2^T(\overline{A'}(\alpha )x- \overline{b'}(\alpha )),\nonumber \\ s.t.\quad&w_1\left[ {\underline{c}}(\alpha )+{\underline{H}}(\alpha )x\right] +w_2\left[ {\overline{c}}(\alpha )+{\overline{H}}(\alpha )x\right] +\underline{A'}(\alpha )^Tu_1+\overline{A'}(\alpha )^Tu_2={0},\nonumber \\&u_1,u_2\ge 0,\quad 0\le \alpha \le 1. \end{aligned}$$

(18)

From multiplying $w_1\left[ {\underline{c}}(\alpha )+{\underline{H}}(\alpha )x\right] +w_2\left[ {\overline{c}}(\alpha )+{\overline{H}}(\alpha )x\right] +\underline{A'}(\alpha )^Tu_1+\overline{A'}(\alpha )^Tu_2={0}$ to x we have $(w_1{\underline{c}}(\alpha )+w_2{\overline{c}}(\alpha ))^Tx+(u_1^T\underline{A'}(\alpha )+u_2^T\overline{A'}(\alpha ))x=-x^T(w_1{\underline{H}}(\alpha )+w_2{\overline{H}}(\alpha ))x$. Substitute this into (18), we derive the fuzzy form of Dorn’s dual quadratic program:

$$\begin{aligned} \max \quad&-\frac{1}{2}x^T(w_1{\underline{H}}(\alpha )+w_2{\overline{H}}(\alpha ))x-(\underline{b'}(\alpha )^Tu_1+\overline{b'}(\alpha )u_2),\\s.t.\quad&w_1{\underline{c}}(\alpha )+w_2{\overline{c}}(\alpha )+(w_1{\underline{H}}(\alpha )+w_2{\overline{H}}(\alpha ))x+\underline{A'}(\alpha )^Tu_1+\overline{A'}(\alpha )^Tu_2=0,\nonumber \\&u_1,u_2\ge 0,\quad 0\le \alpha \le 1. \end{aligned}$$

(19)

Here, by using $x=-(w_1{\underline{H}}(\alpha )+w_2{\overline{H}}(\alpha ))^{-1}(w_1{\underline{c}}(\alpha )+w_2{\overline{c}}(\alpha )+\underline{A'}(\alpha )^Tu_1+\overline{A'}(\alpha )^Tu_2)$ and substituting in (19) we get:

$$\begin{aligned} \max \quad&\frac{1}{2}u^T{D}(\alpha )u+u^T{d}(\alpha )-\frac{1}{2}{c}(\alpha )^T{H(\alpha )^{-1}}{c}(\alpha ),\\s.t.\quad&u\ge 0,\quad 0\le \alpha \le 1, \end{aligned}$$

(20)

where ${D}(\alpha )=-{A'}(\alpha ){H(\alpha )^{-1}}{A'}(\alpha )^T, {d}(\alpha )=-{b'}(\alpha )-{A'}(\alpha ){H(\alpha )^{-1}}{c}(\alpha )$. Also,

$$\begin{aligned} {A'}(\alpha )&=[\underline{A'}(\alpha ), \overline{A'}(\alpha )],\quad&{H}(\alpha )^{-1}=(w_1{\underline{H}}(\alpha )+w_2{\overline{H}}(\alpha ))^{-1},\\ \quad {b'}(\alpha )&=[\underline{b'}(\alpha ), \overline{b'}(\alpha )],\quad&{c}(\alpha )=w_1{\underline{c}}(\alpha )+w_2{\overline{c}}(\alpha ). \end{aligned}$$

Therefore, the problem (1) is converted into the problem (20). In next section, we propose a neural network model for solving the problem (20).

4 Neural network model

In this point of view, we propose a dynamical system for solving the problem (20) as the following:

$$\begin{aligned} \frac{{d_\alpha }u}{dt}={D}(\alpha )u+{d}(\alpha ),\qquad u\in {\mathbb {R}}^{2m+n}_+,\quad 0\le \alpha \le 1, \end{aligned}$$

(21)

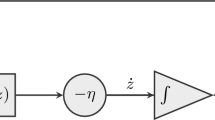
where $\frac{d_\alpha }{dt}$ means for any fixed $\alpha$ we have a particular dynamical system which refers to $\alpha$. The neural network model described by (21) can be easily realized by a recurrent neural network with a single-layer structure as shown in Fig. 1. According to Fig. 1, the circuit realizing the proposed neural network model consists of $2m+n$ activation functions, $2m+n$ summers, and $(2m+n)^2$ multipliers. Also, to solve the above neural network model we use MATLAB (ode45).

Fig. 1

Architecture of the neural network (21)

Lemma 4.1

The dynamical system in (21) is Lipschitz continuous function.

Proof

For any ${\hat{u}},{\bar{u}}\in {\mathbb {R}}^{2m+n}_+$, where ${\hat{u}}=({\hat{u}}_1,\ldots ,{\hat{u}}_{n}), {\bar{u}}=({\bar{u}}_1,\ldots ,{\bar{u}}_{n})$, and assume that ${G_\alpha }(u)={D}(\alpha )u+{d}(\alpha ), 0\le \alpha \le 1$, we have:

$$\begin{aligned} \Vert {G_\alpha }({\hat{u}})-{G_\alpha }({\bar{u}})\Vert&=\Big \Vert {D}(\alpha ){\hat{u}}+{d}(\alpha )-({D}(\alpha ){\bar{u}}+{d}(\alpha ))\Big \Vert \\&\le \Big \Vert {D}(\alpha )({\hat{u}}-{\bar{u}})\Big \Vert \\&\le \Vert {D}(\alpha )\Vert \Big \Vert {\hat{u}}-{\bar{u}}\Big \Vert . \end{aligned}$$

Therefore, by the above notation one can consequently prove that $\Big \Vert {G_\alpha }({\hat{u}})-{G_\alpha }({\bar{u}})\Big \Vert \le \Vert {D}(\alpha )\Vert \Big \Vert {\hat{u}}-{\bar{u}}\Big \Vert$. Thus, ${G_\alpha }(u)={D}(\alpha )u+{d}(\alpha )$ is Lipschitz continuous function with constant $\Vert {D}(\alpha )\Vert$. Note that, $G_\alpha (\cdot )$ means for any fixed $\alpha$ we have a particular ${G_\alpha }(u)={D}(\alpha )u+{d}(\alpha )$ which refers to $\alpha$. $\square$

5 Stability analysis

In this section, we show that the neural network whose dynamic is described by the differential equation (21) is stable. First, some definitions from dynamical system are presented (Khalil 1996).

Definition 5.1

(Equilibrium point) In the following dynamical system:

$$\begin{aligned} {\dot{x}}=f(x(t)) ,\quad x(t_0)=x_0\in {\mathbb {R}}^n, \end{aligned}$$

(22)

where f is a function from ${\mathbb {R}}^n$ to ${\mathbb {R}}^n, x^*$ is called an equilibrium point of (22), if $f(x^*)=0$.

Definition 5.2

(Stability in the sense of Lyapunov) Suppose x(t) is a solution for (22). Equilibrium point $x^*$ is said to be stable in the sense of Lyapunov, if for any $x_0=x(t_0)$ and any $\varepsilon > 0$, there exists a $\delta > 0$, such that:

$$\begin{aligned} \Vert x(t)-x^*\Vert<\varepsilon ,\quad \forall \ t \ge t_0, \quad \Vert x(t_0)-x^*\Vert <\delta . \end{aligned}$$

Definition 5.3

(Lyapunov function) Let ${\varOmega }\subseteq {\mathbb {R}}^n$ be an open neighborhood of ${x^*}$. A continuously differentiable function $V:{\mathbb {R}}^n\longrightarrow {\mathbb {R}}$ is said to be a Lyapunov function at the state ${x^*}$ over the set ${\varOmega }$ for (2) if,

$$\begin{aligned} { {\left\{ \begin{array}{ll} V({x^*})=0,\ V(x)>0,&{}\quad \forall x\in {\varOmega }\backslash \{{x^*}\},\\ \frac{dV(x(t))}{dt}=\nabla V(x(t))^Tf(x(t))\le 0,&{}\quad \forall x\in {\varOmega }. \end{array}\right. }} \end{aligned}$$

Definition 5.4

(Bazaraa et al. 1979) A function $F:{\mathbb {R}}^m\longrightarrow {\mathbb {R}}^m$ is said to be Lipschitz continuous, if there exists a constant $L > 0$, such that $\Vert F(x)-F(y)\Vert \le L\Vert x-y\Vert$ for all $x,y\in {\mathbb {R}}^m$.

Definition 5.5

(Asymptotic stability) An isolated equilibrium point $x^*$ is said to be asymptotically stable, if in addition to being Lyapunov stable, it has the property that $x(t)\rightarrow x^*$ as $t\rightarrow \infty$ for all $\Vert x(t_0)-x^*\Vert <\delta$.

Now, with assumption $Z^*=\{u\ |\ u\$is the solution of (21)$\}\ne \emptyset$, we prove the global convergence of (21). At first, we state basic property of (21) as follow. We assume that ${G_\alpha }(u)={D}(\alpha )u+{d}(\alpha )$.

Theorem 5.6

$u^*$ is the equilibrium point of (21), if and only if, $u^*\in Z^*$ and for any $u_0=u(t_0)\in {\mathbb {R}}^{2m+n}$ there exist a unique continuous solution to Eq. (21) over $[t_0,\infty )$.

Proof

Without loss of generality, assume that ${G_\alpha }(u^*)=0$. And according to the Lemma 4.1, ${G_\alpha }(u)$ is Lipschitz continuous. Using theorem 3.1 in Khalil (1996) the existence and uniqueness of the solution to (21) over $[t_0,\infty )$ are proved. $\square$

Theorem 5.7

The proposed neural dynamical system in (21) is stable in the sense of Lyapunov and is globally convergent to the solution set of (20).

Proof

By Theorem 5.6, one can see that there is a unique continuous solution to (21) over $[t_0,\infty )$. Suppose that $u=u(t)$ is the solution of (21) with initial point $u_0 = u(t_0)$. Also, we propose the following Lyapunov function:

$$\begin{aligned} {V_\alpha }(u)=\frac{1}{2}\left\| D(\alpha )u+d(\alpha )\right\| ^2, \quad u\in {\mathbb {R}}^{2m+n}_+,\quad 0\le \alpha \le 1, \end{aligned}$$

where $V_\alpha$ means for any fixed $\alpha$ we have a particular Lyapunov function which refers to $\alpha$. For $u=u^*, {V_\alpha }(u^*)=0$, and ${V_\alpha }(u)>0$ for $u\ne u^*$. Also, for $0\le \alpha \le 1$, we have:

$$\begin{aligned} \frac{{d}}{dt}{V_\alpha }(u)&=\frac{d{V_\alpha }}{du}\frac{{d_\alpha }u}{dt}\\&= (D(\alpha )u+d(\alpha ))^TD(\alpha ){G}(u)\\&= (D(\alpha )u+d(\alpha ))^TD(\alpha )(D(\alpha )u+d(\alpha ))\le 0. \end{aligned}$$

(23)

The last inequality is verified from the fact that, ${G_\alpha }(u)={D}(\alpha )u+{d}(\alpha )$ and $D(\alpha )$ is a negative semi-definite matrix. Therefore, $\frac{d{V_\alpha }(u)}{dt}<0$ just for $u\ne u^*$. Thus, the neural network (21) is stable and ${V_\alpha }(u)\rightarrow \infty$ as $u\rightarrow \infty$. $\square$

6 Illustrative examples

In this section, some numerical examples are stated in order to demonstrate the validity and applicability of our method. The codes are developed using symbolic computation software MATLAB (ode45) and the calculations are implemented on a machine with Intel core 7 Duo processor 2 GHz and 8 GB RAM.

Example 6.1

Consider the following FQP from Liu (2009):

$$\begin{aligned} \min&{\tilde{f}}=(-6,-5,-4)x_1+(1,1.5,2)x_2\\&\qquad +\frac{1}{2}\left[ (4,6,8)x_1^2+(-6,-4,-2)x_1x_2+(2,4,6)x_2^2\right] \\ s.t.&\quad x_1+(0.5,1,1.5)x_2\le (1,2,3)\\&\qquad (1,2,3)x_1+(-2,-1,-0.5)x_2\le (3,4,5)\\&\qquad x_1,x_2\ge 0, \end{aligned}$$

According to the $\alpha$-cuts of fuzzy coefficients, we have:

$$\begin{aligned}&{\underline{H}}(\alpha )= \begin{bmatrix} 4+2\alpha&\quad -3+\alpha \\ -3+\alpha&\quad 2+2\alpha \end{bmatrix}, \&{\underline{c}}(\alpha )= \begin{bmatrix} -6+\alpha \\ 1+0.5\alpha \end{bmatrix}, \&{\underline{A}}(\alpha )= \begin{bmatrix} 1&0.5+0.5\alpha \\ 1+\alpha&-2+\alpha \end{bmatrix},\&{\underline{b}}(\alpha )= \begin{bmatrix} 1+\alpha \\ 2+2\alpha \end{bmatrix},\\&{\overline{H}}(\alpha )= \begin{bmatrix} 8-2\alpha&\quad -1-\alpha \\ -1-\alpha&\quad 6-2\alpha \end{bmatrix}, \&{\overline{c}}(\alpha )= \begin{bmatrix} -4-\alpha \\ 2-0.5\alpha \end{bmatrix}, \&{\overline{A}}(\alpha )= \begin{bmatrix} 1&\quad 1.5-0.5\alpha \\ 3-\alpha&\quad 0.5-0.5\alpha \end{bmatrix},\&{\overline{b}}(\alpha )= \begin{bmatrix} 3-\alpha \\ 6-2\alpha \end{bmatrix}. \end{aligned}$$

The primal and the dual solutions for various values of $\alpha , w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$ are shown in Table 1.

Table 1 The solution of neural network (21) for different values of $\alpha , w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$ in Example 6.1

One can see all simulation results demonstrate that the neural network (21) is globally asymptotically stable. We solve this problem by letting initial point $(-3, -1.5, -0.5, 1,2,3)$. The $\alpha$-cuts of f represent the possibility that the objective values will appear in the associated range. For instance, at $\alpha =0.4$, the value of $f=-1.8000$ occurs at $x_1=0.7500$ and $x_2=0.0000$ and at $\alpha =0.6$, the value of $f=-1.8897$ occurs at $x_1=0.7766$ and $x_2=0.0000$. Also, Fig. 2 displays the transient behaviour of state trajectories based on (21).

Fig. 2

Transient behaviour of the neural network (21) for $\alpha =0.6, w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$ in Example 6.1

In addition, the primal and the dual solutions for various values of $\alpha , w_1=\frac{1}{4}$ and $w_2=\frac{3}{4}$ are shown in Table 2.

Table 2 The solution of neural network (21) for different values of $\alpha , w_1=\frac{1}{4}$, and $w_2=\frac{3}{4}$ in Example 6.1

One can see all simulation results demonstrate that the neural network (21) is globally asymptotically stable. We solve this problem by letting initial point $(3,1.5,-0.5,-2,2,-1)$. The $\alpha$-cuts of f represent the possibility that the objective values will appear in the associated range. For instance, at $\alpha =0$, the value of $f=-1.4464$ occurs at $x_1=0.6429$ and $x_2=0.0000$ and at $\alpha =0.5$, the value of $f=-1.7356$ occurs at $x_1=0.7308$ and $x_2=0.0000$. Also, Fig. 3 displays the transient behaviour of state trajectories based on (21).

Fig. 3

Transient behaviour of the neural network (21) for $\alpha =0.8, w_1=\frac{1}{4}$, and $w_2=\frac{3}{4}$ in Example 6.1

Furthermore, we compare our neural network results for this example with some other neural networks (for $\alpha =1$, i. e., when the fuzziness goes to zero) in the Table 3.

Table 3 Comparison between the neural network (21) for $\alpha =1$ and $w_1=w_2=\frac{1}{2}$ with random initial point and the methods in Effati et al. (2015), and Xia and Wang (2000) in Example 6.1

In next examples, the FQP with high dimension is investigated, and they show the effectiveness of our method. In fact, we consider a crisp quadratic program as a FQP, but we put the parameters, triangular and symmetric fuzzy numbers.

Example 6.2

Consider the FQP as in (1) with the following properties:

$$\begin{aligned} {\tilde{H}}=\begin{bmatrix} {\tilde{2}}&\quad {\tilde{1}}&\quad {\tilde{1}} \\ {\tilde{1}}&\quad {\tilde{2}}&\quad {\tilde{0}} \\ {\tilde{1}}&\quad {\tilde{0}}&\quad {\tilde{2}} \end{bmatrix},\quad {\tilde{c}}=[-{\tilde{4}}, {\tilde{3}}, -{\tilde{2}}]^T,\quad {\tilde{b}}=[{\tilde{3}}, {\tilde{1}}]^T, \qquad {\tilde{A}}=\begin{bmatrix} {\tilde{3}}&\quad -{\tilde{9}}&\quad {\tilde{9}} \\ {\tilde{1}}&\quad {\tilde{1}}&\quad {\tilde{2}} \end{bmatrix}, \end{aligned}$$

where,

$$\begin{aligned} {\tilde{2}}&=(1, 2, 3),\quad&-{\tilde{2}}=(-3, -2, -1),\quad&{\tilde{3}}=(2, 3, 4),\quad \qquad {\tilde{1}}=(0, 1, 2),\\ -{\tilde{4}}&=(-5, -4, -3), \quad&-{\tilde{9}}=(-10, -9, -8),\quad&{\tilde{9}}=(8, 9, 10). \end{aligned}$$

The primal and the dual solutions for various values of $\alpha , w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$ are shown in Table 4. The optimal solution of the problem for $\alpha =1$ is $x^*=(1, 0, 0)$. One can see all simulation results demonstrate that the neural network (21) is globally asymptotically stable. The $\alpha$-cuts of f represent the possibility that the objective values will appear in the associated range. Also, Figs. 4 and 5 display the transient behaviour of state trajectories based on (21).

Moreover, we compare our neural network results for this example with some other neural networks (for $\alpha =1$, i. e., when the fuzziness goes to zero) in Table 5.

Table 4 The solution of neural network (21) for different values of $\alpha , w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$ in Example 6.2

Fig. 4

Transient behaviour of the neural network (21) for $\alpha =0.5, w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$ in Example 6.2

Fig. 5

Transient behaviour of the neural network (21) for $\alpha =1, w_1=\frac{1}{4}$, and $w_2=\frac{3}{4}$ in Example 6.2

Example 6.3

Consider the FQP as in (1) with the following properties:

$$\begin{aligned} {\tilde{H}}&=\begin{bmatrix} {\tilde{2}}&\quad {\tilde{1}}&\quad {\tilde{0}}&\quad {\tilde{0}}&\quad \ldots&\quad {\tilde{0}}&\quad {\tilde{0}} \\ {\tilde{1}}&\quad {\tilde{2}}&\quad {\tilde{1}}&\quad {\tilde{0}}&\quad \ldots&\quad {\tilde{0}}&\quad {\tilde{0}} \\ {\tilde{0}}&{\tilde{1}}&\quad {\tilde{2}}&\quad {\tilde{1}}&\quad \ldots&\quad {\tilde{0}}&\quad {\tilde{0}} \\ \vdots&\quad&\quad \ddots&\quad \ddots&\quad \ddots&\quad&\quad \vdots \\ {\tilde{0}}&\quad {\tilde{0}}&\quad \ldots&\quad {\tilde{1}}&\quad {\tilde{2}}&\quad {\tilde{1}}&\quad {\tilde{0}} \\ {\tilde{0}}&\quad {\tilde{0}}&\quad \ldots&\quad {\tilde{0}}&\quad {\tilde{1}}&\quad {\tilde{2}}&\quad {\tilde{1}} \\ {\tilde{0}}&\quad {\tilde{0}}&\quad \ldots&\quad {\tilde{0}}&\quad {\tilde{0}}&\quad {\tilde{1}}&\quad {\tilde{2}} \end{bmatrix}_{10\times 10},&{\tilde{c}}=[-{\tilde{1}}, {\tilde{4}}, -{\tilde{1}}, {\tilde{1}}, {\tilde{0}}, {\tilde{0}}, {\tilde{1}}, {\tilde{0}}, {\tilde{1}}, {\tilde{0}}]^T,\\ {\tilde{b}}&=[{\tilde{3}}, {\tilde{1}}, {\tilde{2}}]^T,&{\tilde{A}}=\begin{bmatrix} {\tilde{1}}&-{\tilde{1}}&-{\tilde{1}}&{\tilde{1}}&-{\tilde{1}}&{\tilde{1}}&{\tilde{0}}&{\tilde{1}}&{\tilde{1}}&-{\tilde{1}} \\ {\tilde{0}}&{\tilde{1}}&{\tilde{0}}&{\tilde{1}}&{\tilde{0}}&{\tilde{1}}&{\tilde{1}}&{\tilde{1}}&{\tilde{1}}&{\tilde{0}} \\ -{\tilde{1}}&{\tilde{1}}&-{\tilde{1}}&{\tilde{1}}&{\tilde{0}}&{\tilde{1}}&{\tilde{1}}&{\tilde{0}}&{\tilde{1}}&{\tilde{0}} \end{bmatrix}, \end{aligned}$$

where,

$$\begin{aligned} {\tilde{2}}=(1, 2, 3),\quad {\tilde{1}}=(0, 1, 2),\quad -{\tilde{1}}=(-2, -1, 1),\quad {\tilde{3}}=(2, 3, 4),\quad {\tilde{4}}=(3, 4, 5). \end{aligned}$$

The optimal solution of the problem for various values of $\alpha$ are shown in Table 6.

The optimal solution of the problem for $\alpha =1$ is $x^*=[0.5, 0, 0.5, 0, 0, 0,0,0,0,0]^T$. One can see all simulation results demonstrate that the neural network (21) is globally asymptotically stable. We solve this problem by letting initial point $(-4 , -1, 2, 0, 1, 2,-1, 5, -3, 0, 1, 3,1,7,6,0)$. The $\alpha$-cuts of f represent the possibility that the objective values will appear in the associated range. Also, Figs. 6 and 7 display the transient behaviour of state trajectories based on (21).

Table 5 Comparison between the neural network (21) for $\alpha =1, w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$ with random initial point and the methods in Effati et al. (2015), and Xia and Wang (2000) in Example 6.2

Table 6 The solutions of neural network method for various values of $\alpha$ with different $w_1$ and $w_2$ for Example 6.3

Fig. 6

Transient behaviour of the neural network (21) for $\alpha =0.4, w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$ in Example 6.3

Fig. 7

Transient behaviour of the neural network (21) for $\alpha =1, w_1=\frac{1}{4}$, and $w_2=\frac{3}{4}$ in Example 6.3

Example 6.4

Consider the following FQP:

$$\begin{aligned} \min \quad&{\tilde{f}}(x)={\tilde{c}}^Tx+\frac{1}{2}x^T{\tilde{H}}x,\\s.t.\quad&{\tilde{1}}x_i\le {\tilde{1}},\nonumber \\&x_i\ge 0,\quad i=1,2,\ldots , n \end{aligned}$$

where,

$$\begin{aligned} {\tilde{H}}= \begin{bmatrix} {\tilde{1}}&\quad {\tilde{2}}&\quad {\tilde{2}}&\quad {\tilde{2}}&\quad {\tilde{2}}&\quad \ldots&\quad {\tilde{2}}\\ {\tilde{2}}&\quad {\tilde{5}}&\quad {\tilde{6}}&\quad {\tilde{6}}&\quad {\tilde{6}}&\quad \ldots&\quad {\tilde{6}} \\ {\tilde{2}}&\quad {\tilde{6}}&\quad {\tilde{9}}&\quad {\tilde{10}}&\quad {\tilde{10}}&\quad \ldots&\quad {\tilde{10}} \\ {\tilde{2}}&\quad {\tilde{6}}&\quad {\tilde{10}}&\quad {\tilde{13}}&\quad {\tilde{14}}&\quad \ldots&\quad {\tilde{14}} \\ {\tilde{2}}&\quad {\tilde{6}}&\quad {\tilde{10}}&\quad {\tilde{14}}&\quad {\tilde{17}}&\quad&\quad {\tilde{18}} \\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots&\quad&\quad \ddots&\quad \vdots \\ {\tilde{2}}&\quad {\tilde{6}}&\quad {\tilde{10}}&\quad {\tilde{14}}&\quad {\tilde{18}}&\quad \ldots&\quad \widetilde{4n-3} \end{bmatrix}_{n\times n} ,\quad {\tilde{c}}=\begin{bmatrix} -{\tilde{1}} \\ -{\tilde{1}} \\ -{\tilde{1}} \\ \vdots \\ -{\tilde{1}} \end{bmatrix}_{n\times 1}. \end{aligned}$$

We consider all fuzzy parameters as a triangular and symmetric fuzzy numbers, i. e., ${\tilde{a}}=(a-1,a, a+1)$. The problem is solved for $n=25$ and $n=35$. One can see all simulation results demonstrate that the neural network (21) is globally asymptotically stable. We solve this problem by letting random initial point. Also, Figs. 8 and 9 display the transient behaviour of state trajectories based on (21).

Fig. 8

Transient behaviour of the neural network (21) for $\alpha =1, n=25$, and $w_1=w_2=\frac{1}{2}$ in Example 6.4

Fig. 9

Transient behaviour of the neural network (21) for $\alpha =0.5, n=35, w_1=\frac{1}{4}$, and $w_2=\frac{3}{4}$ in Example 6.4

Example 6.5

Consider the following quadratic programming problem with fuzzy coefficients in the linear term from Silva et al. (2013):

$$\begin{aligned}&\displaystyle \min \quad (-6, -5,-4)x_1+(1, 1.5, 2)x_2+2x^2_1-2x_1x_2+x_2^2,\\&\displaystyle s.t.\quad x_1+x_2\le 2,\\&\displaystyle 2x_1-x_2\le 4\\&\displaystyle x_1,x_2\ge 0. \end{aligned}$$

The optimal solution of the crisp problem is $x^*=(1.45, 0.55)$ and the value of the objective function is $-3.5125$. We apply the neural network (21) for the case that $\alpha =1$ and $w_1=w_2=\frac{1}{2}$. Figure 10 displays the transient behaviour of state trajectories based on (21) with many random initial points.

Also, Fig. 11 displays the transient behaviour of state trajectories based on (21) with many random initial points, $\alpha =0.2, w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$.

Fig. 10

Transient behaviour of the neural network (21) for $\alpha =1$ and $w_1=w_2=\frac{1}{2}$ in Example 6.5

Fig. 11

Transient behaviour of the neural network (21) for $\alpha =0.2, w_1=\frac{1}{3}$, and $w_2=\frac{2}{3}$ in Example 6.5

7 Discussion and conclusion

In this section, we provide a brief description about some issues for the proposed method and findings of the paper.

Table 7 The solutions of neural network method with different $w_1$ and $w_2$ and the Liu’s 2009 method for Example 6.1

In this paper, a neural network model to solve the FQP was proposed. We solved the proposed dynamical system by ODE method. Recently, many neural network models are proposed for solving mathematical programming problems. As we state before, there exist some approaches for solving the FQP. For instance, Ammar and Khalifa (2003) studied the FQP where all decision variables are non negative and the linear term in the objective function does not exist. Also, Liu (2009) discussed a FQP problem as a two-level mathematical programming problem for finding the bounds of the fuzzy objective values. However, in this paper, we solved the FQP by reformulating into a weighting problem. Also, we used some reformulated problems in order to get the Lagrangian dual and the Dorn dual of the FQP. Additionally, by using these transformations, we found both the primal and the dual solutions of the original problem. On the convergence analysis and stability side, we prove some results about the global convergence of the proposed neural network. Table 7 shows the solutions of Liu’s (2009) method and the method which discussed in this paper.

Based on the Table 7, our solutions are feasible. Because the solutions which provide from the neural network method are in the range of the solutions which provided from the Liu’s (2009) method. Indeed, in Liu’s method both upper and lower problems must be solved whereas, in neural network method just an ODE must be solved. Also, in Liu’s method the upper bound problem is a non-linear problem. On the network side, the neural network model has a single-layer structure. Computational results showed that the proposed neural network model is effective for solving the FQP in high dimension. Furthermore, in the neural network method, we have not this limitation that whether we choose the initial point from outside of the convergence region or not and of course, we obtain the unique solution of the problem. In fact, the neural network method does not depend on the initial point. The reason is that our model is globally convergent to the optimal solution of the problem. Thus, we can say that if the model is globally convergent then the trajectories behaviour of the solution for all starting initial points are convergent. Also, we compared our results (for $\alpha =1$, i. e., when the fuzziness goes to zero) with some other crisp neural networks (Effati et al. 2015; Xia and Wang 2000). The results were reported in the Tables 3 and 5. It can be seen that, the proposed neural network after less iterations than the other neural networks obtained the optimal solution. Finally, the works are in progress to extend the other neural network models to solve fuzzy non-linear programming problems and to solve the FQP with fuzzy relations in the constraints.

Appendices

Appendix 1: Some results on fuzzy calculus

Lemma 7.1

Let ${\tilde{f}}, {\tilde{g}}$ be convex fuzzy mappings defined on $C\subseteq {\varOmega }$, and $int\ C\ne \emptyset$, then,

$$\begin{aligned} {\tilde{\partial }}(\lambda {\tilde{f}})(x)=\lambda {\tilde{\partial }} {\tilde{f}}(x),\quad (\lambda >0),\qquad {\tilde{\partial }}({\tilde{f}}+{\tilde{g}})(x)={\tilde{\partial }} {\tilde{f}}(x)+{\tilde{\partial }} {\tilde{g}}(x). \end{aligned}$$

Proof

From Theorem 2.14, $\lambda {\tilde{f}}$ and ${\tilde{f}}+{\tilde{g}}$ are convex fuzzy mapping. The completeness of the proof follows from theorem 23.8 in Zhong and Shi (2002). $\square$

Theorem 7.2

Let ${\tilde{f}}, {\tilde{g}}$ be convex fuzzy mappings defined on $C\subseteq {\varOmega }$, and $int\ C\ne \emptyset$, if ${\tilde{f}}, {\tilde{g}}$ are differential at $x^*$, then $\lambda {\tilde{f}}$ ($\lambda >0$) and ${\tilde{f}}+{\tilde{g}}$ are also differential at $x^*$, i. e.,

$$\begin{aligned} {\tilde{\nabla }} (\lambda {\tilde{f}})(x^*)=\lambda {\tilde{\nabla }} {\tilde{f}}(x^*),\quad {\tilde{\nabla }}({\tilde{f}}+{\tilde{g}})(x^*)={\tilde{\nabla }} {\tilde{f}}(x^*)+{\tilde{\nabla }} {\tilde{g}}(x^*). \end{aligned}$$

Proof

From Theorem 2.14, $\lambda {\tilde{f}}$ and ${\tilde{f}}+{\tilde{g}}$ are convex fuzzy mapping. Using Definition 2.11 and Lemma 7.1, the proof is trivial. $\square$

Appendix 2: Some results on FQP

Lemma 7.3

If fuzzy matrix ${\tilde{H}}$, is positive semi-definite and symmetric, $x\in {\mathbb {R}}^n_+$, then $x^T{\tilde{H}}x$ is a fuzzy number and,

$$\begin{aligned} x^T{\tilde{H}}x&=\left( \left\{ \left( \sum _{i,j=1}^nx_ix_j\underline{h_{ij}}(\alpha ), \sum _{i,j=1}^nx_ix_j\overline{h_{ij}}(\alpha ), \alpha \right) : \alpha \in [0,1]\right\} \right) _{n\times n}\\&=(\{(x^T{\underline{H}}(\alpha )x, x^T{\overline{H}}(\alpha )x, \alpha ): \alpha \in [0,1])\})_{n\times n}, \end{aligned}$$

(24)

where $x=(x_1,x_2,\ldots ,x_n)^T, {\tilde{H}}=(\{(\underline{h_{ij}}(\alpha ), \overline{h_{ij}}(\alpha ), \alpha ): \alpha \in [0,1]\})_{n\times n}$.

Proof

The proof follows from Definition 3.1. $\square$

Lemma 7.4

Let fuzzy matrix ${\tilde{H}}$ be positive semi-definite and symmetric, $x\in {\mathbb {R}}^n_+$, then ${\tilde{h}}(x)=x^T{\tilde{H}}x$ is a convex fuzzy mapping.

Proof

The proof follows from Definition 3.1, Theorem 2.13, and Lemma 7.3. $\square$

Now, consider the FQP defined in (1). Here, we are going to prove some results for the FQP.

Lemma 7.5

Let fuzzy matrix ${\tilde{H}}$ be a positive semi-definite and symmetric, then ${\tilde{f}}(x)={\tilde{c}}^Tx+\frac{1}{2}x^T{\tilde{H}}x$ in (1) is a convex fuzzy mapping.

Proof

Since $x\ge 0, {\tilde{c}}^Tx$ is a convex fuzzy mapping. Using Lemma 7.4 and Theorem 2.14, the proof is complete. $\square$

Remark 7.6

Since in FQP (1), ${\tilde{f}}(x)$ is a convex fuzzy mapping and $T=\{x:\ x\ge 0, {\tilde{A}}x\le {\tilde{b}}\}$ is a convex feasible set, so FQP (1) is a convex fuzzy programming.

Remark 7.7

As in crisp programming problem, we say a fuzzy programming is convex if both objective function and the region solution are convex.

Lemma 7.8

The fuzzy mapping ${\tilde{f}}(x)={\tilde{c}}^Tx+\frac{1}{2}x^T{\tilde{H}}x$ is differentiable on $int\ {\mathbb {R}}^n_+$ and,

$$\begin{aligned} {\tilde{\nabla }}{\tilde{f}}(x)={\tilde{c}}+{\tilde{H}}{x}. \end{aligned}$$

(25)

Proof

The proof follows from Theorem 7.2 and Lemma 7.5. $\square$

Appendix 3: Proof of Theorem 3.2

Proof

Since ${\bar{x}}$ is a local optimal solution, there exists a neighborhood $N({\bar{x}})$ around ${\bar{x}}$, such that:

$$\begin{aligned} {\tilde{f}}({\bar{x}})\le {\tilde{f}}(x),\quad \forall \ x\in N({\bar{x}}). \end{aligned}$$

i.e., according to the Definition 2.3, we get,

$$\begin{aligned} {\underline{f}}({\bar{x}})(\alpha )\le {\underline{f}}(x)(\alpha ),\qquad {\overline{f}}({\bar{x}})(\alpha )\le {\overline{f}}(x)(\alpha ),\qquad 0\le \alpha \le 1. \end{aligned}$$

(26)

By contradiction, suppose that ${\bar{x}}$ is not a global optimal solution, so that ${\tilde{f}}(x^*)<{\tilde{f}}({\bar{x}})$ for some $x^*\in T$, where $T=\{x:\ x\ge 0, {\tilde{A}}x\le {\tilde{b}}\}$ is the feasible set. In other words, we have:

$$\begin{aligned} {\underline{f}}({x}^*)(\alpha )\le {\underline{f}}({\bar{x}})(\alpha ),\qquad {\overline{f}}({x}^*)(\alpha )\le {\overline{f}}({\bar{x}})(\alpha ),\qquad 0\le \alpha \le 1. \end{aligned}$$

From the convexity of ${\tilde{f}}$ for all $\lambda \in (0,1)$, we have:

$$\begin{aligned} \underline{f}(\lambda x^*+(1-\lambda )\bar{x})(\alpha )&\le \lambda \underline{f}(x^*)(\alpha )+ (1-\lambda )\underline{f}(\bar{x})(\alpha )\\&\le \lambda \underline{f}(\bar{x})(\alpha )+(1-\lambda )\underline{f}(\bar{x})(\alpha )=\underline{f}(\bar{x})(\alpha ),\\ \overline{f}(\lambda x^*+(1-\lambda )\bar{x})(\alpha )&\le \lambda \overline{f}(x^*)(\alpha )+(1-\lambda ) \overline{f}(\bar{x})(\alpha )\\ {}&\le \lambda \overline{f}(\bar{x})(\alpha )+(1-\lambda )\overline{f}(\bar{x})(\alpha )=\overline{f}(\bar{x})(\alpha ). \end{aligned}$$

But for $\lambda >0$ and sufficiently small, $\lambda x^*+(1-\lambda ){\bar{x}}\in N({\bar{x}})$. Hence, the above inequalities contradict with (26), this leads to the conclusion that ${\bar{x}}$ is a global optimal solution. Suppose that ${\bar{x}}$ is not the unique global optimal solution, so that there exists a ${\hat{x}}\in T, {\hat{x}}\ne {\bar{x}}$, such that ${\tilde{f}}({\hat{x}})={\tilde{f}}({\bar{x}})$, i. e.,

$$\begin{aligned} {\underline{f}}({\hat{x}})(\alpha )={\underline{f}}({\bar{x}})(\alpha ),\qquad {\overline{f}}({\hat{x}})(\alpha )={\overline{f}}({\bar{x}})(\alpha ),\qquad 0\le \alpha \le 1. \end{aligned}$$

By the strict convexity,

$$\begin{aligned}&{\underline{f}}(\frac{1}{2}{\hat{x}}+\frac{1}{2}{\bar{x}})(\alpha )<\frac{1}{2}{\underline{f}}({\hat{x}})(\alpha )+\frac{1}{2}{\underline{f}}({\bar{x}})(\alpha )={\underline{f}}({\bar{x}})(\alpha ),\\&{\overline{f}}(\frac{1}{2}{\hat{x}}+\frac{1}{2}{\bar{x}})(\alpha )<\frac{1}{2}{\overline{f}}({\hat{x}})(\alpha )+\frac{1}{2}{\overline{f}}({\bar{x}})(\alpha )={\overline{f}}({\bar{x}})(\alpha ). \end{aligned}$$

By the convexity of $T, \frac{1}{2}{\hat{x}}+\frac{1}{2}{\bar{x}}\in T$, and the above inequalities violate global optimality of ${\bar{x}}$. Hence, ${\bar{x}}$ is the unique global minimum. $\square$