1 Introduction

Since Charnes and Cooper (1961) introduced the goal programming to solve a multi-objective linear programming problem by converting it to a linear programming problem, it emerged as a powerful tool for solving various decision making problems in the area of economics and management.

Its growing popularity attracted numerous authors for their contributions both on methodology as well as on applications. Some of the popular methodological extensions of goal programming are weighted goal programming, lexicographical goal programming, integer goal programming, fractional goal programming and stochastic goal programming. The intrinsic feature of the goal programming is to provide an optimal solution to a multi-objective programming problem by accommodating aspiration levels of achieving various goals set by a decision maker. Thus, it has potential to deal with a kind of imprecision in terms of lower and upper aspirations levels set for various goals. A detailed study of various methodologies of goal programming can be obtained in Cohon (1978) and Ignizio (1976) studies.

In modeling of optimization problems arising in real life situations, one is often encountered by conditions where the information available is imprecise or vague. To deal with such situations, Zimmermann (1978) used the fuzzy set given by the Zadeh (1965) and studied the fuzzy linear programming with several objectives. The application of fuzzy sets in decision making was also studied by Narasimhan (1981) and many more and thus a new area of fuzzy goal programming emerged. Further, in studies of decision making under uncertainty, the relationship between goal programming and fuzzy goal programming may be viewed in Mohamed (1997) work and a detailed study of fuzzy programming can be found in Lai and Hwang (1994). In multi-objective programming applied to physical problems, there are many situations in which one has to optimize the efficiency of the system and thus it turns out to be a fractional programming problem. Various authors like (Luhandjula 1984; Dutta et al, 1992; Chakraborty and Gupta 2002; Pal et al, 2003; Mishra and Singh 2013; Kuwano 1996) worked in the area of fuzzy multi objective linear fractional programming problems.

Another approach for dealing with such optimization problems having uncertainty in parameters was developed by using interval valued number approach and numerous authors have worked to get the precise solutions to the optimization problems having imprecise information given in intervals. Some of these interval valued approach in multi objective programming problem can be viewed in work of Inuiguchi and Kume (1991), Inuiguchi and Tanaka (1990) Pal and Sen (2008). A variety of studies in modeling the agriculture production planning problems having various type of uncertainty, imprecision and vagueness can be visualized in work of Biswas and Pal (2005), Mohanty and Vijayaraghawan (1995), Zeng and Kang et al. (2010). Beside the uncertainty of type interval value numbers and fuzzy numbers, there is another kind of uncertainty in which apart of belonging and none belonging, situation needs to deal with hesitation factor. In view of modeling such situations, Atanassov (1986) introduced intuitionistic fuzzy sets. As application of intuitionistic fuzzy set, Angelov (1997) extended the fuzzy optimization methodology to intuitionistic fuzzy environment. Here, it is interesting to note that in many areas like economics, financial planning, agriculture production planning and many more areas, the decisions parameters are neither fully deterministic, nor fully stochastic but are possibilistic and having some degree of non determinacy. Thus, it is noble idea to deal such problems as intuitionistic fuzzy numbers having membership grade, non-membership grade and a hesitation factor.

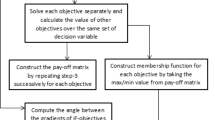
Dubois and Prade (1987) give a method to compute mean value of a fuzzy number and Heilpern (1992) presented a method to compute the expected value of a fuzzy number. These methods were extended in the case of intuitionistic fuzzy numbers by Adrian (2008) and Adrian and Coroiann (2009). Later, Grzegorzewski (2003) discussed a method for distances and ordering for a family of intuitionistic fuzzy numbers and Hassan (2010) extended the ranking of fuzzy number to a method for ranking of intuitionistic fuzzy numbers. Thus motivated with the extension of works of Bharati et al. (2014) and Nishad et al. (2014) for approximation methodology of a fuzzy number to approximation of intuitionistic fuzzy number, objective of the present study is to develop a computational method for goal programming procedure to a real life multi-objective linear programming problem into an intuitionistic fuzzy environment. As a matter of fact, if we consider any agriculture production problem, it involves the parameters which are intuitionistic fuzzy numbers in a natural way. Taking an account of coefficients of objective functions, cost coefficients, the price of many agriculture commodities are uncertain and may be dealt as intuitionistic fuzzy numbers in a more optimistic way. Similarly, the constraints of the resource vectors, the requirement for various factors like man power, water, insecticides, pesticides, are not predefined but are situation/condition dependent and sometimes are purely uncertain. In view of accommodating the above factors of realistic situation, we plan to develop a computational procedure to model such class of optimization problems in intuitionistic fuzzy environment. The study is presented into subsequent sections as follows: Sect. 2 gives the basic notion of fuzzy numbers, its extension to intuitionistic fuzzy number and its approximation. Section 3 describes problem formulation, need and justification of fuzzy goal programming. Sections 4 and 5 present the development of computational methodology to extend fuzzy goal programming to intuitionistic fuzzy goal programming and have been illustrated by implementing on an example. Section 6 deals with fractional programming problem in intuitionistic fuzzy environment and the developed method have been implemented on a real life problem of cropping system followed by conclusion to show its suitability.

2 Intuitionistic fuzzy numbers and its approximations

Definition 1

(Intuitionistic fuzzy set) Let X is a collection of objects then an intuitionistic fuzzy set \(\tilde{A}\) in X is a defined as: \(\tilde{A} = \{ (x,\mu_{{\tilde{A}}} (x),\nu_{{\tilde{A}}} (x),x \in X)\}\) where \(\mu_{{\tilde{A}}} (x)\) and \(\nu_{{\tilde{A}}} (x)\) are called the membership and non-membership functions of x in \(\tilde{A}\) respectively.

Definition 2

[Trapezoidal intuitionistic fuzzy number (TIFN)] An intuitionistic fuzzy set (IFS), \(\tilde{A} = \{ (x,\mu_{{\tilde{A}}} (x),\nu (x),x \in X)\}\) of ℜ is said to be an intuitionistic fuzzy number, if \(\mu_{{\tilde{A}}}\) and are membership and non-membership function respectively and \(\nu_{{\tilde{A}}} (x) \le \,\mu_{{\tilde{A}}}^{c}\) where \(\mu_{{\tilde{A}}}^{c}\) denotes the complement of\(\mathop \mu \nolimits_{{\tilde{A}}}\). A trapezoidal intuitionistic fuzzy number with parameters a′ ≤ a ≤ b ≤ c ≤ d ≤ d′ denoted by \(\tilde{A} = < (a,b,c,d,\mu_{{\tilde{A}}} ),(a',b,c,d',\nu_{{\tilde{A}}} ) >\) is an IFS on real line ℜ whose membership and non-membership functions are defined as follows (Fig. 1):

$$\mu_{{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}l} {\frac{(x - a)w}{(b - a)}} \hfill & {{\rm if}\,a\, \le \,x \,< b} \hfill \\ w \hfill & {{\rm if}\,b\, \le \,x \,< c} \hfill \\ {\frac{(d - x)w}{(d - c)}} \hfill & {{\rm if}\,c\, \le \,x \,< d} \hfill \\ \end{array} } \right.$$
(1)

and

$$\nu_{{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}l} {\frac{(x - a')u + (b - x)}{(b - a')}} \hfill & {{\rm if}\,a' \le \,x \,< b} \hfill \\ u \hfill & {{\rm if}\,b \, \le \,x \,< c} \hfill \\ {\frac{(x - d')u + (c - x)}{(c - d')}} \hfill & {{\rm if}\,c \, \le x \,< d} \hfill \\ \end{array} } \right.$$
(2)

Here, the values w and u represent the maximum degree of membership and the minimum degree of non-membership function, respectively, such that \(\mathop \mu \nolimits_{{\tilde{A}}} :X \to [0,1]\) and \(\nu_{{\tilde{A}}} :X \to [0,1]\) and 0 ≤ w + u ≤ 1.

Fig. 1
figure 1

Membership and non-membership function of trapezoidal intuitionistic fuzzy number

Full size image

Definition 3

[Triangular intuitionistic fuzzy number (TrIFN)] In a trapezoidal intuitionistic fuzzy number, if we put (b = c) then it becomes a triangular intuitionistic fuzzy number with the parameters a′ ≤ a ≤ b ≤ d ≤ d′ and is denoted by (Fig. 2) \(\tilde{A} = < (a,b,d,\mu_{{\tilde{A}}} ),(a',b,d',\nu_{{\tilde{A}}} ) >\)

$$\mu_{{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}l} {\frac{(x - a)w}{(b - a)}} \hfill & {{\rm if}\,a \le \,x < b} \hfill \\ w \hfill & {{\rm if}\,x = b} \hfill \\ {\frac{(d - x)w}{(d - b)}} \hfill & {{\rm if}\,b \le x < d} \hfill \\ \end{array} } \right.$$
(3)

and

$$\nu_{{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}l} {\frac{(x - a')u + (b - x)}{(b - a')}} \hfill & {{\rm if}\,a' \le \,x < b} \hfill \\ u \hfill & {{\rm if}\,x = b} \hfill \\ {\frac{(x - d')u + (b - x)}{(b - d')}} \hfill & {{\rm if}\,b \le x < d} \hfill \\ \end{array} } \right.$$
(4)
Fig. 2
figure 2

Membership and non-membership function of triangular intuitionistic fuzzy number

Full size image

Definition 4

(Expected interval of fuzzy number) Expected interval EI \((\tilde{A})\) of a fuzzy number \(\tilde{A}\) is one of the method to approximate a fuzzy number in form of a deterministic interval. The theory of expected interval of a fuzzy number was introduced by Dubois and Prade (1987). Dubois and Prade considered the approximation of a fuzzy number as a mean value of fuzzy number and give a rigorous definition for mean value of a fuzzy interval to show that the addition of mean value is preserved in possibilistic frame work. Later, Heilpern (1992) defined the expected value of a fuzzy number via a random set and introduced two notations, the expected interval and the expected value of the fuzzy number. He defined the expected value of a fuzzy number as a centre of the expected interval of such a number. Let \(\tilde{A} = \, < (a_{1} ,a_{2} ,a_{3} ,a_{4} ) >\) is a fuzzy number then as fuzzy interval number can be written as

$$EI(\tilde{A}) = [E_{*} (\tilde{A}),E^{*} (\tilde{A})]\, , \quad {\text{where}}$$
(5)
$$E_{*} (\tilde{A}) = a_{2} - \int_{{\mathop a\nolimits_{1} }}^{{\mathop a\nolimits_{2} }} {f_{{\tilde{A}}} (x)dx} \quad {\text{and}}$$
(6)
$$E^{*} (\tilde{A}) = a_{3} - \int_{{\mathop a\nolimits_{3} }}^{{\mathop a\nolimits_{4} }} {g_{{\tilde{A}}} (x)dx}$$
(7)

Here, the two function \(f_{{\tilde{A}}} (x)\) and \(g_{{\tilde{A}}} (x)\) are defined as \(f_{{\tilde{A}}} (x) = \frac{{x - a_{1} }}{{a_{2} - a_{1} }}\) and \(g_{{\tilde{A}}} (x) = \frac{{x - a_{4} }}{{a_{3} - a_{4} }}\)

Definition 5

(Expected interval for intuitionistic fuzzy number) Let there exist numbers: a 1, a 2, a 3, a 4, b 1, b 2, b 3, b 4 ∊ ℜ such thata 1 ≤ a 2 ≤ a 3 ≤ a 4 ≤ b 1 ≤ b 2 ≤ b 3 ≤ b 4 and are four functions \(f_{{\tilde{A}}} ,g_{{\tilde{A}}} ,h_{{\tilde{A}}} ,k_{{\tilde{A}}} :\Re \to [0,1]\): where \(f_{{\tilde{A}}}\) and \(g_{{\tilde{A}}}\) are non decreasing and \(h_{{\tilde{A}}} ,k_{{\tilde{A}}}\) are non increasing function, then an intuitionistic fuzzy number \(\tilde{A} = \{ (x,\mu_{{\tilde{A}}} (x),\nu (x),x \in X)\}\) is defined by membership and non-membership function as given below

$$\mu_{{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}l} {f_{{\tilde{A}}} (x)} \hfill & {{\rm if}\,a_{1}\, \le \, x\, < \,a_{2} } \hfill \\ 1 \hfill & {{\rm if}\,a_{2} \,\le \,x \,< a_{3} } \hfill \\ {g_{{\tilde{A}}} (x)} \hfill & {{\rm if}\,a_{3}\, \le\, x \,< a_{4} } \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(8)

and

$$\nu_{{\tilde{A}}} (x) = \left\{ {\begin{array}{*{20}l} {h_{{\tilde{A}}} (x)} \hfill & {{\rm if}\,b_{1}\, \le\, x \,< b_{2} } \hfill \\ 0 \hfill & {{\rm if}\,b_{2}\, \le \,x\, < b_{3} } \hfill \\ {k_{{\tilde{A}}} (x)} \hfill & {{\rm if}\,b_{3}\, \le \,x \,< b_{4} } \hfill \\ 1 \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(9)

Then the expected interval of the intuitionistic fuzzy number \(\tilde{A} = \langle (a_{1} ,a_{2} ,a_{3} ,a_{4} ),(b_{1} ,b_{2} ,b_{3} ,b_{4} ) \rangle\) introduced by Grzegorzewski (2003) is a crisp interval and is defined as \(EI(\tilde{A}) = [E_{*} (\tilde{A}),E^{*} (\tilde{A})],\)where

$$E_{*} (\tilde{A}) = \frac{{a_{2} + b_{1} }}{2} + \int_{{\mathop b\nolimits_{1} }}^{{\mathop b\nolimits_{2} }} {h_{{\tilde{A}}} (x)dx} - \int_{{\mathop a\nolimits_{1} }}^{{\mathop a\nolimits_{2} }} {f_{{\tilde{A}}} (x)\,dx}$$
(10)
$$E^{*} (\tilde{A}) = \frac{{a_{3} + b_{4} }}{2} + \int_{{\mathop a\nolimits_{3} }}^{{\mathop a\nolimits_{4} }} {g_{{\tilde{A}}} (x)\,dx} - \int_{{\mathop b\nolimits_{3} }}^{{\mathop b\nolimits_{4} }} {k_{{\tilde{A}}} (x)\,dx}$$
(11)

and

$$h_{{\tilde{A}}} (x) = \frac{{x - b_{1} }}{{b_{2} - b_{1} }},\quad f_{{\tilde{A}}} (x) = \frac{{x - a_{1} }}{{a_{2} - a_{1} }}\;,$$
$$g_{{\tilde{A}}} (x) = \frac{{x - a_{4} }}{{a_{3} - a_{4} }},\quad k_{{\tilde{A}}} (x) = \frac{{x - b_{4} }}{{b_{3} - b_{4} }}$$

Definition 6

(Expected interval for a triangular intuitionistic fuzzy number) Let \(\tilde{A} = < (a_{1} ,a,a_{2} ;\mu_{{\tilde{A}}} ),(b_{1} ,a,b_{2} ;\nu_{{\tilde{A}}} ) >\) is an triangular intuitionistic fuzzy number then the above definition of expected interval of triangular intuitionistic fuzzy number gives

$$EI(\tilde{A}) = [E_{*} (\tilde{A}),E^{*} (\tilde{A})]$$
(12)

where

$$\begin{aligned} E_{*} (\tilde{A}) & = \frac{{a_{2} + b_{1} }}{2} + \int_{{\mathop b\nolimits_{1} }}^{{\mathop b\nolimits_{2} }} {h_{{\tilde{A}}} (x)\,dx} - \int_{{\mathop a\nolimits_{1} }}^{{\mathop a\nolimits_{2} }} {f_{{\tilde{A}}} (x)\,dx} \\ \;\;\;\,\,{\kern 1pt} & = \frac{{3a + b_{1} + (a - b_{1} )\nu_{{\tilde{A}}} - (a - a_{1} )\mu_{{\tilde{A}}} }}{4} \\ \end{aligned}$$
(13)

and

$$\begin{aligned} E^{*} (\tilde{A}) & = \frac{{a_{3} + b_{4} }}{2} + \int_{{\mathop a\nolimits_{3} }}^{{\mathop a\nolimits_{4} }} {g_{{\tilde{A}}} (x)\,dx} - \int_{{\mathop b\nolimits_{3} }}^{{\mathop b\nolimits_{4} }} {k_{{\tilde{A}}} (x)\,dx} \\ & = \frac{{3a + b_{2} + (a_{2} - a)\mu_{{\tilde{A}}} + (a - b_{2} )\nu_{{\tilde{A}}} }}{2} \\ \end{aligned}$$
(14)

3 Problem formulation

Consider a multi-objective linear programming problem with k objectives and m constraints in n decision variables which is given as

$$\begin{aligned} {\text{Optimize}}\quad & Z_{k} (X) = C_{k} (X) \\ {\text{Subject to}} \quad & {\text{AX }}\left( { \, \ge , \, = \, , \, \le \, } \right){\text{ b}} \\ & {\text{X }} \ge 0 \\ \end{aligned}$$
(15)

where \({\text{X}} \in \Re^{n} ,b^{T} \in \Re^{m} ,C_{k}^{T} \in \Re^{n}\) and A be a m × n technological matrix.

Here (≥, = ,≤) denotes that inequality which may be in general any of the three types: ≥ or = or ≤.

3.1 Fuzzy goal programming formulation

In many real life problem, a decision maker may be encountered by a situation with imprecise knowledge for setting an aspiration level to be achieved by objective functions. Thus, if we introduce an imprecise aspiration level for each of objective functions, then these objectives of problem (15) can be dealt with fuzzy goals. Thus if g k be the given aspiration level to the kth objective function Z k (X), then the fuzzy goals are represented as

  1. 1.

    \(Z_{k} (X){ \succsim }g_{k}\) for maximization of Z k (X)

and

  1. 2.

    \(Z_{k} (X){ \precsim }g_{k}\) for minimization of Z k (X)

Hence, the problem (15) can be written as the fuzzy multi-objective goal programming problem

$$\begin{aligned} {\text{find}} \quad \quad \quad & {\text{X}} \\ {\text{such that}}\quad & Z_{k} (X){ \succsim }g_{k} \quad{\text{k }} = 1, \, 2, \, . \, . \, .{\text{ k}}_{1} \\ & Z_{k} (X){ \precsim }g_{k} \quad{\text{k }} = k_{1}+1, \, \, . \, . \, .{\text{ k}} \\ & {\text{AX }}\left( { \, \ge , \, = \, , \, \le \, } \right){\text{ b}} \\ & {\text{X }} \ge 0 \\ \end{aligned}$$
(16)

3.2 Constructing membership function

If lk is the lower tolerance limit for the kth fuzzy goal, then the membership function for goal \(Z_{k} (X){ \succsim }g_{k}\) can be expressed as

$$\mu_{{Z_{K} }} (X) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\rm if}\,\,Z_{k} (X) \ge g_{k} } \hfill \\ {\frac{{Z_{k} (X) - l_{k} }}{{g_{k} - l_{k} }}} \hfill & {{\rm if}\,\,l_{k} \le Z_{k} (X) \le g_{k} } \hfill \\ 0 \hfill & {{\rm if}\,\, \, Z_{k} (X) \le l_{k} } \hfill \\ \end{array} } \right.$$
(17)

and if u k is upper tolerance limit for the kth fuzzy goal, then membership function for kth fuzzy goal \(Z_{k} (X){ \precsim }g_{k}\) can be written as

$$\mu_{{Z_{K} }} (X) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\rm if}\,\,Z_{k} (X) \le g_{k} } \hfill \\ {\frac{{u_{k} - Z_{k} (X)}}{{u_{k} - g_{k} }}} \hfill & {{\rm if}\,\,g_{k} \le Z_{k} (X) \le u_{k} } \hfill \\ 0 \hfill & {{\rm if}\,\, \, Z_{k} (X) \ge u_{k} } \hfill \\ \end{array} } \right.$$
(18)

As the highest value of these membership functions be one, then these membership functions can be written in terms of under deviation and over deviation variables as

$$\frac{{Z_{k} (X) - l_{k} }}{{g_{k} - l_{k} }}\,\,\, + d_{k}^{ - } - d_{k}^{ + } = 1$$
(19)
$$\frac{{u_{k} - Z_{k} (X)}}{{u_{k} - g_{k} }} + d_{k}^{ - } - d_{k}^{ + } = 1$$
(20)

where d − k , d + k  ≥ 0, d − k d + k  = 0

Now, we extend this idea of multi-objective fuzzy goal programming problem to a multi-objective intuitionistic fuzzy goal programming problem

4 Multi-objective programming problem with the intuitionistic fuzzy parameters

Let us consider a multi-objective optimization problem with n decision variables, m constraints and k objective functions,

$$\begin{aligned} {\text{Max}}\; & {\text{Z}}\left( {\text{X}} \right) \, = \{ \tilde{C}_{1} X,\tilde{C}_{2} X,\tilde{C}_{3} X,\,.\,.\,.\,\tilde{C}_{k} X\} \\ {\text{s}} . {\text{t}} .\;\; & \tilde{A}_{ij} {\text{X}}_{{{\text{j}} }} \left( { \, \ge , = , \le \, } \right) \tilde{b}_{i} \quad {\text{i }} = \, 1, \, 2, \, 3, \, . \, . \, .{\text{m}} \\ & {\text{X}}_{\text{j}} \ge \, 0\quad \quad {\text{j }} = 1,2,3, \, . \, . \, .{\text{ n}} \\ \end{aligned}$$
(21)

where \({\text{X = }}\left\{ {{\text{x}}_{ 1} , {\text{ x}}_{ 2} , {\text{ x}}_{ 3} , { } . { } . { } . {\text{x}}_{\text{n}} } \right\},\,\tilde{C}_{k} \,\left( {{\text{k = 1,}}\, 2 , { } . { } . . {\text{ k}}} \right)\) and \(\tilde{b}_{i} \, \left( {{\text{i = 1,}}\, 2 ,\, 3 , { } . { } . { } . {\text{ m}}} \right)\). X and \(\tilde{b}_{i} \,\) are n dimensional and m dimensional vectors respectively. \(\tilde{A}\) is a m × n matrix with intuitionistic fuzzy parameter and \(\tilde{b}_{i} \,\) and \(\tilde{C}_{k}\) are intuitionistic fuzzy numbers. Since the above problem (21) has intuitionistic fuzzy coefficients which have possibilistic distribution in an uncertain intervals and hence may be approximated in terms of its expected intervals.

Let EI \((\tilde{A})\) be expected interval of intuitionistic fuzzy number \(\tilde{A}\) described by the definition (5) \(EI(\tilde{A}) = [E_{*} (\tilde{A}),E^{*} (\tilde{A})]\) where \(E_{*} (\tilde{A})\) and \(E^{*} (\tilde{A})\) are the lower and upper bound of the expected interval EI \((\tilde{A})\) of intuitionistic fuzzy number.

Since the coefficients of the objective function \(\tilde{C}_{k}\) are intuitionistic fuzzy numbers, expected interval of \(\tilde{C}_{k}\) can be defined as

$$EI(\tilde{C}_{k} ) = [E_{*} (\tilde{C}_{k} ),E^{*} (\tilde{C}_{k} )]$$

where \(E_{*} (\tilde{C}_{k} )\)

and \(E^{*} (\tilde{C}_{k} )\) is given as in definition of expected interval. Thus EI \((\tilde{C}_{k} )\) can be represented as a closed interval \([E_{*} (\tilde{C}_{k} ),E^{*} (\tilde{C}_{k} )]\), such that \(\tilde{C}_{k} \in [E_{*} (\tilde{C}_{k} ),E^{*} (\tilde{C}_{k} )]\).

Now the lower and upper bound for the respective expected intervals of the objective function are defined as

$$[Z_{k} (x)]^{L} \, = \,\sum\limits_{j = 1}^{n} {E_{*} (\tilde{C}_{kj} )} X_{j}$$
(22)
$$[Z_{k} (x)]^{U} \,\sum\limits_{j = 1}^{n} {E^{*} (\tilde{C}_{kj} )} X_{j}$$
(23)

In the next step, we construct a membership function for the maximization type objective function Z k (X) which can be replaced by the upper bound of its expected interval i.e.

$$[Z_{k} (x)]^{U} \, = \,\sum\limits_{j = 1}^{n} {E^{*} (\tilde{C}_{kj} )} X_{j}$$
(24)

Similarly to construct a membership function for minimization type objective function Z k (X) that is replaced by the lower bound of its expected interval given as

$$[Z_{k} (x)]^{L} \, = \,\sum\limits_{j = 1}^{n} {E_{*} (\tilde{C}_{kj} )} X_{j}$$
(25)

and the constraint inequalities

$$\sum\limits_{j = 1}^{n} {(\tilde{A}_{ij} )} X_{j} { \succsim }\tilde{B}_{i} \quad \left( {{\text{ i = 1, 2, }} . { } . . {\text{ m}}_{ 1} } \right)$$
(26)
$$\sum\limits_{j = 1}^{n} {(\tilde{A}_{ij} )} X_{j} \precsim \tilde{B}_{i} \quad \left( {{\text{i = m}}_{ 1} +{\text{ 1, m}}_{ 1} +{ 2, } . { } . . {\text{ m}}_{ 2} } \right)$$
(27)

Can be written in terms of expected values as

$$\sum\limits_{j = 1}^{n} E^{*} (\tilde{A}_{ij} ) X_{j} \ge E_{*} (\tilde{B}_{i} )\quad \left( {\rm i} = 1,\,2 ,\ldots, {\rm m}_{ 1} \right)$$
(28)
$$\sum\limits_{j = 1}^{n} E_{*} (\tilde{A}_{ij} ) X_{j} \le \,E^{*} (\tilde{B}_{i} )\quad \left( {{\text{i}} = {\rm m}_{ 1} +{\text{ 1, m}}_{ 1} +{ 2, } . { } . . {\text{ m}}_{ 2} } \right)$$
(29)

and the intuitionistic fuzzy equality constraint

$$\sum\limits_{j = 1}^{n} {(\tilde{A}_{ij} )} X_{j} \approx \,\tilde{B}_{i} \, ({\text{i = m}}_{ 2} { + 1,}\, {\text{m}}_{ 2} \,\, { + 2, } . { } . . {\text{ m)}}$$
(30)

can be transformed into two inequalities as

$$\sum\limits_{j = 1}^{n} {E_{*} (\tilde{A}_{ij} )} X_{j} \le E^{*} (\tilde{B}_{i} )\quad ( {\text{i = m}}_{ 2}+ {\text{ 1, m}}_{ 2} +{ 2, } . { } . . {\text{ m)}}$$
(31)
$$\sum\limits_{j = 1}^{n} {E^{*} (\tilde{A}_{ij} )} X_{j} \ge E_{*} (\tilde{B}_{i} )\quad ( {\text{i = m}}_{ 2} +{\text{ 1, m}}_{ 2}+ { 2, } . { } . . {\text{ m)}}$$
(32)

Thus the undertaken maximization problem is transformed into the following multi objective linear programming problem (MOLPP) as

$$\begin{aligned} &{\text{Max}}\; [Z_{k} (x)]^{U} = \sum\limits_{j = 1}^{n} E^{\ast} (\tilde{C}_{kj}) X_{j} \quad ({\rm{k}} = 1, 2, 3,\ldots\,{\rm{k}}\\ & {\rm Subject to} \quad \sum\limits_{j = 1}^{n} E^{\ast} (\tilde{A}_{ij}) X_{j} \ge E_{\ast} (\tilde{B}_{i})\quad ({\rm{i}} = 1,2, \, \ldots \,{\rm{m}}_{1} \\ &\sum\limits_{j = 1}^{n} {E_{\ast}} (\tilde{A}_{ij}) X_{j} \le E^{\ast} (\tilde{B}_{i}) \quad \left({\rm{i}} = {\rm{m}}_{1} + 1, \; {\rm{m}}_{1} + 2, \, \ldots \, {\rm{m}}_{2} \right) \\ &\sum\limits_{j = 1}^{n} E_{\ast} (\tilde{A}_{ij}) X_{j} \le E^{\ast} (\tilde{B}_{i}) \quad ({\rm{i}} = {\rm{m}}_{2} + 1, \; {\rm{m}}_{2} + 2, \, \ldots \,{\rm{m}}) \\ &\sum\limits_{j = 1}^{n} E^{\ast} (\tilde{A}_{ij}) X_{j} \ge E_{\ast} (\tilde{B}_{i})\quad ({\rm{i}} = {\rm{m}}_{2} + 1, \; {\rm{m}}_{2} + 2, \, \ldots \, {\rm{m}}) \\ &X_{j} \ge 0 \quad \left({\rm{j}} = 1, 2, 3, \, \ldots, \, {\rm{n}} \right) \end{aligned}$$
(33)

5 Intuitionistic fuzzy goal programming formulation

Now consider the conversion of objectives to fuzzy goals by means of assigning an aspiration level to each of them. Thus applying the goal programming method, the problem (33) can be transformed into fuzzy goals by taking certain aspiration levels and introducing under and over deviational variables to each of the objective functions. In proposed method the above maximization type objective function, is transformed as

$$\frac{{\sum\nolimits_{j = 1}^{n} {E^{*} (\tilde{C}_{kj} )X_{j} - l_{k} } }}{{g_{k} - l_{k} }} + d_{k}^{ - } - d_{k}^{ + } = 1$$
(34)

where \(d_{k}^{ - } ,d_{k}^{ + } \ge \, 0 \, ,\) with \(d_{k}^{ - } .d_{k}^{ + } = \, 0\) are under and over deviational variables and g k is aspiration level for the kth goal and the highest acceptable level for the kth goal and the lowest acceptable level lk are ideal and anti-ideal solutions and these are computed as

$$g_{k} \, = {\text{ Max}}\,\,\sum\limits_{j = 1}^{n} {E^{*} (\tilde{C}_{kj} )} X_{j} \,\,,\,\quad \left( {{\text{k = 1, 2, 3, }} . { } . . {\text{ k}}} \right)$$
(35)
$${\text{l}}_{\text{k}} = {\text{Min}}\sum\limits_{j = 1}^{n} {E_{*} (\tilde{C}_{kj} )} X_{j} \;,\quad \left( {{\text{k = 1, 2, 3,}} . { } . .\;{\text{k}}} \right)$$
(36)

Now using min sum goal programming method, the above fuzzy goal programming problem is equivalently transformed to a linear programming problem as follows.

$$\begin{aligned} & {\text{find}}\quad {\text{x}} \in {\text{X}}\quad {\text{so that to}} \\ & \hbox{min} \quad {\text{Z}} = \sum\limits_{j = 1}^{n} {w_{k} d_{k}^{ - } } \\ & {\text{subject to}} \\ & \quad \frac{{\sum\limits_{j = 1}^{n} {E^{*} (\tilde{C}_{kj} )} X_{j} - l_{k} }}{{g_{k} - l_{k} }} + d_{k}^{ - } - d_{k}^{ + } = 1 \\ & \quad \sum\limits_{j = 1}^{n} {E^{*} (\tilde{A}_{ij} )} X_{j} \ge E_{*} (\tilde{B}_{i} )\quad \quad \quad \quad \left( {{{\rm i} = 1,\,2 , } . { } . . {\text{ m}}_{ 1} } \right) \\ & \quad \sum\limits_{j = 1}^{n} {E_{*} (\tilde{A}_{ij} )} X_{j} \le \,E^{*} (\tilde{B}_{i} )\quad \quad \quad \quad \left( {{\text{i = m}}_{ 1} +{\text{ 1, m}}_{ 1}+ { 2, } . { } . . {\text{ m}}_{ 2} } \right) \\ & \quad \sum\limits_{j = 1}^{n} {E_{*} (\tilde{A}_{ij} )} X_{j} \le \,E^{*} (\tilde{B}_{i} )\quad \quad \quad \quad ( {\text{i = m}}_{ 2} +{ 1,}\, {\text{m}}_{ 2}+ { 2, } . { } . . {\text{ m)}} \\ & \quad \sum\limits_{j = 1}^{n} {E^{*} (\tilde{A}_{ij} )} X_{j} \ge E_{*} (\tilde{B}_{i} )\quad \quad \quad \quad ( {\text{i = m}}_{ 2} +{ 1,}\, {\text{m}}_{ 2}+ { 2, } . { } . . {\text{ m)}} \\ & \quad X_{j} \ge \, 0,\left( {{\text{j = 1, 2, 3, }} . { } . . , {\text{n}}} \right),d_{k}^{ - } ,d_{k}^{ + } \ge \, 0,{\text{and}}\,d_{k}^{ - } .d_{k}^{ + } = \, 0 \\ \end{aligned}$$
(37)

here, Z represents the achievement function. The weights wk attached to the under deviational variables d − k are given as

$$w_{k} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{g_{k} - l_{k} }}} \hfill & {for\,\,\,\hbox{max} \,case} \hfill \\ {\frac{1}{{u_{k} - l_{k} }}} \hfill & {for\,\,\,\hbox{min} \,case} \hfill \\ \end{array} } \right.$$
(38)

6 Fractional programming problem in intuitionistic fuzzy environment

Consider a problem in which one has to optimize the efficiency of the system. Taking a more general problem, suppose we need to optimize the ratio of two objective functions, out of k objective functions as core of the problem. Let these two linear objectives are \(\tilde{C}_{p} Z_{p} (X) > 0\) and \(\tilde{C}_{q} Z_{q} (X) > \, 0\) with intuitionistic fuzzy parameters in their coefficients, thus it gives rise to a linear fractional programming as

$${\text{Maximize}}\quad \frac{{\tilde{C}_{p} Z_{p} (X)}}{{\tilde{C}_{q} Z_{q} (X)}}$$
(39)

As \(\tilde{C}_{p} Z_{p} (X)\,\, > \, 0\,\,\,{\text{and}}\,\,\tilde{C}_{q} Z_{q} (X) > \, 0 \, ,\) it is equivalent to

$$\begin{aligned} {\text{Maximize}}\quad & \tilde{C}_{p} Z_{p} (X) - \tilde{C}_{q} Z_{q} (X)\,\,\,{\text{and}} \\ & \tilde{C}_{p} Z_{p} (X) - r\,\tilde{C}_{q} Z_{q} (X) > \, 0 \\ \end{aligned}$$

where r is a positive real number, it is a restriction that the ratio should always be greater than a level r. Thus the problem (39) can be equivalently written in an intuitionistic fuzzy goal programming problem as

$$\begin{aligned} {\text{Maximize}}\quad & \tilde{C}_{p} Z_{p} (X) - \tilde{C}_{q} Z_{q} (X) \\ {\text{Such that}}\quad & \tilde{C}_{p} Z_{p} (X) - r\,\tilde{C}_{q} Z_{q} (X) > \, 0 \\ & \tilde{C}_{k} Z_{k} (X){ \succsim }\tilde{b}_{k} \\ & \tilde{C}_{s} Z_{s} (X){ \precsim }\tilde{b}_{s} \\ & \tilde{C}_{t} Z_{t} (X) \approx \tilde{b}_{t} \\ & X_{j} \ge \, 0 \\ \end{aligned}$$
(40)

where \(\left( {{\text{s }} = { 1},{ 2},{ 3 }. \, . \, .{\text{ n}}} \right) \, ,{\text{ k}},{\text{ s}},{\text{ t}}\, \in \left\{ {\left( { 1,{ 2}, \, . \, . \, .{\text{ k}}} \right) \, {-} \, \left( {{\text{p}},{\text{ q}}} \right)} \right\} \, ;\tilde{C}_{k} ,\tilde{C}_{s} ,\tilde{C}_{t} ,\) and \(\tilde{b}_{k} ,\tilde{b}_{s} ,\tilde{b}_{t}\) are intuitionistic fuzzy numbers.

Now the above problem can be solved by approximating the developed expected interval method. Thus the method is being implemented on a real life problem in next section for illustration and testing of its suitability.

6.1 Numerical illustration

In view of illustration of the developed method for modeling a real life problem, we consider a problem of crop planning as undertaken by Biswas and Pal (2005) in which different type of seasonal crops and decision variables are considered in modeling. In the present study, we considered the undertaken problem in more realistic way by considering the modeling in intuitionistic fuzzy environment with a consideration that the coefficients are intuitionistic fuzzy numbers.

Thus the mathematical formulation for all the intuitionistic fuzzy goals of the under taken cropping problem of agriculture production system are as follows (Table 1).

Table 1 The seasonal crops and the associated decision variables
Full size table
  1. 1.

    Land utilization goals

    $$Z_{1} : x_{11} + x_{21} + x_{31} { \precsim }\widetilde{272.135}$$
    $$Z_{2} :x_{21} + x_{42} { \precsim }\widetilde{272.135}$$
    $$Z_{3} : x_{21} + x_{53} + x_{63} + x_{73} + x_{83} { \precsim }\widetilde{272.135}$$
  2. 2.

    Productive resource goals

    1. (a)

      Machine hour goal

      $$\begin{aligned} Z_{4} :\, & 61.02(x_{11} + x_{31} ) + \, 40.52(x_{21} + x_{42} ) \\ & + \,38.51x_{53} + \, 36.6(x_{63} + x_{73} + x_{83} ) \\ & { \succsim }\widetilde{37843.75} \\ \end{aligned}$$
    2. (b)

      Man power goal

      $$\begin{aligned} Z_{5} :\, & 1 2 4x_{11} + { 247}x_{21} + 84x_{31} + 89x_{42} \\ & + \;111x_{53} + 74x_{63} + 47x_{73} + 119x_{83} \\ & { \succsim }\widetilde{46510.66} \\ \end{aligned}$$
    3. (c)

      Water consumption goals

      $$Z_{6} : 60x_{11} + { 3}0x_{21} + 25x_{31} { \succsim }\widetilde{2727.84}$$
      $$Z_{7} :12x_{42} { \succsim }1\widetilde{490.4}0$$
      $$Z_{8} : 4 8x_{53} + 12x_{63} + 6x_{73} + 20x_{83} { \succsim }\widetilde{5675}$$
    4. (d)

      Fertilizer requirement goals

      $$\begin{aligned} Z_{9} :\, & 20(x_{11} + x_{42} ) + 200x_{21} + 40x_{31} \\ & + \,100(x_{53} + x_{63} ) + 80x_{73} + 150x_{83} { \succsim }\widetilde{44500} \\ \end{aligned}$$
      $$\begin{aligned} Z_{10} :\, & 20(x_{11} + x_{31} + x_{42} ) + 100x_{21} \\ & + \,50(x_{53} + x_{63} ) + 40x_{73} + 75x_{83} { \succsim }\widetilde{23000} \\ \end{aligned}$$
      $$\begin{aligned} Z_{11} :\, & 20(x_{11} + x_{31} + x_{42} ) + 100x_{21} \\ & + \,50(x_{53} + x_{63} ) + 40x_{73} + 75x_{83} { \succsim }\widetilde{19000} \\ \end{aligned}$$
      $$\begin{aligned} Z_{12} :\, & 8 5 7 7. 9 8x_{11} + { 23}0 3 1. 5 7x_{21} + 6 700. 9 4x_{31} \\ & + \,\, 6 8 1 1. 5 7x_{42} + 10 50 8. 4 4x_{53} + 7 6 8 5. 7 6x_{63} \\ & + \,\, 50 9 3. 10x_{73} + 2 2 5 2 7.0 5x_{83} { \precsim }\widetilde{6441015.80} \\ \end{aligned}$$
  3. 4.

    Production achievement goals

    $$Z_{13} : 2 5 3 8x_{11} \;{ \succsim }\widetilde{306000} \quad \quad \quad \left( {\text{jute}} \right)$$
    $$Z_{14} : 5 9 2 8 3x_{21} { \succsim }\widetilde{259000} \quad \quad \quad \left( {\text{sugarcane}} \right)$$
    $$Z_{15} : 20 7 6x_{31} + 1 8 8 5x_{42} + 3 40 1x_{53} { \succsim }\widetilde{870000}\quad \quad \quad \left( {\text{rice}} \right)$$
    $$Z_{16} : 2 30 1x_{63} { \succsim }\widetilde{136260} \quad \quad \quad \left( {\text{wheat}} \right)$$
    $$Z_{17} : 7 9 5x_{73} { \succsim }\widetilde{60540} \quad \quad \quad \left( {\text{mustard}} \right)$$
    $$Z_{18} : 1 7 7 7 9x_{83} { \succsim }\widetilde{110000} \quad \quad \quad \left( {\text{potato}} \right)$$
  4. 5.

    Profit goal

    $$\begin{aligned} Z_{19} :\, & 2 4 8 7 2. 4x_{11} + 8 8 9 2 4 5x_{21} + 1 3 4 10. 9 6x_{31} \\ & + \; 10 1 7 9x_{42} + 1 9 1 9 8. 6 4x_{53} + 1 6 10 7x_{63} \\ & + \; 9 1 4 2. 5x_{73} + 3 3 7 80. 1x_{83} { \succsim }\widetilde{12500000} \\ \end{aligned}$$
    (41)

We consider that each resource goals are triangular intuitionistic fuzzy numbers and hence compute its respective expected intervals.

Here, our objective is to maximize the efficiency of the system that is to maximize the ratio of profit to expenditure \(\frac{{Z_{19} (X)}}{{Z_{12} (X)}}\), thus this problem turns out to be a fractional programming problem (40). For shake of simplicity, we assume r = 1. Thus this problem becomes a multi-objective linear goal programming problem with intuitionistic fuzzy goals. The goals Z 12 and Z 19 are transformed to a goal and a constraint as:

$$\begin{aligned} {\text{Maximize}} \quad & Z \, = Z_{19} (X) - Z_{12} (X) \\ {\text{subject to}} \quad & Z_{19} (X) - Z_{12} (X) \ge 0 \\ \end{aligned}$$

Now we solve the problem (41) by applying the developed intuitionistic fuzzy goal programming method described in Sect. 5 and compute various required parameters. We first calculate upper bound (most acceptable solution) g = 51,976,000, and lower bound l = 23,962,000, for the objective function Z, and further compute upper and lower bound of expected value of all the intuitionistic fuzzy goals. We also compute W and w i (i = 1, 2, 3, … 11, 13, … 18) as defined in (38), and thus the problem (41) is transformed to following linear programming problem

$$\begin{aligned} {\text{Minimize}} & \\ {\text{Z}}*\, = & 0.0000000 3 5\quad D^{ - } + \, 0.0 5 8d_{1}^{ - } \\ & + \, 0.0 5 8d_{2}^{ - } + 0.0 5 8d_{3}^{ - } + 0.000 2d_{4}^{ - } + 0.000 8d_{5}^{ - } \\ & + \;0.0 1 1d_{6}^{ - } + 0.0 4 2d_{7}^{ - } + 0.0 3 2d_{8}^{ - } + 0.000 2d_{9}^{ - } \\ & + \;0.000 6d_{10}^{ - } + 0.000 3d_{11}^{ - } + 0.000 6d_{13}^{ - } \\ & + \;0.0000 1d_{14}^{ - } + 0.0000 7d_{15}^{ - } + 0.0000 8d_{16}^{ - } \\ & + \;0.000 3d_{17}^{ - } + 0.000 1d_{18}^{ - } \\ {\text{subject to}} & \\ & 0.000 5 8x_{11} + 0.0 3 90x_{21} + 0.000 2 3x_{31} \\ \quad \, + \;0.000 1 2x_{42} + 0.000 3 1x_{53} + 0.000 30x_{63} \\ & + \;0.000 1 4 4x_{73} + 0.000 40x_{83} + D^{ - } - D^{ + } = { 1}. 8 5 3\\ & - \;0.0 5 8x_{11} - 0.0 5 8x_{21} - 0.0 5 8x_{31} + d_{1}^{ - } - d_{1}^{ + } \\ & \,\, = - 1 7. 2 4 7\\ & - \;0.0 5 8x_{21} - 0.0 5 8x_{42} + d_{2}^{ - } - d_{2}^{ + } = \, - 1 7 2 4 7\\ & - \;0.0 5 8x_{21} - 0.0 5 8x_{53} - 0.0 5 8x_{63} - 0.0 5 8x_{73} \\ & - \;0.0 5 8x_{83} + d_{3}^{ - } - d_{3}^{ + } = \, - 1 7. 2 4 7\\ & 0.0 1 7x_{11} + \, 0.0 1 1x_{21} + 0.0 1 7 { }x_{31} + 0.0 1 1 { }x_{42} \\ & + \;0.0 1x_{53} + 0.0 1 { }x_{63} + 0.0 1 { }x_{73} + 0.0 1 { }x_{83} \\ & + \;d_{4}^{ - } - d_{4}^{ + } = { 1}0. 60 5 { } \\ & 0. 10 6x_{11} + 0. 2 1 1x_{21} + 0.0 7 1x_{31} + 0.0 7 6x_{42} \\ & + \;0.0 9 5x_{53} + 0.0 6 3x_{63} + 0.0 40x_{73} + 0. 10 1x_{83} \\ & + \;d_{5}^{ - } - d_{5}^{ + } = 3 9. 8 3 3\\ & 0.0 6 90x_{11} + 0. 3 4 5x_{21} + 0. 2 8 7x_{31} \\ & + \;d_{6}^{ - } - d_{6}^{ + } = 3 1. 40 5\\ & 0. 5 1 1x_{42} + d_{7}^{ - } - d_{7}^{ + } = 6 3. 5 3 2\\ & 1. 5 5 8x_{53} + 0. 3 8 9x_{63} + 0. 1 9 4x_{73} + 0. 6 4 9x_{83} \\ & \, + \;d_{8}^{ - } - d_{8}^{ + } = 1 8 4. 3 40 \\ & 0.00 5x_{11} + 0.0 5 7x_{21} + 0.0 1 1x_{31} + 0.00 5x_{42} \\ & \, + \;0.0 2 8x_{53} + 0.0 2 8x_{63} + 0.0 2 3x_{73} \\ & \, + 0.0 4 3x_{83} + d_{9}^{ - } - d_{9}^{ + } = 1 2. 8 1 6\\ & 0.0 1 3x_{11} + 0.0 6 5x_{21} + 0.0 1 3x_{31} + 0.0 1 3x_{42} \\ & \, + 0.0 3 2x_{53} + 0.0 3 2x_{63} + 0.0 2 6x_{73} \\ & \, + 0.0 4 8x_{83} + d_{10}^{ - } - d_{10}^{ + } = 1 5.0 1 6\\ & 0.00 6x_{11} + 0.0 3 4x_{21} + 0.00 6x_{31} + 0.00 6x_{42} \\ & \, + 0.0 1 7x_{53} + 0.0 1 7x_{63} + 0.0 1 3x_{73} \\ & \, + 0.0 2 6x_{83} + d_{11}^{ - } - d_{11}^{ + } = 6. 6 4 1\\ & 1. 6 8 2x_{11} + d_{13}^{ - } - d_{13}^{ + } = 6. 6 4 1\\ & 0. 70 3x_{21} + d_{14}^{ - } - d_{14}^{ + } = 3.0 7 1\\ & 0. 1 6 5x_{31} + 0. 1 50x_{42} + 0. 2 7 1x_{53} \\ & \, + d_{15}^{ - } - d_{15}^{ + } = 6 9. 50 4\\ & 0. 20 3x_{63} + d_{16}^{ - } - d_{16}^{ + } = 1 2.0 7\\ & 0. 2 7 2x_{73} + d_{17}^{ - } - d_{17}^{ + } = 20. 7 4\\ & 3. 2 8 1x_{83} + d_{18}^{ - } - d_{18}^{ + } = 20. 30 5\\ & 1 6 2 9 4. 4 2x_{11} + 8 6 6 2 1 3. 4x_{21} + 6 7 10.0 2x_{31} \\ & \, + 3 3 6 7. 4 3x_{42} + 8 6 90. 2 1x_{53} + 8 4 2 1. 2 4x_{63} \\ & \, + 40 4 9. 4x_{73} + 1 1 2 5 3.0 5x_{83} \ge 0 \\ \end{aligned}$$
(42)

The above linear programming problem (42) has been solved by MATLAB®, and solution obtained are

$$\begin{aligned} & x_{11} = 1 9 6. 8 7 6 3,x_{21} = 2 5. 6 30 9,x_{31} = 7 4. 7 5 6 3, \\ & x_{42} = 2 7 1. 7 30 7,x_{53} = 6 4. 1 80 2,x_{63} = 60. 10 30, \\ & x_{73} = 7 6. 2 5 3 1,x_{83} = 7 1. 1 6 9 5,{\text{z}}_{ 1 9} / {\text{z}}_{ 1 2} = { 4}. 7 3\\ \end{aligned}$$

Thus the result obtained for the under taken problem by the proposed intuitionistic method in comparison with past available work have been placed in Table 2 (Appendix)

Table 2 Optimal solution
Full size table

7 Conclusions

The proposed method has been implemented and tested in modeling of agricultural management problem of cropping system planning. Here, we have modeled the agriculture production problem in more realistic way by treating the coefficients as intuitionistic fuzzy numbers. The reason for such assumption is quite obvious as the resource requirements for cropping a system are situation dependent and involve some kind of uncertainty due to uncontrolled natural parameters. It is well established by several studies that the prices of crops and the resource requirements in cropping system are uncertain and many times imprecise. Thus in realistic modeling these quantities cannot be considered crisp and pre determined quantities.

The major superiority of the development method is in modeling of agriculture production planning problem as a linear fractional programming problem. As various studies have suggested modeling such agriculture production problem with imprecise and uncertain parameter, we considered the coefficients as intuitionistic fuzzy numbers in more optimistic way. The modeling of the mentioned problem by intuitionistic fuzzy optimization method provides a better land utilization in all the three prekharif, kharif and ravi seasons. The results obtained by the proposed method have been compared to that obtained by fuzzy method in Table 2. Clearly in most of parameters, the goals are achieved in better way by using the proposed method. Further the efficiency of the cropping system, that is the ratio of profit with expenditure obtained by the proposed method is much higher to a tune of 4.73 to a 2.78 that obtained by the fuzzy optimization method. Thus the proposed method may be used to model the agriculture management problem in cropping system in a better way to improve the efficiency of the system. Such studies may be more reliable to get insight the modeling of agricultural production planning problem in a realistic way.