An inventory model of price and stock dependent demand rate with deterioration under inflation and delay in payment

Abstract

This paper deals with the economic order quantity model for deteriorating items with price and stock dependent demand rate, where deterioration is constant. We have noticed the effect of shortage under inflation and taken into consideration the condition of permissible delay in payment. In first case, the credit period is less than or equal to the cycle time for settling the account and secondly the credit period is greater than the cycle time for settling the account. Then we have obtained the condition for minimizing the total cost. Finally, the results are illustrated by a numerical example for different cases and sensitivity analysis is carried out to analyze the effect of the parameters on the optimal solution.

1 Introduction

In general classical economic order quantity (EOQ) model is developed on the assumption that the demand rate of an item is constant. But in real life demand rate of any item is always in dynamic state. As reported by Levin et al. (1972) and Silver and Peterson (1985), selling of items are proportional to the inventory displayed such that large piles of goods displayed in a supermarket will tempt the customer to buy more. Sana and Chaudhuri (2008) proposed a paper considering various types of demand rates with delay in payment and price discounting. Manna and Chaudhuri (2006) took ramp type demand rate for deteriorating item. Goyal (1985), first investigated an EOQ model considering permissible delay in payment but he ignored the loss due to deterioration. However the real life scenario is different. Chang and Dye (2001) assumed an inventory model for deteriorating item with partial backlogging and permissible delay in payment. Khanra et al. (2011) developed a EOQ model for deteriorating item with time dependent quadratic demand rate under permissible delay in payment. Pal and Chandra (2012) and Jaggi et al. (2012) presented a deterministic inventory model with permissible delay in payment and price discount on backorders. Jamal et al. (2000) developed an inventory model to obtain an optimal payment time by a retailer under delay in payment by the wholesaler. Shah et al. (2011) presented deterioration as Weibull distribution with two credit period. Roy and chaudhuri (2011) considered price and stock dependent demand rate of deteriorating items.

In real life decaying of item is obvious such as electronic item, fruits, etc gradually losses its potential. Again when the increase in price is anticipated, the companies, firms or retailer buy goods in large amount without considering it to be economical or not because the inventory system will deteriorate and sometime large stock creates false impression on the buyers. Misra (1975) developed an EOQ model under incorporating inflationary effects. Hou (2006) derived an inventory model for deteriorating items with stock dependent demand rate and shortage under inflation. Chang et al. (2002) derived an inventory model for deteriorating items with time value of money under finite time horizon and permissible delay in payment. Dey et al. (2008) worked on an inventory model with dynamic demand over finite time horizon under inflation and delay in payment. The paper also have considered the interval valued lead time along with two different storage of the items. Liang and Zhou (2011) considered a two warehouse inventory model for deteriorating model with delay in payment. Shah (2006) investigated an inventory model for deteriorating item under finite time horizon, permissible delay in payment and time value of money. Ouyang et al. (2006) studied an inventory model for non-instantaneous deteriorating items with delay in payment. Singh et al. (2010) studied inventory model of deteriorating item under inflation for two shop under one management system. Liao et al. (2000) developed a inventory model of deteriorating items under inflation and delay in payment. Mandal and Phaujdar (1989) considered deterioration as time dependent variable (i.e., as time passes the material get deteriorated) and stock dependent consumption rate. Hou and Lin (2006) developed an EOQ model of price and stock dependent selling rate for deteriorating items under inflation and time value of money. Ray and Chaudhuri (1997), Chen (1998), Chung and Lin (2001) and Wee and Law (2001) etc. all investigated effects of inflation, time value of money and deteriorating items of inventory model. Roy and Samanta (2010) investigated an inventory model of deteriorating items under two rates of production and delay in payment. Jaggi and Khanna (2010) investigated on the supply chain inventory model for deteriorating items with stock dependent consumption rate and taking into consideration the effect of inflation, delay in payment and shortages. Lo et al. (2007) worked on an intergraded production-inventory model with imperfect production processes and deterioration as Weibull distribution under inflation. Sana (2008) developed an EOQ model with varying demand rate with selling price under permissible delay in payment. The paper also considered the expenditure due to advertisement.

In the supermarket we have seen that not only the amount of the stock but also the price of the item affect the inventory model. So we have considered a deterministic inventory model of deteriorating item where we consider the demand rate as price and stock dependent demand under inflation. We also consider delay in payment i.e., credit period for settling the amount. In Sect. 2 we present some assumptions and denoted some notations that we have used in this paper. We define the inventory model in this section. In Sect. 3 we give detail analysis of the model and obtained the minimization condition of the model in two different cases. Finally we illustrate numerical example and sensitivity analysis in support of the proposed model in Sects. 4 and 5 respectively. Some conclusions are made in Sect. 6.

2 Mathematical formulation of inventory model

The notation and assumptions which are used for developing the model as follows:

Notation:

D(I(t), p):

Demand rate where I(t) is inventory level at time t and p is price of the stock,

k :

Inflation rate,

θ:

Constant rate of deterioration,

T ₁ :

The time when the stock level finishes,

T :

Replenishment cycle,

M :

Credit period settled by the supplier to the retailer,

h :

Holding cost per unit item,

g :

Shortage cost per unit item,

c ₁ :

Purchase cost per unit item,

p :

Selling price per unit item,

I _e :

Rate of interest earned,

I _p :

Rate of interest payable or charged to delay in payment.

Assumption:

• 1. Demand rate is D(I(t), p) = r(p)[α + β I(t)] where r(p) = γ e ^−pδ is the price factor where, γ > 0, δ > 0 are the parameter. β is stock dependent consumption rate parameter 0 ≤ β ≤ 1.

• 2. The demand rate of an item is price and stock dependent.

• 3. Shortages are allowed and these are fully backlogged.

• 4. The deterioration rate is constant on the on-hand inventory per unit time and there is no repair or replenishment for the deteriorating items within the cycle.

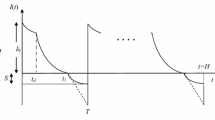
• 5. If the retailer pays by the offered credit period M, then the supplier does not charges any interest to the retailer. If the retailer pays after M then he has to pay interest at the rate I _p to the supplier (Fig. 1).

  Fig. 1

  

  Proposed inventory model with inventory versus time

Therefore the mathematical model of the presented inventory system is as follows:

$$ \frac{dI(t)}{dt}+\theta I(t) =-r(p)[\alpha +\beta I(t)], \quad0\leq t\leq T_{1} $$

(1)

$$ \frac{dI(t)}{dt}+\theta I(t) =-r(p)\alpha, \quad T_{1}\leq t\leq T $$

(2)

where the conditions are I(0) = Q and I(T ₁) = 0

3 Mathematical analysis of the proposed inventory model

The solutions of the differential equations are as follows:

$$ I(t)=\left\{ \begin{array}{l} \frac{e^{-at}(e^{aT_{1}}-e^{at})r(p)\alpha }{a}, \quad if \;0\leq t\leq T_{1} \\ r(p)\alpha (T_{1}-t),\quad if\; T_{1}\leq t\leq T \end{array}\right. $$

(3)

$${\text{where}}\quad a=\theta +\beta r(p) $$

(4)

Therefore the maximum amount of inventory when the cycle began is I(0) = Q i.e.,

$$ Q=I(0)=\frac{\alpha r(p)}{a}(e^{aT_{1}}-1) $$

(5)

The shortage during t = T i.e., highest inventory amount during shortage is Q _s  =  − r(p)α (T ₁ − T) = r(p)α (T − T ₁)

Now the present value of inventory holding cost $(HC)=h\int\nolimits_{0}^{T_{1}}\frac{r(p)\alpha e^{-at}(e^{aT_{1}}-e^{at})}{a}(e^{-kt})dt$

$$ =\frac{hr(p)\alpha }{ak(a+k)}\left(ae^{-kT_{1}}+ke^{aT_{1}}-(a+k)\right) $$

(6)

Now the present value of shortage cost $=SC=-g\int\nolimits_{T_{1}}^{T}I(t)e^{-kt}dt$

$$ \begin{aligned} &=gr(p)\alpha \int\limits_{T_{1}}^{T}(t-T_{1})e^{-kt}dt \\ &=\frac{e^{-k(T+T_{1})}gr(p)\alpha}{k^{2}}\left(e^{kT}-e^{kT_{1}}(1+k(T-T_{1}))\right) \end{aligned} $$

(7)

The present value of purchase cost = PC = $c_{1}Q+c_{1}e^{-kt}\int\nolimits_{0}^{T-T_{1}}r(p)\alpha dt$

$$ =c_{1}Q+c_{1}e^{-kt}r(p)\alpha (T-T_{1}) $$

(8)

${\text{No. of deteriorating item}}\,=\,DI =Q - \int_{0}^{T_{1}}D(I(t),p)dt$

$$ \begin{aligned} &=Q-\int\limits_{0}^{T_{1}}r(p)\left[\alpha +\frac{\alpha \beta r(p)}{a} \left(e^{a(T_{1}-t)}-1\right)\right]dt\\ &=Q-\frac{r(p)\alpha}{a^{2}}\left(a^{2}T_{1}+(e^{{aT_{1}}}-1)r(p)\beta -ar(p)T_{1}\beta \right) \end{aligned} $$

(9)

The deterioration cost (DC) is

$$ DC=c_{1}\left(Q-\frac{r(p)\alpha}{a^{2}} (a^{2}T_{1}+(e^{aT_{1}}-1)r(p)\beta -ar(p)T_{1}\beta)\right) $$

(10)

Ordering cost (OC) is

$$ OC=A $$

(11)

Case 1:

M ≤ T ₁

Interest earned (IE ₁) due to sale up to T ₁ is given by

$$ \begin{aligned} IE_{1}&=c_{1}I_{e}\int\limits_{0}^{T_{1}}tD(I(t),p)dt \\ &=c_{1}I_{e}\int\limits_{0}^{T_{1}}r(p)t\left( { \alpha +\frac{\beta \alpha r(p)}{a}(e^{a(T_{1}-t)}-1)}\right) { dt} \\ &=\frac{c_{1}I_{e}r(p)\alpha }{2a^{3}}(2(e^{aT}-1)r(p)\beta +aT_{1}(a^{2}T_{1}-r(p)(2+aT_{1})\beta )) \end{aligned} $$

(12)

Interest payable (IP ₁) due to arrival of supplier before the stock ends is as follows

$$ \begin{aligned} IP_{1}&=c_{1}I_{p}\int\limits_{M}^{T}I(t)dt =c_{1}I_{p}\left( \int\limits_{M}^{T_{1}}I(t)dt+\int\limits_{T_{1}}^{T}I(t)dt)\right) \\ &=c_{1}I_{p}\left( \int\limits_{M}^{T_{1}}\frac{r(p)\alpha }{a}(e^{a(T_{1}-t)}-1)dt+ \int\limits_{T_{1}}^{T}r(p)\alpha (T_{1}-t)dt\right) \\ &=c_{1}I_{p}\left( \frac{r(p)\alpha (e^{a(T_{1}-M)}-1)-1-a(M-T_{1})}{a^{2}}- \frac{1}{2}r(p)\alpha (T-T_{1})^{2}\right) \end{aligned} $$

(13)

It is evident that the total cost per cycle is the sum of the set-up, production, inventory carrying, interest and depreciation costs.

Therefore the total cost per unit item per unit time = TC ₁

$$ TC_{1}=\frac{1}{T}(OC+HC+SC+DC+PC+IP_{1}-IE_{1}) $$

(14)

$$ \begin{aligned} &=\frac{1}{T}\left[ A+c_{1}r(p)\alpha e^{-kT}(T-T_{1})+\frac{gr(p)\alpha}{k^{2}}(e^{kT_{1}}-e^{kT}(1+k(T-T_{1}))) +\frac{c_{1}r(p)(e^{aT_{1}}-1)\alpha}{a}\right. \\ &\quad+\frac{hr(p)\alpha}{ak(a+k)}(ae^{-kT_{1}}+ke^{aT_{1}}-(a+k))-\frac{ c_{1}r(p)\alpha \theta }{a^{2}}(r(p)T_{1}\beta +(1+T_{1}\theta )-e^{aT_{1}}) \\ &\quad-\frac{c_{1}r(p)I_{e}\alpha}{2a^{3}}(T_{1}^{2}\theta^{3} +r^{2}(p)T_{1}\beta^{2}(T_{1}\theta-2)+2r(p)\beta (-1+e^{aT_{1}}-T_{1}\theta +T_{1}^{2}\theta^{2})) \\ &\left. \quad+\frac{1}{2}c_{1}r(p)I_{p}\alpha \left( -(T_{1}-T)^{2}+\frac{ 2(-1+e^{a(T_{1}-M)}+(M-T_{1})a)}{a^{2}}\right) \right] \end{aligned} $$

(15)

Lemma 1

When $\frac{dTC_{1}}{dT_{1}}|_{T_{1}=t_{1}^{\ast}}=0$ exists for $t_{1}^{\ast}\in [ M,\infty )$ then TC ₁ is minimum at $T_{1}=t_{1}^{\ast}$ if $e^{-kT_{1}}g+c_{1}e^{aT_{1}}(a+\theta)+\frac{h}{a+k}(ke^{-kT_{1}} +ae^{aT_{1}})+c_{1}e^{a(T_{1}-M)}I_{p}-\frac{c_{1}I_{e}}{a}(r(p)e^{aT_{1}}\beta +\theta )>0$ otherwise, $t_{1}^{\ast}=M$ if $\frac{g}{k}(e^{-kT}-e^{-kM})+\frac{h}{a+k}(e^{aM}-e^{-kM}) -c_{1}(e^{-kT}-e^{aM}\left(1-\frac{2I_{e}r(p)\beta }{a^{2}}\right)-\frac{ar(p)\beta(e^{aM}-1-I_{e}M)+a^{2}(1+MI_{e} +MI_{p}-I_{p}T)-r(p)\beta I_{e}}{a^{2}})>0$ and $e^{-kT_{1}}g+c_{1}e^{aT_{1}}(a+\theta)+\frac{h}{a+k}(ke^{-kT_{1}}+ae^{aT_{1}}) +c_{1}e^{a(T_{1}-M)}I_{p}-\frac{c_{1}I_{e}}{a}(r(p)e^{aT_{1}}\beta +\theta )>0$ are satisfied.

Proof

If $\frac{dTC_{1}}{dT_{1}}$ exists for $T_{1}\in[M,\infty)$ then the necessary condition for minimization of TC ₁ for a given value of M is $\frac{dTC_{1}}{dT_{1}}=0$ and we get the extremum of TC ₁. Also the sufficient condition for the minimization of TC ₁ is $\frac{d^{2}TC_{1}}{dT_{1}^{2}}>0$

From the necessary condition $\frac{dTC_{1}}{dT_{1}}=0$ we get,

$$\begin{aligned} \Longrightarrow \frac{1}{T}\left[ {c_{1} r(p)\alpha \left( {e^{{aT_{1} }} - e^{{ - kT}} } \right) - \frac{{r(p)g\alpha (e^{{ - kT_{1} }} - e^{{ - kT}} )}}{k} - \frac{{r(p)h\alpha (e^{{ - kT_{1} }} - e^{{aT_{1} }} )}}{{a + k}} + c_{1} I_{p} r\left( p \right)\alpha \left[( {T - T_{1} } \right) + \frac{{r(p)\alpha (e^{{a(T_{1} - M)}} - 1)}}{a} ]+ c_{1} r\left( p \right)\alpha \left( {e^{{aT_{1} }} - \frac{{r(p)\beta e^{{aT_{1} }} + \theta }}{{a^{2} }}} \right) - \frac{{c_{1} r(p)I_{e} \alpha }}{{2a^{2} }}\left( {2r\left( p \right)e^{{aT_{1} }} \beta + T_{1} (a^{2}-r\left( p \right)\alpha\beta)+ \left( {a_{{}}^{2} T_{1} - r\left( p \right)\beta \left( {2 + aT_{1} } \right)} \right)} \right)} \right] = 0 \end{aligned}$$

(16)

The optimum value of $T_{1}=t_{1}^{\ast}$ is obtained from above if it satisfies the sufficient condition.

Now, using $\frac{dTC_{1}}{dT_{1}}=0$ we get

$$ \begin{aligned} \frac{d^{2}TC_{1}}{dT_{1}^{2}}&=r(p)\left\{e^{-kT_{1}}g\alpha +c_{1}e^{aT_{1}}\alpha (a+\theta)+\frac{h\alpha}{a+k}(ke^{-kT_{1}}+ae^{aT_{1}})\right. \\ &\left.\quad+c_{1}e^{a(T_{1}-M)}I_{p}\alpha -\frac{c_{1}I_{e}\alpha }{a}(r(p)e^{aT_{1}}\beta +\theta )\right\} \end{aligned} $$

Note that $Lt_{T_{1}\rightarrow \infty}\frac{dTC_{1}}{dT_{1}}=\infty$ and now,

$$ \begin{aligned} \frac{dTC_{1}}{dT_{1}}&>0 \\ &\Longrightarrow \frac{1}{T}\left[c_{1}r(p)\alpha (e^{aT_{1}}-e^{-kT})-\frac{r(p)g\alpha (e^{-kT_{1}}-e^{-kT})}{k}-\frac{r(p)h\alpha (e^{-kT_{1}}-e^{aT_{1}})}{a+k}\right. \\ &\quad+c_{1}I_{p}r(p)\alpha \left[ (T-T_{1}) +\frac{r(p)\alpha (e^{a(T_{1}-M)}-1)}{a}\right] +c_{1}r(p)\alpha \left(e^{aT_{1}}-\frac{r(p)\beta e^{aT_{1}}+\theta}{a^{2}}\right) \\ &\left.\quad-\frac{c_{1}r(p)I_{e}\alpha}{2a^{2}}(2r(p)e^{aT_{1}}\beta +T_{1}(a^{2}-r(p)a\beta)+(a^{2}T_{1}-r(p)\beta (2+aT_{1})))\right]>0 \\ &\Rightarrow\frac{g}{k}(e^{-kT}-e^{-kM}) +\frac{h}{a+k}(e^{aM}-e^{-kM})-c_{1}\left(e^{-kT} -e^{aM}\left(1-\frac{2I_{e}r(p)\beta}{a^{2}}\right)\right. \\ &\left.\quad-\frac{ar(p)\beta(e^{aM}-1-I_{e}M)+a^{2}(1+MI_{e}+MI_{p}-I_{p}T)-r(p)\beta I_{e}}{a^{2}}\right)>0 \end{aligned} $$

Now if $e^{-kT_{1}}g+c_{1}e^{aT_{1}}(a+\theta)+\frac{h}{a+k}(ke^{-kT_{1}} +ae^{aT_{1}})+c_{1}e^{a(T_{1}-M)}I_{p} -\frac{c_{1}I_{e}}{a}(r(p)e^{aT_{1}}\beta +\theta)>0$ holds then we get $\frac{d^{2}TC_{1}}{dT_{1}^{2}}>0$ which means TC ₁ has minimum at $T_{1}=t_{1}^{\ast}$, otherwise TC ₁ may be maximum in the interval $[M,\infty)$ or TC ₁ is a monotonic function in $[M,\infty)$. Now $Lt_{T_{1}\rightarrow \infty}\frac{dTC_{1}}{dT_{1}}=\infty$ and $\frac{dTC_{1}}{dT_{1}}|_{T_{1}=M}>0$ imply $TC_{1}(\infty-)<TC_{1}(\infty)$ and TC ₁(M) < TC ₁(M +) respectively. In the neighbourhood of the end point, TC ₁ is a monotonic increasing function of $T_{1}\in [M,\infty)$ and TC ₁ does not have a minimum in $[M,\infty)$. So TC ₁ does not have stationary point in $[M,\infty)$. Therefore $t_{1}^{\ast}=M$ if $Lt_{T_{1}\rightarrow \infty}\frac{dTC_{1}}{dT_{1}}=\infty$ and $\frac{dTC_{1}}{dT_{1}}|_{T_{1}=M}>0$ i.e., if the condition $e^{-kT_{1}}g+c_{1}e^{aT_{1}}(a+\theta)+\frac{h}{a+k}(ke^{-kT_{1}} +ae^{aT_{1}})+c_{1}e^{a(T_{1}-M)}I_{p}-\frac{c_{1}I_{e}}{a}(r(p)e^{aT_{1}}\beta +\theta )>0$ and $\frac{g}{k}(e^{-kT}-e^{-kM})+\frac{h}{a+k}(e^{aM} -e^{-kM})-c_{1}(e^{-kT}-e^{aM}\left(1-\frac{2I_{e}r(p)\beta}{a^{2}}\right) -\frac{ar(p)\beta(e^{aM}-1-I_{e}M)+a^{2}(1+MI_{e}+MI_{p}-I_{p}T)-r(p)\beta I_{e}}{a^{2}})>0$ are satisfied.

Case 2:

T ₁ ≤ M

Interest earned (IE ₂) due to arrival of supplier after the stock ends.

$$ \begin{gathered} = c_{1} I_{e} \left[ {\int\limits_{0}^{{T_{1} }} t D(I(t),p)dt + (M - T_{1} )\int\limits_{0}^{{T_{1} }} D (I(t),p)dt} \right] \hfill \\ = c_{1} I_{e} \left[ {\frac{{r(p)\alpha }}{{2a^{3} }}(2(e^{{aT_{1} }} - 1)r(p)\alpha + aT_{1} (a^{2} T_{1} - r(p)(2 + aT_{1} )\beta ))} \right. + \frac{{(M - T_{1} )\alpha }}{{a^{2} }}(a^{2} T_{1} + (e^{{aT_{1} }} - 1)r(p)\beta - ar(p)T_{1} \beta ) \hfill \\ \end{gathered} $$

(17)

Here the retailer has sold Q unit during [0, T ₁] and is paying c ₁ Q to the supplier in full at time M ≥ T ₁ so the retailer does not have to pay any interest so interest charge is zero i.e.,

$$ IP_{2}=0 $$

Therefore the total cost in this case is

$$ TC_{2}=\frac{1}{T}({OC+HC+DC+SC+PC-IE_{2}+IP}_{2}) $$

(18)

$$ \begin{aligned} &=\frac{1}{T}\left[A+c_{1}r(p)\alpha {e}^{-kT}(T-T_{1}) +\frac{gr(p)\alpha}{k^{2}}(e^{kT_{1}}-e^{kT}(1+k(T-T_{1}))) \right.\\ &\quad+\frac{c_{1}r(p)(e^{aT_{1}}-1)\alpha}{a} \\ &\quad+\frac{hr(p)\alpha}{ak(a+k)}(ae^{-kT_{1}}+ke^{aT_{1}}-(a+k)) -\frac{c_{1}r(p)\alpha\theta}{a^{2}}(r(p)T_{1}\beta +(1+T_{1}\theta )-e^{aT_{1}}) \\ &\quad-\frac{c_{1}r(p)I_{e}\alpha}{2a^{3}}(T_{1}^{2}\theta^{3} +r^{2}(p)T_{1}\beta^{2}(T_{1}\theta -2)+2r(p)\beta (-1+e^{aT_{1}}-T_{1}\theta +T_{1}^{2}\theta^{2})) \\ &\quad\left.-\frac{c_{1}I_{e}(M-T_{1})\alpha}{a^{2}}(T_{1}\theta^{2}+r(p)\beta (-1+e^{aT_{1}}+T_{1}\theta))\right] \end{aligned} $$

(19)

Lemma 2

When $\frac{dTC_{2}}{dT_{1}}|_{T_{1}=t_{2}^{\ast}}=0$ exists for $t_{2}^{\ast}\in (0,\,M]$ then TC ₂ is minimum at $T_{1}=t_{2}^{\ast}$ if $ge^{-kT_{1}}+c_{1}e^{aT_{1}}(a+\theta)+\frac{h}{a+k}(ke^{kT_{1}} +ae^{aT_{1}})+\frac{c_{1}I_{e}\beta e^{aT_{1}}}{a}\left(a(T_{1}-M)+2-r(p)\right) +\frac{c_{1}I_{e}\theta (2-r(p))}{ar(p)}>0$ otherwise, $t_{2}^{\ast}=M$ if $c_{1}(e^{aM}-e^{-kM})+\frac{g}{k}(e^{kM}+e^{kT}) +\frac{h}{a+k}(e^{aM}-e^{-kM})-\frac{c_{1}I_{e}(r(p)-1)}{r(p)a^{2}}(a\theta M+r(p)\beta (e^{aM}-1))+\frac{c_{1}\theta }{a}(e^{aM}-1)>0$

Proof

If $\frac{dTC_{2}}{dT_{1}}$ exists for $T_{1}\in (0,\,M]$, then the necessary condition for minimization of TC ₂ for a given value of M is $\frac{dTC_{2}}{dT_{1}}=0$ and we get the extremum of TC ₂ at $T_{1}=t_{2}^{\ast}$. Also the sufficient condition for the minimization of TC ₂ is $\frac{d^{2}TC_{2}}{dT_{1}^{2}}>0$

From the necessary condition $\frac{dTC_{2}}{dT_{1}}=0$ we get,

$$ \frac{dTC_{2}}{dT_{1}}=0 $$

$$ \begin{aligned} \Longrightarrow &\frac{1}{T}\left[-c_{1}r(p)\alpha (e^{-kT}+e^{aT_{1}})-\frac{1}{k}\alpha r(p)ge^{-k(T+T_{1})}(e^{kT}-e^{kT_{1}}(1+k(T-T_{1}))) \right.\\ &-r(p)g\alpha e^{kT}g(T-T_{1}) +\frac{r(p)h\alpha(e^{-kT_{1}}-e^{aT_{1}})}{a+k} \\ &-\frac{c_{1}I_{e}\alpha (M-T_{1})}{a}(r(p)\beta(e^{aT_{1}}-1)+a) \\ &+\frac{c_{1}I_{e}\alpha}{a^{2}} (r(p)\beta(e^{aT_{1}}-1)-r(p)\beta aT_{1} +a^{2}T_{1})+c_{1}(r(p)e^{aT_{1}}\alpha \\ &-\frac{r(p)\alpha}{a^{2}} (r(p)a\beta +r(p)a\beta e^{aT_{1}}+a^{2})) -\frac{c_{1}r(p)I_{e}\alpha}{2a^{3}}(2r(p)e^{aT_{1}}\beta a \\ &\left. +aT_{1}(a^{2}-r(p)a\beta )+{ a(a^{2}T_{1}-r(p)\beta (2+aT_{1})))}\right]=0 \end{aligned} $$

(20)

The optimum value of $T_{1}=t_{2}^{\ast}$ provided it satisfies the sufficient condition.

Now,

$$\frac{{d^{2} TC_{2} }}{{dT_{1}^{2} }} = \frac{{r(p)}}{T}\left[ {\alpha ge^{{ - kT_{1} }} + c_{1} e^{{aT_{1} }} \alpha (a + \theta ) + \frac{{c_{1} I_{e} \alpha \beta e^{{aT_{1} }} }}{a}\left( {a(T_{1} - M) + 2 - r(p)} \right)} {+ \frac{{c_{1} I_{e} \alpha \theta (2 - r(p))}}{{ar(p)}} + \frac{{h\alpha }}{{a + k}}(ke^{{kT_{1} }} + ae^{{aT_{1} }} )} \right]\;{\text{using}}\;\frac{{dTC_{2} }}{{dT_{1} }} = 0.$$

Note $Lt_{T\rightarrow 0}\frac{dTC_{2}}{dT_{1}}\rightarrow \infty$ and therefore,

$$ \begin{aligned} \frac{dTC_{2}}{dT_{1}}|_{T_{1}=M} &>0 \\ &\Longrightarrow \frac{1}{T}\left[-c_{1}r(p)\alpha (e^{-kT}+e^{aM})-\frac{\alpha r(p)ge^{-k(T+M)}(e^{kT}-e^{kM}(1+k(T-M)))}{k} \right.\\ &\quad-r(p)g\alpha e^{kT}g(T-M) +\frac{r(p)h\alpha (e^{-kM}-e^{aM})}{a+k}+\frac{c_{1}I_{e}\alpha }{a^{2}}(r(p)\beta (e^{aM}-1) \\ &\quad-r(p)\beta aM+a^{2}M)+c_{1}(r(p)e^{aM}\alpha -\frac{r(p)\alpha}{a^{2}}(r(p)a\beta +r(p)a\beta e^{aM}+a^{2})) \\ &\quad-\frac{c_{1}r(p)I_{e}\alpha }{2a^{3}}(2r(p)e^{aM}\beta a+aM(a^{2}-r(p)a\beta) \\ &\left.\quad+a(a^{2}M-r(p)\beta (2+aM)))\right]>0 \\ &\Rightarrow c_{1}(e^{aM}-e^{-kM})+\frac{g}{k}(e^{kM}+e^{kT}) +\frac{h}{a+k}(e^{aM}-e^{-kM}) \\ &\quad-\frac{c_{1}I_{e}(r(p)-1)}{r(p)a^{2}}(a\theta M+r(p)\beta (e^{aM}-1))+\frac{c_{1}\theta }{a}(e^{aM}-1)>0 \end{aligned} $$

Now if $ge^{-kT_{1}}+c_{1}e^{aT_{1}}(a+\theta)+\frac{h}{a+k}(ke^{kT_{1}} +ae^{aT_{1}})+\frac{c_{1}I_{e}\beta e^{aT_{1}}}{a}\left( a(T_{1}-M)+2-r(p)\right) +\frac{c_{1}I_{e}\theta (2-r(p))}{ar(p)}>0$ holds then we get $\frac{d^{2}TC_{2}}{dT_{1}^{2}}>0$ which means TC ₂ has minimum at $T_{1}=t_{2}^{\ast}$, otherwise TC ₂ may be maximum in the interval (0, M] or TC ₂ is a monotonic function in (0, M]. Now $Lt_{T_{1}\rightarrow \infty}\frac{dTC_{2}}{dT_{1}}=\infty$ and $\frac{dTC_{2}}{dT_{1}}|_{T_{1}=M}>0$ imply TC ₂(0) < TC ₂(0 +) and TC ₂(M −) < TC ₂(M) respectively. In the neighbourhood of the end point, TC ₂ is a monotonic increasing function of $T_{1}\in (0, \,M]$ and TC ₂ does not have a minimum in (0, M]. So TC ₂ does not have stationary point in (0, M]. Therefore $t_{2}^{\ast}=M$ if $Lt_{T_{1}\rightarrow \infty }\frac{dTC_{2}}{dT_{1}}=\infty$ and $\frac{dTC_{2}}{dT_{1}}|_{T_{1}=M}>0$ i.e., if the condition $c_{1}(e^{aM}-e^{-kM})+\frac{g}{k}(e^{kM}+e^{kT}) +\frac{h}{a+k}(e^{aM}-e^{-kM})-\frac{c_{1}I_{e}(r(p)-1)}{r(p)a^{2}}(a\theta M+r(p)\beta (e^{aM}-1))+\frac{c_{1}\theta }{a}(e^{aM}-1)>0$ is satisfied.

4 Numerical example

In this section, we have presented an example for numerical exposure of the presented inventory model. In a supermarket the demand rate not only depend upon the amount of the stock but also depends upon the price of the item so that demand rate is D(I(t), p), here γ = 200, δ = 1.3, α = 500 units, β = 0.15. Also let us consider that the item deteriorates 0.1 part of the total inventory which cost $2 per unit item. It takes $250 to order the total inventory. Let the cost price of each item is $3, selling price is $6 and to hold the item it requires $0.6 per unit. The system consider under inflation rate of 12 % and let the retailer earns 15 % of interest and pays 20 % interest where the total inventory system is considered for a full year. Let the supplier comes (1) Monthly (2) 3 months after (3) After 5 months (4) Half yearly. Now we minimize the total cost per unit item per unit time for the above situations.

In put data for the above production inventory model compare to the model presented in Sect. 2 are

$D(I(t),p)=r(p)[\alpha +\beta I(t)]=200e^{(-6\ast1.3)}[500+0.15I(t)], p=6$, θ = 0.1, A = 250 per order, h = 0.6 per year, k = 0.12, c ₁ = 3 per year, g = 2 per year, I _e  = 0.15 per year, I _p  = 0.2 per year, T = 1 year.

Now according to delay in payment as per the inventory model we get solution for four cases. The solutions of the inventory model for different cases are presented in Table 1.

Table 1 Optimal average cost for different delay in payment

In case (1) i.e., delay of payment for 1 month (i.e., M = 0.083) we observe from Table 1 that $t_{1}^{\ast}>M$ and $t_{2}^{\ast}>M$ so here case 2 is contradicts and only case 1 hold and minimum average cost TC ₁. Again for case (2), i.e. payment to supplier after 3 months (i.e., M = 0.25) inventory model follows the fact $t_{1}^{\ast}>M$ and $t_{2}^{\ast}<M$ so both case 1 and case 2 hold together, and here TC ₁ < TC ₂. For case (3), payment to the supplier after 5 months (i.e., M = 0.417) we have the situation here $t_{1}^{\ast}>M$ and $t_{2}^{\ast}<M$ so both case 1 and case 2 hold together. And in this case TC ₂ < TC ₁. Finally for the payment to supplier after 6 months case (4) we obtain optimum time for two cases as $t_{1}^{\ast}<M$ and $t_{2}^{\ast}<M$ so here case 1 contradicts and only case 2 holds and minimum average cost is at case 2.

5 Sensitivity analysis

We study the effect of changes of various parameter θ, p, k, c ₁, I _e , I _p by changing it by −25, −10, 10, 25 %. Taking one parameter at a time and keeping other unchanged.

The analysis is based on case (1) of the above example.

From the sensitivity analysis in Table 2 we summarise the following points:

• 1. $t_{1}^{\ast}$ and $t_{2}^{\ast}$ increases while $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ decreases with the decrease in the value of the parameter θ. Both $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ have low sensitivity to change in θ, and $t_{1}^{\ast}$ and $t_{2}^{\ast}$ are moderately sensitive to change in θ.

• 2. $t_{1}^{\ast}$decreases and $t_{2}^{\ast}$ increases while $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ increases with the decrease in the value of the parameter p. Both $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ are highly sensitive to change in p and $t_{1}^{\ast}$ is moderately sensitive and $t_{2}^{\ast}$ is highly sensitive to change in p.

• 3. $t_{1}^{\ast}$ and $t_{2}^{\ast}$ increases also $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ increases with the decrease in the value of the parameter k. Both $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ are less sensitive to change in k, and $t_{1}^{\ast}$ and $t_{2}^{\ast}$ are moderately sensitive to change in k.

• 4. $t_{1}^{\ast}$ and $t_{2}^{\ast}$ increases while $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ decreases with the decrease in the value of the parameter c ₁. Both $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ are moderately sensitivity to change in c ₁ and $t_{1}^{\ast}$ and $t_{2}^{\ast}$ are also moderately sensitive to change in c ₁.

• 5. $t_{1}^{\ast}$ and $t_{2}^{\ast}$ increases while $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ increases with the decrease in the value of the parameter I _e . Both $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ have low sensitivity to change in I _e , and $t_{1}^{\ast}$ and $t_{2}^{\ast}$ are also less sensitive to change in I _e .

• 6. $t_{1}^{\ast}$ increases and $t_{2}^{\ast}$ remains unchanged while $TC_{1}(t_{1}^{\ast})$ increases and $TC_{2}(t_{2}^{\ast})$ remains same with the decrease in the value of the parameter I _e . $TC_{1}(t_{1}^{\ast})$ is less sensitive to change in I _p and $t_{1}^{\ast}$ is moderately sensitive to change in I _p .

• 7. $t_{1}^{\ast}$ and $t_{2}^{\ast}$ decreases while $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ increases with the decrease in the value of the parameter T. Both $TC_{1}(t_{1}^{\ast})$ and $TC_{2}(t_{2}^{\ast})$ are moderately sensitivity to change in T, and $t_{1}^{\ast}$ and $t_{2}^{\ast}$ are also moderately sensitive to change in T.

Table 2 Sensitivity analysis based on changes of parameters

Now we present few pictorial form for analysis of effect of change of inventory parametric on optimum total cost. We consider for cases of delay payment as describe in numerical example in previous section.

From Fig. 2, we see that when the rate of deterioration (θ) decreases the percentage of total cost decreases in four cases of M and the vice versa. Reason for this is when the deterioration rate has decreased by some percentage then the total cost of the inventory system has decreased (i.e., reduced). We observe from the pattern of the Fig. 2 that for more delay to payment total cost is increased rapidly.

In the Fig. 3 we can see that if the selling price (p) decreases the total cost increases for all in four cases of delay payment. Reason for this is retailer is earning less if he decreases the selling price and hence the total cost of the inventory has increased. From the pattern of the graph we observe that it is logarithmic in nature and more effect on less M.

Fig. 2

Effect of optimal total cost for rate of deterioration

From Fig. 4, we can say that when the inflation (k) increases the total cost decreases in four cases of M. Its reason for common fact that with the increase in selling price the value of money has decreased and hence the total cost has increased. The pattern of the graph is linearly decreasing.

Fig. 3

Effect on optimal total cost for change of selling price

In the Fig. 5 we can see in four cases of M when the purchase cost of item (c ₁) has decreased the total cost has increased. Reason for this is when the price has decreased by some percentage then calculating the percentage of total cost we have to use the decreased purchase cost value which leads to increase in percentage of total cost. We observe that the pattern of the graph is almost linearly decreasing and the change of purchase cost of item is more effective for more delay of payment to the supplier.

Fig. 4

Effect on optimal total cost for change of inflation

From Fig. 6, we observe that when the rate of interest earned (I _e ) has decreased the total cost has increased for all four cases of M. Reason for this is when the interest earned rate has decreased by some percentage so the retailer is earning less which leads to increase in costing of the total inventory system. We observe that the pattern of the graph is almost linearly dependent and more effect for delay of payment to the supplier.

Fig. 5

Effect on optimal total cost for change of purchase cost of item

In the Fig. 7 we can see that when the rate of interest payable (I _p ) has decreased the the total cost has increased in four cases of M. Reason for this is when the interest payable rate has decreased by some percentage so the retailer is paying less to the supplier which leads to increase in total cost. We observe that the pattern of the graph is almost linearly decreasing.

Fig. 6

Effect on optimal total cost for change of rate of interest earned

From Fig. 8, we conclude that the total cost has increased when the replenishment time (T) has decreased in four cases of M and the vice versa. The reason for this that for quick replenishment of inventory means there is a increase in the total cost. The pattern of the graph is logarithmic in nature. We observe that the pattern of the graph is almost logarithmic in nature and more effect for less delay of payment to the supplier.

Fig. 7

Effect on optimal total cost for change of interest payable

Fig. 8

Effect on optimal total cost for change of replenishment time

6 Conclusion

The paper studies the dynamic deterministic inventory model allowing shortage. This model incorporates some realistic feature such as deterioration (a natural phenomenon of goods), shortage, price and amount of the stock displayed in the supermarket. The amount of stock and the price of the item in the market have two aspects, positive as well as negative. Few customer can think that a large amount of stock means the items are in demand where as few customer can think that a large amount of stock means the item is of less demand because other customers are not buying. Same is the case for price of an item. So our task was to optimize the stock amount and minimize the cost. Last but not the least the effect of delay in payment is considered from the retailer point of view and then we optimize the total cost. Example is provided in support of the proposed model and sensitivity analysis is also performed. In sensitivity analysis we have seen the model is highly sensitive with the change in price. Also the model is sensitive with the change in total time of this inventory model. It has been noted that inflation is less sensitive i.e., the inflationary change in the market does not affect the total costing of the system and thus sometime helpful for the retailer. Also we evaluate that at what time should the stock ends so that the total costing is minimum.