Keywords

MSC

7.1 Introduction

With the rapid development of competition and technology between the business enterprises, companies are feeling the necessity of inventory models as a decision-making device for developing their business effectively. It is well-known fact that a general model always represents an enhanced outcome in provisions of maximizing the profit or minimizing the total cost. The traditional inventory models are based on the fact that a retailer has to pay as soon as he received the product. However, this may not be correct. In real-life situations, it is common to observe that the supplier will offer certain time period to the retailer to settle the account. The term is known as trade-credit policy. The company often uses this policy to promote the products. Generally, if the amount is paid before the permissible period, the interest charge is zero and the retailer can use the sale revenue to earn interest. Nevertheless, if the retailer is not able to pay off the amount within the permissible period, an interest is charged by the supplier. This brought up economic advantage to the retailers as they can make some interest from the proceeds. Hence, this model develops a two-level credit policy to reflect a real-life situation. Also, items like fruits, vegetables, dairy products, etc. are perishable with time. It results in loss of marginal values of products, loss of profit and loss of goodwill that lead to reduce the usefulness of the product. Therefore, deterioration plays a vital role and cannot be ignored. Together with rate of deterioration, demand is also one of the factors that influence the sale a lot. Here, in this model instead of taking demand dependent on some specific parameters, to establish model for general cases, the demand rate is considered to be constant. By keeping this in mind, an inventory model is developed with constant demand and deterioration rate. This paper calculates the inventory cycle time where total cost is minimized with respect to decision variables. The paper is structured as follows: Sect. 7.2 is literature review. In Sect. 7.3, notations and assumptions are introduced that are used in proposed model. The inventory model is formulated in Sect. 7.4. Section 7.5 contains computational algorithm. Section 7.6 describes several numerical examples together with sensitivity analysis with respect to inventory parameters. At last, Sect. 7.7 provides conclusion with future scope.

7.2 Literature Review

The trade-credit policy is widely used in inventory models to increase the sale of commodities and to attract more customers. Teng and Chang (2009) developed an EPQ model for two-level credit policy and develop some appropriate results for obtaining optimal solution. Wu et al. (2014) proposed a model for deteriorating items having date of expiration with two-level credit policy. They proved not only the existence of optimal cycle time and trade credit but also the uniqueness of the solution under some numerical examples to modify the problem. Cheng and Kang (2010) developed an integrated model with delay in payment. The model considers vendor–buyer and buyer–customer relationship and presented a price-negotiation scheme to allocate the increased amount of profit. Chung et al. (2014) established an economic production quantity model for exponentially perishable objects under two-level credit periods. The objective is to determine optimal replenishment policy to minimize the relevant cost. Teng et al. (2013) provided a linear non-decreasing demand function of time under permissible credit period. Sarkar et al. (2015) introduced a model for variable deterioration with fixed lifetime products. In this model, numerical examples are illustrated with graphical representation. Sarkar et al. (2013) developed a model for perishable objects where the demand is considered to be time dependent. The objective is to maximize the total profit. Shah et al. (2013) proposed an inventory model with non-instantaneous deteriorating item. In this model, the demand rate is assumed to be a function of selling price and advertisement of an item. Chung (2011) developed an inventory model for two-level credit period policy. The condition that interest charged should be greater than the interest earned is relaxed in this model. Tsao et al. (2011) focused on the production problem under credit policy and reworking of imperfect items. Sang and Tripathi (2012) proposed an EOQ model for deteriorating items with constant demand. The production rate is demand sensitive. Due to continuous demand, shortages occurred and are completely backlogged. Srivastava and Gupta (2007) developed an infinite time-horizon inventory model for perishable objects assuming constant and time-dependent demand rate. Khanra et al. (2011) developed an EOQ model for deteriorating item with trade-credit policy where the demand is time dependent. Sarkar and Sarkar (2013) introduced a model for deteriorating item under stock-dependent demand. They consider backlogging rate and deterioration as time-varying function. Mishra et al. (2013) gave an inventory model for deteriorating items having time-dependent demand and holding cost. The model permits partial backlogging due to shortages.

Tripathi and Mishra (2012) developed an inventory model for constant demand and constant deterioration rate under trade credit. Skouri et al. (2011) proposed a model for ramp-type demand rate where the deterioration rate is constant and the unsatisfied demand is partially backlogged. The model allows permissible delays in payment to attract the customers. Shah (2017) developed a three-layered integrated inventory model for perishable objects under two-level trade-credit policy having quadratic demand. Lio et al. (2018) developed a two-level trade-credit policy for finding feasible order quantity. Cardenas et al. (2020) proposed an EOQ model for nonlinear stock-dependent holding cost in which stock-dependent demand is to be considered. Tiwari et al. (2020) analysed an optimal ordering policy for deteriorating items by assuming complete backlogging. Yang (2004) developed an EOQ model using quantity discount. Li (2014) suggested an optimal control production model under permissible tradable emission. Yang (2019) studied an inventory model for deteriorating items under two-level trade credit with limited storage capacity. This model extends the existing literature of inventory models for deteriorating objects. As with credit periods, deteriorõation is the key factor that influences the objective function directly.

7.3 Notations and Assumptions

The model is formulated using following notations and assumptions.

Notations

\(R\)

Constant demand rate

\(\theta\)

Constant rate of deterioration

\(h\)

Inventory holding cost per unit (dollars/unit)

\(C\)

Purchase cost per unit (dollars/unit)

\(p\)

Selling price per unit (dollars/unit)

\(M\)

The first credit period by the supplier to the retailer’s without spare charges

\(N\)

Second credit period with an interest of \(I_{2}\), where \(N > M\)

\(A\)

Ordering cost per order(dollars/order)

\(I_{{c1}}\)

Interest charge per unit per year during time interval \([M,N]\) (dollars/year)

\(I_{{c2}}\)

Interest charge per unit per year during time interval \([N,T]\) (dollars/year)

\(I_{e}\)

Interest earned per unit per year (dollars/year)

\(T\)

Cycle time (in years)

\(I(t)\)

Inventory level during time \([0,T]\)

\({\text{TC}}(T^{*} )\)

Total cost per year (dollars/year)

\(W_{1}\)

\(\frac{p}{C}M + \frac{{pI_{e} }}{{2C}}N^{2}\)

\(W_{2}\)

\(\frac{p}{C}N + \frac{{pI_{e} }}{{2C}}\left( {M^{2} + \left( {N - M} \right)^{2} } \right)\)

Assumptions

  • Demand rate for object is constant with time.

  • Shortages are not permissible.

  • Replenishment rate is infinite.

  • For \(M > T\), the rate of interest charge is zero and the retailers earn some interest on sales revenue by the time \(M.\)

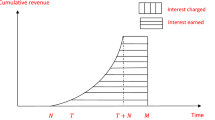
  • For \(M \le T\), different cases are possible. Initially, if the retailer clears the account by \(M\), the interest charge is zero and he/she can earn interest of \(I_{e}\) on sales revenue throughout the cycle time \(T.\) Secondly, if the retailer is unable to pay up to \(M\) or before time period \(N\), then the supplier charges an interest of \(I_{{c1}}\) on the retailer and also utilizes the sales revenue to clear the unpaid amount. Lastly, if the retailer pays after time period \(N\), an interest of \(I_{{c2}}\) is charged on retailer.

7.4 Mathematical Model

In this section, the model is formulated for two-level trade-credit policies for constant demand and deterioration rate. Initially at \(t = 0\), the production rate is \(Q\) given by \(\frac{R}{\theta }\left( {e^{{\theta T}} - 1} \right)\), where the demand is considered to be constant, i.e. \(R\). During time interval \(\left[ {0,T} \right]\), the inventory level decreases due to the effect of deterioration and customer’s consumption rate and reaches zero at the end of cycle time \(t = T\).

The differential equation of the inventory system for the time \(\left[ {0,T} \right]\) is given by

$$\frac{{{\text{d}}I(t)}}{{{\text{d}}t}} = - \theta I(t) - R$$
(7.1)

Using boundary condition \(I(T) = 0\), the inventory level is

$$I(t) = \frac{R}{\theta }\left( {e^{{\theta \left( {T - t} \right)}} - 1} \right)$$
(7.2)

The order quantity \(Q\) is obtained using initial condition \(I(0) = Q\) and is given by

$$Q = \frac{R}{\theta }\left( {e^{{\theta T}} - 1} \right)$$
(7.3)

The costs comprising of the total annual cost are listed below:

  • Ordering cost \(({\text{OC}})\) = \(\frac{A}{T}\)

  • Holding cost \(({\text{HC}})\) = \(\frac{{h}}{T}\int\limits_{0}^{T} {I(t){\text{d}}t}\)

  • Related to the last two assumption, there are four different cases with respect to interest earned and interest charged per year

Case 1: \(T \le M\).

Following Liao et al. (2018), in this case, the credit period \(M\) is greater than the cycle time \(T\), and the retailers sold out all the products before the permissible credit period. So, the interest charge on retailer is zero.

Interest charge \((IC_{1} ) = 0\).

There are two different elements for the interest earned as mentioned bellow:

Firstly, the interest earned by the retailer during time interval \(\left[ {0,M} \right]\) is

Interest earned \(({\text{IE}}11) = \frac{{pI_{e} }}{T}\int\limits_{0}^{T} {Rt{\text{d}}t}\).

Secondly, the interest earned during time \(\left[ {M,T} \right]\) is

Interest earned \(({\text{IE}}12) = \frac{1}{T}\left( {pI_{e} RT + \frac{{pRT^{2} I_{e} ^{2} }}{2}} \right)\left( {M - T} \right)\).

Therefore, the total interest earned is given by

Interest earned

\(({\text{IE}}_{1} ) = {\text{IE}}11 + {\text{IE}}12 = \frac{{pI_{e} }}{T}\int\limits_{0}^{T} {Rt{\text{d}}t} + \frac{1}{T}\left( {pI_{e} RT + \frac{{pRT^{2} I_{e} ^{2} }}{2}} \right)\left( {M - T} \right)\).

Case 2: \(M < T \le W_{1}\).

Here, as \(T \le W_{1}\) it means the retailers clear all its account up to \(M\). Hence, the interest charge is zero.

Interest charge \(({\text{IC}}_{2} ) = 0\).

There are three different elements for interest earned as follows:

Firstly, interest is earned by the retailer on sales revenue during time \(\left[ {0,M} \right]\).

Interest earned \(({\text{IE}}21) = \frac{{pI_{e} }}{T}\int\limits_{0}^{M} {Rt{\text{d}}t}\).

Secondly, the retailer earns interest on sales revenue due to the sale up to cycle time \(T\).

Interest earned \(({\text{IE}}22) = \frac{{pI_{e} }}{T}\int\limits_{0}^{{T - M}} {Rt{\text{d}}t}\).

Lastly, the interest earned by the retailer on the sales revenue during time \(\left[ {M,T} \right]\).

Interest earned \(({\text{IE}}23) = \frac{{I_{e} }}{T}\left( {p\int\limits_{0}^{M} {R{\text{d}}t + pI_{e} \int\limits_{0}^{M} {Rt{\text{d}}t - {\text{CRT}}} } } \right)\left( {T - M} \right)\).

So, the total interest earned in this case is given by

Interest earned

$$({\text{IE}}_{2} ) = {\text{IE}}21 \,+\, {\text{IE}}22 \,+\, {\text{IE}}23 = \left( \begin{gathered} \frac{{pI_{e} }}{T}\int\limits_{0}^{M} {Rt{\text{d}}t} + \frac{{pI_{e} }}{T}\int\limits_{0}^{{T - M}} {Rt{\text{d}}t} \hfill \\ + \frac{{I_{e} }}{T}\left( {p\int\limits_{0}^{M} {R{\text{d}}t + pI_{e} \int\limits_{0}^{M} {Rt{\text{d}}t - {\text{CRT}}} } } \right)\left( {T - M} \right) \hfill \\ \end{gathered} \right)$$

Case 3: \(W_{1} < T \le W_{2}\).

Here, as \(W_{1} < T\) that is, the sales revenue achieved by the retailer is less than the purchase cost up to time period \(M\). Also, \(T \le W_{2}\) which means the retailer decides to decrease the loan amount by the demand and sales revenue and decides to clear its entire purchase amount up to \(N\) or before that. The unpaid balance is given by

Unpaid balance \((U_{1} ) = {\text{CQ}} - p\int\limits_{0}^{M} {R{\text{d}}t - pI_{e} \int\limits_{0}^{M} {Rt{\text{d}}t} }\).

Charges applied on unpaid balance with an interest rate of \(I_{{C1}}\) for time \(M\).

Interest charge \({\text{IC}}_{3} = \frac{{I_{{C1}} U_{1} ^{2} }}{{pQ}}\int\limits_{0}^{{T - M}} {I(t){\text{d}}t}\).

Interest earned for this case is as follows:

Firstly, Interest earned by retailers on sales revenue for time \([0,M]\) is.

Interest earned \(({\text{IE}}31) = \frac{{pI_{e} }}{T}\int\limits_{0}^{M} {Rt{\text{d}}t}\).

Secondly, the retailer uses the sales revenue to gross interest throughout the time from

\(M + \frac{{U_{1} }}{{p\alpha }}\) to \(T\). So, interest earned is given by

Interest earned \(({\text{IE}}32) = \frac{{pI_{e} }}{T}\int\limits_{{M + \frac{{U_{1} }}{{Rp}}}}^{T} {Rt{\text{d}}t}\).

Hence, the total interest earned is given by

Interest earned \(({\text{IE}}_{3} ) = {\text{IE}}31 + {\text{IE}}32 = \frac{{pI_{e} }}{T}\int\limits_{0}^{M} {Rt{\text{d}}t} + \frac{{pI_{e} }}{T}\int\limits_{{M + \frac{{U_{1} }}{{Rp}}}}^{T} {Rt{\text{d}}t}\).

Case 4: \(W_{2} < T\).

Here in this case, the retailer is unable to clear the account at \(M\) and decided to pay it after \(N\).

For interest charges, there are two different elements as follows:

Firstly, the supplier charges an interest of \(I_{1}\) on unpaid balance \(U_{1}\) during time \([M,N]\) is

Interest charged \(({\text{IC}}41) = \frac{{I_{{c1}} \left( {N - M} \right)U_{1} }}{T}\).

Secondly, charge on the unpaid balance with rate of \(I_{{c2}}\) at time period \(N\). Unpaid balance is

Unpaid balance \((U_{2} ) = {\text{CQ}} - pI_{e} \int\limits_{0}^{M} {Rt{\text{d}}t - pI_{e} \int\limits_{0}^{{N - M}} {Rt{\text{d}}t - p\int\limits_{0}^{M} {R{\text{d}}t} } } - p\int\limits_{0}^{{N - M}} {R{\text{d}}t}\), the interest charge

Interest charge \(({\text{IC}}42) = \frac{{I_{{c2}} U_{2} ^{2} }}{{pQ}}\int\limits_{N}^{T} {I(t){\text{d}}t}\).

The total interest charge is

Interest charge \(({\text{IC}}_{4} ) = {\text{IC}}41 + {\text{IC}}42 = \frac{{I_{{c1}} \left( {N - M} \right)U_{1} }}{T} + \frac{{I_{{c2}} U_{2} ^{2} }}{{pQ}}\int\limits_{N}^{T} {I(t){\text{d}}t}\).

The interest earned is given by

Interest earned \(({\text{IE}}_{4} ) = \frac{{pI_{e} }}{T}\int\limits_{0}^{M} {Rt{\text{d}}t}\).

The total annual cost related to the different cases is mentioned below:

$${\text{TC}}_{1} (T) = ({\text{OC}} + {\text{HC}} + {\text{IC}}_{1} - {\text{IE}}_{1} ),\;{\text{for}}\;T \le M$$
(7.4)
$${\text{TC}}_{2} (T) = ({\text{OC}} + {\text{HC}} + {\text{IC}}_{2} - {\text{IE}}_{2} ),\;{\text{for}}\;M < T \le W_{1}$$
(7.5)
$${\text{TC}}_{3} (T) = ({\text{OC}} + {\text{HC}} + {\text{IC}}_{3} - {\text{IE}}_{3} ),\,{\text{for}}\;W_{1} < T \le W_{2}$$
(7.6)
$${\text{TC}}_{4} (T) = ({\text{OC}} + {\text{HC}} + {\text{IC}}_{4} - {\text{IE}}_{4} ),\;{\text{for}}\;W_{2} < T$$
(7.7)

where total cost is given below. Here \(T_{i} ^{*}\) denotes the optimal cycle time for \({\text{TC}}_{i} (T)\) on \(T > 0\) if \(T_{i} ^{*}\) exists for \(i\) = 1 to 4.

$${\text{TC}}(T*) = \max \{ {\text{TC}}_{1} (T_{1} ^{*} ),{\text{TC}}_{2} (T_{2} ^{*} ),{\text{TC}}_{3} (T_{3} ^{*} ),{\text{TC}}_{4} (T_{4} ^{*} )\}$$
(7.8)

Here,

$${\text{TC}}(T_{1} ^{*} ) = \max \{ {\text{TC}}_{1} (T):0 < T \le M\}$$
(7.9)
$${\text{TC}}(T_{2} ^{*} ) = \max \{ {\text{TC}}_{2} (T):M < T \le W_{1} \}$$
(7.10)
$${\text{TC}}(T_{3} ^{*} ) = \max \{ {\text{TC}}_{3} (T):W_{1} < T \le W_{2} \}$$
(7.11)

and

$${\text{TC}}(T_{4} ^{*} ) = \max \{ {\text{TC}}_{4} (T):W_{2} \le T\}$$
(7.12)

7.5 Computational Algorithm

The model uses classical optimization method. The goal is to minimize the total cost for the inventory model. The algorithm is based on the preceding steps.

Step 1: Assign numerical values to the inventory parameters.

Step 2: Compute first-order partial derivative for \({\text{TC}}_{1} (T),{\text{TC}}_{2} (T),{\text{TC}}_{3} (T),{\text{TC}}_{4} (T)\) with respect to the decision variable \(T\) and equating them to zero.

$$\frac{{\partial {\text{TC}}_{1} (T)}}{{\partial T}} = 0,\frac{{\partial {\text{TC}}_{2} (T)}}{{\partial T}} = 0,\frac{{\partial {\text{TC}}_{3} (T)}}{{\partial T}} = 0,\frac{{\partial {\text{TC}}_{4} (T)}}{{\partial T}} = 0$$
(7.13)

An optimal value of decision variable is \(T\) obtained using Eq. (7.13). Hence, the total cost for all the cases can be solved using Eqs. (7.4) to (7.7), and the optimal total annual cost is the one that is satisfied by Eq. (7.8) that also satisfies the respective condition.

Step 3: Convexity of total annual cost is confirmed by means of graphs.

7.6 Numerical Example and Sensitivity Analysis

Example 1

For \(\alpha\) = 9000, \(C\) = $4/unit, \(p\) = $20/unit, \(\theta\) = 0.1, \(h\) = $2/unit/year, \(A\) = $200/order, \(I_{e}\) = $0.11/$/year, \(I_{{c1}}\) = $0.14/$/year, \(I_{{c2}}\) = $0.20/$/year, \(M\) = 0.15 year, \(N\) = 0.2 year. Using the above procedure, the optimal decision variable is \(T_{1} ^{*}\) = 0.103 year that gives \({\text{TC}}(T^{*} )\) = $916.31.

Example 2

For \(\alpha\) = 400, \(C\) = $40/unit, \(p\) = $50/unit, \(\theta\) = 0.2, \(h\) = $38/unit/year, \(A\) = $156/order, \(I_{e}\) = $0.04/$/year, \(I_{{c1}}\) = $0.05/$/year, \(I_{{c2}}\) = $0.06/$/year, \(M\) = 0.12 year, \(N\) = 0.15 year. Using the above procedure, the optimal decision variable is \(T_{2} ^{*}\) = 0.140 year that gives \({\text{TC}}(T^{*} )\) = $2145.23.

Example 3

For \(\alpha\) = 120, \(C\) = $13/unit, \(p\) = $14/unit, \(\theta\) = 0.2, \(h\) = $4/unit/year, \(A\) = $8/order, \(I_{e}\) = $0.04/$/year, \(I_{{c1}}\) = $0.05/$/year, \(I_{{c2}}\) = $0.09/$/year, \(M\) = 0.15 year, \(N\) = 0.17 year. Using the above procedure, the optimal decision variable is \(T_{3} ^{*}\) = 0.170 year that gives \({\text{TC}}(T^{*} )\) = $83.88.

Example 4

For \(\alpha\) = 80, \(C\) = $13/unit, \(p\) = $13.001/unit, \(\theta\) = 0.02, \(h\) = $4/unit/year, \(A\) = $0.8/order, \(I_{e}\) = $0.005/$/year, \(I_{{c1}}\) = $0.0051/$/year, \(I_{{c2}}\) = $0.0052/$/year, \(M\) = 0.05 year, \(N\) = 0.05001 year. Using the above procedure, the optimal decision variable is \(T_{4} ^{*}\) = 0.070 year that gives \({\text{TC}}(T^{*} )\) = $22.55.

Convexity of optimal solutions through graphs is shown below:

Convexity of Example 1

Convexity of Example 2

Convexity of Example 3

Convexity of Example 4

Also, some numerical results depending on the different cases are discussed below in Table 7.1.

Table 7.1 Optimal solutions for different cases with data
Full size table

A sensitivity analysis is done that represents the impact of changing inventory parameters by −20%, −10%, +10% and +20% on decision variable and on the total cost. Here, an analysis is performed for the fourth case as it includes all the cases.

Following results are being observed through Table 7.2.

Table 7.2 Sensitivity analysis
Full size table

  • The more will be the demand rate, less will be the optimal cycle time and larger will be the total cost. Here, the increase is not beneficial as it increases the total cost.

  • With an increase in purchase cost, the demand for the products due to high rate decreases that influences the cycle time. The cycles’ time increases, and it is obvious that the total cost increases. Therefore, the increase is not advisable.

  • Increase in selling price reduces the total cost. So, the change is acceptable.

  • Higher deterioration rate forces the retailer to invest more. The change is not preferable as it increases the optimality cost.

  • The impact is negative as holding cost and ordering cost are the key factors that directly influence the budgets of a company. With an increase in these parameters, the total cost increases.

  • An increase in the total cost decreases with a decrease in cycle time.

  • With an increase in parameters, total cost increases.

  • Credit periods help to boost the products demand. Here, the increase is not sensible as it increases the total cost.

7.7 Conclusion

The paper develops an inventory model for constant demand and constant rate of deterioration. The model considers objects that are getting expired, spoilt and deteriorated with respect to time. It plays a crucial role in environment of marketplace, and the loss that occurs due to that cannot be ignored. The marginal insight shows that higher deterioration rate forces the retailer to spend more. So, it is always preferable to invest more in reducing the rate of deterioration. Also, permissible credit period helps to boost the demand. This model considers a two-level credit period. The model evaluates the optimal cycle time under different cases while minimizing the total cost. The sensitivity analysis shows that the total relevant cost is sensitive to selling price and credit periods. A small change in these parameters highly fluctuates the total cost. The model uses classical optimization method for solution procedure. The present work can be expanded in different ways. One can consider demand to be time dependent or stock dependent with variable deterioration rate having variable holding cost. For smooth business, the companies may offer discounts to attract the customers. To control the rate of deterioration, preservation technology investments are made.