1 Introduction

In the classical inventory models, found in the existing literature are that the life time of an item is infinite while it is in storage. But the effect of deterioration plays an important role in the storage of some commonly used physical goods like fruits, vegetables etc. In these cases, a certain fraction of these goods are either damaged or decayed and are not in a condition to satisfy the future demand of costumers as fresh units. Deterioration in these units is continuous in time and is normally proportional to on-hand inventory. Recently a good number of works have been done by some authors for controlling inventories in which a constant or a variable part of the on-hand inventory gets deteriorated per unit of time. In the existing models, it is normally assumed that the deteriorated units are the complete loss to the inventory management. In reality, it is not always true. These are some units (e.g. fruits, vegetables, food grains, etc) which have a demand to some particular customers even after being partially deteriorated. This phenomenon is very common in the developing countries even majority of people live under poverty line. In business, the partially affected items are being immediately and continuously separated from the lot to save the fresh ones, otherwise the good ones will be affected by getting in contact with the spoiled ones. These damaged units are sold from the adjacent secondary shop. Here, the fresh / good units may be sold with a profit while the deteriorated ones are usually sold at a lower price, even incurring a loss, in such a way that the management makes a profit out of the total sales from the two-shops. The concept of two shops under a single management was introduced by Kar et al. [13]. In their study, they have considered the stock-dependent demand for deteriorating items and they have not considered shortage in the primary and secondary shop. Kar et al. [14] also developed a deterministic inventory model of deteriorating items sold from two-shops under a single management. In that model, they have considered shortage in the primary but not in secondary shop. Das and Maiti [7] developed an inventory model of a differential item sold from two shops under single management with shortages and variable demand. Dey et al. [8] presented an inventory of differential items selling from two shops under a single management with periodically increasing demand over a finite time-horizon. In the above literature, they have not been considered the effect of inflation. But this factor is most important in the present scenario.

In many real-life situations, for certain types of consumer goods (e.g., fruits, vegetables, donuts, and others), the consumption rate is sometimes influenced by the stock-level. It is usually observed that a large pile of goods on shelf in a supermarket will lead the customer to buy more and then generate higher demand. The consumption rate may go up or down with the on-hand stock level. These phenomena attract many marketing researchers to investigate inventory models related to stock-level. The related analysis on such inventory system with stock-dependent consumption rate was studied by Levin et al. [18], Gupta and Vrat [11], Baker and Urban [3], Mandal and Phaujder [22], Dutta and Pal [9], Urban [28], Mandal and Maiti [20, 21], Balkhi and Benkherouf [4], Zhou and Yang [31], Alfares [2], etc. Recently, Goyal and Chang [10] proposed the inventory model with stock-level dependent demand rate.

In the present competitive market, the selling price of a product is one of the decisive factors in selecting the item for use though there is a market for some fashionable goods irrespective of their prices. In practice, higher selling price of a product negates the demand whereas reasonable or low price has the reverse affect. This argument is more appropriate for defective goods whose demand is always price dependent. Whitin [29] first presented an inventory model considering the effect of price dependent demand. Later, Kunreuther and Richard [16], Lee and Rosenblatt [17], Mukherjee [24], Abad [1] presented inventory of joint pricing and inventory planning. Recently, Maiti et al. [19] and Banerjee and Sharma [5] also presented inventory model with price dependent demand.

Generally, in the classical inventory model it is assumed that all the costs associated with the inventory system remains constant over time. Most of the inventory models developed so far does not include inflation and time value of money as parameters of the system. But due to the large scale of inflation the monetary situation in almost of the countries has changed to an extent during the last thirty years. Nowadays inflation has become a permanent feature in the system. Inflation enters in the picture of inventory only because it may have an impact on the present value of the future inventory cost. After the pioneer work of Buzacott in 1975 [6], it is found that inflation plays a vital role in the inventory system and production management though the decision makers may face difficulties in arriving at answers related decision making. At present, it is impossible to ignore the effects of inflation. Between 1975 to 1985 many researchers have been addressing the inflationary effect on an inventory policy. Misra [23], Hwang and Shon [12], Ray and Chaudhuri [25], Sarkar et al. [26], etc. developed an approach of modeling inventory by assuming a constant inflation rate. Yang [30] considered inflation in his two warehouse inventory model. Kumari et al. [15] presented an inventory model for deteriorating items. Singh et al. [27] developed a two-warehouse inventory model for deteriorating items with shortages under inflation and time-value of money.

In this paper, we have developed an inventory model of both non-defective and defective units purchased in a lot and selling separately at two different shops under a single management under the assumption that the demand of the good units is stock dependent whereas the defective ones having only price dependent demand. In primary shop, non-defective units are sold with a profit and the defective units, which are continuously transferred to the adjacent secondary shop, are sold after some re-work repair at a reduced price even incurring a loss. Here shortages are allowed and backlogged. It is also assumed that the rate of replenishment of units for the primary shop is infinite. In the secondary shop, which sells only the deteriorated units, they are continuously transferred from the primary shop with variable rate. We consider three situations for dealing with defective units depending upon the coincidence of the time periods at two shops. In the present model, there are three scenarios:(1) the demand of defective units is so high that the shortages of defective units occur earlier than the shortages at the primary shop, (2) at both the primary and the secondary shops shortages occur at the same time and (3) at the secondary shop for the defective units shortages occur after the occurrence of shortages at the primary shop.

In each scenarios, we have suppose that to meet the shortages an amount of differential units is procured at the beginning of the subsequent scheduling period and from this, both good and defective units are separated in no-time paying an extra price for sorting. Now, due to this, there are three cases. As an attempt is made to meet the shortages of both good and defective units out of specially ordered differentials, let us fulfill one side of those shortages rigidly, i.e. to meet the shortages of goods units, the required amount of differential units are purchased. In that case, as differential units have been calculated on the basis of shortages of good units at the primary shop will be met exactly, but for the secondary shop, we have three cases for the defective units available from the above mentioned process:(a) shortages of defective units are also exactly met, (b) shortages of defective units are more than the available amount. Here we suppose that shortages are partially backorder and (c) shortages are less than the available defective units. In each case under each scenario, profit is maximized and optimum order quantities are valuated using the computer algorithm based on a gradient method. Finally, a numerical example and sensitivity analysis is used to study the behavior of the model.

2 Notations and assumption

To develop an inventory model of differential units with variable demands for primary and secondary shops under a single management, the following notations are used.

cs :

“in-no-time” sorting cost for shortage units only.

θ:

the rate of deterioration.

c0 :

unit cost of the differential item.

For ith (i=1, 2) shop,

pi :

selling price per unit item and pi = mic0

hi :

holding cost per unit quantity per unit time.

μi :

set-up cost per scheduling period.

Qi :

optimum inventory level.

mi :

mark-up price with mi > 1 and 0 < m2 < m1 (m2 is decision variable).

Si :

shortage level at the end of scheduling period.

gi :

shortage cost per unit quantity per unit time.

r:

inflation rate.

qi(t):

inventory level at any time t.

NRi :

net revenue from ith shop.

TCi :

total cost at the ith shop.

(suffices i = 1 and 2 represents the parameters related to the primary and the secondary shops respectively).

In addition to above notations, following assumptions are also considered:

2.1 Assumptions for the primary shop

  1. (1)

    Demand for good units is deterministic and function of current stock level given by \( {{\hbox{D}}_{{1}}}({{\hbox{q}}_{{1}}}({\hbox{t}})) = {a_1} + {b_1}{q_1}(t) \) where a1, b1 are positive constants.

  2. (2)

    Production is instantaneous without lead-time.

  3. (3)

    Shortages are allowed and these are fully backlogged. To meet the shortages for good units, it is required to procure S differential units out of which good and defective units are (1-θ)S (=S1) and (θt)S respectively.

  4. (4)

    Defective unit at any time t is a fraction of on-hand inventory level and is equal to θq1(t), where a and b are constants and 0 < θ < 1. These defective units are continuously transferred to the secondary shop.

  5. (5)

    As shortages for good and defective units are met after sorting the differential units “in-no-time”, sorting cost for shortage units only is dependent on shortage quantity of differential units and is given by

    1. a.

      \( {{\hbox{c}}_{\rm{s}}} = {\hbox{k}}{{\hbox{S}}^{\beta }} \)

    2. b.

      Where k, β (0 < β <1) are positive constants. The continuous sorting cost of defective units at the time of selling of good units at the primary shop is included in the set-up cost as this job is done by the permanent employees of the management.

2.2 Assumptions for the secondary shop

  1. (1)

    Secondary shop sells only the defective units, which are received continuously from the primary shop at a variable rate (θ)q1(t) until the stock of differential items is exhausted in the primary shop. S2 units are also received at the beginning of the next scheduling period to meet the shortages.

  2. (2)

    Shortages are allowed and fully backlogged.

  3. (3)

    In this shop, demand D2 is dependent on the selling price, i.e., it is a function of mark-up price m2, since p2 = m2c0 and D2 = a2–b2c0m2.

3 Primary shop

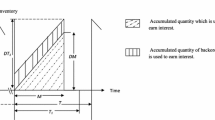
In the present study, we consider that after fulfilling backlogged order quantities of the easier cycle. Initially the inventory stock level of the system is Q1 and up to t = t1 and then the defective units, which are continuously transferred to the secondary shop. The stock level reaches zero at time t = t1, shortages begin after time t = t1 only for good units up to time t = t1+t2. At time t = t1+t2, shortage level is S1 and S units are procured and stored instantaneously. The pictorial representation of the system is given in Fig. 1.

Fig. 1
figure 1

Instantaneous state of inventory for the primary shop

Full size image

The differential equations describing the inventory level q1 (t) in the interval in 0 ≤ t ≤ t1 + t2 are given by

$$ \frac{{d{q_1}(t)}}{{dt}} = \left\{ {\begin{array}{*{20}{c}} { - \theta {q_1}(t) - {D_1}\left( {{q_1}(t)} \right),} \hfill & {0 \leqslant t \leqslant {t_1}} \hfill & {(1)} \hfill \\{ - {D_1}\left( {{q_1}(t)} \right),} \hfill & {{t_1} \leqslant t \leqslant {t_1} + {t_2}} \hfill & {(2)} \hfill \\\end{array} } \right. $$

With the conditions, q1(t) = Q1, 0 and –S1 at t = 0, t1 and t1 + t2 respectively.

Taking \( {D_1}\left( {{q_1}(t)} \right) = {a_1} + {b_1}{q_1}(t) \), the solutions of the above equations are

$$ {q_1}(t) = \frac{{{a_1}}}{\alpha }\left[ {{e^{{\alpha \left( {{t_1} - t} \right)}}} - 1} \right],\;0 \leqslant t \leqslant {t_1} $$
(3)
$$ \begin{array}{*{20}{c}} { = \frac{{{a_1}}}{{{b_1}}}\left[ {{e^{{{b_1}\left( {{t_1} - t} \right)}}} - 1} \right],} & {{t_1} \leqslant t \leqslant {t_1} + {t_2}} \\\end{array} $$
(4)

Where α = b 1 + θ.

If Du be the total defective units during the interval (0, t1 + t2), then

$$ {D_u} = \int\limits_0^{{{t_1}}} {\theta \,{q_1}(t)dt + \theta \,S = } \frac{\theta }{\alpha }\left( {{Q_1} - {a_1}{t_1}} \right) + \theta \,S $$
(6)

Where Q1 and S are given by

$$ \begin{array}{*{20}{c}} {{Q_1} = {q_1}(0) = \frac{{{a_1}}}{\alpha }\left( {{e^{{\alpha {t_1}}}} - 1} \right)} \\{{S_1} = {q_1}\left( {{t_1} + {t_2}} \right) = \frac{{{a_1}}}{{{b_1}}}\left( {1 - {e^{{ - {b_1}{t_2}}}}} \right)\,{\hbox{and}}\,S = \frac{{{S_1}}}{{1 - \theta }}} \\\end{array} $$

The total cost for the primary shop is given by

$$ \begin{array}{*{20}{c}} {{\hbox{T}}{{\hbox{C}}_{{1}}} = {\hbox{Purchase}}\,{\hbox{cost}} + {\hbox{Holding}}\,{\hbox{cost}} + {\hbox{shortage}}\,{\hbox{cost}} + {\hbox{Sorting}}\,{\hbox{cost}} + {\hbox{Setup}}\,{\hbox{cost}}} \\{ = {c_0}({Q_1} + S) + {h_1}\int\limits_0^{{{t_1}}} {({q_1}(t)){e^{{ - rt}}}dt + {g_1}\int\limits_{{{t_1}}}^{{{t_1} + {t_2}}} {( - {q_1}(t)){e^{{ - rt}}}dt + k{S^{\beta }} + {\mu_1}} } } \\{ = {C_0}({Q_1} + S){e^{{ - r{t_1}}}} + \frac{{{h_1}{a_1}}}{\alpha }\left[ {\frac{1}{{\left( {\alpha + r} \right)}}\left( {{e^{{\alpha {t_1}}}} - {e^{{ - r{t_1}}}}} \right) - \frac{1}{r}\left( {1 - {e^{{ - r{t_1}}}}} \right)} \right] + \frac{{{g_1}{a_1}}}{{{b_1}}}\frac{{{e^{{ - r{t_1}}}}}}{r}\left[ {\left( {1 - {e^{{ - r{t_2}}}}} \right) - \frac{{{e^{{ - r{t_1}}}}}}{{\left( {{b_1} + r} \right)}}\left( {1 - {e^{{ - \left( {{b_1} + r} \right){t_2}}}}} \right)} \right] + k{S^{\beta }} + {\mu_1}} \\\end{array} $$
(7)

Net revenue cost for the primary shop is given by

$$ N{R_1} = {m_1}{c_0}\left\{ {\frac{{{b_1}}}{\alpha }{Q_1} + \left( {1 - \theta } \right)S + \frac{{{a_1}\theta {t_1}}}{\alpha }} \right\}\left\{ {\frac{1}{R}\left( {1 - {e^{{ - R({t_1} + {t_2}}}}} \right)} \right\} $$
(8)

3.1 Secondary shop

At the time of sale, the defective units are spotted at the primary shop and then transferred to the secondary shop, at t=0, the amount of inventory in this shop at the beginning of the schedule is zero. It is assumed that initially the amount of defective units received from the primary shop is more than sufficient to meet the demand of defective units, i.e. θ q1(t)>D2. So the inventory level is raised at a rate θ q1(t)-D2 and after some time it will be zero, i.e. θ q1(t)=D2 at t=t3, (\( 0 \leqslant {t_3} \leqslant {t_1} \)), (say). Hence, at t=t3, the process of building up of inventory will be stopped and stock attains its maximum level Q2. Thus, one can get t3 from the relation θ q1(t) =D2 as in scenario-1.

$$ {t_3} = {t_1} - \frac{1}{\alpha }\log \left( {1 + \frac{{\alpha {D_2}}}{{{a_1}\theta }}} \right) $$
(9)

After t=t3, the supply from the primary shop is short of the demand for defective units, i.e. θ q1(t)<D2 and than to fulfill the demand, stock decreases at the rate θ q1(t)-D2 units. After some time, this stick reduces to zero. Thus three scenarios arise depending upon the instants at which the stocks at the primary and the secondary shop are depleted completely. In each scenario, total number of selling units at the secondary shop is equal to the number of defective units that are transferred from the primary shop. But, the available defective units S obtained out of the differential stock S may be less than, equal to or greater than the actual shortage S2 in the secondary shop. In these three cases, net revenue NR2 can be written as follows:

$$ N{R_2} = \left\{ {\begin{array}{*{20}{c}} {{m_2}{c_0}\left\{ {\frac{{{b_1}}}{\alpha }{Q_1} + \left( {1 - \theta } \right)S + \frac{{{a_1}\theta {t_1}}}{\alpha }} \right\}\left\{ {\frac{1}{R}\left( {1 - {e^{{ - R({t_1} + {t_2}}}}} \right)} \right\}}{if\quad \theta S \leqslant {S_2}} \\{{m_2}{c_0}\left\{ {\frac{{{b_1}}}{\alpha }{Q_1} + \left( {1 - \theta } \right)S + \frac{{{a_1}\theta {t_1}}}{\alpha }} \right\}\left\{ {\frac{1}{R}\left( {1 - {e^{{ - R({t_1} + {t_2}}}}} \right)} \right\} + m_2^{\prime }{c_0}\left( {\theta S - {S_2}} \right)}{if\quad \theta S \geqslant {S_2}} \\\end{array} } \right. $$
(10)

Where, \( m_2^{\prime }\left( {0 < m_2^{\prime } \ll {m_2}} \right) \) is the pre-determined markup price for the excess amount, as the excess amount is sold immediately at a much reduced price and the secondary shop starts from zero inventory at the beginning of the scheduling period.

3.1.1 Scenario-1

At the secondary shop, when shortages occurs earlier than the occurrence of shortages at the primary shop.

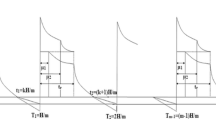
According the assumptions, in this case, the amount of stock is zero initially; the defective units are sold in the adjacent secondary shop. Let the stock Q2 becomes zero at t = t3 + t4 and after that, shortages are allowed. But there will be some gradual decreasing supply of defective units from the primary shop up to t = t1. So during (t3 + t4, t1) shortages increase at the rate and attain shortages level S 12 at t = t1. After t = t1, supply from the primary shop totally stops and shortage increases only due to demand up to t = t1 + t2 when shortage level is S2 (Fig. 2).

Fig. 2
figure 2

Instantaneous state of inventory of scenario-1

Full size image

The differential equations governing the instantaneous state of inventory q2 (t) are

$$ \frac{{d{q_2}(t)}}{{dt}} = \left\{ {\begin{array}{*{20}{c}} {\theta {q_1}(t) - {D_2},} \hfill & {0 \leqslant t \leqslant {t_3}} \hfill & {(11)} \hfill \\{\theta {q_1}(t) - {D_2},} \hfill & {{t_3} \leqslant t \leqslant {t_3} + {t_4}} \hfill & {(12)} \hfill \\{\theta {q_1}(t) - {D_2},} \hfill & {{t_3} + {t_4} \leqslant t \leqslant {t_1}} \hfill & {(13)} \hfill \\{ - {D_2},} \hfill & {{t_1} \leqslant t \leqslant {t_1} + {t_2}} \hfill & {(14)} \hfill \\\end{array} } \right. $$

With the boundary conditions

$$ {q_2}(t) = \left\{ {\begin{array}{*{20}{c}} 0 \hfill & {{\hbox{at}}\,t = 0\,{\hbox{and}}\,t = {t_3} + {t_4}} \hfill \\{{Q_2}} \hfill & {{\hbox{at}}\,t = {t_3}} \hfill \\{ - S_2^{\prime }\,{\hbox{and}} - {S_2},} \hfill & {{\hbox{at}}\,t = {t_1}\,\,{\hbox{and}}\,t = {t_1} + {t_2}} \hfill \\\end{array} } \right. $$

The solution of the differential equation

$$ {q_2}(t) = \left\{ {\begin{array}{*{20}{c}} { - \left\{ {\alpha Y + {D_2}} \right\}t + Y{e^{{\alpha {t_1}}}}\left( {1 - {e^{{ - \alpha t}}}} \right),} \hfill & {0 \leqslant t \leqslant {t_3}} \hfill \\{\left\{ {\alpha Y + {D_2}} \right\}\left( {{t_3} + {t_4} - t} \right) - Y{e^{{\alpha {t_1}}}}\left( {{e^{{ - \alpha t}}} - {e^{{ - \alpha \left( {{t_3} + {t_4}} \right)}}}} \right),} \hfill & {{t_3} \leqslant t \leqslant {t_3} + {t_4}} \hfill \\{ - \left\{ {\alpha Y + {D_2}} \right\}\left( {t - {t_3} - {t_4}} \right) - Y{e^{{\alpha {t_1}}}}\left( {{e^{{ - \alpha t}}} - {e^{{ - \alpha \left( {{t_3} + {t_4}} \right)}}}} \right),} \hfill & {{t_3} + {t_4} \leqslant t \leqslant {t_1}} \hfill \\{ - {S_2} + {D_2}\left( {{t_1} + {t_2} - t} \right),} \hfill & {{t_1} \leqslant t \leqslant {t_1} + {t_2}} \hfill \\\end{array} } \right. $$
(15)

Since q2(t) is continuous at t = t3, one can get an equation related by t3 and t4 as follows:

$$ \left\{ {\alpha Y + {D_2}} \right\}\left( {{t_3} + {t_4}} \right) - Y{e^{{\alpha {t_1}}}}\left( {1 - {e^{{ - \alpha \left( {{t_3} + {t_4}} \right)}}}} \right) = 0,\,{\hbox{where}}\,Y = {a_1}\theta /{\alpha^2}. $$
(16)

Inventory level at t = t3 and the shortage levels at t = t1, t1 + t2 are respectively given by

$$ {Q_2} = - \left\{ {\alpha Y + {D_2}} \right\}{t_3} + Y{e^{{\alpha {t_1}}}}\left( {1 - {e^{{ - \alpha {t_3}}}}} \right) = \left\{ {\alpha Y + {D_2}} \right\}{t_4} + Y{e^{{\alpha \left( {{t_1} - {t_3}} \right)}}}\left( {1 - {e^{{ - \alpha {t_4}}}}} \right) $$
(17)
$$ S_2^{\prime } = \left( {\alpha Y + {D_2}} \right){t_1} - Y\left( {{e^{{\alpha {t_1}}}} - 1} \right) $$
(18)
$$ {S_2} = \left( {\alpha Y + {D_2}} \right){t_1} - Y\left( {{e^{{\alpha {t_1}}}} - 1} \right) + {D_2}{t_2} $$
(19)

The available deteriorated units θS obtained out of the differential stock S may be less than, equal to or greater than the actual shortages S in the secondary shop. In these cases, the relations between t1 and t2 can be written as follows:

  1. Case 1a:

    When S2 = θS, then t1 and t2 are related by

$$ \alpha Y{t_1} + D\left( {{t_1} + {t_2}} \right) - \theta \left( {\frac{{{Q_1}}}{\alpha } + S} \right) = 0 $$
(20)
  1. Case 1b:

    When S2 > θS, then t1, t2 and m2 satisfying the inequation

$$ \alpha Y{t_1} + D\left( {{t_1} + {t_2}} \right) - \theta \left( {\frac{{{Q_1}}}{\alpha } + S} \right) > 0 $$
(21)

With the help of the values \( {S_2} = \left( {\alpha Y + {D_2}} \right){t_1} - Y\left( {{e^{{\alpha {t_1}}}} - 1} \right) + {D_2}{t_2} \) and \( {Q_1} = \frac{{{a_1}}}{\alpha }\left( {{e^{{\alpha {t_1}}}} - 1} \right) \) where \( Y = {a_1}\theta /{\alpha^2} \), we find the above relation.

  1. Case 1c:

    When S2 < θS, then t1, t2 and m2 satisfying the inequation

$$ \alpha Y{t_1} + D\left( {{t_1} + {t_2}} \right) - \theta \left( {\frac{{{Q_1}}}{\alpha } + S} \right) < 0 $$
(22)

Therefore total cost in this scenario is given by

$$ \begin{array}{*{20}{c}} {T{C_2} = {h_2}\left( {\int\limits_0^{{{t_3}}} {{q_2}(t){e^{{ - rt}}}dt + \int\limits_{{{t_3}}}^{{{t_3} + {t_4}}} {{q_2}(t){e^{{ - rt}}}dt} } } \right) + {g_2}\left( {\int\limits_{{{t_3} + {t_4}}}^{{{t_1}}} {\left( { - {q_2}(t)} \right){e^{{ - rt}}}dt + \int\limits_{{{t_1}}}^{{{t_1} + {t_2}}} {\left( { - {q_2}(t)} \right){e^{{ - rt}}}dt} } } \right) + {\mu_2}} \\{T{C_2} = {h_2}\left\{ { - \left( {\alpha Y + {D_2}} \right)\left[ { - \frac{{{t_3}}}{r}{e^{{ - r{t_3}}}} + \frac{1}{{{r^2}}}\left( {1 - {e^{{ - r{t_3}}}}} \right)} \right] + Y{e^{{\alpha {t_1}}}}\left[ {\frac{1}{r}\left( {1 - {e^{{ - r{t_3}}}}} \right) - \frac{1}{{\left( {\alpha + r} \right)}}\left( {1 - {e^{{ - \left( {\alpha + r} \right){t_3}}}}} \right)} \right] + \frac{{\left( {\alpha Y + {D_2}} \right)}}{r}\left( {{t_3} + {t_4}} \right)} \right.} \\{\left( {{e^{{ - r{t_3}}}} - {e^{{ - r\left( {{t_3} + {t_4}} \right)}}}} \right) - \frac{{\left( {\alpha Y + {D_2}} \right)}}{r}\left[ {\left( {{t_3}{e^{{ - r{t_3}}}} - \left( {{t_3} + {t_4}} \right){e^{{ - r\left( {{t_3} + {t_4}} \right)}}}} \right) + \frac{1}{r}\left( {{e^{{ - r{t_3}}}} - {e^{{ - r\left( {{t_3} + {t_4}} \right)}}}} \right)} \right] - \frac{Y}{{\left( {\alpha + r} \right)}}{e^{{\alpha {t_1}}}}\left[ {{e^{{ - \left( {\alpha + r} \right){t_3}}}} - {e^{{ - \left( {\alpha + r} \right)\left( {{t_3} + {t_4}} \right)}}}} \right]} \\{\left. { + \frac{Y}{r}{e^{{\alpha \left( {{t_1} - {t_3} - {t_4}} \right)}}}\left( {{e^{{ - r{t_3}}}} - {e^{{ - r\left( {{t_3} + {t_4}} \right)}}}} \right)} \right\} + {g_2}\left\{ {\left( {\alpha Y + {D_2}} \right)\left\{ {\frac{1}{r}\left[ {\left( {{t_3} + {t_4}} \right){e^{{ - r\left( {{t_3} + {t_4}} \right)}}} - {t_1}{e^{{ - r{t_1}}}}} \right] + \frac{1}{{{r^2}}}\left[ {{e^{{ - r\left( {{t_3} + {t_4}} \right)}}} - {e^{{ - r{t_1}}}}} \right]} \right\} - \frac{{\left( {\alpha Y + {D_2}} \right)}}{r}} \right.} \\{\left( {{t_3} + {t_4}} \right)\left( { - {e^{{ - r{t_1}}}} + {e^{{ - r\left( {{t_3} + {t_4}} \right)}}}} \right) + \left( {\alpha + r} \right)\frac{Y}{r}\left( {{e^{{\alpha {t_1}}}}{e^{{ - \left( {\alpha + r} \right)\left( {{t_3} + {t_4}} \right)}}}} \right.\left. { - {e^{{ - \left( {\alpha + r} \right){t_1}}}}} \right) + \frac{Y}{r}{e^{{\alpha \left( {{t_1} - {t_3} - {t_4}} \right)}}}\left( {{e^{{ - r{t_1}}}} - {e^{{ - r\left( {{t_1} + {t_4}} \right)}}}} \right) + \frac{{\left( {{S_2} - {D_2}\left( {{t_1} + {t_2}} \right)} \right)}}{r}} \\{\left. {\left( {{e^{{ - r{t_1}}}} - {e^{{ - r\left( {{t_1} + {t_2}} \right)}}}} \right) + {D_2}\left\{ {\frac{1}{r}\left[ {{t_1}{e^{{ - r{t_1}}}} - {e^{{ - r\left( {{t_1} + {t_2}} \right)}}}} \right] + \frac{1}{{{r^2}}}\left( {{e^{{ - r{t_1}}}} - {e^{{ - r\left( {{t_1} + {t_2}} \right)}}}} \right)} \right\}} \right\} + {\mu_2}} \\\end{array} $$
(23)

3.1.2 Scenario-2

At both the shops, shortages occur exactly at the same time. Stock is exhausted at t = t1, and then shortages are allowed. As the shortages at both shops occur at the same time, to meet demand of deteriorated units shortages increase at the rate D2 up to t = t1 + t2 when shortage level is S2 (Fig. 3).

Fig. 3
figure 3

Instantaneous state of inventory of scenario-2

Full size image

The differential equations governing the instantaneous state of inventory q2(t) are given by

$$ \frac{{d{q_2}(t)}}{{dt}} = \left\{ {\begin{array}{*{20}{c}} {\theta {q_1}(t) - {D_2},} \hfill & {0 \leqslant t \leqslant {t_3}} \hfill & {(24)} \hfill \\{\theta {q_1}(t) - {D_2},} \hfill & {{t_3} \leqslant t \leqslant {t_1}} \hfill & {(25)} \hfill \\{ - {D_2},} \hfill & {{t_1} \leqslant t \leqslant {t_1} + {t_2}} \hfill & {(26)} \hfill \\\end{array} } \right. $$

With the boundary conditions

$$ \begin{array}{*{20}{c}} {{q_2}(t) = \left\{ {\begin{array}{*{20}{c}} 0 \hfill & {{\hbox{at}}\,t = 0\,{\hbox{and}}\,t = {t_1}} \hfill \\{{Q_2}\,{\hbox{and}} - {S_2},} \hfill & {{\hbox{at}}\,t = {t_3}\,{\hbox{and}}\,t = {t_1} + {t_2}\,{\hbox{respectively}}} \hfill \\\end{array} } \right.} \\{{q_2}(t) = \left\{ {\begin{array}{*{20}{c}} { - \left\{ {\alpha Y + {D_2}} \right\}t + Y{e^{{\alpha {t_1}}}}\left( {1 - {e^{{ - \alpha t}}}} \right),} \hfill & {0 \leqslant t \leqslant {t_3}} \hfill \\{\left\{ {\alpha Y + {D_2}} \right\}\left( {{t_1} - t} \right) + Y{e^{{\alpha {t_1}}}}\left( {1 - {e^{{ - \alpha t}}}} \right),} \hfill & {{t_3} \leqslant t \leqslant {t_1}} \hfill \\{ - {D_2}\left( {t - {t_1}} \right),} \hfill & {{t_1} \leqslant t \leqslant {t_1} + {t_2}} \hfill \\\end{array} } \right.} \\\end{array} $$
(27)

Since q2(t) is continuous at t = t3, one can get t1 from the following equations:

$$ \left\{ {\alpha Y + {D_2}} \right\}{t_1} + Y\left( {{e^{{\alpha {t_1}}}} - 1} \right) = 0 $$
(28)

Inventory level at t=t3 and the shortage level at t=t1+t2 are respectively given by

$$ {Q_2} = - \left\{ {\alpha Y + {D_2}} \right\}{t_3} + Y{e^{{\alpha {t_1}}}}\left( {1 - {e^{{ - \alpha {t_3}}}}} \right) = \left\{ {\alpha Y + {D_2}} \right\}\left( {{t_1} - {t_3}} \right) + Y\left( {1 - {e^{{ - \alpha \left( {{t_1} - {t_3}} \right)}}}} \right) $$
(29)
$$ {{\hbox{S}}_{{2}}} = {{\hbox{D}}_{{2}}}{{\hbox{t}}_{{2}}} $$
(30)
  1. Case (2a):

    When S2 = θS is obtained from-

$$ {D_2}{t_2} - \frac{{{a_1}\theta }}{{{b_1}(1 - \theta )}}\left( {1 - {e^{{{b_1}{t_2}}}}} \right) = 0 $$
(31)
  1. Case (2b): and (2c):

    When S2 > θS or S2 < θS then t2 and m2 satisfying the inequation:

    $$ {D_2}{t_2} - \frac{{{a_1}\theta }}{{{b_1}(1 - \theta )}}\left( {1 - {e^{{{b_1}{t_2}}}}} \right) > 0\,({\hbox{or}}\, < 0) $$
    (32)

One can get the above results directly from the scenario-1 by putting t3+t4=t1 and S2=0.

Therefore the total cost in this scenario is given by

$$ \begin{array}{*{20}{c}} {T{C_2} = {h_2}\left( {\int\limits_0^{{{t_3}}} {{q_2}(t){e^{{ - rt}}}dt + \int\limits_{{{t_3}}}^{{{t_1}}} {{q_2}(t){e^{{ - rt}}}dt} } } \right) + {g_2}\int\limits_{{{t_1}}}^{{{t_1} + {t_2}}} {\left( { - {q_2}(t)} \right){e^{{ - rt}}}dt + {\mu_2}} } \\{T{C_2} = {h_2}\left\{ { - \left( {\alpha Y + {D_2}} \right)\left[ { - \frac{{{t_3}{e^{{ - r{t_3}}}}}}{r} + \frac{1}{{{r^2}}}\left( {1 - {e^{{ - r{t_3}}}}} \right)} \right] + Y{e^{{\alpha {t_1}}}}\left[ {\frac{1}{r}\left( {1 - {e^{{ - r{t_3}}}}} \right) - \frac{1}{{\left( {\alpha + r} \right)}}\left( {1 - {e^{{ - \left( {\alpha + r} \right){t_3}}}}} \right)} \right] + \frac{{\left( {\alpha Y + {D_2}} \right){t_1}}}{r}\left( {{e^{{ - r{t_3}}}} - {e^{{ - r{t_1}}}}} \right)} \right.} \\{\left. { - \left( {\alpha Y + {D_2}} \right)\left[ {\frac{1}{r}\left( {{t_3}{e^{{ - r{t_3}}}} - {t_2}{e^{{ - r{t_1}}}}} \right) + \frac{1}{{{r^2}}}\left( {{e^{{ - r{t_3}}}} - {e^{{ - r{t_1}}}}} \right)} \right] + \frac{Y}{r}\left( {{e^{{ - r{t_3}}}} - {e^{{ - r{t_1}}}}} \right) + \frac{{Y{e^{{\alpha {t_1}}}}}}{{\left( {\alpha + r} \right)}}\left( {{e^{{ - \left( {\alpha + r} \right){t_3}}}} - {e^{{ - \left( {\alpha + r} \right){t_1}}}}} \right)} \right\} + \frac{{{g_2}{D_2}}}{r}\left[ { - \left( {{t_2} - {t_5}} \right)} \right.} \\{{e^{{ - r\left( {{t_1} + {t_2}} \right)}}}\left. { + \frac{1}{r}{e^{{ - r{t_1}}}}\left( {1 - {e^{{ - r{t_2}}}}} \right)} \right] + {\mu_2}} \\\end{array} $$
(33)

3.1.3 Scenario-3

Shortages at the primary shop occur before the occurrence of shortages at the secondary shop. Here the stock is not exhausted at t = t1, through the supply of deteriorated units at t = t1. So, the stock at that time decreases due to demand after t = t1 and becomes zero at t = t1 + t5. Then the shortages at this shop increases at a rate D2 up to t = t1 + t2 when shortages level is S2 (Fig. 4).

Fig. 4
figure 4

Instantaneous state of inventory of scenario-3

Full size image

The differential equations governing the instantaneous state of inventory q2(t) are

$$ \frac{{d{q_2}(t)}}{{dt}} = \left\{ {\begin{array}{*{20}{c}} {\theta {q_1}(t) - {D_2},} \hfill & {0 \leqslant t \leqslant {t_3}} \hfill & {(34)} \hfill \\{} \hfill & {} \hfill & {} \hfill \\{\theta {q_1}(t) - {D_2},} \hfill & {{t_3} \leqslant t \leqslant {t_1}} \hfill & {(35)} \hfill \\{ - {D_2},} \hfill & {{t_1} \leqslant t \leqslant {t_1} + {t_5}} \hfill & {(36)} \hfill \\{ - {D_2},} \hfill & {{t_1} + {t_5} \leqslant t \leqslant {t_1} + {t_2}} \hfill & {(37)} \hfill \\\end{array} } \right. $$

With the boundary conditions

$$ {q_2}(t) = \left\{ {\begin{array}{*{20}{c}} {0,} \hfill & {{\hbox{at}}\,t = 0\,{\hbox{and}}\,t = {t_1} + {t_5}} \hfill \\{{Q_2},\,Q_2^1\,{\hbox{and}} - {S_2},} \hfill & {{\hbox{at}}\,t = {t_3},\,t = {t_1}\,{\hbox{and}}\,t = {t_1} + {t_2}} \hfill \\\end{array} } \right. $$
$$ {q_2}(t) = \left\{ {\begin{array}{*{20}{c}} { - \left\{ {\alpha Y + {D_2}} \right\}t + Y{e^{{\alpha {t_1}}}}\left( {1 - {e^{{ - \alpha t}}}} \right){e^{{\alpha {t_1}}}},} \hfill & {0 \leqslant t \leqslant {t_3}} \hfill & {(38)} \hfill \\{Q_2^{\prime } + \left\{ {\alpha Y + {D_2}} \right\}\left( {{t_1} - t} \right) + Y\left( {1 - {e^{{ - \alpha \left( {{t_1} - t} \right)}}}} \right),} \hfill & {{t_3} \leqslant t \leqslant {t_1}} \hfill & {(39)} \hfill \\{{D_2}({t_1} + {t_5} - t),} \hfill & {{t_1} \leqslant t \leqslant {t_1} + {t_5}} \hfill & {(40)} \hfill \\{ - {D_2}(t - {t_1} - {t_5}),} \hfill & {{t_1} + {t_5} \leqslant {t_1} + {t_2}} \hfill & {(41)} \hfill \\\end{array} } \right. $$

Where \( Q_2^{\prime } = {{\hbox{D}}_{{2}}}\,{{\hbox{t}}_{{5}}} \)..

Using the continuity of q2(t) at t = t3, one can get a relation between t1 and t5 as follows

$$ {D_2}\left( {{t_1} + {t_5}} \right) + \alpha Y{t_1} + Y\left( {1 - {e^{{\alpha {t_1}}}}} \right) = 0 $$
(42)

Inventory level at t = t3 and the shortages level at t = t1 + t2 are respectively given by

$$ {Q_2} = - \left\{ {\alpha Y + {D_2}} \right\}{t_3} + Y{e^{{\alpha {t_1}}}}\left( {1 - {e^{{ - \alpha {t_3}}}}} \right) = {D_2}{t_5} + \left\{ {\alpha Y + {D_2}} \right\}\left( {{t_1} - {t_3}} \right) + Y\left( {1 - {e^{{ - \alpha \left( {{t_1} - {t_3}} \right)}}}} \right) $$
(43)
$$ {{\hbox{S}}_{{2}}} = {{\hbox{D}}_{{2}}}\left( {{{\hbox{t}}_{{2}}}-{{\hbox{t}}_{{5}}}} \right) $$
(44)
  1. Case (3a):

    When S2 = θS, t2 and t5 are related by

$$ {{\hbox{D}}_{{2}}}\left( {{{\hbox{t}}_{{2}}}--{{\hbox{t}}_{{5}}}} \right) - \theta {\hbox{S}} = 0 $$
(45)
  1. Case (3b) or (3c):

    When S2 > θS or S2 < θS then t1, t2 and m2 satisfying

    $$ {D_2}({t_2} - {t_5}) - \theta \,S > 0\,({\hbox{or}}\, < 0) $$
    (46)

Therefore the total cost in this scenario is given by

$$ \begin{array}{*{20}{c}} {T{C_2} = {h_2}\left( {\int\limits_0^{{{t_3}}} {{q_2}(t){e^{{ - rt}}}dt + \int\limits_{{{t_3}}}^{{{t_1}}} {{q_2}(t){e^{{ - rt}}}dt} } + \int\limits_{{{t_1}}}^{{{t_1} + {t_5}}} {{q_2}(t){e^{{ - rt}}}dt} } \right) + {g_2}\int\limits_{{{t_1}}}^{{{t_1} + {t_2}}} {\left( { - {q_2}(t)} \right){e^{{ - rt}}}dt + } {\mu_2}} \\{T{C_2} = {h_2}\left\{ { - \left( {\alpha \gamma + {D_2}} \right)\left[ { - \frac{{{t_3}{e^{{ - r{t_3}}}}}}{r} + \frac{1}{{{r^2}}}\left( {1 - {e^{{ - r{t_3}}}}} \right)} \right] + \gamma {e^{{\alpha {t_1}}}}\left[ {\frac{1}{r}\left( {1 - {e^{{ - r{t_3}}}}} \right) - \frac{1}{{\left( {\alpha + r} \right)}}\left( {1 - {e^{{ - \left( {\alpha + r} \right){t_3}}}}} \right)} \right] + Q_2^1\left( {{t_1} - {t_3}} \right) + \frac{{\left( {\alpha \gamma + {D_2}} \right){t_1}}}{r}\left( {{e^{{ - r{t_3}}}} - {e^{{ - r{t_1}}}}} \right)} \right.} \\{ - \left( {\alpha \gamma + {D_2}} \right)\left[ {\frac{1}{r}\left( {{t_3}{e^{{ - r{t_3}}}} - {t_2}{e^{{ - r{t_1}}}}} \right) + \frac{1}{{{r^2}}}\left( {{e^{{ - r{t_3}}}} - {e^{{ - r{t_1}}}}} \right)} \right] + \frac{\gamma }{r}\left( {{e^{{ - r{t_3}}}} - {e^{{ - r{t_1}}}}} \right) + \frac{{\gamma {e^{{\alpha {t_1}}}}}}{{\left( {\alpha + r} \right)}}\left( {{e^{{ - \left( {\alpha + r} \right){t_3}}}} - {e^{{ - \left( {\alpha + r} \right){t_1}}}}} \right)\left. { + \frac{{{D_2}}}{\gamma }\left[ {\frac{{{e^{{ - r{t_1}}}}}}{r}\left( {{e^{{ - r{t_1}}}} - 1} \right) + {t_5}{e^{{ - r{t_1}}}}} \right]} \right\}} \\{ + \frac{{{g_2}{D_2}}}{r}\left[ { - \left( {{t_2} - {t_5}} \right){e^{{ - r\left( {{t_1} + {t_2}} \right)}}} + \frac{1}{r}{e^{{ - r{t_1}}}}\left( {1 - {e^{{ - r{t_2}}}}} \right)} \right] + {\mu_2}} \\\end{array} $$
(47)

4 Profit for management

If π be the total average profit out of proceeds from both the shops then

$$ \pi = \frac{1}{{{t_1} + {t_2}}}\sum\limits_{{i = 1}}^2 {\left( {N{R_i} - T{C_i}} \right)} $$
(48)

Where net revenue NR1 and the total cost TC1 for the primary shop are given by (8) and (7) respectively. Also, for the secondary shop net revenue NR2 and the total cost TC2 for different scenarios and cases are shown in (10) (23) (33) and (47). Thus nine different problems may arise. Hence, the objective is to maximize the total average profit given by (48) with the appropriate constraints for different scenarios and cases.

4.1 Solution procedure

Generalized reduced gradient (GRG) method

We have used GRG method [13] to find the optimal solution of the problem mentioned earlier. The GRG method is a method for solving problems with linear constraint only. Let us consider the non-linear problems as;

$$ \begin{array}{*{20}{c}} {\hbox{Maximize }} \hfill & {{\hbox{f}}\left( {\hbox{X}} \right)} \hfill \\{{\hbox{Subject}}\,{\hbox{to}}} \hfill & {{{\hbox{h}}_{\rm{j}}}\left( {\hbox{X}} \right) < 0,\,{\hbox{j}} = {1},\,{2} \ldots \,{\hbox{m}}} \hfill \\{} \hfill & {{{\hbox{l}}_{\rm{k}}}\left( {\hbox{X}} \right) = 0,\,{\hbox{k}} = {1},\,{2}, \ldots \ldots {\hbox{l}}} \hfill \\{} \hfill & {{\hbox{X}} = \left[ {{{\hbox{x}}_{{1}}},{{\hbox{x}}_{{2}}} \ldots {{\hbox{x}}_{\rm{n}}}} \right]{\hbox{T}}} \hfill \\{} \hfill & {{{\hbox{x}}_{\rm{i}}} < {{\hbox{x}}_{\rm{i}}} < {{\hbox{x}}_{\rm{i}}},\,{\hbox{i}} = {1},{2}, \ldots ..,{\hbox{n}}.} \hfill \\\end{array} $$

By adding a non-negative slack variable to each of the inequality constraints, the above problem can be reduced to the form,

$$ \begin{array}{*{20}{c}} {\hbox{Maximize}} \hfill & {{\hbox{f}}\left( {\hbox{X}} \right)} \hfill \\{{\hbox{Subject}}\,{\hbox{to}}} \hfill & {{{\hbox{h}}_{\rm{j}}}\left( {\hbox{X}} \right) + {{\hbox{x}}_{{{\rm{i}} + {\rm{j}}}}} = 0,\,{\hbox{j}} = {1},{2}, \ldots .,{\hbox{m}}} \hfill \\{} \hfill & {{{\hbox{l}}_{\rm{k}}}\left( {\hbox{X}} \right) = 0,\,{\hbox{k}} = {1},{2}, \ldots \ldots {\hbox{l}}} \hfill \\{} \hfill & {{{\hbox{x}}_{\rm{i}}} < {{\hbox{x}}_{\rm{i}}} < {{\hbox{x}}_{\rm{i}}},\,{\hbox{i}} = {1},{2}, \ldots ..,{\hbox{n}}.} \hfill \\{} \hfill & {{{\hbox{x}}_{{{\rm{i}} + {\rm{j}}}}} > 0,\,{\hbox{j}} = {1},{2}, \ldots .,{\hbox{m}}} \hfill \\\end{array} $$

with (n + m) variables (x1,x2,…xn,xn+1,…xn+m). The problem can be rewritten in a general form as:

$$ \begin{aligned} {\text{Maximize f}}{\left( {\text{X}} \right)} \\ {\text{Subject to g}}_{{\text{j}}} {\left( {\text{X}} \right)}{\text{ = 0,j = 1,2,}}....{\text{,m + 1}} \\ \quad \,{\text{X = }}{\left[ {{\text{x}}_{{\text{1}}} {\text{,x}}_{{\text{2}}} {\text{,}}...{\text{x}}_{{\text{n}}} {\text{,x}}_{{{\text{n + 1}}}} {\text{,}}...{\text{x}}_{{\text{n}}} {\text{ + }}_{{\text{m}}} } \right]}^{{\text{T}}} \\ \quad {\text{x}}_{{\text{i}}} {\text{ $<$ x}}_{{\text{i}}} {\text{ $<$ x}}_{{\text{i}}} {\text{,i = 1,2,}}.....{\text{,n + m}} \\ \end{aligned} $$

where the lower and upper bounds on the slack variables, xi (i = n+1,n+2,…..,n + m) are taken as zero and a sufficiently large number respectively.

This method is based on the idea of elimination of variables using the equality constraints. Here, (n + m) design variables can be classified into two sets, the first set is of (n-l) design or independent variables and the other set is of (m + l) state or dependent variables and where the design variables are completely independent and the state variables are dependent on the design variables used to satisfy the constraints gj(X) < 0, j=1, 2,…m + l. To determine the search direction, GRG is calculated in terms of above two sets of variables. Geometrically, the reduced gradient can be desired as a projection of the original n-dimensional gradient into the (n-m) dimensional feasible region described by the design variables.

Now, to find the local maximum of the objective along the search direction, any one of the one-dimensional maximization procedures may be used. Here, we have used the quadratic interpolation method for finding the optimal step length.

Now, GRG method is used to optimize the profit functions given by (48) for different scenarios and cases subject to the appropriate constraints. To illustrate it explicitly, the problem of case-1b of scenario-1 can be mathematically written as

$$ \begin{array}{*{20}{c}} {\hbox{Maximize}} \hfill & {\pi \left( {{{\hbox{t}}_{{1}}},\,{{\hbox{t}}_{{2}}},\,{{\hbox{t}}_{{4}}},\,{{\hbox{m}}_{{2}}}} \right)} \hfill \\{\hbox{Subject to}} \hfill & {\left\{ {\alpha Y + {D_2}} \right\}\left( {{t_3} + {t_4}} \right) - Y{e^{{\alpha {t_1}}}}\left( {1 - {e^{{ - \alpha \left( {{t_3} + {t_4}} \right)}}}} \right) = 0} \hfill \\{} \hfill & {\alpha Y{t_1} + D\left( {{t_1} + {t_2}} \right) - \theta \left( {\frac{{{Q_1}}}{\alpha } + S} \right) > 0} \hfill \\\end{array} $$

Here, t1, t2, t4, and m2 are the decision variables and using their optimum values, the optimum order quantity and shortage level at the primary shop and then corresponding quantities at the secondary shop and the optimum selling price of the defective units are obtained.

5 Numerical example

To illustrate the model, we suppose c0 = 1.1, h1 = 1.5, g1 = 2.0, μ1 = 70, h2 = 1.2, g2 = 1.8, μ2 = 35, b1 = 0.15, b2 = 2.50, k = 2, β = 0.40, θ = 0.30, r = 0.2. In addition to the above

Table-1 Different parametric values for different cases

 

Scenario-1

Scenario-2

Scenario-3

a1

75

50

20

a2

32

50

20

m1

7.0

5.5

5.5

m’2

0.12

0.40

0.40

Applying the above solution procedure the computational result shows the following optimal values:

  • Profit for the scenario-1 is 2,223.26.

  • Profit for the scenario-2 is 1,645.26.

  • Profit for the scenario-3 is 608.58.

Table-2 Comparison of policy by varying inflation rate

Inflation rate (r)

Profit for the Scenario-1

Profit for the Scenario-2

Profit for the Scenario-3

0.2

2,223.26

1,645.26

608.58

0.4

1,233.55

1,002.21

346.83

0.6

895.441

750.41

243.42

0.8

718.36

602.17

182.41

1.0

605.144

500.33

140.68

1.2

523.985

425.03

110.05

figure 5

Table-3 Comparison of policy by varying holding cost in primary shop

g1

Profit for the Scenario-1

Profit for the Scenario-2

Profit for the Scenario-3

2.5

2,370.11

1,709.07

635.47

3.0

2,516.97

1,772.89

662.35

3.5

2,663.83

1,836.70

689.24

4.0

2,810.68

1,900.52

716.13

4.5

2,957.54

1,964.33

743.02

5.0

3,104.39

2,028.15

769.91

figure 6

Table-4 Comparison of policy by varying holding cost in secondary shop

g2

Profit for the Scenario-1

Profit for the Scenario-2

Profit for the Scenario-3

2

2,235.17

1,641.07

605.37

4

2,354.29

1,599.21

573.29

6

2,473.40

1,557.34

541.21

8

2,592.52

1,515.48

509.13

figure 7

Sensitivity analysis

The change in the values of parameters may happen due to uncertainties in any decision-making situation. In order to examine the implications of these changes, the sensitivity analysis will be of great help in decision-making. Using the numerical example given in the preceding section, the sensitivity analysis of various parameters has been done. The results of sensitivity analysis are summarized in Table 5. The following inferences can be made.

Table-5 Effects of changing various parameters on the profit

Parameter

Percentage change in the Parameter

Profit for the Scenario-1

Percentage change in the Profit for the Scenario-1

Profit for the Scenario-2

Percentage change in the Profit for the Scenario-2

Profit for the Scenario-3

Percentage change in the Profit for the Scenario-3

c0

−20

1,977.02

−11.07

1,397.88

−15.03

504.03

−17.17

−10

2,100.14

−5.53

1,521.57

−7.51

556.30

−8.58

10

2,346.38

5.53

1,768.94

7.51

660.85

8.59

20

2,469.50

11.07

1,892.63

15.03

713.13

17.17

h1

−20

2,210.12

−0.59

1,639.16

−0.30

607.08

−0.24

−10

2,216.69

−0.29

1,642.21

−0.18

607.83

−0.12

10

2,229.83

0.29

1,648.30

0.18

609.33

0.12

20

2,236.40

0.59

1,651.35

0.37

610.08

0.24

g1

−20

2,105.78

−5.28

1,594.20

−3.10

587.07

−3.53

−10

2,164.52

−2.64

1,619.73

−1.15

597.82

−1.76

10

2,282.00

2.64

1,670.78

1.15

619.33

1.76

20

2,340.74

5.28

1,696.31

3.10

630.09

3.53

h2

−20

2,161.47

−2.77

1,604.67

−2.46

601.17

−1.21

−10

2,192.37

−1.38

1,624.96

−1.23

604.87

−0.60

10

2,254.15

1.38

1,665.55

1.23

612.28

0.60

20

2,285.05

2.77

1,685.84

2.46

615.99

1.21

g2

−20

2,201.82

−0.96

1,652.79

0.45

614.35

0.94

−10

2,212.54

−0.48

1,649.02

0.22

611.47

0.47

10

2,223.98

0.48

1,641.49

−0.22

605.69

−0.47

20

2,244.70

0.96

1,637.72

−0.45

602.80

−0.94

b1

−20

2,296.90

3.31

1,633.37

−0.72

602.09

−1.06

−10

2,251.61

1.27

1,635.48

−0.59

603.69

−0.80

10

2,207.24

−0.70

1,660.62

0.93

615.87

1.19

20

2,200.46

−1.02

1,680.16

2.12

624.96

2.69

b2

−20

2,223.26

0.00

1,645.26

−0.0001

608.58

0.0005

−10

2,223.26

0.00

1,645.26

−0.0001

608.58

0.0005

10

2,223.26

0.00

1,645.26

−0.0001

608.58

0.0005

20

2,223.26

0.00

1,645.26

−0.0001

608.58

0.0005

θ

−20

2,128.06

−4.28

1,578.45

−4.06

577.09

−5.17

−10

2,175.66

−2.14

1,611.86

−2.03

592.84

−2.58

10

2,270.86

2.14

1,678.66

2.02

624.32

2.58

20

2,318.48

4.28

1,712.06

4.06

640.06

5.17

r

−20

2,715.48

22.13

1,948.96

18.45

731.68

20.22

−10

2,442.11

9.84

1,780.87

8.24

663.57

9.03

10

2,044.06

−8.06

1,533.23

−6.80

563.13

−7.46

20

1,894.60

−14.78

1,438.89

−12.54

524.82

−13.76

6 Observations

The main point’s draws from the numerical example are as follow:

  1. 1.

    It is clear from the Table 2; the total profit is fluctuating due to inflation. Total profit decrease as inflation rate r increases in all scenarios because as the inflation rate r increases, the total inventory cost increases. The profit is maximum for the scenario 1. So, it is very important to take consideration of inflation in model otherwise model will not represent the realistic situation.

  2. 2.

    It is clear from the Table 3; changes in the holding cost (g1) for the primary shop do have a significant effect in the total profit. The total profit for the scenario - 1 is more in comparison from the scenario - 2 and 3.

  3. 3.

    It is clear from the Table 4; changes in the holding cost (g2) for the secondary shop do have a significant effect in the total profit. The total profit for the scenario - 1 is more in comparison from the scenario - 2 and 3.

Finally, the profit is maximum for the scenario-1 with respects all the parameters e i. when the shortages in the primary and secondary shop occurs at the same time, then the profit is maximum.

The main point’s draws from the sensitivity analysis are as follow:

  1. 1.

    As the value of unit cost (c0) increases, the total profit in all three scenarios is also increases.

  2. 2.

    As the value of holding cost (h1) for the primary shop increases, the total profit in all three scenarios is also increases.

  3. 3.

    As the value of shortage cost (g1) for the primary shop increases, the total profit in all three scenarios is also increases.

  4. 4.

    As the value of holding cost (h2) for the secondary shop increases, the total profit in all three scenarios is also increases.

  5. 5.

    As the value of shortage cost (g2) for the secondary shop increases, the total profit for the scenarios-1 increases, whereas the total profit for the scenarios-2 and scenario-3 decrease.

  6. 6.

    As the value of (b1) for the primary shop increases, the total profit for the scenarios-1 increases, whereas the total profit for the scenarios-2 and scenario-3 decrease.

  7. 7.

    The effect of changes in b2 on the profit for all the three scenarios is not significant.

  8. 8.

    The total profit in all the three scenarios is highly sensible with respect to θ and the rate of inflation (r). As the value of θ increases, the total profit in all three scenarios is also increase. Whereas total profit decrease with the increase of inflation rate.

7 Conclusion

In this study, a deterministic inventory model has been framed for deteriorating items sold from two shops under one management. The demand rate for the primary shop is stock-dependent and for the secondary shop is price-dependent. In both shops, shortages are allowed and fully backlogged under the effect of inflation. Here, three different scenarios are also presented for the secondary shop. Retailers purchase the items in a lot from wholesalers and sell the fresh and deteriorated ones separately. The main aim is to maximize the retailer’s total inventory profit by considering the effect of inflation. Sensitivity analysis with respect to various parameters has been carried out. With the help of numerical example and sensitivity analysis, we conclude that the profit for the scenario-1 is maximum in comparison of the scenario-2 and 3 i.e., when the shortages in the primary and secondary shop occur at the same time, then the profit is maximum. The total profit in all the three scenarios is highly sensible with respect to the deterioration rate (θ) and the rate of inflation (r). As the value of the deterioration rate (θ) increases, the total profit in all three scenarios is also increase. Whereas total profit decrease with the increase of inflation rate (r). These results are applicable for the products like shoes, ready-made garments, fruits, etc. where the product is not sold immediately. So, the cost of these types of products is affected by inflation and deterioration. The extent to which inflation has affected the business world is clearly elucidated through the sensitivity analysis, where the effect of inflation is visibly shown over the total profit.

A future study should further incorporate the proposed model into more realistic assumptions, such as probabilistic demand, shortages are fully backlogged, deterioration rate with a two-parameter Weibull distribution and the parameters are in fuzzy nature.