An inventory model for non-instantaneous deteriorating items with partial backlogging, permissible delay in payments, inflation- and selling price-dependent demand and customer returns

Abstract

This paper develops an economic ordering policy model for non-instantaneous deteriorating items with selling price- and inflation-induced demand under the effect of inflation, permissible delay in payments and customer returns. Shortages are allowed and partially backlogged. The customer returns are assumed to increase with both the quantity sold and the product price. The main objective is to determine the optimal selling price, the optimal length of time in which there is no inventory shortage, and the optimal replenishment cycle simultaneously, to minimize the present value of the total profit. An efficient algorithm is presented to find the optimal solution of the developed model. Finally, a numerical example is extracted to solve the presented inventory model using the proposed algorithm.

1 Introduction

Recently, many researchers have studied the inventory problems for deteriorating items such as fashionable items, electronics products, fruits, and green vegetables, and many others. Ghare and Schrader (1963) was the first to establish an economic order quantity (EOQ) model for deteriorating items. Afterward, Covert and Philip (1973) extended their work by presenting a variable rate of deterioration. Goyal and Giri (2001) presented a great literature review on deteriorating inventory items. Later, there are many papers presented in the analysis of deteriorating inventory, such as Dye et al. (2007a), Balkhi (2011), Skouri et al. (2011), and Wang and Lin (2012).

In all the above-mentioned models, it is assumed that the items in the inventory start to deteriorate from the instant of their arrival in the stock. However, in practice, an item would have a span of maintaining original state or quality, i.e., there is no deterioration occurring during that period, such as fashionable items, electronics products, fruits, and green vegetables. Wu et al. (2006) introduced the phenomenon as “non-instantaneous deterioration” and developed the optimal replenishment policy for non-instantaneous deteriorating item with stock dependent demand and partial backlogging. For these types of items the assumption that the deterioration starts from the instant of arrival in stock may lead to make an unsuitable replenishment policy due to overstating relevant inventory cost. As a result, it is necessary to consider the inventory models for non-instantaneous deteriorating items.

When the demand depends on the price of an item, the inventory control model should incorporate the selling price as a decision variable. Therefore, Optimal pricing strategy is one of the major policies for sellers or retailers to obtain its maximum profit. Thus, several researchers have studied the pricing and inventory control problem under a variety of conditions, such as Abad (1996, 2001), You (2005), Dye (2007), Dye et al. (2007b), Chang et al. (2006), Shi et al. (2012), Tsao and Sheen (2008), Samadi et al. (2013), and Chao et al. (2014).

In the classical inventory model, it is tacitly assumed that the retailer must pay off from the instant of reception of the items. However, in today’s competitive business environment, the supplier could encourage the retailer to buy more by allowing a certain fixed period for settling the account and there is no charge on the amount owed during this period.

Recently, some researchers have studied the problem of joint pricing and inventory control for non-instantaneously deteriorating items. Ouyang et al. (2006) investigated the inventory model for non-instantaneous deteriorating items considering permissible delay in payments. Yang et al. (2009) considered the optimal pricing and ordering strategies for non-instantaneous deteriorating items with partial backlogging and price dependent demand. Chang et al. (2010) developed the inventory model for non-instantaneous deteriorating items with stock dependent demand. Geetha and Uthayakumar (2010) studied the EOQ inventory model for non-instantaneous deteriorating items with permissible delay in payments and partial backlogging. Musa and Sani (2010) proposed the inventory model for non-instantaneous deteriorating items with permissible delay in payments. Maihami and Nakhai-Kamalabadi (2012) developed the joint pricing and inventory control model for non-instantaneous deteriorating items with price and time dependent demand and partial backlogging.

Since 1975, a series of related papers appeared that considered the effects of time value of money and inflation on the inventory system. Buzacott (1975) was the first to establish EOQ model with inflation subject to different types of pricing policies. Later, there are many papers considered the effects of time value of money and inflation on the inventory system, such as Misra (1979), Park (1986), Datta and Pal (1991), Hall (1992), Goal et al. (1991), Bose et al. (1995), Hariga and Ben-Daya (1996), Horowitz (2000), Sarker and Pan (1994), Moon and Lee (2000), Dye et al. (2007a, b), Mirzazadeh et al. (2009), Sarkar and Moon (2011), Sarkar et al. (2011), Taheri-Tolgari et al. (2012), Wee and Law (2001), Hsieh and Dye (2010), Gholami-Qadikolaei et al. (2013), Ghoreishi et al. (2013a), Ghoreishi et al. (2014), Tripathi et al. (2014) and Guria et al. (2013). Ghoreishi et al. (2013b) studied the optimal pricing and inventory control policy for non-instantaneously deteriorating items with the finite replenishment rate considering time- and price-dependent demand, customer returns and time value of money. Our paper include the following new, more realistic assumptions, when compared with Ghoreishi et al. (2013b) study: (1) In our proposed paper, we discuss the effects of permissible delay in payments, however, in the Ghoreishi et al. (2013b), the effects of permissible delay in payments is not considered. (2) In the Ghoreishi et al. (2013b), shortages are not allowed, but in our presented work, shortages are allowed and partially backlogged. (3) In our current paper, we consider selling price- and inflation-induced demand, but in Ghoreishi et al. (2013b), the demand is function of price and time. (4) Our current work considers infinite replenishment rate, while Ghoreishi et al. (2013b) discussed finite replenishment rate.

Hess and Mayhew (1997) found that the number of returns has a strong positive linear relationship with the quantity sold by using regression models. Anderson et al. (2006) provided evidence to show that customer returns increase with both the quantity sold and the price set for the product. Chen and Bell (2009) showed that customer returns affect the firm’s pricing and inventory policies. In this model, the quantity of returned product is a function of both the quantity sold and the price.

In dealing with these shortcomings above, we investigate an inventory model for non-instantaneous deteriorating items with price- and inflation-dependent demand rate and partial backlogging. The effects of permissible delay in payments, customer returns and time value of money on replenishment policy are also discussed. In the classical inventory model, it is tacitly assumed that the retailer must pay off from the instant of reception of the items. However, in today’s competitive business environment, the supplier could encourage the retailer to buy more by allowing a certain fixed period for settling the account and there is no charge on the amount owed during this period. Also, in the traditional inventory model, it is assumed that the items in the inventory start to deteriorate from the instant of their arrival in the stock. However, in practice, an item would have a span of maintaining original state or quality, i.e., there is no deterioration occurring during that period, such as fashionable items, electronics products, fruits, and green vegetables. Therefore, in order to incorporate realistic conditions, in is necessary to consider inventory problems for non-instantaneous deteriorating items. In addition, today, inflation has become a perpetual feature of the economy and affects the demand of certain products. As inflation increases, the value of money goes down and erodes the future worth of saving and forces one for more current spending. Usually, these spending are on peripherals and luxury items that give rise to demand of these items. Consequently, the effect of inflation and time value of the money cannot be ignored for determining the optimal inventory policy. Moreover, in practice, customer returns increase with both the quantity sold and the product price. Furthermore, when the demand depends on the price of an item, the inventory control model should incorporate the selling price as a decision variable. Therefore, optimal pricing strategy is one of the major policies for sellers or retailers to obtain its maximum profit. Thus, in this work, we develop the problem of simultaneously determining a pricing and inventory replenishment strategy for non-instantaneous deteriorating items with price- and inflation-dependent demand rate, partial backlogging, permissible delay in payments and customer returns. A computational procedure is proposed to derive the optimal selling price, the optimal length of time in which there is no inventory shortage, and the optimal replenishment cycle simultaneously when the present value of total profit is maximized. A numerical example is provided to illustrate the proposed model. The impact of customer returns, inflation, non-instantaneous deterioration, and permissible delay in payments on the optimal solution are also discussed.

To the authors’ best knowledge, nobody considered a pricing and inventory control model with permissible delay in payments, price- and inflation-induced demand, partial backlogging shortage, non-instantaneously deteriorating items, and customer returns. The backlogging rate is variable and dependent on the time of waiting for the next replenishment. The main objective is to determine the optimal selling price, the optimal length of time in which there is no inventory shortage, and the optimal replenishment cycle simultaneously such that the present value of total profit is maximized. This is the first work that follows the above more realistic assumptions.

2 Notation and assumptions

The following notation and assumptions are used throughout the paper:

2.1 Notation

$A$ :

Constant purchasing cost per order,

$c$ :

Purchasing cost per unit,

$c_1$ :

Holding-cost per unit per unit time,

$c_2$ :

Backorder-cost per unit per unit time,

$c_3$ :

Cost of lost sale per unit,

$p$ :

Selling price per unit, where $p>c$ (decision variable),

$\theta$ :

Constant deterioration rate,

$r$ :

Constant representing the difference between the discount (cost of capital) and the inflation rate,

$Q$ :

Order quantity,

$T$ :

Length of replenishment cycle time (decision variable),

$t_1$ :

Length of time in which there is no inventory shortage (decision variable),

$t_{d}$ :

Length of time in which the product exhibits no deterioration,

$SV$ :

Salvage value per unit,

$H$ :

Length of planning horizon,

$N$ :

Number of replenishments during the time horizon $H$,

$T^{*}$ :

Optimal length of the replenishment cycle time,

$Q^{*}$ :

Optimal order quantity,

$t_1^*$ :

Optimal length of time in which there is no inventory shortage,

$p^{*}$ :

Optimal selling price per unit,

$I_1 (t)$ :

Inventory level at time $t\in [0,t_d ]$,

$I_2 (t)$ :

Inventory level at time $t\in [t_d, t_1 ]$,

$I_3 (t)$ :

Inventory level at time $t\in [t_1, T]$,

$I_{0}$ :

Maximum inventory level,

$S$ :

Maximum amount of demand backlogged,

$f(p,t_1,N)$ :

Present value of total profit over the time horizon,

$I_{e}$ :

Interest earned per dollar per unit time,

$I_{p}$ :

Interest charged per dollar per unit time,

$M$ :

Trade-credit period.

2.2 Assumptions

In this paper, the following assumptions are considered:

• 1. There is a constant fraction of the on-hand inventory deteriorates per unit of time and there is no repair or replacement of the deteriorated inventory.

• 2. A single non-instantaneous deteriorating item is assumed.

• 3. The replenishment rate is infinite and the lead time is zero.

• 4. Demand is inflation rate and selling price dependent, i.e., $D(t)=(a-bp)e^{krt}$ (where 0 $< k < 1, a > 0, b > 0$).

• 5. Shortages are allowed. The unsatisfied demand is backlogged, and the fraction of shortage backordered is $\beta \left( x \right) =k_{0} e^{-\delta x}\left( {\delta >0,0<k_0 \le 1} \right)$, where $x$ is the waiting time up to the next replenishment and $\delta$ is a positive constant and $0\le \beta \left( x \right) \le 1,\beta \left( 0 \right) =1 \ [1].$

• 6. Following the empirical findings of Anderson et al. (2006), we assume that customer returns increase with both the quantity sold and the price. We use the general form: $R\left( {p,t} \right) =\alpha D\left( {p,t} \right) +\beta p\left( {\beta \ge 0,0\le \alpha <1} \right)$ that was presented by Chen and Bell (2009). Customers are assumed to return $R\left( {p,t} \right)$ products during the period for full credit and these units are available for resale in the following period. We assume that the salvage value of the product at the end of the last period is SV per unit.

• 7. The time horizon is finite.

3 Model formulation

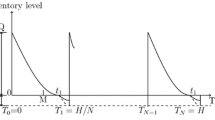
Here, we use the Yang et al.’s (2009) inventory shortage model as follows: $I_{0}$ units of item arrive at the inventory system at the beginning of each cycle. During the time interval [0, $t_{d}$], the inventory level decreases due to demand only. Afterwards, during the time interval [$t_{d}, t_{1}$], the inventory level drops to zero due to both demand and deterioration. Finally, a shortage occurs due to demand and partial backlogging during the time interval [$t_{1}, T$] (see Fig. 1).

Fig. 1

Graphical representation of the inventory system

The equation representing the inventory status in the system for the first interval is derived as follows:

During the time interval [0, $t_{d}$], the differential equation representing the inventory status is given by

$$\begin{aligned} \frac{dI_1 (t)}{dt}=-D\left( t \right) =-(a-bp)e^{krt}. \end{aligned}$$

(1)

With the condition $I_{1}$(0)= $I_{0}$, solving Eq. (1) yields

$$\begin{aligned} I_1 \left( t \right) =\frac{\left( {-a+bp} \right) e^{krt}-bp+I_0 kr+a}{kr} \quad \left( {0\le t\le t_d } \right) . \end{aligned}$$

(2)

In the second interval [$t_{d}, t_{1}$], the inventory level decreases due to demand and deterioration. Thus, the differential equation below represents the inventory status:

$$\begin{aligned} \frac{dI_2 (t)}{dt}+\theta I_2 \left( t \right) =-D\left( t \right) . \end{aligned}$$

(3)

By the condition $I_2 \left( {t_1 } \right) =0$, the solution of Eq. (3) is

$$\begin{aligned} I_2 \left( t \right) =-\frac{\left( {a-bp} \right) (e^{t\left( {kr+\theta } \right) }-e^{t_1 \left( {kr+\theta } \right) })e^{-\theta t}}{kr+\theta }\quad \quad \left( {t_d \le t\le t_1 } \right) . \end{aligned}$$

(4)

It is clear from Fig. 1 that $I_1(t_d) = I_2(t_d)$, therefore, the maximum inventory level $I_{0}$ can be obtained

$$\begin{aligned} \,\,I_0 =\frac{1}{\left( {kr+\theta } \right) kr}\left( {\left( {a-bp} \right) \left( {e^{-\theta t_d }kre^{t_1 \left( {kr+\theta } \right) }-e^{-\theta t_d }kre^{t_d \left( {kr+\theta } \right) }+\left( {-1+e^{krt_d }} \right) \left( {kr+\theta } \right) } \right) } \right) .\nonumber \\ \end{aligned}$$

(5)

In the third interval, $[t_1,T]$, shortage is partially backlogged according to fraction $\beta \cdot (T-t)$. Therefore, the inventory level at time $t$ is obtained by the following equation:

$$\begin{aligned} \frac{dI_3 (t)}{dt}=-D\left( t \right) \cdot \beta \left( {T-t} \right) =\frac{-D(t)}{e^{\delta (T-t)}}\qquad \qquad (t_1 \le t\le T). \end{aligned}$$

(6)

The solution of the above differential equation, after applying the initial value condition $I_3 (t_1 )=0$, is

$$\begin{aligned} I_3 \left( t \right) =-\frac{\left( {a-bp} \right) (e^{\left( {-T+t} \right) \delta +krt}-e^{\left( {kr+\delta } \right) t_1 -\delta T})}{kr+\delta }\quad \left( {t_1 \le t\le T} \right) .\end{aligned}$$

(7)

If we put $t=T$ into $I_3 \left( t \right)$, the maximum amount of demand backlogging ($S)$ will be obtained:

$$\begin{aligned} S=-I_3 \left( T \right) =\frac{\left( {a-bp} \right) (e^{krT}-e^{\left( {kr+\delta } \right) t_1 -\delta T})}{kr+\delta }. \end{aligned}$$

(8)

The order quantity per cycle ($Q)$ is the sum of $S$ and $I_{0}$, i.e.,

$$\begin{aligned} Q&= S+I_0 = \frac{1}{\left( {kr+\theta } \right) kr\left( {kr+\delta } \right) }\left( \left( {a-bp} \right) \left( \left( {-k^{2}r^{2}-\theta kr} \right) e^{\left( {kr+\delta } \right) t_1 -\delta T}\right. \right. \nonumber \\&\quad \left. \left. +\,ke^{-\theta t_d }r\left( {kr+\delta } \right) e^{t_1 \left( {kr+\theta } \right) }-ke^{-\theta t_d }r\left( {kr+\delta } \right) e^{t_d \left( {kr+\theta } \right) }\right. \right. \nonumber \\&\quad \left. \left. +\,\left( {\left( {kr+\delta } \right) e^{krt_d }-kr+kre^{krT}-\delta } \right) \left( {kr+\theta } \right) \right) \right) . \end{aligned}$$

(9)

So far, we derived the equations representing the inventory status. Equations (2) and (4) represent the inventory level when there is no inventory shortage, while Eq. (7) represents inventory level when there is inventory shortage. Therefore, using the above mentioned equations, we can obtain the present value inventory costs and sales revenue for the one cycle, which consists of the following elements:

• 1. Since replenishment in each cycle has been done at the start of each cycle, the present value of replenishment cost for the one cycle will be $A$, which is a constant value.

• 2. Inventory occurs during period $t_{1}$, therefore, the present value of holding cost (HC) for the one cycle is

  $$\begin{aligned} HC=c_1 \left( {\int _0^{t_d } I_1 \left( t \right) \cdot e^{-r\cdot t}dt+e^{-r\cdot t_d }\int _{t_d }^{t_1 } I_2 \left( t \right) \cdot e^{-r\cdot t}dt} \right) . \end{aligned}$$

  (10)

• 3. The present value of shortage cost (SC) due to backlog for the one cycle is

  $$\begin{aligned} SC=c_2 \left( {e^{-r\cdot t_1 }\int _{t_1 }^T -I_3 (t)\cdot e^{-r\cdot t}dt} \right) . \end{aligned}$$

  (11)

• 4. The present value of opportunity cost due to lost sales (OC) for the one cycle is

  $$\begin{aligned} OC=c_3 \left( {e^{-r\cdot t_1 }\int _{t_1 }^T D\left( t \right) (1-\beta \cdot \left( {T-t} \right) )\cdot e^{-r\cdot t}dt} \right) . \end{aligned}$$

  (12)

• 5. The present value of purchase cost (PC) for the one cycle is

  $$\begin{aligned} PC=c\left( {I_0 +Se^{-r\cdot T}} \right) . \end{aligned}$$

  (13)

• 6. The present value of return cost for each cycle. We assume that returns from period $i-1$ are available for resale at the beginning of period $i$ (except of the first period in which there is no cycle previous to it). It is also assumed that the salvage value of the product at the end of the last period ($i=N$) is SV. Therefore, the present value of return cost and resale revenue for each cycle is obtained as follows:

  $$\begin{aligned} RC_i =\left\{ {{\begin{array}{ll} p\displaystyle \int _0^{t_1 } \left( {\alpha D\left( t \right) +\beta p} \right) e^{-r\cdot t}dt, &{} \quad \hbox {for}\;\; i=1, \\ RC=p\displaystyle \int _0^{t_1 } \left( {\alpha D\left( t \right) +\beta p} \right) e^{-r\cdot t}dt\,-\,c\int _0^{t_1 } \left( {\alpha D( t)+\beta p} \right) dt, &{} \\ &{} \quad {\hbox {for}\;\; i=2,3,\ldots ,N-1,} \\ p\displaystyle \int _0^{t_1 } \!\!\left( {\alpha D\left( t \right) \!+\!\beta p} \right) e^{-r\cdot t}dt \!-\!c\int _0^{t_1 }\!\! \left( {\alpha D\left( t \right) \!+\!\beta p} \right) dt\!-\!SVe^{-r\cdot T}\int _0^{t_1 } \!\!\left( {\alpha D\left( t \right) \!+\!\beta p} \right) dt,&{} \\ \qquad &{} \quad {\hbox {for}\;\; i=N.} \end{array}}} \right. \nonumber \\ \end{aligned}$$

  (14)

• 7. The present value of sales revenue (SR) for the one cycle is

  $$\begin{aligned} SR=p\left( {\int _0^{t_1 } D(t)\cdot e^{-r\cdot t}dt+S\cdot e^{-r\cdot T}} \right) . \end{aligned}$$

  (15)

• 8. The present value of interest payable for the one cycle. For each cycle, we need to consider cases where the length of the credit period is longer or shorter than the length of time in which the product exhibits no deterioration ($t_{d})$ and the length of time in which there is no inventory shortage ($t_{1})$. Thus, we calculate the present value of interest payable for the items kept in stock under the following three cases.

Case 1

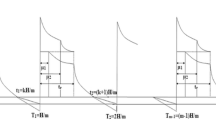
The delay time of payments occurs before deteriorating time or 0 $< M \le t_{d}$ (see Fig. 2).

In this case, payment for items is settled and the retailer starts paying the interest charged for all unsold items in inventory with rate $I_{p}$. Thus, the present value of interest payable for the one cycle is given by

$$\begin{aligned} IP_1 =cI_p \left[ {e^{-r\cdot M}\int _M^{t_d } I_1 \left( t \right) \cdot e^{-r\cdot t}dt+e^{-r\cdot t_d }\int _{t_d }^{t_1 } I_2 \left( t \right) \cdot e^{-r\cdot t}dt} \right] . \end{aligned}$$

(16)

Fig. 2

$0 < M \le t_{d}$ (Case 1: the delay time of payments occurs before the the deteriorating time)

Case 2

The delay time of payments occurs after deteriorating time and before the length of time in which there is no inventory shortage; i.e., $t_{d} < M \le t_{1}$ (see Fig. 3).

Fig. 3

$t_{d} < M \le t_{1 }$ (Case 2: the delay time of payments occurs after the deteriorating time and before the production period time)

The conditions of this case are similar to those for Case 1. Thus, the present value of interest payable for the one cycle is given below:

$$\begin{aligned} IP_2 =cI_p \left[ {e^{-r\cdot M}\int _M^{t_1 } I_2 \left( t \right) \cdot e^{-r\cdot t}dt} \right] . \end{aligned}$$

(17)

Case 3

The delay time of payments occurs after the length of time in which there is no inventory shortage and before the duration of inventory cycle or $t_{1} < M \le T$ (see Fig. 4).

Fig. 4

$t_{1} < M \le T$ (Case 3: the delay time of payments occurs after the production period time and before the duration of inventory cycle)

In this case there is no opportunity cost. Therefore, $IP_3 =0$.

• 9. The present value of interest earned for the one cycle.

There are different ways to tackle the interest earned. Here, we use the approach used in Geetha and Uthayakumar (2010). We assume that during the time when the account is not settled, the retailer sells the goods and continues to accumulate sales revenue and earns interest with rate $I_{e}$. Therefore, the present value of the interest earned for the one cycle is as given below for the three different cases.

Case 1

The delay time of payments occurs before the deteriorating time or $0 < M \le t_{d}$:

$$\begin{aligned} IE _1 =pI_e \int _0^M t\cdot D\left( {p,t} \right) \cdot e^{-r\cdot t}dt. \end{aligned}$$

(18)

Case 2

The delay time of payments occurs after the deteriorating time and before the production period time; i.e., $t_{d} < M \le t_{1}$:

$$\begin{aligned} IE _2 =pI_e \int _0^M t\cdot D\left( {p,t} \right) \cdot e^{-r\cdot t}dt. \end{aligned}$$

(19)

Case 3

The delay time of payments occurs after the production period time and before the duration of inventory cycle or $t_{1} < M \le T$:

$$\begin{aligned} IE _3 =pI_e \left[ {\int _0^{t_1 } t\cdot D\left( {p,t} \right) \cdot e^{-r\cdot t}dt+(M-t_1 )\int _0^{t_1 } D(p,t)\cdot e^{-r\cdot t}dt} \right] . \end{aligned}$$

(20)

There are $N$ cycles during the planning horizon. Since inventory is assumed to start and end at zero, an extra replenishment at $t=H$ is required to satisfy the backorders of the last cycle in the planning horizon. Therefore, the total number of replenishment will be $N+1$ times; the first replenishment lot size is $I_{0}$, and the 2nd, 3rd, ..., $N$th replenishment lot size is as follows:

$$\begin{aligned} Q=S+I_0. \end{aligned}$$

Finally, the last or ($N+1$)th replenishment lot size is $S$. Therefore, the present value of total profit during the planning horizon, denoted by $f(p,t_1,N)$, is derived as follows:

which we want to maximize subject to the following constraints:

$$\begin{aligned} p>0,0<t_1 <T,\, N\in \mathbb {N}. \end{aligned}$$

The value of the variable $T$ can be replaced by the equation $T=H/N$, for some constant $H>0$, and we will use the geometric series formula for the following explanation: $\mathop \sum \nolimits _{i=0}^{N-1} e^{-r\cdot i\cdot T}=(1-e^{-r\cdot N\cdot T})/(1-e^{-r\cdot T})$. Thus, the objective of this paper is to determine the values of $t_1, p$ and $N$ that maximize $f(p,t_1,N)$ subject to $p>0$ and $0<t_1 <T$, where $N$ is a discrete variable and $p$ and $t_1$ are continuous variables. However, since $f\left( {p,t_1,N} \right)$ is a very complicated function due to high-power expressions in the exponential function, it is difficult to show analytically the validity of the sufficient optimality conditions. Hence, if more than one local maximum exists, we would attain the largest of the local maximum values over the regions subject to $p>0$ and $0<t_1 <T$. The largest value is referred to as the global maximum value of $f\left( {p,t_1,N} \right)$. So far, the procedure is to locate the optimal values of $p$ and $t_1$ when $N$ is fixed. Since $N$ is a discrete variable, the following approximate algorithm can be used to determine the optimal values of $p, t_1$ and $N$.

4 The optimal solution procedure

The objective function has three variables. The number of production cycles ($N)$ is a discrete variable, the production period in an inventory cycle ($t_{1})$ and the selling price per unit ($p)$ are continuous variables. We use the algorithm for Case 1, 0 $< M \le t_{d}$, to obtain the optimal amount of $t_{1}, p$ and $N$. One can develop this algorithm for Cases 2 and 3.

The proposed algorithm has two parts. In the first part, for simplicity, we solve our model without constraints and then we can use the following algorithm, where, without loss of generality, we focus on $f_1$ rather than $f_2$ or $f_3$:

Step 1-1 Let $N=1$.

Step 1-2 Take the partial derivatives of $f_1 \left( {p,t_1,N} \right)$ with respect to $p$ and $t_1$, and equate the results to zero, the necessary conditions for optimality are

$$\begin{aligned} \frac{\partial }{\partial p}f_1 \left( {p,t_1,N} \right) =0 \end{aligned}$$

(22)

and

$$\begin{aligned} \frac{\partial }{\partial t_p }f_1 \left( {p,t_1,N} \right) =0. \end{aligned}$$

(23)

In “Appendix”, we use the formula of $f_1 \left( {p,t_1,N} \right)$ from Eq. (21a), inserted into Eqs. (22) and (23).

Step 1-3 For given values of $N$, derive $t_1^*$ and $p^{*}$ from Eqs. (22) and (23). Substitute $(p^{*},t_1^{*},N)$ into $f_1 \left( {p,t_1,N} \right)$ from Eq. (21a) to derive $f_1 (p^{*},t_1^{*},N)$.

Step 1-4 Add one unit to $N$ and repeat Steps 1-2 and 1-3 for the new $N$ until the maximum $f_1 \left( {p^{*},t_1^{*},N^{*}} \right)$ is found.

The point $(p^{*},t_1^{*},N^{*})$ and the value $f_1 (p^{*},t_1^{*},N^{*})$ constitute the optimal solution and satisfy the following conditions:

$$\begin{aligned} \Delta f_1 \left( {p^{*},t_1^{*},N^{*}} \right) <0<\Delta f_1 \left( {p^{*},t_1^*,N^{*}-1} \right) , \end{aligned}$$

(24)

where

$$\begin{aligned} \Delta f_1 \left( {p^{*},t_1^*,N^{*}} \right) =f_1 \left( {p^{*},t_1^*,N^{*}+1} \right) -f_1 \left( {p^{*},t_{1}^*,N^{*}} \right) . \end{aligned}$$

(25)

We substitute $(p^{*},t_1^*,N^{*})$ into Eq. (9) to derive the $N$th replenishment lot size.

If the objective function was strictly concave, the following sufficient conditions should be satisfied:

$$\begin{aligned} \left( {\frac{\partial ^{2}f_1 }{\partial p\partial t_1 }} \right) ^{2}-\left( {\frac{\partial ^{2}f_1 }{\partial t_1^2 }} \right) \left( {\frac{\partial ^{2}f_1 }{\partial p^{2}}} \right) <0, \end{aligned}$$

(26)

and anyone of the following conditions:

$$\begin{aligned} \frac{\partial ^{2}f_1 }{\partial t_1^2 }<0,\quad \frac{\partial ^{2}f_1 }{\partial p^{2}}<0. \end{aligned}$$

(27)

It is difficult to show the validity of the above sufficient conditions analytically, due to involvement of a high-power expression of the exponential function. However, in most practical cases it can be assessed numerically.

Step 1-5 Check whether the optimal solution satisfies all constraints. If at least one of the constraints is not satisfied, then use the second part of the algorithm.

In the second part of the algorithm, the model is solved using Lagrange multiplier method. Therefore, the Lagrange function will be as follows:

$$\begin{aligned} L\left( {p,t_1 ,\lambda _1 ,\lambda _2 ,\lambda _3 ,N} \right) =f_1 \left( {p,t_1 ,N} \right) +\lambda _1 p+\lambda _2 t_1 +\lambda _3 \left( {T-t_1 } \right) . \end{aligned}$$

(28)

In the real world, this situation would rarely occur. However, for the sake of theoretical clarity, we will discuss this situation in the following second part of the algorithm for the above unconstrained function:

Step 2-1 Let $N=1$.

Step 2-2 Take the partial derivatives of $L\left( {p,t_1 ,\lambda _1 ,\lambda _2 ,\lambda _3 ,N} \right)$ with respect to $p, t_1 , \lambda _1 ,\lambda _2$ and $\lambda _3$ and equate the results to zero, the necessary conditions for optimality are

$$\begin{aligned}&\frac{\partial }{\partial p}L\left( {p,t_1 ,\lambda _1 ,\lambda _2 ,\lambda _3 ,N} \right) =0,\end{aligned}$$

(29)

$$\begin{aligned}&\frac{\partial }{\partial t_p }L\left( {p,t_1 ,\lambda _1 ,\lambda _2 ,\lambda _3 ,N} \right) =0,\end{aligned}$$

(30)

$$\begin{aligned}&\frac{\partial }{\partial \lambda _1 }L\left( {p,t_1 ,\lambda _1 ,\lambda _2 ,\lambda _3 ,N} \right) =0,\end{aligned}$$

(31)

$$\begin{aligned}&\frac{\partial }{\partial \lambda _2 }L\left( {p,t_1 ,\lambda _1 ,\lambda _2 ,\lambda _3 ,N} \right) =0 \end{aligned}$$

(32)

and

$$\begin{aligned} \frac{\partial }{\partial \lambda _3}L\left( {p,t_1 ,\lambda _1 ,\lambda _2 ,\lambda _3 ,N} \right) =0. \end{aligned}$$

(33)

Step 2-3 For given values of $N$, derive $p^{*},t_1^*, \lambda _1^*,\lambda _2^*$ and $\lambda _3^*$ from Eqs. (29)–(33). Substitute $(p^{*},t_1^*, \lambda _1^*,\lambda _2^*, \lambda _3^*,N)$ into $L\left( {p,t_1 ,\lambda _1 ,\lambda _2,\lambda _3 ,N} \right)$ from Eq. (28) to derive $L(p^{*},t_1^*, \lambda _1^*,\lambda _2^*, \lambda _3^*,N)$.

Step 2-4 Add one unit to $N$ and repeat Steps 2-2 and 2-3 for the new $N$ until the maximum $L(p^{*},t_1^*, \lambda _1^*,\lambda _2^*, \lambda _3^*,N^{*})$ is found.

The point $(p^{*},t_1^*, \lambda _1^*,\lambda _2^*, \lambda _3^*,N^{*})$ and the value $L(p^{*},t_1^*, \lambda _1^*,\lambda _2^*, \lambda _3^*,N^{*})$ constitute the optimal solution and satisfy the following conditions:

$$\begin{aligned} \Delta L\left( {p^{*},t_1^*,\lambda _1^*,\lambda _2^*,\lambda _3^*,N^{*}} \right) <0<\Delta L\left( {p^{*},t_1^*,\lambda _1^*,\lambda _2^*,\lambda _3^*,N^{*}-1} \right) , \end{aligned}$$

(34)

where

$$\begin{aligned} \Delta L\left( {p^{*},t_1^*,\lambda _1^*,\lambda _2^*,\lambda _3^*,N^{*}} \right)&= L\left( {p^{*},t_1^*,\lambda _1^*,\lambda _2^*,\lambda _3^*,N^{*}+1} \right) \nonumber \\&\quad -\,L\left( {p^{*},t_{1}^*,\lambda _1^*,\lambda _2^*,\lambda _3^*,N^{*}} \right) . \end{aligned}$$

(35)

We substitute $(p^{*},t_1^*,N^{*})$ into Eq. (9) to derive the $N$th replenishment lot size.

If the objective function was strictly concave, the Hessian matrix at the stationary point $\left( {p^{*},t_1^*,\lambda _1^*,\lambda _2^*,\lambda _3^*,N^{*}} \right)$ should be negative definite.

5 A numerical example

To illustrate the solution procedure and the results, let us apply the proposed algorithm to solve the following numerical example. The results can be found by using Maple 13. This example is based on the following parameters and functions:

$c = \$10$ per unit, $c_{1 }= \$1$ per unit/per unite time, $c_{2 }= \$5$ per unit/per unite time, $c_{3 }= \$25$ per unit, $t_{d }= 0.08$ unit time, $A = \$250$ per order run, $\theta = 0.08, r = 0.12, \delta = 0.1, H = 40$ unit time, $\alpha = 0.2, \beta = 0.3, SV = \$3$ per unit, $a = 200, b = 4, k = 0.03, M = 0.01$ unit time, $I_{p}= 0.15/{\$}$ per unit time, $I_{e }$= 0.12/$ per unit time.

From Table 1, the maximum present value of total profit is found in 40th cycle. The total number of order therefore is $N+1$ or 41. With 41 orders, the optimal solution is as follows:

$$\begin{aligned} p^{*}=30.357, \quad t_1^*=0.288,\quad T^{*}=1.000,\quad f_1^*=7901.628,\quad Q^{*}=76.897. \end{aligned}$$

It is observed that all constraints are satisfied, and as a result, it is not required to use the second part of the algorithm. In practice, it could be expected to solve most problems just by the first part of the algorithm.

Table 1 Optimal solution of the example

By substituting the optimal values of $N^{*}, p^{*}$ and $t_1^*$ into Eq. (27), it will be shown that $f_{1}$ is strictly concave (see Fig. 5 for an illustration):

$$\begin{aligned} \frac{\partial ^{2}f_1 }{\partial t_1^2 }=-10{,}209.452, \quad \frac{\partial ^{2}f_1 }{\partial p^{2}}=-60.255. \end{aligned}$$

Fig. 5

The graphical representation of the concavity of the present value of total profit function $f_1 \left( {p,t_1,40} \right)$ which optimal value is derived from Table 1

From Table 2 it is observed that when the returns only depended on the quantity sold (i.e., $\beta = 0$), the price increases and the order quantity decreases, but if the returns are dependent on the price only (i.e., $\alpha =0$), the price goes down and the order quantity increases. The results verify that when returns increase with the product price (when purchase costs are constant), the firm should set a lower price (in order to discourage returns). Increasing $\alpha$ and/or $\beta$ reduces the firm’s profit.

Table 2 The impact of customer returns on the optimal solution of the example which optimal solution is derived from Table 1

The numerical results of the Table 3 are summarized in Fig. 6a–c.

Fig. 6

The numerical results of the Table 3 which include the impact of the discount rate of inflation $(r)$ on the optimal solution of the Example. a Impact of $r$ on optimal cycle time. b Impact of $r$ on optimal order quantity. c Impact of $r$ on optimal present value of total profit

Table 3 The impact of the discount rate of inflation on the optimal solution of the Example which optimal solution is derived from Table 1

Moreover, as it can be seen in Table 3, when the net discount rate of inflation ($r$) decreases, then, the optimal order quantity, the optimal cycle time, and the optimal present value of total profit increase. Thus, the results confirm that when the discount rate of inflation decreases, the purchasing power will be raised, which will lead to an enhancement in order quantity. As a result, it is important to consider the effects of inflation and the time value of money on inventory policy.

Also, If $t_{d}= 0$, the model convert to the instantaneous deterioration items case, and the optimal present value of total profit can be found as follows: $f_1^*= 7{,}749.093$. It can be seen that the optimal present value of total profit in the instantaneous deterioration items case decreases. This implies that the optimal present value of total profit could be increased by changing the instantaneously to non-instantaneously items using the improved stock condition.

In addition, when the supplier does not provide a credit period (i.e., $M = 0$), the optimal present value of retailer total profit and cycle time can be found as follows: $f_1^*=7{,}892.824$. It can be seen that the optimal present value of total profit decreases. Thus, retailers should try to get credit periods for their payments if they wish to increase their profit.

6 Conclusion and outlook

In this paper, we consider the effects of permissible delay in payments, inflation and customer returns on joint pricing and inventory control model for non-instantaneous deteriorating items with inflation- and selling price-dependent demand and partial backlogging. The backlogging rate is variable and dependent on the time of waiting for the next replenishment. The customer returns are assumed as a function of price and demand simultaneously. The mathematical models are derived to determine the optimal selling price and replenishment policy. An optimization algorithm is presented to derive the optimal decision variables. Finally, a numerical example is solved and the effects of the customer returns, inflation, non-instantaneous deterioration, and delay in payments are also discussed.

From Table 2 it can be observed that when the customer returns depend on the quantity of product sold only (i.e., $\beta = 0$), the price increases and order quantity decreases. On the other hand, when the customer returns increase with price only (i.e., $\alpha =0$), the price reduces and the order quantity increases. Also, observed in Table 3, it can be seen that there is an improvement in the optimal cycle time, optimal order quantity, and in the optimal present value of total profit when the discount rate of inflation decreases. Moreover, from Table 4 it can be observed that the optimal present value of total profit in the instantaneous deterioration items case decreases. In addition, the results show that when a delay in payments is allowed, the optimal present value of the total profit for the retailer does enhance. Thus, retailers should try to get credit periods for their payments if they wish to increase their profit.

Table 4 The results of the example with instantaneous and non-instantaneous deteriorating models

Our model could be implemented in engineering and management sciences, business administration, financing and economics.

To the best of our knowledge, this is the first model in pricing and inventory control models that consider permissible delay in payments, inflation- and selling price-dependent demand rate, partial backlogging, and customer returns for non-instantaneously deteriorating items. The proposed model can be further extended in several ways. For example, we could incorporate: (i) stochastic demand function, (ii) two warehouse, (iii) quantity discount, (iv) stochastic inflation (v) two-level trade credit or trade credit linked to order quantity and (vi) deteriorating cost. In addition, we consider to extend our model which consists of ordinary differential equations to the presence of random fluctuation as included by a system of stochastic differential equations, and solve our optimization problem within such a new setting. Finally, a detailed complexity investigation of our research, in terms of class identification and complexity reductions, may be conducted in future. In fact, we could consider methods of nonlinear mixed-integer programming, and look for a priori information, e.g., on data structures, identifying the problem in the classes $P$ or NP, or as NP complete even, and for conditions under which complexity can be diminished in our study.

Appendix

For a given value of $N$, the necessary optimality conditions for finding the optimal values $p^{*}$ and $t_1^*$ are given as follows and were implemented by us:

$$\begin{aligned}&\frac{\partial }{\partial p}f_1 \left( {p,t_1 ,T}\right) =((bkr^{2}c_3 e^{-rt_1 }(r+\theta )(k-1)(kr+\theta )(kr+\delta )e^{\left( {\delta +\left( {k-1} \right) r} \right) t_1 -\delta T} \\&\quad +\,bkr^{2}c_1 e^{-rt_d }\left( {k-1} \right) \left( {kr+\delta } \right) \left( {-r+kr+\delta } \right) e^{t_1 \left( {kr+\theta } \right) -t_d \left( {r+\theta } \right) } \\&\quad -\,\left( {kr+\theta } \right) \left( {-r+kr+\delta } \right) \left( {k-1} \right) \left( b( {( {e^{-rt_1 }}))^{2}c_2 -c_2 e^{-rt_1 }be^{-rT}+r\left( {\left( {c-2p} \right) b+a} \right) e^{-rT}} \right) \\&\qquad r\left( {r+\theta } \right) ke^{\left( {kr+\delta } \right) t_1 -\delta T}- bkrc_{2} e^{-rt_1 }\left( {r+\theta } \right) \left( {k-1} \right) \left( {kr+\theta } \right) \left( {-e^{-rt_1 }+e^{-rT}} \right) \\&\qquad \left( {-r+kr+\delta } \right) e^{\left( {-T+t} \right) \delta +krt} + bkre^{-t_d \left( {r+\theta } \right) }c_1 \left( {k-1} \right) \left( {kr+\delta } \right) \left( {-r+kr+\delta } \right) \left( {r+\theta } \right) \\&\qquad e^{t_1 \left( {kr+\theta } \right) +rt_d }+ b\theta e^{-t_d \left( {r+\theta } \right) }c_1 (k-1)\left( {kr+\delta } \right) \left( {-r+kr+\delta } \right) \left( {r+\theta } \right) e^{\left( {\left( {1+k} \right) r+\theta } \right) t_d} \\&\qquad bkr\left( {k-1} \right) \left( {kr+\delta } \right) \left( {-r+kr+\delta } \right) \left( {r+\theta } \right) \left( {e^{-\theta t_d }cr-e^{-t_d \left( {r+\theta } \right) }c_1 } \right) e^{t_1 \left( {kr+\theta } \right) } \\&\quad -\,\left( {c_1 \left( {r+\theta } \right) e^{-t_d \left( {r+\theta } \right) }+ ce^{-\theta t_d }r^{2}(k-1}) \right) b\left( {-r+kr+\delta } \right) \left( {r+\theta } \right) k\left( {kr+\delta } \right) \\&\qquad e^{t_d \left( {kr+\theta } \right) } + \left( {kr+\theta } \right) \left( {-r+kr+\delta } \right) rk(-bc_3 \left( {r+\theta } \right) e^{-rt_1 }-e^{-rt_d }bc_1 \\&\quad +\,\left( {r+\theta } \right) \left( {-2bp+a} \right) \left( {kr+\delta } \right) e^{rt_1 \left( {k-1} \right) }+ (bkrc_1 e^{-rt_d }\left( {kr+\delta } \right) \left( {-r+kr+\delta } \right) e^{rt_d \left( {k-11} \right) } \end{aligned}$$

$$\begin{aligned}&\quad +\,kr + \theta )(bc_1 e^{t_d \left( {r+\theta } \right) }\left( {kr+\delta } \right) \left( {-r+kr+\delta } \right) e^{-t_d \left( {r+\theta } \right) } + r(bkc_3 e^{-rt_1 }\delta \left( {kr+\delta } \right) e^{rT\left( {k-1} \right) } \\&\quad +\,(-r+kr + \delta )(\left( {kr+\delta } \right) k\left( -\alpha \left( {-2bp+a} \right) e^{krt_1 }+\left( {-2\beta pk-2\alpha bp+2\beta p+\alpha a} \right) e^{rt_1 }\right. \\&\quad +\,2p\beta ( {k-1} ) \Big )e^{-rt_1 } - bc\alpha \left( {k-1} \right) \left( {kr+\delta } \right) e^{krt_1 } + r\left( {\left( {c-2p} \right) b+a} \right) ke^{krT}\left( {k-1} \right) e^{-rT} \\&\quad -\,\left( {-bc\left( {k-1} \right) e^{krt_d }-\beta t_1 crk^{2}+\left( {\beta t_1 cr+\left( {-2p+c-c\alpha } \right) b+a} \right) k+bc\left( {-1+\alpha } \right) } \right) \\&\qquad \left( {kr+\delta } \right) ))))(r+\theta ))(-1+e^{-rH})/\left( (kr+\theta )(k-1)r^{2}(kr+\delta )k(r+\theta )(-r+kr+\delta )\right. \\&\qquad \left. (-1+e^{-\frac{rH}{N}}))+ \frac{SVe^{-rH}\left( {\alpha b-\alpha be^{krt_1 }+\beta t_1 kr} \right) }{kr}+\frac{c(-\beta t_1 kr+\alpha be^{krt_1 }-\alpha b}{kr}\right) \\&\quad +\,\frac{1}{r\left( {r+\theta } \right) \left( {-1+e^{-\frac{rH}{N}}} \right) }\left( I_p c\left( {a-bp} \right) \left( {-1+e^{-rH}} \right) \left( e^{-rM}\left( {e^{\left( {kr+\theta } \right) t_1 +rM}-e^{\left( {kr+\theta } \right) t_1 +rt_d }} \right) \right. \right. \\&\qquad \left( {r+\theta }\right) e^{\left( {-r-\theta } \right) t_d -rM} \left. \left. +re^{-rt_d }\left( {-e^{\left( {kr+\theta } \right) t_1 -\left( {r+\theta } \right) t_d }+e^{rt_1 \left( {k-1} \right) }} \right) \right) \right) =0 \end{aligned}$$

and

$$\begin{aligned}&\frac{\partial }{\partial t_1 }f_1 ( {p,t_1,T} )=(-(k-1)( {r+\theta } )e^{-rt_1 }r( {a-bp} )( {-1+e^{-rH}} )( {( {-2+k} )r+\delta } )( {kr+\delta } )\\&\qquad c_3 e^{( {\delta +(k-1)r} )t_1 -\delta T}-(k-1)r(\delta +(k-1)r)(a-bp)c_1 (-1+e^{-rH})(kr+\delta )e^{-rt_d } \\&\qquad e^{t_1 ( {kr+\theta } )-t_d ( {r+\theta } )}+ (k-1)(( {( {-2+k} )r+\delta } )c_2 ( ( e^{-rt_1 } ))^{2}-e^{-rT}( {\delta +(k-1)r} )c_2 e^{-rt_1 } \\&\quad +\,e^{-rT}r( {kr+\delta } )( {c-p} ) ) ({r+\theta } )( {\delta +(k-1)r} )( {a-bp} )( {-1+e^{-rH}} )e^{( {kr+\delta } )t_1 -\delta T} \\&\quad -\,(k-1)( {r+\theta } )e^{-rt_1 }r( {\delta +k-1} )r )( {a-bp} )(-1+e^{-rH})c_2 ( {-2e^{-rt_1 }+e^{rT}} )e^{( {-T+t} )\delta +krt}\\&\quad +\,(-(k-1)( {r+\theta } )(\delta +(k-1)r( {a-bp} ) c_1 (-1+e^{-rH}) e^{-t_d ( {r+\theta } )}e^{t_1 ( {kr+\theta } )+rt_d } \\&\quad -\,(k-1)( {r+\theta } )r( {\delta +(k-1)r} )( {\alpha ( {a-bp} )e^{krt_1 }+\beta p} )( {c-SVe^{-rH}} )e^{-\frac{rH}{N}}\\&\quad -\,(k-1)(r+\theta )(\delta +(k-1)r)(e^{-\theta t_d }cr-e^{-t_d ( {r+\theta } )}c_1 )(a-bp)(-1+e^{-rH})e^{t_1 ( {kr+\theta } )} \\&\quad +\,r( ( c_3 ( {r+\theta } )( {-2+k} )e^{-rt_1 }+(k-1)( {e^{-rt_d }c_1 +p( {r+\theta } )} )( {\delta +(k-1)r} )( {a-bp} )\\&\qquad ({-1+e^{-rH}} ) e^{-rt_1 (k-1)}+( {r+\theta } )( \delta c_3 e^{-rt_1 }( {-1+e^{-rH}} )( {a-bp} )e^{rT(k-1)}+(k-1)\\&\qquad (({-SV+c-pe^{-rt_1 }} )e^{-rH} +pe^{-rt_1 } ) ({\delta +(k-1)r} )( {\alpha ( {a-bp} )e^{krt_1 }+\beta p} ) ) ) ) \\&\qquad (kr+\delta ))/((k-1)( {r+\theta } )r(\delta +(k-1)r)(-1+e^{-\frac{rH}{N}})(kr+\delta )) \\&\quad +\,\frac{1}{(k-1)^{2}( {kr+\theta } )kr^{2}( {r+\theta } )( {-1+e^{-\frac{rH}{N}}} )}(( {-1+e^{-rH}} ) \\&\qquad (-( {r+\theta } )(k-1)I_p be^{-rM}c(-(k-1)kre^{( {kr+\theta } )t_1 +rM}+( {r+\theta } )ke^{( {kr+\theta } )t_d +rM}\\&\quad +\,( {-kr-\theta } )e^{( {r+\theta } )t_d +krM}-e^{( {( {k+1} )r+\theta } )t_d }\theta (k-1) ) e^{( {-r-\theta } )t_d -rM}\\&\quad +\,k+k( r^{2}cI_p be^{-rt_d }(k-1)^{2}e^{( {kr+\theta } )t_1 -( {r+\theta } )t_d }\\&\quad +\,( {r+\theta } )I_e ( {kr+\theta } )( {-2bp+a} )( {krM-1-rM} )e^{rM(k-1)}+cbrI_p e^{-rt_d }( {r+\theta } )(k-1) \\&\qquad e^{rt_d (k-1)}+ ({-cbrI_p e^{-rt_d }(k-1)e^{rt_1 (k-1)}+( {r+\theta } )I_e ({-2bp+a})( {kr+\theta } )}) ))=0. \end{aligned}$$