1 Introduction

Renewable energy systems (RES) are growing global interest as fossil fuel resources are depleted, electricity demand is increasing in developing countries, and costs of the photovoltaic (PV) modules have been reduced. Solar energy is the most popular source of energy that includes several applications such as irrigation, solar farming, street light, water heating, and is another most popular RES. The significant advantage of the PV system is that it can convert solar energy directly to a direct current. PV systems, including standalone, grid-tied, and hybrid systems, have a broad range of options (Premkumar et al. 2020c, d). Using an exact model with respect to the experimental I–V data, the most significant task is to improve the PV system performance throughout the operation. The cell manufacturers verify the I–V curve against standard test conditions (STC). The performance of the PV system can be severely impacted by ambient pressure, temperature, and irradiance changes in the environment (Premkumar et al. 2020b). Therefore, several PV models are proposed, such as the single-diode model (SDM), double-diode model (DDM), and three-diode model (TDM), to analyze the behavior of the PV cell/module. Such models differ in precision or complexity, with the most frequently accepted models being the SDM and DDM. In general, the precision of the PV system is dependent upon the model parameters, so it is necessary to estimate such parameters in order to maximize the effectiveness (Chin et al. 2015).

Using different optimization methods that can be classified as analytical, deterministic, and metaheuristic methods, investigators have attempted to improve the operation of the PV system. In order to define the value of unknown variables, the analytical methods use several mathematical formulas (Navabi et al. 2015; Batzelis and Papathanassiou 2016). Although the ease of processing and rate of getting the results, the analytical techniques could be unreliable and, depending on certain assumptions planned in advance within STC (Wolf and Benda 2013), lead to a significant gap between the measured and simulated output of the real PV model. The methods, such as the Newton–Raphson, Lambert W-functions, etc., are few examples of deterministic approaches that include limitations on the design, including convexity and differentiability. Identifying the PV model parameters is multi-modal and non-linear, which causes the deterministic approaches to fall towards premature convergence and can lead to low output if the initial parameters are far from the global solutions (Ishaque et al. 2012; Liang et al. 2020).

To overcome the deficiency in existing techniques, metaheuristic techniques are considered to obtain the most promising solution to the PV parameter identification optimization problem. Consequently, to prevent stagnation in the local minimum, they must balance both the exploitation and exploration phases (Li et al. 2020). The various real-world applications were motivated by the exceptional advancement of metaheuristic techniques and the significance of solar power and its variety of real-world applications to devise a new meta-heuristic optimization to identify the PV model parameters (Wong and Ming 2019). Different optimization techniques have been successfully used to characterize the photovoltaic system with such PV parameters, including differential evolution (DE) algorithm (Xiong et al. 2018b), genetic algorithm (GA) (Kumari and Geethanjali 2017), Jaya algorithm (Venkata Rao 2016), improved Jaya algorithm (IJAYA) (Yu et al. 2017b; Premkumar et al. 2021b), Rao algorithm (Premkumar et al. 2020a), teaching–learning-based optimization (TLBO) algorithm (Liao et al. 2020), particle swarm optimization (PSO) algorithm (Khanna et al. 2015), gravitational search algorithm (Mosavi et al. 2019), stochastic fractal search algorithm (Khishe et al. 2018), autonomous PSO (Mosavi and Khishe 2017), Artificial Bee Colony (ABC) (Jamadi et al. 2016), biogeography-based optimization (Kaveh et al. 2019; Mosavi et al. 2017), moth-flame optimization (MFO) algorithm (Sheng et al. 2019), bacterial foraging algorithm (BFA) (Krishnakumar et al. 2013), shuffled frog leaping algorithm (SFLA) (Hasanien 2015), cuckoo search (CS) (Yang and Deb 2010), firefly optimization (FFO) (Louzazni et al. 2017), grey wolf optimization (GWO) algorithm (Long et al. 2020), whale optimization algorithm (WOA) (Oliva et al. 2017; Khishe and Mosavi 2019; Qiao et al. 2021), sine–cosine algorithm (SCA) (Montoya et al. 2020), salp-swarm algorithm (SSA) (Abbassi et al. 2019; Khishe and Mohammadi 2019), coyote optimization algorithm (COA) (Diab et al. 2020), dragonfly optimization (Khishe and Safari 2019), Harris Hawks optimizer (HHO) (Jiao et al. 2020), marine-predator algorithm (MPA) (Soliman and Hasanien 2020), slime mould algorithm (SMA) (Kumar et al. 2020), equilibrium optimizer (Abdel-basset et al. 2020), and chimps optimization (Khishe and Mosavi 2020a, b). A detailed review of all the algorithms for the solar parameter estimation problem is provided as a supplementary file.

Ishaque and Salam (2011) introduced the DE to calculate the model parameters at various irradiances and temperatures for several types of photovoltaic cells. Ishaque et al. (2012) introduced a penalty-based DE algorithm to determine the variables of the module using artificial data. The authors of Biswas et al. (2019) suggested that the L-SHADE method adjusts its variables based on the performance history of such variables in past iterations. Yu et al. (2017a) presented a self-adaptive TLBO technique that accurately assesses the PV model parameters. The findings found that compared to other comparative approaches, the suggested technique demonstrates sharpness and high precision. Besides, the BFA (Rajasekar et al. 2013) has been implemented with new objective functions to determine maximum power and open-circuit voltage that help to estimate characteristics of the solar PV cell/module correctly. The SCA technique is integrated with the Nelder-Mead simplex method and the learning system based on the opposition to improve the solution accuracy (Chen et al. 2019). Xiong et al. (2018a) suggested a different extraction approach based on using enhanced WOA to obtain the parameters of different PV models selectively. The traditional WOA has good local search exposure, but it struggles from premature convergence when dealing with numerous multi-modal issues. Allam et al. (2016) introduced an optimized method of parameter optimization using the MFO algorithm. The suggested technique has been applied to estimate the three models (i.e., SDM, DDM, and TDM) based on data measured in the research laboratory.

Metaheuristics are not optimal, with a few of these having many problems affecting the accuracy and efficiency. The opposition-based learning (OBL) mechanism was already implemented to prevent these conditions and the OBL considers the solution of the individual candidate and produces the opposite position in the search space (Tizhoosh 2005). The OBL validates whether the candidate solution or the opposite function has the best value of the objective function through a single rule. This method might be implemented at initialization or when the population changes a pair of possible results based on the procedure. The OBL has shown that effectiveness enhances many metaheuristic algorithms. For numerical solution space, the firefly algorithm has also been updated using OBL (Verma et al. 2016). The opposition-based rule was also used to determine the parameters using the SFLA in industrial automation (Ahandani and Alavi-Rad 2015). Many of these experiments demonstrate that OBL is an exciting process for optimization problems to produce better performance.

The gradient-based optimization algorithm (GOA) is a recently reported metaheuristic algorithm (Ahmadianfar et al. 2020). And it has been developed for a numerical optimization problem. However, when GOA is applied to real-world engineering problems, including solar parameter estimation problems, the GOA suffers due to the local optima trap. To avoid this trapping and to improve the convergence rate of the basic GOA, the OBL scheme is integrated with the GOA to formulate a new algorithm called opposition-based gradient-based optimization algorithm (OBGOA). The no-free lunch (NFL) theory states that no optimization algorithm can outperform another on any measure across all problems (Wolpert and Macready 1997). However, OBGOA can quickly distinguish between the exploration and exploitation phases and converges on more accurate results. This study proposes the use of OBGOA to extract the electrical parameters of the PV cell and module with high accuracy and in real-time, based on the arguments stated in the NFL theory OBGOA’s capacity to regulate the exploitation and exploration phases. The  key contributions of this paper are as follows.

  • The usage of OBL, in conjunction with GOA, greatly increases the accuracy and efficiency of the traditional GOA. However, such enhancement meets the limitations of the GOA, retaining the excellent potential for optimization.

  • To prove that the proposed OBGOA can solve real-time applications, the proposed algorithm is validated over the solar PV parameter estimation problem.

  • Comparisons with several other existing techniques revealed that in terms of effectiveness and accuracy, the OBGOA could produce positive performance.

  • Various metrics and statistical validations support the experiments and comparisons.

The rest of the paper is structured as follows. Section 2 presents a mathematical model of the single-diode and double-diode model of the photovoltaic cell/module, in addition to the objective function formulation for the above-said problem. Section 3 briefly explains the basic concepts of the traditional GOA and describes the development process of the proposed OBGOA. Section 4 discusses the experimental results and the performance comparison with other metaheuristic techniques. Finally, the findings are provided in Sect. 5 with concluding remarks.

2 Mathematical model of the photovoltaic cell/module and problem formulation

Several PV models have defined the I–V characteristics of the solar cell and panel. SDM and DDM are the most widely used models in practical applications. This section presents the photovoltaic cell and module’s equivalent circuit for both SDM and DDM, along with the objective functions (Mohamed et al. 2013; Drouiche et al. 2018).

2.1 Single-diode model (SDM) of the PV cell

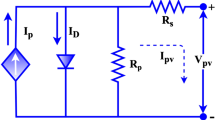
The single-diode model has been widely utilized in numerous applications, particularly when defining the characteristics of the PV cell. The equivalent circuit of the single diode model is illustrated in Fig. 1, including photocurrent Ip, the current through the diode Id, and shunt resistor current Ish. Furthermore, in Eq. (1), the output current (I) is described.

Fig. 1
figure 1

Single-diode photovoltaic cell model

Full size image
$$I={I}_{p}-{I}_{d}-{I}_{sh}$$
(1)

As per the Shockley equation, the diode current Id is given in Eq. (2), in which the reverse saturation current of the diode is denoted as Isd, the ohmic resistance of the PV cell is represented as Rp and Rs, the output voltage of the PV cell is V, the output current is I, and the diode ideality factor is denoted n. In addition, the expression for Ish is presented in Eq. (3).

$${I}_{d}={I}_{sd}\left[\mathrm{exp}\left(\frac{q(V+I{R}_{s})}{nkT}\right)-1\right]$$
(2)
$${I}_{sh}=\frac{V+I{R}_{s}}{{R}_{p}}$$
(3)

where the electron charge q is equal to 1.602*10−19 C, the Boltzmann constant k equals 1.3806*10−23 J/K, and the absolute temperature is denoted as T in Kelvin. Therefore, Eq. (1) is rewritten as follows.

$$I={I}_{p}-{I}_{sd}\left[\mathrm{exp}\left(\frac{q(V+I{R}_{s})}{nkT}\right)-1\right]-\frac{V+I{R}_{s}}{{R}_{p}}$$
(4)

The five unknown parameters of the SDM of the PV cell is observed from Eq. (4) and is presented as \({I}_{p},{I}_{sd},n, {R}_{s}\) and \({R}_{p}\).

2.2 Double-diode model (DDM) of the PV cell

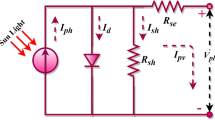
The DDM is established considering the impact of the recombination losses in the depletion region. In the double-diode model, the controlled current source has two diodes connected in parallel and parallel resistance. The circuit structure of the DDM is shown in Fig. 2. The total photovoltaic cell current is given as follows.

Fig. 2
figure 2

Double-diode photovoltaic cell model

Full size image
$$I={{I}_{p}-{I}_{d}-{I}_{sh}=I}_{p}-{I}_{sd1}\left[\mathrm{exp}\left(\frac{q\left(V+I{R}_{s}\right)}{{n}_{1}kT}\right)-1\right]-{I}_{sd2}\left[\mathrm{exp}\left(\frac{q(V+I{R}_{s})}{{n}_{2}kT}\right)-1\right]-\frac{V+I{R}_{s}}{{R}_{p}}$$
(5)

The reverse saturation current and the diffusion current are denoted as Isd1 and Isd2, and the diffusion and recombination diode ideality factors are denoted as n1 and n2. The seven unknown parameters of the DDM of the PV cell is observed from Eq. (5) and is presented as \({I}_{p},{ n}_{1}, {n}_{2}, {{ I}_{sd1}, {I}_{sd2}, R}_{s},\) and \({R}_{p}\).

2.3 Mathematical models of the solar photovoltaic module

The PV module contains multiple series or parallel cells whose arrangement is shown in Fig. 3. The PV module focused on SDM and DDM can be defined by Eqs. (6) as well as (7).

Fig. 3
figure 3

Equivalent circuit of the solar PV module

Full size image
$$I={I}_{p}{N}_{sh}-{I}_{sd}{N}_{sh}\left[\mathrm{exp}\left(\frac{q(V+I{R}_{s}\left({N}_{s}/{N}_{sh}\right))}{{N}_{s}nkT}\right)-1\right]-\frac{V+I{R}_{s}\left({N}_{s}/{N}_{sh}\right)}{{R}_{p}\left({N}_{s}/{N}_{sh}\right)}$$
(6)
$$I={I}_{p}{N}_{sh}-{I}_{sd1}{N}_{sh}\left[\mathrm{exp}\left(\frac{q(V+I{R}_{s}\left({N}_{s}/{N}_{sh}\right))}{{N}_{s}{n}_{1}kT}\right)-1\right]-{I}_{sd2}{N}_{sh}\left[\mathrm{exp}\left(\frac{q(V+I{R}_{s}\left({N}_{s}/{N}_{sh}\right))}{{N}_{s}{n}_{2}kT}\right)-1\right]-\frac{V+I{R}_{s}\left({N}_{s}/{N}_{sh}\right)}{{R}_{p}\left({N}_{s}/{N}_{sh}\right)}$$
(7)

The series-connected PV cells are referred to as Ns, the parallel-connected PV cells are referred to as Nsh, the total voltage of the module is referred to as V, and the total current of the module is referred to as I.

2.4 Objective function formulation

To optimize the model parameters from the estimated current and the variation between experimental current, identifying the PV cell parameters for various models is probably converted into an optimization problem. During the optimization procedure, the current of the PV cell/module is obtained by optimizing the design variables. First, identify the optimal values of unknown parameters, as previously discussed, such that the error between the estimated current and the experimental current is as minimal as possible. Equation (8) introduces the fitness function of the optimization problem, which would also be considered the root mean square error (RMSE) (Jordehi 2016). Owing to its non-linear transcendental nature, the fitness function is challenging to solve. This study’s key objective is to check for a vector Y that allows the RMSE(Y) value to achieve the lowest value.

$$RMSE\left({Y}_{i}\right)=\sqrt{\frac{1}{X}\sum_{k=1}^{X}{{f}_{k}\left(V,I,{Y}_{i}\right)}^{2}}$$
(8)

The number of samples is referred to as X, and the decision/optimization/design variables are referred to as Y.

3 Improved gradient-based optimization algorithm

This section of the paper briefly introduces the concept of the GOA and extend the discussions to the formulation of the OBGOA.

3.1 Gradient-based optimization algorithm (GOA)

In the traditional GOA that incorporates the gradient and population-based methods, Newton’s approach for exploring the search domain using a set of variables and two major operators, such as local escaping operators and gradient search rule, define the search path (Ahmadianfar et al. 2020). The initialization phase of the GOA is similar to other metaheuristics algorithms. Therefore, the initialization phase is not discussed in this paper.

3.1.1 Gradient search rule (GSR)

The migration of vectors is supervised in the gradient search rule (GSR) to improve search in the possible area and obtain good positions. The GSR allows the GOA to adjust for the random actions during the optimization procedure, supporting exploration and avoiding premature convergence. The convergence rate of the GOA technique is facilitated using the direction of movement (DM) to establish an acceptable local search propensity. Therefore, the current vector position is updated using Eq. (11).

$${X1}_{n}^{t}={x}_{n}^{t}-GSR+DM$$
(9)
$$GSR=randn\times {\rho }_{1}\times \frac{2\Delta x\times {x}_{n}^{t}}{\left({x}_{\text{worst}}-{x}_{best}+\varepsilon \right)}$$
(10)
$$DM=rand\times {\rho }_{2}\times \left({x}_{best}-{x}_{n}^{t}\right)$$
(11)

The current vector \({x}_{n}^{t}\) is updated using Eq. (9), and the newly updated vector is denoted as \({X1}_{n}^{t}\). The term \({\rho }_{1}\) is the critical control parameter to balance the exploitation and exploration phases. The best solution and the worst solutions during the optimization are represented as \({x}_{best}\) and \({x}_{\text{worst}}\), respectively. The value of \(\varepsilon\) is inside the range of [0, 0.1]

$${\rho }_{1}=2\times rand\times \alpha -\alpha$$
(12)
$$\alpha =\left|\beta \times {\sin}\left(\frac{3\pi }{2}+ {\sin}\left(\beta \times \frac{3\pi }{2}\right)\right)\right|$$
(13)
$$\beta ={\beta }_{\min}+\left({\beta }_{\max}-{\beta }_{\min}\right)\times {\left(1-{\left(\frac{t}{{IT}_{\max}}\right)}^{3}\right)}^{2}$$
(14)

where the current iteration is denoted as t, the values of \({\beta }_{\max}\) and \({\beta }_{\min}\) are equal to 1.2 and 0.2, respectively, and \(randn\) is a uniformly distributed random number. The difference between the randomly selected position and the current best solution is represented as \(\Delta x\). The variable \(\delta\) has been presented to verify that the \(\Delta x\) is changed during each iteration.

$$\delta =2\times rand\times \left|\frac{{x}_{{r}_{1}}^{t}+{x}_{{r}_{2}}^{t}+{x}_{{r}_{3}}^{t}+{x}_{{r}_{4}}^{t}}{4}-{x}_{n}^{t}\right|$$
(15)

where \(rand\) is a random number with D-dimensions, the integers, such as \({r}_{1}\text{,} {r}_{2}\text{,} {r}_{3}, \,\mathrm{and} \, {r}_{4} ({r}_{1}\ne {r}_{2}\ne {r}_{3}\ne {r}_{4}\ne n\)) are randomly selected between [1, D]. Another random parameter that supports the exploration phase of the GOA is referred to as \({\rho }_{2}\) and it helps each vector in the population to have various step sizes. The expression for \({\rho }_{2}\) as follows.

$${\rho }_{2}=2\times rand\times \alpha -\alpha$$
(16)

After introducing Newton’s method to improve the exploration and diversity and generate a strong population-based search process, Eq. (9) can be rewritten as follows.

$${X1}_{n}^{t}={x}_{n}^{t}-randn\times {\rho }_{1}\times \frac{2\Delta x\times {x}_{n}^{t}}{\left({yp}_{n}^{t}-{yq}_{n}^{t}+\varepsilon \right)}+rand\times {\rho }_{2}\times \left({x}_{best}-{x}_{n}^{t}\right)$$
(17)

Replace the best vector position with the current vector position in Eq. (17). Therefore, a new vector (\({X2}_{n}^{t}\)) is generated, and it is expressed as follows.

$${X2}_{n}^{t}={x}_{\text{best}}-randn\times {\rho }_{1}\times \frac{2\Delta x\times {x}_{n}^{t}}{\left({yp}_{n}^{t}-{yq}_{n}^{t}+\varepsilon \right)}+rand\times {\rho }_{2}\times \left({x}_{r1}^{t}-{x}_{r2}^{t}\right)$$
(18)
$${yp}_{n}=rand\times \left(\frac{\left[{z}_{n+1}{+x}_{n}\right]}{2}+rand\times \Delta x\right)$$
(19)
$${yq}_{n}=rand\times \left(\frac{\left[{z}_{n+1}{+x}_{n}\right]}{2}-rand\times \Delta x\right)$$
(20)

The search process as represented in Eq. (18) is useful for local search but is restricted to global search, while Eq. (17) implemented the search process that is perfect for global search, but local search is restricted. Therefore, to improve both the exploration and exploitation ability of the algorithm, both search strategies are utilized in GOA. Based on Eqs. (17) and (18), along with the current vector position, the updated solution during the next iteration \({x}_{n}^{t+1}\) is written as follows.

$${x}_{n}^{t+1}={r}_{a}\times \left({r}_{b}\times {X1}_{n}^{t}+\left(1-{r}_{b}\right)\times {X2}_{n}^{t}\right)+\left(1-{r}_{a}\right){\times X3}_{n}^{t}$$
(21)
$${X3}_{n}^{t}={X}_{n}^{t}-{\rho }_{1}\times \left({X2}_{n}^{t}-{X1}_{n}^{t}\right)$$
(22)

3.1.2 Local escaping operator (LEO)

The LEO is applied to facilitate the validity of the GOA in solving difficult problems. By exploiting numerous probable solutions, the LEO produces a superior solution \({X}_{LEO}^{t}\) including random solutions, such as \({x}_{r1}^{t}\) and \({x}_{r2}^{t}\), the position of the best solution \({x}_{\text{best}}\), updated random solution \({x}_{k}^{t}\), and the solutions \({X1}_{n}^{t}\) and \({X2}_{n}^{t}\).

$$\begin{gathered} {\mathbf{if}}\;~rand < P_{r} \hfill \\ \quad {\mathbf{if}}\;rand < 0.5 \hfill \\ \quad \quad X_{{LEO}}^{t} = {{X_{n}^{{t + 1}} + a \times \left( {u_{1} \times x_{{{\text{best}}}} - u_{2} \times x_{k}^{t} } \right) + b \times \rho _{1} \times \left( {u_{3} \times \left( {X2_{n}^{t} - X1_{n}^{t} } \right) + u_{2} \times \left( {x_{{r1}}^{t} - x_{{r2}}^{t} } \right)} \right)} \mathord{\left/ {\vphantom {{X_{n}^{{t + 1}} + a \times \left( {u_{1} \times x_{{{\text{best}}}} - u_{2} \times x_{k}^{t} } \right) + b \times \rho _{1} \times \left( {u_{3} \times \left( {X2_{n}^{t} - X1_{n}^{t} } \right) + u_{2} \times \left( {x_{{r1}}^{t} - x_{{r2}}^{t} } \right)} \right)} 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ \quad \quad X_{n}^{{t + 1}} = X_{{LEO}}^{t} \hfill \\ \quad {\mathbf{else}} \hfill \\ \quad \quad X_{{LEO}}^{t} = {{x_{{{\text{best}}}} + a \times \left( {u_{1} \times x_{{{\text{best}}}} - u_{2} \times x_{k}^{t} } \right) + b \times \rho _{1} \times \left( {u_{3} \times \left( {X2_{n}^{t} - X1_{n}^{t} } \right) + u_{2} \times \left( {x_{{r1}}^{t} - x_{{r2}}^{t} } \right)} \right)} \mathord{\left/ {\vphantom {{x_{{{\text{best}}}} + a \times \left( {u_{1} \times x_{{{\text{best}}}} - u_{2} \times x_{k}^{t} } \right) + b \times \rho _{1} \times \left( {u_{3} \times \left( {X2_{n}^{t} - X1_{n}^{t} } \right) + u_{2} \times \left( {x_{{r1}}^{t} - x_{{r2}}^{t} } \right)} \right)} 2}} \right. \kern-\nulldelimiterspace} 2} \hfill \\ ~\quad \quad X_{n}^{{t + 1}} = X_{{LEO}}^{t} \hfill \\ \quad {\mathbf{end}} \hfill \\ {\mathbf{end}} \hfill \\ \end{gathered}$$
(23)

The value of a is a uniform random number in the range of [− 1, 1], the value of b is a normal distributed random number with a standard deviation (SD) of 1 and a mean of 0, \({P}_{r}\) is the probability rate, and the random numbers, such as \({u}_{1}\), \({u}_{2}\), and \({u}_{3}\) are written as follows.

$${u}_{1}=\left\{\begin{array}{l}2\times rand, if {\mu }_{1}<0\text{.}5\\ 1, otherwise\end{array}\right.$$
(24)
$${u}_{2}=\left\{\begin{array}{l}rand, if {\mu }_{1}<0\text{.}5\\ 1, otherwise\end{array}\right.$$
(25)
$${u}_{3}=\left\{\begin{array}{l}rand, if {\mu }_{1}<0\text{.}5\\ 1, otherwise\end{array}\right.$$
(26)

The value of \({\mu }_{1}\) is varies between [0, 1] and \(rand\) is a random number between [0, 1]. Equations (24–26) are rewritten as follows.

$${u}_{1}={L}_{1}\times 2\times rand+\left(1-{L}_{1}\right)$$
(27)
$${u}_{2}={L}_{1}\times rand+\left(1-{L}_{1}\right)$$
(28)
$${u}_{3}={L}_{1}\times rand+\left(1-{L}_{1}\right)$$
(29)

The value of \({L}_{1}\) is 0 when the value of \({\mu }_{1}\) is larger than or equal to 0.5; otherwise, the value is 1. The following update scheme is used in Eq. (23) to find the solution \({x}_{k}^{t}\).

$${x}_{k}^{t}=\left\{\begin{array}{l}{x}_{rand}, if {\mu }_{2}<0\text{.}5\\ {x}_{p}^{t}, otherwise\end{array}\right.$$
(30)
$${x}_{rand}={X}_{lb}+rand \times ({X}_{ub}-{X}_{lb})$$
(31)

where \({\mu }_{2}\) is a random number between [0, 1], the randomly selected population solution is \({x}_{rand}\), and the new solution is \({x}_{p}^{t}\). Therefore, Eq. (30) is rewritten as follows.

$${x}_{k}^{t}={L}_{2}\times {x}_{p}^{t}+\left(1-{L}_{2}\right)\times {x}_{rand}$$
(32)

As similar to \({L}_{1}\), \({L}_{2}\) is also a binary parameter. The value of \({L}_{2}\) is 0 when the value of \({\mu }_{2}\) is larger than or equal to 0.5; otherwise, the value is 1. The pseudocode of the basic version of the GOA is shown in the Algorithm.

figure a

3.2 Opposition-based learning (OBL)

The opposition-based learning concept has been adopted to enhance the integration of heuristic approaches to explore a global optimization solution. Generally, the metaheuristic approaches generate the initial population and random solutions to discover the optimal solution. However, the initial solutions are randomly generated or based on previous information, including specifying domain search or other parameters. In the lack of such information, these methods can neither converge to a global optimal because their function is randomly in the solution space. Such methods are often laborious since they rely on the difference between current and best solutions. The OBL proposes a technique to try for a solution oppositely to the current solution to overcome these problems, so the solution gets nearer to the desired solution, and the convergence gets smoother (Cuevas et al. 2012). The opposite value of the real number \(x\in [lb, ub]\) is denoted as \(\overline{x }\) and is given in Eq. (33).

$$\overline{x }=ub+lb-x$$
(33)

For the multi-dimensional search space, Eq. (33) is rewritten as follows.

$$\overline{{x }_{i}}={ub}_{i}+{lb}_{i}-{x}_{i}, i=1, 2, \ldots , D$$
(34)

The opposite point \(\overline{{x }_{i}}\) is replaced with the respective solution x depending on the fitness function value. If \(f(x)\) is greater than \(f(\overline{x })\), then x does not alter, else \(x=\overline{x }\); thus, population solutions are changed based on the better value of \(\overline{x }\) and \(x\).

3.3 Proposed opposition-based gradient-based optimization algorithm (OBGOA)

A few limitations of the conventional GOA are being trapped in the optimal local solution, high computational complexity, and poor convergence and such restrictions are attributable to the fact that specific solutions are modified to the optimal solution though few solutions are removed from this solution. However, when taking the opposite solution into account, the OBGOA removes these disadvantages. Besides, the OBGOA integrates the basic GOA’s search functionality with the OBL to improve solution space exploration. Thus, the proposed technique has fewer parameters to be adjusted relative to similar techniques, and the introduction of OBL doesn’t impact the GOA specification, while on the other hand, the reliability of the optimum solution is improved. In this context, the size of the initial population owing to enhancing convergence can be reduced to the best solution, as OBGOA can discover the search space widely.

Nevertheless, the OBGOA population setting may also influence the call functions provided in the optimization problem. An assessment of the objective function requires more computation time, relying on the execution. This reality explicitly correlates to the NFL statement, stating that an algorithm cannot be enhanced without losing any benefit. This is the primary reason to create OBGOA. The suggested methodology enhances the GOA over two phases: primarily, the OBL has been utilized to increase the rate of converge in the population initialization and stop trapped in local optimal by looking for solutions in the entire search space. Second, the OBL has been used in updating the population approach to test whether the change in the opposite track is higher than the current improvement. The suggested strategy randomly generates the population X with size Np, in which the solution xj = [xj1, xj2, …, xjD], j = 1, 2, …, Np. Therefore, each opposite solution is determined by OBL, and afterward, the opposite population \(\overline{X }\) is developed. The optimal Np solution is chosen based on the \(\overline{X }\) and X populations.

Phase I : initialization phase

  1. i.

    Initialize the random population solutions X.

  2. ii.

    Determine the opposite population \(\overline{X }\) as follows.

    $$\overline{{x }_{n,i}}={ub}_{n,i}+{lb}_{n,i}-{x}_{n,i}, i=1, 2, \ldots , D, n=1, 2, \ldots , {N}_{p}$$
  3. iii.

    Choose the best population solutions from \(X\cup \overline{X }\) to generate a new population.

Phase II: updated phase—After deciding the proper population solutions that have created a new population, the OBGOA decides the optimal population solution. Using the GOA, the population solution X is revised, and the objective functions are measured, and the opposite population \(\overline{X }\) is calculated based on the OBL, and the objective function is assessed for each \(\overline{x }\). Focused on the objective function, the next stage in the OBGOA is to choose the best population solutions from \(X\cup \overline{X }\). The processes are repeated till the stopping conditions, as shown in Fig. 4.

Fig. 4
figure 4

Flowchart of the proposed OBGOA

Full size image

4 Experimental results and discussions

This section shows the effectiveness of the proposed OBGOA, and the experimental findings were presented. The OBGOA is mainly implemented in three different models: SDM, DDM, and PV models, to estimate uncertain parameters. The description of the datasets used is discussed as follows. The experimental data samples of RTC France Si solar cell, PhotoWatt-PWP201, KC200GT, and SM55 are considered to examine the effectiveness of the proposed algorithm. The first set from which includes 26 samples of voltage and current are obtained from an RTC France Si solar cell at an irradiance of 1000 W/m2 and temperature of 33 °C (Premkumar et al. 2021a), and the second set is the data obtained from a PhotoWatt-PWP201 module (Premkumar et al. 2021a). Two commercial versions are also being evaluated: monocrystalline SM55 (Chaibi et al. 2019) and multi-crystalline KC200GT (Ma 2014), from the manufacturer’s datasheet to show the robustness and accuracy of the OBGOA at various temperature and irradiance levels. The findings of which would be contrasted to those of other successful and very recent algorithms, such as EO, GOA, MPA, SMA, COA, SSA, and HHO. The OBGOA and other algorithms are executed using MATLAB software installed on a laptop with a 2.44 GHz clock frequency and 8 GB of memory. Each method performs 30 times on each problem independently, with ITmax is equal to 1000 and a search agent of 50. The control parameters of all algorithms are listed in Appendix B. In Table 1, the range of design variables for each model is listed. Each algorithm’s efficiency is contrasted based on the RMSE values, convergence curve, and statistical data analysis.

Table 1 Upper and lower bounds for PV models
Full size table

4.1 Results of the PV cell and the PV module

This section discusses comprehensive experimental findings of the RTC France Si solar cell and PhotoWatt-PWP201 for both SDM and DDM. The lower the RMSE, the nearer the estimated value towards the experimental data, which indicates that the selected algorithm holds high efficiency in estimating unknown cell/module parameters. Thus, the error value tends to be reduced as low as possible. In the meantime, relative error (RE) and integral absolute error (IAEi) are used to emphasize the value of the error between the experimental data and estimated data at each set value of the voltage, as described below.

$$RE=\frac{\left|{I}_{exp}-{I}_{est}\right|}{{I}_{exp}}$$
(35)
$$IAE_{i}=\left|{I}_{exp}-{I}_{est}\right|$$
(36)

where Iexp signifies the experimental current sample and Iest denotes the estimated current.

4.1.1 Results of the RTC France Si solar cell

By comparison, the reliability of the OBGOA has been dramatically increased relative to the standard GOA. Compared to several other techniques comprising COA, SSA, SMA, EO, HHO, MPA, GOA, as seen in Tables 2 and 3, the OBGOA obtained the best RSME with a result of 9.8602E − 04 for SDM and 9.8258E − 04 for DDM, suggesting that OBGOA is a robust tool for solving the problem of identification of uncertain parameters of the PV cell. The ‘+’ sign in all tables indicates that the results obtained by OBGOA are better than other algorithms. Figure 5 illustrates OBGOA’s convergence curve and other selected algorithms, implying the value of mean RMSE after 30 individual runs of each algorithm for both SDM and DDM of the PV cell. Compared to other algorithms, OBGOA’s convergence speed is excellent, i.e., early convergence to global minima. It is more straightforward to see that the convergence curve of the OBGOA has a better performance and is higher than other competitive algorithms. The OBGOA extracts the I–V characteristic of the SDM and DDM of the PV cell accurately, and it can be observed in Fig. 6. From Fig. 6, it is seen that the estimated data values and experimental data values are significantly suited over the experimental voltage points, which shows the reliability of the OBGOA and also, OBGOA’s performance is significantly observed, and the current and power values are estimated from the experiment data. The RE and IAE between the experimental and simulated current at each voltage sample point are low enough to confirm that the OBGOA can reliably indicate solar cells’ real characteristics. The value of IAE with respect to the current and power is calculated and listed in Tables 13 and 14 (refer Appendix A), respectively, for SDM and DDM, in addition to the value of RE at each experimental point. The boldface in all tables indicates the best values. 

Table 2 Uncertain parameters estimated by various algorithms for SDM of the cell (RTC France Si solar cell)
Full size table
Table 3 Uncertain parameters estimated by various algorithms for DDM of the cell (RTC France Si solar cell)
Full size table
Fig. 5
figure 5

Convergence curves of all algorithms (RTC France Si cell); a SDM, b DDM

Full size image
Fig. 6
figure 6

I–V characteristics obtained by OBGOA (RTC France Si cell); a SDM, b DDM

Full size image

From Table 13, it is observed that the value of IAE is less than 1.627E − 03, and the value of RE is less than 5.908E − 03. The average values of IAE with respect to the power and current are 8.781E − 05 and 7.225E − 04, respectively, and the average value of RE is 4.507E − 03, which indicates OBGOA can able to realize the real characteristics of the SDM. Table 14 displays explicitly that the IAE (with respect to current and power) and RE values are smaller than 1.604E − 03 (with respect to current), 8.051E − 04 (with respect to current), and 6.957E − 03, respectively. The average values of IAE with respect to the power and current are 4.197E − 04 and 7.175E − 04, respectively, and the average value of RE is 7.536E − 05, which indicates OBGOA can able to realize the real characteristics of the DDM. Based on above-all discussions, it is claimed that OBGOA helps analyze both SDM and DDM model’s unknown parameters.

4.1.2 Results of the PhotoWatt-PWP201 PV module

As in SDM/DDM of the PV cell, in SDM/DDM PV module model also the reliability of the OBGOA has been dramatically increased relative to the basic GOA version. Furthermore, compared to several other techniques, as seen in Tables 4 and 5, the proposed OBGOA obtained the best RSME with 2.4115E − 03 for SDM and 2.4018E − 03 for DDM, suggesting that OBGOA is a robust tool for solving the problem of identification of uncertain parameters of the PV model.

Table 4 Parameters estimated by various algorithms for SDM of the PV module (PhotoWatt-PWP201)
Full size table
Table 5 Parameters estimated by various algorithms for DDM of the PV module (PhotoWatt-PWP201)
Full size table

Figure 7 illustrates convergence curves, implying the value of mean RMSE after 30 individual runs of each algorithm for both SDM and DDM of the PhotoWatt-PWP201 PV module.

Fig. 7
figure 7

Convergence curves of all algorithms (PhotoWatt-PWP201 PV module); a SDM, b DDM

Full size image

Compared to other techniques, OBGOA’s convergence speed is excellent, i.e., early convergence to global minima. The proposed OBGOA extracts the I–V characteristic of the SDM and DDM of the PV module accurately, and it can be observed in Fig. 8. From Fig. 8, it is seen that the estimated data values and experimental data values are significantly suited over the experimental voltage points, which shows the reliability of the proposed OBGOA. The RE and IAE values are low enough to confirm that the OBGOA can reliably indicate the solar module’s real characteristics. The value of IAE with respect to the current and power is calculated and listed in Tables 15 and 16 (refer Appendix A), respectively for SDM and DDM, in addition to the value of RE at each experimental point. From Table 15, it is observed that the value of IAE is less than 5.000E − 03, and the value of RE is less than 6.553E − 03. The average values of IAE with respect to the power and current are 5.599E − 03, and 0.0020, respectively, and the average value of RE is 1.0007E − 03, which indicates OBGOA can realize the real characteristics of the SDM. Table 16 displays explicitly that the IAE (with respect to current and power) and RE values are smaller than 4.415E − 03 (with respect to current), 5.321E − 02 (with respect to power), and 4.021E − 02, respectively. The average values of IAE with respect to the power and current are 1.992E − 02, and 0.0019, respectively, and the average value of RE is 5.534E − 03, which indicates that OBGOA can realize the real characteristics of the DDM. Based on above-all discussions, it is claimed that OBGOA helps analyze both SDM and DDM model’s unknown parameters. The above discussions show minimal IAE and RE between the estimated data and experimental data and are enough to show OBGOA reliability and solution accuracy.

Fig. 8
figure 8

I–V characteristics obtained by OBGOA (PhotoWatt-PWP201 module); a SDM, b DDM

Full size image

4.1.3 Average run time

The computation cost is indeed a significant metric for assessing the efficiency of the algorithm. The average CPU computation time of all algorithms is reported in Table 6. From Fig. 9, it can be noticed that the time required by each method to address the problem on various models is different. The HHO has the highest total CPU time, no matter which model and the basic variant of GOA needs the shortest time. Even though OBGOA is not the fastest compared to GOA (better than other peers), other techniques are relatively similar to the OBGOA. Thus, it is declared that a more successful method is OBGOA.

Table 6 Average CPU time of various algorithms
Full size table
Fig. 9
figure 9

Mean CPU time for different PV models

Full size image

4.2 Results of commercial PV modules

The authors wanted to investigate the feasibility of the OBGOA by defining SDM variables for two commercial PV modules, namely KC200GT and SM55. The KC200GT is a high-performance multi-crystalline module, and the SM55 is a monocrystalline module intended for industrial applications. The short-circuit current Isc of the PV module finds the initial range of the Ip, the temperature coefficient of the short-circuit current is denoted as α, and the value is taken from the specification sheet. The value of Isc is calculated using the datasheet at STC, and the expression to calculate Isc is given as follows.

$${I}_{sc}\left(T,G\right)={I}_{sc-STC}\times \frac{G}{{G}_{STC}}+\alpha \left(T-{T}_{STC}\right)$$
(37)

where G and T denote the actual solar irradiance and temperature, GSTC and TSTC denote the solar irradiance and temperature at STC, and Isc-STC refers to the short-circuit current at STC.

The approximate findings of the five parameters for SDM of those two PV modules are listed in Tables 7, 8, 9 and 10. For such models, the OBGOA determines the optimal parameters at various irradiation levels (200 W/m2, 400 W/m2, 600 W/m2, 800 W/m2, and 1000 W/m2) with a temperature of 25 °C. Similarly, the values of the parameters are extracted for KC200GT at temperatures of 25 °C, 50 °C, and 75 °C, and SM55 at temperatures of 25 °C, 40 °C, and 60 °C with the solar irradiance of 1000 W/m2. Figures 10, 11, 12 and 13 demonstrates the high degree of fitting under different operating conditions between the experimental value and estimated value of the two PV modules, presenting conclusive proof even further to demonstrate the effectiveness of the OBGOA.

Table 7 Optimized variables by OBGOA for KC200GT PV module at a temperature of 25 ℃
Full size table
Table 8 Optimized variables by OBGOA for SM55 PV module at a temperature of 25 ℃
Full size table
Table 9 Optimized parameters by OBGOA for KC200GT PV module at G = 1000 W/m2
Full size table
Table 10 Optimized parameters by OBGOA for SM55 PV module at G = 1000 W/m2
Full size table
Fig. 10
figure 10

I–V curves of KC200GT at various irradiations

Full size image
Fig. 11
figure 11

I–V curves of SM55 at various irradiations

Full size image
Fig. 12
figure 12

I–V curves of KC200GT at various temperatures

Full size image
Fig. 13
figure 13

I–V curves of SM55 at various temperatures

Full size image

4.2.1 Different solar irradiation conditions

Tables 7 and 8 lists the estimated parameters by OBGOA on different irradiation conditions for all two commercial PV modules. In Table 7, the estimated parameters for SDM of the KC200GT PV module by the proposed algorithm for different irradiation conditions. The I–V characteristics of KC200GT are shown in Fig. 10.

Table 8 shows the estimated parameters of the SM55 PV module by the OBGOA for different irradiation conditions. The I–V characteristics of SM55 are depicted in Fig. 11.

4.2.2 Different temperature conditions

Tables 9 and 10 lists the estimated parameters by OBGOA on different temperature conditions for all two commercial modules, similar to previous discussions. In Table 9, the estimated parameters of the KC200GT PV module by the proposed algorithm for different temperature conditions. The I–V characteristics of KC200GT for different temperatures are depicted in Fig. 12.

Table 10 shows the estimated parameters of the SM55 PV module by the proposed algorithm for different temperature conditions. The I–V characteristics of SM55 for different temperatures are depicted in Fig. 13.

The estimated value and experimental sample collected under different temperatures and different irradiation conditions fit well with all two PV modules. Therefore, the proposed OBGOA can achieve a low RMSE value on such test data sets. In addition, the I–V curves prove OBGOA’s accuracy as the irradiance values, and temperature values differ. PV models encounter multiple environmental problems in actual situations, mainly as soon as the outdoor temperature is not appropriate or the solar irradiation is inadequate. Nevertheless, it can be seen in the findings that the OBGOA can still achieve low RSME under low temperature and irradiance. In summary, it can reasonably be demonstrated that the OBGOA is an accurate and appropriate tool for obtaining unknown parameters under different irradiance and temperature conditions.

4.3 Performance comparisons

Numerous comparisons and statistical measures with other existing techniques were performed to demonstrate the effectiveness of the OBGOA. Besides, the selection of these algorithms depends on choosing the most recent and efficient techniques that have been established to solve the problem of parameter identification in PV systems. The algorithms are SSA, COA, SMA, EO, HHO, MPA, and GOA, as discussed earlier. The statistical analysis has been carried out only for SDM/DDM of the PV cell, SDM/DDM of the PV module, and SDM of three commercial PV modules under different irradiation conditions as a sample analysis. The performance indicators, namely Min, Mean, Max, and SD values attained by different methods, are mentioned in Table 11 for the SDM and DDM. To rate the algorithms according to each evaluation metric, the rank (R) has been used. Considering the Min RMSE, it is evident that OBGOA finds the optimal RMSE with a value of 9.8602E − 4 for SDM and 9.8258E − 04 for DDM. Other methods have lower RMSE values, and with 8.796E − 3 for SDM and 3.7764E − 04, HHO is the worst method among various other methods. Besides, OBGOA reports a tremendous outperformance for the Mean and Max; in addition, the value of SD is also minimal compared to other algorithms. Few algorithms, such as HHO and SSA, display poor performance by examining the RMSE values. On the other hand, a few algorithms, such as MPA, SMA, COA, and EO, have demonstrated satisfactory results. The basic GOA also achieves the minimum RSME value, i.e., 9.929E − 04 for SDM and 9.8602E − 04 for DDM, but the OBGOA outperforms GOA in terms of Min, Mean, Max, and SD values and the remaining algorithms. Therefore, it is concluded that the OBGOA stands first for parameter estimation of the PV cell.

Table 11 Statistical results of various algorithms for SDM/DDM of the RTC France Si cell
Full size table

As similar to the statistical analysis of the RTC France Si cell, the PhotoWatt-PWP201 is also analyzed. The performance indicators attained by different methods are mentioned in Table 12 for the SDM and DDM. Considering the Min RMSE, it is obvious that OBGOA finds the optimal RMSE with a value of 2.4018E − 03 for SDM and 2.4115E − 03 for DDM. On the other hand, other methods have lower RMSE values, and with 7.335E − 03 for SDM and 9.339E − 02, HHO is the worst method among various other methods. Besides, OBGOA reports a tremendous outperformance for the Mean and Max; in addition, the value of SD is also minimal compared to other algorithms.

Table 12 Statistical results of various selected algorithms for SDM/DDM of the PhotoWatt-PWP201
Full size table

In Tables 11 and 12, a ranking of all the algorithms is provided. R provides the order of each method, considering the order of that algorithm relative to the other methods in all other parameters. As seen, OBGOA has the lowest R-value (1) and noticed that GOA performs second best, preceded by EO, SSA, COA, MPA, and SMA. As per the Min RMSE, in almost all situations, it is observed that the performance of OBGOA exceeds the other techniques, while OBGOA deservingly succeeds throughout all situations based on Mean RMSE.

The suggested algorithm is superior to all others in extracting the best parameters for the SDM, DDM, and PV module models with the help of the earlier observations and the statistical analysis of such outcomes, and the comparison with several other techniques. The proposed OBGOA can extract the variables of two commercial PV modules obtained from the supplier for practical application. It relies on many performance measures to estimate the effectiveness of OBGOA, including Min, Mean, Max, SD, computation time, and R. Especially compared to all algorithms except GOA, OBGOA is effective in terms of computation time. Besides, in terms of RMSE and R, OBGOA outperforms all existing algorithms. In addition to using an opposition-based learning scheme, the excellent results of OBGOA benefit from the strong exploration and exploitation abilities.

4.4 Discussions

This paper provides a robust approach for estimating the PV cell or PV module parameters to maximize its performance in solar photovoltaic systems. Considering the proposed method’s findings, the proposed OBGOA estimates the value of the unknown variables promptly relative to the other techniques for the various PV models. The new algorithm significantly reduces the current and power losses relative to the experimental current and power. Furthermore, it is seen how the results indicate that the estimated values are very well adapted to the experimental values as the irradiance and the temperature levels are changed, and this is proof of the effectiveness of the proposed OBGOA. Besides, for real-time systems, OBGOA output is checked using commercial information retrieved from the datasheet provided by the manufacturers, such as the KC200GT and SM55. The proposed OBGOA is thus a conveniently applied and realistic solution, and it is an excellent alternative to identify the optimum parameters of the PV system. The average values of RMSE, SD, IAE, RE, and RT obtained by the proposed OBGOA have percentage decrease of 1.152%, 175%, 1.25%, 1.35%, and − 5%, respectively, with respect to the basic version of GOA. The average values of RMSE, SD, IAE, RE, and RT obtained by the proposed OBGOA have percentage decrease of 18%, 200%, 1.3%, 1.5%, and 50%, respectively, with respect to the other selected algorithms. It is worth stating that the proposed OBGOA finds exact parameters at various operating conditions, which is expressive for the maximum power point tracking of a photovoltaic system, since few modules in photovoltaic systems are subject to critical conditions, such as static shading, dynamic shading, and partial shading (Premkumar et al. 2021c; Manoharan et al. 2021). Besides, the obtained results can be utilized while modeling the maximum power point tracking system to track the maximum output power, as varying irradiation and temperature in real-time applications. The limitations of the proposed OBGOA are as follows. The computing efforts of OBGOA are greater than those for standard algorithms since more iterations are required, which might become computationally expensive if the simulation tool takes a long time to evaluate a single objective. Furthermore, the final solutions generated by OBGOA could be reproduced exactly; therefore, numerous runs must be performed to assure reliability and some relevant statistical analysis.

To summarize, the OBGOA has the highest SDM/DDM of PV cell and module convergence speeds. The enhanced capabilities in escaping local optima are because the OBL allows GOA to search optimal solutions faster than other widely used algorithms. As a result, the populations are less likely to become stuck in local optimal, achieving global optima more quickly than traditional approaches.

5 Conclusions

Identifying unknown parameters is a great challenge in photovoltaic systems to improve the accuracy of the power and current. This paper suggests an enhanced variant of the basic GOA to correctly predict the best parameters of the various models, such as SDM, DDM, and PV modules. In recent times, the OBL has gained further attention, which is used to enhance the effectiveness of heuristic methods. It has a significant characteristic that uses the basic variant of GOA to search in the solution space in the opposite direction to the current solution. The authors demonstrated the effect of OBL in this paper to enhance the accuracy of the GOA to solve the parameter estimation optimization problem. Numerous investigations were carried to allow contrasts with other state-of-the-art algorithms to evaluate the effectiveness of OBGOA. The findings and the statistical measures illustrate OBGOA’s superior performance for all the various PV models in terms of RMSE, computation time, SD, RE, IAE, and R. Furthermore, the graphical illustration of the I–V curves shows that the estimated value is in good agreement with the experimental value. In addition, the effectiveness of OBGOA has been evaluated at various temperature and irradiance levels using data from the manufacturer’s datasheet, and the OBGOA can be an alternative tool for parameter estimation of PV models.

The proposed method is expected to be extended in the future to many other energy sectors, such as PV array fault detection, PV array reconfiguration, maximum power point tracking, and energy scheduling in PV systems. Furthermore, the development of more successful strategies for the proposed method to be capable of solving several other optimization problems is also an ultimate goal, particularly for multi-objective and constrained problems. Additionally, the extension of the OBGOA to many other important topics, including image segmentation, feature selection problems, underwater targets classification, underwater acoustical dataset classification, multi-layer perceptron neural network trainer, and feed-forward neural network trainer, will be explored in the future.