1 Introduction

Many attempts have been made to speed up the change of energy infrastructure and increase the research on renewable energy to address environmental pollution and the growing energy shortage. Solar PV is considered the most feasible candidate among various renewable energy technologies for meeting growing energy requirements. For the eighth year now, creative investment in renewable energy has increased the majority of solar energy [1]. The PV modules with higher efficiency and lower price are released to the market, powered by government support and the competition between PV manufacturers. The cumulative installed annual solar capacity by the end of 2017 reached 98 GW with projections of 162 GW by 2021 [2, 3]. PV technology advances attracted significant attention in assessing, simulating, and harvesting maximum power for PV systems [4,5,6]. The I–V characteristic is a nonlinear relationship that is highly influenced by variation in temperature and solar insolation; however, it means that PV modelling is a challenging problem. In recent decades, various PV equivalent circuit models are used to represent the PV cell/module. However, three parameter-equivalent circuit models are used frequently by the researchers, such as SDM, DDM, and TDM, despite the different models designed to describe the behaviour of solar cells/modules [3,4,5,6,7]. The SDM is the most preferred model due to its simplicity; however, this model is inaccurate because it lacks accuracy at low-irradiance, with open-circuit voltage ignored carriage recombination losses in the depletion region [7, 8]. To solve this problem, the DDM is introduced. An extra diode suggests the recombination losses. The model with double-diode showed more accuracy, but this is due to a more complex model with more unknowns; the previous unknowns are complemented by an additional diode saturation current and its ideality factor for the other diode.

A better model with three diodes addressing the effects of grain limits and leakage currents is presented [9]. Despite the model's ability to meet the majority of the physical needs of the solar cell, nine parameters are calculated [10]. Therefore, there are five unknown parameters in SDM, such as the photocurrent, Ip, the diode saturation current, Id, the diode ideality factor, n, the series resistance, Rs, and the shunt resistance, Rp, seven unknown parameters in DDM, such as Ip, Id1, Id2, n1, n2, Rs, Rp and nine parameters in TDM, such as Ip, Id1, Id2, Id3 n1, n2, n3, Rs, Rp have to be precisely determined. The exact information of these unknown parameters is essential not only for the PV module performance assessment but also for maximum power point tracking (MPPT) in PV systems [11,12,13,14,15]. Regrettably, the SDM, DDM, and TDM are implicitly transcendental equations and lack explicit insolubility with general functions [16]. This implicit character not only affects the estimation of the solar cell/module parameters [17] but also the simulation of the PV system. Briefly, all PV models are described as follows. The SDM is very simple to adopt but results in inaccurate results. The ideal factors of n1 and n2 for the DDM are 1 and 2, respectively; however, for commercial models with a scale of about 154.8 cm2 and an efficiency of about 16%, n1 was reported to be between 1 and 1.5, and n2 was reported to be between 2 and 5 [18]. These results showed that the DDM was insufficient to adequately reflect various current components of the experimental solar cells. The diode current (Id1) is contributed by the first diode in the TDM model due to diffusion and recombination in the quasi-neutral regions of the emitter and bulk regions with n1 = 1, and the diode current (Id2) is contributed by recombination in the space charge area with n2 = 2. The addition of a third diode in parallel with the two diodes accounts for the diode current (Id3) affected by recombination in defect areas, grain sites, and other factors. The third diode's ideality factor, n3, must be calculated along with the model's other parameters and is expected to range between 2 and 5 [18, 19]. Therefore, it is essential to develop a reliable and effective way of extracting the parameters accurately from the experimental data or the datasheet details of solar cells/modules.

Numerous literature techniques have been developed to determine the model parameters of SDM, DDM, and TDM. These approaches may typically be categorized as numerical methods and analytical methods. In addition to sufficient simplification norms, analytical methods rely on the precision of some I–V curve distinct points, i.e. Voc, Isc, maximum power point, and gradients at the intersection axis. Thus, analytical approaches choose the points chosen to generalize every I–V data measured. When the selection of the point is wrongly assigned, there may be very significant errors in the extracted parameters. Therefore, research methods are usually unpredictable and, in most situations, yield unsatisfactory results. Alternatively, numerical approaches find all experimental I–V data to extract the cell/module parameters at a higher degree of assurance. Therefore, numerical approaches have successfully resolved the cell/module parameter estimation problem using computer science and mathematics advances. Different deterministic methodologies [20,21,22], evolutionary algorithms [23,24,25,26,27], and evolutionary bionics [28,29,30,31,32,33,34,35,36,37] have been used for these past years. However, deterministic approaches are susceptible and vulnerable to local minima trapping of initial values. While evolutionary algorithms offer greater precision and improved efficiency, and its effectiveness relies on the correct adjustment of control parameters. Every wrong selection would lead to the premature end of iterations and slow convergence speed. Searches continue, thus, for accurate and effective numerical algorithms to solve the solar cell parameter estimation problems.

The strategies of swarm intelligence mimic creatures that live in natural communities. Such strategies emulate the groups of creatures to their own primary objective of survival [36] through a traditional problem-solving approach. In recent times, the most complex, multi-variant problems have been solved by meta-heuristic techniques. Many of the meta-heuristic techniques that have been developed have been applied in relation to the PV parameter extraction problem, namely particle swarm algorithm (PSO) [23], flower pollination algorithms (FPA) [34], cuckoo search (CS) [36], whale optimization algorithm (WOA) [38], fireworks algorithm [39], salp swarm algorithm [40], multiverse optimizer [41], grey wolf optimization (GWO) [42], ant lion optimization (ALO) [43], Harris hawk optimization [44], Rao algorithm [45], slime mould algorithm [46], and hybrid techniques, such as PSOGWO [47], GWOCS [48], Jaya algorithm and its variants [49], Marine predator algorithm [19], and Coyote optimization [50]. Each algorithm is different in approach, and each algorithm is ranked based on the accuracy of the extracted parameters, computation time, and computational complexity.

In 2020, a new meta-heuristic technique inspired by physics was developed, known as the equilibrium optimization (EO) algorithm [51]. The EO is a recently developed meta-heuristic algorithm based on a mass-volume balance model. The EO proved its performance in handling the single-objective benchmark functions and real-time applications, such as pressure vessel, gear-train problem, economic load dispatch, optimal power flow problem, feature selection, and truss design, including solar parameter estimation problem [52,53,54,55,56]. The EO algorithm proved its better performance over other well-known algorithms, such as GWO, PSO, FPA, WOA, ant lion optimizer, Harris hawks optimizer, and slime mould algorithm. However, the EO algorithm is stuck at local optima when the problem dimension is increased. This motivates the authors to focus on the EO algorithm to improve its performance. Opposition-based learning (OBL) was applied to improve the solution accuracy. OBL is a recently developed approach for speeding up the search for well computational intelligence techniques, including fuzzy logic systems, reinforcement learning, artificial neural networks, and swarm and evolutionary algorithms. By concurrently observing the actual candidate solution and its opposite, it is possible to increase the exploration capability using the OBL. Based on this statement from the literature, the OBL scheme is used in this paper to improve the solution accuracy. OBL considers the individual candidate solution and generates the opposite location in the search space. OBL checks whether the opposite function or the candidate solution has the optimal solution of the respective objective function. The OBL is utilized in the initialization phase and update phase to increase the solution. This paper utilizes a new algorithm called OBEO to extract the PV module parameters, and it is based on dynamic source and sink models based on physics used to approximate equilibrium states. EO is in the third class of meta-heuristic algorithms as it originates like physical laws. The performance of the proposed EO algorithm is compared with the state-of-the-art techniques, such as GWO, EO, ALO, WOA, PSOGWO, and GWOCS algorithms. This paper contains major contributions as follows.

  • Evolution of an error function based on the information from the datasheet provided by the manufacturers

  • The proposed OBEO algorithm is utilized for the PV models, such as SDM, DDM, and TDM of three commercial PV modules, such as Adani ASB-7-355, Adani ASM-7-PERC-365, and Tata TP280.

  • OBEO algorithm optimizes the evolved error function for different commercial and non-commercial PV modules, and the optimal parameters are obtained from 20 individual runs

  • The obtained statistical results are compared with the state-of-the-art algorithms. Also, the Friedman rank test (FRT) is carried out to rank the algorithms

The rest of the paper is structured accordingly. Section 2 of the paper analyses the PV models, such as SDM, DDM, and TDM, and defines the error function for estimating the solar photovoltaic module parameters. Section 3 provides a brief overview of the EO algorithm, proposed OBEO algorithm, and explains how the OBEO algorithm is implemented for the parameter estimation problem. Section 4 describes the findings of the experiment, a systematic review, and comparisons. Section 5 concludes the paper with the final remarks.

2 Modelling of the PV module and problem formulation

The solar cell/module can be viewed from the physical perspective as a large-scale diode exposed to the sun [57,58,59,60]. For decades, the equivalent circuits based on the Shockley-diode were, therefore, the standard way of describing the electrical behaviour of solar cells/modules. An ideal solar cell is represented by a current source in parallel with an ideal diode in theory. But since, in reality, no solar cell is ideal, this optimal model is substantially different from real I–V characteristics. Being rational, it is important to take into consideration non-ideal behaviours like parallel parasitic losses, series parasitic loss, and several conduction phenomena for the accurate models of solar cells. The three most common models in the literature are the SDM, DDM, and TDM models listed below.

2.1 Photovoltaic module modelling

2.1.1 Single-diode model

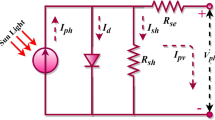
Several photovoltaic cells in series (Ns) or parallel (Np) form a PV module. The series-connected cells were taken into account in this paper because they produce a high output voltage. The PV module’s equivalent circuit is addressed in this subsection by considering a single-diode with serial photovoltaic cells [26,27,28]. Figure 1 illustrates the PV module’s equivalent circuit of the SDM.

Fig. 1
figure 1

Equivalent circuit of the SDM for PV module

Full size image

The modelling initially starts with the photovoltaic cell and is then extended to the module. As discussed earlier, the photovoltaic cell is pictorially represented by a single current source, i.e. photocurrent, Ip, parallel with a single-diode, as depicted in Fig. 1. This photocurrent depends on solar irradiation. The ohmic losses are denoted by the Rs and Rp, and Id denotes the diode's reverse saturation current. The expression for the total current of the PV module, Ipv, is derived as follows.

$$I_{{{\text{pv}}}} = I_{{\text{p}}} - I_{{\text{d}}} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{pv}}}} + I_{{{\text{pv}}}} R_{{\text{s}}} } \right)}}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{\left( {V_{{{\text{pv}}}} + I_{{{\text{pv}}}} R_{{\text{s}}} } \right)}}{{R_{{\text{p}}} }}$$
(1)

where q represents the electron charge and is equal to 1.60217646 × 10−19 C, k represents the Boltzmann constant and is equal to 1.3806503 × 10−23 J/K, the absolute cell temperature is represented by T, and the PV module output voltage is denoted as Vpv. To analyse further, the operating cases, such as open-circuit, short-circuit, and maximum power output is considered, and Eq. 1 is rewritten as follows.

Case 1—Short-circuit During this case, the value of Vpv is equal to zero, and the value of Ipv is equal to Isc. By substituting these settings in Eq. 1, the equation for the photocurrent is derived as follows.

$$I_{{{\text{sc}}}} = I_{{\text{p}}} - I_{{\text{d}}} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }}$$
(2)
$$I_{{\text{p}}} = I_{{{\text{sc}}}} + I_{{\text{d}}} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }}$$
(3)

Case 2—Open-circuit During this case, the value of Vpv is equal to Voc, and the value of Ipv, is equal to zero. By substituting these settings in Eq. 1, the equation for the photocurrent is further derived as follows.

$$0 = I_{{\text{p}}} - I_{{\text{d}}} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }}$$
(4)
$$I_{{\text{p}}} = I_{{\text{d}}} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }}$$
(5)

The equation for the reverse saturation current of the diode, Id, is obtained by solving both Eqs. 3 and 5.

$$I_{{\text{d}}} = \frac{{I_{{{\text{sc}}}} - \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }} + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }}}}{{\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{nkTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{nkTN_{{\text{s}}} }}} \right\}}}$$
(6)

The equation for the photocurrent is derived by substituting Eq. 6 in Eq. 5.

$$I_{{\text{p}}} = \frac{{\left[ {I_{{{\text{sc}}}} - \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }} + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }}} \right]\left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right]}}{{\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{nkTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{nkTN_{{\text{s}}} }}} \right\}}} + \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }}$$
(7)

Case 3—Maximum power point During this case, the value of the Vpv is equal to Vmpp, and the value of the Ipv is equal to Impp. The output current of the PV module during maximum power operating conditions is derived by substituting these settings in Eq. 1.

$$I_{{{\text{mpp}}}} = I_{{\text{p}}} - I_{{\text{d}}} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{R_{{\text{p}}} }}$$
(8)

2.1.2 Double-diode model

The corresponding DDM equivalent circuit, as shown in Fig. 2, in which the diode D1 simulates diffusion processes in the depletion layer of minority carriers, while the diode D2 reflects the recombination of the carriers in the junction area for the space charge region [12, 30,31,32]. As a result, ID1 and ID2 represent current components in the diffusion and recombination, respectively. The resistances, like Rp and Rs, are similar to those of the SDM. The diode ideality factors are represented as n1 and n2. The expression for the total current of the PV module, Ipv, is derived as follows.

$$I_{{{\text{pv}}}} = I_{{\text{p}}} - I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{pv}}}} + I_{{{\text{pv}}}} R_{{\text{s}}} } \right)}}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] - I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{pv}}}} + I_{{{\text{pv}}}} R_{{\text{s}}} } \right)}}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{\left( {V_{{{\text{pv}}}} + I_{{{\text{pv}}}} R_{{\text{s}}} } \right)}}{{R_{{\text{p}}} }}$$
(9)
Fig. 2
figure 2

Equivalent circuit of the DDM for PV module

Full size image

The photocurrent equation is derived in three operating conditions as similar to the SDM of the PV module. During case-1, substitute Vpv = 0 and Ipv = Isc in Eq. 9, and the equation for the photocurrent is obtained as follows.

$$I_{{\text{p}}} = I_{{{\text{sc}}}} + I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }}$$
(10)

During case-2, substitute Vpv = Voc and Ipv = 0 in Eq. 9, and the photocurrent equation is written as follows.

$$I_{{\text{p}}} = I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }}$$
(11)

The equation for the reverse saturation current of the diode, Id2, is derived by solving Eq. 10 and Eq. 11 and is written as follows.

$$I_{{{\text{d}}_{2} }} = \frac{{I_{{{\text{sc}}}} - \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }} - I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{s} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\}} \right] + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }}}}{{\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\}}}$$
(12)

The photocurrent equation is obtained by substituting Eq. 12 in Eq. 11 and is written as follows.

$$I_{{\text{p}}} = I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{I_{{{\text{sc}}}} - \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }} - I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\}} \right] + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }}}}{{\left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right]^{ - 1} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\}} \right]}} + \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }}$$
(13)

During case-3, substitute Vpv = Vmpp and Ipv = Impp in Eq. 9, and the equation for the total current of the PV module is written as follows.

$$I_{{{\text{mpp}}}} = I_{{\text{p}}} - I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] - I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{R_{{\text{p}}} }}$$
(14)

2.1.3 Three-diode model

Nevertheless, in the three-diode model, the current source is connected parallel to three diodes, as shown in Fig. 3 [14, 49, 50, 60]. The current components of the diodes, such as ID1, ID2, and ID3, due to the diffusion processes in the depletion layer of minority carriers, space charge recombination, and defect region recombination, respectively. The reverse saturation current of the diodes is represented as Id1, Id2, and Id3, and its respective ideality factors are represented as n1, n2, and n3. The values of n1 and n2 are varied between 1 and 2, and the value of n3 is varied between 2 and 5. The resistances similar to the SDM and DDM are identical, such as Rp and Rs. The expression for the total current of the PV module, Ipv, is derived as follows.

$$\begin{aligned} I_{{{\text{pv}}}} & = I_{{\text{p}}} - I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{pv}}}} + I_{{{\text{pv}}}} R_{{\text{s}}} } \right)}}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] - I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{pv}}}} + I_{{{\text{pv}}}} R_{{\text{s}}} } \right)}}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] \\ & \quad - I_{{{\text{d}}_{3} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{pv}}}} + I_{{{\text{pv}}}} R_{{\text{s}}} } \right)}}{{n_{3} kTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{\left( {V_{{{\text{pv}}}} + I_{{{\text{pv}}}} R_{{\text{s}}} } \right)}}{{R_{{\text{p}}} }} \\ \end{aligned}$$
(15)
Fig. 3
figure 3

Equivalent circuit of the TDM for PV module

Full size image

The photocurrent equation is derived in three operating conditions as similar to the SDM of the PV module. During case-1, substitute Vpv = 0 and Ipv = Isc in Eq. 15, and the equation for the photocurrent is obtained as follows.

$$I_{{\text{p}}} = I_{{{\text{sc}}}} + I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{3} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }}$$
(16)

During case-2, substitute Vpv = Voc and Ipv = 0 in Eq. 15, and the photocurrent equation is written as follows.

$$I_{{\text{p}}} = I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{3} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }}$$
(17)

The equation for the reverse saturation current of the diode, Id2, is derived by solving Eqs. 16 and 17 and is written as follows.

$$\begin{aligned} I_{{{\text{d}}_{3} }} & = \frac{{I_{{{\text{sc}}}} + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }} - \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }}}}{{\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{s} I_{{{\text{sc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\}}} - \frac{{I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\}} \right]}}{{\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\}}} \\ & \quad - \frac{{I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\}} \right]}}{{\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\}}} \\ \end{aligned}$$
(18)

The photocurrent equation is obtained by substituting Eq. 18 in Eq. 19 and is written as follows.

$$\begin{aligned} I_{{\text{p}}} & = I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] \\ & \quad + \left[ {\frac{{I_{{{\text{sc}}}} + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }} - \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }}}}{{\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\}}} - \frac{{I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\}} \right]}}{{\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\}}}} \right. \\ & \quad \left. { - \frac{{I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{s} I_{{{\text{sc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\}} \right]}}{{\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - \exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\}}}} \right]\left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }} \\ \end{aligned}$$
(19)

During case-3, substitute Vpv = Vmpp and Ipv = Impp in Eq. 15, and the equation for the total current of the PV module is written as follows.

$$\begin{aligned} I_{{{\text{mpp}}}} & = I_{{\text{p}}} - I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] - I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] \\ & \quad - I_{{{\text{d}}_{3} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{3} kTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{R_{{\text{p}}} }} \\ \end{aligned}$$
(20)

Following a comprehensive study of literature, the models, such as SDM, DDM, and TDM for the PV modules, are used to estimate parameters because of their simplicity and accuracy. No literature discusses the TDM mathematical model of the photovoltaic module for three operating regions. This is one of the unique contents of this article.

2.2 Manufacturers datasheet information

In the present study, three distinct types of commercial PV modules are considered in India, such as monocrystalline, polycrystalline, and bifacial PV modules. Three PV modules are selected due to their availability in the commercial market of India. However, the proposed algorithm can be used for estimating the parameters of any PV modules at any PV capacity. The typical manufacturer’s information is shown in Table 1. It is to be remembered that, under standard test conditions (STC), i.e. 25 °C temperature and 1000 W/m2 solar radiation, the voltage and current data at three operating points, such as open-circuit, short-circuit, and maximum power point (MPP), are clearly mentioned in the datasheet provided by the manufacturer.

Table 1 Electrical specification of the selected PV modules
Full size table

2.3 Objective function

The objective is to precisely extract the PV module parameters in order to enable data shown in Table 1 to be fulfilled in three cases: open-circuit, short-circuit, and MPP. In the objective function formulation, all three operating conditions are considered, which is considered a unique point in this paper. Because some of the researchers in the literature extracted the parameters of the PV modules by considering the MPP alone. The parameters to be optimized and the parameters estimated using the proposed EO algorithm are listed in Table 2 for the PV models, such as SDM, DDM, and TDM. For instance, three parameters to be optimized (n, Rs, and Rp) and two parameters to be estimated (Ip and Id) for the SDM, five parameters to be optimized (n1, n2, Id1, Rs, and Rp), and two parameters to be estimated (Ip and Id2) for the DDM, and seven parameters to be optimized (n1, n2, n3, Id1, Id2, Rs, and Rp) and two parameters to be estimated (Ip and Id3) for the TDM. The estimated parameters are derived from the operating points at the open-circuit and short-circuit. Table 2 provides detailed information about the analytical calculation along with its respective equation.

Table 2 Optimized and calculated variables for the SDM, DDM, and TDM
Full size table

The target strategies shall ensure that the photovoltaic module results in all three operating points comply with the I–V relationship. The parameters estimated must generate the voltage and current data of the operating environment, such as short-circuit, open-circuit, and MPP following V–I relationships. Therefore, a more sophisticated optimization algorithm is necessary to minimize errors at three operating points. The error functions at the short-circuit, open-circuit, and MPP, respectively, are obtained as follows for the SDM.

$$E_{{{\text{SC}}}} = I_{{{\text{sc}}}} + I_{{\text{d}}} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }} - I_{{\text{p}}}$$
(21)
$$E_{{{\text{OC}}}} = I_{{\text{d}}} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }} - I_{{\text{p}}}$$
(22)
$$E_{{{\text{MPP}}}} = I_{{\text{p}}} - I_{{\text{d}}} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{nkTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{R_{{\text{p}}} }} - I_{{{\text{mpp}}}}$$
(23)

Similarly, the error functions at the short-circuit, open-circuit, and MPP, respectively, for the DDM are obtained as follows.

$$E_{{{\text{SC}}}} = I_{{{\text{sc}}}} + I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }} - I_{{\text{p}}}$$
(24)
$$E_{{{\text{OC}}}} = I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }} - I_{{\text{p}}}$$
(25)
$$E_{{{\text{MPP}}}} = I_{{\text{p}}} - I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] - I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{R_{{\text{p}}} }} - I_{{{\text{mpp}}}}$$
(26)

Similarly, the error functions at the short-circuit, open-circuit, and MPP, respectively, for the TDM are obtained as follows.

$$E_{{{\text{SC}}}} = I_{{{\text{sc}}}} + I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{3} }} \left[ {\exp \left\{ {\frac{{qR_{{\text{s}}} I_{{{\text{sc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{R_{{\text{s}}} I_{{{\text{sc}}}} }}{{R_{{\text{p}}} }} - I_{{\text{p}}}$$
(27)
$$E_{{{\text{OC}}}} = I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{1} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] + I_{{{\text{d}}_{3} }} \left[ {\exp \left\{ {\frac{{qV_{{{\text{oc}}}} }}{{n_{3} kTN_{{\text{s}}} }}} \right\} - 1} \right] + \frac{{V_{{{\text{oc}}}} }}{{R_{{\text{p}}} }} - I_{{\text{p}}}$$
(28)
$$\begin{aligned} E_{{{\text{MPP}}}} & = I_{{\text{p}}} - I_{{{\text{d}}_{1} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{1} kTN_{s} }}} \right\} - 1} \right] - I_{{{\text{d}}_{2} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{2} kTN_{{\text{s}}} }}} \right\} - 1} \right] \\ & \quad - I_{{{\text{d}}_{3} }} \left[ {\exp \left\{ {\frac{{q\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{n_{3} kTN_{{\text{s}}} }}} \right\} - 1} \right] - \frac{{\left( {V_{{{\text{mpp}}}} + I_{{{\text{mpp}}}} R_{{\text{s}}} } \right)}}{{R_{{\text{p}}} }} - I_{{{\text{mpp}}}} \\ \end{aligned}$$
(29)

The objective or error function for all SDM, DDM, and TDM is written as follows.

$$E = E_{{{\text{SC}}}}^{2} + E_{{{\text{OC}}}}^{2} + E_{{{\text{MPP}}}}^{2}$$
(30)

Using data from the manufacturer’s datasheet, the error function value is reduced as small as possible. The PV module parameters are estimated to change the variables generated by the solution vectors, E as small as possible, by optimizing the parameters (i.e. 3 parameters for SDM, 5 parameters for DDM, and 7 parameters for TDM).

3 Opposition-based equilibrium optimizer (OBEO) and its applications in parameter estimation problem

3.1 Concept of EO algorithm

Another meta-heuristic algorithm that inspires in the laws of physics, namely the equilibrium optimizer (EO), is presented in [47]. EO uses a mass balance equation to calculate the numbers of mass inputs, generates in volume over time, and attempts to find the status which achieves the equilibrium state. The calculation is based on a dynamic mass balance on the control volume. EO is holding the advantages known as a good algorithm, such as balancing, efficiently implementing, and diversity among individuals in a population by exploration and exploitation operators. It can, therefore, be used in real-world problems to solve many problems of optimization, like image segmentation, DNA fragmentation assembly problem, power systems, and so on. In this paper, the performance of the EO algorithm is reviewed for the solar photovoltaic parameter estimation problems. More details on the inscription of EO can be found in [47]. The following three steps to be followed to model the EO algorithm mathematically.

Step-1: Initialization EO takes a group of particles in this stage, in which each particle constitutes the concentration vector containing the solution to the problem of optimization. Randomly in the search area, the initial concentration vector is generated with the following formula.

$$X_{i}^{{{\text{initial}}}} = X_{{{\text{lb}}}} + \left( {X_{{{\text{ub}}}} - X_{{{\text{lb}}}} } \right) \times {\text{rand}}_{i} ,\quad i = 0, 1, 2, \ldots {\text{np}}$$
(31)

where \(X_{i}^{{{\text{initial}}}}\) denotes the concentration vector of the particle, i, lb, and ub denote lower and upper limit for each dimension, np denotes the number of particles and a random number of the ith particle in range of [0,1].

Step-2: Equilibrium pool and candidates (\(\vec{D}_{{{\text{eq}},{\text{pool}}}}\)) There is an aim for each meta-heuristic algorithm intended to achieve based on its architecture. For instance, GWO, WOA, ALO searches for prey [39,40,41]. In [29], the bee searches for the source of food. Similarly, EO is searching for a system equilibrium. EO can achieve a near-optimal solution to the optimization problem when it reaches an equilibrium state. EO does not know the concentration level that attains an equilibrium state during the optimization process. Therefore, it assigns such candidates of the four most productive particles found in the optimizing process, plus a further particle, whose concentration is the arithmetic mean of the four particles. The four candidates and the average candidate support the EO algorithm to improve exploration and exploitation capability. Finally, such five particles are nominated for equilibrium and used to create a vector known as the equilibrium pool.

$$\vec{D}_{{{\text{eq}},{\text{pool}}}} = \left\{ {\vec{D}_{{{\text{eq}},(1)}} ,\vec{D}_{{{\text{eq}},(2)}} ,\vec{D}_{{{\text{eq}},(3)}} ,\vec{D}_{{{\text{eq}},(4)}} ,\vec{D}_{{{\text{eq}},({\text{avg}})}} } \right\}$$
(32)

Every particle updates its concentration in every iteration with a random choice of candidates with the same probability. The particle undergoes an update process by the end of the optimization process, with all the candidate solutions receiving around a similar number of updates.

Step-3: Concentration update The exponential term (F) is the next term contributing to the key concentration updating rule. A proper definition of this term helps EO to balance exploitation and exploration reasonably. As the turnover rate can vary with time in an accurate control volume, the λ random vector is assumed at [0,1] interval.

$$\vec{F} = e^{{ - \vec{\lambda }\left( {t - t_{0} } \right)}}$$
(33)

where t is a time and is defined as a function of iteration (l), therefore, t is decreased with an increase in the number of iterations.

$$t = \left[ {1 - \frac{l}{{l_{\max } }}} \right]^{{\left( {a_{2} \times \frac{l}{{l_{\max } }}} \right)}}$$
(34)

where the current iteration is denoted by l, the maximum iteration is denoted by lmax, and the constant that manages the ability of exploitation is denoted by a2. This study also considers convergence by slowing the search speed and enhancing the exploitation and exploration ability of the algorithm.

$$t_{0} = \frac{1}{{\vec{\lambda }}}\ln \left( { - a_{1} {\text{sign}}\left( {\vec{r} - 0.5} \right)\left[ {1 - e^{{ - \vec{\lambda }t}} } \right]} \right) + t$$
(35)

where the value which controls the ability of exploration is denoted by a1. The exploration ability is improved by increasing the value of a1, while exploitation performance is reduced. Similarly, the exploitation ability is increased by increasing the a2, however, the exploration performance is reduced. The random vector is denoted by \(\vec{r}\) and varied between [0,1]. The values of a1 and a2 are selected as 2 and 1, respectively, in this paper. The generation rate (Gr) is used to deliver a precise solution by refining the phase of exploitation.

$$\vec{G}_{r} = \vec{G}_{0} e^{{ - \vec{\lambda }\left( {t - t_{0} } \right)}}$$
(36)

where the initial value is represented by R0 and is derived as follows.

$$\vec{G}_{0} = \overrightarrow {{{\text{GRCP}}}} \times \left( {\vec{D}_{{{\text{eq}}}} - \vec{\lambda } \times \vec{D}} \right)$$
(37)
$$\overrightarrow {{{\text{GRCP}}}} = \left\{ {\begin{array}{*{20}l} {0.5r_{a} } \hfill & {\quad r_{b} > {\text{RP}}} \hfill \\ 0 \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(38)

where the random numbers are represented as ra and rb and vary between [0,1]. The generation rate control parameters are denoted as \(\overrightarrow {{{\text{GRCP}}}}\) that finds whether Gr is applied to the update rate based on the rate of probability, RP. Lastly, EO is updated using the following equation.

$$\vec{D} = \vec{D}_{eq} + \left( {\vec{D} - \vec{D}_{eq} } \right) \times \vec{F} + \frac{{\overrightarrow {G}_{r} }}{{\overrightarrow {\lambda } \times V}} \times \left( {1 - \vec{F}} \right)$$
(39)

where the value of V is equal to 1. The detailed information can be found in [47]. The pseudocode of the basic version of the EO algorithm is shown in the Algorithm.

figure a

3.2 Opposition-based learning

The OBL framework was established to develop heuristic methods to discover a global optimization solution. Meta-heuristic methods produce an initial population, including random solutions, to find the optimal solution. Nevertheless, initial solutions are created randomly or based on past knowledge, including location search or other variables. In the absence of such details, these approaches cannot converge to an optimal global since they operate randomly in solution space. Such strategies are also time-consuming since they depend on the discrepancy between the existing and best solutions. The OBL suggests a strategy to address these problems opposite the current solution, so the result gets closer to a real solution, and the convergence becomes better. The opposite real number x ∈ [lb, ub] is represented as \(\overline{x }\) and is stated as follows.

$$\overline{x} = {\text{ub}} + {\text{lb}} - x$$
(40)

For multi-dimensional search space, Eq. 40 can be modified in Eq. 41.

$$\overline{x}_{i} = {\text{ub}}_{i} + {\text{lb}}_{i} - x_{i} ,\quad i = 1,2, \ldots ,D$$
(41)

The \(\overline{{x }_{i}}\) is substituted with the respective x reliant on the objective function. If f(x) is larger than f(\(\overline{x }\)), then x is same, else x = \(\overline{x }\). Consequently, population solution is altered based on the best values of \(\overline{x }\) and x.

3.3 Proposed OBEO algorithm

The traditional EO algorithm has some drawbacks, such as being stuck in the optimal local solution, time-consuming, and slow convergence. Such constraints are based on the fact that, while a few solutions are excluded from this solution, particular solutions are changed to optimal solutions. However, considering the opposite direction, the proposed methodology eliminates such drawbacks. The OBEO algorithm combines the simple version of EO's search features with OBL to enhance exploration. The suggested methodology has fewer parameters to be modified than similar strategies, and the implementation of OBL does not affect the EO requirement, although the optimum solution's efficiency is increased. In this sense, the initial population's size due to increasing convergence could still be decreased to the optimum solution, as OBEO can broadly explore the search space. The presented approach improves the EO algorithm over two stages: initially, the OBL is being used to improve the convergence rate in the initialization of the population and avoid trapping in the optimal local. Second, OBL was used to update the population method to evaluate if the opposite direction transition is greater than the present development. The overall process of the OBEO algorithm is illustrated in Fig. 4. The variables required to utilize the OBEO algorithm for the above-said problem are listed in Table 3.

Fig. 4
figure 4

Flowchart of the OBEO algorithm

Full size image
Table 3 Input parameters of the EO algorithm
Full size table

The use of a broader range of decision variables leads to greater fitness measures for optimizing SDM, DDM, and TDM. The EO algorithm suggested that the particle number, np be 10 times the problem dimension [47]. Therefore, the number of particles is selected after several trials for good performance. The EO algorithm is executed by MATLAB 9.4, and the simulations are carried out via a laptop with Core i5-4210 and 4 GB RAM.

4 Simulation results and performance comparisons

The simulation results of the proposed OBEO algorithm were applied to the different commercial PV modules, such as SDM, DDM, and TDM. To check the validity of the proposed algorithm, 20 individual runs of simulation are carried out. The I–V characteristic of the different PV modules is developed by utilizing the steps as follows.

  1. a.

    Select and categorize the optimized parameters and estimated parameters for each PV models

  2. b.

    Reduce the voltage in steps of 1 V from zero to Voc and assign the maximum output voltage of the module as Voc

  3. c.

    For each discrete value of the output voltage of the module, the parameters are optimized by solving Eq. 1. The MATLAB command ‘FSOLVE’ is used to solve the equations

  4. d.

    As the maximum power point voltage is not chosen in the output voltage of the module due to the fractional Vmpp, the output current is individually calculated for the voltage at MPP.

  5. e.

    Repeat steps b–d for other sets of parameters to be optimized.

The control parameters of various algorithms are listed in Table 4 for the simulation study, and it has been selected after several trials of the algorithms. The stopping criteria of each algorithm are set by a maximum number of iterations. The search agents are selected based on 5–10 times the problem dimension.

Table 4 Various parameters of algorithms for the parameter estimation problems
Full size table

4.1 Results of the single-diode model

The I–V characteristics of the ASB-7–355 PV module for 20 individual runs are depicted in Fig. 5, and the variations in I–V characteristics are not only due to the values of the Rp and Rs but also the ideality factor of the diode, n. The optimized and estimated parameters of the ASB-7-355 PV module are listed in Table 5. It is observed from Table 5 that the limitations on three points are all seen for all the PV module parameter sets.

Fig. 5.
figure 5

Twenty feasible I–V curves of the ASB-7-355 PV module for the SDM

Full size image
Table 5 Calculated and optimized parameters of the ASB-7-355 PV module for the SDM
Full size table

As illustrated in Fig. 5, the I–V characteristic of 20 individual runs is passed through the points, such as 0 V, 9.74 A; 37.9 V, 9.37 A; 46.4 V, 0 A. Figure 6a displays a scatter plot and shows how the optimized parameters are distributed across the algorithm's search space. During each run, the solution set reaches zero error at the operating points. It is discussed that there may be one I–V characteristic is shown in most of the literature. However, the solution is not unique, and therefore, the I–V curve is also not unique when the three points on I–V are considered. There are multiple numbers of I–V curves in Fig. 5, and each curve has an optimal solution. In reality, there will be only one I–V curve matching to its equivalent circuit parameters. However, as long as the experimental values are available, the researcher can extract the unique I–V curve. In this paper, the I–V curve is extracted only when the target error reaches zero while optimizing the parameters of the module. The I–V curve accuracy can be increased by selecting many points on the I–V characteristic. However, all the optimal parameter is considered to be sufficient since most of the researchers target primarily on the MPPs. Therefore, one of the optimal curves (best solution obtained from the 20 individual runs) is compared with the I–V curve provided in the manufacturer datasheet. The same is illustrated in Fig. 6b. It is observed from Fig. 6b that the estimated curve and the curve provided by the manufacturer are almost matching. From Fig. 6a, it is observed that a wide search has occurred on the shunt resistance, Rp.

Fig. 6
figure 6

SDM of the ASB-7-355 PV module; a scattered plot; b I–V curve comparison between estimated and datasheet

Full size image

The same study is extended to the other two commercial PV panels, such as TP280 and ASM-7-PERC-365 PV panels. During 20 individual runs, the I–V curves are illustrated in Fig. 7, and observed that all the curves are passes through the operating points, such as 0 V, 9.93 A; 39 V, 9.36 A; 47.31 V, 0 A. The calculated and optimized parameters of the PV module during 20 individual runs are listed in Table 6. As discussed, the optimum parameters of the PV module are extracted by targeting zero value at the above-said operating points during 20 individual runs.

Fig. 7.
figure 7

Twenty feasible I–V curves of the ASM-7-PERC-365 PV module for the SDM

Full size image
Table 6 Calculated and optimized parameters of the ASM-7-PERC-365 PV module for the SDM
Full size table

The normalized values of the optimized parameters during 20 individual runs are illustrated in Fig. 8a. It is observed from Fig. 8a that the wide search has happened in series resistance and diode ideality factor. Similarly, the estimated I–V curve is compared with the I–V curve in the datasheet provided by the manufacturer and is illustrated in Fig. 8b.

Fig. 8
figure 8

SDM of the ASM-7-PERC-365 PV module; a scattered plot; b I–V curve comparison between estimated and datasheet

Full size image

As similar to the previous discussion, The I–V characteristics of the TP280 PV module are illustrated in Fig. 9 for 20 individual runs. The optimized and calculated parameters of the same PV module are listed in Table 7 for all runs.

Fig. 9.
figure 9

Twenty feasible I–V curves of the TP280 PV module for the SDM

Full size image
Table 7 Calculated and optimized parameters of the TP280 PV module for the SDM
Full size table

The scatter plot of the parameters optimized during 20 individual runs is displayed in Fig. 10a. The distribution of the optimized parameters is wider in the given range and finds the optimal value by targeting the zero error in the operating points, such as 0 V, 8.33 A; 36.1 V, 7.78 A; 44.5 V, 0 A. The I–V curve comparison between the estimated and manufacturer datasheet is illustrated in Fig. 10b.

Fig. 10
figure 10

SDM of the TP280 PV module; a scattered plot; b I–V curve comparison between estimated and datasheet

Full size image

To check the superiority of the proposed algorithm, the scattered plot of all algorithms for all the PV modules is illustrated in Figs. 6a, 8a, and 10a, respectively. It is observed from the scatter plot that the proposed OBEO algorithm is widely searching for the solution in the search space provided during 20 individual runs. The optimal solutions provided by the OBEO algorithm are acceptable compared to other algorithms discussed in the literature.

4.2 Results of the double-diode model

As similar to SDM, the simulation is also carried out for DDM of all the PV modules listed in Table 1. First, the I–V curves for all 20 individual run of the ASB-7-355 PV module. As shown in Fig. 11, all the I–V curves pass through the operating points, such as 0 V, 9.74 A; 37.9 V, 9.37 A; 46.4 V, 0 A. The estimated and optimized parameters during 20 runs are listed in Table 8 for ASB-7-355 PV modules with the error value during all 20 runs of the algorithm. It is observed that the algorithm can achieve zero error during all the runs by optimizing the parameters.

Fig. 11.
figure 11

Twenty feasible I–V curves of the ASB-7-355 PV module for the DDM

Full size image
Table 8 Calculated and optimized parameters of the ASB-7-355 PV module for the DDM
Full size table

Each I–V characteristic is different, and it can be attributed not only due to the variation in shunt and series resistance of the module but also to the diode saturation current and ideality factor. The normalized values of all the optimized parameters are illustrated in Fig. 12a. The parameter search is spread across a wide range of given search spaces. A wide range of searches has occurred on the shunt resistance and the diode saturation current of the module. It is also observed from Table 8 that zero error is achieved during all individual runs of the simulation. To check the effectiveness of the proposed algorithm, one of the best solutions achieved during 20 runs is compared with the I–V curve provided by the manufacturer, and the same is illustrated in Fig. 12b.

Fig. 12
figure 12

DDM of the ASB-7-355 PV module; a parallel coordinated plot; b I–V curve comparison between estimated and datasheet

Full size image

The simulation is also carried out for the PV modules, such as ASM-7-PERC-365 and TP280. The I–V characteristics of the ASM-7-PERC-365 PV module for all individual runs are illustrated in Fig. 13, and it is observed that all the I–V curves are passes through the points, such as 0 V, 9.93 A; 39.01 V, 9.36 A; 47.31 V, 0 A. Besides, the estimated and optimized parameters of the module for all runs are listed in Table 9. As similar to the previous discussion, the algorithm can extract the parameters by achieving zero error during all the runs.

Fig. 13.
figure 13

Twenty feasible I–V curves of the ASM-7-PERC-365 PV module for the DDM

Full size image
Table 9 Calculated and optimized parameters of ASM-7-PERC-365 module for the DDM
Full size table

The normalized values of the optimized parameters are illustrated in Fig. 14a, in which the wide search has happened at diode saturation current, diode ideality factors, and shunt resistance of the module. The variation of diode saturation current is dominant during all individual runs; however, the impact on the I–V curve is significantly less due to its less magnitude. The comparison is made between one of the best solutions obtained so far and the I–V curve provided by the manufacturer, and the same is illustrated in Fig. 14b.

Fig. 14
figure 14

DDM of the ASM-7-PERC-365 PV module; a parallel coordinated plot; b I–V curve comparison between estimated and datasheet

Full size image

As similar to the previous discussion, the I–V characteristics of the TP280 PV module for DDM are illustrated in Fig. 15 for 20 individual runs. The optimized and calculated parameters of the same PV module are listed in Table 10 for all runs. The normalized value plot of the parameters optimized during 20 individual runs is displayed in Fig. 16a. The distribution of the optimized parameters is wider in the given range and finds the optimal value by targeting the zero error in the operating points, such as 0 V, 8.33 A; 36.1 V, 7.78 A; 44.5 V, 0 A. The wide search has happened at diode saturation current and shunt resistance of the PV panel. The comparison between one of the best estimated I–V curves and the I–V curve given in the manufacturer datasheet is illustrated in Fig. 16b.

Fig. 15.
figure 15

Twenty feasible I–V curves of the TP280 PV module for the DDM

Full size image
Table 10 Calculated and optimized parameters of the TP280 PV module for the DDM
Full size table
Fig. 16
figure 16

DDM of the TP280 PV module; a parallel coordinated plot; b I–V curve comparison between estimated and datasheet

Full size image

To check the superiority of the proposed algorithm, the parallel coordinated plot of the OBEO algorithm for all the PV modules is illustrated in Figs. 12a, 14a, and 16a, respectively. It is observed from the parallel coordinated plot that the proposed OBEO algorithm is widely searching for the solution in the search space provided during 20 individual runs. The optimal solutions provided by the OBEO algorithm are acceptable compared to other algorithms discussed in the literature. The detailed statistics results of all the algorithms are presented in the further subsection of this paper for better understanding. The solutions provided by the DDM are more accurate than the solutions provided by the SDM of all the PV modules.

4.3 Results of the three-diode model

As discussed in the literature, the solution accuracy of the TDM is more than the solution provided by the SDM and DDM of the PV modules. The simulation is also carried out for the TDM of all the PV modules presented in Table 1. The proposed OBEO algorithm optimizes seven variables. Two other variables are estimated or calculated based on the relation between the estimated data and optimized data. The I–V curves of the ASB-7-355 PV module during all 20 runs are illustrated in Fig. 17 and observed that all I–V curves are successfully passed through the operating points, such as 0 V, 9.74 A; 37.9 V, 9.37 A; 46.4 V, 0 A. The estimated or calculated parameters and the optimized parameters of the OBEO algorithm for all 20 runs are listed in Table 11. It is observed from Table 10 that the OBEO algorithm can able to achieve zero error during all the runs by optimizing the seven parameters. Based on these seven optimized parameters, the other two parameters are calculated and listed in Table 11.

Fig. 17.
figure 17

Twenty feasible I–V curves of the ASB-7-355 PV module for the DDM

Full size image
Table 11 Calculated and optimized parameters of the ASB-7-355 PV module for the TDM
Full size table

The normalized values of the optimized parameters of the ASB-7-355 PV module are illustrated in Fig. 18a. As observed in Fig. 18a, the wide search has happened at the diode’s saturation current, such as Id1 and Id2, and the normalized values vary between 0.01 and 0.95 p.u. Since the magnitude of these currents is very small, there will not be much impact on the I–V curves of the PV module. The comparison between one of the best solutions obtained so far and the I–V curve provided in the datasheet is illustrated in Fig. 18b to check the effectiveness of the OBEO algorithm.

Fig. 18
figure 18

TDM of the ASB-7-355 PV module; a parallel coordinated plot; b I–V curve comparison between estimated and datasheet

Full size image

The simulation is also carried out for the three-diode model of the TP280 and ASM-7-PERC-365 PV modules, and the I–V curves of both modules during all 20 individual runs are illustrated in Figs. 19 and 20, respectively. It is observed from Figs. 19 and 20 that all 20 I–V curves are passes through the three operating points of the PV module, such as 0 V, 9.93 A; 39.01 V, 9.36 A; 47.31 V, 0 A, and 0 V, 8.33 A; 36.1 V, 7.78 A; 44.5 V, 0 A, respectively. The seven optimized parameters and two estimated parameters and the error values of the PV modules are listed in Tables 12 and 13, respectively, for 20 runs and observed zero error while optimizing the parameters during all 20 runs of the simulation.

Fig. 19.
figure 19

Twenty feasible I–V curves of the ASM-7-PERC-365 PV module for the TDM

Full size image
Fig. 20.
figure 20

Twenty feasible I–V curves of the TP280 PV module for the TDM

Full size image
Table 12 Calculated and optimized parameters of the ASM-7-PERC-365 PV module for the TDM
Full size table
Table 13 Calculated and optimized parameters of the ASM-7-PERC-365 PV module for the TDM
Full size table

To understand the distribution of the optimized parameters, normalized values of both modules are plotted in parallel coordinated plots, and the same is displayed in Figs. 21a and 22a, respectively. For both the modules, the wide search has happened at the reverse saturation currents of the diode for both PV modules. Since the magnitude of such currents is very small, the impact on the I–V curve is also very small. The comparison between the estimated I–V curve and the I–V curve provided in the PV modules datasheet is illustrated in Figs. 21b and 22b.

Fig. 21
figure 21

TDM of the ASM-7-PERC-365 PV module; a parallel coordinated plot; b I–V curve comparison between estimated and datasheet

Full size image
Fig. 22
figure 22

TDM of the ASM-7-PERC-365 PV module; a parallel coordinated plot; b I–V curve comparison between estimated and datasheet

Full size image

In short, irrespective of which PV module types we consider or which PV models (SDM, DDM, and TDM) for parameter estimation problems we follow, no single I–V curve could be obtained for the specific module with three different operating points. The parameter optimization based on the datasheet information, i.e. three operating points, such as Voc, Isc, Vmpp, and Impp, always results in various I–V curves during all simulation runs.

4.4 Comparison study

To prove the effectiveness of the proposed OBEO algorithm applied to parameter estimation problems is compared with other state-of-the-art meta-heuristic algorithms, such as ALO, GWO, EO, and WOA, and hybrid algorithms, such as PSOGWO and GWOCS. All the algorithms use the same objective function to minimize the error by targeting zero error. All the PV models, such as SDM, DDM, and TDM for the optimization problems of the PV modules, such as ASB-7-355, ASM-7-PERC-365, and TP280 are discussed in this paper.

For better comparison, the statistical results of different algorithms are listed in Table 14. The algorithms, such as OBEO and EO, can produce almost zero error during 20 individual runs. However, EO fails to produce zero error for TDM of the PV modules. Next to OBEO and EO, the algorithms, such as ALO, WOA, PSOGWO, GWO, and GWOCS, show less errors during all runs of the simulation. The worst error values of ALO, WOA, PSOGWO, GWO, and GWOCS algorithms range from 10−25 to 10−11. This error can also be seen as a zero error for all practical applications. Table 14 concludes that in three operating points, the intended results of the PV module can be obtained with different PV parameter sets, irrespective of the algorithm used. The CPU run time of 20 runs for all the algorithms is listed in Table 14. From Table 14, it is observed that the proposed OBEO algorithm is quickest, followed by GWOCS, GWO, PSOGWO, WOA, EO, and ALO. Nevertheless, this paper aims not to assert OBEO’s superiority over other algorithms but instead to show that datasheet information is insufficient to determine the characteristic of I–V on just three points of the PV module. In order to rank the algorithms, Friedman’s rank test (FRT) is carried out based on the minimum fitness values. FRT is a nonparametric tool for determining error variations through several trials. The term nonparametric refers to a test that does not presume the data comes from a specific distribution. The ranking of all algorithms is provided in Table 14.

Table 14 Summary of the statistical results of various algorithms
Full size table

From Table 14, it is observed that the proposed OBEO algorithm performs better for all PV models in terms of Min, standard deviations, runtime, and FRT rank, followed by EO, ALO, WOA, PSOGWO, GWO, and GWOCS. The minimum value of standard deviation indicates the reliability of the algorithms. Based on obtained Min and standard deviation values, it is concluded that the proposed OBEO algorithm is a robust tool for estimating the parameters of the solar PV module.

5 Conclusion

This paper presents an estimation of the PV module parameters by using the datasheet information at three I–V operating points, such as Isc, Voc, and MPP, by applying the selected meta-heuristic algorithms. The optimization of parameters is carried out for the three different PV models of three different commercial PV modules. For all the PV models, partial parameters are estimated (2 for all PV models) through the analytical method, and partial parameters are optimized (3 for SDM, 5 for DDM, and 7 for TDM) through optimization algorithms. The application of the OBEO algorithm for the parameter estimation problem is explained in detail, whereas other algorithms, such as GWO, ALO, WOA, EO, PSOGWO, and GWOCS, are directly applied to the parameter estimation problem without any comprehensive explanation. The simulation study and further statistical analysis showed that no single I–V curve is possible with a few information from the manufacturer datasheet. The I–V relation would be satisfied by different sets of optimum parameters at all three points. Therefore, the researcher can select any one of the optimal set of parameters from the set of results for their further applications. For an accurate and unique I–V curve of the PV module, more experimental data are required. Although the studies are carried out in standard testing conditions for the PV modules, the results are also valid for other solar irradiation and temperature. Many optimal parameter sets can be achieved at any temperature or solar irradiation in several runs, and the I–V relation in three points can be followed by each parameter set.

In future studies, the proposed OBEO algorithm can also be applied to other engineering problems, such as optimal power flow, charge scheduling, charging station placement in electric vehicles, economic load dispatch, power system stability, image enhancement, image segmentation, vehicle routing, and wireless sensor networks. Also, the OBEO algorithms can be extended as binary versions, multi-objective, and many-objective versions.