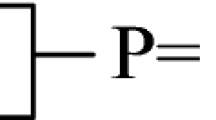1 Introduction

According Moore’s law that the number of transistors will be doubled on the chipsets every 18–24 months, the area occupied and energy losses of the chipsets are very important parameters. One of the methods suggested to reduce the occupied area, increasing speed, and reducing the complexity of the chipsets, is the use of multi-value logic (MVL) in circuit design. Ternary logic is one of the most popular multi-value logic that has attracted researchers in the recent years (Mc Hugh and Twamley 2005). Another issue that is very important in the design of integrated circuits which is increasingly getting significant, is the issue of power consumption and energy losses reduction otherwise the smallest loss of energy in VLSI circuits causes too much heat and thus reduces the life and efficiency of the circuits. A solution that has attracted the attention of many digital designers in the recent years is reversible circuits. Bennett (1973) has proven that circuit design in reversible form can remove the energy losses caused by missing information in the circuit. A circuit is reversible if the number of inputs is equal the number of outputs and there is a one-to-one correspondence between inputs and outputs (Amirthalakshmi and Raja 2018; Ariafar and Mosleh 2019; Islam et al. 2009; Karthikeyan and Jagadeeswari 2020; Noorallahzadeh and Mosleh 2019a, b; PourAliAkbar and Mosleh 2019).

Due to the prominent features of quantum reversible MVL circuits, so far many circuits including adders/subtractors (Asadi et al. 2020; Deibuk and Biloshytskyi 2015b; Haghparast et al. 2017; Khan 2008a; Khan and Perkowski 2007; Khan 2002; Lisa and Babu 2015; Monfared and Haghparast 2016, 2017a, b; Panahi et al. 2018), multipliers (Monfared and Haghparast 2019; Panahi et al. 2019), comparators (Deibuk and Biloshytskyi 2015a; Khan 2008b; Monfared and Haghparast 2015) as well as various base circuits and synthesis methods(Barbieri and Moraga 2020; Haghparast et al. 2017; Hu and Deibuk 2018; Khan 2014, 2020; Mercy Nesa Rani and Datta 2020; Mohammadi et al. 2008; Niknafs and Mohammadi 2013) have been designed and implemented. Full-adders are essential components of arithmetic and logic units and are the basis of almost all computing circuits so that designing an efficient full-adder can improve the efficiency of digital systems.

So far, several quantum reversible ternary full-adders have been designed which will be discussed in more details in Sect. 3. One of the major problems of all previous designs is the absence of full use of the capacity of the full-adder. A full-adder at the base of r is called comprehensive full-adder, if it is capable of receiving (r + 1) inputs and produce two outputs with different values. In this paper, we use this potential and propose a new reversible ternary full-adder which is called comprehensive reversible ternary full-adder (CRTFA). The most prominent feature of the proposed circuit compared to all previous traditional reversible ternary full-adders is that it does not produce an extra digit in consecutive additions and can therefore perform computations with the least circuit complexity and fastest speed compared to existing traditional reversible ternary full-adders. To show performance of the proposed quantum reversible ternary full-adder, an effective design of quantum reversible ternary coded decimal adder/subtractor is designed and implemented.

The contributions of this work is summarized as follows:

  • Introducing a novel approach for designing reversible ternary full-adder.

  • Presenting a new reversible 3-qutrit ripple carry adder (3-qutrit RCA) using the proposed reversible ternary full-adder.

  • Proposing a new reversible ternary coded decimal error detector circuit.

  • Providing effective circuits of reversible ternary coded decimal adder and subtractor using the proposed reversible 3-qutrit RCA and reversible ternary coded decimal error detector.

  • Developing a novel design of the reversible ternary coded decimal adder/subtractor using the proposed circuits.

The paper is composed of the following sections: In the second section, an overview of ternary logic, reversible logic, and quantum reversible ternary circuits are proposed. In the third section, we will review the previous reversible ternary full-adder/subtractor as well as reversible ternary code decimal adder/subtractor circuits. The proposed circuits including comprehensive reversible ternary full-adder as well as reversible ternary coded decimal adder, subtractor and adder/subtractor are provided in the fourth section. The full comparisons are presented in the fifth section. Finally, the paper finalizes with conclusions and future works.

2 Foundations of the research

In this section, we first introduce a background of ternary logic. In the following, the reversible logic is introduced, and finally, the quantum reversible ternary gates will be presented.

2.1 Ternary logic

Designing the first computational machines using ternary logic precedes the design of binary machines. Developed by Thomas Fowler in 1840 and Brusentzov in the 1950s and 1970s, these machines had a high speed and a low power consumption. With the advent of quantum computers, predictions suggest that reversible ternary logic will again be widely used for computing. In ternary logic, the smallest unit of memory is called Qutrit which can store three values of 0, 1, and 2 such that each of these values is represented by 3 × 1 vectors as |0 ≥ [1 0 0]T, |1 ≥ [0 1 0]T, |2 ≥ [0 0 1]T are displayed.

In general, a ternary n-Qutrit memory unit has 3n discrete states that are displayed as |0 0… 0 > , |0 0… 1 > and … |2 2… 2 > . In addition, all possible states of a ternary n-Qutrit system can be obtained by Tensor multiplication (Klimov et al. 2003).

A ternary GF3 is a algebraic structure containing a set of elements {0, 1, 2} with two addition and multiplication operations as in Table 1. It should be noted that GF3 operations are ternary (Monfared and Haghparast 2017a).

Table 1 (a) The addition and (b) multiplication of two ternary number
Full size table

2.2 Reversible logic

One of the main factors in designing VLSI circuits is the issue of power consumption and energy losses. Landauer relied on the thermodynamic technology to show that the design of digital circuits using conventional logic known as irreversible logic causes an unintended waste of electrical energy. In addition, he showed that the heat energy produced by the loss of one bit of information during processing is equal KTLn2 where K = 1.3807 × 10−23 (J/K) Boltzmann constant, and T absolute temperature (K) (Landauer 1961).

Bennet (1973) proved that in order to avoid energy loss in computational circuits, processes must be reversible; This means if one uses reversible logic gates, there will be no additional power consumption and no energy will be wasted. A gate is reversible if the number of inputs is equal the number of outputs and there is a one-to-one correspondence between them which means that the input vector can be obtained by output vector (Perkowski et al. 2001).

Feedback and fan-out in reversible logic are not allowed (fan-out = 1). The main application of reversible logic is in quantum computing because quantum circuits must be reversible. This method has been widely used in various fields of research such as optical computing, very low power CMOS design, DNA computing, quantum computing, thermodynamic technology, bioinformatics and nanotechnology (Biswas 2008; Babu and Mia 2016). Several criteria have already been proposed for the synthesis of reversible circuits, some of which are(Islam et al. 2009):

Gate count (GC) It is a measure that refers to the total number of reversible gates used in circuit design.

Number of constant inputs (CI) This criterion refers to the number of inputs that must be set to a constant value (0 or 1) to synthesize the logical function.

Number of garbage outputs (GO) Unwanted or unused outputs of the reversible gate (or circuit) are known as garbage outputs. In the other words, outputs that are only needed to maintain reversibility are called garbage outputs.

Quantum cost (QC) This criterion indicates the cost of a reversible logic circuit in terms of basic quantum gates.

Delay The delay of a logic circuit is the maximum number of gates in the path from each input line to each output line.

Hardware complexity (HC) This criterion refers to the total number of logical operations in a reversible circuit. In hardware complexity, the following terms are used:

α:

Number of two-input Ex-OR gates

β:

Number of two-input AND gates

γ :

Number of NOT gates

T:

total logical calculation

2.3 Quantum reversible ternary gates

In this section, the most important quantum reversible ternary gates are introduced.


(A) Quantum reversible ternary shift gate


If Z is initialized with values of 0, 1 or 2, then Z (01) replaces 0 and 1, Z (02) replaces 0 and 2, and finally Z (12) replaces values 1 and 2 (Table 2) (Khan and Perkowski 2007; Khan 2006). Conversions Z (+ 1) and Z (+ 2) sum up the initial states by values 1 and 2 (Table 3). As shown in Fig. 1, A is a quantum ternary shift gate input and the P is output that is Z conversion of the input A where Z can be one of the five above mentioned values, that is {Z (01), Z (02), Z (12), Z (+1), Z (+2)}.

Table 2 Different displacement functions in quantum reversible ternary logic
Full size table
Table 3 Quantum reversible ternary addition functions
Full size table
Fig. 1
figure 1

Schematic representation of a quantum reversible ternary shift gate

Full size image

Each of these conversions has a name based on what they do (Table 4), and the quantum cost of each of these conversions is 1.

Table 4 Different functions in quantum reversible ternary logic and their names
Full size table

(B) Quantum reversible ternary Muthukrishnan-Stroud gate (M-S gate)


A quantum reversible ternary M-S gate with two inputs that performs Z = {+ 1, + 2, 01, 02, 12} operation on one of the inputs where the other input having a value of 2. The quantum cost of this gate is also 1.

In addition, this gate was first introduced by Muthukrishnan and Stroud (2000), as shown in Fig. 2.

Fig. 2
figure 2

Quantum reversible ternary M-S gate (Muthukrishnan and Stroud 2000)

Full size image

(C) Quantum reversible ternary Feynman gate


Feynman’s quantum reversible ternary gate is presented in both normal and controlled modes as shown in Fig. 3a, normal condition is a quantum reversible ternary 2 × 2 gate where the first output is equal the first input and the second output is the sum of two inputs in the base 3. Its quantum cost is 4 (Khan 2006)

Fig. 3
figure 3

Different representations of the quantum reversible ternary Feynman gate and its implementation using the M-S gate. a Normal mode and b controlled mode (Khan 2006)

Full size image

As shown in Fig. 3b, in the controlled mode, that is a 3 × 3 quantum reversible ternary gate. The first output is the first input, the second output is the second input, and the third output is sum of second and third inputs in base 3 provided the first input has a value of 2, and otherwise it results in the third input. The quantum cost of this gate is also 4.


(D) Generalized quantum ternary gate (GTG)


The generalized quantum ternary gate is one of the most applicable quantum reversible ternary basic gates. It is a quantum reversible ternary 2 × 2 gate which its quantum realization is shown in Fig. 4. Depending on the value of the first input, three different basic operations can be performed on the other input, including {12, 02, 01, + 1, +2} (Khan 2004) .

Fig. 4
figure 4

GTG quantum reversible ternary gate a circuit structure and b its implementation using M-S gate (Khan 2004)

Full size image

(E) Quantum reversible ternary Toffoli gate


This gate, which is one of the important quantum reversible ternary gates, has been used in circuits in three different forms as follows (Miller et al. 2004):

Normal quantum reversible ternary Toffoli gate In this form, it has three main inputs and one implicit constant input whose two general symbols are shown in Fig. 5a. As can be seen, when two inputs A and B are 2, output R performs the Z transform of the input C. Moreover, as shown in Fig. 5b, the quantum cost of this gate is 5.

Fig. 5
figure 5

Normal quantum reversible ternary Toffoli gate a two different symbols and b realization using M-S gate (Miller et al. 2004)

Full size image

General quantum reversible ternary Toffoli gate In this form, it has three main inputs and one implicit constant input whose general symbol is illustrated in Fig. 6a. As can be observed, when two inputs A and B are equal the values specified in the corresponding circles, the output R performs Z transform on the input C. The quantum cost of this gate as shown in Fig. 6b, for each circle not equal 2, two units are added to the quantum cost of a Normal quantum reversible ternary Toffoli gate, which is 5.

Fig. 6
figure 6

General quantum reversible ternary Toffoli gate a general symbol and b realization using the normal quantum reversible ternary Toffoli gate (Miller et al. 2004)

Full size image

Four-input quantum reversible ternary Toffoli gate This gate has 4 main inputs and two implicit constant inputs whose general symbol is demonstrated in Fig. 7a. In this form, when the three inputs A, B and C are equal 2, the output S performs Z transform on the input D. As shown in Fig. 7b, the quantum cost of this gate is 9. In addition to calculate the quantum cost of this gate, for each circle that is opposite 2, two units are added to this quantum cost.

Fig. 7
figure 7

Four-input Toffoli quantum ternary-reversible gate a general symbol and b realization using M-S gate (Miller et al. 2004)

Full size image

(F) Quantum reversible ternary C2NOT gate


This quantum reversible ternary base gate was first introduced by Mandal et al. (2011). This gate has three main inputs. If inputs A and B are values 2 and 1, or 1 and 2, then the input C will be inverted (NOT (C)). Figure 8a shows the symbol of a quantum reversible ternary C2NOT gate and Fig. 8b shows its realization using the M-S gate. Moreover, its quantum cost is 8.

Fig. 8
figure 8

Quantum reversible ternary C2NOT gate a general symbol and b realization using M-S gate (Mandal et al. 2011)

Full size image

3 Previous works

Since the circuits presented in this paper have led to the implementation of the two main circuits of reversible ternary full-adder/subtractor and reversible ternary code decimal (TCD) adder/subtractor, this section reviews the background of these two main circuits.

3.1 An overview of reversible ternary coded decimal adder/subtractor

Because many people use the decimal system, so computing in the decimal system is one of the branches of computing in computer science. One way to implement it is to perform all the calculations in ternary and then convert the ternary results to decimal. This method requires that the decimal numbers be converted into ternary first. Compute on them and convert them to decimal, which is very time consuming and complex. To solve this problem, we convert these decimal numbers into ternary code to perform all computes directly on that code; which is called Ternary Code Decimal (TCD).

Table 5 assigns each 3-qutrit code to a decimal digit. A decimal K-digit, requires 3 K-qutrit in TCD for presentation. For example, the number 396 is displayed in TCD with 9 qutrits as 010100020 where each 3-qutrit group represents a decimal digit. Whenever a decimal number in a TCD is between 0 and 9, it is equivalent to its ternary. But a TCD number greater than 9 isn’t equivalent to a ternary number. Thus the ternary numbers 101 through 222, which are not in Table 5, have no meaning in TCD.

Table 5 3-qutrits ternary code decimal equivalent to decimal values
Full size table

Haghparast et al. (2017) presented a reversible TCD-adder. Its overall architecture is shown in Fig. 9. As can be seen, two 3-qutrit adder were used in the implementation of the scheme, which, after error detection by the Error Detector module, corrected for the output of the first 3-qutrit full-adder by another 3-qutrit adder by added with the number 17 = (122)3. However, if the output of the first 3-qutrit adder is within the permissible range of 0–9, then the second 3-qutrit adder will be added with the number 0 so that the output does not change.

Fig. 9
figure 9

Reversible TCD adder block diagram provided by Haghparast et al. (2017)

Full size image

In this design, 3-qutrit adders is designed, once with a carry input and again without a carry input, with quantum costs of 42 and 35, respectively, and the Error Detector module, which is one of the most important parts of any TCD adder, is designed in two different ways, as illustrated in Figs. 10 and 11.

Fig. 10
figure 10

Quantum representation of reversible ternary Error Detector circuit(approach#1) provided by Haghparast et al. (2017)

Full size image
Fig. 11
figure 11

Quantum representation of reversible ternary Error Detector circuit (approach#2) provided by Haghparast et al. (2017)

Full size image

In Fig. 10, all unauthorized states for Z0, Z1, and Z2, which are the outputs of first adder, are investigated, and if one of these states is generated, the number 17 is generated to be added to the output of the first adder, until the final output is corrected. The final quantum cost of the Error Detector circuit in this paper by this method is 38.

In the second method presented in Fig. 11, the permissible states for Z0, Z1, and Z2 are examined, and in the absence of these states, the number 17 is generated to be added to the output of the first adder, until the final output is corrected. The final quantum cost of the Error Detector circuit in this paper by this method is 21. Finally, using the above circuits, two different designs for TCD adder are presented which have a quantum cost of 115 and 98.These quantum costs include, respectively, the first 3-qutrit adder with carry input (quantum cost 42), the second 3-qutrit adder without carry input (quantum cost 35), and finally two different perspectives for the Error Detector block (quantum costs 38 and 21).

Panahi et al. (2018) presented a reversible TCD adder. The overall architecture is illustrated in Fig. 12. As shown in Fig. 12, in the implementation of this design, as in the previous design, two 3-qutritadder were used which, after error detection by the Error Detector block, corrected the output of the first 3-qutrit adder by another 3-qutrit adder will be added with 17 = (122)3. However, if the output of the first 3-qutrit adder is within the permissible range of 0 to 9, then the second 3-qutrit adder will be added with the number 0 so that the output does not change.

Fig. 12
figure 12

Reversible TCD adder block diagram provided by Panahi et al. (2018)

Full size image

In this design, 3-qutrit adder is designed in three different blocks with different conditions that have a quantum cost of 29, 22 and 14, respectively. The Error Detector block, which is one of the most important parts of any TCD adder, is also designed with the quantum cost of 16 shown in Fig. 13 and is exactly the same as the Error Detector block of the previous article. That is, when an error occurs in the output of the first adder, this circuit produces a number 17 to correct the error in the next adder.

Fig. 13
figure 13

Quantum representation of reversible ternary Error Detector block provided by Panahi et al. (2018)

Full size image

Finally, using the above circuits, a scheme for TCD adder is presented which has a quantum cost of 67. This quantum cost comprises the first 3-qutrit adder block with quantum cost 29, the second 3-qutrit adder block with quantum cost 22 and finally the Error Detector block with quantum cost 16. The third 3-qutrit adder block, is used for 9’s complement in decimal subtraction. So they first get the 9’s complement of B and then add the result to the digit A. Now if the result is invalid, it must be added by 18 to make the result valid. Finally, in this paper, a reversible TCD adder/subtractor circuit with a quantum cost of 91 is obtained.

4 Proposing reversible ternary circuits

In this section, we first introduce a novel reversible ternary full-adder, called Comprehensive Reversible Ternary Full-Adder (CRTFA). Then we implement a reversible 3-qutrit adder with 3-input, by three CRTFAs. Next, we present quantum reversible ternary coded decimal adder as well as a reversible ternary coded decimal error detector circuit. In the following, a reversible ternary coded decimal adder and a reversible ternary coded decimal subtractor are designed. Finally, by merging the last two circuits, we introduce an effective design of reversible ternary coded decimal adder/subtractor.

4.1 Proposing reversible 3-qutrit ripple carry adder

As discussed in previous section, one of the major problems of the previous reversible ternary full-adders is the absence of full use of the capacity of the ternary full adder; a full adder at the base of r is called a comprehensive full-adder if it is capable of receiving (r + 1) inputs and produce two outputs with different values. This important potential is being applied here and a comprehensive reversible ternary full-adder, called CRTFA is suggested which is capable of utilizing the full capacity of ternary computation. The most prominent feature of the proposed full-adder is that unlike all previous designs, it does not produce an extra digit in consecutive summaries; thereby computation is done with lowest circuit and fastest speed compared to existing full-adders. Moreover, using the proposed full-adder, we implement a reversible 3-qutrit ripple carry adder (3-qutrit RCA) which is able to sum three 3-qutrit numbers.

To design a reversible ternary full-adder with the above attributes, that is, a reversible ternary full-adder that can compute sum of three 1-qutrit and one Cin and produce one 1-qutrit and one Cout, we utilize the proposed reversible ternary half-adder in Fig. 14a. As Fig. 14a shows, quantum cost of this half-adder is 6 and it has one constant input and one garbage output. Moreover, two special cases of the proposed half-adder are given in Fig. 14b, c which are discussed in the following. The proposed half-adder, which is the basis of our designs in this article, works correctly for all of its input states. The proposed reversible ternary full-adder using three proposed half-adders is illustrated in Fig. 15.

Fig. 14
figure 14

Quantum realization of a the reversible ternary half-adder, b the reversible ternary semi half-adderblock#1 and c the reversible ternary semi half-adder block#2

Full size image
Fig. 15
figure 15

Quantum realization of a the comprehensive reversible ternary full-adder along with b its block diagram

Full size image

By connecting three proposed full-adders, we can easily design a reversible 3-qutrit RCA (as seen in Fig. 16).

Fig. 16
figure 16

Block diagram of the proposed reversible 3-qutrit RCA

Full size image

With a simple look at Fig. 16 and since the quantum cost of each CRTFA block is 18, therefore, the quantum cost of the proposed reversible 3-qutrit RCA is 54. This circuit is called the General 3-qutrit RCA.

Given that we suppose to use the proposed reversible RCA for designing reversible ternary coded decimal adder, so the values of C2, C1and C0 can only be 000 or 122, hence the values of A2, B2 and C2 will never be 2 and the values of C0 and C1 will never be 1. And since to implement any of the Qutrits, we have to use the half-adder at a quantum cost of 6, thus the semi half-adder block#1 in Fig. 14b can be used to generate A2, B2 and C2, which has a quantum cost of 5 and the semi half-adder block#2 in Fig. 14c can be used to generate C0 and C1, which has a quantum cost of 3. With the explanations provided if we were to remove never-to-be-seen scenarios from our general design, the quantum cost of the reversible 3-qutrit RCA for reversible ternary coded decimal adder is 45. This circuit is called the Optimized 3-qutrit RCA.

4.2 Proposing reversible ternary error detector circuit

In this section, we introduce the proposed reversible ternary Error Detector circuit, which is one of the most important parts of the reversible ternary code decimal adder. The proposed circuit is illustrated in Fig. 17 that its quantum cost is 15. This circuit works as follows: when an error occurs in the output of the first reversible 3-qutrit RCA, the Error detector circuit produces the number 17 to correct the error in the second reversible 3-qutrit RCA, but there are no other adders in this design, and all of that happens in the first adder. Just like the block diagram in Fig. 18. To implement this circuit, we first assume that the output is invalid. That is, we set the value of the constant input, which is supposed to detect the error, to 2. And then we examine the condition of the TCD number, which includes the following two conditions:

Fig. 17
figure 17

Quantum representation of the proposed error detection and correction block

Full size image
Fig. 18
figure 18

Proposed reversible TCD adder block diagram

Full size image
  1. 1.

    If Z2 (most valuable qutrit) is 0, that’s true.

  2. 2.

    If Z2 = 1, then the number is true if Z1 and Z0 are both 0. Figure 17 is exactly the way to implement these terms and generate numbers 17 or 0 to correct the existing TCD number at the output.

So the circuit designed in Fig. 17 can be analyzed as follows:

  1. 1.

    If v = 0, then the output is valid and the values of C2C1C0 will be equal 000.

  2. 2.

    If v = 2, the output is invalid and the values of C2C1C0 will be 122 (i.e. 17), to reproduce the correct value by adding this value to the inputs.

4.3 Proposing reversible TCD adder

Since the comprehensive reversible ternary full-adder that has been discussed in this article, instead of the addition of two numbers and a Cin, it brings out the sum of three numbers and one Cin. Therefore, in cases where we want to sum multiple sequential numbers, this kind of adder can be used. As it is observed in the previous designs, there are need two adders to design a reversible TCD adder. Therefore, due to the specific feature of the proposed adder, by using a proposed adder module can be done sum of two previous sequential additions. The block diagram of this operation is shown in Fig. 18.

Since the output of Fig. 18 is constantly changing, only when V = 0 output is valid and if V = 2, the output has an invalid value, which must be corrected. Note that in the designed circuit, V can never be 1.

In the block diagram of Fig. 18, two main blocks are observed. The adder block, which is a 3-qutrit RCA adder, is once designed generally (General Design), and again designed without cases that never occur (Optimized Design) and the detector block is represented by a new design that is better than earlier designs in terms of quantum cost.

4.4 Proposing reversible TCD subtractor

When we want to perform the subtraction operation using the addition operation, we will face with two challenges as follows:

  1. 1.

    The subtraction operation must be implemented by addition operation

  2. 2.

    The subtraction result may be a negative number while TCD values are inherently for unsigned numbers.

To solve these two problems, we operate in the following way. Assume A and B be two TCD number.

If A > B then \({\text{A}} - {\text{B}} = {\text{A}} + \left( {{\bar{\text{B}}} + 1} \right)\) and the result is between 0 and 9,while the result on the right side of this equation has a Carry more than the left side of it. To remove this Carry, we need to add it by the value 2. Since the position of the Carry is 27, we have to add the result by the value 54, that is:

$$\varvec{A} - \varvec{B} = \varvec{A} + \left( {\bar{\varvec{B}} + 1} \right) + 54 = \varvec{A} + \bar{\varvec{B}} + 55$$

To implement the above formula using a reversible 3-qutrit RCA with 3-input, the following must be done:

  1. (a)

    Inputs A remain unchanged.

  2. (b)

    Inputs B must be 2’s complemented.

  3. (c)

    The inputs C are given the maximum value, namely: 2223 = 2610 which is, of course, the 2’s complement of 0003 = 010.

  4. (d)

    We also fill the input of a Cin with a maximum value, means 2 (2’s complement of 0).

  5. e)

    Increase the Cout output (which has 27th position) by one unit.

Thus, the above formula is implemented with the 3-qutrit adder with 3-input provided as follows:

$$\varvec{A} + \bar{\varvec{B}} + 55 = \left[ {\varvec{ A} + \bar{\varvec{B}} + 26\left( {\varvec{C} = 222} \right) + 2\left( {\varvec{Cin} = 2} \right)} \right] + 27\left( {\varvec{Cout} = \varvec{Cout} + 1} \right)$$

If A < B, then \({\text{A}} - {\text{B}} = {\text{A}} + \left( {\bar{B} + 1} \right)\) and the result is negative andit will exceed 9. So the result of TCD and its ternary is not equal. Therefore, we acted exactly like the solution to the first problem and just instead of the number 2610 = 2223 to the inputs C, the number 910 = 1003(that is 2’s complement of numbers 1710 = 1223) is used. The following formula illustrates the proposed method for solving this challenge:

$$\varvec{A} + \bar{\varvec{B}} + 38 = \left[ {\varvec{ A} + \bar{\varvec{B}} + 9\left( {\varvec{C} = 100} \right) + 2\left( {\varvec{Cin} = 2} \right)} \right] + 27\left( {\varvec{Cout} = \varvec{Cout} + 1} \right)$$

By performing the above formula on negative numbers, Cout assigns a value of 2. So this (Cout = 2) indicates that the number is negative and the 3-qutrit final output is 10’s complemented of result. For example, if we want to get 3–5 in TCD method, we will do the following:

$$3 - 5 = 3\left( {010} \right)_{3} + \overline{{5\left( {012} \right)_{3} }} + 38\left( {1102} \right)_{3} = \left( {010} \right)_{3} + \left( {210} \right)_{3} + \left( {1102} \right)_{3} = \left( {2022} \right)_{3}$$

As shown in the example above, the leftmost number is 2 (the value shown in red) which indicates that the result is negative. And the number shown in green is (022) = 8. That’s the 10’s complement of 8 is 2. So the result will be − 2.

The blocks in Fig. 19 are exactly the blocks proposed in the Figs. 17 and 16. So if we take them generally, this TCD subtractor will have a quantum cost of (77 = (3 * 18) + 15 + 8). But if we eliminate situations that never happen, its quantum cost will be reduced to 70. The V output also represents the validity or invalidity of the output as in the previous design.

Fig. 19
figure 19

Proposed reversible TCD subtractor block diagram

Full size image

4.5 Proposing reversible TCD adder/subtractor

Now, with the explanation given in the preceding sections, if we add a Select base to the above circuits, a new circuit can be designed that is both reversible TCD adder and subtractor. Just like in Fig. 19, if Select = 2, subtraction of two TCDs is performed, otherwise, when Select = 0 or 1, the addition of two TCDs is performed.

As shown in Fig. 20, just like a subtractor, the blocks in Fig. 20 are exactly the blocks introduced in the previous parts in Figs. 17 and 16. So if we take them generally (General Design), this TCD subtractor will have a quantum cost of (77 = (3 * 18) + 15 + 8) and if we eliminate situations that never happen (Optimized Design), its quantum cost will be reduced to 70.

Fig. 20
figure 20

Proposed reversible TCD adder/subtractor block diagram

Full size image

5 Results and comparisons

As seen in the previous parts, a reversible TCD adder, subtractor, or adder/subtractor composes two main blocks the reversible 3-qutrit RCA and Error Detector. The first comparison is made between reversible 3-qutrit RCAs. A comprehensive comparison of reversible 3-qutrit RCAs is given in Table 6.

Table 6 Comparison of the proposed reversible 3-qutrit RCA with previous designs
Full size table

As can be seen in Table 6, Haghparast et al. (2017) and Panahi et al. (2018) used two reversible 3-qutrit adders with 2-input (A2A1A0 and B2B1B0) to implement the TCD adder that their specifications come in different colors in the Table 6, and as can be seen, it performs best in the most important indicator (the quantum cost) of the Optimized circuit provided.

As mentioned earlier, two adders are used in the previous designs, as the first adder combines two decimal numbers and one Cin to create one output, so the first adder does not need to be a Cout design. The second adder has two states: first, if the output of the first adder is correct (a number between 0 and 9), the second adder adds it to zero, and if the first adder’s output is false, the second adder adds it to seventeen. In both cases, the second adder does not require a Cin design. But since we use a single adder instead of two separate adders, we need both Cin and Cout.

Since we have used three full-adder modules for our design, each of them has three half-adder modules. While in the design presented by Panahi et al. (2018), each adder is designed as a module. Therefore, our design has a more complete form and the number of constant inputs to our scheme and, consequently, the number of garbage outputs, is greater than Panahi’s design. But the most important feature that is quantum cost, in the proposed Optimized Design (eliminating situations that never happen) is lower than previous designs.

The second comparison is between the reversible ternary Error Detector blocks that is provided in Table 7.

Table 7 Comparison of the proposed reversible ternary Error Detector with previous designs
Full size table

As can be seen in Table 7, in the proposed design, all the evaluation criteria are optimized better than the other circuits. The number of garbage outputs in this circuit is zero because in the circuit designed in this section, the only garbage output available is used to verify the correct circuit result.

In the third comparison of this section, we look at the reversible TCD adder. The results of these comparisons are presented in Table 8.

Table 8 Comparison of the proposed reversible TCD adder with previous designs
Full size table

By looking at Table 8, it is clear that OPTIMIZED-DESIGN is the best quantum cost circuit ever offered.

In the fourth and final comparison in this section, we intend to compare the reversible TCD adder/subtractor presented in this paper with the only one presented by Panahi et al. (2018). Table 9 shows these comparisons easily.

Table 9 Comparison of the proposed reversible TCD adder/subtractor with the previous design
Full size table

As shown in Table 9, since the previous circuit in Panahi et al. (2018) was not modular, they had to add new blocks to design the new circuit. While the circuit presented in this article has made this feature without any changes to the circuit principle. In addition, the circuit presented for all 300 states shows the correct answer while the previous circuit has 122 correct states in sum mode and 200 correct states in subtraction mode.

6 Conclusions and future works

In this paper, at first, using the available potentials in the ternary logic, a new reversible ternary full-adder is designed. This circuit, considered as the basic circuit in this article, consists of three half-adders that are connected in series. The half-adder circuit is also designed in two special cases, which we call the semi half-adder block #1 and block #2. Comprehensive full adder that designed in this article is capable of adding up to three numbers and one Cin at a time and producing one output and one Cout. Therefore, it is very useful in places where it is necessary to have successive additions. One of them is TCD adder/subtractor, because the structure of this circuit consists of two consecutive adders. The TCD adder circuit presented in this article is better than the previous one provided by Panahi in terms of quantum cost 10% and finally, the TCD adder/subtractor circuit presented in this article is 23% better than the previous circuit (which is true for special cases) in term of quantum cost, which presented by Panahi et al. (2018).

For future works, the proposed designs in this paper can be applied for designing complicated circuits in quantum reversible ternary logic like compressors, multipliers and dividers.