1 Introduction

It is well known that patterns in the nature are ubiquitous and they constitute the colorful world we live. Understanding the formation of patterns is great significant to the research of biological invasion and epidemic diffusion. In his seminal work [23], Turing explained successfully the changes of some animal surface patterns by means of a reaction–diffusion system coupled by two parabolic partial differential equations with homogeneous Neumann boundary conditions. Turing’s findings revealed that different random diffusions of two substances may lead to that a stable spatially uniform steady state loses its stability and then arises the spatially nonuniform patterns. This is called as Turing instability (or diffusion-driven instability). Since Turing’s pioneering work, Turing instability or Turing bifurcation for various reaction–diffusion ecosystems has attracted great interest of lots of researchers [4, 6, 8, 10, 11, 13, 15, 16, 21, 22, 25, 27, 28, 30,31,32].

In the real world, the interactions among species are various and the one of predator–prey type between two species is of great importance. Assume that there exist only predator and prey species in the same habitat and in the absence of predator species, the growth rate of prey species follows the Logistic growth law and the functional response of predator to prey is of Holling-II type. Then the normalized growth dynamics between two species can be described by the following reaction–diffusion system [20, 29]

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=d_{11}\Delta u+u\left( 1-\frac{u}{c}\right) -\frac{muv}{1+u},&{} x\in \Omega ,t>0,\\ \frac{\partial v}{\partial t}=d_{22}\Delta v-\theta v+ \frac{muv}{1+u},&{} x\in \Omega ,t>0,\\ \frac{\partial u}{\partial n}=\frac{\partial v}{\partial n}=0,&{} x\in \partial \Omega ,t>0, \end{array}\right. } \end{aligned}$$
(1.1)

where \(\Omega \subset R^{N}(N\ge 1)\) is a bounded domain with a smooth boundary \(\partial \Omega \) and \(\pmb {n}\) is the outside unit normal vector on \(\partial \Omega \); the Laplace operator \(\Delta \) implies that the spatial diffusion of prey and predator species are random and free; the variables u(x, t) and v(x, t) represent respectively the population densities of prey and predator species at space location \(x\in \Omega \) and time \(t>0\); \(d_{11},d_{22}>0\) are separately the diffusion coefficients of prey and predator species; \(c>0\) is the maximum environment carrying capacity of prey species; \(\theta >0\) is the natural death rate of the predator species in the absence of prey species; \(m>0\) is the maximum capture rate of the predator to prey and the function \(u/(1+u)\) is the functional response function of predator species to prey species. The homogenous Neumann boundary condition imposed in (1.1) is to guarantee that system (1.1) is self-contained.

Under the assumption that the distribution in space of prey and predator species is homogeneous, namely, in the case when there is no the effect on spatial diffusion, model (1.1) can take the corresponding ordinary differential equation (ODE) model

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\text {d} u}{\text {d} t}=u\left( 1-\frac{u}{c}\right) -\frac{muv}{1+u},\\ \frac{\text {d} v}{\text {d} t}=-\theta v+ \frac{muv}{1+u}. \end{array}\right. } \end{aligned}$$
(1.2)

It is easy to reveal that when the condition

  1. (H)

    \(c,m>0\) and \(0<\theta <\frac{cm}{c+1}\)

holds, system (1.2) has the unique positive equilibrium \(E_*=(u_{*},v_{*})\), where

$$\begin{aligned} u_*=\frac{\theta }{m-\theta },~~v_*=\frac{cm-(c+1)\theta }{c(m-\theta )^{2}}. \end{aligned}$$
(1.3)

The asymptotical stability of the unique positive equilibrium \(E_*\) of ODE system (1.2) has been investigated extensively by several authors and the following main result has been obtained [7, 12]:

Theorem 1.1

Assume that the condition (H) holds.

  1. (i)

    If \((c-1)/2<u_{*}<c\), then the unique positive equilibrium \(E_*\) of (1.2) is globally asymptotically stable;

  2. (ii)

    If \(c>1\) and \(0<u_{*}<(c-1)/2\), then the unique positive equilibrium \(E_*\) of (1.2) is unstable and (1.2) has a globally asymptotically stable periodic orbit surrounding \(E_*\);

  3. (iii)

    When \(c>1\), \(u_{*}=(c-1)/2\) is the subcritical Hopf bifurcation value of system (1.2) at \(E_*\).

On the other hand, dynamics of reaction–diffusion system (1.1) has been also investigated deeply by several researchers [20, 29]. For example, under the condition (H), Yi et al. [29] analyzed in detail the spatiotemporal dynamics of (1.1) near the constant coexistence equilibrium \(E_*\) including Hopf bifurcation and steady state bifurcation. Peng and Shi [20] further gave some results regarding equilibrium of (1.1) and they obtained that when m is sufficiently large, system (1.1) has no nonconstant positive equilibrium. Meanwhile, it has been found that spatial diffusion in (1.1) does not affect the stability of the constant coexistence equilibrium \(E_*\). Therefore, Turing instability and Turing bifurcation of (1.1) at the constant coexistence equilibrium are impossible and the associated Hopf bifurcation and spatially heterogeneous steady-state solution bifurcation of (1.1) at \(E_*\) occur only in the instability regime of the ODE system (1.2). For the dynamics of system (1.1) with delay, see [5, 26]. Also, one can refer to references [1,2,3, 9] for Hopf bifurcation and steady state bifurcation of the constant coexistence equilibrium in some reaction–diffusion epidemic models.

It should be pointed out that the diffusive system (1.1) can predict more accurately the development of some species than the associated ODE system. However, in modelling (1.1) it is assumed that the diffusion of prey and predator species depends only upon gradients of the concentration of species but not on the spatial distribution of any other species [17]. Therefore, system (1.1) incorporates only the diffusion terms \(\Delta u\) and \(\Delta v\). In practice, in addition to the self-diffusion in the interior of species, there should also exist cross-diffusion effect among different species [14, 24]. As a result, reaction–diffusion systems with cross-diffusion effect can more practically describe the interactions between different species. Following the idea in [24], the flux of a species should be also induced by a gradient of the other species and according to the Fickian interpretation of the diffusion process, the cross-diffusion term of predator to prey species should take the form \(d_{12}v\) and the one of prey to predator species should take the form \(d_{21}u\), where \(d_{12},d_{21}\ge 0\) are respectively referred to as the cross-diffusion coefficients of predator to prey and prey to predator. Based on these considerations and model (1.1), a more reasonable predator–prey system should be described by the following reaction–diffusion system with the linear cross-diffusion

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=d_{11}\Delta u+d_{12}\Delta v+u(1-\frac{u}{c}) -\frac{muv}{1+u},&{} x\in \Omega ,t>0,\\ \frac{\partial v}{\partial t}=d_{21}\Delta u+d_{22}\Delta v-\theta v+ \frac{muv}{1+u},&{} x\in \Omega ,t>0,\\ \frac{\partial u}{\partial n}=\frac{\partial v}{\partial n}=0,&{} x\in \partial \Omega ,t>0. \end{array}\right. } \end{aligned}$$
(1.4)

If we restrict the spatial domain \(\Omega \) to the planar rectangle domain \(\Omega _L=(0,L_{x})\times (0,L_{y})\) with \(L_x,L_y>0\), then model (1.4) can be read as the following form

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=d_{11}\left( \frac{ \partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial y^{2}}\right) +d_{12}\left( \frac{ \partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}v}{\partial y^{2}}\right) +u(1-\frac{u}{c}) -\frac{muv}{1+u},&{}(x,y)\in \Omega _L,t>0,\\[2mm] \frac{\partial v}{\partial t}=d_{21}\left( \frac{ \partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial y^{2}}\right) +d_{22}\left( \frac{ \partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}v}{\partial y^{2}}\right) -\theta v+ \frac{muv}{1+u},&{}(x,y)\in \Omega _L,t>0,\\[2mm] \frac{\partial u}{\partial n}=\frac{\partial v}{\partial n}=0,&{}(x,y)\in \partial \Omega _L,t>0. \end{array}\right. }\nonumber \\ \end{aligned}$$
(1.5)

Recently, Wang and Peng [25] investigated numerically the spatiotemporal dynamics of the unique constant coexistence equilibrium \(E_*\) of system (1.5) and they found that the linear cross-diffusion effect in (1.5) can induce more complicated spatiotemporal dynamics such as Turing instability and Turing patterns. Since the work in [25] is only numerical but not analytical, the classification and stability of Turing patterns of (1.5) near the unique constant coexistence equilibrium \(E_*\) cannot be determined. However, it is more important and interesting to analyze theoretically the classification and stability of Turing patterns of reaction–diffusion systems. Based on these reasons, the main aim of this paper is to explore in detail the classification and stability of Turing patterns of (1.5) near the unique constant coexistence equilibrium \(E_*\).

The layout of this paper is organized as follows. In Sect. 2, we determine the spatially homogeneous Hopf bifurcation curve and Turing bifurcation curve of system (1.5) at the unique constant coexistence equilibrium \(E_*\). In Sect. 3, through multiple-scale time analysis and successive approximations, the amplitude equations of system (1.5) near the unique constant coexistence equilibrium \(E_*\) are obtained. In Sect. 4, the existence and stability for different types of patterns arising near the Turing threshold are discussed in detail with the help of the amplitude equations obtained in the previous section. Some numerical simulations are carried out in Sect. 5 to verify the obtained theoretical predictions. Finally, some important conclusions are included also in Sect. 6.

2 Spatially Homogeneous Hopf and Turing Bifurcation Curves

In this section, we obtain the spatial homogeneous Hopf curve and Turing bifurcation curve of the unique constant coexistence equilibrium \(E_*\) of system (1.5) and determine the parameter range in which system (1.5) possesses Turing patterns near the constant coexistence equilibrium \(E_*\).

It is easy to see that under the condition (H), system (1.5) has the unique constant coexistence equilibrium \(E_*=(u_{*},v_{*})\), where \(u_{*}\) and \(v_{*}\) are given by (1.3). The Jacobian matrix of system (1.5) at \(E_*\) is

$$\begin{aligned} J:=\left( \begin{array}{cc} a_{11}(\theta ) &{}\quad a_{12}(\theta )\\ a_{21}(\theta ) &{}\quad a_{22}(\theta ) \\ \end{array} \right) =\left( \begin{array}{cc} \frac{\theta [(c-1)m-(c+1)\theta ]}{cm(m-\theta )} &{} -\theta \\ \frac{cm-(c+1)\theta }{cm} &{} 0 \\ \end{array} \right) . \end{aligned}$$

Let

$$\begin{aligned} U:=\left( \begin{array}{cc} u-u_{*} \\ v-v_{*} \\ \end{array} \right) ~\text {and}~ D:=\left( \begin{array}{cc} d_{11} &{} d_{12}\\ d_{21} &{} d_{22} \\ \end{array} \right) . \end{aligned}$$

Then the linearized form of system (1.5) at \(E_*\) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial U}{\partial t}=D\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) U+JU,&{}(x,y)\in \Omega _L,\\ \frac{\partial U}{\partial n}=0,&{}(x,y)\in \partial \Omega _L. \end{array}\right. } \end{aligned}$$
(2.1)

It follows from [17, 26] that all the eigenvalues of the eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) u+\mu u=0,&{}(x,y)\in \Omega _L,\\ \frac{\partial u}{\partial n}=0,&{}(x,y)\in \partial \Omega _L \end{array}\right. } \end{aligned}$$

are nonnegative and hence they can be written into \(k^2\) such that they are usually said to be the wavenumbers. For a certain wavenumber \(k^2\) and \(0<\theta <\frac{cm}{c+1}\), define \(T_{k}(\theta )\) and \(D_{k}(\theta )\) by

$$\begin{aligned} T_k(\theta ){} & {} =a_{11}(\theta )+a_{22}(\theta )-(d_{11}+d_{22})k^{2},\\ D_k(\theta ){} & {} =a_{11}(\theta )a_{22}(\theta )-a_{12}(\theta )a_{21}(\theta ) - [a_{11}(\theta )d_{22}+a_{22}(\theta )d_{11}-a_{12}(\theta )d_{21}\\{} & {} \quad -a_{21}(\theta )d_{12}]k^{2} +(d_{11}d_{22}-d_{12}d_{21})k^{4}. \end{aligned}$$

Then the characteristic equation of the linear system (2.1) has the form

$$\begin{aligned} \lambda ^{2}-T_{k}(\theta )\lambda +D_{k}(\theta )=0. \end{aligned}$$
(2.2)

If Eq. (2.2) with \(k=0\) has a pair of purely imaginary roots and the associated transversality condition holds, then system (1.5) has a spatially homogeneous Hopf bifurcation at the coexistence equilibrium \(E_*\). When \(c>1\), let

$$\begin{aligned} \theta _H:=\frac{(c-1)m}{c+1}. \end{aligned}$$
(2.3)

Then one can see that when \(c>1\),

$$\begin{aligned} T_0(\theta _H)=a_{11}(\theta _H)+a_{22}(\theta _H)=a_{11}(\theta _H)=0 \end{aligned}$$

and

$$\begin{aligned} D_0(\theta _H){} & {} =a_{11}(\theta _H)a_{22}(\theta _H)-a_{12}(\theta _H)a_{21}(\theta _H)=-a_{12}(\theta _H)a_{21}(\theta _H)\\{} & {} =\frac{\theta _H[cm-(c+1)\theta _H]}{cm}=\frac{\theta _H}{c}>0. \end{aligned}$$

In addition, when \(c>1\) and \(k^2>0\),

$$\begin{aligned} T_k(\theta _H)=-(d_{11}+d_{22})k^{2}<0. \end{aligned}$$

Therefore, we can obtain that when \(c>1\), the spatially homogeneous Hopf bifurcation curve of (1.5) at \(E_*\) is

$$\begin{aligned} \theta =\theta _H. \end{aligned}$$
(2.4)

Now we deduce the Turing bifurcation curve of (1.5) at \(E_*\). To achieve this end, we need that the unique positive equilibrium \(E_*\) of the ODE system (1.2) is stable, that is,

$$\begin{aligned} {\left\{ \begin{array}{ll} T_0(\theta )=a_{11}(\theta )+a_{22}(\theta )=\frac{\theta [(c-1)m-(c+1)\theta ]}{cm(m-\theta )}<0,\\ D_0(\theta =a_{11}(\theta )a_{22}(\theta )-a_{12}(\theta )a_{21}(\theta )=\frac{\theta [cm-(c+1)\theta ]}{cm}>0. \end{array}\right. } \end{aligned}$$
(2.5)

In fact, we can see easily that (2.5) holds when \(c>1\) and

$$\begin{aligned} \theta _H<\theta <\frac{cm}{c+1}. \end{aligned}$$
(2.6)

Under the condition (2.6), if for some \(k>0\), (2.2) has a root \(\lambda _k\) such that

$$\begin{aligned} \Re (\lambda _k)=0,\quad \Im (\lambda _k)=0, \end{aligned}$$

then (1.5) has a Turing bifurcation at \(E_*\). It follows from [22] that under (2.6), if \(d_{11}d_{22}-d_{12}d_{21}>0\), the wave number \(k^2\) takes the critical value \(k_{T}^{2}=\sqrt{\frac{a_{11}a_{22}-a_{12}a_{21}}{d_{11}d_{22}-d_{12}d_{21}}}\) and

$$\begin{aligned} a_{11}d_{22}+a_{22}d_{11}-a_{12}d_{21}-a_{21}d_{12}-2\sqrt{(d_{11}d_{22}-d_{12}d_{21})(a_{11}a_{22}-a_{12}a_{21})}=0, \end{aligned}$$

then system (1.5) has Turing bifurcation at \(E_*\). Therefore, when (2.6) holds and \(d_{11}d_{22}-d_{12}d_{21}>0\), the Turing bifurcation curve of (1.5) at \(E_*\) is given by

$$\begin{aligned} \begin{array}{l} d_{22}\frac{\theta [(c-1)m-(c+1)\theta ]}{cm(m-\theta )}+d_{21}\theta -d_{12}\frac{cm-(c+1)\theta }{cm} -2\sqrt{(d_{11}d_{22}-d_{12}d_{21})\frac{\theta [cm-(c+1)\theta ]}{cm}}=0. \end{array}\nonumber \\ \end{aligned}$$
(2.7)

In addition, if (2.6) holds and \(d_{11}d_{22}-d_{12}d_{21}>0\), then the constant coexistence equilibrium \(E_*\) of system (1.5) is Turing unstable when

$$\begin{aligned} \begin{array}{l} d_{22}\frac{\theta [(c-1)m-(c+1)\theta ]}{cm(m-\theta )}+d_{21}\theta -d_{12}\frac{cm-(c+1)\theta }{cm} -2\sqrt{(d_{11}d_{22}-d_{12}d_{21})\frac{\theta [cm-(c+1)\theta ]}{cm}}>0, \end{array} \end{aligned}$$

and hence the Turing patterns exist. However, when

$$\begin{aligned} \begin{array}{l} d_{22}\frac{\theta [(c-1)m-(c+1)\theta ]}{cm(m-\theta )}+d_{21}\theta -d_{12}\frac{cm-(c+1)\theta }{cm} -2\sqrt{(d_{11}d_{22}-d_{12}d_{21})\frac{\theta [cm-(c+1)\theta ]}{cm}}<0, \end{array} \end{aligned}$$

the constant coexistence equilibrium \(E_*\) of system (1.5) is locally asymptotically stable.

Summarize the above analysis, we have the following result.

Theorem 2.1

Suppose that \(c > 1\) the condition (2.6) holds, \(d_{11}d_{22}-d_{12}d_{21}>0\) and \(\theta =\theta _T(m)\) is defined by Eq. (2.7). Then the constant coexistence equilibrium \(E_*\) of system (1.5) is locally asymptotically stable when \(\theta >\max \left\{ \theta _H,\theta _T(m)\right\} \), is Turing unstable as \(\theta _H<\theta <\theta _T(m)\) and system (1.5) can undergo a Turing bifurcation at \(E_*\) when \(\theta \) crosses through decreasingly \(\theta _T\) from up to down. In addition, the constant coexistence equilibrium \(E_*\) of system (1.5) is always unstable when \(c>1\) and \(0<\theta <\theta _H\), see Figs. 1 and 2.

Fig. 1
figure 1

Spatially homogeneous Hopf bifurcation and Turing bifurcation curves in m-\(\theta \) plane of (1.5) at the constant coexistence equilibrium \(E_*\)

Full size image
Fig. 2
figure 2

Graph to relation between \(\text {Re}(\lambda )\) of the characteristic Eq. (2.2) and the wavenumber \(k^{2}\) when m and \(d_{ij}(i,j=1,2)\) are fixed and \(\theta \) varies

Full size image

Remark 2.2

Under the conditions (2.6) and \(d_{11}d_{22}-d_{12}d_{21}>0\). If \(d_{12}=d_{21}=0\), then we can see that the left hand side of (2.7) becomes

$$\begin{aligned} \begin{array}{l} d_{22}\frac{\theta [(c-1)m-(c+1)\theta ]}{cm(m-\theta )}-2\sqrt{d_{11}d_{22}\frac{\theta [cm-(c+1)\theta ]}{cm}}<0. \end{array} \end{aligned}$$

This implies that for all \(k^2\in [0,+\infty )\), all the roots of (2.2) have negative real parts and therefore the constant coexistence equilibrium \(E_*\) of system (1.5) is locally asymptotically stable. Thus, the Turing pattern cannot appear in (1.5) and this shows as well that the cross-diffusion plays an important role in the Turing pattern formation of (1.5).

Remark 2.3

If \(c>1\), \(0<\theta <\theta _H\) and \(\theta _{T}(m)\) is defined by the Eq. (2.7), then system (1.5) can bifurcate the spatially heterogeneous steady states from the constant coexistence equilibrium \(E_*\) when \(\theta \) passes through \(\theta _{T}(m)\) from up to down.

3 Amplitude Equations

This section is mainly devoted to obtaining the amplitude equations of system (1.5) at the constant coexistence equilibrium \(E_*\) when \(0<\theta _{T}-\theta \ll 1\) by using multi-scale time analysis.

Assume that \(0<\theta _{T}-\theta \ll 1\) and let \(\hat{u}=u-u_{*}\), \(\hat{v}=v-v_{*}\). Still denote \(\hat{u}\) and \(\hat{v}\) by u and v. Then system (1.5) is transformed into the following system

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=d_{11}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) u+d_{12}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) v\\ \hspace{1cm}+(u+u_{*})(1-\frac{u+u_{*}}{c}) -\frac{m(u+u_{*})(v+v_{*})}{1+u+u_{*}},&{} (x,y)\in \Omega _L,t>0,\\ \frac{\partial v}{\partial t}=d_{21}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) u+d_{22}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) v\\ \hspace{1cm}-\theta (v+v_{*})+\frac{m(u+u_{*})(v+v_{*})}{1+u+u_{*}},&{} (x,y)\in \Omega _L,t>0,\\ \frac{\partial u}{\partial n}=\frac{\partial v}{\partial n}=0,&{} (x,y)\in \partial \Omega _L,t>0. \end{array} \right. \end{aligned}$$
(3.1)

It is easy to see that the constant coexistence equilibrium \(E_*\) of system (1.5) corresponds to zero solution of system (3.1).

Define the real-valued Sobolev space X by

$$\begin{aligned} X=\left\{ u\in H^{2}(\Omega _L)\left| \frac{\partial u}{\partial n}=0,(x,y)\in \partial \Omega _L\right. \right\} \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} f(u,v)=(u+u_{*})(1-\frac{u+u_{*}}{c}) -\frac{m(u+u_{*})(v+v_{*})}{1+u+u_{*}},\\ g(u,v)=-\theta (v+v_{*})+ \frac{m(u+u_{*})(v+v_{*})}{1+u+u_{*}}. \end{array}\right. } \end{aligned}$$

Then system (3.1) can be further expressed in view of Taylor expansion of f(u, v) and g(u, v) at (0, 0) as

$$\begin{aligned} \frac{\partial U}{\partial t}=L(\theta )U+N(\theta ;U,U), \end{aligned}$$
(3.2)

where \(U=(u,v)^{T}\in X^{2}\), the linear operator \(L(\theta ): X^2\rightarrow [L^2(\Omega )]^2\) is defined by

$$\begin{aligned} L(\theta )= \left( \begin{array}{cc} a_{11}(\theta )+d_{11}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) &{} a_{12}(\theta )+d_{12}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) \\[2mm] a_{21}(\theta )+d_{21}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) &{} a_{22}(\theta )+d_{22}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) \\ \end{array} \right) \end{aligned}$$

with

$$\begin{aligned}{} & {} a_{11}(\theta )=\frac{\theta [(c-1)m-(c+1)\theta ]}{cm(m-\theta )}, ~~a_{12}(\theta )=-\theta ,~~ a_{21}(\theta )=\frac{cm-(c+1)\theta }{cm},\\{} & {} a_{22}(\theta )=0, \end{aligned}$$

and the nonlinear mapping \(N(\theta ;\cdot ,\cdot ): X^2\times X^2\rightarrow [L^2(\Omega )]^2\) is given by

$$\begin{aligned}{} & {} N(\theta ;U,U)\nonumber \\{} & {} \qquad = \left( \begin{array}{cc} \frac{f_{uu}(\theta )}{2}u^{2}+f_{uv}(\theta )uv+\frac{f_{vv}(\theta )}{2}v^{2}+ \frac{f_{uuu}(\theta )}{3!}u^{3}+\frac{f_{uuv}(\theta )}{2}u^{2}v+\frac{f_{uvv}(\theta )}{2}uv^{2} +\frac{f_{vvv}(\theta )}{3!}v^{3} \\ \frac{g_{uu}(\theta )}{2}u^{2}+g_{uv}(\theta )uv+\frac{g_{vv}(\theta )}{2}v^{2}+ \frac{g_{uuu}(\theta )}{3!}u^{3}+\frac{g_{uuv}(\theta )}{2}u^{2}v+\frac{g_{uvv}(\theta )}{2}uv^{2} +\frac{g_{vvv}(\theta )}{3!}v^{3} \\ \end{array} \right) ,\nonumber \\ \end{aligned}$$
(3.3)

here

$$\begin{aligned}{} & {} f_{uu}(\theta )=\frac{2(c-1)m^2-2(2c+1)m\theta +2(c+1)\theta ^2}{cm^2},~~f_{uv}(\theta )=-\frac{(m-\theta )^{2}}{m},\\{} & {} f_{vv}(\theta )=0, \end{aligned}$$
$$\begin{aligned}{} & {} f_{uuu}(\theta )=-\frac{6(m-\theta )^2[c(m-\theta )-\theta ]}{cm^3},~~f_{uuv}(\theta )=\frac{2(m-\theta )^3}{m^2},~~ f_{uvv}(\theta )=0,\\{} & {} f_{vvv}(\theta )=0, \end{aligned}$$
$$\begin{aligned} g_{uu}(\theta )=-\frac{2(m-\theta )[c(m-\theta )-\theta ]}{cm^2},~~ g_{uv}(\theta )=\frac{(m-\theta )^{2}}{m},~~ g_{vv}(\theta )=0, \end{aligned}$$
$$\begin{aligned}{} & {} g_{uuu}(\theta )=\frac{6(m-\theta )^2[c(m-\theta )-\theta ]}{cm^3},~~ g_{uuv}(\theta )=-\frac{2(m-\theta )^3}{m^2},~~ g_{uvv}(\theta )=0, \\{} & {} g_{vvv}(\theta )=0. \end{aligned}$$

Since the calculation is only limited to the case when \(0<\theta _{T}-\theta \ll 1\), it follows that \(\theta \) can be expressed as

$$\begin{aligned} \theta -\theta _{T}=\epsilon \theta _{1}+\epsilon ^{2}\theta _{2}+O(\epsilon ^{3}), \end{aligned}$$
(3.4)

where \(\epsilon \) is a very small positive number. Making use of the expansion (3.4), U can be expanded as the following power series

$$\begin{aligned} U= \left( \begin{array}{cc} u \\ v \\ \end{array} \right) =\epsilon \left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) +\epsilon ^{2}\left( \begin{array}{cc} u_{2} \\ v_{2} \\ \end{array} \right) +\epsilon ^{3}\left( \begin{array}{cc} u_{3} \\ v_{3} \\ \end{array} \right) +O(\epsilon ^{4}). \end{aligned}$$
(3.5)

Thus the nonlinear mapping \(N(\theta ;U,U)\) defined by (3.3) has the form

$$\begin{aligned} N(\theta ;U,U)=\epsilon ^{2}N_{2}(\theta _T)+\epsilon ^{3}[N_{31}(\theta _T)+\theta _{1}N_{32}(\theta _T)]+O(\epsilon ^{4}), \end{aligned}$$
(3.6)

where

$$\begin{aligned} N_{2}(\theta _T)= \left( \begin{array}{cc} \frac{f_{uu}^{*}}{2}u_{1}^{2}+f_{uv}^{*}u_{1}v_{1}+\frac{f_{vv}^{*}}{2}v_{1}^{2} \\ \frac{g_{uu}^{*}}{2}u_{1}^{2}+g_{uv}^{*}u_{1}v_{1}+\frac{g_{vv}^{*}}{2}v_{1}^{2} \\ \end{array} \right) , \end{aligned}$$
$$\begin{aligned}{} & {} N_{31}(\theta _T) \\{} & {} \quad = \left( \begin{array}{cc} f_{uu}^{*}u_{1}u_{2}+f_{uv}^{*}(u_{1}v_{2}+u_{2}v_{1})+f_{vv}^{*}v_{1}v_{2}+ \frac{f_{uuu}^{*}}{3!}u_{1}^{3}+\frac{f_{uuv}^{*}}{2}u_{1}^{2}v_{1}+ \frac{f_{uvv}^{*}}{2}u_{1}v_{1}^{2}+\frac{f_{vvv}^{*}}{3!}v_{1}^{3} \\ g_{uu}^{*}u_{1}u_{2}+g_{uv}^{*}(u_{1}v_{2}+u_{2}v_{1})+g_{vv}^{*}v_{1}v_{2}+ \frac{g_{uuu}^{*}}{3!}u_{1}^{3}+\frac{g_{uuv}^{*}}{2}u_{1}^{2}v_{1}+ \frac{g_{uvv}^{*}}{2}u_{1}v_{1}^{2}+\frac{g_{vvv}^{*}}{3!}v_{1}^{3} \\ \end{array} \right) , \end{aligned}$$

as well as

$$\begin{aligned} N_{32}(\theta _{T})= \left( \begin{array}{cc} \frac{f_{uu\theta }^{*}}{2}u^{2}+f_{uv\theta }^{*}uv+\frac{f_{vv\theta }^{*}}{2}v^{2} \\ \frac{g_{uu\theta }^{*}}{2}u^{2}+g_{uv\theta }^{*}uv+\frac{g_{vv\theta }^{*}}{2}v^{2} \\ \end{array} \right) , \end{aligned}$$

here all the partial derivatives with the superscript stars represent the values of the corresponding partial derivatives when \(\theta =\theta _{T}\). Set

$$\begin{aligned} a_{11}'(\theta _{T})= & {} \frac{(c-1)m^{2}-2(c+1)m\theta _T+(c+1)\theta _T^{2}}{cm(m-\theta _T)^{2}},~~a_{12}'(\theta _{T})=-1,\\ a_{21}'(\theta _{T})= & {} -\frac{c+1}{cm},~~ a_{22}'(\theta _{T})=0 \end{aligned}$$

and

$$\begin{aligned} a''_{11}(\theta _{T})=\frac{-2m}{c(m-\theta _T)^{3}}. \end{aligned}$$

Define the second order matrices \(M_1\) and \(M_2\) by

$$\begin{aligned} M_{1}= \left( \begin{array}{cc} a_{11}'(\theta _{T}) &{}\quad a_{12}'(\theta _{T})\\ a_{21}'(\theta _{T}) &{}\quad a_{22}'(\theta _{T})\\ \end{array} \right) ,~~~~ M_{2}= \left( \begin{array}{cc} a_{11}^{''}(\theta _{T}) &{}\quad 0\\ 0 &{}\quad 0 \\ \end{array} \right) . \end{aligned}$$

Then the linear operator \(L(\theta )\) can be approximately decomposed into the following form:

$$\begin{aligned} L(\theta )=L_{T}+(\theta -\theta _{T})M_{1}+(\theta -\theta _{T})^{2}M_{2}+O((\theta -\theta _{T})^{3}), \end{aligned}$$
(3.7)

where

$$\begin{aligned} L_{T}= \left( \begin{array}{cc} a_{11}(\theta _{T})+d_{11}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) &{} a_{12}(\theta _{T})+d_{12}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) \\[2mm] a_{21}(\theta _{T})+d_{21}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) &{} a_{22}(\theta _{T})+d_{22}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) \\ \end{array} \right) . \end{aligned}$$

Now we let

$$\begin{aligned} \frac{\partial }{\partial t}=\epsilon \frac{\partial }{\partial T_{1}}+\epsilon ^{2}\frac{\partial }{\partial T_{2}}+O(\epsilon ^{3}). \end{aligned}$$
(3.8)

Substitute the decomposition formulas (3.4)–(3.8) into (3.2), and compare the coefficients of different orders of \(\epsilon \), it is obtained that

$$\begin{aligned} L_{T} \left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) =0, \end{aligned}$$
(3.9)
$$\begin{aligned} L_{T} \left( \begin{array}{cc} u_{2} \\ v_{2} \\ \end{array} \right) =\frac{\partial }{\partial T_{1}}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -\theta _{1}M_{1}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -N_{2}(\theta _{T}), \end{aligned}$$
(3.10)

and

$$\begin{aligned} \begin{aligned} L_{T} \left( \begin{array}{cc} u_{3} \\ v_{3} \\ \end{array} \right) =&\frac{\partial }{\partial T_{1}}\left( \begin{array}{cc} u_{2} \\ v_{2} \\ \end{array} \right) +\frac{\partial }{\partial T_{2}}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -\theta _{1}M_{1}\left( \begin{array}{cc} u_{2} \\ v_{2} \\ \end{array} \right) \\&-\theta _{1}^{2}M_{2}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -\theta _{2}M_{1}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -N_{31}(\theta _{T})-\theta _{1}N_{32}(\theta _{T}). \end{aligned}\nonumber \\ \end{aligned}$$
(3.11)

Define respectively \(\Phi \) and \(\Psi \) by and

$$\begin{aligned} \Phi =-\frac{a_{12}(\theta _{T})-k_{T}^{2}d_{12}}{a_{11}(\theta _{T})-k_{T}^{2}d_{11}} =-\frac{a_{22}(\theta _{T})-k_{T}^{2}d_{22}}{a_{21}(\theta _{T})-k_{T}^{2}d_{21}} \end{aligned}$$

and

$$\begin{aligned} \Psi =-\frac{a_{11}(\theta _{T})-k_{T}^{2}d_{11}}{a_{21}(\theta _{T})-k_{T}^{2}d_{21}} =-\frac{a_{12}(\theta _{T})-k_{T}^{2}d_{12}}{a_{22}(\theta _{T})-k_{T}^{2}d_{22}}. \end{aligned}$$

Then the general solution of the linear homogeneous Eq. (3.9) can be expressed as the form

$$\begin{aligned} \left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) =\left( \begin{array}{c} \Phi \\ 1 \\ \end{array} \right) \left( \begin{array}{c} \sum \limits _{j=1}^{3}W_{j}e^{\text {i}\pmb {k}_{j}\cdot \pmb {r}}+\sum \limits _{j=1}^{3}\overline{W}_{j}e^{-\text {i}\pmb {k}_{j}\cdot \pmb {r}} \\ \end{array} \right) , \end{aligned}$$
(3.12)

where \(W_{j}\) are the amplitudes corresponding to the modes of \(e^{\text {i}\pmb {k}_{j}\cdot \pmb {r}}(j=1,2,3)\). Here \(\pmb {k}_{j}(j=1,2,3)\) are called as wave vectors such that \(|\pmb {k}_{j}|=k_T\) and \(\pmb {k}_{1}+\pmb {k}_{2}+\pmb {k}_{3}=\pmb {0}\), see [18, 32].

According to the Fredholm solvability condition [19], Eq. (3.10) has a nontrivial solution if the vector function at the right end of Eq. (3.10) is orthogonal to the eigenfunction of operator \(L_{T}^{+}\) corresponding to zero eigenvalue, where

$$\begin{aligned} L_{T}^{+}= \left( \begin{array}{cc} a_{11}(\theta _{T})+d_{11}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) &{} a_{21}(\theta _{T})+d_{21}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) \\ a_{12}(\theta _{T})+d_{12}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) &{} a_{22}(\theta _{T})+d_{22}\left( \frac{ \partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}\right) \\ \end{array} \right) . \end{aligned}$$

Notice that the zero eigenvector of \(L_{T}^{+}\) is

$$\begin{aligned} \left( \begin{array}{c} 1 \\ \Psi \\ \end{array} \right) \left( \begin{array}{c} \sum \limits _{j=1}^{3}W_{j}e^{\text {i}\pmb {k}_{j}\pmb {r}}+\sum \limits _{j=1}^{3}\overline{W}_{j}e^{-\text {i}\pmb {k}_{j}\pmb {r}} \\ \end{array} \right) . \end{aligned}$$
(3.13)

Let

$$\begin{aligned} \left( \begin{array}{c} F_{u} \\ F_{v} \\ \end{array} \right) =\frac{\partial }{\partial T_{1}}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -\theta _{1}M_{1}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -N_{2}(\theta _{T}). \end{aligned}$$

Then when \((F_{u},F_{v})^{T}\) and (3.13) are orthogonal, we have

$$\begin{aligned} (1,\Psi ) \left( \begin{array}{c} F_{u}^{j} \\ F_{v}^{j} \\ \end{array} \right) =0, j=1,2,3, \end{aligned}$$
(3.14)

where \(F_{u}^{j}\) and \(F_{v}^{j}\) are the coefficients of \(e^{\text {i}\pmb {k}_{j}\cdot \pmb {r}}(j=1,2,3)\) in \(F_{u}\) and \(F_{v}\). Denote

$$\begin{aligned} H_{1}^{*}=\Phi a_{11}'(\theta _{T})+a_{12}'(\theta _{T})+\Psi (\Phi a_{21}'(\theta _{T})+a_{22}')(\theta _{T}), \end{aligned}$$
(3.15)

and

$$\begin{aligned} H_{2}(\theta )=2[h_{1}(\theta )+\Psi h_{2}(\theta )], \end{aligned}$$
(3.16)

where

$$\begin{aligned} h_{1}(\theta )=\frac{f_{uu}(\theta )}{2}\Phi ^{2}+f_{uv}(\theta )\Phi +\frac{f_{vv}(\theta )}{2}, \end{aligned}$$

and

$$\begin{aligned} h_{2}(\theta )=\frac{g_{uu}(\theta )}{2}\Phi ^{2}+g_{uv}(\theta )\Phi +\frac{g_{vv}(\theta )}{2}. \end{aligned}$$

Then from (3.14) we can get the equations about amplitudes \(W_{j}\) are

$$\begin{aligned} \begin{aligned} (\Phi +\Psi )\frac{\partial W_{1}}{\partial T_{1}}=\theta _{1}H_{1}^{*}W_{1}+H_{2}^{*}\overline{W}_{2}\overline{W}_{3} \\ (\Phi +\Psi )\frac{\partial W_{2}}{\partial T_{1}}=\theta _{1}H_{1}^{*}W_{2}+H_{2}^{*}\overline{W}_{1}\overline{W}_{3} \\ (\Phi +\Psi )\frac{\partial W_{3}}{\partial T_{1}}=\theta _{1}H_{1}^{*}W_{3}+H_{2}^{*}\overline{W}_{1}\overline{W}_{2}, \end{aligned} \end{aligned}$$
(3.17)

where \(H_{2}^{*}\) denotes the value of \(H_{2}\) at \(\theta =\theta _{T}\).

In the next, we need to solve Eq. (3.10). To ensure the convergence of \(W_{j}(j=1,2,3)\) in (3.17), the higher order terms like \(e^{2\textbf{i}\textbf{k}_{j}\cdot \textbf{r}}\) and \(e^{\textbf{i}(\textbf{k}_{i}-\textbf{k}_{j})\cdot \textbf{r}}\) should be considered in \(u_2\) and \(v_2\). Let

$$\begin{aligned} \left( \begin{array}{c} A_{0} \\ B_{0} \\ \end{array} \right)= & {} \left( \begin{array}{c} -2\frac{a_{22}(\theta _{T})h_{1}-a_{12}(\theta _{T})h_{2}}{a_{11}(\theta _{T})a_{22}(\theta _{T})-a_{12}(\theta _{T})a_{21}(\theta _{T})} \\ -2\frac{a_{11}(\theta _{T})h_{2}-a_{21}(\theta _{T})h_{1}}{a_{11}(\theta _{T})a_{22}(\theta _{T})-a_{12}(\theta _{T})a_{21}(\theta _{T})} \\ \end{array} \right) \\ \left( \begin{array}{c} A_{1} \\ B_{1} \\ \end{array} \right)= & {} \left( \begin{array}{c} -\frac{(a_{22}(\theta _{T})-4d_{22}k_{T}^{2})h_{1} -(a_{12}(\theta _{T})-4d_{12}k_{T}^{2})h_{2}}{(a_{11}(\theta _{T})-4d_{11}k_{T}^{2}) (a_{22}(\theta _{T})-4d_{22}k_{T}^{2})-(a_{12}(\theta _{T})-4d_{12}k_{T}^{2})(a_{21}(\theta _{T})- 4d_{21}k_{T}^{2})} \\ -\frac{(a_{11}(\theta _{T})-4d_{11}k_{T}^{2})h_{2} -(a_{21}(\theta _{T})-4d_{21}k_{T}^{2})h_{1}}{(a_{11}(\theta _{T})-4d_{11}k_{T}^{2}) (a_{22}(\theta _{T})-4d_{22}k_{T}^{2})-(a_{12}(\theta _{T})-4d_{12}k_{T}^{2})(a_{21}(\theta _{T})- 4d_{21}k_{T}^{2})} \\ \end{array} \right) \\ \left( \begin{array}{c} A_{2} \\ B_{2} \\ \end{array} \right)= & {} \left( \begin{array}{c} -2\frac{(a_{22}(\theta _{T})-3d_{22}k_{T}^{2})h_{1} -(a_{12}(\theta _{T})-3d_{12}k_{T}^{2})h_{2}}{(a_{11}(\theta _{T})-3d_{11}k_{T}^{2}) (a_{22}(\theta _{T})-3d_{22}k_{T}^{2})-(a_{12}(\theta _{T})-3d_{12}k_{T}^{2})(a_{21}(\theta _{T})- 3d_{21}k_{T}^{2})} \\ -2\frac{(a_{11}(\theta _{T})-3d_{11}k_{T}^{2})h_{1} -(a_{21}(\theta _{T})-3d_{21}k_{T}^{2})h_{2}}{(a_{11}(\theta _{T})-3d_{11}k_{T}^{2}) (a_{22}(\theta _{T})-3d_{22}k_{T}^{2})-(a_{12}(\theta _{T})-3d_{12}k_{T}^{2})(a_{21}(\theta _{T})- 3d_{21}k_{T}^{2})} \\ \end{array} \right) . \end{aligned}$$

Then the solution of Eq. (3.10) is given by

$$\begin{aligned} \begin{aligned} \left( \begin{array}{c} u_{2} \\ v_{2} \\ \end{array} \right) =&\left( \begin{array}{c} U_{0} \\ V_{0} \\ \end{array} \right) +\sum \limits _{j=1}^{3}\left( \begin{array}{c} U_{j} \\ V_{j} \\ \end{array} \right) e^{\text {i}\pmb {k}_{j}\cdot \pmb {r}}+\sum \limits _{j=1}^{3}\left( \begin{array}{c} U_{jj} \\ V_{jj} \\ \end{array} \right) e^{2\text {i}\pmb {k}_{j}\cdot \pmb {r}}\\&+\sum \limits _{{\mathop {i<j}\limits ^{i,j=1}}}^{3}\left( \begin{array}{c} U_{ij} \\ V_{ij} \\ \end{array} \right) e^{\text {i}(\pmb {k}_{i}-\pmb {k}_{j})\cdot \pmb {r}} +c.c., \end{aligned} \end{aligned}$$
(3.18)

in which

$$\begin{aligned} \left( \begin{array}{c} U_{0} \\ V_{0} \\ \end{array} \right) =\left( \begin{array}{c} A_{0}^{*} \\ B_{0}^{*} \\ \end{array} \right) (\mid W_{1}^{2}\mid +\mid W_{2}^{2}\mid +\mid W_{3}^{2}\mid ), \qquad U_{j}=\Phi V_{j}, \end{aligned}$$

and

$$\begin{aligned} \left( \begin{array}{c} U_{jj} \\ V_{jj} \\ \end{array} \right) =\left( \begin{array}{c} A_{1}^{*} \\ B_{1}^{*} \\ \end{array} \right) W_{j}^{2}, \qquad \left( \begin{array}{c} U_{ij} \\ V_{ij} \\ \end{array} \right) =\left( \begin{array}{c} A_{2}^{*} \\ B_{2}^{*} \\ \end{array} \right) W_{i}\overline{W}_{j}, \end{aligned}$$

here \(A_{i}^{*}\) and \(B_{i}^{*}(j=0,1,2)\) denote the values of \(A_{i}\) and \(B_{i}(j=0,1,2)\) when \(\theta =\theta _{T}\).

Set

$$\begin{aligned} \begin{aligned} \left( \begin{array}{c} \widetilde{F}_{u} \\ \widetilde{F}_{v} \\ \end{array} \right) =&\frac{\partial }{\partial T_{1}}\left( \begin{array}{cc} u_{2} \\ v_{2} \\ \end{array} \right) +\frac{\partial }{\partial T_{2}}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -\theta _{1}M_{1}\left( \begin{array}{cc} u_{2} \\ v_{2} \\ \end{array} \right) \\&-\theta _{1}^{2}M_{2}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -\theta _{2}M_{1}\left( \begin{array}{cc} u_{1} \\ v_{1} \\ \end{array} \right) -N_{31}(\theta _T)-\theta _{1}N_{32}(\theta _T), \end{aligned} \end{aligned}$$
(3.19)

and \(\widetilde{F}_{u}^{j}\) and \(\widetilde{F}_{v}^{j}\) denote separately the coefficients of \(e^{\text {i}\pmb {k}_{j}\cdot \pmb {r}}(j=1,2,3)\) in \(\widetilde{F}_{u}\) and \(\widetilde{F}_{v}\). Then, the orthogonality of \((\widetilde{F}_{u},\widetilde{F}_{v})^{T}\) and (3.13) gives

$$\begin{aligned} (1,\Psi ) \left( \begin{array}{c} \widetilde{F}_{u}^{j} \\ \widetilde{F}_{v}^{j} \\ \end{array} \right) =0, j=1,2,3. \end{aligned}$$

Let

$$\begin{aligned} H_{3}^{*}=\Phi a_{11}'(\theta _{T})+a_{12}'(\theta _{T})+\Psi (\Phi a_{21}'(\theta _{T})+a_{22}'(\theta _{T})),~~ H_{4}^{*}=2(h_{3}^{*}+\Psi h_{4}^{*}), \end{aligned}$$

where

$$\begin{aligned} h_{3}^{*}=\frac{f_{uu\theta }^{*}}{2}\Phi ^{2}+f_{uv\theta }^{*}\Phi +\frac{f_{vv\theta }^{*}}{2},~~ h_{4}^{*}=\frac{g_{uu\theta }^{*}}{2}\Phi ^{2}+g_{uv\theta }^{*}\Phi +\frac{g_{vv\theta }^{*}}{2}. \end{aligned}$$

Furthermore, define \(G_1(\theta )\) and \(G_2(\theta )\) by

$$\begin{aligned} \begin{aligned} G_{1}(\theta )=~&(A_{0}+A_{1})[f_{uu}(\theta )\Phi +f_{uv}(\theta )]+(B_{0}+B_{1})[f_{uv}(\theta )\Phi +f_{vv}(\theta )]\\&+\frac{f_{uuu}(\theta )}{2}\Phi ^{3}+\frac{3f_{uuv}(\theta )}{2}\Phi ^{2}+\frac{3f_{uvv}(\theta )}{2}\Phi +\frac{f_{vvv}(\theta )}{2}\\&+\Psi [(A_{0}+A_{1})[g_{uu}(\theta )\Phi +g_{uv}(\theta )]+(B_{0}+B_{1})[g_{uv}(\theta )\Phi +g_{vv}(\theta )]\\&+\frac{g_{uuu}(\theta )}{2}\Phi ^{3}+\frac{3g_{uuv}(\theta )}{2}\Phi ^{2}+\frac{3g_{uvv}(\theta )}{2}\Phi +\frac{g_{vvv}(\theta )}{2}, \end{aligned} \nonumber \\ \end{aligned}$$
(3.20)

and

$$\begin{aligned} \begin{aligned} G_{2}(\theta )=~&\,(A_{0}+A_{2})[f_{uu}(\theta )\Phi +f_{uv}(\theta )]+(B_{0}+B_{2})[f_{uv}(\theta )\Phi +f_{vv}(\theta )]\\&+f_{uuu}(\theta )\Phi ^{3}+3f_{uuv}(\theta )\Phi ^{2}+3f_{uvv}(\theta )\Phi +f_{vvv}(\theta )\\&+\Psi [(A_{0}+A_{2})[g_{uu}(\theta )\Phi +g_{uv}(\theta )]+(B_{0}+B_{2})[g_{uv}(\theta )\Phi +g_{vv}(\theta )]\\&+g_{uuu}(\theta )\Phi ^{3}+3g_{uuv}(\theta )\Phi ^{2}+3g_{uvv}(\theta )\Phi +g_{vvv}(\theta ). \end{aligned}\nonumber \\ \end{aligned}$$
(3.21)

Then putting (3.12) and (3.18) into (3.11), we can obtain the equations about amplitudes \(V_{j}\) and \(W_{j}\) are as follows:

$$\begin{aligned} \begin{aligned} (\Phi +\Psi )\left( \frac{\partial V_{1}}{\partial T_{1}}+\frac{\partial W_{1}}{\partial T_{2}}\right) =&H_{1}^{*}(\theta _{1}V_{1}+\theta _{2}W_{1})+H_{2}^{*}(\overline{V}_{2}\overline{W}_{3} +\overline{V}_{3}\overline{W}_{2}+\theta _{1}^{2}H_{3}^{*}W_{1}\\&+[G_{1}^{*}\mid W_{1}\mid ^{2}+G_{2}^{*}(\mid W_{2} \mid ^{2}+\mid W_{3} \mid ^{2})]W_{1}+\theta _{1}H_{4}^{*}\overline{W}_{2}\overline{W}_{3}\\ (\Phi +\Psi )\left( \frac{\partial V_{2}}{\partial T_{1}}+\frac{\partial W_{2}}{\partial T_{2}}\right) =&H_{1}^{*}(\theta _{1}V_{2}+\theta _{2}W_{2})+H_{2}^{*}(\overline{V}_{3}\overline{W}_{1} +\overline{V}_{1}\overline{W}_{3}+\theta _{1}^{2}H_{3}^{*}W_{2}\\&+[G_{1}^{*}\mid W_{2}\mid ^{2}+G_{2}^{*}(\mid W_{1} \mid ^{2}+\mid W_{3} \mid ^{2})]W_{2}+\theta _{1}H_{4}^{*}\overline{W}_{1}\overline{W}_{3} \\ (\Phi +\Psi )\left( \frac{\partial V_{3}}{\partial T_{1}}+\frac{\partial W_{3}}{\partial T_{2}}\right) =&H_{1}^{*}(\theta _{1}V_{3}+\theta _{2}W_{3})+H_{2}^{*}(\overline{V}_{1}\overline{W}_{2} +\overline{V}_{2}\overline{W}_{1}+\theta _{1}^{2}H_{3}^{*}W_{3}\\&+[G_{1}^{*}\mid W_{3}\mid ^{2}+G_{2}^{*}(\mid W_{1} \mid ^{2}+\mid W_{2} \mid ^{2})]W_{3}+\theta _{1}H_{4}^{*}\overline{W}_{1}\overline{W}_{2}, \end{aligned} \nonumber \\ \end{aligned}$$
(3.22)

where \(G_{1}^{*}=G_{1}(\theta _{T})\) and \(G_{2}^{*}=G_{2}(\theta _{T})\).

Now in system (3.1) let

$$\begin{aligned} \left( \begin{array}{cc} u \\ v \\ \end{array} \right) =\sum _{j=1}^3\left( \begin{array}{cc} A_j \\ B_j\\ \end{array} \right) \left( \begin{array}{c} \sum \limits _{j=1}^{3}W_{j}e^{\text {i}\pmb {k}_{j}\cdot \pmb {r}}+\sum \limits _{j=1}^{3}\overline{W}_{j}e^{-\text {i}\pmb {k}_{j}\cdot \pmb {r}} \\ \end{array} \right) +\cdots . \end{aligned}$$

Then it follows from [18, 30] that \(A_{j}=\Phi B_{j}(j=1,2,3)\) and the amplitudes \(A_{j}\) can be expanded as

$$\begin{aligned} A_{j}=\epsilon W_{j}+\epsilon ^{2}V_{j}+O(\epsilon ^{3}), j=1,2,3. \end{aligned}$$

According to the decomposition (3.8), the partial derivative of amplitudes \(A_{j}(j=1,2,3)\) with respect to time t has the form

$$\begin{aligned} \frac{\partial A_{j}}{\partial t}=\epsilon ^{2}\frac{\partial W_{j}}{\partial T_{1}}+\epsilon ^{3}\frac{\partial W_{j}}{\partial T_{2}}+\epsilon ^{3}\frac{\partial V_{j}}{\partial T_{1}}+O(\epsilon ^{4}). \end{aligned}$$

Let \(H(\theta )\) be given by

$$\begin{aligned} \begin{aligned} H(\theta )&=\Phi (a_{11}(\theta )-a_{11}(\theta _{T}))+a_{12}(\theta )-a_{12}(\theta _{T})\\&\quad +\Psi [\Phi (a_{21}(\theta )-a_{21}(\theta _{T}))+a_{22}(\theta )-a_{22}(\theta _{T})] \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \mu =\frac{H(\theta )}{\Phi +\Psi },~h=\frac{H_{2}(\theta )}{\Phi +\Psi },~g_{1}=-\frac{G_{1}(\theta )}{\Phi +\Psi },~g_{2}=-\frac{G_{2}(\theta )}{\Phi +\Psi }, \end{aligned}$$

where \(H_{2}(\theta )\), \(G_{1}(\theta )\) and \(G_{2}(\theta )\) are given respectively by (3.16) and (3.21). It follows from (3.17) and (3.22) that the amplitude equations of model (1.4) near \((u_{*},v_{*})\) are

$$\begin{aligned} \begin{aligned} \frac{\partial A_{1}}{\partial t}=\mu A_{1}+h\overline{A}_{2}\overline{A}_{3}- [g_{1}| A_{1}|^{2}+g_{2}(|A_{2}|^{2}+|A_{3}|^{2})]A_{1},\\ \frac{\partial A_{2}}{\partial t}=\mu A_{2}+h\overline{A}_{1}\overline{A}_{3}- [g_{1}| A_{2}|^{2}+g_{2}(| A_{1}|^{2}+|A_{3}|^{2})]A_{2},\\ \frac{\partial A_{3}}{\partial t}=\mu A_{3}+h\overline{A}_{1}\overline{A}_{2}- [g_{1}|A_{3}|^{2}+g_{2}(|A_{1}|^{2}+|A_{2}|^{2})]A_{3}. \end{aligned} \end{aligned}$$
(3.23)

4 Classification and Stability of Turing Patterns

In the present section, we discuss the existence and stability of Turing patterns arising near the Turing threshold in system (1.5) through the amplitude equations obtained in the previous section. A stable Turing pattern corresponds to a stable steady state solution of Eq. (3.23). Since each amplitude in (3.23) can be expressed into the function of a mode \(\rho _{i}=|A_{i}|\) and a phase angle \(\varphi _{i}\), one can know that \(A_j\) can be written into \(A_{j}=\rho _{j}e^{\text {i}\varphi _{j}}(j=1,2,3)\). Putting \(A_{j}=\rho _{j}e^{\text {i}\varphi _{j}}(j=1,2,3)\) into Eq. (3.23) and separating the real and the imaginary parts, we have the following equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial \varphi }{\partial t}=-h\frac{\rho _{1}^{2}\rho _{2}^{2}+\rho _{1}^{2}\rho _{3}^{2}+\rho _{2}^{2}\rho _{3}^{2}}{\rho _{1}\rho _{2}\rho _{3}}\sin \varphi ,\\ \frac{\partial \rho _{1}}{\partial t}=\mu \rho _{1}+h\rho _{2}\rho _{3}\cos \varphi -g_{1}\rho _{1}^{3} -g_{2}(\rho _{2}^{2}+\rho _{3}^{2})\rho _{1},\\ \frac{\partial \rho _{2}}{\partial t}=\mu \rho _{2}+h\rho _{1}\rho _{3}\cos \varphi -g_{1}\rho _{2}^{3} -g_{2}(\rho _{1}^{2}+\rho _{3}^{2})\rho _{2},\\ \frac{\partial \rho _{3}}{\partial t}=\mu \rho _{3}+h\rho _{1}\rho _{2}\cos \varphi -g_{1}\rho _{3}^{3} -g_{2}(\rho _{1}^{2}+\rho _{2}^{2})\rho _{3},\\ \end{array}\right. } \end{aligned}$$
(4.1)

where \(\varphi =\varphi _{1}+\varphi _{2}+\varphi _{3}\). According to [18, 19], we know that system (4.1) has the following four kinds of stationary solutions when \(g_1,g_2>0\).

  1. (1)

    The stationary state

    $$\begin{aligned} \rho _{1}=\rho _{2}=\rho _{3}=0 \end{aligned}$$

    is stable if \(\mu <0\triangleq \mu _{2}\) and unstable for \(\mu >\mu _{2}\).

  2. (2)

    The stripe pattern solution

    $$\begin{aligned} S: \rho _{1}=\sqrt{\frac{\mu }{g_{1}}}, \rho _{2}=\rho _{3}=0 \end{aligned}$$

    exists when \(\mu >0\). The stripe solution \((\sqrt{\frac{\mu }{g_{1}}},0,0)\) is stable for

    $$\begin{aligned} \mu >\frac{h^{2}g_{1}}{(g_{2}-g_{1})^{2}}\triangleq \mu _{3} \end{aligned}$$

    and unstable for \(0<\mu <\mu _{3}\).

  3. (3)

    The hexagon pattern solutions

    $$\begin{aligned} H_{0}: \rho _{1}=\rho _{2}=\rho _{3}=\frac{\mid h\mid + \sqrt{h^{2}+4(g_{1}+2g_{2})\mu }}{2(g_{1}+2g_{2})},\\ H_{\pi }: \rho _{1}=\rho _{2}=\rho _{3}=\frac{\mid h\mid - \sqrt{h^{2}+4(g_{1}+2g_{2})\mu }}{2(g_{1}+2g_{2})}, \end{aligned}$$

    exist when

    $$\begin{aligned} \mu >\frac{-h^{2}}{4(g_{1}+2g_{2})}\triangleq \mu _{1}. \end{aligned}$$

    The solution \(H_{0}\) is stable only for

    $$\begin{aligned} \mu <\frac{h^{2}(2g_{1}+g_{2})}{(g_{2}-g_{1})^{2}}\triangleq \mu _{4}, \end{aligned}$$

    while \(H_{\pi }\) is always unstable.

  4. (4)

    The mixed state

    $$\begin{aligned} \rho _{1}=\frac{\mid h\mid }{g_{2}-g_{1}}, \rho _{2}=\rho _{3}=\sqrt{\frac{\mu -g_{1}\rho _{1}^{2}}{g_{1}+g_{2}}}, \end{aligned}$$

    exists when \(g_{2}>g_{1}\), \(\mu >g_{1}\rho _{1}^{2}\) and it is always unstable.

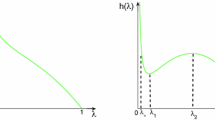
It is easy to know that under the condition \(g_{1},g_{2}>0\), the critical value \(\mu _k(k=1, 2, 3, 4)\) have the relationship \(\mu _1<\mu _2<\mu _3<\mu _4\). The curves of \(S, H_0\) and \(H_\pi \) against \(\mu \) are demonstrated in Fig. 3 and we can see that when \(\mu _{1}<\mu <\mu _{2}\), both the uniform stationary solution and the hexagonal pattern \(H_{0}\) are stable; when \(\mu _{2}<\mu <\mu _{3}\), only the hexagonal pattern \(H_{0}\) is stable; when \(\mu _{3}<\mu <\mu _{4}\), both the stripe pattern S and hexagonal pattern \(H_{0}\) are stable; when \(\mu >\mu _{4}\), only the stripe is stable. In addition, when \(\mu >\mu _{4}\), the hexagonal pattern \(H_{\pi }\) is always unstable.

Fig. 3
figure 3

Chart of stationary solutions of system (4.1) in \(\mu \)-\(\rho \) plane. The solid line shows that the stationary solution of (4.1) is stable and the dotted one shows that it is unstable

Full size image
Table 1 Range of \(\mu \) with respect to different values of \(\theta \)
Full size table
Fig. 4
figure 4

Simulation diagrams of the prey species of system (1.5) with \(d_{11}=0.5\), \(d_{12}=0.5\), \(d_{21}=1.45\), \(d_{22}=1.5\), \(m=0.8\), \(c=2\) and \(\theta =0.345\) at different instants. a \(t=200\), b \(t=400\), c \(t=1000\), d \(t=2000\)

Full size image

5 Numerical Simulations for Pattern Formations

In this section, we shall give some numerical simulations in order to verify the theoretical results obtained in Sects. 2 and 3. To carry out our numerical simulations, initial conditions in system (1.5) is taken as the random ones, \(L_x=L_y=200\), and system (1.5) is numerically integrated by using the finite difference approximation of spatial derivatives and the explicit Euler method of time derivative, in which the time step is 1/100. Set the parameters in system (1.5) as \(d_{11}=0.5, d_{12}=0.5, d_{21}=1.45, d_{22}=1.5, m=0.8, c=2\). Then in this case \(\theta _H=0.2667\) and \(\theta _T=0.3892\). Take \(\theta =0.345\), \(\theta =0.36\) and \(\theta =0.376\) respectively. Then the values for \(\mu _k(k=1,2,3,4)\) and \(\mu \) are set in the Table 1.

When \(\theta =0.345\), \(\mu \) is between \(\mu _{2}\) and \(\mu _{3}\). According to the previous theoretical analysis, system (1.5) will have a stable spot pattern and the stable \(H_{0}\) hexagon pattern, see Fig. 4. According to Fig. 4d, except for the yellow spots, the prey population is mainly distributed in the blue square area. The numerical simulation shows that the numerical results are consistent with the theoretical ones.

When \(\theta =0.36\), it can be seen that \(\mu \in (\mu _{3},\mu _{4})\) and hence the stripe and \(H_{0}\) hexagon patterns of system (1.5) are stable, see Fig. 5. It is shown that spot patterns and stripe patterns occur simultaneously and they compete each other. The dynamics of the model shows the transition from spot patterns to stripe patterns growth, that is, spot patterns decay and stripe patterns occur.

Fig. 5
figure 5

Simulation diagrams of the prey species of system (1.5) with \(d_{11}=0.5\), \(d_{12}=0.5\), \(d_{21}=1.45\), \(d_{22}=1.5\), \(m=0.8\), \(c=2\) and \(\theta =0.36\) at different instants. a \(t=200\), b \(t=600\), c \(t=1000\), d \(t=2000\)

Full size image
Fig. 6
figure 6

Simulation diagrams of the prey species of system (1.5) with \(d_{11}=0.5\), \(d_{12}=0.5\), \(d_{21}=1.45\), \(d_{22}=1.5\), \(m=0.8\), \(c=2\) and \(\theta =0.376\) at different instants. a \(t=400\), b \(t=1000\), c \(t=2000\), d \(t=4000\)

Full size image

When \(\theta \) is selected as 0.376, one can find from Table 1 that \(\mu >\mu _{4}\) and so only the stripe patterns are stable. The numerical results show that the final pattern is the stripe pattern, see Fig. 6. It can be found that the labyrinth pattern occupies the entire spatial area.

6 Conclusions

Although reaction–diffusion systems with self-diffusion can more reasonably predict the development of some species than the associated ODE models, under some particular situations cross-diffusion among species cannot still be omitted. Consequently, we regarded a classical two-species predator–prey reaction–diffusion system with the linear self-diffusion and cross-diffusion and subject to homogeneous Neumann boundary condition on a planar rectangle domain in this paper.

It has been found in [29] that only random freedom diffusion in the classical predator–prey system with the Holling-II type functional response and subject to homogeneous Neumann boundary condition on a bounded domain with a smooth boundary doesn’t affect the stability of the constant coexistence equilibrium. Whether or not the cross-diffusion can bring out more complicated dynamical behaviors in reaction–diffusion systems is an important and interesting subject. Here, we explored mainly the effect of cross-diffusion on dynamical behaviors of system in [29] and it was shown that the occurrence of linear cross-diffusion can arise more complicated dynamical behaviors such as various Turing patterns.

The effect of linear cross-diffusion on dynamical behaviors of model (1.5) have been concerned in [25], however, they gave only numerical simulations for the associated phenomena but not the detailed theoretical analysis. Therefore, the classification and stability of Turing patterns of system (1.5) near the unique constant coexistence equilibrium cannot be determined. The main contribution of this paper is that the classification and stability of Turing patterns of (1.5) near the unique constant coexistence equilibrium were gave in detail.