1 Introduction

Pattern formation is an important research aspect of modern science and technology. It can be used to describe the structure changes of interacting species or reactants of ecology, chemical reaction, and gene formation in nature. Spatial, temporal, and spatiotemporal patterns could occur in the reaction–diffusion models via Turing instability, Hopf bifurcation, and nonconstant positive solutions.

Turing instability is an important way to study spatial inhomogeneous patterns. In the early 1950s, the British mathematician Alan M. Turing [42] proposed a model that accounts for pattern formation in morphogenesis. Turing showed mathematically that a system of coupled reaction–diffusion equations could give rise to spatial concentration patterns of a fixed characteristic length from an arbitrary initial configuration due to so-called diffusion-driven instability, that is, diffusion could destabilize an otherwise stable equilibrium of the reaction–diffusion system and lead to nonuniform spatial patterns. Turing’s analysis stimulated considerable theoretical research on mathematical models of pattern formation, and a great deal of research have been devoted to the study of Turing instability in chemical and biology contexts (see [4, 10, 17, 43, 57] for Brusselator model; [6, 12, 24, 48] for Gray–Scott model; [15, 16, 27, 53, 55] for Lengyel–Epstein model; [32, 52, 56] for Oregonator model, [14, 36, 47, 49] for Schnakenberg model, [5, 29, 33, 45] for Sel’klov model, [18, 19, 23, 37, 51] for predator–prey model).

Hopf bifurcation is used to study the temporal periodic patterns. In [54], the authors gave a detailed Hopf bifurcation analysis for both the ODE and PDE models, deriving a formula for determining the direction of the Hopf bifurcation and the stability of the bifurcating spatially homogeneous periodic solutions (see also [1, 11, 21, 34, 35, 41, 46] for the studies of Hopf bifurcation in diffusive predator–prey models).

In spatially inhomogeneous case, the existence of a nonconstant time-independent positive solution, also called stationary patterns, is an indication of the richness of the corresponding partial differential equation dynamics. In recent years, stationary patterns induced by diffusion have been studied extensively, and many important phenomena have been observed (see [3, 7, 8, 20, 22, 26, 30] and references therein).

In this paper, we investigate the spatial, temporal, and spatiotemporal patterns of the following diffusive predator–prey model with ratio-dependent Holling type III functional response

(1)

To study the stationary patterns, we also consider the steady-state equations associated with (1):

$$\begin{aligned} \left\{ \begin{aligned}&-d_1{\varDelta } u=u(1-u)-\frac{\alpha (m+1) u^2v}{u^2+mv^2},&x\in {\varOmega },\\&-d_2{\varDelta } v=\lambda v\left( 1-\frac{v}{u}\right) ,&x\in {\varOmega },\\&\frac{\partial u}{\partial \nu }=\frac{\partial v}{\partial \nu }=0,&x\in \partial {\varOmega }. \end{aligned} \right. \end{aligned}$$
(2)

Here, u and v stand for the densities of the prey and predator; \({\varOmega }\) is a bounded domain of \(\mathbf {R}^N\), with smooth boundary \(\partial {\varOmega }, {\varDelta }\) is the Laplace operator with respect to the spatial variable \(x=(x_1,\ldots ,x_N), \nu \) is the unit outward normal on \(\partial {\varOmega }\). The homogeneous Neumann boundary conditions indicate that the predator–prey system is self-contained with zero population flux across the boundary. The positive constants \(d_1\) and \(d_2\) are diffusion coefficients, and the initial data \(u_0(x)\) and \(v_0(x)\) are nonnegative functions. The parameters \(m,\lambda \) are positive constants and \(0<\alpha <1\). Then it is easy to see that (2) possesses a unique positive constant steady-state solution

$$\begin{aligned} (u,v)=(1-\alpha ,1-\alpha ). \end{aligned}$$
(3)

Problem (1) was studied in [39] recently, and the uniform persistence of the solution semiflows, the existence of global attractors, local and global stability of the positive constant steady state were derived. On the other hand, the understanding of patterns and mechanisms of spatial dispersal of interacting species is an issue of significant current interest in conservation biology and ecology, and biochemical reactions [2, 9, 25, 28, 38].

The goal of this paper was to give a comprehensive mathematical study of the model (1). In particular, we are interested in the spatiotemporal pattern formation, Turing instability, bifurcation, and the effect of system parameters and diffusion coefficients on the dynamics of the solutions of (1).

The organization of the remaining part of this paper is as follows. In Sect. 2, we investigate the asymptotical behavior of the positive equilibrium \((1-\alpha ,1-\alpha )\) and occurrence of Hopf bifurcation of the local system (4) of (1). In Sect. 3, we firstly consider the asymptotical behavior and Turing instability of the positive equilibrium \((1-\alpha ,1-\alpha )\) for the reaction–diffusion system (1), and then we study the existence of Hopf bifurcation and the stability of the bifurcating periodic solution. In Sect. s4, we consider the existence and nonexistence of positive solutions for problem (2) by bifurcation theory and energy method. Throughout this paper, \(\mathbf {N}\) is the set of natural numbers and \(\mathbf {N}_0=\mathbf {N}\cup \{0\}\). The eigenvalues of the operator \(-{\varDelta }\) with homogeneous Neumann boundary condition in \({\varOmega }\) are denoted by \(0=\mu _0<\mu _1\le \mu _2\le \ldots \le \mu _n\le \ldots \), and the eigenfunction corresponding to \(\mu _n\) is \(\phi _n(x)\).

2 Analysis of the local system

For the diffusive predator–prey model (1), the local system is an ordinary differential equation in the form of

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}u}{\mathrm{d}t}=u(1-u)-\frac{\alpha (m+1) u^2v}{u^2+mv^2},&t>0,\\&\frac{\mathrm{d}v}{\mathrm{d}t}=\lambda v\left( 1-\frac{v}{u}\right) ,&t>0. \end{aligned} \right. \end{aligned}$$
(4)

By (3), \((1-\alpha ,1-\alpha )\) is the unique positive equilibrium of (4). We consider the stability of the constant equilibrium \((1-\alpha ,1-\alpha )\) with respect to problem (4) and study the existence of periodic solutions of problem (4) by analyzing the Hopf bifurcations from the constant equilibrium \((1-\alpha ,1-\alpha )\).

2.1 Stability analysis

The Jacobian matrix of system (4) at \((1-\alpha ,1-\alpha )\) is

$$\begin{aligned} L_0(\lambda )=\left( \begin{array}{cc} \displaystyle \frac{2\alpha }{m+1}-1 &{} \displaystyle \frac{(m-1)\alpha }{m+1} \\ \displaystyle \lambda &{} \displaystyle -\lambda \\ \end{array} \right) . \end{aligned}$$
(5)

The characteristic equation of \(L_0(\lambda )\) is

$$\begin{aligned} \xi ^2-T(\lambda )\xi +D(\lambda )=0, \end{aligned}$$
(6)

where

$$\begin{aligned} T(\lambda )=\frac{2\alpha }{m+1}-1-\lambda ,\ \ D(\lambda )=\lambda (1-\alpha )>0. \end{aligned}$$

Then the equilibrium \((1-\alpha ,1-\alpha )\) is locally asymptotically stable if \(T(\lambda )<0\), and it is unstable if \(T(\lambda )>0\). Thus, we have the following conclusions

Theorem 1

The unique positive equilibrium \((1-\alpha ,1-\alpha )\) of the local system (4) is locally asymptotically stable if \(\alpha \le \frac{m+1}{2}\) or \(\alpha >\frac{m+1}{2}\) and \(\lambda >\frac{2\alpha }{m+1}-1\), and it is unstable if \(\alpha >\frac{m+1}{2}\) and \(\lambda <\frac{2\alpha }{m+1}-1\).

2.2 Hopf bifurcation

In this part, we analyze the Hopf bifurcation occurring at \((1-\alpha ,1-\alpha )\) under the assumption \(\alpha >\frac{m+1}{2}\). Denote

$$\begin{aligned} \lambda _0:=\frac{2\alpha }{m+1}-1. \end{aligned}$$
(7)

Then \(L_0(\lambda )\) has a pair of purely imaginary eigenvalues \(\xi =\pm \sqrt{\lambda _0(1-\alpha )}\) when \(\lambda =\lambda _0\). Therefore, according to Poincaré–Andronov–Hopf Bifurcation Theorem [50], Theorem3.1.3], system (4) has a small amplitude nonconstant periodic solution bifurcated from the interior equilibrium \((1-\alpha ,1-\alpha )\) when \(\lambda \) crosses through \(\lambda _0\) if the transversal condition is satisfied.

Let \(\xi (\lambda )=\beta (\lambda )\pm i w(\lambda )\) be the roots of (6). Then

$$\begin{aligned} \beta (\lambda )= & {} \frac{1}{2}T(\lambda )=\frac{\alpha }{m+1}-\frac{1}{2}(1+\lambda ), \\ w(\lambda )= & {} \frac{1}{2}\sqrt{4D(\lambda )-T(\lambda )^2}\\= & {} \sqrt{\lambda (1-\alpha )-\left( \frac{\alpha }{m+1}-\frac{1}{2}(1+\lambda )\right) ^2}. \end{aligned}$$

Hence, \(\beta (\lambda _0)=0\) and \(\beta '(\lambda _0)=-\frac{1}{2}<0\). This shows that the transversal condition holds. Thus, (4) undergoes a Hopf bifurcation at \((1-\alpha ,1-\alpha )\) as \(\lambda \) passes through the \(\lambda _0\).

However, the detailed property of the Hopf bifurcation needs further analysis of the normal form of the system. To this end, we translate the equilibrium \((1-\alpha ,1-\alpha )\) to the origin by the translation \(\tilde{u}=u-(1-\alpha ), \tilde{v}=v-(1-\alpha )\). For the sake of convenience, we still denote \(\tilde{u}\) and \(\tilde{v}\) by u and v, respectively. Thus, the local system (4) becomes

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}u}{\mathrm{d}t}=&(2\alpha -1)u-u^2+\alpha (1-\alpha )\\&-\frac{\alpha (m\!+\!1)(u\!+\!1-\alpha )^2(v+1-\alpha )}{(u\!+\!1-\alpha )^2+m(v\!+\!1-\alpha )^2},&t\!>\!0,\\ \frac{\mathrm{d}v}{\mathrm{d}t}=&\lambda (v\!+\!1-\alpha )\left( 1-\frac{v\!+\!1-\alpha }{u+\!1\!-\alpha }\right) ,&t\!>\!0. \end{aligned} \right. \end{aligned}$$
(8)

Rewrite (8) to

$$\begin{aligned} \left( \begin{array}{c} \displaystyle \frac{\mathrm{d}u}{\mathrm{d}t} \\ \displaystyle \frac{\mathrm{d}v}{\mathrm{d}t} \\ \end{array} \right) =L_0(\lambda )\left( \begin{array}{c} u \\ v \\ \end{array} \right) +\left( \begin{array}{c} f(u,v,\lambda ) \\ g(u,v,\lambda ) \\ \end{array} \right) , \end{aligned}$$
(9)

where

$$\begin{aligned} f(u,v,\lambda )= & {} a_1u^2+a_2uv+a_3v^2+a_4u^3\nonumber \\&+\,\, a_5 u^2v+a_6v^3+\cdots \\ g(u,v,\lambda )= & {} b_1u^2+b_2uv+b_3v^2+b_4u^3\nonumber \\&+\,\, b_5 u^2v+b_6v^3+\cdots \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&a_1 = \frac{\alpha m(3-m)}{(m+1)^2(1-\alpha )}-1,\\&\quad a_2=-a_3=\frac{\alpha m(m-3)}{(m+1)^2(1-\alpha )}, \\&a_4=\frac{4\alpha m(m-1)}{(m+1)^3(1-\alpha )^2},\ a_5 = \frac{\alpha m(m^2-14m+9)}{3(m+1)^3(1-\alpha )^2},\\&\quad a_6=\frac{\alpha m(m^2-6m+1)}{(m+1)^3(1-\alpha )^2},\\&b_1=b_3=-b_2=-\frac{\lambda }{1-\alpha },\ b_4=\frac{\lambda }{(1-\alpha )^2},\\&\quad b_5=-\frac{2\lambda }{3(1-\alpha )^2},\ b_6=0. \end{aligned} \end{aligned}$$
Fig. 1
figure 1

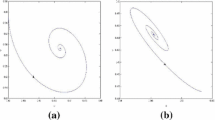
When \(\lambda =0.156>\lambda _0\approx 0.1429\), the solution trajectories spiral toward the positive equilibrium \((0.4,0.4)\) (see left-hand side of the above figure). When \(\lambda =0.14<\lambda _0\approx 0.1429\), there is a limit cycle surrounding the positive equilibrium \((0.4,0.4)\) (see right-hand side of the above figure)

Full size image

Set the matrix

$$\begin{aligned} P=\left( \begin{array}{cc} 1 &{} 0 \\ N(\lambda ) &{} M(\lambda ) \\ \end{array} \right) \end{aligned}$$

where

$$\begin{aligned} N(\lambda )=\frac{2\alpha +(m+1)(\lambda {-}1)}{2\alpha (1{-}m)},\ M(\lambda )=\frac{(m+1)w(\lambda )}{\alpha (1-m)}. \end{aligned}$$

Clearly,

$$\begin{aligned} P^{-1}=\left( \begin{array}{cc} 1 &{} 0 \\ \displaystyle -\frac{N(\lambda )}{M(\lambda )} &{} \displaystyle \frac{1}{M(\lambda )} \\ \end{array} \right) , \end{aligned}$$

and when \(\lambda =\lambda _0\),

$$\begin{aligned}&N_0:=N(\lambda _0)=\frac{2m\alpha +(m+1)(1-m)}{\alpha (m+1)(1-m)},\\&\quad M_0:=M(\lambda _0)=\frac{m+1}{\alpha (1-m)}\sqrt{\lambda _0(1-\alpha )}. \end{aligned}$$

By the transformation \((u,v)^T=P(x,y)^T\), system (8) becomes

$$\begin{aligned} \left( \begin{array}{c} \displaystyle \frac{dx}{dt} \\ \displaystyle \frac{dy}{dt} \\ \end{array} \right) ={\varPhi }(\lambda )\left( \begin{array}{c} x \\ y \\ \end{array} \right) +\left( \begin{array}{c} \tilde{f}(x,y,\lambda ) \\ \tilde{g}(x,y,\lambda ) \\ \end{array} \right) , \end{aligned}$$
(10)

where

$$\begin{aligned} {\varPhi }(\lambda )=\left( \begin{array}{cc} \beta (\lambda ) &{} -w(\lambda ) \\ w(\lambda ) &{} \beta (\lambda ) \\ \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned}&\begin{aligned} \tilde{f}(x,y,\lambda )=&f(x,Nx+My,\lambda )\\ =&\left( a_1+a_2N+a_3N^2\right) x^2\\&+(a_2M+2a_3MN)xy+a_3M^2y^2\\&+\left( a_4+a_5N+a_6N^3\right) x^3\\&+\left( a_5M+3a_6MN^2\right) x^2y\\&+3a_6M^2Nxy^2+a_6M^3y^3+\cdots , \end{aligned} \\&\begin{aligned} \tilde{g}(x,y,\lambda )=&\frac{1}{M}\left( g(x,Nx+My,\lambda ){-}Nf(x,Nx+My,\lambda )\right) \\ =&\frac{b_1+(b_2-a_1)N+(b_3-a_2)N^2-a_3N^3}{M}x^2\\&+\left( b_2+(2b_3-a_2)N-2a_3N^2\right) xy\\&+(b_3M-a_3MN)y^2\\&+\frac{b_4+(b_5-a_4)N-a_5N^2-a_6N^4}{M}x^3\\&+\left( b_5-a_5N-3a_6N^3\right) x^2y\\&-3a_6MN^2xy^2-a_6M^2Ny^3+\cdots \\ \end{aligned}\\ \end{aligned}$$

Rewrite (9) in the following polar coordinates form

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}r}{\mathrm{d}t}=\beta (\lambda )r+a(\lambda )r^3+\cdots ,\\&\frac{\mathrm{d}\theta }{\mathrm{d}t}=w(\lambda )+c(\lambda )r^2+\cdots , \end{aligned} \right. \end{aligned}$$
(11)

then the Taylor expansion of (11) at \(\lambda =\lambda _0\) yields

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}r}{\mathrm{d}t}=\beta '(\lambda _0)(\lambda -\lambda _0)r+a(\lambda _0)r^3\\&\qquad \quad +o\left( (\lambda -\lambda _0)^2r,(\lambda -\lambda _0)r^3,r^5\right) ,\\&\frac{\mathrm{d}\theta }{\mathrm{d}t}=w(\lambda _0)+w'(\lambda _0)(\lambda -\lambda _0)+c(\lambda _0)r^2\\&\qquad \quad +o\left( (\lambda -\lambda _0)^2,(\lambda -\lambda _0)r^2,r^4\right) . \end{aligned} \right. \end{aligned}$$
(12)

In order to determine the stability of the periodic solution, we need to calculate the sign of the coefficient \(a(\lambda _0)\), which is give by

$$\begin{aligned} \begin{aligned} a(\lambda _0)&:=\frac{1}{16}\left( \tilde{f}_{xxx}+\tilde{f}_{xyy}+\tilde{g}_{xxy}+\tilde{g}_{yyy}\right) (0,0,\lambda _0)\\&\qquad +\frac{1}{16w(\lambda _0)}\left( \tilde{f}_{xy}\left( \tilde{f}_{xx}+\tilde{f}_{yy}\right) \right. \\&\qquad \left. -\,\tilde{g}_{xy}\left( \tilde{g}_{xx}+\tilde{g}_{yy}\right) {-}\tilde{f}_{xx}\tilde{g}_{xx}+\tilde{f}_{yy}\tilde{g}_{yy}\right) (0,0,\lambda _0), \end{aligned} \end{aligned}$$
(13)

where

$$\begin{aligned} \begin{aligned}&\tilde{f}_{xxx}(0,0,\lambda _0)=6\left( a_4+a_5+a_6N_0^3\right) ,\\&\quad f_{xyy}(0,0,\lambda _0)=6a_6M_0^2N_0,\\&\tilde{g}_{xxy}(0,0,\lambda _0)=2\left( b_5-a_5N_0-3a_6N_0^3\right) ,\\&\quad g_{yyy}(0,0,\lambda _0)=-6a_6M_0^2N_0,\\&\tilde{f}_{xx}(0,0,\lambda _0)=2\left( a_1+a_2N_0+a_3N_0^2\right) ,\\&\quad f_{xy}(0,0,\lambda _0)=a_2M_0+2a_3M_0N_0,\\&\tilde{f}_{yy}(0,0,\lambda _0)=2a_3M_0^2,\\&\quad g_{xx}(0,0,\lambda _0)=2\\&\quad \times \left( \frac{b_1+(b_2-a_1)N_0+(b_3-a_2)N_0^2-a_3N_0^3}{M_0}\right) ,\\&\tilde{g}_{xy}(0,0,\lambda _0)=b_2+(2b_3-a_2)N_0-2a_3N_0^2,\\&\quad g_{yy}=2(b_3M_0-a_3M_0N_0). \end{aligned} \end{aligned}$$

Now from Poincaré-Andronov-Hopf Bifurcation Theorem, \(\beta '(\lambda _0)=-\frac{1}{2}<0\) and the above calculation of \(a(\lambda _0)\), we summarize our results as follows.

Theorem 2

Suppose \(\frac{m+1}{2}<\alpha <1\) and let \(a(\lambda _0)\) be defined as in (13). Then system (4) undergoes a Hopf bifurcation at \((1-\alpha ,1-\alpha )\) when \(\lambda =\lambda _0\). Furthermore,

  1. 1.

    if \(a(\lambda _0)<0\), then the direct of the Hopf bifurcation is subcritical and the bifurcating periodic solutions are orbitally asymptotically stable;

  2. 2.

    if \(a(\lambda _0)>0\), then the direct of the Hopf bifurcation is supercritical and the bifurcating periodic solutions are unstable.

2.3 Numerical simulations

To illustrate Theorem 2, we give some numerical simulations for the following particular case of system (4) with fixed parameters \(\alpha =0.6, m=0.05\).

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}u}{\mathrm{d}t}=u(1-u)-\frac{0.6(0.05+1) u^2v}{u^2+0.05v^2},&t>0,\\&\frac{\mathrm{d}v}{\mathrm{d}t}=\lambda v\left( 1-\frac{v}{u}\right) ,&t>0. \end{aligned} \right. \end{aligned}$$
(14)

It is easy to see \(1.05=m+1<1.2=2\alpha \), and system (14) has a unique positive equilibrium \((0.4,0.4)\). Noticing that \(\lambda _0\approx 0.1429\) and \(a(\lambda _0)\approx -0.2907\), it follows from Theorem1 that \((0.4,0.4)\) is locally asymptotically stable when \(\lambda >\lambda _0\approx 0.1429\) and unstable when \(\lambda <\lambda _0\approx 0.1429\). Moreover, when \(\lambda \) passuses through \(\lambda _0\) from the right side of \(\lambda _0, (0.4,0.4)\) will lose its stability and Hopf bifurcation occurs, that is, a family of periodic solutions bifurcate from \((0.4,0.4)\). Since \(a(\lambda _0)\approx -0.2907<0\), it follows from Theorem 2 that the Hopf bifurcation is subcritical and the bifurcating periodic solutions are orbitally asymptotically stable. Numerical simulations are presented in Fig. 1. The left of Fig. 1 shows the stable behavior of the prey and predator when \(\lambda >\lambda _0\). The right of Fig. 1 is the phase portrait of the problem (14), which depicts the limit cycle arising out of Hopf bifurcation around \((0.4,0.4)\).

3 Analysis of the PDE model (1)

In this section, we consider the stability of the constant equilibrium \((1-\alpha ,1-\alpha )\) with respect to problem (1) and study the existence of periodic solutions of problem (1) by analyzing the Hopf bifurcations from the constant equilibrium \((1-\alpha ,1-\alpha )\).

3.1 Stability analysis

The stability of \((1-\alpha ,1-\alpha )\) with respect to (1) is determined by the following eigenvalue problem, which is got by linearizing the system (2) about the constant equilibrium \((1-\alpha ,1-\alpha )\)

$$\begin{aligned} \left\{ \begin{aligned}&d_1{\varDelta }\phi +\left( \frac{2\alpha }{m+1}-1\right) \phi +\frac{(m-1)\alpha }{m+1}\psi =\mu \phi ,&x\in {\varOmega },\\&d_2{\varDelta }\psi +\lambda \phi -\lambda \psi =\mu \psi ,&x\in {\varOmega },\\&\frac{\partial \phi }{\partial \nu }=\frac{\partial \psi }{\partial \nu }=0,&x\in \partial {\varOmega }. \end{aligned} \right. \end{aligned}$$
(15)

Denote

$$\begin{aligned} L(\lambda )=\left( \begin{array}{cc} d_1{\varDelta }+\frac{2\alpha }{m+1}-1 &{} \frac{(m-1)\alpha }{m+1} \\ \lambda &{} d_2{\varDelta }-\lambda \\ \end{array} \right) . \end{aligned}$$
(16)

For each \(n\in \mathbf {N}_0\), we define a \(2\times 2\) matrix

$$\begin{aligned} L_n(\lambda )=\left( \begin{array}{cc} -d_1\mu _n+\frac{2\alpha }{m+1}-1 &{} \frac{(m-1)\alpha }{m+1} \\ \lambda &{} -d_2\mu _n-\lambda \\ \end{array} \right) . \end{aligned}$$
(17)

The following statements hold true by using Fourier decomposition:

  1. 1.

    If \(\mu \) is an eigenvalue of (15), then there exists \(n\in \mathbf {N}_0\) such that \(\mu \) is an eigenvalue of \(L_n(\lambda )\).

  2. 2.

    The constant equilibrium \((1-\alpha ,1-\alpha )\) is locally asymptotically stable with respect to (1) if and only if for every \(n\in \mathbf {N}_0\), all eigenvalues of \(L_n(\lambda )\) have negative real part.

  3. 3.

    The constant equilibrium \((1-\alpha ,1-\alpha )\) is unstable with respect to (1) if there exists an \(n\in \mathbf {N}_0\) such that \(L_n(\lambda )\) has at least one eigenvalue with positive real part.

The characteristic equation of \(L_n(\lambda )\) is

$$\begin{aligned} \mu ^2-T_n(\lambda )\mu +D_n(\lambda )=0, \end{aligned}$$
(18)

where

$$\begin{aligned} T_n(\lambda )= & {} -(d_1+d_2)\mu _n+\frac{2\alpha }{m+1}-1-\lambda ,\\ D_n(\lambda )= & {} d_1d_2\mu _n^2+\left( d_1\lambda +d_2-\frac{2\alpha }{m+1}d_2\right) \mu _n\\&+\,\lambda (1-\alpha ). \end{aligned}$$

Then \((1-\alpha ,1-\alpha )\) is locally asymptotically stable if \(T_n(\lambda )<0\) and \(D_n(\lambda )>0\) for all \(n\in \mathbf {N}_0\), and \((1-\alpha ,1-\alpha )\) is unstable if there exists \(n\in \mathbf {N}_0\) such that \(T_n(\lambda )>0\) or \(D_n(\lambda )<0\).

Obviously, if \(2\alpha \le m+1\), then \(T_n(\lambda )<0\) and \(D_n(\lambda )>0\) for all \(n\in \mathbf {N}_0\). We get \((1-\alpha ,1-\alpha )\) is locally asymptotically stable.

Next, we consider the case \(\alpha >(m+1)/2\), which implies \(m<1\) since \(\alpha <1\).

We define

$$\begin{aligned} T(\lambda ,\mu )= & {} -\lambda -(d_1+d_2)\mu +\frac{2\alpha }{m+1}-1, \\ D(\lambda ,\mu )= & {} (1-\alpha )\lambda +d_1\mu \lambda +d_1d_2\mu ^2 \nonumber \\&+\,d_2 \left( 1-\frac{2\alpha }{m+1}\right) \mu ,\nonumber \end{aligned}$$
(19)

and

$$\begin{aligned} H= & {} \left\{ (\lambda ,\mu )\in (0,\infty )\times [0,\infty ):T(\lambda ,\mu )=0\right\} , \\ S= & {} \left\{ (\lambda ,\mu )\in (0,\infty )\times [0,\infty ):D(\lambda ,\mu )=0\right\} . \end{aligned}$$

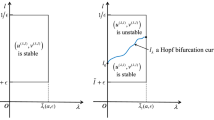
Then \(H\) is the Hopf bifurcation curve, and \(S\) is the steady-state bifurcation curve. Furthermore, the sets \(H\) and \(S\) are graphs of functions defined as follows

$$\begin{aligned} \lambda _H(\mu )= & {} -(d_1+d_2)\mu +\lambda _0, \end{aligned}$$
(20)
$$\begin{aligned} \lambda _S(\mu )= & {} \frac{\lambda _0d_2\mu -d_1d_2\mu ^2}{d_1\mu -\alpha +1}, \end{aligned}$$
(21)

where \(\lambda _0\) is defined as in (7), which is positive since \(\alpha >(m+1)/2\).

The following properties of the functions \(\lambda _H(\mu )\) and \(\lambda _S(\mu )\) can be derived by direct calculations.

Lemma 1

Suppose \(1>\alpha >(m+1)/2\). Let \(\lambda _0\) be defined as in (7), and let \(\lambda _H(\mu )\) and \(\lambda _S(\mu )\) be the functions defined as in (20) and (21), respectively. Define

$$\begin{aligned} \mu _1^*:= & {} \frac{\sqrt{(1-\alpha )^2+(1-\alpha )\lambda _0}+\alpha -1}{d_1}\in \left( 0,\frac{\lambda _0}{d_1}\right) , \end{aligned}$$
(22)
$$\begin{aligned} \mu _2^*:= & {} \frac{\lambda _0}{d_1+d_2}, \end{aligned}$$
(23)
$$\begin{aligned} \mu _3^*:= & {} \frac{\lambda _0}{d_1}, \end{aligned}$$
(24)
$$\begin{aligned} \mu ^H:= & {} \frac{-\zeta +\sqrt{\zeta ^2+4\lambda _0(1-\alpha )d_1^2}}{2d_1^2},\nonumber \\&\quad \zeta :=(d_1+d_2)(1-\alpha )+(d_2-d_1)\lambda _0, \end{aligned}$$
(25)
$$\begin{aligned} \mu ^l:= & {} \frac{(d_2{-}d_1)\lambda _0{-}\sqrt{(d_2{-}d_1)^2\lambda _0^2{-}4d_1d_2(1{-}\alpha )\lambda _0}}{2d_1d_2}, \end{aligned}$$
(26)
$$\begin{aligned} \mu ^r:= & {} \frac{(d_2{-}d_1)\lambda _0\!+\!\sqrt{(d_2{-}d_1)^2\lambda _0^2{-}4d_1d_2(1{-}\alpha )\lambda _0}}{2d_1d_2}, \end{aligned}$$
(27)
$$\begin{aligned} D_1^*:= & {} \sqrt{\frac{\lambda _0}{1-\alpha }+1}, \end{aligned}$$
(28)
$$\begin{aligned} D_2^*:= & {} \frac{1}{\lambda _0}\left( \lambda _0+2(1{-}\alpha )+2\sqrt{(1{-}\alpha )^2+(1{-}\alpha )\lambda _0}\right) , \end{aligned}$$
(29)
$$\begin{aligned} \alpha ^*:= & {} \frac{(m+1)(1+\sqrt{2})}{2(m+\sqrt{2})}\in \left( \frac{m+1}{2},1\right) , \end{aligned}$$
(30)
$$\begin{aligned} \lambda _S^*:= & {} \lambda _S(\mu _1^*)\nonumber \\= & {} \frac{d_2\left( \lambda _0+1{-}\alpha {-}\sqrt{(1{-}\alpha )^2+(1{-}\alpha )\lambda _0}\right) ^2}{d_1(\lambda _0+1{-}\alpha )}>0, \end{aligned}$$
(31)
$$\begin{aligned} \lambda _H^*:= & {} \lambda _H(\mu _1^*)\nonumber \\= & {} \lambda _0{-}\left( 1\!+\!\frac{d_2}{d_1}\right) \left( \sqrt{(1{-}\alpha )^2\!+\!(1{-}\alpha )\lambda _0}{-}(1{-}\alpha )\right) . \end{aligned}$$
(32)
  1. 1.

    The function \(\lambda _H(\mu )\) is strictly decreasing for \(\mu \in (0,\infty )\) such that

    $$\begin{aligned}&\lambda _H(0)\!=\!\lambda _0,\ \lambda _H\left( \mu _2^*\right) \!=\!0,\ \lambda _H(\mu )<0\ \mathrm{for}\ \\&\quad \mu >\mu _2^*, \lim _{\mu \rightarrow +\infty }\lambda _H(\mu )=-\infty . \end{aligned}$$
  2. 2.

    \(\mu =\mu _1^*\) is the unique critical value of \(\lambda _S(\mu )\), the function \(\lambda _S(\mu )\) is strictly increasing for \(\mu \in (0,\mu _1^*)\), and \(\lambda _S(\mu )\) is strictly decreasing for \(\mu \in (\mu _1^*,+\infty )\). Furthermore,

    $$\begin{aligned}&\lambda _S(0)=\lambda _S\left( \mu _3^*\right) =0,\ \max _{\mu \in [0,+\infty )}\lambda _S(\mu )=\lambda _S^*,\\&\quad \lim _{\mu \rightarrow +\infty }\lambda _S(\mu )=-\infty . \end{aligned}$$
  3. 3.

    \(\lambda _H(\mu )\) and \(\lambda _S^{\mu }\) cross at the point \(\left( \mu ^H,\lambda _H\left( \mu ^H\right) \right) \) and \(\lambda _H(\mu )>\lambda _S(\mu )\) for \(0\le \mu <\mu ^H, \lambda _H(\mu )<\lambda _S(\mu )\) for \(\mu ^H<\mu \le \mu _3^*\).

  4. 4.

    \(\lambda _H^*>\lambda _S^*\) if \(\frac{d_2}{d_1}<1, \lambda _H^*=\lambda _S^*\) if \(\frac{d_2}{d_1}=1\), and \(\lambda _H^*<\lambda _S^*\) if \(\frac{d_2}{d_1}>1\).

  5. 5.

    \(\mu _1^*>\mu _2^*\) if \(\frac{d_2}{d_1}>D_1^*, \mu _1^*=\mu _2^*\) if \(\frac{d_2}{d_1}=D_1^*\), and \(\mu _1^*<\mu _2^*\) if \(\frac{d_2}{d_1}<D_1^*\).

  6. 6.

    \(\lambda _S^*>\lambda _0\) if \(\frac{d_2}{d_1}>D_2^*, \lambda _S^*=\lambda _0\) if \(\frac{d_2}{d_1}=D_2^*\), and \(\lambda _S^*<\lambda _0\) if \(\frac{d_2}{d_1}<D_2^*\). Moreover, if \(\frac{d_2}{d_1}>D_2^*\), then

    1. (a)

      \(0<\mu ^l<\mu _1^*<\mu ^r\) and \(\lambda _S\left( \mu ^l\right) =\lambda _S\left( \mu ^r\right) =0\);

    2. (b)

      \(\lambda _S(\mu )>\lambda _0\) for \(\mu \in \left( \mu ^l,\mu ^r\right) \) and \(0<\lambda _S(\mu )<\lambda _0\) for \(\mu \in \left( 0,\mu ^l\right) \cup \left( \mu ^r,\mu _3^*\right) \).

  7. 7.

    Let us view \(D_1^*\) and \(D_2^*\) as functions of \(\alpha \in \left( (m+1)/2,1\right) \). Then \(D_1^*\) is strictly increasing, and \(D_2^*\) is strictly decreasing. Furthermore,

    $$\begin{aligned} \begin{aligned}&\lim _{\alpha \rightarrow \frac{m+1}{2}^+}D_1^*=1,\ \lim _{\alpha \rightarrow 1^-}D_1^*=+\infty ,\\&\lim _{\alpha \rightarrow \frac{m+1}{2}^+}D_2^*=+\infty ,\ \lim _{\alpha \rightarrow 1^-}D_1^*=1,\\&D_1^*(\alpha ^*)=D_2^*(\alpha ^*)=\sqrt{2\sqrt{2}+3}. \end{aligned} \end{aligned}$$

    Moreover, \(D_1^*<D_2^*\) if \(\frac{m+1}{2}<\alpha <\alpha ^*\) and \(D_1^*>D_2^*\) if \(\alpha ^*<\alpha <1\).

Now we can give a stability result regarding the constant equilibrium \((1-\alpha ,1-\alpha )\) by above analysis. We define

$$\begin{aligned} \overline{\lambda }:=\max _{n\in \mathbf {N}}\lambda _S(\mu _n)\le \lambda _S^*. \end{aligned}$$
(33)
Fig. 2
figure 2

The line is the graph of \(\lambda _H(\mu )\). The curves are the graphs of \(\lambda _S(\mu )\). Left is for \(\frac{d_2}{d_1}<D_1^*\), in which (1) is the case of \(\frac{d_2}{d_1}<1\), (2) is the case of \(\frac{d_2}{d_1}=1\), (3) is the case of \(\frac{d_2}{d_1}>1\) and \(\frac{d_2}{d_1}<D_2^*\), (4) is the case of \(\frac{d_2}{d_1}>1\) and \(\frac{d_2}{d_1}=D_2^*\), and (5) is the case of \(\frac{d_2}{d_1}>1\) and \(\frac{d_2}{d_1}>D_2^*\). Middle is for \(\frac{d_2}{d_1}=D_1^*\), in which (1) is the case of \(\frac{d_2}{d_1}<D_2^*\), (2) is the case of \(\frac{d_2}{d_1}=D_2^*\), and (3) is the case of \(\frac{d_2}{d_1}>D_2^*\). Right is for \(\frac{d_2}{d_1}>D_1^*\), in which (1) is the case of \(\frac{d_2}{d_1}<D_2^*\), (2) is the case of \(\frac{d_2}{d_1}=D_2^*\), and (3) is the case of \(\frac{d_2}{d_1}>D_2^*\)

Full size image

Theorem 3

Let \(\lambda _0, \lambda _S^*, \overline{\lambda }\), and \(D_2^*\) be the constants defined as (7), (31 32), (33), and (29 30), respectively. The constant equilibrium \((1-\alpha ,1-\alpha )\) is locally asymptotically stable with respect to (1) if \(2\alpha \le m+1\); or \(2\alpha >m+1\) and

$$\begin{aligned} \lambda >\max \{\lambda _0,\overline{\lambda }\}. \end{aligned}$$
(34)

In particular, (34) holds if

$$\begin{aligned} \begin{aligned} \lambda >\max \{\lambda _0,\lambda _S^*\}=\left\{ \begin{array}{ll} \lambda _S^*, &{} \hbox {if }\frac{d_2}{d_1}>D_2^*; \\ \lambda _0, &{} \hbox {otherwise.} \end{array} \right. \end{aligned} \end{aligned}$$

The constant equilibrium \((1-\alpha ,1-\alpha )\) is unstable with respect to (1) if \(\lambda <\max \{\lambda _0,\overline{\lambda }\}\).

Remark 1

In [39], the authors also studied the locally asymptotic stability of \((1-\alpha ,1-\alpha )\) for \(N=1\), i.e., \({\varOmega }=(0,\ell )\) for some constant \(\ell >0\), and they got \((1-\alpha ,1-\alpha )\) is locally asymptotically sable if \(2\alpha \le m+1\). In view of above theorem, we extend their results about two aspects:

  • The condition \(2\alpha \le m+1\) also ensures the locally asymptotic stability of \((1-\alpha ,1-\alpha )\) for general dimensional \(N\ge 1\).

  • The are also some stability results when \(2\alpha >m+1\), which includes the effects of the diffusion coefficients \(d_1\) and \(d_2\).

For global stability results of the constant equilibrium \((1-\alpha ,1-\alpha )\), we refer [39], Theorem2.7].

Next, we derive conditions for the Turing instability with respect to constant equilibrium \((1-\alpha ,1-\alpha )\), which means \((1-\alpha ,1-\alpha )\) is locally asymptotically stable with respect to (4), and it is unstable with respect to (1). In view of Theorem 1, Lemma 1 and Theorem 3, we have

Theorem 4

Let fix \(m\in (0,1)\) and \(\alpha \in \left( \frac{m+1}{2},1\right) \). Then Turing instability happens if

  1. (i)

    \(\displaystyle \frac{d_2}{d_1}>D_2^*\),

  2. (ii)

    there exists \(k\in \mathbf {N}\) such that \(\mu _k\in \left( \mu ^l,\mu ^r\right) \), and \(\lambda _0<\lambda <\lambda _S(\mu _k)\),

where \(\lambda _0, \lambda _S(\mu ), \mu ^l, \mu ^r, D_2^*\), and \(\lambda _S^*\) are defined as (7), (21), (26), (27), (29 30), and (31 32), respectively.

3.2 Hopf bifurcations

In this part, we study the existence of periodic solutions of (1) by analyzing the Hopf bifurcations from the positive constant equilibrium \((1-\alpha ,1-\alpha )\) for \(2\alpha >m+1\) since \((1-\alpha ,1-\alpha )\) is locally asymptotic stable when \(2\alpha \le m+1\), and we will show the existence of spatially homogeneous and spatially nonhomogeneous periodic orbits. In this part and Sect. 4.1, we assume that all eigenvalues \(\mu _i\) are simple and denote the corresponding eigenfunction by \(\phi _i(x)\), where \(i\in \mathbf {N}_0\). Note that this assumption always holds when \(N=1\) for \({\varOmega }=(0,\ell \pi )\), as for \(i\in \mathbf {N}_0, \mu _i=i^2/\ell ^2\) and \(\phi _i(x)=\cos (ix/\ell )\), where \(\ell \) is a positive constant, and it also holds for generic class of domain in higher dimensions. We use \(\lambda \) as the main bifurcation parameter. To identify possible Hopf bifurcation value \(\lambda ^H\), we recall the following necessary and sufficient condition from [13, 54].

\((A_H)\) :

There exists \(i\in \mathbf {N}_0\) such that

$$\begin{aligned}&T_i(\lambda ^H)=0,\;D_i(\lambda ^H)>0\;\mathrm{and}\;T_j(\lambda ^H)\not =0,\nonumber \\&\quad D_j(\lambda ^H)\not =0\;\mathrm{for}\;j\in \mathbf {N}_0\setminus \{i\}, \end{aligned}$$
(35)

where \(T_i(\lambda )\) and \(D_i(\lambda )\) are defined as (18), and for the unique pair of complex eigenvalues \(\alpha (\lambda )\pm i\omega (\lambda )\) near the imaginary axis,

$$\begin{aligned} \alpha '(\lambda ^H)\not =0\;\mathrm{and}\;\omega (\lambda ^H)>0. \end{aligned}$$
(36)

For \(i\in \mathbf {N}_0\), we define

$$\begin{aligned} \lambda _i^H=\lambda _H(\mu _i), \end{aligned}$$
(37)

where the function \(\lambda _H(\mu )\) is defined as (20). Then \(T_i(\lambda _i^H)=0\) and \(T_j(\lambda _i^H)\not =0\) for \(j\not =i\).

By (35), we need \(D_i(\lambda _i^H)>0\) to make \(\lambda _i^H\) as a possible bifurcation value, which means \(\mu _i<\mu ^H\) by part 3 of Lemma 1, where \(\mu ^H\) is defined as in (25). Let \(n_0\in \mathbf {N}_0\) such that \(\mu _{n_0}<\mu ^H\le \mu _{n_0+1}\), then we can see (35) holds with \(\lambda ^H=\lambda _i^H\) for \(0\le i\le n_0\) (see Fig. 2). Finally, we consider the conditions in (36). Let the eigenvalues close to the pure imaginary one at \(\lambda =\lambda _i^H, 0\le i\le n_0\) be \(\alpha (\lambda )\pm i\omega (\lambda )\). Then

$$\begin{aligned} \alpha '(\lambda _i^H)= & {} \frac{T'_i(\lambda _i^H)}{2}=-\frac{1}{2}<0, \\ \omega (\lambda _i^H)= & {} \sqrt{D_i(\lambda _i^H)}>0. \end{aligned}$$

Then all conditions in \((A_H)\) are satisfied if \(0\le i\le n_0\). Now, by using the Hopf bifurcation theorem in [54], we have

Theorem 5

Suppose that \(\alpha , m,d_1,d_2\) are fixed such that \((m+1)/2<\alpha <1\). Let \(\lambda _0, L(\lambda ), D_i(\lambda ), \mu ^H\) be defined as in (7), (16), (19), and (25), respectively. Let \({\varOmega }\) be a smooth domain so that all eigenvalues \(\mu _i, i\in \mathbf {N}_0\) are simple. Then there exists \(n_0\in \mathbf {N}_0\) such that \(\mu _{n_0}<\mu ^H\le \mu _{n_0+1}\), and \(\lambda _i^H\) is a Hopf bifurcation value for \(i\in \{0,\ldots ,n_0\}\). At each \(\lambda _i^H\), the system (1) undergoes a Hopf bifurcation, and the bifurcation periodic orbits near \((\lambda ,u,v)=\left( \lambda _i^H, 1-\alpha , 1-\alpha \right) \) can be parameterized as \((\lambda (s),u(s),v(s))\), so that \(\lambda (s)\in C^\infty \) in the form of \(\lambda (s)=\lambda _i^H+o(s)\) for \(s\in (0,\delta )\) for some small constant \(\delta >0\), and

$$\begin{aligned} u(s)(x,t)= & {} 1-\alpha +sa_i\cos \left( \omega \left( \lambda _i^H\right) t\right) \phi _i(x)+o(s), \\ v(s)(x,t)= & {} 1-\alpha +sb_i\cos \left( \omega \left( \lambda _i^H\right) t\right) \phi _i(x)+o(s), \end{aligned}$$

where \(\omega \left( \lambda _i^H\right) =\sqrt{D_i\left( \lambda _i^H\right) }\) is the corresponding time frequency, \(\phi _i(x)\) is the corresponding spatial eigenfunction, and \((a_i,b_i)\) is the corresponding eigenvector, i.e.,

$$\begin{aligned} \left( L\left( \lambda _i^H\right) -i\omega \left( \lambda _i^H\right) I\right) \left( \begin{array}{c} a_i\phi _i(x) \\ b_i\phi _i(x) \\ \end{array} \right) =\left( \begin{array}{c} 0 \\ 0 \\ \end{array} \right) . \end{aligned}$$

Moreover,

  1. 1.

    The bifurcation periodic orbits from \(\lambda =\lambda _0^H=\lambda _0\) are spatially homogeneous, which coincide with the periodic orbits of the corresponding local system (4);

  2. 2.

    The bifurcation periodic orbits from \(\lambda _i^H, 1\le i\le n_0\), are spatially nonhomogeneous.

Next, we consider the bifurcation direction (\(\lambda '(0)>0\) or \(\lambda '(0)<0\)) and stability of the bifurcating periodic solutions bifurcating from \(\lambda =\lambda _0\), and we have the following theorem.

Theorem 6

Suppose the assumptions in Theorem 5 hold, and let

$$\begin{aligned} \rho (\alpha ,m):= & {} -(\alpha +2)(1-\alpha )m^3-\left( 6\alpha ^2+21\alpha -14\right) m^2\nonumber \\&+\left( 9\alpha ^2+19\alpha +10\right) m-15\alpha -6. \end{aligned}$$
(38)

Then,

  1. 1.

    if \(\rho (\alpha ,m)<0\), the Hopf bifurcation at \(\lambda =\lambda _0\) is subcritical and the bifurcating periodic solutions are orbitally asymptotical stable;

  2. 2.

    if \(\rho (\alpha ,m)>0\), the Hopf bifurcation at \(\lambda =\lambda _0\) is supercritical and the bifurcating periodic solutions are unstable.

Proof

We use the normal form method and center manifold theorem in [13] to prove this theorem. Let \(L^*(\lambda )\) be the conjugate operator of \(L(\lambda )\) defined as (16):

$$\begin{aligned} L^*(\lambda )\left( \begin{array}{c} u \\ v \\ \end{array} \right) =\left( \begin{array}{cc} d_1{\varDelta }+\frac{2\alpha }{m+1}-1 &{} \lambda \\ \frac{(m-1)\alpha }{m+1} &{} d_2{\varDelta }-\lambda \\ \end{array} \right) \left( \begin{array}{c} u \\ v \\ \end{array} \right) \nonumber \\ \end{aligned}$$
(39)

with domain \(D_{L^*}=D_L=X_C:=X\oplus iX=\{x_1+ix_2:x_1,x_2\in X\}\), where

$$\begin{aligned}&X :=\left\{ (u,v)\in H^2({\varOmega })\times H^2({\varOmega }):\frac{\partial u}{\partial \nu }\right. \nonumber \\&\quad \left. =\frac{\partial v}{\partial \nu }=0,\ x\in \partial {\varOmega }\right\} . \end{aligned}$$

Let

$$\begin{aligned}&q:=\left( \begin{array}{c} 1 \\ \frac{1}{1+\lambda _0-\alpha }\left( \lambda _0-\sqrt{\lambda _0(1-\alpha )}i\right) \\ \end{array} \right) ,\\&\quad q^*:=\left( \begin{array}{c} \frac{1}{2|{\varOmega }|}\left( 1+\sqrt{\frac{\lambda _0}{1-\alpha }}i\right) \\ -\frac{1+\lambda _0-\alpha }{2|{\varOmega }|\sqrt{\lambda _0(1-\alpha )}} i\\ \end{array} \right) . \end{aligned}$$

It is easy to see that

  1. 1.

    \(\langle L^*(\lambda )\xi ,\eta \rangle =\langle \xi ,L(\lambda )\eta \rangle \) for any \(\xi \in D_{L^*}\) and \(\eta \in D_L\),

  2. 2.

    \(L^*(\lambda )q^*=-i\sqrt{\lambda _0(1{\!-}\alpha )}q^*, L(\lambda )q=i\sqrt{\lambda _0(1-\alpha )}q\),

  3. 3.

    \(\langle q^*,q\rangle \)=1, \(\langle q^*,\overline{q}\rangle =0\).

Here \(\langle \xi ,\eta \rangle :=\int _{\varOmega }\overline{\xi }^T\eta dx\) denotes the inner product in \(L^2({\varOmega })\times L^2({\varOmega })\).

According to [13], we decompose \(X=X^C\oplus X^S\) with \(X^C:=\left\{ zq+\overline{z}\overline{q}:z\in \mathbf {C}\right\} \) and \(X^S:=\left\{ \omega \in X:\langle q^*,\omega \rangle =0\right\} \). For any \((u,v)\in X\), there exits \(z\in \mathbf {C}\) and \(\omega =(\omega _1,\omega _2)\) such that

$$\begin{aligned} (u,v)^T=zq+\overline{z}\overline{q}+(\omega _1,\omega _2)^T,\ z=\left\langle q^*,(u,v)^T\right\rangle . \end{aligned}$$

Thus,

$$\begin{aligned} \left\{ \begin{aligned} u&=z+\overline{z}+\omega _1,\\ v&=\frac{z}{1+\lambda _0-\alpha }\left( \lambda _0-\sqrt{\lambda _0(1-\alpha )}i\right) \\&\quad + \frac{\overline{z}}{1+\lambda _0-\alpha }\left( \lambda _0+\sqrt{\lambda _0(1-\alpha )}i\right) +\omega _2. \end{aligned} \right. \end{aligned}$$

Our system in \((z,\omega )\) coordinates becomes

$$\begin{aligned} \left\{ \begin{aligned} \frac{\mathrm{d}z}{\mathrm{d}t}&=i\sqrt{\lambda _0(1-\alpha )}z+\left\langle q^*, \varphi \right\rangle ,\\ \frac{\mathrm{d}\omega }{\mathrm{d}t}&=L(\lambda )\omega +\left( \varphi -\left\langle q^*, \varphi \right\rangle q-\left\langle \overline{q}^*, \varphi \right\rangle \overline{q}\right) , \end{aligned} \right. \end{aligned}$$
(40)

with \(\varphi =(f,g)^T\), where f and g are defined as (9). Straightforward calculations show that

$$\begin{aligned}&\left\langle q^*, \varphi \right\rangle = \frac{1}{2}\left( f-i\left( \sqrt{\frac{\lambda _0}{1-\alpha }}f-\frac{1+\lambda _0-\alpha }{\sqrt{\lambda _0(1-\alpha )}}g\right) \right) , \\&\left\langle \overline{q}^*, \varphi \right\rangle = \frac{1}{2}\left( f+i\left( \sqrt{\frac{\lambda _0}{1-\alpha }}f-\frac{1+\lambda _0-\alpha }{\sqrt{\lambda _0(1-\alpha )}}g\right) \right) , \\&\left\langle q^*, \varphi \right\rangle q=\frac{1}{2}\left( \begin{array}{c} f-i\left( \sqrt{\frac{\lambda _0}{1-\alpha }}f-\frac{1+\lambda _0-\alpha }{\sqrt{\lambda _0(1-\alpha )}}g\right) \\ g+i\left( \sqrt{\frac{\lambda _0}{1-\alpha }}g-\frac{1}{1+\lambda _0-\alpha }\left( \sqrt{\lambda _0(1-\alpha )}+\lambda _0\sqrt{\frac{\lambda _0}{1-\alpha }}\right) f\right) \\ \end{array} \right) , \\&\left\langle \overline{q}^*, \varphi \right\rangle \overline{q}=\frac{1}{2}\left( \begin{array}{c} f+i\left( \sqrt{\frac{\lambda _0}{1-\alpha }}f-\frac{1+\lambda _0-\alpha }{\sqrt{\lambda _0(1-\alpha )}}g\right) \\ g-i\left( \sqrt{\frac{\lambda _0}{1-\alpha }}g-\frac{1}{1+\lambda _0-\alpha }\left( \sqrt{\lambda _0(1-\alpha )}+\lambda _0\sqrt{\frac{\lambda _0}{1-\alpha }}\right) f\right) \\ \end{array} \right) , \\&\qquad \quad \left\langle q^*, \varphi \right\rangle q+ \left\langle \overline{q}^*, \varphi \right\rangle \overline{q}=\left( \begin{array}{c} f \\ g \\ \end{array} \right) , \\&H(z,\overline{z},\omega ):=\varphi - \left\langle q^*, \varphi \right\rangle q- \left\langle \overline{q}^*, \varphi \right\rangle \overline{q}=\left( \begin{array}{c} 0 \\ 0 \end{array} \right) . \end{aligned}$$

Let \(H=\frac{1}{2}H_{20}z^2+H_{11}z\overline{z}+\frac{1}{2}H_{02}\overline{z}^2+o\left( |z|^2\right) \). It follows [13], Appendix A] that the system (40) possesses a center manifold, and then we can write \(\omega \) in the form \(\omega =\frac{1}{2}\omega _{20}z^2+\omega _{11}z\overline{z}+\frac{1}{2}\omega _{02}\overline{z}^2+o\left( |z|^2\right) \). Thus, we have

$$\begin{aligned}&\overline{\omega }_{02}=\omega _{20}=\left( 2i\sqrt{\lambda _0(1-\alpha )}I-L\right) ^{-1}H_{20}=0,\\&\quad \omega _{11}=(-L)^{-1}H_{11}=0. \end{aligned}$$

Thus, the equation on the center manifold in \(z, \overline{z}\) coordinate now is

$$\begin{aligned} \frac{dz}{dt}= & {} i\sqrt{\lambda _0(1-\alpha )}z+\frac{1}{2}g_{20}z^2+g_{11}z\overline{z}+\frac{1}{2}g_{02}\overline{z}^2\\&+\,\, \frac{1}{2}g_{21}z^2\overline{z}+o\left( |z|^3\right) , \end{aligned}$$

where

$$\begin{aligned} g_{20}= & {} \frac{1}{2}\left( f_{uu}(0,0)+2f_{uv}(0,0)q_2\right) =a_1+a_2q_2\\= & {} \frac{\alpha m(3-m)}{(m+1)^2(1+\lambda _0-\alpha )}-1\\&+\frac{\alpha m(3-m)}{(m+1)^2(1-\alpha )} \frac{\sqrt{\lambda _0(1-\alpha )}}{1+\lambda _0-\alpha }i, \\ g_{11}= & {} \frac{1}{2}\left( f_{uu}(0,0)+f_{uv}(0,0)(\overline{q}_2+q_2)\right) \\= & {} a_1+a_2\frac{\lambda _0}{1+\lambda _0-\alpha }\\= & {} \frac{\alpha m(3-m)}{(m+1)^2(1+\lambda _0-\alpha )}-1\\ g_{02}= & {} \frac{1}{2}\left( f_{uu}(0,0)+2f_{uv}(0,0)\overline{q}_2\right) \\= & {} a_1+a_2\overline{q}_2=\overline{g}_{20} \end{aligned}$$
$$\begin{aligned}= & {} \frac{\alpha m(3-m)}{(m+1)^2(1+\lambda _0-\alpha )}-1\\&-\frac{\alpha m(3-m)}{(m+1)^2(1-\alpha )} \frac{\sqrt{\lambda _0(1-\alpha )}}{1+\lambda _0-\alpha }i, \\ g_{21}= & {} \frac{1}{2}\left( f_{uuu}(0,0)+f_{uuv}(0,0)\overline{q}_2+2f_{uuv}(0,0)q_2\right) \\= & {} 3a_4+a_5\overline{q}_2+2a_5q_2\\= & {} \frac{12\alpha m(m-1)}{(m+1)^3(1-\alpha )^2}\\&+\frac{\alpha m\lambda _0(m^2-14m+9)}{(m+1)^3(1-\alpha )^2(1+\lambda _0-\alpha )}\\&-\frac{\alpha m(m^2-14m+9)\sqrt{\lambda _0(1-\alpha )}}{3(m+1)^3(1-\alpha )^2(1+\lambda _0-\alpha )}i. \end{aligned}$$

According to [13],

$$\begin{aligned} c_1(\lambda _0)= & {} \frac{i}{2\sqrt{\lambda _0(1-\alpha )}}\left( g_{20}g_{11}-2|g_{11}|^2\right. \\&\left. -\frac{1}{3}|g_{02}|^2\right) +\frac{g_{21}}{2}. \end{aligned}$$

Then,

$$\begin{aligned} \mathrm{Re}\ c_1(\lambda _0)= & {} \mathrm{Re}\left\{ \frac{i}{2\sqrt{\lambda _0(1-\alpha )}}g_{20}g_{11}+\frac{g_{21}}{2}\right\} \\= & {} \frac{\alpha m(3-m)}{2(m+1)^2(1-\alpha )(1+\lambda _0-\alpha )}\\&+\frac{\alpha m\lambda _0(m^2-14m+9)}{2(m+1)^3(1-\alpha )^2(1+\lambda _0-\alpha )}\\&-\frac{6\alpha m(1-m)}{(m+1)^3(1-\alpha )^2}\\&-\frac{\alpha ^2m^2(3-m)^2}{2(m+1)^4(1-\alpha )(1+\lambda _0-\alpha )^2}. \end{aligned}$$

Since \(\lambda _0=\frac{2\alpha }{m+1}-1\), we get

$$\begin{aligned} \mathrm{Re}\ c_1(\lambda _0)=\frac{m\rho (\alpha ,m)}{2(1-\alpha )^2(1-m)(m+1)^3}, \end{aligned}$$

where \(\rho (\alpha ,m)\) is defined as (38). \(\square \)

3.3 Numerical simulations

We give some numerical simulations in this part to illustrate the results got in Theorems 3, 4, and 5. We consider the following particular case of system (1) in one-dimensional interval \({\varOmega }=\left( 0,\sqrt{2.5}\pi \right) \) with fixed parameters \(\alpha =0.6\) and \(m=0.05\):

(41)

Then \(\mu _n=\frac{n^2}{2.5}, \lambda _0\approx 0.1429, D_2^*\approx 13.1204\), and \(\rho =-13.77\). It is easy to see \(1.05=m+1<1.2=2\alpha \), and system (41) has a unique positive equilibrium \((0.4,0.4)\).

Fig. 3
figure 3

Numerical simulations of the system (41) with \(d_1=0.05, d_2=20\) such that \(\frac{d_2}{d_1}>D_2^*\approx 13.1204\) and \(\lambda =5>\lambda _S^*\approx 4.3566\), the solution converges to the unique positive equilibrium \((0.4,0.4)\)

Full size image
Fig. 4
figure 4

Numerical simulations of Turing instability of the system (41) with \(d_1=0.05, d_2=20\) such that \(\frac{d_2}{d_1}>D_2^*\approx 13.1204\) and \(\lambda =0.2\) such that \(\lambda _0\approx 0.1429<0.2=\lambda <\lambda _S(\mu _1)=\lambda _S(0.4)\approx 2.341\)

Full size image
Fig. 5
figure 5

Numerical simulations of the stable periodic solutions for the system (41) with \(d_1=0.05, d_2=20\) such that \(\frac{d_2}{d_1}>D_2^*\approx 13.1204\) and \(\lambda =0.12\) such that \(\lambda =0.12<\lambda _0\approx 0.1429\)

Full size image
Fig. 6
figure 6

Numerical simulations of the system (41) with \(d_1=d_2=1\) such that \(\frac{d_2}{d_1}<D_2^*\approx 13.1204\) and \(\lambda =0.16>\lambda _0\approx 0.1429\), the solution converges to the unique positive equilibrium \((0.4,0.4)\)

Full size image
Fig. 7
figure 7

Numerical simulations of the stable periodic solutions for the system (41) with \(d_1=d_2=1\) such that \(\frac{d_2}{d_1}<D_2^*\approx 13.1204\) and \(\lambda =0.13<\lambda _0\approx 0.1429\)

Full size image
  1. 1.

    Firstly, we choose \(d_1=0.05\) and \(d_2=20\) so that \(\frac{d_2}{d_1}>D_2^*\). Then \(\mu ^l\approx 0.02, \mu ^r\approx 2.8307, \lambda _S(\mu _1)=\lambda _S(0.4)\approx 2.341\), and \(\lambda _S^*\approx 4.3566\) it follows from Theorem 3, (0.4,0.4) is locally asymptotic stable if \(\lambda >\lambda _S^*\) (see Fig. 3), it follows from Theorem 4 that Turing instability happens if \(\lambda _0<\lambda <\lambda _S(\mu _1)\) (see Fig. 4), and it follows from Theorems 5 and 6 that Hopf bifurcation occurs at \(\lambda =\lambda _0\), and the bifurcation periodic solutions exist when \(\lambda <\lambda _0\), and they are orbitally asymptotically stable since \(\rho <0\) (see Fig. 5).

  2. 2.

    Secondly, we choose \(d_1=d_2=1\) so that \(\frac{d_2}{d_1}<D_2^*\). Then it follows from Theorem 4 that no Turing instability happens, it follows from Theorem 3, (0.4,0.4) is locally asymptotic stable if \(\lambda >\lambda _0\) (see Fig. 6), and it follows from Theorems 5 and 6 that Hopf bifurcation occurs at \(\lambda =\lambda _0\), and the bifurcation periodic solutions exist when \(\lambda <\lambda _0\), and they are orbitally asymptotically stable since \(\rho <0\) (see Fig. 7).

4 Analysis of the steady-state model (2)

In this section, we analyze the steady-state model (2) by studying the existence and nonexistence of nonconstant solutions.

4.1 Existence of nonconstant solutions

In this part, we consider the existence of nonconstant solutions for problem (2) by bifurcation theory. The following a priori estimate can be easily established via maximum principle.

Lemma 2

Suppose \(m>0\) and \(0<\alpha <1\) are fixed such that

$$\begin{aligned} \alpha <\frac{2\sqrt{m}}{m+1}. \end{aligned}$$
(42)

Then for any \(\lambda >0\), the positive solution \((u,v)\) of problem (2) satisfies

$$\begin{aligned} 1-\frac{\alpha (m+1)}{2\sqrt{m}}\le u(x),\;v(x)\le 1,\ x\in \overline{{\varOmega }}. \end{aligned}$$
(43)

Proof

It follows from the first equation of (2) that \(-d_1{\varDelta } u\le u(1-u)\). Then we get \(u\le 1\) by maximum principle. Similarly, by the second equation of (2), we obtain \(v\le 1\). So the upper bounds follows.

Next, we derive the lower bounds. By the first equation of (2), we have

$$\begin{aligned} -d_1{\varDelta } u= & {} u\left( 1-u-\frac{\alpha (m+1)uv}{u^2+mv^2}\right) \\\ge & {} u\left( 1-u-\frac{\alpha (m+1)uv}{2\sqrt{m}uv}\right) . \end{aligned}$$

Then we get \(u\ge 1-\frac{\alpha (m+1)}{2\sqrt{m}}\). The inequality combining with the second equation of (2) implies \(v\ge 1-\frac{\alpha (m+1)}{2\sqrt{m}}\). \(\square \)

As in the previous section, we use \(\lambda \) as the bifurcation parameter to consider the bifurcation solutions. We identify steady- state bifurcation value \(\lambda ^S\) of (2), which satisfies the following steady-state bifurcation conditions [54]:

\((A_S)\) :

There exists \(i\in \mathbf {N}_0\) such that

$$\begin{aligned}&D_i(\lambda ^S)=0,\;T_i(\lambda ^S)\not =0,\;D_j(\lambda ^S)\not =0\;\mathrm{and}\nonumber \\&\quad T_j(\lambda ^S)\not =0,\;\mathrm{for}\;j\in \mathbf {N}_0\setminus \{i\}, \end{aligned}$$
(44)

and

$$\begin{aligned} D'_i(\lambda ^S)\not =0, \end{aligned}$$
(45)

where \(T_i(\lambda )\) and \(D_i(\lambda )\) are defined as (18).

Apparently, \(D_0(\lambda )\not =0\); hence, we only consider the case \(i\in \mathbf {N}\). If the following we fix \(\alpha \) and \(m\) to satisfy \((m+1)/2<\alpha <1\), to determine \(\lambda \) values satisfying \((A_S)\), we notice that \(D_i(\lambda )=0\) is equivalent to \(\lambda =\lambda _S(\mu _i)\), where \(\lambda _S(\mu )\) is defined as (21). Then we make the following assumption on the spectral set \(\{\mu _n\}_{n\in \mathbf {N}_0}\) according to Lemma 1:

\((SP)\) :

there exist \(p,q\in \mathbf {N}\) such that \(\mu _{p-1}<\mu ^H<\mu _p\le \mu _q<\mu _3^*\le \mu _{q+1}\), where \(\mu _3^*\) and \(\mu ^H\) are as (24) and (25), respectively.

In the following, we denote

$$\begin{aligned} \langle p,q\rangle:= & {} \left\{ \begin{array}{ll} [p,q]\cap \mathbf {N}, &{} \hbox {if }p<q; \\ p, &{} \hbox {if }p=q, \end{array} \right. \end{aligned}$$
(46)
$$\begin{aligned} \lambda _i^S:= & {} \lambda _S(\mu _i),\ \mathrm{for}\ i\in \langle p,q\rangle . \end{aligned}$$
(47)

Points \(\lambda _i^S\) are potential steady-state bifurcation points. It follows from Lemma 1 that for each \(i\in \langle p,q\rangle \), there exists only one point \(\lambda _i^S\) such that \(D_i(\lambda _i^S)=0\) and \(T_i(\lambda _i^S)\not =0\). On the other hand, it is possible that for some \(\tilde{\lambda }\in (0,\lambda _S^*)\) with \(\lambda _S^*\) defined as (31 32) such that

\((SS)\) :

\(\lambda _i^S=\lambda _j^S=\tilde{\lambda }\) for some \(i,j\in \langle p,q\rangle \) and \(i\not =j\),

i.e., \(D_i(\tilde{\lambda })=D_j(\tilde{\lambda })\). Then for \(\lambda =\tilde{\lambda }, (A_S)\) is not satisfied, and we shall not consider bifurcations at such a point. On the other hand, it is also possible such that

\((HS)\) :

\(\lambda _i^S=\lambda _j^H\), for some \(i,j\in \langle p,q\rangle \) and \(i\not = j\), where \(\lambda _j^H\) is a Hopf bifurcation point defined as (37).

However, from an argument in [54], for \(\mathbf {N}=1\) and \({\varOmega }=(0,\ell \pi )\), there are only countably many \(\ell \), such that \((SS)\) or \((HS)\) occurs for some \(i\not =j\). For general bounded domains in \(\mathbf {R}^N\), one can also show \((SS)\) or \((HS)\) does not occur for generic domains [44].

According to above analysis, to satisfy the bifurcation condition \((A_S)\), we only need to verify \(D'_i(\lambda _i^S)\not =0\). In fact, since \(\alpha <1\), we obtain

$$\begin{aligned} D'_i(\lambda _i^S)=d_1\mu _i+1-\alpha \ge 1-\alpha >0. \end{aligned}$$
Fig. 8
figure 8

Numerical simulations of the system (41) with \(d_1=0.05, d_2=10\) and \(\lambda =3.5\). The solution converges to a spatially nonhomogeneous steady-state solution

Full size image

Summarizing the above discussion and using a general bifurcation theorem [54], we obtain the main result of this part on bifurcation of steady-state solutions:

Theorem 7

Suppose that \(\alpha , m,d_1,d_2\) are fixed such that \((m+1)/2<\alpha <1\). Let \((SP)\) holds and let \({\varOmega }\) be a smooth domain so that all eigenvalues \(\mu _i, i\in \mathbf {N}_0\) are simple. Then for any \(i\in \langle p,q\rangle \), which is defined as (46), there exists unique \(\lambda _i^S\in (0,\lambda _S^*]\) with \(\lambda _S^*\) defined as (31 32) and \(\lambda _i^S\) defined as (47) such that \(D_i(\lambda _i^S)=0\) and \(T_i(\lambda _i^S)\not =0\), where \(D_i(\lambda )\) and \(D_i(\lambda )\) are defined as (18). If in addition, we assume (SS) and (HS) hold. The following conclusions are valid.

  1. 1.

    There is a smooth curve \({\varGamma }_i\) of positive solutions of (2) bifurcating from \((\lambda ,u,v)=(\lambda _i^S,1-\alpha ,1-\alpha )\). Near \((\lambda ,u,v)=(\lambda _i^S,1-\alpha ,1-\alpha ), {\varGamma }_i=\{(\lambda _i(s),u_i(s),v_i(s)):s\in (-\epsilon ,\epsilon )\}\), where

    $$\begin{aligned} \left\{ \begin{array}{ll} u_i(s)=1-\alpha +sl_i\phi _i(x)+s\psi _{1,i}(s), \\ v_i(s)=1-\alpha +sm_i\phi _i(x)+s\psi _{2,i}(s), \end{array} \right. \end{aligned}$$

    for some \(C^\infty \) functions \(\lambda _i,\psi _{1,i},\psi _{2,i}\) such that \(\lambda _i(0)=\lambda _i^S\) and \(\psi _{1,i}(0)=\psi _{2,i}(0)=0\). Here \((l_i,m_i)\) satisfies

    $$\begin{aligned} L(\lambda _i^S)[(l_i,m_i)^T\phi _i(x)]=(0,0)^T, \end{aligned}$$

    where \(L(\lambda )\) is defined as (16).

  2. 2.

    In addition, if we assume (42) holds, then \({\varGamma }_i\) contained in a global branch \({\varSigma }_i\) of positive nontrivial solutions of the problem (2), and either \(\overline{{\varSigma }_i}\) contains another \(\left( \lambda _j^S,1-\alpha ,1-\alpha \right) \) or the projection of \(\overline{{\varSigma }_i}\) onto \(\lambda \)-axis contains the interval \(\left( 0,\lambda _i^S\right) \), or the projection of \(\overline{{\varSigma }_i}\) onto \(\lambda \)-axis contains the interval \(\left( \lambda _i^S,\infty \right) \).

Proof

The condition \((A_S)\) has been proved in the previous paragraphs, and the bifurcation of solutions to (2) occurs at \(\lambda =\lambda _i^S\). Note that we assume \((SS)\) and \((HS)\) hold, so \(\lambda =\lambda _i^S\) is always a bifurcation from simple eigenvalue point. By (43), we know that \((u,v)\) has positive upper and lower bounds, which are uniformly in \(\lambda \). From the global bifurcation theorem in [40], \({\varGamma }_i\) contained in a global branch \({\varSigma }_i\) of positive solutions, and either \(\overline{{\varSigma }_i}\) contains another \(\left( \lambda _j^S,1-\alpha ,1-\alpha \right) \) or \(\overline{{\varSigma }_i}\) is not compact. Furthermore, if \(\overline{{\varSigma }_i}\) is not compact, then \(\overline{{\varSigma }_i}\) contains a boundary point \((\tilde{\lambda },\tilde{u},\tilde{v})\), and since \((\tilde{u},\tilde{v})\) satisfies (43), it follows that \(\tilde{\lambda }\) must satisfy \(\tilde{\lambda }=0\) or \(\tilde{\lambda }=\infty \) and the conclusion follows. \(\square \)

4.2 Numerical simulations

We give some numerical simulations in this part to illustrate the results got in Theorem 7. We consider problem (41) with \(d_1=0.05\) and \(d_2=20\) again. Then \(\mu _n=\frac{n^2}{2.5}, \lambda _0\approx 0.1429, \mu ^H\approx 0.053, \mu _3^*\approx 2.8571, \lambda _S^*\approx 4.3566\). It is easy to see \(1.05=m+1<1.2=2\alpha \), and system (41) has a unique positive equilibrium \((0.4,0.4)\). We can find that

$$\begin{aligned} 0=\mu _0<\mu ^H<\mu _1=0.4<\mu _2=1.6<\mu _3^*<\mu _3=3.6. \end{aligned}$$

This gives possible steady-state bifurcation points \(\lambda _1^S=\lambda _S(\mu _1)\approx 2.3401\) and \(\lambda _2^S=\lambda _S(\mu _2)\approx 4.1905\), while the largest Hopf bifurcation point \(\lambda _0^H=\lambda _0\approx 0.1429\) is much smaller. Hence, for this parameter set \((d_1,d_2)=(0.05,20)\), when \(\lambda \) decreases, the first bifurcation point encountered is \(\lambda _2^S\approx 4.1905\), and a steady-state bifurcation (Turing bifurcation) occurs. A numerical simulation for \(\lambda =3.5\) is shown in Fig. 8, where a nonhomogeneous steady-state solution can be observed for large \(t\).

4.3 Nonexistence of nonconstant solutions

We consider the nonexistence of nonconstant solutions in this part by energy methods, and the main result is the following theorem.

Theorem 8

Suppose \(m>0\) and \(0<\alpha <1\) are fixed such that (42) holds. Let \(\mu _1\) be large enough such that

$$\begin{aligned} \mu _1>{\varPsi }:=\frac{\lambda }{d_2}\left( \frac{\alpha (m+1)}{\sqrt{m}}-1\right) \end{aligned}$$
(48)

and

$$\begin{aligned} \begin{aligned}&\mu _1>{\varPhi }:=\frac{\alpha (m+1)}{\sqrt{m}}\left( 1-\frac{\sqrt{m}}{\alpha (m+1)}\right. \\&\left. +\frac{4\lambda m^2(4\sqrt{m}-\alpha (m+1))}{(2\sqrt{m}-\alpha (m+1))^3(d_2\sqrt{m}\mu _1+\lambda (\sqrt{m}{-}\alpha (m+1))}\right) , \end{aligned} \end{aligned}$$
(49)

then (2) has no positive nonconstant solution.

Remark 2

It is clear that Theorem 8 holds if \(\mu _1\) is large enough. Note that large \(\mu _1\) is reflected by small “size” of the domain \({\varOmega }\) (here, the “size” should be understood under a rescaling without changing the geometry of \({\varOmega }\). For precise explanation of this, one may refer to [31]). Therefore, the prey \(u\) and the predator \(v\) will be spatially homogeneous distributed when the “size” of \({\varOmega }\) is sufficiently small. On the other hand, we observe that \(\lim _{\alpha \rightarrow 0}{\varPsi }=-\lambda /d\) and \(\lim _{\alpha \rightarrow 0}{\varPhi }=-1\). So Theorem 8 holds for any “size” of the domain \({\varOmega }\) if \(\alpha \) is small enough.

Proof of Theorem 8

In the proof, we denote \(|{\varOmega }|^{-1}\int _{\varOmega }fdx\) by \(\overline{f}\) for \(f\in L^1({\varOmega })\). Let \((u,v)\) be a positive solution of (2), then it is obvious that \(\int _{\varOmega }(u-\overline{u})dx=\int _{\varOmega }(v-\overline{v})dx=0\). Multiplying the first equation of (2) by \(u-\overline{u}\), we obtain

$$\begin{aligned} \begin{aligned}&d_1\int _{\varOmega }|\nabla (u-\overline{u})|^2dx\\&\quad =\int _{\varOmega }\left( u-u^2-\frac{\alpha (m+1)u^2v}{u^2+mv^2}\right) (u-\overline{u})dx\\ =&\int _{\varOmega }\left( u-\overline{u}-\left( u^2-\overline{u}^2\right) -\alpha (m+1)\right. \\&\left. \quad \left( \frac{u^2v}{u^2+mv^2}-\frac{\overline{u}^2\overline{v}}{\overline{u}^2+m\overline{v}^2}\right) \right) (u-\overline{u})dx\\ =&\int _{\varOmega }\left( 1{-}(u+\overline{u})-\frac{\alpha m(m+1)(u+\overline{u})v^2\overline{v}}{(u^2+mv^2)(\overline{u}^2+m\overline{v}^2)}\right) (u{-}\overline{u})^2dx\\&+\int _{\varOmega }\frac{\alpha (m+1)(u^2\overline{u}^2-mu^2v\overline{v})}{(u^2+m v^2)(\overline{u}^2+m\overline{v}^2)}(u-\overline{u})(v-\overline{v})dx. \end{aligned} \end{aligned}$$

By (43), we get

$$\begin{aligned} \begin{aligned}&d_1\int _{\varOmega }|\nabla (u-\overline{u})|^2dx \\&\quad \le \left( \frac{\alpha (m+1)}{\sqrt{m}}-1\right) \int _{\varOmega }(u-\overline{u})^2dx\\ {}&\qquad +\alpha (m+1)\left( 1+\frac{2\sqrt{m}}{2\sqrt{m}-\alpha (m+1)}\right) \\&\qquad \times \int _{\varOmega }|u-\overline{u}||v-\overline{v}|dx. \end{aligned} \end{aligned}$$
(50)

Similarly, we obtain the following inequality by the second equation of (2) and (43)

$$\begin{aligned} \begin{aligned}&d_2\int _{\varOmega }|\nabla (v{-}\overline{v})|^2dx\le \lambda \left( \frac{\alpha (m+1)}{\sqrt{m}}{-}1\right) \int _{\varOmega }(v{-}\overline{v})^2dx\\ {}&\quad +\frac{4\lambda m}{\left( 2\sqrt{m}-\alpha (m+1)\right) ^2}\int _{\varOmega }|u-\overline{u}||v-\overline{v}|dx. \end{aligned} \end{aligned}$$
(51)

Thus, thanks to the well-known Poincaré’s inequality

$$\begin{aligned} \mu _1\int _{\varOmega }(f-\overline{f})dx\le \int _{\varOmega }|\nabla (f-\overline{f})|^2dx,\ \forall f\in H^1({\varOmega }), \end{aligned}$$

we find

$$\begin{aligned}&\left( d_2\mu _1+\lambda \left( 1-\frac{\alpha (m+1)}{\sqrt{m}}\right) \right) \int _{\varOmega }(v-\overline{v})^2dx\nonumber \\&\le \frac{4\lambda m}{\left( 2\sqrt{m}-\alpha (m+1)\right) ^2}\int _{\varOmega }|u-\overline{u}||v-\overline{v}|dx\nonumber \\&\le \frac{4\lambda m}{\left( 2\sqrt{m}-\alpha (m+1)\right) ^2}\left( \int _{\varOmega }(u-\overline{u})^2dx\right) ^{\frac{1}{2}}\nonumber \\&\quad \left( \int _{\varOmega }(v-\overline{v})^2dx\right) ^{\frac{1}{2}}. \end{aligned}$$
(52)

If \(v\equiv \overline{v}\) on \(\overline{{\varOmega }}\), the second equation of (2) shows \(u\equiv \overline{v}\). We assume that \(v\not \equiv \overline{v}\). Thus, the above inequality direct leads to

$$\begin{aligned}&\left( d_2\mu _1+\lambda \left( 1-\frac{\alpha (m+1)}{\sqrt{m}}\right) \right) \left( \int _{\varOmega }(v-\overline{v})^2dx\right) ^{\frac{1}{2}}\\&\le \frac{4\lambda m}{\left( 2\sqrt{m}-\alpha (m+1)\right) ^2}\left( \int _{\varOmega }(u-\overline{u})^2dx\right) ^{\frac{1}{2}}, \end{aligned}$$

which, together with (52), infers

$$\begin{aligned}&\int _{\varOmega }|u-\overline{u}||v-\overline{v}|dx\nonumber \\&\le \frac{4\lambda m}{\left( 2\sqrt{m}-\alpha (m+1)\right) ^2\left( d_2\mu _1+\lambda \left( 1-\frac{\alpha (m+1)}{\sqrt{m}}\right) \right) }\nonumber \\&\quad \int _{\varOmega }(u-\overline{u})^2dx \end{aligned}$$
(53)

By virtue of (50), (53), and Poincaré’s inequality again, we obtain

$$\begin{aligned} \begin{aligned} \mu _1\int _{\varOmega }(u-\overline{u})^2dx\le {\varPhi }\int _{\varOmega }(u-\overline{u})^2dx, \end{aligned} \end{aligned}$$
(54)

where \({\varPhi }\) is defined as (49). Under our hypothesis, (54) deduces \(u\equiv \overline{u}\), which in turn indicates \(v\equiv \overline{v}\). \(\square \)