1 Introduction

A fundamental goal of theoretical ecology is to understand how the interactions of individual organisms with each other and with the environment determine the distribution of populations and the structure of communities. In recent decades the role of spatial effects in maintaining biodiversity has received a great deal of attention in the literature on conservation, see for example [35, 57]. One way to try to understand how spatial effects such as habitat fragmentation influence populations and communities is by using mathematical models [6]. The dynamical relationship between predators and their prey has been investigated widely in recent years due to its universal existence and importance in mathematical biology and ecology. The spatiotemporal dynamics of a predator–prey system in a homogeneous environment can be described by a system of nonlinear parabolic partial differential equations or reaction–diffusion equations, see for examples in [41, 44, 48]:

$$\begin{aligned}&\dfrac{\partial H(X,T)}{\partial T}=D_1\Delta H+F(H)H-G(H)P,\nonumber \\&\dfrac{\partial P(X,T)}{\partial T}=D_2\Delta P+kG(H)P-M(P)P, \end{aligned}$$
(1.1)

where H(X, T) and P(X, T) are the densities of prey and predator at time T and position X respectively; here \(X\in \Omega _O\subseteq {\mathbb {R}}^n\) is the spatial habitat of the two species; the Laplacian operator \(\Delta \) describes the spatial dispersal with passive diffusion; \(D_1\) and \(D_2\) are the diffusion coefficients of species and k is the food utilization coefficient. The function F(H) describes the per capita growth rate of the prey, G(H) is the functional response of the predator, which corresponds to the saturation of their appetites and reproductive capacity, and M(P) stands for predator mortality.

The functions F(H), G(H) and M(P) can be of different types in various specific situations. Since the first differential equation model of predator–prey type Lotka–Volterra equation was formulated [43, 61] in 1920s, a logistic type growth F(H) is usually assumed for the prey species in the models, while a linear mortality rate M(P) is assumed for the predator. Some conventional functional response functions G(H) include Holling type I, II, III (see [30, 62]), Ivlev type (see [36]), Beddington–DeAngelis type (see [4, 15]). the Crowley–Martin type (see [12]), and the recent well-known ratio dependence type, which was first proposed by Arditi and Ginzburg (see [2]). Of them, the Holling type I-III was labeled prey-dependent(see [34]) and the other types that consider the interference among predators were labeled predator-dependent (see [2]).

When F(H) is of a logistic growth, the dynamics of (1.1) has been considered in many articles. [18–20, 63, 67, 70] consider the bifurcation solutions and pattern formations of traditional Holling Type II functional response used to describe the plant consumption by the herbivore in the interaction of plant and herbivore; Wang et al. [62] investigates the global dynamics of traditional Holling Type II functional response and strong Allee effect growth. Strongly coupled parabolic and elliptic predator–prey models have received considerable attention in [16, 17, 21, 22, 39, 40, 47, 49, 54].

Since the traditional Holling III predator–prey model received great attention among theoretical and mathematical biologists, we will focus our attention here on the following reaction diffusion system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle U_{t}-d_{1}\Delta U=AU\left( 1- \frac{U}{H}\right) -\frac{BU^{p}V}{\alpha ^{p} + U^{p}},&{}\quad x\in \Omega , \ t>0,\\ \displaystyle V_{t}-d_{2}\Delta V = - CV + \frac{DU^{p}V}{\alpha ^{p} + U^{p}}, &{}\quad x\in \Omega , \ t>0, \\ \displaystyle \frac{\partial U}{\partial n}=\displaystyle \frac{\partial V}{\partial n}=0, &{} \quad x\in \partial \Omega , \ t>0, \\ \displaystyle U(x,0)=U_{0}(x) \geqslant 0, \ \ V(x,0)=V_{0}(x) \geqslant 0,&{}\quad x\in \Omega ,\\ \end{array}\right. } \end{aligned}$$
(1.2)

where \(\Omega \) is a bounded domain in \({\mathbb {R}^N}\)(\(N \ge 1\)) with a smooth boundary \(\partial \Omega \); n is the unit outer normal, and no flux boundary condition is imposed so the system is a closed one; \(U=U(x,t)\) and \(V=V(x,t)\) represent the densities of the prey and predator at time \(t>0\) and a spatial position \(x \in \Omega \) respectively; \(d_1, d_2>0\) are the diffusion coefficients of the species; the parameters A, B, C, D, H are positive real numbers,the prey population follows a logistic growth and A is the intrinsic growth rate; H is the carrying capacity; C is the death rate of the predator; B and D represent the strength of the relative effect of the interaction on the two species; the function \(\dfrac{U^{p}}{\alpha ^{p} + U^{p}}\) denotes the functional response of the predator to the prey density (see [9]), which refers to the change in the density of prey attached per unit time per predator as the prey density changes. The topical Holling Type II functional response is referred to \(p=1\), Holling Type III functional response with \(p=2\), both of which are monotonic increasing function with respect to the prey U.

By rescaling as follows:

$$\begin{aligned} s=At, \ \ u=U/H,\ \ v=BV/DH,\ \ d_{1}^{'}=A^{-1}d_1,\ \ d_{2}^{'}=A^{-1}d_2,\ \ a=\dfrac{\alpha }{H} ,\ \ m=\dfrac{D}{A},\ \ d=\dfrac{C}{A}, \end{aligned}$$

(1.2) with Holling III functional response is equivalently rewritten as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle u_{t}-d_{1}\Delta u= u (1-u)- \frac{mu^{2}v}{a^{2}+u^{2}},&{}\quad x\in \Omega , \ t>0,\\ \displaystyle v_{t}-d_{2}\Delta v=-dv+\frac{mu^{2}v}{a^{2}+u^{2}},&{}\quad x\in \Omega , \ t>0, \\ \displaystyle \frac{\partial u}{\partial n}=\displaystyle \frac{\partial v}{\partial n}=0, &{}\quad x\in \partial \Omega , \ t>0, \\ \displaystyle u(x, 0)=u_{0}(x)\ge 0, \ \displaystyle v(x, 0)=v_{0}(x)\ge 0, &{}\quad x\in \Omega , \end{array}\right. } \end{aligned}$$
(1.3)

where d is the death rate of the predator, m is the strength of the interaction and \(a, d_1, d_2\) are positive constants. System (1.3) is an important model on population dynamics (refer to [24, 31, 38, 53] and references therein). Many attempts have been made to give sufficient conditions and necessary conditions to guarantee the existence and the uniqueness of limit cycles of kinetic system of (1.3). For example, see [10, 33, 59]. Recently, Eduardo and Alejandro [23] described the multiple limit cycles in a Gause Type predator–prey model with Holling Type III functional response and Allee effect on prey. For the diffusive predator prey system (1.3), Li and Wu [42] established the existence of traveling wave solutions and small amplitude traveling wave train solutions; Su et al. [58] investigated dynamic complexities with impulsive effects; Das and Kar [13] highlighted a delayed predator-prey model with Holling type III functional response and harvesting to predator; Song and Wan [56] focused on the Hopf bifurcation analysis.

In the early 1950s, the British mathematician Turing [60] proposed a model that accounts for pattern formation in morphogenesis. Turing showed mathematically that a system of coupled reaction–diffusion equations could give rise to spatial concentration patterns of a fixed characteristic length from an arbitrary initial congratulation due to so called diffusion-driven instability, that is, diffusion could destabilize an otherwise stable equilibrium of the reaction–diffusion system and lead to nonuniform spatial patterns. Turing’s analysis stimulated considerable theoretical research on mathematical models of pattern formation, and a great deal of research have been devoted to the study of Turing instability in chemical and biology contexts, see for example, [3, 5, 8, 25, 37, 50, 69] for Brusselator model; [14, 51] for Gray–Scott model; [45, 66] for Lengyel–Epstein model, and [26, 65] for Schnakenberg model.

In this paper, our main contribution is a comprehensive mathematical study of (1.3). In particular we are interested in the spatiotemporal pattern formations and bifurcations in the model, and the effect of system parameters and diffusion coefficients on the model dynamics. The organization of the remaining part of the paper is as follows. In Sect. 2, we obtain the existence and boundedness of solutions to system (1.3). In Sect. 3, we analyze the stability of the constant steady state, and we obtain the global stability by constructing Lyapunov functionals. Also we use bifurcation theory to prove the existence of periodic orbits. In Sect. 4, we prove the existence and non-existence of positive non-constant steady state solutions by using a priori estimates, energy estimates and Leray–Schauder degree theory and bifurcation theory. Throughout this paper, \(\mathbb {N}\) is the set of natural numbers and \(\mathbb {N}_0=\mathbb {N}\cup \{0\}\). The eigenvalues of operator \(-\Delta \) with homogeneous Neumann boundary condition in \(\Omega \) are denoted by \(0=\mu _0<\mu _1\le \mu _2 \le \cdots \le \cdots \), and the eigenfunction corresponding to \(\mu _n\) is \(\phi _n(x)\).

2 Basic Dynamics of the Reaction–Diffusion System

The global existence and boundedness of the non-negative solutions to (1.3) can be obtained from a general result of Hollis, Martin and Pierre [32] (see Theorems 1 and 2). Here we can show the precise bounds of the solutions:

Lemma 2.1

Suppose that \(\left( u(x,t),v(x,t)\right) \) is a nonnegative solution of (1.3). Then (u(x, t), v(x, t)) must satisfy \(\displaystyle \limsup _{t\rightarrow +\infty }u(x,t)\le 1\), \(\int _{\Omega }v(x,t)dx\le 1+|\Omega |/(4d)\) as \(t\rightarrow \infty \). Furthermore, \(\displaystyle \limsup _{t\rightarrow +\infty } v(x,t)\le C\) with C independent of \(u_0,v_0,d_1,d_2\) but only on a lower bound of \(d_2\).

Proof

Let \(\left( u(x,t), v(x,t)\right) \) be the unique non-negative solution of (1.3). Then the first equation of (1.3) shows that:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t\le d_1\Delta u+u(1-u),\;\;&{}\quad x\in \Omega , \;\; t>0,\\ \displaystyle \frac{\partial u}{\partial n}=0,\;\;\;&{}\quad x\in \partial \Omega . \end{array}\right. } \end{aligned}$$
(2.1)

It is well-known that

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t= d_1\Delta u+u(1-u),\;\;&{}\quad x\in \Omega , \;\; t>0,\\ \displaystyle \frac{\partial u}{\partial n}=0,\;\;\;&{}\quad x\in \partial \Omega \end{array}\right. } \end{aligned}$$
(2.2)

is a gradient system, and every orbit of (2.2) converges to the unique positive steady state \(u=1\) (see [11, 27]). Then from the comparison principle of parabolic equation, the solution u(x, t) to (1.3) satisfies \(\displaystyle \limsup _{t\rightarrow +\infty }u(x,t)\le 1\).

For the estimate of v(x, t), let \(\int _{\Omega }u(x,t)dx=U(t)\), \(\int _{\Omega }v(x,t)dx=V(t)\), then

$$\begin{aligned} \frac{dU}{dt}= & {} \int _{\Omega } u_t dx=\int _{\Omega } d_1\Delta u dx+\int _{\Omega }\left[ u(1-u)-\dfrac{mu^2v}{a^2+u^2}\right] dx\nonumber \\= & {} \int _{\Omega }\left[ u(1-u)-\dfrac{mu^2v}{a^2+u^2}\right] dx, \end{aligned}$$
(2.3)
$$\begin{aligned} \frac{dV}{dt}= & {} \int _{\Omega } v_t dx=\int _{\Omega } d_2\Delta v dx-d\int _{\Omega } v dx+\int _{\Omega }\dfrac{mu^2}{a^2+u^2}vdx\nonumber \\= & {} -dV+\int _{\Omega }\dfrac{mu^2}{a^2+u^2}vdx. \end{aligned}$$
(2.4)

Adding (2.3) and (2.4), we obtain

$$\begin{aligned} (U+V)_t= & {} -dV+\int _{\Omega }u(1-u)dx\\= & {} -d(U+V)+dU+\int _{\Omega }u(1-u)dx\\\le & {} -d(U+V)+d+\dfrac{|\Omega |(1+\varepsilon )}{4},\quad \quad \text {for}\;t\;\text {large enough}. \end{aligned}$$

Integration of the inequality leads to

$$\begin{aligned} \int _{\Omega }v(x,t)dx=V(t)<U(t)+V(t)\le 1+|\Omega |(1+\varepsilon )/(4d)\quad \quad \text {for}\;t\;\text {large enough}. \end{aligned}$$
(2.5)

From (2.5), we know that any solution v(x, t) satisfies an \(L^1\) a priori estimate \(K_1=1+|\Omega |/(4d)\), which only depends on d and \(\Omega \). Furthermore we can use the \(L^1\) bound to obtain an \(L^{\infty }\) bound C, such that \(\displaystyle \limsup _{t\rightarrow +\infty } v(x,t)\le C\) with C independent of \(u_0,v_0,d_1,d_2\) but only on a lower bound of \(d_2\) (see Theorem 3.1 in [1] and Lemma 4.7 in [7]). \(\square \)

3 Stability Analysis and Oscillatory Patterns

In this section, we will analyze the stability of the positive equilibrium and Hopf bifurcations.

3.1 Local and Global Stability

System (1.3) has three nonnegative constant equilibrium solutions: (0, 0), (1, 0) and (\(\lambda \), \(v_{\lambda })\), where (\(\lambda \), \(v_{\lambda })\) satisfies

$$\begin{aligned} \lambda ^{2}=\dfrac{a^{2}d}{m-d},\;\; v_{\lambda }= \dfrac{(1-\lambda )(a^{2}+ \lambda ^{2})}{m\lambda }. \end{aligned}$$
(3.1)

Clearly, the positive equilibrium solution (\(\lambda \), \(v_{\lambda }\)) exists if and only if \(0< \lambda <1\). In the proceeding discussion, we fix parameters \(a, m, d_1, d_2\) and choose \(\lambda \) (or equivalently d) as the bifurcation parameter. Linearizing the system (1.3) about the positive equilibrium \((\lambda , v_{\lambda })\), we obtain an eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} d_1 \Delta \phi +A(\lambda )\phi +B(\lambda )\psi =\mu \phi ,\,\, &{}\quad x\in \Omega ,\\ d_2 \Delta \psi +C(\lambda )\phi =\mu \psi ,\,\, &{}\quad x\in \Omega ,\\ \dfrac{\partial \phi }{\partial n}=\dfrac{\partial \psi }{\partial n}=0,\,\, &{}\quad x\in \partial \Omega , \end{array}\right. } \end{aligned}$$
(3.2)

where

$$\begin{aligned} A(\lambda )=\dfrac{-2\lambda ^3+\lambda ^2-a^2}{a^2+\lambda ^2}, \quad B(\lambda )=-d , \quad C(\lambda )=\dfrac{2a^2(1-\lambda )}{a^2+\lambda ^2}. \end{aligned}$$

Denote

$$\begin{aligned} L(\lambda )= \begin{pmatrix} d_{1} \Delta +A(\lambda ) &{} B(\lambda ) \\ C(\lambda ) &{} d_{2} \Delta \ \ \\ \end{pmatrix}. \end{aligned}$$
(3.3)

For each \(n\in \mathbb {N}_0\), we denote a \(2\times 2\) matrix:

$$\begin{aligned} L_n(\lambda )= \begin{pmatrix} -d_{1}\mu _n+A(\lambda ) &{} B(\lambda ) \\ C(\lambda ) &{} -d_{2}\mu _n \ \ \\ \end{pmatrix}. \end{aligned}$$
(3.4)

Then the following statements hold true by using Fourier decomposition:

  1. (1)

    If \(\mu \) is an eigenvalue of (3.2), then there exists \(n\in \mathbb {N}_0\) such that \(\mu \) is an eigenvalue of \(L_n(\lambda )\).

  2. (2)

    The positive equilibrium \((\lambda ,v_{\lambda })\) is locally asymptotically stable with respect to (1.3) if and only if for every \(n\in \mathbb {N}_0\), all eigenvalues of \(L_n(\lambda )\) have negative real part.

  3. (3)

    The positive equilibrium \((\lambda ,v_{\lambda })\) is unstable with respect to (1.3) if there exists an \(n\in \mathbb {N}_0\) such that \(L_n(\lambda )\) has at least one eigenvalue with nonnegative real part.

Now the characteristic equation of (3.4) is given by:

$$\begin{aligned} \beta ^2-T_n(\lambda )\beta +D_n(\lambda )=0,\ \ \ n\in \mathbb {N}_0, \end{aligned}$$
(3.5)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle T_n(\lambda )=A(\lambda )-(d_1+d_2)\mu _n ,\\ \displaystyle D_n(\lambda )= d_1d_2\mu _n^2-A(\lambda )d_2\mu _n-B(\lambda )C(\lambda ). \end{array}\right. } \end{aligned}$$
(3.6)

Then \((\lambda ,v_{\lambda })\) is locally asymptotically stable if \(T_n(\lambda )<0\) and \(D_n(\lambda )>0\) for all \(n\in \mathbb {N}_0\), and \((\lambda ,v_{\lambda })\) is unstable if there exists \(n\in \mathbb {N}_0\) such that \(T_n(\lambda )>0\) or \(D_n(\lambda )<0\). To obtain more precise stability results, we define \(h(\lambda ): =v_{\lambda }\), then

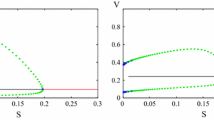
$$\begin{aligned} h(\lambda )=\dfrac{(1-\lambda )(a^{2}+ \lambda ^{2})}{m\lambda }, \quad \quad h'(\lambda )=\dfrac{-2\lambda ^{3}+\lambda ^{2}-a^{2}}{m\lambda ^{2}}. \end{aligned}$$

In particular, the signs of \(h'(\lambda )\) and \(A(\lambda )\) are identical for all \(\lambda \). By \(h'(\lambda )=h''(\lambda ) =0\), we get \(a=a^{*}=\sqrt{3}/9\). After straight forward calculations, we have the following properties of the functions of \(h(\lambda )\) (see Fig. 1):

Fig. 1
figure 1

(left) \(a>a^*\), parameter \(a=2\); (right) \(0<a<a^*\), parameter \(a=0.15\) with \(\lambda _{*}=0.1149\), \(\lambda _{1}=0.191\), \(\lambda _{2}=0.443\), \( \lambda ^{*}=0.6186\)

Full size image

Lemma 3.1

If \(a>a^*\), then \(h(\lambda )\) is strictly decreasing for all \(\lambda >0\); If \(0<a<a^*\), then there exists \(\lambda _*,\lambda _1,\lambda _2,\lambda ^*\in (0,1)\) with \(0<\lambda _*<\lambda _1<\lambda _2<\lambda ^*<1\) such that \(h(\lambda )\) is strictly decreasing in \((0,\lambda _1)\cup (\lambda _2,\infty )\) and strictly increasing in \((\lambda _1, \lambda _2)\), where \(h'(\lambda _1)=h'(\lambda _2)=0\) and \(h(\lambda _*)=h(\lambda _2)\), \(h(\lambda ^*)=h(\lambda _1)\). Moreover, there exists a unique \(\lambda _3\in (\lambda _1,\lambda _2)\) such that \(h'(\lambda )>0\) in \((\lambda _1,\lambda _3)\) and \(h'(\lambda )<0\) in \((\lambda _3,\lambda _2)\).

Proof

In fact, \(h''(\lambda )=\dfrac{2(a^2-\lambda ^3)}{m\lambda ^3}\) leads to the existence of the unique \(\lambda _3\in (\lambda _1,\lambda _2)\). \(\square \)

Now we can give a stability result regarding the constant equilibrium \((\lambda , v_{\lambda })\) by the analysis above and the restriction on a.

Suppose that \(a>a^*\) holds. Then, for any \(n\in \mathbb {N}_0\) and \(0<\lambda <1\), we have \(T_n(\lambda )< 0\) since \(A(\lambda )<0\) and \(D_n(\lambda )>0\) since \(-B(\lambda )C(\lambda )=\dfrac{2m\lambda ^{2}(1-\lambda )a^{2}}{(a^{2}+\lambda ^{2})^{2}}>0\) . Therefore, all eigenvalues of the operator \(L_n(\lambda )\), \(n\in \mathbb {N}_0\) have strictly negative real parts. Hence the positive equilibrium \((\lambda , v_{\lambda })\) is locally asymptotically stable for the reaction–diffusion system (1.3). In addition, the theorem below shows that if \(a>a^*\), then the locally asymptotic stability of \((\lambda , v_{\lambda })\) implies the globally asymptotic stability of \((\lambda ,v_{\lambda })\) for the reaction–diffusion system (1.3):

Theorem 3.2

Suppose that \(m,d_1,d_2>0\), \(a>a^*\) and \(0<\lambda <1\). Then \((\lambda ,v_{\lambda })\) is globally asymptotically stable in \(\{(u,v): u\ge 0, v\ge 0\}\) for the system (1.3).

Proof

We define the following Lyapunov functional \(E:C(\bar{\Omega })\times C(\bar{\Omega })\rightarrow {\mathbb {R}}\):

$$\begin{aligned} E(u,v)=\int _{\Omega }\int _\lambda ^u \dfrac{mg(\xi )-d}{g(\xi )}\,d\xi dx +m\int _{\Omega }\int _{v_\lambda }^v\dfrac{\eta -v_\lambda }{\eta }\,d\eta dx, \end{aligned}$$

where \(g(u)=\dfrac{u^2}{a^2+u^2}\). Then

$$\begin{aligned} \dfrac{d}{dt}E(u(x,t),v(x,t))= & {} \int _{\Omega }\dfrac{mg(u)-d}{g(u)}\,u_t dx +m\int _{\Omega }\dfrac{v-v_\lambda }{v}\,v_t dx\\= & {} m\int _{\Omega }\left( g(u)-g(\lambda )\right) \left( z(u)-z(\lambda )\right) dx-I(t), \end{aligned}$$

where \(z(u)=\dfrac{(1-u)(a^2+u^2)}{u}\), and

$$\begin{aligned} I(t):=d_1 \int _{\Omega }\dfrac{g'(u)}{g^2(u)}\,\nabla {u}^2 dx +d_2 v_\lambda m \int _{\Omega }\dfrac{1}{v^2}\,\nabla {v}^2 dx. \end{aligned}$$

Notice that

$$\begin{aligned} g'(u)=\dfrac{2a^{2}u}{(a^2+u^2)^2}>0,\quad z'(u)=\dfrac{-2u^{3}+u^{2}-a^{2}}{u^2}<0 \end{aligned}$$

for all \(u>0\) from Lemma 3.1. Therefore,

$$\begin{aligned} \left[ g(u)-g(\lambda )\right] \left[ z(u)-z(\lambda )\right] \le 0, \end{aligned}$$

which implies that E decreases monotonically along the solution orbit. Then, it follows that for any \(0<\lambda <1\), the unique positive equilibrium \((\lambda ,v_{\lambda })\) of the reaction–diffusion system (1.3) is globally asymptotically stable in \({\mathbb {R}}^2_{+}\) by [14, 68]. \(\square \)

Suppose that \(0<a<a^*\) holds , we have the following stability of \((\lambda , v_{\lambda })\):

Theorem 3.3

  1. (1)

    If \(\lambda \in (0,\lambda _*)\cup (\lambda ^*,1)\), then \((\lambda , v_{\lambda })\) is globally asymptotically stable;

  2. (2)

    If \(\lambda \in (\lambda _*,\lambda _1)\cup (\lambda _2,\lambda ^*)\), then \((\lambda , v_{\lambda })\) is locally asymptotically stable;

  3. (3)

    If \(\lambda \in (\lambda _1,\lambda _2)\), then \((\lambda , v_{\lambda })\) is unstable.

Proof

  1. 1.

    From the discussion above and Theorem 3.2, when \(0<a<a^{*}\) and \(\lambda \in (0, \lambda _{*})\) or \(\lambda \in (\lambda ^{*}, 1)\), \(A(\lambda )<0\) and

    $$\begin{aligned} \left[ g(u)-g(\lambda )\right] \left[ z(u)-z(\lambda )\right] \le 0 . \end{aligned}$$

    still hold. So the same Lyapunov function can still be used.

  2. 2.

    If \(\lambda \in (\lambda _*,\lambda _1)\cup (\lambda _2,\lambda ^*)\), then \(A(\lambda )<0\). Therefore, for any \(n\in \mathbb {N}_0\) and \(0<\lambda <1\), we have \(T_n(\lambda )< 0\) and \(D_n(\lambda )>0\).

  3. 3.

    If \(\lambda \in (\lambda _1,\lambda _2)\), then \(A(\lambda )>0\). For \(i=0\),

    $$\begin{aligned} \text {trace} (T_0)=A(\lambda )>0, \end{aligned}$$

    which implies that (3.5) has at least one root with positive real part.

\(\square \)

It is pointed out that the positive equilibrium \((\lambda ,v_{\lambda })\) does not exist if \(\lambda >1\). In this case, we can show that the boundary equilibrium (1, 0) is globally stable for all \(a>0\).

Theorem 3.4

Suppose that \(a,m,d_1,d_2>0\). If \(\lambda >1\) (equivalently \(d>m/(a^2+1)\)), then (1, 0) is globally asymptotically stable to the system (1.3).

Proof

When \(\lambda >1\), we construct a similar Lyapunov functional as follows:

$$\begin{aligned} E(u,v)=\int _{\Omega }\int _1^u \dfrac{mg(\xi )-mg(1)}{g(\xi )}\,d\xi dx +m\int _{\Omega }vdx, \end{aligned}$$

where \(g(u)=\dfrac{u^2}{a^2+u^2}\). Then

$$\begin{aligned} \dfrac{d}{dt}E(u(x,t),v(x,t))= & {} \int _{\Omega }\dfrac{mg(u)-mg(1)}{g(u)}\,u_t dx +m\int _{\Omega }v_t dx\\= & {} \int _{\Omega }u(1-u)\left( m-\dfrac{d(a^2+u^2)}{{u^2}}\right) dx-I(t), \end{aligned}$$

where

$$\begin{aligned} I(t):=md_1g(1) \int _{\Omega }\dfrac{g'(u)}{g^2(u)}\,\nabla {u}^2 dx. \end{aligned}$$

Recall \(u(x,t)\le 1\) as \(t\rightarrow +\infty \) and \(g'(u)=\dfrac{2a^{2}u}{(a^2+u^2)^2}>0\) for all \(u>0\). Therefore, \(E_{t}(u,v)\le 0\) if \(\lambda >1\) (equivalently \(d>m/(a^2+1)\)), which again implies that E decreases monotonically along the solution orbit. It follows that the equilibrium (0, 1) of the reaction–diffusion system (1.3) is globally asymptotically stable. \(\square \)

Remark 3.5

Compared with the reaction–diffusion system, it is more feasible to observe the dynamics as the parameter \(\lambda \) changes for the ODE system. Here we collect some known results on the ODE dynamics of (1.3) (see for example [33, 59]) via some phases portraits, see Figs. 2 and 3.

Fig. 2
figure 2

\(a=0.3>a^*\). (left) \(d=0.6\), \((\lambda ,v_{\lambda })\) is globally stable in \({\mathbb {R}}^2_{+}\); (middle) \(d\approx 0.15\), then \(\lambda <\lambda _1\approx 0.19\), \((\lambda ,v_{\lambda })\) is globally stable in \({\mathbb {R}}^2_{+}\); (right) \(d\approx 0.64\), then \(0.44 \approx \lambda _2>\lambda >\lambda _1\approx 0.19\), there exists a unique limit cycle

Full size image
Fig. 3
figure 3

\(a=0.15<a^*\). (left) \(d\approx 0.95\) and \(\lambda >\lambda _2\), \((\lambda ,v_{\lambda })\) is globally stable in \({\mathbb {R}}^2_{+}\); (right) \(d\approx 0.99\) and (1, 0) is globally stable in \({\mathbb {R}}^2_{+}\)

Full size image

3.2 Bifurcation Analysis and Oscillatory Patterns

In this subsection, we investigate the Hopf bifurcations from the positive equilibrium \((\lambda ,v_{\lambda })\) for (1.3), and we will show the existence of spatially homogeneous and spatially inhomogeneous periodic orbits of system (1.3). In this subsection, we assume that all eigenvalues \(\mu _i\) of \(-\Delta \) in \(H_1(\Omega )\) are simple, and denote the corresponding eigenfunction by \(\phi _i(x)\) where \(i\in \mathbb {N}_0\). Note that this assumption always holds when \(\mathbb {N}=1\) for domain \((0,l\pi )\), as for \(i\in \mathbb {N}_0\), \(\mu _i=i^2/l^2\) and \(\phi _i(x)=\cos (ix/l)\), where l is a positive constant; and it also holds for generic class of domains in higher dimensions.

From [62, 67], it follows that if for certain critical value \(\lambda ^H\), there exists \(n\in \mathbb {N}_0\), such that

$$\begin{aligned} T_n(\lambda ^H)=0 , D_n(\lambda ^H)>0 ,\;\text {and}\;T_j(\lambda ^H)\ne 0, D_j(\lambda ^H)\ne 0, \; \text {for}\; j\ne n; \end{aligned}$$
(3.7)

and for unique pair of complex eigenvalues near the imaginary axis \(\alpha (\lambda ) \pm i \omega (\lambda )\) ,

$$\begin{aligned} \alpha '(\lambda ^H)\ne 0, \end{aligned}$$
(3.8)

then there is a Hopf bifurcation emanating from the unique constant steady state \((\lambda ,v_{\lambda })\) near \(\lambda =\lambda ^H\).

Theorem 3.3 implies that the trivial steady state \((\lambda ,v_{\lambda })\) is globally asymptotically stable for all \(\lambda \) if \(a>a^*\) and locally asymptotically stable for \(\lambda \in (0,\lambda _1)\cup (\lambda _2,1)\) if \(0<a<a^*\). Hence any potential Hopf bifurcation point \(\lambda ^H\) must be in the interval \(\lambda \in [\lambda _1,\lambda _2]\) for \(0<a<a^*\).

Firstly, \(\lambda _1^H=\lambda _1\), \(\lambda _2^H=\lambda _2\) are always Hopf bifurcation points since \(T_0(\lambda _{1,2}^H)=A(\lambda _{1,2}^H)=0\) and \(T_j(\lambda _{1,2}^H)=-(d_1+d_2)\mu _j<0\) for any \(j\ge 1\); and

$$\begin{aligned} D_i(\lambda _{1,2}^H)=-B(\lambda _{1,2}^H)C(\lambda _{1,2}^H)+d_1d_2\mu _j^2>0 \end{aligned}$$

for any \(j\in {\mathbb N}_0\). This corresponds to the Hopf bifurcation of spatially homogeneous periodic orbits which have been known from the studies in [33]. Apparently \(\lambda _{1,2}^H\) are also the two unique value \(\lambda \) for the Hopf bifurcation of spatially homogeneous periodic orbits from the uniqueness result of limit cycle in [23, 33].

Fig. 4
figure 4

The figure of \(A(\lambda )\), parameter a = 0.15

Full size image

Hence in the following we search for spatially non-homogeneous Hopf bifurcations for \(i\ge 1\). From Eq.(3.6), it follows that \(T_n(\lambda )=0\) is equivalent to

$$\begin{aligned} A(\lambda )=(d_1+d_2)\mu _n. \end{aligned}$$

Notice that \(A(\lambda _1)=A(\lambda _2)=0\) and \(A(\lambda )>0\) in \((\lambda _1,\lambda _2)\). Denote \(A(\lambda )\) achieves a local maximum \(A(\lambda _{1*})=M^*\) in \((\lambda _1,\lambda _2)\), see Fig. 4.

From Lemma 3.1, we define \(\lambda _{i,\pm }^H\) to be the two solution of \(A(\lambda )=(d_1+d_2)\mu _i\) satisfying \(\lambda _1<\lambda <\lambda _2\). These points satisfy

$$\begin{aligned} \lambda _1<\lambda _{1,-}^H<\lambda _{2,-}^H<\cdots <\lambda _{m,-}^H<\lambda _{1*}<\lambda _{m,+}^H<\cdots <\lambda _{2,+}^H<\lambda _{1,+}^H<\lambda _2, \end{aligned}$$

where m is the largest integer so that \(\mu _m\le M^*/(d_1+d_2)\).

Clearly \(T_i(\lambda _{i,\pm }^H)=0\) and \(T_j(\lambda _{i,\pm }^H)\ne 0\) for any \(j\ne i\). We will derive the condition \(D_i(\lambda _{i,\pm }^H)>0\) hold for all i satisfying \(1\le i\le m\). In fact, if \(\lambda _{i,\pm }\in (\lambda _1,\lambda _2)\), then

$$\begin{aligned} \begin{aligned} D_i(\lambda _{i,\pm }^H)&=-B(\lambda _{i,\pm }^H)C(\lambda _{i,\pm }^H)-A(\lambda _{i,\pm }^H)d_2\mu _i+d_1d_2\mu _i^2\\&=-B(\lambda _{i,\pm }^H)C(\lambda _{i,\pm }^H)-(d_1+d_2)d_2\mu _i^2+d_1d_2\mu _i^2\\&=-B(\lambda _{i,\pm }^H)C(\lambda _{i,\pm }^H)-d_2^2\mu _i^2\\&=\frac{2a^2m(\lambda _{i,\pm }^H)^2(1-\lambda _{i,\pm }^H)}{(a^2+\lambda _{i,\pm }^H)^2}- \frac{d_2^2A^2(\lambda _{i,\pm }^H)}{(d_1+d_2)^2}\\&=\dfrac{1}{(a^2+(\lambda _{i,\pm }^H)^2)^2}\left[ 2a^2m(\lambda _{i,\pm }^H)^2(1-\lambda _{i,\pm }^H)\right. \\&\quad \left. -\frac{d_2^2}{(d_1+d_2)^2}\left( -2(\lambda _{i,\pm }^H)^3+(\lambda _{i,\pm }^H)^2-a^2\right) ^2\right] >0, \end{aligned} \end{aligned}$$
(3.9)

if \(d_1, d_2\) satisfy

$$\begin{aligned} \dfrac{d_2}{d_1+d_2}<\inf _{\lambda \in ( \lambda _1,\lambda _2)}\sqrt{\dfrac{2a^2m\lambda ^2(1-\lambda )}{(-2\lambda ^3+\lambda ^2-a^2)^2}}. \end{aligned}$$
(3.10)

Finally let the eigenvalues close to the pure imaginary one near at \(\lambda =\lambda _{i,\pm }^H\), \(0\le i\le m\) be \(\alpha (\lambda )\pm i\omega (\lambda )\). Then

$$\begin{aligned} \alpha (\lambda )=\frac{A(\lambda )}{2}-(d_1+d_2)\mu _i, \end{aligned}$$
(3.11)

and

$$\begin{aligned} \alpha '(\lambda )=\frac{A'(\lambda )}{2}= {\left\{ \begin{array}{ll} \displaystyle >0, \quad \lambda _1\le \lambda _0<\lambda _{1*},\\ \displaystyle <0, \quad \lambda _{1*}<\lambda _0\le \lambda _2. \end{array}\right. } \end{aligned}$$
(3.12)

Hence the transversality condition is always satisfied as long as \(\lambda _{i,\pm }^H\ne \lambda _{1*}\).

Summarizing our analysis above, by using the Hopf bifurcation theorem in [67], we obtain our main result in this subsection:

Theorem 3.6

Recall \(A(\lambda )\) reaches its maximum \(A(\lambda _{1*})=M^*\) in \((\lambda _1,\lambda _2)\). Suppose that \(m>0\), \(0<a<a^*\) and the constants \(d_1, d_2\) satisfy (3.10). Let \(\Omega \) be a bounded smooth domain so that the spectral set \(S=\{\mu _i\}_{i\in \mathbb {N}_0}\) satisfies that:

  1. (S1)

    All eigenvalues \(\mu _i\) are simple for \(i\in \mathbb {N}_0\).

Then there exist \(2(m+1)\) points \(\lambda ^{H}_{j,\pm }\) satisfying

$$\begin{aligned} \lambda _1=\lambda _{1}^{H}<\lambda _{1,-}^{H}<\lambda _{2,-}^{H}<\cdots <\lambda _{m,-}^{H}<\lambda _{1*}<\lambda _{m,+}^{H}<\cdots <\lambda _{2,+}^{H}<\lambda _{1,+}^{H}<\lambda _{2}^{H}=\lambda _2. \end{aligned}$$

such that the system (1.3) undergoes a Hopf bifurcation at \(\lambda =\lambda ^{H}_{j,\pm }\) or \(\lambda =\lambda _{1, 2}^{H}\), and the bifurcating periodic orbits near near \((\lambda ,v_{\lambda })\) can be parameterized in the form:

$$\begin{aligned} (\lambda ,u,v)= & {} (\lambda ^H_i+o(s),\lambda ^H_i+se_i\cos (\omega (\lambda _i^H)t)\phi _i(x)\\&+\,o(s), v_{\lambda ^H_i}+sf_i\cos (\omega (\lambda _i^H)t)\phi _i(x)+o(s)), \end{aligned}$$

for \(s\in (0,\delta )\), where \(\omega (\lambda _i^H)=\sqrt{D_i(\lambda _i^H)}\) is the corresponding time frequency, \(\phi _i(x)\) is the corresponding spatial eigenfunction, and \((e_i,f_i)\) is a corresponding eigenvector. Moreover,

  1. (1)

    The periodic solutions bifurcating from \(\lambda =\lambda _{1, 2}^{H}\) are spatially homogeneous, which coincides with the periodic solutions of the corresponding ODE system.

  2. (2)

    The bifurcating periodic solutions from \(\lambda =\lambda ^{H}_{j,\pm }\) are spatially nonhomogeneous.

The spatially nonhomogeneous periodic orbits bifurcating from \(\lambda _{j,\pm }^H\), \(1\le j\le m\) are all unstable as \(L(\lambda _{j,\pm }^H)\) possesses at least one pair of eigenvalues with positive real part.

Relying on the abstract results obtained in [67] or [28], we can determine the stability and bifurcation direction of the homogeneous periodic solutions. To that end, we calculate \(Re(c_1(\lambda _{1, 2}^H))\) in the context of [67] when \(\Omega =(0,l\pi )\).

According to \(c_1(\lambda _0^H)\) of the definition in references [67], we need to calculate the symbols of \(Re(c_1(\lambda _{1, 2}^H))\). To simplify the notation, we denote \(\lambda _0=\lambda _{1, 2}\) in the following calculation. Let

$$\begin{aligned} q:=(a_0, b_0)^T=\left( \displaystyle {1}, \dfrac{-i\omega _0}{d}\right) ^\top ,\;\; \text {and}\;\;q^*:=(a_0^*, b_0^*)^T=\left( \displaystyle \dfrac{1}{2l\pi }, \dfrac{-di}{2\omega _0l\pi }\right) ^\top , \end{aligned}$$

where

$$\begin{aligned} \omega _0=\sqrt{\dfrac{2a^2d(1-\lambda )}{a^2+\lambda ^2}}. \end{aligned}$$

Recall that in our context,

$$\begin{aligned} f(\lambda , u, v)= & {} (u+\lambda ) (1-u-\lambda )- \frac{m(u+\lambda )^{2}(v+v_\lambda )}{\alpha ^{2} +(u+\lambda )^{2}} ,\\ g(\lambda , u, v)= & {} -d(v+v_\lambda ) + \frac{m(u+\lambda )^{2}(v+v_\lambda )}{\alpha ^{2} + (u+\lambda )^{2}}. \end{aligned}$$

Then the direct calculation can lead to

$$\begin{aligned} f_0= & {} g_{uu}\mid a_{0} \mid ^{2}+ g_{uv}(a_{0}\overline{b_{0}}+\overline{a_{0}}b_{0})+g_{vv}\mid b_{0}\mid ^{2}=\frac{2(1-\lambda )a^2(a^2-3\lambda ^2)}{(a^2+\lambda ^2)^2 \lambda },\\ e_0= & {} -2-f_0,\\ c_0= & {} f_{uu}a_{0}^{2}+ 2f_{uv}a_{0}b_{0}+f_{vv}b_{0}^{2}=-2-\frac{2(1-\lambda )a^2(a^2-3\lambda ^2)}{(a^2+\lambda ^2)^2 \lambda }+\frac{4m\lambda a^2}{(a^2+\lambda ^2)^2}\frac{\omega _0}{d}i,\\ d_0= & {} g_{uu}a_{0}^{2}+ 2g_{uv}a_{0}b_{0}+g_{vv}b_{0}^{2}=-2-c_0,\\ g_0= & {} f_{uuu}\mid a_0 \mid ^{2}a_{0}+f_{uuv}(2\mid a_0 \mid ^{2}b_{0}+ a_{0} ^{2}\overline{b_{0}})+f_{uvv}(2\mid b_0 \mid ^{2}a_{0}+ b_{0} ^{2}\overline{a_{0}})+f_{vvv}\mid b_0 \mid ^{2}b_{0}\\= & {} \frac{24a^2(a^2-\lambda ^2)(1-\lambda )}{(a^2+\lambda ^2)^3 }+\frac{2ma^2(a^2-3\lambda ^2)}{(a^2+\lambda ^2)^3}\frac{\omega _0}{d}i,\\ h_0= & {} -g_0, \end{aligned}$$

and

$$\begin{aligned} \langle q^*,Q_{qq}\rangle= & {} \frac{1}{2l\pi }c_0+\frac{di}{2\omega _0l\pi }d_0, \ \langle q^*, Q_{q\bar{q}}\rangle =\frac{1}{2l\pi }e_0+\frac{di}{2\omega _0l\pi }f_0,\\ \langle \bar{q}^*, Q_{qq}\rangle= & {} \frac{1}{2l\pi }c_0-\frac{di}{2\omega _0l\pi }d_0, \langle \bar{q}^*, Q_{q\bar{q}}\rangle =\frac{1}{2l\pi }e_0-\frac{di}{2\omega _0l\pi }f_0,\\ \langle q^*, C_{qq\bar{q}}\rangle= & {} \frac{1}{2l\pi }g_0+\frac{di}{2\omega _0l\pi }h_0 . \end{aligned}$$

Hence it is straightforward to obtain

$$\begin{aligned} \begin{aligned} H_{20}&=(c_0, d_0)^T-\langle q^*, Q_{qq}\rangle (a_0, b_0)^T-\langle \bar{q}^*, Q_{qq}\rangle (\overline{a_0}, \overline{b_0})^T=0,\\ H_{11}&=(e_0, f_0)^T-\langle q^*, Q_{q\bar{q}}\rangle (a_0, b_0)^T-\langle \bar{q}^*, Q_{q\bar{q}}\rangle (\overline{a_0}, \overline{b_0})^T=0, \end{aligned} \end{aligned}$$
(3.13)

which implies that \(\omega _{20}=\omega _{11}=0\). So

$$\begin{aligned} \langle q^*, Q_{\omega _{11}q}\rangle =\langle q^*, Q_{\omega _{20}\bar{q}}\rangle =0. \end{aligned}$$

Therefore,

$$\begin{aligned} Re(c_1(\lambda _{1, 2}^H))&=Re\left\{ \frac{i}{2\omega _0}\langle q^*, Q_{qq}\rangle \cdot \langle q^*, Q_{q\bar{q}}\rangle +\frac{1}{2}\langle q^*, C_{qq\bar{q}}\rangle \right\} \\&= Re\left\{ \frac{i}{2\omega _0}\left( \frac{1}{2l\pi }c_0+\frac{di}{2\omega _0l\pi }d_0\right) \left( \frac{1}{2l\pi }e_0+\frac{di}{2\omega _0l\pi }f_0\right) +\frac{1}{2}\left( \frac{1}{2l\pi }g_0+\frac{di}{2\omega _0l\pi }h_0\right) \right\} \\&=\frac{a^2}{\lambda _{1, 2}^H(a^2+(\lambda _{1, 2}^H)^2)}+\frac{a^4(1-\lambda _{1, 2}^H)(a^2-3(\lambda _{1, 2}^H)^2)}{(\lambda _{1, 2}^H)^2(a^2+(\lambda _{1, 2}^H)^2)^3}+\frac{(a^2-3(\lambda _{1, 2}^H)^2)}{2\lambda _{1, 2}^H(a^2+(\lambda _{1, 2}^H)^2)}\\&\quad +\,\frac{a^2(1-\lambda _{1, 2}^H)(a^2-3(\lambda _{1, 2}^H)^2)^2}{2(\lambda _{1, 2}^H)^2(a^2+(\lambda _{1, 2}^H)^2)^3} +\frac{6a^2(1-\lambda _{1, 2}^H)(a^2-3(\lambda _{1, 2}^H)^2)}{(a^2+(\lambda _{1, 2}^H)^2)^3}\\&=\frac{3}{2(\lambda _{1, 2}^H)^{2}(a^2+(\lambda _{1, 2}^H)^2)^3}\left( a^{6}+a^4(\lambda _{1, 2}^H)^3 -9a^2(\lambda _{1, 2}^H)^4 +8a^2(\lambda _{1, 2}^H)^5-(\lambda _{1, 2}^H)^7\right) . \end{aligned}$$

Let \(M=a^{6}+a^4(\lambda _{1, 2}^H)^3 -9a^2(\lambda _{1, 2}^H)^4 +8a^2(\lambda _{1, 2}^H)^5-(\lambda _{1, 2}^H)^7\). Recall \(\lambda _1^H, \lambda _2^H\) are the two positive roots of \(\mathcal {A}(\lambda )=-2\lambda ^3+\lambda ^2-a^2=0\). It is easy to verify \(\mathcal {A}(a)<0\) and \(\mathcal {A}(1/3)>0\). Combining \(0<a<a^*=\sqrt{3}/9<1/3\), we can obtain \(a<\lambda _1^H<\lambda _2^H<1\). Then

$$\begin{aligned} \begin{aligned} M&=a^{6}+a^4(\lambda _{1, 2}^H)^3 -9a^2(\lambda _{1, 2}^H)^4 +8a^2(\lambda _{1, 2}^H)^5-(\lambda _{1, 2}^H)^7\\&=a^6+(\lambda _{1, 2}^H)^3(a^4-(\lambda _{1, 2}^H)^4-8a^2(\lambda _{1, 2}^H)+8a^2(\lambda _{1, 2}^H)^2-a^2(\lambda _{1, 2}^H)^2)\\&=a^6+(\lambda _{1, 2}^H)^3(a^4-(\lambda _{1, 2}^H)^4+8a^2\lambda _{1, 2}^H(\lambda _{1, 2}^H-1)-a^2(\lambda _{1, 2}^H)^2)\\&\quad <a^6-a^2(\lambda _{1, 2}^H)^4=a^2(a^4-(\lambda _{1, 2}^H)^4)<0. \end{aligned} \end{aligned}$$

Combining the symbols of \(Re(c_1(\lambda _{1, 2}^H))\) and the transaction condition (3.12), we have the following stability of homogeneous periodic solutions bifurcating from the positive equilibrium of (1.3):

Theorem 3.7

The Hopf bifurcation at \(\lambda =\lambda _1\) is forward and the corresponding bifurcating spatially homogeneous periodic solutions are always locally orbitally stable; the Hopf bifurcation at \(\lambda =\lambda _2\) is backward and the corresponding bifurcating spatially homogeneous periodic solutions are always locally orbitally stable.

Proof

It has been observed that \(T_0(\lambda _{1,2}^H)=0\), \(T_j(\lambda _{1,2}^H)=-(d_1+d_2)\mu _j<0\) for any \(j\ge 1\); and

$$\begin{aligned} D_j(\lambda _{1,2}^H)=-B(\lambda _{1,2}^H)C(\lambda _{1,2}^H)+d_1d_2\mu _j^2>0 \end{aligned}$$

for any \(j\in {\mathbb N}_0\). Therefore, at \(\lambda _0=\lambda _{1,2}^H\), apart from the purely imaginary eigenvalues, all the other eigenvalues of the linearized operators have strictly negative real parts. Thus the bifurcating periodic solutions are stable when \(Re(c_1(\lambda _{1,2}^H))<0\) (also see [28]).

Moreover, \(\alpha '(\lambda _1^H)>0\) and \(\alpha '(\lambda _2^H)<0\). Then the conclusion can be obtained from Theorem 2.3 in [67]. \(\square \)

We find that \(M<0\) always holds for all \(a\in (0,a^*)\), which also identifies the uniqueness of limit cycle for the corresponding ODE system (see [10, 33, 59]). One condition to ensure the uniqueness of limit cycle in [59] is \(\lambda <(2d-m)/(2d)\). Since the values of \(\lambda _1, \lambda _2\) are only determined by a, Theorem 3.7 implies that the limit cycle bifurcating is unique if \(\lambda _2<1-m/(2d)\) for fixed \(m>0, 0<a<a^*\). Specifically, we can give the homogeneous periodic solutions of the system (1.3) (see Figs. 5, 6) with parameters \(a=0.15, m=1\) and \(\Omega =(0,3\pi )\).

Fig. 5
figure 5

The periodic solutions of the system (1.3), where the initial value \((u_0(x)=0.1374, v_0(x)=0.267)\), \(d=0.6185\) and \(\lambda _1\approx 0.191\)

Full size image
Fig. 6
figure 6

Periodic solutions of the system (1.3), where the initial value \((u_0(x)=\cos (x)+1.5, v_0(x)=\sin (x)+1.6)\), \(d=0.8971\) and \(\lambda _2\approx 0.443\)

Full size image

4 Analysis of the Steady State Solutions

In this section we discuss the existence and nonexistence of non-constant positive steady state solutions of (1.3), which satisfies:

$$\begin{aligned} {\left\{ \begin{array}{ll} d_{1}\Delta u+u (1-u)- \dfrac{mu^{2}v}{a^{2}+u^{2}}=0,&{}\quad x\in \Omega , \\ d_{2}\Delta v-dv+\dfrac{mu^{2}v}{a^{2}+u^{2}}=0,&{}\quad x\in \Omega , \\ \displaystyle \frac{\partial u}{\partial n}=\displaystyle \frac{\partial v}{\partial n}=0,\;\;\;&{}\quad x\in \partial \Omega . \end{array}\right. } \end{aligned}$$
(4.1)

Throughout the remaining part of this paper, the solutions refer to the classical solutions, by which we mean solutions in \(C^2(\Omega )\cap C^1(\overline{\Omega })\). We will give a priori upper and lower bounds for the positive solutions of (4.1).

4.1 A Priori Estimates and Nonexistence of Solutions

In this subsection we discuss the nonexistence of non-constant positive solutions to (4.1). To derive some a priori estimates for nonnegative solutions of (4.1), we recall the following maximum principle ([52]):

Lemma 4.1

Let \(\Omega \) be a bounded Lipschitz domain in \(\mathbb {R}^n\), and let \(g\in C(\overline{\Omega }\times \mathbb {R})\). If \(z\in H^{1}(\Omega )\) is a weak solution of the inequalities

$$\begin{aligned} \Delta z+g(x,z(x))\ge 0\;\;\text {in}\;\;\Omega , \quad \quad \frac{\partial z}{\partial n}(x)\le 0\;\;\text {on}\;\;\partial \Omega , \end{aligned}$$

and if there is a constant K such that \(g(x,z)<0\) for \(z>K\), then \(z\le K\) a.e. in \(\Omega \).

Firstly we have the following a priori estimate for any nonnegative solution to (4.1):

Lemma 4.2

Suppose that \(\left( u(x),v(x)\right) \) is a nonnegative solution of (4.1). Then either (u, v) is one of constant solutions: (0, 0), (1, 0), or for \(x\in \overline{\Omega }\), \(\left( u(x),v(x)\right) \) satisfies

$$\begin{aligned} 0<u(x)<1,\quad \quad \text {and}\quad 0<v(x)<C^*=\dfrac{1}{4d}+\dfrac{d_1}{d_2}, \end{aligned}$$
(4.2)

where \(d,d_1,d_2>0\).

Proof

Let \(\left( u(x),v(x)\right) \) be a nonnegative solution to (4.1). If there exists \(x_0\in \overline{\Omega }\) such that \(v(x_0)=0\), then \(v(x)\equiv 0\) from the strong maximum principle and u(x) satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} -d_1\Delta u=u(1-u),\;\;&{}x\in \Omega ,\\ \displaystyle \frac{\partial u}{\partial n}=0,\;\;&{}x\in \partial \Omega . \end{array}\right. } \end{aligned}$$
(4.3)

From Theorem 10.1.6 of [29], \(u\equiv 0\) or \(u\equiv 1\). Hence if (u, v) is not (0, 0) or (1, 0), then \(u(x)>0\) and \(v(x)>0\) for \(x\in \overline{\Omega }\).

From Lemma 4.1, \(u(x)\le 1\) and from the strong maximum principle, \(u(x)<1\) for all \(x\in \overline{\Omega }\). By adding the two equations in (4.1), we have

$$\begin{aligned} \begin{aligned} -(d_1\Delta u+d_2\Delta v)=\,&u(1-u)-dv\\ =&\left( u(1-u)+\displaystyle \frac{dd_1u}{d_2}\right) -\displaystyle \frac{d}{d_2}(d_1u+d_2v)\\&\quad \le \left( \dfrac{1}{4}+\displaystyle \frac{dd_1}{d_2}\right) -\displaystyle \frac{d}{d_2}(d_1u+d_2v).\\ \end{aligned} \end{aligned}$$

Then Lemma 4.1 and the maximum principle implies that

$$\begin{aligned} d_1u+d_2v<\displaystyle \frac{d_2}{4d}+d_1, \end{aligned}$$

which implies the desired estimate. \(\square \)

Now we can obtain the nonexistence of positive steady state solutions for some parameters.

Corollary 4.3

Suppose \(d_1,d_2>0\) and \(\Omega \) is a bounded domain with smooth boundary. Let (u(x), v(x)) be a nonnegative solution to (4.1). If \(\lambda \ge 1\), then (u(x), v(x)) is either (0, 0) or (1, 0).

Proof

From Lemma 4.2, \(u(x)\le 1\) and \(\displaystyle -d+m/(a^2+1)\le 0\). By integrating the second equation of (4.1), we obtain

$$\begin{aligned} 0\le d_2\int _{\Omega }|\nabla v|^2 dx=\int _{\Omega }v^2 \left( -d+\dfrac{mu^2}{a^2+u^2}\right) dx\le 0. \end{aligned}$$

Hence \(v\equiv 0\) on \(\overline{\Omega }\). \(\square \)

Moreover, we can show that the nonexistence of positive steady state solutions when the diffusion coefficients \(d_1\) and \(d_2\) are large.

Theorem 4.4

For any fixed \(d>0\), there exists \(d^*=d^*(d,\Omega )\) such that if \(\min \{d_1, d_2\}>d^*\), then the only nonnegative solutions to (4.1) are (0, 0), (1, 0) and \((\lambda ,v_{\lambda })\). \(\square \)

Proof

Let (u, v) be a nonnegative solution to (4.1), and denote \(\bar{u}=|\Omega |^{-1}\int _{\Omega } u dx\), \(\bar{v}=|\Omega |^{-1}\int _{\Omega } v dx\). Then

$$\begin{aligned} \int _{\Omega }(u-\bar{u})dx=\int _{\Omega }(v-\bar{v})dx=0. \end{aligned}$$
(4.4)

Multiplying the first equation in (4.1) by \(u-\bar{u}\) and applying Lemma 4.2, we get

$$\begin{aligned} \begin{aligned}&d_1\int _{\Omega }|\nabla (u-\bar{u})|^2 dx\\&\quad =\int _{\Omega }(u-\bar{u})u(1-u)dx-\int _{\Omega }(u-\bar{u})\dfrac{mu^2v}{a^2+u^2}dx\\&\quad =\int _{\Omega }(u-\bar{u})\left[ u(1-u)-\bar{u}(1-\bar{u})\right] dx-\int _{\Omega }(u-\bar{u})\left[ \dfrac{mu^2v}{a^2+u^2}-\dfrac{m\bar{u}^2\bar{v}}{a^2+\bar{u}^2}\right] dx\\&\quad =\int _{\Omega }(u-\bar{u})^2[1-(u+\bar{u})^2]dx+\int _{\Omega }(u-\bar{u})\left[ -\dfrac{mu^2v}{a^2+u^2}+\dfrac{m\bar{u}^2\bar{v}}{a^2+\bar{u}^2}\right] dx\\&\quad \le \int _{\Omega }(u-\bar{u})^2dx+\int _{\Omega }(u-\bar{u})(\bar{v}-v)\dfrac{mu^2}{a^2+u^2}dx+\int _{\Omega }(u-\bar{u})\bar{v}\left[ \dfrac{m\bar{u}^2}{a^2+\bar{u}^2}-\dfrac{mu^2}{a^2+u^2}\right] dx\\&\quad \le \int _{\Omega }(u-\bar{u})^2dx+\dfrac{m}{2}\int _{\Omega }(u-\bar{u})^2dx+\dfrac{m}{2}\int _{\Omega }(\bar{v}-v)^2dx\\&\qquad -\int _{\Omega }(u-\bar{u})^2\bar{v}\dfrac{2ma^2\xi }{(a^2+\xi ^2)^2}dx,\ \, \text {where}\;\xi \in (\bar{u},u)\\&\quad \le \left( \dfrac{m}{2}+1\right) \int _{\Omega }(u-\bar{u})^2dx+\dfrac{m}{2}\int _{\Omega }(v-\bar{v})^2dx. \end{aligned} \end{aligned}$$
(4.5)

Furthermore, adding the two equations in (4.1) and integrating over \(\Omega \), we get

$$\begin{aligned} \int _{\Omega }(-d_1\Delta u-d_2\Delta v) dx=\int _{\Omega } \left[ u(1-u)-dv \right] dx, \end{aligned}$$
(4.6)

then the Neumann boundary conditions lead to

$$\begin{aligned} d\int _{\Omega } v dx =\int _{\Omega }u(1-u)dx \le \dfrac{|\Omega |}{4}. \end{aligned}$$
(4.7)

Thus

$$\begin{aligned} \bar{v}=\displaystyle \frac{1}{|\Omega |}\int _{\Omega }v dx\le \displaystyle \frac{1}{4d}. \end{aligned}$$
(4.8)

In a similar manner, we multiply the second equation in (4.1) by \(v-\bar{v}\) to have

$$\begin{aligned}&d_2\int _{\Omega }|\nabla (v-\bar{v})|^2 dx =\int _{\Omega }(v-\bar{v})\left( -dv+\dfrac{mu^2}{a^2+u^2}v\right) dx\nonumber \\&\quad =\int _{\Omega }(v-\bar{v})\left[ \left( -dv+\dfrac{mu^2}{a^2+u^2}v\right) -\left( -d\bar{v}+\dfrac{m\bar{u}^2}{a^2+\bar{u}^2}\bar{v}\right) \right] dx\nonumber \\&\quad =-d\int _{\Omega }(v-\bar{v})^2dx+\int _{\Omega }(v-\bar{v})\left[ \dfrac{mu^2}{a^2+u^2}v-\dfrac{m\bar{u}^2}{a^2+\bar{u}^2}\bar{v}\right] dx\nonumber \\&\quad \le \int _{\Omega }(v-\bar{v})\left[ \dfrac{mu^2}{a^2+u^2}v-\dfrac{mu^2}{a^2+u^2}\bar{v}+\dfrac{mu^2}{a^2+u^2}\bar{v}-\dfrac{m\bar{u}^2}{a^2+\bar{u}^2}\bar{v}\right] dx\nonumber \\&\quad =\int _{\Omega }(v-\bar{v})^2\dfrac{mu^2}{a^2+u^2}dx+\int _{\Omega }(v-\bar{v})\bar{v}\left[ \dfrac{mu^2}{a^2+u^2}-\dfrac{m\bar{u}^2}{a^2+\bar{u}^2}\right] dx\nonumber \\&\quad \le \dfrac{m}{a^2+1}\int _{\Omega }(v-\bar{v})^2dx+\int _{\Omega }(v-\bar{v})\bar{v}(u-\bar{u})\dfrac{2ma^2\xi }{(a^2+\xi ^2)^2}dx, \,\; \text {where}\;\xi \in (\bar{u},u)\nonumber \\&\quad \le \dfrac{m}{a^2+1}\int _{\Omega }(v-\bar{v})^2dx+\dfrac{1}{32d^2}\int _{\Omega }(v-\bar{v})^2dx+\dfrac{ma^2}{(a^2+1)^2}\int _{\Omega }(u-\bar{u})^2dx. \end{aligned}$$
(4.9)

From (4.5), (4.9) and the Poincaré inequality, we obtain that

$$\begin{aligned} \begin{aligned}&d_2\int _{\Omega }|\nabla (v-\bar{v})^2|dx +d_1\int _{\Omega }|\nabla (u-\bar{u})^2| dx \\ \le&\displaystyle \frac{1}{\mu _1}\left( A\int _{\Omega }|\nabla (v-\bar{v})^2|dx+B\int _{\Omega }|\nabla (u-\bar{u})^2| dx\right) , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} A=\dfrac{m}{a^2+1}+\dfrac{1}{32d^2}+\dfrac{m}{2},\;\;\;B=\dfrac{ma^2}{(a^2+1)^2}+\dfrac{m}{2}+1. \end{aligned}$$

This shows that if

$$\begin{aligned} \min \{d_1,d_2\}>\frac{1}{\mu _1}\max \{A,B\}, \end{aligned}$$

then

$$\begin{aligned} \nabla (u-\bar{u})=\nabla (v-\bar{v})=0, \end{aligned}$$

and (u, v) must be a constant solution. \(\square \)

4.2 Existence of Non-constant Positive Steady State Solutions

In this subsection we use degree theory to prove the existence of non-constant solutions to (4.1) for certain parameter range. For that purpose, we cite a Harnack inequality for weak solutions in [52].

Lemma 4.5

Let \(\Omega \) be a bounded Lipschitz domain in \(\mathbb {R}^n\), and let \(c(x)\in L^q(\Omega )\) for some \(q>n/2\). If \(z\in H^1(\Omega )\) is a nonnegative weak solution of the boundary value problem

$$\begin{aligned} \Delta z+c(x)z=0\;\;\text { in}\;\;\Omega , \quad \quad \frac{\partial z(x)}{\partial n}\le 0\;\;\text { on}\;\;\partial \Omega , \end{aligned}$$

then there is a constant \(C_1\), determined only by \(\parallel c\parallel _q\), q and \(\Omega \) such that

$$\begin{aligned} \sup _{\overline{\Omega }} z\le C_1\inf _{\overline{\Omega }} z. \end{aligned}$$

Based on the above preparation, we are ready to derive a priori upper and lower bounds for all positive solutions to (4.1). More precisely, we have

Theorem 4.6

Let \(\Omega \) be a bounded smooth domain in \(\mathbb {R}^n\). Then, for \(\sigma \le \lambda \le 1\) with some \(\sigma >0\) small enough, there exist two positive constants \(\underline{\mathcal {C}}\) and \(\overline{\mathcal {C}}\) with \(\underline{\mathcal {C}}<\overline{\mathcal {C}}\) depending possibly on \(d_1,d_2, d, \sigma \) and \(\Omega \), such that any positive solution \(\left( u(x),v(x)\right) \) of (4.1) satisfies

$$\begin{aligned} \underline{\mathcal {C}}\le u(x),\; v(x)\le \overline{\mathcal {C}} \quad \text {for any}\;\;x\in \overline{\Omega }. \end{aligned}$$
(4.10)

Proof

From Lemma 4.2, we obtain that for any \(x\in \overline{\Omega }\),

$$\begin{aligned} u(x), v(x)\le \overline{\mathcal {C}}:=\max \left\{ 1, \dfrac{1}{4d}+\dfrac{d_1}{d_2}\right\} , \end{aligned}$$

where \(\overline{\mathcal {C}}\) depends on \(d_1,d_2,d\).

Now we give the lower bound. Let

$$\begin{aligned} L_1(x): =\dfrac{1}{d_1}\left[ 1-u(x)-\dfrac{mu(x)v(x)}{a^2+u^2(x)}\right] ,\;\;\; L_2(x): =\dfrac{1}{d_2}\left[ -d+\dfrac{mu^2(x)}{a^2+u^2(x)}\right] , \end{aligned}$$

then the mean value theorem implies that

$$\begin{aligned} \dfrac{mu^2}{a^2+u^2}:=g(u)=g(u)-g(0)=g'(\xi )u,\;\;\xi \in (0,u). \end{aligned}$$

Then we have

$$\begin{aligned} |L_1(x)| \le \dfrac{1}{d_1}\left( 2+\dfrac{m\overline{\mathcal {C}}}{2a}\right) ,\quad \quad |L_2(x)| \le \dfrac{1}{d_2}\left( d+\dfrac{m}{a^2+1}\right) . \end{aligned}$$

Lemma 4.5 implies that there exists a positive constant \(C_2\) depending on \(d_1,d_2, d\) and \(\Omega \) such that

$$\begin{aligned} \sup _{\overline{\Omega }}u(x)\le C_2\inf _{\overline{\Omega }}u(x),\quad \sup _{\overline{\Omega }}v(x)\le C_2\inf _{\overline{\Omega }}v(x). \end{aligned}$$

Hence it remains to prove that there exists \(C_3>0\) such that

$$\begin{aligned} \sup _{\overline{\Omega }}u(x)\ge C_3\;\; \text {and}\;\;\mathbf {} \sup _{\overline{\Omega }}v(x)\ge C_3. \end{aligned}$$
(4.11)

Suppose this is not true, then there exists a sequence of positive solutions \((u_n(x),v_n(x))\) such that

$$\begin{aligned} \sup _{\overline{\Omega }} u_n(x)\rightarrow 0\quad \text {or}\quad \sup _{\overline{\Omega }} v_n(x)\rightarrow 0 \quad \text { as} \;\; n\rightarrow +\infty . \end{aligned}$$
(4.12)

From the Sobolev embedding theorem and elliptic estimates, there exists a subsequence of \((u_n, v_n)\), which we still denote by \((u_n, v_n)\), such that \(u_n\rightarrow u_0\) and \(v_n\rightarrow v_0\) in \(C^2(\overline{\Omega })\) as \(n\rightarrow +\infty \). Observe that \(u_0\le 1\) and from (4.12), either \(u_0\equiv 0\) or \(v_0\equiv 0\) and \((u_0,v_0)\) satisfies (4.1). Therefore, we have the following two cases:

  1. (i)

    \(u_0\equiv 0\), \(v_0\not \equiv 0\); or \(u_0\equiv 0\), \(v_0\equiv 0\).

  2. (ii)

    \(u_0\not \equiv 0\), \(v_0\equiv 0\).

Since \((u_n,v_n)\) is a positive solution of (4.1), we can obtain the following integral equation by integrating the second equation in (4.1) for \(v_n\) over \(\Omega \),

$$\begin{aligned} \int _{\Omega }v_n\left[ -d+g(u_n)\right] dx=0. \end{aligned}$$
  1. (i)

    If \(u_0\equiv 0\), then we have

    $$\begin{aligned} -d+g(u_n)\rightarrow -d+g(u_0)=-g(\lambda )+g(0)\le -g(\sigma )<0 \end{aligned}$$

    for any \(x\in \overline{\Omega }\) as \(n\rightarrow \infty \). Since \(v_n>0\), then for sufficient large n, we obtain

    $$\begin{aligned} \int _{\Omega }v_n\left( -d+g(u_n)\right) dx<0, \end{aligned}$$
    (4.13)

    that is a contradiction.

  2. (ii)

    If \(u_0\not \equiv 0\) and \(v_0\equiv 0\), then this implies that \(u_0\) satisfies (4.3). So \(u_0\equiv 1\) for large n. Thus, we have

    $$\begin{aligned} -d+g\left( u_n\right) \rightarrow -d+g(1)\ge 0 \end{aligned}$$

    for large n since \(d=g(\lambda )\le g(1)\).

Then the contradiction with (4.13) is reached. Therefore (4.11) holds and we complete the proof. It is remarkable that the lower bound \(\underline{\mathcal {C}}\) depends only on \(d_1,d_2, d\). \(\square \)

Recall the definition of \(\underline{\mathcal {C}}\) and \(\overline{\mathcal {C}}\) from Theorem 4.6, we set

$$\begin{aligned} \begin{aligned} \mathbf {X}&=\{(u,v)\in [C^1(\overline{\Omega })]^2 |\; \frac{\partial u}{\partial n}= \frac{\partial v}{\partial n}=0\; \text {on}\; \partial \Omega \},\;\;\;\; \mathbf {X}^+=\{(u,v) | u, v\ge 0, (u,v) \in \mathbf {X}\},\\ \Lambda&=\{(u,v)\in \mathbf {X} \;|\;\underline{\mathcal {C}}/2\le u(x),\; v(x)\le 2\overline{\mathcal {C}} \; \text {for}\;x\in \overline{\Omega }\}. \end{aligned} \end{aligned}$$

Denote \(\mathbf {u}=(u,v)\) and \(e^*=(\lambda ,v_{\lambda })\), and

$$\begin{aligned} G(\mathbf {u})=\left( {{\begin{array}{*{20}c} {u(1-u)-\dfrac{mu^2v}{a^2+u^2}}\\ {v\left( -d+\dfrac{mu^2}{a^2+u^2}\right) }\\ \end{array}}}\right) ,\;\;\;\;\quad G_{\mathbf {u}}(e^*)=\left( {{\begin{array}{*{20}c} {A(\lambda )}&{}{B(\lambda )}\\ {C(\lambda )}&{}{0}\\ \end{array}}}\right) , \end{aligned}$$

where \(A(\lambda ), B(\lambda ), C(\lambda )\) are defined as in Sect. 2.2. Thus, (4.1) can be written as

$$\begin{aligned} -\Delta \Phi (\mathbf {u})=G(\mathbf {u}) \;\;\text {in}\; {\Omega }, \quad \quad \frac{\partial \mathbf {u}}{\partial n}=0\;\;\text {on}\;\partial \Omega , \end{aligned}$$
(4.14)

with \(\Phi (\mathbf {u})=(d_1u, d_2v)^T\). Since the determinant \(det \Phi (\mathbf {u})\) is positive for all non-negative \(\mathbf {u}\), \(\Phi _{\mathbf {u}}^{-1}\) exists and for \(\sigma \le \lambda < K\), \(\mathbf {u}\) is a positive solution of (4.14) if and only if

$$\begin{aligned} \mathcal {F}(d_1, d_2, \lambda ; \mathbf {u})\equiv \mathbf {u}-(\mathbf {I}-\Delta )^{-1} [\Phi _{\mathbf {u}}^{-1}G(\mathbf {u})+\mathbf {u}]=0, \;\;\mathbf {u}\; \text {in}\;\mathbf {X}^{+}. \end{aligned}$$

And \((\mathbf {I}-\Delta )^{-1}\) is the inverse of \(\mathbf {I}-\Delta \) in \(\mathbf {X}\) with the Neumann boundary condition. As \(\mathcal {F}(d_1, d_2, \lambda ; \cdot )\) is a compact perturbation of the identity operator, the Leray–Schauder degree \(deg(\mathcal {F}(d_1, d_2, \lambda ; \cdot ), \Lambda , 0)\) is well defined from Theorem 4.6, and by the homotopy invariance, it is constant for all \(\lambda \ge \sigma \). Direct computation gives

$$\begin{aligned} \mathcal {F}_{\mathbf {u}}(d_1,d_2,\lambda ; e^*)=\mathbf {I}-(\mathbf {I}-\Delta )^{-1} [\Phi _{\mathbf {u}}^{-1}(e^*)G_{\mathbf {u}}(e^*)+\mathbf {I}]. \end{aligned}$$

If \(\mathcal {F_{\mathbf {u}}}(d_1,d_2,\lambda ; e^*)\) is invertible, i.e. 0 is not an eigenvalue \(\mathcal {F_{\mathbf {u}}}(d_1,d_2,\lambda ; e^*)\), then the Leray–Schauder Theorem (Theorem 2.8.1 in [46]) implies that

$$\begin{aligned} index(\mathcal {F}(d_1,d_2,\lambda ;e^*))=(-1)^{\gamma }, \end{aligned}$$

where \(\gamma =\sum M_{\beta }\) and \(M_{\beta }\) is the multiplicity of any negative eigenvalue \(\beta \) of \(\mathcal {F_{\mathbf {u}}}(d_1,d_2,\lambda ; e^*)\). The \(deg(\mathcal {F}(d_1, d_2, \lambda ; \cdot ), \Lambda , 0)\) is then equal to the summation of the indexes over all solutions to \(\mathcal {F}=0\) in \(\Lambda \).

To calculate \(\gamma \), we firstly define

$$\begin{aligned} \begin{aligned} \widetilde{H}(d_1,d_2,\lambda ;\mu )&=det [\mu \mathbf {I}-\Phi _{\mathbf {u}}^{-1}(e^*)G_{\mathbf {u}}(e^*)]\\&=\dfrac{1}{d_1d_2}[d_1d_2\mu _i^2-A(\lambda )d_2 \mu _i-B(\lambda )C(\lambda )]. \end{aligned} \end{aligned}$$
(4.15)

By the same arguments as in [52, 64], \(\beta \) is an eigenvalue of \(\mathcal {F_{\mathbf {u}}}(d_1,d_2,\lambda ; e^*)\) on \(X_j\) if and only if \(\beta (1+\mu _j)\) is an eigenvalue of the matrix

$$\begin{aligned} M(\mu _j):=\mu _j\mathbf {I}-\Phi _{\mathbf {u}}^{-1}(e^*)G_{\mathbf {u}}(e^*)= \left( {{\begin{array}{*{20}c} {\mu _j-\displaystyle \frac{A(\lambda )}{d_1}}&{}{-\displaystyle \frac{B(\lambda )}{d_1}}\\ {-\displaystyle \frac{C(\lambda )}{d_2}}&{}{\mu _j}\\ \end{array}}}\right) . \end{aligned}$$

Thus, \(\mathcal {F_{\mathbf {u}}}(d_1,d_2,\lambda ; e^*)\) is invertible if and only if the matrix \(M(\mu _j)\) is non-singular for all \(j\ge 0\). We also have that if \(\widetilde{H}(d_1,d_2,\lambda ;\mu _j)\not =0\), then \(\widetilde{H}(d_1,d_2,\lambda ;\mu _j)<0\) if and only if the number of negative eigenvalues of \(\mathcal {F_{\mathbf {u}}}(d_1,d_2,\lambda ; e^*)\) in \(X_j\) is odd. Then the following lemma (Theorem 6.1.1 in [64]) gives the explicit formula of calculating the index:

Lemma 4.7

If \(\widetilde{H}(d_1,d_2,\lambda ;\mu _i)\ne 0\) for all \(i\ge 0\), then

$$\begin{aligned} index (\mathcal {F}(d_1,d_2,\lambda ; e^*))=(-1)^{\gamma }, \;\;\;\;\;\gamma =\sum _{i\ge 0,\; \widetilde{H}(d_1,d_2,\lambda ;\mu _i)<0} m(\mu _i), \end{aligned}$$

where \(m(\mu _i)\) is the algebraic multiplicity of \(\mu _i\).

From Lemma 4.7 we see that to calculate the index of \(\mathcal {F}(d_1,d_2,\lambda ; e^*)\), the key step is to determine the range of \(\mu \) for which \(\widetilde{H}(d_1,d_2,\lambda ;\mu )<0\).

If \(i=0\), then \(\widetilde{H}(d_1,d_2,\lambda ;0)=\dfrac{-B(\lambda )C(\lambda )}{d_1d_2} =\dfrac{\lambda (1-\lambda )g'(\lambda )}{d_1d_2}>0\) for all \(\sigma \le \lambda <1\), which has no contribution to the sum \(\gamma \) in Lemma 4.7. We assume that \(i\ge 1\) in the following.

Indeed nonnegative roots to (4.15) exist if and only if \(-4d_1B(\lambda )C(\lambda )-d_2A^2(\lambda )<0\). Define \(\mu ^+(\lambda ,d_1,d_2)\) and \(\mu ^-(\lambda ,d_1,d_2)\) be the two roots of

$$\begin{aligned} \widetilde{H}(d_1,d_2,\lambda ;\mu )=0. \end{aligned}$$

Now by using the same method as in [52, 64] , we have the following existence result for the non-constant steady state solutions:

Theorem 4.8

Let \(S=\bigcup _{i=1}^{\infty }\{\mu _i\}\) be the set of all eigenvalues of \(-\Delta \) in \(H^1(\Omega )\), and let \(A(\lambda )\), \(B(\lambda )\) and \(C(\lambda )\) be defined as in Sect. 2. Assume that

$$\begin{aligned} \frac{d_2}{d_1}> \frac{-4B(\lambda )C(\lambda )}{A^2(\lambda )} \end{aligned}$$
(4.16)

and there exists \(i,j\in N_0\), such that

  1. (1)

    \(0\le \mu _j<\mu ^{-}(\lambda ,d_1,d_2)<\mu _{j+1}\le \mu _i<\mu ^{+}(\lambda ,d_1,d_2)<\mu _{i+1}\);

  2. (2)

    \(\sum _{k=j+1}^{i}m(\mu _k)\) is odd.

Then (4.1) has at least one non-constant positive solution \(\left( u(x),v(x)\right) \) when \(\sigma \le \lambda <1\).

Proof

Consider a mapping \(\hat{H}:\Lambda \times [0,1]\rightarrow C(\Omega )\times C(\Omega )\) by

$$\begin{aligned} \hat{H}(\mathbf {u},t)=(-\Delta +I)^{-1} \left( {{\begin{array}{*{20}c} {u+\left( \dfrac{1-t}{d^*}+\dfrac{t}{d_1}\right) u(1-u)-g(u)v}\\ {v+\left( \dfrac{1-t}{d^*}+\dfrac{t}{d_2}\right) v\left( -d+g(u)\right) }\\ \end{array}}}\right) , \end{aligned}$$

where \(d^*\) is defined as in Theorem 4.4. It is easy to see that solving (4.1) is equivalent to find a fixed point of \(\hat{H}(\cdot ,1)\) in \(\Lambda \). According to the choice of \(d^*\) in Theorem 4.4, we have that \(e^*=(\lambda ,v_{\lambda })\) is the only fixed point of \(\hat{H}(\cdot ,0)\).

Furthermore, we have

$$\begin{aligned} deg (I-\hat{H}(\cdot ,0),\Lambda ,e^*)=index (I-\hat{H}(\cdot ,0),e^*)=1. \end{aligned}$$

Since \(I-\hat{H}(\cdot ,1)=\mathcal {F}\), and if (4.1) has no other positive solutions except the constant one \(e^*\), we have

$$\begin{aligned} deg(I-\hat{H}(\cdot ,1),\Lambda ,(0,0))=index (\mathcal {F},e^*)=(-1)^{\sum _{k=j+1}^{i}m(\mu _k)}=-1. \end{aligned}$$

On the other hand, from the homotopy invariance of the Leray–Schauder degree, we have

$$\begin{aligned} 1=deg (I-\hat{H}(\cdot ,0),\Lambda ,(0,0))=deg(I-\hat{H}(\cdot ,1),\Lambda ,(0,0))=-1. \end{aligned}$$

which is a contradiction. Therefore, there exists at least one non-constant positive solution \(\left( u(x),v(x)\right) \) to (4.1). \(\square \)

The conditions (1) and (2) in Theorem 4.8 defines a region in the parameter space \(\{(\lambda ; d_1; d_2)\}\) for which a non-constant solution to (4.1) exists. This parameter region is usually a union of smaller connected components. When fixing all other parameters but freeing one, the parameter set is usually a union of non-overlapping intervals. This can be seen in the following corollary.

Corollary 4.9

Let \(d (or \lambda ), d_1\) be fixed so that (4.16) holds. Define

$$\begin{aligned} d_2^n=\dfrac{B(\lambda )C(\lambda )}{d_1\mu _n^2-A(\lambda )\mu _n} \end{aligned}$$

for some \(n\in \{n\in \mathbb {N}:d_1\mu _n-A(\lambda )<0\}\). Assume that each of \(\mu _j\) has odd multiplicity for \(j\in M\) and the set \(\{d_2^n:n\in \mathbb {N}, d_1\mu _n-A(\lambda )<0 \}\) can be relabeled to \(\{\widehat{d_2^n}:n\in \mathbb {N}\}\) such that

$$\begin{aligned} d_2^*\le \widehat{d_2^1}<\widehat{d_2^2}<\cdots <\widehat{d_2^i}<\widehat{d_2^{i+1}}<\cdots , \end{aligned}$$

where \(\dfrac{B(\lambda )C(\lambda )}{d_1\mu -A(\lambda )\mu }\) achieves its minimum \(d_2^*\) for \(d_1\mu -A(\lambda )<0\). Then (4.1) has at least one non-constant solution for \(d_2\in \bigcup _{i\in \mathbb {N}}(\widehat{d_2^{2i}},\widehat{d_2^{2i+1}})\).

Proof

It is easy to see that \(\gamma \) is odd when \(d_2\in \bigcup _{i\in \mathbb {N}}(\widehat{d_2^{2i}},\widehat{d_2^{2i+1}})\). \(\square \)

4.3 Steady State Bifurcation and Stationary Patterns

In this section we will identify bifurcation points \(\lambda ^S\) along the branch of the constant steady states \(\{(\lambda ,\lambda ,v_{\lambda }):\lambda _1<\lambda <\lambda _2\}\) where non-constant steady state solutions bifurcate from. In this subsection, we assume that all eigenvalues \(\mu _i\) of \(-\Delta \) in \(H^1(\Omega )\) are simple, and denote corresponding eigenfunction by \(\phi _i(x)\). Note that this assumption always holds when \(n=1\) for domain \(\Omega =(0,\ell \pi )\) that for \(i\in {\mathbb N}_0\). From [67], we know that a bifurcation point \(\lambda ^S\) satisfies the following condition:

\(\mathbf{(H2)}\)::

there exists \(i\in {\mathbb N}_0\) such that

$$\begin{aligned} D_i(\lambda ^S)=0,\;\;T_i(\lambda ^S)\ne 0,\;\text { and }\; D_j(\lambda ^S)\ne 0,\; T_j(\lambda ^S)\ne 0\;\text { for }\;j\ne i; \end{aligned}$$

and

$$\begin{aligned} \displaystyle \frac{d}{d\lambda }D_i(\lambda ^S)\ne 0. \end{aligned}$$

It is well known that the first eigenvalue of \(-\Delta \) under the Neumann boundary is \(\mu _0=0\). Then \(D_0(\lambda )=\lambda (1-\lambda )g'(\lambda )\ne 0\) for any \(0<\lambda <1\). Moreover, \(D_n(\lambda )>0\) for \(\lambda \in (0, \lambda _{1}]\) or \(\lambda \in [\lambda _{2}, 1)\), hence we only consider \(n\in {\mathbb N}\) and determine the set

$$\begin{aligned} \Omega _2:=\{\lambda \in (\lambda _{1},\lambda _{2}):\;\text {for some}\;n\in {\mathbb N},\;\mathbf{(H_2)}\;\text {is satisfied}\}, \end{aligned}$$
(4.17)

when a set of parameters \((d,d_1,d_2)\) are given.

Now for the steady state bifurcation curve \(D_n(\lambda )=0\), we notice that it is equivalent to \(\tilde{D}(\lambda )= (a^2+\lambda ^2)D_n(\lambda )=0\) for \(\lambda \ge 0\). For fixed \(\mu _n\), \(\tilde{D}\) is a degree 3 polynomial of \(\lambda \), and for fixed \(\lambda \), it is a quadratic in p. Suppose \(S(\lambda )=d_2^2A^2(\lambda )+4d_1d_2B(\lambda )C(\lambda )>0\), which is equivalent to

$$\begin{aligned} \dfrac{d_1}{d_2}<\dfrac{(-2\lambda ^3+\lambda ^2-a^2)^2}{8ma^2(1-\lambda )\lambda ^2}. \end{aligned}$$
(4.18)

From Lemma 4.10, there exists at least two roots of \(S(\lambda )=0\), the minimal and maximal one are denoted by \(\lambda _1<\lambda _{-}<\lambda _{+}<\lambda _2\). Thus we can solve \(\mu _n\) from \(D_n(\lambda )=0\). Let

$$\begin{aligned} \begin{aligned} \mu =\mu _{\pm }(\lambda ):&=\displaystyle \frac{d_2A(\lambda )\pm \sqrt{d_2^2A^2(\lambda )+4d_1d_2B(\lambda )C(\lambda )}}{2d_1d_2}\\&=\dfrac{d_2A(\lambda ) \pm \sqrt{C(\lambda )(d_2^2\alpha (\lambda )-4d_1d_2d)}}{2d_1d_2}, \end{aligned} \end{aligned}$$
(4.19)

where \(\alpha (\lambda )=\dfrac{A(\lambda )^2}{C(\lambda )}=\dfrac{(-2\lambda ^3+\lambda ^2-a^2)^2}{2a^2(1-\lambda )(a^2+\lambda ^2)}\). It is mentioned that \(\mu _{\pm }(\lambda )\) exists only for

$$\begin{aligned} \lambda \in \Lambda _S=\{\lambda |\lambda _{-}<\lambda <\lambda _{+}: (4.18) \;\text {holds}\}. \end{aligned}$$

One can also see that the function \(D_n(\lambda )\) has no critical points in the first quadrant, hence the set \(\{(\lambda ,\mu _n)\in {\mathbb {R}}^2_+: D_n(\lambda )=0\}\) must a bounded connected smooth curve. We have the following basic property of the function \(\alpha (\lambda )\).

Lemma 4.10

For all \(\lambda \in (\lambda _1,\lambda _2)\), \(\alpha (\lambda )>0\); \(\alpha (\lambda _1)=\alpha (\lambda _2)=0\). \(\alpha '(\lambda _1+0)>0\), \(\alpha '(\lambda _2-0)<0\) and there exists a unique \(\lambda ^{\dag }\in (\lambda _1, \lambda _2)\) such that \(\alpha '(\lambda ^{\dag })=0\) and \(\alpha (\lambda ^{\dag })=\max _{\lambda _1<\lambda <\lambda _2}\alpha (\lambda )\).

Proof

From the expression of \(\alpha (\lambda )\) and \(A(\lambda _1)=A(\lambda _2)=0\), it is clearly that \(\alpha (\lambda _1)=\alpha (\lambda _2)=0\). By direct calculation, it follows that

$$\begin{aligned} \alpha '(\lambda )=\dfrac{A(\lambda )[2A'(\lambda )C(\lambda )-A(\lambda )C'(\lambda )]}{C(\lambda )^2}. \end{aligned}$$

Denote \(\widetilde{\alpha }(\lambda )=2A'(\lambda )C(\lambda )-A(\lambda )C'(\lambda )\). Since \(\widetilde{\alpha }(\lambda _1)=2A'(\lambda _1)C(\lambda _1)>0\) and \(\widetilde{\alpha }(\lambda _2)=2A'(\lambda _2)C(\lambda _2)<0\), there exists at least one root of \(\widetilde{\alpha }(\lambda )=0\) in \((\lambda _1,\lambda _2)\). Moreover, it can denote such \(\lambda \) as \(\lambda ^{\dag }\) such that \(\alpha (\lambda ^{\dag })=\max _{\lambda _1<\lambda <\lambda _2}\alpha (\lambda )\). \(\square \)

We can summarize the properties of \(\mu _{\pm }(\lambda )\) as follows:

Lemma 4.11

Suppose that \(a>0, m>0\) and the constants \(d_1, d_2\) satisfy (4.18). Let \(\mu _{\pm }(\lambda )\) be the functions defined in (4.19). Then there exists \(\lambda _1<\lambda _{-}<\lambda _{+}<\lambda _2\) such that \(\mu _{\pm }(\lambda )\) exists for \(\lambda \in \Lambda _S\). Moreover \(\mu _{+}(\lambda )\ge \mu _{-}(\lambda )\) and

$$\begin{aligned} \lim _{\lambda \rightarrow \lambda _+}\mu _{\pm }(\lambda )=\frac{A(\lambda _+)}{2d_1},\quad \quad \lim _{\lambda \rightarrow \lambda _{-}}\mu _{\pm }(\lambda )=\frac{A(\lambda _{-})}{2d_1}. \end{aligned}$$

Hence the steady state bifurcation curve \(\{D_n(\lambda ,\mu )=0:\mu \ge 0, \lambda \ge 0\}\) is a smooth curve connecting \((\lambda ,\mu )=\left( \lambda _{-},\frac{A(\lambda _{-})}{2d_1}\right) \), \((\lambda ,\mu )=\left( \lambda _{+},\frac{A(\lambda _{+})}{2d_1}\right) \). Moreover, \(\mu _{+}(\lambda )\) attains its maximum value \(M^{**}\) at \(\lambda ^{**}\in [\lambda _{-},\lambda _{+}]\) and \(\mu _{-}(\lambda )\) attains its minimum value \(M_{**}\) at \(\lambda _{**}\in [\lambda _{-},\lambda _{+}]\), thus the steady state bifurcation curve exists only for \(\mu \in [M_{**}, M^{**}]\).

From Lemma 4.11, if \(M_{**}>\mu _i=\mu >M^{**}\), then there no \(\lambda \in (\lambda _{-},\lambda _{+}]\) such that \(D_i(\lambda )=0\). But for any \(M_{**}\le \mu _i\le M^{**}\), there exists \(\lambda ^S_i\) such that \(D_i(\lambda ^S_i)=0\) and these \(\lambda _i^S\) are potential steady state bifurcation points. Note that from Lemma 4.11 in Sect. 4.1, for each given \(i\in {\mathbb N}\), there are at least two \(\lambda \) such that \(D(\lambda ,\mu _i)=0\).

On the other hand, it is possible that for some \(\lambda \in (\lambda _{-},\lambda _{+})\) and some \(i\ne j\), we have

$$\begin{aligned} \mu _j=\mu _{-}(\lambda ), \;\;\; \text { and } \;\; \mu _i=\mu _{+}(\lambda ). \end{aligned}$$
(4.20)

Then for this \(\lambda \), 0 is not a simple eigenvalue of \(L(\lambda )\) and we shall not consider bifurcations at such points. However from an argument in [67], for \(n=1\) and \(\Omega =(0,\ell \pi )\), there are only countably many \(\ell \), such that (4.20) occurs for some \(i\ne j\). For general bounded domains in \({\mathbb {R}}^n\), one can also show that (4.20) does not occur for generic domains.

Next we verify \(\displaystyle \frac{d D_i}{d\lambda }(\lambda _i^S)\ne 0\) if \(\lambda _i^S\in \Lambda _{S}\) and \(S(\lambda _i^S)\ne 0\). Indeed one has \(D_i'(\lambda )=-B(\lambda )C'(\lambda )-d_2 \mu _i A'(\lambda )\), and from the expression of \(\mu _{\pm }\),

$$\begin{aligned} \mu '_{\pm }(\lambda )=\dfrac{B(\lambda )C'(\lambda )+d_2A'(\lambda )\mu _{\pm }(\lambda )}{d_2(2d_1\mu _{\pm }(\lambda )-A(\lambda ))}. \end{aligned}$$

Therefore from Lemma 4.11, if \(\mu '_{\pm }(\lambda _i^S)\ne 0\), then \(\displaystyle \frac{d D_i}{d\lambda }(\lambda _i^S)\ne 0\) for \(\lambda _i^S\in \Lambda _{S}\) and \(S(\lambda _i^S)\ne 0\).

Summarizing the above discussion and using a general bifurcation theorem ([55]), we obtain the main result of this section on the global bifurcation of steady state solutions:

Theorem 4.12

Suppose that \(d,d_1,d_2>0\) are fixed. Let \(\Omega \) be a bounded smooth domain so that its spectral set \(S=\{ \mu _i\}\) satisfy that

[S1] :

All eigenvalues \(\mu _i\) are simple for \(i\ge 0\);

[S2] :

There exists \(l,k\in {\mathbb N}\) such that \(0=\mu _0<\cdots <\mu _{l-1}<M_{**}<\mu _l<\cdots <\mu _k<M^{**}<\mu _{k+1}\), where \(M_{**}\), \(M^{**}\) are constants depending on \(d,d_1,d_2\) which is defined in Lemma 4.11,

then for each \(l\le i\le k\), there exist at least two \(\lambda _{i,-}^S<\lambda _{i,+}^S\in (\lambda _{-},\lambda _{+})\) such that \(D(\lambda _{i,\pm }^S,\mu _i)=0\). If in addition, we assume

$$\begin{aligned} \lambda _{i}^S\ne \lambda _j^S, \;\;\; \text {for any }l\le i\ne j\le k, \text { and}\;\; S(\lambda _i^S)\ne 0, p'_{\pm }(\lambda _i^S)\ne 0 \text { for any } l\le i\le k, \end{aligned}$$
(4.21)

then

  1. 1.

    There is a smooth curve \(\Gamma _i\) of positive solutions of (4.1) bifurcating from \((\lambda ,u,v)=(\lambda ^S_i,\lambda ^S_i,v_{\lambda ^S_i})\), with \(\Gamma _i\) contained in a global branch \(\mathcal {C}_i\) of positive solutions of (4.1);

  2. 2.

    Near \((\lambda ,u,v)=(\lambda ^S_i,\lambda ^S_i,v_{\lambda ^S_i})\), \(\Gamma _i=\{(\lambda _i(s),u_i(s),v_i(s)): s\in (-\epsilon ,\epsilon )\}\), where \(u_i(s)=\lambda ^S_i+s a_i \phi _i(x)+s\psi _{1,i}(s)\), \(v_i(s)=\lambda ^S_i+s b_i \phi _i(x)+s\psi _{2,i}(s)\) for some \(C^{\infty }\) smooth functions \(\lambda _i, \psi _{1,i}, \psi _{2,i}\) such that \(\lambda _i(0)=\lambda ^S_i\) and \(\psi _{1,i}(0)=\psi _{2,i}(0)=0\); Here \((a_i,b_i)\) satisfies

    $$\begin{aligned} L(\lambda ^S_i)[(a_i,b_i)^{\top } \phi _i(x)]=(0,0)^{\top }. \end{aligned}$$
  3. 3.

    Either \(\overline{\mathcal {C}_i}\) contains another \((\lambda ^S_j,\lambda ^S_j,v_{\lambda ^S_j})\) for \(j\ne i\) and \(1\le j\le k\), or the projection of \(\overline{\mathcal {C}_i}\) onto \(\lambda -\)axis contains the interval \((0,\lambda ^S_{i})\).

Proof

The existence and uniqueness of \(\lambda _i^S\) follows from discussions above. Then the local bifurcation result follows from Theorem 3.2 in [67], and it is an application of a more general result Theorem 4.3 in [55].

For the global bifurcation, we apply Theorem 4.3 in [55]. After the change of variables:

$$\begin{aligned} w_1=u-\lambda ,\;\;w_2=v-v_{\lambda }, \end{aligned}$$

we define a nonlinear equation:

$$\begin{aligned} \begin{aligned}&F\left( \lambda ,\left( {{\begin{array}{*{20}c} {w_1}\\ {w_2}\\ \end{array} }}\right) \right) \\&\quad = \left( {{\begin{array}{*{20}c} {d_1\Delta w_1+\left[ (\lambda +w_1)(1-\lambda -w_1)-g(\lambda +w_1)(v_{\lambda }+w_2)\right] }\\ {d_2\Delta w_2+(v_{\lambda }+w_2)\left[ -d+g(\lambda +w_1)\right] }\\ \end{array} }}\right) , \end{aligned} \end{aligned}$$

with domain

$$\begin{aligned} V=\left\{ \left( \lambda ,\left( {{\begin{array}{*{20}c} {w_1}\\ {w_2}\\ \end{array} }}\right) \right) : 0<\lambda <1, \;\; w_1, w_2\in X\;\text {and}\;w_1+\lambda \ge 0,\;\;w_2+v_{\lambda }\ge 0\right\} . \end{aligned}$$

Then \(\{(\lambda ,0,0): 0<\lambda <1\}\) is a line of trivial solutions for \(F=0\) and Theorem 4.3 in [55] can be applied to each continuum \(\mathcal {C}_i\) bifurcated from \((\lambda _i^S,0,0)\). For each continuum \(\mathcal {C}_i\), either \(\overline{\mathcal {C}_i}\) contains another \((\lambda _j^S,0,0)\) or \(\mathcal {C}_i\) is not compact. (Here we do not make an extinction between the solutions of (4.1) and \(F=0\) as they are essentially same, hence we use \(\mathcal {C}_i\) for solution continuum for both equations.)

From Lemma 4.2, every solution (u, v) of (4.1) is bounded in \(L^{\infty }\), then it is also bounded in X from \(L^p\) estimates and Schauder estimates. Therefore, if \(\mathcal {C}_i\) is not compact, then \(\overline{\mathcal {C}_i}\) contains a boundary point \((\widetilde{\lambda }, \widetilde{w_1}, \widetilde{w_2})\).

  1. (a)

    If \(\widetilde{\lambda }=0\), then the projection of \(\overline{\mathcal {C}_i}\) onto \(\lambda -\)axis contains \((0,\lambda _i^S)\);

  2. (b)

    If \(\widetilde{\lambda }=1\), then Corollary 4.3 implies that \((\widetilde{\lambda }+\widetilde{w_1}, v_{\widetilde{\lambda }}+\widetilde{w_2})=(0,0)\) or (1, 0). But \((u,v)=(0,0)\) is not a bifurcation point since the linearization of (1.3) implies that the constant equilibrium (0, 0) is unstable. Hence \((\widetilde{w_1}+\widetilde{\lambda },\widetilde{w_2}+v_{\widetilde{\lambda }})\) must be in a form of (1, 0);

  3. (c)

    If \(0<\widetilde{\lambda }<1\), then there exists \(x_0\in \bar{\Omega }\) such that \((\widetilde{w_1}+\widetilde{\lambda })(x_0)=0\) or \((\widetilde{w_2}+v_{\widetilde{\lambda }})(x_0)=0\) since \(\widetilde{w_1}\) and \(\widetilde{w_2}\) are bounded from Theorem 4.6. The strong maximum principle implies that \((\widetilde{w_1}+\widetilde{\lambda })(x)\equiv 0\) or \((\widetilde{w_2}+v_{\widetilde{\lambda }})(x)\equiv 0\) for all \(x\in \Omega \). If \(v\equiv 0\), then \((\widetilde{\lambda }, u, v)\) is a solution in form \((\widetilde{\lambda }, 0, 0)\) or \((\widetilde{\lambda }, 1, 0)\). If \(u\equiv 0\), then \(v\equiv 0\) from maximum principle. Same as in (b), \((\widetilde{w_1}+\widetilde{\lambda },\widetilde{w_2}+v_{\widetilde{\lambda }})\) also must be in a form of (1, 0).

\(\square \)

Remark 4.13

We remark that one can indeed show that \(\lambda =\lambda _n^S\) and \(d_2=d_2^n\) defined in Corollary 4.9 are bifurcation points where non constant positive solutions stem out from the branch of constant solutions by using of the global bifurcation theorem in [55]. This would partially generalize the result in Theorem 4.12 where the eigenvalues \(\mu _i\) are assumed to be simple. However the result in Corollary 4.9 shows the existence of non constant solutions in some more specific parameter regions, which cannot be achieved in bifurcation results.