Introduction

Friction stir welding process

Friction Stir Welding, a relatively new welding process, was developed in 1991 at The Welding Institute (Cambridge, England). It is a process that, although in its development stage, has been successfully used to join pieces of materials with poor weldability, such as high strength aluminium alloys, some dissimilar metals and plastics. The FSW process has many advantages compared to conventional welding. The process uses a non-consumable tool, doesn’t need filler wire and, in many cases, gas shielding is not needed. The welding takes place in solid phase, below the melting point, thus improving the quality of the weld: the weld has very low distortion, almost no porosity and very good mechanical properties. However, despite its great use in industry, the mechanisms that govern the process are not yet known in detail.

The welding tool is very simple. It is composed of two metal cylinders: the shoulder and the pin. The pin can be cylindrical or slightly conical, and plain or threaded, thus promoting the transport of material. The shoulder is a greater cylinder placed onto the pin. Figure 1 presents a sketch of a cylindrical pin and shoulder.

Fig. 1
figure 1

Rotating tool

Full size image

Before the welding process starts, the two plates or sheets must be butted together. The plates have to be clamped onto a backing bar in a manner that prevents the abutting joint faces from being forced apart. The first step of the welding process is the heating of the material, by placing the pin onto the welding line and rotating it very fast (about 1000 revolutions per minute). Due to the friction, heat is generated, temperature of the plates is increased and the strength of the materials is reduced. Then the rotating pin is sunken into the sheets until the tool shoulder is in full contact with the sheets or plates surface, generating more friction and heating. Once the pin is completely inserted, it is moved with a small nutting angle in the welding direction. Due to the advancing and rotating effect of the pin and shoulder of the tool along the seam, an advancing side and a retreating side are formed and the softened and heated material flows around the pin to its backside where the material is consolidated to create a high-quality, solid-state weld. A schematic representation of the process is shown in Fig. 2.

Fig. 2
figure 2

Schematic representation of the FSW

Full size image

The rotation of the tool has two objectives: on one hand it generates, due to the friction, the necessary heat to reach high temperatures so as to soften both materials. However, the temperature never reaches the melting temperature, because when temperature increases the resistance of the material reduces, and so does the heat generated by friction.

The second objective of the rotation is the mixing of both solids, generating the welding line with a mixed new material. The rotation process also drags the materials of both plates, mixing them. When the pin has spiral form this mixing is more effective. Since the rotation speed is very high, the resultant material is very homogeneous.

The heat source is very localized, therefore only a small zone along the welding line is mixed and modified, the rest of material preserve the original properties. In fact, it is possible to separate the region in three zones: the most remote does not suffer any transformation (unaffected material), the region closer to the weld centre experience only a thermal process equivalent to the one that would suffer in a standard welding process (heat affected zone), and in the zone under the tool (thermo-mechanically affected zone) the material has been plastically deformed by the friction stir welding tool, and the heat from the process will also have exerted some influence on it. The microstructure of the material placed in this latter zone is modified, being able in occasions manage to re-crystallize.

Numerical simulation of friction stir welding

In this paper we focus on the numerical simulation of the process, rather than the experimental characterization. From the numerical point of view, such a process presents several challenging difficulties. First of all, the extremely large deformations present during the process, although very localized in a region around the pin, always introduce numerical problems. Second, there is a strong coupling between these large deformations and heat generation, that in turn affects the behaviour of the material. Last, it is important to notice the difficulty of simulating the FSW of two plates of different materials.

Up to our knowledge, few numerical attempts have been made in order to simulate this process, and almost all of them are based on the Finite Element Method. On the first attempts [1] only the evolution of the temperature in the stationary phase was simulated. The steady-state of the FSW process can be simulated easily using Eulerian approaches [2], including complex thermomechanical models, but the transient phase can not be solved using this method. In [3] a Lagrangian approach with intensive remeshing is employed. Similar approaches have been employed in [4] and [5]. Remeshing, however, is well-known as a potential source of numerical diffusion in the results. Other authors use arbitrary Lagrangian Eulerian (ALE) formulations [6], studying and taking into account the diffusion related to the mapping inherent to this numerical method. Extended finite element methods (X-FEM) could also be employed to this end, see for instance [7].

In this paper we employ a somewhat different approach based on the use of meshless methods. Meshless methods allow for a Lagrangian description of the motion, while avoiding the need for remeshing (a review of the state of the art in meshless methods can be consulted in [8]). Thus, the nodes, that in our implementation transport all the variables linked to material’s history, remain the same throughout the simulation. Mappings between old and new meshes are not necessary and hence the avoidance of numerical diffusion.

Among the many meshless methods available nowadays, we have chosen the Natural Element Method [9, 10]. It possesses some noteworthy advantages over other meshless methods that will be described on the following section.

The natural element method

Essentially, the NEM is a Galerkin procedure that relies on natural neighbour interpolation to construct the trial and test functions characteristic of this method. Prior to the definition of these interpolation functions, it is necessary to introduce some basic geometrical entities that are needed for further developments.

Voronoi/Dirichlet diagrams

Consider a model composed by a cloud of points \(\boldsymbol{N}=\{n_1, n_2, \ldots, n_m \}\subset \mathbb{R}^d\), for which there is a unique decomposition of the space into regions such that each point within these regions is closer to the node to which the region is associated than to any other in the cloud. This kind of space decomposition is called a Voronoi diagram (also Dirichlet tessellation) of the cloud of points and each Voronoi cell is formally defined as (see Fig. 3):

$$\label{eq:1} T_I=\{ \boldsymbol{x} \in \mathbb{R}^{d} :d( \boldsymbol{x}, \boldsymbol{x}_I)<d( \boldsymbol{x}, \boldsymbol{x}_J) \; \forall \; J\neq I\}, $$
(1)

where d(·,·) is the Euclidean distance function.

Fig. 3
figure 3

Delaunay triangulation and Voronoi diagram of a cloud of points

Full size image

The dual structure of the Voronoi diagram is the Delaunay triangulation, obtained by connecting nodes that share a common (d − 1)-dimensional facet. While the Voronoi structure is unique, the Delaunay triangulation is not, there being some so-called degenerate cases in which there are two or more possible Delaunay triangulations (consider, for example, the case of triangulating a square in 2D, as depicted in Fig. 3 (right)). Another way to define the Delaunay triangulation of a set of nodes is by invoking the empty circumcircle property, which means that no node of the cloud lies within the circle covering a Delaunay triangle. Two nodes sharing a facet of their Voronoi cell are called natural neighbours and hence the name of the technique.

Equivalently, the second-order Voronoi diagram of the cloud is defined as

$$\label{eq:2} \begin{array}{rcl} T_{IJ}&=&\{\boldsymbol{x} \in \mathbb{R}^d : d( \boldsymbol{x}, \boldsymbol{x}_I)<d( \boldsymbol{x}, \boldsymbol{x}_J)<d(\boldsymbol{x}, \boldsymbol{x}_K) \nonumber\\&& \times\, \forall \; J\neq I\neq K\}. \end{array} $$
(2)

Based on these definitions, different natural neighbour interpolation schemes have been proposed. In this paper we have used the so-called Sibson interpolation for velocities and Thiessen interpolation for pressure, following the analysis done in [11].

Thiessen interpolation

The simplest of the natural neighbour-based interpolants is the so-called Thiessen’s interpolant [12]. Its interpolating functions are defined as

$$\label{thiessen} \psi_I(\boldsymbol{x})={\Bigg \{ } \begin{array}{l} 1\quad \textnormal{ if }\boldsymbol{x}\in T_I \\[2pt] 0\quad \textnormal{ elsewhere} \\ \end{array}. $$
(3)

The Thiessen interpolant is a piece-wise constant function, defined over each Voronoi cell. It defines a method of interpolation often referred to as nearest neighbour interpolation, since a point is given a value defined by its nearest neighbour. Although it is obviously not valid for the solution of second-order partial differential equations, it can be used to interpolate the pressure in formulations arising from Hellinger-Reissner-like mixed variational principles, as proved in [11].

Sibson’s interpolation

The most extended natural neighbour interpolation method is the Sibson interpolant [13, 14]. Consider the introduction of the point \(\boldsymbol{x}\) in the cloud of nodes. Due to this introduction, the Voronoi diagram will be altered, affecting the Voronoi cells of the natural neighbours of \(\boldsymbol{x}\). Sibson [13] defined the natural neighbour coordinates of a point \(\boldsymbol{x}\) with respect to one of its neighbours I as the ratio of the cell T I that is transferred to T x when adding \(\boldsymbol{x}\) to the initial cloud of points to the total volume of T x . In other words, if \(\kappa(\boldsymbol{x})\) and \(\kappa_I(\boldsymbol{x})\) are the Lebesgue measures of T x and T xI respectively, the natural neighbour coordinates of \(\boldsymbol{x}\) with respect to the node I is defined as

$$ \label{ffor} \phi_I(\boldsymbol{x})=\frac{\kappa_I(\boldsymbol{x})}{\kappa(\boldsymbol{x})}. $$
(4)

In Fig. 4 the shape function associated to node 1 at point \(\boldsymbol{x}\) may be expressed as

$$\label{eq:5} \phi_1(\boldsymbol{x})=\frac{A_{abfe}}{A_{abcd}}. $$
(5)
Fig. 4
figure 4

Definition of the Natural Neighbour coordinates of a point \(\boldsymbol{x}\)

Full size image

Sibson’s interpolation scheme possesses the usual reproducing properties for this class of problems, i.e., verify the partition of unity property (constant consistency), linear consistency (and therefore are suitable for the solution of second-order PDE). Other interesting properties such as the Kronecker delta property [9] and linear interpolation on the boundary [15, 16] are also verified by the NEM.

Governing equations

FSW processes involve large deformation and high velocities of the rotating pin that make the elastic strains to be negligible. Although an elastic recovery exists, it is obvious negligible as a first approximation. The obvious advantage of this assumption is that the material can then be modeled as a non-Newtonian (visco-plastic) fluid. This assumption is known as the flow formulation in the forming processes community [17]. Thus, the essential variables of the problem will be velocities and pressures, instead of displacements and pressures.

The stresses will be, under this assumption,

$$\label{eq:6} \boldsymbol{\sigma}=2\mu\boldsymbol{d}-p\boldsymbol{I} $$
(6)

where \(p=-tr(\boldsymbol{\sigma})/3\), \(\boldsymbol{d}\) is the strain rate tensor and \(\boldsymbol{I}\) stands for the second-order identity tensor. According with the flow formulation, the viscosity μ can be rewritten as

$$\label{eq:7} \mu=\frac{\sigma_y}{3\bar d} $$
(7)

where σ y is the yield stress, which can depend on the strain, the strain rate, the temperature and other variables, and \(\bar d= \sqrt{\frac{2}{3}\boldsymbol{d}:\boldsymbol{d}}\) is the equivalent strain rate.

We consider, for the plates being welded, the balance of momentum equations without inertia and mass terms and the assumed incompressibility of a von Mises-like flow:

$$\label{equil} \nabla{\boldsymbol\sigma}=\boldsymbol 0,\;\;\;\; \nabla{\boldsymbol{v}}=0 $$
(8)

where \(\boldsymbol{v}\) represents the velocity field. Velocities are interpolated by means of the Sibson shape functions, while pressures are considered constant over the whole Voronoi cell associated to each node and thus interpolated with Thiessen shape functions.

Temperature is also an essential variable in the problem. To study the evolution and distribution of temperatures, the rigid-plastic material equations are coupled with the following heat transfer equations:

$$\label{heat} \nabla (k\nabla T) + \dot{r} -(\rho c_p \dot{T}) =0 $$
(9)

where k denotes the thermal conductivity, \(\dot{r}\) the heat generation rate, ρ the specific density and c p the specific heat of the metal. The rate of heat generation due to plastic deformation is calculated as

$$\label{heatrate} \dot{r} = \beta \boldsymbol{\sigma}:\boldsymbol{d} $$
(10)

where β represents the fraction of mechanical energy transformed to heat and is assumed to be 0.9 [18].

Together with these equations, appropriate boundary conditions are considered:

$$\label{eq:11} \boldsymbol{\sigma}\cdot \boldsymbol{n} = \overline{\boldsymbol{t}} \textnormal{ on }\Gamma_t $$
(11)
$$\label{eq:12} \boldsymbol{v} = \overline{\boldsymbol{v}}\textnormal{ on }\Gamma_v $$
(12)

where Γ t and Γ v represent, respectively, the part of the boundary \(\Gamma = \partial \Omega\) where tractions and velocities are prescribed. In addition, along the boundary, either temperature or heat flux is prescribed.

The coupling has been made through a block-iterative semi-implicit method, together with a fixed-point algorithm to treat the non-linear coupling (see Fig. 5). This strategy has also been employed successfully in previous works of the authors [19]. Numerical integration of the weak form of the problems given by Eqs. 8 and 9 is achieved through the use of three-point quadrature rules on the Delaunay triangles for simplicity, although more sophisticated techniques, such as Stabilized Conforming Nodal Integration (SCNI), could equally be used.

Fig. 5
figure 5

Staggered implicit thermo-mechanical procedure

Full size image

Examples and numerical results

The aim of the examples shown here is to check the ability of the NEM to solve different difficulties related to the simulation of the FSW process.

The first aspect to consider is the extremely high strain which would distort the mesh if the simulation is done using FEM. At the beginning of the simulations, a more or less regular cloud of nodes is used, but the same cloud of nodes, which will become very irregularly distributed, will be used during the whole process. An updated Lagrangian procedure is used in all simulations.

The nonlinear thermomechanical behaviour is another source of complexity. Then, on the first example real material properties, corresponding to aluminium AA7075, are used to check the robustness of the NEM procedure. The simulation will also show the influence of the temperature evolution on the mechanical properties.

A third aspect to consider is the possibility of welding plates of different materials. Material properties are here associated to the nodes of the model. On the second example, two dissimilar materials are used (namely, aluminium and copper), and the path of the nodes close to the pin is studied.

On both the examples, a very simple two-dimensional plane stress model is used. This simple assumption has obvious consequences on the final result, since it has been experimentally observed that fully three-dimensional material flow exists surrounding the pin. Nevertheless, for the time being, plane stress assumption is judged necessary to firstly validate the proposed model and the associated numerical technique.

The pin is considered cylindrical and rigid. Despite that the usual friction coefficient between the pin and the sheet has been established to be around 0.5, we have considered here perfect adhesion between them. This will overestimate the strain produced by the pin rotation. In addition, no micro-mechanical model has been considered for the aluminium, i.e., no re-crystallization phenomena is being considered, that could eventually take into account the heat affected zone.

Thermomechanical simulation

As said before, the material chosen for both plates of this first example corresponds to aluminium AA7075, whose properties are taken from [4]:

$$\label{const} \mu =\frac{K T^A \bar{d}^{n-1}}{3} $$
(13)

with \(K=2.69\cdot 10^{10}\frac{N}{mm^2}\), A = − 3.3155, n = 0.1324, and the following thermal properties:

$$\label{eq:14} k=180\frac{N}{sK},\;\; \rho c_p=2.39\frac{N}{mm^2K} $$
(14)

The pin has a diameter of 3 mm and rotates at \(1000\frac{rev}{min}\). The time step increment used in the simulation is 5 ×10 − 4 s. Temperature at the beginning of the process is 298K.

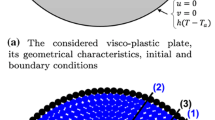
Each slab is a rectangle of 6 ×12 mm2 of aluminium AA7075. The geometry, the initial cloud of 240 nodes and its corresponding Delaunay triangulation can be seen at Fig. 6.

Fig. 6
figure 6

Delaunay triangulation at initial step

Full size image

Since no remeshing is done, the node distribution can become highly irregular, but this fact does not affect the accuracy of the results, as mentioned before. Figure 7 shows a detail of the node distribution, the Delaunay triangulation and the temperature distribution after some calculation time. The high distortion of the Delaunay triangulation of the nodes can be noticed.

Fig. 7
figure 7

Detail of the temperature distribution (K) on an irregular cloud of nodes. 50-th time step

Full size image

In Fig. 8 the evolution of the temperature is shown at different time steps. The simulation can be maintained for very long times, but we show some representative snapshots of intermediate states. In Figs. 9 and 10 the equivalent strain rate and the viscosity are depicted at the same time steps. In all cases results show an overall good qualitative agreement with the experiments. Note that although the displacement of the pin is small at the early stages of the simulation, it is still present in the simulations.

Fig. 8
figure 8

Temperature evolution. a 1st time step b 100th time step c 400th time step

Full size image
Fig. 9
figure 9

Equivalent strain rate evolution. a 1st time step b 100th time step c 400th time step

Full size image
Fig. 10
figure 10

Viscosity evolution a 1st time step b 100th time step c 400th time step

Full size image

FSW of two plates of different materials

The most important advantage of the presented technique is the possibility of tracking the material particles throughout the process. In this example two plates of different materials, both with viscosity defined by Eq. 13, are used.

The pin has a diameter of 6 mm, rotates at \(1000\frac{rev}{min}\) and advances at \(1\frac{mm}{s}\). The time step increment used in the simulation is again 10 − 4 s.

In Figs. 11, 12 and 13, several steps of the simulation are shown. Nodes of each plate have been labelled, and are depicted in blue and red, respectively, in the figures that follow. This tracking can be performed since no addition or deletion of nodes is performed (although it is possible, if refinement is necessary for different reasons). In this way, the numerical diffusion provoked by continuous remeshing is avoided. In addition, if some kind of nodal integration is performed (see [20]), all history variables can be linked to the nodes, thus avoiding any projection procedures. In this technique, the material associated to each Voronoi cell is assumed to be that of the node.

Fig. 11
figure 11

Material distribution at 50th time step

Full size image
Fig. 12
figure 12

Material distribution at 150th time step

Full size image
Fig. 13
figure 13

Material distribution at 6000th time step

Full size image

Throughout Figs. 11 to 13 an helical distribution of the mixing materials is observed. This is in good agreement with the experiments performed. In Fig. 14 the result of an experiment with plasticine and a purely cylindrical tool can be observed. Although the absence of the shoulder provokes a big defect in the welding, the purpose of the experiment is to show how the tool removes material from the lower part of the image (advancing side) and places it in the upper part, thus generating onion ring-like structures, similar to those observed in the simulation.

Fig. 14
figure 14

Experiments with plasticine and cylindrical tool. Depth of the layers formed by the pin

Full size image

This can also be observed from the experiments made with two plates of aluminium 1050 and copper b1, whose final result is shown in Fig. 15. In Fig. 16 the mixing of different layers of aluminium and copper can be noticed at different scales. Obviously, the numerical technique presented here is not able to obtained this different multi-scale mixing, but shows a good accordance with the macro scale of the problem.

Fig. 15
figure 15

Final result of the welding of two plates composed by Al 1050 and Cu b1

Full size image
Fig. 16
figure 16

Micrographs of the different microstructures obtained by stirring Al 1050 and Cu b1

Full size image

Figures 17, 18 and 19 present the equivalent strain rate distribution at three time steps. It can be seen that the mixture of the nodes modify the material properties and thus the velocity distribution around the pin.

Fig. 17
figure 17

Equivalent strain rate at 50th time step

Full size image
Fig. 18
figure 18

Equivalent strain rate at 150th time step

Full size image
Fig. 19
figure 19

Equivalent strain rate at 6000th time step

Full size image

Concerning the computational cost of the simulations, it can be said that NEM procedures are much costly than equivalent FEM formulations, in a ratio from 2 to 4 times slower. A thorough analysis of timings and computational cost of FEM techniques in a similar environment can be found in [21]. Nevertheless, the most important part of the time employed in solving the problem is spent in Newton-Raphson iterations, which consume similar CPU times for both techniques.

Conclusions

In this paper we have presented the results of the first attempt—up to our knowledge—of applying meshless methods to the simulation of Friction Stir Welding processes. The use of meshless methods (in particular, the Natural Element Method) was motivated by the need to avoid extensive remeshing procedures associated with the large deformations present in this kind of processes.

Although the presented results can be considered as very preliminary, and further refinement of the models (especially relative to contact and friction) is needed, we can conclude that the Natural Element Method constitutes a valuable tool for the simulation of such a complex forming process. In particular, it has been shown how a large number of time steps (up to six thousands) have been accomplished maintaining the initial set of nodes. Despite the high distortion of the triangulation, good qualitative agreement with previous results, both experimental and numerical, has been found.

Note, however, that the true interest of the proposed technique relies in its extension to three-dimensional settings, where the true complexity of the process should be analyzed. This constitutes the ongoing work of the authors.