A 2D mechanical–thermal coupled model to simulate material mixing observed in friction stir welding process

Abstract

The aim of our work is the numerical modeling of two dimensional mechanical–thermal material mixing observed in stir welding process using a high order algorithm. This algorithm is based on coupling a meshless approach, a time discretization, a homotopy transformation, a development in Taylor series and a continuation method. The performance of the proposed model is the consideration of large deformations in the formulation of the posed problem. For the spatial treatment, we use the moving least squares approximation which will be applied directly to the strong form formulation of conservation equations. Each collocation point holds mechanical–thermal variables. The high order algorithm and the homotopy transformation allow reducing the number of tangent matrices to decompose and to avoid iterative procedure. Comparisons with the classical iterative solver (Jamal et al. in J Comput Mech 28:375–380, 2002) are performed. Numerical results reveal that a few number of matrix factorization is needed with the proposed approach, decreasing the computation time.

1 Introduction

Numerical simulation of friction stir welding (FSW) process is a major challenge for researchers because of the complexity of the process and the coupled physical phenomena [19]. Indeed, this process involves the coupling between mechanical, thermal and metallurgical problems. In recent literature, contributions concerning numerical modeling of FSW can be classified into two main classes. The first one uses Eulerian formulations and is based on fluid dynamics codes to study material flow around the welding tool. Usually these studies are conducted to search for stationary solution which excludes cases of welding tools with complex geometries. A second class uses the finite element method in Lagrangian formulation. It can deal with unsteady state problems considering more or less complex geometries of the tool. However, these methods suffer from the complexity of the formulation which has to manage the large deformations induced in the vicinity of the tool by re-meshing this area or using the arbitrary Lagrangian Eulerian formalism and also these methods require very large computation time making their use less convenient for the engineer. To overcome this drawback, some contributions proposed to address the problem using mesh-free methods. The aim is to avoid remeshing and then to reduce diffusion problems in the numerical solution [4, 6, 21, 22]. Some works have been done for the 3D simulation of friction stir welding using natural element method [1, 2], particle tracing method [16], finite element method [8] and particle method [9].

In a previous paper [20], we have proposed a 2D mechanical formulation to model material mixing using a meshless method and a high order algorithm which is applied on a strongly formulation. Indeed, we have chosen to use the moving least squares (MLS) approximation which has been used for the first time to construct smooth functions for a scatter. This method allows to build a local approximation of the solution using low degree of polynomials whose coefficients depend on spatial coordinates. However, in the case of the element-free Galerkin method (EFG), the MLS approximation is used within a weak formulation [11, 18].

In the work [20], we have applied the algorithm on a strong form formulation of the mechanical problem to avoid difficulties related to numerical integration. As the problem is temporal, the classical implicit Euler scheme is used for the time discretization. During material mixing, the deformations are important. We therefore used a nonlinear constitutive law dependent on the strain rate. To reduce the computation time and the number of tangent matrix decompositions, we have proposed a high order algorithm. After the time discretization, the obtained nonlinear problem is transformed using the homotopy technique which consists in introducing an arbitrary matrix and a scalar parameter. If this homotopy parameter is set to zero, we obtain an easy problem to solve and when this parameter is equal to one we recover the initial problem before homotopy transformation. The solution of the modified nonlinear problem is sought by expanding the unknowns in the form of Taylor series with respect to homotopy parameter. Our experience shows that when the arbitrary matrix introduced in the modified problem is chosen judiciously, only one tangent matrix decomposition is required to compute tens of time steps which allows one to reduce significantly the total computation time.

In the present work, we propose to extend the application field of the model used in [20] to the case of 2D mechanical–thermal material mixing observed in friction stir welding process. We present the thermo-mechanical problem under a strong formulation. The coupling between the mechanical and thermal problem is due to the heat source and the law giving the viscosity depending on the temperature and the equivalent strain rate. According to these relations, the considered problem is strongly nonlinear. For the spatial discretization, we use the MLS approximation which will be applied directly to the strong form formulation. Each collocation point holds mechanical and thermal unknowns. The high order algorithm and the homotopy transformation used in [20] allow reducing the number of tangent matrices to decompose and to avoid iterative procedure. Let us recall that in the used algorithm, we did not need any iterative corrections.

The layout of this paper is as follows. In Sect. 2, we present the governing equations of the mechanical–thermal problem. We consider sticking conditions for the contact interface between welding tool and piece. In Sect. 3, we give details of the used algorithm. To search the solution in the form of power series, the different equations of the nonlinear problem are transformed in a quadratic framework. This allows the algorithm to be optimal. After that a time discretization is applied and the obtained nonlinear problem is discretized using MLS approximation. Thereafter the homotopy technique and the development in Taylor series are used in continuation procedure. In Sect. 4, numerical application is proposed and a comparison with an implicit iterative algorithm [10] based on the MLS approximation is performed to assess the validity of our algorithm. Finally, some conclusions are presented in Sect. 5.

2 Governing equations

The general laws of physics, especially the mechanics of deformable media, are based on the principle of conservation laws. This principle expresses stock of influences affecting the physical quantities such as quantity of motion, mass and energy to establish equations to solve. The resulting problem is described by the two first conservation laws for an incompressible material including:

$$\begin{aligned} \left\{ \begin{array}{l} \rho \dot{V}={\rm div}(\sigma )\\ {\rm div}(V)=0 \end{array} \right. , \end{aligned}$$

(1)

where $\rho$ is the material density, V is the velocity vector of components u and v, $\dot{V}= \partial {V}/\partial {t}$, $\sigma$ is the stress tensor and the gravity is neglected. The constitutive law is given by the deviatoric stress tensor under the following form:

$$\begin{aligned} S=2\mu \dot{\epsilon } , \end{aligned}$$

(2)

where $\mu$ is the material dynamic viscosity and $\dot{\epsilon }$ is the strain rate tensor defined as:

$$\begin{aligned} \dot{\epsilon }=\frac{1}{2}({}^t\nabla {V}+\nabla {V}) \end{aligned}$$

(3)

The equation of energy conservation, in our case, is written as follows:

$$\begin{aligned} \rho {C_{\rm p}}\dot{T}={\rm div}(k_{\rm c}\nabla T)+q_{\rm v} \end{aligned}$$

(4)

where T is the temperature, $\dot{T}=\partial {T}/\partial {t}$, $C_{\rm p}$ is the coefficient of specific heat, ${k_{\rm c}}$ is the thermal conductivity of the material and $q_{\rm v}$ denotes the volume source. This volume source $q_{\rm v}$ in the heat equation corresponding to the mechanical power dissipated per unit volume. It can be written from the velocity field of the mechanical problem as follows:

$$\begin{aligned} q_{\rm v}=\beta S:\dot{\epsilon } \end{aligned}$$

(5)

where $\beta$ is a coefficient taken equal to 0.9. Taking into account the relation (2), the Eq. (5) can be written as follows:

$$\begin{aligned} q_{\rm v}=3\beta \mu \bar{\dot{\epsilon }}^2 \end{aligned}$$

(6)

where $\bar{\dot{\epsilon }}$ is the equivalent strain rate given by:

$$\begin{aligned} \bar{\dot{\epsilon }}=\sqrt{\frac{2}{3}\dot{\epsilon }:\dot{\epsilon }} \end{aligned}$$

(7)

For the dynamic viscosity, we choose a power law as in [3] given by:

$$\begin{aligned} \mu =\frac{1}{3}{K}T^A{\bar{\dot{\epsilon }}}^{n-1} \end{aligned}$$

(8)

where K, A and n are the material properties. To satisfy the condition of incompressibility numerically in the Eq. (1), we introduce, in general, a pressure term penalized by a large factor noted $\lambda$. This means that the incompressibility condition (1) is replaced by a viscous law [17]:

$$\begin{aligned} p=-\lambda {\rm Tr}(\dot{\epsilon }) \end{aligned}$$

(9)

where ${\rm Tr}(.)$ denotes the trace. The stress tensor $\sigma$, under this assumption, is given by:

$$\begin{aligned} \sigma =\lambda {\rm Tr}(\dot{\epsilon })I+2\mu \dot{\epsilon } \end{aligned}$$

(10)

where I is the unity tensor. Finally, the mechanical–thermal equations and the constitutive laws can be written as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \rho \dot{V} = {\rm div}(\sigma )\\ \rho C_{\rm p}\dot{T} = {\rm div}(k_{\rm c}\nabla T)+q_{\rm v}\\ \sigma =\lambda {\rm Tr}(\dot{\epsilon })I+2\mu \dot{\epsilon }\\ \dot{\epsilon } = \frac{1}{2}({}^t\nabla {V}+\nabla {V})\\ \bar{\dot{\epsilon }}= \sqrt{\frac{2}{3}\dot{\epsilon }:\dot{\epsilon }}\\ \mu =\frac{1}{3}KT^A{\bar{\dot{\epsilon }}}^{n-1}\\ q_{\rm v} = 3\beta \mu {\bar{\dot{\epsilon }}}^{2} \end{array} \right. \end{aligned}$$

(11)

The Eq. (11) will be completed by the boundary and initial conditions of mechanical and thermal type.

3 The proposed algorithm

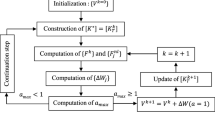
To solve the problem (11), we propose, in this work, a high order implicit algorithm which combines: a temporal implicit scheme, a meshless approach, a homotopy transformation, a development in Taylor series and a continuation procedure. With the aim to write the problem (11) in quadratic form, we introduce the following changes of variables and the differential forms:

$$\begin{aligned} \left\{ \begin{array}{l} \alpha = T^A \\ \gamma = {\bar{\dot{\epsilon }}}^{n-1} \\ \varphi = {\bar{\dot{\epsilon }}}^{2}\\ T {\rm d}\alpha = A\alpha {\rm d}T\\ {\bar{\dot{\epsilon }}} {\rm d}\gamma = (n-1)\gamma {\rm d}{\bar{\dot{\epsilon }}} \end{array} \right. \end{aligned}$$

(12)

Once the strongly nonlinear relationships of the problem (11) have been transformed into quadratic equations, it is easy to develop the unknown in Taylor series and to calculate numerically these series to a high order. Thus, the quadratic problem is written as:

$$\begin{aligned} \left\{ \begin{array}{l} \rho \dot{V} = {\rm div}(\sigma )\\ \rho C_{\rm p}\dot{T} = {\rm div}(k_{\rm c}\nabla T)+q_{\rm v}\\ \sigma = \lambda {\rm Tr}(\dot{\epsilon })I+2\mu \dot{\epsilon }\\ \dot{\epsilon } = \frac{1}{2}({}^t\nabla {V}+\nabla {V})\\ \bar{\dot{\epsilon }}^2 = \frac{2}{3}\dot{\epsilon }:\dot{\epsilon }\\ \mu = \frac{K}{3}\alpha \gamma \\ T {\rm d}\alpha = A\alpha {\rm d}T\\ {\bar{\dot{\epsilon }}} {\rm d}\gamma = (n-1)\gamma {\rm d}{\bar{\dot{\epsilon }}}\\ q_{\rm v} = 3\beta \mu \varphi \\ \varphi = \bar{\dot{\epsilon }}^2 \end{array} \right. \end{aligned}$$

(13)

3.1 Temporal implicit scheme

For solving the nonlinear unsteady problem (13), we use here the Euler implicit scheme widely used in the resolution of this problems. Using the Euler implicit scheme, the time discretization of the problem (13) leads to the following nonlinear system in terms of the new unknown at time $t^{k+1}=(k+1)\Delta {t}$:

$$\begin{aligned} \left\{ \begin{array}{l} \rho (V^{k+1}-V^{k})=\Delta {t}{\rm div}(\sigma ^{k+1})\\ \rho {C_{\rm p}}(T^{k+1}-T^{k})=\Delta {t}{\rm div}(k_{\rm c}\nabla T^{k+1})+\Delta {t}q^{k+1}_{\rm v}\\ \sigma ^{k+1}=\lambda {\rm Tr}(\dot{\epsilon }^{k+1})I+2\mu ^{k+1}\dot{\epsilon }^{k+1}\\ \dot{\epsilon }^{k+1}=\frac{1}{2}({}^t\nabla {V}^{k+1}+\nabla {V}^{k+1})\\ (\bar{\dot{\epsilon }}^{k+1})^2=\frac{2}{3}\dot{\epsilon }^{k+1}:\dot{\epsilon }^{k+1}\\ \mu ^{k+1}=\frac{K}{3}\alpha ^{k+1}\gamma ^{k+1}\\ T^{k+1} {\rm d}\alpha ^{k+1}=A\alpha ^{k+1} {\rm d}T^{k+1}\\ {\bar{\dot{\epsilon }}}^{k+1} {\rm d}\gamma ^{k+1}=(n-1)\gamma ^{k+1} {\rm d}{\bar{\dot{\epsilon }}}^{k+1}\\ q^{k+1}_{\rm v}=3\frac{\beta }{C_{\rm p}}\mu ^{k+1}\varphi ^{k+1}\\ \varphi ^{k+1}=(\bar{\dot{\epsilon }}^{k+1})^2 \end{array} \right. \end{aligned}$$

(14)

where $(.)^{k+1}$ represent the unknowns at time $t^{k+1}=(k+1)\Delta {t}$ with $\Delta {t}$ is the time step. We introduce the increments $\Delta V$, $\Delta T$, $\Delta \sigma$, $\Delta \dot{\epsilon }$, $\Delta \bar{\dot{\epsilon }}$, $\Delta \mu$, $\Delta q_{\rm v}$, $\Delta \alpha$, $\Delta \gamma$ and $\Delta \varphi$ as new unknowns of the problem (14) given by:

$$\begin{aligned} \left\{ \begin{array}{l} \Delta V=V^{k+1}-V^{k}\\ \Delta T=T^{k+1}-T^{k}\\ \Delta \sigma =\sigma ^{k+1}-\sigma ^{k}\\ \Delta \dot{\epsilon }=\dot{\epsilon }^{k+1}-\dot{\epsilon }^{k}\\ \Delta \bar{\dot{\epsilon }}=\bar{\dot{\epsilon }}^{k+1}-\bar{\dot{\epsilon }}^{k}\\ \Delta \mu =\mu ^{k+1}-\mu ^{k}\\ \Delta q_{\rm v}=q^{k+1}_{\rm v}-q^{k}_{\rm v}\\ \Delta \alpha =\alpha ^{k+1}_{\rm v}-\alpha ^{k}\\ \Delta \gamma =\gamma ^{k+1}-\gamma ^{k}\\ \Delta \varphi =\varphi ^{k+1}-\varphi ^{k} \end{array} \right. \end{aligned}$$

(15)

Taking account of the Eq. (15), the problem verified by new unknowns can be written as:

$$\begin{aligned} \left\{ \begin{array}{l} \rho \Delta V = \Delta t {\rm div}(\sigma ^{k}) + \Delta t {\rm div} (\Delta \sigma )\\ \rho {C_{\rm p}}\Delta T = \Delta {t} {\rm div}(k_{\rm c}\nabla T^{k})+\Delta {t} {\rm div}(k_{\rm c}\nabla \Delta T)+\Delta {t}q^{k}_{\rm v}+\Delta {t}\Delta q_{\rm v}\\ \Delta \sigma = \lambda {\rm Tr}(\Delta \dot{\epsilon })I+2\mu ^{k}\Delta \dot{\epsilon }+2\dot{\epsilon }^{k}\Delta \mu +2\Delta \mu \Delta \dot{\epsilon }\\ \Delta \dot{\epsilon } = \frac{1}{2}({}^t\nabla {\Delta V}+\nabla {\Delta V})\\ 2 \bar{\dot{\epsilon }}^k\Delta \bar{\dot{\epsilon }} = \frac{2}{3}(2\dot{\epsilon }^k:\Delta \dot{\epsilon }+\Delta \dot{\epsilon }:\Delta \dot{\epsilon }) -\Delta \bar{\dot{\epsilon }}^2\\ \Delta \mu = \frac{K}{3}(\alpha ^{k}\Delta \gamma +\gamma ^{k}\Delta \alpha + \Delta \alpha \Delta \gamma )\\ T^{k} {\rm d}\Delta \alpha = A\alpha ^{k} {\rm d}\Delta T+A\Delta \alpha {\rm d}\Delta T-\Delta T {\rm d}\Delta \alpha \\ {\bar{\dot{\epsilon }}}^{k} {\rm d}\Delta \gamma = (n-1)\gamma ^{k} {\rm d}\Delta {\bar{\dot{\epsilon }}}+(n-1)\Delta \gamma {{\rm d}}\Delta {\bar{\dot{\epsilon }}}-\Delta {\bar{\dot{\epsilon }}} {\rm d}\Delta \gamma \\ \Delta q_{\rm v} = 3{\beta }(\mu ^{k}\Delta \varphi +\varphi ^{k}\Delta \mu +\Delta \mu \Delta \varphi )\\ \Delta \varphi = 2\bar{\dot{\epsilon }}^{k}\Delta {\bar{\dot{\epsilon }}}+\Delta {\bar{\dot{\epsilon }}}^{2} \end{array} \right. \end{aligned}$$

(16)

In the resolution, we precede to write the equations (16)a and (16)b in a single equation. Then we combine the unknowns $\Delta {u}$, $\Delta {v}$ and $\Delta {T}$ at point x into a single vector $\{\Delta {X}_x\}$ given by:

$$\left\{ {\Delta {X_x}\; = {\;^t} < \Delta u,\;\Delta v,\;\Delta T> } \right\}$$

(17)

3.2 Moving least squares (MLS) approximation

The MLS approximation was devised by mathematicians in data fitting and surface construction [11]. It can be categorized as a method of series representation of functions. An excellent description of the MLS approximation can be found in a paper by Lancaster and Salkauskas [11]. The MLS approximation is now widely used in MFree methods for constructing MFree shape functions. The MLS approximation of unknown vector $\{\Delta {X_x}\}$ is defined at point x as:

$$\begin{aligned} { \{\Delta {X}_x\}=[\varPhi (x)]\{\Delta X_m\} } \end{aligned}$$

(18)

where $[\varPhi (x)]$ is the matrix of MLS shape functions corresponding to m nodes in the support domain of the point x and $\{\Delta X_m\}$ is the vector that collects the nodal unknowns for all the nodes in the support domain. The quantities $\{\Delta X_m\}$ and $[\varPhi (x)]$ are given by:

$$\begin{aligned} \left\{ \begin{array}{l} {}^t\{\Delta X_m\}=\langle \langle \Delta X_{1}\rangle , \langle \Delta X_{2}\rangle ,\ldots ,\langle \Delta X_{m}\rangle \rangle \\ \left[ {{\varPhi (x)}_{(3\times 3m)}} \right] =\left[ {\begin{array}{*{20}{c}} {\varPhi _{1}}&{}0&{}0&{}{\ldots }&{}{\varPhi _m}&{}0&{}0\\ 0&{}\varPhi _1&{}0&{}{\ldots }&{}0&{}\varPhi _m&{}0\\ 0&{}0&{}\varPhi _1&{}{\ldots }&{}0&{}0&{}\varPhi _m \end{array}} \right] \end{array} \right. \end{aligned}$$

(19)

with $\varPhi _i$; $i=1\ldots m$ are the MLS shape functions. Taking account of the approximation (18) and after substitution and assembly techniques, the problem (16) is written in the following condensed form:

$$\begin{aligned} \left\{ \begin{array}{lll} [K^k_T]\{\Delta X\}+ \Delta t\{Fq(\{\Delta X\},\{\Delta X\})\}=\Delta t\{F^{k}\} \\ \{\Delta \dot{\epsilon }_{x}\}=[B]\{\Delta X_m\}\\ 2 \bar{\dot{\epsilon }}_{x}^k \Delta \bar{\dot{\epsilon }}_{x}=\frac{2}{3} (2{}^t\{{\dot{\epsilon }_{x}}^k\}[R]\{\Delta \dot{\epsilon }_{x}\})+\bar{\dot{\epsilon }}_{x}^{nl}\\ T_{x}^{k} {\rm d}\Delta \alpha _{x}=A\alpha _{x}^{k} {\rm d}\Delta T_{x}+\alpha _{x}^{nl}\\ {\bar{\dot{\epsilon }}_{x}}^{k} {\rm d}\Delta \gamma _{x}=(n-1)\gamma _{x}^{k} {\rm d}\Delta \bar{\dot{\epsilon }}_{x}+\gamma _{x}^{nl}\\ \Delta \varphi _{x}=2\bar{\dot{\epsilon }}_{x}^{k}\Delta \bar{\dot{\epsilon }}_{x}+\varphi _{x}^{nl}\\ \Delta \mu _{x}=\frac{K}{3}(\alpha _{x}^{k}\Delta \gamma _{x}+\gamma _{x}^{k}\Delta \alpha _{x})+ \mu _{x}^{nl}\\ \{\Delta \sigma _{x}\}=[C^k]\{\Delta \dot{\epsilon }_{x}\}+\{\sigma _{x}^{nl}\}\\ \Delta q_{\rm v}=3\frac{\beta }{C_{\rm p}}(\mu _{x}^{k}\Delta \varphi _{x}+\varphi _{x}^{k}\Delta \mu _{x})+ q_{\rm v}^{nl} \end{array} \right. \end{aligned}$$

(20)

where $[K_T^k ]$ is the tangent matrix that depends on the solution at time $t^k=k\Delta {t}$, $\{\Delta X\}$ is the unknown global vector containing $3N_{\rm p}$ components; with $N_{\rm p}$ is the total number of points, $\{F_Q({\{}\Delta {X}{\}},{\{}\Delta {X}{\}})\}$ is a quadratic form and $\{F^{k}\}$ is the right-hand side that depends on the solution at time $t^k=k\Delta {t}$ and $\bar{\dot{\epsilon }}_{x}^{nl}$, $\alpha _{x}^{nl}$, $\gamma _{x}^{nl}$, $\varphi _{x}^{nl}$, $\mu _{x}^{nl}$, $\{\sigma _{x}^{nl}\}$ and $q_{\rm v}^{nl}$ are the quadratic terms, the vectorial quantities are given by:

$$\begin{aligned} \begin{array}{l} \{\Delta \dot{\epsilon }_{x}\}=\left\{ \begin{array}{*{20}{l}} \Delta \dot{\epsilon }_{11}\\ \Delta \dot{\epsilon }_{22}\\ 2\Delta \dot{\epsilon }_{12} \end{array} \right\} ; \quad \left[ {{B}_{(3\times 3m)}} \right] =\left[ {\begin{array}{*{20}{c}} {\frac{\partial {\varPhi _{1}}}{\partial x}}&{}0&{}0&{}{\ldots }&{}{\frac{\partial {\varPhi _m}}{\partial x}}&{}0&{}0\\ 0&{}{\frac{\partial {\varPhi _1}}{\partial y}}&{}0&{}{\ldots }&{}0&{}{\frac{\partial {\varPhi _m}}{\partial y}}&{}0\\ {\frac{\partial {\varPhi _1}}{\partial y}}&{}{\frac{\partial {\varPhi _1}}{\partial x}}&{}0&{}{\ldots }&{}{\frac{\partial {\varPhi _m}}{\partial y}}&{}{\frac{\partial {\varPhi _m}}{\partial x}}&{}0 \end{array}} \right] \\ \\ \{\Delta \sigma _{x}\}=\left\{ \begin{array}{*{20}{l}} \Delta \sigma _{11}\\ \Delta \sigma _{22}\\ \Delta \sigma _{12} \end{array} \right\} ; \quad \left[ C^k\right] =\left[ {\begin{array}{*{20}{c}} 2\mu ^k+\lambda \left( 1-\frac{\lambda }{2\mu ^k+\lambda }\right) &{}\lambda \left( 1-\frac{\lambda }{2\mu ^k+\lambda }\right) &{}0\\ \lambda \left( 1-\frac{\lambda }{2\mu ^k+\lambda }\right) &{}2\mu ^k+\lambda \left( 1-\frac{\lambda }{2\mu ^k+\lambda }\right) &{}0\\ 0&{}0&{}\mu ^k\\ \end{array}} \right] \\ \\ \left[ R\right] =\left[ \begin{array}{*{20}{l}} 1&{}0&{}0\\ 0&{}1&{}0\\ 0&{}0&{}\frac{1}{2} \end{array} \right] \end{array} \end{aligned}$$

(21)

3.3 Homotopy transformation

To avoid the decomposition of the tangent matrix to each time step, we use an homotopy transformation by introducing, in the problem (20), an arbitrary matrix $[K^{*}]$ and an artificial parameter “a” under the following form:

$$\begin{aligned} \left\{ \begin{array}{l} [K^*]\{\Delta \chi (a)\}+a([K_T^k]-[K^*])\{\Delta \chi (a)\}+a\Delta {t}\{F_Q(\{\Delta \chi (a)\},\{\Delta \chi (a)\}) \}=a\Delta {t}\{F^{k}\} \\ \{\Delta \dot{E_{x}}(a)\}=[B]\{\Delta \chi _{m}(a)\}\\ 2 \bar{\dot{\epsilon }}_{x}^k\Delta \bar{\dot{E}}_{x}(a)=\frac{4}{3}{}^t\{{\dot{\epsilon }_{x}}^k\}[R]\{\Delta {\dot{E}_{x}}(a)\}+\bar{\dot{E}}_{x}^{nl}(a)\\ T_{x}^{k} {\rm d}\Delta \varLambda _{x}(a)=A\alpha _{x}^{k} {\rm d}\Delta T_{x}(a)+\varLambda _{x}^{nl}(a)\\ \bar{\dot{\epsilon }}_{x}^{k} {\rm d}\Delta \varGamma _{x}(a)=(n-1)\gamma _{x}^{k} {\rm d}\Delta \bar{\dot{E}}_{x}+\varGamma _{x}^{nl}(a)\\ \Delta \phi _{x}(a)=2\bar{\dot{\epsilon }}_{x}^{k}\Delta \bar{\dot{E}}_{x}(a)+\phi _{x}^{nl}(a)\\ \Delta MU_{x}(a)=\frac{K}{3} (\alpha _{x}^{k}\Delta \varGamma _{x}(a)+\gamma _{x}^{k}\Delta \varLambda _{x}(a))+MU_{x}^{nl}(a)\\ \{\Delta \varSigma _{x}(a)\}=[C^k]\{\Delta \dot{E_{x}}(a)\}+2\Delta MU_{x}\{\dot{\epsilon }_{x}^k\}+\{\varSigma _{x}^{nl}(a)\}\\ \Delta Q^v_{x}(a)=\frac{3\beta }{C_{\rm p}} (\mu _{x}^k \Delta \phi _{x}(a)+\varphi _{x}^k\Delta MU_{x}(a))+Q^{vnl}_{x}(a) \end{array} \right. \end{aligned}$$

(22)

where $\{\Delta \chi (a)\}$ and the others are new unknowns of the problem (22) such that if $a=0$ it is null and if $a=1$ it coincides with the solution of the problem (20), the quantities $\bar{\dot{E}}_{x}^{nl}(a)$, $\varLambda _{x}^{nl}(a)$, $\varGamma _{x}^{nl}(a)$, $\phi _{x}^{nl}(a)$, $MU_{x}^{nl}(a)$, $\{\varSigma _{x}^{nl}(a)\}$ and $Q^{vnl}_{x}(a)$ are the quadratic forms.

3.4 Development in Taylor series

The unknown of artificial problem (22) is sought here as developments in Taylor series truncated at order p with respect to homotopy parameter “a” in the following form:

$$\begin{aligned} \left\{ {\begin{array}{l} \{\Delta \chi \} = a\{\Delta \chi _{1}\} + a^2\{\Delta \chi _{2}\} + \ldots + a^p\{\Delta \chi _{\rm p}\}\\ \{\Delta \dot{E}_{x}\} = a\{\Delta \dot{E_{1}}\} + a^2\{\Delta \dot{E_{2}}\} + \ldots + a^p\{\Delta \dot{E_{\rm p}}\}\\ \Delta \bar{\dot{E_{x}}} = a\Delta \bar{\dot{E}}_{1} + a^2\Delta \bar{\dot{E}}_{2} + \ldots + a^p\Delta \bar{\dot{E}}_{\rm p}\\ \Delta \varLambda _{x} = a\Delta \varLambda _{1} + a^2\Delta \varLambda _{2} + \cdots + a^p\Delta \varLambda _{\rm p}\\ \Delta \varGamma _{x} = a\Delta \varGamma _{1} + a^2\Delta \varGamma _{2} + \cdots + a^p\Delta \varGamma _{\rm p}\\ \Delta \phi _{x} = a\Delta \phi _{1} + a^2\Delta \phi _{2} + \cdots + a^p\Delta \phi _{\rm p}\\ \Delta MU_{x} = a\Delta MU_{1} + a^2\Delta MU_{2} + \cdots + a^p\Delta MU_{\rm p}\\ \{\Delta \varSigma _{x}\} = a\{\Delta \varSigma _{1}\} + a^2\{\Delta \varSigma _{2}\} + \cdots + a^p\{\Delta \varSigma _{\rm p}\}\\ \Delta Q^{v}_{x} = a\Delta Q_{1} + a^2\Delta Q_{2} + \cdots + a^p\Delta Q_{\rm p} \end{array}}\right. \end{aligned}$$

(23)

The developments in Taylor series (23) are introduced into the equations to be solved and by equating like powers of “a”, the nonlinear problem (22) is transformed into a sequence of linear ones. When the problem contains soft nonlinearity which is quadratic with respect to the unknown $\{\chi (a)\}$, the use of developments is relatively simple and easy. The linear problems obtained at each order of truncation can be written:

$$\begin{aligned} \begin{array}{l} {\rm Order}\; 1{:} \left\{ \begin{array}{l} [K^*]\{\Delta \chi _1\}=\Delta {t}\{F^{k}\}\\ \{\Delta {\dot{E}}_{1}\} = [B]\{\chi _{1}\}\\ \Delta \bar{\dot{E}}_{1} = \frac{2}{3\bar{\dot{\epsilon }}_{x}^{k}}{2}^t\{\dot{\epsilon }_{x}^{k}\}[R]\{\Delta {\dot{E}}_{1}\}\\ \Delta \varLambda _{1}=\frac{1}{T_{x}^k} A \alpha _{x}^k \Delta T_{1}\\ \Delta \varGamma _{1}=\frac{1}{\bar{\dot{\epsilon }}_{x}^{k}}(n-1)\gamma _{x}^k \Delta \bar{\dot{E}_{1}}\\ \Delta \phi _{1}=2 \bar{\dot{\epsilon }}_{x}^k\Delta \bar{\dot{E}}_{1}\\ \Delta MU_{1}=\frac{K}{3} (\alpha _{x}^k\Delta \varGamma _{1}+\gamma _{x}^k\Delta \varLambda _{1} )\\ \{\Delta \varSigma _{1}\} =[C^k]\{\Delta \dot{E}_{1}\}+2\Delta MU_{1}\{\dot{\epsilon }_{x}^k\}\\ \Delta Q_{1}=\frac{3\beta }{C_{\rm p}} (\mu _{x}^k \Delta \phi _1+\varphi _{x}^k\Delta MU_{1}) \end{array}\right. \end{array} \end{aligned}$$

(24)

$$\begin{aligned} \begin{array}{l} {\rm Order}\;j, 2\le j \le p {:} \left\{ {\begin{array}{l} [K^{*}]\{\Delta \chi _{j}\}=\left( [K^{*}]-[K^{k}_T]\right) \{\Delta \chi _{j-1}\}+\Delta t{\{F^{nl}_{j}\}}\\ \{\Delta {\dot{E}}_{j}\} = [B]\{\Delta \chi _{j}\}\\ \Delta \bar{\dot{E}}_{j}=\frac{2}{3\bar{\dot{\epsilon }}^{k}}{}^t\{\dot{\epsilon }_{x}^{k}\} [R]\{\Delta \dot{E}_{j}\} +\bar{\dot{E}}^{nl}_{j}\\ \Delta \varLambda _{j}=\frac{A}{T_{x}^k}\alpha _{x}^k\Delta T_{j}+\varLambda ^{nl}_{j}\\ \Delta \varGamma _{j}=\frac{1}{\bar{\dot{\epsilon }}_{x}^{k}}(n-1)\gamma _{x}^k\Delta \bar{\dot{E}}_j+\varGamma ^{nl}_{j}\\ \Delta \phi _{j}=2 \bar{\dot{\epsilon }}_{x}^{k}\Delta \bar{\dot{E}}_j+\phi ^{nl}_{j}\\ \Delta MU_{j}=\frac{K}{3} (\alpha _{x}^k\Delta \varGamma _j+\gamma ^k\Delta \varLambda _{j} )+MU^{nl}_{j}\\ \{\Delta {\varSigma }_{j}\}=[C^k]\{\Delta \dot{E}_j\}+2\Delta MU_j\{\dot{\epsilon }_{x}^k\}+\{{\varSigma }^{nl}_{j}\}\\ \Delta Q_{j}=\frac{3\beta }{C_{\rm p}} (\mu _{x}^k\Delta \phi _{j}+\varphi _{x}^k\Delta MU_{j})+Q^{nl}_{j} \end{array}} \right. \end{array} \end{aligned}$$

(25)

where $\{(.)^{nl}_j\}$ are the second member vectors depending of terms of the lower orders of Taylor series. The previous linear problems have all the same tangent matrix which is defined by the arbitrary matrix $[K^*]$. With this technique a part of the nonlinear solution branch can be computed.

3.5 Continuation procedure

To determine the whole nonlinear solution, a continuation procedure based on the developments in Taylor series has been proposed in [5]. The key point is to define the validity range of the developments in Taylor series (23). The definition of the validity range of the Eq. (23) is easily obtained by requiring that the difference between two developments in Taylor series solutions (23) at consecutive orders remains smaller at the end of the step than a chosen parameter tolerance “$\eta$”. Hence, the maximum value “$a_{\rm max}$ of a homotopy parameter “a” can be defined with the following equation [5, 12–15]:

$$\begin{aligned} a_{\rm max} = \left( \eta \frac{\left\| \{\Delta \chi _1\}\right\| }{\left\| \{\Delta \chi _{\rm p}\}\right\| }\right) ^{\left( \frac{1}{p-1}\right) } \end{aligned}$$

(26)

For unsteady problems, the parameter “$a_{\rm max}$” which depends of time allows us to determine the maximum time “$t_{\rm max}$” of validity of the series which is defined by the following inequality:

$$\begin{aligned} a_{\rm max}\ge 1 \end{aligned}$$

(27)

The solution of the problem (14) is obtained by writing:

$$\begin{aligned} \left\{ \begin{array}{l} \{X^{k+1}\}=\{X^{k}\}+\{\Delta \chi (a=1)\}\\ \{{\dot{\epsilon }_{x}}^{k+1}\}=\{{\dot{\epsilon }_{x}}^{k}\}+\{\Delta {{\dot{E_{x}}(a=1)}}\}\\ \bar{\dot{\epsilon }}_{x}^{k+1}=\bar{\dot{\epsilon }}_{x}^{k}+\Delta \bar{\dot{E}}_{x}(a=1)\\ \alpha _{x}^{k+1}=\alpha _{x}^{k}+\Delta \varLambda _{x}(a=1)\\ \gamma _{x}^{k+1}=\gamma _{x}^{k}+\Delta \varGamma _{x}(a=1)\\ \varphi _{x}^{k+1}=\varphi _{x}^{k} + \Delta \phi _{x}(a=1)\\ \mu _{x}^{k+1}=\mu _{x}^{k}+\Delta MU_{x}(a=1)\\ \{\sigma _{x}^{k+1}\} =\{\sigma _{x}^{k}\}+\{\Delta \varSigma _{x}(a=1)\}\\ q_{\rm v}^{k+1}=q_{\rm v}^{k}+\Delta Q^{v}_{x}(a=1) \end{array} \right. \end{aligned}$$

(28)

This maximum time will be considered later as an initial condition for the next step of the continuation procedure. The whole solution of the problem (20) is determined branch by branch [20].

4 Numerical application

In this section, we present a numerical analysis to demonstrate the efficiency of the algorithm derived from our numerical modeling for the simulation of friction stir welding. The area affected thermo-mechanically is assumed small compared to the area occupied by the welded plates. This area is considered as an assembly of two holed plates which have the shape of a half-disc (see Fig. 1a). These circular plates of interior radius $R_1=1.5 \ {\rm mm}$ and exterior radius $R_2=6 \ {\rm mm}$, respectively, are made of a visco-plastic material of aluminum alloy AA7075. The interior radius $R_1$ corresponds here to the radius of the welding tool. The mechanical data used in this application are: for circular plates; $k=2.69\;10^{10} \ {\rm N} \ {\rm mm}^{-2},$ $A=-3.3155,$ ${n}=0.1324,$ $\rho =2780 \ {\rm kg/m}^3,$ $C_{\rm p}=920 \ {\rm J/kg} \ {\rm K}$ and $k_{\rm c}=140 \ {\rm W/m} \ {\rm K}$ [3] and for welding tool; $\rho _t = 7800 \ {\rm kg/m}^3$, $C_{p_t} = 450 \ {\rm J/kg} \ {\rm K}$ and $k_{c_t} = 36 \ {\rm W/m} \ {\rm K}$. The initial and boundary conditions adopted in this example (see Fig. 1a) are given by:

$$\begin{aligned} \left\{ \begin{array}{ll} u(x,y,t)=-\sqrt{x^2+y^2}\omega \sin (\omega t) &{} {\rm for} \quad x^2+y^2\le R_1^2 \quad {\rm and} \quad \forall \;t\ge 0\\ v(x,y,t)= \sqrt{x^2+y^2}\omega \cos (\omega t) &{} {\rm for} \quad x^2+y^2\le R_1^2\quad {\rm and}\quad \forall \;t\ge 0\\ u(x,y,t)=0 &{} {\rm for} \quad x^2+y^2=R_2^2 \quad {\rm and} \quad \forall \; t\ge 0\\ v(x,y,t)=0 &{} {\rm for} \quad x^2+y^2=R_2^2 \quad {\rm and} \quad \forall \; t\ge 0\\ -k_{\rm c}\frac{\partial T(x,y,t)}{\partial N}=h(T(x,y,t)-T_{\rm a}) &{} {\rm for} \quad x^2+y^2=R_2^2 \quad {\rm and} \quad \forall \; t\ge 0\\ u(x,y,t)=0 &{} {\rm for} \quad R_1^2<x^2+y^2<R_2^2\quad {\rm and} \quad t=0\\ v(x,y,t)=0 &{} {\rm for} \quad R_1^2<x^2+y^2<R_2^2\quad {\rm and} \quad t=0\\ T(x,y,t)= 300 \ {\rm K} &{} {\rm for} \quad 0 \le x^2+y^2 \le R_2^2 \quad {\rm and} \quad t=0 \end{array} \right. \end{aligned}$$

(29)

where $\omega =20 \ {\rm rad/s}$ is the rotational speed of the welding tool, N is the normal to the circular contour of radius $R_2$, $T_{\rm a}$ is the ambient temperature taken equal to 300 K and $h=1000 \ {\rm W/m}^2 \ {\rm K}$ is the heat transfer coefficient.

Fig. 1

Data of considered example

The analysis is made in the time range [0, 0.7 s] with a time step $\Delta {t}=10^{-4} \ {\rm s}$ for the Euler scheme. The size of the influence domain $h_{\rm I}$ is taken equal to $3 {\rm d}r$ with dr being the inter-point distance taken equal to $3.7510^{-4} \ {\rm m}$ and the weight function is chosen as:

$$\begin{aligned} w(r)=\left\{ \begin{array}{ll} {\rm e}^{-(\frac{r}{c})^{2q}} &{} {\rm if} \ r\le 1\\ 0&{} {\rm if} \ r> 1 \end{array} \right. \end{aligned}$$

(30)

where $r=\parallel x-x_m\parallel /h_{\rm I}$, $c=0.2$ and $q=1$. With these data, the area occupied by the plates which are represented by colors blue and red, respectively and the welding tool is replaced by 846 points (see Fig. 1b). The pre-conditioner matrix $[K^{*}]$ is taken equal to the tangent matrix $[K_T^{t_{\rm max}}]$ evaluated at the started time of each step.

In this application, we will discuss the influence of the truncation order p on the maximum time $t_{\rm max}$ during a step of the continuation technique. The Table 1 shows that when the truncation order p increases the size of the average validity range $t_{\rm max}$ increases and stabilizes from the truncation order $p=15$ for a fixed tolerance parameter $\eta =10^{-6}$. Similarly, if we increase the order of truncation the number of steps of the proposed algorithm decreases and stabilizes from the order $p=15$ (see Table 1).

Table 1 Influence of the truncation order p on the average validity range $t_{\rm max}$ and number of steps of the proposed algorithm in the time range [0, 0.7 s].

After these numerical tests we choose thereafter the truncation order $p=7$ and the tolerance parameter $\eta = 10^{-6}$ for the proposed algorithm and the tolerance parameter $\delta = 10^{-6}$ for the iterative method. The obtained solution is compared with that obtained by the conventional method using the Euler scheme coupled with an iterative method [21] similar to that used in various areas of physics [7], it is described in [10]. In this iterative method,the convergence is evaluated by assuming that the relative difference between two consecutive iterations is less than a given tolerance parameter. The two plates are stained with the colors blue and red, respectively, to show the material mixing.

In Fig. 2, we plot the evolution of u and v components of the velocity along the time axis t at points (1) and (2) near the tool (see Fig. 1b), obtained by the proposed algorithm and the iterative method. We remark that the two solutions are confounded. It is worth noting that the solution obtained by the proposed algorithm requires 46 steps of continuation (46 inversions of the matrix $[K^*]$), whereas that obtained by the iterative method requires 15,000 inversions of matrix $[K^*]$.

Fig. 2

Evolution of u and v components of the velocity vector according to the time t at the registration points (1) and (2) presented in Fig. 1b

Also, the Fig. 3 represents the evolution of the temperature T along the time axis t at points (1) and (3) (see Fig. 1b). The solutions obtained by the two algorithms are in good agreement. From this figure, we see that the temperature saved at point (1) is greater than that saved at point (3). This is due to the deformations which are stronger near the welding tool.

Fig. 3

Temporal evolution of the temperature T at the registration points (1) and (3) presented in Fig. 1b

Thereafter, we proceed to make the registration sections of the components of the velocity and temperature on the lines $y = 0$, $x\in [-R_2,R_2]$ $(A-A)$ and $x=0$, $y\in [-R_2,R_2]$ $(B-B)$ (see Fig. 4).

Fig. 4

Registration sections $(A-A)$ and $(B-B)$

The Fig. 5 shows the evolution of u and v along the horizontal and vertical sections and the comparison between the proposed algorithm and the iterative algorithm at time $t=0.7 {\rm s}$. One can observe that the two algorithms are in good agreement.

Fig. 5

Evolution of u and v components of the velocity vector according to the registration sections $(B-B)$ and $(A-A)$, respectively

The Figs. 6, 7, 8 and 9 show the evolution of temperature T along the horizontal section or vertical section and the state of material mixing at times $t = 0.01 \ {\rm s}$, $t = 0.3 \ {\rm s}$, $t = 0.5 \ {\rm s}$ and $t = 0.7 \ {\rm s}$, respectively. From these figures, we remark that the material flow (deformation) is circular about the tool because the mixing process is controlled only by rotating speed.

Fig. 6

Evolution of the temperature T along the registration section $(A-A)$ and material mixing state at time $t = 0.01\ {\rm s}$.

Fig. 7

Evolution of the temperature T along the registration section $(A-A)$ and material mixing state at time $t = 0.3\ {\rm s}$.

Fig. 8

Evolution of the temperature T along the registration section $(A-A)$ and material mixing state at time $t = 0.5\ {\rm s}$.

Fig. 9

Evolution of the temperature T along the registration section $(A-A)$ and material mixing state at time $t = 0.7\ {\rm s}$.

The Fig. 10 shows the temperature distribution T at time $t = 0.001\ {\rm s}$ and $t = 0.7\ {\rm s}$, respectively.

Fig. 10

Temperature distribution at times $t = 0.001\ {\rm s}$ and $t = 0.7\ {\rm s}$

The Fig. 11 illustrates the temperature distribution in the welded plate and in the considered tool for times $t=0.05 \ {\rm s}$ and $t=0.08 \ {\rm s}$. The temperature distribution is symmetric because the heat generation near the tool during the mixing process is dominated by rotating speed of the tool.

Fig. 11

Temperature distribution at times $t = 0.05 \ {\rm s}$ and $t = 0.08 \ {\rm s}$

5 Conclusion

In this work, we have used the high order algorithm for the simulation of mechanical–thermal material mixing observed during the FSW process in the bi-dimensional case. This algorithm combines the high order implicit technique based on developments in Taylor series and meshless method based on MLS. A mechanical–thermal formulation is used under a strong form. The obtained results are convincing compared to the iterative method. The used algorithm requires no correction and one inversion of the iteration matrix allows us to get a good part of the solution. The key points in this high order implicit algorithm are, first a high order solver based on developments in Taylor series, second the possibility of choosing the tangent matrix $[K^*]$ which limits the number of matrices to be triangulated. Let us recall that the used algorithm solves the nonlinear visco-plastic problem with a high order predictor without any correction. The used algorithm can easily be adapted to other nonlinear problems. This comparison confirms the robustness, accuracy and efficiency of the algorithm. Compared to the iterative method, the algorithm is found competitive in terms of computational cost versus accuracy, and benefit from a simple implementation. This work is currently in progress to other application fields as the three-dimensional mixing process.