Challenges in Thermo-mechanical Analysis of Friction Stir Welding Processes

Abstract

This paper deals with the numerical simulation of friction stir welding (FSW) processes. FSW techniques are used in many industrial applications and particularly in the aeronautic and aerospace industries, where the quality of the joining is of essential importance. The analysis is focused either at global level, considering the full component to be jointed, or locally, studying more in detail the heat affected zone (HAZ). The analysis at global (structural component) level is performed defining the problem in the Lagrangian setting while, at local level, an apropos kinematic framework which makes use of an efficient combination of Lagrangian (pin), Eulerian (metal sheet) and ALE (stirring zone) descriptions for the different computational sub-domains is introduced for the numerical modeling. As a result, the analysis can deal with complex (non-cylindrical) pin-shapes and the extremely large deformation of the material at the HAZ without requiring any remeshing or remapping tools. A fully coupled thermo-mechanical framework is proposed for the computational modeling of the FSW processes proposed both at local and global level. A staggered algorithm based on an isothermal fractional step method is introduced. To account for the isochoric behavior of the material when the temperature range is close to the melting point or due to the predominant deviatoric deformations induced by the visco-plastic response, a mixed finite element technology is introduced. The Variational Multi Scale method is used to circumvent the LBB stability condition allowing the use of linear/linear P1/P1 interpolations for displacement (or velocity, ALE/Eulerian formulation) and pressure fields, respectively. The same stabilization strategy is adopted to tackle the instabilities of the temperature field, inherent characteristic of convective dominated problems (thermal analysis in ALE/Eulerian kinematic framework). At global level, the material behavior is characterized by a thermo–elasto–viscoplastic constitutive model. The analysis at local level is characterized by a rigid thermo–visco-plastic constitutive model. Different thermally coupled (non-Newtonian) fluid-like models as Norton–Hoff, Carreau or Sheppard–Wright, among others are tested. To better understand the material flow pattern in the stirring zone, a (Lagrangian based) particle tracing is carried out while post-processing FSW results. A coupling strategy between the analysis of the process zone nearby the pin-tool (local level analysis) and the simulation carried out for the entire structure to be welded (global level analysis) is implemented to accurately predict the temperature histories and, thereby, the residual stresses in FSW.

1 Introduction

1.1 Industrial Background of FSW

Friction stir welding (FSW) is a solid state joining technology in which no gross melting of the welded material takes place. It is a relatively new technique [developed by The Welding Institute (TWI), in Cambridge, UK, in 1991] widely used over the past decades for joining aluminium alloys. Recently, FSW has been applied to the joining of a wide variety of other metals and alloys such as magnesium, titanium, steel and others. FSW is considered to be the most significant development in metal joining in decades and, in addition, is a “green” technology due to its energy efficiency, environmental friendliness, and versatility. This process offers a number of advantages over conventional joining processes (such as e.g. fusion welding). The main advantages, often mentioned, include: (a) absence of the need for expensive consumables such as a cover gas or flux; (b) ease of automation of the machinery involved; (c) low distortion of the work-piece; and (d) good mechanical properties of the resultant joint [80, 104]. Additionally, since it allows avoiding all the problems associated to the cooling from the liquid phase, issues such as porosity, solute redistribution, solidification cracking and liquation cracking are not encountered during FSW.¹ In general, FSW has been found to produce a low concentration of defects and is very tolerant to variations in parameters and materials. Furthermore, since welding occurs by the deformation of material at temperatures below the melting temperature, many problems commonly associated with joining of dissimilar alloys can be avoided, thus high-quality welds are produced. Due to this fact, it has been widely used in different industrial applications where metallurgical characteristics should be retained, such as in aeronautic, naval and automotive industry.

Fig. 1

FSW process

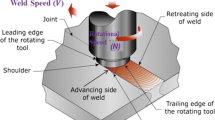
During FSW, the work-piece is placed on a backup plate and it is clamped rigidly to eliminate any degrees of freedom (Fig. 1). A nonconsumable tool, rotating at a constant speed, is inserted into the welding line between two pieces of sheet or plate material (which are butted together) and generates heat. This heat is produced, on one hand, by the friction between the tool shoulder and the work-pieces, and, on the other hand, by the mechanical mixing (stirring) process in the solid state. This results in the plastification of the material close to the tool at very high strain rates and leads to the formation of the joint. In detail, the plasticized material is stirred by the tool and the heated material is forced to flow around the pin tool to its backside thus filling the hole in the tool wake as the tool moves forward. As the material cools down, a solid continuous joint between the two plates emerges.

Usually the tool is tilted at an angle of 1°–3° away from the direction of travel, although some tool designs allow it to be positioned orthogonally to the work-piece. The welding tool consists of a shoulder and a pin. The length of the pin tool is slightly less than the depth of weld and the tool shoulder is kept in close contact with the work-piece surface (see Fig. 2). The tool serves three primary functions, that is, heating of the work-piece, movement of material to produce the joint (stirring), and containment of the hot metal beneath the tool shoulder. The function of the pin tool is to heat up the weld metal by means of friction and plastic dissipation, and, through its shape and rotation, force the metal to move around its form and create a weld. The function of the shoulder is to heat up the metal through friction and to prevent it from being forced out of the weld. The tool shoulder restricts metal flow to a level equivalent to the shoulder position, that is, approximately to the initial work-piece top surface.

Fig. 2

Schematic representation of the friction stir welding process

Depending on the geometrical configuration of the tool, material movement around the pin can become complex, with severe gradients in temperature and strain rate. This environment creates a challenge for modelers due to the resulting coupled thermo-mechanical nature, the large deformation and strain rates near the pin. Since FSW is not a symmetric process, two sides of the tool are differentiated. One can see in Fig. 3 that the work-pieces being joined by the weld are either on the retreating or advancing side of the rotating tool. The retreating side is the one where the tool rotating direction is opposite to the tool moving direction and parallel to the metal flow direction. In contrast, the advancing side is the one where the tool rotation direction is the same as the tool moving direction and opposite to the metal flow direction. This unsymmetric nature results in a different material flow on the different sides of the tool and has a large effect on many applications, especially lap joints [23]. The periodic “onion flow” pattern that is left behind as the tool advances is schematically illustrated in Fig. 3.

Fig. 3

Definition of Friction Stir Welding zones [49]

During the early development of FSW, the process appeared simple, compared to many conventional welding practices. However, as development continued, the complexity of FSW was realized. It is now known that properties following FSW are a function of both controlled and uncontrolled variables (response variables) as well as external boundary conditions. For example, investigators have now illustrated that post-weld properties depend on:

• Tool travel speed: influences total heat, porosity and weld quality.

• Tool rotation rate: influences total heat and weld quality.

• Tool design: shoulder diameter, scroll or concave shoulder, features on the pin and pin length influence the extent of the material (Fig. 4).

• Tool tilt: It influences the contact pressure. There exists lower contact pressure (or incomplete contact) on the leading edge of the shoulder due to tool tilt (typically between 0° and 3°).

• Material thickness: influences cooling rate and through-thickness temperature gradients.

Fig. 4

Different pin shapes

These parameters must be carefully calibrated according to the welding process and the selected material, respectively. The strong coupling between the temperature field and the mechanical behavior is the key-point in FSW and its highly non-linear relationship makes the process setup complex. The operative range for most of the welding process parameters is rather narrow requiring a tedious characterization and sensitivity analysis. This is why, despite the apparent simplicity of this novel welding procedure, computational modeling is considered a very helpful tool to understand the leading mechanisms that govern the material behavior, attracting more and more the research interest.

Finite element modeling is an option which can help to determine process parameters that would otherwise require further experimental testing for validation and analysis. The weld quality depends largely on how the material is heated, cooled and deformed. Hence a prior knowledge of the temperature evolution within the work-piece would help in designing the process parameters for a welding application. Research in the field of FSW joints has been limited possibly due to proprietary publishing restriction within industry. For this reason, Finite Element Analysis (FEA) could be also very beneficial. Two process parameters of interest for FSW welds are tool travel rates and rotational tool velocities. With respect to this, a lot of emphasis has been laid on FEA analysis, as it may broaden the scope of application of FSW. Another important process parameter in FSW is the heat flux. This can be also easily included in the FEA. The heat flux should be high enough to keep the maximum temperature in the work-piece around 80–90 % of the melting temperature of the work-piece material, so that welding defects are avoided [29].

Moreover, analytical and numerical methods have a role to play, although numerical methods dominate due to the accuracy and ease-to-use of modern workstations and software. Numerical modeling is based on discretized representations of specific welds, using finite element, finite difference, or finite volume techniques. These methods can capture much of the complexity in material constitutive behavior, boundary conditions, and geometry, but in practice, a limited range of conditions tends to be studied in depth. Therefore, it is good modeling practice to explore simplifications to the problem that give useful insight across a wider domain, for example, making valid two-dimensional (2-D) approximations to inherently three dimensional (3-D) behavior. It is also essential to deliver a model that is properly validated and whose sensitivity is known to uncertainty in the input material and process data—ideals that are rarely carried through in practice.

1.2 Challenges for the Simulation of FSW

Information about the shape, dimensions and residual stresses in a component after welding and mechanical properties of the welded joint are of great interest in order to improve the quality and to prevent failures during manufacturing or in service. The FSW process can be analyzed either experimentally or numerically.

FSW is difficult to analyze experimentally; however, process parameters and different fixture set-ups can be evaluated without doing a large number of experiments. An experiment can be designed to answer one or more carefully formulated questions. The goals must be clarified perfectly to choose the appropriate parameters and factors. Otherwise the goal is not achieved and the experiment must be repeated. Different welded specimens are produced by varying the process parameter. The properties and microstructure changes in weld are investigated. For instance, the tensile strength of the produced joint is tested at room temperature. Microstructure of the weld is analyzed by means of optical microscopy or microhardness measurements.

The alternative to the experimental FSW analysis is numerical modeling and simulation. Computer-based models provide the opportunity to improve theories of design and increase their acceptance. Simulations are useful in designing the manufacturing process as well as the manufactured component itself. To do an appropriate modeling, the physics of the problem must be well-understood.

1.2.1 Physical Model

FSW is a problem of complex nature; the process is highly nonlinear and coupled. Different physical phenomena occur during the welding process, involving the thermal and mechanical interactions. The temperature field is a function of many welding parameters such as welding speed, welding sequence and environmental conditions. Formation of distortions and residual stresses in work-pieces depend on many interrelated factors such as thermal field, material properties, structural boundary conditions and welding conditions.

The challenging issues in physical modeling of the FSW process are divided into three parts:

1.2.1.1 Complex Thermal Behavior

Heat transfer mechanisms including convection, radiation and conduction have a significant role on the process behavior. Convection and radiation fluxes dissipate heat significantly through the work-pieces to the surrounding environment while conduction heat flux occurs between the work-pieces and the support.

1.2.1.2 Non-linear Behavior and Localized Nature

In FSW, the mechanical behavior is non-linear due to the high strain rates and visco-plastic material. The strong non-linear region is limited to a small area and the remaining part of the model is mostly linear. However, the exact boundaries of the non-linear zone are not known a-priori. It is generally believed that strain rate during the welding is high. Knowledge of strain rate is important for understanding the subsequent evolution of grain structure, and it serves as a basis for verification of various models as well.

1.2.1.3 Coupled Nature

The thermal and mechanical problems are strongly coupled (the thermal loads generate changes in the mechanical field). The mechanical effects coupled to the thermal ones include internal heat generation due to plastic deformations or viscous effects, heat transfer between contacting bodies, heat generation due to friction, etc. The thermal effects are also coupled to the mechanical ones; for instance, thermal expansion, temperature-dependent mechanical properties, temperature gradients in work-pieces, etc.

An adequate physical model of the welding process must account for all these phenomena including thermal, mechanical and coupling aspects.

1.2.2 Numerical Model

Among several numerical modeling techniques, the Finite Element (FE) framework is found to be suitable for the simulation of welding and proven to be a versatile tool for predicting a component’s response to the various thermal and mechanical loads. The FE method also offers the possibility to examine different aspects of the manufacturing process without having a physical prototype of the product. To this end, a specialized thermo-mechanical coupled model needs to be implemented in a finite element program, and the predictive capabilities of the theory and its numerical implementation must be validated.

The numerical simulation of the FSW process has many complex and challenging aspects that are difficult to deal with: the welding process is described by the equilibrium and energy equations governing the mechanical and thermal problems and they are coupled. Additionally, both of them are non-linear. This has important implications upon the complexity of the numerical model. Consequently, a robust and efficient numerical strategy is crucial for solving such highly non-linear coupled finite element equations. In such process, several assumptions are commonly assumed.

It is important to distinguish between two different kinds of welding analyses carried out at local or global level, respectively.

In local level analysis, the focus of the simulation is the heat affected zone. The simulation is intended to compute the heat power generated either by visco-plastic dissipation or by friction at the contact interface. At this level, the process phenomena that can be studied are the relationship between welding parameters, the contact mechanisms in terms of applied normal pressure and friction coefficient, the setting geometry, the material flow within the heat affected zone, its size and the corresponding consequences on the microstructure evolution, etc.

A simulation carried out at global level studies the entire component to be welded. In this case, a moving heat power source is applied to a control volume representing the actual heat affected zone at each time-step of the analysis. The effects induced by the welding process on the structural behavior are the target of this kind of study. These effects are distortions, residual stresses or weaknesses along the welding line, among others.

The aim of this work is to develop a robust numerical tool able to simulate the welding process considering its complex features at local level as well as global level.

1.2.2.1 Mechanical Problem

A quasi-static mechanical analysis can be assumed as the inertia effects in welding processes are negligible due to the high viscosity characterization. At local level, the volumetric changes are found to be negligible, and incompressibility can be assumed. To deal with the incompressible behavior, a very convenient and common choice is to describe the formulation splitting the stress tensor into its deviatoric and volumetric parts. Dealing with the incompressible limit requires the use of mixed velocity-pressure interpolations. The problem suffers from instability if the standard Galerkin FE formulation is used, unless compatible spaces for the pressure and the velocity field are selected [Ladyzhenskaya–Babuška–Brezzi (LBB) stability condition]. Due to this, pressure instabilities appear if equal velocity-pressure interpolations are used. Thus, the challenging issue of pressure stabilization rises up.

The welding process is characterized by very high strain rates as well as a wide temperature range going from the environmental temperature to the melting point. Hence, the constitutive laws adopted should depend on both variables. The constitutive theory applied must be specialized to capture the features of the thermo-mechanically coupled strain rate and temperature dependent large deformation. According to the split of the stress tensor, different rate-dependent constitutive models can be used for modeling of the welding process. At typical welding temperatures, the large strain deformation is mainly visco-plastic. Depending on the scope of the analysis, rigid-visco-plastic or elasto-visco-plastic constitutive models can be used. Not only the prediction of the temperature evolution, but the accurate residual stress evaluation field generated during the process is the objective of the FSW simulation. The selected constitutive model must appropriately define the material behavior and has to be calibrated by the temperature evolution. The challenge arises from the extremely non-linear behavior of these constitutive models and, therefore, from the numerical point of view, a special treatment is obligatory. Moreover, the localized large strain rates usually involved in FSW processes make the problem even more complex.

1.2.2.2 Thermal Problem

The thermal problem is defined by the balance of energy equation. In FSW simulation, the plastic dissipation term appearing in the energy equation has a critical role on the process behavior and it is the main source of heat generation.

The definition of the heat source is one of the key points when studying the welding process. In global level simulations, the mesh density used to discretize the geometry is not usually fine enough to define the welding pool shape or a non-uniform heat source. This is only done if the simulation of the welding pool is the objective itself (local level analysis). If the global structure is considered, the size of the heat source is of the same dimension than the element size generally used for a thermo-mechanical analysis. Therefore, when the global model is taken into account, the resulting mesh density is usually too coarse to represent the actual shape of the heat source.

Depending on the framework used to describe the formulation of the coupled thermo-mechanical problem, a convective term might appear in the thermal governing equations. Therefore convection instabilities of the temperature appear for convection dominated problems. It is well known that in diffusion dominated problems, the solution is stable. However, in convection dominated problems, the stabilizing effect of the diffusion term becomes insufficient and oscillations appear in the temperature field. The threshold between stable and unstable solutions is usually expressed in terms of the Peclet number.

1.2.2.3 Kinematic Framework

Establishing an appropriate kinematic framework for the simulation of welding is one of the main objectives of this paper.

If the welding process is studied at global level, a Lagrangian framework is an appropriate choice for the description of the problem. Lagrangian settings, in which each individual node of the computational mesh represents an associated material particle during motion, are mainly used in structural mechanics. Classical applications of the Lagrangian description in large deformation problems are the simulation of vehicle crash tests and the modeling of metal forming operations. In these processes, the Lagrangian description is used in combination with both solid and structural (beam, plate, shell) elements. Numerical solutions are often characterized by large displacements and deformations and history-dependent constitutive relations are employed to describe elasto-plastic and visco-plastic material behavior. The Lagrangian reference frame allows easy tracking of free surfaces and interfaces between different materials.

In a local simulation, the main focus of the simulation is the heat affected zone (HAZ) where the use of a Lagrangian framework is not always advantageous. In the HAZ, the large distortions would require continuous re-meshing. The alternative is to use Eulerian or Arbitrary Lagrangian Eulerian (ALE) methods. Eulerian settings are widely used in fluid mechanics. Here, the computational domain and reference mesh are fixed and the fluid moves with respect to the grid. The Eulerian formulation facilitates the treatment of large distortions in the fluid motion. Its handicap is the difficulty to follow free surfaces and interfaces between different materials or different media (e.g., fluid-fluid and fluid-solid interfaces).

An Arbitrary Lagrangian Eulerian (ALE) formulation which generalizes the classical Lagrangian and Eulerian descriptions is particularly useful in flow problems involving large distortions in the presence of mobile and deforming boundaries. Typical examples are problems describing the interaction between a fluid and a flexible structure and the simulation of metal forming processes. The key idea in the ALE formulation is the introduction of a computational mesh which can move with a velocity different from (but related to) the velocity of the material particles. With this additional freedom with respect to the Eulerian and Lagrangian descriptions, the ALE method succeeds to a certain extend in minimizing the problems encountered in the classical kinematical descriptions, while combining their respective advantages at best.

In the simulation of FSW, it is adroit to introduce an apropos kinematic framework for the description of different parts of the computational domain. Despite the efficiency of the idea, the mesh moving strategy and the treatment of the domains interaction are challenging.

1.2.2.4 Coupled Problem

The numerical solution of the coupled thermo-mechanical problem involves the transformation of an infinite dimensional transient system into a sequence of discrete non-linear algebraic problems. This is achieved by means of the FE spatial descritization procedure, a time-marching scheme for the advancement of the primary nodal variables, and with a time iteration algorithm to update the internal variables of the constitutive equations.

Regarding the time-stepping schemes, two types of strategies can be applied to the solution of the coupled thermo-mechanical problems:

The first possibility is a monolithic (simultaneous) time-stepping algorithm which solves both the mechanical and the thermal equilibrium equations together. It advances all the primary nodal variables of the problem simultaneously. The main advantage of this method is that it enables stability and convergence of the whole coupled problem. However, in simultaneous solution procedures, the time-step as well as time-stepping algorithm has to be equal for all subproblems, which may be inefficient if different time scales are involved in the thermal and the mechanical problem. Another important disadvantage is the considerably high computational effort required to solve the monolithic algebraic system and the necessity to develop software and solution methods specifically for each coupled problem.

A second possibility is a staggered algorithm (block-iterative or fractional-step), where the two subproblems are solved sequentially. Usually, a staggered solution [arising from an operator split and a product formula algorithm (PFA)] yields superior computational efficiency.

Staggered solutions are based on an operator split, applied to the coupled system of non-linear ordinary differential equations, and a product formula algorithm, which leads to splitting of the original monolithic problem into two smaller and better conditioned subproblems (within the framework of classical fractional step methods). This leads to the partition of the original problem into smaller and typically symmetric (physical) subproblems. After this, the use of different standard time-stepping algorithms developed for the uncoupled subproblems is straightforward, and it is possible to take advantage of the different time scales involved. The major drawback of these methods is the possible loss of accuracy and stability. However, it is possible to obtain unconditionally stable schemes using this approach, providing that the operator split preserves the underlying dissipative structure of the original problem.

1.2.2.5 Particle Tracing

One of the main issues in the study of FSW at local level, is the heat generation. The generated heat must be enough to allow for the material to flow and to obtain a deep heat affected zone. Insufficient heat forms voids as the material is not softened enough to flow properly. The visualization of the material flow is very useful to understand its behavior during the weld. A method approving the quality of the created weld by visualization of the joint pattern is advantageous. It can be used to investigate the appropriate process parameters to create a qualified joint. However, following the position of the material during the welding process is not an easy task, neither experimentally or numerically.

The experimental material visualization is difficult and needs metallographic tools. This is why establishing a numerical method for the visualization of the material trajectory in order to gain insight to the heat affected zone and the material penetration within the work-piece thickness is one of the main objective of the work. Particle tracing is a method used to simulate the motion of material points, following their positions at each time-step of the analysis. This method can be naturally applied to the study of the material flow in the welding process. In the Lagrangian framework, as the mesh nodes represent the material points, the trajectories are the solution of the governing system of equations. When using Eulerian and ALE framework the solution does not give directly information about the material position. However, the velocity field obtained can be integrated to get an insight of the extent of material mixing during the weld.

Integration of the velocity field is proposed at postprocess level to follow the material motion (displacement field). This obliges the modeler to use an appropriate time integration method for the solution of the ODE in order to track the particles. Moreover, a search algorithm must be executed to find the position of the material points in the Eulerian or ALE meshes.

1.2.2.6 Residual Stresses

Since FSW occurs by the deformation of material at temperatures below the melting point, many problems commonly associated with fusion welding technologies can be avoided and high-quality welds are produced.

Generally, FSW yields fine microstructures, absence of cracking, low residual distortion and no loss of alloying elements. Nevertheless, as in the traditional fusion welds, a softened heat affected zone and a tensile residual stress field appear.

Although the residual stresses and distortion are smaller in comparison with those of traditional fusion welding, they cannot be ignored, specially when welding thin plates of large size.

In the local level analysis, the focus of the study is the HAZ and a viscoplastic model is used to chareacterize the material behavior. Elastic stresses are neglected and the calculation of residual stresses is not possible. However, at global level, the residual stresses are one of the main outcomes of the process simulation using an elasto-viscoplastic constitutive model. Therefore, in this work, a local-global coupling strategy is proposed in order to obtain the residual stress field.

1.3 State of the Art on the Numerical Modeling of FSW

The FSW simulation typically involves studies of the transient temperature and its dependence on the rotation and advancing speed, residual stresses in the work-piece, etc. This simulation is not an easy task since it involves the interaction of thermal, mechanical and metallurgical phenomena. Up to now several researchers have carried out computational modeling of FSW.

1.3.1 Thermal Modeling

To date, most of the research interest devoted to the topic was focused on the heat transfer and thermal analysis in FSW while the mechanical aspects were neglected. Among others, Gould and Feng [57] proposed a simple heat transfer model to predict the temperature distribution in the work-piece. Chao and Qi [27, 28] developed a moving heat source model in a finite element analysis and simulated the transient evolution of the temperature field, residual stresses and residual distortions induced by the FSW process. Their model was based on the assumption that the heat generation came from sliding friction between the tool and material. This was done by using Coulomb’s law to estimate the friction force. Moreover, the pressure at the tool surface was set constant and thereby enabled a radially dependent surface heat flux distribution generated by the tool shoulder. In this model the heat generated by the pin was neglected.

Nguyen and Weckman [77] demonstrated a transient thermal FEM model for friction welding which was used to predict the microstructure of 1045 steel. Measured power data was used to calculate the heat input and a constant temperature boundary condition at the welding interface was invoked. In another FEM thermal model by Mitelea and Radu [74] friction welding of dissimilar materials was modeled. The paper compared different heat flux distributions to determine which gave the best agreement with experimental results. To conclude both analytical and numerical techniques were used to describe the heat flow in friction welding, with a more accurate solution being obtained with the latter. Because friction welding is a short duration process, a transient model was more appropriate than one that used a steady state solution.

Colegrove et al. [40, 41] and Frigaard et al. [54] developed 3D heat flow models for the prediction of the temperature field. They used the CFD commercial software FLUENT for a 2D and 3D numerical investigation on the influence of pin geometry, comparing different pin shapes in terms of their influence upon the material flow and welding forces on the basis of both stick and slip conditions at the tool/work-piece interface. It was only the tool pin that was modeled. Several different tool shapes were considered. The modeling result showed that the difference between the result corresponding to slip and stick conditions was small and the pressure and forces were similar. In spite of the good obtained results, the accuracy of the analysis was limited by the assumption of isothermal conditions. Midling [73] and Russell and Sheercliff [86] investigated the effect of tool shoulder of the pin tool on the heat generation during the FSW operation. Generally, those early flow models and others (e.g. Askari et al. [8]) were uncoupled or sequentially coupled to the heat solvers, and limited by the computational power and software capabilities of that time.

1.3.2 Thermo-Mechanical Modeling

More recently, a coupled thermomechanical modeling and simulation of the FSW process can be found in Zhu and Chao [106], Jorge and Balancín [65] or De Vuyst et al. [44, 45]. Zhu et al. [106] used a 3D nonlinear thermal and thermo-mechanical numerical model using the finite element analysis code WELDSIM. The objective was to study the variation of transient temperature and residual stress in a friction stir welded plate of 304L stainless steel. Based on the experimental records of transient temperatures, an inverse analysis method for thermal numerical simulation was developed. After the transient temperature field was determined, the residual stresses in the welded plate were calculated using a three-dimensional elasto-plastic thermo-mechanical model. In this model the plastic deformation of the material was assumed to follow the Von Mises yield criterion and the associated flow rule.

In a more sophisticated way, De Vuyst et al. [44, 45] used the coupled thermo-mechanical FE code MORFEO to simulate the flow around tools of simplified geometry. The rotation and advancing speed of the tool were modeled using prescribed velocity fields. An attempt to consider features associated to the geometrical details of the probe and shoulder, which had not been discretized in the FE model in order to avoid very large meshes, was taken into account using additional velocity boundary conditions. In spite of that, the mesh used resulted to be large: a mesh of roughly 250,000 nodes and almost 1.5 million of linear tetrahedral elements was used. A Norton–Hoff rigid-visco-plastic constitutive equation was considered, with averaged values of the consistency and strain rate sensitivity constitutive parameters determined from hot torsion tests performed over a range of temperatures and strain rates. The computed streamlines were compared with the flow visualization experimental results obtained using copper marker material sheets inserted transversally or longitudinally to the weld line. The simulation results correlated well when compared to markers inserted transversely to the welding direction. However, when compared to a marker inserted along the weld center line only qualitative match could be obtained. The correlation could have been improved by modeling the effective weld thickness of the experiment, using a more realistic material model, for instance, by incorporating a yield stress or temperature dependent properties, more exact prescription of the velocity boundary conditions or refining the mesh in specific zones, for instance, under the probe. The authors concluded that it was essential to take into account the effects of the probe thread and shoulder thread in order to get realistic flow fields.

Fourment [51] performed the simulation of transient phases of FSW with FEM using an ALE formulation, in order to take the large deformation of a 3D coupled thermo-mechanical model into account. This method permitted both transient and steady state analysis. The formulation was developed in [52, 58] to simulate the different stages of the FSW process. Assidi [10] presented a 3D FSW simulation based on friction models calibration using Eulerian and ALE formulation. An interesting comparison of the heat energy generated by the FSW between numerical methods and experimental data was presented in Dong et al. [50] and Chao et al. [29].

In [29], Chao used a FE formulation to model the heat transfer of the FSW process in two boundary values problems: a steady state problem for the tool and transient one for the work-piece. To validate the result, the temperature evolution was recorded in the tool and in the work-piece. The heat input from the tool shoulder was assumed to be linearly proportional to the distance from the center of the tool due to heat generation by friction. To model the work-piece the code WELDSIM was used. It was a transient, nonlinear, 3D FE code. In this model only half of the work-piece was modeled due to symmetry meaning that the advancing and retreating sides of the weld were not differentiated. The conclusions from this work indicated that 95 % of the heat generated goes into the work-piece and only 5% goes to the tool. It gave a very high heat efficiency estimate.

As the model predictions are not always in agreement with experimental results. In [82], the Levenberg-Marquardt (LM) method is used in order to perform a non-linear estimation of the unknown parameters present in the heat transfer and fluid flow models, by adjusting the temperatures results obtained with the models to temperature experimental measurements. The unknown parameters are: the friction coefficient and the amount of adhesion of material to the surface of the tool, the heat transfer coefficient on the bottom surface and the amount of viscous dissipation converted into heat.

1.3.3 Global Level Modeling

Most of the above-mentioned works were performed at global level. These studies typically analyzed the effect of the welding process on the structural behavior in terms of distortions, residual stresses or weakness along the welding line, among others. As the simulations carried out at global level consider the generated heat as input parameter, several techniques were used to determine the heat input to the model. One way was to measure the temperature experimentally, and adjust the heat input of the model till the numerical and experimental temperature profiles match [27, 28, 40, 94–96]. Another technique involved estimating the power input analytically and then artificially limiting the peak temperature [54, 94] or introducing latent heat effects [94, 95] to avoid over-predicting the weld temperature. The most satisfactory approach involved measuring the weld power experimentally and using this as an input to the model [66–68, 70, 93].

Khandkar et al. [67] used a finite element method based on a 3D thermal model to study the temperature distributions during the FSW process. The moving heat source generated by the rotation and linear traverse of the pin-tool was correlated to input torque data obtained from experimental investigation of butt-welding. The moving heat source included heat generation due to torques at the interface between the tool shoulder and the work-piece, the horizontal interface between the pin bottom and the work-piece, and the vertical interface between the cylindrical pin surface and the work-piece. Temperature-dependent properties of the weld-material were used for the numerical modeling.

In Hamilton et al. [59] and Khandkar et al. [68] a torque-based heat input was used. Various aluminium alloys were included into the model and the maximum welding temperature could be predicted from tool geometry, welding parameters and material parameters. The thermal model involved an energy-slip factor which was developed by a relationship between the solidus temperature and the energy per unit length of the weld. In Khandkar et al. latest models, the thermal models were coupled with the mechanical behavior and thereby not only the heat transport was modeled, the residual stress was also an outcome of the model [69]. Khandkar et al. [69] used a coupled thermo-mechanical FE model based on torque input for calculating temperature and residual stresses in aluminium alloys and 304L stainless steel.

Reynolds et al. used two models in [85] to explain the FSW process. The first was a thermal model to simulate temperature profiles in friction stir welds. The total torque at the shoulder was divided into shoulder, pin bottom and vertical pin surface. The required inputs for the model were total input power, tool geometry, thermo-physical properties of the material being welded, welding speed and boundary conditions. The output from the model could be used to rationalize observed hardness and microstructure distributions. The second model was a fully coupled, two-dimensional fluid dynamics based model that was used to make parametric studies of variations in properties of the material to be welded (mechanical and thermo-physical) and variations in welding parameters. This was done by a non slip boundary condition at the tool work-piece interface. The deformation behavior was based on deviatoric flow stress using the Zener-Hollomon parameter. Results from this model provided insight regarding the effect of material properties on friction stir weldability and on potential mechanisms of defect formation.

Some other authors presented thermo-mechanical models for the prediction of the distribution of the residual stresses in the process of friction stir welding. A steady-state simulation of FSW was carried out by Bastier et al. [12]. The simulation included two main steps. The first one uses an Eulerian description of the thermo-mechanical problem together with a steady-state algorithm detailed in [43], in order to avoid remeshing due to the pin motion. In the second step, a steady-state algorithm based on an elasto-visco-plastic constitutive law was used to estimate the residual state induced by the process.

Some other authors used both experimental and numerical methods for computing the residual stresses. McCune et al. [72] studied computationally and experimentally the effect of FSW improvements in terms of panel weight and manufacturing cost on the prediction of residual stress and distortion in order to determine the minimum required modeling fidelity for airframe assembly simulations. They proved the importance of accurately representing the welding forging force and the process speed.

Paulo et al. [81] used a numerical-experimental procedure (contour method) to predict the residual stresses arising from FSW operations on stiffened panels. The contour method allowed for the evaluation of the normal residual stress distribution on a specimen section. The residual stress distribution was evaluated by means of an elastic finite element model of a cut sample, using the measured and digitalized out-of-plane displacements as input nodal boundary conditions.

Yan et al. [102] adopted a general method with several stiffeners designed on the sheet before welding. Based on the numerical simulation of the process for sheet with stiffeners, the residual distortion of the structure was predicted and the effect of the stiffeners was investigated. They verified first the numerical model experimentally and then applied the verified model on the structure to compute the residual stresses.

Fratini and Pasta [53] used the cut-compliance and the inverse weight-function methodologies for skin stringer FSW geometries via finite element analysis to measure residual stresses.

Rahmati Darvazi and Iranmanesh [84] presented a thermo-mechanical model to predict the longitudinal residual stress applying a so-called advancing retreating factor. The uncoupled thermo-mechanically equations were solved using ABAQUS.

1.3.4 Local Level Modeling

Since the temperature is crucial in the FSW simulation, the heat source needs to be modeled accurately. This consideration obliges the researchers to study the process at the local level where the simulation is concentrated on the stirring zone. For this type of simulation, the heat power is assumed to be generated either by the visco-plastic dissipation or by the friction at the contact interface. At this level the majority of the process phenomena can be analyzed: the relationship between rotation and advancing speed, the contact mechanisms, the effect of pin shape, the material flow within stir zone, the size of the stir zone and the corresponding consequences on the microstructure evolution, etc.

Most models of FSW consider the FEM in a Lagrangian mesh [55, 56, 71], which is used to study the process globally and to predict the weld temperature and deformation structure. However, the number of simulations using other numerical methods such as finite volume or other kinematic frameworks such as Eulerian or ALE is also considerable.

In the model by Maol and Massoni [71] (FEM with a Lagrangian mesh), the material was assumed to be visco-plastic, with temperature-dependent properties. A frictional interface was used between the two parts and its value was determined experimentally from the pressure and velocity between the two parts. Bendzsak and North [15] used the finite volume method to predict the flow field in the fully plasticized region of a friction weld. Similar and dissimilar welds were analyzed. In the similar welds the viscosity was found from a heuristic relationship, which was independent of temperature. The dissimilar welds used a transient thermal model, a complex viscosity relationship and an Eulerian-Lagrangian mesh.

A thermo-mechanical model for FSW was proposed by Dong et al. [49]. There, an axis-symmetrical FE Lagrangian formulation was used. Ulysse in [97] modeled 3D FSW for aluminium thick plates. Forces acting on the tool were studied for various welding and rotational speeds. The deviatoric stress tensor was used by Ulysse to model the stir-welding process using 3D visco-plastic modeling. Parametric studies were conducted to determine the effect of tool speed on plate temperatures and to validate the model predictions by comparing with available measurements. In addition, forces acting on the tool were computed for various welding and rotational speeds. It was found that pin forces increased with increasing welding speeds, but the opposite effect was observed for increasing rotational speeds.

Askari et al. [9] used the CTH finite volume hydrocode coupled to an advection-diffusion solver for the energy balance equation. This model predicts important fields like strain, strain rate and temperature distribution. The elastic response was taken into account in this case. The results proved encouraging with respect to gaining an understanding of the material flow around the tool. However, simplified friction conditions were used. They used particle tracking and the mixing fraction to visualize the flow. The mixing fraction determines the ratio of advancing to retreating side material in the welded joint. These techniques enabled very impressive flow visualization, with the large dispersion of material that occurs with an advancing side marker being correctly predicted. The work also predicted that material, particularly that starting on the advancing side, flows more than one revolution around the tool.

Xu et al. [99] used finite element models to describe the material flow around the pin. This was done by using a solid mechanical 2D FE model. It included heat transfer, material flow, and continuum mechanics. The pin was included but not the threads of the pin. Xu and Deng [100, 101] developed a 3D finite element procedure to simulate the FSW process using the commercial FEM code ABAQUS, focusing on the velocity field, the material flow characteristics and the equivalent plastic strain distribution. The authors used an ALE formulation with adaptive meshing and considered large elasto-plastic deformations and temperature dependent material properties. However, the authors did not perform a fully coupled thermo-mechanical simulation, super imposing the temperature map obtained from the experiments as a prescribed temperature field to perform the mechanical analysis. The numerical results were compared to experimental data available, showing a reasonably good correlation between the equivalent plastic strain distributions and the distribution of the microstructure zones in the weld. They examined the velocity gradient around the pin and found that it was higher on the advancing than retreating side and higher in front than behind the pin. Maps of the strain on the transverse cross section were compared against typical weld macrosections.

Seidel and Reynolds [90] also used the CFD commercial software FLUENT to model the 2D steady-state flow around a cylindrical tool. The paper describes the progressive development of a finite volume model in FLUENT that used a visco-plastic material whose viscous properties were based on the Sellars-Tegart relationship. Even though the model was 2D, heat generation and conduction were included. To avoid over-predicting the weld temperature, the viscosity was reduced by 3 orders of magnitude near the solidus. The model correctly predicted material flow around the retreating side of the tool.

Bendzsak et al. [13, 14] used the Eulerian code Stir3D to model the flow around a FSW tool, including the tool thread and tilt angle in the tool geometry and obtaining complex flow patterns. The temperature effects on the viscosity were neglected. They used the finite volume method to predict the flow field in the fully plasticized region of a friction weld. Similar and dissimilar welds were analyzed. In the similar welds the viscosity was found from a heuristic relationship, which was independent of temperature. The dissimilar welds used a transient thermal model, a complex viscosity relationship and an Eulerian-Lagrangian mesh.

Schmidt and Hattel [89] presented a 3D fully coupled thermo-mechanical FE model in ABAQUS/Explicit using the ALE formulation and the Johnson--Cook material law. The flexibility of the FSW machine was taken into account connecting the rigid tool to a spring. The work-piece was modeled as a cylindrical volume with inlet and outlet boundary conditions. A rigid back-plate was used. The contact forces were modeled using a Coulomb friction law, and the surface was allowed to separate. Heat generated by friction and plastic deformation was considered. The simulation modeled the dwell and weld phases of the process. A constant contact conductance was used everywhere under the sheet. They used the generated heat from three different areas, the shoulder, pin and pin tip, and used both sticking and sliding conditions. Despite the wealth of information that this model can provide (e.g. material velocity, plastic strains, and temperatures across the weld), a major shortcoming for it was the long processing time for reaching the steady-state (14 days on a 3 GHz Pentium PC to reach only 10 s of model time).

The model developed by Chen and Kovacevic [30] uses the commercial FEM software ANSYS for a thermo-mechanically coupled Lagrangian finite element model of aluminium alloy AA-6061-T6. The welding tool was modeled as a heat source. The model only included the shoulder and so the effect of the pin was ignored. This simple model severely limited the accuracy of the stress and force and the strain rate dependence was not included in the material model. However, the authors were able to investigate the effect of the heat moving source on the work-piece material. Finally the model predicted the welding forces in the x, y and z directions.

Nikiforakis [78] used a finite difference method to model the FSW process. Despite the fact that he was only presenting 2D results, the model proposed had the advantage of minimizing calibration of model parameters, taking into account a maximum of physical effects. A transient and fully coupled thermo-fluid analysis was performed. The rotation of the tool was handled through the use of the overlapping grid method. A rigid-visco-plastic material law was used and sticking contact at the tool work-piece interface was assumed. Hence, heating was due to plastic deformation only.

Heurtier et al. [60] used a 3D semi-analytical coupled thermo-mechanical FE model to simulate FSW processes. The model uses an analytical velocity field and considers heat input from the tool shoulder and plastic strain of the bulk material. Trajectories, temperature, strain, strain rate fields and micro-hardness in various weld zones are computed and compared to experimental results obtained on a AA 2024-T351 alloy FSW joint.

1.3.5 Kinematic Framework

Among the distinctive local level studies, Cho et al. [39] used an Eulerian approach including thermomechanical models without considering the transient temperature in simulation. The strain hardening and texture evolution in the friction stir welds of stainless steel was studied in this paper. A Lagrangian approach with intensive re-meshing was employed in [31] while similar approaches were applied in [17] and [18], which are not numerically efficient.

Buffa et al. [17] using the commercial FE software DEFORM-3D, proposed a 3D Lagrangian, implicit, coupled thermo-mechanical numerical model for the simulation of FSW processes, using a rigid-visco-plastic material description and a continuum assumption for the weld seam. The proposed model is able to predict the effect of process parameters on process variables, such as the temperature, strain and strain rate fields, as well as material flow and forces. Reasonably good agreement between the numerically predicted results, on forces and temperature distribution, and experimental data was obtained. The authors found that the temperature distribution about the weld line is nearly symmetric because the heat generation during FSW is dominated by rotating speed of the tool, which is much higher than the advancing speed. On the other hand, the material flow in the weld zone is non symmetrically distributed about the weld line because the material flow during FSW is mainly controlled by both advancing and rotating speeds.

Nandan et al. in [75] and [76] employed a control volume approach for discretization of the FSW domain. They investigated visco-plastic flow and heat transfer during friction stir welding in mild steel. The temperature, cooling rates and plastic flows were solved by the equations of conservation of mass, momentum and energy together with the boundary conditions. In this model the non-Newtonian viscosity was determined from the computed values of strain rate, temperature and material properties. Temperatures and total torque was compared with experimental values showing good agreement. The computed temperatures were in good agreement with the corresponding experimental values.

Aspects that are ignored by most authors are the effect of convective heat flow due to material deformation and the asymmetry of heat generation due to the much higher pressure at the back of the shoulder. The former requires a prediction of the material flow around the tool, which is difficult to implement in most (non-fluid) solvers, which only predict weld temperature.

Recently, Assidi et al. [11] used an ALE formulation implemented into the Forge3® software with a splitting approach and an adaptive re-meshing scheme based on error estimation. In [19] the residual stresses in a 3D FE model were predicted for the FSW simulation of butt joints through a single block approach. The model was able to predict the residual stresses by considering only thermal actions. Buffa et al. [19] simulated the welding process using a continuous rigid-viscoplastic finite element model in a single block approach through the Lagrangian implicit software, DEFORM-3DTM. Then, the temperature histories extracted at each node of the model were transferred to another finite element model considering elasto-plastic behavior of the material. The map of the residual stress was extrapolated from the numerical model along several directions by considering thermal actions only.

Santiago et al. [87] developed a simplified computational model taking into account the real geometry of the tool, i.e. the probe thread, and using an ALE formulation. They considered also a simplified friction model to take into account different slip/stick conditions at the pin shoulder/work-piece interface.

The more recent works performed in this direction are those presented in this paper. Agelet de Saracibar et al. [3, 4], Agelet de Saracibar et al. [5, 6], Chiumenti et al. [36], and Dialami et al. [46–48] used a sub-grid scale finite element stabilized mixed velocity/pressure/temperature formulation for coupled thermo-rigid-plastic models, using Eulerian and Arbitrary Lagrangian Eulerian (ALE) formalisms, for the numerical simulation of FSW processes. They used ASGS and OSGS methods and quasi-static sub-grid scales, neglecting the sub-grid scale pressure and using the finite element component of the velocity in the convective term of the energy balance equation. Chiumenti et al. [36], Dialami et al. [46], and Chiumenti et al. [37] developed an apropos kinematic framework for the numerical simulation of FSW processes and compared with a solid approach in [20, 21]. A combination of ALE, Eulerian and Lagrangian descriptions at different zones of the computational domain and an efficient coupling strategy was proposed. The resulting apropos kinematic setting efficiently permitted to treat arbitrary pin geometries and facilitates the application of boundary conditions. The formulation was implemented in an enhanced version of the finite element code COMET [26] developed by the authors at the International Centre for Numerical Methods in Engineering (CIMNE). Chiumenti et al. [37] used a novel stress-accurate FE technology for highly nonlinear analysis with incompressibility constraints typically found in the numerical simulation of FSW processes. They used a mixed linear piece-wise interpolation for displacement, pressure and stress fields, respectively, resulting in an enhanced stress field approximation which enables for stress accurate results in nonlinear computational mechanics.

1.4 Outline

The outline of this paper is as follows:

In Sect. 2 the thermal problem for the simulation of the FSW process at both local and global level is formulated. The thermal problem is governed by the enthalpy based balance of energy equation. Heat generation via viscous dissipation as well as frictional heating due to the contact is taken into account. Thermal convection and radiation boundary conditions are also considered.

In Sect. 3 the mechanical problem for the simulation of the welding process is formulated. The mechanical problem is described by the balance of momentum equation.

The material behavior is either thermo–elasto–visco-plastic (global level analysis) or thermo-rigid-visco-plastic (local level analysis).

Section 4 describes the discrete FE modeling and sub-grid scale stabilization to deal with incompressibility and heat convection dominated problems. The multiscale stabilization method is introduced and an approximation of the sub-grid scale variables together with the stabilization parameters is given. Algebraic Sub-grid Scale (ASGS) and Orthogonal Sub-grid Scale (OSGS) methods for mixed velocity, pressure and temperature linear elements are used. It is shown how the classical GLS and SUPG methods can be recovered as a particular case of the ASGS method.

Section 5 is devoted to the description of the proposed kinematic framework to simulate the FSW process. A novel numerical strategy to model FSW is presented. Using the Arbitrary-Lagrangian-Eulerian kinematic framework, the overall computational domain is divided into sub-domains associating an apropos kinematic framework to each one of them. A combination of ALE, Lagrangian and Eulerian formulations for the different domain parts is proposed. Coupling between each domain is explained in detail including the friction contact. The strategy adopted to deal with an accurate definition of the boundary conditions is presented.

Section 6 deals with the visualization of material flow during the welding process. A particle tracing technique is used, to visualize the trajectories of any material points. This method can be naturally applied to the simulation of the material flow in welding simulations. The trajectories of the material points are integrated from the velocity field obtained in the simulation at the post-process level.

Section 7 is devoted to the description of the Local-global strategy for the calculation of residual stresses in FSW process. The heat power is obtained at local level and then is transferred to the global one in order to compute the residual stresses.

Section 8 summarizes the work and provides a critical overview of the goals achieved in the simulation of FSW processes. Innovative features of the work are highlighted. Conclusions are drawn with regard to the fields of application and the intrinsic limits of the presented methods.

2 Thermal Problem

The governing equation representing the thermal problem is the balance of energy equation. This equation controls the temperature evolution and can be stated as ([1, 24, 34]):

$$\begin{aligned} \rho _{o}c\frac{dT}{dt}=\dot{R}-{\varvec{\nabla }}\cdot \mathbf {q} \end{aligned}$$

(1)

where $\rho _{o},$ c, T, $\dot{R}$ and $\mathbf {q}$ are the density at the reference configuration, the specific heat, temperature, the volumetric heat source introduced into the system by plastic dissipation and the heat flux, respectively.

Depending on the aim of the analysis, whether it is local or global, there are different definitions for the heat source, $\dot{R}$:

• Power dissipated through plastic deformation (i.e. local analysis).

• Known input (i.e. global analysis).

2.1 Thermal Problem at the Global Level

Fig. 5

Temperature field in a FSW process (global level)

Fig. 6

Temperature evolution obtained from global level analysis compared with experiment

At the global level, the Lagrangian framework is used to describe the thermal problem. According to this framework, the energy equation reads simply

$$\begin{aligned} \rho _{o}c\dfrac{\partial T}{\partial t}=\dot{R}-{\varvec{\nabla }}\cdot \mathbf {q} \end{aligned}$$

(2)

In global level analysis, the heat source is the (known) power input for the problem, obtained by solving the local level analysis.

Figure 5 shows the temperature field and moving heat source in a global level simulation.

The temperature field obtained from a global level analysis for different lines parallel to the weld line at the bottom surface is compared with those obtained from experiments is depicted in Fig. 6.

2.2 Thermal Problem at the Local Level

At the local level, where the focus of the simulation is the heat affected zone (fixed in the space together with the reference frame), the Eulerian framework is considered. According to this kinematic setting, the energy equation can be rewritten as

$$\begin{aligned} \rho _{o}c\left( \dfrac{\partial T}{\partial t}+\mathbf {v}\cdot {\varvec{ \nabla }}T\right) =\dot{R}-{\varvec{\nabla }}\cdot \mathbf {q} \end{aligned}$$

(3)

where $\mathbf {v}$ is the (spatial) velocity (see Sect. 5 for further details).

Fig. 7

Temperature contour field in FSW process (local level)

Fig. 8

Temperature evolution obtained from local level analysis compared with experiment

In the FSW process, the heat source introduced into the system is due to the mechanical dissipation and it is computed as a function of the plastic strain rate, ${\dot{\mathbf{e}}}$, and the deviatoric stresses, $\mathbf {s}$, as:

$$\begin{aligned} \dot{R}=\gamma \mathbf {s}:\dot{\mathbf{e}} \end{aligned}$$

(4)

where $\gamma \simeq 90\%$ is the fraction of the total plastic energy converted into heat.

Application of the local level analysis in FSW process can be seen in Fig. 7.

The temperature field obtained from a local level analysis for different lines parallel to the weld line at the bottom surface is compared with those obtained from experiments is depicted in Fig. 8.

2.3 Boundary Conditions

Let us denote by $\Omega$ an open and bounded domain. The boundary $\partial \Omega$ can be split into $\partial \Omega _{q}$ and $\partial \Omega _{T}$ such that $\partial \Omega =\partial \Omega _{q}\cup \partial \Omega _{T}$ , where fluxes (on $\partial \Omega _{q}$) and temperatures (on $\partial \Omega _{T}$) are prescribed for the heat transfer analysis as

$$\begin{aligned} \begin{array}{ccc} \mathbf {q\cdot n}=\bar{q} &{} \quad \text {on} &{} \partial \Omega _{q} \\ T=\bar{T} &{} \quad \text {on} &{} \partial \Omega _{T} \end{array} \end{aligned}$$

(5)

In Fig. 9, $\Omega _{1}$ and $\Omega _{2}$ represent the tool and the work-piece domains, respectively.

Fig. 9

Thermal boundary condition

The initial condition for the transient thermal problem in terms of the initial temperature field is: $T\left( t=0\right) =T_{o}$.

On free surfaces, the heat flux is dissipated through the boundaries to the environment by heat convection, expressed by Newton’s law as:

$$\begin{aligned} q_{conv}=h_{conv}(T-T_{env}) \end{aligned}$$

(6)

where $h_{conv}$ is the heat transfer coefficient by convection, $T_{env}$ is the surrounding environment temperature and T is the temperature of the body surface.

Another heat dissipation mechanism is heat loss due to radiation. Heat radiation flux is computed using the Stefan–Boltzmann law:

$$\begin{aligned} q_{rad}=\sigma _{0}\varepsilon (T^{4}-T_{env}^{4}) \end{aligned}$$

(7)

where $\sigma _{0}$ is the Stefan–Boltzmann constant and $\varepsilon$ is the emissivity factor.

2.4 Thermal Constitutive Model

Heat transfer by conduction involves transfer of energy within a material without material flow. The thermal constitutive model for conductive heat flux is defined according to the isotropic conduction law of Fourier. It is computed in terms of the temperature gradient, $\nabla T$, and the (temperature dependent) thermal conductivity, k, as:

$$\begin{aligned} \mathbf {q}=-k\,\nabla T \end{aligned}$$

(8)

2.5 Friction Model

The thermal exchanges at the contact boundary ($\partial \Omega _{c}$ in Fig. 9) can also result from a friction type dissipation process (Fig. 10). The heat generated by frictional dissipation at the contact interface is absorbed by the two bodies in contact according to their respective thermal diffusivity. In this section the frictional contact is described by two models: Coulomb’s law used when Lagrangian setting is considered in global studies; and Norton’s law considered when Eulerian/ALE setting is used in local studies.

Fig. 10

Velocity (top) and temperature fields (bottom) obtained with fully stick condition between pin and work-piece

2.5.1 Coulomb’s Friction Law

Adopting the classical friction model based on Coulomb’s law, the so called slip function is defined as [7]:

$$\begin{aligned} \phi \left( \mathbf {t}_{N},\mathbf {t}_{T}\right) =\left\| \mathbf {t} _{T}\right\| -\eta \left\| \mathbf {t}_{N}\right\| \le 0 \end{aligned}$$

(9)

where $\eta \left( T,\Delta \mathbf {u}_{c}\right)$ is the friction coefficient, which can result in a nonlinear function of temperature and slip displacement $\Delta \mathbf {u}_{c}$. $\mathbf {t}_{N}$ and $\mathbf {t} _{T}$ are the normal and tangential components of the traction vector, $\mathbf {t}_{c}={\varvec{\sigma }}\cdot \mathbf {n}$, at the contact interface, respectively:

$$\begin{aligned} \mathbf {t}_{N}= & {} \left( \mathbf {n}\otimes \mathbf {n}\right) \cdot \mathbf {t} _{c}=\left( \mathbf {t}_{c}\cdot \mathbf {n}\right) \mathbf {n} \end{aligned}$$

(10)

$$\begin{aligned} \mathbf {t}_{T}= & {} \left( \mathbf {I}-\mathbf {n}\otimes \mathbf {n}\right) \cdot \mathbf {t}_{c}=\mathbf {t}_{c}-\mathbf {t}_{N} \end{aligned}$$

(11)

where $\mathbf {n}$ is the unit vector normal to the contact interface.

This given, both stick and slip mechanisms can be recovered using the unified format:

$$\begin{aligned} \left\| \mathbf {t}_{T}\right\| =\varepsilon _{T}\left( \left\| \Delta \mathbf {u}_{T}\right\| -\gamma \frac{\partial \phi }{\partial \left\| \mathbf {t}_{T}\right\| }\right) =\varepsilon _{T}\left( \left\| \Delta \mathbf {u}_{T}\right\| -\gamma \right) \end{aligned}$$

(12)

together with the Kuhn-Tucker conditions defined in terms of the slip function, $\phi$, and the slip multiplier, $\gamma$, as:

$$\begin{aligned} \begin{array}{c} \phi \le 0 \\ \gamma \ge 0 \\ \phi \dot{\gamma }=0 \end{array} \end{aligned}$$

(13)

where $\varepsilon _{T}$ is a penalty parameter (regularization of the Heaviside function).

$\Delta \mathbf {u}_{T}$ and $\Delta \mathbf {u}_{N}$ are the tangential and the normal components of the total relative displacement, $\Delta \mathbf {u} _{c},$ computed as:

$$\Delta \mathbf {u}_{T}= \left( \mathbf {I}-\mathbf {n}\otimes \mathbf {n} \right) \cdot \Delta \mathbf {u}_{c}$$

(14)

$$\Delta \mathbf {u}_{N}= \Delta \mathbf {u}_{c}-\Delta \mathbf {u}_{T}$$

(15)

• The sliding condition allows for relative slip between the contact surfaces. The tangential traction vector, $\mathbf {t}_{T}$, is computed from (9) assuming $\phi =0$, as:

  $$\begin{aligned} \mathbf {t}_{T}=\eta \left\| \mathbf {t}_{N}\right\| \frac{\Delta \mathbf {u}_{T}}{\left\| \Delta \mathbf {u}_{T}\right\| } \end{aligned}$$

  (16)

  The normal traction vector is obtained with a further penalization as:

  $$\begin{aligned} \mathbf {t}_{N}=\varepsilon _{N}\Delta \mathbf {u}_{N} \end{aligned}$$

  (17)

  where $\varepsilon _{N}$ is the normal penalty parameter (not necessarily equal to $\varepsilon _{T}$), which enforces non-penetration in the normal direction.

• The stick condition is obtained for $\dot{\gamma }=0$, when the contact surfaces are sticked to each other and there is no relative slip between them. The tangential traction vector reads:

  $$\begin{aligned} \mathbf {t}_{T}=\varepsilon _{T}\Delta \mathbf {u}_{T} \end{aligned}$$

  (18)

  while the normal component of the traction vector is given by Eq. (17).

2.5.2 Norton’s Friction Law

The relative velocity between two bodies in contact is the cause of heat generation by friction. This is one of the key mechanisms of generating heat in the FSW process. When the driving variable is the velocity field, $\mathbf {v}$, it is very convenient to use a Norton type friction law.

The tangential component of the traction vector at the contact interface, $\mathbf {t}_{T}$, is defined as:

$$\begin{aligned} \mathbf {t}_{T}=\eta _{eq}\mathbf {n}_{T}=a\left( T\right) \left\| \Delta \mathbf {v}_{T}\right\| ^{q}\mathbf {n}_{T} \end{aligned}$$

(19)

where $\eta _{eq}\left( T,\Delta \mathbf {v}_{T}\right) =a\left( T\right) \left\| \Delta \mathbf {v}_{T}\right\| ^{q}$ is the equivalent friction coefficient. $a\left( T\right)$ is the (temperature dependent) material consistency, $0\le q\le 1$ is the strain rate sensitivity and $\mathbf {n}_{T}=\dfrac{\Delta \mathbf {v}_{T}}{\left\| \Delta \mathbf {v} _{T}\right\| }$ is the tangential unit vector, defined in terms of the relative tangential velocity at the contact interface.

This given, the heat flux generated by Norton’s friction law reads:

$$\begin{aligned} q_{\textit{frict}}^{\left( 1\right) }= & {} -\varsigma ^{\left( 1\right) }\mathbf {t} _{T}\cdot \Delta \mathbf {v}_{T}=-\varsigma ^{\left( 1\right) }a\left( T\right) \left\| \Delta \mathbf {v}_{T}\right\| ^{q+1} \\ q_{\textit{frict}}^{\left( 2\right) }= & {} -\varsigma ^{\left( 2\right) }\mathbf {t} _{T}\cdot \Delta \mathbf {v}_{T}=-\varsigma ^{\left( 2\right) }a\left( T\right) \left\| \Delta \mathbf {v}_{T}\right\| ^{q+1} \nonumber \end{aligned}$$

(20)

The total amount of heat generated by the friction dissipation is split into the fraction absorbed by the bodies in contact. The amount of heat absorbed by the first body, $\varsigma ^{\left( 1\right) }$, and by the second body, $\varsigma ^{\left( 2\right) }$, depends on the thermal diffusivity, $\alpha = \dfrac{k}{\rho _{0}c}$, of the two materials in contact as:

$$\begin{aligned} \varsigma ^{\left( 1\right) }= & {} \dfrac{\alpha ^{\left( 1\right) }}{\alpha ^{\left( 1\right) }+\alpha ^{\left( 2\right) }} \\ \varsigma ^{\left( 2\right) }= & {} \dfrac{\alpha ^{\left( 2\right) }}{\alpha ^{\left( 2\right) }+\alpha ^{\left( 1\right) }} \nonumber \end{aligned}$$

(21)

The more diffusive is the material of one part in comparison with the other part, the more heat is absorbed by it.

2.6 Weak Form of the Thermal Problem

Considering Eqs. (2) and (8), the weak form of the thermal problem at global level is defined over the integration domain $\Omega$ and its boundary $\partial \Omega$ as:

$$\begin{aligned}&\int \limits _{\Omega }\left( \left[ \rho _{o}c\dfrac{\partial T}{\partial t}\right] \delta T\right) dV \\&\quad +\int \limits _{\Omega }\left[ k\nabla T\cdot \nabla \left( \delta T\right) \ \right] dV =W_{\textit{ther}} \quad \forall \delta T\nonumber \end{aligned}$$

(22)

where $\delta T$ is the test function of the temperature field, while the thermal work, $W_{\textit{ther}}$, is defined as:

$$\begin{aligned} W_{\textit{ther}}=\int \limits _{\Omega }\left( \dot{R} \delta T\right) \ dV-\int \limits _{\partial \Omega q}\left( \bar{q}\delta T\right) dS-\int \limits _{\partial \Omega _{c}}\left( q_{\textit{frict}}\delta T\right) dS \end{aligned}$$

(23)

Note that the term due to friction ($q_{\textit{frict}}$) appears only at local level.

Similarly, considering Eqs. (3) and (8), the weak form of the problem at local level is written as

$$\begin{aligned}&\int \limits _{\Omega }\left( \left[ \rho _{o}c\left( \dfrac{\partial T}{ \partial t}+\mathbf {v}\cdot {\varvec{\nabla }}T\right) \right] \ \delta T\right) dV \\&\quad +\int \limits _{\Omega }\left[ k\nabla T\cdot \nabla \left( \delta T\right) \ \right] \ dV =W_{\textit{ther}}\quad \forall \delta T \nonumber \end{aligned}$$

(24)

2.7 Discrete Weak Form of the Thermal Problem

In the framework of the standard Galerkin finite element method, the discrete counterpart of the weak form for the thermal problem can be written as

• Global form

  $$\begin{aligned}&\int \limits _{\Omega }\left[ \left( \rho _{o}c\dfrac{\partial T_{h}}{\partial t}\right) \ \delta T_{h}\right] \ dV \\&\quad +\int \limits _{\Omega }\ k\nabla T_{h}{\varvec{\cdot \nabla }}\left( \delta T_{h}\right) dV\ =W_{\textit{ther}}^{\textit{ext}}\left( \delta T_{h}\right) \quad \forall \delta T_{h} \nonumber \end{aligned}$$

  (25)

• Local form

  $$\begin{aligned}&\int \limits _{\Omega }\left[ \left( \rho _{o}c\left( \dfrac{\partial T_{h}}{ \partial t}+\mathbf {v}_{h}\cdot {\varvec{\nabla }}T_{h}\right) \right) \ \delta T_{h}\right] \ dV \\&\quad +\int \limits _{\Omega }\ k\nabla T_{h}{\varvec{\cdot \nabla }}\left( \delta T_{h}\right) dV\ =W_{\textit{ther}}^{\textit{ext}}\left( \delta T_{h}\right) \quad \forall \delta T_{h} \nonumber \end{aligned}$$

  (26)

  where $T_{h}$ is the discrete temperature field.

3 Mechanical Problem

In this section, the general framework for the description of the mechanical problem in FSW processes is presented. This framework is developed both for local and global analysis. In global level analyses, the effect of a moving heat source on the entire structure is studied. The heat source is introduced into the system and moves along the weld line while the structure is fixed. In this case the Lagrangian framework is used for the definition of the problem, as the reference frame is attached to the structure. The moving heat source generates thermal deformation in the structure. Therefore, definition of the problem in terms of displacements is a natural choice for the computation of the mechanical problem. On the other side, in local level analysis, the focus of the study is the heat affected zone. The heat source is fixed together with the reference frame while the structure moves with the imposed velocity (relative movement). In this case, the Eulerian model is a suitable choice and the problem can be conveniently defined in terms of the velocity field.

Fig. 11

Mechanical results in a FSW process (local analysis)

In both cases, assuming quasi-static conditions, the local form of the balance of momentum equation, also known as Cauchy’s equation of motion, is given by

$$\begin{aligned} {\varvec{\nabla }}\cdot {\varvec{\sigma }}+\rho _{o}\mathbf {b}=0 \end{aligned}$$

(27)

where ${\varvec{\sigma }}$ is the Cauchy’s stress tensor, $\mathbf {b}$ is the body forces vector per unit of mass, $\rho _{o}$ is the density in the reference configuration and ${\varvec{\nabla }}\cdot \left( \circ \right)$ is the divergence operator.

In the case of metallic materials where the behavior of inelastic (plastic) strains is isochoric (plastic deformations are deviatoric), it is convenient to split the stress tensor, ${\varvec{\sigma }}$, into volumetric and deviatoric parts:

$$\begin{aligned} {\varvec{\sigma }}=p\mathbf {I}+\mathbf {s} \end{aligned}$$

(28)

where $p=\frac{1}{3}\mathrm {tr}\left( {\varvec{\sigma }}\right)$ is the pressure and $\mathbf {s}=\mathrm {dev}\left( {\varvec{\sigma }}\right)$ is the stress deviator. Similarly, the strain tensor, ${\varvec{\varepsilon }},$ can be split into volumetric, $e_{vol},$ and the deviatoric, $\mathbf {e,}$ parts.

$$\begin{aligned} {\varvec{\varepsilon }}=\frac{1}{3}e_{vol}\mathbf {I}+\mathbf {e} \end{aligned}$$

(29)

Therefore, the local form of the mechanical problem can be stated as:

$$\begin{aligned} {\varvec{\nabla }}\cdot \mathbf {s+\nabla }p+\rho _{o}\mathbf {b}=\mathbf {0} \end{aligned}$$

(30)

where p and $\mathbf {s}$ are defined according to the constitutive equations selected for the local or global analysis, respectively.

Fig. 12

Velocity streamlines around a triangular pin (left) and a trivex pin (right)

Fig. 13

Plastic dissipation under a FSW tool

Fig. 14

Longitudinal stress (XX) field in a global level simulation of FSW after cooling

Figure 11 shows the results of the mechanical simulation at the local level. Pressure, velocity, strain-rate and stress fields are presented around the rotating triangular pin. The peaks in mechanical variables around the pin can be seen. Due to the high rotational velocity of the pin, the asymmetry of the results are not visible.

The streamlines and velocity vectors around the triangular pin are shown in Fig. 12. One can see the strong effect of rotational velocity and the differences between retreating and advancing sides.

Plastic dissipation under the FSW tool with cylindrical pin is illustrated in Fig. 13. Note that plastic dissipation is one of the main sources of heat in FSW. Effect of the shoulder is clearly important and cannot be neglected. This obliges modelers to perform simulation in 3D in order to obtain accurate results.

Figure 14 shows the results of the mechanical simulation at global level (residual stresses). The figure illustrates the effect of a moving heat source on the stress XX field after fixture release and cooling phase.

3.1 Constitutive Model

According to the general perspective of the paper, which studies the FSW process at both local and global level, this section is divided into two parts: the first part describes the mechanical constitutive equations used at global level; the second part is devoted to the description of the mechanical constitutive model used at the local level.

3.1.1 Mechanical Constitutive Model at Global Level

When the effects induced by the process on the structural behavior are the target of the study, the global level analysis is preferred. These effects are distortions, residual stresses or weaknesses along the welding line, among others and the displacement field is the driving variable.

At global level, the stress deviator, $\mathbf {s}\left( \mathbf {u},T\right)$ , is generally defined through the constitutive equation as a function of displacements $\mathbf {u}$ and temperature T. The heat source moves along the welding path and the temperature range varies from room temperature to very high temperatures close to the melting point. Consequently, the material behavior changes from elasto-plastic (at room temperature) to pure viscous (close to the melting point). This evolution can be defined by a thermo–elasto–visco-plastic constitutive model. Close to the melting point, the viscous behavior dominates and the elastic limit gradually decreases.

To this end, it can be written:

$$\begin{aligned} p &= K\,e^{e}=K\,\,\left( e\mathbf {-}e^{\theta \,\,}\right) =K\,\,\left( \nabla \cdot \mathbf {u}-e^{\theta \,\,}\right) \end{aligned}$$

(31)

$$\begin{aligned} \mathbf {s} & =G\mathbf {e}^{e}=\,G\,\left( \,\,\mathbf { e-e}^{vp}\right) \end{aligned}$$

(32)

where K(T) is the bulk modulus, which controls the material compressibility and G is the shear modulus. Deformations $e^{\theta },e^{e},\mathbf {e}^{vp}$ and $\mathbf {e}^{e}$ are the volumetric thermal deformation, the elastic volumetric strain, the viscoplastic and the elastic deviatoric strain, respectively. The thermal deformation $e^{\theta }$ is expressed as

$$\begin{aligned} e^{\theta }=3\left[ \alpha \left( T\right) \left( T-T_{\textit{ref}}\right) -\alpha \left( T_{0}\right) \left( T_{0}-T_{\textit{ref}}\right) \right] \end{aligned}$$

(33)

where $\alpha (T)$ is the thermal expansion coefficient.

Fig. 15

Temperature dependent material properties of 304L stainless steel

Figure 15 shows the temperature-dependent material property for 304L stainless steel. The mechanical material parameters can be obtained by fitting the constitutive model with uniaxial, tensile stress–strain curves obtained at different temperatures.

The viscoplastic deformation ${\dot{\mathbf{e}}}^{vp}$ is defined through appropriate evolution laws

$$\begin{aligned} {\dot{\mathbf{e}}}^{vp}= \gamma ^{vp}\,\dfrac{{\varvec{{\partial }}\Phi }}{ \partial \mathbf {s}}=\gamma ^{vp}\mathbf {n} \end{aligned}$$

(34)

$$\begin{aligned} \dot{\xi }= \gamma ^{vp}\,\sqrt{\dfrac{2}{3}} \end{aligned}$$

(35)

where $\Phi \left( \mathbf {s,\,}T\right)$ is the viscoplastic yield surface, $\mathbf {n}=\dfrac{\mathbf {s}}{\left\| \mathbf {s}\right\| }$ is the unit normal to the yield surface and $\gamma ^{vp}\,=\left\langle \dfrac{\Phi }{\eta }\right\rangle$ is the visco-plastic parameter, when a rate-dependent evolution law is assumed. $\eta \left( T\right)$ is the plastic viscosity associated to the visco-plastic model.

3.1.2 Mechanical Constitutive Model at Local Level

When the heat affected zone is the focus of the study, the local level analysis in Eulerian format is preferred. The stress deviator $\mathbf {s} \left( \mathbf {v},T\right)$ is defined as a function of temperature, T,  and the velocities, $\mathbf {v,}$ rather than displacements. The constitutive laws are typically formulated in terms of strain-rate rather than strain. The FSW process is characterized by very high strain rates as well as a wide temperature range going from the environmental temperature to the one close to the melting point. Hence, instead of a thermo–elasto–visco-plastic model (generally adopted for metals in the Lagrangian formulation), a thermo-rigid-visco-plastic behavior is usually introduced within an Eulerian/ALE framework. The elastic strains are neglected compared to the viscoplastic flow and, therefore, precluding the computation of residual stresses.

The incompressibility constraint is often adopted by assuming that the volumetric changes, including thermal deformation, are negligible in comparison with elasto-plastic (deviatoric) deformation:

$$\begin{aligned} \dot{e}_{{\textit{vol}}}={\varvec{\nabla }}\cdot \mathbf {v}\cong 0 \end{aligned}$$

(36)

so that ${\dot{\mathbf{e}}}={\dot{\mathbf{\varepsilon }}}=\nabla ^{s}\mathbf {v}$.

According to the split of the stress tensor introduced in Eq. (28), different rate-dependent constitutive models can be used for modeling the welding process. The constitutive models are usually defined by the relationship between the deviatoric parts of the stress and the strain rate, ${\dot{\mathbf{e}}}$. This reduces into the definition of visco-plastic constitutive models of the form:

$$\begin{aligned} \mathbf {s}=\eta {\dot{\mathbf{e}}}=2\overline{ \mu }{\dot{\mathbf{e}}} \end{aligned}$$

(37)

where $\overline{ \mu }$ is the effective viscosity coefficient of the material. The following additive decomposition of the deviatoric strain rate is assumed:

$$\begin{aligned} {\dot{\mathbf{e}}}={\dot{\mathbf{e}}}^{e}+{\dot{\mathbf{e}}}^{vp} \end{aligned}$$

(38)

where ${\dot{\mathbf{e}}}^{e}$ and ${\dot{\mathbf{e}}}^{vp}$ are the elastic and visco-plastic parts, respectively. In local level FSW, the elastic part of the strain tensor, ${\dot{\mathbf{e}}}^{e}$, is negligible compared with the visco-plastic component, ${\dot{\mathbf{e}}}^{vp}$, so that:

$$\begin{aligned} {\dot{\mathbf{e}}}\equiv {\dot{\mathbf{e}}}^{vp} \end{aligned}$$

(39)

This means that the total deformation is visco-plastic and a rigid-visco-plastic model is recovered. The rigid-visco-plastic models can be interpreted as non-Newtonian laws where the viscosity $\overline{ \mu }$ is a nonlinear function of the strain-rate ${\dot{\mathbf{e}}}.$ Typical constitutive equations used for non-Newtonian modeling are listed in Table 1. The coefficients $\mu _{0}$ and $\mu _{\infty }$ in these models represent the asymptotic values of the viscosity $\overline{ \mu }$ at zero and infinite strain-rates, respectively. In the Newtonian case $\overline{ \mu }= \mu _{0}= \mu _{\infty }= \mu .$

Table 1 Various constitutive models for the viscosity

In the present paper, depending on the definition for $\overline{ \mu }$, three models are introduced from the groups (b), (c) and (f): Norton–Hoff, Sheppard–Wright and Carreau constitutive models.

3.1.2.1 Norton–Hoff Model

The Norton–Hoff model was originally introduced by Norton [79] in order to describe the unidimensional creep of steel at high temperature, and extended by Hoff [61] to multi-dimensional situations. This model can be easily characterized by simple mechanical tests and accurately describes the behavior of materials with significant viscous and creep response to loading. The Norton–Hoff model is best suited for the materials that are tough and highly rate sensitive.

According to this constitutive model, the effective viscosity is expressed as a function of the temperature and the equivalent plastic strain rate, $\overset{\cdot }{\bar{\varepsilon }}=\sqrt{2/3}\left\| {\dot{\mathbf{e}}} ^{vp}\right\| =\sqrt{2/3}\left( {\dot{\mathbf{e}}}^{vp}:{\dot{\mathbf{e}}} ^{vp}\right) ^{1/2}$, as:

$$\begin{aligned} \bar{ \mu }= \mu \left( \sqrt{3}\overset{\cdot }{\bar{\varepsilon }}\right) ^{(m-1)} \end{aligned}$$

(40)

where $0\le m\left( T\right) \le 1$ and $\mu \left( T\right)$ are the (temperature dependent) rate sensitivity and viscosity parameters, respectively (Fig. 16). Note that:

• $m=0$ leads to the expression of a rigid plastic constitutive law.

  $$\begin{aligned} \mathbf {s}=\sqrt{2} \mu \mathbf {n} \end{aligned}$$

  (41)

  where $\mathbf {n=}\dfrac{{\dot{\mathbf{\varepsilon }}}}{\left\| {\dot{\mathbf{\varepsilon }}}\right\| }=\dfrac{\mathbf {s}}{\left\| \mathbf {s} \right\| }$ defines the plastic-flow direction.

• $m=1$ leads to the linear behavior of a Newtonian fluid.

  $$\begin{aligned} \mathbf {s}=2 \mu {\dot{\mathbf{\varepsilon }}} \end{aligned}$$

  (42)

  that is, a linear relationship between stresses and strain-rates where the constant of proportionality is the viscosity parameter.

The great advantage of the Norton–Hoff model is its simplicity as it only depends on two (temperature dependent) parameters.

For the majority of metals, the rate-sensitivity parameter is usually within the range $0.1\le m\le 0.2$ which results in a very non-linear (non-Newtonian) material behavior (e.g. aluminium and steel alloys).

The nonlinearity of the Norton–Hoff model increases as m diminishes. To deal with this nonlinearity, m can be computed in a series of steps starting from the value $m=1$ in the first step and reaching its real value at step N. This implies that at each time-step i $<N$ the problem is solved with constitutive rate sensitivity $m_{i}$:

$$\begin{aligned} m_{i}=1-\left( 1-m\right) *\left( \left( 1-i\right) /\left( 1-N\right) \right) ^{m} \end{aligned}$$

(43)

Fig. 16

Stress versus strain rate affected by rate sensitivity variation

3.1.2.2 Sheppard–Wright Model

The equation used to describe the flow strength of alloys was introduced initially by Sellars and Tegart [91]. Sheppard and Wright [92] introduced an alternative rigid visco-plastic formulation extending this formulation.

According to the Sheppard–Wright model, the effective viscosity coefficient is defined in terms of effective flow stress $\sigma _{e}$ (i.e. norm of deviatoric stress) and effective strain rate $\overset{\cdot }{\bar{ \varepsilon }}$ (i.e. norm of deviatoric strain rate) as

$$\begin{aligned} \bar{\mu }=\frac{\sigma _{e}}{3\overset{\cdot }{\bar{\varepsilon }}} \end{aligned}$$

(44)

where the effective stress $\sigma _{e}$ depends on the strain rate and the temperature field (below the metals solidus temperature) and it is defined as

$$\begin{aligned} \sigma _{e}\left( \overset{\cdot }{\bar{\varepsilon }},T\right) =\frac{1}{ \alpha }\sinh ^{-1}\left( \left( \frac{Z}{A}\right) ^{1/n}\right) =\frac{1}{ \alpha }\ln \left[ \left( \frac{Z}{A}\right) ^{1/n}+\sqrt{1+\left( \frac{Z}{A }\right) ^{2/n}}\right] \end{aligned}$$

(45)

where Z, the Zener–Hollomon parameter, represents the temperature compensated effective strain rate [105]

$$\begin{aligned} Z=\overset{\cdot }{\bar{\varepsilon }}\exp \left( \frac{Q}{RT}\right) \end{aligned}$$

(46)

R is the universal gas constant and T is the absolute temperature (in Kelvin). The material constants $\alpha$, A, n and the apparent activation energy, Q,  are derived by fitting experimental response of the material, and are all independent of temperature (Fig. 17).

Fig. 17

Effect of activation energy on stress versus strain rate

The advantage of the Sheppard–Wright model in comparison with the Norton–Hoff model is the possibility of a better calibration of the material behavior in the entire temperature range from the environment temperature to the melting point.

3.1.2.3 Carreau Model

According to Carreau’s constitutive model [22, 88], the effective viscosity coefficient is defined as

$$\begin{aligned} \bar{\mu }=\left[ 1+\left( \left( \frac{\sigma _{0}}{3\dot{\varepsilon } _{0}\mu _{0}}\right) ^{\frac{n}{1-n}}\frac{\sqrt{\frac{2}{3}}\left\| {\dot{\mathbf{e}}}\right\| }{\dot{\varepsilon }_{0}}\right) ^{2}\right] ^{ \frac{1-n}{2n}}\left( \mu _{0}-\mu _{\infty }\right) +\mu _{\infty } \end{aligned}$$

(47)

where $\mu _{0}$, $\mu _{\infty }$, $\dot{\varepsilon }_{0}$ and n are the saturation viscosities at zero and infinite limits, the plastic strain rate corresponding to the yield limit $\sigma _{0}$ and n the exponent, respectively. The yield limit $\sigma _{0}$ is defined by a Johnson–Cook power of the form

$$\begin{aligned} \sigma _{0}=\left\{ \begin{array}{ll} \sigma _{0,R}\left[ 1-\left( \frac{T-T_{R}}{T_{M}-T_{R}}\right) ^{m}\right] &{}\quad T<T_{M} \\ 0 &{}\quad T\ge T_{M} \end{array} \right. \end{aligned}$$

(48)

where $T_{M}$, $T_{R}$, $\sigma _{0,R}$ and m are melting temperature, room temperature, yield limit at room temperature and Johnson–Cook exponent, respectively.

Fig. 18

Stress–Strain rate behavior of a Carreau model with temperature change

The main advantage of this constitutive model is that the range of admissible viscosity values is bounded by the viscosity at room temperature and for the liquid phase. These limit bounds will resolve the problem related to singularity of the non-Newtonian constitutive models and thus use of numerical tricks such as definition of cut-off values on the strain rates.

Figure 18 shows the stress–strain rate behavior of a Carreau model for different temperatures.

3.2 Weak Form of the Mechanical Problem

The mixed $\mathbf {u}/p$ formulation is the most classical formulation to tackle the incompressible limit, where both displacements and pressures are used as master fields. It is often used for modeling nearly incompressible (Poisson’s ratio above 0.49) or completely incompressible material behavior (Poisson’s ratio equal to 0.50). The standard irreducible formulation is simply not suitable for incompressible conditions.

The mixed $\mathbf {u}/p$ formulation solves the balance of momentum equation (30) and the volumetric part of the constitutive Eq. ( 31) in the weak form. Taking into account that $\mathbf {s}\left( {\mathbf {u}}\right)$ is defined as a function of displacement, the weak form of the mixed $\mathbf {u}/p$ mechanical problem at global level is defined over the integration domain $\Omega$ and its boundary $\partial \Omega$ as:

$$\begin{aligned} \left\{ \begin{array}{ll} \int \limits _{\Omega }\left( \mathbf {s}\left( \mathbf {u}\right) :\nabla ^{s}\delta {\mathbf {u}}\right) \; dV+\int \limits _{\Omega }\left( p{\varvec{\nabla }}\cdot \delta {\mathbf {u}}\right) \ dV=W_{\textit{mech}} &{} \quad \forall \delta \mathbf {v} \\ \int \limits _{\Omega }\left[ \left( {\varvec{\nabla }}\cdot \mathbf {u}\right) \;\delta p\right] \ dV-\int \limits _{\Omega }\left[ \left( e^{\theta }+\dfrac{p}{K}\right) \;\delta p\right] \ dV=0 &{} \quad \forall \delta p \end{array} \right. \end{aligned}$$

(49)

where $\delta {\mathbf {u}}$ and $\delta p$ are the test functions of the displacement and pressure fields, respectively, while the mechanical work is defined as:

$$\begin{aligned} W_{\textit{mech}}=\int \limits _{\Omega }\left( \rho _{o}\mathbf {b}\cdot \delta \mathbf { u}\right) \;dV+\int \limits _{\partial \Omega _{\sigma }}\left( {\bar{\mathbf{t}}}\cdot \delta {\mathbf {u}}\right) \;dS \end{aligned}$$

(50)

Definition of the problem in the mixed $\mathbf {u/}p$ format is not obligatory, however it is convenient for including both the compressible and incompressible cases. If $e^{\theta }\rightarrow 0$ and the bulk modulus $K\rightarrow \infty ,$ such as in the liquid-like phase, the incompressibility condition is recovered: ${\varvec{\nabla }}\cdot \mathbf {u} =0$. In this case, the second Eq. (49) enforces (in weak sense) the incompressibility condition as a purely kinematic constraint.

Similarly, according to Eqs. (30) and (36), and taking into account that $\mathbf {s}\left( {\mathbf {v}}\right)$ is defined as a function of the velocity field, the weak form of the mixed $\mathbf {v}/p$ mechanical problem at local level is defined over the integration domain $\Omega$ and its boundary $\partial \Omega$ as:

$$\begin{aligned} \left\{ \begin{array}{ll} \int \limits _{\Omega }\left( \mathbf {s}\left( \mathbf {v}\right) :\nabla ^{s}\delta \mathbf {v}\right) \;dV+\int \limits _{\Omega }\left( p {\varvec{\nabla }}\cdot \delta {\mathbf {v}}\right) \ dV=W_{{\textit{mech}}} &{} \quad \forall \delta \mathbf {v} \\ \int \limits _{\Omega }\left[ \left( {\varvec{\nabla }}\cdot \mathbf {v}\right) \;\delta p\right] \ dV=0 &{} \quad \forall \delta p \end{array} \right. \end{aligned}$$

(51)

where $\delta {\mathbf {v}}$ is the test function of the velocity field.

3.2.1 Boundary Conditions

For the global level analysis, the boundary $\partial \Omega$ is split into $\partial \Omega _{\sigma }$ and $\partial \Omega _{u}$, being $\partial \Omega =$ $\partial \Omega _{\sigma }$ $\cup$ $\partial \Omega _{u}$ such that the tractions are prescribed on $\partial \Omega _{\sigma }$ while displacements are specified on $\partial \Omega _{u}$. The corresponding Neumann and Dirichlet boundary conditions on $\partial \Omega _{\sigma }$ and $\partial \Omega _{u}$ are defined as

$$\begin{aligned} \begin{array}{ccc} {\varvec{\sigma }}\cdot \mathbf {n}={\bar{\mathbf{t}}} &{} \text {on} &{} \partial \Omega _{\sigma } \\ \mathbf {u}={\bar{\mathbf{u}}} &{} \text {on} &{} \partial \Omega _{u} \end{array} \end{aligned}$$

(52)

where ${\bar{\mathbf{t}}}$ and ${\bar{\mathbf{u}}}$ are the prescribed traction and velocity field, respectively and $\mathbf {n}$ is the unit outward normal to the surface $\partial \Omega _{\sigma }$.

Similarly, for the local level analysis, the boundary $\partial \Omega$ is split into $\partial \Omega _{\sigma }$ and $\partial \Omega _{v}$, being $\partial \Omega =$ $\partial \Omega _{\sigma }$ $\cup$ $\partial \Omega _{v}$ such that the velocities are specified on $\partial \Omega _{v}$ and the corresponding Dirichlet and Neumann boundary conditions on $\partial \Omega _{\sigma }$ and $\partial \Omega _{v}$ are defined.

3.3 Discrete Weak Form of the Mechanical Problem

In the framework of the standard Galerkin finite element method, the discrete counterparts of the weak forms for the mechanical problem can be written as

• Global form:

$$\begin{aligned} \left\{ \begin{array}{ll} \int \limits _{\Omega }\left( \mathbf {s}_{h}\left( {\mathbf {u}} _{h}\right) :\nabla ^{s}\delta {\mathbf {u}}_{h}\right) \; dV+\int \limits _{\Omega }\left( p_{h}\ {\varvec{\nabla }}\cdot \delta { \mathbf {u}}_{h}\right) \ dV=W_{\textit{mech}}^{\textit{ext}}\left( \delta {\mathbf {u}} _{h}\right) & \forall \delta {\mathbf {u}}_{h}\\ \int \limits _{\Omega }\left[ \left( {\varvec{\nabla }}\cdot \mathbf {u} _{h}\right) \;\delta p_{h}\right] \ dV-\int \limits _{\Omega }\left[ \left( e^{\theta }\left( T_{h}\right) +\frac{p_{h}}{K}\right) \; \delta p_{h}\right] \ dV=0 & \forall \delta p_{h} \end{array} \right. \end{aligned}$$

(53)

• Local form:

$$\begin{aligned} \left\{ \begin{array}{ll} \int \limits _{\Omega }\left( \mathbf {s}_{h}\left( {\mathbf {v}} _{h}\right) :\nabla ^{s}\delta {\mathbf {v}}_{h}\right) \; dV+\int \limits _{\Omega }\left( p_{h}\ {\varvec{\nabla }}\cdot \delta { \mathbf {v}}_{h}\right) \ dV=W_{\textit{mech}}^{\textit{ext}}\left( \delta {\mathbf {v}} _{h}\right) & \forall \delta {\mathbf {v}}_{h} \\ \int \limits _{\Omega }\left[ \left( {\varvec{\nabla }}\cdot \mathbf {v} _{h}\right) \;\delta p_{h}\right] \ dV=0 & \forall \delta p_{h} \end{array} \right. \end{aligned}$$

(54)

where ${\mathbf {u}}_{h}, {\mathbf {v}}_{h},$ $p_{h},$ $\mathbf {s}_{h}$ and $T_{h}$ are the discrete counterparts of the respective fields.

4 Stabilization Methods

In this section, a stabilized finite element formulation based on the Variational Multiscale (VMS) stabilization method is adopted. This stabilization method allows the use of equal order interpolation for the velocity and pressure fields, bypassing the need to satisfy the inf-sup condition (see Sect. 4.1), and avoiding the oscillations arising in convective dominated problems (see Sect. 4.2).

4.1 Pressure Stabilization

It is known that the incompressibility constraint or under isochoric strain conditions, the use of an irreducible velocity-based (or displacement-based) formulation leads to pressure locking situations. It must be pointed out that when using a J2-plasticity model (in solid mechanics) or one of the non-Newtonian laws presented in the previous section (for the Eulerian framework), it is usual to get an isochoric strain field, that is, most of the deformations are deviatoric and the volumetric part is negligible. The use of a mixed $\mathbf {v}/p$ formulation is a well-known remedy. However, when the mixed Galerkin formulation is used, compatible spaces for the pressure and the velocity field have to be considered and they must satisfy the Ladyzhenskaya–Babuška–Brezzi (LBB) stability condition [16].

The LBB compatibility condition restricts the choice of finite element spaces $V_{h}$ and $P_{h}$ for velocities (or displacements) and pressure, respectively. It states that in order to obtain a stable formulation, $V_{h}$ and $P_{h}$ must be chosen such that the following inf–sup condition is satisfied:

$$\begin{aligned} \underset{\delta p_{h}\in P_{h}}{\inf }\underset{\delta {\mathbf {v}} _{h}\in V_{h}}{\sup }\frac{\left( \delta p_{h},\nabla \cdot \delta {\mathbf {v}}_{h}\right) }{\left\| \delta p_{h}\right\| _{0}\left\| \delta {\mathbf {v}}_{h}\right\| _{1}}\ge \alpha >0, \end{aligned}$$

(55)

where parameter $\alpha$ is independent of the mesh size h. If the LBB compatibility condition is satisfied, there exists a unique solution ${\mathbf {v}}_{h}\in V_{h}$ and a $p_{h}\in P_{h}$ (determined up to an arbitrary constant in the case of purely Dirichlet boundary conditions).

Unfortunately, standard Galerkin mixed elements with continuous equal order linear velocity/pressure interpolation violate the LBB condition, leading to instabilities in the pressure field and poor numerical performance. Stable formulations can be obtained either by choosing velocity/pressure pairs that satisfies the LBB condition (e.g. P2/P0 [62]) or by using pressure stabilization methods.

Using LBB stable elements, such as the Q2/Q1 (Taylor–Hood element, based upon continuous quadratic velocity, continuous bilinear pressure) or the mini element (continuous linear velocity+bubble function, continuous linear pressure) is difficult in practice, due to the complexity of the associated implementation and lower computational efficiency than that of simplicial elements. Fortunately, there exist possibilities for circumventing the LBB condition, which permit the use of equal order velocity/pressure interpolations, by modifying the original Galerkin problem, adding stabilization terms.

Essentially, in the majority of stabilization methods, the stabilizing terms added to the original Galerkin formulation involve the residual of the balance of momentum equation. These methods are called residual-based. A stabilization method is consistent if, on convergence, the solution of the modified problem is exactly the solution of the original problem.

The sub-grid method was originally introduced in [64] as a powerful technology known for its enhanced accuracy properties. The exact solution is split into two parts, corresponding to different scales or levels of resolution: the one that can be captured by the finite element mesh (coarse) and the other one, called the sub-grid (finer) part. While the first one can be resolved by the finite element method, the latter one cannot. The particular approximation used for the sub-grid scale defines the numerical strategy. The solution of the continuous problem contains components from both scales. It is necessary to, somehow, include the effect of both scales in the approximation to get the stable solution of the discrete problem. The aim is to find an approximate solution for the sub-grid scale and to include it into the discrete finite element solution. The effect of this finer scale can be included, at least locally, to enhance the stability of the pressure in the mixed formulation [2, 25, 32, 33].

To this end, the solution space, $\Psi$, is split into two parts:

$$\begin{aligned} \Psi =\Psi _{h}\oplus \tilde{\Psi } \end{aligned}$$

(56)

$\Psi _{h}$ denotes the finite element solution while $\tilde{\Psi }$, is the one that completes $\Psi _{h}$ in $\Psi$ and it is called the sub-grid scale [63, 64]. Accordingly, the velocity and pressure fields of the mixed problem are expressed as (Fig. 19)

$$\begin{aligned} \mathbf {v} &= \mathbf {v}_{h}+\widetilde{\mathbf {v}} \\ p &= p_{h} \nonumber \end{aligned}$$

(57)

where $\mathbf {v}_{h}\in$ $\Psi _{h}$ is the velocity field of the finite element scale and $\widetilde{\mathbf {v}}\in \tilde{\Psi }$ is the enhancement of the velocity field belonging to the sub-grid scale. Note that no sub-grid scale contribution is considered for the pressure field. It is reasonable to assume that the sub-grid velocities $\widetilde{\mathbf {v}}$ are sufficiently small compared to $\mathbf {v}_{h}$. They can be viewed as a high frequency perturbation of the finite element field, which cannot be resolved in $\Psi _{h}$. It can also be assumed that $\widetilde{ \mathbf {v}}$ and its variation $\delta \widetilde{\mathbf {v}}$ vanish on the boundary $\partial \Omega.$

Fig. 19

Finite element and sub-grid scale parts of the solution ${\mathbf{U}}= \left(\begin{array}{l}{\mathbf {v}} \\ {p} \end{array}\right)$

Different choices are available for the approximation of the velocity sub-grid scale. Two possible options correspond to the ASGS and the OSGS methods.

Using ASGS method, $\widetilde{\mathbf {v}}$ is approximated as $\widetilde{ \mathbf {v}}=\tau _{v}r_{h}$, where $r_{h}$ is the residual of the momentum equation in finite element space.

$$\begin{aligned} r_{h}=r_{h}\left( {\mathbf {v}}_{h},p_{h}\right) ={\varvec{\nabla }} \cdot \mathbf {s}_{h}+{\varvec{\nabla }}p_{h}+\rho _{o}\mathbf {b\simeq \nabla } p_{h} \end{aligned}$$

(58)

where ${\varvec{\nabla }}\cdot \mathbf {s}_{h}$ vanishes when using linear triangular or tetrahedral elements and the body forces, $\rho _{o}\mathbf {b}$, are negligible. This given:

$$\begin{aligned} \widetilde{\mathbf {v}}=\tau _{v}{\varvec{\nabla }}p_{h} \end{aligned}$$

(59)

After substituting into the weak form of both the balance of momentum equation and the constitutive equation, the discrete ASGS stabilized weak form of the mechanical problem for linear elements simplifies to:

$$\begin{aligned} \left\{ \begin{array}{ll} \int \limits _{\Omega }\left( \mathbf {s}_{h}:\nabla ^{s}\delta {\mathbf {v}}_{h}\right) \;dV+{\int \limits _{{\varvec{\Omega }} }}\left( p_{h}\ {\varvec{\nabla }}\cdot \delta {\mathbf {v}}_{h}\right) \ dV=W_{\textit{mech}}^{\textit{ext}}\left( \delta \mathbf {v}_{h}\right) &{} \quad \forall \delta \mathbf {v}_{h} \\ \int \limits _{\Omega }\left[ \left( {\varvec{\nabla }}\cdot \mathbf {v} _{h}\right) \;\delta p_{h}\right] \ dV+\int \limits _{\Omega }\tau _{v}\left( {\varvec{\nabla }}\delta p_{h}\cdot {\varvec{\nabla }}p_{h}\right) dV=0 &{} \quad \forall \delta p_{h} \end{array} \right. \end{aligned}$$

(60)

where $\int \limits _{\Omega }\tau _{v}\left( {\varvec{\nabla }}\delta p_{h}\cdot {\varvec{\nabla }}p_{h}\right) dV$ is the resulting stabilization term to be considered.

A further approximation for the unknown sub-grid space $\tilde{\Psi },$ is the space orthogonal to the finite element space, referred to hereafter as $\Psi _{h}^{\perp }$. This means approximating the solution space as $\Psi \simeq \Psi _{h}\oplus \Psi _{h}^{\perp }$. The subsequent stabilization method is called OSGS method, and it has already been successfully applied to several problems in fluid and solid mechanics. According to OSGS, $\widetilde{\mathbf {v}}$ is approximated as $\widetilde{\mathbf {v}}=$ $\tau _{v}P_{h}^{\perp }\left( r_{h}\right)$, where $P_{h}^{\perp }$ is the orthogonal projection onto the space orthogonal to the finite element space (Fig. 20).

Fig. 20

Representation of OSGS solution space

The orthogonal projection of a variable $\left( \cdot \right)$ can be computed as: $P_{h}^{\perp }\left( \cdot \right) =\left( \cdot \right) -P_{h}\left( \cdot \right)$. The resulting discrete OSGS stabilized weak form of the mechanical problem is:

$$\begin{aligned} \left\{ \begin{array}{ll} \int \limits _{\Omega }\left( \mathbf {s}_{h}:\nabla ^{s}\delta { \mathbf {v}}_{h}\right) \;dV+\int \limits _{\Omega }\left( p_{h}\ {\varvec{\nabla }}\cdot \delta {\mathbf {v}}_{h}\right) \ dV=W_{\textit{mech}}^{\textit{ext}}\left( \delta \mathbf {v}_{h}\right) &{} \quad \forall \delta \mathbf {v}_{h} \\ \int \limits _{\Omega }\left[ \left( {\varvec{\nabla }}\cdot \mathbf {v} _{h}\right) \;\delta p_{h}\right] \ dV+\int \limits _{\Omega }\tau _{v}\left[ {\varvec{\nabla }}\delta p_{h}\cdot \left( {\varvec{\nabla }} p_{h}-\Pi _{h}\right) \right] dV=0 & \quad \forall \delta p_{h} \\ \int \limits _{\Omega }\left( {\varvec{\nabla }}p_{h}\cdot \delta \Pi _{h}\right) dV-\int \limits _{\Omega }\left( \Pi _{h}\cdot \delta \Pi _{h}\right) dV=0 & \quad \forall \delta \Pi _{h} \end{array} \right. \end{aligned}$$

(61)

where $\Pi _{h}=P_{h}\left( {\varvec{\nabla }}p_{h}\right)$ and $\delta \Pi _{h}$ are the smooth projection of the pressure gradient and its variation onto the finite element space, respectively.

The resulting system is an accurate, stable and consistent formulation for the solution of the mechanical problem subjected to the incompressibility constraint.

Fig. 21

Pressure field (left) and streamlines (right) obtained using ASGS (top) and OSGS (bottom) stabilization method

The stabilization parameter $\tau _{v}$, is computed as:

$$\begin{aligned} \tau _{v}=c_{u}\frac{h^{2}}{2\bar{\mu }} \end{aligned}$$

(62)

where h is the element size, $c_{u}$ is a constant and $\bar{\mu }$ is the parameter defined according to the constitutive model (either effective viscosity or shear modulus). $\bar{\mu }\left( T\right)$ is usually temperature dependent and therefore the stabilization term $\tau _{v}\left( T\right)$ is a temperature dependent parameter.

Figure 21 compares results of ASGS and OSGS pressure stabilization methods in a parallel flow passing through a tube. The results obtained using OSGS are nodally exact, and totally unaffected by the boundary conditions [6].

4.2 Convective Stabilization

When using an ALE or Eulerian framework for the description of the problem, a convective term coming from the material time derivative arises in the equations.

It is well-known that in diffusion dominated problem, the solution of the balance of energy equation is stable. However, in convection dominated problem, the stabilizing effect of the diffusion term is insufficient and instabilities appear in the solution. The threshold between stable and unstable conditions is usually expressed in terms of the Peclet number. The typical Peclet number for FSW processes ranges from $10^{1}$ to $10^{3}$. For this range of the Peclet number, the effect of the convective term cannot be neglected and the solution of the thermal problem is found to be instable.

According to the sub-grid scale method, the solution space $\Theta$ of the temperature field is split into two parts: the finite element space and the space for the sub-grid scale.

$$\begin{aligned} \Theta =\Theta _{h}+\tilde{\Theta } \end{aligned}$$

(63)

Therefore, the temperature field can be approximated as

$$\begin{aligned} T=T_{h}+\tilde{T} \end{aligned}$$

(64)

where $T_{h}\in \Theta _{h}$ is the temperature component of the (coarse) finite element scale and $\tilde{T}\in \tilde{\Theta }$ is the enhancement of the temperature field corresponding to the (finer) sub-grid scale. Let us also consider the corresponding variations $\delta T_{h}\in \Theta _{h}$ and $\delta \tilde{T}$ $\in \tilde{\Theta }$, respectively.

Also in this case, we consider two possible choices for the approximation of the temperature sub-grid scales corresponding to the ASGS and the OSGS methods.

In the ASGS method, $\tilde{T}$ is approximated as $\tilde{T}\mathbf {=} \tau _{\theta }r_{h}^{\theta }$, where $r_{h}^{\theta }$ is the residual of the energy balance equation in the finite element scale.

$$\begin{aligned} r_{h}^{\theta }=\rho _{o}c\left( \frac{\partial T_{h}}{\partial t}+\mathbf {v} _{h}\cdot {\varvec{\nabla }}T_{h}\right) \ -{\varvec{\nabla \cdot }}\left( k {\varvec{\nabla }}T_{h}\right) \simeq \rho _{o}c\left( \frac{\partial T_{h}}{ \partial t}+\mathbf {v}_{h}\cdot {\varvec{\nabla }}T_{h}\right) \end{aligned}$$

(65)

where the diffusive term, ${\varvec{\nabla \cdot }}\left( k{\varvec{\nabla }} T_{h}\right) ,$ vanishes when using linear triangular or tetrahedral meshes.

In this case, the discrete thermal equation for linear elements can be stabilized by adding a residual based ASGS stabilization term of the form:

$$\begin{aligned} \int \limits _{\Omega }\tau _{\theta }\left[ \rho _{o}c\left( \mathbf {v} _{h}\cdot {\varvec{\nabla }}\left( \delta T_{h}\right) \right) \right] \ \left[ \rho _{o}c\left( \mathbf {v}_{h}\cdot {\varvec{\nabla }}T_{h}\right) \ \right] dV \end{aligned}$$

(66)

to the Galerkin weak form of the problem. This given:

$$\begin{aligned}&\int \limits _{\Omega }\left[ \rho _{o}c\left( \frac{\partial T_{h}}{ \partial t}+\mathbf {v}_{h}\cdot {\varvec{\nabla }}T_{h}\right) \ \delta T_{h} \right] \ dV+\int \limits _{\Omega }\ \left( k\nabla T_{h}\right) \mathbf {\cdot }\nabla \left( \delta T_{h}\right) dV \nonumber \\&\quad +\int \limits _{\Omega }\tau _{\theta }\left[ \rho _{o}c\left( \mathbf {v} _{h}\cdot {\varvec{\nabla }}\left( \delta T_{h}\right) \right) \right] \ \left[ \rho _{o}c\left( \mathbf {v}_{h}\cdot {\varvec{\nabla }}T_{h}\right) \ \right] dV=W_{\textit{ther}}^{\textit{ext}}\left( \delta T_{h}\right) \quad \forall \delta T_{h} \end{aligned}$$

(67)

It can be observed that for linear elements, the ASGS method coincides with the SUPG method.

As an alternative, the space orthogonal to the finite element space $\Theta _{h}^{\perp }$ can be adopted for the approximation of the unknown sub-grid space $\tilde{\Theta }$. This means that the solution space is approximated as $\Theta \simeq \Theta _{h}\oplus \Theta _{h}^{\perp }$. According to the OSGS method, $\tilde{T}$ is defined as $\tilde{T}\mathbf {=} \tau _{\theta }P_{h}^{\perp }\left( r_{h}^{\theta }\right)$.

Taking into account that $P_{h}^{\perp }\left( \cdot \right) =\left( \cdot \right) -P_{h}\left( \cdot \right)$, the resulting discrete OSGS stabilized weak form of the thermal problem for linear elements simplifies to:

$$\begin{aligned}&\int \limits _{\Omega }\left[ \rho _{o}c\left( \dfrac{\partial T_{h}}{ \partial t}+\mathbf {v}_{h}\cdot {\varvec{\nabla }}T_{h}\right) \ \delta T_{h} \right] \ dV+\int \limits _{\Omega }\left( k\nabla T_{h}\right) {\varvec{\cdot \nabla }}\left( \delta T_{h}\right) dV\ \\&\quad +\int \limits _{\Omega }\tau _{\theta }\left[ \rho _{o}c\left( \mathbf {v} _{h}\cdot {\varvec{\nabla }}\left( \delta T_{h}\right) \right) \right] \ \left[ \rho _{o}c\left( \mathbf {v}_{h}\cdot {\varvec{\nabla }}T_{h}\right) -\Pi _{h}^{\theta }\ \right] dV=W_{\textit{ther}}^{\textit{ext}}\left( \delta T_{h}\right) \quad \forall \delta T_{h} \\&\int \limits _{\Omega }\left[ \left( \mathbf {v}_{h}\cdot {\varvec{\nabla }} T_{h}\right) \text { }\delta \Pi _{h}^{\theta }\ \right] dV-\int \limits _{ \Omega }\left[ \Pi _{h}^{\theta }\cdot \text { }\delta \Pi _{h}^{\theta }\ \right] dV=0 \quad \forall \delta \Pi _{h}^{\theta } \end{aligned}$$

(68)

where $\Pi _{h}^{\theta }$ is the smooth projection of the convective term.

$$\begin{aligned} \Pi _{h}^{\theta }=P_{h}\left[ \rho _{o}c\left( \mathbf {v}_{h}\cdot {\varvec{\nabla }}T_{h}\right) \ \right] \end{aligned}$$

(69)

The mesh dependent stabilization parameter defined for the thermal (convective) problem is

$$\begin{aligned} \tau _{\theta }=\left( c_{1}\frac{k}{h^{2}}+c_{2}\frac{\left\| \mathbf {v} _{h}\right\| }{h}\right) ^{-1} \end{aligned}$$

(70)

where h is the element size, $c_{1}$ and $c_{2}$ are algorithmic constants.

Fig. 22

Comparison between the temperature distribution at different times (10, 40 and 70) and at the steady state

Comparison between the temperature distribution at the center line at different times (10, 40 and 70) and at the steady state, obtained using GLS pressure stabilization method and OSGS and SUPG convection stabilization methods are shown in Fig. 22 in a parallel flow passing through a tube.

5 Apropos Kinematic Framework

The kinematic framework used for the simulation of FSW process is different if a local or global analysis is performed. When the process is simulated at global level, the Lagrangian framework is preferred. In this case the movement of the material points, $\mathbf {X}$, coincides with the mesh nodes. The material and local time derivative of the temperature concide:

$$\begin{aligned} \dfrac{dT\left( \mathbf {X},t\right) }{dt}=\dfrac{\partial T\left( \mathbf {X} ,t\right) }{\partial t} \end{aligned}$$

(71)

If the process is studied at the local level, ALE or Eulerian frameworks are a convenient choice. In this case, the material derivative depends on the local derivative plus a convective term of the form:

$$\begin{aligned} \dfrac{dT\left( \mathbf {x},t\right) }{dt}=\dfrac{\partial T\left( \mathbf {x} ,t\right) }{\partial t}+\dfrac{\partial T\left( \mathbf {x},t\right) }{ \partial \mathbf {x}}\dfrac{d\mathbf {x}}{dt}=\dfrac{\partial T\left( \mathbf {x },t\right) }{\partial t}+\mathbf {v}\left( \mathbf {x},t\right) \cdot \nabla _{ \mathbf {x}}T\left( \mathbf {x},t\right) \end{aligned}$$

(72)

where $\mathbf {v}\left( \mathbf {x},t\right)$ is the spatial velocity and $\nabla _{\mathbf {x}}T\left( \mathbf {x},t\right)$ is the spatial gradient. The convective term accounts for the movement of the material points with respect to a fixed mesh.

In the ALE framework, the reference system neither moves together with the material (Lagrangian) nor is fixed (Eulerian) but it can move arbitrary. In this case, the material derivative depends on the local derivative plus a convective term as a function of the relative velocity $\mathbf {c}$. It is defined as

$$\begin{aligned} \dfrac{dT\left( {\varvec{\chi }},t\right) }{dt}\cong & {} \dfrac{\partial T\left( {\varvec{\chi }},t\right) }{\partial t}+\dfrac{\partial T\left( {\varvec{\chi }},t\right) }{\partial {\varvec{\chi }}}\dfrac{d{\varvec{\chi }}}{dt}\nonumber \\= & {} \dfrac{\partial T\left( {\varvec{\chi }},t\right) }{\partial t}+\mathbf {c} \cdot \nabla _{{\varvec{\chi }}}T\left( {\varvec{\chi }},t\right) \end{aligned}$$

(73)

where the relative velocity is $\mathbf {c}=\mathbf {v}\left( {\varvec{\chi }} ,t\right) -\mathbf {v}_{\textit{mesh}}$. $\mathbf {v}\left( {\varvec{\chi }},t\right)$ and $\mathbf {v}_{\textit{mesh}}$ are the material and the mesh velocities, respectively .

In this case, the movement of the mesh must be calculated at each time-step. In general, an ad-hoc methodology is necessary to compute the position of the mesh at each time-step of the analysis. This is known to be one of the main difficulties of the ALE method.

At this point, it is convenient to introduce a feasible strategy and an apropos kinematic framework for the simulation of the FSW process. In the FSW process, the pin rotates at constant angular velocity and, at the same time, advances with a constant speed. For the sake of convenience, in the numerical simulation, the movement of the pin is defined by the pure rotation around its axis while the advancing speed (in the opposite direction) is imposed to both the work-piece and the back-plate.

Taking into account that, during the welding process, the pin is rotating with a very high speed (e.g. 50–5000 RPM, depending on the work-piece material), a fully Lagrangian approach (which follows the material particles of the continuum in their motion) leads to a computational overhead. The reason is that in a Lagrangian analysis, the mesh is attached to the material and thus the mesh deforms with it. The material in the stirring zone suffers very large deformations at high strain-rates. As a consequence, a fine mesh and a continuous re-meshing are required to avoid an excessive mesh distortion. This usually leads to computationally intensive analyses, as well as, to a general loss of solution accuracy due to the interpolation process necessary to move both nodal and Gaussian variables from mesh to mesh.

Application of a fully Eulerian approach is feasible exclusively for pins with a circular cross-section. When the pin is not cylindrical, the boundaries of the model are continuously changing according to the actual position/rotation of the pin. As a consequence, the integration domain must be re-defined at each time-step of the simulation.

In modeling FSW, the choice of kinematic frameworks for different domain zones (regions) crucially impacts on the computational efficiency and the solution quality. For defining the suitable frameworks several observations must be made:

• The extent of the material deformation varies in different regions of the analysis domain.

• Pins used in practice are not necessarily cylindrical (Fig. 4).

• Boundary conditions must be applied conveniently according to the movement of the pin.

• Re-definition of the integration domain and re-meshing is preferably to be avoided.

Fig. 23

The geometry discretization

In the proposed methodology, the original geometry is divided into three distinct zones (Fig. 23) which are: the pin, the work-piece and the stir-zone (process zone close to the pin where most of the material deformation takes place). An apropos kinematic framework is adopted for each one of these zones.

• The pin is assumed to be rigid and it is defined in the Lagrangian framework as at each time-step of the analysis, the mesh moves according to the rotation of the pin.

• The work-piece, excluding the stir-zone close to the pin, is modeled in the Eulerian framework, as in this area the domain neither changes its shape nor contains moving boundaries. The fixed mesh in Eulerian zone enables the application of boundary conditions in the inflow and outflow of the work-piece.

• In the stir-zone, the material is subjected to extremely high strains. Thus, the ALE kinematic framework is chosen to study the stir-zone. The stir-zone is modeled as a circular region around the pin. The size of this area strongly depends on the viscosity and thermal diffusivity of the material. The key idea consists in using the so-called mesh sliding techniques, meaning that the mesh rigidly rotates at each time-step according to the pin movement, decoupling the material motion from the motion of the mesh. Consequently, the integration domain moves in such a way that the inner boundary of the stir-zone is connected to the contour surface of the pin. In the ALE approach, the calculation of the mesh velocity can be a difficulty while in the proposed strategy, this is not an issue. When studying a FSW process, the mesh velocity can be prescribed according to the pin rotation as:

  $$\begin{aligned} \mathbf {v}_{\textit{mesh}}={\varvec{\varpi }} \times {\varvec{r}} \end{aligned}$$

  (74)

  where ${\varvec{\varpi }}$ is the angular velocity of the pin and $\mathbf {r}$ is the position of any grid point with respect to the rotation axis.

The ALE kinematic framework can recover the Lagrangian and the Eulerian frameworks as limit cases. Denoting by $\mathbf {v}_{\textit{mesh}}$ the mesh velocity, the convective term can be written as $\rho _{o}c\left[ \left( \mathbf {v}-\mathbf {v}_{\textit{mesh}}\right) \cdot {\varvec{\nabla }}T\right]$, the convective term vanishes in the Lagrangian framework ($\mathbf {v=v}_{\textit{mesh}}$) and simplifies to $\rho _{o}c$ $\mathbf {v}\cdot {\varvec{\nabla }}T$ in the Eulerian zone ($\mathbf {v}_{\textit{mesh}}=\mathbf {0}$). Table 2 summarizes the computational framework together with the solution hypotheses for the pin, the work-piece and the stir-zone.

Table 2 Convective velocity, material derivative and spatial gradient in Lagrangian (pin), Eulerian (work-piece) and ALE (stir-zone) formulations

According to the geometry subdivision and kinematic frameworks introduced, two different types of domain interactions exist. The coupling between each part needs a special attention: on one hand, the connection between the fixed mesh of the work-piece and the ALE mesh used for the stir-zone must be considered. On the other hand, the frictional contact between the stir-zone and the pin (see Sect. 2.5) must be defined.

The coupling at the interface between the ALE (stir-zone) and the Eulerian (work-piece) parts requires a special treatment as the mesh is fixed on one side (Eulerian) and it moves on the other side (ALE). Physically, work-piece and stir-zone are not separated, they belong to the same metal sheet even if in the numerical model, a relative movement of the two computational sub-domains exists. Therefore, the objective is to get continuous fields for all the state variables $\mathbf {v,}$ p and T at the interface between the two zones. The coupling is performed using a node-to-node link or node-to-face contact approach.

Fig. 24

Node-to-node link approach

In the first and simpler case, each node of the mesh on the interface is duplicated (Fig. 24). One node belongs to the ALE region and the other one to the Eulerian region. At every mesh movement, for a given node of the ALE surface, the corresponding node of the Eulerian side is found and a link between the two nodes is created. A search algorithm restricted to the interface nodes is performed in order to identify all the node-to-node connections at the interface. This leads to an ad-hoc assembling procedure, where the contributions (elemental residuals and tangent matrices) of the stir-zone nodes are summed to the corresponding contributions of the work-piece nodes. This approach requires a coincident mesh at the interface. The time-step is chosen such that the two meshes (ALE and Eulerian) are synchronized to keep the Courant number, $Cu=1$ at the sliding interface.

The node-to-node linking approach is simple to achieve for 2D analysis but it becomes complex when an automatic 3D mesh generator (which usually supports unstructured tetrahedral meshes) is used. This approach can be applied in 3D analysis if a structured mesh is defined at the interface surfaces. It should be meshed in such way that at each time-step, the ALE mesh at the interface slides from one node to another. This requires coincident and equi-spaced mesh at the contact surfaces.

If the surface meshes are not coincident, a node-to-face approach can be used. For this more complex approach, the mesh is not sychronized. Therefore, at the sliding interface, contact elements are created. At the contact interface, each node of the stir-zone is projected on the work-piece surface. Once the contact elements are generated, whether the Lagrange multiplier method, the augmented Lagrange method, or the penalty method can be used to apply the constraint between the problem variables, T, p, $\mathbf {v}$.

In the penalty method, very large values of both stiffness and thermal resistivity representing the penalty parameters are assigned to the contact elements. This is performed to ensure the most rigid/conductive link between the two domains in both the mechanical and the thermal problems. In this case, the integration domains are connected by forcing coincident heat fluxes and normal tractions on both sides of the contact surface.

In this approach, at each time-step, the contact elements need to be regenerated according to a (rather time-consuming) closest-point-projection algorithm.

6 Particle Tracing Technique

One of the main issues in the study of FSW is heat generation. In the FSW process, welding is achieved by the heat generated due to friction and the material mixing/stirring process. The heat generated must be enough to allow for the material to flow and to obtain a deep heat affected zone. The visualization of the material flow is very useful to understand its behavior during the weld (Fig. 25). A method assessing the quality of the created weld by visualization of the joint pattern is advantageous. It can be used to have a pre-knowledge of the appropriate process parameters.

Fig. 25

Material flow visualization in horizontal and vertical directions

In this paper, a numerical particle tracing technology is introduced to study the extent of material stirring during the FSW process and to study the weld quality.

Using the Lagrangian framework, the solution obtained at the mesh points represents the material movement: points of the mesh are material particles. Therefore, no special technique for the tracking of the material is necessary. A particle tracing technique needs to be used when the solution of the problem is performed in ALE or Eulerian kinematic frameworks.

Due to the ALE framework of the finite element analysis used, the motion of the mesh is not necessarily tied to the motion of the material. During the analysis, a material particle moves through the mesh and at different time, it is located inside different elements. To observe material movement around the pin, it is necessary to construct and analyze material particle trajectories. This is possible with the use of a particle tracing method to follow the motion of material points. This method can be naturally applied to the study of the material flow in the welding process.

Fig. 26

Material points distribution

Fig. 27

Tracer position in time

Fig. 28

Velocity effect on the weld quality

In this method, firstly, a set of points representing the material points (tracers) are distributed in the domain and then, an Ordinary Differential Equation (ODE) for the computation of material displacement at a post-process level must be solved (Fig. 26). Each particle position is integrated from:

$$\begin{aligned} \frac{D\left( \mathbf {X}\left( t\right) \right) }{Dt}=\mathbf {V}\left( \mathbf {X}\left( t\right) ,t\right) \end{aligned}$$

(75)

with the initial condition

$$\begin{aligned} \mathbf {X}\left( t=0\right) =\mathbf {X}_{0} \end{aligned}$$

where $\mathbf {X}\left( t\right)$ is the position of the material points at time t and $\mathbf {V}\left( \mathbf {X}\left( t\right) ,t\right)$ is the velocity of the tracer in the position $\mathbf {X}\left( t\right)$ and time t. The tracer velocity is obtained interpolating the nodal velocity of the background mesh. To this end, firstly, a search algorithm is necessary in order to identify the element containing the tracer (Fig. 27).

To solve Eq. (77), there exist a large amount of integration techniques ranging from the simple first order Backward Euler (BE) scheme to higher order Runge-Kutta schemes. The RK4 method is the best choice among the other integration techniques because it can integrate exactly a circular trajectory, which is the most common particle path in FSW.

Fig. 29

Material particles after the weld with a threaded pin

Figure 28 demonstrates the velocity effect on the final weld quality. It demonstrates that the rotational and advancing velocities can not be selected arbitrarily.

Figure 29 shows the final state of the material particles (a colorful set) after FSW process.

7 Residual Stresses

In this section, the two-step strategy for computing the residual stresses is based upon combining global and local level analysis. The strategy is shown in Fig. 30.

Fig. 30

Coupling strategy at local and global level

The first step consists of computing the heat generated by the FSW tool at the thermo-mechanically affected zone (TMAZ). This is performed within the local level analysis.

7.1 Step 1: The Local Level Analysis

In the local level analysis, the focus of the simulation is a small domain (typically, its size is the double of the pin-shoulder) including the TMAZ. Because of this, the size of the local domain is not necessarily the whole component. It can be much smaller as big as the HAZ surrounded by artificial boundary (Fig. 23). The local model provides a highly detailed description of the heat generation in order to capture accurately the temperature field.

At local level, the analysis data are the pin geometry, rotation and advancing speeds, tool pressure and thermo-physical material properties. The process phenomena studied are the relationship between the welding parameters, the contact mechanisms in terms of applied normal pressure and friction coefficient, the pin geometry, the material flow within the HAZ (or stirring zone), its size and, eventually, the corresponding consequences on the microstructure evolution.

The local level analysis requires a very fine mesh in the TMAZ as in this region (basically a narrow area close to the pin) the strain rate gradient is extremely steep. This strain rate localization is mainly due to the highly non-linear behavior of the constitutive models that characterize the material.

The output of the local analysis, which is the heat power ($\dot{P}$) to be used at global level, is calculated once the steady-state is achieved. It is computed taking into account the heat generated from both friction ($q_{fric}$) and plastic dissipation ($\dot{D}$) integrated over the TMAZ domain:

$$\begin{aligned} \dot{P}=\int \nolimits _{{\small \Omega }_{\textit{TMAZ}}}\dot{Q} \mathrm {d}V=\int \nolimits _{{\small \Omega }_{\textit{TMAZ}}}\dot{D}\mathrm {d} V+\int \nolimits _{\partial {\small \Omega }_{\textit{TMAZ}}}q_{fric}\mathrm {d}S \end{aligned}$$

(76)

where $\dot{Q}$ is the power density introduced into the system.

Thus, performing the local level analysis provides the input data for the global study.

Fig. 31

Schematic of a global model with a moving heat source

7.2 Step 2: The Global Level Analysis

A simulation carried out at the global level studies the entire component to be welded. In this case, a moving heat power source is applied to a control volume representing the actual TMAZ at each time-step of the analysis. The effects induced by the welding process on the structural behavior are the target of the study. These are the distortions, residual stresses or weaknesses along the welding line, among others. At global level, the analysis data are the heat source, gravity load, clamping system and cooling device (clamping, release and cooling down). In the model, the small differences in the temperature resulting from the characteristics of the retreating or advancing sides of the welds are not considered (Fig. 31).

Fig. 32

TMAZ schematic

Fig. 33

Mesh resolution at local (left) and global (right) levels

Fig. 34

Temperature field at local (left) and global (right) levels

For the performance of the global level analysis, the definition of the input power is required. Since no filler material is needed for joining in FSW, the power input does not form part of the industrial setting and is generally unknown. Apart from experiments and calibration, the power can be approximated mathematically or by use of inverse analysis. In this work, it is proposed to compute it from the local level simulation.

The principal effect of the material processing at the stirring zone on the structure is the thermal expansion. The clamping system prevents the expansion of the material due to the thermal deformations which transform into plastic strains and, therefore, producing residual stresses in both longitudinal and transversal directions in the weld and its vicinity.

The only data transferred between the two analysis levels is the heat source, as the deformations are negligible in the size of stirring zone comparing with the structure dimension.

Keeping the same input power obtained from local level analysis, the global level FSW simulation can be performed for desired component dimensions and welding paths, independently of the domain and mesh used in the local level analysis.

Fig. 35

Temperature evolution obtained from local and global level analyses compared with experiment

Fig. 36

Comparison between the stresses obtained from global level analysis and experiment at a line orthogonal to the weld line

The numerical simulation at global level needs an ad-hoc procedure in order to apply the power energy to the elements representing the Thermo-Mechanically Affected Zone (TMAZ) (Fig. 32). Therefore, a search algorithm is required to identify those elements at each time step of the simulation. The total power input ($\dot{P}$) delivered within the time-step, $\Delta t$, is distributed among the elements of the TMAZ volume during the current time-step. The upper surface of the volume is a rectangle with dimension of advancing speed (v) $\times$ time step ($\Delta t$) $\times$ pin diameter ($d_{p}$). The diameter of the profile of this volume ($d_{0}$) decreases parabolically with depth z in the work-piece thickness (d):

$$\begin{aligned} \begin{array}{cc} d_{0}\left( z\right) =d_{p}\sqrt{\frac{z+d}{z}}&-d\le z\le 0 \end{array} \end{aligned}$$

(77)

The mesh resolution of the TMAZ in the global analysis needs to be sufficient for the definition of the volume where the power input is inserted. According to the search algorithm, the volumes ($V_{\textit{TMAZ}}$) of all the elements representing the TMAZ are added up as

$$\begin{aligned} V_{\textit{TMAZ}}=\sum \limits _{e=1}^{n_{e\in TMAZ}}V^{\left( e\right) } \end{aligned}$$

(78)

so that the heat source distribution is defined as (Fig. 31)

$$\begin{aligned} \dot{Q}=\frac{\dot{P}}{V_{\textit{TMAZ}}} \end{aligned}$$

(79)

This power re-distribution preserves the total amount of energy input independently of the mesh used [35].

7.3 Experimental Validation

In this section, firstly, the comparison between the temperature fields obtained at local and global levels are shown to validate the local-global coupling strategy. Then, the residual stresses computed using the strategy are illustrated.

The meshes at local and global levels are shown in Fig. 33. The total dissipated power is obtained at the steady state and used as the heat input energy for the global level analysis. It is applied to the control volume representing the TMAZ at each time-step of the analysis. The temperature fields at local and global levels at the end of the process is shown in Fig. 34. The comparison between the temperature fields obtained from both local and global level analyses for different lines parallel to the weld line at the bottom surface or thermocouples placed at identical locations with those obtained from experiments are presented in Fig. 35.

The global level analysis provides the residual stress field. The comparison between the variations of the residual stress (normal stresses in x direction) along the transverse direction (along the line perpendicular to the weld line) and experimental results are plotted in Fig. 36 at the same location. Longitudinal stresses after fixture release and cooling are depicted in this figure.

8 Conclusion

This paper presents the challenges and achievements in the numerical simulation of coupled thermo-mechanical FSW problems. The existing methodologies are designed to simulate FSW process either at global or local level.

In the global level approach, the objective is to study the effect of a moving heat source, in a Lagrangian framework, on the behavior of the whole structure to be welded (the input energy is known).

In the local level approach, the objective is to analyze the heat affected zone and to study the heat source locally. This can be used as energy input for the global analysis (the heat generation comes from plastic dissipation and frictional effects).

Generally, more attention has been paid to local level simulation as the complex coupled thermo-mechanical phenomenon are mostly concentrated in the HAZ. In the local level approach, the effect of high rotational velocity is studied. Contact, strain-rate localization, strongly non-linear and isochoric material behaviors and convective domination make the local analysis more complicated and important.

In this paper, several aspects of FSW modeling are highlighted:

• Coupled thermo-mechnical model A robust and accurate thermo-mechanical solver for the simulation of FSW processes has been developed. The transient thermal model proposed in both Lagrangian and Eulerian kinematic frameworks allows for local and global level analysis. Suitable boundary conditions based on Newton’s law are introduced to deal with heat conduction at contact interface and heat convection at the external boundaries.

• Apropos kinematic framework To study FSW process, a suitable and robust kinematic setting has been proposed. The apropos kinematic setting, combines ALE, Eulerian and Lagrangian frameworks for different parts of the domain avoiding remeshing and variable remapping procedures. Moreover, it permits to account for the arbitrary and complex pin shapes typically found in FSW process.

• Mixed stabilized formulation for the mechanical problem In the hypothesis of isochoric material behavior as for liquid-like phase or more generally when the deformations are mainly deviatoric (J2 plasticity model used for metals), the stabilized mixed $\mathbf {v}/p$ formulation has been introduced. Due to the good performance, this technology must be used especially for industrial simulations with triangular/tetrahedral meshes for the domain discretization . Pressure locking is overcome using VMS stabilization methods. Two stabilization methods are compared: ASGS and OSGS. The OSGS stabilization method shows higher accuracy even if the necessary computational effort is superior.

• Mixed stabilized formulation for convective dominated thermal problem To deal with thermal analysis where the convective term dominates (ALE/Eulerian framework), the convection instabilities has been overcome using VMS stabilization methods. This leads to a very accurate treatment of this numerical problem. The stabilization method based on the sub-grid scales approach circumvents the Ladyženskaja–Babuška–Brezzi (LBB) condition, allowing an accurate and robust formulation for linear elements. Classical GLS and SUPG stabilization methods can be recovered as a particular case of the sub-grid scale stabilization framework.

• Constitutive modeling The thermo–elasto–visco-plastic constitutive model used for the simulation of FSW process at global level has been developed. This model covers the full temperature range leading to an accurate evolution of temperature, distortions and the residual stresses. Thermo-rigid-visco-plastic constitutive models such as Norton–Hoff, Carreau or Sheppard–Wright have been used for the simulations of FSW processes at local level. These kind of models neglect both the elastic and the thermal strains. They are intended to solve mechanical problem dominated by very high deviatoric strains as well as high strain rates. It is important to observe that also in this case the thermal coupling is essential to capture the real material behavior. This leads to highly non-linear models strongly coupled with the temperature field, which can be treated as non-Newtonian flows, with a temperature dependent viscosity.

• Strain localization problemThe FSW process produces a strong strain localization in the stirring zone close to the pin. A sliding zone concentrates in a thin layer under a pure shear stress field. The solution of such problem is not feasible using a standard velocity-based element. However, the use of mixed $\mathbf {v}/p$ element is able to capture the strain localization satisfactorily. Also in this case the proposed VMS-based stabilization technique is suitable to treat such complex problem.

• Material flow visualization The paper also deals with the problem of material tracking in the stirring zone. The simulation is carried out using a rigid visco-plastic constitutive model and this reduces into a non-Newtonian fluid-like analysis where it is important to visualize the material flow. The model provides this insight by tracking the particles position during the full motion of the FSW process in the stirring zone. The trend observed is consistent with the results of experiments, showing the motion of the markers inserted into the weld. The model correctly predicts the material flow around the retreating side of the pin. Results of the simulation correctly demonstrate that the material is moved away from the direction of travel and material sticking could occur at the tool interface. The resulting material flow is not symmetric with respect to the joint line and the flow patterns on the advancing and retreating sides are different. The model is able to include the effect of complex tool geometries as threaded pins. Some distinctive 3D features of the flow can be appreciated. These included: the material flow within the thickness direction and a centrifugal material flow pattern around the pin. Among the integration methods (BES, BFECC and RK4) used for the problem of interest, RK4 is found to be the most accurate when a larger time-step is used.

• Residual stress computation The paper proposes a local-global two level strategy for the prediction of residual stresses in FSW processes. At the first step, the heat power is calculated at local level from both viscous dissipation and friction. Then the heat power is transferred into the global level simulation in order to obtain the residual stresses.