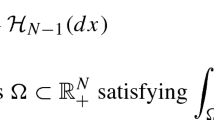Existence of Isoperimetric Sets with Densities “Converging from Below” on ${\mathbb {R}}^N$

Abstract

In this paper, we consider the isoperimetric problem in the space ${\mathbb {R}}^N$ with a density. Our result states that, if the density f is lower semi-continuous and converges to a limit $a>0$ at infinity, with $f\le a$ far from the origin, then isoperimetric sets exist for all volumes. Several known results or counterexamples show that the present result is essentially sharp. The special case of our result for radial and increasing densities positively answers a conjecture of Morgan and Pratelli (Ann Glob Anal Geom 43(4):331–365, 2013.

1 Introduction

In this paper we are interested in the isoperimetric problem with density. This means that we are given a positive lower semi-continuous function $f:{\mathbb {R}}^N\rightarrow {\mathbb {R}}^+$, usually called a “density”, and we measure volume and perimeter of a generic subset E of ${\mathbb {R}}^N$ as

where the essential boundary of E (which coincides with the usual topological boundary when E is regular) is defined as

$B_r(x)$ stands for the ball of radius r centered at x, and $\omega _N$ is the Euclidean volume of a ball of radius 1. The isoperimetric problem with density then consists, as always, in minimizing the perimeter among all the sets with a given volume. This generalization of the classical isoperimetric problem, as well as many specific cases, has been extensively studied in recent years and has many important applications. Without trying to describe precisely the history of this problem, we limit ourselves to recalling its main steps. The idea of studying the isoperimetric problem with a density first appeared in the paper [9], and it can be seen as a generalization of the well-studied isoperimetric problem in a Riemannian manifold (see, for instance, [12]). Some preliminary results, such as the regularity of isoperimetric sets, come from the classical regularity papers of the 1970s; recall, for instance, the fundamental contribution of Almgren [1, 2]. Several authors have recently studied other aspects of the problem. For instance, the papers [4, 14] consider the general problem, its main properties and some open questions. The papers [3, 8] study some of the isoperimetric properties of spheres: this means that, in some particular cases, balls are isoperimetric sets. An important example of these properties is the celebrated “log-convex density conjecture”, see [11], which has been studied by several authors and finally positively answered by Chambers in [5]. Finally, the most recent general results about the existence of isoperimetric sets are in [13], while those about the regularity are in [6, 7].

In this paper we will consider the most basic question in this setting, which is of course the existence of isoperimetric sets, i.e., sets E with the property that $P_f(E)= {\mathfrak {J}}(|E|_f)$ where, for any $V\ge 0$,

$$\begin{aligned} {\mathfrak {J}}(V):=\inf \big \{P_f(F):\, |F|_f=V\big \}\,. \end{aligned}$$

Depending on the assumptions on f, the answer to this question can either be trivial or extremely complicated.

Let us start with a very simple, yet fundamental, observation. Fix a volume $V>0$ and let $\{E_i\}$ be an isoperimetric sequence of volume V: this means that $|E_i|_f=V$ for every $i\in {\mathbb {N}}$, and $P_f(E_i) \rightarrow {\mathfrak {J}}(V)$. Thus, possibly up to a subsequence, the sets $E_i$ converge to some set E in the $L^1_\mathrm{loc}$ sense. As a consequence, standard lower semi-continuity results in BV ensure that $P_f(E)\le \liminf P_f(E_i)={\mathfrak {J}}(V)$; therefore, if actually $|E|_f=V$, then obviously E is an isoperimetric set. Unfortunately, this simple observation is not sufficient, in general, to show the existence of isoperimetric sets, because there is no general reason why the volume of E should be exactly V (while it is obviously at most V). In fact, volume can disappear at infinity.

A second remark is the following: if the weighted volume of the whole space ${\mathbb {R}}^N$ is finite, then in the argument above it becomes obvious that $|E|_f=V$. In other words, the mass cannot vanish to infinity. Hence, in this case isoperimetric sets exist for all volumes.

Let us then consider the more interesting problem when $f\not \in L^1({\mathbb {R}}^N)$. In this case, by the different scaling properties of volume and perimeter, roughly speaking we can say that “isoperimetric sets like small density”. Let us be somewhat more precise: one can immediately check that, if two different balls $B_1$ and $B_2$ lie in two regions where the density is constantly $d_1$ resp. $d_2$, and if $|B_1|_f=|B_2|_f$, then $P_f(B_1)< P_f(B_2)$ when $d_1<d_2$. More generally, all the simplest examples show that isoperimetric sets tend to prefer the zones where density is lower, and it is very reasonable to expect that this behavior is common. Of course, this argument does not predict anything in situations where the density varies quickly (for instance, it would be very convenient for a set to lie where the density is large if at the same time the boundary stays where the density is small!), but nevertheless having this “general rule” in mind may help a lot.

With the aid of the above observations, let us now return to the question of the existence of isoperimetric sets. First of all, let us consider the case when the density converges to 0 at infinity. In this case, following the argument above one should expect that isoperimetric sequences diverge at infinity, to reach the zones with lowest density, and that the isoperimetric function ${\mathfrak {J}}$ is identically 0, so that no isoperimetric set exists. A formal proof of this fact is quite easy in specific cases, for instance, when the density goes to 0 as a polynomial, or as an exponential. The general proof is currently a work in progress.

On the contrary, if the density f blows up at infinity, one may expect isoperimetric sets to exist, because isoperimetric sequences should remain bounded to avoid zones where the density is high, so there would be no loss of mass at infinity. A complete answer to this issue has already been given in [13]: if the density is also radial, then isoperimetric sets exist for every volume, as expected (Theorem 3.3 in [13]), but if the density is not radial, then existence might fail (Proposition 5.3 in [13]), contrary to intuition.

Let us move on and consider the case when the density, at infinity, is neither converging to 0 nor diverging. Again, it is very simple to observe that existence generally fails if the density is decreasing, at least definitively. Similarly, it is easy to build examples of both existence and non-existence for oscillating densities (that is, densities for which the $\liminf$ and the $\limsup$, at infinity, are different). Summarizing, with regard to the existence problem, the only interesting case left is when the density has a finite limit at infinity and it is converging to that limit from below. This leads us to the following definition.

Definition 1.1

We say that the l.s.c. function $f:{\mathbb {R}}^N\rightarrow {\mathbb {R}}$ is converging from below if there exists $0<a <+\infty$ such that $f(x) \rightarrow a$ when $|x|\rightarrow \infty$, and $f(x) \le a$ for |x| large enough.

Basically, the observations above mean that, for functions f which are not converging densities, there is in general no interesting open question about the issue of existence. Indeed, as explained above, in each of these cases it is already known whether isoperimetric sets exist for all volumes or not. Conversely, for some special cases of densities converging from below, the existence problem has already been discussed. In particular, combining the results of [6, 13], the existence of isoperimetric sets follows for densities which are continuous and converging from below and which satisfy some technical assumptions. For instance it is enough that f is superharmonic, or that f is radial and for every $c>0$ there is some $R\gg 1$ for which $f(R)\le a-e^{-cR}$. Moreover, in [13] it was conjectured that isoperimetric sets exist for all volumes if the density is radial and increasing.

In this paper we are able to prove the existence for any density converging from below (this is even stronger than the above-mentioned conjecture). As explained above, this result is sharp.

Theorem 1.2

Let $f\in L^1_\mathrm{loc}({\mathbb {R}}^N)$ be a density converging from below. Then isoperimetric sets exist for every volume.

Let us conclude the Introduction with a quick description of our main argument. The starting point is the following idea, taken from [13]. Let us consider an isoperimetric sequence $\{E_i\}$, converging in $L^1_\mathrm{loc}$ to some set E. As explained above, if $|E|_f=V$ then E is already an isoperimetric set, thus there is nothing to prove. Otherwise, one can easily notice (see Lemma 2.1) that ${\mathfrak {J}}(V)$ equals the perimeter of E plus the perimeter of a “ball at infinity”, that is, the perimeter that a ball of volume $V-|E|_f$ has in the space ${\mathbb {R}}^N$ with constant density a. As a consequence, one is led to looking for a set behaving better than a ball at infinity; in other words, one aims at finding a set F with volume $V-|E|_f$ and with perimeter smaller than the one of a ball at infinity. This last property can be equivalently expressed by saying that the “mean density” of F is smaller than a; see Definition 3.1. If such a set F exists, and it does not intersect E, then $E\cup F$ is clearly isoperimetric, and we are done. Moreover, since one can show that the set E is bounded (see Lemma 2.3), then the non-intersection with the (a priori not known) set E is automatic if F is far enough from the origin. Summarizing, the whole problem has been easily reduced to finding a set, arbitrarily far from the origin, with a given volume and mean density smaller than a. By making use of this observation, the existence of isoperimetric sets was already proved in some particular cases in [13]. More precisely, the authors of that paper observed that the needed existence of a set F with mean density smaller than a follows under some technical assumptions, such as the rate of convergence of f at a at infinity, or the superharmonicity of f, or other specific cases.

In the present paper, we are able to show the existence of such a set F with no additional assumptions, thus getting the sharp Theorem 1.2. To obtain our result, we start with the same idea as above, but we drastically change strategy. Roughly speaking, the additional assumptions used in [13] ensured that every ball far from the origin has mean density smaller than a, while it is enough to find only a single set—and not necessarily a ball—with this property. Since f is converging to a from below, it is reasonable to expect that the mean density of a generic ball far from the origin should be smaller than a. This is not necessarily true for a randomly taken ball; however, we show that it is impossible that this is false for every ball, because otherwise an averaging argument would give a contradiction with the fact that f is converging from below to a. Hence, we have found a ball with mean density smaller than a far from the origin. Unfortunately, this is only the first big step of the proof, still not enough to conclude. Indeed, keep in mind that we need to find a set with mean density smaller than a and given volume, while with our averaging argument we are able to consider balls with given radius. As a consequence, the second and last big step of the proof, which is actually more delicate than the first one, consists in deforming the balls found above. We are able to do this deformation in such a way to adjust the volume, but without destroying the property of having the mean density smaller than a. As explained above, this concludes the proof.

2 General Results About Isoperimetric Sets

In this section we present some general lemmas about the existence and the boundedness of isoperimetric sets.

As already briefly described in the Introduction, let us fix some $V>0$ and an isoperimetric sequence of volume V, that is, a sequence of sets $E_j\subseteq {\mathbb {R}}^N$ such that $|E_j|_f=V$ for any j, and $P_f(E_j)\rightarrow {\mathfrak {J}}(V)$ for $j\rightarrow \infty$. As already observed, if (a subsequence of) $\{E_j\}$ converges in $L^1_\mathrm{loc}$ to a set E, then by lower semicontinuity $P_f(E)\le {\mathfrak {J}}(V)$, and $|E|_f\le V$; thus, the set E is automatically isoperimetric of volume V if $|E|_f=V$. However, it is always true that E is isoperimetric for its own volume. We stress that this fact is widely known, but we prefer to give the proof for the sake of completeness, and also because in the literature we could not find any proof which works in such a generality. After this lemma, we will show that if there was loss of mass at infinity (that is, if $|E|_f< V$), then E is necessarily bounded.

Lemma 2.1

Assume that $f\in L^1_\mathrm{loc}({\mathbb {R}}^N)$ and that f is locally bounded from above far enough from the origin. Let $\{E_j\}$ be an isoperimetric sequence of volume V converging in $L^1_\mathrm{loc}$ to some set E. Then E is an isoperimetric set for the volume $|E|_f$. If in addition f is converging to some $a>0$, then

$$\begin{aligned} {\mathfrak {J}}(V) = P_f(E) + N(\omega _N a)^{\frac{1}{N}} (V-|E|_f )^{\frac{N-1}{N}}\,. \end{aligned}$$

(2.1)

Proof

Let us start by proving that E is isoperimetric. As we already observed, $P_f(E)\le {\mathfrak {J}}(V)$ and $|E|_f\le V$; as a consequence, if $|E|_f=V$ it is clear that E is isoperimetric, and on the other hand if $|E|_f=0$ then the empty set E is still clearly isoperimetric for the volume 0. As a consequence, we can assume without loss of generality that $0< |E|_f < V$.

Suppose now that the claim is false, and then let $F_1$ be a set satisfying

$$\begin{aligned} |F_1|_f=|E|_f, \quad \eta :=\frac{P_f(E)-P_f(F_1)}{6} >0. \end{aligned}$$

Now choose $x\in {\mathbb {R}}^N$ being a point of density 1 in $F_1$ and a Lebesgue point for f with $f(x)>0$: such a point exists; in particular, -a.e. point of $F_1$ can be taken. The assumptions on x ensure that, for every radius $\bar{r}$ small enough,

$$\begin{aligned} \frac{1}{2} \,\omega _N f(x) \bar{r}^N \le |B_{\bar{r}}(x) \cap F_1|_f \le |B_{\bar{r}}(x)|_f \le 2 \omega _N f(x) {\bar{r}}^N, \end{aligned}$$

(2.2)

and in turn this implies that there exist arbitrarily small radii r (not necessarily all those small enough) such that

(2.3)

Indeed, if the last inequality were false for every $0<r<\bar{r}$, then by integrating we would get that (2.2) is false.

Similarly, let y be a point of density 0 for $F_1$ which is a Lebesgue point for f with $f(y)>0$ (the existence of such a point requires that $f\notin L^1({\mathbb {R}}^N)$, and in turn this is surely true because $|E|_f<V$). Since we can find such a point arbitrarily far from the origin (and far from x), by assumption it is admissible to assume that $f\le M$ in a small neighborhood of y. As a consequence, there exists some radius $\bar{\rho }>0$ such that, for every $0<\rho <\bar{\rho }$,

(2.4)

Let us now fix a constant $\delta >0$ such that (possibly decreasing $\bar{\rho }$)

$$\begin{aligned} \delta< \eta , \quad \frac{f(y)}{2}\, \omega _N \bar{\rho }^N > \delta , \quad M N \omega _N \bar{\rho }^{N-1} < \eta . \end{aligned}$$

(2.5)

We claim the existence of some set $F\subseteq {\mathbb {R}}^N$ and of a big constant $R>0$ (in particular, much bigger than both |x| and |y|) such that

$$\begin{aligned} F \subseteq B_R, \quad P_f(F)< P_f(E) - 5\eta , \quad 0< \delta ':= |E|_f -|F|_f< \frac{\delta }{2}, \end{aligned}$$

(2.6)

writing for brevity $B_R=B_R(0)$. To show this, it is useful to consider two possible cases. If $F_1$ is bounded, we define $F=F_1\setminus B_r(x)$ for some r very small such that both (2.2) and (2.3) hold true. Then the inclusion $F\subseteq B_R$ is true for every R big enough, and the two inequalities in (2.6) immediately follow by (2.2), (2.3) and the definition of $\eta$ as soon as r is sufficiently small. Otherwise, if $F_1$ is not bounded, then we define $F=F_1\cap B_R$ for a big constant R: of course, the inclusion $F\subseteq B_R$ is automatically satisfied, and the inequality about $\delta '$ is also true for every R big enough, say $R>R_0$. Concerning the inequality on $P_f(F)$, if it were false for every $R>R_0$, then for every $R>R_0$ it would be

and then by integrating we would get

The contradiction shows the existence of some suitable R, thus the existence of F satisfying (2.6) is proved.

We can now select some $R'>R$ such that

(2.7)

Since $E_j\cap B_{R'}$ (resp., $E_j \cap B_{R'+1}$) converges in the $L^1$ sense to $E\cap B_{R'}$ (resp., $E \cap B_{R'+1}$), for every j big enough we have

$$\begin{aligned} |E|_f -\delta '< |E_j\cap B_{R'}|_f \le |E_j\cap B_{R'+1}|_f < |E|_f+ \delta ', \end{aligned}$$

(2.8)

(2.9)

Arguing as above, by (2.8) we have

so we can find some $R_j\in (R',R'+1)$ such that, also recalling (2.5),

(2.10)

Observe that, since $|E_j|=V$ by definition, (2.8) implies

$$\begin{aligned} V - |E|_f -\delta '< |E_j\setminus B_{R_j}|_f < V - |E|_f +\delta '. \end{aligned}$$

As a consequence, calling $G_j = F \cup \big ( E_j \setminus B_{R_j}\big )$ and also recalling (2.6), (2.7), (2.9) and (2.10), we can estimate the volume of $G_j$ by

$$\begin{aligned} |G_j|_f = |F|_f + |E_j \setminus B_{R_j}|_f = |E|_f - \delta ' + |E_j \setminus B_{R_j}|_f \in (V- \delta , V), \end{aligned}$$

(2.11)

and the perimeter of $G_j$ by

(2.12)

Finally, we define the competitor $\widetilde{E}_j = G_j \cup B_{\rho _j}(y)$, where $\rho _j<\bar{\rho }$ is the constant such that $|\widetilde{E}_j|_f = V$—this is possible by (2.11), (2.4), and (2.5). Then again applying (2.4) and (2.5), from (2.12) we deduce

$$\begin{aligned} P_f(\widetilde{E}_j) < P_f(E_j) - \eta \end{aligned}$$

for every j big enough, and this gives the desired contradiction with the fact that the sequence $E_j$ was isoperimetric. This finally shows that E is an isoperimetric set for the volume $|E|_f$.

We now move to the second part of the proof, namely, we assume that f is converging to some $a>0$ (not necessarily from below), and we aim to prove (2.1). Notice that we can assume without loss of generality that $|E|_f < V$, because otherwise (2.1) would be a direct consequence of the fact that E is isoperimetric.

Arguing as in the first part of the proof, for every $\varepsilon >0$ we can find a very big R such that, calling $F=E\cap B_R$, it is

$$\begin{aligned} |F|_f \ge |E|_f - \varepsilon , \quad P_f(F) \le P_f(E) +\varepsilon . \end{aligned}$$

Then let B be a ball with volume $|B|_f = V - |F|_f$: if we take this ball far enough from the origin, then $B\cap F=\emptyset$, thus $|G|_f=V$, where $G=F\cup B$. Moreover, again taking the ball far enough, we have $a-\varepsilon \le f \le a+\varepsilon$ on the whole B. As a consequence, calling r the radius of B, we have

$$\begin{aligned} V-|E|_f + \varepsilon \ge V-|F|_f = |B|_f \ge (a-\varepsilon ) \omega _N r^N, \end{aligned}$$

from which we get

$$\begin{aligned} \begin{aligned} {\mathfrak {J}}(V)&\le P_f(G) = P_f(F) + P_f(B) \le P_f(E) + \varepsilon + (a+\varepsilon ) N \omega _N r^{N-1}\\&\le P_f(E) + \varepsilon + \frac{a+\varepsilon }{(a-\varepsilon )^{\frac{N-1}{N}}}\,N\omega _N^{\frac{1}{N}}\,\Big (V-|E|_f + \varepsilon \Big )^{\frac{N-1}{N}}, \end{aligned} \end{aligned}$$

which in turn implies an inequality in (2.1) by letting $\varepsilon \rightarrow 0$.

To show the other inequality, consider again the isoperimetric sequence $\{E_j\}$; for any given $\varepsilon >0$, exactly as in the first part we can find an arbitrarily big R so that $a-\varepsilon \le f\le a+\varepsilon$ out of $B_R$ and

$$\begin{aligned} |E\cap B_R|_f \ge |E|_f - \varepsilon , \quad P_f (E\setminus B_R) \le \varepsilon . \end{aligned}$$

For every $j\gg 1$, then, we can find some $R_j \in (R,R+1)$ so that

Since $a-\varepsilon \le f\le a+\varepsilon$ out of $B_R$ we deduce, using the Euclidean isoperimetric inequality,

$$\begin{aligned} \begin{aligned} P_f (E_j\setminus B_{R_j})&\ge (a-\varepsilon ) P_\mathrm{eucl} (E_j\setminus B_{R_j}) \ge (a-\varepsilon ) N\omega _N^{\frac{1}{N}}|E_j\setminus B_{R_j}|_\mathrm{eucl}^{\frac{N-1}{N}}\\&\ge \frac{a-\varepsilon }{(a+\varepsilon )^{\frac{N-1}{N}}}\,N\omega _N^{\frac{1}{N}}|E_j\setminus B_{R_j}|_f^{\frac{N-1}{N}} \\&\ge \frac{a-\varepsilon }{(a+\varepsilon )^{\frac{N-1}{N}}}\,N\omega _N^{\frac{1}{N}}\Big (V-|E|_f -\varepsilon \Big )^{\frac{N-1}{N}}, \end{aligned} \end{aligned}$$

which in turn gives

Since $P_f(E_j)\rightarrow {\mathfrak {J}}(V)$ for $j\rightarrow \infty$, sending $\varepsilon \rightarrow 0$ in the last estimate yields the second inequality for (2.1), thus the proof is concluded.

Remark 2.2

Actually, the claim of Lemma 2.1 can be proved even with weaker assumptions. More precisely, one could apply the results of [6] to extend the validity to the more general case when f is “essentially bounded” in the sense of [6].

The second result that we present is a clever observation, which we owe to Frank Morgan. It shows that whenever a density converges to a limit $a>0$ (not necessarily from below), then if an isoperimetric sequence is losing mass at infinity the remaining limiting set—which is isoperimetric thanks to Lemma 2.1—is bounded.

Lemma 2.3

[10, Lemma 13.6] Let the density f converge to some $a>0$, and let the isoperimetric sequence $\{E_j\}$ of volume V converge in $L^1_\mathrm{loc}$ to a set E with $|E|_f<V$. Then E is bounded.

Proof

Assume that $|E|_f<V$. Then for every $t>0$ define

For every t, we can select a ball B of volume $V-|E|_f+ m(t)$ far away from the origin, in order to have no intersection with $E\cap B_t$; thus, the set $(E\cap B_t) \cup B$ has precisely volume V, hence ${\mathfrak {J}}(V) \le P_f (E\cap B_t) + P_f(B)$. Since the ball B can be taken arbitrarily far from the origin, thus in a region where f is arbitrarily close to a, exactly as in the second part of the proof of Lemma 2.1 we deduce

$$\begin{aligned} {\mathfrak {J}}(V) \le P_f (E \cap B_t) + N (a\omega _N)^{\frac{1}{N}} \big (V-|E|_f+ m(t)\big )^{\frac{N-1}{N}}. \end{aligned}$$

Recalling that $|E|_f<V$ and comparing the last inequality with (2.1), we obtain

$$\begin{aligned} P_f(E) \le P_f (E\cap B_t) + C m(t) \end{aligned}$$

for some strictly positive constant C. Notice now that

and in turn by the (Euclidean) isoperimetric inequality if $t\gg 1$ we have

$$\begin{aligned} P_f(E\setminus B_t)\ge & {} (a-\varepsilon ) P_\mathrm{eucl}(E\setminus B_t)\\\ge & {} (a-\varepsilon ) N\omega _N^{\frac{1}{N}} |E\setminus B_t|^{\frac{N-1}{N}}_\mathrm{eucl} \ge \frac{a-\varepsilon }{(a+\varepsilon )^{\frac{N-1}{N}}}\, N\omega _N^{\frac{1}{N}} m(t)^{\frac{N-1}{N}}. \end{aligned}$$

Putting everything together, we get

$$\begin{aligned} Cm(t) \ge 2 m'(t) + \frac{1}{C_1} m(t)^{\frac{N-1}{N}} \end{aligned}$$

for some other constant $C_1>0$. And in turn, if $t\gg 1$ then $m(t)\ll 1$, thus the last estimate implies

$$\begin{aligned} m(t) \le C_2 \big (- m'(t)\big )^{\frac{N}{N-1}}. \end{aligned}$$

Finally, it is well known that a positive decreasing function m which satisfies the above differential inequality vanishes in a finite time. Hence, $m(t)=0$ for t big enough, and this means precisely that E is bounded.

3 Proof of the Main Result

This section is devoted to showing the main result of the paper, namely, Theorem 1.2. The overall idea is to take an isoperimetric sequence of volume V, and to consider a limiting set E (up to a subsequence, this is always possible). If $|E|_f=V$, then there is nothing to prove because, as we already saw several times, the set E is already the desired isoperimetric set of volume V. Instead, if $|E|_f<V$, we know by Lemma 2.1 that E is an isoperimetric set for volume $|E|_f$, and by Lemma 2.3 that E is bounded. Moreover, formula (2.1) says that an isoperimetric set of volume V can be found as the union of E and a “ball at infinity” with volume $V-|E|_f$. By “ball at infinity” we mean a hypothetical ball where the density is constantly a: such a ball does not really exist, but a sequence of balls of correct volume which escape at infinity will have a perimeter which converges to that of this “ball at infinity”. In other words, a sequence of sets consisting of the union of E and a ball escaping at infinity is isoperimetric thanks to (2.1). Our strategy is then simple: we look for a set B, far away from the origin, which is better than a ball at infinity, in other words, which has the same volume and less perimeter than it. Since E is bounded (this is a crucial point, coming from Lemma 2.3) the sets E and B have no intersection, thus the union of E with B is isoperimetric. As one can see, the only thing that needs to be done is to find a set of given volume, arbitrarily far from the origin, which is “better” than a ball at infinity.

First of all, let us express in a useful way the property of being better than a ball at infinity, by means of the following definition, first given in [13].

Definition 3.1

We say that the set $E\subseteq {\mathbb {R}}^N$ of finite volume has mean density $\rho$ if

$$\begin{aligned} P_f(E) = N(\omega _N \rho )^\frac{1}{N} |E|_f^\frac{N-1}{N}. \end{aligned}$$

The meaning of this definition is evident: $\rho$ is the unique number such that, if we endow ${\mathbb {R}}^N$ with the constant density $\rho$, then balls of volume $|E|_f$ have perimeter $P_f(E)$. The convenience of this notion is also clear: being “better than a ball at infinity” simply means having mean density less than a.

We can then continue our description of the proof of Theorem 1.2: as said above, one needs only to find a set of volume $V-|E|_f$ arbitrarily far from the origin and having mean density at most a. Since we want to find an isoperimetric set for any volume V, and we cannot know a priori how big $|E|_f$ is, we need to find sets of mean density less than a of any volume and arbitrarily far from the origin. Actually, by a trivial rescaling argument, we can assume that $a=1$ and search for a set of volume $\omega _N$. Since f is converging to 1 and we must work very far from the origin, everything will be very close to the Euclidean case; hence a set of volume $\omega _N$ and mean density less than 1 (or, equivalently, with perimeter less than $N \omega _N$) must be extremely close to a ball of radius 1. The first big step in our proof will then consist in finding a ball of radius 1 arbitrarily far from the origin and with mean density less than 1.

Surprisingly enough, this will by no means conclude the proof, due to a seemingly minor problem: since f converges to 1 from below, the ball of radius 1 that we have found does not have exactly volume $\omega _N$, but a bit less. The further from the origin the ball is, the smaller this gap will be, yet still positive. Notice that at this point we cannot rely on a rescaling argument again: we have already rescaled to the case of volume $\omega _N$, so another volume will not solve the problem (in principle, it could be true that there are sets of mean density less than 1 only for all the rational volumes, and for no irrational one...). Hence, the second big step in our proof will be to slightly modify the ball found in the first big step, in such a way that the volume increases up to exactly $\omega _N$, while the mean density remains smaller than 1. At that point, the proof will be concluded. We should mention that the proof of this second fact is more delicate than the proof of the first!

Let us now state the claims of the two big steps with more precision, and then use them to give the formal proof of Theorem 1.2—which is more or less exactly what we have just described informally. We will then conclude the paper with two sections, devoted to presenting the proof of the two big claims.

Proposition 3.2

Let f be a density converging from below to 1, and set $g=1-f$. Then for every $\varepsilon >0$ there exists a ball B with radius 1 and arbitrarily far from the origin such that

$$\begin{aligned} P_g(B)\ge (N-\varepsilon )|B|_g. \end{aligned}$$

Proposition 3.3

Let f be a density converging from below to 1. Then there exists a set E with volume $\omega _N$ and mean density smaller than 1 arbitrarily far from the origin.

Proof of Theorem 1.2

Let $\{E_j\}$ be an isoperimetric sequence of volume V, and let E be the $L^1_\mathrm{loc}$ limit of a suitable subsequence. If $|E|_f=V$ then the proof is already concluded. Otherwise, we know that E is bounded by Lemma 2.3 and that (2.1) holds. Up to a rescaling, we can assume that f converges from below to 1, and that $V-|E|_f=\omega _N$. By Proposition 3.3 we can find a set F not intersecting E with volume $\omega _N$ and mean density less than 1, which means $P_f(F)\le N\omega _N$. The set $E\cup F$ then has volume V, and by (2.1) we obtain $P(E\cup F)\le {\mathfrak {J}}(V)$, which means that $E\cup F$ is an isoperimetric set. $\square$

3.1 Proof of Proposition 3.2

This section is devoted to the proof of Proposition 3.2. Before presenting it, it is convenient to prove a couple of technical lemmas.

Lemma 3.4

Let $g: (0,\infty )\rightarrow [0,\infty )$ and $\alpha :(-1,1)\rightarrow {\mathbb {R}}$ be $L^1$ functions such that

$$\begin{aligned} \lim _{t\rightarrow \infty } g(t)=0, \quad \int _{-1}^1\alpha (t)\,dt = 0, \quad \int _{-1}^\sigma \alpha (t) \,dt >0 \quad \forall \,\sigma \in (-1,1). \end{aligned}$$

(3.1)

Then there exists an arbitrarily large R such that

$$\begin{aligned} \int _{-1}^1\alpha (t)g(t+R)\,dt\ge 0, \end{aligned}$$

with strict inequality unless $g(t)=0$ for all t big enough.

Proof

If the claim were false, then for every choice of $R',\,R''$ with $R''\ge R'+2$ one has

$$\begin{aligned} \begin{aligned} 0&>\,\int _{R'}^{R''}\int _{-1}^1\alpha (t)g(t+R)\,dt\,dR\\&=\,\int _{R'-1}^{R'+1}g(s)\int _{-1}^{s-R'}\alpha (t)\,dt\,ds\\&\quad +\,\int _{R''-1}^{R''+1}g(s)\int _{s-R''}^{1}\alpha (t)\,dt\,ds\\&=\,A(R')+B(R''), \end{aligned} \end{aligned}$$

where there is no integral over $(R'+1,R''-1)$ because it cancels thanks to (3.1). The conditions on $\alpha$ and g also ensure that $A(R')\ge 0\ge B(R'')$ for every $R',\, R''$. Now suppose that for some arbitrarily large $R'$ one has $A(R')>0$. We can then fix $R'$ and send $R''\rightarrow \infty$: since $g\rightarrow 0$, we get $B(R'')\rightarrow 0$, and then there is some $R''\gg 1$ such that $A(R')+B(R'')>0$, against the above inequality. As a consequence, it must be that $A(R')=0$ for every $R'$ big enough, and in turn this means that g is definitively zero, hence any R big enough satisfies the claim. $\square$

Lemma 3.5

Let $g: (0,\infty )\rightarrow [0,\infty )$ and $\beta :(-1,1)\rightarrow {\mathbb {R}}$ be $L^1$ functions such that g and $\alpha (t)=\int _{-1}^t\beta (\sigma )\,d\sigma$ satisfy condition (3.1), and $\alpha (1)=0$. Then there exists an arbitrarily large R such that

$$\begin{aligned} \int _{-1}^1\beta (t)g(t+R)\,dt\ge 0, \end{aligned}$$

(3.2)

with strict inequality unless $g(t)=0$ for all t big enough.

Proof

The proof is analogous to the one of Lemma 3.4 above. Take $R'\gg 1$ and assume that the conclusion fails for every $R\ge R'$; then for every $R''> R' +2$ we have

$$\begin{aligned} 0&>\,\int _{R'}^{R''}\int _{-1}^{1} \beta (t)g(t+R)\,dt\,dR\\&=\,\int _{R'-1}^{R'+1}g(s)\int _{-1}^{s-R'}\beta (t)\,dt\,ds\\&\quad +\,\int _{R''-1}^{R''+1}g(s)\int _{s-R''}^{1}\beta (t)\,dt\,ds. \end{aligned}$$

Exactly as before, since the last term in the right goes to 0 when $R''\rightarrow \infty$, we find a contradiction as soon as the first term in the right is strictly positive. In other words, the proof is concluded as soon as we find some $R'$ such that

$$\begin{aligned} 0&<\int _{R'-1}^{R'+1}g(s)\int _{-1}^{s-R'}\beta (t)\,dt\,ds\\&=\,\int _{R'-1}^{R'+1} g(s) \alpha (s-R')\,ds\\&=\,\int _{-1}^1 \alpha (t)g(t+R')\,dt. \end{aligned}$$

And in turn, the existence of such an $R'$ is ensured by Lemma 3.4 since $\alpha$ satisfies condition (3.1), unless g is definitively zero. And in this latter case, of course any R big enough would satisfy the required condition. $\square$

We are now ready to prove Proposition 3.2.

Proof of Proposition 3.2

For simplicity, we split the proof in two steps: first we show that one can always reduce to the case of a radial density, and then we prove the claim for this case.

Step I Reduction to radial case.

Let us assume that the claim holds for any radial density, and let f be not necessarily radial. Define then the density ${\tilde{f}}$ as the radial average of f, namely,

(3.3)

Of course, then ${\tilde{g}}=1-{\tilde{f}}$ is also the radial average of g. Since the claim holds for the radial density ${\tilde{f}}$, for any $\varepsilon >0$ we can find a ball B satisfying $P_{{\tilde{g}}}(B) \ge (N-\varepsilon ) |B|_{{\tilde{g}}}$. Let us then call $B^\theta$, for $\theta \in {\mathbb {S}}^{N-1}$, the ball having the same distance from the origin as B, and which is rotated by an angle $\theta$: all the different balls $B^\theta$ are equivalent for the density ${\tilde{f}}$, but not for the original density f. Now observe that by definition

and then of course there exists some $\theta \in {\mathbb {S}}^{N-1}$ such that $P_g(B^\theta )\ge (N-\varepsilon ) |B^\theta |_g$.

Step II Proof of the radial case.

Thanks to Step I we can assume without loss of generality that f is radial. For a ball $B_R$ having radius 1 and center at a distance R from the origin, we can then calculate perimeter and volume by integrating over the radial layers, that is, we have

$$\begin{aligned} P_g(B_R) = \int _{-1}^1 \varphi _R(t) g(t+R) \, dt, \quad |B_R|_g = \int _{-1}^1 \psi _R(t) g(t+R) \, dt, \end{aligned}$$

(3.4)

where $\varphi _R(t)$ and $\psi _R(t)$ can be calculated by the Fubini theorem and the co-area formula. Actually, it is not important to write down the exact formula, while it is easy to observe that (basically, since the layers become flat in the limit) the following uniform limits hold

$$\begin{aligned} \frac{\varphi _R(t)}{\widetilde{\varphi }(t)} \xrightarrow [\ R\rightarrow \infty ]{} 1, \quad \frac{\psi _R(t)}{\widetilde{\psi }(t)} \xrightarrow [\ R\rightarrow \infty ]{} 1, \end{aligned}$$

(3.5)

the limit functions being simply

$$\begin{aligned} \widetilde{\varphi }(t) = (N-1)\omega _{N-1} (1-t^2)^{\frac{N-3}{2}}, \quad \widetilde{\psi }(t) = \omega _{N-1} (1-t^2)^{\frac{N-1}{2}}. \end{aligned}$$

As a consequence, we can work with the approximated functions $\widetilde{\varphi }$ and $\widetilde{\psi }$ in place of $\varphi$ and $\psi$: more precisely, we call “approximated” perimeter and volume of $B_R$ the functions $\widetilde{P}_g(B_R)$ and $\widetilde{V}_g(B)$ obtained by substituting $\varphi$ and $\psi$ into (3.4) with $\widetilde{\varphi }$ and $\widetilde{\psi }$. The claim will then be automatically obtained, thanks to (3.5), if we can find an arbitrarily large R such that

$$\begin{aligned} \widetilde{P}_g(B_R)\ge N \widetilde{V}_g(B_R). \end{aligned}$$

We can now define $\beta :(-1,1)\rightarrow {\mathbb {R}}$ as $\beta (t)={\tilde{\varphi }}(t)-N{\tilde{\psi }}(t)$, so that we can limit ourselves to finding an arbitrarily large R such that (3.2) holds. It is elementary to check that the assumptions of Lemma 3.5 are satisfied: one can either do the simple calculations, or just observe that $\alpha (t)$ coincides with the perimeter minus N times the volume of the portion of the unit ball centered at the origin whose first coordinate is between $-1$ and t, so that all the conditions to check become trivial. Therefore, the existence of the sought R directly comes from Lemma 3.5 and the proof is completed. $\square$

3.2 Proof of Proposition 3.3

This last section is entirely devoted to giving the proof of Proposition 3.3, again divided into a few steps. For the reader’s convenience, in Steps I and II we start with two particular cases, namely, when f is non-decreasing along the half-lines starting at the origin, and when f is radial: even though these two particular cases are not really needed for the proof, the argument is similar to the general one but works more easily, so this helps to understand the general case.

Proof of Proposition 3.3

Let us set $\varepsilon \ll 1$: thanks to Proposition 3.2, there is a ball $B=B_R^{\bar{\theta }}$ of radius 1 and centered at the point $R\bar{\theta }$, with some arbitrarily large R and some $\bar{\theta }\in {\mathbb {S}}^{N-1}$, which satisfies $P_g(B)\ge (N-\varepsilon ) |B|_g$. Since $f\le 1$ on B, we have $|B|_f\le \omega _N$: if $|B|_f=\omega _N$ we are already done, because $P_f(B)\le P_\mathrm{eucl}(B)=N\omega _N$, and this automatically implies that the mean density of B is less than 1. Then let us suppose that $|B|_f <\omega _N$, or equivalently that $|B|_g>0$, and let us try to enlarge B so as to reach volume $\omega _N$, but still having mean density less than 1. We will do this in some steps.

Step I The case of non-decreasing densities.

Let us start with the case when f is a “non-decreasing density”. This means that, for every $\theta \in {\mathbb {S}}^{N-1}$, the function $t\mapsto f(t\theta )$ is non-decreasing, at least for large t.

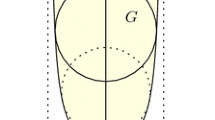
In this case, let us define a new set E as follows. First of all, we decompose $B=B_l \cup B_r$, where $B_l$ and $B_r$ are the “left” and the “right” part of the ball $B_R^{\bar{\theta }}$: formally, a point $x\in B$ is said to belong to $B_l$ or $B_r$ if $x\cdot \bar{\theta }$ is smaller or bigger than R respectively. Then for any small $\delta$ we call $B_{l,\delta }$ the half-ball centered at $(R-\delta )\bar{\theta }$ with radius $(R-\delta )/R$, and $C_\delta$ the cylinder of radius 1 and height $\delta$ whose axis is the segment connecting $(R-\delta )\bar{\theta }$ and $R\bar{\theta }$; finally, we let $E_\delta =B_r \cup B_{l,\delta } \cup C_\delta$; see Fig. 1, left. Since f is converging to 1, and R can be taken arbitrarily big, we have

$$\begin{aligned} |E_\delta |_f - |B|_f \ge (1-\varepsilon ) \omega _{N-1} \delta \,; \end{aligned}$$

as a consequence, by continuity we can fix $\bar{\delta }$ such that $E=E_{\bar{\delta }}$ has exactly volume $\omega _N$, and we have

$$\begin{aligned} \bar{\delta }\le (1+2 \varepsilon ) \,\frac{|B|_g}{\omega _{N-1}}. \end{aligned}$$

(3.6)

Thanks to the assumption that f is non-decreasing, we know that

(3.7)

where we call $\partial ^l B_{l,\delta }$ and $\partial ^l B_\delta$ the “left parts” of the boundaries, that is,

$$\begin{aligned} \partial ^l B_l = \Big \{y \in \partial B_l :\, y \cdot \bar{\theta }\le R \Big \}, \quad \partial ^l B_{l,\delta } = \Big \{y \in \partial B_{l,\delta } :\, y \cdot \bar{\theta }\le R-\delta \Big \}. \end{aligned}$$

As a consequence, again using the facts that $f\le 1$ and that R can be taken arbitrarily big, thanks to (3.6) and (3.7) we can evaluate

$$\begin{aligned} \begin{aligned} P_f(E)&\le P_f(B) +(N-1+\varepsilon )\omega _{N-1}\bar{\delta }\le N\omega _N - P_g(B) +(N-1+\varepsilon ) (1+2\varepsilon ) |B|_g\\&\le N\omega _N - (N-\varepsilon ) |B|_g +(N-1+\varepsilon ) (1+2\varepsilon ) |B|_g < N\omega _N. \end{aligned} \end{aligned}$$

Summarizing, we have built a set E arbitrarily far from the origin, with volume exactly $\omega _N$, and perimeter less than $N\omega _N$, thus having mean density less than 1. The proof is then concluded for this case.

Fig. 1

The sets E of Step I (left) and of Step II (right). The half-balls $B_r$ and $B_{l,\delta }$, as well as the half-balls $B^-$ and $B^+_\delta$, are light shaded; the cylinder $C_\delta$, as well as the region $E\setminus (B^-\cup B^+_\delta )$, is dark shaded

Step II The case of radial densities.

Let us now assume that the density is radial. In this case, we cannot use the same argument as in the previous step, because there would be no way to extend the validity of (3.7). Nevertheless, we can use a similar idea to enlarge the ball B: instead of translating half of the ball B we rotate it. More formally, let us take a hyperplane passing through the origin and the center of the ball $B_R^{\bar{\theta }}$, and let us denote by $B^\pm$ the two corresponding half-balls into which $B_R^{\bar{\theta }}$ is subdivided. Let us then consider the circle contained in ${\mathbb {S}}^{N-1}$ which contains the direction $\bar{\theta }$ and the direction orthogonal to the hyperplane, and for any small $\sigma >0$ let $\rho _\sigma$ denote rotation through angle $\sigma$ in this circle. Then let $B^+_\sigma =\rho _\sigma (B^+)$ and finally let $E_\delta$ be the union of $B^-$ with all the half-balls $B^+_\sigma$ for $0<\sigma <\delta$, as in Fig. 1, right. As in the previous step, since f is converging to 1 we can evaluate the difference of the volumes as

$$\begin{aligned} |E_\delta |_f - |B|_f \ge \omega _{N-1}(R-1)(1-\varepsilon ) \delta . \end{aligned}$$

Then we can again select $\bar{\delta }$ such that $E=E_{\bar{\delta }}$ has volume exactly $\omega _N$ and we have

$$\begin{aligned} \bar{\delta }\le (1+2 \varepsilon )\,\frac{|B|_g}{\omega _{N-1}(R-1)}. \end{aligned}$$

(3.8)

This time, the radial assumption on f gives

where $\partial ^+ B^+_\delta$ and $\partial ^+ B^+$ denote the “upper” parts of the boundaries in the obvious sense. And finally, almost exactly as in last step we can estimate the perimeter of E as

$$\begin{aligned} \begin{aligned} P_f(E)&\le P_f(B) + (N-1)\omega _{N-1} (R+1) \bar{\delta }\\&\le N\omega _N - P_g(B) + (N-1)(1+2\varepsilon )\,\frac{R+1}{R-1}\,|B|_g\\&\le N\omega _N - (N-\varepsilon )|B|_g + (N-1)(1+2\varepsilon )\,\frac{R+1}{R-1}\,|B|_g< N\omega _N, \end{aligned} \end{aligned}$$

where the last inequality again is true if we have chosen $\varepsilon \ll 1$ and then $R\gg 1$. Thus, the set E has volume $\omega _N$ and mean density less than 1, and the proof is obtained also in this case.

Step III The general case in dimension 2.

Let us now treat the case of a general density f. For simplicity of notation we now assume that we are in the two-dimensional situation $N=2$. In the next step we generalize our argument to any dimension.

As in the proof of Proposition 3.2, let us call ${\tilde{f}}$ the radial average of f according to (3.3), and ${\tilde{g}}=1-{\tilde{f}}$ the radial average of g. Proposition 3.2 then provides us with a ball $B_R$, of radius 1 and distance $R\gg 1$ from the origin, such that

$$\begin{aligned} P_{{\tilde{g}}}(B_R)\ge (N-\varepsilon ) |B_R|_{{\tilde{g}}}. \end{aligned}$$

(3.9)

For any $\theta \in {\mathbb {S}}^1$, as usual, we then call $B_R^\theta$ the ball of radius 1 centered at $R\theta$. Let us now argue as in Step II: we call $B_R^{\theta ,\pm }$ (resp., $\partial ^\pm B_R^\theta$) the two half-balls (resp., half-circles) made by the points of $B_R^\theta$ (resp., $\partial B^\theta _R$) having direction bigger or smaller than $\theta$; thus, for any small $\delta >0$, we define $E_\delta ^\theta$ the union of $B^{\theta ,-}_R$ with all the half-balls $B^{\theta +\sigma ,+}_R$ for $0<\sigma <\delta$. Since the sets $E^\theta _\delta$ are increasing for $\delta$ increasing, if $R\gg 1$ there is a unique $\bar{\delta }=\bar{\delta }(\theta )$ such that $|E^\theta _{\bar{\delta }}|_f=\omega _N$, and exactly as in Step II we have the estimate (3.8) for $\bar{\delta }$, which for R big enough (since $f\rightarrow 1$ and then $g\rightarrow 0$) implies

$$\begin{aligned} \bar{\delta }(\theta ) \le \frac{(1+3\varepsilon )|B_R^\theta |_g}{\omega _{N-1}(R-1)}. \end{aligned}$$

(3.10)

Let us then define the function $\tau :{\mathbb {S}}^1\rightarrow {\mathbb {S}}^1$ as $\tau (\theta )=\theta +\bar{\delta }(\theta )$, and notice that by construction this is a strictly increasing bijection of ${\mathbb {S}}^1$ onto itself, with $\tau (\theta )>\theta$ (if $\tau (\theta )=\theta$ then the ball $B^\theta _R$ has already volume $\omega _N$, and in this case there is nothing to prove, as already observed). Let us now fix a generic $\theta \in {\mathbb {S}}^1$, and let $\eta \ll \tau (\theta )-\theta$: if we call

$$\begin{aligned} A=\Big (\bigcup \nolimits _{0<\sigma<\eta } B_R^{\theta +\sigma } \Big )\setminus B_R^{\theta +\eta }, \quad B=\Big (\bigcup \nolimits _{0<\sigma <\eta } B_R^{\tau (\theta +\sigma )} \Big )\setminus B_R^{\tau (\theta )}, \end{aligned}$$

then, since

$$\begin{aligned} \big |E^\theta _{\bar{\delta }(\theta )}\big |_f = \omega _N = \big |E^{\theta +\eta }_{\bar{\delta }(\theta +\eta )}\big |_f, \quad E^{\theta +\eta }_{\bar{\delta }(\theta +\eta )}=\big (E^\theta _{\bar{\delta }(\theta )}\cup B\big ) \setminus A, \end{aligned}$$

one has $|A|_g =|B|_g$. On the other hand, one clearly has

$$\begin{aligned} \frac{|B|_\mathrm{eucl}}{|A|_\mathrm{eucl}}= \frac{\tau (\theta +\eta )-\tau (\theta )}{\eta }. \end{aligned}$$

Taking R big enough, we can assume without loss of generality that $1-\varepsilon \le f \le 1$ for points having distance at least $R-1$ from the origin, and this yields

$$\begin{aligned} 1-\varepsilon \le \frac{\tau (\theta +\eta ) - \tau (\eta )}{\eta }\le \frac{1}{1-\varepsilon }. \end{aligned}$$

As an immediate consequence we obtain that the function $\tau$ is bi-Lipschitz and $1-\varepsilon \le \tau '\le (1-\varepsilon )^{-1}$. Let us now observe that, by construction, all the sets $E^\theta =E^\theta _{\tau (\theta )-\theta }$ have exactly volume $\omega _N$: we then want to find some $\bar{\theta }\in {\mathbb {S}}^1$ such that $P_f(E^{\bar{\theta }})\le N\omega _N$, so $E^{\bar{\theta }}$ has mean density less than 1 and we are done. Now, since a simple change of variables gives

we can readily evaluate by (3.9)

and hence get the existence of some $\bar{\theta }\in {\mathbb {S}}^1$ such that

Thanks to (3.10), we then have

where the last inequality holds as soon as $\varepsilon$ was chosen small enough at the beginning. The set $E^{\bar{\theta }}$ is then as sought and this step is done.

Step IV The general case.

We are now ready to present the proof in the general case. We start by noticing that in the argument of Step III the assumption $N=2$ was used only to work with ${\mathbb {S}}^1$, hence to get the validity of (3.9). More precisely, let us assume that there exists some arbitrarily large R and some circle ${\mathcal {C}}\approx {\mathbb {S}}^1$ in ${\mathbb {S}}^{N-1}$ such that the estimate

(3.11)

holds true. Then we can repeat verbatim the proof of Step III: we get the existence of some $\bar{\theta }\in {\mathcal {C}}$ such that the set $E_R^{\bar{\theta }}$ has volume $\omega _N$ and mean density less than 1, and the proof is concluded. Hence, it remains to find some R and some circle ${\mathcal {C}}$ so that (3.11) holds; notice that, if $N=2$, then ${\mathcal {C}}={\mathbb {S}}^1$ and (3.11) reduces to (3.9), which in turn holds for some arbitrarily large R thanks to Proposition 3.2.

Let us then consider the case of dimension $N=3$. By Proposition 3.2 we can take $R\gg 1$ such that (3.9) holds true; for any $\theta \in {\mathbb {S}}^2$, then we denote by ${\mathcal {C}}_\theta$ the circle in ${\mathbb {S}}^2$ which is orthogonal to $\theta$, and we observe that, by homogeneity,

so thanks to (3.9) we get the existence of a circle ${\mathcal {C}}={\mathcal {C}}_{\bar{\theta }}$ for which (3.11) holds true: the proof is then concluded also in dimension $N=3$.

Notice that the argument above can be rephrased as follows: if there exists some sphere $\mathcal S\approx {\mathbb {S}}^2 \subseteq {\mathbb {S}}^{N-1}$ such that the average estimate (3.11) holds with $\mathcal S$ in place of ${\mathcal {C}}$ (and in turn in dimension $N=3$ this reduces to (3.9) and hence holds), then the proof is concluded. As a consequence, the claim follows also in dimension $N=4$, arguing exactly as above with the spheres $\mathcal S_\theta \approx {\mathbb {S}}^2$ orthogonal to any $\theta \in {\mathbb {S}}^3$, and the obvious argument by induction then gives the thesis for any dimension. $\square$

Remark 3.6

Notice that, in the proof of Proposition 3.3, we have actually found a set which has mean density strictly less than 1, unless $g\equiv 0$ on some ball of radius 1. On the other hand, as it clearly appears from the proof of Theorem 1.2, it is impossible to find such a set if some isoperimetric sequence is losing mass at infinity, otherwise the argument of Theorem 1.2 would give a set with perimeter strictly less than the infimum. There are then only two possibilities: either there are balls where $f\equiv 1$ arbitrarily far from the origin, or no isoperimetric sequence can lose mass at infinity.

In particular, our proof shows that no isoperimetric sequence can lose mass at infinity if $f<1$ out of some big ball.