Some Weighted Isoperimetric Problems on ${\mathbb {R}}^N _+$ with Stable Half Balls Have No Solutions

Abstract

We show the counter-intuitive fact that some weighted isoperimetric problems on the half-space ${\mathbb {R}}^N _+$, for which half-balls centered at the origin are stable, have no solutions. A particular case is the measure $d\mu = x_N ^{\alpha } \, dx$, with $\alpha \in (-1,0)$. Some results on stability and nonexistence for weighted isoperimetric problems on ${\mathbb {R}}^N$ are also obtained.

1 Introduction

A manifold with density is a manifold endowed with a positive function, the density, which weights both the volume and the perimeter. This mathematical subject is attracting an increasing attention from the mathematical community. The related bibliography is very wide and, in this short note, it is impossible to give an exhaustive account of it. Hence we remind the interested reader to [19] and [21] and the references therein. One natural issue in this setting consists of finding families of densities for which one can determine the explicit form of the isoperimetric set, see for instance [5,6,7,8,9,10, 12, 17, 23].

The problem becomes more challenging when perimeter and volume carry two different weights. One important example is when the manifold is ${\mathbb {R}}^N$, ($N\ge 2$), and the two weight functions are powers of the distance from the origin, see [1], and the references cited therein. The theorem proved in [1] states that all spheres about the origin are isoperimetric for a certain range of the powers. One can modify this problem by inserting a further homogeneous perturbation term, namely $x_{N}^{\alpha }$, both in the volume and in the perimeter, see [2] and [3]:

where ${\mathbb {R}}^{N} _{+} := \{ x \in {\mathbb {R}}^N :\, x_N >0\}$ and $k,\ell , \alpha \in {\mathbb {R}}$.

Adapting some new methods introduced in [1], in [2] and [3] the authors find, for any given positive number $\alpha$, a range of parameters k and $\ell$ for which the isoperimetric sets are intersections of balls centered at the origin, denoted in the sequel by $B_{R}$, with ${\mathbb {R}}^N_{+}$.

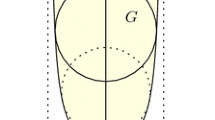
In the present paper we discuss again problem (P), but for $\alpha \in (-1,0)$. It turns out that for a certain range of the parameters k and $\ell$, the problem has no solution despite the fact that half-balls $B_{R} \cap {\mathbb {R}}^N _+$ are stable. By this, we mean that the first variation of the weighted perimeter vanishes while the second variation is nonnegative under every smooth perturbation of $\partial B_{R} \cap {\mathbb {R}}^N _+$ which preserves the measure constraint contained in problem (P) (for a precise definition of stability see Sect. 4).

Our main result is the following

Theorem 1.1

Assume that $\alpha \in (-1,0)$, and that the conditions

$$\begin{aligned}&k+N+\alpha -1 < \sqrt{(N-1)(N+\alpha -1)}, \end{aligned}$$

(1.1)

$$\begin{aligned}&N(k+ N+\alpha -1) < (\ell +N+\alpha ) (N-1), \end{aligned}$$

(1.2)

$$\begin{aligned}&\ell +1 \le k +\frac{N+\alpha -1}{k+N+\alpha -1 } \end{aligned}$$

(1.3)

are satisfied. Then the isoperimetric problem (P) has no solution, nevertheless half-balls $B_R \cap {\mathbb {R}}^N _{+}$ are stable.

Note that the conditions (1.1), (1.2) and (1.3) are satisfied in the model case $k=\ell =0$.

The delicate part in the proof of Theorem 1.1 relies on finding the best constant, $\mu _1 ^{\alpha } ( {\mathbb {S}}^{N-1}_+)$, in a weighted Poincaré-Wirtinger inequality on the half-sphere ${\mathbb {S}}^{N-1} _+ := {\mathbb {S}}^{N-1} \cap {\mathbb {R}}^{N}_ {+}$.

In Sect. 2 we prove a compact imbedding property for some weighted spaces for functions defined on the upper half-sphere. To this aim we use stereographic coordinates, since, in this coordinate system, the metric is just the conformal factor times the identity. This allows us to use an already known compact imbedding result for weighted spaces in ${\mathbb {R}}^{N-1}$.

In Sect. 3 we first note that $\mu _1 ^{\alpha } ( {\mathbb {S}}^{N-1}_+ )$ represents the first nontrivial Neumann eigenvalue of some self-adjoint compact operator on the half-sphere. In view of the imbedding result this implies that $\mu _1 ^{\alpha } ( {\mathbb {S}}^{N-1}_+ )$ appears as a minimum of an appropriate Rayleigh quotient. Then we write the operator in spherical coordinates and, using separation of variables and comparing the eigenvalues of two Sturm-Liouville problems, we show that the exact value of $\mu _1 ^{\alpha } ( {\mathbb {S}}^{N-1}_+ )$ is $N+\alpha -1$. This implies the stability of half-spheres in view of Theorem 4.1 in [2], which holds true irrespectively of the sign of $\alpha$.

In order to prove that the problem has no solution, we show in Sect. 4 that the “isoperimetric ratio” (see (4.8)) for a unit ball centered at $(0, \ldots , 0, t)$ tends to zero when t goes to infinity. This completes the proof of Theorem 1.1.

Our paper concludes with a few remarks on stability and nonexistence for some weighted isoperimetric problems on ${\mathbb {R}}^N$ in Sect. 5.

2 Notation and preliminary results

Throughout this paper the following notation will be in force:

$$\begin{aligned}&{\mathbb {R}}_{+}^{N}=\left\{ x=(x_{1},...,x_{N})\in {\mathbb {R}} ^{N}: x_{N}>0\right\} , \ |x|:= \sqrt{\sum _{i=1} ^N x_i ^2 },\ N\ge 2 ,\\&H= \{ x= (x_1 , \ldots , x_N ):\, x_N =0 \} ,\\&B_R (x^0):= \left\{ x \in {\mathbb {R}}^{N}: \, |x-x^0 |<R \right\} , \quad ( x^{0} \in {\mathbb {R}}^{N}, \ R>0 ),\\&B_R:=B_R (0), \quad B_R ^+ := B_R \cap {\mathbb {R}}^N _+ ,\\&{\mathbb {S}}^{N-1}=\partial B_1 , \ {\mathbb {S}}_{+}^{N-1}:= {\mathbb {S}}^{N-1}\cap {\mathbb {R}}_{+}^{N},\\&{\mathbb {B}}_{1}:= \left\{ y = (y_1 , \ldots y_{N-1}) \in {\mathbb {R}}^{N-1}: \, |y| := \sqrt{\displaystyle \sum \limits _{i=1}^{N-1}y_{i}^{2}}<1 \right\} . \end{aligned}$$

The stereographic projection

$$\begin{aligned} {\mathbb {S}}_{+}^{N-1} \ni \zeta \longmapsto y = S(\zeta ) \in {\mathbb {B}} _1 \end{aligned}$$

from the south pole $P_{S}=(0,..,0,-1)$ and its inverse are given by

$$\begin{aligned} y_{i}=\dfrac{\zeta _{i}}{1+\zeta _{N}}\text { for }1\le i\le N-1, \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{ccc} \zeta _{i}=\dfrac{2y_{i}}{\left| y\right| ^{2}+1} &{}\quad \text {for} &{} 1\le i\le N-1 \\ &{} &{} \\ \zeta _{N}=\dfrac{1-\left| y\right| ^{2}}{\left| y\right| ^{2}+1} &{}\quad \text {for} &{} i=N \end{array} \right. \end{aligned}$$

respectively. As well known, in this coordinate system, see e.g. [13] p. 444, the metric on ${\mathbb {S}}^{N-1}$ is

$$\begin{aligned} g_{ij}(y)=\left( \dfrac{2}{\left| y \right| ^{2}+1}\right) ^{2}\delta _{ij}. \end{aligned}$$

Hence $d\sigma$, the volume element on ${\mathbb {S}}^{N-1}$, is given by

$$\begin{aligned} d\sigma =\sqrt{\det g_{ij}(y)}\, dy=\left( \dfrac{2}{\left| y\right| ^{2}+1 }\right) ^{N-1}\, dy. \end{aligned}$$

For any function $u: {\mathbb {S}}^{N-1 } _+ \rightarrow {\mathbb {R}}$ we define ${\hat{u}} : {\mathbb {B}}_1 \rightarrow {\mathbb {R}}$ by

$$\begin{aligned} {\hat{u}}(y) := u(\zeta ) , \quad (y= S(\zeta ), \, \zeta \in {\mathbb {S}} ^{N-1} _+). \end{aligned}$$

Note that, if u is a smooth function, then

$$\begin{aligned} |\nabla _{\mathbb {S}} u (\zeta ) | = \sqrt{g^{ij} {\hat{u}}_{y_i} (x) {\hat{u}}_{y_j } (y) } = |\nabla {\hat{u}} (y) | \cdot \frac{2}{|y|^2 +1} , \quad (\zeta \in {\mathbb {S}}^{N-1} _+ ). \end{aligned}$$

For $\alpha \in \left( -1, +\infty \right)$, we consider the measure $d\sigma _{\alpha }$, defined on ${\mathbb {S}}_{+}^{N-1}$, given by $d\sigma$ times $\zeta _{N}^{\alpha }$. In stereographic coordinates, such a measure takes the following form

$$\begin{aligned} d\sigma _{\alpha }=\left( \dfrac{1-\left| y\right| ^{2}}{\left| y\right| ^{2}+1}\right) ^{\alpha } \cdot \left( \dfrac{2}{\left| y\right| ^{2}+1}\right) ^{N-1}\, dy. \end{aligned}$$

Define the weighted Sobolev space $W^{1,2}\left( {\mathbb {S}} _{+}^{N-1};\, d\sigma _{\alpha }\right)$ as the closure of $C^{\infty }( {\mathbb {S}}_{+}^{N-1})$ under the norm

$$\begin{aligned} \left\| u\right\| _{W^{1,2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }^{2} := \left\| u\right\| _{L^{2}\left( {\mathbb {S}} _{+}^{N-1};\, d\sigma _{\alpha }\right) }^{2} + \left\| \nabla _{{\mathbb {S}}} u \right\| _{L^{2} \left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }^{2}. \end{aligned}$$

Theorem 2.1

The space $W^{1,2}\left( {\mathbb {S}} _{+}^{N-1};\, d\sigma _{\alpha }\right)$ is compactly embedded in $L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) .$

Proof

As already noticed the stereographic projection from the south pole of ${\mathbb {S}} _{+}^{N-1}$ is just ${\mathbb {B}}_{1}.$ Let us first write the weighted norm of a function in stereographic coordinates.

$$\begin{aligned} \left\| \nabla _{{\mathbb {S}}} u\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }^{2}= & {} \sum _{i,j}\int _{{\mathbb {B}}_{1}}\left[ g^{ij}\frac{ \partial {\hat{u}}}{\partial y_{i}}\frac{\partial {\hat{u}}}{\partial y_{j}}\right] \left( \dfrac{2}{\left| y\right| ^{2}+1}\right) ^{N-1}\left( \dfrac{ 1-\left| y\right| ^{2}}{\left| y\right| ^{2}+1}\right) ^{\alpha }\, dy \\= & {} \int _{{\mathbb {B}}_{1}}\left[ \left( \dfrac{2}{\left| y\right| ^{2}+1} \right) ^{-2}\left| \nabla {\hat{u}}\right| ^{2}\right] \left( \dfrac{2}{ \left| y\right| ^{2}+1}\right) ^{N-1}\left( \dfrac{1-\left| y\right| ^{2}}{\left| y\right| ^{2}+1}\right) ^{\alpha }\, dy\\= & {} \int _{{\mathbb {B}}_{1}}\left| \nabla {\hat{u}}\right| ^{2}\dfrac{2^{N-3} \left( \left| y\right| +1\right) ^{\alpha } }{\left( \left| y\right| ^{2}+1\right) ^{N-3+\alpha }} \cdot \left( 1-\left| y\right| \right) ^{\alpha } \, dy \end{aligned}$$

and

$$\begin{aligned} \left\| u\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1}\, d\sigma _{\alpha }\right) }^{2} = \int _{{\mathbb {B}}_{1}}{\hat{u}}^{2} \frac{2^{N-1}\left( |y|+1 \right) ^{\alpha } }{ \left( |y| ^{2}+1 \right) ^{N-1+\alpha }} \cdot \left( 1- \left| y\right| \right) ^{\alpha } \, dy. \end{aligned}$$

Note that there exists $C\in \left( 0,1 \right)$ such that for any $y\in {\mathbb {B}}_{1}$ there holds

$$\begin{aligned} C\le \dfrac{2^{N-3}\left( \left| y\right| +1\right) ^{\alpha } }{\left( \left| y\right| ^{2}+1\right) ^{N-3+\alpha }}\le \frac{1}{C} \end{aligned}$$

(2.1)

and

$$\begin{aligned} C\le 2^{N-1}\left( \dfrac{1}{\left| y\right| ^{2}+1}\right) ^{N-1+\alpha }\left( \left| y\right| +1\right) ^{\alpha }\le \frac{1 }{C}. \end{aligned}$$

(2.2)

Now consider a bounded sequence $\left\{ u_{n}\right\} _{n\in {\mathbb {N}}}$ of functions in $W^{1,2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) ,$ that is,

$$\begin{aligned} \left\| u_{n}\right\| _{W^{1,2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) } \le C \quad \forall n\in {\mathbb {N}}. \end{aligned}$$

(2.3)

Writing

$$\begin{aligned} d(y)=\text {dist}\left( y,\partial {\mathbb {B}}_{1}\right) =1-|y| , \end{aligned}$$

and using (2.1) and (2.2) one immediately realizes that (2.3) is equivalent to

$$\begin{aligned} \int _{{\mathbb {B}}_{1}}\left| \nabla {\hat{u}}_{n}\right| ^{2}d(y)^{\alpha }\, dy+\int _{{\mathbb {B}}_{1}}{\hat{u}}_{n}^{2}\, d(y)^{\alpha }\, dy\le C. \end{aligned}$$

Now using Theorem 8.8 in [14] we deduce that, up to a not relabelled subsequence, we have that there exists a function $u\in W^{1,2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right)$ such that

$$\begin{aligned} \int _{{\mathbb {B}}_{1}}\left| \hat{u_{n}}-{\hat{u}}\right| ^{2}\, d(y)^{\alpha }\, dy\rightarrow 0 \end{aligned}$$

and therefore

$$\begin{aligned} u_{n}\rightarrow u\text { strongly in }L^{2}\left( {\mathbb {S}} _{+}^{N-1};\, d\sigma _{\alpha }\right) . \end{aligned}$$

$\square$

Theorem 2.2

The following Weighted Poincaré inequality holds true

$$\begin{aligned} \left\| u-\frac{1}{\sigma _{\alpha }\left( {\mathbb {S}}_{+}^{N-1}\right) } \int _{{\mathbb {S}}_{+}^{N-1}}u\, d\sigma _{\alpha }\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) } \le C \left\| \nabla _{\mathbb {S}} u\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }, \end{aligned}$$

(2.4)

where $C\in (0,+\infty )$ is a constant which does not depend on u.

Proof

One can obtain the proof repeating the arguments of the classical one for the unweighted case (see, e.g., [16], Th. 8.11, page 218). We include it for reader’s convenience. Assume, arguing by contradiction, that there exists a sequence $\left\{ u_{k}\right\} _{k\in {\mathbb {N}} }\subset W^{1,2}\left( {\mathbb {S}}_{+}^{N-1};d\sigma _{\alpha }\right)$ such that

$$\begin{aligned} \left\| u_{k}-\frac{1}{\sigma _{\alpha }\left( {\mathbb {S}} _{+}^{N-1}\right) }\int _{{\mathbb {S}}_{+}^{N-1}}u_{k}\, d\sigma _{\alpha }\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) } \ge k\left\| \nabla _S u_{k}\right\| _{L^{2}\left( {\mathbb {S}} _{+}^{N-1};\, d\sigma _{\alpha }\right) } \end{aligned}$$

Consider now the normalized sequence

$$\begin{aligned} v_{k}:= \frac{u_{k}-\dfrac{1}{\sigma _{\alpha }\left( {\mathbb {S}} _{+}^{N-1}\right) }\displaystyle \int _{{\mathbb {S}}_{+}^{N-1}}u_{k}\, d\sigma _{\alpha }}{\left\| u_{k}-\dfrac{1}{\sigma _{\alpha }\left( {\mathbb {S}} _{+}^{N-1}\right) }\displaystyle \int _{{\mathbb {S}}_{+}^{N-1}}u_{k}\, d\sigma _{\alpha }\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }} \, \quad \ \forall k\in {\mathbb {N}}. \end{aligned}$$

Clearly

$$\begin{aligned} \int _{{\mathbb {S}}_{+}^{N-1}}v_{k}\, d\sigma _{\alpha }=0\,, \left\| v_{k}\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }=1\text { and }\left\| \nabla _S v_{k}\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }\le \frac{1}{k} \end{aligned}$$

(2.5)

for any $k\in {\mathbb {N}}.$

Thanks to Theorem 2.1 we have that there exists a function $v\in W^{1,2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right)$ such that, up to a subsequence,

$$\begin{aligned} v_{k}\rightarrow v\text { strongly in }L^{2}\left( {\mathbb {S}} _{+}^{N-1};\, d\sigma _{\alpha }\right) . \end{aligned}$$

Finally from (2.5) we deduce that

$$\begin{aligned} \int _{{\mathbb {S}}_{+}^{N-1}}v\, d\sigma _{\alpha }=0, \quad \left\| v\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }=1, \quad \text{ and } \ \nabla _{{\mathbb {S}}} v =0 \ \text{ a.e. } \text{ on } {\mathbb {S}} ^{N-1}_+ , \end{aligned}$$

which is impossible. $\square$

Remark 2.1

Note the aim of the next Section is to find the best constant in (2.4).

Using Theorem 2.1 and Theorem 2.2 we immediately deduce the following

Theorem 2.3

Let

$$\begin{aligned} V_{\alpha }:=\left\{ u\in W^{1,2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) :\, \int _{{\mathbb {S}}_{+}^{N-1}}u\, d\sigma _{\alpha }=0\right\} . \end{aligned}$$

Every sequence $\left\{ u_{n}\right\} _{n\in {\mathbb {N}}}\subset V_{\alpha }$ such that

$$\begin{aligned} \left\| \nabla _{\mathbb {S}} u_{n}\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }\le C\, \forall n\in {\mathbb {N}} \end{aligned}$$

for some $C\in (0,+\infty ),$ admits a subsequence, still denoted by $u_{n},$ such that

$$\begin{aligned} \left\| u_{n}-u\right\| _{L^{2}\left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) }\rightarrow 0\text { for some }u\in V_{\alpha }. \end{aligned}$$

(2.6)

3 An optimal weighted Wirtinger inequality

The spherical coordinates on ${\mathbb {S}}_{+}^{N-1}$ are given by

$$\begin{aligned} \left\{ \begin{array}{lll} \zeta _{N} &{} = &{} \cos \theta _{1} \\ \zeta _{N-1} &{} = &{} \sin \theta _{1}\cos \theta _{2}\, \\ \zeta _{N-2} &{} = &{} \sin \theta _{1}\sin \theta _{2}\cos \theta _{3} \\ &{} . &{} \\ &{} . &{} \\ \zeta _{2} &{} = &{} \sin \theta _{1}\sin \theta _{2}\cdot ...\cdot \sin \theta _{N-2}\cos \theta _{N-1} \\ \zeta _{1} &{} = &{} \sin \theta _{1}\sin \theta _{2}\cdot ...\cdot \sin \theta _{N-2}\sin \theta _{N-1} \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} \theta _{1}\in \left( 0,\frac{\pi }{2}\right) ; \theta _{2},...,\theta _{N-2}\left( 0,\pi \right) ; \theta _{N-1}\in \left( 0,2\pi \right) . \end{aligned}$$

Let $\Delta _{{\mathbb {S}}^{m}}$ be the classical Laplace Beltrami operator on ${\mathbb {S}}^{m}$. We consider the following differential operator

$$\begin{aligned} \Delta _{{\mathbb {S}}^{N-1}}^{\alpha }u:=\frac{1}{\sin ^{N-2}\theta _{1}}\frac{ \partial }{\partial \theta _{1}}\left( \sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}\frac{\partial u}{\partial \theta _{1}}\right) +\frac{\cos ^{\alpha }\theta _{1}}{\sin ^{2}\theta _{1}}\Delta _{{\mathbb {S}}^{N-2}}u. \end{aligned}$$

Note that

$$\begin{aligned} \Delta _{{\mathbb {S}}^{N-1}}^{0 }u =\Delta _{{\mathbb {S}}^{N-1}}u. \end{aligned}$$

Finally we will denote by $\mu _{1}^{\alpha }({\mathbb {S}}_{+}^{N-1})$ the first non-trivial eigenvalue of the following problem

$$\begin{aligned} \left\{ \begin{array}{cc} -\Delta _{{\mathbb {S}}^{N-1}}^{\alpha }u=\mu \cos ^{\alpha }\theta _{1}u &{} \text {on }{\mathbb {S}}_{+}^{N-1} \\ &{} \\ \displaystyle \int _{{\mathbb {S}}_{+}^{N-1}}ud\sigma _{\alpha }=0.{ \ \ \ \ \ \ } &{} \end{array} \right. \end{aligned}$$

(3.1)

Note that, by Theorem  2.3, $\mu _{1}^{\alpha }({\mathbb {S}} _{+}^{N-1})$ has the following variational characterization

$$\begin{aligned} \mu _{1}^{\alpha }({\mathbb {S}}_{+}^{N-1})= & {} \min \left\{ \frac{ \displaystyle \int _{{\mathbb {S}} _{+}^{N-1}}\left| \nabla _{{\mathbb {S}}}u\right| ^{2}\, d\sigma _{\alpha } }{\displaystyle \int _{{\mathbb {S}}_{+}^{N-1}}u^{2}\, d\sigma _{\alpha }},\text { with }u\in W^{1,2}\right. \nonumber \\&\left. \left( {\mathbb {S}}_{+}^{N-1};\, d\sigma _{\alpha }\right) \backslash \left\{ 0\right\} :\, \int _{{\mathbb {S}}_{+}^{N-1}}u\, d\sigma _{\alpha }=0\right\} . \end{aligned}$$

Indeed, the differential operator appearing in (3.1) is self-adjoint and compact.

Theorem 3.1

The following holds true:

$$\begin{aligned} \mu _{1}^{\alpha }({\mathbb {S}}_{+}^{N-1})=N+\alpha -1. \end{aligned}$$

Proof

We start by using standard separation of variables. Hence let

$$\begin{aligned} \psi =g\left( \theta _{1}\right) f(\theta _{2},...,\theta _{N-1}):{\mathbb {S}} _{+}^{N-1}\rightarrow {\mathbb {R}} \end{aligned}$$

be an eigenfunction of problem (3.1) corresponding to an eigenvalue $\mu$. A straightforward computation yields

$$\begin{aligned} -\frac{1}{g}\frac{1}{\sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}}\frac{d }{d\theta _{1}}\left( \sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}\frac{ dg}{d\theta _{1}}\right) +\frac{1}{g}\frac{1}{\sin ^{2}\theta _{1}}\frac{ \Delta _{{\mathbb {S}}^{N-2}}f}{f}=\mu . \end{aligned}$$

Since, see [11] and [22],

$$\begin{aligned} \frac{\Delta _{{\mathbb {S}}^{N-2}}f}{f}=\text {Constant }\Leftrightarrow {\ \ } \frac{\Delta _{{\mathbb {S}}^{N-2}}f}{f}=k\left( k+N-3\right) ,\text { with }k \in {\mathbb {N}} \cup \left\{ 0\right\} , \end{aligned}$$

we have

$$\begin{aligned} -\frac{1}{\sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}}\frac{d}{d\theta _{1}}\left( \sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}\frac{d}{d\theta _{1}}g\right) +\frac{k\left( k+N-3\right) }{\sin ^{2}\theta _{1}}g=g\mu . \nonumber \\ \end{aligned}$$

(3.2)

Let us denote with $\left\{ \mu _{k} \right\} _{k\in {\mathbb {N}}_{0}}$ the sequence of eigenvalues of the Sturm-Liouville problem (3.2).

We claim that

$$\begin{aligned} \mu _{0}>(N-1)(1-\alpha ). \end{aligned}$$

(3.3)

Clearly the first “radial” eigenfunction, $g_{0}(\theta _{1})$, of (3.1) corresponds to $k=0$. Since $g_{0}(\theta _{1})$ has exactly two nodal domains there exists ${\widehat{\theta }}\in \left( 0,\frac{\pi }{2} \right)$ such that

$$\begin{aligned} g_{0}(\theta _{1})=0\text { if and only if }\theta =\widehat{\theta }. \end{aligned}$$

Therefore

$$\begin{aligned} \mu _{0}=\lambda _{1}({\widehat{\theta }}), \end{aligned}$$

where $\lambda _{1}\left( {\widetilde{\theta }}\right)$ is the first eigenvalue of the following Dirichlet problem

$$\begin{aligned} \left\{ \begin{array}{lll} -\Delta _{{\mathbb {S}}^{N-1}}^{\alpha }v=\lambda \cos ^{\alpha }\theta _{1}v &{} \quad \text {on} &{} {\mathbb {S}}_{+}^{N-1}\cap \left\{ 0<\theta _{1}<\widetilde{\theta }\right\} \\ &{} &{} \\ v=0 &{}\quad \text {on} &{} \partial \left[ {\mathbb {S}}_{+}^{N-1}\cap \left\{ 0<\theta _{1}<{\widetilde{\theta }}\right\} \right] . \end{array} \right. \end{aligned}$$

(3.4)

Since, as well known, the Dirichlet eigenvalues are monotone with respect to the inclusion of sets, we have

$$\begin{aligned} \lambda _{1}\left( {\widehat{\theta }}\right) >\lambda _{1}\left( \frac{\pi }{2 }\right) . \end{aligned}$$

Let us conclude the proof of the claim by showing that

$$\begin{aligned} \lambda _{1}\left( \frac{\pi }{2}\right) =(N-1)(1-\alpha ). \end{aligned}$$

A straightforward computation shows that

$$\begin{aligned} \psi _{0}(\theta _{1}):=\cos ^{1-\alpha }\theta _{1} \end{aligned}$$

is an eigenfunction of problem (3.4) with $\widetilde{\theta }=\frac{ \pi }{2},$ corresponding to the eigenvalue $(N-1)(1-\alpha )$. Indeed we have

$$\begin{aligned}&\left. -\frac{1}{\sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}}\frac{d}{ d\theta _{1}}\left( \sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}\frac{d}{ d\theta _{1}}g\right) +\frac{k\left( k+N-3\right) }{\sin ^{2}\theta _{1}} g\right| _{k=0,{ \ }g=\cos ^{1-\alpha }\theta _{1}}\\&\quad =\frac{ 1-\alpha }{\sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}}\frac{d}{d\theta _{1}}\left( \sin ^{N-1}\theta _{1}\right) = \left( 1-\alpha \right) \left( N-1\right) \cos ^{1-\alpha }\theta _{1}. \end{aligned}$$

Since $\psi _{0}(\theta _{1})$ does not change sign on ${\mathbb {S}} _{+}^{N-1}\cap \left\{ 0<\theta _{1}<\frac{\pi }{2}\right\}$, it must be an eigenfunction corresponding to $\lambda _{1}\left( \frac{\pi }{2}\right)$ , and the claim follows.

Now let us turn our attention to the case $k=1$, which corresponds to the first “angular” eigenfunction. That is an eigenfunction $\varphi$ of problem (3.1) in the form

$$\begin{aligned} \varphi =g_{1}(\theta _{1})f(\theta _{2},...,\theta _{N-1}) \end{aligned}$$

where

$$\begin{aligned} g_{1}(\theta _{1})>0 \quad \forall \theta \in \left( 0,\frac{\pi }{2} \right) . \end{aligned}$$

Note that, since any eigenvalue of the problem (3.2) is simple, the function $g_{1}(\theta _{1})$ is unique, up to a multiplicative constant.

We claim that

$$\begin{aligned} g_{1}(\theta _{1})=\sin \theta _{1}. \end{aligned}$$

Indeed we have

$$\begin{aligned}&-\frac{1}{\sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}}\frac{d}{d\theta _{1}}\left( \sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}\frac{dg_{1}}{ d\theta _{1}}\right) +\frac{N-2}{\sin ^{2}\theta _{1}}g_{1}\\&\quad =-\frac{1}{\sin ^{N-2}\theta _{1}\cos ^{\alpha }\theta _{1}}\left( \left( N-2\right) \sin ^{N-3}\theta _{1}\cos ^{\alpha +2}\theta _{1}\right. \nonumber \\&\qquad \left. -\left( \alpha +1\right) \sin ^{N-1}\theta _{1}\cos ^{\alpha }\theta _{1}\right) +\frac{N-2 }{\sin \theta _{1}}\\&\quad =-\left( N-2\right) \frac{\cos ^{2}\theta _{1}}{\sin \theta _{1}}+\left( \alpha +1\right) \sin \theta _{1}+\frac{N-2}{\sin \theta _{1}}\\&\quad =\left( N+\alpha -1\right) \sin \theta _{1} =\left( N+\alpha -1\right) g_{1}(\theta _{1}). \end{aligned}$$

The claim is proved.

Gathering the above estimates, taking into account that $\alpha \in \left( -1,0\right)$, we have

$$\begin{aligned} \mu _{0}=\lambda _{1}({\widehat{\theta }})>\lambda _{1}\left( \frac{\pi }{2} \right) =(N-1)(1-\alpha )=-N\alpha +N+\alpha -1>N+\alpha -1=\mu _{1}. \end{aligned}$$

$\square$

Remark 3.1

By equality (4.11) of [2], we have just proven that, the second variation of the perimeter w.r.t. volume-preserving smooth perturbations at the half ball is nonnegative for $\alpha \in (-1 , +\infty )$. Note that in [7], see Proposition 2.1, the case of nonnegative $\alpha$ is addressed.

4 An isoperimetric problem in the half space and a curious example

In this section we consider an isoperimetric problem that we have studied in [2], but we will change the range of one of the parameters in it.

Let k, $\ell$ and $\alpha$ be real numbers satisfying

$$\begin{aligned}&\alpha >-1, \end{aligned}$$

(4.1)

$$\begin{aligned}&\ell +N+ \alpha >0, \end{aligned}$$

(4.2)

$$\begin{aligned}&k+N+\alpha >0. \end{aligned}$$

(4.3)

We define a measure $\mu _{\ell , \alpha }$ on ${\mathbb {R}}^{N}_+$ by

$$\begin{aligned} d\mu _{\ell , \alpha }(x)=|x|^{\ell } x_N^\alpha \,dx. \end{aligned}$$

(4.4)

If $M \subset$${{\mathbb {R}}}^{N}_{+}$ is a measurable set with finite $\mu _{\ell , \alpha }$-measure, then we define $M^{\star }$, the

$\mu _{\ell ,\alpha }$-symmetrization of M, as

$$\begin{aligned} M^{\star } := B_R ^+ , \end{aligned}$$

(4.5)

where R is given by

$$\begin{aligned} \mu _{\ell , \alpha } \left( B_{R} ^+ \right) = \mu _{\ell , \alpha } \left( M\right) = \int _M d\mu _{\ell , \alpha } (x) . \end{aligned}$$

(4.6)

Following [21], the $\mu _{k, \alpha }$–perimeter relative to${\mathbb {R}}^N _+$ of a measurable set M of locally finite perimeter - henceforth simply called the relative$\mu _{k, \alpha }$–perimeter - is given by

$$\begin{aligned} P_{\mu _{k, \alpha }}(M , {\mathbb {R}}^N _+ ):= \int _{\partial M\cap {\mathbb {R}} ^N_+ } \, x_N^\alpha |x|^{k} \, {\mathcal {H}}_{N-1} (dx) . \end{aligned}$$

(4.7)

Here and throughout, $\partial M$ and ${{\mathcal {H}}} _{N-1}$ will denote the essential boundary of M and $(N-1)$-dimensional Hausdorff-measure, respectively.

We will call a set $\Omega \subset {\mathbb {R}}^N _+$ a $C^n$-set, ($n\in {\mathbb {N}}$), if for every $x^0 \in \partial \Omega \cap {\mathbb {R}}^N _+$, there is a number $r >0$ such that $B_r (x^0 ) \cap \Omega$ has exactly one connected component and $B_r (x^0 ) \cap \partial \Omega$ is the graph of a $C^n$-function on an open set in ${\mathbb {R}} ^{N-1}$.

We consider a one-parameter family $\{ \varphi _t \}_{t}$ of $C^n$-variations

$$\begin{aligned} {\mathbb {R}}^N _+ \times (-\varepsilon , \varepsilon ) \ni (x,t) \longmapsto \varphi (x,t) \equiv \varphi _t (x) \in {\mathbb {R}}^N _+, \end{aligned}$$

with $\varphi (x, 0)=x$, for any $x\in {\mathbb {R}}^N_+$. The measure and perimeter functions of the variation are $m(t) := \mu _{\ell ,\alpha }(\varphi _t (\Omega ))$ and $p (t) := P_{\mu _{k,\alpha }} (\varphi _t (\Omega ))$, respectively. We say that the variation $\{ \varphi _t \} _t$ of $\Omega$ is measure-preserving if m(t) is constant for any small t. We say that a $C^1$-set $\Omega$ is stationary if $p'(0) = 0$ for any measure-preserving $C^1$-variation. Finally, we call a $C^2$-set $\Omega$stable if it is stationary and $p''(0) \ge 0$ for any measure-preserving $C^2$-variation of $\Omega$.

If M is any measurable subset of ${\mathbb {R}}^{N}_{+}$, with $0<\mu _{\ell ,\alpha } (M)<+\infty$, we set

$$\begin{aligned} {{\mathcal {R}}}_{k,\ell ,N, \alpha } (M) := \frac{P_{\mu _{k, \alpha }}(M , {\mathbb {R}}^N _+ )}{ \left( \mu _{\ell ,\alpha } (M) \right) ^{(k+N+\alpha -1)/(\ell +N+\alpha )} }. \end{aligned}$$

(4.8)

Finally, we define

$$\begin{aligned} C_{k,\ell ,N, \alpha }^{rad} := {{\mathcal {R}}}_{k,\ell ,N, \alpha } (B_1 ^+ ). \end{aligned}$$

(4.9)

We study the following isoperimetric problem:

Find the constant$C_{k,\ell ,N, \alpha } \in [0, + \infty )$, such that

$$\begin{aligned} C _{k,\ell ,N, \alpha }:= & {} \inf \{ {\mathcal R}_{k,\ell ,N, \alpha } (M):\, M \textit{ is a measurable set with locally finite perimeter}\nonumber \\&\textit{and } 0<\mu _{\ell ,\alpha } (M) <+\infty \} . \end{aligned}$$

(4.10)

Moreover, we are interested in conditions on k, $\ell$ and $\alpha$ such that

$$\begin{aligned} {{\mathcal {R}}}_{k,\ell ,N, \alpha } (M) \ge {\mathcal R}_{k,\ell ,N, \alpha } (M^{ \star } ) \end{aligned}$$

(4.11)

holds for all measurable sets $M\subset {{\mathbb {R}} ^N_+ }$ with $0<\mu _{\ell ,\alpha }(M)<+\infty$ and locally finite perimeter.

Let us begin with some immediate observations.

The conditions (4.1), (4.3) and (4.2) have been made to ensure that the integrals (4.6) and (4.7) converge. The cases $\alpha =0$ and $\alpha >0$ were analysed in the articles [1] and [2], respectively. Here we are only interested in the case

$$\begin{aligned} \alpha \in (-1, 0), \end{aligned}$$

that is, our weight functions are singular on the hyperplane $\{ x_N =0\}$.

The functional ${{\mathcal {R}}}_{k,\ell ,N, \alpha }$ has the following homogeneity properties,

$$\begin{aligned} {{\mathcal {R}}}_{k,\ell ,N, \alpha } (M )= & {} {\mathcal R}_{k,\ell ,N, \alpha } (tM ) , \end{aligned}$$

(4.12)

where $t>0$, M is a measurable set with $0<\mu _{\ell , \alpha } (M)<+\infty$ and $tM := \{t \zeta :\, \zeta \in M \}$, and there holds

$$\begin{aligned} C_{k,\ell ,N, \alpha } ^{rad} = {\mathcal R}_{k,\ell ,N, \alpha } (B_1 ^+ ). \end{aligned}$$

(4.13)

Hence we have that

$$\begin{aligned} C_{k,\ell ,N, \alpha } \le C_{k,\ell ,N, \alpha } ^{rad} , \end{aligned}$$

(4.14)

and (4.11) holds if and only if

$$\begin{aligned} C_{k,\ell ,N,\alpha } = C_{k,\ell ,N,\alpha } ^{rad} . \end{aligned}$$

(4.15)

We have the following

Lemma 4.1

Let $\alpha \in (-1,0)$. Then a necessary condition for the existence of minimizers of problem (P) is

$$\begin{aligned} kN \ge \ell (N-1) -\alpha . \end{aligned}$$

(4.16)

Proof

In the following we write for any two continuous functions $f,g: (0, +\infty ) \rightarrow (0,+\infty )$,

$$\begin{aligned} f \simeq g \quad \Longleftrightarrow \quad c_1 f(t) \le g(t) \le c_2 g(t) \ \ \forall t\in [1, +\infty ), \end{aligned}$$

for some constants $0<c_1 <c_2$.

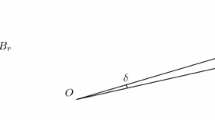
Assume that (4.16) does not hold. Let $\Omega (t) := B_1 (0, \ldots , 0 , t)$, ($t>1$). Then we have

$$\begin{aligned} {\mathcal {R}}_{k,\ell ,N,\alpha } (\Omega (t) ) \simeq t^{\alpha +k - (k+N+\alpha -1)(\alpha +\ell )/(\ell +N+\alpha )} . \end{aligned}$$

Since $KN < \ell (N-1) -\alpha$, it follows that

$$\begin{aligned} \lim _{t\rightarrow \infty } {\mathcal {R}}_{k,\ell ,N,\alpha } (\Omega (t) ) =0, \end{aligned}$$

that is, problem (P) has no minimizer. $\square$

Remark 4.1

(a) :

Observe that (4.16) is equivalent to

$$\begin{aligned} N(k+ N+\alpha -1 ) \ge (N-1) (\ell +N+\alpha ). \end{aligned}$$

(4.17)

Note also that (4.16) is not satisfied if

$$\begin{aligned} k=\ell =0, \end{aligned}$$

that is, problem (P) has no minimizer in this case.

(b) :

Using trial domains

$$\begin{aligned} \Omega (t) = B_1 (t, 0,\ldots ,0), \end{aligned}$$

and proceeding similarly as in the above proof, leads to another necessary condition for existence of minimizers of (P), namely:

$$\begin{aligned} k(N+ \alpha )\ge \ell (N+\alpha -1). \end{aligned}$$

(4.18)

This necessary condition has been obtained in the case $\alpha \ge 0$ in [2], Lemma 4.1. Note that in our case, $\alpha \in (-1,0)$, it holds true, too. However, if $\alpha \in (-1,0)$, then (4.16) is more restrictive than (4.18).

Lemma 4.2

A necessary condition for radiality of the minimizers of problem (P) is

$$\begin{aligned} \ell +1 \le k +\frac{N+\alpha -1}{k+N+\alpha -1 } . \end{aligned}$$

(4.19)

Moreover, if (4.19) is satisfied, then half-balls $B_R^+$, ($R>0$), are stable for problem (P).

Proof

This property has been obtained for the case $\alpha \ge 0$ in [2], Theorem 4.1. The proof essentially depends on the fact that the first eigenvalue of the problem (3.1), $\mu _1 ^{\alpha }( {\mathbb {S}} ^{N-1} _+ )$ is equal to $N+\alpha -1$. As we have proven above in Theorem 3.1, that property still holds for $\alpha \in (-1,0)$. Hence the proof of [2] carries over to our case. $\square$

Now we are the position to prove our main result.

Proof of Theorem 1.1:

Non-existence follows from Lemma 4.1, while the fact that half-balls are stable for problem (P) follows from Lemma 4.2—see also [2], Theorem 4.1 and Theorem 5.2 for the special case $N=2$, $k=\ell =0$. $\square$

Remark 4.2

Observe that for each $\alpha \in (-1,0)$, the set of pairs $(k,\ell )$ satisfying the conditions (1.2) and (4.19) is non-empty in view of (1.1). In particular, it contains the point (0, 0).

We conclude with a result that has been obtained for the cases $\alpha =0$ and $\alpha >0$ in the papers [1] and [2], respectively.

Theorem 4.1

Let $k\ge \ell + 1$ and $\alpha \in (-1,0)$. Then (4.15) holds. Moreover, if $k> \ell + 1$ and

$$\begin{aligned} {{\mathcal {R}}} _{k,\ell ,N,\alpha } (M) = C^{rad} _{k,\ell , N,\alpha } \quad \text{ for } \text{ some } \text{ measurable } \text{ set } M \subset {\mathbb {R}}^N_+ \text{ with } 0< \mu _{\ell , \alpha } (M) < +\infty ,\nonumber \\ \end{aligned}$$

(4.20)

then $M = B_R ^+$ for some $R > 0$.

For the proof we need a property that has been known for the cases $\alpha \ge 0$, see [2], Lemma 4.1. The proof carries over to our situation without changes.

Lemma 4.3

Let $k,\ell$ and $\alpha$ be as above and $\ell ' \in (-N-\alpha , \ell )$. Further, assume that $C_{k,\ell , N,\alpha } = C_{k,\ell ,N, \alpha } ^{rad}$. Then we also have $C_{k,\ell ', N,\alpha } = C_{k,\ell ',N, \alpha } ^{rad}$. Moreover, if ${\mathcal R}_{k,\ell ' ,N,\alpha }(M) = C_{k,\ell ' , N, \alpha } ^{rad}$ for some measurable set $M \subset {\mathbb {R}}^N_+$, with $0< \mu _{\ell ', \alpha }(M) < +\infty$, then $M = B _R ^+$ for some $R>0$.

Proof of Theorem 4.1:

We proceed similarly as in [2], proof of Theorem 4.1. The idea is to use Gauss’ Divergence Theorem. We split into two cases.

1. Assume that $k= \ell + 1$, and let $\Omega$ a $C^1$-set. Define the domain

$$\begin{aligned} {\widetilde{\Omega }} := \Omega \cup (H\cap \partial \Omega ) \cup \{ x= (x_1 , \ldots , -x_N ) :\, x\in \Omega \} . \end{aligned}$$

Then we have in view of the assumptions (4.1), (4.3) and (4.2),

$$\begin{aligned} 2 \int _{\partial \Omega \cap {\mathbb {R}}^N _+ } |x| ^{\ell } x _N ^{\alpha } (x \cdot \nu ) \, {\mathcal {H}}_{N-1} (dx )= & {} \int _{\partial {\widetilde{\Omega }} } |x| ^{\ell } x _N ^{\alpha } (x \cdot \nu ) \, {\mathcal {H}}_{N-1} (dx ) ,\nonumber \\&(\nu : \text{ exterior } \text{ unit } \text{ normal } ), \end{aligned}$$

(4.21)

$$\begin{aligned} 2 \int _{\Omega } |x| ^{\ell } x _N ^{\alpha } \, dx= & {} \int _{{\widetilde{\Omega }} } |x| ^{\ell } x _N ^{\alpha } \, dx. \end{aligned}$$

(4.22)

Furthermore, Gauss’ Divergence Theorem yields

$$\begin{aligned} \int _{{\widetilde{\Omega }} } |x|^{\ell } x_N ^{\alpha } \, dx= & {} \frac{1}{\ell +N +\alpha } \int _{{\widetilde{\Omega }} } \text{ div }\, \left( |x|^{\ell } x_N ^{\alpha } x \right) \, dx\nonumber \\= & {} \int _{\partial {\widetilde{\Omega }} } |x|^{\ell } x_N ^{\alpha } (x\cdot \nu ) {{\mathcal {H}}} _{N-1} (dx)\nonumber \\\le & {} \int _{\partial {\widetilde{\Omega }} } |x|^{\ell +1 } x_N ^{\alpha } {{\mathcal {H}}} _{N-1} (dx), \end{aligned}$$

(4.23)

with equality for ${\widetilde{\Omega }} = B_R$. Using this, (4.21), and (4.22), we obtain (4.15) for $C^1$-sets when $k= \ell +1$, and then by approximation also for sets with locally finite perimeter.

2. Let $k> \ell +1$. Then, using Lemma 4.3 and the result for $k=\ell +1$, we again obtain (4.15), and (4.20) can hold only if $M = B_R ^+$. $\square$

5 Some remarks on isoperimetric problems on ${\mathbb {R}}^N$

Ideas as they were used in the last section are useful in other situations as well. In this section we are interested in criteria for nonexistence and nonradiality of solutions to some weighted isoperimetric problems on ${\mathbb {R}}^N$. More results to these and related questions can be found in the papers [12, 15, 20, 21] and in [18].

Let f, g be two positive functions on ${\mathbb {R}}^N$ with g locally integrable and f lower semi-continuous. For any measurable set $M\subset {\mathbb {R}}^N$ we define its weighted measure and perimeter by

$$\begin{aligned} |M|_g:= & {} \int _M g(x)\, dx , \quad \text{ and } \end{aligned}$$

(5.1)

$$\begin{aligned} P_f (M):= & {} \int _{\partial M} f(x) \, {\mathcal {H}}_{N-1} (dx) . \end{aligned}$$

(5.2)

Then $C^n$-sets, stationary and stable sets are defined analogously as in Sect. 4, replacing ${\mathbb {R}}_+ ^N$, $P_{\mu _{k,\alpha } } (M)$ and $\mu _{\ell , \alpha } (M)$ by ${\mathbb {R}}^N$, $P_f (M)$ and $|M|_g$, respectively.

We consider the isoperimetric problem

$$\begin{aligned} {{ Find }} \ \ \ \inf \Big \{ P_f (M): \, \, M \ {{ has~ locally~ finite~perimeter~ and }} |M|_g =d \ \Big \} , \ \ (d>0).\nonumber \\ \end{aligned}$$

(5.3)

Let us first assume that f and g are equal and radial, that is, there is a function $h: [0, +\infty ) \rightarrow (0,\infty )$ such that

$$\begin{aligned} f(x) = g(x) = h(|x|) \quad \forall x\in {\mathbb {R}}^N . \end{aligned}$$

(5.4)

It has been known for some time—see for instance [4], Corollary 3.11—that if $h\in C^2 (0,+\infty )$, and if $\log h$ is convex (equivalently, if h is log-convex) then balls centered at the origin are stable for the isoperimetric problem (5.3). Recently G. Chambers, see [10] proved the beautiful Log-convex Theorem:

If$f=g$, $f\in C^1$andhis log-convex, then balls centered at the origin solve problem (5.3).

Note that the smoothness assumption for f at zero in the theorem forces h to be non-decreasing.

We will show below that the situation is different when h is log-convex, but decreasing on some interval.

Lemma 5.1

Assume that f satisfies (5.4), where $r\mapsto h(r)$ is log-convex and strictly decreasing for $r\in (0,R_0 )$, for some $R_0 >0$. Then there exists a number $d_0 >0$, which depends only on $R_0$, such that for any $d\in (0,d_0 ]$, balls centered at the origin with measure d are not isoperimetric for problem (5.3).

Proof

For any $d>0$ choose positive numbers R(d), $\rho (d)$, such that

$$\begin{aligned} |B_{R(d)} |_f= & {} |B_{\rho (d)} (y(d))|_f =d,\nonumber \\ \text{ where } y(d)= & {} (R_0 -\rho (d), 0, \ldots , 0). \end{aligned}$$

(5.5)

If d is small enough—say $d\in (0, d_0 ]$—then we have that

$$\begin{aligned}&R(d) \le R_0 -2 \rho (d) \quad \text{ and } \end{aligned}$$

(5.6)

$$\begin{aligned}&\left[ h(R_0 - 2d) \right] ^N < h(R(d)) \left[ h(R_0 ) \right] ^{N-1} . \end{aligned}$$

(5.7)

From (5.5) we find, using the monotonicity of h,

$$\begin{aligned} \omega _N h(R(d)) (R(d))^N > \omega _N h(R_0 ) (\rho (d))^N, \end{aligned}$$

that is,

$$\begin{aligned} \rho (d) < \left( \frac{h(R(d))}{h(R_0 )} \right) ^{1/N} R(d). \end{aligned}$$

(5.8)

Hence the monotonicity of h, (5.6) (5.7) and (5.8) yield

$$\begin{aligned} P_f (B_{\rho (d)} (y(d))< & {} N\omega _N h(R_0 - 2\rho (d)) (\rho (d) )^{N-1}\nonumber \\< & {} N\omega _N h(R_0 - 2\rho (d)) \cdot \left( \frac{h(R(d))}{h(R_0 )} \right) ^{(N-1)/N} \cdot (R(d)) ^{N-1}\nonumber \\< & {} N\omega _N h(R(d)) (R(d))^{N-1}\nonumber \\< & {} P_f (B_{R(d)} ). \end{aligned}$$

(5.9)

This proves the Lemma. $\square$

We conclude this section with a non-existence result.

Theorem 5.1

Assume that f and g satisfy

$$\begin{aligned}&f(x) \le c_1 |x|^{- \alpha } \ \ \text{ and } \end{aligned}$$

(5.10)

$$\begin{aligned}&g(x) \ge c_2 |x|^{-\beta } \quad \text{ for } |x| \ge R_1 , \end{aligned}$$

(5.11)

where $\alpha$, $\beta$, $R_1$, $c_1$ and $c_2$ are positive numbers and

$$\begin{aligned} \beta \le N \ \ \ \text{ and } \ \ \alpha > \frac{N-1}{N} \cdot \beta . \end{aligned}$$

(5.12)

Then the isoperimetric problem (5.3) has no solution.

Proof

Fix $d>0$, and set $z(t):= (t, 0, \ldots ,0)$ for every $t>0$. Choose $R(t)>0$ such that

$$\begin{aligned} |B_{R(t)} (z(t))|_g =d. \end{aligned}$$

(5.13)

In view of (5.11) this implies that

$$\begin{aligned} \lim _{t\rightarrow +\infty } (t-R(t)) = +\infty . \end{aligned}$$

(5.14)

When t is large enough—say $t\ge t_0$—assumption (5.11) and (5.14) yield

$$\begin{aligned} |B_{R(t)} (z(t)) |_g= & {} \int _{B_{R(t)} (z(t)) } g(x)\, dx = t^{N } \int _{B_{R(t)/t} (z(1))} g(ty)\, dy\nonumber \\\ge & {} c_2 t^{N-\beta } \int _{B_{R(t)/t} (z(1))} |y|^{-\beta } \, dy . \end{aligned}$$

(5.15)

Now from (5.15) we obtain the following alternative:

$$\begin{aligned}&\text{ If } \beta <N, \text{ then } \lim _{t\rightarrow +\infty } \frac{R(t)}{t} =0, \text{ and } \end{aligned}$$

(5.16)

$$\begin{aligned}&\text{ if } \beta =N, \text{ then } \frac{R(t)}{t} \le 1-\delta \text{ for } t\ge t_0 , \text{ for } \text{ some } \delta \in (0,1). \end{aligned}$$

(5.17)

Further, from (5.13) we have

$$\begin{aligned} d\ge \omega _N (R(t))^N c_2 (t+ R(t)) ^{-\beta } . \end{aligned}$$

(5.18)

Using this, (5.16), (5.17), (5.12) and again (5.10), leads to

$$\begin{aligned} P_f (B_{R(t)} (z(t)))= & {} \int _{\partial B_{R(t)} (z(t))} f(x) \, {\mathcal {H}} _{N-1} (dx) \nonumber \\\le & {} c_1 (t-R(t)) ^{-\alpha } N\omega _N (R(t))^{N-1}\nonumber \\\le & {} c_1 (t-R(t)) ^{-\alpha } N\omega _N \left( \frac{ d(t+R(t))^{\beta } }{ c_2 \omega _N } \right) ^{(N-1)/N}\nonumber \\&\longrightarrow 0 \quad \text{ as } t\rightarrow +\infty . \end{aligned}$$

(5.19)

The theorem is proved.$\square$

Remark 5.1

The case that $f(x) = |x|^{-\alpha }$, $g(x)= |x|^{-\beta }$, ($x\in {\mathbb {R}} ^N$), with $\beta <N$, was treated in [1], Lemma 4.1. See also [12], Proposition 7.3 for the special case $f(x)=g(x)=|x|^{-\beta }$.