Regularity of isoperimetric sets in $\mathbb R^2$ with density

Abstract

We consider the isoperimetric problem in $\mathbb R^2$ with density. We show that, if the density is $\mathrm{C}^{0,\alpha }$, then the boundary of any isoperimetric set is of class $\mathrm{C}^{1,\frac{\alpha }{3-2\alpha }}$. This improves the previously known regularity.

1 Introduction

The isoperimetric problem in $\mathbb R^n$ with density is a classical problem, which has received much attention in the last decade. The idea is quite simple: given a lower semicontinuous function $f:\mathbb R^n\rightarrow (0,+\infty )$, usually called “density”, for any set $E\subseteq \mathbb R^n$ we define the volume $V_f(E)$ and the perimeter $P_f(E)$ as

$$\begin{aligned} V_f(E) := \int _E f(x)\, dx, \quad P_f(E) := \int _{\partial ^* E} f(x)\, d{\text{ H }\;}^{n-1}(x), \end{aligned}$$

where the subscript reminds us that volume and perimeter are computed with respect to f, and where $\partial ^* E$ is the reduced boundary of E (to read this paper there is no need to know what the reduced boundary is, since under our assumptions it always coincides with the usual topological boundary $\partial E$). The literature on problems of this kind is vast, here we can give just a very sketchy outline.

In the 1970–1980’s, the way for the study of the regularity in a completely general case was paved, see the papers [2, 4, 7, 26]. After that, people started to focus on isoperimetric problems in a non-Euclidean setting, considering finer notions of minimality [19] and investigating the case of Riemannian manifolds [21]. In the last ten years, finally, the above-described question of isoperimetric problems with density was explicitly considered; in [8, 24] the first fundamental, general properties were studied, the papers [13, 16] consider some specific examples, namely the sectors with density and the mixed Euclidean–Gaussian densities, and the more recent papers [10, 12, 23] (see also the references therein) contain more or less the state-of-the-art on this problem.

The main questions about the isoperimetric problem with density are of course the existence and regularity of isoperimetric sets. A lot is known about the existence (see for instance [9, 12, 23]). Since in this paper we are dealing with the regularity, let us briefly recall the main known results. The first, very important one, can be found in [20, Proposition 3.5 and Corollary 3.8] (see also [1, 3]).

Theorem 1.1

Let f be a $\mathrm{C}^{k,\alpha }$ density on $\mathbb R^n$, with $k\ge 1$. Then the boundary of any isoperimetric set is $\mathrm{C}^{k+1,\alpha }$, except for a singular set of Hausdorff dimension at most $n-8$. If f is just Lipschitz, then the boundary is of class $\mathrm{C}^{1,\alpha }$ for every $0<\alpha <1$.

It is important to point out that the above result requires at least a Lipschitz regularity for f. The reason is rather simple: most of the standard techniques to get regularity make sense only if f is at least Lipschitz (for a discussion on this fact, see [10, Section 5]). In particular, the following simple observation can be useful. In order to get regularity of an isoperimetric set E, a standard idea is to build some “competitor” F, which behaves better than E where the boundary of E is not regular enough; however, in order to get some contradiction, we must ensure that F has the same volume as E, since otherwise the isoperimetric property of E cannot be used. On the other hand, it can be complicated to build the set F taking its volume into account, since while defining F one is interested in its perimeter. As a consequence, it is extremely useful to have the so-called “$\varepsilon -\varepsilon$ property”, which roughly speaking says the following: it is always possible to modify the volume of a set F of a small quantity $\varepsilon$, increasing its perimeter of at most $C|\varepsilon |$ for some fixed constant C. If this is the case, one can then “adjust” the volume of F so that it coincides with the one of E. This property has already been discussed by Allard, Almgren and Bombieri since the 1970’s (see for instance [1–4, 7]), and it has been widely used in most of the papers about regularity in this context since then. Unfortunately, while the $\varepsilon -\varepsilon$ property is rather simple to establish when f is at least Lipschitz, it is false if f is not Lipschitz.

To get some regularity for isoperimetric sets in the case of low regularity of f, in the recent paper [10] we introduced and proved a weaker property, called the “$\varepsilon -\varepsilon ^\beta$ property”, which basically says that the volume of a set can be modified by $\varepsilon$, increasing the perimeter by at most $C|\varepsilon |^\beta$. Since we will use this property in the present paper, we provide the result below (the actual result proved in [10] is more general, but here we prefer to state the simpler version that we are going to need).

Theorem 1.2

[10, Theorem B] Let $E\subseteq \mathbb R^n$ be a set of locally finite perimeter, and f an $\alpha$-Hölder density for some $0<\alpha \le 1$. Then, for every ball B with nonempty intersection with $\partial ^* E$, there exist two constants $\bar{\varepsilon },\, C>0$ such that, for every $|\varepsilon | < \bar{\varepsilon }$, there is a set $\widetilde{E}$ satisfying

$$\begin{aligned} \widetilde{E}\Delta E\subset \subset B, \quad V_f(\widetilde{E}) = V_f (E) + \varepsilon , \quad P_f(\widetilde{E}) \le P_f(E) + C |\varepsilon |^\beta , \end{aligned}$$

(1.1)

where $\beta =\beta (\alpha ,n)$ is defined by

$$\begin{aligned} \beta =\beta (\alpha ,n) := \frac{\alpha +(n-1)(1-\alpha )}{\alpha +n(1-\alpha )}\,, \end{aligned}$$

so for $n=2$ it is $\beta =\frac{1}{2-\alpha }$.

By using the classical regularity results (see for instance [5, 25]), and modifying the arguments in order to make use of the $\varepsilon -\varepsilon ^\beta$ property instead of the $\varepsilon -\varepsilon$ one (which is false), we obtained the following regularity result (see [25] for a definition of porosity).

Theorem 1.3

[10, Theorem 5.7] Let E be an isoperimetric set in $\mathbb R^n$ with a density $f\in \mathrm{C}^{0,\alpha }$, with $0<\alpha \le 1$. Then $\partial ^* E=\partial E$ is of class $C^{1,\frac{\alpha }{2n(1-\alpha )+2\alpha }}$. In particular, if $n=2$ then $\partial E$ is $\mathrm{C}^{1,\frac{\alpha }{4-2\alpha }}$. If f is only bounded above and below, then it is still true that $\partial ^* E=\partial E$, and moreover E is porous.

The main result of the present paper is a stronger regularity result for the bi-dimensional case, stated as follows.

Theorem A

(Regularity of isoperimetric sets) Let $f:\mathbb R^2\rightarrow (0,+\infty )$ be a $\mathrm{C}^{0,\alpha }$ density, for some $0<\alpha \le 1$. Then, every isoperimetric set E has a boundary of class $\mathrm{C}^{1,\frac{\alpha }{3-2\alpha }}$.

It is worth observing that the regularity obtained above is still less than the $\mathrm{C}^{1,\alpha }$ regularity that one could expect just by looking at Theorem 1.1, but it is better than the previously known regularity given by Theorem 1.3. In particular, notice that there is a substantial improvement between $\mathrm{C}^{1,\frac{\alpha }{4-2\alpha }}$ and $\mathrm{C}^{1,\frac{\alpha }{3-2\alpha }}$. Indeed, the second exponent is not just merely bigger than the first one, there is also a much deeper difference: namely, when $\alpha$ goes to 1, the first exponent goes to 1 / 2, while the second goes to 1. In particular, our Theorem A gives also a proof that for f Lipschitz an isoperimetric set is $\mathrm{C}^{1,1}$, as stated in Theorem 1.1.

Let us give now some remarks. First of all, the fact that the regularity of the “old” Theorem 1.3 never exceeds $\mathrm{C}^{1,\frac{1}{2}}$ is not strange: indeed, this is the best regularity that can be obtained via the classical methods, without fully using the isoperimetric property of a set E, but only the (weaker) fact that E is an $\omega$-minimizer of the perimeter. To get anything better than $\mathrm{C}^{1,\frac{1}{2}}$, one must use the fact that E is isoperimetric (at least in a “local” sense), as we do in the present paper by using the $\varepsilon -\varepsilon ^\beta$ property.

A second remark is about the sharp regularity exponent that one can obtain for an isoperimetric set with a $\mathrm{C}^{0,\alpha }$ density: we do not believe that our exponent of Theorem A is sharp, but we are also not sure whether it is possible to reach the $\mathrm{C}^{1,\alpha }$ regularity, similarly to what happens for $k\ge 1$ in the classical case.

Lastly, let us notice that most of our arguments also work in a Riemannian surface with minor modifications. More precisely, a Riemannian surface behaves more or less as $\mathbb R^n$ with density, but the density corresponding to the volume and the one corresponding to the perimeter are different. A work in progress considers the more general setting with two distinct densities (which covers the case of a Riemannian surface, but is in fact much more general). Similarly, the same technique also gives results in the more general case of the $(M,\varepsilon ,\delta )$ curves (see for instance [19, 26]); results in this direction are also currently being investigated in a work in progress.

We conclude the introduction by quickly describing how the proof works. The idea is to take two points $x,\,y$ in the boundary of E, very close to each other, and to replace the arc of $\partial E$ connecting them with the segment xy. If the points are well chosen, then the new curve is still the boundary of a set, say F, very similar to E. While the Euclidean perimeter of F is obviously smaller than that of E, this is not sure for the (weighted) perimeter; however, since f is continuous, one has also $P_f(F)<P_f(E)$ unless the curve between x and y is sufficiently close to the segment. The set F need not have the same volume as E, hence we cannot directly use it as a competitor for the isoperimetric problem; however, we can do so after having “adjusted” its volume by means of Theorem 1.2. Summarizing, we have obtained an estimate of how much three points in $\partial E$, sufficiently close to each other, can deviate from being aligned. Finally, applying this estimate subsequently to a suitable sequence of triples of points, we can show that, for any two points a and z in $\partial E$, the tangent vectors $\nu _a$ and $\nu _z$ to $\partial E$ at a and z satisfy

$$\begin{aligned} |\nu _a-\nu _z|\le C \rho ^{\frac{\alpha }{3-2\alpha }}\,, \end{aligned}$$

where $\rho$ is the distance between a and z. This will provide the required regularity, hence concluding the proof.

1.1 Notation

Let us briefly present the notation of the present paper. The density will always be denoted by $f:\mathbb R^2\rightarrow (0,+\infty )$; keep in mind that, since we want to prove Theorem A, the function f will always be at least continuous. For any set $E\subseteq \mathbb R^2$, we denote by $V_f(E)$ and $P_f(E)$ its volume and perimeter. For any $z\in \mathbb R^2$ and $\rho >0$, we denote by $B_\rho (z)$ the ball centered at z with radius $\rho$. Given two points $x,\,y\in \mathbb R^2$, we denote by $xy,\, \ell (xy)$, and $\ell _f(xy)$ the segment connecting the two points, its Euclidean length, and its length with respect to the density f (that is, $\int _{xy} f(t) dt$). Given three points $a,\,b,\, c$, we denote by the angle between the segments ab and bc. Let now $E\subseteq \mathbb R^2$ be an isoperimetric set; then, through Theorem 1.3 we already know that the boundary of E is of class $\mathrm{C}^{1,\frac{\alpha }{4-2\alpha }}$; hence in particular Lipschitz. As a consequence, for any two points $x,\,y$ which belong to the same connected component of $\partial E$ and which are very close to each other (with respect to the diameter of this connected component), the shortest curve in $\partial E$ connecting x and y is well-defined. We denote this curve by , and again by and we denote its Euclidean length and its length with respect to the density f. The letter C is always used to denote a large constant, which can increase from line to line, while M is a fixed constant, coming from the $\alpha$-Hölder property.

2 Proof of the main result

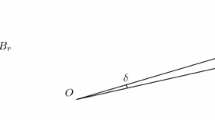
This section is devoted to the proof of our main result, Theorem A. Most of the proof consists in studying the situation around a few given points, so let us set some useful specific notation; Fig. 1 illustrates the names of the points. Let us fix an isoperimetric set E and a point z on $\partial E$. Let $\rho \ll 1$ be a very small constant, much smaller than the length of the connected component $\gamma \subseteq \partial E$ containing z, and of the distance between z and the other connected components of $\partial E$ (if any). Since we know that $\gamma$ is a $\mathrm{C}^{1,\frac{\alpha }{4-2\alpha }}$ curve, we can decide arbitrarily an orientation on it; hence, let us define four points $x,\, \bar{x},\,y,\,\bar{y}$ in $\partial B_\rho (z)$ as follows: among the points of $\gamma$ which belong to $\partial B_\rho (z)$ and which are before z, we call $\bar{x}$ the closest one to z, and x the farthest one (in the sense of the parameterization of $\gamma$). We define analogously $\bar{y}$ and y after z: of course, $\bar{x}$ and x may coincide, as well as y and $\bar{y}$. Moreover, we call $\delta$ the angle , and

Finally, we introduce the following set F, which we will use as a competitor to E (after adjusting its area).

Fig. 1

Position of the points for Lemma 2.2

Definition 2.1

With the above notation, we let $F\subseteq \mathbb R^2$ be the bounded set whose boundary is .

Notice that the above definition makes sense: indeed, by [10, Theorem 1.1] we already know that E is bounded, and by construction the segment xy cannot intersect any point of . In particular, all the connected components of E whose boundary is not $\gamma$ also belong to F; instead, the connected component of E with $\gamma$ as boundary has been slightly modified near z. Recalling that f is real-valued and strictly positive, as well as $\alpha$-Hölder, we can find a constant M such that

$$\begin{aligned} \frac{1}{M} \le f(p)\le M\,,\quad |f(p)-f(q)| \le M |p-q|^\alpha \end{aligned}$$

(2.1)

for every $p,\, q$ in some neighborhood of E, containing all the points that we are going to use in our argument. This is not a problem, since all our arguments will be local. Let us now give the first easy estimates about the above quantities.

Lemma 2.2

With the above notation, one has

$$\begin{aligned} l \le C\rho ^{\frac{2}{2-\alpha }},\quad \delta \le C\rho ^{\frac{\alpha }{4-2\alpha }}\,, \end{aligned}$$

(2.2)

and moreover

(2.3)

Proof

First of all, let us consider a point $p\in E\Delta F$ in the symmetric difference between E and F; by construction, either p belongs to the ball $B_\rho (z)$, or it has a distance at most l / 2 from that ball. As a consequence, p has distance at most $\rho +l/2$ from z, and this gives

$$\begin{aligned} |V_f(E)-V_f(F)| \le V_f(E\Delta F) \le M\big (\pi (\rho +l/2)^2\big ) \le 2M\pi (\rho ^2 + l^2). \end{aligned}$$

(2.4)

Let us now apply Theorem 1.2 to the set E, with a ball B intersecting $\partial E$ far away from the point z. We get a constant $\bar{\varepsilon }$ and of course, up to have taken $\rho$ small enough, we can assume that $|\varepsilon |\le \bar{\varepsilon }$, being $\varepsilon = V_f(E)-V_f(F)$. Then, Theorem 1.2 provides us with a set $\widetilde{E}$ satisfying (1.1). As a consequence, if we define $\widetilde{F}= F {\setminus } B \cup (B\cap \widetilde{E})$, we get $V_f(\widetilde{F}) = V_f(F) + V_f(\widetilde{E}) - V_f(E) = V_f(E)$, and then, since E is isoperimetric, by (2.4) we get

$$\begin{aligned} P_f(E)\le P_f(\widetilde{F}) = P_f(F) + P_f(\widetilde{E}) - P_f(E) \le P_f(F)+ C \big (\rho ^2+l^2\big )^{\frac{1}{2-\alpha }}, \end{aligned}$$

which implies

(2.5)

Let us now evaluate the term : if we call $f_\mathrm{min}$ and $f_\mathrm{max}$ the minimum and the maximum of f inside $B_z(\rho )$, by (2.1) we have

$$\begin{aligned} f_\mathrm{max} \le f_\mathrm{min} + 2M\rho ^\alpha ,&\quad f_\mathrm{min}\ge \frac{1}{M}, \end{aligned}$$

and then

Inserting this estimate in (2.5), we obtain

$$\begin{aligned} 2\,\frac{1-\cos \delta }{M}\, \rho +\frac{l}{M} \le C\big (\rho ^2+l^2\big )^{\frac{1}{2-\alpha }}+4M \rho ^{\alpha +1}\,. \end{aligned}$$

Since

$$\begin{aligned} \frac{2}{2-\alpha } > 1, \quad \alpha +1 \ge \frac{2}{2-\alpha }\,, \end{aligned}$$

we immediately derive, first, that $\delta$ is very small, so that $1-\cos \delta \ge \delta ^2/3$, and, then,

$$\begin{aligned} \delta ^2 \rho + l \le C \rho ^{\frac{2}{2-\alpha }}\,. \end{aligned}$$

This gives the validity of both the inequalities in (2.2). Finally, (2.5) together with (2.2) and the fact that, since $\delta \ll 1$, one has $\ell (xy)\approx 2\rho$, gives (2.3). $\square$

Corollary 2.3

For any two points $a,\,b\in \gamma$ sufficiently close to each other, one always has

(2.6)

Proof

Let be a point such that $\rho =\ell (az)=\ell (zb)$, and let us call $x,\,\bar{x},\, y$ and $\bar{y}$ as before. Of course, and , so that $\ell (a\bar{x})+\ell (b\bar{y})\le l$. Since by (2.2) we have $l\ll \rho$, we get and , as well as $\ell _f(ab)\approx \ell _f(xy)$. Hence, (2.3) gives us

and then the first estimate in (2.6) is established. The second one immediately follows, simply because f is continuous. $\square$

A similar argument to the one proving Lemma 2.2 then gives the following estimate.

Lemma 2.4

Given any two sufficiently close points $r,\, s\in \gamma$, one has

(2.7)

Proof

Let us call t the maximal distance between points of the arc and the segment rs, and let us denote $2d=\ell (rs)$ for brevity. Of course, concerning the Euclidean distances, one has

(2.8)

Let us call $\pi$ the projection of $\mathbb R^2$ on the line containing the segment rs, so that for every one has $|a-\pi (a)|\le t$ by definition; moreover, define the density $g:\mathbb R^2\rightarrow \mathbb R^+$ as $g(a)=f(\pi (a))$, so that by the $\alpha$-Hölder property (2.1) of f we get

$$\begin{aligned} f(a) \ge g(a) - M t^\alpha \end{aligned}$$

(2.9)

for every . Since $\pi (a)=a$ for every $a\in rs$, by (2.8) and (2.1) we can then easily evaluate

On the other hand, by (2.9) and by (2.6) we have also

Putting together the last two estimates, we obtain

As a consequence, we can assume that $t\ll d$, since otherwise we readily get , and in this case of course (2.7) holds. Therefore, the last inequality can be rewritten as

(2.10)

There are then two cases: if the term between parenthesis is positive, then again (2.7) clearly holds. If, instead, it is negative, this implies

$$\begin{aligned} t\le 6M^3 d^{\frac{2}{2-\alpha }}\,, \end{aligned}$$

and then (2.10) gives

which is (2.7). $\square$

We can now show a more refined estimate for , which takes into account the maximal angle of deviation of the curve with respect to the segment pq. Let us be more precise: for every we define $H=H(w)$ the projection of w on the line containing pq. Moreover, we call $\theta =\theta (w)$ the angle if H is closer to p than to q, and otherwise, and we let $\bar{\theta }$ be the maximum among all the angles $\theta (w)$ for : Fig. 2 depicts the situation.

Fig. 2

Definition of $\bar{\theta }$

Lemma 2.5

With the above notation, and calling $\rho =\ell (pq)$, there is $C=C(\alpha ,M)$ for which

(2.11)

Proof

Let us fix a point such that $\theta (w)=\bar{\theta }$, and assume without loss of generality that , as in Fig. 2. We can then apply Lemma 2.4, first with $rs=pw$, and then with $rs=wq$, to get, also keeping in mind (2.6), that

(2.12)

Now we have to compare the lengths of the segments pw and qw with those of the segments pH and qH. We can again argue defining the density g as $g(a)=f(\pi (a))$, $\pi$ being the projection on the line containing the segment pq: then

$$\begin{aligned} \ell _f(pw)-\ell _f(pH)&= \ell _g(pw)-\ell _g(pH) + \ell _f(pw)-\ell _g(pw)\\&\ge \frac{1}{M}\, \Big (\ell (pw)-\ell (pH)\Big ) - M\ell _f(pw) \ell (wH)^\alpha \,, \end{aligned}$$

and the analogous estimate of course works for $\ell _f(wq)-\ell _f(wH)$. Putting them together, and recalling that $\ell _f(pH)+\ell _f(qH)\ge \ell _f(pq)$, with strict inequality if H is outside pq, we obtain

$$\begin{aligned} \ell _f(pw)+\ell _f(wq)-\ell _f(pq)&\ge \frac{1}{M}\, \Big (\ell (pw)+\ell (wq)-\ell (pq)\Big )\\&\quad - M\big (\ell _f(pw)+\ell _f(wq)\big ) \ell (wH)^\alpha \\&\ge \frac{\rho }{6M} \bar{\theta }^2 - 2M^2 \rho ^{1+\alpha }\bar{\theta }^\alpha \,, \end{aligned}$$

where we have again used $\bar{\theta }\ll 1$, which comes as usual by (2.6). Putting this estimate together with (2.12), we get

(2.13)

Now, notice that

$$\begin{aligned} \rho ^{1+\alpha }\bar{\theta }^\alpha \ge \rho ^{\frac{2+\alpha }{2-\alpha }} \quad \Longleftrightarrow \quad \bar{\theta }\ge \rho ^{\frac{\alpha }{2-\alpha }}\qquad \Longleftrightarrow \qquad \rho \bar{\theta }^2 \ge \rho ^{1+\alpha }\bar{\theta }^\alpha \,. \end{aligned}$$

As a consequence, (2.13) implies the validity of both the cases in (2.11), up to have chosen a sufficiently large constant $C=C(M,\alpha )$. $\square$

We are now ready to find a first result about the behaviour of the direction of the chords connecting points of the curve $\gamma$. Indeed, putting together Lemma 2.5 and Lemma 2.2, we get the next estimate.

Lemma 2.6

Let $a,\, z$ be two points in $\gamma$ sufficiently close to each other, call $\rho =\ell (az)$, and let be a point closer to a than to z. Then, there is $C=C(M,\alpha )$ such that

Proof

Having a point $z\in \gamma$ and some $\rho >0$ very small, we can define the points $x,\, \bar{x},\, y,\, \bar{y}$ as for Lemma 2.2, and by symmetry we can think . We now apply Lemma 2.5 two times, once with $p_1=x$ and $q_1=z$, and once with $p_2=y$ and $q_2=z$. Thus, we obtain the validity of (2.11) for the two angles $\bar{\theta }_1$ and $\bar{\theta }_2$; we claim that

$$\begin{aligned} \bar{\theta }:= \max \big \{ \bar{\theta }_1,\, \bar{\theta }_2\big \} \le C \rho ^{\frac{\alpha }{3-2\alpha }}\,. \end{aligned}$$

(2.14)

Let us first see that this estimate implies the thesis. If the point w is closer to x than to z, then by definition and by (2.14)

As a consequence, by (2.2) we have

(2.15)

and the thesis is obtained. Suppose, instead, that w is closer to z than to x; since by assumption it is anyhow closer to a than to z, and $\ell (ax)\le l\ll \ell (wz)$ by (2.2), again using (2.14) we have

then the very same argument as in (2.15) again shows the thesis. Summarizing, we have proved that (2.14) implies the thesis, and hence to conclude we only have to show the validity of (2.14).

We argue as in Lemma 2.2, defining the competitor set F which has as boundary. Notice that this is very similar to what we did in Definition 2.1, the only difference being that we are putting the two segments xz and zy instead of the segment xy. The very same argument that we presented after Definition 2.1 ensures that the set F is well defined. As in Lemma 2.2, then, we now have to evaluate $|V_f(F)-V_f(E)|$ and $P_f(F)-P_f(E)$. Concerning the first quantity, we can get an estimate which is much better than (2.4), thanks to the definition of $\bar{\theta }_1$ and $\bar{\theta }_2$.

Fig. 3

Constraint on the position of the curve

Let us be more precise. The curve is composed by two parts; the first one, , by definition remains within a distance of at most from x. The second one, , is contained in the shaded region of Fig. 3, which is the intersection between the ball $B_\rho (z)$ and the region of the points w such that . Repeating the same argument with $\bar{\theta }_2,\, y$ and $\bar{y}$, and recalling that , we have

$$\begin{aligned} |V_f(E) - V_f(F)| \le 9M\rho ^2 \big (\bar{\theta }_1+\bar{\theta }_2) + \pi M l^2 \le 18M\rho ^2\bar{\theta }+ \pi M l^2\,. \end{aligned}$$

Let us now observe that by (2.2) one has $l^2\le C\rho ^{\frac{4}{2-\alpha }}$, and then

$$\begin{aligned} l^2 \le \rho ^2\bar{\theta }\quad \Longleftarrow \quad C\rho ^{\frac{4}{2-\alpha }} \le \rho ^2\bar{\theta }\quad \Longleftrightarrow \quad \bar{\theta }\ge C\rho ^{\frac{2\alpha }{2-\alpha }}\,. \end{aligned}$$

Then there are two possibilities: either $\bar{\theta }\le C\rho ^{\frac{2\alpha }{2-\alpha }}$, so we already have the validity of (2.14) and the proof is concluded, or $\bar{\theta }\ge C\rho ^{\frac{2\alpha }{2-\alpha }}$, and then the last two estimates imply

$$\begin{aligned} |V_f(E) - V_f(F)| \le 22M\rho ^2\bar{\theta }\,. \end{aligned}$$

Therefore, using Theorem 1.2 exactly as in the proof of Lemma 2.2, we find a set $\widetilde{F}$ having the same volume as E (and then more perimeter) satisfying

$$\begin{aligned} P_f(E) \le P_f(\widetilde{F}) \le P_f(F) + C \big (22M\rho ^2 \bar{\theta }\big )^{\frac{1}{2-\alpha }} = P_f(F) + C \rho ^{\frac{2}{2-\alpha }}\bar{\theta }^{\frac{1}{2-\alpha }} \,, \end{aligned}$$

from which we directly get

(2.16)

We now use the fact that (2.11) is valid both with $\bar{\theta }_1$ and with $\bar{\theta }_2$, as pointed out before. One has to distinguish three possible cases.

Since $\rho ^{\frac{\alpha }{2-\alpha }}\le \rho ^{\frac{\alpha }{3-2\alpha }}$, if both $\bar{\theta }_1$ and $\bar{\theta }_2$ are smaller than $C\rho ^{\frac{\alpha }{2-\alpha }}$ then so is $\bar{\theta }$, so (2.14) is true and there is nothing more to prove.

Suppose now that both $\bar{\theta }_1$ and $\bar{\theta }_2$ are bigger than $C\rho ^{\frac{\alpha }{2-\alpha }}$. In this case, (2.11) gives

which together with (2.16) gives

$$\begin{aligned} \rho \bar{\theta }^2 \le C \rho ^{\frac{2}{2-\alpha }}\bar{\theta }^{\frac{1}{2-\alpha }}\,, \end{aligned}$$

which is equivalent to (2.14), and then also in this case the proof is completed.

Finally, we have to consider what happens when only one between $\bar{\theta }_1$ and $\bar{\theta }_2$ is bigger than $C\rho ^{\frac{\alpha }{2-\alpha }}$; just to fix the ideas, we can suppose that $\bar{\theta }_1\ge C\rho ^{\frac{\alpha }{2-\alpha }}\ge \bar{\theta }_2$, hence in particular $\bar{\theta }=\bar{\theta }_1$. Applying then (2.11), this time we find

where the last inequality is true precisely because $\bar{\theta }\ge C \rho ^{\frac{\alpha }{2-\alpha }}$. Exactly as before, putting this estimate together with (2.16) implies (2.14), and then also in the last possible case we obtain the proof. $\square$

The last lemma is exactly what we needed to obtain the proof of our main Theorem A.

Proof (of Theorem A)

Let E be an isoperimetric set for the $\mathrm{C}^{0,\alpha }$ density f. To show that $\partial E$ is of class $\mathrm{C}^{1,\frac{\alpha }{3-2\alpha }}$, let us select two generic points $z,\,a\in \partial E$ such that $\rho =\ell (za)\ll 1$. We want to show that

(2.17)

as this readily implies the thesis. Indeed, suppose that (2.17) has been established, and call $\nu \in \S ^1$ the direction of the segment az; since we already know that $\partial E$ is of class $\mathrm{C}^1$ by Theorem 1.3, considering points which converge to z we deduce by (2.17) that $|\nu -\nu _z|\le C \rho ^{\frac{\alpha }{3-2\alpha }}$, where $\nu _z\in \S ^1$ is the tangent vector to $\partial E$ at z. Since the situation of a and of z is perfectly symmetric, the same argument also shows that $|\nu -\nu _a|\le C \rho ^{\frac{\alpha }{3-2\alpha }}$, thus by triangular inequality we have found

$$\begin{aligned} |\nu _a-\nu _z|\le C \rho ^{\frac{\alpha }{3-2\alpha }}\,. \end{aligned}$$

Since a and z are two generic points having distance $\rho$, and since C only depends on M and on $\alpha$, this estimate shows that $\partial E$ is of class $\mathrm{C}^{\frac{\alpha }{3-2\alpha }}$; therefore, the proof will be concluded once we show (2.17). Notice that (2.17) simply says that the estimate of Lemma 2.6 holds also without requiring the point w to be closer to a than to z.

To do so, let us recall that by (2.6), let us write $a_0=a$, and let us define recursively the sequence $a_j$ by letting be the point such that

Observe that $a_j$ is a sequence inside the curve , which converges to z, and moreover for every $j\in \mathbb N$ one has

(2.18)

Let us now take a point ; again recalling (2.6), by the definition of the points $a_j$ it is obvious that w is closer to $a_j$ than to z; as a consequence, Lemma 2.6 applied to $a_j$ and z ensures that

where we have also used (2.18), and where $\kappa =(2/3)^{\frac{\alpha }{3-2\alpha }}<1$. Keeping in mind the obvious fact that for every j, and then that the above estimate is valid in particular for the point $a_{j+1}$, we deduce that for the generic it holds

where the last inequality is true because $\kappa \!=\!\kappa (\alpha )<1$. We have then established (2.17), and the proof is concluded. $\square$