Introduction

The electrowetting (EW) process is a useful physical mechanism and a promising tool for control and manipulation of microfluidic objects (particles, drops, bubbles) (Chen and Bonaccurso 2014; Mugele and Baret 2005). The special case of electrowetting-on-dielectric (EWOD) is equally important (Chung et al. 2010; Nelson and Kim 2012; Zhao and Wang 2013). Nowadays, EWOD has found wide applications in various fields, such as electronic variable-focus liquid lenses (Kuiper and Hendriks 2004; Li and Jiang 2014), display technology (Hayes and Feenstra 2003; Roques-Carmes et al. 2004), digital (droplet) microfluidal devices for bioanalysis (lab-on-a-chip) (Hua et al. 2010; Li et al. 2014), etc. The contact angle is given by the Young–Lippmann equation (Berge 1993; Mugele and Baret 2005; Quilliet and Berge 2001; Zhao and Wang 2013). However, the obtained experimental results proved to be very much different from the theoretical predictions of this equation. Thus, it might be expected that the contact angle would be zero just after some critical voltage value (complete wetting and the contact angle is tend to zero), but in fact the experimental value of the contact angle is always finite (Chevalliot et al. 2012; Mugele and Baret 2005; Zhao and Wang 2013). The mechanism of the contact angle saturation is not clearly understood and is still the question under discussion (Mugele and Baret 2005).

The liquid bridge is a well-known testbed used to analyze the surface tension-dominated phenomena (Demin 2008; Ferrera and Montanero 2007)including those encountered in EWOD-based microfluidic devices (Mampallil et al. 2013; Mugele and Baret 2005). An important problem of research in this field is the movement of the contact line, and changes in the contact angle and surface tension (Antonov et al. 2019; De Gennes 1985; Wang et al. 2019). The viscosity is significant only in thin boundary layers near the rigid surface under high-frequency forced vibrations (Klimenko and Lyubimov 2012, 2018; Shklyaev and Straube 2008). Consequently, the flow in large can be considered as an inviscid one, in which the viscosity effect should be taken into account only in the dynamic boundary layer near the rigid plate (Borkar and Tsamopoulus 1991). For periodic or quasi-periodic motion the most frequently used condition for contact line velocity is the one applied by (Hocking 1987) for investigation of standing waves between two vertical walls. It was also used to study the oscillations of drops (Alabuzhev 2016; Alabuzhev and Lyubimov 2007), bubbles (Alabuzhev and Kaysina 2016; Shklyaev and Straube 2008), and liquid bridge (Borkar and Tsamopoulus 1991), etc. This condition allows us to consider an inviscid fluid, in which only the movement of the contact line leads to energy dissipation (Dolmatova and Goldobin 2018; Goldobin 2017; Shklyaev and Straube 2008). In (Fayzrakhmanova and Straube 2009; Fayzrakhmanova et al. 2011; Hocking 1987), it is suggested to use a more complicated boundary condition, which states a non-unique dependence of the contact angle on the contact line velocity. In this case, a plane capacitor (horizontal layer) is much easier to create in a physical experiment (Il’in and Kartavykh 2018; Kartavykh et al. 2015; Mampallil et al. 2013).

An effective boundary condition for EWOD was formulated based on the Hocking equation (Hocking 1987) for a cylindrical drop in (Alabuzhev and Kashina 2016):

$$\begin{aligned} \frac{{\partial {\zeta ^*}}}{{\partial {t^*}}} = \pm {\Lambda ^*}\left( {\frac{{\partial {\zeta ^*}}}{{\partial {z^*}}} + {A^*}\cos \left( {2{\omega ^*}{t^*}} \right) } \right) , \end{aligned}$$
(1)

where \({\zeta ^*}\) is the deviation of the drop interface from the equilibrium position, \({z^*}\) is the axial coordinate, \({\Lambda ^*}\) is a phenomenological constant (the so-called wetting parameter or the Hocking parameter), having the dimension of velocity, \({A^*}\) is the effective amplitude, \({\omega ^*}\) is the AC frequency. Note that the conditions of a fixed contact line and constant contact angle are particular cases of the boundary conditions \({\Lambda ^*} = 0\) and \(\partial \zeta ^{*}/\partial z^{*}= 0\), respectively. Consequently, this coefficient describes the interaction between the contact line and the substrate. Thus Hocking’s condition (Hocking 1987) specifies the energy dissipation due to the fluid motion near the contact line on the assumption that the fluid is inviscid. The boundary condition 1 was also used to study the dynamics of a cylindrical bubble (Kashina and Alabuzhev 2018c) and a oblate drop (Alabuzhev and Kashina 2017).

The Hocking parameter \({\Lambda ^{*}}\) (see Eq. 1 or (Hocking 1987)) is a real constant in all the above articles. This parameter as a complex number is proposed in (Miles 1991). Inhomogeneous plates were considered in (Alabuzhev 2018; Kashina and Alabuzhev 2018a, b), where the Hocking parameter was taken as a function of coordinates. The surfaces with different Hocking parameters were investigated in (Alabuzhev and Kashina 2019; Kashina and Alabuzhev 2019). We study only the isothermal problem, therefore, a change in the surface tension due to heating (Joule’s law) is not taken into account (Hayat et al. 2015; Samoilova and Lobov 2014; Samoilova and Shklyaev 2015).

In this paper, we consider the behavior of a cylindrical drop (like a liquid bridge) between two heterogeneous plates under the applied AC-voltage. In order to describe the motion of the contact line, we use the modified boundary condition 1 with the Hocking parameter as a function of coordinates (by analogy to (Kashina and Alabuzhev 2018)). In accordance with (Alabuzhev and Kashina 2019), it is also possible to use different Hocking parameters for solid plates.

Note, that free oscillations of a cylindrical drop were studied in (Alabuzhev and Lyubimov 2007) (identical plate surfaces) and (Alabuzhev and Kashina 2019) (different surfaces).

Problem Formulation

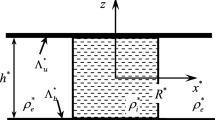
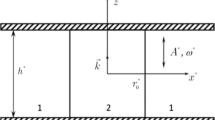
Consider an incompressible liquid drop of density \(\rho _{i}^{*}\) sandwiched between two parallel solid surfaces (separated by a distance \(h^*\)) and surrounded by another liquid of density \(\rho _{e}^{*}\) (see Fig. 1). We suppose that the drop is sufficiently small, so that its shape can hardly be distorted by gravity. In other words, in the examined case the drop shape is characterized by a small Bond number \(Bo \approx \rho ^{*}_{i,e} g R^{*}/ \sigma ^{*}\), where \(R^{*}\) is the drop radius, \(\sigma ^{*}\) is the surface tension coefficient, g is the acceleration due to gravity. This means that in equilibrium the free surface is the lateral surface of a circular cylinder of radius \(R^{*}\) and height \(h^{*}\). The equilibrium contact angle \({\gamma _{0}}\) between the lateral surface of the drop and the solid surface is equal to \(\pi / 2\).

The system is subjected to vibrations with the amplitude \(A^{*}\) and frequency \(\omega ^{*}\). The vibration force is directed parallel to the symmetry axis of the drop. The vibration frequency is large in terms of viscosity but comparable with the fundamental frequencies of the shape oscillations \(\Omega ^{*2} \approx m(m^{2}-1)\sigma ^{*}(\rho _{i,e}R^{*3})^{-1}\), i.e. the capillary number \(Ca=\sigma ^{*} R^{*} \left( \rho ^{*}_{i,e} \nu ^{*2}_{i,e} \right) ^{-1}\) is large. Here \(\nu ^{*2}_{i,e}\) are kinematic viscosity coefficients of the drop and the external liquid, respectively. It is also assumed that the compressibility of the drop and the surrounding liquid is inessential, i.e. \(\omega ^{*} R^{*} \ll c\), where c is the speed of sound. For example, for water drops \((\rho _{i}^{*})\) of radius 1mm (Mampallil et al. 2013) in air\(\omega ^{*} \approx 10-10^3 rad/s\).

Fig. 1
figure 1

Problem geometry (1 – electrode, 2 – dielectric layer)

Full size image

We apply the cylindrical reference frame with the coordinates \({r^*}\), \(\alpha\), \({z^*}\) and the axis of cylinder symmetry, which is parallel to the \({z^*}\)-axis because of the problem symmetry. Let the surface of the drop be described by the equation \({r^{*}} ={R^{*}} + {\zeta ^{*}}\left( {\alpha ,{z^*},{t^*}} \right)\). In the accepted approximations, the liquid motion is irrotational, which makes it convenient to introduce the velocity potential \({\mathbf {v}^*} = \mathbf {\nabla }{\varphi ^*}\). Taking the length \(R_0^*\), the height \({h^*}\), the density \(\rho _e^* + \rho _i^*\), the time \({\sigma ^{ - 1/2}}\sqrt{\left( {\rho _e^* + \rho _i^*} \right) R_0^{*3}}\), the velocity potential \({A^*}\sqrt{\sigma }{\left( {\left( {\rho _e^* + \rho _i^*} \right) R_0^{*3}} \right) ^{ - 1/2}}\), the pressure \({A^*}\sigma {\left( {R_0^*} \right) ^{ - 2}}\) and the deviation of the surface \(A^*\) as characteristic quantities, we go to the dimensionless variables and obtain the following linear problem

$$\begin{aligned} {p_j}= & {} - {\rho _j}{\varphi _j}_t, \Delta {\varphi _j} = 0, j = i,e, \end{aligned}$$
(2)
$$\begin{aligned} \Delta= & {} \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{\partial }{{\partial r}}} \right) + \frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {\alpha ^2}}} + {b^2}\frac{{{\partial ^2}}}{{\partial {z^2}}}, \nonumber \\ r= & {} 1: \left[ \varphi _r\right] = 0, {\zeta _t} = {\varphi _r}, \left[ p \right] = \zeta + {\zeta _{\alpha \alpha }} + {b^2}{\zeta _{zz}}, \end{aligned}$$
(3)
$$\begin{aligned} z= & {} \pm \frac{1}{2}: {\varphi _z} = 0, \end{aligned}$$
(4)
$$\begin{aligned} r= & {} 1, z = \pm \frac{1}{2}: {\zeta _{t}} = \mp \Lambda _{u,b} \left( \alpha \right) \left( {{\zeta _z} + a\cos \left( {2\omega t} \right) } \right) , \end{aligned}$$
(5)

where p is the fluid pressure, \(\varphi\) is the velocity potential, the square brackets denote the jump in the quantity at the interface between the external liquid and the drop, \(\Lambda \left( \alpha \right)\) describes the heterogeneity condition for plates, \(\Lambda _{u} \left( \alpha \right)\) and \(\Lambda _{b} \left( \alpha \right)\) are the Hocking parameter of the “top” \(\left( z=0.5 \right)\) and “bottom” \(\left( z=-0.5\right)\) substrate, respectively. The boundary-value problem (2)–(5) involves six parameters:

The aspect ratio is

$$\begin{aligned} b = \frac{R^{*}}{h^{*}}, \end{aligned}$$

the dimensionless densities are

$$\begin{aligned} {\rho _i} = \frac{\rho _i^*}{\left( {\rho _e^* + \rho _i^*} \right) } \quad \text{ and } \quad {\rho _e} = \frac{\rho _e^*}{\left( {\rho _e^* + \rho _i^*} \right) }, \end{aligned}$$

the wetting parameter is

$$\begin{aligned} \Lambda = {\Lambda ^{*}} \sqrt{ \frac{\left( {\rho _e^* + \rho _i^*} \right) R^*}{\sigma ^{*}}}, \end{aligned}$$

the AC frequency is

$$\begin{aligned} \omega = {\omega ^*} \sqrt{ \frac{\left( \rho _e^* + \rho _i^* \right) R^{*3}}{\sigma ^{*}} }, \end{aligned}$$

the AC amplitude is

$$\begin{aligned} a = 0.5{A^*}C \sqrt{ \frac{\left( \rho _e^* + \rho _i^* \right) R^{*3}}{\sigma ^{*}} }. \end{aligned}$$

Here C is capacitance per unit area.

Forced Oscillations

The functions \(\Lambda _{u,b} \left( \alpha \right)\) are represented as a Fourier series in eigenfunctions of the Laplace operator. Let us consider a particular case of uniform electric field and heterogeneous plates: \(\Lambda _{u,b}=\lambda _{u,b} |\cos (\alpha )|\). The solutions for the velocity potential \(\varphi\) and the surface deviation \(\zeta\) are written as

$$\begin{aligned} {\varphi _i}\left( {r,\alpha ,z,t} \right) = \mathrm {Re} \left( i2\omega \sum \limits _{m,k = 0}^\infty {F_{mk}\left( r,\alpha , z\right) {e^{i2\omega t}}} \right) , \end{aligned}$$
(6)
$$\begin{aligned} {\varphi _e}\left( {r,\alpha ,z,t} \right) = \mathrm {Re} \left( i2\omega \sum \limits _{m,k = 0}^\infty { G_{mk}\left( r,\alpha , z\right) {e^{i2\omega t}}}\right) , \end{aligned}$$
(7)
$$\begin{aligned}& \zeta \left( {z,t} \right) = \mathrm {Re} \left( \left( \sum \limits _{m,k = 0}^\infty H_{mk}{\left( \alpha ,z \right) }+\sum \limits _{m = 0}^\infty D_{m}{\left( \alpha ,z \right) } \right) {e^{i2\omega t}} \right) , \\& F_{mk}(r,\alpha , z)=\left( {a_{mk}^{(0)}}R_{mk}^{(0)i}\left( r \right) Z_{k}^{(0)}\left( z\right) \;+ \right. \nonumber \\& \qquad \qquad \qquad \left. + a_{mk}^{(1)}R_{mk}^{(1)i}\left( r \right) Z_{n}^{(1)}\left( z\right) \right) A_m\left( \alpha \right) , \nonumber \\& G_{mk}(r,\alpha , z)=\left( {b_{mk}^{(0)}}R_{mk}^{(0)e}\left( r \right) Z_{k}^{(0)}\left( z\right) \;+ \right. \nonumber \\ &\left. + b_{mk}^{(1)}R_{mk}^{(1)e}\left( r \right) Z_{n}^{(1)}\left( z\right) \right) A_m\left( \alpha \right) , \nonumber \\ &H_{mk}(\alpha , z)= \left( {{c_{mk}^{(0)}}{Z_k^{(0)}}\left( z \right) } \;+ \right. \nonumber \\ &\left. + {{c_{mk}^{(1)}}{Z_k^{(1)}}\left( z \right) } \right) {A_m}\left( \alpha \right) ,\nonumber \\ &D_{0}\left( \alpha ,z \right) ={d_0^{(0)}}\cos \left( {\frac{z}{b}} \right) +{d_0^{(1)}}\sin \left( {\frac{z}{b}} \right) , \nonumber \\ &D_{m}\left( \alpha ,z \right) = \left( d_{m}^{(0)}\cosh \left( {\frac{{\sqrt{4{m^2} - 1} }}{b}z} \right) + \right. \nonumber \\ &\left. + d_{m}^{(1)}\sinh \left( {\frac{{\sqrt{4{m^2} - 1} }}{b}z} \right) \right) A_{m}\left( z \right) , \nonumber \\ &R_{m0}^{(0)i}(r)=r^{m}, \quad R_{mk}^{(0)e}(r)=\frac{1}{r^{m}}, \nonumber \\ &R_{mk}^{(0)i}(r)=I_{m}(2k \pi b r), \quad R_{mk}^{(0)e}(r)=K_{m}{\left( 2k \pi b r\right) }, \nonumber \\ &R_{mk}^{(1)i}(r)=I_{m}({\left( {2k + 1} \right) \pi b r}), \quad R_{mk}^{(1)e}(r)=K_{m}({\left( {2k + 1} \right) \pi b r}), \nonumber \\ &Z_k^{(0)}\left( z\right) =\cos {\left( {2k \pi z} \right) }, \quad Z_k^{(1)}\left( z\right) =\sin {\left( {\left( {2k + 1} \right) \pi z} \right) }, \nonumber \\& A_m\left( \alpha \right) = \cos \left( {2m\alpha } \right) , \nonumber \end{aligned}$$
(8)

where \(F_{mk}(r,\alpha , z)\) and \(G_{mk}(r,\alpha , z)\) are the eigenfunctions of the Laplace operator, \(I_{m}\) and \(K_{m}\) are the modified Bessel functions of m-th order. Substituting solutions (6)–(8) into (2)–(5), we obtain the expressions for the unknown amplitudes \({a_{mk}}\), \({b_{mk}}\), \({c_{mk}}\) and \({d_{m}}\). We do not write explicit expressions for these coefficients because they are far too cumbersome. These expressions are equivalent to the similar solutions obtained for \(\Lambda _{u,b} \left( \alpha \right) =\lambda =const\) in (Alabuzhev and Kashina 2016) and \(\Lambda _{u,b} \left( \alpha \right) =\lambda _{u,b}\) in (Alabuzhev and Kashina 2019; Kashina and Alabuzhev 2019). One can easily verify the complex nature of these coefficients for any set of parameters, except for the limiting cases corresponding to the fixed contact line or contact angle. This complexity leads to a phase shift between different spatial modes of oscillations, i.e., the appearance of traveling capillary waves on the lateral surface (Alabuzhev 2016; Alabuzhev and Kashina 2019).

For convenience, we prescribe the following maximum deviations of the drop surface from the equilibrium position: on the “upper” plate \(z=0.5\) – \(\zeta _{u}=\max {\left( \zeta (0,0.5,0)\right) }\), on the “bottom” plate \(z-=0.5\) – \(\zeta _{b}=\max {\left( \zeta (0,-0.5,0)\right) }\), in the center of the layer \(z=0\) – \(\zeta _{0}=\max {\left( \zeta (0,0,0)\right) }\) and a “quarter” position \(z=0.5\) – \(\zeta _{q}=\max {\left( \zeta (0,0.25,0)\right) }\); the values of the internal contact angle \(\gamma\) on the “upper” plate are \(\gamma _{u}\), at the “bottom” plate – \(\gamma _{b}\).

Uniform Plates

The dynamics of the drop significantly depends on the amplitude \(\lambda\) of the function \(\Lambda \left( \alpha \right)\). First consider the behaviour of the drop in the case of homogeneous plates, i.e. \(\Lambda _{u,b} \left( \alpha \right) =\lambda _{u,b}\) (Alabuzhev and Kashina 2019; Kashina and Alabuzhev 2019). Therefore, the solution (6)–(8) of problem (2)–(5) does not depend on the polar angle \(\alpha\), since the external force excites only axisymmetric vibrations. In this case the amplitudes of the solution (6)–(8) are defined by expressions

$$\begin{aligned} &d_{0}^{(0)}=a \frac{\lambda _{b} \left( 2 i \omega B C+1 \right) + 2 i \omega B G}{2i \omega \left( F-DS \right) }, \quad d_{0}^{(1)}=B a+D d_{0}^{(0)}, \nonumber \\& B=-\frac{\lambda _{u}}{2i\omega \left( { \lambda _{u}C+G }\right) } , \quad D=\frac{\lambda _{u}S-F}{\lambda _{u}C+G}, \nonumber \\& F=4\omega ^2 \sum \limits _{k = 1}^\infty \frac{(-1)^k f_k}{\Omega ^{(0)2}_k-4\omega ^2} - f_{0} +\cos \left( {\frac{1}{2b}} \right) , \nonumber \\& G=4\omega ^2 \sum \limits _{k = 0}^\infty \frac{(-1)^k g_k}{\Omega ^{(1)2}_k-4\omega ^2} + \sin \left( {\frac{1}{2b}} \right) , \nonumber \\ &C=\frac{1}{2i\omega b}\cos \left( {\frac{1}{2b}} \right) , \quad S=\frac{1}{2i\omega b}\sin \left( {\frac{1}{2b}} \right) , \nonumber \\ &c^{(0)}_{00}=-f_0, \quad c^{(0)}_{0k}=\frac{4\omega ^2 f_k d_0^{(0)}}{\Omega ^{(0)2}_k-4\omega ^2}, \quad c^{(1)}_{k}=\frac{4\omega ^2 g_k d_{0}^{(1)}}{\Omega ^{(1)2}_k-4\omega ^2},\nonumber \\ &a^{(0)}_{0k}R^{(0)i}_{0kr}(1)= 2i\omega \left( {c^{(0)}_{k}+f_k d_{0}^{(0)}}\right) , \nonumber \\ &a^{(1)}_{0k}R^{(1)i}_{0kr}(1)= 2i\omega \left( {c^{(1)}_{k}+g_k d_{0}^{(1)}}\right) , \nonumber \\ &a^{(0)}_{00}=0, \quad b^{(0)}_{00}=0, \quad a^{(0)}_{0k}R^{(0)i}_{0kr}(1)=b^{(0)}_{k}R^{(0)e}_{0kr}(1), \nonumber \\ &a^{(1)}_{0k}R^{(1)i}_{0kr}(1)=b^{(1)}_{0k}R^{(1)e}_{0kr}(1), \nonumber \end{aligned}$$

where \(f_{k}\) and \(g_{k}\) are the coefficients of the Fourier series expansions of the functions \(\cos (z/b)\) and \(\sin (z/b)\), respectively, and \(\Omega ^{(0)2}_{k}\) and \(\Omega ^{(1)2}_{k}\) are the eigenfrequencies of the drop with a freely moving contact line (i.e., at \(\lambda \rightarrow \infty\)) (Alabuzhev and Lyubimov 2007).

The results of the solution are presented in Figs. 2, 3 and 4. Figure 2 shows the oscillation amplitude of the drop surface and the deviation of the contact angle as a function of the frequency of the uniform electric field for several values of the Hocking parameters \(\lambda _{u}\) and \(\lambda _{b}\). The amplitudes of the surface oscillations and the contact angle reach maximum values in a linear resonance. It is also seen from the graphs that the values of the resonant frequencies decrease with an increase of parameter \(\lambda _{u}\) or \(\lambda _{b}\). Despite weak dissipation at small values of the parameter \(\lambda _{b}\), the amplitude of surface oscillations is finite (Fig. 2a) and the amplitude of oscillations of the contact line is small (Fig. 2d). The contact angle varies in a wide range (Fig. 2e, f). It is important to note that if at least one of the parameters \(\lambda _{u}\) or \(\lambda _{b}\) is finite, the amplitude of surface oscillations is always finite. Consequently, dissipation is determined by the largest damping parameter. In the general case, the amplitude of drop surface oscillations depends on the amplitude of contact line oscillations. Therefore, the deviations of the contact line are small for small parameters \(\lambda \ll 1\), which leads to slight deviations of the lateral surface (not in resonance).

The external force excites only odd shape modes \(\sin \left( {\left( {2k + 1} \right) \pi z} \right)\) (6)–(8) in the case of equality of the Hocking parameters \(\lambda _{u}=\lambda _{b}=1\), so that there is no deviation of the drop surface in the center of the layer (Fig. 2c) and the form of the drop surface is described by the odd function (Fig. 3a). The excitation of even modes \(\cos {\left( {2k \pi z} \right) }\) is also due to the asymmetry with respect to the z-coordinate at different Hocking parameters \(\lambda _{u} \ne \lambda _{b}\). This leads to the appearance of paired resonance peaks on the amplitude-frequency characteristic curve (see Fig. 2). In most cases, the resonant amplitude of the odd mode is higher than that of the corresponding even mode. Note, that in the general case the form of the drop lateral surface is also close to the description in terms of the odd function, despite different values of \(\lambda\) (Fig. 3b). The drop shape governed by an even function is observed only at the “even” resonant frequency (Fig. 3c), when the amplitudes of the even harmonics are much hiher than the amplitudes of the odd ones.

There are “antiresonant” frequencies, i.e. such frequencies, at which the line of contact is motionless (Fig. 2). Such frequencies lie between the pairs of resonance frequencies of the mode shapes. In the first such region (\(\omega <6\) in our case, see Fig. 2), there is only one resonant frequency - the main frequency of the axisymmetric mode, or, in other words, the zero odd mode shape \(k=0\). An zero even shape mode is absent, since it corresponds to volume oscillations, which are absent for an incompressible drop.

Traveling capillary waves propagating along the lateral surface of the drop are caused by the oscillations of the contact line and the contact angle (Fig. 4). At equal values of the parameter \(\lambda\), there are no traveling waves and only standing waves are initiated on the surface of the drop (Fig. 4a). Note that traveling waves arising due to the action of axisymmetric external vibrations are observed on the drop surface only when the values of \(\lambda\)are finite (Alabuzhev 2016). If the values of\(\lambda _{u}\) and \(\lambda _{b}\) are different, the waves propagate at any values of these parameters. Figure 4b, c show the oscillations of the wave crest position, i.e. the traveling waves propagate along the entire surface in the absence of symmetry.

Fig. 2
figure 2

Plots of the amplitudes of contact line oscillations \(\zeta _{u}\) (a) and \(\zeta _{b}\) (d), the position of the lateral surface \(\zeta _{q}\) (b) and \(\zeta _{0}\) (c), and the contact angle \(\gamma _{u}\) (e) and \(\gamma _{b}\) (f) as a function of the frequency \(\omega\) of the external vibrations for different values of the Hocking parameter \(\lambda _{b}\) (\(b = 1\), \(\lambda _{u}=1\), \(a=10\), \(\rho _{i}=0.7\)). The cases of \(\lambda _{b}\) = 0.01, 1, and 100 correspond to the solid, dashed and dotted lines, respectively

Full size image
Fig. 3
figure 3

Evolution of the drop surface shape. \(T=\pi \omega ^{-1}\) is the oscillation period (\(b = 1\), \(a=10\), \(\rho _{i}=0.7\), \(\lambda _{u}=1\)), (a) \(\lambda _{b} = 1\), \(\omega = 4\), (b) \(\lambda _{b} = 100\), \(\omega = 4\), (c) \(\lambda _{b} = 100\), \(\omega = 9.5\). \(t=0\) – solid line, \(t=0.125T\) – dashed, \(t=0.25T\) – dotted, \(t=0.375T\) – dash-dotted

Full size image
Fig. 4
figure 4

Propagation of maxima of traveling waves over the drop surface (\(b = 1\), \(a=10\), \(\rho _{i}=0.7\), \(\lambda _{u}=1\)), (a) \(\lambda _{b} = 1\), \(\omega = 4\), (b) \(\lambda _{b} = 100\), \(\omega = 4\), (c) \(\lambda _{b} = 100\), \(\omega = 9.5\)

Full size image

Non-Uniform Plates

Now we consider the plates, the surfaces of which are rough, that is, they have a spatially heterogeneous structure, which is described by the relation \(\Lambda _{u,b}=\lambda _{u,b} |\cos (\alpha )|\). In this case, due to the surface inhomogeneity, the application of the external force will excite only azimuthal oscillation modes (see the boundary condition (5)), consequently the dynamics of the drop differs significantly from its behavior in the uniform field “Uniform Plates”. Dependencies similar to Figs. 2, 3 and 4 are shown in Figs. 5, 6 and 7.

Fig. 5
figure 5

Plots of the amplitudes of contact line oscillations \(\zeta _{u}\) (a) and \(\zeta _{b}\) (d), the side-surface position \(\zeta _{q}\) (b) and \(\zeta _{0}\) (c), and the contact angle \(\gamma _{u}\) (e) and \(\gamma _{b}\) (f)as a functions of the frequency \(\omega\) of the external vibrations for non-uniform plates at \(\alpha =0\) (\(b = 1\), \(\lambda _{u}=1\), \(a=10\), \(\rho _{i}=0.7\)). The cases of \(\lambda _{b}\) = 0.01, 1, and 100 correspond to the solid, dashed and dotted lines, respectively

Full size image
Fig. 6
figure 6

Evolution of the drop surface shape at \(\alpha =0^{o}\) and \(\alpha =90^{o}\). \(T=\pi \omega ^{-1}\) is the oscillation period (\(b = 1\), \(a=10\), \(\rho _{i}=0.7\), \(\lambda _{u}=1\)), (a) \(\lambda _{b} = 0.01\), \(\omega = 1\), (b) \(\lambda _{b} = 100\), \(\omega = 1\), (c) \(\lambda _{b} = 100\), \(\omega = 10\). \(t=0\) – solid line, \(t=0.125T\) – dashed, \(t=0.25T\) – dotted, \(t=0.375T\) – dash-dotted. line 0 - \(\alpha =0^{o}\), line 90 - \(\alpha =90^{o}\)

Full size image
Fig. 7
figure 7

Propagation of maxima of traveling waves over the drop surface (\(b = 1\), \(a=10\), \(\rho _{i}=0.7\), \(\lambda _{u}=1\)), (a) \(\lambda _{b} = 0.01\), \(\omega = 1\), (b) \(\lambda _{b} = 100\), \(\omega = 1\), (c) \(\lambda _{b} = 100\), \(\omega = 10\)

Full size image

In our case, the even azimuthal modes occur due to the nonuniformity of the substrate, which leads to the appearance of additional resonance peaks (see Fig. 5). The Fourier coefficients of the function \(\Lambda _{u,b}=\lambda _{u,b} |\cos (\alpha )|\) are given by:

$$\begin{aligned} &l_{0}=\frac{1}{2\pi }\int _0^{2 \pi } \Lambda _{u,b}{\left( \alpha \right) }\,d\alpha =\lambda _{u,b}\frac{2}{\pi }, \nonumber \\ &l_{m}=\frac{1}{\Vert \cos (2m \alpha ) \Vert ^{2}}\int _0^{2 \pi } \Lambda _{u,b}{\left( \alpha \right) } \cos {\left( 2m \alpha \right) }\,d\alpha = \nonumber \\ &=\lambda _{u,b}\frac{4(-1)^{m+1}}{(4m^2-1)\pi }, \quad m \ge 1 \nonumber . \end{aligned}$$

These expansion coefficients, and, accordingly, the contribution of the external force energy decrease by \(m^{-2}\) for each azimuthal mode. Consequently, the largest part of the energy is transferred to the first few modes and the zero (azimuthal) mode makes the main contribution to the droplet shape.

As noted above, the external force excites both the odd and even longitudinal vibrational modes (along the symmetry axis z) as noted above. The odd amplitude coefficient is \(d_{1} \sim \lambda _{u}+\lambda _{b}\), but the even amplitude coefficient is \(d_{0} \sim \lambda _{b}-\lambda _{u}\). In the limit case of close values \(\lambda _{b}=\lambda _{u}+\delta\), \(\delta \ll 1\), these amplitude coefficients are defined as (in the case of uniform plates “Uniform Plates”)

$$\begin{aligned} d_{0}^{(0)}= &\;a \delta \frac{2 i \omega B C+1}{4 i \omega \left( F- \lambda _{u} S \right) }, \nonumber \\ d_{0}^{(1)}=&\; \frac{\lambda _{u} a}{2 i \omega \left( \lambda _{u} C+G \right) }. \nonumber \end{aligned}$$

Accordingly, the odd amplitude \(d_{0}^{(1)}\) is much higher than the even amplitude \(d_{0}^{(0)}\). However, this amplitude \(d_{0}^{(0)}\) becomes significant in the resonance mode at the frequency of an even harmonic: \(F-\lambda _{u} S = 0\).

A new resonance peak appears in front of the axisymmetric mode already existing at the main frequency (compare Fig. 2 with Fig. 5). This peak corresponds to resonance at the fundamental frequency of the quadrupole mode of natural oscillations (azimuthal number \(m=2\), wave number \(k=0\)). In this case, the fundamental frequency of the quadrupole mode is less than the main frequency of the axisymmetric mode (\(m=0\), \(k=1\)), since the fundamental frequency of volume (radial) oscillations does not exist in the case of drop incompressibility. Consequently, the inhomogeneity of the plate surface gives rise to additional quadrupole oscillations of the drop. Note that there are additional resonance peaks at the frequency of the next mode, but they are less pronounced compared to the quadrupole oscillations.

The oscillations amplitude of the drop lateral surface near the main frequencies is maximum and decreases at subsequent resonant frequencies (see Fig. 5). A similar dependence was obtained in the case of equal Hocking parameters (Alabuzhev and Kashina 2017; Kashina and Alabuzhev 2018a, b). For a homogeneous surface, the opposite effect is observed - the amplitude increases and the amplitude values for even and odd modes are different (see Fig. 2). Consequently, the heterogeneity neutralizes the influence of the difference in Hocking parameters.

The lateral surface deviation at different times of the oscillation period is shown in Fig. 6 for two cross sections \(\alpha = 0^{o}\) and \(\alpha = 90^{o}\). This is attributed to the fact that the non-symmetric vibration modes are excited due to inhomogeneity and therefore, the vibration amplitude at \(\alpha = 0^{o}\) is greater than at \(\alpha = 90^{o}\). The positions of the maxima are shown in Fig. 7. The subsequent positions of the maxima are shown on the lateral surface of the drop in contrast to Fig. 4. It is seen that traveling waves propagate along the axis of symmetry only in the limited areas, but change their position with respect to the azimuthal angle.

Figure 8 shows the variation in the shape of the contact line during the oscillation period \(T=\pi \omega ^{-1}\). It can be seen that the drop extends along the surface inhomogeneity, i.e. along the x-axis (Fig. 8a). At large values of the parameter \(\lambda _{b}\), the interaction of the line of contact with the substrate decreases, which leads to the appearance of pronounced quadrupole oscillations (Figs. 5 and 8b). The axisymmetric oscillations become dominant again with increasing frequency (Figs. 5 and 8c). The axisymmetric oscillations are the main oscillation mode of forced oscillations in the case of non-uniform field and homogeneous surfaces.

Fig. 8
figure 8

The shape of the contact line at the upper plate during the oscillation period \(T=\pi \omega ^{-1}\) \((a=10, \lambda _{u}=1, \rho _i=0.7, b=1, \omega =1, \epsilon =0.1)\), (a) \(\lambda _{b} = 0.01\), \(\omega = 1\), (b) \(\lambda _{b} = 100\), \(\omega = 1\), (c) \(\lambda _{b} = 100\), \(\omega = 10\). \(t = 0.\) – solid line, \(t = 0.125T\)– dotted, \(t = 0.25T\)– dashed, \(t = 0.375T\)– dot-dashed

Full size image

Conclusions

The behavior of the cylindrical drop between two solid plates has been considered taking into account the dynamics of the contact angle under the action of the electric field. The solid plates have heterogeneous surfaces described by the functions \(\Lambda _{u,b}(\alpha )=\lambda _{u,b} |\cos (\alpha )|\), where \(\Lambda _{u} \left( \alpha \right)\) and \(\Lambda _{b} \left( \alpha \right)\) are the Hocking parameter of the “upper” \(\left( z=0.5 \right)\) and “bottom” \(\left( z=-0.5\right)\) substrate, respectively.

It is shown that in the case of homogeneous plates, the drop performs axisymmetric oscillations. Traveling waves on the lateral surface exist only at different values of the Hocking parameter (i.e at \(\lambda _{b} \ne \lambda _{b}\)). A standing wave exists with at equal parameters: \(\lambda _{b} = \lambda _{b}\). In the latter case, only the odd modes of surface vibrations are resonant, while for \(\lambda _{b} \ne \lambda _{b}\) the even modes are also resonant. The “antiresonant” frequencies lie between pairs of such resonant frequencies.

The azimuthal vibration modes are excited in the case of non-uniform plate surfaces. At low frequencies, the main type of vibrations is a quadrupole mode. At higher frequencies, there are axisymmetric oscillations, which are modulated by the azimuthal modes. Large values of the parameter \(\lambda _{b}\) (at finite \(\lambda _{u}\)) the interaction between the line of contact and the substrate decreases, which leads to the appearance of pronounced quadrupole oscillations. The traveling waves propagate along the axis of symmetry only in the limited areas, but change their position with respect to the azimuthal angle.

It is obvious that the type of inhomogeneity has a significant effect on the drop dynamics. However, it can be expected that similar inhomogeneities affect the droplet behavior in the same way. Consequently, based on the results of stydying this particular case one can qualitatively describe the oscillations of a drop in the case of even functions \(\Lambda _{u,b}(\alpha )\).