Forced Axisymmetric Oscillations of a Drop, which is Clamped Between Different Surfaces

Abstract

We consider forced oscillations of a oblate fluid drop, which is surrounded by another liquid and confined between two parallel rigid plates subject to vibrations. The axisymmetrical vibration force is parallel to the symmetry axis of the drop. The velocity of the contact line motion is proportional to the deviation of the contact angle from its equilibrium value. The proportionality factors are different for each solid plate , which accounts for the reason of excitation of additional shape oscillation modes and the appearance of new resonant frequencies. The solution of the boundary value problem is found using the Fourier series expansion into eigenfunctions of the Laplace operator.

Introduction

The surface properties of the substrate have a significant impact on the dynamics of the contact line and the contact angle (Benilov 2010; Borcia et al. 2019; Savva and Kalliadasis 2013). Introduction of a coupling coefficient accounting for the interaction between the contact line and substrate is an effective and and well established approach. The author of work (Hocking 1987a) have proposed an effective boundary condition that linearly relates the velocity of movement of the contact line and the deviation of the contact angle

$$ \frac{{\partial {\zeta^{*}}}}{{\partial {t^{*}}}} = {\varLambda^{*}}\mathbf{k} \cdot \mathbf \nabla {\zeta^{*}}, $$

(1)

where ζ^∗ is the deviation of the interface from the equilibrium position, k is the external normal to the solid surface, Λ^∗ is a phenomenological constant (the so-called wetting parameter or Hocking parameter) having a dimension of a velocity. The accepted boundary condition (1) is associated with two important constraints: (a) ζ^∗ = 0 – the requirement of a fixed contact line (pinned-end edge condition, for example Benilov (2016) and Demin (2008)), (b) k ⋅∇ζ^∗ = 0 – a constant contact angle (free contact line, for example Alabuzhev and Lyubimov (2005)). Many other authors used condition (1) in tackling a variety of problems (Alabuzhev 2016; Alabuzhev and Kaysina 2016; Borkar and Tsamopoulus 1991; Perlin et al. 2004; Shklyaev and Straube 2008). The problems Alabuzhev and Kashina (2019); Kashina and Alabuzhev (2018, 2019a), included the modified condition (1) with an external force, whereas the general case of the condition (1) in the problems (Hocking 1987b; Fayzrakhmanova and Straube 2009; Fayzrakhmanova et al. 2011) allowed for the hysteresis of the contact angle. In Viola et al. (2018) and Viola and Gallaire (2018) authors adopted the linear model (1) to a nonlinear empiric law (Dussan 1979; Voinov 1976) for the contact line, which takes into account the contact angle hysteresis trough adding a non-linear term.

The effect of viscosity becomes significant only in thin boundary layers near a solid surface under high-frequency vibrations, and the motion of the contact line is determined mainly by the rapidly oscillating pressure field (Benilov 2016; Klimenko and Lyubimov 2012; 2018). Thus, it is possible to describe the non-viscous behavior of a fluid in the core by considering only the viscosity of the dynamic boundary layer near the solid substrate (about vanishing kinematic viscosity (Goldobin 2017)). Complex processes occurring in the immediate vicinity of the contact line are excluded from consideration due to the use of the effective boundary conditions (1) imposed on the dynamics of the visible contact angle. So, in the framework of the inviscid fluid model, the attempts made in Benilov (2010,2011); Benilov and Billingham (2011); Benilov and Cummins (2013); Bradshaw and Billingham(2018) were directed toward finding a reasonable explanation of the nontrivial behavior of a drop on an inclined plane under vertical vibrations (e.g. the drop can climb uphill) (Brunet et al. 2007; Brunet et al. 2009).

The Hocking parameter is a constant in most of the works listed above. Authors Miles (1991) suggested that the contact line variation should not necessarily coincide in phase with the contact angle, i.e., the Hocking parameter is complex. The force oscillations was considered in Alabuzhev (2016) and Alabuzhev and Lyubimov (2007), and the free oscillations in Alabuzhev and Lyubimov (2007) for the case of an identical homogeneous plate surfaces. The problem of an identical inhomogeneous surfaces was considered in Alabuzhev (2018) (with b.c. (1)), Kashina and Alabuzhev (2019b) (with modified b.c. (1) (Alabuzhev and Kashina 2019)). The Hocking parameter was represented as a coordinate function just as a tensorial local slip boundary condition (Asmolov et al. 2018; Dubov et al. 2018). The natural oscillations of a drop in the case of different plate surfaces were studied in Alabuzhev and Kashina (2019). In this article we consider the axisymmetrical forced oscillations of a cylindrical fluid drop, which is surrounded by another ideal liquid. The drop is sandwiched between two plates with different surfaces, the same as considered in Alabuzhev and Kashina (2019). The force of the external electric field acts only on the contact line at a double frequency in Alabuzhev and Kashina (2019), while in our research, the vibration force acts on the this system at a single frequency as a whole. This difference significantly changes the behavior of the system, especially for small Hocking parameters. Furthermore, our results can be potentially interesting in studying the thermocapillary Marangoni effect and the dynamics of drops (bubbles) in both isothermal and non-isothermal flows (Bekezhanova and Goncharova 2019).

Problem Formulation

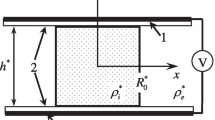
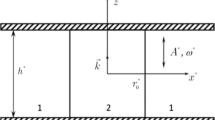
Let us consider an oblate drop of incompressible liquid of density $\rho _{i}^{*}$ and kinematic viscosity $\nu _{i}^{*}$, as shown in Fig. 1. This drop is placed between two parallel plates and surrounded an incompressible liquid of density $\rho _{e}^{*}$ and kinematic viscosity $\nu _{e}^{*}$. We admit that the drop is small enough so that its shape can be hardly distorted by gravity and hence the interface has the form of a circular cylinder of radius R^∗ and the equilibrium contact angle equals π/2. We assume that the solid substrates are subjected to transverse vibrations with an amplitude a^∗ and a frequency ω^∗.

Fig. 1

Geometry of problem

The amplitude of external force is considered small in the sense that $a^{*}\ll R^{*}$ and the frequency of the substrate oscillations is high enough $\omega ^{*}R^{*2} \gg \nu ^{*}$. Viscous boundary layers, which arise near the rigid plates and near the interface, become very thin at such frequency. In another way, the frequency constraints allow us to neglect viscous dissipation in fluids, which renders the use of inviscid liquid approximation quite reasonable. However, the frequency is assumed comparable with the eigenfrequencies of free oscillations for a cylindrical drop of radius R^∗: ${\varOmega }_{m}^{*2}=m(m^{2}-1)*\sigma ^{*}/\left (\left (\rho _{i}^{*}+\rho _{e}^{*}\right )R^{*3} \right )$, where m is an azimuthal number, σ^∗ is the surface tension coefficient. Moreover the fluid motion in the drop (or external liquid) is assumed to be incompressible, i.e. $\omega ^{*} R^{*} \ll c^{*}$, where c^∗ is the sound velocity. For example, for water drop in air ($\sigma ^{*} \sim 10^{2} \enskip g/s^{2}$, $\rho _{i}^{*} \sim 1 \enskip g/cm^{3}$, $\rho _{e}^{*} \sim 10^{-3} \enskip g/cm^{3}$, $\nu ^{*} \sim 10^{-2} \enskip cm^{2}/s$, $c^{*} \sim 1.5 \cdot 10^{5} \enskip cm/s$) of radius $R^{*} \sim 1 cm$ – 0.1 rad/s ≪ ω^∗≪ 10⁵rad/s and ${\varOmega }_{m}^{*} \sim 10\sqrt {m(m^{2}-1)} rad/s$.

Let the drop’s shape be described by the equation ${r^{*}} = R_{0}^{*} + {\zeta ^{*}}\left ({\alpha ,{z^{*}},{t^{*}}} \right )$ in the cylindrical coordinates r^∗, α, z^∗ with the origin in the center of the cylinder.On the assumption of a potential liquid motion, we introduce the velocity potential ${\mathbf v^{*}} = \mathbf {\nabla } {\varphi ^{*}}$. We note again (see Section “Introduction”) that in the problem under consideration, the energy dissipation is due to the Hocking condition, even despite the model of an inviscid fluid. This allows us to use the potential flow according to the Kelvin’s circulation theorem.

The dimensionless amplitude of oscillations is given as $\epsilon ={A^{*}}/R^{*} \ll 1$, which allows us to linearize the governing equations and simplify the boundary conditions. Taking the length $R_{0}^{*}$, the height h^∗, the density $\rho _{e}^{*} + \rho _{i}^{*}$, the time ${\sigma ^{- 1/2}}\sqrt {\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )R^{*3}}$, the velocity potential ${A^{*}}\sqrt \sigma {\left ({\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )R^{*3}} \right )^{- 1/2}}$, the pressure ${A^{*}}\sigma {\left ({R^{*}} \right )^{- 2}}$ and the deviation of the surface A^∗ as characteristic quantities, we pass to dimensionless variables and obtain the following linear problem

$$ \begin{array}{@{}rcl@{}} {p_{j}} &=& - {\rho_{j}}\left( \frac{\partial \varphi_{j}}{\partial t}-\omega^{2} z e^{i\omega t} \right), \quad {\Delta} {\varphi_{j}} = 0, \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} {\Delta} &=& \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{\partial }{{\partial r}}} \right) + {b^{2}}\frac{{{\partial^{2}}}}{{\partial {z^{2}}}}, \\ r &=& 1: \left[\frac{\partial \varphi}{\partial r}\right] = 0, \quad \frac{\partial \zeta}{\partial t} = \frac{\partial \varphi}{\partial r}, \quad \left[ p \right] = \zeta+{b^{2}}\frac{\partial^{2} \zeta}{\partial z^{2}}, \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} z &=& \pm \frac{1}{2}: \quad \frac{\partial \varphi}{\partial z} = 0, \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} r &=& 1, z = \pm \frac{1}{2}: \quad \frac{\partial \zeta}{\partial t} = \mp \lambda_{u,b} \frac{\partial \zeta}{\partial z}, \end{array} $$

(5)

where p is the fluid pressure, j = i, e, λ_u and λ_b are Hocking parameters parameters on the “upper” $\left (z=0.5 \right )$ and “bottom” $\left (z=-0.5 \right )$ plates, respectively, the square brackets denote the jump in the quantity at the interface between the surrounding liquid and the drop. The external force (2) excites only axisymmetrical oscillations (independent of the azimuth angle α), therefore the angle derivative is omitted in the equations and the boundary conditions.

The boundary-value problem (2)–(5) involves five parameters:

the small vibrations amplitude – $\epsilon = {A^{*}}{\left (R^{*}\right )^{- 1}}$,

the aspect ratio – $b = {R^{*}}{h^{- 1}}$,

the dimensionless densities – ${\rho _{i}} = \rho _{i}^{*}{\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )^{- 1}}$ and ${\rho _{e}} = \rho _{e}^{*}{\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )^{- 1}}$,

the wetting parameter – $\lambda = {\varLambda ^{*}}b{\sigma ^{- 1/2}} \sqrt {\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )R^{*}}$,

the force frequency – $\omega = {\omega ^{*}}{\sigma ^{- 1/2}} \sqrt {\left (\rho _{e}^{*} + \rho _{i}^{*} \right )R^{*3}}$.

Method of Solution

We will consider only an axisymmetrical mode of the forced oscillations of the drop. Note, the natural axisymmetrical oscillations of this system were studied in Alabuzhev and Kashina (2019). We will search for the solution of problem (2) - (5) in the form of a Fourier series expansion into the basis functions of the Laplace operator taking into account the boundary conditions (4)

$$ \begin{array}{@{}rcl@{}} {\varphi_{i}}\left( {r,z,t} \right) &=& \operatorname{Re} {\left( i\omega {\phi_{i}}\left( {r,z} \right) {e^{i\omega t}} \right)}, \end{array} $$

(6)

$$ \begin{array}{@{}rcl@{}} {\varphi_{e}}\left( {r,z,t} \right) &=& \operatorname{Re} {\left( i\omega {\phi_{e}}\left( {r,z} \right) {e^{i\omega t}}\right)}, \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} \zeta \left( {z,t} \right) &=& \operatorname{Re} {\left( \xi\left( {z} \right) {e^{i\omega t}} \right)}, \end{array} $$

(8)

$$ \begin{array}{@{}rcl@{}} {\phi_{i}}\left( {r,z} \right)&=&\sum\limits_{k = 0}^{\infty} {\left( {a^{(0)}_{k}F^{(0)}_{k}\left( r,z\right)+a^{(1)}_{k}F^{(1)}_{k}\left( r,z\right)} \right)},\\ {\phi_{e}}\left( {r,z} \right)&=&\sum\limits_{k = 0}^{\infty} {\left( {b^{(0)}_{k}G^{(0)}_{k}\left( r,z\right)+b^{(1)}_{k}G^{(1)}_{k}\left( r,z\right)} \right)},\\ \xi\left( {z} \right)&=&\sum\limits_{k = 0}^{\infty} \left( {c^{(0)}_{k}}{Z^{(0)}_{k}}\left( z \right) + {c^{(1)}_{k}}{Z^{(1)}_{k}}\left( z\right)\right)+ \\ \qquad \qquad &&+{d_{0}}\cos \left( {\frac{z}{b}} \right)+ {d_{1}}\sin \left( {\frac{z}{b}} \right),\\ F^{(0)}_{k}(r, z)&=&R^{(0i)}_{k} (r) Z^{(0)}_{k}\left( z\right), \\ \quad F^{(1)}_{k}(r, z)&=&R^{(1i)}_{k} (r) Z^{(1)}_{k}\left( z\right), \\ G^{(0)}_{k}(r, z)&=&R^{(0e)}_{k} (r) Z^{(0)}_{k}\left( z\right), \\ \quad G^{(1)}_{k}(r, z)&=&R^{(1e)}_{k} (r) Z^{(1)}_{k}\left( z\right), \\ R^{(0i)}_{0} (r)&=&const, \quad R^{(0e)}_{0} (r)=const, \\ R^{(0i)}_{k} (r)&=&I_{0}\left( { 2k \pi b r} \right), \quad R^{(1i)}_{k} (r)=I_{0}\left( {\left( {2k + 1} \right)\pi b r} \right), \\ R^{(0e)}_{k} (r)&=&K_{0}\left( { 2k \pi b r} \right), \quad R^{(1e)}_{k} (r)=K_{0}\left( {\left( {2k + 1} \right)\pi b r} \right), \\ Z^{(0)}_{k}\left( z\right)&=&\cos {\left( {2k \pi z} \right)}, \quad Z^{(1)}_{k}\left( z\right)=\sin {\left( {\left( {2k + 1} \right)\pi z} \right)}, \end{array} $$

where $I_{0}\left (r\right )$ and $K_{0}\left (r\right )$ are the modified Bessel functions of the first and second kinds, respectively, $a^{(0)}_{k}$, $a^{(1)}_{k}$, $b^{(0)}_{k}$, $b^{(1)}_{k}$, $c^{(0)}_{k}$, $c^{(1)}_{k}$, d₀ and d₁ are unknown amplitudes. The last two terms in the solution for $\zeta \left ({z, t} \right )$ (8) are a particular solution to the normal stress balance condition (3) for even and odd mod, respectively. Modes parity means the parity of the functions (6)-(8) with respect to a change in the sign of the z coordinate. These expressions are equivalent to the similar solutions obtained in Alabuzhev (2016) for λ_u = λ_b = λ.

Substituting solutions (6)-(8) into the problem (2)-(5), we obtain the expressions for the unknowns amplitudes:

$$ \begin{array}{@{}rcl@{}} d_{0}&=&\frac{\left( N_{u}-N_{b} \right)L}{M_{b}N_{u}+M_{u}N_{b}}, \quad d_{1}=\frac{\left( M_{u}+M_{b} \right)L}{M_{b}N_{u}+M_{u}N_{b}},\\ M_{j}&=&M+\lambda_{j}B, \quad N_{j}=N-\lambda_{j}A, \enskip j=u,b, \\ M&=&\omega^{2} \sum\limits_{k = 1}^{\infty} \frac{(-1)^{k} f_{k}}{{\varOmega}^{(0)2}_{k}-\omega^{2}} - f_{0} +\cos\left( {\frac{1}{2b}} \right), \end{array} $$

$$ \begin{array}{@{}rcl@{}} N&=&\omega^{2} \sum\limits_{k = 0}^{\infty} \frac{(-1)^{k} g_{k}}{{\varOmega}^{(1)2}_{k}-\omega^{2}} + \sin\left( {\frac{1}{2b}} \right), \\ L&=&\omega^{2}\left( \rho_{i} - \rho_{e} \right) \sum\limits_{k = 0}^{\infty} \frac{(-1)^{k} {\varOmega}_{k}^{(1)2} l_{n}}{ {\left( (2k+1)^{2} \pi^{2} b^{2} - 1 \right)} {\left( {\varOmega}^{(1)2}_{k} - \omega^{2} \right)} }, \\ A&=&\frac{1}{2i\omega b}\cos \left( {\frac{1}{2b}} \right), \quad B = \frac{1}{2i\omega b}\sin \left( {\frac{1}{2b}} \right), \\ c^{(0)}_{0}&=&-f_{0}d_{0}, \quad c^{(0)}_{k}=\frac{\omega^{2} f_{k} d_{0}}{{\varOmega}^{(0)2}_{k}-\omega^{2}}, \\ c^{(1)}_{k}&=&\frac{\omega^{2} g_{k} d_{1}}{{\varOmega}^{(1)2}_{k}-\omega^{2}}- \frac{ \omega^{2}\left( \rho_{i}-\rho_{e}\right){\varOmega}_{k}^{(1)2} l_{n}}{ {\left( (2k+1)^{2} \pi^{2} b^{2}-1 \right)} {\left( {\varOmega}^{(1)2}_{k}-\omega^{2} \right)} }, \\ a^{(0)}_{k}R^{0i}_{kr}(1)&=& \omega \left( {c^{(0)}_{k}+f_{k} d_{0} }\right), \\ a^{(1)}_{k}R^{1i}_{kr}(1)&=& \omega \left( {c^{(1)}_{k}+g_{k} d_{1} }\right), \\ -\rho_{i}\omega^{2}a^{(0)}_{0}&=&c^{(0)}, \quad \quad a^{(0)}_{k}R^{0i}_{kr}(1)=b^{(0)}_{k}R^{0e}_{kr}(1), \\ b^{(0)}_{0}&=&0, \quad a^{(1)}_{k}R^{1i}_{kr}(1)={b^{1}_{k}}R^{1e}_{kr}(1), \\ {\varOmega}^{(0)2}_{k}&=&\frac{4\pi^{2} k^{2} b^{2}-1}{\rho_{i} \frac{R^{(0i)}_{k} (1)}{R^{(0i)}_{kr} (1)}-\rho_{e} \frac{R^{(0e)}_{k} (1)}{R^{(0e)}_{kr} (1)}}, \\ {\varOmega}^{(1)2}_{k}&=&\frac{(2k+1)^{2} \pi^{2} b^{2}-1}{\rho_{i} \frac{R^{(1i)}_{k} (1)}{R^{(1i)}_{kr} (1)}-\rho_{e} \frac{R^{(1e)}_{k} (1)}{R^{(1e)}_{kr} (1)}}, \\ R^{(0i)}_{kr} (r)&=&\frac{d}{dr}I_{k}\left( { 2k \pi b r} \right), \\ R^{(1i)}_{kr} (r)&=&\frac{d}{dr}I_{k}\left( { \left( {2k + 1} \right)\pi b r} \right), \\ R^{(0e)}_{kr} (r)&=&\frac{d}{dr}K_{k}\left( { 2k \pi b r} \right),\\ R^{(1e)}_{kr} (r)&=&\frac{d}{dr}K_{k}\left( { \left( {2k + 1} \right)\pi b r} \right), \end{array} $$

(9)

where f_k, g_k and l_k are the coefficients of the Fourier series expansions of the functions ${\cos \limits } \left ({b^{(-1)} z} \right )$, ${\sin \limits } \left ({b^{(-1)} z} \right )$ and z, respectively, ${\varOmega }^{(0)}_{k}$ and ${\varOmega }^{(1)}_{k}$ are the eigenfrequencies of the drop with a freely moving contact line (i.e., at $\lambda \rightarrow \infty$) (Alabuzhev 2016). In study (Alabuzhev 2016) only odd modes of forced oscillations were detected; in our case, both even and odd modes are excited due to different Hocking parameters.

It is easy to verify that these amplitudes are complex for any set of parameters, except for the limiting cases corresponding to a fixed contact line or a constant contact angle. This fact leads to a phase shift between different shape modes of oscillations, i.e. to the appearance of traveling capillary waves on the lateral surface of the drop. It should be noted that, despite the presence of factors ${{\varOmega }_{k}^{2}}-\omega ^{2}$ in the denominators, the natural frequencies of oscillation of a cylindrical drop Ω_k are not resonant, except for the limiting case of a fixed contact angle (λ_u ≫ 1, λ_b ≫ 1). There are no forced oscillations if the liquids densities are equal, i.e. $\rho _{i}=\rho _{e}$.

Results and discussion

For convenience, we introduce the following notation: ξ(0.5) = ζ_u and ξ(− 0.5) = ζ_b are the oscillation amplitude of the contact line at the “upper” plate and the “bottom” plate respectively, ξ(0) = ζ₀ is the surface oscillation amplitude at z = 0, ξ(0.25) = ζ_q is the surface oscillation amplitudes at z = 0.25, γ_u and γ_b are the inner contact angle, i.e. the contact angle inside the drop, which is counted from the substrate towards the interface, δ_u = γ_u − 0.5π and $\delta _{u}=\gamma _{b}-0.5\pi$ are deviations of the contact angles. In fact, the last expression refers to the boundary angle, which is measured with respect to the interface.

The dependence of the surface oscillations amplitudes and the contact angle are given in Figs. 2, 3 for different values of the Hocking parameter λ_u and the aspect ratio b.

Fig. 2

Plots of the amplitudes of oscillations of the contact lines ζ_u (a) and ζ_b (d), the side-surface position ζ_q (b) and ζ₀ (c), and the contact angles γ_u (e) and γ_b as functions of the frequency ω of the external vibrations for different values of the Hocking parameter λ_b (b = 1, λ_u = 1, ρ_i = 0.7). The cases of λ_b = 0.1, 1 and 10 correspond to the solid, dashed and dotted lines, respectively

Fig. 3

Plots of the amplitudes of oscillations of the contact lines ζ_u (a) and ζ_b (d), the side-surface position ζ_q (b) and ζ₀ (c), and the contact angles γ_u (e) and γ_b as functions of the frequency ω of the external vibrations for different values of the Hocking parameter λ_b (b = 0.32, λ_u = 1, ρ_i = 0.7). The cases of λ_b = 0.1, 1 and 10 correspond to the solid, dashed and dotted lines, respectively

The amplitudes of the drop surface oscillations and the contact angle reach maximum values in the linear resonance mode (Fig. 2). It is also seen from the pictures that the values of the resonant frequencies decrease with an increase of λ_u or λ_b. Despite weak dissipation at small values of the parameter λ_b, the amplitude of contact line oscillations at z = 0.5 is greater than it is at z = − 0.5 (Fig. 2a, d). In the opposite case, for large λ_b, the amplitude of oscillations of the contact line on the “bottom” plate is larger than on the “upper” one. The contact angle varies in a wide range (Fig. 2e, f). It is important to note that if at least one of the parameters λ_u or λ_b is finite, the amplitude of the surface oscillations is always limited. The damping coefficient of the free oscillations is maximum at finite values of the Hocking parameters λ_u = O(1) and λ_b = O(1). Consequently, dissipation is determined by the total contribution of damping ratios and the curves have the shape of a resonance curve (Fig. 2b). The amplitude of the contact line oscillations tends to infinity at $\lambda \rightarrow \infty$, but the amplitude of the drop surface oscillations is also limited to infinity at $\lambda \rightarrow 0$. The damping coefficients are small in these limiting cases. The results for identical plates are discussed in greater detail in paper (Alabuzhev 2016). For example, zero amplitude of the drop surface oscillations is observed at the center of the layer with λ_u = λ_b = 1 (Fig. 2c). In this situation, the external force excites only odd shape modes.

At certain frequencies ω, the motion of a drop does not depend on the parameters λ_{u, b}: the contact line looks like a fixed contact line at any values of λ_{u, b} (Fig. 2). The values of such “anti-resonant” frequencies are determined from the solution (6)-(8):

$$ d_{0}=0, \quad d_{1}=\frac{L}{N}=0, $$

(10)

i.e. L = 0 and this solution yields only odd oscillations modes. In this case the contact line is stationary:

$$ c_{k}^{(1)}=-\frac{\omega^{2}\left( \rho_{i}-\rho_{e}\right){\varOmega}_{k}^{(1)2} l_{n}}{{\left( (2k+1)^{2} \pi^{2} b^{2}-1 \right)}{\left( {\varOmega}^{(1)2}_{k}-\omega^{2} \right)}}, $$

For example, in the limiting case where the contact line is free ($\lambda _{u,b} \to \infty$ and d_0,1 = 0), the amplitudes $c_{k}^{(1)}$ are described by this expression for ${\lambda _{u}} = \lambda _{b} = \lambda$. The amplitude of the k − th harmonic $c_{k}^{(1)}$ begins to increase without limitation and the influence of even weak dissipation becomes significant for $\omega \to {\varOmega }_{k}^{(1)}$.

In the vicinity of the resonance frequency $\omega \approx {\varOmega }_{k}^{(1)}$ the deviation of the surface can be expressed as

$$ \begin{array}{@{}rcl@{}} \zeta = -A_{k} \sin{\left( (2k + 1)\pi z\right)} \cos{\left( {\varOmega}_{k}^{(1)} + \beta_{k}\right)}, \\ A_{k}=\frac{\left( \rho_{i}-\rho_{e}\right){\varOmega}_{k}^{(1)3} l_{n}}{{2\left( (2k+1)^{2} \pi^{2} b^{2}-1 \right)}\sqrt{\left( {\varOmega}^{(1)2}_{k}-\omega^{2} \right)+{\kappa_{k}^{2}}}}, \\ \tan{\beta_{k}}=\frac{\kappa_{k}}{{\varOmega}^{(1)}_{k}-\omega}, \kappa_{k}=\frac{2b^{2}{\varOmega}^{(1)2}_{k}}{\left( (2k+1)^{2} \pi^{2} b^{2}-1 \right)\lambda}. \end{array} $$

Here κ_k is the damping ratio of free oscillations, similar to the attenuation coefficient of natural oscillations (Alabuzhev 2016; Fayzrakhmanova and Straube 2009). The dependence of the amplitude and phase shift of the oscillations on the frequency in the neighborhood of the resonance takes the form, which is typical of the systems with weak dissipation. From the last expression, it follows that at the frequency ${\varOmega }^{(1)}_{k}$ (the resonance frequency shift is proportional to $\lambda ^{-2}$ (Alabuzhev 2016; Fayzrakhmanova and Straube 2009)) the oscillation amplitude takes the maximum value

$$ \max\left( A_{k} \right)=\lambda \frac{\left( \rho_{i}-\rho_{e}\right){\varOmega}_{k}^{(1)} l_{n}}{4b^{2}}. $$

(11)

At the resonance point, the oscillation amplitude increases with increasing mode number and the proportionality coefficient for a large wetting parameter is $(2k+1)^{-2}{\varOmega }_{k}^{(1)}$. These conclusions are valid for λ𝜖 ≪ 1. In the limiting case where the contact line is fixed, the solution is given by the general formulas (6)-(9), but the coefficients $c^{(0),(1)}_{k}$ and d_0,1 are real, i.e. the oscillations of the substrate and droplet occur in the same phase.

Vibrations excite both odd and even longitudinal vibrational modes (along the symmetry axis z) as noted above. Odd modes exist only with equal Hocking parameters $\lambda _{u}=\lambda _{b}=\lambda$ (see Alabuzhev (2016)). As a result, each shape oscillation mode has two close resonant peaks (see Figs. 2, 3). The amplitude of the “odd” peak is greater than that of the “even” peak because the vibration force pumps energy into the shape odd modes. This energy is redistributed into an even mode due to the difference in the properties of the surfaces (in fact, due to dissymmetry with respect to the coordinate z). Resonance amplitudes can be comparable in the center of the layer (at z = 0.5), since the amplitude of the “odd” peak is zero for equal Hocking parameters. Moreover, these peaks are more observable at large values of the parameter λ.

Let’s consider the case of close values of Hocking parameters: λ_u = λ + β, λ_b = λ, β ≪ λ. The amplitudes d₀ and d₁ defined in the solution (9) are represented as

$$ \begin{array}{@{}rcl@{}} d_{0}=\frac{\beta a B}{2\left( {M+\lambda B } \right)}, \quad d_{1}=a+\frac{\beta a A}{2\left( {N-\lambda A} \right)}, \\ a=\frac{L}{\left( {N-\lambda A} \right)}, \end{array} $$

so the correction to amplitude of the shape modes are proportional to β. Nevertheless, the resonance can occur at the frequencies of even modes and the resonance amplitude will be noticeable. In the limiting cases of large and small parameters λ_b ($\lambda _{u}=\mathcal {O}(1)$), the solution (9) takes on a simpler form:

$$ \begin{array}{@{}rcl@{}} \lambda_{b} \to \infty : \\ d_{0}=\frac{AL}{N_{u}B-M_{u}A }, \quad d_{1}=\frac{BL}{N_{u}B-M_{u}A }, \\ \lambda_{b} \to 0 : \\ d_{0}=-\frac{\lambda_{u}AL}{N_{u}M+M_{u}N}, \quad d_{1}=\frac{\lambda_{u}BL}{N_{u}M+M_{u}N}. \end{array} $$

Even in the dissipationless case of limiting resonant frequencies (a fixed contact line or a fixed contact angle on the bottom plate), these amplitudes will be finite. As b decreases, the eigenfrequency of the first mode can vanish in a certain interval of the values of the Hocking parameter λ_u (λ_b is fixed) (Alabuzhev and Lyubimov 2007; Alabuzhev and Kashina 2019). The width of this interval decreases with increasing the aspect ratio b. The reason for frequency vanishing is following: damping is so intensive (the parameter λ_u is finite) that the excitation of free oscillations becomes impossible. For the surface modes of eigenoscillations, the energy dissipation is proportional to the surface area of the drop (the kinetic energy of drop oscillations is proportional to the drop volume and the energy of surface waves is proportional to the area of the drop surface). Therefore, for a fixed volume of the drop, an increase of value b corresponds to a decrease of the area of the side surface of the drop, i.e., lower dissipation for surface waves. At higher frequencies, this effect appears when the aspect ratio b < π^− 1 (Alabuzhev and Lyubimov 2007; Alabuzhev and Kashina 2019), which corresponds to one half of the wavelength of the Rayleigh-Plateau instability for a liquid liquid column for h^∗ = 2πR^∗, i.e., for b = (2π)^− 1 (Plateau 1863; Rayleigh 1892). Thus, for b = π^− 1, the critical thickness of the layer (and the height of the cylindrical drop) is equal to the Rayleigh-Plateau instability half-wavelength. As a result, the first resonant maximum disappears at a minimum value b = 0.32 (Fig. 3) and exist at b = 1 (Fig. 2). The values of eigenfrequencies decrease with decreasing the aspect ratio b, therefore, the resonant peaks are shifted to the left along ω–axis.

Figure 4 shows the profile of the lateral surface (Fig. 4a,e,i), the contact line (Fig. 4b,c,f,g,j,k) and changes in the internal contact angle (Fig. 4d,h,l) for several values ω and λ_{u, b} at different moments of the oscillation period. The shape of the drop surface depends on the frequency of the vibrational field. For example, in Fig. 4, most of the vibration energy at a given frequency ω ≈ 10 (see Fig. 2a) is transferred to the lowest shape mode at λ_u = 1, λ_b = 0.1 (Fig. 2a) and the resonance frequency ω ≈ 7 is at λ_u = 1, λ_b = 10. The case of “anti-resonant” frequency ω ≈ 25 (λ_u = λ_b = 1) is also shown in Fig. 2e-h.

Fig. 4

Evolution of the drop surface shape (a,e,i), the shape of the contact line (b,c,f,g,j,k) and the contact angles (d,h,l). T = 2πω^− 1 is the oscillation period (b = 1, ρ_i = 0.7, λ_u = 1, 𝜖 = 0.1), (a-d) ω = 10, λ_b = 0.1, (e-h) ω = 25, λ_b = 1, (i-l) ω = 7, λ_b = 10, (a-c, e-g,i-k) t = 0 – solid line, t = 0.125T – dashed , t = 0.25T – dotted, t = 0.375T – dash-dotted

The drop shape is described by an odd function in the most cases (see Fig. 4a,e,i), despite the presence of two sets of spatial harmonics (odd and even) in the solution (6)–(8). The combination of even and odd functions describes the shape of a drop in the vicinity of “even” resonances (see Fig. 5a). Thus, the odd vibrations contain most of the energy. However, the wave propagation patterns along the lateral surface are significantly different in these two cases. Figures 5b-d show variations of the wave crest position. In the case of an odd droplet shape the waves propagate in the limited areas (Fig. 5c,d). They propagate along the entire surface in the absence of symmetry (Fig. 5b), i.e. the amplitude of even vibrations is comparable to the amplitude of odd harmonics or even more.

Fig. 5

Evolution of the drop surface shape (a) and propagation of waves along the drop surface (b-d). T = 2πω^− 1 is the oscillation period (b = 1, ρ_i = 0.7, λ_u = 1), (a,b) ω = 19, λ_b = 0.1, 𝜖 = 0.1, (c) ω = 7, λ_b = 10, (d) ω = 7, λ_b = 1, (a) t = 0 – solid line, t = 0.125T – dashed , t = 0.25T – dotted, t = 0.375T – dash-dotted

Conclusion

The behavior of a cylindrical drop confined between solid plates has been considered taking into account the dynamics of the contact angle under axisymmetrical vibrations. The solid plates have different Hocking parameters. The boundary condition imposed on the contact line leads to the damping of oscillations. In addition, there is a phase shift between the oscillations of different parts of the liquid, which leads to the appearance of traveling capillary surface waves.

It is shown that an external force excites both the odd and even spatial harmonics of oscillations due to different values of Hocking parameters on the plates. The equality of these parameters implies the occurrence of odd harmonics, only.

The study of forced vibrations revealed the existence of resonance phenomena. Vibrations excite both the odd and even longitudinal oscillation modes and as a result, each shape oscillation mode has two close resonant peaks. It is shown that dissipation at the contact line leads to a limitation of the maximum amplitude of oscillations in the resonance mode, as well as to a shift of the resonance frequency. At finite values of the Hocking parameter λ, due to dissipation in the process of the contact line motion, the amplitude of oscillations remains limited.

In most cases, the drop shape is described by an odd function, despite the presence of two sets of spatial harmonics (odd and even) in the solution. The combination of even and odd functions describes the shape of a drop near “even” resonances. Thus, the odd vibrations contain most of the energy. It is shown that the patterns of capillary wave propagation along the lateral surface are significantly different in these two cases. Capillary waves propagate in the limited areas in the case of an odd droplet shape and along the entire surface in the absence of symmetry, i.e. the amplitude of even vibrations is comparable to the amplitude of odd harmonics or even more.

The eigenfrequency of the first mode can be vanishes in a certain interval of the values of the Hocking parameter λ_{u, b}. The reason for frequency vanishing is that damping is so intensive that the excitation of free oscillations is impossible: for the surface modes of eigenoscillations, the energy dissipation is proportional to the surface area of the drop (the kinetic energy of drop oscillations is proportional to the drop volume and the energy of surface waves is proportional to the area of the drop surface). As a result, the first resonant maximum disappears at small values of the aspect ratio (radius-to-height ratio) b. Thus, one can set such an aspect ratio of the drop that the characteristic frequency of any mode is equal to zero, and, ultimately, determine the Hocking parameter λ.