Introduction

The oscillations of a fluid drops (or a gas bubbles) on a substrate and methods of controlling such objects have been the focus of many research works. For example, the forced oscillations of a hemispherical droplet on the substrate subjected to tangential and normal vibrations are studied in Mettu and Chaudhury (2012) and Sudo et al. (2010). A review of studies into the behavior of a drop on the dielectric substrate (EWOD) in an alternating electric field is given in Mugele and Baret (2005). The influence of liquid evaporation from the droplet surface on the oscillations of sessile drop was investigated in Korenchenko and Beskachko (2013) and Sanyal and Basu (2016). The effect of the substrate surface properties on the motion of a drop lying on the inclined surface was studied in Savva and Kalliadasis (2013) and Savva and Kalliadasis (2014). Studies of oscillations of a liquid bridge (Liang and Kawaji 2009; Shevtsova and Melnikov 2006) and a cylindrical drop (Alabuzhev and Lyubimov 2005; Demin 2008) are of interest not only because of a variety of peculiar effects in such systems, but also for technological reasons.

The research of drop oscillations involves the study of the motion of the contact line of three immiscible media, such as the solid-liquid-gaseous contact line or the solid-liquid-liquid contact line (Brutin et al. 2009; Diana et al. 2012; Fernandez et al. 2017; van Lengerichal and Steen 2012). Despite widespread use of wetting in modern technologies, this phenomenon is not well understood, since the interfacial interaction significantly depends on the impurities contained in the examined system and the state of the surface (roughness, dislocations).

When considering the high-frequency vibrational motion of a contact line, the effect of viscosity becomes significant only in thin boundary layers near a solid surface, and the motion of the contact line is determined mainly by a rapidly oscillating pressure field. Thus, the inviscid behavior of a liquid in the drop core can be considered, taking into account only the viscosity of the dynamic boundary layer near the solid substrate. Complex processes occurring in the immediate vicinity of the contact line are excluded from consideration by imposing the effective boundary conditions on the dynamics of the visible contact angle (Bostwick and Steen 2014; Zhang and Thiessen 2013).

Damping of standing waves on the surface of a liquid between two vertical walls was studied in Hocking (1987). The effective boundary condition describing the dynamics of the contact line assumes that the relationship between the velocity of the contact line and the deviation of the contact angle from the equilibrium value (for simplicity, this angle is considered equal to 90o) is linear:

$$ \frac{{\partial {\zeta^{*}}}}{{\partial {t^{*}}}} = {{\Lambda}^{*}}\mathbf{k} \cdot \boldsymbol{\nabla}{\zeta^{*}} $$
(1)

where ζ ∗ is the deviation of the interface from the equilibrium position, k is the external normal to the solid surface, Λ∗ is a phenomenological constant (the so-called wetting parameter or Hocking parameter) having the dimension of the velocity. The accepted boundary conditions (1) are associated with two important constraints: (a) ζ ∗ = 0 the requirement of a fixed contact line (pinned-end edge condition), (b) k ⋅∇ ζ ∗ = 0 a constant contact angle. A qualitative comparison with experimental work is also carried out in this work . It was shown that appreciable discrepancies between the experimentally measured damping decrements of oscillations and their theoretical values obtained in other studies (only viscous friction in the boundary layer was taken into account) can be explained by energy dissipation in the vicinity of the contact line.

Condition (1) was used, for example, to study the oscillations of a hemispherical droplet of an incompressible liquid on a substrate (Lyubimov et al. 2004, 2006), a hemispherical gas bubble in a liquid of finite depth on a substrate (Shklyaev and Straube 2008), a cylindrical drop in an infinite volume of liquid (Alabuzhev and Lyubimov 2007), a cylindrical bubble in a liquid of a finite volume (Alabuzhev 2014; Alabuzhev and Kaysina 2015), a ”sandwiched” droplet (having the shape of a rotation figure) (Alabuzhev and Lyubimov 2012) and a capillary bridge in weightlessness (Borkar and Tsamopoulus 1991). In all the works listed, it was shown that the damping of the oscillations is mainly due to the motion of the contact line (with the exception of the limiting cases of a fixed contact line and a fixed edge angle). In Miles (1991), it was assumed that a change in the contact line does not necessarily occur in one phase with a contact angle, i.e. the Hocking constant is complex.

The condition of the fixed contact line, which is the limiting case (1), was used to study the natural oscillations of a capillary bridge (liquid zone) in a gravity field (Demin 2008) and the parametric instability of a semicylindrical drop of a weakly viscous liquid on a substrate (Kartavyh and Shklyaev 2007). Another limiting case, namely, a fixed contact angle, was considered, for example, in the study of oscillations of a compressible hemispherical droplet on a substrate (Ivantsov 2012) and a cylindrical drop of an incompressible fluid under multifrequency vibrations (Alabuzhev and Lyubimov 2005).

In experiments (Ting and Perlin 1995; Perlin et al. 2004), the investigation of the motion of a solid-liquid contact line along a vertical solid wall was made with intent to obtain a phenomenological formula for the Hocking parameter, which was a variable. It was shown that for small-amplitude oscillations (small Reynolds numbers) the behavior of the contact line is well described by the condition specified by the contact line. With increasing amplitude the contact line is found to be in the slippage mode, i.e. the contact line is moving.

Another important problem is non-uniform wetting of the surface along which the contact line moves (Savva and Kalliadasis 2013, 2014). Heterogeneous substrates can cause different effects (Brunet et al. 2007), for example, hysteresis of the contact angle (Fayzrakhmanova and Straube 2009; Fayzrakhmanova et al. 2011).

In this article, we consider the axisymmetrical oscillations of cylindrical fluid drop, which is surrounded by another ideal liquid. We assume that the Hocking parameter is a function of coordinates. The natural and forced axisymmetrical oscillations of the cylindrical drop for the case of uniform plates were investigated in Alabuzhev (2016) and Alabuzhev and Lyubimov (2007).

Problem Formulation

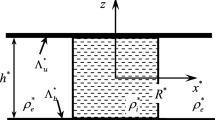
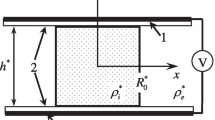
Following (Alabuzhev 2016; Alabuzhev and Lyubimov 2007), consider the oscillations of an incompressible fluid drop of density \( \rho_{i}^{*} \) and kinematic viscosity \( \nu_{i}^{*} \) surrounded by another fluid of density \( \rho_{e}^{*} \) and kinematic viscosity \( \nu_{e}^{*} \). The system is bounded by two parallel solid surfaces which are separated by a distance h ∗ (see Fig. 1). In equilibrium the drop has a circular cylindrical form with radius \( r_{0}^{*} \). The equilibrium contact angle 𝜗 0 is equal to 0.5π. The system is subjected to a vibration field with amplitude A ∗ and frequency ω ∗. The vibration force is directed parallel to the symmetry axis of the drop. We assume that the frequency is high enough to neglect the dissipative effects caused by acoustic radiation and viscous dissipation, i.e. ω ∗ \( R_{0}^{*} \) ≪ c and \(\delta =\sqrt {\nu ^{*}/\omega ^{*}}\), where c is the sound velocity, δ is the viscous boundary-layer thickness. The amplitude of the external force is considered small in the sense that A ∗ ≪ \( R_{0}^{*} \).

Fig. 1
figure 1

Problem geometry. 1 – surrounding liquid, 2 – drop

Full size image

We work in cylindrical coordinates r ∗, α and z ∗ because of the problem symmetry. Let the lateral surface of the drop be described by \(r^{*}=r^{*}_{0}+\zeta ^{*}\left (z^{*},t^{*}\right )\), where ζ ∗ is the surface deviation from equilibrium. In the accepted approximations the liquid motion is irrotational, which is convenient for introducing the velocity potential. Thus, the dynamics of the liquid is described by the Bernoulli and Laplace equations. We use the following quantities as the measurement units: \( r_{0}^{*} \) for length, h ∗ for height, \({\sigma ^{- 1/2}}\sqrt {\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )r_{0}^{*3}}\) for time, \({A^{*}}\sqrt \sigma {\left ({\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )r_{0}^{*3}} \right )^{- 1/2}}\) for velocity, \({A^{*}}{r^{*}_{0}}\sqrt \sigma {\left ({\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )r_{0}^{*3}} \right )^{- 1/2}}\) for velocity potential, \({A^{*}}\sigma {\left ({r_{0}^{*}} \right )^{- 2}}\) for pressure, A ∗ for surface deviation. The amplitude of oscillations is given as 𝜖 = A ∗/\( r_{0}^{*} \) ≪ 1, which allows us to linearize the governing equations and simplify the boundary conditions. Thus, the dimensionless linear boundary value problem is determined by

$$\begin{array}{@{}rcl@{}} {p_{j}} \!&=&\! - {\rho_{j}}\left( \frac{\partial \varphi_{j}}{\partial t}-\omega^{2} z e^{i\omega t} \right), \,\,{\Delta} {\varphi_{j}} \,=\, 0, j \,=\, i,e, \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} {\Delta} \!&=&\! \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{\partial }{{\partial r}}} \right) \,+\, \frac{1}{{{r^{2}}}}\frac{{{\partial^{2}}}}{{\partial {\alpha^{2}}}} \,+\, {b^{2}}\frac{{{\partial^{2}}}}{{\partial {z^{2}}}}, \\ r \!&=&\! 1: \left[\frac{\partial \varphi}{\partial r}\right] \,=\, 0, \frac{\partial \zeta}{\partial t} \,=\, {\varphi_{r}}, \left[ p \right] \,=\, \zeta \,+\,\frac{\partial^{2} \zeta}{\partial \alpha^{2}} \,+\, {b^{2}}\frac{\partial^{2} \zeta}{\partial z^{2}}, \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} z \!&=&\! \pm \frac{1}{2}: \frac{\partial \varphi}{\partial z} \,=\, 0, \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} r \!&=&\! 1, z \,=\, \pm \frac{1}{2}: \frac{\partial \zeta}{\partial t} \,=\, \mp \lambda \left( \alpha \right) \frac{\partial \zeta}{\partial z}, \end{array} $$
(5)

where p is the fluid pressure, \(\lambda \left (\alpha \right )\) describes the heterogeneity condition for plates, the square brackets denote the jump in the quantity at the interface between the external liquid and the drop. The boundary-value problem (2)-(5) involves five parameters:

the aspect ratio – b = r 0 h −1,

the dimensionless densities – \({\rho _{i}} = \rho _{i}^{*}{\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )^{- 1}}\) and \({\rho _{e}} = \rho _{e}^{*}{\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )^{- 1}}\),

the wetting parameter – λ =Λ∗ bσ −1/2 \(\sqrt {\left ({\rho _{e}^{*} + \rho _{i}^{*}} \right )r_{0}^{*}}\),

the frequency – ω = ω ∗ σ −1/2 \(\sqrt {\left (\rho _{e}^{*} + \rho _{i}^{*} \right )r_{0}^{*3}} \).

Natural Oscillations

It is convenient to begin our investigation with a consideration of the natural oscillations of a cylindrical drop. Later we will focus on the even azimuthal oscillation modes governed by the function \(\lambda \left (\alpha \right )\) and odd vertical modes due to the external force. The system of equations and boundary conditions (2)–(5) can be written without considering the vibrational force. The fields of velocity potentials and surface deviation can be represented as

$$\begin{array}{@{}rcl@{}} {\varphi_{i}}\left( {r,\alpha,z,t} \right) &=& Re \left( i{\Omega} \sum\limits_{m,k = 0}^{\infty} {F_{mk}\left( r,\alpha, z\right) {e^{i{\Omega} t}}} \right), \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} {\varphi_{e}}\left( {r,\alpha,z,t} \right) &=& Re \left( i{\Omega} \sum\limits_{m,k = 0}^{\infty} { G_{mk}\left( r,\alpha, z\right) {e^{i{\Omega} t}}}\right), \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} \zeta \left( {z,t} \right) &=& Re \left( {\left( {\sum\limits_{m,k = 0}^{\infty} {{c_{mk}}{Z_{k}}\left( z \right){A_{m}}\left( \alpha \right)} } \right. + {d_{0}}\sin \left( {\frac{z}{b}} \right) + } \right. \\ &&\left. \left. + \sum\limits_{m = 1}^{\infty} {{d_{m}}\sinh \left( {\frac{{\sqrt {4{m^{2}} - 1} }}{b}z} \right){A_{m}}\left( \alpha \right)} \right){e^{i{\Omega} t}} \right), \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} F_{mk}(r,\alpha, z)&=&{a_{mk}}R_{mk}^{i}\left( r \right) Z_{n}\left( z\right) A_{m}\left( \alpha\right), \\ G_{mk}(r,\alpha, z)&=&{b_{mk}} R_{mk}^{e}\left( r \right) Z_{n}\left( z\right)A_{m}\left( \alpha\right), \\ R_{mk}^{i}(r)&=&I_{m}({\left( {2k + 1} \right)\pi b r}), \\ R_{mk}^{e}(r)&=&K_{m}({\left( {2k + 1} \right)\pi b r}), \\ Z_{n}\left( z\right)&=&\sin {\left( {\left( {2k + 1} \right)\pi z} \right)}, A_{m}\left( \alpha\right) = \cos \left( {2m\alpha } \right), \end{array} $$

where F m k (r, α, z) and G m k (r, α, z) are eigenfunctions of the Laplace operator, I m and K m are the modified Bessel functions of m-th order. Substituting solutions (6)–(8) into (2)–(5), we obtain a spectral-amplitude problem, whose eigenvalues are values of the natural oscillation frequency Ω. These complex algebraic equations have complex solutions, which lead to damping of oscillations. This attenuation is caused only by the condition on the contact line, not by viscosity. We also note that damping times are of the order of magnitude comparable with the period of oscillation, i.e. at a finite value of the wetting parameter, the droplet is able to execute only a few oscillations.

For an arbitrary value of λ, the equations of our spectral-amplitude problem were solved numerically by the two-dimensional secant method. By analogy with Alabuzhev and Kaysina (2015), for convenience we will denote the frequencies of the even modes as Ω m,2k (k = 0, 1, 2, …), and the frequencies of the odd modes as Ω m,2k+ 1 (k = 0, 1, 2, …). Here, the first index m is a azimuthal number and the second index 2k (or 2k + 1) is wavenumber. Thus, the frequencies Ω m,n of the natural oscillations with the odd index n will correspond to the odd modes and an even index n to the even mode.

The dependence of the natural frequency \(Re\left ({\Omega }\right )\) and the damping decrement \(Im\left ({\Omega }\right )\) of several first modes on the Hocking parameter λ for various values of the geometric parameter is shown in Figs. 2, 3 and 4. Note that only one solution of \(Re\left ({\Omega }\right )\) is constructed, the conjugate solution (even with respect to the abscissa axis) is not shown in the graphs. It can be seen from Figs. 2–4. that, except for the axisymmetrical mode, the frequencies decrease monotonically with increasing λ: the drop with the fixed contact line has the highest frequency, and the smallest with a fixed contact angle. Damping decimals have a maximum at a finite capillary parameter, and is limited to zero for \(\lambda \rightarrow 0\) and \(\lambda \rightarrow \infty \). As the aspect ratio b increases, the values of the frequencies \(Re\left ({\Omega }\right )\) and decrements \(Re\left ({\Omega }\right )\) increase.

Fig. 2
figure 2

Frequency (a) and damping ratio (b) of natural oscillations vs wetting parameter λ for Ω01 \(\left (b = 1, \rho _{i}= 0.7 \right )\). λ = λ 0 – solid line, k λ = 0.1 – dashed, k λ = 1 – dot-dashed, k λ = 10 – dotted

Full size image
Fig. 3
figure 3

Frequency (a) and damping ratio (b) of natural oscillations vs wetting parameter λ for Ω21 \(\left (b = 1, \rho _{i}= 0.7 \right )\). λ = λ 0 – solid line, k λ = 0.1 – dashed, k λ = 1 – dot-dashed, k λ = 10 – dotted

Full size image
Fig. 4
figure 4

Frequency (a) and damping ratio (b) of natural oscillations vs wetting parameter λ for Ω01 \(\left (b = 0.4, \rho _{i}= 0.7 \right )\). λ = λ 0 – solid line, k λ = 0.1 – dashed, k λ = 1 – dot-dashed, k λ = 10 – dotted

Full size image

The frequency \(Re\left ({\Omega }_{0,1}\right )\) of the zero-th mode of natural oscillations shows a very interesting feature: this frequency can vanish over a certain interval of the Hocking parameter (Fig. 4). The width of this interval decreases with increasing b (Figs. 2 and 4). On this interval, the damping rate \(Im\left ({\Omega }_{0,1}\right )\) has three values (Fig. 4), and the boundaries of the interval correspond to the branch points of the solution \(Im\left ({\Omega }_{0,1}\right )\). The reason of vanishing frequency is the dissipation (the parameter λ is finite), which is so high that the oscillations become impossible: for surface modes (n > 0) of natural oscillations, the dissipation power is proportional to the area of the lateral surface (the larger the surface, the more energy is needed for surface waves, and the energy of the droplet oscillations is proportional to volume). Consequently, for a constant droplet volume, an increase in the geometric parameter b corresponds to a decrease in the lateral surface of the drop, that is, a decrease in the dissipation contributing to surface oscillations. We note that the frequency nullification effect also exists for other higher modes of oscillation. However, this effect manifests itself above the threshold of the Rayleigh-Plateau instability of the fundamental mode.

Note that the frequency of the volumetric oscillations of the bubble (Alabuzhev 2014) and the fundamental frequencies of the azimuthal modes (n = 0) of the drop (Alabuzhev and Lyubimov 2007; Lyubimov et al. 2004) can vanish, beginning with a certain value of the aspect ratio b, over a certain range of values λ, and the length of this interval increases with increasing b. In this case, the dissipation power is proportional to the length of the contact line, since it is the interaction of the contact line and the solid substrate that causes dissipation. Consequently, with increase of the parameter b at a constant volume of the drop, the length of the contact line increases, which leads to a growth of dissipation.

The wavenumber k λ plays the role of an effe ctive wetting coefficient λ. The small parameter λ fits the strong interaction of the contact line with the substrate and the small amplitude of the oscillations (see Figs. 2–4). Consequently, the long-wave heterogeneity of the substrate leads to a decrease in the oscillations amplitude. Also, the long-wave heterogeneity of the plate suppresses the effect of frequency zeroing see Fig. 4).

Forced Oscillations

Here we consider the problem of forced oscillations. The solution in this case is similar to solution (6)–(8) with exception for the time dependence: oscillation frequency is the forced frequency ω.

The dependence of the surface oscillations amplitude at the upper plate ζ, the shape of the contact line and deviation of the contact angle with the upper plate γ = 𝜗 − π on the forced frequency ω is given in Figs. 5 and 6 for different values of the Hocking parameter λ 0 and of the aspect ratio b. Note that the curves have a resonant shape in the limiting case λ 0 → 0. The amplitude of the contact line oscillations limits to infinity for \({\lambda _{0}} \rightarrow \infty \). Results for homogenous plates can be seen in Alabuzhev (2016) and Lyubimov et al. (2004) more details.

Fig. 5
figure 5

Deviation of contact line (a-c) and contact angle at upper plate (d-f) vs frequency. (b = 1, ρ i = 0.7), λ = λ 0– solid line, k λ = 0.1– dashed, k λ = 1 – dash-dotted, k λ = 1 – dotted, (a,d) – λ 0 = 0.01, (b,e) – λ 0 = 1, (c,f) – λ 0 = 100

Full size image
Fig. 6
figure 6

Deviation of the contact line (a-c) and contact angle at the upper plate (d-f) vs frequency. (b = 0.4, ρ i = 0.7), λ = λ 0– solid line, k λ = 0.1– dashed, k λ = 1 – dash-dotted, k λ = 1 – dotted, (a,d) – λ 0 = 0.01, (b,e) – λ 0 = 1, (c,f) – λ 0 = 100

Full size image

The first frequency of axisymmetric mode is excited first (Figs. 5 and 6) for any wavenumber k. This mode exists at λ 0 = 1 and b = 1 and the first resonance peak corresponds to first axysimmetrical frequency (Fig. 5a and b). Note that there are antiresonance frequencies such that the contact line amplitude goes to zero. The contact angle also remains intact at these points (Fig. 5). As it has been shown above, the first mode disappears at some parameters λ 0, b and k λ (Figs. 4a and 6b). Figures 5 and 6 show how the amplitude of the contact line changes with increase in the wavenumber k. Value of k λ plays the role of an effective wetting parameter, the same as λ 0.

Conclusions

The behavior of cylindrical drop between solid plates has been considered taking into account the dynamics of the contact angle under axisymmetrical vibrations. The solid plates have nonuniform surfaces described by function \(\lambda \left (\alpha \right ) = {\lambda _{0}}\left | {\sin \left ({k_{\lambda }\cos \left (\alpha \right )} \right )} \right |\). The main purpose of this paper is to develop a method for studying the drop forced oscillation on an inhomogeneous substrates and determining λ. The investigation of natural oscillations has shown that the wavenumber k λ plays the role of effective wetting parameter. Also the main frequency of axial mode may not disappear at different values of k λ , in contrast to the homogeneous case.

For small values of the parameter λ 0, i.. with a weak energy dissipation, the amplitude of the surface forced oscillations is large and tends to infinity in the limit λ 0 → 0 or \({\lambda _{0}} \to \infty \). The amplitude of the contact line oscillations is finite for any values of λ 0 except \({\lambda _{0}} \to \infty \). There are ”antiresonant” frequencies, i.e. such vibration frequencies, for which the contact line does not move for any values of λ 0, and the contact angle does not change. Moreover the change in the drop volume (i.e. aspect ratio b) can suppress resonances.