Abstract
The main motive and, at the same time, the goal of this work is to investigate a revisited Nicholson’s blowflies equation that involves a time varying delay and an iterative term. We make use of Schauder’s fixed point theorem to tackle the existence of positive periodic solutions and under an additional condition, we apply the Banach contraction principle for establishing the existence, uniqueness and stability results. Finally, we give two examples to illustrate the effectiveness of our main results that are completely new and complement some earlier investigations to some extent.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This work fits into the overall framework of the study of delayed phenomena in population dynamics. More precisely, the study carried out in this article concerns one of the most important biological models Nicholson’s blowflies model which describes the evolution, over time, of populations of a sheep blowfly called Lucilia cuprina. Despite its harmless appearance, Lucilia cuprina is a parasitic fly of major global economic importance since it is responsible for \(90\%\) of severe sheep illnesses or what they are commonly referred to as flystrikes. This dipteran fly causes significant economic losses amounting to hundreds of millions of dollars per year for the animal, food and textile industries in many parts of Europe, North America , Australia as well as several countries such as New Zealand and South Africa. To be honest, the fly itself is harmless, as the adult fly usually feeds on pollen and nectar, but the danger lies in its maggots that cause fatal cutaneous infections in the lamb. More precisely, after the hatching of maggots from fly eggs that are laid on the skin of the host, they start to parasitize and invade the living flesh for feeding off excretions and damaged tissues and hence creating painful wounds that can lead to the death of the lamb if it has left without treatment.
For sheep farmers, Lucilia cuprina is difficult to fight and the strategies for fighting against it, have until now been based on preventive approaches wether chemical, mechanical or biological ones. For instance, they have used and still use the mulesing which is a very painful and inexpensive surgical procedure for reducing the risk of the flystrike. It consists of removing parts of the skin from around the lamb’s breech and cutting its tail by means of special sharp shears for leaving a smooth and glabrous epidermis and hence avoiding the aggression of maggots. They have also tried to use organochlorine insecticides such as cyclodienes (dieldrin) to reduce fly breeding. But unfortunately this blowfly has rapidly developed resistance to chemical treatments. On the other hand, some scientists have adopted the sterile insect technique by changing the characteristics of male insects, while others have chosen to use a more-efficient and less-costly approach where larvae have been modified to be dependent on the tetracycline. In the absence of this antibiotic, the female larvae will die before reaching the pupal stage and the male ones will transmit this lethal dependence on the antibiotic to their female offspring. Unfortunately, this technique has also been abandoned, mainly due to high costs and hence the mulsing remains the only current preventive measure.
In the early fifties of the last century, the famous entomologist Alexander. John. Nicholson has conducted a series of experiments aimed at tackling this serious problem by studying the dynamics of this annoying fly. As a result of his laboratory researches, he observed a regular periodic oscillation of about 35 to 40 days which corresponds to a delay ranging from 9 to 15 days. Gurney et al. [10] have modelled mathematically these experiments where they have proposed the following first-order differential equation with a constant delay:
with \(x\left( t\right) \) represents the size of the population of sexually mature flies at time t, \(\beta \) is the maximum egg production per fly per day, k is the maximum number of the Australian sheep blowflies that the environment can support, \(\alpha \) is the mortality rate and \(\tau \) is the time needed to complete the four life cycle stages, starting with the oviposition and ending with the emergence of new flies from pupae.
It’s worth noting here that this delay differential equation and its generalizations are commonly used for describing the development of some insect populations, but this does not preclude their use for describing other phenomena in population dynamics since it has found many useful applications in system control theory, biomathematics, neural networks models, models for fisheries management and optimization problems. In fact, for a long time, delay differential equations have received a great deal of attention due to their significant nature that allows for a more realistic modelling of many real phenomena. Concerning Nicholson’s differential equation with two delays, many researchers pay great attention to it. For example, Huang et al. [11] used differential inequality techniques and dynamical system approaches to investigate the following Nicholson’s blowflies equation with two different constant delays:
I would like to point out that the time-varying environment influences environmental models by playing a significant role in their modelling which translates the fact that coefficients and delays in models of population dynamics and ecology are usually time-varying. For this, many scholars investigated Nicholson’s blowflies models with time-varying coefficients and delays. For instance, Long and Gong [15], used differential inequality techniques and the fluctuation lemmas to study the below Nicholson’s blowflies equation with variable parameters and multiple pairs of time-varying delays.
One of the most common and frequently encountered class of delay differential equations in life sciences is iterative differential equations which appear as models for several vital phenomena, ranging from ecological, biological and epidemiological phenomena to electrodynamic ones (see for instance [2, 4, 9, 12, 16]). Most recently, many scholars have tried to deal with iterative differential equations (see [1,2,3,4,5,6,7,8, 12,13,14, 16, 23]). However, to the best of our knowledge, it seems that little has been done for iterative Nicholson’s blowflies equations except our work [4], where we have investigated the following Nicholson’s blowflies equation with iterations in the harvesting effort:
where q \(x\left( t-\tau \right) \) \(E\left( t,x\left( t\right) ,x^{\left[ 2\right] }\left( t\right) \right) \) stands for the harvesting term which represents live-capture, hunting or trapping blowflies, \(x\left( t-\tau \right) \) denotes the delayed estimate of the true population, \(E\left( t,x\left( t\right) ,x^{\left[ 2\right] }\left( t\right) \right) \) is the harvesting effort which can be defined as the intensity of human activities to harvest blowflies and \(q>0\) is the so-called the catchability or capturability coefficient, which expresses the fraction of the population that is caught by one unit of harvesting effort.
In fact, the above equation involves two different types of delays where the recruitment term incorporates the same constant delay while the harvesting term involves this lag as well as the iterations in the harvesting effort that have resulted from other delays depending on the time and state. As we said before, this kind of equation is of great interest in the mathematical modelling of many phenomena in life sciences and electrodynamics, yet it is challenging to deal with it, if not impossible. In fact, the dilemma resides in the lack of a basic theory and also in its iterative terms which often hinder the use of classical mathematical methods or make these latter difficult to apply.
Based on the above discussions and motivated by the desire to continue the investigation in this direction, in the present paper, we study the following revisited Nicholson’s blowflies equation:
where \(\alpha ,\beta ,\gamma \in C\left( \left[ 0,w\right] ,\left( 0,+\infty \right) \right) \) are \(w-\)periodic functions, \(\tau \in C\left( {\mathbb {R}},{\mathbb {R}}\right) \) is a \(w-\)periodic function and \(x^{\left[ 2\right] }\left( t\right) =x\left( x\left( t\right) \right) .\) Here we assume that the recruitment term involves two different delays, the first one is \(\tau (t)\) which represents the developmental or maturation time whereas the second one is of the form \(\tau _{1}(t,x\left( t\right) )=t-x\left( t\right) \). This latter lag which depends on both the time and the size of the population and gives rise to what is known as the second iterate of the state \(x^{\left[ 2\right] }\left( t\right) \), stands for the delay that occurs due to the competition for food during the three larval stages. Indeed, the huge number of larvae leads to the crowding of the individuals which has impact on their survival and reproduction during the life cycle. In other words, since the larvae superimpose on each other, so the larvae on the bottom complete their development before the ones sitting on the top, and this leads to occur the aforementioned delay that depends on the time and the number of larvae.
The key features of the current work can be summarized as follows:
-
(i)
The recruitment term in our problem involves two distinctive delays which have shown to be more realistic in modelling the development of Lucilia cuprina populations. The maturation delay \(\tau (t)\) is a time-varying lag while the other one depends on the time and the density of adult Australian sheep blowflies which gives in turn the second iterate of the state.
-
(ii)
Up to now, there are no manuscripts that deal with Nicholson’s blowflies equation with an iterative recruitment term. So, our obtained results will enrich some previous ones to some extent.
-
(iii)
The aim of this work is to provide some new criteria for the existence, uniqueness and stability of positive periodic solutions. We follow an approach that is based on reducing the existence of the solution to that of a fixed point of an integral operator constructed after the conversion of the considered equation into an integral one whose kernel is a Green’s function. In light of this, our technique encompasses the use of Schauder’s and Banach fixed point theorems together with some properties of the obtained kernel. This technique allows us to achieve our desired targets whether mathematical or biological ones where the construction of a Banach space and a subset of it, is its main cornerstone.
The rest of this article is structured as follows. Section 2, collects some preliminary results, definitions and an established estimate. In Sect. 3, we first establish some equivalence between our problem and an equivalent nonlinear integral equation and we also state some properties of the obtained Green’s kernel that will be needed for establishing our main results. Then, we make use of Schauder’s fixed point theorem to give fairly some sufficient conditions that guarantee the existence of at least one positive periodic solution of the considered model; on the other hand we investigate the existence, uniqueness and stability of positive periodic solutions by virtue of the Banach contraction principle. In Sect. 4, we give two examples to illustrate that our results are feasible and effective. Finally, we conclude the paper with a summary and some discussions in Sect. 5.
2 Mathematical background
To begin with, we will first define an appropriate Banach space and a suitable subset of it for fulfilling some basic mathematical and biological facts as well as we will prove an interesting estimate and we will recall a lemma that will be crucially important to reach our targets.
For \(c_{1},c_{2},w>0\), let \({\mathbb {D}}\) be defined by
be a compact and convex subset of the following Banach space:
furnished with the supremum norm
In addition, if \(x_{1},x_{2}\in {\mathbb {D}}\), then
So
Also, if \(x_{1},x_{2}\in {\mathbb {D}}\), then
By applying the mean value theorem to the function \(f\left( z\right) =\exp \left( -z\right) \) over the interval \(\left[ \gamma \left( s\right) x_{1}^{\left[ 2\right] }\left( s\right) ,\gamma \left( s\right) x_{2}^{\left[ 2\right] }\left( s\right) \right] \), we obtain
where \(\zeta \left( s\right) \) is between \(\gamma \left( s\right) x_{1}^{\left[ 2\right] }\left( s\right) \) and \(\gamma \left( s\right) x_{2}^{\left[ 2\right] }\left( s\right) .\)So
where
It follows from (2.1) and (2.2) that
Lemma 1
[23] It holds
From now on, we adopt the following notations:
3 Main findings
The main focus of this section is to investigate the existence, uniqueness and stability of positive periodic solutions for Eq. (1.1). Firstly, by using the periodic properties, we will convert Eq. (1.1) into an integral one with a Green’s kernel where we also give some properties of this obtained Green’s function, secondly, we apply Schauder’s fixed point theorem to establish the existence result and finally, we prove the existence, and stability of the unique solution by using the Banach contraction principle.
We begin our investigation by the conversion of the given problem into an equivalent integral equation.
Lemma 2
The following assertions are equivalent:
-
(1)
\(x\in {\mathbb {D}}\cap {\mathcal {C}}^{1}\left( {\mathbb {R}},{\mathbb {R}}\right) \) is a solution of Eq. (1.1).
-
(2)
\(x\in {\mathbb {D}}\) is a solution of the following integral equation:
$$\begin{aligned} x\left( t\right) =\int _{t}^{t+w}{\mathcal {G}}\left( t,s\right) \beta \left( s\right) x\left( s-\tau \left( s\right) \right) e^{-\gamma \left( s\right) x^{\left[ 2\right] }\left( s\right) }ds, \end{aligned}$$(3.1)where
$$\begin{aligned} {\mathcal {G}}\left( t,s\right) =\frac{\exp \left( \int _{t}^{s}\alpha \left( u\right) du\right) }{\exp \left( \int _{0}^{w}\alpha \left( u\right) du\right) -1}. \end{aligned}$$(3.2)
Furthermore, we have
and since
then
In addition, it follows from the mean value theorem that
for all \(t_{2},t_{1}\in \left[ 0,w\right] \) with \(t_{1}<t_{2}\).Thanks to Lemma 2, we define an integral operator \({\mathcal {S}} :{\mathbb {D}}\rightarrow {\mathbb {X}}\) as follows:
So, fixed points of operator \({\mathcal {S}}\) are solutions of Eq. (1.1) and vice versa.
3.1 Existence of positive periodic solutions
Now, using Schauder’s fixed point theorem and some properties of the Green’s kernel, we will state and prove our first existence theorem.
Theorem 1
Assume that \(k_{1}\le c_{1},\) \(k_{2}\le c_{2}\) and \(\tau \in {\mathbb {D}}\), then Eq. (1.1) has at least one positive periodic solution in \({\mathbb {D}}.\)
Proof
The proof of this theorem is based on using Schauder’s fixed point theorem. For this, we must show that operator \({\mathcal {S}}:{\mathbb {D}}\rightarrow {\mathbb {X}}\) is continuous and that \({\mathcal {S}}\) maps the compact set \({\mathbb {D}}\) into itself.First and foremost, it follows from (3.3) and the periodic properties that \(\left( {\mathcal {S}}x\right) \left( t\right) \in {\mathbb {X}}\), for all \(x\in {\mathbb {D}}.\) Next, we proceed in two steps.
Step 1: Let us prove that \({\mathcal {S}}\) is continuous. Indeed, if \(x_{1},x_{2}\in {\mathbb {D}}\), then
Taking into account (2.3) , (3.4), one can see that
Consequently,
This last estimate shows that \({\mathcal {S}}\) is Lipschitz continuous which entails that it is continuous.
Step 2: Now, we show that \({\mathcal {S}}\) maps \({\mathbb {D}}\) into itself. Let \(x\in {\mathbb {D}}\) and \(t,t_{1},t_{2}\in \left[ 0,w\right] \). It is obvious that \(\left( {\mathcal {S}}x\right) \left( t\right) \ge 0\) and
Since \(k_{1}\le c_{1}\), then
On the other hand, we get
Thanks to (3.4) and (3.5), we arrive at
In view of the fact that \(k_{2}\le c_{2}\) together with (3.9) and Lemma 1, we obtain
From (3.9) and (3.10) we infer that \({\mathcal {S}}\) maps \({\mathbb {D}}\) into itself.
Accordingly, in view of the previous two steps, all requirements of Schauder’s fixed point theorem are fulfilled and, consequently, \({\mathcal {S}}\) admits at least one fixed point x residing in \({\mathbb {D}}\) which ensures that x is a solution of Eq. (1.1). \(\square \)
3.2 Uniqueness and stability
The uniqueness and continuous dependence on parameters of solutions are presented in the following two theorems which show that adding another condition to the assumptions of Theorem 1 makes Eq. (1.1) possible to admit a unique positive periodic solution that depends continuously on the mortality rate \(\alpha \), the maximum daily egg production \(\beta \) and the population’s carrying capacity\(\frac{1}{\gamma }.\)
Theorem 2
Besides the hypotheses of Theorem 1, if \(k_{3}<1,\) then Eq. (1.1) admits a unique positive periodic solution \(x\in {\mathbb {D}}.\)
Proof
One can follow the argument of the proof of Theorem 1, to demonstrate that operator \({\mathcal {T}}\) maps \({\mathbb {D}}\) into itself and
This implies that \({\mathcal {S}}\) is a contraction mapping. So, the Banach contraction principle ensures that \({\mathcal {S}}\) has a unique fixed point which is the unique positive periodic solution of Eq. (1.1). \(\square \)
Theorem 3
Under the assumptions of Theorem 2, the unique solution of Eq. (1.1) depends continuously on functions \(\alpha ,\) \(\beta \) and \(\gamma .\)
Proof
Let x be a solution of Eq. (1.1), so x satisfies the integral Eq. (3.1) i.e.,
and let \({\widetilde{x}}\) be a solution of the perturbed equation with small perturbations in \(\alpha ,\) \(\beta \) and \(\gamma \) that fulfill all requirements of Theorem 2. So, \({\widetilde{x}}\) satisfies the following integral equation:
where
and \({\widetilde{\alpha }},{\widetilde{\beta }},{\widetilde{\gamma }}\) are the perturbed parameters.Estimating the difference between \(x\left( t\right) \) and \({\widetilde{x}}\left( t\right) \), we find that
By using the same techniques as that in the proofs of (2.2) and (2.3), we can establish
and
where
Thanks to (3.12) and (3.13), we get
Accordingly,
This finishes the proof. \(\square \)
Remark 1
So far, Nicholson’s blowflies model with a time varying delay and an iteration in the recruitment term is considered for the first time. Moreover, the main results of this paper generalize to certain extent those of some interesting works (see for example [11, 15, 16]and references therein) that have underscored the importance of incorporating two different delays in the recruitment term since in such a case, the dynamics of Nicholson’s blowflies model becomes even more enriching than the case where the two delays are identical. Unlike the aforementioned works that have dealt with models involving the same lag or different constant or time varying delays in the recruitment function, we have supposed that this latter incorporates an iterative delayed recruitment function. So such a situation does not seem to have been discussed previously which means that our theoretical findings are completely new and can also be regarded as a generalization of some earlier investigations.
Remark 2
Our work contributes in enriching the few existing literature on iterative problems that are often connected to the study of many phenomena in life sciences. In [4], the authors have investigated the existence of at least one positive periodic solution which is not necessarily unique. They did not proved the uniqueness and stability of solutions whereas in this work we have established the existence of a unique positive periodic solution where the stability is preserved under small perturbations of its maximum production rate, its death rate and its size at which the blowfly population reproduces at its maximum rate. We draw attention here to the fact that involving different delays in the model can create a new dynamics and hence lead to chaotic oscillations. That is to say, the stability of a system with the same lag can become unstable with different delays. So, our results in this work complete the ones in the aforementioned paper and references cited therein.
4 Examples
In this section, we present two examples to validate our main theoretical findings obtained in the previous section.
Example 1
In this example, we set \(w=37,\) \(c_{1}=\pi ,\) \(c_{2}=2\pi \) and
In this case, we obtain
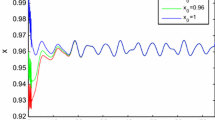
We conclude by Theorem 2 that Eq. (1.1) has one and only one positive periodic solution in the closed, convex and bounded subset
where the period is \(w=37\) days. Moreover, we have
where \({\widetilde{\alpha }},{\widetilde{\beta }}\) and \({\widetilde{\gamma }}\) are the perturbed parameters. So, the unique solution depends continuously on parameters \(\alpha ,\) \(\beta \) and \(\gamma \).
Example 2
In this example, we have the same constants and the same functions as the previous example, we change only the function \(\beta \) as follows:
In this case, we obtain
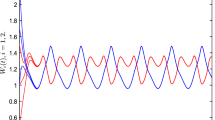
Here, the additional condition of Theorem 2 is not fulfilled and since all assumptions of Theorem 1 are satisfied, then Eq. (1.1) has at least one positive periodic solution in
which is not necessarily unique.
5 Conclusion
This work shed light on the importance of considering state and time dependent delays in modelling realistic phenomena in insect population dynamics. Herein, we have first noticed that most of investigations in the literature concerning the Nicholson’s blowflies equation did not deal with the case of an iterative recruitment term with a time varying delay. We have therefore aimed at enriching this literature and hence contributing in filling some of the existing gaps by combining the fixed point theory with the Green’s functions method for establishing some new criteria that ensure the existence, uniqueness and continuous dependence on parameters of positive periodic solutions for our Nicholson’s blowflies equation with a time varying delay and an iterative term in the recruitment term. To be more precise, we have revisited the Nicholson’s blowflies model by assuming that the maturation delay depends only on the time while the other lag that results from the competition for food during the three larval stages, depends on both the time and the number of adult blowflies, which in turn gives the second iterate in the recruitment term. So, for paving the way for applying our technique, we have needed, firstly, to construct an appropriate Banach space and a subset of it under which the iterative term will be well controlled and the sought results will be more realistic and credible. Next, we have converted our considered equation with the periodic properties into an equivalent integral equation where the kernel is a Green’s function. Then, by virtue of Schauder’s fixed point theorem together with some properties of the obtained kernel we have proved that at least one positive periodic solution can exist but not necessarily unique and also by means of the Banach contraction principle and under an additional criterion, we have shown the existence and stability of the unique positive periodic solution. Our obtained theoretical results are of great practical significance for doing more in-depth research on various generalizations of the classical Nicholson’s blowflies equation or for dealing with many natural models such as neural networks models and models for fisheries management especially those that can be regarded as a generalization of Nicholson’s models (see for example [17,18,19,20,21,22]). Finally, two examples are provided to show the effectiveness of our main findings.
Data availability
Not applicable.
References
Bouakkaz, A.: Bounded solutions to a three-point fourth-order iterative boundary value problem. Rocky Mt. J. Math. 52(3), 793–803 (2022). https://doi.org/10.1216/rmj.2022.52.793
Bouakkaz, A.: Positive periodic solutions for a class of first-order iterative differential equations with an application to a hematopoiesis model. Carpathian J. Math. 38(2), 347–355 (2022). https://doi.org/10.37193/CJM.2022.02.07
Bouakkaz, A., Khemis, R.: Positive periodic solutions for a class of second-order differential equations with state dependent delays. Turkish J. Math. 44(4), 1412–1426 (2020). https://doi.org/10.3906/mat-2004-52
Bouakkaz, A., Khemis, R.: Positive periodic solutions for revisited Nicholson’s blowflies equation with iterative harvesting term. J. Math. Anal. Appl. 494(2), 124663 (2021). https://doi.org/10.1016/j.jmaa.2020.124663
Cheraiet, S., Bouakkaz, A., Khemis, R.: Bounded positive solutions of an iterative three-point boundary-value problem with integral boundary conditions. J. Appl. Math. Comput. 65, 597–610 (2021). https://doi.org/10.1007/s12190-020-01406-8
Cheraiet, S., Bouakkaz, A., Khemis, R.: Some new findings on bounded solution of a third order iterative boundary-value problem. J. Interdiscip. Math. 25(4), 1153–1162 (2022). https://doi.org/10.1080/09720502.2021.1995215
Chouaf, S., Bouakkaz, A., Khemis, R.: On bounded solutions of a second-order iterative boundary value problem. Turkish J. Math. 46(2), 453–464 (2022). https://doi.org/10.3906/mat-2106-45
Chouaf, S., Khemis, R., Bouakkaz, A.: Some existence results on positive solutions for an iterative second-order boundary-value problem with integral boundary conditions. Bol. Soc. Parana. Mat. 3(40), 1–10 (2022). https://doi.org/10.5269/bspm.52461
Fečkan, M., Wang, J., Zhao, H.Y.: Maximal and minimal nondecreasing bounded solutions of iterative functional differential equations. Appl. Math. Lett. 113, 106886 (2021). https://doi.org/10.1016/j.aml.2020.106886
Gurney, W., Blythe, S., Nisbet, R.: Nicholson’s blowflies revisited. Nature 287, 17–21 (1980). https://doi.org/10.1038/287017a0
Huang, C., Yang, X., Cao, J.: Stability analysis of Nicholson’s blowflies equation with two different delays. Math. Comput. Simul. 171(9), 201–206 (2020). https://doi.org/10.1016/j.matcom.2019.09.023
Khemis, M., Bouakkaz, A.: Existence, uniqueness and stability results of an iterative survival model of red blood cells with a delayed nonlinear harvesting term. J. Math. Model. 10(3), 515–528 (2022). https://doi.org/10.22124/JMM.2022.21577.1892
Khemis, R., Ardjouni, A., Bouakkaz, A., Djoudi, A.: Periodic solutions of a class of third-order differential equations with two delays depending on time and state. Comment. Math. Univ. Carolin. 60(3), 379–399 (2019). https://doi.org/10.14712/1213-7243.2019.018
Khuddush, M., Prasad, K.R.: Nonlinear two-point iterative functional boundary value problems on time scales. J. Appl. Math. Comput. (2022). https://doi.org/10.1007/s12190-022-01703-4
Long, X., Gong, S.: New results on stability of Nicholson’s blowflies equation with multiple pairs of time-varying delays. Appl. Math. Lett. 100, 106027 (2020). https://doi.org/10.1016/j.aml.2019.106027
Mezghiche, L., Khemis, R., Bouakkaz, A.: Positive periodic solutions for a neutral differential equation with iterative terms arising in biology and population dynamics. Int. J. Nonlinear Anal. Appl. (2022). https://doi.org/10.22075/IJNAA.2022.26264.3281
Xu, C., Liao, M., Li, P., Guo, Y., Liu, Z.: Bifurcation properties for fractional order delayed BAM neural networks. Cogn. Comput. 13, 322–356 (2021). https://doi.org/10.1007/s12559-020-09782-w
Xu, C., Liao, M., Li, P., Xiao, Q., Yuan, S.: A new method to investigate almost periodic solutions for an Nicholson’s blowflies model with time-varying delays and a linear harvesting term. Math. Biosci. Eng. 16(5), 3830–3840 (2019). https://doi.org/10.3934/mbe.2019189
Xu, C., Liao, M., Pang, Y.: Existence and convergence dynamics of pseudo almost periodic solutions for Nicholson’s blowflies model with time-varying delays and a harvesting term. Acta Appl. Math. 146, 95–112 (2016). https://doi.org/10.1007/s10440-016-0060-7
Xu, C., Li, P., Yuan, S.: New findings on exponential convergence of a Nicholson’s blowflies model with proportional delay. Adv. Differ. Equ. 2019, 358 (2019). https://doi.org/10.1186/s13662-019-2248-4
Xu, C., Liu, Z., Aouiti, C., Li, P., Yao, L., Yan, J.: New exploration on bifurcation for fractional-order quaternion-valued neural networks involving leakage delays. Cogn. Neurodyn. 16, 1233–1248 (2022). https://doi.org/10.1007/s11571-021-09763-1
Xu, C., Zhang, W., Aouiti, C., Liu, Z., Yao, L.: Further analysis on dynamical properties of fractional-order bi-directional associative memory neural networks involving double delays. Math. Methods Appl. Sci. (2022). https://doi.org/10.1002/mma.8477
Zhao, H.Y., Fečkan, M.: Periodic solutions for a class of differential equations with delays depending on state. Math. Commun. 23, 29–42 (2018)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Khemis, R. Existence, uniqueness and stability of positive periodic solutions for an iterative Nicholson’s blowflies equation. J. Appl. Math. Comput. 69, 1903–1916 (2023). https://doi.org/10.1007/s12190-022-01820-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12190-022-01820-0
Keywords
- Banach contraction principle
- Schauder’s fixed point theorem
- Nicholson’s blowflies equation
- Periodic solution