Almost Periodic Dynamics of a Delayed Patch-Constructed Nicholson’s Blowflies System

Abstract

In this paper, we consider a delayed patch-constructed Nicholson’s blowflies system in almost periodic environment. By combining the innovative inequality technique with the basic properties of almost periodic functions and the fluctuation lemma, some testable criteria are achieved to verify the global exponential stability of the addressed almost periodic system under more general conditions, which improve and complement the existing literature. In particular, the assumptions employed in the established exponential stability criteria are sharp when the addressed system degenerates into the scalar Nicholson’s blowflies equation. Moreover, a numerical example is presented to illustrate the effectiveness of the theoretical results.

1 Introduction

The following known delay differential equation consistent with Nicholson’s classic blowfly data [1] was established by Gurney in 1980 [2].

$$\begin{aligned} x^{\prime }(t)=-d x(t)+\beta x(t-\tau ) e^{-x(t-\tau )}, \ d, \beta , \tau \in (0, \ +\infty ). \end{aligned}$$

(1.1)

Here, x(t) labels for the size of the population at time t, d stands for the per capita daily adult death rate, $\beta$ denotes the maximum per capita daily egg production and $\tau$ represents the generation time, which refers to the time taken from birth to maturity. This model was studied in detail in [3]. Considering that the external conditions surrounding the actual biological model tend to undergo periodic or almost periodic changes in line with seasonal and climatic variations, Eq. (1.1) can be naturally promoted as the following non-autonomous version:

$$\begin{aligned} x^{\prime }(t)=-d(t) x(t)+\beta (t) x(t-\tau (t)) e^{-x(t-\tau (t))}, \end{aligned}$$

(1.2)

in which $t\ge t_{0}$, $d(t)>0$, $\beta (t)>0$ and $\tau (t)\ge 0$ are almost periodic on $\mathbb {R}$. Recently, the author of [4] has successively studied the global asymptotic stability issue of periodic equation (1.2) under the following key conditions:

$$\begin{aligned} 1<\min \limits _{t\in [t_0,t_0+\omega ]} \frac{\beta (t)}{d(t)}\le \max \limits _{t\in [t_0,t_0+\omega ]} \frac{\beta (t)}{d(t)} \le \max \limits _{t\in [t_0,t_0+\omega ]} \frac{\beta (t)}{d(t)-\tau (t)\beta (t)\sup \nolimits _{t\in \mathbb {R}}\beta (t)} \le e^{2},\nonumber \\ \end{aligned}$$

(1.3)

here $\omega >0$ is the period.

It is widely recognized that populations evolve influenced by external effects which are roughly in nature, but not exactly periodic, or under environmental forcing which exhibits different, noncommensurate periods. This sort of time dependence can arise from the interplay of short-term weather cycles and seasonal climate variations, or from the superposition of daily and annually periodic phenomena, and so on. Growth processes, for instance, depend on the length of days and nights which varies during the year. Models with such time dependence are characterized more appropriately by quasi-periodic or almost periodic equations or even by certain nonautonomous equations rather than by periodic ones [5]. Due to this fact, the biological parameters in model (1.2) may all not be periodic, but fall into the class of almost periodic functions. For example, Li et al. in [6] has systematically demonstrated the existence and global exponential attractivity of a unique positive almost periodic solution for equation (1.2) based on the subsequent pivotal assumption:

$$\begin{aligned} 1<\inf \limits _{t\in \mathbb {R}} \frac{\beta (t)}{d(t)}\le \sup \nolimits _{t\in \mathbb {R}} \frac{\beta (t)}{d(t)-\tau (t)\beta (t)\sup \nolimits _{t\in \mathbb {R}}\beta (t)} < e^{2}, \end{aligned}$$

(1.4)

which is a sharp condition ensuring the stability of scalar delayed Nicholson’s blowflies equation with almost periodic biological or environmental parameters.

As pointed out in [7], patch dynamics models in biological systems are typically utilized to describe the spatial distribution of populations as influenced by many factors, such as habitats with different food-rich patches, ecological systems with protected and non-protected areas, single species structured into several stages according to age or size, and many other situations of heterogeneous environments. Given the prevalence of patch environments, mathematicians and biologists are increasingly focused on understanding the dynamic evolution of populations at regional or local scales. Consequently, with the recognition that the habitats of many species are fragmented and spatial domains exhibit discrete physical regionalization (often referred to as patches), the following time-varying delayed Nicholson’s blowflies system incorporated with patch structure has been proposed and analyzed [8,9,10,11,12,13,14,15,16].

$$\begin{aligned} \begin{array}{lll} u_p^\prime (t) & =& -d_p(t)u_p(t)+\sum \limits _{q=1, q\ne p}^n a_{pq}(t)u_q(t)\\ & & +\sum \limits _{q=1}^m\beta _{pq}(t)u_p(t-\tau _{pq}(t)) e^{-c_{pq}(t)u_p(t-\tau _{pq}(t))},\ t\ge t_{0}, \end{array} \end{aligned}$$

(1.5)

where $u_p(t)$ stands for the number of the denseness of the pth-species at time t, $a_{pq}(t)$($p\ne q$) represents the percentage of the species moving from patch q to patch p at time t, $d_p (t)$ is the coefficient of instantaneous loss for patch p at time t (which integrates both death rate and migration rate of the species in patch p moving to other patches), and they subject to the conditions listed below:

$$\begin{aligned} \begin{array}{lll} d_p (t)>\sum \limits _{q=1,q\ne p }^{n} a_{ pq} (t). \end{array} \end{aligned}$$

(1.6)

Besides, $\beta _{pq}(t)u_p(t-\tau _{pq}(t))e^{-c_{pq}(t)u_p(t-\tau _{pq}(t))}$ stands for the reproductive function for class p at time t, $\beta _{pq} (t)$ labels the birth rate for the species, $\tau _{pq}(t)$ represents the generation time, $\frac{1}{c_{pq}(t)}$ denotes the size at which the population reproduces at its maximum rate, where $p\in P:= \{1, \ldots , n\}$, $q \in Q:= \{1, \ldots , m\}$.

Very recently, some excellent results on the dynamics of Nicholson’s blowflies system with patch structure have been established. For instance, Faria in [17] obtained the periodic attractivity on patch-constructed Nicholson’s blowflies system with multiple delays of the forms

$$\begin{aligned} \begin{aligned} u_p'(t)&=-d_p(t)u_p(t)+\sum _{q=1, q\ne p}^n a_{pq}(t)u_q(t) \\&\quad +\beta _{p}(t)u_p(t-n_p m)e^{-\gamma _p(t)u_p(t-n_pm)}, \ t \ge t_0, \end{aligned} \end{aligned}$$

(1.7)

where $m >0$, $n_p \in \mathbb {N}$, $d_p(t), \beta _p(t), \gamma _p(t)$ are positive, continuous and $m-$periodic, $a_{pq}(t)$ is nonnegative, continuous and $m-$periodic, for all p, q. Subsequently, based on Faria’s conclusions, Zhao et al. [18] infer that sufficient criteria ensuring the existence of a unique positive periodic solution of system (1.5) that is globally asymptotically stable can be established only under the following assumptions:

$$\begin{aligned} & d_{p}(t)v_{p}-\sum \limits _{q=1, q\ne p}^n a_{pq}(t)v_{q}-\sum \limits _{q=1}^m\beta _{pq}(t) \left[ \sum \limits _{q=1, q\ne p}^na_{pq}^{+}v_{q}+\sum \limits _{q=1}^m \beta _{pq}^{+}v_{p}\right] \tau _{pq}(t)>0,\nonumber \\ & \quad c_{pq}(t)v_{p}\alpha \le 2, \end{aligned}$$

(1.8)

and

$$\begin{aligned} \left. \begin{array}{ll} 1<\bigg \{ \frac{\sum \nolimits _{q=1}^{m}\beta _{pq}(t) v_{p}}{d_{p}(t) v_{p}-\sum \nolimits _{q = 1, q \ne p}^n a_{pq}(t) v_{q}}\bigg \}^{-},\\ \bigg \{\frac{\sum \nolimits _{q = 1}^m\beta _{pq}(t)v_{p} e^{ - c_{pq}(t)v_{p}\alpha } }{ d_{p} (t)v_{p}- \sum \nolimits _{q = 1, q \ne p}^n a_{pq}(t)v_{q } - \sum \nolimits _{q = 1}^m \beta _{pq}(t) [ \sum \nolimits _{q = 1, q \ne p}^n a_{pq} ^{+}v_{q } + \sum \nolimits _{q = 1}^m \beta _{pq}^{+}v_{p} ] \tau _{pq}(t)}\bigg \}^{+}\le 1, \end{array} \right\} \nonumber \\ \end{aligned}$$

(1.9)

for each $t\in \mathbb {R}, \ p\in P$ and $q\in Q$, where $\alpha >0$, and $v=(v_{1}, v_{2}, \ldots , v_{n})$ is a positive vector.

In view of the practical background of biomathematical models with almost periodic parameters, and the non-autonomous ones are more difficult to analyse in general. It is important and interesting to establish sharp sufficient criteria for ascertaining the existence and globally exponential stability on positive almost periodic solutions of patch-constructed Nicholson’s blowflies system with multiple delays. On the other hand, it is preferable and desirable that the biological model not only converges, but also converges as fast as possible in the real world, as we also know that exponential stability gives a fast convergence rate to the almost periodic solution. However, there are few existing results on the research of establishing sharp criteria for ensuring the stability problem of almost periodic system (1.5) up to now. Addressing this problem constitutes the purpose of this paper, which will innovate and promote the theory and application of delay differential equations to some extent. More precisely, the main contributions of this paper can be summarized as the following three aspects.:

• 1) A class of delay patch-constructed model for Nicholson’s blowflies system is proposed, meanwhile, the basic problems for system (1.5) such as positiveness, persistence, and boundedness are achieved.

• 2) Under some assumptions, the global exponential stability of positive almost periodic solutions for system (1.5) is established through the fluctuation lemma alongside innovative inequality analyses, which enhancing and extending the key findings in [6, 20,21,22]. In particular, the sharp conditions ensuring the almost periodic stability of scalar delayed Nicholson’s blowflies established in the above literature are comprehensively covered by the conclusions of this present paper.

• 3) A numerical simulation example and some comparative analyses are provided to reveal the uniformity of the theoretical results.

The rest of this article is listed as below. Section 2 presents some preliminaries that will be used in the later sections. Global exponential stability of almost periodic system (1.5) is shown in Sect. 3. In Sects. 4 and 5, numerical simulations and conclusions are given, respectively.

2 Preliminaries

Let $C(\mathbb {R},\Omega )$ represent the set comprising all continuous functions mapping from $\mathbb {R}$ to $\Omega$, with $\Omega \subseteq \mathbb {R}$. As to $p\in P$ and $q\in Q$, suppose that $d_{p }, c_{pq}, a _{pq}(p\ne q), \beta _{pq}, \tau _{pq}\in C(\mathbb {R}, [0, +\infty ))$ are almost periodic and

$$\begin{aligned} \begin{array}{lll} f^{+}=\sup \nolimits _{t\in \mathbb {R}}f(t), ~f^{-} =\inf \limits _{t\in \mathbb {R}}f(t), \ \text{ where } \ f\in C(\mathbb {R}, \mathbb {R}). \end{array} \end{aligned}$$

For $u=(u_1, \dots , u_n)\in \mathbb {R}^n$, define

$$\begin{aligned} |u|=(|u_1|, \dots , |u_n|), \ \ \Vert u\Vert =\max _{p \in P}|u_p|. \end{aligned}$$

Definition 2.1

(see [27]). $u\in C(\mathbb {R},\Omega )$ is referred to an almost periodic function on $\mathbb {R}$, if for any $\varepsilon >0$, the set

$$\begin{aligned} T(u,\varepsilon )=\{\delta : |u(t+\delta )-u(t) |<\varepsilon , \ \forall t\in \mathbb {R}\} \end{aligned}$$

is relatively dense on $\mathbb {R}$.

Designate

$$\begin{aligned} \begin{array}{lll} \tau _{p}=\max \limits _{q\in Q}\tau _{pq}^{+}, \ \tau =\max \limits _{p \in P} \tau _{p}, \ B_{+}=\prod \limits _{p=1}^{n}C([-\tau _{p}, 0],[0, +\infty )), \end{array} \end{aligned}$$

and label $u_{t}(t_{0}, \varphi )(u(t; t_{0}, \varphi ))$ as the solution of system (1.5) accompanying the initial conditions:

$$\begin{aligned} \begin{array}{lll} u_{t_{0}}=\varphi , \ \ \ \varphi \in B_+, \ \text{ in } \text{ which } \ \varphi _{p}(0)>0 \ \text{ for } \text{ every } \ p\in P. \end{array} \end{aligned}$$

(2.1)

Throughout the paper, when all components of a vector are positive, it is defined as the positive vector. For a positive vector $v=(v_{1}, v_{2}, \ldots , v_{n})$, we label

$$\begin{aligned} L_{p}^*:= \left( \frac{1}{c_{pq}(t) }\ln {\bigg \{\frac{\sum \nolimits _{q = 1}^m\beta _{pq}(t)v_{p} }{ d_{p} (t)v_{p}- \sum \nolimits _{q = 1, q \ne p}^n a_{pq}(t)v_{q } - \sum \nolimits _{q = 1}^m \beta _{pq}(t) [ \sum \nolimits _{q = 1, q \ne p}^n a_{pq} ^{+}v_{q } + \sum \nolimits _{q = 1}^m \beta _{pq}^{+}v_{p} ] \tau _{pq}(t)} \bigg \}} \right) ^+, \end{aligned}$$

$$\begin{aligned} l^*_{p}:=\sup \left\{ \rho | \rho>0, \sum \limits _{q=1}^m \beta _{{p}q}(t)v_p e^{-c_{{p}q}(t) \rho }> d_{p}(t) v_p- \sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(t) v_q, \ \forall t \in \mathbb {R}\right\} , \end{aligned}$$

$$\begin{aligned} c _0:=\min \limits _{p\in P,q\in Q}c^{-}_{{pq}}, \ c ^0:=\max \limits _{p\in P,q\in Q}c^{+}_{{pq}}, \end{aligned}$$

and

$$\begin{aligned} L ^*:=\max \limits _{p\in P}L_{p}^*,\ k^* \in (0,1) \ \text{ with } \ k^* e^{-k^*}=c ^0L^* e^{-c ^0L^*}, \ l^*:=\min \left\{ \min \limits _{p\in P}l_{p}^*, \frac{k^*}{c ^0}\right\} . \end{aligned}$$

For arbitrary $p\in P$ and $q\in Q$, we suppose further that

$$\begin{aligned} & 0<\left\{ d_{p}(t) v_{p}-\sum \limits _{q = 1, q \ne p}^n a_{pq}(t) v_{q} \right\} ^{-}, \ 1<\left\{ \frac{\sum \nolimits _{q=1}^{m}\beta _{pq}(t) v_{p}}{d_{p}(t) v_{p}-\sum \nolimits _{q = 1, q \ne p}^n a_{pq}(t) v_{q}}\right\} ^{-},\nonumber \\ \end{aligned}$$

(2.2)

$$\begin{aligned} & \begin{array}{ll} \left\{ d_{p}(t)v_{p}-\sum \limits _{q=1, q\ne p}^n a_{pq}(t)v_{q}-\sum \limits _{q=1}^m\beta _{pq}(t) \left[ \sum \limits _{q=1, q\ne p}^na_{pq}^{+}v_{q}+\sum \limits _{q=1}^m \beta _{pq}^{+}v_{p}\right] \tau _{pq}(t)\right\} ^{-} >0, \end{array}\nonumber \\ \end{aligned}$$

(2.3)

and

$$\begin{aligned} L^*c_{pq}(t) < 2 \ \ \text {for all} \ t \in \mathbb {R}, q \in Q \ \text {and} \ p \in P. \end{aligned}$$

(2.4)

In what follows, we present five lemmas that will play vital roles in establishing our principal results.

Lemma 2.2

(See [22, Proposition 3.1]) Suppose that $\mu (t)$ is an almost periodic function defined on $\mathbb {R}$. Then

$$\begin{aligned} \mathop {\liminf }\limits _{t \rightarrow + \infty } \mu (t) = \mu ^ -,\quad \textrm{and}\quad \mathop {\limsup }\limits _{t \rightarrow + \infty } \mu (t) = \mu ^ +. \end{aligned}$$

Lemma 2.3

Suppose that (2.2) holds. Then $u(t; t_{0}, \varphi )$ exists on $[t_{0}, +\infty )$, and is unique. Moreover, $u(t; t_{0}, \varphi )$ is positive and permanent.

Proof

Let $[t_0, \eta (\varphi ))$ be the maximal existence right-interval of $u(t; t_{0}, \varphi )$, and denote $u(t)=u(t; t_{0}, \varphi )$ for any $t\in [t_0, \eta (\varphi ))$. According to $u_{t_{0}}=\varphi \in B_+$ and Theorem 5.2.1 in [24], it is easy to see that $u_{t} \in B_+$ for arbitrary $t\in [t_0, \eta (\varphi ))$. This, combining (1.5) and the facts that $a _{pq}(p\ne q)$ and $\beta _{pq} \in C(\mathbb {R}, [0, +\infty ))$, leads to

$$\begin{aligned} & \int _{t_0}^{t} e^{-\int _{\varrho }^{t} d_p(s)ds} \left[ \sum \limits _{q=1, q\ne p}^n a_{pq}(\varrho )u_q(\varrho ) +\sum \limits _{q=1}^m\beta _{pq}(\varrho )u_p(\varrho -\tau _{pq}(\varrho ))e^{-c_{pq}(\varrho )u_p(\varrho -\tau _{pq}(\varrho ))}\right] \\ & \quad d\varrho \ge 0, \end{aligned}$$

and

$$\begin{aligned} u_p (t)&=u_p(t_0)e^{-\int _{t_0}^t d_p(s)ds}+ \int _{t_0}^{t} e^{-\int _{\varrho }^{t} d_p(s)ds} \left[ \sum \limits _{q=1, q\ne p}^n a_{pq}(\varrho )u_q(\varrho ) \right. \\&\quad \left. +\sum \limits _{q=1}^m\beta _{pq}(\varrho )u_p(\varrho -\tau _{pq}(\varrho )) e^{-c_{pq}(\varrho )u_p(\varrho -\tau _{pq}(\varrho ))}\right] d\varrho \\&\ge u_p(t_0)e^{-\int _{t_0}^t d_p(s)ds} \\&>0 ,\ \ \text {for any} \ t \in [t_0, \eta (\varphi )) \ \text {and} \ p \in P. \end{aligned}$$

Next, one can substantiate $\eta (\varphi )=+\infty$. To do this, for $t \in [t_0, \eta (\varphi ))$ and $p \in P$, we set

$$\begin{aligned} m_p(t)=\max \limits _{t_0-\tau _p \le s \le t} u_p(s), \ M(t)=\max \limits _{p \in P} m_p(t). \end{aligned}$$

Then

$$\begin{aligned} u_p^{\prime }(s) \le \bigg ( \sum \limits _{q=1, q\ne p}^n a_{pq}(s)+\sum \limits _{q=1}^m\beta _{pq}(s) \bigg ) M(s) \ \ \text {for arbitrary}\ s \in [t_0, t]\ \text {and} \ p \in P,\end{aligned}$$

and thus

$$\begin{aligned} u_p (s)&\le u_p(t_0)+ \int _{t_0}^{s} \left( \sum \limits _{q=1, q\ne p}^n a_{pq}(\varrho )+\sum \limits _{q=1}^m\beta _{pq}(\varrho ) \right) M(\varrho ) d\varrho \\&\le ||\varphi ||+ \int _{t_0}^{t} \max _{p \in P} \left( \sum \limits _{q=1, q\ne p}^n a_{pq}(\varrho )+\sum \limits _{q=1}^m\beta _{pq}(\varrho ) \right) M(\varrho ) d\varrho \ \\ &\quad \text {for all}\ s \in [t_0, t]\ \text {and} \ p \in P, \end{aligned}$$

which produces

$$\begin{aligned} M(t)\le & ||\varphi ||+ \int _{t_0}^{t} \max _{p \in P} \left( \sum \limits _{q=1, q\ne p}^n a_{pq}(\varrho )+\sum \limits _{q=1}^m\beta _{pq}(\varrho ) \right) M(\varrho ) d\varrho \ \\ & \quad \mathrm{for\ all}\ t \in [t_0, \eta (\varphi )). \end{aligned}$$

According to Gronwall–Bellman inequality, we obtain that

$$\begin{aligned} 0&<u_p(t) \\&\le m_p(t) \\&\le M(t) \\&\le ||\varphi || e^{\int _{t_0}^{t} \max \limits _{p \in P} \bigg ( \sum \limits _{q=1, q\ne p}^n a_{pq}(\varrho )+\sum \limits _{q=1}^m\beta _{pq}(\varrho ) \bigg ) d\varrho }\ \text {for all}\ t \in [t_0, \eta (\varphi ))\ \text {and} \ p \in P, \end{aligned}$$

which combining with [25, Theorem 2.3.1] shows that $\eta (\varphi )=+\infty$.

Choose $p^l \in P$ such that

$$\begin{aligned} 0 \le l:=\mathop {\liminf }\limits _{t \rightarrow + \infty } u_{p^l} (t)=\min _{p \in P} \mathop {\liminf }\limits _{t \rightarrow + \infty } u_{p} (t). \end{aligned}$$

Hereafter, we demonstrate $l>0$. In contradiction, we suppose that

$$\begin{aligned} \mathop {\liminf }\limits _{t \rightarrow + \infty } u_{p^l} (t)=\min _{p \in P} \mathop {\liminf }\limits _{t \rightarrow + \infty } u_{p} (t) =0. \end{aligned}$$

(2.5)

Let

$$\begin{aligned} w_p(t)=\max \left\{ \xi : \xi \le t, u_p(\xi ) =\min \limits _{t_0 \le s \le t} u_p(s) \right\} \end{aligned}$$

for $t \ge t_0$. (2.5) allows one can select $p^{**} \in P$ and a strictly monotone increasing sequence $\{\xi _n\}_{n=1}^{+\infty }$ satisfying $\mathop {\lim } \nolimits _{n \rightarrow +\infty } \xi _n =+\infty$,

$$\begin{aligned} u_{p^{**}}(w_{p^{**}}(\xi _n))=\min _{p \in P}u_{p}(w_{p}(\xi _n)), \ \mathop {\lim }\limits _{n \rightarrow +\infty } u_{p^{**}}(w_{p^{**}}(\xi _n))=0, \end{aligned}$$

(2.6)

and then

$$\begin{aligned} \mathop {\lim } \limits _{n \rightarrow +\infty } w_{p^{**}}(\xi _n) =+\infty . \end{aligned}$$

(2.7)

Without loss of generality, we further assume the following limits

$$\begin{aligned} \mathop {\lim } \limits _{n \rightarrow +\infty } d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}, \ \mathop {\lim } \limits _{n \rightarrow +\infty }\beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}} (q\in Q) \end{aligned}$$

and

$$\begin{aligned} \mathop {\lim } \limits _{n \rightarrow +\infty }a_{p^{**}q}(w_{p^{**}}(\xi _n))v_q (q\in Q\setminus \{p^{**}\}) \end{aligned}$$

exist. In addition, we can denote $Q=Q_{1}\cup Q_{2}$ with

$$\begin{aligned} Q_{1}=\left\{ q\in Q|\mathop {\lim } \limits _{n \rightarrow +\infty }\beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}>0 \right\} \end{aligned}$$

and

$$\begin{aligned} Q_{2}=\left\{ q\in Q|\mathop {\lim } \limits _{n \rightarrow +\infty }\beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}=0 \right\} . \end{aligned}$$

Based on (2.7), it can be observed that there exists $n^{**}>0$ such that

$$\begin{aligned} w_{p^{**}}(\xi _n)> t_0+\tau _{p^{**}} \ \ \text {for} \ n>n^{**}. \end{aligned}$$

Let $x_{p}(t)=v_{p}^{-1}u_{p}(t)$, then

$$\begin{aligned} x_{p}^{\prime }(t)&= v_{p}^{-1}\left[ -d_{p}(t)v_{p}x_{p}(t)+\sum \limits _{q=1, q\ne p}^na_{pq}v_qx_q(t)\right. \\&\quad \left. +\sum \limits _{q=1}^m \beta _{pq}(t)v_px_p(t-\tau _{pq}(t))e^{-c_{pq}(t)v_p x_p(t-\tau _{pq}(t))}\right] \ \ \text {for all} \ p \in P. \end{aligned}$$

Therefore,

$$\begin{aligned} 0&\ge x_{p^{**}}^{\prime }(w_{p^{**}}(\xi _n)) \\&= v_{p^{**}}^{-1}\left[ -d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n))\right. \\ &\quad +\sum \limits _{q=1, q\ne p^{**}}^n a_{p^{**}q}(w_{p^{**}}(\xi _n))v_qx_q(w_{p^{**}}(\xi _n))\\&\quad +\sum \limits _{q=1}^m\beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n))) \\&\quad \left. \times e^{-c_{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n)))} \right] \\&\ge v_{p^{**}}^{-1}\left[ -d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n))\right. \\ &\quad +\sum \limits _{q=1, q\ne p^{**}}^n a_{p^{**}q}(w_{p^{**}}(\xi _n))v_qx_{p^{**}}(w_{p^{**}}(\xi _n))\\&\quad +\sum \limits _{q=1}^m\beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n))) \\&\quad \left. \times e^{-c_{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n)))} \right] \\&=v_{p^{**}}^{-1}\left[ x_{p^{**}}(w_{p^{**}}(\xi _n))(-d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}+\sum \limits _{q=1, q\ne p^{**}}^n a_{p^{**}q}(w_{p^{**}}(\xi _n))v_q)\right. \\&\quad +\sum \limits _{q=1}^m\beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n))) \\&\quad \left. \times e^{-c_{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n)))}\right] \end{aligned}$$

and

$$\begin{aligned}&x_{p^{**}}(w_{p^{**}}(\xi _n))\left[ d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}-\sum \limits _{q=1, q\ne p^{**}}^n a_{p^{**}q}(w_{p^{**}}(\xi _n))v_q\right] \\ &\ge \sum \limits _{q=1}^m\beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n))) \\ &\quad \times e^{-c_{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n)))}, \ n>n^{**}, \end{aligned}$$

which, together with (2.2) and (2.6), produce

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow +\infty } x_{p^{**}}(w_{p^{**}}(\xi _n))=0, \end{aligned}$$

and

$$\begin{aligned} \mathop {\lim }\limits _{n \rightarrow +\infty } x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n))) =0, \ q \in Q_{1}. \end{aligned}$$

(2.8)

Note that

$$\begin{aligned} 1&\ge \frac{\sum \nolimits _{q=1}^m \beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n)))}{x_{p^{**}}(w_{p^{**}}(\xi _n))[d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}-\sum \nolimits _{q=1, q\ne p^{**}}^n a_{p^{**}q}(w_{p^{**}}(\xi _n))v_q]} \\&\quad \times e^{-c_{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n)))} \\&\ge \frac{\sum \nolimits _{q=1}^m \beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}}{d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}-\sum \nolimits _{q=1, q\ne p^{**}}^n a_{p^{**}q}(w_{p^{**}}(\xi _n))v_q} \\&\quad \times e^{-c_{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}x_{p^{**}}(w_{p^{**}}(\xi _n)-\tau _{p^{**}q}(w_{p^{**}}(\xi _n)))}, \ n>n^{**}, \end{aligned}$$

Letting $n \rightarrow +\infty$, it follows from (2.2), (2.8) and Lemma 2.2 that

$$\begin{aligned} 1&\ge \frac{\sum \nolimits _{q\in Q_{1}} \mathop {\lim } \nolimits _{n \rightarrow +\infty }\beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}}{ \mathop {\lim } \nolimits _{n \rightarrow +\infty }d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}-\sum \limits _{q=1, q\ne p^{**}}^n \mathop {\lim } \nolimits _{n \rightarrow +\infty }a_{p^{**}q}(w_{p^{**}}(\xi _n))v_q} \\ &= \frac{\sum \nolimits _{q=1}^m \mathop {\lim } \nolimits _{n \rightarrow +\infty }\beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}}{ \mathop {\lim } \nolimits _{n \rightarrow +\infty }d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}-\sum \nolimits _{q=1, q\ne p^{**}}^n \mathop {\lim } \nolimits _{n \rightarrow +\infty }a_{p^{**}q}(w_{p^{**}}(\xi _n))v_q} \\ &= \mathop {\lim } \nolimits _{n \rightarrow +\infty }\bigg [ \frac{\sum \nolimits _{q=1}^m \beta _{p^{**}q}(w_{p^{**}}(\xi _n))v_{p^{**}}}{d_{p^{**}}(w_{p^{**}}(\xi _n))v_{p^{**}}-\sum \nolimits _{q=1, q\ne p^{**}}^n a_{p^{**}q}(w_{p^{**}}(\xi _n))v_q}\bigg ] \\&\ge \mathop {\liminf } \nolimits _{t \rightarrow +\infty }\bigg [ \frac{\sum \nolimits _{q=1}^m \beta _{p^{**}q}(t)v_{p^{**}}}{d_{p^{**}}(t)v_{p^{**}}-\sum \nolimits _{q=1, q\ne p^{**}}^n a_{p^{**}q}(t)v_q} \bigg ] \\&= \bigg \{\frac{\sum \nolimits _{q=1}^m \beta _{p^{**}q}(t)v_{p^{**}}}{d_{p^{**}}(t)v_{p^{**}}-\sum \nolimits _{q=1, q\ne p^{**}}^n a_{p^{**}q}(t)v_q}\bigg \}^{-} \\&>1. \end{aligned}$$

This is a contradiction, and hence, $l>0$. $\square$

Remark 2.4

In Lemma 2.3, we have not required the assumption that $\liminf \nolimits _{t\rightarrow +\infty }\beta _{pq} (t)>0$ for $p\in P, \ q\in Q$, which is crucial for achieving persistence in [22]. This indicates that the persistence result obtained in this paper extends the corresponding ones in the aforementioned literature.

Lemma 2.5

(See [7, Lemma 2.3]) For arbitrary $X\in (0, 2], K>0 \ \text{ and } \ K\ne X$,

$$\begin{aligned} \begin{array}{lll} e^{-X}|K-X|> \left| K e^{-K}-X e^{-X}\right| . \end{array} \end{aligned}$$

Lemma 2.6

Denote $u(t)=u(t;t_0,\varphi )$ for arbitrary $t \in [t_0, +\infty )$ and choose $p^l, p^L \in P$ such that

$$\begin{aligned} L=\mathop {\limsup }\limits _{t \rightarrow + \infty } u_{p^L} (t)=\max _{p \in P} \mathop {\limsup }\limits _{t \rightarrow + \infty } u_{p} (t), \ l=\mathop {\liminf }\limits _{t \rightarrow + \infty } u_{p^l} (t)=\min _{p \in P} \mathop {\liminf }\limits _{t \rightarrow + \infty } u_{p} (t).\end{aligned}$$

Moreover, assume that (2.2)-(2.3) are satisfied. Then

$$\begin{aligned} l^* \le l=\mathop {\liminf }\limits _{t \rightarrow + \infty } u_{p^l} (t) \le \mathop {\limsup }\limits _{t \rightarrow + \infty } u_{p^L} (t) =L \le L^*. \end{aligned}$$

Proof

With the aid of Lemma 2.3 and the fluctuation Lemma [26, Lemma A.1], we can select $\left\{ {{t_k}} \right\} _{k = 1}^{ + \infty }$ and $\left\{ {{h_k}} \right\} _{k = 1}^{ + \infty }$ satisfying that

$$\begin{aligned} \begin{array}{lll} \mathop {\lim }\limits _{k \rightarrow + \infty } {t_k} =+\infty , \mathop {\lim }\limits _{k \rightarrow +\infty }u_{p^{L}}({t_k}) =L \ \text{ with } \ \mathop {\lim }\limits _{k \rightarrow +\infty } u_{p^{L}}'({t_k})=0, \end{array} \end{aligned}$$

(2.9)

and

$$\begin{aligned} \begin{array}{lll} \mathop {\lim }\limits _{k \rightarrow + \infty } {h_k} =+\infty , \mathop {\lim }\limits _{k \rightarrow +\infty }u_{p^{l}}({h_k}) =l \ \text{ with } \ \mathop {\lim }\limits _{k \rightarrow +\infty } u_{p^{l}}'({h_k})=0. \end{array} \end{aligned}$$

(2.10)

Without compromising generality, we can also assume that the following limits exist.

$$\begin{aligned} & \lim \limits _{k \rightarrow + \infty }d_{p ^{L}}(t_k), \ \lim \limits _{k \rightarrow + \infty }u_q(t_k)(q\ne p^{L}), \ \mathop {\lim }\limits _{k \rightarrow + \infty }\beta _{p^{L}q}({t_k}),\\ & \mathop {\lim }\limits _{k \rightarrow + \infty }c_{p^{L}q}({t_k}), \ \mathop {\lim }\limits _{k \rightarrow + \infty }a_{p^{L}q}({t_k}), \ \mathop {\lim }\limits _{k \rightarrow + \infty }u_{p^{L}}({t_k}-\tau _{p^{L}q}(t_k)),\\ & \lim \limits _{k \rightarrow + \infty }d_{p ^{l}}(h_k), \ \lim \limits _{k \rightarrow + \infty }u_q(h_k)(q\ne p^{l}), \ \mathop {\lim }\limits _{k \rightarrow + \infty }\beta _{p^{l}q}({h_k}),\\ & \mathop {\lim }\limits _{k \rightarrow + \infty }c_{p^{l}q}({h_k}), \ \mathop {\lim }\limits _{k \rightarrow + \infty }a_{p^{l}q}({h_k}), \ \mathop {\lim }\limits _{k \rightarrow + \infty }u_{p^{l}}({h_k}-\tau _{p^{l}q}(h_k)). \end{aligned}$$

For arbitrary $\varepsilon >0$, there exists $T>0$ such that

$$\begin{aligned} u_{p ^{L}}(t)<L+\varepsilon \quad \mathrm{for\ every}\ t >T. \end{aligned}$$

Thus, for each $t \in (T+\tau _{p ^{L}}, +\infty )$, one has

$$\begin{aligned} \begin{aligned} -d_{p ^{L}}(t)(L+\varepsilon )&< v_{p^{L}}^{-1} \left[ -d_{p ^{L}}(t) v_{p^{L}} u_{p ^{L}}(t) +\sum \limits _{q=1, q\ne {p ^{L}}}^n a_{{p ^{L}}q}(t) v_{q} u_q(t) \right. \\ &\ \ \ \ \ \left. +\sum \limits _{q=1}^m\beta _{{p ^{L}}q}(t)v_{p^{L}} u_{p ^{L}}(t-\tau _{{p ^{L}}q}(t)) e^{-c_{{p ^{L}}q}(t) u_{p ^{L}}(t-\tau _{{p ^{L}}q}(t))} \right] \\&< v_{p^{L}}^{-1}\left( \sum \limits _{q=1, q\ne {p ^{L}}}^n a_{{p ^{L}}q}(t)v_{p^{L}}+\sum \limits _{q=1}^m\beta _{{p ^{L}}q}(t)v_{p^{L}}\right) (L+\varepsilon ), \end{aligned} \end{aligned}$$

which, combined with the second inequality in (2.2), suggests that

$$\begin{aligned} \begin{aligned} |u_{p ^{L}}'(t)|&< v_{p^{L}}^{-1}\left( \sum \limits _{q=1, q\ne {p ^{L}}}^n a_{{p ^{L}}q}(t)v_{p^{L}}+\sum \limits _{q=1}^m\beta _{{p ^{L}}q}(t)v_{p^{L}}\right) (L+\varepsilon )\\&\le v_{p^{L}}^{-1}\left( \sum \limits _{q=1, q\ne {p ^{L}}}^n a_{{p ^{L}}q}^{+}v_{p^{L}}+\sum \limits _{q=1}^m\beta _{{p ^{L}}q} ^{+}v_{p^{L}}\right) (L+\varepsilon ), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} u_{p^L}'(t_k)&= v_{p^{L}}^{-1}\left\{ -d_{p^L}(t_k)v_{p^{L}}u_{p^L}(t_k)+\sum \limits _{q=1, q\ne {p^L}}^n a_{{p^L}q}(t_k)v_{q}u_q(t_k) \right. \nonumber \\&\ \ \ \ \ \left. +\sum \limits _{q=1}^m\beta _{{p^L}q}(t_k)v_{p^{L}}u_{p^L}(t_k-\tau _{{p^L}q}(t_k)) e^{-c_{{p^L}q}(t_k)u_{p^L}(t_k-\tau _{{p^L}q}(t_k))} \right\} \nonumber \\&= v_{p^{L}}^{-1} \left\{ -d_{p^L}(t_k)v_{p^{L}}u_{p^L}(t_k)+\sum \limits _{q=1, q\ne {p^L}}^n a_{{p^L}q}(t_k)v_{q}u_q(t_k) \right. \nonumber \\&\ \ \ \ \ \left. +\sum \limits _{q=1}^m \frac{\beta _{{p^L}q}(t_k)v_{p^{L}}}{c_{{p^L}q}(t_k)} c_{{p^L}q}(t_k) u_{p^L}(t_k)e^{-c_{{p^L}q}(t_k) u_{p^L}(t_k)} \right. \nonumber \\&\ \ \ \ \ \left. +\sum \limits _{q=1}^m \frac{\beta _{{p^L}q}(t_k)v_{p^{L}}}{c_{{p^L}q}(t_k)} \left[ c_{{p^L}q}(t_k) u_{p^L}(t_k-\tau _{{p^L}q}(t_k)) e^{-c_{{p^L}q}(t_k) u_{p^L}(t_k-\tau _{{p^L}q}(t_k))} \right. \right. \nonumber \\&\ \ \ \ \ \left. \left. -c_{{p^L}q}(t_k) u_{p^L}(t_k) e^{-c_{{p^L}q}(t_k) u_{p^L}(t_k)}\right] \right\} \nonumber \\&\le v_{p^{L}}^{-1} \left\{ -d_{p^L}(t_k)v_{p^{L}}u_{p^L}(t_k)+\sum \limits _{q=1, q\ne {p^L}}^n a_{{p^L}q}(t_k)v_{q}u_q(t_k) \right. \nonumber \\&\ \ \ \ \ \left. +\sum \limits _{q=1}^m \beta _{{p^L}q}(t_k) v_{p^{L}}u_{p^L}(t_k)e^{-c_{{p^L}q}(t_k) u_{p^L}(t_k)} \right. \nonumber \\&\ \ \ \ \ \left. +\sum \limits _{q=1}^m \beta _{{p^L}q}(t_k) v_{p^{L}}|(1-\theta _q)e^{-\theta _q}||u_{p^{L}}(t_k)-u_{p^{L}}(t_k-\tau _{p^Lq}(t_k))| \right\} \nonumber \\&\le v_{p^{L}}^{-1} \left\{ -d_{p^L}(t_k)v_{p^{L}}u_{p^L}(t_k)+\sum \limits _{q=1, q\ne {p^L}}^n a_{{p^L}q}(t_k)v_{q}u_q(t_k) \right. \nonumber \\&\ \ \ \ \ \left. +\sum \limits _{q=1}^m \beta _{{p^L}q}(t_k) v_{p^{L}}u_{p^L}(t_k)e^{-c_{{p^L}q}(t_k) u_{p^L}(t_k)} \right. \nonumber \\&\ \ \ \ \ \left. +\sum \limits _{q=1}^m \beta _{{p^L}q}(t_k) v_{p^{L}} \int _{t_k-\tau _{p^Lq}(t_k)}^{t_k} |u_{p ^{L}}^{\prime }(s)| ds \right\} \nonumber \\&\le v_{p^{L}}^{-1} \left\{ -d_{p^L}(t_k)v_{p^{L}}u_{p^L}(t_k)+\sum \limits _{q=1, q\ne {p^L}}^n a_{{p^L}q}(t_k)v_{q}u_q(t_k) \right. \nonumber \\&\ \ \ \ \ \left. +\sum \limits _{q=1}^m \beta _{{p^L}q}(t_k) v_{p^{L}}u_{p^L}(t_k)e^{-c_{{p^L}q}(t_k)u_{p^L}(t_k)} \right. \nonumber \\&\ \ \ \ \ \left. +\sum \limits _{q=1}^m \beta _{{p^L}q}(t_k) \left( \sum \limits _{q=1, q\ne {p ^{L}}}^n a_{{p ^{L}}q}^+ v_{q}+\sum \limits _{q=1}^m\beta _{{p ^{L}}q}^+v_{p^{L}}\right) (L+\varepsilon ) \cdot \tau _{p^Lq}(t_k) \right\} ,\nonumber \\&\ t_k > T+\tau _{p ^{L}}, \end{aligned}$$

(2.11)

where $\theta _q$ represents the intermediate point of the differential mean value theorem and $q \in Q$.

By taking the limits on both sides of (2.11), it follows from (2.9) that

$$\begin{aligned} 0&\le v_{p^{L}}^{-1} L\left[ -\mathop {\lim }\limits _{k \rightarrow +\infty }d_{p^L}(t_k)v_{p^{L}}+\mathop {\lim }\limits _{k \rightarrow +\infty }\sum \limits _{q=1, q\ne {p^L}}^n a_{{p^L}q}(t_k)v_{q} \right. \\&\ \ \ \ \ +\mathop {\lim }\limits _{k \rightarrow +\infty }\sum \limits _{q=1}^m \beta _{{p^L}q}(t_k) v_{p^{L}} e^{-\mathop {\lim }\limits _{k \rightarrow +\infty }c_{{p^L}q}(t_k) L} \\&\ \ \ \ \ \left. +\frac{L+\varepsilon }{L}\mathop {\lim }\limits _{k \rightarrow +\infty }\sum \limits _{q=1}^m \beta _{{p^L}q}(t_k) \left( \sum \limits _{q=1, q\ne {p ^{L}}}^n a_{{p ^{L}}q}^{+}v_{q}+\sum \limits _{q=1}^m\beta _{{p ^{L}}q}^+v_{p^{L}}\right) \cdot \tau _{p^Lq}(t_k)\right] \end{aligned}$$

and

$$\begin{aligned}&\mathop {\lim }\limits _{k \rightarrow +\infty }\sum \limits _{q=1}^m \beta _{{p^L}q}(t_k) v_{p^{L}} e^{-\mathop {\lim }\limits _{k \rightarrow +\infty }c_{{p^L}q}(t_k) L} \nonumber \\&\quad \ge \mathop {\lim }\limits _{k \rightarrow +\infty } \left\{ d_{p^L}(t_k)v_{p^{L}}-\sum \limits _{q=1, q\ne {p^L}}^n a_{{p^L}q}(t_k)v_{q} \right. \nonumber \\&\quad \left. -\sum \limits _{q=1}^m\beta _{{p^L}q}(t_k)\left[ \sum \limits _{q=1, q\ne {p^L}}^n a_{{p^L}q}^+ v_{q}+\sum \limits _{q=1}^m\beta _{{p^L}q}^+v_{p^{L}} \right] \tau _{p^Lq}(t_k) \frac{L+\varepsilon }{L} \right\} . \end{aligned}$$

(2.12)

Letting $\varepsilon \rightarrow 0$, (2.3), (2.12) and Lemma 2.2 yield

$$\begin{aligned} \begin{aligned} L&\le \mathop {\lim }\limits _{k \rightarrow +\infty } \frac{1}{c_{{p^L}q}(t_k) } \\&\quad \ \ \ \times \ln \left\{ \frac{\sum \nolimits _{q=1}^m \beta _{{p^L}q}(t_k) v_{p^{L}}}{d_{p^L}(t_k)v_{p^{L}}-\sum \nolimits _{q=1, q\ne p}^n a_{{p^L}q}(t_k)v_{q}-\sum \nolimits _{q=1}^m\beta _{{p^L}q}(t) {\Big [}\sum \nolimits _{q=1, q\ne p}^n a_{{p^L}q}^+ v_{q} +\sum \nolimits _{q=1}^m\beta _{{p^L}q}^+ v_{p^{L}}{\Big ]} \tau _{p^Lq}(t_k) } \right\} , \end{aligned} \end{aligned}$$

which combined the definition of $L^*$ implies that $L \le L^*$.

It still needs to confirm that $l^* \le l =\mathop {\liminf }\nolimits _{t \rightarrow + \infty } u_{p^l} (t)$. Otherwise, $l^* > \mathop {\liminf }\nolimits _{t \rightarrow + \infty } u_{p^l} (t)$. Note that

$$\begin{aligned} l\lim \limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) \le \lim \limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) \lim \limits _{k \rightarrow +\infty } u_{p^l}(h_k-\tau _{{p^l}q}(h_k))\le c ^0L^*, \end{aligned}$$

and

$$\begin{aligned} & l\lim \limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) \le k^*<1, \ l\lim \limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) e^{-l\lim \limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) }\\ & \quad =\min _{s\in [l\lim \limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k), \ c ^0L^*]}se^{-s}. \end{aligned}$$

From (2.10) and the definition of $l^*$, we acquire

$$\begin{aligned} 0&= -\mathop {\lim }\limits _{k \rightarrow +\infty }d_{p^l}(h_k) v_{p^l} \mathop {\lim }\limits _{k \rightarrow +\infty } u_{p^l}(h_k)+\sum \limits _{q=1, q\ne {p^L}}^n \mathop {\lim }\limits _{k \rightarrow +\infty } a_{{p^l}q}(h_k) v_{q} \mathop {\lim }\limits _{k \rightarrow +\infty } u_q(h_k)\\&\ \ \ \ \ +\sum \limits _{q=1}^m \frac{{\mathop {\lim }\nolimits _{k \rightarrow +\infty }\beta _{{p^l}q}(h_k) v_{p^l}}}{\mathop {\lim }\nolimits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) } \mathop {\lim }\limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) \mathop {\lim }\limits _{k \rightarrow +\infty } u_{p^l}(h_k-\tau _{{p^l}q}(h_k))\\&\quad e^{-\mathop {\lim }\limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) \mathop {\lim }\limits _{k \rightarrow +\infty } u_{p^l}(h_k-\tau _{{p^l}q}(h_k))} \\&\ge -\mathop {\lim }\limits _{k \rightarrow +\infty }d_{p^l}(h_k) v_{p^l} \mathop {\lim }\limits _{k \rightarrow +\infty } u_{p^l}(h_k)+\sum \limits _{q=1, q\ne {p^L}}^n \mathop {\lim }\limits _{k \rightarrow +\infty } a_{{p^l}q}(h_k) v_{q} \mathop {\lim }\limits _{k \rightarrow +\infty } u_q(h_k) \\ &\ \ \ \ \ +\sum \limits _{q=1}^m \mathop {\lim }\limits _{k \rightarrow +\infty } \beta _{{p^l}q}(h_k) v_{p^l} l e^{-l\mathop {\lim }\limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) } \\ &\ge \left[ -\mathop {\lim }\limits _{k \rightarrow +\infty }d_{p^l}(h_k)v_{p^l}+\mathop {\lim }\limits _{k \rightarrow +\infty }\sum \limits _{q=1, q\ne {p^L}}^n a_{{p^l}q}(h_k)v_{q}\right. \\&\quad \left. +\mathop {\lim }\limits _{k \rightarrow +\infty }\sum \limits _{q=1}^m \beta _{{p^l}q}(h_k) v_{p^l} e^{-l\mathop {\lim }\limits _{k \rightarrow +\infty }c_{{p^l}q}(h_k) } \right] \\&>0, \end{aligned}$$

a clear contradiction, indicating that $l^* \le l=\liminf \nolimits _{t \rightarrow +\infty } u_{p^l}(t)$. This proves Lemma 2.6. $\square$

Lemma 2.7

Let ${\bar{u}}_p(t)={\bar{u}}_p (t;t_0,\varphi )$ be a solution of (1.5) with the initial data (2.1) and $\varphi _p' \in C([-\tau _p,0], \mathbb {R})$. If the assumptions of Lemma 2.6 and (2.4) are satisfied. Then, for any $\varepsilon >0$, there exists a relatively dense subset $\Lambda _\varepsilon$ of $\mathbb {R}$ incorporating the property that, for each $\theta \in \Lambda _\varepsilon$, there is a sufficiently large $N>0$ such that

$$\begin{aligned} |{\bar{u}}_p(t+\theta )-{\bar{u}}_p(t)| < \frac{\varepsilon }{2} \ \ \text {for arbitrary} \ t>N, \ p \in P.\end{aligned}$$

Proof

Define

$$\begin{aligned} {\bar{u}}_p(t) \equiv {\bar{u}}_p(t_0- \tau _p ),\ \ \text {for arbitrary}\ t \in (-\infty , t_0-\tau _p). \end{aligned}$$

(2.13)

For $\theta \in \mathbb {R}$, from (2.4) and Lemma 2.5, one can take ${N_0} \in ( \max \left\{ {{t_0},{t_0}\mathrm{{ - }}\theta } \right\} , \ +\infty )$, $\bar{l} \in (0, \ l^{*})$ and ${\bar{L}}> L^{*}$ satisfying that

$$\begin{aligned} {\bar{L}} c_{pq}(t)< 2 \ \ \text {for any} \ t \in \mathbb {R}, q \in Q, p \in P,\end{aligned}$$

and

$$\begin{aligned} {\bar{l}}< {\bar{u}}_p(t), {\bar{u}}_p\left( {t + \theta } \right) < {\bar{L}} \ \ \text{ for } \text{ arbitrary } \ t \ge {N_0}. \end{aligned}$$

As to $t \in \mathbb {R}$, set

$$\begin{aligned} U(t)=(U_1(t), U_2(t), \ldots , U_n(t)), \ \ U_p(t) = \frac{{\bar{u}_p\left( {t + \theta } \right) }}{{\bar{u}_p(t)}} - 1, \end{aligned}$$

and

$$\begin{aligned} \Pi _p(\theta , t)= & -[d_p(t+\theta )-d_p(t)] \bar{u}_p(t+\theta )+\sum \limits _{q=1, q\ne {p}}^n[ a_{{p}q}(t+\theta )-a_{{p}q}(t)] \bar{u}_q(t+\theta ) \\ & +\sum \limits _{q=1}^m [\beta _{{p}q}(t+\theta )- \beta _{{p}q}(t)] \bar{u}_p(t+\theta -\tau _{pq}(t+\theta )) e^{-c_{pq}(t+\theta )\bar{u}_p(t+\theta -\tau _{pq}(t+\theta ))} \\ & +\sum \limits _{q=1}^m \beta _{{p}q}(t)\Big [{\bar{u}}_p(t+\theta -\tau _{pq}(t+\theta ))e^{-c_{pq}(t+\theta ){\bar{u}}_p(t+\theta -\tau _{pq}(t+\theta ))}\\ & -{\bar{u}}_p(t-\tau _{pq}(t)+\theta )e^{-c_{pq}(t+\theta ){\bar{u}}_p(t-\tau _{pq}(t)+\theta )}\Big ] \\ & +\sum \limits _{q=1}^m \beta _{{p}q}(t)\Big [{\bar{u}}_p(t-\tau _{pq}(t)+\theta )e^{-c_{pq}(t+\theta ){\bar{u}}_p(t-\tau _{pq}(t)+\theta )}\\ & -{\bar{u}}_p(t-\tau _{pq}(t)+\theta )e^{-c_{pq}(t)\bar{u}_p(t-\tau _{pq}(t)+\theta )}\Big ]. \end{aligned}$$

Let $K_0=\max \{t_0+N_0+\tau ,t_0+N_0+\tau -\theta \}$. Then, for all $t > {K_0}$, we have

$$\begin{aligned} U_p'(t)&= \frac{{\bar{u}_p' ( {t + \theta } )\bar{u}_p(t) - \bar{u}_p ( {t + \theta } )\bar{u}_p'(t)}}{{{{ [ {\bar{u}_p(t)} ]}^2}}} \nonumber \\&= \frac{1}{{{{\left[ {\bar{u}_p(t)} \right] }^2}}} \left\{ \bar{u}_p(t) \left[ \Pi _p \left( {\theta ,t} \right) - d_p (t)\bar{u}_p\left( {t + \theta } \right) +\sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(t) {\bar{u}}_q(t+\theta ) \right. \right. \nonumber \\&\quad \left. +\sum \limits _{q=1}^m \beta _{{p}q}(t){\bar{u}}_p(t-\tau _{pq}(t)+\theta )e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t)+\theta )} \right] - \bar{u}_p ( {t + \theta } ) \nonumber \\&\quad \times \left[ -d_p(t) {\bar{u}}_p(t)+\sum \limits _{q=1, q\ne p}^n a_{pq}(t) {\bar{u}}_q(t) \right. \nonumber \\&\quad \left. \left. +\sum \limits _{q=1}^m\beta _{pq}(t) {\bar{u}}_p(t-\tau _{pq}(t)) e^{-c_{pq}(t) {\bar{u}}_p(t-\tau _{pq}(t))}\right] \right\} \nonumber \\&= \frac{1}{{{{\left[ {\bar{u}_p(t)} \right] }^2}}} \left\{ \bar{u}_p(t) \Pi _p \left( {\theta ,t} \right) +{\bar{u}_p(t)}\sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(t) {\bar{u}}_q(t+\theta ) \right. \nonumber \\&\quad +{\bar{u}_p(t)}\sum \limits _{q=1}^m \beta _{{p}q}(t){\bar{u}}_p(t-\tau _{pq}(t)+\theta )e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t)+\theta )} \nonumber \\&\quad - \bar{u}_p ( {t + \theta } ) \sum \limits _{q=1, q\ne p}^n a_{pq}(t) {\bar{u}}_q(t) \nonumber \\&\quad \left. - \bar{u}_p ( {t + \theta } )\sum \limits _{q=1}^m\beta _{pq}(t) {\bar{u}}_p(t-\tau _{pq}(t)) e^{-c_{pq}(t) {\bar{u}}_p(t-\tau _{pq}(t))} \right\} \nonumber \\&= \frac{\Pi _p \left( {\theta ,t} \right) }{\bar{u}_p(t)} +\frac{1}{[\bar{u}_p(t)]^2}\left\{ \bar{u}_p(t) \sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(t) {\bar{u}}_q(t+\theta )\right. \nonumber \\&\quad \left. - \bar{u}_p ( {t + \theta } ) \sum \limits _{q=1, q\ne p}^n a_{pq}(t) {\bar{u}}_q(t)\right\} \nonumber \\&\quad +\frac{1}{[\bar{u}_p(t)]^2}\left\{ {\bar{u}_p(t)}\sum \limits _{q=1}^m \beta _{{p}q}(t){\bar{u}}_p(t-\tau _{pq}(t)+\theta )e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t)+\theta )}\right. \nonumber \\&\quad \left. - \bar{u}_p ( {t + \theta } )\sum \limits _{q=1}^m\beta _{pq}(t) {\bar{u}}_p(t-\tau _{pq}(t)) e^{-c_{pq}(t) {\bar{u}}_p(t-\tau _{pq}(t))} \right\} \nonumber \\&= \frac{\Pi _p \left( {\theta ,t} \right) }{\bar{u}_p(t)} +\frac{\sum \nolimits _{q=1, q\ne {p}}^n a_{{p}q}(t)}{\bar{u}_p(t)}\left\{ ({\bar{u}}_q(t+\theta )- \bar{u}_q (t))- {\bar{u}}_q(t)\frac{{\bar{u}}_p(t+\theta )- \bar{u}_p(t)}{\bar{u}_p(t)}\right\} \nonumber \\&\quad +\frac{1}{[\bar{u}_p(t)]^2}\left\{ {\bar{u}_p(t)}\sum \limits _{q=1}^m \beta _{{p}q}(t){\bar{u}}_p(t-\tau _{pq}(t)+\theta )e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t)+\theta )}\right. \nonumber \\&\quad - \bar{u}_p (t) \sum \limits _{q=1}^m \beta _{{p}q}(t){\bar{u}}_p(t-\tau _{pq}(t))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))} \nonumber \\&\quad + \bar{u}_p (t) \sum \limits _{q=1}^m \beta _{{p}q}(t){\bar{u}}_p(t-\tau _{pq}(t))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))} \nonumber \\&\quad \left. - \bar{u}_p ( {t + \theta } )\sum \limits _{q=1}^m\beta _{pq}(t) {\bar{u}}_p(t-\tau _{pq}(t)) e^{-c_{pq}(t) {\bar{u}}_p(t-\tau _{pq}(t))} \right\} \nonumber \\&= \frac{\Pi _p \left( {\theta ,t} \right) }{\bar{u}_p(t)} +\frac{\sum \nolimits _{q=1, q\ne {p}}^n a_{{p}q}(t)}{\bar{u}_p(t)}\left\{ ({\bar{u}}_q(t+\theta )- \bar{u}_q (t))- {\bar{u}}_q(t)\frac{{\bar{u}}_p(t+\theta )- \bar{u}_p(t)}{\bar{u}_p(t)}\right\} \nonumber \\&\quad +\frac{1}{[\bar{u}_p(t)]^2}\left\{ {\bar{u}_p(t)}\sum \limits _{q=1}^m \beta _{{p}q}(t) \left[ {\bar{u}}_p(t-\tau _{pq}(t)+\theta )e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t)+\theta )} \right. \right. \nonumber \\&\quad \left. \left. - {\bar{u}}_p(t-\tau _{pq}(t))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))} \right] \right. \nonumber \\&\quad \left. - \sum \limits _{q=1}^m \beta _{{p}q}(t){\bar{u}}_p(t-\tau _{pq}(t))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))} [\bar{u}_p ( {t + \theta }) -\bar{u}_p (t) ] \right\} \nonumber \\&= \frac{\Pi _p \left( {\theta ,t} \right) }{\bar{u}_p(t)} +\frac{\sum \nolimits _{q=1, q\ne {p}}^n a_{{p}q}(t)}{\bar{u}_p(t)}\bar{u}_q (t)(U_q(t)-U_p(t)) \nonumber \\&\quad +\frac{\sum \nolimits _{q=1}^m \beta _{{p}q}(t)}{\bar{u}_p(t)} \left\{ \left[ {\bar{u}}_p(t-\tau _{pq}(t))(1+U_p(t-\tau _{pq}(t)))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))(1+U_p(t-\tau _{pq}(t)))} \right. \right. \nonumber \\&\quad \left. \left. - {\bar{u}}_p(t-\tau _{pq}(t))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))} \right] - {\bar{u}}_p(t-\tau _{pq}(t))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))} U_p (t) \right\} \nonumber \\&= \frac{\Pi _p \left( {\theta ,t} \right) }{\bar{u}_p(t)} +\frac{\sum \nolimits _{q=1, q\ne {p}}^n a_{{p}q}(t)}{\bar{u}_p(t)}\bar{u}_q (t)U_q(t) \nonumber \\&\quad +\frac{\sum \nolimits _{q=1}^m \beta _{{p}q}(t)}{\bar{u}_p(t)} \left[ {\bar{u}}_p(t-\tau _{pq}(t))(1+U_p(t-\tau _{pq}(t)))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))(1+U_p(t-\tau _{pq}(t)))} \right. \nonumber \\&\quad \left. - {\bar{u}}_p(t-\tau _{pq}(t))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))} \right] \nonumber \\&- \left\{ \frac{\sum \nolimits _{q=1, q\ne {p}}^n a_{{p}q}(t)}{\bar{u}_p(t)}\bar{u}_q (t)U_p(t) + \frac{\sum \nolimits _{q=1}^m \beta _{{p}q}(t)}{\bar{u}_p(t)} \bar{u}_p(t-\tau _{pq}(t))e^{-c_{pq}(t){\bar{u}}_p(t-\tau _{pq}(t))} U_p (t) \right\} . \end{aligned}$$

(2.14)

Define

$$\begin{aligned} G(x, y):[c_0\bar{l}, c^0\bar{L}] \times [c_0\bar{l}, c^0\bar{L}] \rightarrow \mathbb {R}, \quad G(x, y)=\left\{ \begin{array}{l} \frac{x e^{-x}-y e^{-y}}{x-y}, x \ne y, \\ (1-x) e^{-x}, x=y. \end{array}\right. \nonumber \\ \end{aligned}$$

(2.15)

Clearly, G(x, y) is continuous on $\mathbb {R}^{2}$. It follows from Lemma 2.5 that

$$\begin{aligned} |G(x, y)|<e^{-x} \text{ for } \text{ all } (x, y) \in D:=[c_0\bar{l}, c^0\bar{L}] \times [c_0\bar{l}, c^0\bar{L}]. \end{aligned}$$

Therefore, it is possible to choose an enough small $r>0$ obeying that, for arbitrary $(u, v) \in D , p \in P$ and $t \in \mathbb {R}$,

$$\begin{aligned} |G(u, v)|<\frac{1}{e^{r \tau _p}}\left[ e^{-u}-\frac{2 r \bar{u}_p(t)}{\sum \nolimits _{q=1}^m \beta _{{p}q}(t) {\bar{l}}}\right] , \end{aligned}$$

(2.16)

and then

$$\begin{aligned} |u e^{-u}-v e^{-v}| \le \frac{1}{e^{r \tau _p}}\left[ e^{-u}-\frac{2 r \bar{u}_p(t)}{\sum \nolimits _{q=1}^m \beta _{{p}q}(t) \bar{l}}\right] |u-v|. \end{aligned}$$

(2.17)

In view of Lemma 2.6, it is evident that ${\bar{u}}_p(t)$ and ${{\bar{u}}_p^{\prime }(t)}$ are bounded on $[t_{0}, \ +\infty )$. It follows from (2.13) that ${\bar{u}}_p(t)$ is uniformly continuous on $\mathbb {R}$. Hence, for arbitrary $\varepsilon > 0$, we are able to select a small enough ${\tilde{\varepsilon }} > 0$ satisfying that

$$\begin{aligned}&|a_{pq}(t)-a_{pq}(t+\theta )|<{\tilde{\varepsilon }}, \ \ |\beta _{pq}(t)-\beta _{pq}(t+\theta )|<{\tilde{\varepsilon }}, \\&|c_{pq}(t)-c_{pq}(t+\theta )|<{\tilde{\varepsilon }}, \ \ |\tau _{pq}(t)-\tau _{pq}(t+\theta )|<{\tilde{\varepsilon }}, \end{aligned}$$

it then follows that

$$\begin{aligned} \frac{ |\Pi _p ( \theta ,t )| }{{\bar{u}_p(t)}} < \frac{1}{{4\bar{L}}}r\varepsilon , \end{aligned}$$

(2.18)

where $t \in \mathbb {R}, p \in P, q \in Q$. Furthermore, for $\tilde{\varepsilon }> 0$, by exploiting the characteristics of the set of uniform almost periodic functions [27, P. 19, corollary 2.3], it’s possible to select a relatively dense subset $\Lambda _{\tilde{\varepsilon }}$ of $\mathbb {R}$ agreeing that

$$\begin{aligned} \begin{aligned}&\left. \begin{array}{l} |a_{pq}(t)-a_{pq}(t+\theta )|<{\tilde{\varepsilon }}, \ \ |\beta _{pq}(t)-\beta _{pq}(t+\theta )|<{\tilde{\varepsilon }}, \\ |c_{pq}(t)-c_{pq}(t+\theta )|<{\tilde{\varepsilon }}, \ \ |\tau _{pq}(t)-\tau _{pq}(t+\theta )|<{\tilde{\varepsilon }}, \end{array} \right\} \\&\quad \ \theta \in \Lambda _{{\tilde{\varepsilon }}}, t \in \mathbb {R}, p \in P, q \in Q. \end{aligned} \end{aligned}$$

(2.19)

For the simplicity of notation, we designate $\Lambda _{\varepsilon }=\Lambda _{{\tilde{\varepsilon }}}$. Then, for any $\theta \in \Lambda _{\varepsilon }$, (2.18) and (2.19) give us

$$\begin{aligned} \frac{ |\Pi _p ( \theta ,t )| }{{\bar{u}_p(t)}} < \frac{1}{{4\bar{L}}}r\varepsilon . \end{aligned}$$

(2.20)

Denote

$$\begin{aligned} Y(t)=(Y_1(t), Y_2(t), \dots , Y_n(t)), \ \ Y_{p}(t)=e^{rt}U_{p}(t), \ \text{ where } \ p \in P. \end{aligned}$$

Let $I(t)=\sup \nolimits _{t_{0}-\tau < s\le t}\{e^{rs}\Vert U(s)\Vert \}$, and $p_t$ be an index such that

$$\begin{aligned} |Y_{p_t}(t)|=\Vert Y(t)\Vert . \end{aligned}$$

(2.21)

It is easy to see that $e^{rt}\Vert U(t)\Vert \le I(t)$, and I(t) is nondecreasing.

We are now in a position to complete the subsequent verification in two cases.

Case 1. If

$$\begin{aligned} I(t)> {e^{r t}}\Vert U(t)\Vert \ \text {for arbitrary} \ t > {K_0}, \end{aligned}$$

(2.22)

we assert that

$$\begin{aligned} I(t) \equiv \Vert I(K_0)\Vert \ \text{ for } \text{ any } t > {K_0}. \end{aligned}$$

(2.23)

Assume contrarily that there exists ${s_1} > {K_0}$ obeying that $I(s_1) > I(K_0)$. Since

$$\begin{aligned} I(s_1) > {e^{r s_1}}\Vert U(s_1)\Vert , \ \text{ and } \ {e^{r t}}\Vert U(t)\Vert \le I(K_0) \text{ for } \text{ arbitrary } t \in [t_{0}-\tau , \ {K_0}], \end{aligned}$$

there must be a constant $\alpha \in ( {{K_0}, \ {s_1}} )$ such that

$$\begin{aligned} {e^{r \alpha }}\Vert U(\alpha )\Vert = I(s_1) \ge I(\alpha ), \end{aligned}$$

which leads to a contradiction with (2.22). Hence, the aforementioned assertion is true and we can choose ${s_2} > {K_0}$ satisfying

$$\begin{aligned} \Vert U(t)\Vert \le {e^{ - rt}}I( t ) = {e^{ - rt}}I(K_0) < \frac{\varepsilon }{{4{\bar{L}}}} \ \ \text{ for } \text{ arbitrary }\ t \ge {s_2}. \end{aligned}$$

(2.24)

Case 2. If there is a ${s^*}$ obeying that ${s^*} \ge {K_0}$ and $I(s^*)=e^{rs^*}\Vert U(s^*)\Vert$. It can be deduced from (2.14), (2.17), (2.20) and the definition of Dini derivative that

$$\begin{aligned} 0\le & {D^ - }(e^{rs}|U_{p_{s^{*}}}(s)|)\bigg |_{s = s^*} \\\le & r e^{rs^*}|U_{p_{s^*}}(s^*)|+e^{rs^*}\frac{|\Pi _{p_{s^*}} \left( {\theta ,s^*} \right) |}{\bar{u}_{p_{s^*}}(s^*)} + e^{rs^*} \frac{\sum \nolimits _{q=1, q\ne {p_{s^*}}}^n a_{{p_{s^*}}q}(s^*)}{\bar{u}_{p_{s^*}}(s^*)}\\ & \bar{u}_q (s^*) ( |U_q(s^*)|-|U_{p_{s^*}}(s^*)|) \\ & -\frac{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*)}{\bar{u}_{p_{s^*}}(s^*)}{\bar{u}}_{p_{s^*}}(s^*-\tau _{{p_{s^*}}q}(s^*)) e^{rs^*-c_{{p_{s^*}}q}(s^*){\bar{u}}_{p_{s^*}}(s^*-\tau _{{p_{s^*}}q}(s^*))} |U_{p_{s^*}} (s^*)| \\ & +\,e^{rs^*} \frac{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*)}{\bar{u}_{p_{s^*}}(s^*)} \frac{1}{c_{p_{s^*}q}(s^*)}{\Bigg |}c_{p_{s^*}q}(s^*){\bar{u}}_{p_{s^*}}(t-\tau _{p_{s^*}q}(s^*))\\ & \times \, (1+U_{p_{s^*}}(t-\tau _{p_{s^*}q}(s^*)))e^{-c_{p_{s^*}q}(s^*){\bar{u}}_{p_{s^*}}(t-\tau _{p_{s^*}q}(s^*))(1+U_{p_{s^*}}(t-\tau _{p_{s^*}q}(s^*)))} \\ & -\, c_{p_{s^*}q}(s^*)\bar{u}_{p_{s^*}}(t-\tau _{p_{s^*}q}(s^*))e^{-c_{p_{s^*}q}(s^*)\bar{u}_{p_{s^*}}(t-\tau _{p_{s^*}q}(s^*))} {\Bigg |} \\\le & r e^{rs^*}|U_{p_{s^*}}(s^*)|+e^{rs^*}\frac{|\Pi _{p_{s^*}} \left( {\theta ,s^*} \right) |}{\bar{u}_{p_{s^*}}(s^*)}+ e^{rs^*} \frac{\sum \nolimits _{q=1, q\ne {p_{s^*}}}^n a_{{p_{s^*}}q}(s^*)}{\bar{u}_{p_{s^*}}(s^*)}\\ & \bar{u}_q (s^*) ( |U_q(s^*)|-|U_{p_{s^*}}(s^*)|) \\ & -\,\frac{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*)}{\bar{u}_{p_{s^*}}(s^*)}{\bar{u}}_{p_{s^*}}(s^*-\tau _{{p_{s^*}}q}(s^*)) \left\{ e^{rs^*-c_{{p_{s^*}}q}(s^*){\bar{u}}_{p_{s^*}}(s^*-\tau _{{p_{s^*}}q}(s^*))} |U_{p_{s^*}} (s^*)| \right. \\ & \left. -\,e^{rs^*}\frac{1}{e^{r \tau _{p_{s^*}}}} |U_{p_{s^*}}(s^*-\tau _{p_{s^*}q}(s^*))| \left[ e^{-c_{p_{s^*} q}(s^*){\bar{u}}_{p_{s^*}}(s^*-\tau _{{p_{s^*}}q}(s^*))}-\frac{2r {\bar{u}}_{p_{s^*}}(s^*)}{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*) {\bar{l}}}\right] \right\} \\= & r e^{rs^*}|U_{p_{s^*}}(s^*)|+e^{rs^*}\frac{|\Pi _{p_{s^*}} \left( {\theta ,s^*} \right) |}{\bar{u}_{p_{s^*}}(s^*)}+ \frac{\sum \nolimits _{q=1, q\ne {p_{s^*}}}^n a_{{p_{s^*}}q}(s^*)}{\bar{u}_{p_{s^*}}(s^*)}\\ & \bar{u}_q (s^*) (e^{rs^*} |U_q(s^*)|-e^{rs^*}|U_{p_{s^*}}(s^*)|) \\ & -\,\frac{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*)}{\bar{u}_{p_{s^*}}(s^*)}{\bar{u}}_{p_{s^*}}(s^*-\tau _{{p_{s^*}}q}(s^*)) \Bigg \{ e^{rs^*-c_{{p_{s^*}}q}(s^*){\bar{u}}_{p_{s^*}}(s^*-\tau _{{p_{s^*}}q}(s^*))} |U_{p_{s^*}} (s^*)| \\ & -\,e^{rs^*}\frac{1}{e^{r \tau _{p_{s^*}}}} |U_{p_{s^*}}(s^*-\tau _{p_{s^*}q}(s^*))| \Bigg [e^{-c_{p_{s^*} q}(s^*){\bar{u}}_{p_{s^*}}(s^*-\tau _{{p_{s^*}}q}(s^*))}-\frac{2r {\bar{u}}_{p_{s^*}}(s^*)}{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*) {\bar{l}}}\Bigg ] \Bigg \} \\\le & e^{rs^*}\frac{|\Pi _{p_{s^*}} \left( {\theta ,s^*} \right) |}{\bar{u}_{p_{s^*}}(s^*)}\\ & +\,\frac{\sum \nolimits _{q=1}^n \beta _{{p_{s^*}}q}(s^*)}{\bar{u}_{p_{s^*}}(s^*)} \left\{ -\Bigg [\bar{u}_{p_{s^*}}(s^*-\tau _{p_{s^*} q}(s^*))e^{-c_{p_{s^*}q}{\bar{u}}_{p_{s^*}}(s^*-\tau _{p_{s^*}q}(s^*))}-\frac{r{\bar{u}}_{p_{s^*}}(s^*)}{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*)} \Bigg ]\right. \\ & e^{r s^*}|U_{p_{s^*}}(s^*)| \left. +{\bar{u}}_{p_{s^*}}(s^*-\tau _{p_{s^*}q}(s^*)) \frac{e^{r \tau _{p_{s^*}q}(s^*) }}{e^{r \tau _{p_{s^*}}}}e^{r (s^*-\tau _{p_{s^*}q}(s^*))}|U_{p_{s^*}}(s^*-\tau _{p_{s^*}q}(s^*))| \right. \\ & \left. \times \, \Bigg [ e^{-c_{p_{s^*}q}(s^*){\bar{u}}_{p_{s^*}}(s^*-\tau _{p_{s^*}q}(s^*))} -\frac{2r {\bar{u}}_{p_{s^*}}(s^*)}{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*) {\bar{l}}} \Bigg ] \right\} \\\le & \frac{\sum \nolimits _{q=1}^n \beta _{{{p_{s^*}}}q}(s^*)}{\bar{u}_{p_{s^*}}(s^*)} \left\{ -\Bigg [\bar{u}_{p_{s^*}}(s^*-\tau _{p_{s^*} q}(s^*))e^{-c_{p_{s^*}q}{\bar{u}}_{p_{s^*}}(s^*-\tau _{p_{s^*}q}(s^*))}-\frac{r{\bar{u}}_{p_{s^*}}(s^*)}{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*)} \Bigg ] I(s^*) \right. \\ & \left. +\,{\bar{u}}_{p_{s^*}}(s^*-\tau _{p_{s^*}q}(s^*)) \Bigg [ e^{-c_{p_{s^*}q}(s^*){\bar{u}}_{p_{s^*}}(s^*-\tau _{p_{s^*}q}(s^*))} -\frac{2r {\bar{u}}_{p_{s^*}}(s^*)}{\sum \nolimits _{q=1}^m \beta _{{p_{s^*}}q}(s^*) {\bar{l}}} \Bigg ] I(s^*) \right\} \\ & +e^{rs^*}\frac{|\Pi _{p_{s^*}} \left( {\theta ,s^*} \right) |}{\bar{u}_{p_{s^*}}(s^*)} \\\le & rI( s^*) +e^{rs^*}\frac{|\Pi _{p_s} \left( {\theta ,s^*} \right) |}{\bar{u}_{p_s}(s^*)} -{2r} I(s^*) \\= & - rI(s^*) +e^{rs^*}\frac{|\Pi _{p_s} \left( {\theta ,s^*} \right) |}{\bar{u}_{p_s}(s^*)} \\\le & - rI( s^*) + e^{rs^*}\frac{1}{4{\bar{L}}}r\varepsilon . \end{aligned}$$

This indicates

$$\begin{aligned} e^{rs^*}\Vert U(s^*)\Vert = I(s^*) \le \frac{1}{4{\bar{L}}}\varepsilon e^{rs^*} \ \text{ and } \ \Vert U(s^*)\Vert \le \frac{1}{4\bar{L}}\varepsilon . \end{aligned}$$

Similarly, we drive

$$\begin{aligned} e^{r\bar{t}}\Vert U(\bar{t})\Vert \le \frac{1}{4{\bar{L}}}\varepsilon e^{r\bar{t}} \ \text{ with } \ \Vert U(\bar{t})\Vert \le \frac{1}{4\bar{L}}\varepsilon \ \ \text{ if } \ I( \bar{t} ) = e^{r \bar{t}}\Vert U(\bar{t})\Vert \ \text{ and } \ \bar{t} > s^*.\nonumber \\ \end{aligned}$$

(2.25)

Furthermore, when $I(\tilde{t}) > e^{r \tilde{t}}\Vert U(\tilde{t})\Vert$ for $\tilde{t} > s^*$, we can take $s^* \le {s_3} < \tilde{t}$ such that

$$\begin{aligned} I(s_3) = e^{rs_3}\Vert U(s_3)\Vert , \ \text{ and } \ I(s) > e^{r s} \Vert U(s)\Vert \ \text{ for } \text{ all } \ s \in ( s_3,\ \tilde{t}]. \end{aligned}$$

(2.26)

It follows from (2.25) that

$$\begin{aligned} \Vert U(s_3) \Vert \le \frac{\varepsilon }{4{\bar{L}}}. \end{aligned}$$

A similar reasoning as that employed in Case 1 shows that

$$\begin{aligned} I( s ) \equiv I( s_3) \ \text{ for } \text{ all } \ s \in ( s_3, \ \tilde{t} ]. \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert U(\tilde{t})\Vert< e^{ - r\tilde{t}}I( \tilde{t} ) = e^{ - r \tilde{t}}I(s_3) = \Vert U(s_3)\Vert e^{ -r(\tilde{t}-s_3)} < \frac{\varepsilon }{4{\bar{L}}}, \end{aligned}$$

which implies that there exists $N > \max \{ s^*, s_2\}$ such that

$$\begin{aligned} \Vert U(t) \Vert \le \frac{\varepsilon }{4{\bar{L}}}, \ \text{ and } \ | \bar{u}_{p}( t + \theta ) - \bar{u}_{p}(t) | < \frac{\varepsilon }{2} \ \text {for arbitrary}\ t > N, \ p \in P. \end{aligned}$$

This completes the proof of Lemma 2.7. $\square$

3 Global Exponential Stability Analysis

In this section, we will confine ourselves to prove the main results on existence and global exponential stability of positive almost periodic solution for system (1.5).

Theorem 3.1

If all the conditions in Lemma 2.7 are valid, then system (1.5) admits a unique almost periodic solution which is globally exponentially stable.

Proof

The proof will be subdivided into three steps.

Step 1. Consider $z_p( t ) = z_p( t;t_0,\varphi )$ as a solution of system (1.5) that fulfills the initial data in Lemma 2.7, and designate

$$\begin{aligned} z_p( t ) \equiv z_p( t - \tau _p ) \ \ \ \text{ for } \text{ arbitrary } \ t \in ( - \infty ,t_0 - \tau _p ), \end{aligned}$$

(3.1)

and

$$\begin{aligned} \pi _p ( i,t )&=-[d_p(t+t_i)-d_p(t)] z_p(t+t_i)+\sum \limits _{q=1, q\ne {p}}^n[ a_{{p}q}(t+t_i)-a_{{p}q}(t)] z_q(t+t_i) \nonumber \\&\quad +\sum \limits _{q=1}^m [\beta _{{p}q}(t+t_i)- \beta _{{p}q}(t)] z_p(t+t_i-\tau _{pq}(t+t_i)) e^{-c_{pq}(t+t_i)z_p(t+t_i-\tau _{pq}(t+t_i))} \nonumber \\&\quad +\sum \limits _{q=1}^m \beta _{{p}q}(t)[z_p(t+t_i-\tau _{pq}(t+t_i))e^{-c_{pq}(t+t_i)z_p(t+t_i-\tau _{pq}(t+t_i))} \nonumber \\&\quad -z_p(t-\tau _{pq}(t)+t_i)e^{-c_{pq}(t+t_i)z_p(t-\tau _{pq}(t)+t_i)}] \nonumber \\&\quad +\sum \limits _{q=1}^m \beta _{{p}q}(t)[z_p(t-\tau _{pq}(t)+t_i)e^{-c_{pq}(t+t_i)z_p(t-\tau _{pq}(t)+t_i)} \nonumber \\&\quad -z_p(t-\tau _{pq}(t)+t_i)e^{-c_{pq}(t)z_p(t-\tau _{pq}(t)+t_i)}] \ \ \text {for all} \ t \in \mathbb {R}\ \text {and}\ p\in P, \end{aligned}$$

(3.2)

where $\ \{t_i \}_{i = 1}^{ + \infty }$ is an arbitrary sequence of real numbers. Observing the boundedness of $z_p( t )$ and $z_p'( t )$ on $[t_{0}, \ +\infty )$, one can obtain from (3.1) that $z_p( t )$ exhibits uniform continuity on $\mathbb {R}$. This follows from [27, p.19, Corollary 2.3], along with the characteristics of almost periodic function family $\Big \{ \sum \nolimits _{q=1}^m \beta _{{p}q}(t), \sum \nolimits _{q=1, q\ne {p}}^n a_{{p}q}(t), d_p(t), c_{pq}(t), \tau _{pq} ( t )\Big \}$, we can take a sequence $\{ t_i\}_{i = 1}^{ + \infty }$ which satisfies $\mathop {\lim } \nolimits _{i \rightarrow + \infty } {t_i} = + \infty$ and

$$\begin{aligned} \Big | \sum \limits _{q=1}^m \beta _{{p}q}(t + t_i) - \sum \limits _{q=1}^m \beta _{{p}q}(t)\Big |< & \frac{1}{i},\Big | \sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(t+t_i) - \sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(t)\Big |\\< & \frac{1}{i}, | d_p(t+t_i) - d_p(t)| < \frac{1}{i}, \end{aligned}$$

$$\begin{aligned} |c_{pq}(t+t_i)-c_{pq}(t)|<\frac{1}{i}, |\tau _{pq} ( t +t_i)-\tau _{pq} ( t )|<\frac{1}{i}, | \pi _p ( i,t) | < \frac{1}{i}, \end{aligned}$$

(3.3)

for any $t \in \mathbb {R}$ and $i \in \{1,2,3, \dots \}$.

From the boundedness of $z_p'( t )$ on $[t_{0}, \ +\infty )$, $\varphi _p' \in C([-\tau _p,0], \mathbb {R})$, and (3.1), one can see that $\{ z_p( t + t_i)\}_{i = 1}^{ + \infty }$ is uniformly bounded and equiuniformly continuous on $\mathbb {R}$. It is readily seen from Arzalà-Ascoli Lemma that there exists a subsequence $\{z_p(t+t_{i_{n}})\}_{n\ge 1}$ of $\{z_p(t+t_{i})\}_{i\ge 1}$ such that $z_p(t+t_{i_{n}})$ (To maintain simplicity, we continue to use $z_p(t+t_{i})$) uniformly converges to a continuous function $z_p^{*}(t)$ on any bounded closed subinterval of $\mathbb {R}$. This, combined with Lemma 2.6, results in

$$\begin{aligned} l^* \le {z_p^*}(t) \le L^* \ \text{ for } \text{ arbitrary } \ t \in \mathbb {R}, \ p \in P. \end{aligned}$$

(3.4)

Due to (3.2) and (3.3), for any $\Delta t \in \mathbb {R}$ and $t \ge {t_0}$, one gets

$$\begin{aligned}&z_p^*(t + \Delta t) - z_p^*(t) \nonumber \\&\quad = \mathop {\lim } \limits _{i \rightarrow + \infty } [ z_p(t + \Delta t + t_i) - z_p(t + t_i)] \nonumber \\&\quad = \mathop {\lim }\limits _{i \rightarrow + \infty } \int _t^{t + \Delta t} {z_p'(s + t_i)} ds \nonumber \\&\quad = \mathop {\lim }\limits _{i \rightarrow + \infty } \int _t^{t + \Delta t} \left[ -d_p(s + t_i)z_p(s + t_i)+\sum \limits _{q=1, q\ne p}^n a_{pq}(s + t_i)z_q(s + t_i) \right. \nonumber \\&\qquad \left. +\sum \limits _{q=1}^m\beta _{pq}(s + t_i)z_p(s + t_i-\tau _{pq}(s+t_i)) e^{-c_{pq}(s + t_i)z_p(s+t_i-\tau _{pq}(s+t_i))} \right] ds \nonumber \\&\quad = \mathop {\lim }\limits _{i \rightarrow + \infty } \int _t^{t + \Delta t} \left[ - d_p (s)z_p\left( {s + t_i } \right) +\sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(s) z_q(s + t_i) \right. \nonumber \\&\qquad \left. +\sum \limits _{q=1}^m \beta _{{p}q}(s)z_p(s + t_i-\tau _{pq}(s))e^{-c_{pq}(s)z_p(s + t_i-\tau _{pq}(s))} + \pi _p ( {i,s} ) \right] ds \nonumber \\&\quad = \mathop {\lim }\limits _{i \rightarrow + \infty } \int _t^{t + \Delta t} \pi _p ( i,s ) ds+ \int _t^{t + \Delta t} \left[ - d_p (s)z_p^*(s) + \sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(s) z_q^*(s) \right. \nonumber \\&\quad \left. +\sum \limits _{q=1}^m \beta _{{p}q}(s)z_p^*(s -\tau _{pq}(s))e^{-c_{pq}(s)z_p^*(s -\tau _{pq}(s))} \right] ds \nonumber \\&\quad = \int _t^{t + \Delta t} \left[ - d_p (s)z_p^*(s) + \sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(s) z_q^*(s) \right. \nonumber \\&\qquad \left. +\sum \limits _{q=1}^m \beta _{{p}q}(s)z_p^*(s -\tau _{pq}(s))e^{-c_{pq}(s)z_p^*(s -\tau _{pq}(s))} \right] ds, \end{aligned}$$

(3.5)

where $t + {t_i}, \ t + {t_i} + \Delta t \ge {t_0}$. Apparently, (3.5) leads to

$$\begin{aligned} \begin{aligned} {( {{z_p^*}(t)} )^\prime }&= - d_p (t)z_p^*(t) + \sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(t) z_q^*(t)\\&\quad +\sum \limits _{q=1}^m \beta _{{p}q}(t)z_p^*(t -\tau _{pq}(t))e^{-c_{pq}(t)z_p^*(t -\tau _{pq}(t))}, \end{aligned} \end{aligned}$$

(3.6)

for all $t\ge {t_0}$. This shows that ${z_p^*}(t)$ is a solution of system (1.5).

Step 2. We will confirm that ${z_p^*}(t)$ is almost periodic on $\mathbb {R}$. In accordance with Lemma 2.7, for any given $\varepsilon > 0$, there exists a relatively dense subset $\Lambda _{\varepsilon }$ of $\mathbb {R}$ incorporating the characteristic of having a sufficiently large $N> 0$ corresponding to that

$$\begin{aligned} | {z_p( {t + \theta } ) - z_p( t )} | < \frac{\varepsilon }{2} \ \text{ for } \text{ arbitrary } \ t> N, \ p \in P. \end{aligned}$$

(3.7)

For every fixed $s \in \mathbb {R}$, select ${N_1} > N$ such that for each $i > {N_1}$,

$$\begin{aligned} s + {t_i} > N \ \text{ and } \ | {z_p(s + {t_i} + \theta ) - z_p(s + {t_i})}| < \frac{\varepsilon }{2}. \end{aligned}$$

(3.8)

Letting ${i \rightarrow + \infty }$, (3.8) implies that

$$\begin{aligned} |{z_p^*}(s + \theta ) - {z_p^*}(s)| = \mathop {\lim }\limits _{i \rightarrow + \infty } | {z_p(s + {t_i} + \theta ) - z_p(s + {t_i})} | \le \frac{\varepsilon }{2} < \varepsilon , \end{aligned}$$

which means that ${z_p^*}(t)$ is a positively almost periodic function.

Step 3. We shall validate that ${z_p^*}(t)$ is globally exponentially stable. For this purpose, we label

$$\begin{aligned} x _{p}^{*}(t )=v_{p}^{-1}z_{p}^{*}(t), \ x _{p}(t )=v_{p}^{-1}z_{p}(t; t_{0}, \varphi ), \end{aligned}$$

and set

$$\begin{aligned} w(t)=(w_1 (t), w_2 (t), \dots ,w_n (t)), \ \ w_p (t) = \frac{{x_{p}(t)}}{{{x_{p}^*}(t)}} - 1 \ \text{ for } \text{ all }\ t\in [t_{0}- \tau _p,\ +\infty ). \end{aligned}$$

Then, for arbitrary $p \in P$ and $t \ge t_0$, produces

$$\begin{aligned} \left. \begin{array}{ll} x_p^\prime (t) =v_{p}^{-1}\Big [ - d_p(t)v_{p}x_p(t) + \sum \limits _{q = 1, q \ne p}^n a_{pq}(t)v_{q } x_q(t) \\ \ \ \ \ \ \ \ \ \ \ \ \quad + \sum \limits _{q = 1}^m \beta _{pq}(t)v_{p} x_p( t - \tau _{pq}(t) )e^{ - c_{pq}(t)v_{p}x_p( t - \tau _{pq}(t) )}\Big ], \\ (x_{p}^*)_{t_{0}}=v_{p}^{-1}\varphi _{p}, \ \ \ \varphi \in B_+ \ \text{ with } \ \varphi _{p}(0)>0, \end{array} \right\} \end{aligned}$$

(3.9)

and

$$\begin{aligned} w_p '(t)&= \frac{{x_p'(t){x_p^*}(t) - x_p(t)({x_p^*}(t))'}}{{{{({x_p^*}(t))}^2}}} \nonumber \\&= \frac{v_p^{-1}}{{{{({x_p^*}(t))}^2}}}\Bigg \{ {x_p^*}(t)\Bigg [-d_p(t)v_px_p(t)+\sum \limits _{q=1, q\ne p}^n a_{pq}(t)v_qx_q(t) \nonumber \\&\quad +\sum \limits _{q=1}^m\beta _{pq}(t)v_px_p(t-\tau _{pq}(t)) e^{-c_{pq}(t)v_px_p(t-\tau _{pq}(t))}\Bigg ] \nonumber \\&\quad - x_p(t)\Bigg [ - d_p (t)v_px_p^*(t) + \sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(t)v_qx_q^*(t) \nonumber \\&\quad +\sum \limits _{q=1}^m \beta _{{p}q}(t)v_px_p^*(t -\tau _{pq}(t))e^{-c_{pq}(t)v_px_p^*(t -\tau _{pq}(t))}\Bigg ]\Bigg \} \nonumber \\&= \frac{1}{{{v_p{x_p^*}(t)}}}\left\{ -d_p(t)v_px_p(t)+\sum \limits _{q=1, q\ne p}^n a_{pq}(t)v_qx_q(t) \right. \nonumber \\&\quad \left. +\sum \limits _{q=1}^m\beta _{pq}(t)v_px_p(t-\tau _{pq}(t)) e^{-c_{pq}(t)v_px_p(t-\tau _{pq}(t))} \right. \nonumber \\&\quad \left. - \Bigg [ - d_p (t)v_px_p(t) + \sum \limits _{q=1, q\ne {p}}^n a_{{p}q}(t)v_qx_q^*(t)\frac{x_p(t)}{x_p^*(t)}\right. \nonumber \\&\quad \left. +\sum \limits _{q=1}^m \beta _{{p}q}(t)v_p\frac{x_p(t)}{x_p^*(t)}x_p^*(t -\tau _{pq}(t))e^{-c_{pq}(t)v_px_p^*(t -\tau _{pq}(t))}\Bigg ]\right\} \nonumber \\&= \frac{1}{{{v_p{x_p^*}(t)}}}\left\{ \sum \limits _{q=1, q\ne p}^n a_{pq}(t)v_qx_q^*(t)[w_q(t)-w_p(t)] \right. \nonumber \\&\quad \left. +\sum \limits _{q=1}^m\beta _{pq}(t)v_p\Bigg [x_p^*(t-\tau _{pq}(t))(w_p(t-\tau _{pq}(t))+1)\right. \nonumber \\ &\quad \left. e^{-c_{pq}(t)v_px_p^*(t-\tau _{pq}(t))(w_p(t-\tau _{pq}(t))+1)} \right. \nonumber \\&\left. - (w_p(t)+1)x_p^*(t-\tau _{pq}(t))e^{-c_{pq}(t)v_px_p^*(t -\tau _{pq}(t))}\Bigg ]\right\} . \end{aligned}$$

(3.10)

Now, we prove that $z_p^*(t)$ is stable. For any $\varepsilon >0$, let

$$\begin{aligned} \begin{array}{lll} k^*=\min \limits _{p \in P}v_p^{-1} l^*,\\ H = \frac{{{k^*}\varepsilon }}{L^*} \ \text{ and } \ | (x_{p})_{t_{0}}(\theta )-v_{p}^{-1}\varphi _{p}(\theta )| < H \ \text{ with } \ p\in P \ \text{ and } \ t\in [-\tau _{p}, \ t_{0}], \end{array} \end{aligned}$$

we now verify that

$$\begin{aligned} | {x_p(t) - {x_p^*}(t)} | < \varepsilon \ \text{ with } \ \ p \in P \ \text {and} \ t \in [-\tau _p, +\infty ). \end{aligned}$$

(3.11)

It is easy to see that for every $t \in [ {{t_0} - \tau _p , \ t_{0}} ]$,

$$\begin{aligned} | {w_p (t)} | = {\Big |} {\frac{{x_p(t) - {x_p^*}(t)}}{{{x_p^*}(t)}}}{\Big |} < \frac{H}{{{x_p^*}(t)}} \le \frac{H}{k^* }. \end{aligned}$$

(3.12)

We assert

$$\begin{aligned} | {w_p (t)} |< \frac{H}{k^*} \ \text{ for } \text{ all } \ t>t_{0} \ \text {and} \ p \in P. \end{aligned}$$

(3.13)

If the assertion would not hold, then there exist $p_1 \in P$ and $S_{1}>t_0$ satisfying that either

$$\begin{aligned} w_{p_1} ({S_1}) = \frac{H}{k^*}, \ \text{ and } \ | {w_q (t)} | < \frac{H}{k^*} \ \ \text {for arbitrary }t \in [{t_0} - \tau _q, \ S_1 )\text { and }q \in P,\nonumber \\ \end{aligned}$$

(3.14)

or

$$\begin{aligned} w_{p_1} ({S_1}) = -\frac{H}{k^*}, \ \text{ and } \ | {w_q (t)} | < \frac{H}{k^*}\ \ \text {for arbitrary }t \in [{t_0} - \tau _q, \ S_1 )\text { and }q \in P.\nonumber \\ \end{aligned}$$

(3.15)

If (3.14) is satisfied, and there is a $q \in Q$ such that $\beta _{p_1q}(S_1)w_{q} ({S_1} - \tau _{{p_1}q} ({S_1})) \ne 0$, we get from (3.23), (3.10), (2.4), Lemmas 2.5 and 2.6 that

$$\begin{aligned} 0&\le w_{p_1} '({S_1})\\&= \frac{1}{v_{p_1}{x_{p_1}^*}(S_1)}\left\{ \sum \limits _{q=1, q\ne {p_1}}^n a_{{p_1}q}(S_1)v_qx_q^*(S_1)[w_q(S_1)-w_{p_1}(S_1)] \right. \\&\quad \left. +\sum \limits _{q=1}^m\beta _{{p_1}q}(S_1)v_{p_1}\Bigg [x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))(w_{p_1}(S_1-\tau _{{p_1}q}(S_1))+1)\right. \\&\quad \left. \times e^{-c_{{p_1}q}(S_1)v_{p_1}x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))(w_{p_1}(S_1-\tau _{{p_1}q}(S_1))+1)}\right. \\&\quad \left. - (w_{p_1}(S_1)+1)x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))e^{-c_{{p_1}q}(S_1)v_{p_1}x_{p_1}^*(S_1 -\tau _{{p_1}q}(S_1))}\Bigg ]\right\} \\&\le \frac{\sum \nolimits _{q=1}^m\beta _{{p_1}q}(S_1)}{v_{p_1}{x_{p_1}^*}(S_1)c_{p_1q}(S_1)}\Bigg \{ c_{p_1q}(S_1)v_{p_1}x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))(w_{p_1}(S_1-\tau _{{p_1}q}(S_1))+1) \\&\quad \times e^{-c_{{p_1}q}(S_1)v_{p_1}x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))(w_{p_1}(S_1-\tau _{{p_1}q}(S_1))+1)} \\&\quad -c_{{p_1}q}(S_1)v_{p_1}x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))e^{-c_{{p_1}q}(S_1)v_{p_1}x_{p_1}^*(S_1 -\tau _{{p_1}q}(S_1))} \\&\quad - c_{{p_1}q}(S_1)v_{p_1}w_{p_1}(S_1)x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))e^{-c_{{p_1}q}(S_1)v_{p_1}x_{p_1}^*(S_1 -\tau _{{p_1}q}(S_1))} \Bigg \} \\&< \frac{\sum \nolimits _{q=1}^m\beta _{{p_1}q}(S_1)}{v_{p_1}{x_{p_1}^*}(S_1)c_{p_1q}(S_1)}\Bigg \{ c_{p_1q}(S_1)v_{p_1}x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))\\&\quad \times |w_{p_1}(S_1-\tau _{{p_1}q}(S_1))| e^{-c_{{p_1}q}(S_1)v_{p_1}x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))} \\&\quad - c_{{p_1}q}(S_1)v_{p_1}\frac{H}{k^*}x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))e^{-c_{{p_1}q}(S_1)v_{p_1}x_{p_1}^*(S_1 -\tau _{{p_1}q}(S_1))} \Bigg \} \\&= \frac{\sum \nolimits _{q=1}^m\beta _{{p_1}q}(S_1)}{x_{p_1}^*(S_1)}x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))e^{-c_{{p_1}q}(S_1)v_{p_1}x_{p_1}^*(S_1-\tau _{{p_1}q}(S_1))}\\&\qquad \Big [-\frac{H}{k^*}+|w_{p_1}(S_1-\tau _{p_1 q}(S_1)){|}\Big ] \\&\le 0, \end{aligned}$$

which is a contradiction. In addition, when $\beta _{p_1q}(S_1) w_{q}({S_1} - \tau _{{p_1}q}({S_1})) = 0$ for all $q \in Q$, we can establish the aforementioned contradiction as well.

If (3.15) is true, a contradiction arises such that (3.13) holds by a similar manner, so (3.11) follows, and then

$$\begin{aligned} |w_p(t)|&=\bigg |\frac{x_p(t)-x_p^*(t)}{x_p^*(t)}\bigg | \\&= \bigg |\frac{v_p^{-1}z_p(t)-v_p^{-1}z_p^*(t)}{v_p^{-1}z_p^*(t)}\bigg | \\&= \bigg |\frac{z_p(t)-z_p^*(t)}{z_p^*(t)}\bigg | \\&<\frac{H}{k^*}. \end{aligned}$$

Thus,

$$\begin{aligned} |z_p(t)-z_p^*(t)|<z_p^*(t)\frac{H}{k^*} \le L^*\frac{H}{k^*}=\varepsilon \ \text {for all}\ t \ge t_0 \ \text {and} \ p \in P,\end{aligned}$$

which implies that $z_p^ {*}(t)$ is stable.

Finally, it suffices to prove the global exponential attractiveness of $z_p^{*}(t)$. From (2.4) and Lemma 2.6, one can choose $0<{\bar{l}}< l^{*} \le l \le L \le L^{*}< {\bar{L}}$ such that

$$\begin{aligned} {\bar{L}} c_{pq}(t) < 2 \ \ \text {for all} \ t \in \mathbb {R}, q \in Q, p \in P.\end{aligned}$$

According to (2.15) and Lemma 2.5, one can choose a small enough positive constant r obeying that, for arbitrary $(u, v) \in D , p \in P$ and $t \in \mathbb {R}$,

$$\begin{aligned} |G(u, v)|<\frac{1}{e^{r \tau _p}}\left[ e^{-u}-\frac{2 r x_p^*(t)}{\sum \nolimits _{q=1}^m \beta _{{p}q}(t) {\bar{l}}}\right] , \end{aligned}$$

(3.16)

and then

$$\begin{aligned} \left| u e^{-u}-v e^{-v}\right| \le \frac{1}{e^{r \tau _p}}\left[ e^{-u}-\frac{2 r x_p^*(t)}{\sum \nolimits _{q=1}^m \beta _{{p}q}(t) {\bar{l}}}\right] |u-v|. \end{aligned}$$

(3.17)

Define

$$\begin{aligned} W_p(t) = e^{rt}|w_{p}(t)| \ \text{ for } \text{ all } t\in \mathbb {R} \ \text {and} \ p \in P. \end{aligned}$$

(3.18)

In light of (3.4) and Lemma 2.6, there exists a large enough $T^{*}>t_0$ such that

$$\begin{aligned} 0< {\bar{l}}< {z_p^*}(t),\ z_p(t) < {\bar{L}} \ \text {for any} \ t>T^{*} \text {and} \ p \in P. \end{aligned}$$

(3.19)

Clearly, for any $t\in [t_0- \tau , \ T^{*}]$ and $p \in P$,

$$\begin{aligned} W_p(t) < \mathop {\max }\limits _{s \in [ t_{0} - \tau , \ {T^*}]} \Vert e^{rs}w(s)\Vert + 1 \mathop = \limits ^\Delta {M_{\varphi }}. \end{aligned}$$

(3.20)

We claim that

$$\begin{aligned} W_p(t)< {M_{\varphi }} \ \text{ for } \text{ all } \ t>T^{*} \ \text {and} \ p \in P. \end{aligned}$$

(3.21)

Assume that, in contradiction to the conclusion (3.21), there exist $p_2 \in P$ and $T_0>T^{*}$ satisfying that

$$\begin{aligned} W_{p_2}(T_0)= {M_{\varphi }}\ \text{ and } \ W_q(t)< {M_{\varphi }} \ \text{ for } \text{ arbitrary } \ t\in [t_0-\tau _q, \ T_0 )\ \text {and}\ q \in P.\nonumber \\ \end{aligned}$$

(3.22)

Using (3.10), (3.16) and (3.19), we obtain that

$$\begin{aligned} 0\le & D^ - ( e^{rs} | w_{p_2}(s) |)\bigg |_{s = T_0 }\\\le & re^{r T_0}|w_{p_2}(T_0)| +e^{r T_0} \frac{1}{v_{p_2}x_{p_2}^*(T_0)} \\ & \left\{ \sum \limits _{q=1,q \ne p_2}^na_{p_2q}(T_0)v_qx_q^*(T_0)[|w_q(T_0)|-|w_{p_2}(T_0)|]\right. \\ & +\,\sum \limits _{q=1}^m \beta _{{p_2}q}(T_0)v_{p_2}\Bigg |x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))(w_{p_2}(T_0-\tau _{{p_2}q}(T_0))+1)\\ & \times \, e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))(w_{p_2}(T_0-\tau _{{p_2}q}(T_0))+1)} \\ & -\,x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))}\Bigg | \\ & \left. -\,\sum \limits _{q=1}^m \beta _{{p_2}q}(T_0)v_{p_2}|w_{p_2}(T_0)|x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))}\right\} \\\le & re^{r T_0}|w_{p_2}(T_0)| +e^{r T_0} \frac{1}{v_{p_2}x_{p_2}^*(T_0)} \Bigg \{ \frac{\sum \nolimits _{q=1}^m\beta _{{p_2}q}(T_0)}{c_{p_2q}(T_0)}\Bigg [\Big |c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0)) \\ & \times \, (w_{p_2}(T_0-\tau _{{p_2}q}(T_0))+1) e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))(w_{p_2}(T_0-\tau _{{p_2}q}(T_0))+1)} \\ & -\,c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))} \Big | \\ & -\,c_{{p_2}q}(T_0)v_{p_2}|w_{p_2}(T_0)|x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))} \Bigg ] \Bigg \} \\\le & re^{r T_0}|w_{p_2}(T_0)| + \frac{\sum \nolimits _{q=1}^m \beta _{{p_2}q}(T_0)}{x_{p_2}^*(T_0)} \left\{ x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))e^{r T_0}|w_{p_2}(T_0-\tau _{{p_2}q}(T_0))| \right. \\ & \times \,\Bigg [e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))}-\frac{2rx_{p_2}^*(T_0)}{\sum _{q=1}^m \beta _{{p_2}q}(T_0) {\bar{l}}}\Bigg ] \frac{1}{e^{r \tau _{p_2}}}\\ & \left. -\,e^{r T_0}|w_{p_2}(T_0)|x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))} \right\} \\< & re^{r T_0}|w_{p_2}(T_0)| + \frac{\sum \nolimits _{q=1}^m \beta _{{p_2}q}(T_0)}{x_{p_2}^*(T_0)} \left\{ x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))M_{\varphi }\right. \\ & \times \,\bigg [e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))}-\frac{2rx_{p_2}^*(T_0)}{\sum _{q=1}^m \beta _{{p_2}q}(T_0) {\bar{l}}}\bigg ] \\ & \left. -\,M_{\varphi }x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))e^{-c_{{p_2}q}(T_0)v_{p_2}x_{p_2}^*(T_0-\tau _{{p_2}q}(T_0))} \right\} \\< & rM_{\varphi }-2rM_{\varphi } \\= & -rM_{\varphi } \\< & 0. \end{aligned}$$

This contradicts and suggests that (3.21) is valid. Thus,

$$\begin{aligned} W_p(t)&= e^{rt}|w_{p}(t)| \\&=e^{rt} \frac{|x_p(t)-x_p^*(t)|}{x_p^*(t)} \\&=e^{rt} \frac{|v_p^{-1}z_p(t)-v_p^{-1}z_p^*(t)|}{v_p^{-1}z_p^*(t)} \\&=e^{rt} \frac{|z_p(t)-z_p^*(t)|}{z_p^*(t)} \\&<M_\varphi , \end{aligned}$$

which means that

$$\begin{aligned}|z_p(t)-z_p^*(t)|< z_p^*(t) M_\varphi {e^{ - r t}} \le \bar{L} M_\varphi {e^{ - r t}}, \ \text{ for } \text{ any } \ t>T^{*}\ \text {and}\ p \in P. \end{aligned}$$

This concludes the proof of Theorem 3.1. $\square$

For $n=m=1$ and $c \equiv 1$, system (1.5) becomes the following Nicholson’s blowflies equation [6] :

$$\begin{aligned} u'(t)=-d(t)u(t)+\beta (t)u(t-\tau (t)) e^{-u(t-\tau (t))}. \end{aligned}$$

(3.23)

One can easily check that the hypotheses (2.2)–(2.4) are satisfied. Then, from Theorem 3.1, the following corollary can be deduced.

Corollary 3.2

Assume that the conditions of Lemma 2.7 hold, Eq. (3.23) admits a unique positive almost periodic solution which is globally exponentially stable.

Remark 3.3

Especially, when the impact of delay vanishes, the sharp conditions (2.2)–(2.4) become

$$\begin{aligned} & 0<\left\{ d_{p}(t) v_{p}-\sum \limits _{q = 1, q \ne p}^n a_{pq}(t) v_{q} \right\} ^{-}, \ 1<\left\{ \frac{\sum \nolimits _{q=1}^{m}\beta _{pq}(t) v_{p}}{d_{p}(t) v_{p}-\sum \nolimits _{q = 1, q \ne p}^n a_{pq}(t) v_{q}}\right\} ^{-},\nonumber \\ \end{aligned}$$

(3.24)

$$\begin{aligned} & \begin{array}{lll} \left\{ d_{p}(t)v_{p}-\sum \limits _{q=1, q\ne p}^n a_{pq}(t)v_{q}\right\} ^{-}>0, \end{array} \end{aligned}$$

(3.25)

$$\begin{aligned} & \left\{ \frac{\sum \nolimits _{q = 1}^m\beta _{pq}(t)v_{p} }{ d_{p} (t)v_{p}- \sum \nolimits _{q = 1, q \ne p}^n a_{pq}(t)v_{q } } \right\} ^+ <e^2. \end{aligned}$$

(3.26)

These time-delay independent conditions guarantee that system (1.5) has a unique globally exponentially stable positive almost periodic solution. Specifically, we have the following corollary:

Corollary 3.4

Given that (3.24)–(3.26) are satisfied, then there exists a positive almost periodic solution of system (1.5) which is globally exponentially stable.

4 A Numerical Example

In this section, we give a numerical example to support the validity of our results.

Example 4.1

Consider the two-dimensional delay Nicholson’s blowflies system with patch-structure as follows,

$$\begin{aligned} \left\{ \begin{array}{lll} W'_{1}(t)& =& -(2+2|\cos 2 t|) W_{1}(t)+(1+1|\cos 2 t|) W_{2}(t)\\ & & +(0.5+0.06|\cos 2 t|)|\sin t|(4.05 +(e^{ 2}-4.1)) \\ & & \times W_{1}(t-\frac{1}{60e^{4}}|\cos t|)e^{-W_{1}(t-\frac{1}{60e^{4}}|\cos t|)}\\ & & +(0.5+0.04|\cos 2 t|)(4.05 +(e^{ 2}-4.1)|\sin t|)\\ & & \times W_{1}(t-\frac{1}{50e^{4}}|\sin 2t|)e^{-W_{1}(t-\frac{1}{50e^{4}}|\sin 2t|)},\\ W'_{2}(t)& =& -(3+3|\sin 2 t|) W_{2}(t)+(1+1|\sin 2 t|) W_{1}(t)\\ & & +(0.6+0.2|\sin 2 t|)|\cos t|(4.05 +(e^{ 2}-4.1))\\ & & \times W_{2}(t-\frac{1}{70e^{4}}|\cos 6t|)e^{-W_{2}(t-\frac{1}{70e^{4}}|\cos 6t|)}\\ & & +(1+0.2|\sin 2 t|)(4.05 +(e^{2}-4.1)|\cos t|)\\ & & \times W_{2}(t-\frac{1}{70e^{4}}|\sin 8t|)e^{-W_{2}(t-\frac{1}{70e^{4}}|\sin 8t|)}, \end{array} \right. \end{aligned}$$

(4.1)

where $\ t\ge t_{0}=0.$

It is straightforward to verify that (4.1) adheres to

$$\begin{aligned} \left\{ \begin{array}{ll}v_{p}=c_{pq}(t)=1, \ m=n=2, \\ \bigg \{ \frac{\sum \nolimits _{q=1}^{m}\beta _{pq}(t) v_{p}}{d_{p}(t) v_{p}-\sum \nolimits _{q = 1, q \ne p}^n a_{pq}(t) v_{q}}\bigg \}^{-}\approx 1.09>1, \\ \bigg \{\frac{ \sum \nolimits _{q = 1}^m \beta _{pq}(t) v_{p} }{ d_{p} (t)v_{p}- \sum \nolimits _{q = 1, q \ne p}^n a_{pq}(t)v_{q } - \sum \nolimits _{q = 1}^m \beta _{pq}(t) [ \sum \nolimits _{q = 1, q \ne p}^n a_{pq} ^{+}v_{q } + \sum \nolimits _{q = 1}^m \beta _{pq}^{+}v_{p} ] \tau _{pq}(t)} \bigg \}^+\\ \approx 6.04 <e^2, \end{array} \right. \nonumber \\ \end{aligned}$$

(4.2)

and $L^* c_{pq}(t) \approx \ln {6.04} <2$.

Fig. 1

Transient states of system (4.1) with initial values $(W_{1}(t), W_{2}(t))=(0.5,1),(1,1.7),(1.5,2.3)$

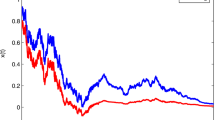
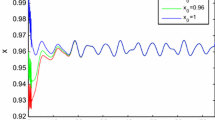
Hence, according to Theorem 3.1, it can be demonstrated that Eq. (4.1) possesses a positive globally exponentially stable almost periodic solution. The findings are validated by the subsequent numerical simulations depicted in Fig. 1. The trajectory of the solutions robustly validates the efficacy and accuracy of the results presented in this study.

Remark 4.2

Clearly, the results reported in [19,20,21,22] and the references therein are not applicable to system (4.1) because (4.2) fails to meet the requirement of (1.7) and incorporates time-varying delays. This suggests that our findings significantly extend the current results, even under constant delay. It is evident that the model we have examined is highly versatile, and the outcomes of this study both broaden and enhance the existing findings from [17, 19,20,21,22, 27] and the referenced sources.

5 Conclusions

We remark that, in nature, there is no phenomenon that is purely periodic, and this gives the idea to consider the almost-periodic situations. So, in this paper, motivated by prior literature addressing the stringent condition for ensuring global exponential stability of the positive equilibrium for the autonomous delay Nicholson’s blowflies equation, this study investigates the global exponential stability of a positive almost periodic patch-constructed Nicholson’s blowflies system with time-varying delays. Employing the fundamental properties of almost periodic functions, the fluctuation lemma, and analysis techniques, this paper establishes several new adequate criteria guaranteeing the existence and global exponential stability of the positive almost periodic solution for the addressed system under less stringent conditions. It is notable that in the absence of delay effects, our findings fully encompass the current results regarding the stringent criterion ensuring the global exponential stability on the positive equilibrium of the scalar delay Nicholson’s blowflies equation. We also claim that many results in the literature dealing with equilibria or periodic solutions of patch-constructed Nicholson’s blowflies system are special cases of the results in this paper. Hence, the findings presented in this paper serve to complement and improve the corresponding scalar almost periodic equation. The approach outlined in this paper can be readily applied to investigate the sharp stability criteria for other types of biological models that incorporate multiple time-varying delays, as discussed in [20, 21]. We defer this endeavor to our future work.