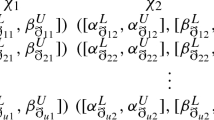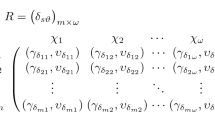1 Introduction

Atanassov [1] developed the intuitionistic fuzzy set (IFS) by taking into consideration of the pairings of membership degree (MD) and non-membership degree (NMD) in such a way that their entire sum does not exceed one, which is a generalisation of the fuzzy set [2]. Following its launch, scientists have employed these speculations in various directions and realized that they are more productive in dealing with the vulnerabilities throughout the investigation. Considering that the aforementioned hypotheses have already been effectively characterized, but sometimes, it struggles to deal with the circumstances by IFS. As an example, if a DM might take the MD and NMD of any component as 0.7 and 0.4, respectively, then obviously their total sum exceeds one, but the sum of their squares is less than one. Henceforth, in those circumstances, IFS has a type of inadequacy. To be able to address these challenges, the Pythagorean fuzzy set (PFS) [3, 4], an expansion of IFSs, has arisen as a powerful tool for portraying the vulnerability in the information. Henceforth, the PFS is more general compared to the IFS.

Leading to a shortage of existing knowledge, it could be challenging for DMs to characterize their feelings accurately with a crisp number in certain genuine decision-making situations, yet they can be addressed via an interval number within [0,1]. As a result, the concept of interval-valued PFSs (IVPFSs) is essential, as it allows MDs and NMDs to be authorized to a specific set with an interval value. Zhang [5] presented the notion of IVPFS. They should also satisfy the criterion that the squares of the upper limits of two intervals’ are less than or equal to one [6]. Because of their amazing ability to deal with more faulty and ambiguous data and supervise sophisticated vulnerabilities in practice-oriented decision situations, IVPF sets have wider potential applications. According to this viewpoint, the utilization of the IVPFS hypothesis to MADM issues gets quite possibly the most encouraging directions in displaying unsure data for practical dynamic issues [7, 8]. IVPFSs allow the NMD and MD of a certain set to have an interval value within [0, 1]. Concurrently, IVPFSs are needed to fulfil the requirement that the sum of the square of both upper limits of the interval-valued MDs and NMDs be less than or equal to one.

A few valuable decision theories and strategies have been developed for managing MADM difficulties. For example, MADM with probabilities in an IVPF setting [9], IVPF Maclaurin symmetric mean operators in MADM difficulties [10], IVPF Frank power aggregation operators based on an isomorphic frank dual triple [11], methods for MADM with IVPF data [12], IVPF power average based MULTIMOORA technique for MADM issues [13], a novel outranking technique for MCDM with IVPF linguistic data [14], approaches to MAGDM based on induced IVPF Einstein hybrid aggregation operators [15], new operations and algorithms for IVPFSs [16, 17], a novel methodology for MADM concerns with IVPF linguistic data [18], IVPF dual Muirhead mean operators for MADM difficulties [19], some new generalized IVPF aggregation operators based on Einstein t-norms [20].

IVPF MADM has been widely employed in a variety of domains, for example, evaluation of solar photovoltaic technology development [21], bridge construction [22], green suppliers’ selection [19], potential evaluation of emerging technology commercialization [23, 24], the configuration of a telecommunication network [25], sustainable supplier selection [26], car selection problem [27], risk assessment of technological innovation in high-tech companies [28, 29], providing financial support for the infrastructure development [30], treatment and management of health care waste [31].

We can see from these models and discussions that the majority of contemporary IVPF aggregation techniques are set up with the help of the algebraic product and algebraic sum of IVPFSs to express the aggregation technique. A standard t-norm and t-conorm could be used to create a generalised union and intersection on IVPFSs. Aczel-Alsina [32] presented two new operations in 1982 named Aczel-Alsina t-norm (AA t-norm) and Aczel-Alsina t-conorm (AA t-conorm), which place a high premium on parameter adaptability. Recently, Senapati and his associates have opened new horizons in decision-making theories using the AA t-norms. They applied AA t-norms to decision-making difficulties under IFS [33], interval-valued IFS [34], hesitant fuzzy [35] and picture fuzzy [36] environments. To handle MADM issues including IVPF data, the motivation behind this paper is to produce some new aggregation operators dependent on AA t-norm and AA t-conorm. Besides, this research provides an adaptable and helpful way to manage different sorts of inclination data to adjust to the peculiarities of actual decision circumstances (figure 1).

Figure 1
figure 1

The framework of the study.

Full size image

We propose these sections in this paper: in section 2, we concisely discuss certain essential ideas of Aczel-Alsina triangular norms, IVPFSs, and a few working principles of IVPFEs. We suggest Aczel-Alsina operations for IVPFEs in section 3. In section 4, we propose certain IVPF aggregation operators by virtue of Aczel-Alsina operations, like the IVPFAAWA operator, IVPFAAOWA operator, and IVPFAAHA operator, and analyzed several attractive characteristics of the recommended operators. We determine the details of these new aggregation operators as well as specific situations. In section 5, we create a MADM strategy on the basis of the recommended operators under an induced IVPF situation. In section 6, a practical example is given to demonstrate the legitimacy and superiority of the recommended methodology. In section 7, we examine how a parameter influences decision outcomes. In section 8, then created a comparative study with the prevailing techniques. Finally, section 9 illustrates and discusses the conclusion and scope of future research.

2 Preliminaries

In the accompanying, we acquaint a few fundamental concepts closely tied with t-norm, t-conorm, AA t-norm, AA t-conorm and IVPFS.

2.1 t-norm, t-conorm, AA t-norm and AA t-conorm

Definition 1

[37] A t-norm is a binary operation on the unit interval [0, 1], i.e., a function \(T:[0,1]^{2}\rightarrow [0,1]\) such that, for all \(w, h, y \in [0, 1]\), the following axioms are satisfied:

(i):

\(T(w,h) = T(h,w)\) (commutativity);

(ii):

\(T(w,h)\le T(w, y)\) if \(h \le y\) (monotonicity);

(iii):

\(T(w, T(h, y))= T(T(w,h), y)\) (associativity);

(iv):

\(T(w, 1) = w\) (one identity).

Example 1

Examples of popular t-norms:

(i):

\(T_{P}(w,h)=w.h\) (product t-norm);

(ii):

\(T_{M}(w,h)=\min (w,h)\) (minimum t-norm);

(iii):

\(T_{L}(w,h)=\max (w + h-1, 0)\) (Lukasiewicz t-norm);

(iv):

\(T_D(w,h) =\left\{ \begin{array}{ll} w, &{} \text{ if } h=1\\ h, &{} \text{ if } w=1\\ 0, &{} \text{ otherwise } \end{array}\right.\) (Drastic t-norm);

for all \(w, h\in [0, 1]\).

Definition 2

[37] A t-conorm is a binary operation on the unit interval [0, 1], i.e., a function \(S:[0,1]^{2}\rightarrow [0,1]\) such that, for all \(w, h, y \in [0, 1]\), the following axioms are satisfied:

(i):

\(S (w,h) = S (h,w)\) (commutativity);

(ii):

\(S (w,h)\le S (w, y)\) if \(h\le y\) (monotonicity);

(iii):

\(S(w, S(h, y))= S (S(w,h), y)\) (associativity);

(iv):

\(S (w, 0) = w\) (one identity).

Example 2

Examples of popular t-conorms:

(i):

\(S_{P}(w,h)=w+h-w.h\) (probabilistic sum);

(ii):

\(S_{M}(w,h)=\max (w,h)\) (maximum t-conorm);

(iii):

\(S_{L}(w,h)=\min (w + h, 1)\) (Lukasiewicz t-conorm);

(iv):

\(S_D(w,h)=\left\{ \begin{array}{ll} w, &{} \text{ if } h=0\\ h, &{} \text{ if } w=0\\ 1, &{} \text{ otherwise } \end{array}\right.\) (Drastic t-conorm);

for every \(w, h \in [0, 1]\).

Additionally, it provided evidence that when T is a t-norm and S is a t-conorm, then \(T(w,h)\le \min \{w, h\}\) and \(S(w,h)\ge \max \{w, h\}\) for all \(w, h \in [0, 1]\) [37].

Definition 3

[32, 38](AA t-norm) In the early 1980s, Aczel-Alsina constructed the t-norm class within the context of analytic functions.

The class \((T_{A}^{\zeta })_{\zeta \in [0,\infty ]}\) of AA t-norms is portrayed through

$$\begin{array}{ll} T_{A}^{\zeta }(w,h)=\left\{ \begin{array}{ll} T_D(w,h), &{} \mathrm{if} \,\, \zeta =0\\ \min (w,h), &{} \mathrm{if} \,\, \zeta =\infty \\ e^{-((-\ln w)^\zeta +(-\ln h)^\zeta )^{1/\zeta }}, &{} \mathrm{otherwise} \end{array}\right. \end{array}$$

The class \((S_{A}^{\zeta })_{\zeta \in [0,\infty ]}\) of AA t-conorms is portrayed through

$$\begin{array}{ll} S_{A}^{\zeta }(w,h)=\left\{ \begin{array}{ll} S_D(w,h), &{} \mathrm{if} \,\, \zeta =0\\ \max (w,h), &{} \mathrm{if} \,\, \zeta =\infty \\ 1-e^{-((-\ln (1- w))^\zeta +(-\ln (1-h))^\zeta )^{1/\zeta }}, &{} \mathrm{otherwise} \end{array}\right. \end{array}$$

Borderline Cases: \(T_{A}^{0}=T_D\), \(T_{A}^{1}=T_P\), \(T_{A}^{\infty }=\min\), \(S_{A}^{0}=S_D\), \(S_{A}^{1}=S_P\), \(S_{A}^{\infty }=\max\).

For each \(\zeta \in [0,\infty ]\), the t-norm \(T_{A}^{\zeta }\) and t-conorm \(S_{A}^{\zeta }\) are dual to each other. The class of AA t-norms increases strictly and the class of AA t-conorms decreases strictly.

2.2 IVPFSs

Zhang and Xu [4] presented the general mathematical form of PFS in the following way:

Definition 4

Let \(\digamma\) be a fixed set, a PFS \(\Upsilon\) on \(\digamma\) ascertained as

$$\begin{aligned} \Upsilon =\{\langle \omega , \alpha _{\Upsilon }(\omega ), \beta _{\Upsilon }(\omega )\rangle |\omega \in \digamma \} \end{aligned}$$

where MD \(\alpha _{\Upsilon }: \digamma \rightarrow [0,1]\) and NMD \(\beta _{\Upsilon }: \digamma \rightarrow [0,1]\) for all \(\omega \in \digamma\) fulfilling the condition \(0\le \alpha _{\Upsilon }^{2}(\omega )+\beta _{\Upsilon }^{2}(\omega )\le 1\), where the degree of indeterminacy \(\pi _{\Upsilon }(\omega )=\sqrt{1-\alpha _{\Upsilon }^{2}(\omega )-\beta _{\Upsilon }^{2}(\omega )}\).

Zhang [5] delivered the definition of IVPFSs by means of the following:

Definition 5

[5] Assume that \(\Theta ([0, 1])\) contains all closed subintervals of the unit interval [0, 1]. An IVPFS \({\tilde{\Upsilon }}\) on \(\digamma\) with MD \({\tilde{\alpha }}_\Upsilon (\omega ):\digamma \rightarrow \Theta ([0, 1])\) and NMD \({\tilde{\beta }}_\Upsilon (\omega ):\digamma \rightarrow \Theta ([0, 1])\) is assigned as

$$\begin{aligned} {\tilde{\Upsilon }}=\{\langle \omega , {\tilde{\alpha }}_{\Upsilon }(\omega ), {\tilde{\beta }}_{\Upsilon }(\omega )\rangle |\omega \in \digamma \}, \end{aligned}$$

where \({\tilde{\alpha }}_\Upsilon (\omega )=[\alpha ^L_\Upsilon (\omega ),\alpha ^U_\Upsilon (\omega )]\) and \({\tilde{\beta }}_\Upsilon (\omega )=[\beta ^L_\Upsilon (\omega ),\beta ^U_\Upsilon (\omega )]\), for all \(\omega \in \digamma\), including the condition \(0 \le (\alpha ^U_\Upsilon (\omega ))^2+ (\beta ^U_\Upsilon (\omega ))^2\) \(\le 1\). \(\pi _{{\tilde{\Upsilon }}}(\omega )=[\pi ^L_\Upsilon (\omega ),\pi ^U_\Upsilon (\omega )]\) denotes the indeterminacy degree of element \(\omega\) that belongs to \({\tilde{\Upsilon }}\), where

$$\begin{aligned} \pi ^L_\Upsilon (\omega )=\sqrt{1-(\alpha ^U_\Upsilon (\omega ))^2-(\beta ^U_\Upsilon (\omega ))^2} \end{aligned}$$

and

$$\begin{aligned} \pi ^U_\Upsilon (\omega )=\sqrt{1-(\alpha ^L_\Upsilon (\omega ))^2-(\beta ^L_\Upsilon (\omega ))^2}. \end{aligned}$$

For benefit, we called \({\tilde{\Upsilon }}=\{\langle \omega , [\alpha ^L_\Upsilon (\omega ),\alpha ^U_\Upsilon (\omega )], [\beta ^L_\Upsilon (\omega ),\) \(\beta ^U_\Upsilon (\omega )]\rangle |\omega \in \digamma \}\) as IVPF element (IVPFE) defined by \({\tilde{\Upsilon }}=([\alpha ^L_\Upsilon ,\alpha ^U_\Upsilon ],\) \([\beta ^L_\Upsilon ,\beta ^U_\Upsilon ])\).

Liang et al [28] outlined score and accuracy function for contrasting two IVPFEs in this way:

Definition 6

[28] For an IVPFE \({\tilde{\Upsilon }}=([\alpha ^L_\Upsilon ,\alpha ^U_\Upsilon ], [\beta ^L_\Upsilon ,\beta ^U_\Upsilon ])\), score function \({\mathbb {Q}}({\tilde{\Upsilon }})\) and accuracy function \({\mathbb {W}}({\tilde{\Upsilon }})\) can be computed as:

$$\begin{aligned} {\mathbb {Q}}({\tilde{\Upsilon }})=\frac{1}{2}\Big [(\alpha ^L_{\Upsilon })^{2}+(\alpha ^U_{\Upsilon })^{2}-(\beta ^L_{\Upsilon })^{2}-(\beta ^U_{\Upsilon })^{2}\Big ], \end{aligned}$$
(1)
$$\begin{aligned} {\mathbb {W}}({\tilde{\Upsilon }})=\frac{1}{2}\Big [(\alpha ^L_{\Upsilon })^{2}+(\alpha ^U_{\Upsilon })^{2}+(\beta ^L_{\Upsilon })^{2}+(\beta ^U_{\Upsilon })^{2}\Big ], \end{aligned}$$
(2)

where \({\mathbb {Q}}({\tilde{\Upsilon }})\in [-1,1]\) and \({\mathbb {W}}({\tilde{\Upsilon }})\in [0,1]\).

In this way, the ordering of two IVPFEs can be carried out dependent on score and accuracy function listed as follows.

Definition 7

[28] Assume that \({\tilde{\Upsilon }}_1=([\alpha ^L_{\Upsilon _1}, \alpha ^U_{\Upsilon _1}], [\beta ^L_{\Upsilon _1}, \beta ^U_{\Upsilon _1}])\) and \({\tilde{\Upsilon }}_2=([\alpha ^L_{\Upsilon _2},\) \(\alpha ^U_{\Upsilon _2}], [\beta ^L_{\Upsilon _2}, \beta ^U_{\Upsilon _2}])\) are any two IVPFEs. Then:

  1. (1)

    if \({\mathbb {Q}}({\tilde{\Upsilon }}_1) < {\mathbb {Q}}({\tilde{\Upsilon }}_2)\) then \({\tilde{\Upsilon }}_1\prec {\tilde{\Upsilon }}_2\),

  2. (2)

    if \({\mathbb {Q}}({\tilde{\Upsilon }}_1)> {\mathbb {Q}}({\tilde{\Upsilon }}_2)\) then \({\tilde{\Upsilon }}_1\succ {\tilde{\Upsilon }}_2\),

  3. (3)

    if \({\mathbb {Q}}({\tilde{\Upsilon }}_1)= {\mathbb {Q}}({\tilde{\Upsilon }}_2)\) then

    1. (i)

      if \({\mathbb {W}}({\tilde{\Upsilon }}_1) < {\mathbb {W}}({\tilde{\Upsilon }}_2)\) then \({\tilde{\Upsilon }}_1\prec {\tilde{\Upsilon }}_2\),

    2. (ii)

      if \({\mathbb {W}}({\tilde{\Upsilon }}_1) > {\mathbb {W}}({\tilde{\Upsilon }}_2)\) then \({\tilde{\Upsilon }}_1\succ {\tilde{\Upsilon }}_2\),

    3. (iii)

      if \({\mathbb {W}}({\tilde{\Upsilon }}_1)= {\mathbb {W}}({\tilde{\Upsilon }}_2)\) then \({\tilde{\Upsilon }}_1\sim {\tilde{\Upsilon }}_2\).

The fundamental operations of IVPFEs are constructed by Liang et al [28] and Zhang [5] in the following way.

Definition 8

Let \({\tilde{\Upsilon }}=([\alpha ^L_\Upsilon ,\alpha ^U_\Upsilon ], [\beta ^L_\Upsilon ,\beta ^U_\Upsilon ]),\) \({\tilde{\Upsilon }}_1=([\alpha ^L_{\Upsilon _1}, \alpha ^U_{\Upsilon _1}],\) \([\beta ^L_{\Upsilon _1}, \beta ^U_{\Upsilon _1}])\) and \({\tilde{\Upsilon }}_2=([\alpha ^L_{\Upsilon _2},\) \(\alpha ^U_{\Upsilon _2}], [\beta ^L_{\Upsilon _2}, \beta ^U_{\Upsilon _2}])\) be three IVPFEs, then:

  1. (i)

    \(\bigoplus\)-union:

    $$\begin{aligned}&{\tilde{\Upsilon }}_1 \bigoplus {\tilde{\Upsilon }}_2=\Big (\Big [\sqrt{(\alpha ^L_{\Upsilon _1})^{2}+(\alpha ^L_{\Upsilon _2})^{2}-(\alpha ^L_{\Upsilon _1})^{2}(\alpha ^L_{\Upsilon _2})^{2}}, \\&\quad \sqrt{(\alpha ^U_{\Upsilon _1})^{2}+(\alpha ^U_{\Upsilon _2})^{2}-(\alpha ^U_{\Upsilon _1})^{2}(\alpha ^U_{\Upsilon _2})^{2}}\Big ], \Big [\beta ^L_{\Upsilon _1} \beta ^L_{\Upsilon _2}, \beta ^U_{\Upsilon _1} \beta ^U_{\Upsilon _2}\Big ]\Big ),\end{aligned}$$
  2. (ii)

    \(\bigotimes\)-intersection:

    $$\begin{aligned}&{\tilde{\Upsilon }}_1 \bigotimes {\tilde{\Upsilon }}_2= \Big (\Big [\alpha ^L_{\Upsilon _1} \alpha ^L_{\Upsilon _2}, \alpha ^U_{\Upsilon _1} \alpha ^U_{\Upsilon _2}\Big ], \\&\quad \Big [\sqrt{(\beta ^L_{\Upsilon _1})^{2}+(\beta ^L_{\Upsilon _2})^{2}-(\beta ^L_{\Upsilon _1})^{2}(\beta ^L_{\Upsilon _2})^{2}},\\&\quad \sqrt{(\beta ^U_{\Upsilon _1})^{2}+(\beta ^U_{\Upsilon _2})^{2}-(\beta ^U_{\Upsilon _1})^{2}(\beta ^U_{\Upsilon _2})^{2}}\Big ]\Big ),\end{aligned}$$
  3. (iii)

    Multiplication:

    $$\begin{aligned}&\zeta \;{\tilde{\Upsilon }}=\Big (\Big [\sqrt{1-(1-(\alpha ^L_{\Upsilon })^{2})^{\zeta }}, \\&\quad \sqrt{1-(1-(\alpha ^U_{\Upsilon })^{2})^{\zeta }},\Big ], \Big [(\beta ^L_{\Upsilon })^{\zeta }, (\beta ^U_{\Upsilon })^{\zeta }\Big ]\Big ), \zeta > 0, \end{aligned}$$
  4. (iv)

    Exponentiation:

    $$\begin{aligned}&{\tilde{\Upsilon }}^{\zeta }=\Big (\Big [(\alpha ^L_{\Upsilon })^{\zeta }, (\alpha ^U_{\Upsilon })^{\zeta }\Big ], \\&\quad \Big [\sqrt{1-(1-(\beta ^L_{\Upsilon })^{2})^{\zeta }},\\&\quad \sqrt{1-(1-(\beta ^U_{\Upsilon })^{2})^{\zeta }}\Big ]\Big ), \zeta > 0, \end{aligned}$$
  5. (v)

    Complement:

    $$\begin{aligned} {\tilde{\Upsilon }}^c=([\beta ^L_\Upsilon ,\beta ^U_\Upsilon ], [\alpha ^L_\Upsilon ,\alpha ^U_\Upsilon ]).\end{aligned}$$

3 Aczel-Alsina operations on IVPFEs

We explained Aczel-Alsina operations for IVPFEs in the context of AA t-norm and AA t-conorm.

Definition 9

Let \({\tilde{\Upsilon }}=([\alpha ^L_\Upsilon ,\alpha ^U_\Upsilon ], [\beta ^L_\Upsilon ,\beta ^U_\Upsilon ]),\) \({\tilde{\Upsilon }}_1=([\alpha ^L_{\Upsilon _1}, \alpha ^U_{\Upsilon _1}],\) \([\beta ^L_{\Upsilon _1}, \beta ^U_{\Upsilon _1}])\) and \({\tilde{\Upsilon }}_2=([\alpha ^L_{\Upsilon _2},\) \(\alpha ^U_{\Upsilon _2}], [\beta ^L_{\Upsilon _2}, \beta ^U_{\Upsilon _2}])\) be three IVPFEs, \(\lambda \ge 1\) and \(\zeta >0\). Then, we describe the AA t-norm and t-conorm operations by means of the following:

  1. (i)
    $$\begin{aligned}{\tilde{\Upsilon }}_1\bigoplus {\tilde{\Upsilon }}_2= & {} \bigg ( \bigg [ \sqrt{1-e^{-((-\ln (1- (\alpha ^L_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}, \;\ \;\ \\&\sqrt{1-e^{-((-\ln (1- (\alpha ^U_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}} \bigg ], \;\ \;\ \\&\bigg [\sqrt{e^{-((-\ln (\beta ^L_{\Upsilon _1})^2)^\lambda +(-\ln (\beta ^L_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}, \;\ \;\ \\&\sqrt{e^{-((-\ln (\beta ^U_{\Upsilon _1})^2)^\lambda +(-\ln (\beta ^U_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}\bigg ]\bigg ),\end{aligned}$$
  2. (ii)
    $$\begin{aligned}&{\tilde{\Upsilon }}_1\bigotimes {\tilde{\Upsilon }}_2\\&\quad = \bigg (\bigg [ \sqrt{e^{-((-\ln (\alpha ^L_{\Upsilon _1})^2)^\lambda +(-\ln (\alpha ^L_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-((-\ln (\alpha ^U_{\Upsilon _1})^2)^\lambda +(-\ln (\alpha ^U_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}\bigg ], \;\ \;\ \\&\qquad \bigg [\sqrt{1-e^{-((-\ln (1- (\beta ^L_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\beta ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}, \;\ \;\ \\&\qquad \sqrt{1-e^{-((-\ln (1- (\beta ^U_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\beta ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\bigg ]\bigg ), \end{aligned}$$
  3. (iii)
    $$\begin{aligned}\zeta {\tilde{\Upsilon }}= & {} \Big ( \Big [\sqrt{1-e^{-(\zeta (-\ln (1- (\alpha ^L_{\Upsilon })^2))^\lambda )^{1/\lambda }}}, \;\ \\&\sqrt{1-e^{-(\zeta (-\ln (1- (\alpha ^U_{\Upsilon })^2))^\lambda )^{1/\lambda }}}\Big ], \;\ \\&\Big [\sqrt{e^{-(\zeta (-\ln (\beta ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}}, \sqrt{e^{-(\zeta (-\ln (\beta ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}} \Big ]\Big ), \end{aligned}$$
  4. (iv)
    $$\begin{aligned}&{\tilde{\Upsilon }}^{\zeta }\\&\quad =\Big ( \Big [ \sqrt{e^{-(\zeta (-\ln (\alpha ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}}, \sqrt{e^{-(\zeta (-\ln (\alpha ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}} \Big ], \;\ \\&\qquad \Big [ \sqrt{1-e^{-(\zeta (-\ln (1- (\beta ^L_{\Upsilon })^2))^\lambda )^{1/\lambda }}}, \;\ \\&\qquad \sqrt{1-e^{-(\zeta (-\ln (1- (\beta ^U_{\Upsilon })^2))^\lambda )^{1/\lambda }}}\Big ] \Big ),\end{aligned}$$

Example 3

Let \({\tilde{\Upsilon }}=([0.12, 0.19], [0.74,0.84]),\) \({\tilde{\Upsilon }}_1=([0.62,\) 0.67], [0.33, 0.40]) and \({\tilde{\Upsilon }}_2=([0.51, 0.56], [0.42,0.48])\) be three IVPFEs, then utilizing Aczel-Alsina operation in accordance with Definition 9 for \(\lambda =4\) and \(\zeta =7,\) we get

  1. (i)
    $$\begin{aligned}&{\tilde{\Upsilon }}_1\bigoplus {\tilde{\Upsilon }}_2 \\&\quad =\Big ( \Big [ \sqrt{1-e^{-((-\ln (1- (0.62)^2))^4+(-\ln (1-(0.51)^2))^4)^{1/4}}}, \\&\qquad \sqrt{1-e^{-((-\ln (1- (0.67)^2))^4+(-\ln (1-(0.56)^2))^4)^{1/4}}}\Big ],\\&\qquad \Big [\sqrt{e^{-((-\ln (0.33)^2)^4+(-\ln (0.42)^2)^4)^{1/4}}}, \\&\qquad \sqrt{e^{-((-\ln (0.40)^2)^4+(-\ln (0.48)^2)^4)^{1/4}}} \Big ]\Big )\\&\quad =([0.628362, 0.679049], [0.301041, 0.368329]), \end{aligned}$$
  2. (ii)
    $$\begin{aligned}&{\tilde{\Upsilon }}_1\bigotimes {\tilde{\Upsilon }}_2\\&\quad =\Big ( \Big [\sqrt{e^{-((-\ln (0.62)^2)^4+(-\ln (0.51)^2)^4)^{1/4}}}, \\&\qquad \sqrt{e^{-((-\ln (0.67)^2)^4+(-\ln (0.56)^2)^4)^{1/4}}}\Big ], \\&\qquad \Big [\sqrt{1-e^{-((-\ln (1- (0.33)^2))^4+(-\ln (1-(0.42)^2))^4)^{1/4}}}, \\&\qquad \sqrt{1-e^{-((-\ln (1- (0.40)^2))^4+(-\ln (1-(0.48)^2))^4)^{1/4}}} \Big ]\Big ) \\&\quad =([0.490393, 0.543179], [0.425614, 0.489478]), \end{aligned}$$
  3. (iii)
    $$\begin{aligned}7 {\tilde{\Upsilon }}= & {} \Big ( \Big [ \sqrt{1-e^{-(7(-\ln (1- (0.12)^2))^4)^{1/4}}}, \\&\sqrt{1-e^{-(7(-\ln (1- (0.19)^2))^4)^{1/4}}}\Big ], \\&\Big [ \sqrt{e^{-(7(-\ln (0.74)^2)^4)^{1/4}}},\sqrt{e^{-(7(-\ln (0.84)^2)^4)^{1/4}}} \Big ]\Big ) \\= & {} ([0.152699, 0.240940], [0.612767, 0.753068]), \end{aligned}$$
  4. (iv)
    $$\begin{aligned}{\tilde{\Upsilon }}^{7}= & {} \Big ( \Big [\sqrt{e^{-(7(-\ln (0.12)^2)^4)^{1/4}}},\sqrt{e^{-(7(-\ln (0.19)^2)^4)^{1/4}}}\Big ],\\&\Big [ \sqrt{1-e^{-(7(-\ln (1- (0.74)^2))^4)^{1/4}}},\\&\sqrt{1-e^{-(7(-\ln (1- (0.84)^2))^4)^{1/4}}} \Big ] \Big ) \\= & {} ([0.031785, 0.0671178], [0.851340, 0.929069]), \end{aligned}$$

Theorem 1

Let \({\tilde{\Upsilon }}=([\alpha ^L_\Upsilon ,\alpha ^U_\Upsilon ], [\beta ^L_\Upsilon ,\beta ^U_\Upsilon ]),\) \({\tilde{\Upsilon }}_1=([\alpha ^L_{\Upsilon _1}, \alpha ^U_{\Upsilon _1}],\) \([\beta ^L_{\Upsilon _1}, \beta ^U_{\Upsilon _1}])\) and \({\tilde{\Upsilon }}_2=([\alpha ^L_{\Upsilon _2},\) \(\alpha ^U_{\Upsilon _2}], [\beta ^L_{\Upsilon _2}, \beta ^U_{\Upsilon _2}])\) be three IVPFEs, then we have

(i):

\({\tilde{\Upsilon }}_1 \bigoplus {\tilde{\Upsilon }}_2={\tilde{\Upsilon }}_2 \bigoplus {\tilde{\Upsilon }}_1;\)

(ii):

\({\tilde{\Upsilon }}_1 \bigotimes {\tilde{\Upsilon }}_2={\tilde{\Upsilon }}_2 \bigotimes {\tilde{\Upsilon }}_1;\)

(iii):

\(\zeta ({\tilde{\Upsilon }}_1 \bigoplus {\tilde{\Upsilon }}_2)=\zeta {\tilde{\Upsilon }}_1 \bigoplus \zeta {\tilde{\Upsilon }}_2,\) \(\zeta >0\);

(iv):

\((\zeta _1+\zeta _2 ){\tilde{\Upsilon }}=\zeta _1 {\tilde{\Upsilon }} \bigoplus \zeta _2 {\tilde{\Upsilon }}\), \(\zeta _1, \zeta _2 >0\);

(v):

\(({\tilde{\Upsilon }}_1 \bigotimes {\tilde{\Upsilon }}_2)^\zeta ={\tilde{\Upsilon }}_1^\zeta \bigotimes {\tilde{\Upsilon }}_2^\zeta\), \(\zeta >0\);

(vi):

\({\tilde{\Upsilon }}^{\zeta _1} \bigotimes {\tilde{\Upsilon }}^{\zeta _2}={\tilde{\Upsilon }}^{(\zeta _1+\zeta _2 )}\), \(\zeta _1, \zeta _2 >0\).

Proof

For the three PFEs \({\tilde{\Upsilon }}\), \({\tilde{\Upsilon }}_1\) and \({\tilde{\Upsilon }}_2\), and \(\zeta , \zeta _1, \zeta _2 > 0\), as stated in Definition 9, we can get

(i):
$$\begin{aligned}&{\tilde{\Upsilon }}_1 \bigoplus {\tilde{\Upsilon }}_2\\&\quad = \bigg ( \bigg [\sqrt{1-e^{-((-\ln (1- (\alpha ^L_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}},\\&\qquad \sqrt{1-e^{-((-\ln (1- (\alpha ^U_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\bigg ], \\&\qquad \bigg [\sqrt{e^{-((-\ln (\beta ^L_{\Upsilon _1})^2)^\lambda +(-\ln (\beta ^L_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-((-\ln (\beta ^U_{\Upsilon _1})^2)^\lambda +(-\ln (\beta ^U_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}\bigg ]\bigg ) \\&\quad =\bigg ( \bigg [ \sqrt{1-e^{-((-\ln (1- (\alpha ^L_{\Upsilon _2})^2))^\lambda +(-\ln (1-(\alpha ^L_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-((-\ln (1- (\alpha ^U_{\Upsilon _2})^2))^\lambda +(-\ln (1-(\alpha ^U_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}}\bigg ], \\&\qquad \bigg [\sqrt{e^{-((-\ln (\beta ^L_{\Upsilon _2})^2)^\lambda +(-\ln (\beta ^L_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-((-\ln (\beta ^U_{\Upsilon _2})^2)^\lambda +(-\ln (\beta ^U_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}}\bigg ]\bigg ) \\&\quad ={\tilde{\Upsilon }}_2 \bigoplus {\tilde{\Upsilon }}_1\end{aligned}$$

.

(ii):

It is not complicated at all.

(iii):

Let \(t= \sqrt{1-e^{-((-\ln (1- (\alpha ^L_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\).

Then \(\ln (1-t^2)=-((-\ln (1- (\alpha ^L_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }\). Using this, we get

$$\begin{aligned}&\zeta ({\tilde{\Upsilon }}_1 \bigoplus {\tilde{\Upsilon }}_2) \\&\quad =\zeta \bigg ( \bigg [\sqrt{1-e^{-((-\ln (1- (\alpha ^L_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-((-\ln (1- (\alpha ^U_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\bigg ],\\&\qquad \bigg [\sqrt{e^{-((-\ln (\beta ^L_{\Upsilon _1})^2)^\lambda +(-\ln (\beta ^L_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-((-\ln (\beta ^U_{\Upsilon _1})^2)^\lambda +(-\ln (\beta ^U_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}\bigg ]\bigg )\\&\quad =\bigg ( \bigg [\sqrt{1-e^{-(\zeta ((-\ln (1- (\alpha ^L_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^L_{\Upsilon _2})^2))^\lambda ))^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-(\zeta ((-\ln (1- (\alpha ^U_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\alpha ^U_{\Upsilon _2})^2))^\lambda ))^{1/\lambda }}}\bigg ],\\&\qquad \bigg [\sqrt{e^{-(\zeta ((-\ln (\beta ^L_{\Upsilon _1})^2)^\lambda +(-\ln (\beta ^L_{\Upsilon _2})^2)^\lambda ))^{1/\lambda }}}, \\&\qquad \sqrt{e^{-(\zeta ((-\ln (\beta ^U_{\Upsilon _1})^2)^\lambda +(-\ln (\beta ^U_{\Upsilon _2})^2)^\lambda ))^{1/\lambda }}}\bigg ]\bigg )\\&\quad =\bigg ( \bigg [\sqrt{1-e^{-(\zeta (-\ln (1- (\alpha ^L_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}},\\&\qquad \sqrt{1-e^{-(\zeta (-\ln (1- (\alpha ^U_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}}\bigg ],\\&\qquad \bigg [\sqrt{e^{-(\zeta (-\ln (\beta ^L_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}}, \sqrt{e^{-(\zeta (-\ln (\beta ^U_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}}\bigg ]\bigg ) \\&\qquad \bigoplus \bigg ( \bigg [\sqrt{1-e^{-(\zeta (-\ln (1- (\alpha ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}},\\&\qquad \sqrt{1-e^{-(\zeta (-\ln (1- (\alpha ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\bigg ], \bigg [\sqrt{e^{-(\zeta (-\ln (\beta ^L_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-(\zeta (-\ln (\beta ^U_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}\bigg ]\bigg )=\zeta {\tilde{\Upsilon }}_1 \bigoplus \zeta {\tilde{\Upsilon }}_2\end{aligned}$$

.

(iv):
$$\begin{aligned}&\zeta _1 {\tilde{\Upsilon }} \bigoplus \zeta _2 {\tilde{\Upsilon }}=\Big ( \Big [ \sqrt{1-e^{-(\zeta _1(-\ln (1- (\alpha ^L_{\Upsilon })^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-(\zeta _1(-\ln (1- (\alpha ^U_{\Upsilon })^2))^\lambda )^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{e^{-(\zeta _1(-\ln (\beta ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-(\zeta _1(-\ln (\beta ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}}\Big ]\Big ) \\&\qquad \bigoplus \Big ( \Big [\sqrt{1-e^{-(\zeta _2(-\ln (1- (\alpha ^L_{\Upsilon })^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-(\zeta _2(-\ln (1- (\alpha ^U_{\Upsilon })^2))^\lambda )^{1/\lambda }}} \Big ], \\&\qquad \Big [ \sqrt{e^{-(\zeta _2(-\ln (\beta ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-(\zeta _2(-\ln (\beta ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}} \Big ] \Big )\\&\quad =\Big ( \Big [\sqrt{1-e^{-((\zeta _1+\zeta _2)(-\ln (1- (\alpha ^L_{\Upsilon })^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-((\zeta _1+\zeta _2)(-\ln (1- (\alpha ^U_{\Upsilon })^2))^\lambda )^{1/\lambda }}} \Big ], \\&\qquad \Big [ \sqrt{e^{-((\zeta _1+\zeta _2)(-\ln (\beta ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-((\zeta _1+\zeta _2)(-\ln (\beta ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}} \Big ]\Big ) =(\zeta _1+\zeta _2 ){\tilde{\Upsilon }}. \end{aligned}$$
(v):
$$\begin{aligned}&({\tilde{\Upsilon }}_1 \bigotimes {\tilde{\Upsilon }}_2)^\zeta = \Big ( \Big [\sqrt{e^{-((-\ln (\alpha ^L_{\Upsilon _1})^2)^\lambda +(-\ln (\alpha ^L_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-((-\ln (\alpha ^U_{\Upsilon _1})^2)^\lambda +(-\ln (\alpha ^U_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{1-e^{-((-\ln (1- (\beta ^L_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\beta ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-((-\ln (1- (\beta ^U_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\beta ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\Big ]\Big )^\zeta \\&\quad =\Big ( \Big [\sqrt{e^{-(\zeta ((-\ln (\alpha ^L_{\Upsilon _1})^2)^\lambda +(-\ln (\alpha ^L_{\Upsilon _2})^2)^\lambda ))^{1/\lambda }}}, \\&\qquad \sqrt{e^{-(\zeta ((-\ln (\alpha ^U_{\Upsilon _1})^2)^\lambda +(-\ln (\alpha ^U_{\Upsilon _2})^2)^\lambda ))^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{1-e^{-(\zeta ((-\ln (1- (\beta ^L_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\beta ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-(\zeta ((-\ln (1- (\beta ^U_{\Upsilon _1})^2))^\lambda +(-\ln (1-(\beta ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\Big ]\Big )\\&\quad =\Big ( \Big [\sqrt{e^{-(\zeta (-\ln (\alpha ^L_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}},\sqrt{e^{-(\zeta (-\ln (\alpha ^U_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{1-e^{-(\zeta (-\ln (1- (\beta ^L_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}},\\&\qquad \sqrt{1-e^{-(\zeta (-\ln (1- (\beta ^U_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}} \Big ]\Big ) \\&\qquad \bigoplus \Big ( \Big [\sqrt{e^{-(\zeta (-\ln (\alpha ^L_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}},\sqrt{e^{-(\zeta (-\ln (\alpha ^U_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{1-e^{-(\zeta (-\ln (1- (\beta ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-(\zeta (-\ln (1- (\beta ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\Big ]\Big )\\&\quad ={\tilde{\Upsilon }}_1^\zeta \bigotimes {\tilde{\Upsilon }}_2^\zeta . \end{aligned}$$
(vi):
$$\begin{aligned}&{\tilde{\Upsilon }}^{\zeta _1} \bigotimes {\tilde{\Upsilon }}^{\zeta _2} =\Big ( \Big [\sqrt{e^{-(\zeta _1(-\ln (\alpha ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-(\zeta _1(-\ln (\alpha ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{1-e^{-(\zeta _1(-\ln (1- (\beta ^L_{\Upsilon })^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-(\zeta _1(-\ln (1- (\beta ^U_{\Upsilon })^2))^\lambda )^{1/\lambda }}}\Big ] \Big ) \\&\qquad \bigotimes \Big ( \Big [\sqrt{e^{-(\zeta _2(-\ln (\alpha ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}},\\&\qquad \sqrt{e^{-(\zeta _2(-\ln (\alpha ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{1-e^{-(\zeta _2(-\ln (1- (\beta ^L_{\Upsilon })^2))^\lambda )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-(\zeta _2(-\ln (1- (\beta ^U_{\Upsilon })^2))^\lambda )^{1/\lambda }}}\Big ] \Big )\\&\quad =\Big ( \Big [\sqrt{e^{-((\zeta _1+\zeta _2)(-\ln (\alpha ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}},\\&\qquad \sqrt{e^{-((\zeta _1+\zeta _2)(-\ln (\alpha ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{1-e^{-((\zeta _1+\zeta _2)(-\ln (1- (\beta ^L_{\Upsilon })^2))^\lambda )^{1/\lambda }}},\\&\qquad \sqrt{1-e^{-((\zeta _1+\zeta _2)(-\ln (1- (\beta ^U_{\Upsilon })^2))^\lambda )^{1/\lambda }}}\Big ]\Big ) \\&\quad ={\tilde{\Upsilon }}^{(\zeta _1+\zeta _2 )}. \end{aligned}$$

\(\square\)

4 IVPF Aczel-Alsina average aggregation operators

In this section, we define three IVPF average aggregation operators through using Aczel-Alsina operations.

Definition 10

Let \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\) \(\psi )\) be a collection of IVPFEs. An IVPF Aczel-Alsina weighted average (IVPFAAWA) operator is a mapping \(IVPFAAWA: IVPFE^{\psi }\rightarrow IVPFE\) such that

$$\begin{aligned}&IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )=\mathop \bigoplus \limits _{\xi =1}^{\psi }(\varsigma _\xi {\tilde{\Upsilon }}_\xi )\\&\quad =\varsigma _1 {\tilde{\Upsilon }}_1 \bigoplus \varsigma _2 {\tilde{\Upsilon }}_2 \bigoplus \cdots \bigoplus \varsigma _\psi {\tilde{\Upsilon }}_\psi \end{aligned}$$

where \(\varsigma =(\varsigma _1,\varsigma _2,\ldots ,\varsigma _\psi )^{T}\) be the weight vector of \({\tilde{\Upsilon }}_\xi\) \((\xi =1,2,\ldots ,\psi )\) with \(\varsigma _{\Upsilon }> 0\) and \(\mathop \sum \nolimits _{\xi =1}^{\psi }\varsigma _\xi =1\).

In view of the Aczel-Alsina operation laws from Theorem 1, we can determine the accompanying Theorem 2.

Theorem 2

Let \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\) \(\psi )\) be a collection of IVPFEs, then their aggregated value by employing the IVPFAAWA operator is also an IVPFE, and

$$\begin{aligned}&IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )=\mathop \bigoplus \limits _{\xi =1}^{\psi }(\varsigma _\xi {\tilde{\Upsilon }}_\xi )\nonumber \\&\quad =\left( \left[ \sqrt{1-e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha ^L_{\Upsilon _\xi })^2))^\lambda )^{1/\lambda }}}, \right. \right. \nonumber \\&\quad \left. \left. \sqrt{1-e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha ^U_{\Upsilon _\xi })^2))^\lambda )^{1/\lambda }}} \right] , \right. \nonumber \\&\left. \left[ \sqrt{e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta ^L_{\Upsilon _\xi })^2)^\lambda )^{1/\lambda }}}, \sqrt{e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta ^U_{\Upsilon _\xi })^2)^\lambda )^{1/\lambda }}}\right] \right) \end{aligned}$$
(3)

where \(\varsigma =(\varsigma _1,\varsigma _2,\ldots ,\varsigma _\psi )\) be the weight vector of \({\tilde{\Upsilon }}_\xi\) \((\xi =1,2,\ldots ,\psi )\), and \(\varsigma _\xi > 0\), \(\mathop \sum \nolimits _{\xi =1}^{\psi }\varsigma _\xi =1\), \(\lambda >0\).

Proof

Using the process of mathematical induction, we can illustrate Theorem  2 as follows:

(i) When \(\psi =2\), on the basis of Aczel-Alsina operations of IVPFEs, we get

$$\begin{aligned}&\varsigma _1 {\tilde{\Upsilon }}_1=\Big ( \Big [\sqrt{1-e^{-(\varsigma _1(-\ln (1- (\alpha ^L_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}},\\&\quad \sqrt{1-e^{-(\varsigma _1(-\ln (1- (\alpha ^U_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}}\Big ], \Big [\sqrt{e^{-(\varsigma _1(-\ln (\beta ^L_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}}, \\&\quad \sqrt{e^{-(\varsigma _1(-\ln (\beta ^U_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}} \Big ]\Big ),\\&\quad \varsigma _2 {\tilde{\Upsilon }}_2=\Big ( \Big [\sqrt{1-e^{-(\varsigma _2(-\ln (1- (\alpha ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}},\\&\quad \sqrt{1-e^{-(\varsigma _2(-\ln (1- (\alpha ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\Big ], \Big [\sqrt{e^{-(\varsigma _2(-\ln (\beta ^L_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}, \\&\quad \sqrt{e^{-(\varsigma _2(-\ln (\beta ^U_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}} \Big ]\Big ). \end{aligned}$$

Based on Definition 9, we obtain

$$\begin{aligned}&IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1, \tilde{\Upsilon }_2)=\varsigma _1 {\tilde{\Upsilon }}_1\bigoplus \varsigma _2 {\tilde{\Upsilon }}_2\\&\quad =\Big ( \Big [\sqrt{1-e^{-(\varsigma _1(-\ln (1- (\alpha ^L_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}},\\&\qquad \sqrt{1-e^{-(\varsigma _1(-\ln (1- (\alpha ^U_{\Upsilon _1})^2))^\lambda )^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{e^{-(\varsigma _1(-\ln (\beta ^L_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}}, \sqrt{e^{-(\varsigma _1(-\ln (\beta ^U_{\Upsilon _1})^2)^\lambda )^{1/\lambda }}} \Big ]\Big )\\&\qquad \bigoplus \Big ( \Big [\sqrt{1-e^{-(\varsigma _2(-\ln (1- (\alpha ^L_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}},\\&\qquad \sqrt{1-e^{-(\varsigma _2(-\ln (1- (\alpha ^U_{\Upsilon _2})^2))^\lambda )^{1/\lambda }}}\Big ], \\&\qquad \Big [\sqrt{e^{-(\varsigma _2(-\ln (\beta ^L_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}}, \sqrt{e^{-(\varsigma _2(-\ln (\beta ^U_{\Upsilon _2})^2)^\lambda )^{1/\lambda }}} \Big ]\Big )\\&\quad =\Bigg ( \Bigg [\sqrt{1-e^{-\big (\varsigma _1(-\ln (1- (\alpha ^L_{\Upsilon _1})^2 ))^\lambda +\varsigma _2(-\ln (1- (\alpha ^L_{\Upsilon _2})^2))^\lambda \big )^{1/\lambda }}},\\&\qquad \sqrt{1-e^{-\big (\varsigma _1(-\ln (1- (\alpha ^U_{\Upsilon _1})^2 ))^\lambda +\varsigma _2(-\ln (1- (\alpha ^U_{\Upsilon _2})^2))^\lambda \big )^{1/\lambda }}} \Bigg ],\\&\qquad \Bigg [\sqrt{e^{-\big (\varsigma _1(-\ln (\beta ^L_{\Upsilon _1})^2)^\lambda +\varsigma _2(-\ln (\beta ^L_{\Upsilon _2})^2)^\lambda \big )^{1/\lambda }}},\\&\qquad \sqrt{e^{-\big (\varsigma _1(-\ln (\beta ^U_{\Upsilon _1})^2)^\lambda +\varsigma _2(-\ln (\beta ^U_{\Upsilon _2})^2)^\lambda \big )^{1/\lambda }}}\Bigg ]\Bigg )\\&\quad =\Bigg ( \Bigg [\sqrt{1-e^{-\big (\mathop \sum \limits _{\xi =1}^{2}\varsigma _\xi (-\ln (1-(\alpha ^L_{\Upsilon _\xi })^2))^\lambda \big )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-\big (\mathop \sum \limits _{\xi =1}^{2}\varsigma _\xi (-\ln (1-(\alpha ^U_{\Upsilon _\xi })^2))^\lambda \big )^{1/\lambda }}}\Bigg ],\\&\qquad \Bigg [\sqrt{e^{-\big (\mathop \sum \limits _{\xi =1}^{2}\varsigma _\xi (-\ln (\beta ^L_{\Upsilon _\xi })^2)^\lambda \big )^{1/\lambda }}}, \sqrt{e^{-\big (\mathop \sum \limits _{\xi =1}^{2}\varsigma _\xi (-\ln (\beta ^U_{\Upsilon _\xi })^2)^\lambda \big )^{1/\lambda }}}\Bigg ]\Bigg ). \end{aligned}$$

Hence, (3) is right for \(\psi =2\).

(ii) Suppose that (3) is valid for \(\psi =k\), then we have

$$\begin{aligned}&IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_k)=\mathop \bigoplus \limits _{\xi =1}^{k}(\varsigma _\xi \tilde{\Upsilon }_\xi )\\&\quad =\left( \left[ \sqrt{1-e^{-(\mathop \sum \limits _{\xi =1}^{k}\varsigma _\xi (-\ln (1- (\alpha ^L_{\Upsilon _\xi })^2))^\lambda )^{1/\lambda }}},\right. \right. \\&\qquad \left. \sqrt{1-e^{-(\mathop \sum \limits _{\xi =1}^{k}\varsigma _\xi (-\ln (1- (\alpha ^U_{\Upsilon _\xi })^2))^\lambda )^{1/\lambda }}} \right] , \\&\qquad \left[ \sqrt{e^{-(\mathop \sum \limits _{\xi =1}^{k}\varsigma _\xi (-\ln (\beta ^L_{\Upsilon _\xi })^2)^\lambda )^{1/\lambda }}},\right. \\&\qquad \left. \left. \sqrt{e^{-(\mathop \sum \limits _{\xi =1}^{k}\varsigma _\xi (-\ln (\beta ^U_{\Upsilon _\xi })^2)^\lambda )^{1/\lambda }}}\right] \right) . \end{aligned}$$

Now for \(\psi =k+1\), then

$$\begin{aligned}&IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1,\tilde{\Upsilon }_2,\ldots ,{\tilde{\Upsilon }}_k,{\tilde{\Upsilon }}_{k+1})\\&\quad =\mathop \bigoplus \limits _{\xi =1}^{k}(\varsigma _\xi \tilde{\Upsilon }_\xi )\bigoplus (\varsigma _{k+1}{\tilde{\Upsilon }}_{k+1})\\&\quad =\Bigg (\Bigg [ \sqrt{1-e^{-\big (\mathop \sum \limits _{\xi =1}^{k}\varsigma _\xi (-\ln (1- (\alpha ^L_{\Upsilon _\xi })^2))^\lambda \big )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-\big (\mathop \sum \limits _{\xi =1}^{k}\varsigma _\xi (-\ln (1- (\alpha ^U_{\Upsilon _\xi })^2))^\lambda \big )^{1/\lambda }}}\Bigg ],\\&\qquad \Bigg [\sqrt{e^{-\big (\mathop \sum \limits _{\xi =1}^{k}\varsigma _\xi (-\ln (\beta ^L_{\Upsilon _\xi })^2)^\lambda \big )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-\big (\mathop \sum \limits _{\xi =1}^{k}\varsigma _\xi (-\ln (\beta ^U_{\Upsilon _\xi })^2)^\lambda \big )^{1/\lambda }}}\Bigg ]\Bigg )\\&\qquad \bigoplus \Bigg (\Bigg [ \sqrt{1-e^{-\big (\varsigma _{k+1}(-\ln (1-(\alpha ^L_{\Upsilon _{k+1}})^2))^\lambda \big )^{1/\lambda }}}, \\&\qquad \sqrt{1-e^{-\big (\varsigma _{k+1}(-\ln (1-(\alpha ^U_{\Upsilon _{k+1}})^2))^\lambda \big )^{1/\lambda }}}\Bigg ],\\&\qquad \Bigg [\sqrt{e^{-\big (\varsigma _{k+1}(-\ln (\beta ^L_{\Upsilon _{k+1}})^2)^\lambda \big )^{1/\lambda }}},\\&\qquad \sqrt{e^{-\big (\varsigma _{k+1}(-\ln (\beta ^U_{\Upsilon _{k+1}})^2)^\lambda \big )^{1/\lambda }}}\Bigg ]\Bigg )\\&\quad =\Bigg ( \Bigg [\sqrt{1-e^{-\big (\mathop \sum \limits _{\xi =1}^{k+1}\varsigma _\xi (-\ln (1-(\alpha ^L_{\Upsilon _\xi })^2))^\lambda \big )^{1/\lambda }}},\\&\qquad \sqrt{1-e^{-\big (\mathop \sum \limits _{\xi =1}^{k+1}\varsigma _\xi (-\ln (1-(\alpha ^U_{\Upsilon _\xi })^2))^\lambda \big )^{1/\lambda }}}\Bigg ],\\&\qquad \Bigg [\sqrt{e^{-\big (\mathop \sum \limits _{\xi =1}^{k+1}\varsigma _\xi (-\ln (\beta ^L_{\Upsilon _\xi })^2)^\lambda \big )^{1/\lambda }}}, \\&\qquad \sqrt{e^{-\big (\mathop \sum \limits _{\xi =1}^{k+1}\varsigma _\xi (-\ln (\beta ^U_{\Upsilon _\xi })^2)^\lambda \big )^{1/\lambda }}}\Bigg ]\Bigg ). \end{aligned}$$

Thus, (3) is true for \(\psi =k+1\).

Therefore, from (i) and (ii), it must be concluded that (3) are true for any \(\psi\). \(\square\)

By employing the IVPFAAWA operator, it is simple to demonstrate the subsequent properties.

Theorem 3

(Idempotency) If \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])\) \((\xi\) \(=1,2,\ldots ,\psi )\) is a collection of IVPFEs that are all identical, i.e., \({\tilde{\Upsilon }}_\xi ={\tilde{\Upsilon }}\) for every \(\xi\), then

$$\begin{aligned} IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )={\tilde{\Upsilon }}. \end{aligned}$$

Proof

Since \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])={\tilde{\Upsilon }}\) \((\xi =1,2,\) \(\ldots ,\psi )\), then we have by equation (3),

$$\begin{aligned}&IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2, \ldots , {\tilde{\Upsilon }}_\psi )=\mathop \bigoplus \limits _{\xi =1}^{\psi }(\varsigma _\xi {\tilde{\Upsilon }}_\xi )\\&\quad =\left( \left[ \sqrt{1-e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha ^L_{\Upsilon _\xi })^2))^\lambda )^{1/\lambda }}},\right. \right. \\&\quad \left. \left. \sqrt{1-e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha ^U_{\Upsilon _\xi })^2))^\lambda )^{1/\lambda }}} \right] , \right. \left. \left[ \sqrt{e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta ^L_{\Upsilon _\xi })^2)^\lambda )^{1/\lambda }}},\right. \right. \\&\quad \left. \left. \sqrt{e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta ^U_{\Upsilon _\xi })^2)^\lambda )^{1/\lambda }}}\right] \right) =\left( \left[ \sqrt{1-e^{-(-\ln (1- (\alpha ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}},\right. \right. \\&\quad \left. \left. \sqrt{1-e^{-(-\ln (1- (\alpha ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}} \right] , \right. \left. \left[ \sqrt{e^{-((-\ln (\beta ^L_{\Upsilon })^2)^\lambda )^{1/\lambda }}},\right. \right. \\&\quad \left. \left. \sqrt{e^{-((-\ln (\beta ^U_{\Upsilon })^2)^\lambda )^{1/\lambda }}}\right] \right) =\left( \left[ \sqrt{1-e^{\ln (1- (\alpha ^L_{\Upsilon })^2)}}, \sqrt{1-e^{\ln (1- (\alpha ^U_{\Upsilon })^2)}} \right] ,\right. \\&\quad \left. \left[ \sqrt{e^{\ln (\beta ^L_{\Upsilon })^2}}, \sqrt{e^{\ln (\beta ^U_{\Upsilon })^2}}\right] \right) =\left( \left[ \sqrt{(\alpha ^L_{\Upsilon })^2}, \sqrt{(\alpha ^U_{\Upsilon })^2} \right] ,\right. \\&\quad \left. \left[ \sqrt{(\beta ^L_{\Upsilon })^2},\sqrt{(\beta ^U_{\Upsilon })^2}\right] \right) =([\alpha ^L_{\Upsilon },\alpha ^U_{\Upsilon }], [\beta ^L_{\Upsilon }, \beta ^U_{\Upsilon }])={\tilde{\Upsilon }}. \end{aligned}$$

Thus, \(IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )={\tilde{\Upsilon }}\) holds. \(\square\)

Theorem 4

(Boundedness) Let \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi },\beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\psi )\) be an accumulation of IVPFEs. Let \({\tilde{\Upsilon }}^{-}=\min ({\tilde{\Upsilon }}_1,{\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )\) and \({\tilde{\Upsilon }}^{+}=\max ({\tilde{\Upsilon }}_1,{\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )\). Then, \({\tilde{\Upsilon }}^{-}\le IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1,{\tilde{\Upsilon }}_2,\ldots ,{\tilde{\Upsilon }}_\psi )\le {\tilde{\Upsilon }}^{+}.\)

Proof

Let \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi },\beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\psi )\) be an accumulation of IVPFEs. Let \({\tilde{\Upsilon }}^{-}=\min ({\tilde{\Upsilon }}_1,{\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )=([\alpha _{\Upsilon }^{L-},\alpha _{\Upsilon }^{U-}], [\beta _{\Upsilon }^{L-}, \beta _{\Upsilon }^{U-}])\) and \({\tilde{\Upsilon }}^{+}=\max ({\tilde{\Upsilon }}_1,{\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )=([\alpha _{\Upsilon }^{L+},\alpha _{\Upsilon }^{U+}], [\beta _{\Upsilon }^{L+},\beta _{\Upsilon }^{U+}])\). We have, \(\alpha _{\Upsilon }^{L-}=\underset{\xi }{\min }\{\alpha ^L_{\Upsilon _\xi }\}\), \(\alpha _{\Upsilon }^{U-}=\underset{\xi }{\min }\{\alpha ^U_{\Upsilon _\xi }\}\), \(\beta _{\Upsilon }^{L-}=\underset{\xi }{\max }\{\beta ^L_{\Upsilon _\xi }\}\), \(\beta _{\Upsilon }^{U-}=\underset{\xi }{\max }\{\beta ^U_{\Upsilon _\xi }\}\), \(\alpha _{\Upsilon }^{L+}=\underset{\xi }{\max }\{\alpha ^L_{\Upsilon _\xi }\}\), \(\alpha _{\Upsilon }^{U+}=\underset{\xi }{\max }\{\alpha ^U_{\Upsilon _\xi }\}\), \(\beta _{\Upsilon }^{L+}=\underset{\xi }{\min }\{\beta ^L_{\Upsilon _\xi }\}\), and \(\beta _{\Upsilon }^{U+}=\underset{\xi }{\min }\{\beta ^U_{\Upsilon _\xi }\}\). Consequently, there are the ensuing inequities,

$$\begin{aligned}&\sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha _{\Upsilon }^{L-})^2))^\lambda \Big )^{1/\lambda }}} \\&\quad \le \sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha ^L_{\Upsilon _\xi })^2))^\lambda \Big )^{1/\lambda }}}\\&\quad \le \sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha _{\Upsilon }^{L+})^2))^\lambda \Big )^{1/\lambda }}},\\&\sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha _{\Upsilon }^{U-})^2))^\lambda \Big )^{1/\lambda }}} \\&\quad \le \sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha ^U_{\Upsilon _\xi })^2))^\lambda \Big )^{1/\lambda }}}\\&\quad \le \sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha _{\Upsilon }^{U+})^2))^\lambda \Big )^{1/\lambda }}},\\&\sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta _{\Upsilon }^{L+})^2)^\lambda \Big )^{1/\lambda }}} \le \sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta ^L_{\Upsilon _\xi })^2)^\lambda \Big )^{1/\lambda }}} \\&\quad \le \sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta _{\Upsilon }^{L-})^2)^\lambda \Big )^{1/\lambda }}},\\&\sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta _{\Upsilon }^{U+})^2)^\lambda \Big )^{1/\lambda }}} \le \sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta ^U_{\Upsilon _\xi })^2)^\lambda \Big )^{1/\lambda }}} \\&\quad \le \sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta _{\Upsilon }^{U-})^2)^\lambda \Big )^{1/\lambda }}}. \end{aligned}$$

Therefore, \({\tilde{\Upsilon }}^{-}\le IVIFAAWA_{\varsigma }({\tilde{\Upsilon }}_1,{\tilde{\Upsilon }}_2,\ldots ,{\tilde{\Upsilon }}_\psi )\le {\tilde{\Upsilon }}^{+}.\) \(\square\)

Theorem 5

(Monotonicity) Assume that \({\tilde{\Upsilon }}_\xi\) and \({\tilde{\Upsilon }}^{'}_\xi\) \((\xi =1,2,\) \(\ldots ,\psi )\) are two IVPFEs, if \({\tilde{\Upsilon }}_\xi \le {\tilde{\Upsilon }}^{'}_\xi\) for all \(\xi\), then

\(IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )\le IVPFAAWA_{\varsigma }({\tilde{\Upsilon }}^{'}_1, {\tilde{\Upsilon }}^{'}_2,\ldots ,\) \({\tilde{\Upsilon }}^{'}_\psi ).\)

Now, we introduce IVPF Aczel-Alsina ordered weighted averaging (IVPFAAOWA) operator.

Definition 11

Assume that \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\psi )\) is a collection of IVPFEs. A \(\psi\)-dimension IVPF Aczel-Alsina ordered weighted average (IVPFAAOWA) operator is a function \(IVPFAAOWA: IVPFE^{\psi }\) \(\rightarrow IVPFE\) along with corresponding vector \(\varpi =(\varpi _1,\varpi _2,\ldots ,\varpi _\psi )^{T}\) intended to enable \(\varpi _\xi >0\), and \(\mathop \sum \nolimits _{\xi =1}^{\psi }\varpi _\xi =1\). Therefore,

$$\begin{aligned}&IVPFAAOWA_{\varpi }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )=\mathop \bigoplus \limits _{\xi =1}^{\psi }(\varpi _\xi {\tilde{\Upsilon }}_{\varrho (\xi )})\\&\quad = \varpi _1 {\tilde{\Upsilon }}_{\varrho (1)} \bigoplus \varpi _2 {\tilde{\Upsilon }}_{\varrho (2)} \bigoplus \cdots \bigoplus \varpi _\psi {\tilde{\Upsilon }}_{\varrho (\psi )} \end{aligned}$$

where \((\varrho (1),\varrho (2),\ldots ,\varrho (\psi ))\) are the permutation of \((\xi =1,2,\) \(\ldots ,\psi )\), with the property that \({\tilde{\Upsilon }}_{\varrho (\xi -1)}\ge {\tilde{\Upsilon }}_{\varrho (\xi )}\) for all \(\xi =1,2,\ldots ,\psi\).

The succeeding theorem is developed on the basis of the Aczel-Alsina product operation on IVPFEs.

Theorem 6

Let \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\psi )\) denotes the set of IVPFEs. A \(\psi\)-dimension IVPF Aczel-Alsina ordered weighted average (IVPFAAOWA) operator is a function \(IVPFAAOWA: IVPFE^{\psi }\rightarrow IVPFE\) with related vector \(\varpi =(\varpi _1,\varpi _2,\ldots ,\varpi _\psi )^{T}\) such that \(\varpi _\xi >0\), and \(\mathop \sum \nolimits _{\xi =1}^{\psi }\varpi _\xi =1\). Then,

$$\begin{aligned}&IVPFAAOWA_{\varpi }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )=\mathop \bigoplus \limits _{\xi =1}^{\psi }(\varpi _\xi {\tilde{\Upsilon }}_{\varrho (\xi )})\\&\quad =\left( \left[ \sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varpi _\xi \big (-\ln \big (1- \big (\alpha ^L_{\Upsilon _{\varrho (\xi )}}\big )^2 \big )\big )^\lambda \Big )^{1/\lambda }}},\right. \right. \\&\qquad \left. \sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varpi _\xi \big (-\ln \big (1- \big (\alpha ^U_{\Upsilon _{\varrho (\xi )}}\big )^2\big )\big )^\lambda \Big )^{1/\lambda }}}\right] , \\&\qquad \left[ \sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varpi _\xi \big (-\ln \big (\beta ^L_{\Upsilon _{\varrho (\xi )}}\big )^2\big )^\lambda \Big )^{1/\lambda }}},\right. \\&\qquad \left. \left. \sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varpi _\xi \big (-\ln \big (\beta ^U_{\Upsilon _{\varrho (\xi )}}\big )^2\big )^\lambda \Big )^{1/\lambda }}}\right] \right) \end{aligned}$$

where \((\varrho (1),\varrho (2),\ldots ,\varrho (\psi ))\) are the permutation of \((\xi =1,2,\) \(\ldots ,\psi )\), for which \({\tilde{\Upsilon }}_{\varrho (\xi -1)}\ge {\tilde{\Upsilon }}_{\varrho (\xi )}\) for every \(\xi =1,2,\ldots ,\psi\).

The following properties of the IVPFAAOWA operator can readily be demonstrated.

Theorem 7

(Idempotency) If all \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\psi )\) are identical, i.e. \({\tilde{\Upsilon }}_\xi ={\tilde{\Upsilon }}\) for every \(\xi\), then \({IVPFAAOWA}_{\varpi }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )={\tilde{\Upsilon }}.\)

Theorem 8

(Boundedness) Let \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\psi )\) denotes the set of IVPFEs. Assume \({\tilde{\Upsilon }}^{-}=\underset{\xi }{\min } {\tilde{\Upsilon }}_\xi\), and \(\Upsilon ^{+}=\underset{\xi }{\max }{\tilde{\Upsilon }}_\xi\). Subsequently

$$\begin{aligned} {\tilde{\Upsilon }}^{-}\le {IVPFAAOWA}_{\varpi }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )\le {\tilde{\Upsilon }}^{+}. \end{aligned}$$

Theorem 9

(Monotonicity) Let \({\tilde{\Upsilon }}_\xi\) and \({\tilde{\Upsilon }}^{'}_\xi\) \((\xi =1,2,\ldots ,\psi )\) be two sets of IVPFEs, if \({\tilde{\Upsilon }}_\xi \le {\tilde{\Upsilon }}^{'}_\xi\) for all \(\xi\), then

$$\begin{aligned}&{IVPFAAOWA}_{\varpi }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )\\&\quad \le {IVPFAAOWA}_{\varpi }({\tilde{\Upsilon }}^{'}_1, {\tilde{\Upsilon }}^{'}_2, \ldots , {\tilde{\Upsilon }}^{'}_\psi ). \end{aligned}$$

Theorem 10

(Commutativity) Let \({\tilde{\Upsilon }}_\xi\) and \(\Upsilon ^{'}_\xi\) \((\xi =1,2,\ldots ,\) \(\psi )\) be two IVPFEs, then \({IVPFAAOWA}_{\varpi }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )= {IVPFAAOWA}_{\varpi }({\tilde{\Upsilon }}^{'}_1,\) \({\tilde{\Upsilon }}^{'}_2, \ldots , {\tilde{\Upsilon }}^{'}_\psi )\) where \({\tilde{\Upsilon }}^{'}_\xi\) is any permutation of \({\tilde{\Upsilon }}_\xi\) \((\xi =1,2,\ldots ,\psi )\).

We can see in Definitions 10 and 11 that the IVPFAAWA operator only weights the IVPF values, whereas the IVPFAAOWA operator only weights the ordered positions of the IVPF values, not the weights of the IVPF values itself. Weights expressed in both the operators IVPFAAWA and IVPFAAOWA have been in various situations in this way. They are, however, regarded as simply one of them. We introduce the IVPF Aczel-Alsina hybrid averaging (IVPFAAHA) operator to avoid this flaw.

Definition 12

Assume that \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\psi )\) is a collection of IVPFEs. A \(\psi\)-dimension IVPFAAHA operator is a mapping \(IVPFAAHA: IVPFE^{\psi }\) \(\rightarrow IVPFE\), with related weight vector \(\varpi =(\varpi _1,\varpi _2,\ldots ,\varpi _\psi )^{T}\) such that \(\varpi _\xi > 0\), and \(\mathop \sum \nolimits _{\xi =1}^{\psi }\varpi _\xi =1\). Therefore,

$$\begin{aligned}&IVPFAAHA_{\varsigma ,\varpi }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )=\mathop \bigoplus \limits _{\xi =1}^{\psi }(\varpi _\xi \dot{{\tilde{\Upsilon }}}_{\varrho (\xi )})\\&\quad = \varpi _1\dot{{\tilde{\Upsilon }}}_{\varrho (1)} \bigoplus \varpi _2\dot{{\tilde{\Upsilon }}}_{\varrho (2)} \bigoplus \cdots \bigoplus \varpi _\psi \dot{{\tilde{\Upsilon }}}_{\varrho (\psi )} \end{aligned}$$

where \(\dot{{\tilde{\Upsilon }}}_{\varrho (\xi )}\) is the \(\xi\)-th largest weighted IVPF values \(\dot{{\tilde{\Upsilon }}}_{\xi }\) \((\dot{{\tilde{\Upsilon }}}_\xi =\psi \varsigma _\xi {{\tilde{\Upsilon }}}_\xi , \xi =1,2,\ldots ,\psi )\), and \(\varsigma =(\varsigma _1,\varsigma _2,\ldots , \varsigma _\psi )^{T}\) represents weight vector of \({{\tilde{\Upsilon }}}_\xi\) with \(\varsigma _\xi > 0\) and \(\mathop \sum \nolimits _{\xi =1}^{\psi }\varsigma _\xi =1\), where \(\psi\) is balancing constant.

Specifically, if \(\varpi =(1/\psi ,1/\psi ,\ldots ,1/\psi )^T\), the IVPFAAHA operator becomes an IVPFAAWA operator and if \(\varsigma =(1/\psi ,\) \(1/\psi ,\ldots ,1/\psi )^T\), the IVPFAAHA operator becomes an IVPFAAOWA operator.

We can prove the following Theorem 11 by using Aczel-Alsina sum operations of the IVPFEs.

Theorem 11

Let \({\tilde{\Upsilon }}_\xi =([\alpha ^L_{\Upsilon _\xi },\alpha ^U_{\Upsilon _\xi }], [\beta ^L_{\Upsilon _\xi }, \beta ^U_{\Upsilon _\xi }])\) \((\xi =1,2,\ldots ,\) \(\psi )\) be a collection of IVPFEs. A \(\psi\)-dimension IVPFAAHA operator is a mapping \(IVPFAAHA: IVPFE^{\psi }\rightarrow IVPFE\), with related weight vector \(\varpi =(\varpi _1,\varpi _2,\ldots ,\varpi _\psi )^{T}\) such that \(\varpi _\xi > 0\), and \(\mathop \sum \nolimits _{\xi =1}^{\psi }\varpi _\xi =1\). Therefore, IVPFAAHA operator can be evaluated as

$$\begin{aligned}&IVPFAAHA_{\varsigma ,\varpi }({\tilde{\Upsilon }}_1, {\tilde{\Upsilon }}_2,\ldots , {\tilde{\Upsilon }}_\psi )=\mathop \bigoplus \limits _{\xi =1}^{\psi }(\varpi _\xi \dot{{\tilde{\Upsilon }}}_{\varrho (\xi )})\\&\quad =\left( \left[ \sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varpi _\xi \big (-\ln \big (1- \big ({\dot{\alpha }}^L_{\Upsilon _{\varrho (\xi )}}\big )^2\big )\big )^\lambda \Big )^{1/\lambda }}},\right. \right. \\&\qquad \left. \left. \sqrt{1-e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varpi _\xi \big (-\ln \big (1- \big ({\dot{\alpha }}^U_{\Upsilon _{\varrho (\xi )}}\big )^2\big )\big )^\lambda \Big )^{1/\lambda }}}\right] \right. ,\\&\qquad \left[ \sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varpi _\xi \big (-\ln \big ({\dot{\beta }}^L_{\Upsilon _{\varrho (\xi )}}\big )^2 \big )^\lambda \Big )^{1/\lambda }}},\right. \\&\qquad \left. \left. \sqrt{e^{-\Big (\mathop \sum \limits _{\xi =1}^{\psi }\varpi _\xi \big (-\ln \big ({\dot{\beta }}^U_{\Upsilon _{\varrho (\xi )}}\big )^2\big )^\lambda \Big )^{1/\lambda }}} \right] \right) \end{aligned}$$

where \(\dot{{\tilde{\Upsilon }}}_{\varrho (\xi )}\) is the \(\xi\)-th biggest weighted IVPFEs \(\dot{{\tilde{\Upsilon }}}_{\xi }\) \((\dot{{\tilde{\Upsilon }}}_\xi =\psi \varsigma _\xi {{\tilde{\Upsilon }}}_\xi , \xi =1,2,\ldots ,\psi )\), and \(\varsigma =(\varsigma _1,\varsigma _2,\ldots , \varsigma _\psi )^{T}\) is weight vector of \({{\tilde{\Upsilon }}}_\xi\) with \(\varsigma _\xi > 0\) and \(\mathop \sum \nolimits _{\xi =1}^{\psi }\varsigma _\xi =1\), where \(\psi\) is the balancing coefficient.

Proof

Similarly to Theorem 2, Theorem 11 is simply obtained. \(\square\)

5 Recommended decision framework

In the following, we will use the suggested IVPFAAWA operator to create a technique to MADM utilizing IVPF data.

Indicate a discrete set of alternatives by \(\aleph =\{\aleph _1, \aleph _2,\ldots ,\) \(\aleph _u\}\) and the set of attributes by \(\chi =\{\chi _1,\chi _2, \ldots , \chi _\psi \}\). Let \(\varsigma =(\varsigma _1,\varsigma _2,\ldots ,\varsigma _\psi )^T\) be the weight vector of attributes, fulfilling \(\varsigma _\xi >0\) and \(\mathop \sum \nolimits _{\xi =1}^{\psi } \varsigma _\xi =1\). We denote the preference values of every alternative \(\aleph _g\) with regard to the criterion \(\chi _\xi\) by an IVPFE \({{\widetilde{\varphi }}}_{\eta \xi } =([\alpha ^L_{\Upsilon _{\eta \xi }}, \alpha ^U_{\Upsilon _{\eta \xi }}], [\beta ^L_{\Upsilon _{\eta \xi }},\beta ^U_{\Upsilon _{\eta \xi }}])\), where \([\alpha ^L_{\Upsilon _{\eta \xi }}, \alpha ^U_{\Upsilon _{\eta \xi }}]\) states the positive MD that DM considers what the alternative \(\aleph _g\) should satisfy the criteria \(\chi _\xi\), and \([\beta ^L_{\Upsilon _{\eta \xi }},\beta ^U_{\Upsilon _{\eta \xi }}]\) indicates the uncertain degree that DM considers what the alternative \(\aleph _g\) should not fulfill the criteria \(\chi _\xi\), where \([\alpha ^L_{\Upsilon _{\eta \xi }}, \alpha ^U_{\Upsilon _{\eta \xi }}] \subset D[0,1]\), \([\beta ^L_{\Upsilon _{\eta \xi }},\beta ^U_{\Upsilon _{\eta \xi }}] \subset D[0,1]\) and \(0\le (\alpha ^U_{\Upsilon _{\eta \xi }})^2+(\beta ^U_{\Upsilon _{\eta \xi }})^2 \le 1\), \((\eta =1,2,\ldots ,\phi )\). Therefore we are able to elicit an IVPF decision matrix \(R =\big ({{\widetilde{\varphi }}}_{\eta \xi }\big )_{\phi \times \psi }\) in the following form:

$$\begin{aligned}&R =\big ({{\widetilde{\varphi }}}_{\eta \xi } \big )_{\phi \times \psi } \\&\quad = \begin{array}{cc} &{} \chi _1 \;\ \; \chi _2 \cdots \chi _\psi \\ \begin{array}{c} \aleph _1 \\ \aleph _2 \\ \vdots \\ \aleph _u \end{array} &{} \left( \begin{array}{cccc} ([\alpha ^L_{\Upsilon _{11}},\alpha ^U_{\Upsilon _{11}}], [\beta ^L_{\Upsilon _{11}},\beta ^U_{\Upsilon _{11}}]) &{} ([\alpha ^L_{\Upsilon _{12}},\alpha ^U_{\Upsilon _{12}}], [\beta ^L_{\Upsilon _{12}},\beta ^U_{\Upsilon _{12}}]) &{} \cdots &{} ([\alpha ^L_{\Upsilon _{1\psi }},\alpha ^U_{\Upsilon _{1\psi }}], [\beta ^L_{\Upsilon _{1\psi }},\beta ^U_{\Upsilon _{1\psi }}])\\ ([\alpha ^L_{\Upsilon _{21}},\alpha ^U_{\Upsilon _{21}}], [\beta ^L_{\Upsilon _{21}},\beta ^U_{\Upsilon _{21}}]) &{} ([\alpha ^L_{\Upsilon _{22}},\alpha ^U_{\Upsilon _{22}}], [\beta ^L_{\Upsilon _{22}},\beta ^U_{\Upsilon _{22}}]) &{} \cdots &{} ([\alpha ^L_{\Upsilon _{2\psi }},\alpha ^U_{\Upsilon _{2\psi }}], [\beta ^L_{\Upsilon _{2\psi }},\beta ^U_{\Upsilon _{2\psi }}])\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ ([\alpha ^L_{\Upsilon _{\phi 1}},\alpha ^U_{\Upsilon _{\phi 1}}], [\beta ^L_{\Upsilon _{\phi 1}},\beta ^U_{\Upsilon _{\phi 1}}]) &{} ([\alpha ^L_{\Upsilon _{\phi 2}},\alpha ^U_{\Upsilon _{\phi 2}}], [\beta ^L_{\Upsilon _{\phi 2}},\beta ^U_{\Upsilon _{\phi 2}}]) &{} \cdots &{} ([\alpha ^L_{\Upsilon _{\phi \psi }},\alpha ^U_{\Upsilon _{\phi \psi }}], [\beta ^L_{\Upsilon _{\phi \psi }},\beta ^U_{\Upsilon _{\phi \psi }}]) \end{array}\right) \end{array} \end{aligned}$$

The following steps are included in the analysis focusing on the IVPFAAWA operator to evaluate the MADM concerns with IVIFEs:

Step 1. Convert decision matrix \(R =\big ({{\widetilde{\varphi }}}_{\eta \xi } \big )_{\phi \times \psi }\) into the normalization matrix \({\overline{R}} =\big (\overline{{{\widetilde{\varphi }}}}_{\eta \xi } \big )_{\phi \times \psi }\).

$$\begin{aligned} \overline{{{\widetilde{\varphi }}}}_{\eta \xi }=\left\{ \begin{array}{ll} {{\widetilde{\varphi }}}_{\eta \xi } \text{ for } \text{ benefit } \text{ attribute } \chi _\xi \\ ({{\widetilde{\varphi }}}_{\eta \xi })^c \text{ for } \text{ cost } \text{ attribute } \chi _\xi \end{array}\right. \end{aligned}$$
(4)

where \(({{\widetilde{\varphi }}}_{\eta \xi })^c\) is complement of \({{\widetilde{\varphi }}}_{\eta \xi }\), so as \(({{\widetilde{\varphi }}}_{\eta \xi })^c=([\beta ^L_{\Upsilon _{\eta \xi }},\) \(\beta ^U_{\Upsilon _{\eta \xi }}],[\alpha ^L_{\Upsilon _{\eta \xi }},\) \(\alpha ^U_{\Upsilon _{\eta \xi }}])\).

If all of the attributes \(\chi _\xi\) \((\xi =1,2,\ldots ,\psi )\) are of an identical type, there is no need to normalize the attribute values. However, if a MADM issue has both benefit and cost attributes, we are able to transform cost type rating values into the benefit type rating values. As a consequence \(R =\big ({{\widetilde{\varphi }}}_{\eta \xi } \big )_{\phi \times \psi }\) change into IVPF decision matrix \({\overline{R}} =\big (\overline{{{\widetilde{\varphi }}}}_{\eta \xi } \big )_{\phi \times \psi }\).

Step 2. Use the IVPFAAWA operator with the decision information expressed in matrix R to acquire the overall preference values \({{\widetilde{\varphi }}}_\eta\) \((\eta =1,2,\ldots ,\phi )\) of the alternative \(\aleph _\eta\) i.e.,

$$\begin{aligned}&{{\widetilde{\varphi }}}_\eta =IVPFAAWA_{\varsigma }({{\widetilde{\varphi }}}_{\eta 1},{{\widetilde{\varphi }}}_{\eta 2},\ldots ,{{\widetilde{\varphi }}}_{\eta \psi })=\mathop \bigoplus \limits _{\xi =1}^{\psi }(\varsigma _\xi {{\widetilde{\varphi }}}_{\eta \xi })\\&\quad =\left( \left[ \sqrt{1-e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha ^L_{\Upsilon _\xi })^2))^\lambda )^{1/\lambda }}}, \right. \right. \\&\qquad \left. \sqrt{1-e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (1- (\alpha ^U_{\Upsilon _\xi })^2))^\lambda )^{1/\lambda }}} \right] , \\&\quad \left. \left[ \sqrt{e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta ^L_{\Upsilon _\xi })^2)^\lambda )^{1/\lambda }}}, \sqrt{e^{-(\mathop \sum \limits _{\xi =1}^{\psi }\varsigma _\xi (-\ln (\beta ^U_{\Upsilon _\xi })^2)^\lambda )^{1/\lambda }}}\right] \right) . \end{aligned}$$

Step 3. Determine the scores \({\mathbb {Q}}({{\widetilde{\varphi }}}_\eta )\) \((\eta =1,2,\ldots ,\phi )\) of the ultimate IVPFEs \({{\widetilde{\varphi }}}_\eta\) \((\eta =1,2,\ldots ,\phi )\) to evaluate all of the alternatives \(\aleph _\eta\) \((\eta =1,2,\ldots ,\phi )\) and then to choose the most effective one(s) (if there is no difference between two scores \({\mathbb {Q}}({{\widetilde{\varphi }}}_\eta )\) and \({\mathbb {Q}}({{\widetilde{\varphi }}}_\xi )\), then we must evaluate the accuracy degrees \({\mathbb {W}}({{\widetilde{\varphi }}}_\eta )\) and \({\mathbb {W}}({{\widetilde{\varphi }}}_\xi )\) of the collective overall preference values \({{\widetilde{\varphi }}}_\eta\) and \({{\widetilde{\varphi }}}_\xi\), respectively, and then rank the alternatives \(\aleph _\eta\) and \(\aleph _\xi\) by means of accuracy degrees \({\mathbb {W}}({{\widetilde{\varphi }}}_\eta )\) and \({\mathbb {W}}({{\widetilde{\varphi }}}_\xi ))\).

Step 4. Rank all the possibilities \(\aleph _\eta\) \((\eta =1,2,\ldots ,\phi )\) and pick the optimal one(s) according to \({\mathbb {Q}}({{\widetilde{\varphi }}}_\eta )\) \((\eta =1,2,\ldots ,\phi )\).

Step 5. End.

6 Numerical analysis

MADM’s technique can be applied to a broader range of human choices and decisions, ranging from commercial to governmental to socioeconomically frameworks. Let’s look at an example of a professional decision-making difficulty.

6.1 Problem description

A travel agency named Chongqing China International Travel Service has dominated in giving travel-related services to international tourists from different countries. The agency’s consumers should be offered additional services, such as comprehensive briefings, online reservation capabilities, the ability to reserve and sell airline tickets, and certain other transport services. As a result, the corporation intends to locate an appropriate information technology (IT) software development company capable of delivering affordable arrangements via software development. To accomplish the above rationale, the organisation establishes a group of five alternatives (companies), to be specific, Chongqing Temiluo Technology Co Ltd \((\aleph _1)\), Chongqing Zhuangwang Technology Co Ltd \((\aleph _2)\), Chongqing Zhangzhiwo Technology Co Ltd \((\aleph _3)\), Chongqing Siyuan Software Company \((\aleph _4)\), and Wujue Software Co Ltd \((\aleph _5)\). They use the following criteria to evaluate five possible software companies:

\(\chi _1\):

: Technical ability (Technical abilities are the specific skills and knowledge necessary to successfully accomplish complex actions, activities, and processes in the fields of physical and computational technology, including a wide range of other businesses. The key challenges in technical abilities include standard operating systems, programming languages, software proficiency, graphic designing, and analytical techniques),

\(\chi _2\):

: High-quality service management (Generally speaking, service quality refers to a customer’s evaluation of service results in terms of the organization’s business. An organisation with superior service quality is more likely to successfully fulfil customers’ needs while being globally competitive in its sector), (figure 2).

\(\chi _3\):

: Management of projects (Project management is the utilization of explicit information, abilities, apparatuses and strategies to provide something of value to individuals. A project management life cycle comprises five particular stages including initiation, planning, execution, monitoring, and closure that consolidate to transform a project idea into a working product) (figure 3).

\(\chi _4\):

: Professional background (A professional experience is a summary of prior work experience and performance. It’s most commonly used throughout the application process for a job. This is more than a list of previous roles; it should showcase your most important and relevant accomplishments).

The DM gives weight of the attribute as \(\varsigma = (0.30, 0.30, 0.25,\) \(0.15)^T\). The DM utilizes the IVPFEs to give assessment data of five alternatives \(\aleph _\eta\) \((\eta =1,2,\ldots , 5)\) in relation to aforesaid four attributes \(\chi _\xi\) \((\xi = 1, 2, 3, 4)\), as indexed in table 1.

Figure 2
figure 2

High service quality management.

Full size image
Figure 3
figure 3

Project management.

Full size image
Table 1 IVPF decision matrix.
Full size table

As every one of the criteria values are of the same kind, the initial decision matrix does not need to be normalized. With the aim of designating proper IT companies \(\aleph _\eta\) \((\eta =1,2,\ldots ,\) 5), we utilize the IVPFAAWA operator. The IVPFEs presented in table 1 are assessed accordance with the following arrangements:

  • Step 1. Expect to be that \(\lambda =5\). Then, at that point, by employing the IVPFAAWA operator to assess the overall decision values \({{\widetilde{\varphi }}}_\eta\) of software systems \(\aleph _\eta\) are as \(\widetilde{\varphi }_1=([0.59526, 0.67766], [0.21049, 0.31484])\),

    \(\widetilde{\varphi }_2=([0.51168, 0.60141], [0.35793, 0.42258])\),

    \(\widetilde{\varphi }_3=([0.70605, 0.74565], [0.21936, 0.27472])\),

    \(\widetilde{\varphi }_4=([0.60963, 0.66228], [0.28787, 0.35181])\),

    \(\widetilde{\varphi }_5=([0.59392, 0.68748],[0.27990, 0.33633])\).

  • Step 2. Calculate the score values \({\mathbb {Q}}({{\widetilde{\varphi }}}_\eta )\) \((\eta =1,2,\ldots ,\) 5) of the entire IVPFEs \({{\widetilde{\varphi }}}_\eta\) \((\eta =1,2,\ldots ,5)\) by Definition 6, and get \({\mathbb {Q}}({{\widetilde{\varphi }}}_1)=0.33506\), \({\mathbb {Q}}({{\widetilde{\varphi }}}_2)=0.15841\), \({\mathbb {Q}}({{\widetilde{\varphi }}}_3)=0.46545\), \({\mathbb {Q}}({{\widetilde{\varphi }}}_4)=0.30181\), \({\mathbb {Q}}({{\widetilde{\varphi }}}_5)=0.31695\).

  • Step 3. Subsequently \({\mathbb {Q}}({{\widetilde{\varphi }}}_3)>{\mathbb {Q}}({{\widetilde{\varphi }}}_1)>{\mathbb {Q}}({{\widetilde{\varphi }}}_5)>{\mathbb {Q}}({{\widetilde{\varphi }}}_4)>{\mathbb {Q}}({{\widetilde{\varphi }}}_2)\), then \({{\widetilde{\varphi }}}_3>{{\widetilde{\varphi }}}_1>{{\widetilde{\varphi }}}_5>{{\widetilde{\varphi }}}_4>{{\widetilde{\varphi }}}_2\), and thus we have \(\aleph _3\succ \aleph _1\succ \aleph _5\succ \aleph _4\succ \aleph _2\), where \(``\succ ''\) represents “be superior to”.

  • Step 4. According to the priority ranking of alternatives, \(\aleph _3\) is selected as the supreme IT software company.

7 The effects of parameter \(\lambda\) on the ranking results

It is noted that we accept \(\lambda =10\) in the aforementioned analysis. In general, DMs can assign different values to the parameter with respect to their preferences. To be able to demonstrate the effects of the parameter \(\lambda\) on the decision-making outcome of this example, we use the different values \(\lambda\) to rank the alternatives. We set the values within 1 and 100 and generate the score values of five IT software companies \(\aleph _\eta\) \((\eta =1,2,\ldots , 5)\) to evaluate the variation in the ranking of these companies concerning the values of the parameter. The differences in the rankings regarding the parameter values \(\lambda\) can be seen explicitly in table 2, and graphically in figure 4. Table 2 portrays the score values of alternatives produced by employing the IVPFAAWA operator, where we have the ability to recognize that score values of each alternative grow significantly whilst the values of \(\lambda\) change from 1 to 100. When \(1 \le \lambda \le 8\), the order of preference is \(\aleph _3\succ \aleph _1\succ \aleph _5\succ \aleph _4\succ \aleph _2\) and when \(9 \le \lambda \le 100\), the order of preference is \(\aleph _3\succ \aleph _5\succ \aleph _1\succ \aleph _4\succ \aleph _2\). It is observed that there are two different orders of preference but the corresponding best choice is always \(\aleph _3\).

Table 2 Preference order of alternatives by IVPFAAWA operator with different parameter values \(\lambda .\)
Full size table
Figure 4
figure 4

Score values of the alternatives for different values \(\lambda\) by IVPFAAWA operator.

Full size image

8 Comparative analysis

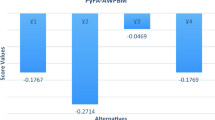
We compare our proposed method to a variety of other classical techniques namely the IVPF weighted averaging (IVPFWA) operator [39], IVPF weighted geometric (IVPFWG) operator [39], IVPF Einstein weighted averaging (IVPFEWA) operator [40] and IVPF Einstein weighted geometric (IVPFEWG) operator [41] in this section. Table 3 summarises the comparison outcomes, which are represented graphically in figure 5. Tables 2 and 3 show that the IVPFWA operator is a particular case of our recommended IVPFAAWA operator, and that it occurs when \(\lambda =1\).

As a result, our suggested techniques are much more comprehensive and diverse than many conventional techniques for dealing with IVPF MADM difficulties.

Table 3 Comparison analysis with several commonly used methodologies.
Full size table
Figure 5
figure 5

Comparative analysis employing a few prevalent approaches.

Full size image
Table 4 Comparisons with several existing techniques in terms of their characteristics.
Full size table

9 Conclusions

In this paper, bearing in mind AA t-norm and AA t-conorm, we have presented different operational rules for IVPFEs. Subsequently, we have proposed the IVPFAAWA operator, IVPFAAOWA operator, and IVPFAAHA operator based on the proposed Aczel-Alsina operations and analyzed a lot of important characteristics of these operators. Based on IVPFAAWA operator, we developed a methodology to manage conventional MADM issue, delivered a representative example to adequately justify the methodology, and examined the impacts of the adaptable parameter on the ultimate aggregation results. The relative investigation further exhibited and found that the outcomes coincide with the current procedures which confirms the constancy of the methodology.

When it comes to future research, we will additionally sum up these operators by the utilization of the power operator and Bonferroni mean operator or expand the uses of the aggregation operators to different areas, as for example multi-objective optimization problem, clustering, supply chain management, and pattern recognition. Moreover, we will stretch out the suggested methodology to tackle the MADM issues under a dual probabilistic linguistic environment [42], etc.