A novel outranking method for multiple criteria decision making with interval-valued Pythagorean fuzzy linguistic information

Abstract

This paper aim to propose a novel outranking method based on interval-valued Pythagorean fuzzy linguistic set (IVPFLS) to estimate alternatives for decision makers. With the rapid increase of the complexity, the challenges of a group of decision makers, a high degree of uncertainty and conflicting criteria are associated with multiple criteria decision making (MCDM) problems and few studies for these. In this regard, the outranking-VIKOR (O-VIKOR) method with the construction of compromise solution considers “group utility” and “individual regret” in pairwise alternatives. To fully show the compromise outranking relation, the O-VIKOR method allows decision makers reach consensus by mutual concessions when the dominant position from alternatives is extant. Subsequently, we define the credibility formula that constitutes a complementary judgment matrix for devoting to ranking the alternatives more precision. When it is necessary to process the evaluation information of multiple decision makers, the interval-value Pythagorean fuzzy linguistic entropic induced ordered weighted averaging (IVPFLEIOWA) operator is proposed with entropic order-inducing variable which includes a new interval-value Pythagorean fuzzy linguistic entropy for measuring uncertainty to capture the interrelationship among the primary preference of decision makers. Finally, a case study on site selection problem for a manufacturer is presented to illustrate the efficiency of our proposed method and make comparative analysis with other methods.

1 Introduction

Multiple criteria decision making (MCDM) is a significant technique to handle preference information of decision makers on the practical decision making and widely applies in many domains, such as investment strategy (Xian et al. 2018b), robot selection (Liu et al. 2019), green supply chain initiatives (Zhang and Xing 2017) and energy project selection (Liang and Xu 2017). These MCDM problems are generally considered in fuzzy environment. On the basis of fuzzy sets (Zadeh 1965), Atanassov (1986) depicted the concept of intuitionistic fuzzy set (IFSs) to capture imprecision information with membership function and non-membership function. Pythagorean fuzzy set (Yager 2013) as a special type with nonstandard fuzzy set, it allows the sum of the membership degree and the non-membership degree is over 1, nevertheless the square sum is less or equal than 1. And many fundamental studies are contributed in Pythagorean fuzzy circumstances; Yager (2014) gave some operators on PFSs and discusses properties of Pythagorean fuzzy number (PFN) such as membership grade. Xian et al. (2018a) investigated principal-value Pythagorean fuzzy set (p-PFS) with the consideration of principal-value and introduced a ranking method to find the idea alternative. For adapting demand of decision making, Zhang (2016) extended PFSs to interval-valued Pythagorean fuzzy sets (IVPFSs). Because people tend to use linguistic information indicating the preference in assessment, Du et al. (2017) proposed interval-valued Pythagorean fuzzy linguistic number (IVPFLN) that use linguistic information with the reliability degree to express evaluation for highly uncertain condition and make some research on operators. It is not sufficient for study of measuring uncertainty on IVPFLS, but the entropy is an useful way in this. Therefore, we develop an interval-value Pythagorean fuzzy linguistic entropic induced ordered weighted averaging (IVPFLEIOWA) operator with interval-value Pythagorean fuzzy linguistic entropy which can capture uncertainty in IVPFLSs and aggregate evaluation information.

Generally, establishing evaluation criteria system is a sophisticated process for constructing mathematical model of preference information. In the literature, researchers have utilized a variety of MCDM methods for finding the acceptable final solution, such as aggregated decision method (Wei 2019; Wu et al. 2019; Tang et al. 2019), bidirectional project method (Lu et al. 2019), prospect theory (Ding et al. 2019), TOPSIS method (Xian et al. 2018b) and VIKOR method (Chen 2018). Among these methods, the merit of the VIKOR (Vlsekriterijumska Optimizacija I Kompromisno Resenje) method is dedicated to obtain the compromise solution considering the maximum group utility and minimum individual regret for realistic decision-making environments. Recently, some studies of VIKOR method have extended on a variety of uncertain environmental conditions. Sanayei et al. (2010) developed an extended VIKOR method for solving MCDM problem in fuzzy environment and applied in supplier selection problem. Chen (2018) defined remoteness index for different ideal solution: displaced or fixed, and proposed remoteness index-based Pythagorean fuzzy VIKOR methods. For taking linguistic information into account MCDM problem, Liao et al. (2015) proposed some hesitant fuzzy linguistic distance measures and extended to the hesitant fuzzy linguistic VIKOR method based on these measures. There are many useful applications of VIKOR method in uncertainty MCDM problems (Chen 2018; Meksavang et al. 2019; Liu and Wu 2012; Park et al. 2011). It is understood that there are some gaps on VIKOR method. While using the form like the closest to the ideal to achieve the consensus by mutual concessions, the VIKOR method neglects many critical information of alternatives in pairs. Because of its characteristics, it is difficult to handle highly uncertain information.

The outranking methods not only can avoid these drawbacks but also by pairwise comparison can effectively reduce the high degree of uncertainty. As for the classical method, the outranking methods, with multiple morphologies have a significant feature that forms an outranking relation by the action of comparing pairs on each criteria. Meanwhile, the indifference information is also adequately involved in consideration, which is more in line with realistic situation. The first outranking method called ELECTRE I (ELimination Et Choix Traduisant la REalit I) is an effective MCDM method(Roy 1968). The ELECTRE I method is used to compute a partial prioritization and determine a set of ponderable alternatives. And other ELECTRE method, such as ELECTRE II, ELECTRE III, ELECTRE IV, ELECTRE IS, ELECTRE TRI (Figueira et al. 2005), which is more elaborate than the original method. The ELECTRE I is used for selection problem. After that, the ELECTRE II is designed by Roy and Bertier (1973) to construct outranking relation of alternatives which one alternative is preferred to another on each criteria. ELECTRE III was proposed to improve ELECTRE II (Roy 1978) and provides indifference, preference and veto thresholds that is more detailed to establish outranking relation in decision matrices. It is particularly used in quantifying the relative importance of criteria and reduce the uncertainty of information by comparison in pairwise. Thus, to demonstrate the applications of ELECTRE III, Papadopoulos and Karagiannidis (2008) used the ELECTRE III in the selection of decentralized energy systems. Radziszewska-Zielina (2010) applied ELECTRE III to pick out the most suitable construction enterprise for cooperation in terms of partnering relations. Hashemi et al. (2016) extended ELECTRE III to handle interval-valued fuzzy information to determine the best investment project. Based on ELECTRE III, Peng and Wang (2018) developed an improved outranking method combined QUALIFLEX to enhance effective ranking capability for solving cognitive information. Nevertheless, the ELECTRE III method directly negates the value which exceeds veto thresholds in relation model, without considering the impact of this part of the information on the final ranking and ignore the subjective will of the DMs in consensus by mutual concessions.

Motivated by the conflict compromise of VIKOR and the pairwise comparison of ELECTRE III, The outranking-VIKOR (O-VIKOR) in interval-valued Pythagorean fuzzy linguistic environment is proposed for treating group decision making problems with high uncertainty and conflicting criteria. The contributions of this paper can be summarized briefly as follows:

• (1) The interval-value Pythagorean fuzzy linguistic entropic induced ordered weighted average operator (IVPFLEIOWA) is proposed to utilize the entropy order-inducing variable to describe the uncertainty and the sequential position information of IVPFLS.

• (2) An compromise outranking method is proposed to remedy the drawbacks in ELECTRE III. This method has fully integration of the advantages of relation model of ELECTRE III and the successful reaching consensus by compromise. In the proposed method, we define the compromise outranking degree that represents the superiority of action one over another with consensus parameter based on outranking index and veto index.

• (3) Because the compromise outranking relation is difficult to obtain a complete sorting result, a credibility formula is proposed to construct the complementary judgment matrix and help rank the results. The advantages of this method are clearly illustrated in modified parameter analysis and comparative analyses.

The remainder of this paper is organized as follows. Section 2 briefly recalls some basic concepts of IVPFLSs and two MCDM methods, VIKOR and ELECTRE III. Section 3 defines an interval-valued Pythagorean fuzzy linguistic entropy and IVPFLEIOWA operation which considering entropy order-inducing variable. In Sect. 4, we propose O-VIKOR model and introduce the steps for solving MCDM problems. In Sect. 5, the example that involves site selection to interpret the flexibility and validity of the proposed method. This section also provides some comparative analyses to demonstrate the superior performance of the proposed method. Section 6 presents the conclusions and outlines the aims of the future work.

2 Preliminaries

In this section, we briefly introduce some basic concepts of linguistic term sets, interval-valued intuitionistic fuzzy set, interval-valued Pythagorean fuzzy set and interval-valued intuitionistic fuzzy entropy. And two traditional MCDM methods that call VIKOR and ELECTRE III are also briefly described.

2.1 Linguistic term sets

As practical decision making, personal preference information is fuzziness from linguistic term sets rather than numerical numbers. Sometimes it is difficult to evaluate preference information with numerical numbers, especially for qualitative information. Basic concept is introduced in the following.

Definition 2.1

(Du et al. 2017) Let $S = \left\{ {{s_i}|i = 1,2,\ldots ,t} \right\}$ be a linguistic term set, S is a consecutive finite subset of ordered linguistic term set. Here the t denotes furthest value of linguistic term set. ${s_i}$ which subscript as i is the ith language variable of S. Let $S = \left\{ {{s_1},{s_2},\ldots ,{s_9}} \right\}$ be a linguistic term set, it can be given as follows:

$$\begin{aligned}&S = \{s_1=\text {extremely poor}, s_2 =\text {very low}, s_3=\text {poor},s_4 =\text {slightly poor}, \\&\quad s_5 =\text {fair}, s_6 = \text {slightly good}, s_7 =\text {good}, s_8 =\text {very good}, s_9 =\text {extremely good}\}. \end{aligned}$$

in which $s_i<s_k$ iff $i<k$. It would be satisfied the following additional characteristics:

• (1) The negation operator: $Neg(s_i)=s_k,k=T-1$. ($T+1$ is the cardinality).

• (2) Maximization and Minimization operator: Max$(s_i, s_k)=s_i$ if $s_i\ge s_k$, Min $(s_i, s_k)=s_i$ if $s_i\le s_k$.

2.2 Interval-valued Pythagorean fuzzy linguistic set

Definition 2.2

(Zhang 2016) Let X be a fix set. An interval-valued Pythagorean fuzzy set (IVPFS) ${\tilde{P}}$ on X is defined as:

$$\begin{aligned} {\tilde{P}} = \left\{ {\left\langle {{{{\tilde{\mu }}}_{{\tilde{P}}}}(x),{{{\tilde{\nu }}}_{{\tilde{P}}}}(x)} \right\rangle \left| {x \in X} \right. } \right\} \end{aligned}$$

(1)

where the function: ${{\tilde{\mu }} _{{\tilde{P}}}}(x) = [\mu _{{\tilde{P}}}^{\mathrm{L}}(x),\mu _{{\tilde{P}}}^{\mathrm{U}}(x)] \subseteq {\mathrm{[0,1]}}$, ${{\tilde{\nu }} _{{\tilde{P}}}}(x) = [\nu _{{\tilde{P}}}^{\mathrm{L}}(x),\nu _{{\tilde{P}}}^{\mathrm{U}}(x)] \subseteq [0,1]$, $0 \le {(\mu _{{\tilde{P}}}^{\mathrm{U}}(x))^2} + {(\nu _{{\tilde{P}}}^{\mathrm{U}}(x))^2} \le 1$ for $\forall x \in X$; ${{\tilde{\mu }} _{{\tilde{P}}}}(x)$, ${{\tilde{\nu }} _{{\tilde{P}}}}(x)$ present degree of interval-valued membership and degree of interval-valued non-membership, respectively. The degree of interval-valued hesitancy denotes: ${{\tilde{\pi }} _{{\tilde{P}}}}(x) = [\sqrt{1 - \mu _{{\tilde{P}}}^{\mathrm{U}}(x){^2} - \nu _{{\tilde{P}}}^{\mathrm{U}}(x){^2}} , \sqrt{1 - \mu _{{\tilde{P}}}^{\mathrm{L}}(x){^2} - \nu _{{\tilde{P}}}^{\mathrm{L}}(x){^2}} ]$.

Definition 2.3

(Du et al. 2017) Let X be a fix set, S be a finite linguistic term, then the interval-valued Pythagorean fuzzy linguistic set (IVPFLS) ${\tilde{s}}$ in X is defined as:

$$\begin{aligned} {\tilde{s}} = \left\{ {\left\langle {{s_{\alpha (x)}};[\mu _{\tilde{s}}^{\mathrm{L}}(x),\mu _{\tilde{s}}^{\mathrm{U}}(x)],[\nu _{\tilde{s}}^{\mathrm{L}}(x),\nu _{\tilde{s}}^{\mathrm{U}}(x)]} \right\rangle \left| {x \in X} \right. } \right\} \end{aligned}$$

(2)

where ${s_{\alpha (x)}} \in S$, the function: $[\mu _{\tilde{s}}^{\mathrm{L}}(x),\mu _{\tilde{s}}^{\mathrm{U}}(x)] \subseteq [0,1]$, $[\nu _{\tilde{s}}^{\mathrm{L}}(x),\nu _{\tilde{s}}^{\mathrm{U}}(x)] \subseteq [0,1]$, denoting the degree of interval-valued membership ($\mu _{\tilde{s}}^{\mathrm{L}}(x)$ and $\mu _{\tilde{s}}^{\mathrm{U}}(x)$ is the lower and the upper of membership) and the degree of interval-valued non-membership ($\nu _{\tilde{s}}^{\mathrm{L}}(x)$ and $\nu _{\tilde{s}}^{\mathrm{U}}(x)$ is the lower and the upper of non-membership), satisfies the condition: $0 \le {(\mu _{\tilde{s}}^{\mathrm{U}}(x))^2} + {(\nu _{\tilde{s}}^{\mathrm{U}}(x))^2} \le 1$, $\forall x \in X$, and the degree of interval-valued hesitancy denotes:

$$\begin{aligned} {{\tilde{\pi }} _{\tilde{s}}}(x) = \left[ \sqrt{1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}(x))}^2} - {{(\nu _{\tilde{s}}^{\mathrm{U}}(x))}^2}}, \sqrt{1 - {{(\mu _{\tilde{s}}^{\mathrm{L}}(x))}^2} - {{(\nu _{\tilde{s}}^{\mathrm{L}}(x))}^2}} \right] \subseteq [0,1]. \end{aligned}$$

Definition 2.4

(Du et al. 2017) Let ${\tilde{s}} = ({s_{\alpha (x)}};[\mu _{\tilde{s}}^{\mathrm{L}}(x),\mu _{\tilde{s}}^{\mathrm{U}}(x)],[\nu _{\tilde{s}}^{\mathrm{L}}(x),\nu _{\tilde{s}}^{\mathrm{U}}(x)])$, ${{\tilde{s}}_1} = ({s_\alpha }({x_1});[\mu _{\tilde{s}}^{\mathrm{L}}({x_1}),\mu _{\tilde{s}}^{\mathrm{U}}({x_1})],$$[\nu _{\tilde{s}}^{\mathrm{L}}({x_1}),\nu _{\tilde{s}}^{\mathrm{U}}({x_1})])$ and ${{\tilde{s}}_2} = ({s_\alpha }({x_2});[\mu _{\tilde{s}}^{\mathrm{L}}({x_2}),\mu _{\tilde{s}}^{\mathrm{U}}({x_2})],[\nu _{\tilde{s}}^{\mathrm{L}}({x_2}),\nu _{\tilde{s}}^{\mathrm{U}}({x_2})])$ be three IVPFLSs, the operational laws of interval-valued Pythagorean fuzzy linguistic variable set $(\lambda > 0)$ are defined as:

• 1. ${{\tilde{s}}_1} \oplus {{\tilde{s}}_2} = ({s_{\alpha ({x_1}) + \alpha ({x_2})}};[\sqrt{{{(\mu _{\tilde{s}}^{\mathrm{L}}({x_1}))}^2} + {{(\mu _{\tilde{s}}^{\mathrm{L}}({x_2}))}^2} - {{(\mu _{\tilde{s}}^{\mathrm{L}}({x_1}))}^2}{{(\mu _{\tilde{s}}^{\mathrm{L}}({x_2}))}^2}}$,

  $\sqrt{{{(\mu _{\tilde{s}}^{\mathrm{U}}({x_1}))}^2} + {{(\mu _{\tilde{s}}^{\mathrm{U}}({x_2}))}^2} - {{(\mu _{\tilde{s}}^{\mathrm{U}}({x_1}))}^2}{{(\mu _{\tilde{s}}^{\mathrm{U}}({x_2}))}^2}} ],[\nu _{\tilde{s}}^{\mathrm{L}}({x_1})\nu _{\tilde{s}}^{\mathrm{L}}({x_2}),\nu _{\tilde{s}}^{\mathrm{U}}({x_1})\nu _{\tilde{s}}^{\mathrm{U}}({x_2})])$;

• 2. ${{\tilde{s}}_1} \otimes {{\tilde{s}}_2} = ({s_{\alpha ({x_1}) \times \alpha ({x_2})}};[\mu _{\tilde{s}}^{\mathrm{L}}({x_1})\mu _{\tilde{s}}^{\mathrm{L}}({x_2}),\mu _{\tilde{s}}^{\mathrm{U}}({x_1})\mu _{\tilde{s}}^{\mathrm{U}}({x_2})]$, $[\sqrt{{{(\nu _{\tilde{s}}^{\mathrm{L}}({x_1}))}^2} + {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_2}))}^2} - {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_1}))}^2}{{(\nu _{\tilde{s}}^{\mathrm{L}}({x_2}))}^2}}$,

  $\sqrt{{{(\nu _{\tilde{s}}^{\mathrm{U}}({x_1}))}^2} + {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_2}))}^2} - {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_1}))}^2}{{(\nu _{\tilde{s}}^{\mathrm{U}}({x_2}))}^2}} ])$;

• 3. $\lambda {\tilde{s}} = ({s_{\lambda \alpha (x)}};[\sqrt{1 - {{(1 - {{(\mu _{\tilde{s}}^{\mathrm{L}}(x))}^2})}^\lambda }} ,\sqrt{1 - {{(1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}(x))}^2})}^\lambda }} ],[{(\nu _{\tilde{s}}^{\mathrm{L}}(x))^\lambda },{(\nu _{\tilde{s}}^{\mathrm{U}}(x))^\lambda }])$;

• 4. ${{\tilde{s}}^\lambda } = ({s_{{{(\alpha (x))}^\lambda }}};[{(\mu _{\tilde{s}}^{\mathrm{L}}(x))^\lambda },{(\mu _{\tilde{s}}^{\mathrm{U}}(x))^\lambda }],[\sqrt{1 - {{(1 - {{(\nu _{\tilde{s}}^{\mathrm{L}}(x))}^2})}^\lambda }} ,\sqrt{1 - {{(1 - {{(\nu _{\tilde{s}}^{\mathrm{U}}(x))}^2})}^\lambda }} ])$;

• 5. ${{\tilde{s}}^c} = ({s_{t - \alpha (x)}};[\nu _{\tilde{s}}^{\mathrm{L}}(x),\nu _{\tilde{s}}^{\mathrm{U}}(x)],[\mu _{\tilde{s}}^{\mathrm{L}}(x),\mu _{\tilde{s}}^{\mathrm{U}}(x)])$, (${{\tilde{s}}^c}$ is the complementary set of ${\tilde{s}}$).

Definition 2.5

(Du et al. 2017) Let ${\tilde{s}} = ({s_{\alpha (x)}};[\mu _{\tilde{s}}^{\mathrm{L}}(x),\mu _{\tilde{s}}^{\mathrm{U}}(x)],[\nu _{\tilde{s}}^{\mathrm{L}}(x),\nu _{\tilde{s}}^{\mathrm{U}}(x)])$, ${{\tilde{s}}_1} = ({s_\alpha }({x_1});[\mu _{\tilde{s}}^{\mathrm{L}}({x_1}),\mu _{\tilde{s}}^{\mathrm{U}}({x_1})],$$[\nu _{\tilde{s}}^{\mathrm{L}}({x_1}),\nu _{\tilde{s}}^{\mathrm{U}}({x_1})])$ and ${{\tilde{s}}_2} = ({s_\alpha }({x_2});[\mu _{\tilde{s}}^{\mathrm{L}}({x_2}),\mu _{\tilde{s}}^{\mathrm{U}}({x_2})],[\nu _{\tilde{s}}^{\mathrm{L}}({x_2}),\nu _{\tilde{s}}^{\mathrm{U}}({x_2})])$ be any three IVPFLSs, then the score function $h({\tilde{s}})$ can be represent as:

$$\begin{aligned} h({\tilde{s}}) = \frac{1}{2} \times \left( \frac{{{{(\mu _{\tilde{s}}^{\mathrm{L}}(x))}^2} + {{(\mu _{\tilde{s}}^{\mathrm{U}}(x))}^2}}}{2} + 1 - \frac{{{{(\nu _{\tilde{s}}^{\mathrm{L}}(x))}^2} + {{(\nu _{\tilde{s}}^{\mathrm{U}}(x))}^2}}}{2}\right) \times {s_{\alpha (x)}} \end{aligned}$$

(3)

The accuracy function $a({\tilde{s}})$ can be represent as:

$$\begin{aligned} a({\tilde{s}}) = \left( \frac{{{{(\mu _{\tilde{s}}^{\mathrm{L}}(x))}^2} + {{(\mu _{\tilde{s}}^{\mathrm{U}}(x))}^2}}}{2} + \frac{{{{(\nu _{\tilde{s}}^{\mathrm{L}}(x))}^2} + {{(\nu _{\tilde{s}}^{\mathrm{U}}(x))}^2}}}{2}\right) \times {s_{\alpha (x)}} \end{aligned}$$

(4)

then we have

• 1. If $h({{\tilde{s}}_1}) < h({{\tilde{s}}_2})$, then ${{\tilde{s}}_1} < {{\tilde{s}}_2}$;

• 2. If $h({{\tilde{s}}_1}) = h({{\tilde{s}}_2})$, then

• (1) If $a({{\tilde{s}}_1}) < a({{\tilde{s}}_2})$, then ${{\tilde{s}}_1} < {{\tilde{s}}_2}$

• (2) If $a({{\tilde{s}}_1}) = a({{\tilde{s}}_2})$, then ${{\tilde{s}}_1} = {{\tilde{s}}_2}$

Definition 2.6

(Du et al. 2017) Let ${{\tilde{s}}_i} = ({s_\alpha }({x_i});[\mu _{\tilde{s}}^{\mathrm{L}}({x_i}),\mu _{\tilde{s}}^{\mathrm{U}}({x_i})],[\nu _{\tilde{s}}^{\mathrm{L}}({x_i}),\nu _{\tilde{s}}^{\mathrm{U}}({x_i})])$, $(i = 1,2,\ldots ,n)$ be a collection of the IVPFLSs, then an interval-valued Pythagorean fuzzy linguistic ordered weighted average (IVPFLOWA) operator of dimension n is a function ${R^n} \otimes {{\tilde{S}}^n} \rightarrow {\tilde{S}}$ that is associated with weight vector $\omega = {({\omega _1},{\omega _2},\ldots ,{\omega _n})^T}$, such that ${\omega _i} \in [0,1]$ and $\sum \nolimits _{i = 1}^n {{\omega _i}} = 1$, and as follows:

$$\begin{aligned} \text {LIVPFLOWA}({{\tilde{s}}_1},{{\tilde{s}}_2},\ldots ,{{\tilde{s}}_n}) = \mathop \oplus \limits _{i = 1}^n {\omega _i}{{\tilde{s}}_{{\sigma _i}}} \end{aligned}$$

(5)

where ${{\tilde{s}}_{{\sigma _i}}}$ is the ith largest ${{\tilde{s}}_i}$ value of the IVPFLOWA. If $\omega = {(1/n,1/n,\ldots ,1/n)^T}$, then IVPFLOWA operator reduces to then IVPFLA operator.

Fig. 1

The compromise solution of VIKOR

2.3 Two multiple criteria decision making methods

2.3.1 VIKOR method

As a classical method, the VIKOR is one useful MCDM method of decision techniques to find compromise solution from a set of conflict criteria. It can consider both the group utility and individual regret. The compromise solution by the VIKOR method is based on the form of ${L_n} - metric$ (Opricovic 1998):

$$\begin{aligned} L{}_{pi} = {\left\{ \sum \limits _{j = 1}^n \left( {\omega _j}\frac{{f_j^ + - {f_{ij}}}}{{f_j^ + - f_j^ - }} \right) ^p \right\} ^{1/p}},\quad (1 \le p \le \infty ;\;\; i = 1,2,\ldots ,n) \end{aligned}$$

(6)

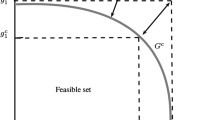
where ${\omega _j}(j = 1,2,\ldots ,m)$ are the weights of the criterion, ${f^ + } = \mathop {\max }\nolimits _j {f_{ij}}$ and ${f^ - } = \mathop {\min }\nolimits _j {f_{ij}}$ are the best and worst values, respectively. The compromise solution ${F_c}$ is a feasible solution that is the closest to the ideal solution which is shown in Fig. 1 (Qin et al. 2015).

2.3.2 ELECTRE III

ELECTRE III takes the pairwise comparison of alternatives to build the mutual outranking relation even criterion are different scale, and reduces the uncertain degree of vague information. This method is an interaction method (Yoon and Hwang 1995) that confers the indifference and preference threshold definition to apply in determining that the contrast of alternatives and another is equal or preference. Assume $x_1$ and $x_2$ are two alternatives, then the evaluation of them are $g(x_1)$ and $g(x_2)$. Consequently, with the multi-criteria weight ${\omega _j}(j = 1,2,\ldots ,m)$, evaluation of alternative $x_1$ will be represented by the vector $g({x_1}) = ({g_1}({x_1}),{g_2}({x_1}),\ldots ,{g_m}({x_1}))$. Let q(g) and p(g) expresses the indifference and preference thresholds, respectively (Hashemi et al. 2016). If $g(x_1) \ge g(x_2)$, then $g(x_1) \succ g(x_2) + p(g(x_2)) \Leftrightarrow x_1Px_2$, $g(x_2) + q(g(x_2)) \prec g(x_1) \prec g(x_2) + p(g(x_2)) \Leftrightarrow x_1Qx_2$$g(x_2) \prec g(x_1) \prec g(x_2) + q(g(x_2)) \Leftrightarrow x_1Ix_2$, where P denotes a strong preference, Q denotes a weak preference, I denotes indifference.

Definition 2.7

The concordance index $c(x_1,x_2)$ for each pair is defined as:

$$\begin{aligned} c(x_1,x_2) = \frac{{\sum \nolimits _{j = 1}^n {{\omega _j}{c_j}(x_1,x_2)}}}{{\sum \nolimits _{j = 1}^n {{\omega _j}}}} \end{aligned}$$

(7)

where ${\omega _j}$ is the weight of jth criteria, such that ${\omega _i} \in [0,1]$ and $\sum \nolimits _{i = 1}^n {{\omega _i}} = 1$; ${c_j}(x_1,x_2)$ is the partial concordance index under jth criteria and defined as:

$$\begin{aligned} {c_j}(x_1,x_2)=\left\{ \begin{array}{ll} 0, &{}\quad {{\mathrm{if }}\ {g_j}(x_2) - {g_j}(x_1) \le {q_j}}\\ 1, &{}\quad {{\mathrm{if }}\ {g_j}(x_2) - {g_j}(x_1) \ge {p_j}}\\ \frac{{{p_j} + {g_j}(x_1) - {g_j}(x_2)}}{{{p_j} - {q_j}}}, &{}\quad \text {otherwise} \end{array} \right. \end{aligned}$$

(8)

The discordance matrix can be calculated by veto threshold $v_j$ which allows the complete rejection if ${g_j}(x_2) - {g_j}(x_1) > {v_j}$ for jth criteria.

Definition 2.8

The discordance index $d(x_1,x_2)$ for each pair is defined as:

$$\begin{aligned} {d_j}(x_1,x_2)=\left\{ \begin{array}{ll} 0, &{}\quad {{\mathrm{if }}\ {g_j}(x_2) - {g_j}(x_1) \le {p_j}}\\ 1, &{}\quad {{\mathrm{if }}\ {g_j}(x_2) - {g_j}(x_1) \ge {v_j}}\\ {\frac{{{g_j}(x_2) - {g_j}(x_1) - {p_j}}}{{{v_j} - {p_j}}}}, &{}\quad \text {otherwise} \end{array} \right. \end{aligned}$$

(9)

Definition 2.9

The outranking degree $S(x_1,x_2)$ based on concordance index $c(x_1,x_2)$ and discordance index $d(x_1,x_2)$ is defined as:

$$\begin{aligned} S(x_1,x_2)=\left\{ \begin{array}{ll} c(x_1,x_2), &{}\quad {{\mathrm{if }}\ {d_j}({x_1},{x_2}) \le c({x_1},{x_2}),\forall j \in J}\\ {c({x_1},{x_2}) \times \prod \limits _{j \in J({x_1},{x_2})} {\frac{{1 - {d_j}({x_1},{x_2})}}{{1 - c({x_1},{x_2})}}}}, &{}\quad \text {otherwise}\\ \end{array} \right. \end{aligned}$$

(10)

where, $J(x_1,x_2)$ is the group of criteria for which ${d_j}(x_1,x_2) > c(x_1,x_2)$.

In addition, to determine the completely ranking order of the alternatives, hierarchy of the alternative solutions is created from the reliability matrix, and hierarchy rank is achieved by superiority ratio for every project (Papadopoulos and Karagiannidis 2008). Another ranking method can get a net credibility degree calculating by two value function which represents concordance credibility degree and discordance credibility degree (Hashemi et al. 2016).

3 Interval-valued Pythagorean fuzzy linguistic entropic induced ordered weighted averaging Operator

In this section, we propose interval-valued Pythagorean fuzzy linguistic entropic induced ordered weighted averaging (IVPFLEIOWA) operator includes an entropy order-inducing variable which determines order position information based on IVPFLSs.

3.1 Interval-valued Pythagorean fuzzy linguistic entropy

The IVPFLS is based on the linguistic information part and the fuzzy information part reflecting the evaluation of DMs and its reliability. It is essential for entropy in interval-valued Pythagorean fuzzy linguistic environment to estimate the reliability by the degree of membership and the degree of non-membership that both can express the hesitant of DMs. In the case of extreme conditions: $[\mu _{\tilde{s}}^{\mathrm{L}}({x_i}),\mu _{\tilde{s}}^{\mathrm{U}}({x_i})] = [\nu _{\tilde{s}}^{\mathrm{L}}({x_i}),\nu _{\tilde{s}}^{\mathrm{U}}({x_i})] = [0,0]$, indicating that DMs cannot make a judgment, the uncertainty of the information is largest. For the above situation, we extend interval-valued intuitionistic fuzzy entropy in Guo and Song (2014) to interval-valued Pythagorean fuzzy linguistic entropy, and discuss the properties.

Definition 3.1

Let ${\tilde{S}}$ be an IVPFLS, a function e: IVPFLS$({\tilde{S}}) \rightarrow [0,1]$ is defined as interval-value Pythagorean fuzzy linguistic entropy. Then the entropy e is defined as following:

$$\begin{aligned} e({{\tilde{s}}_i})= & {} 0.5 \times \left( 1 - \frac{1}{2}(|{(\mu _{\tilde{s}}^{\mathrm{L}}({x_i}))^2} - {(\nu _{\tilde{s}}^{\mathrm{L}}({x_i}))^2}| + |{(\mu _{\tilde{s}}^{\mathrm{U}}({x_i}))^2} - {(\nu _{\tilde{s}}^{\mathrm{U}}({x_i}))^2}|)\right) \nonumber \\&\times (1 + 0.5({(\pi _{\tilde{s}}^{\mathrm{L}}({x_i}))^2} + {(\pi _{\tilde{s}}^{\mathrm{U}}({x_i}))^2})) \end{aligned}$$

(11)

where $e({{\tilde{s}}_i}) \in [0,1]$ for $i = 1,2,\ldots ,n$; ${{{\tilde{\pi }}} _{\tilde{s}}}({x_i})$ is the hesitance degree of IVPFLS and can be computed as: ${{{\tilde{\pi }}} _{\tilde{s}}}({x_i}) = [\sqrt{1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}({x_i}))}^2} - {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_i}))}^2}}, \sqrt{1 - {{(\mu _{\tilde{s}}^{\mathrm{L}}({x_i}))}^2} - {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_i}))}^2}} ]$.

Theorem 3.1

Let ${\tilde{S}}$ be an IVPFLS, ${{\tilde{s}}_i} \in \text {IVPFLS}$. A real function $e({{\tilde{s}}_i}) \in [0,1]$ defined by Eq. (11) is an interval-valued Pythagorean fuzzy linguistic entropy. Assume two interval-valued Pythagorean fuzzy linguistic entropy $e({{\tilde{s}}_1})$ and $e({{\tilde{s}}_2})$, then the entropy should satisfy following properties:

• 1. $e({{\tilde{s}}_i}) = 0$ iff ${{\tilde{s}}_i}$ is a crisp set;

• 2. $e({{\tilde{s}}_i}) = 1$ iff $[\mu _{\tilde{s}}^{\mathrm{L}}({x_i}),\mu _{\tilde{s}}^{\mathrm{U}}({x_i})] = [\nu _{\tilde{s}}^{\mathrm{L}}({x_i}),\nu _{\tilde{s}}^{\mathrm{U}}({x_i})] = [0,0]$ for $\forall {{\tilde{s}}_i} \in {\tilde{S}}$.

• 3. $e({{\tilde{s}}_1}) \le e({{\tilde{s}}_2})$ if ${{\tilde{s}}_1}$ is less fuzzy than ${{\tilde{s}}_2}$, i.e.

  $$\begin{aligned}&{{\tilde{s}}_1} \subseteq {{\tilde{s}}_2},\text { for }\mu _{\tilde{s}}^{\mathrm{L}}({x_2}) \le \nu _{\tilde{s}}^{\mathrm{L}}({x_2})\text { and }\mu _{\tilde{s}}^{\mathrm{U}}({x_2}) \le \nu _{\tilde{s}}^{\mathrm{U}}({x_2});\\&{{\tilde{s}}_1} \supseteq {{\tilde{s}}_2}, for \mu _{\tilde{s}}^{\mathrm{L}}({x_2}) \ge \nu _{\tilde{s}}^{\mathrm{L}}({x_2})\text { and }\mu _{\tilde{s}}^{\mathrm{U}}({x_2}) \ge \nu _{\tilde{s}}^{\mathrm{U}}({x_2}). \end{aligned}$$

• 4. $e({{\tilde{s}}_i}) = e({\tilde{s}}_i^c)$

Proof

• 1. When ${{\tilde{s}}_i}$ is crisp set, we have $\mu _{\tilde{s}}^{\mathrm{L}}({x_i}) = \mu _{\tilde{s}}^{\mathrm{U}}({x_i}) = 1$ or $\nu _{\tilde{s}}^{\mathrm{L}}({x_i}) = \nu _{\tilde{s}}^{\mathrm{U}}({x_i}) = 1$ for $\forall {{\tilde{s}}_i} \in {\tilde{S}}$ , it is simple to obtain $e({{\tilde{s}}_i}) = 0$.

• 2. Let ${{\tilde{\mu }} _{\tilde{s}}}({x_i}) = {{\tilde{\nu }} _{\tilde{s}}}({x_i}) = [0,0]$, for $\forall {{\tilde{s}}_i} \in {\tilde{S}}$ , after calculation we have $e({{\tilde{s}}_i}) = 1$.

• 3. For $\forall {{\tilde{s}}_1},{{\tilde{s}}_2} \in \text {IVPFLS}$, assume ${{\tilde{s}}_1} \subseteq {{\tilde{s}}_2}$ for $\mu _{\tilde{s}}^{\mathrm{L}}({x_2}) \le \nu _{\tilde{s}}^{\mathrm{L}}({x_2})$, $\mu _{\tilde{s}}^{\mathrm{U}}({x_2}) \le \nu _{\tilde{s}}^{\mathrm{L}}({x_2})$, $\forall {{\tilde{s}}_i} \in {\tilde{S}}$, we have inequality $\mu _{\tilde{s}}^{\mathrm{L}}({x_1}) \le \mu _{\tilde{s}}^{\mathrm{L}}({x_2}) \le \nu _{\tilde{s}}^{\mathrm{L}}({x_2}) \le \nu _{\tilde{s}}^{\mathrm{L}}({x_1})$ and $\mu _{\tilde{s}}^{\mathrm{U}}({x_1}) \le \mu _{\tilde{s}}^{\mathrm{U}}({x_2}) \le \nu _{\tilde{s}}^{\mathrm{U}}({x_2}) \le \nu _{\tilde{s}}^{\mathrm{U}}({x_1})$, for $\forall {{\tilde{s}}_i} \in {\tilde{S}}$, then we have

  $$\begin{aligned} e({{\tilde{s}}_1})= & {} 0.5 \times \left( 1 - \frac{1}{2}\left( \left| {{{(\mu _{\tilde{s}}^{\mathrm{L}}({x_1}))}^2} - {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_1}))}^2}} \right| + \left| {{{(\mu _{\tilde{s}}^{\mathrm{U}}({x_1}))}^2} - {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_1}))}^2}} \right| \right) \right) \\&\times \, (1 + 0.5({(\pi _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + {(\pi _{\tilde{s}}^{\mathrm{U}}({x_1}))^2}))\\= & {} 0.5 \times \left( 1 - \frac{1}{2}({(\nu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} - {(\mu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + {(\nu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2} - {(\mu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2}\right) \\&\times \, (1 + 0.5((1 - {(\mu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} - {(\nu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + 1 - {(\mu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2} - {(\nu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2}))\\= & {} 1 + \frac{1}{4}({(\mu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + {(\mu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2}) - \frac{3}{4}({(\nu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + {(\nu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2}) \\&+\,\frac{1}{8}({({(\nu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + {(\nu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2})^2} - {(\mu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + {(\mu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2}) \end{aligned}$$

  similarity, we can get $E({{\tilde{s}}_2})$.then

  $$\begin{aligned} e({{\tilde{s}}_1}) - e({{\tilde{s}}_2})= & {} ({(\mu _{\tilde{s}}^{\mathrm{L}}({x_2}))^2} + {(\mu _{\tilde{s}}^{\mathrm{U}}({x_2}))^2} - {(\mu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} - {(\mu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2})(1 - 0.5({(\mu _{\tilde{s}}^{\mathrm{L}}({x_2}))^2}\\&+\, {(\mu _{\tilde{s}}^{\mathrm{U}}({x_2}))^2} + {(\mu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + {(\mu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2})) + ({(\nu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + {(\nu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2}\\&-\, {(\nu _{\tilde{s}}^{\mathrm{L}}({x_2}))^2} - {(\nu _{\tilde{s}}^{\mathrm{U}}({x_2}))^2})(3 - 0.5({(\nu _{\tilde{s}}^{\mathrm{L}}({x_1}))^2} + {(\nu _{\tilde{s}}^{\mathrm{U}}({x_1}))^2} + {(\nu _{\tilde{s}}^{\mathrm{L}}({x_2}))^2}\\&+ \,{(\nu _{\tilde{s}}^{\mathrm{U}}({x_2}))^2})) \end{aligned}$$

  Since $\mu _{\tilde{s}}^{\mathrm{U}}({x_1}) \le \nu _{\tilde{s}}^{\mathrm{U}}({x_1}) \wedge \mu _{\tilde{s}}^{\mathrm{U}}({x_2}) \le \nu _{\tilde{s}}^{\mathrm{U}}({x_2})$ we can get $\mu _{\tilde{s}}^{\mathrm{U}}({x_1}) \le 0.5 \wedge \mu _{\tilde{s}}^{\mathrm{U}}({x_2}) \le 0.5$, for $\forall {{\tilde{s}}_i} \in {\tilde{S}}$. So we infer $\mu _{\tilde{s}}^{\mathrm{U}}({x_1}) + \nu _{\tilde{s}}^{\mathrm{U}}({x_2}) \le 1$, $\forall {{\tilde{s}}_i} \in {\tilde{S}}$. And $\mu _{\tilde{s}}^{\mathrm{L}}({x_1}) + \mu _{\tilde{s}}^{\mathrm{U}}({x_1}) + \mu _{\tilde{s}}^{\mathrm{L}}({x_2}) + \mu _{\tilde{s}}^{\mathrm{U}}({x_2}) \le 2$, for $\forall {{\tilde{s}}_i} \in {\tilde{S}}$. Thus we get $e({{\tilde{s}}_1}) \le e({{\tilde{s}}_2})$. Similarity as ${{\tilde{s}}_1} \supseteq {{\tilde{s}}_2}$, for $\mu _{{{\tilde{s}}_1}}^{\mathrm{L}} \ge \nu _{{{\tilde{s}}_1}}^{\mathrm{L}}$ and $\mu _{{{\tilde{s}}_1}}^{\mathrm{U}} \ge \nu _{{{\tilde{s}}_1}}^{\mathrm{U}}$, $\forall {{\tilde{s}}_i} \in {\tilde{S}}$, we also get $e({{\tilde{s}}_1}) \le e({{\tilde{s}}_2})$.

• 4. It is straightforward from the definition of ${\tilde{s}}^c$. $\square$

Remark 3.1

The interval-valued Pythagorean fuzzy linguistic entropy ${e_i}(i=1,2,\ldots ,n)$ is used to acquire entropy order-inducing variable $u_i(i=1,2,\ldots ,n)$ of interval-valued Pythagorean fuzzy linguistic entropic induced ordered weighted averaging operator in Sect. 3.2. Entropy order-inducing variable $u_i$ satisfies the descending order only if the ascending order of ${e_i}$ (The greater entropy ${e_i}$, the smaller entropy order-inducing variable $u_i$).

3.2 Interval-valued Pythagorean fuzzy linguistic entropic induced ordered weighted averaging operator

The IVPFLEIOWA operator is first proposed in this part. This operator not only considers the self-value and ordinal information of the argument variables, but also measures the uncertainty of the argument variables with entropy order-inducing variable.

Definition 3.2

Let ${{\tilde{s}}_i} = ({s_\alpha }({x_i});[\mu _{\tilde{s}}^{\mathrm{L}}({x_i}),\mu _{\tilde{s}}^{\mathrm{U}}({x_i})],[\nu _{\tilde{s}}^{\mathrm{L}}({x_i}),\nu _{\tilde{s}}^{\mathrm{U}}({x_i})])$, $(i = 1,2,\ldots ,n)$ be a collection of the interval-valued Pythagorean fuzzy linguistic numbers, then an interval-valued Pythagorean fuzzy linguistic entropic induced ordered weighted average (IVPFLEIOWA) operator of dimension n is a function ${E^n} \otimes {{\tilde{S}}^n} \rightarrow {\tilde{S}}$ that has an associated weighting vector $\omega = {({\omega _1},{\omega _2},\ldots ,{\omega _n})^T}$, such that ${\omega _i} \in [0,1]$ and $\sum \nolimits _{i = 1}^n {{\omega _i}} = 1$, and it is defined to aggregate the set of second argument of a list of n pairs $\{ ({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})\}$ according to the following formula:

$$\begin{aligned} \textit{IVPFLEIOWA}(({u_1},{{\tilde{s}}_1}),({u_2},{{\tilde{s}}_2}),\ldots ,({u_n},{{\tilde{s}}_n})) = \mathop \oplus \limits _{i = 1}^n {\omega _i}{{\tilde{s}}_{{\hat{\sigma }_i}}}, \end{aligned}$$

(12)

where $u_i$ is entropy order-inducing variable, and ${{\tilde{s}}_{{\hat{\sigma }_i}}}$ is ${{\tilde{s}}_{{\hat{i}}}}$ value of IVPFLEIOWA pair $\{ ({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})\}$ having the jth $(j = 1,2,\ldots ,n)$ largest $u_i$, $\{ {{\tilde{s}}_1},{{\tilde{s}}_2},\ldots ,{{\tilde{s}}_n}\}$ is induced by the order-inducing value of ${u_1},{u_2},\ldots ,{u_n}$ associated with them.

Theorem 3.2

Let $({e_i},{{\tilde{s}}_i})(i = 1,2,\ldots ,n)$ be a collection of IVPFLEIOWA pairs, ${{\tilde{s}}_i}$ in $({e_i},{{\tilde{s}}_i})$ is referred to as the IVPFLN denoted by ${{\tilde{s}}_i} = ({s_\alpha }({x_i});[\mu _{\tilde{s}}^{\mathrm{L}}({x_i}),\mu _{\tilde{s}}^{\mathrm{U}}({x_i})],[\nu _{\tilde{s}}^{\mathrm{L}}({x_i}),\nu _{\tilde{s}}^{\mathrm{U}}({x_i})])$, so final aggregated value by using the IVPFLEIOWA operator is also an IVPFLN, and

$$\begin{aligned}&\textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) = \mathop \oplus \limits _{i = 1}^n {\omega _i}{{\tilde{s}}_{{\hat{\sigma }_i}}}\nonumber \\&\quad = \left( {s_{\sum \limits _{i = 1}^n {{\omega _i}\alpha ({x_{{\hat{\sigma }_i}}})}}};\left[ \left( \sqrt{1 - \prod \limits _{i = 1}^n {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}))}^2})}^{{\omega _i}}}}} \right) ,\right. \right. \nonumber \\&\qquad \times \,\left. \left. \left( \sqrt{1 - \prod \limits _{i = 1}^n {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2})}^{{\omega _i}}}}} \right) \right] ,\right. \nonumber \\&\qquad \times \,\left. \left[ \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^n {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } ,\right. \right. \nonumber \\&\qquad \left. \left. \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^n {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } \right] \right) \end{aligned}$$

(13)

where ${{\tilde{s}}_{{\hat{\sigma }_i}}} = ({s_{\alpha ({x_{{\hat{\sigma }_i}}})}};[\mu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}),\mu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}})],[\nu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}),\nu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}})])$, $({{\tilde{s}}_{{\hat{1}}}},{{\tilde{s}}_{{\hat{2}}}},\ldots ,{{\tilde{s}}_{{\hat{n}}}}) \rightarrow ({{\tilde{s}}_{{\hat{\sigma }_1}}},{{\tilde{s}}_{{\hat{\sigma }_2}}},\ldots ,{{\tilde{s}}_{{\hat{\sigma }_n}}})$ being a permutation such that ${u_i} \ge {u_{i + 1}}$ in IVIFLEIOWA pair for $\{ ({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})\}$ for $\forall i = 1,2,\ldots ,n - 1$. $\omega = {({\omega _1},{\omega _2},\ldots ,{\omega _n})^T}$ is an associated weighting vector with ${\omega _i} \in [0,1]$ and $\sum \nolimits _{i = 1}^n {{\omega _i} = 1}$.

Proof

The first result follows from Definition 2.6. In the next, we only prove Eq. (13) by using mathematical induction on n.

For $n = 2$, since

$$\begin{aligned} {{\tilde{s}}_1}= & {} ({s_{\alpha ({x_1})}};[\mu _{\tilde{s}}^{\mathrm{L}}({x_1}),\mu _{\tilde{s}}^{\mathrm{U}}({x_1})],[\nu _{\tilde{s}}^{\mathrm{L}}({x_1}),\nu _{\tilde{s}}^{\mathrm{U}}({x_1})]),\\ {{\tilde{s}}_2}= & {} ({s_{\alpha ({x_2})}};[\mu _{\tilde{s}}^{\mathrm{L}}({x_2}),\mu _{\tilde{s}}^{\mathrm{U}}({x_2})],[\nu _{\tilde{s}}^{\mathrm{L}}({x_2}),\nu _{\tilde{s}}^{\mathrm{U}}({x_2})]), \end{aligned}$$

then

$$\begin{aligned}&{\omega _1} \odot {{\tilde{s}}_{{\hat{\sigma }_1}}} \oplus {\omega _2} \odot {{\tilde{s}}_{{\hat{\sigma }_2}}}\\&\quad = \left( [{s_{{\omega _1}\alpha ({x_{{\hat{\sigma }_1}}}) + {\omega _1}\alpha ({x_{{\hat{\sigma }_2}}})}}];\left[ \left( \sqrt{1 - \prod \limits _{i = 1}^2 {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}))}^2})}^{{\omega _i}}}}} \right) ,\right. \right. \\&\qquad \left. \left. \left( \sqrt{1 - \prod \limits _{i = 1}^2 {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2})}^{{\omega _i}}}}} \right) \right] ,\right. \\&\qquad \left. \left. \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^n {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } ,\right. \right. \\&\qquad \left. \left. \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^n {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } \right] \right) \end{aligned}$$

Suppose that if Eq. (13) holds for $n = k$, $k \in N$, that is

$$\begin{aligned}&{\omega _1} \odot {{\tilde{s}}_{{\hat{\sigma }_1}}} \oplus {\omega _2} \odot {{\tilde{s}}_{{\hat{\sigma }_2}}} \oplus \cdots \oplus {\omega _k} \odot {{\tilde{s}}_{{\hat{\sigma }_k}}}\\&\quad = \left( {s_{\sum \limits _{i = 1}^k {{\omega _i}\alpha ({x_{{\hat{\sigma }_i}}})}}};\left[ \left( \sqrt{1 - \prod \limits _{i = 1}^k {{{(1 - {{(\mu _{{{{\tilde{P}}}_{{\hat{\sigma }_i}}}}^{\mathrm{L}}({x_{\tilde{s}}}))}^2})}^{{\omega _i}}}}} \right) ,\right. \right. \\&\qquad \left. \left( \sqrt{1 - \prod \limits _{i = 1}^k {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2})}^{{\omega _i}}}}} \right) \right] ,\\&\qquad \left[ \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^k {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } ,\right. \\&\qquad \left. \left. \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^k {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } \right] \right) \end{aligned}$$

Then, when $n = k + 1$, using the operational laws in Definition 2.4, we have

$$\begin{aligned}&{\omega _1} \odot {{\tilde{s}}_{{\hat{\sigma }_1}}} \oplus {\omega _2} \odot {{\tilde{s}}_{{\hat{\sigma }_2}}} \oplus \cdots \oplus {\omega _{k + 1}} \odot {{\tilde{s}}_{{\hat{\sigma }_{k + 1}}}}\\&\quad = \left( {s_{\sum \limits _{i = 1}^k {{\omega _i}\alpha ({x_{{\hat{\sigma }_i}}})}}};\left[ \left( \sqrt{1 - \prod \limits _{i = 1}^k {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}))}^2})}^{{\omega _i}}}}} \right) ,\right. \right. \\&\qquad \left. \left. \left( \sqrt{1 - \prod \limits _{i = 1}^k {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2})}^{{\omega _i}}}}} \right) \right] ,\right. \\&\qquad \left. \left[ \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^k {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } ,\right. \right. \\&\quad \left. \left. \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^k {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } \right] \right) \oplus \\&\qquad \left( {s_{{\omega _{k + 1}}\alpha ({x_{{\hat{\sigma }_{k + 1}}}})}};\left[ \left( \sqrt{1 - {{(1 - {{(\mu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_{k + 1}}}}))}^2})}^{{\omega _{k + 1}}}}} \right) ,\right. \right. \\&\qquad \left. \left. \left( \sqrt{1 - {{(1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_{k + 1}}}}))}^2})}^{{\omega _{k + 1}}}}} \right) \right] ,\right. \\&\qquad \left. \left[ \sqrt{1 - (1 - {{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_{k + 1}}}}))}^2}))}^{{\omega _{k + 1}}}})} ,\right. \right. \\&\qquad \left. \left. \sqrt{1 - (1 - {{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_{k + 1}}}}))}^2}))}^{{\omega _{k + 1}}}})} \right] \right) \\&\quad = \left( {s_{\sum \limits _{i = 1}^{k + 1} {{\omega _i}\alpha ({x_{{\hat{\sigma }_i}}})}}};\left[ \left( \sqrt{1 - \prod \limits _{i = 1}^{k + 1} {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}))}^2})}^{{\omega _i}}}}} \right) ,\right. \right. \\&\qquad \left. \left. \left( \sqrt{1 - \prod \limits _{i = 1}^{k + 1} {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2})}^{{\omega _i}}}}} \right) \right] ,\right. \\&\qquad \left. \left[ \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^{k + 1} {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } ,\right. \right. \\&\qquad \left. \left. \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^{k + 1} {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}}))}^2}))}^{{\omega _i}}}} \right) } \right] \right) \end{aligned}$$

That is , Eq. (13) holds for $n = k + 1$. Thus, Eq. (16) holds for all. The IVPFLEIOWA operator has the following properties. $\square$

Theorem 3.3

(Commutativity) Let $((e_1^\#,{\tilde{s}}_1^\#),(e_2^\#,{\tilde{s}}_2^\#),\ldots ,(e_n^\#,{\tilde{s}}_n^\#))$ is any permutation of the interval-valued intuitionistic fuzzy linguistic variable $(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n}))$ then

$$\begin{aligned}&\textit{IVPFLEIOWA}((e_1^\#,{\tilde{s}}_1^\#),(e_2^\#,{\tilde{s}}_2^\#),\ldots , (e_n^\#,{\tilde{s}}_n^\#))\nonumber \\&\quad = \textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) \end{aligned}$$

(14)

Proof

Let

$$\begin{aligned} \textit{IVPFLEIOWA}((e_1^\#,{\tilde{s}}_1^\#),(e_2^\#,{\tilde{s}}_2^\#) ,\ldots ,(e_n^\#,{\tilde{s}}_n^\#))= & {} \mathop \oplus \limits _{i = 1}^n {\omega _i} \odot {\tilde{s}}_{{\hat{\sigma }_i}}^\#\\ \textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n}))= & {} \mathop \oplus \limits _{i = 1}^n {\omega _i} \odot {{\tilde{s}}_{{\hat{\sigma }_i}}} \end{aligned}$$

Since $((e_1^\#,{\tilde{s}}_1^\#),(e_2^\#,{\tilde{s}}_2^\#),\ldots ,(e_n^\#,{\tilde{s}}_n^\#))$ is any permutation of $(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n}))$ then we have ${\tilde{s}}_{{\hat{\sigma }_i}}^* = {{\tilde{s}}_{{\hat{\sigma }_i}}}$ for all $i(i = 1,2,\ldots ,n)$, so

$$\begin{aligned}&\text {IVPFLIOWA}((e_1^\#,{\tilde{s}}_1^\#),(e_2^\#,{\tilde{s}}_2^\#),\ldots ,(e_n^\#,{\tilde{s}}_n^\#))\\&\quad = \text {IVPFLIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) \end{aligned}$$

$\square$

Theorem 3.4

(Monotonicity) Let $((e_1^\#,{\tilde{s}}_1^\#),(e_2^\#,{\tilde{s}}_2^\#),\ldots ,(e_n^\#,{\tilde{s}}_n^\#))$ and $(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n}))$ are two interval-valued Pythagorean fuzzy linguistic variables. $\omega = ({\omega _1},{\omega _2},\ldots ,{\omega _n})^T$ is the weighting vector of ${{\tilde{s}}_i}$ and ${\tilde{s}}_i^\#(i = 1,2,\ldots ,n)$ with ${\omega _i} \in [0,1]$ and $\sum \nolimits _{i = 1}^n {{\omega _i}} = 1$. If ${{\tilde{s}}_i} \le {\tilde{s}}_i^\#$, for all $i(i = 1,2,\ldots ,n)$, then

$$\begin{aligned}&\textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n}, {{\tilde{s}}_n}))\nonumber \\&\quad \le \textit{IVPFLEIOWA}((e_1^\#,{\tilde{s}}_1^\#),(e_2^\#,{\tilde{s}}_2^\#),\ldots , (e_n^\#,{\tilde{s}}_n^\#)) \end{aligned}$$

(15)

Proof

Let

$$\begin{aligned} \textit{IVPFLEIOWA}((e_1^\#,{\tilde{s}}_1^\#),(e_2^\#,{\tilde{s}}_2^\#),\ldots ,(e_n^\#,{\tilde{s}}_n^\#))= & {} \mathop \oplus \limits _{i = 1}^n {\omega _i} \odot {\tilde{s}}_{{\hat{\sigma }_i}}^\#\\ \textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n}))= & {} \mathop \oplus \limits _{i = 1}^n {\omega _i} \odot {{\tilde{s}}_{{\hat{\sigma }_i}}} \end{aligned}$$

Since ${{\tilde{s}}_i} \le {\tilde{s}}_i^\#$ for all $i(i = 1,2,\ldots ,n)$. Then, we have

$$\begin{aligned}&\textit{IVPFLEIOWA}(({u_1},{{\tilde{s}}_1}),({u_2},{{\tilde{s}}_2}),\ldots , ({u_n},{{\tilde{s}}_n}))\\&\quad \le \textit{IVPFLEIOWA}((u_1^*,{\tilde{s}}_1^*),(u_2^*,{\tilde{s}}_2^*),\ldots , (u_n^*,{\tilde{s}}_n^*)) \end{aligned}$$

$\square$

Theorem 3.5

(Idempotency) Let $\omega = {({\omega _1},{\omega _2},\ldots ,{\omega _n})^T}$ be the weight vector of ${{\tilde{s}}_i}$ and ${\tilde{s}}_i^\#(i = 1,2,\ldots ,n)$ with ${\omega _i} \in [0,1]$ and $\sum \nolimits _{i = 1}^n {{\omega _i}} = 1$. If ${{\tilde{s}}_i},{\tilde{s}} \in {\tilde{S}}$, for all $i(i = 1,2,\ldots ,n)$, where ${{\tilde{s}}_{{\hat{\sigma }_i}}} = ({s_{\alpha ({x_{{\hat{\sigma }_i}}})}};[\mu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}),\mu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}})],[\nu _{\tilde{s}}^{\mathrm{L}}({x_{{\hat{\sigma }_i}}}),\nu _{\tilde{s}}^{\mathrm{U}}({x_{{\hat{\sigma }_i}}})])$, then

$$\begin{aligned} \textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) = {\tilde{s}} \end{aligned}$$

(16)

Proof

Since ${{\tilde{s}}_i}{ = _{\mathrm{IVPFL}}}{\tilde{s}}$ for all $i(i = 1,2,\ldots ,n)$, let

$$\begin{aligned}&\textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots , ({e_n},{{\tilde{s}}_n}))\\&\quad = {\omega _1} \odot {{\tilde{s}}_{{\hat{\sigma }_1}}} \oplus {\omega _2} \odot {{\tilde{s}}_{{\hat{\sigma }_2}}} \oplus \cdots \oplus {\omega _n} \odot {{\tilde{s}}_{{\hat{\sigma }_n}}} \\&\quad = {\omega _1} \odot {\tilde{s}} \oplus {\omega _2} \odot {\tilde{s}} \oplus \cdots \oplus {\omega _n} \odot {\tilde{s}}\\&\quad = ({\omega _1} + {\omega _2} + \cdots + {\omega _n}) \odot {\tilde{s}} \end{aligned}$$

According to Theorem 3.1 and $\sum \nolimits _{i = 1}^n {{\omega _i}} = 1$, we have

$$\begin{aligned}&({\omega _1} + {\omega _2} + \cdots + {\omega _n}) \odot {\tilde{s}}\\&\quad = {}_{IVPF}\left( {s_{\sum \limits _{i = 1}^n {{\omega _i}\alpha (x)}}};\left[ \left( \sqrt{1 - \prod \limits _{i = 1}^n {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{L}}(x))}^2})}^{{\omega _i}}}}} \right) ,\right. \right. \\&\qquad \left. \left( \sqrt{1 - \prod \limits _{i = 1}^n {{{(1 - {{(\mu _{\tilde{s}}^{\mathrm{U}}(x))}^2})}^{{\omega _i}}}}} \right) \right] ,\\&\qquad \left[ \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^n {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{L}}(x))}^2}))}^{{\omega _i}}}} \right) } ,\right. \\&\qquad \left. \left. \sqrt{1 - \left( 1 - \prod \limits _{i = 1}^n {{{(1 - (1 - {{(\nu _{\tilde{s}}^{\mathrm{U}}(x))}^2}))}^{{\omega _i}}}} \right) } \right] \right) \\&\quad = _{IVPF}({s_{\alpha (x)}};[\mu _{\tilde{s}}^{\mathrm{L}}(x),\mu _{\tilde{s}}^{\mathrm{U}}(x)],[\nu _{\tilde{s}}^{\mathrm{L}}(x),\nu _{\tilde{s}}^{\mathrm{U}}(x)])\\&\quad = {\tilde{s}} \end{aligned}$$

so, $\textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) = {\tilde{s}}$. $\square$

Theorem 3.6

(Boundedness) Let ${{\tilde{s}}_m} = \mathop {\min }\limits _i ({{\tilde{s}}_1},{{\tilde{s}}_2},\ldots ,{{\tilde{s}}_n})$, ${{\tilde{s}}_M} = \mathop {\max }\limits _i ({{\tilde{s}}_1},{{\tilde{s}}_2},\ldots ,{{\tilde{s}}_n})$, then

$$\begin{aligned} {{\tilde{s}}_m} \le \textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) \le {{\tilde{s}}_M} \end{aligned}$$

(17)

Proof

Since ${{\tilde{s}}_m} \le {{\tilde{s}}_i} \le {{\tilde{s}}_M}$ for all $i(i = 1,2,\ldots ,n)$ and $\sum \nolimits _{i = 1}^n {{\omega _i}} = 1$, using Theorems 3.1-3.4, then

$$\begin{aligned}&\textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) \\&\quad = {\omega _1} \odot {{\tilde{s}}_{{\hat{\sigma }_1}}} \oplus {\omega _2} \odot {{\tilde{s}}_{{\hat{\sigma }_2}}} \oplus \cdots \oplus {\omega _n} \odot {{\tilde{s}}_{{\hat{\sigma }_n}}} \ge {\omega _1} \odot {{\tilde{s}}_m} \oplus {\omega _2} \odot {{\tilde{s}}_m} \oplus \cdots \oplus {\omega _n} \odot {{\tilde{s}}_m}\\&\quad = ({\omega _1} + {\omega _2} + \cdots + {\omega _n}) \odot {{\tilde{s}}_m}\\&\quad = {{\tilde{s}}_m} \\&\textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) \\&\quad = {\omega _1} \odot {{\tilde{s}}_{{\hat{\sigma }_1}}} \oplus {\omega _2} \odot {{\tilde{s}}_{{\hat{\sigma }_2}}} \oplus \cdots \oplus {\omega _n} \odot {{\tilde{s}}_{{\hat{\sigma }_n}}} \le {\omega _1} \odot {{\tilde{s}}_M} \oplus {\omega _2} \odot {{\tilde{s}}_M} \oplus \cdots \oplus {\omega _n} \odot {{\tilde{s}}_M}\\&\quad = ({\omega _1} + {\omega _2} + \cdots + {\omega _n}) \odot {{\tilde{s}}_M}\\&\quad = {{\tilde{s}}_M} \end{aligned}$$

so ${{\tilde{s}}_m} \le \textit{IVPFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) \le {{\tilde{s}}_M}$. $\square$

Remark 3.2

If $\omega = {({\omega _1},{\omega _2},\ldots ,{\omega _n})^T} = {(\frac{1}{n},\frac{1}{n},\ldots ,\frac{1}{n})^T}$, then we get the interval-value Pythagorean fuzzy linguistic averaging (IVPFLA) operator (Du et al. 2017).

$$\begin{aligned} \text {IVPFLA}({{\tilde{s}}_1},{{\tilde{s}}_2},\ldots ,{{\tilde{s}}_n}) = \mathop \oplus \limits _{i = 1}^n \frac{1}{n} \odot {{\tilde{s}}_i} = {{\tilde{s}}_{\sum \limits _{i = 1}^n {\frac{i}{n}}}} \end{aligned}$$

(18)

Remark 3.3

If $\mu _{\tilde{s}}^{\mathrm{L}}({x_i}) = \mu _{\tilde{s}}^{\mathrm{U}}({x_i})$, $\nu _{\tilde{s}}^{\mathrm{L}}({x_i}) = \nu _{\tilde{s}}^{\mathrm{U}}({x_i})$, for all $i(i = 1,2,\ldots ,n)$, then we get the Pythagorean fuzzy linguistic entropic induced ordered weighted averaging (PFLEIOWA) operator.

$$\begin{aligned} \textit{PFLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) = \mathop \oplus \limits _{i = 1}^n {\omega _i} \odot {{\tilde{s}}_{{\hat{\sigma }_i}}} \end{aligned}$$

(19)

where ${{\tilde{s}}_{{\hat{\sigma }_i}}}$ is ${{\tilde{s}}_i}$ value of the PFLEIOWA pair $\{ ({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})\}$ having the $(j = 1,2,\ldots ,n)$ largest ${u_i}$.

Remark 3.4

If $\mu _{\tilde{s}}^{\mathrm{L}}({x_i}) = \mu _{\tilde{s}}^{\mathrm{U}}({x_i}) = 1$, $\nu _{\tilde{s}}^{\mathrm{L}}({x_i}) = \nu _{\tilde{s}}^{\mathrm{U}}({x_i}) = 0$ for all $i(i = 1,2,\ldots ,n)$, then we get the fuzzy linguistic entropic induced ordered weighted averaging (FLEIOWA) operator.

$$\begin{aligned} \textit{FLEIOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) = \mathop \oplus \limits _{i = 1}^n {\omega _i} \odot {{\tilde{s}}_{{\hat{\sigma }_i}}} \end{aligned}$$

(20)

where ${{\tilde{s}}_{{\hat{\sigma }_i}}}$ is ${{\tilde{s}}_i}$ value of FLEIOWA pair $\{ ({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})\}$ having the jth$(j = 1,2,\ldots ,n)$ largest ${u_i}$.

Remark 3.5

If ${e_i} > {e_{i + 1}}$ for all $i(i = 1,2,\ldots ,n)$, and the ordered position of ${e_i}$ is the same as the ordered position of ${{\tilde{s}}_i}$, the interval-value Pythagorean fuzzy linguistic ordered weighted averaging (IVPFLOWA) operator (Du et al. 2017) is obtained.

$$\begin{aligned} \text {IVPFLOWA}(({e_1},{{\tilde{s}}_1}),({e_2},{{\tilde{s}}_2}),\ldots ,({e_n},{{\tilde{s}}_n})) = \mathop \oplus \limits _{i = 1}^n {\omega _i} \odot {{\tilde{s}}_i} \end{aligned}$$

(21)

Remark 3.6

If entropy order-inducing variable degenerates to traditional order-inducing variable, we get the traditional interval-value Pythagorean fuzzy linguistic induced ordered weighted averaging (IVPFLIOWA) operator.

4 The O-VIKOR method in interval-value Pythagorean fuzzy linguistic environment

4.1 The O-VIKOR model

This section aims to propose the O-VIKOR method to solve complex MCDM problems involving full of uncertainty and conflict criterion based on compromise outranking degree and a novel ranking approach.

Support ${z_i} = \{ {z_1},{z_2},\ldots ,{z_m}\}$ be a finite set of alternatives and $c = \{ {c_1},{c_2},\ldots ,{c_n}\}$ be a set of criteria, the score value ${h_j}({z_i})$ under criteria ${c_j}$ is calculated by Eq. (4). Let $\omega = {({\omega _1},{\omega _2},\ldots ,{\omega _n})^T}$ be a weight vector of criterion, such that ${\omega _j} \in [0,1]$ and $\sum \nolimits _{j = 1}^n {{\omega _j}} = 1$. and ${p_j}$, ${q_j}$ and ${v_j}$ represent preference threshold, indifference threshold and veto threshold, respectively, with the condition: $0 \le {q_j}< {p_j} < {v_j} \le 1$.

4.1.1 The compromise outranking degree

This part mainly discusses how to calculate the compromise outranking degree of pairwise alternatives. In this regard, the outranking indices and veto indices which express as group utility for the majority and individual regret for the opponent are first defined. Subsequently, the compromise outranking degree based on outranking index and veto index is proposed to form the compromise outranking relation which means reaching consensus by mutual concessions.

The compromise outranking relations are determined based on IVPFLSs. The outranking index C and the veto index D of alternative $z_i$ over $z_k$ on criteria $c_j$ are defined as following and the property is analyzed.

Definition 4.1

The outranking index $C({z_i},{z_k})$ for pairwise alternatives $z_i$ and $z_k$ is defined as:

$$\begin{aligned} C({z_i},{z_k}) = \frac{{\sum \limits _{j = 1}^n {{\omega _j}{C_j}({z_i},{z_k})}}}{{\sum \limits _{j = 1}^n {{\omega _j}}}} \end{aligned}$$

(22)

where ${z_k} \ne {z_i}$; the partial outranking index ${C_j}({z_i},{z_k})$ is presented as follows:

$$\begin{aligned} {C_j}({z_i},{z_k})=\left\{ \begin{array}{ll} 0, &{}\quad {{\mathrm{if }}\ {h_j}({z_i}) - {h_j}({z_k}) \le {q_j}}\\ 1, &{}\quad {{\mathrm{if }}\ {h_j}({z_i}) - {h_j}({z_k}) \ge {p_j}}\\ {\frac{{{h_j}({z_i}) - {h_j}({z_k}) - {q_j}}}{{{p_j} - {q_j}}}}, &{}\quad {{\mathrm{otherwise}}} \end{array} \right. \end{aligned}$$

(23)

and ${C_j}({z_i},{z_k}) \in [0,1]$, ${p_j}$, ${q_j}$ represent preference threshold and indifference threshold.

Theorem 4.1

If ${h_j}({z_i})$ or ${h_j}({z_k})$ is a fixed value, ${C_j}({z_i},{z_k})$ is monotonous along the corresponding cross section. Let ${h_j}({z_1})$, ${h_j}({z_2})$ and ${h_j}({z_3})$ are three score value of $z_1$, $z_2$ and $z_1$ under jth criteria.

• (1) If ${h_j}({z_1}) \ge {h_j}({z_2}) \ge {h_j}({z_3})$, then ${C_j}({z_1},{z_3}) - {C_j}({z_1},{z_2}) \ge 0$.

• (2) If ${h_j}({z_1}) \ge {h_j}({z_2}) \ge {h_j}({z_3})$, then ${C_j}({z_1},{z_3}) - {C_j}({z_2},{z_3}) \ge 0$.

Proof

(1)We know ${C_j}({z_i},{z_k})$ from Eq. (28) have three situations: 1, 0, $\frac{{{h_j}({z_i}) - {h_j}({z_k}) - {q_j}}}{{{p_j} - {q_j}}}$. If ${h_j}({z_i}) - {h_j}({z_k}) = {q_j}$, then we can obtain ${C_j}({z_i},{z_k}) = 0 = \frac{{{h_j}({z_i}) - {h_j}({z_k}) - {q_j}}}{{{p_j} - {q_j}}}$. If ${h_j}({z_i}) - {h_j}({z_k}) = {p_j}$, then we can obtain ${C_j}({z_i},{z_k}) = 1 = \frac{{{h_j}({z_i}) - {h_j}({z_k}) - {q_j}}}{{{p_j} - {q_j}}}$.

Then, if ${h_j}({z_i}) - {h_j}({z_k}) < {q_j}$ (or ${h_j}({z_i}) - {h_j}({z_k}) > {p_j}$), we have ${C_j}({z_i},{z_k}) = 1$ (or ${C_j}({z_i},{z_k}) = 0$). Thus, we can regard ${h_j}({z_i}) - {h_j}({z_k})$ as ${q_j}$ (or ${p_j}$) when ${h_j}({z_i}) - {h_j}({z_k}) < {q_j}$ (or ${h_j}({z_i}) - {h_j}({z_k}) > {p_j}$).

Now, if ${h_j}({z_1}) \ge {h_j}({z_2}) \ge {h_j}({z_3})$, we can conclude

$$\begin{aligned}&{C_j}({z_1},{z_3}) - {C_j}({z_1},{z_2}) \\&\quad = \frac{{{h_j}({z_1}) - {h_j}({z_3}) - {q_j}}}{{{p_j} - {q_j}}} - \frac{{{h_j}({z_1}) - {h_j}({z_2}) - {q_j}}}{{{p_j} - {q_j}}} = \frac{{{h_j}({z_2}) - {h_j}({z_3})}}{{{p_j} - {q_j}}} \ge 0 \end{aligned}$$

(2) The proof is similar to (1). $\square$

Theorem 4.2

If ${z_1} \supseteq {z_2} \supseteq {z_3}$, from Eq. (22) and Theorem 4.1, it is obvious that the outranking index $C({z_i},{z_k})$ has similar property as $C({z_i},{z_k})$.

Definition 4.2

The veto index $D({z_i},{z_k})$ for pairwise alternatives $z_i$ and $z_k$ is defined as

$$\begin{aligned} {D}({z_i},{z_k})=\left\{ \begin{array}{ll} 0, &{}\quad {\mathrm{if }}\max [{\omega _j}({h_j}({z_k}) - {h_j}({z_i}))] \le {\omega _j}{q_j}\\ 1, &{}\quad {\mathrm{if }}\max [{\omega _j}({h_j}({z_k}) - {h_j}({z_i}))] \ge {\omega _j}{v_j}\\ \frac{{\max [{\omega _j}({h_j}({z_k}) - {h_j}({z_i}))] - {\omega _j}{q_j}}}{{{\omega _j}[{v_j} - {q_j}]}}, &{}\quad {{\mathrm{otherwise}}} \end{array} \right. \end{aligned}$$

(24)

where ${z_k} \ne {z_i}$; $0 \le D({z_i},{z_k}) \le 1$; ${q_j}$ and ${v_j}$ represent indifference threshold and veto threshold.

Remark 4.1

The veto index $D({z_i},{z_k})$ means that $z_i$ with maximum lower score value than another $z_k$ under a certain criteria, it forms the maximum veto relationship if the variance for $z_i$ over $z_k$ is more than veto threshold. If this variance is less than indifference threshold, it can be concluded that there is no veto relationship for pairwise alternatives.

Definition 4.3

The compromise outranking degree indicates to obtain the consensus by mutual concessions. Then, the compromise outranking degree $S({z_i},{z_k})$ for pairwise alternatives $z_i$ and $z_k$ is defined as:

$$\begin{aligned} S({z_i},{z_k})=\left\{ \begin{array}{ll} {C({z_i},{z_k})}, &{}\quad \text {if } D({z_i},{z_k}) \le C({z_i},{z_k})\\ {\zeta C({z_i},{z_k}) + (1 - \zeta )C({z_i},{z_k})\frac{{1 - D({z_i},{z_k})}}{{1 - C({z_i},{z_k})}}}, &{}\quad \text {otherwise} \end{array} \right. \end{aligned}$$

(25)

where $0 \le S({z_i},{z_k}) \le 1$; ${C({z_i},{z_k})}$ is the outranking index, $D({z_i},{z_k})$ is the veto index; $\zeta$ is the weight vector of the outranking index which means “group utility”, and $\zeta \in [0,1]$. If we have a larger $\zeta$, it explains that decision makers consider a greater preference of group utility.

4.1.2 A ranking approach of the compromise outranking degree

Since the compromise outranking degree of alternatives is determined, the compromise outranking degree matrix can be constructed as the mainstay for ranking order. However, it is a hard issue given how to suitably deal with the compromise outranking degree matrix in the study. Therefore, we propose the credibility degree formula to transform the compromise outranking degree matrix into the preference relation matrix to reflect the superiority among alternatives.

Definition 4.4

Let $z_i$ and $z_k$ be two alternatives. the credibility degree formula presents the possibility degree of $z_i$ being not less than $z_k$ which considering overall criterion is defined as:

$$\begin{aligned} p({z_i} \ge {z_k}) = 0.5 \times (1 + (S({z_i},{z_k}) - S({z_i},{z_k}))) \end{aligned}$$

(26)

where $S({z_i},{z_k})$ is the compromise outranking degree in pairwise and calculated by Eq. (25).

Theorem 4.3

The formula satisfies the boundness and the complementarity. Let $z_1$ and $z_2$ be two alternatives, then $0 \le p({z_1} \ge {z_2}) \le 1$ and $p({z_1} \ge {z_2}) + p({z_2} \ge {z_1}) = 1$. From Eq. (26), it is obvious.

Theorem 4.4

(Transitivity) Let ${z_1}$, ${z_2}$ and ${z_3}$ be three alternatives. If ${z_1} \supseteq {z_2} \supseteq {z_3}$, it implies $S({z_1},{z_3}) \ge S({z_1},{z_2}) \ge S({z_2},{z_3})$ and $S({z_3},{z_1}) \le S({z_2},{z_1}) \le S({z_3},{z_2})$, then $p({z_1} \ge {z_3}) \ge p({z_1} \ge {z_2})$ or $p({z_1} \ge {z_3}) \ge p({z_2} \ge {z_3})$.

Proof

If ${z_1} \supseteq {z_2} \supseteq {z_3}$, it is known that $S({z_1},{z_3}) \ge S({z_1},{z_2})$ and $S({z_3},{z_1}) \le S({z_2},{z_1})$. Meanwhile, it is easy to see that $p({z_1} \ge {z_3}) = S({z_1},{z_3}) - S({z_3},{z_1})$ and $p({z_1} \ge {z_2}) = S({z_1},{z_2}) - S({z_2},{z_1})$. Thus, it is obtained that $p({z_1} \ge {z_3}) \ge p({z_1} \ge {z_2})$. Similarly, it can be proofed that $p({z_1} \ge {z_3}) \ge p({z_2} \ge {z_3})$. $\square$

Remark 4.2

In the calculation of credibility degree, the characteristics of IVPFL information and the preference of decision makers for conflicting attributes are fully considered. Then, multiple sets of credibility degree $p({z_i} \ge {z_k})$ construct the complementary judgment matrix ${P_S}$ as:

$$\begin{aligned} {P_S} = {({p_{ij}})_{m \times m}} = \left[ {\begin{array}{*{20}{c}} {0.5}&{}\quad {{p_{12}}}&{}\quad \ldots &{}\quad {{p_{1m}}}\\ {{p_{21}}}&{}\quad {0.5}&{}\quad \ldots &{}\quad {{p_{2m}}}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ {{p_{m1}}}&{}\quad {{p_{m2}}}&{}\quad \ldots &{}\quad {0.5} \end{array}} \right] \end{aligned}$$

(27)

From these credibility degree in pairwise, an acceptable ranking order of alternatives can be derived. To obtain the reasonable ranking result, we use the precise solution given in (Xu 2002) as:

$$\begin{aligned} Y = {({y_1},{y_2},\ldots ,{y_n})^T} = \left( \frac{1}{{\sum \limits _{i = 1}^n {({p_{i1}}/{p_{1i}})}}},\frac{1}{{\sum \limits _{i = 1}^n {({p_{i2}}/{p_{2i}})}}},\ldots ,\frac{1}{{\sum \limits _{i = 1}^n {({p_{in}}/{p_{1n}})}}}\right) ^T \end{aligned}$$

(28)

Fig. 2

The process of the O-VIKOR model

4.2 Decision-making steps

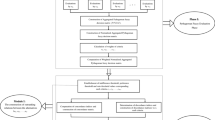
Based on the above, with the integration of the preceding decision model, the steps for addressing group decision making problems are shown in Fig. 2 and presented in the following:

Step 1.:

Obtain all evaluation information of alternatives, characteristic actions and thresholds by using IVPFLNs.

Step 2.:

Aggregate overall decision maker matrices with weight vector of DMs by using IVPFLEIOWA operator from Eq. (12).

Step 3.:

Calculate the score value of evaluation information and determine indifference, preference thresholds and veto threshold by Eq. (4).

The performance of alternatives demand a way to evaluate certain accuracy even fuzzy linguistic set is difficult to estimate. It would be a standard that tackles difference of pairwise to find the mutual relationship. Therefore, assume $z_i$ and $z_k$ be two IVPFLSs, it can offer the precise evaluation values by score function from Eq. (4) and get the following:

If $h({z_i}) < h({z_k})$, then ${z_i} < {z_k}$.

Step 4.:

Calculate the weight vector of the criteria. As a key factor that directly influences the decision results, the acquisition of criteria weight vector is very important. Thus, we use the score value by Eq. (4) to calculate the attribute weights as following:

$$\begin{aligned} {\omega _j} = \frac{{\sum \nolimits _i^m {{h_j}({z_i})}}}{{\sum \nolimits _j^n {\sum \nolimits _i^m {{h_j}({z_i})}} }} \end{aligned}$$

(29)

where ${h_j}({z_i})$ indicates the score value of alternatives ${z_i}$.

Step 5.:

Calculate the outranking indices and veto indices. Following steps 3 and 4, we computed the outranking and veto indices of all pairwise alternatives using Eqs. (22)–(24). Then, the outranking index and veto index matrices then can be constructed.

Step 6.:

Calculate the compromise outranking degree.With the step 4, we utilize the above elements to get the compromise outranking degree according to Eq. (25).

Step 7.:

Calculate the credibility formula from Eq. (26) and form the complementary judgment matrix ${P_S}$.

Step 8.:

Determine the ranking of all alternatives. According to the obtained complementary judgment matrix ${P_S}$, the ranking results are computed using Eq. (28). Then, the final results can be deduced.

Table 1 The preference degree ${\tilde{s}}_{ij}^{(k)}$ of the decision matrix ${D^1}$

Table 2 The preference degree ${\tilde{s}}_{ij}^{(k)}$ of the decision matrix ${D^2}$

Table 3 The preference degree ${\tilde{s}}_{ij}^{(k)}$ of the decision matrix ${D^3}$

5 Numerical example and comparison

In this section, the O-VIKOR method is implemented to select the best candidate for site location problem in China and comparative analyses between the proposed method and others are given to interpret the efficiency of our proposed method.

5.1 Numerical example

Site selection is a fundamental, strategic and critical decision making activity of an enterprise (Pace and Shieh 2010). The problem of site selection is to select the optimal location for the “facilities” to be set up. It is an optimization problem with broad practical significance and a complex system engineering, which needs to comprehensively consider engineering geology, resource environment, transportation conditions and other factors (Wu et al. 2018). Site selection is directly related to the size of the project, the amount of investment and construction progress, but also related to the quality of the economic and technical indicators after the completion and operation (Boostani et al. 2018). Selecting a suitable site location, to achieve the goals of reasonable allocation of costs and resources, the site location is an significant issue for a manufacturer.

Many factors have been suggested as being important criteria for the location problem by researchers. To obtain a fitting ranking of site location in Chongqing, China, refer to (Zandi and Roghanian 2013), decision makers consider six critical factors ${C_j}(j = 1,2,\ldots ,6)$: (1) ${C_1}$: Investment cost control; (2) ${C_2}$: Expansion possibility; (3) ${C_3}$: Availability of acquirement material; (4) ${C_4}$: Human resource; (5) ${C_5}$: Transportation availability; (6) ${C_6}$: Climatic conditions. Then, there are four candidate locations ${z_i}(i = 1,2,\ldots ,4)$, which is evaluated by three decision makers ${{\mathrm{D}}_k}(k = 1,2,3)$, with fixed decision makers’ weight vector $\varpi = {(0.35,0.40,0.25)^T}$. The information collected in fact is limited and incomplete. If decision maker is required to give the implicit number, there will be inaccurate information in the aggregation and treating phases. However, the IVPFLS is very suitable for responding to the cognitive preference information of decision maker with inner hesitation and chosen to express the preference information in the paper.

Step 1.:

From professional analysis and discussion, decision maker provide evaluation information of candidate locations in the interval-valued Pythagorean fuzzy linguistic environment shown in Tables 1, 2 and 3, and the preference threshold $p_j$, indifference threshold $q_j$ and veto threshold $v_j$ on each criterion shown in Table 4.

Step 2.:

The aggregated of preference matrices of decision makers are calculated based on IVPFLEIOWA operator by Eq. (17) is shown in Table 5.

Step 3.:

Compute the score value by Eq. (3) of each IVPFLSs in Table 6.

Step 4.:

Determine the weights of the criteria, we can obtain the weight vector of criteria as $\omega = (0.186,0.156,0 .154,0 .181,0.161,0.162)$ using Eq. (27).

Step 5.:

Calculate the outranking index and veto index according to Eqs. (22)–(24), and the matrices are shown in Tables 7 and 8.

Table 4 The matrix of the alternatives thresholds

Table 5 The aggregated matrix of experts preferences

Table 6 The score value of alternatives and thresholds

Table 7 The outranking index matrix

Table 8 The veto index matrix

Table 9 The compromise outranking matrix

Table 10 The complementary judgment matrix ${P_S}$

Step 6.:

Following step 5, calculate the compromise outranking degree by Eq. (25) with $\zeta = 0.5$ which represents the equal consideration of the proportion of comprehensive outranking ratio and another ratio under the influence of veto factors, and is shown in Table 9.

Step 7.:

Determine the complementary judgment matrix of the credibility degree by using Eq. (26), the complementary judgment matrix ${P_S}$ is shown in Table 10.

Step 8.:

Derive the ranking results by Eq. (28):

$$\begin{aligned} y({z_1}) = 0.295, y({z_2}) = 0.319, y({z_3}) = 0.118, y({z_4}) = 0.264 \end{aligned}$$

According to ranking results, we can get the ranking order of alternatives is ${z_2}> {z_1}> {z_4} > {z_3}$, and $x_2$ is the best option for site location.

5.2 Influence analysis of modified parameter

The proposed method makes a choice in “group utility” and “individual regret” to get the compromise outranking relation with the parameters $\zeta$. As the important part, the parameters $\zeta$ is analyzed here in detail. When satisfying the condition: $D({x_i},{x_k}) > C({x_i},{x_k})$, different parameter $\zeta$ is taken to be discussed: when the DMs want both group utility and individual one, simultaneously, then we let parameter $\zeta = 0.5$; when the DMs are more inclined to group utility or individual regret, then we let parameter $0.5< \zeta < 1$ or $0< \zeta < 0.5$; when the DM is fully inclined to individual regret, then $\zeta = 0$, it means veto index reaches the maximum influence of compromise outranking degree. When the parameter $\zeta = 1$, it means not consider individual regret and veto threshold, then only outranking index impacts the decision result.

Here the parameter $\zeta$ is assigned different numerical values to analyse the effect of the ranking results. To facilitate the comparison of results, we choose the following three parameters to analyse: $\zeta = 0,0.5,1$, and the decision results are shown in Fig. 3. Apparently, if the parameter $\zeta = 0$ or $\zeta = 0.5$, we can get the same results as: ${z_2}> {z_1}> {z_4} > {z_3}$; if the parameter $\zeta = 1$, we can obtain the different ranking order as: ${z_1}> {z_4}> {z_2} > {z_3}$. The main reason is the preference of decision makers between group utility and individual regret according to current situation. It can be derived that the final results of site location problem is a compromise solution.

Fig. 3

Compare difference parameter $\zeta$ of the proposed method

5.3 Comparative analyses

In this section, the site locations are ranked by other previous researches including the VIKOR method (Park et al. 2011), the interval-valued Pythagorean fuzzy linguistic aggregated operator decision method (Du et al. 2017) and the ELECTRE III (Hashemi et al. 2016). The comparative analyses between the proposed method and those existing methods are discussed in detail, and the final results of difference methods are listed in Table 11.

The ELECTRE III method calculates the outranking degree based on concordance index and discordance index, but the way has certain defects. If the pairwise comparison has large difference under criteria and even more than veto threshold, leading to discordance index which does not consider the influence of weight vector is great. From the outranking degree in Eq. (10), ELECTRE III directly denies the possibility of advantage in pairwise with great difference over veto threshold, and in the case some information is ignored. However, the veto index in the proposed method is used as one of the elements for reaching a consensus. Whether this part information is retained is determined by how to reach consensus. As we can see, the proposed method and ELECTRE III has the similar results for site location problem only if the parameter $\zeta = 1$. Through the above discussion, it can be inferred that two methods can be transformed into each other only when the veto factor plays a minimal role.

Table 11 Comparison with Refs. (Du et al. 2017; Park et al. 2011; Hashemi et al. 2016)

With the IVPFL aggregated operation decision method and the VIKOR method, the difference among all rankings is due to the essential differences is information measuring pattern and ranking principles. The VIKOR method in reference (Park et al. 2011) based on distance measure by closest ideal solution for obtaining the results, whereas the proposed method is an improved outranking method based on a compromise outranking measure for determining the results. The VIKOR method is a function model and assume the results to be subject to complete compensation among criteria, but this process leads to information loss. However, the proposed method is a relation model, which sufficiently considers the non-compensation principle among criteria. Compared with the aggregated operator method (Du et al. 2017) which emphasis on measuring the information about the alternative itself, the proposed method is more adapted to complex and highly uncertain decision making environment. The proposed method is also able to reduce the uncertainty in decision information by building compromise relation in pairwise alternatives.

Based on the above analysis, the advantages of the proposed O-VIKOR method can be summarized as follows:

• (1) The proposed method introduces the cognitive complex linguistic information in the form of IVPFLSs. It is efficient to express the subjective judgment and inherent uncertainty of decision making.

• (2) The proposed method gives IVPFLEIOWA operator to aggregate evaluation information. The IVPFLEIOWA operator both considers the self-value and ordinal information of the argument variables, and measures the uncertainty of the argument variables with entropy order-inducing variable.

• (3) The proposed method is an pairwise comparison method by using interactive computing to reduce the high degree of uncertainty. It can construct the compromise outranking relation which involves outranking index and veto index. Then, for obtaining convincing results, the proposed method gives the credibility degree approach to handle compromise outranking relation. Thus, it is more comprehensive to measure information than the ELECTRE III method.

6 Conclusion

Compared with fuzzy number, intuitionistic fuzzy number, etc., interval-value Pythagorean fuzzy linguistic information includes special characters in assessing the subjective judgment and inherent uncertainty of decision makers. It has the ability to demonstrate fuzzy information reliability to describe preference information of decision making for MCDM problems. Then, the IVPFLEIOWA operator is proposed to aggregate decision matrices of preference information. The IVPFLEIOWA operator is induced by the uncertainty of entropy order-inducing variable for considering the self-value and ordinal information of the argument variables. Subsequently, this paper develops the O-VIKOR method including compromise outranking relations and ranking approach for addressing situations of MCDM problems. The compromise outranking relations are discussed in detail and the corresponding outranking indices and veto indices for IVPFLSs were obtained. Lastly, for the practicality of application, we give a detailed procedure of the O-VIKOR method to solve complex MCDM problems. The advantages of this method are clearly illustrated by a numerical example concerning the site location selection. This method can overcome the shortcomings of existing methods. By different parameter and different ranking methods, the decision making would lead to different rankings. As discussed in the influence analysis of modified parameter and comparative analyses, the proposed method can handle MCDM problems more flexible and practical.

Nevertheless, there is still the limitation that is the need for a large number of computation with the increasing complexity of decision making information. In the future, the proposed method shall consider other linguistic term sets, such as hesitant fuzzy linguistic term sets and probabilistic linguistic term sets. And we will also consider other entropy in our method and extend the applications to other domains.