1 Introduction

Harris [1] first presented the economic order quantity (EOQ) to minimize the total inventory cost. Since the EOQ model consists of some assumptions, by relaxing the assumption that all orders are obtained together, the economic manufacturing quantity (EMQ) model is introduced by Taft [2]. The basic EOQ and EPQ models suppose that the demand rate is constant; however, it is not realistic in practice, and generally customer’s demand varies with time. Therefore, many researchers are interested in studying inventory systems when demand depends on time. For example, Silver and Meal [3] proposed an approximation to find an optimum lot size when demand varies with time. Donaldson [4] presented an inventory system, whose demand has a linear time-varying trend and then proposed an approach to obtain the optimal solutions of it. Ritchie [5] considered an inventory system in which demand increases linearly. Bose et al [6] investigated an EOQ model with a demand that changes with time positively and linearly, considering shortages and deterioration. Teng [7] proposed a method to obtain optimal inventory policies, considering a linear trend in deterministic demand. There was little published work on inventory systems with decreasing trend in demand before the paper presented by Zhao et al [8]. They presented an analytic algorithm to solve such problems. Lo et al [9] introduced an optimum policy for the problem of inventory management, where demand changes linearly and used a model called the “two-equation model”.

Yang et al [10] proposed a parametric eclectic model with demand decreasing non-linearly. Omar and Yeo [11] considered a manufacturing system for a situation that new products are manufactured using one kind of raw material, used products are repaired and demand is assumed to vary with time continuously. Maihami and Kamalabadi [12] adopted a demand function dependent on both time and price for an inventory model with decaying items. Pando et al [13] studied a model with the holding cost non-linearly dependent on both quantity and time and the stock level dependent demand rate.

There are different ways to take out items during the cycle length to supply demand. They are referred to as demand patterns. Various types of these patterns are discussed by researchers. When the demand rate is constant during the scheduling period, its pattern is known as uniform. However, it is not suitable for many practical situations. In real world situations, there are some other ways to take out products from the stock. Demand of customers can be dependent on time, price, stock level, etc. Since time is one of the most common inputs of demand functions in practice, there are some patterns considering it as an input like linear, quadratic, exponential, non-linear and power. Demand used in this study is supposed to follow a power law, because of the wide-ranging uses and being more applicable than the others. This pattern can be used for the situations that a high percentage of demand happens at the beginning of the cycle, because of approaching to the expiry date or demanding for the fresh products (e.g., prepared food, breads, fresh meat, fruits, yogurts and vegetables), or at the end of the scheduling period, because of becoming scarce or daily use (e.g., sugar, tea, coffee and oil). Also, it consists of the situation that demand occurs uniformly. Several papers have been published in this category.

Naddor [14] studied a power demand pattern in an order-level system. Lee and Wu [15] analyzed an EOQ model with backordering, power demand for decaying item. Then, Dye [16] completed Lee and Wu’s model by proposing a model, in which backordering rate changes pro rata with time. Singh et al [17] proposed an inventory system considering partial backordering and power demand pattern for perishable items. Abdul-Jalbar et al [18] investigated a one-warehouse N-retailer problem, in which the demand pattern is power and backorders are allowed. Rajeswari and Vanjikkodi [19] developed a deterministic EOQ model considering constant deterioration, partially backlogged shortages and power demand pattern. Sicilia et al [20] analyzed inventory systems, in which deterministic demand changes with time and follows a power pattern. They discussed several scenarios: the inventory systems with and without shortages, the systems with full backlogging or entirely lost sales. Sicilia et al [21, 22] extended a lot-sizing system with a power demand pattern for deteriorating items.

Sicilia et al [23] investigated an EOQ system, in which deterioration occurs with a constant rate and deterministic demand pattern is power. Sicilia et al [24] developed an EPQ system, in which demand follows a time-dependent power law and production rate changes pro rata with the demand rate, allowing for backlogged shortage. San-José et al [25] optimized an inventory system with power demand pattern and partial backlogging. Keshavarzfard et al [26] developed an inventory-pricing model for multiple products in which the production rate is proportional to power demand rate.

One of the conventional assumptions in the EPQ model is perfect quality of all produced items. Resulting from process deterioration, defective raw materials or other reasons, producing items with imperfect quality is unavoidable. In the last years, several studies have been done to deal with production of defective items. Shih [27] discussed the impact of imperfect items on the replenishment size and the objective function. Schwaller [28] incorporated inspection costs in the EOQ system and assumed that a known proportion of an incoming lot is defective. Salameh and Jaber [29] considered that defective products are sold as one batch after finishing 100% inspection process. Hayek and Salameh [30] developed a manufacturing system with a random defective production rate, in which all defective items can be reworked. They derived an optimal production policy, in which backordered products are allowed. Goyal et al [31] presented an easy procedure to find the production policy of a vendor and buyer system with defective items. They assumed that a specified portion of imperfect products are produced during the replenishment process. Chiu [32] investigated an EPQ system for a situation that imperfect products are produced with a random rate and assumed that reworking of them starts immediately after production time, however a fraction of imperfect products are scrapped. Jamal et al [33] adopted two policies to find the optimum lot quantity in a production model considering rework. Ojha et al [34] studied a manufacturing process that manufactures imperfect products with a constant rate. They assumed that products can be delivered just after checking quality of entire batch and imperfect products have to be reworked. Also three scenarios were investigated by them. Cárdenas-Barrón [35] presented an extension of [33] by adding planned backorders. Taleizadeh et al [36] studied a production system with limited capacity and allowing for backorders, in which manufacturing imperfect items follows either a normal or a uniform probability distribution. Taleizadeh et al [37] modeled an inventory system with rework process, multiple products and single machine, to find the optimal lot size. Ouyang et al [38] discussed a situation that management invests capital to improve quality. Also, they considered defective products and inspection policy in their model. Furthermore, Taleizadeh et al [39] analyzed a manufacturing system considering defective items, rework process and multiple products. Taleizadeh et al [40] presented a production system with one machine, multiple products, and interruption in process, scrap, rework and backordering.

Jaber et al [41] extended [29] to a situation that replacing defective products is impossible due to the distance of the supplier. They modeled two different cases to deal with this condition. Taleizadeh et al [42] and Taleizadeh and Noori [43] suggested an inventory system for a three-layer supply chain considering defective items. They assumed three scenarios. First, all imperfect products are disposed. Second, imperfect products are reworked and sold as perfect items. Third, scenario consists of selling imperfect products as a batch with a lower price than price of perfect items. Treviño-Garza et al [44] obtained the optimal value for the replenishment quantity models using two solution procedures. They considered a system of both vendor and buyer and assumed that the imperfect items are produced as well. Taleizadeh and Wee [45] proposed a production system by assuming one machine, multiple products, manufacturing limitations, defective items, rework, and partial backlogging. Tai [46] analyzed an inventory system, in which a different screening process is considered for each single quality characteristic. Each screening process has independent screening rate and defective percentage. Taleizadeh et al [47] worked on an EPQ model with multiple shipments and rework of imperfect products to find the number of shipments, replenishment size and the price. Hsu and Hsu [48] studied optimal replenishment size models with defective products by assuming three scenarios according to the time of selling imperfect products. Taleizadeh and Moshtagh [49] worked on imperfect production processes, quality dependent return and lot sales in a closed loop supply chain. Table 1 shows some terms and their codes and explanations to categorize all reviewed papers. Then in table 2, a categorization of those papers is provided.

Table 1 Codes and explanations to categorize papers.
Full size table
Table 2 Categorization of reviewed papers.
Full size table

This work differs from the existing papers in some directions. With regard to the literature review until now no research is done on the jointly considering inventory systems with power demand rate dependent production rate, backlogging and defective items. In the real world, producing defective items is part of the production process. As regards it is not included in models with a power demand pattern. Also, such problems do not involve the costs (e.g., inspection and production) that are impartible parts of a production process. Actually inspection is a process itself and so that the cost associated with it should be considered in the model. As well when the cost of a production process for each item is not assumed, the results of modeling a system may be unreal. In practice, holding of defective items has cost; however, it is rarely applied in the existing studies. Therefore, firstly we extend model presented in [24] by allowing for defective items. Secondly, we consider three different situations for the proposed model regarding to the date that imperfect products are drawn from the stock. Thirdly, our model consists of production and inspection costs as well as holding cost of imperfect items. The arrangement of the rest of this work is as follows. Problem definition is available in section 2. Moreover, three developed models and the related procedure to solve them, are presented in sections 3 and 4, respectively. Then in section 5, an example is investigated. Section 6 consists of some sensitivity analyses and managerial insights. Finally, conclusions are provided in section 7.

2 Problem definition

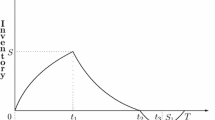
We consider a manufacturing factory with production and inspection stages. The demand of the product has a power pattern in each inventory cycle. It is supposed that the production rate changes pro rata with the demand rate. Due to many reasons a fraction of the produced lot is assumed to be imperfect. Such products are discovered in the inspection stage. Management of the factory desires to determine the minimum inventory costs of the system, and satisfy the customer demand simultaneously. Behavior of the inventory is studied for three cases, dependent on when defective items are drawn from the inventory. In case I, we investigate the situation that imperfect items are scrapped or sold at the time that they are identified. So that in this case, the holding cost of defective items is zero. In order to reduce some costs (e.g., holding cost), it seems to be better to scrap or sell imperfect products as soon as possible; however in practice, selling or scrapping items day-to-day may be infeasible. However, in some industries (e.g., pharmaceutical companies) it is inescapable. In cases II and III, imperfect products are held in the stock and sold when the replenishment and scheduling periods are finished, respectively. The cycle length and the reorder point are two decision variables of the system. A minimizing approach is applied to specify the optimum replenishment policies of the inventory system. Figure 1 shows the system of processing a lot size.

Figure 1
figure 1

Processing a lot size.

Full size image

We apply the following notations in our model.

  • T: Cycle length or scheduling period (time).

  • s: Reorder point per lot (units).

  • Q: Production lot size (units).

  • \( t^{{\prime }} \): Production cycle length (time).

  • d: Total demand during the scheduling period (units).

  • r: Average demand (r = d/T) (units).

  • \( C_{h} \): Carrying cost ($/unit/unit time).

  • \( C_{b} \): Cost of backordering ($/unit/unit time).

  • \( C_{i} \): Cost of inspecting ($/unit).

  • \( C_{p} \): Cost of producing ($/unit).

  • \( C_{o} \): Setup cost per cycle ($/replenishment).

  • \( \lambda \): Defective rate.

  • CD(t): Demand up to time t (\( 0 \le t \le T \)).

  • D(t): Demand rate at time t (\( 0 \le t \le T \)).

  • P(t): Production rate at time t (\( 0 \le t \le T \)).

  • I(t): Net stock level at time t (\( 0 \le t \le T \)).

  • ID(t): Stock level of imperfect products at time t.

  • \( I_{h} \left( {s,T} \right) \): Average number of items holding in stock (units).

  • \( I_{b} \left( {s,T} \right) \): Average number of backordered items (units).

  • \( I_{d} \left( T \right): \) Average amount of defective items carried in inventory (units).

  • \( CH\left( {s,T} \right) \): Cost of carrying products ($/unit time).

  • \( CB\left( {s,T} \right) \): Backordering cost ($/unit time).

  • \( CO\left( {s,T} \right) \): Setup cost ($/unit time).

  • \( CI\left( {s,T} \right) \): Inspection cost ($/unit time).

  • \( CP\left( {s,T} \right) \): Production cost ($/unit time).

  • \( CD\left( T \right) \): Holding cost of defective items ($/unit time).

  • \( TC_{j} \left( {s,T} \right) \): Total cost for case j (j = I, II, III) ($/unit time).

We keep the main assumptions given in [24].

  1. (1)

    Infinite-horizon is assumed.

  2. (2)

    The amount of demand throughout the inventory cycle T is considered to be d, and average demand rate is r = d/t units per cycle.

  3. (3)

    The inventory system consists of a single item.

  4. (4)

    The demand rate is less than the production rate.

  5. (5)

    The production rate P(t) is proportional to demand rate at any time t (\( 0 \le t \le t^{{\prime }} \)) and is defined by P(t) = αD(t) with \( \upalpha > 1 \).

  6. (6)

    We suppose that producing defective items is unavoidable and the fraction of defective items or defective rate is denoted by \( \lambda \), which is a constant value.

  7. (7)

    The produced items of perfect quality are added to inventory with rate \( \left( {1 - \lambda } \right)P\left( t \right) - D\left( t \right) \), during the production cycle.

  8. (8)

    To warrant that the consumer demand is totally covered by the products of perfect quality, it is assumed that \( \alpha \left( {1 - \lambda } \right) - 1 > 0 \) or \( 1 - \frac{1}{\alpha } > \lambda \).

  9. (9)

    Shortages are allowed and fully backordered.

  10. (10)

    To warrant that there is enough replenishment capacity to meet the demand, we assume that inspection occurs immediately after producing an item.

  11. (11)

    However, the average demand per cycle d is deterministic, the number of items withdrawn from stock is dependent on the time at which they are removed. Therefore, we suppose that the cumulative demand \( CD\left( t \right) \) up to time \( t \) (\( 0 \le t \le T \)) follows a power pattern and is given by \( CD\left( t \right) = d\left( {\frac{t}{T}} \right)^{1/n} \), Where \( d \) is the demand quantity during the inventory cycle and \( n \) is the demand pattern index, with \( 0 < n < \infty \).

The demand rate at time \( t \) (\( 0 \le t \le T \)), follows a time-power pattern too and is the derivative of the function \( CD\left( t \right) \), that is \( D\left( t \right) = \frac{{rt^{{\left( {1 - n} \right)/n}} }}{{nT^{{\left( {1 - n} \right)/n}} }} \), with \( 0 \le t < T \). The nature of this demand pattern is completely defined by \( n \). If the demand pattern index is \( n = 1 \), then demand is uniform (has a constant rate) and the inventory decreases linearly. When a great portion of demand happens mainly at the beginning of the cycle, then demand follows a pattern law with index \( n > 1 \). But if a larger percentage of demand occurs at the end of the scheduling period, then the demand of the inventory system is defined by a power pattern index \( n < 1 \). Also by using this kind of demand function, it is supposed that the demand is dependent on both time and the length of the scheduling period. The length of the inventory cycle or scheduling period is a fraction of the unit time. For example, assume that the unit time is a year. If \( T = \frac{1}{2},\frac{1}{3}, \ldots \) then a year consists of 2, 3, … inventory cycles, respectively.

The decision variables are cycle length T and reorder point s.

3 Mathematical models

This section extends the model proposed by [24] in some directions. Let \( I\left( t \right) \) be the net stock level at time \( t \left( {0 \le t \le T} \right) \). Inventory cycle starts with s units net stock at time 0. Also production period starts at time t = 0 and continues until \( t = t^{{\prime }} \). We suppose that the demand rate is less than the production rate in interval \( 0 \le t \le t^{{\prime }} \). With regard to that in real world situations the production process is usually imperfect, a certain fraction \( \lambda \) of defective items is supposed to be produced in each production period. Thus, the production rate of non-defective items can be obtained by\( \left( {1 - \lambda } \right)P\left( t \right) \). Therefore, inventory is accumulated during the production period \( \left[ {0,t^{{\prime }} } \right] \), at a rate \( \left( {1 - \lambda } \right)P\left( t \right) - D\left( t \right) \).

Under these conditions, the following differential equations govern the system:

$$ \frac{dI\left( t \right)}{dt} = \left( {1 - \lambda } \right)P\left( t \right) - D\left( t \right) = \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)D\left( t \right) = \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)\frac{{rt^{{\left( {1 - n} \right)/n}} }}{{nT^{{\left( {1 - n} \right)/n}} }},\quad 0 \le t \le t^{{\prime }} $$
(1)
$$ \frac{dI\left( t \right)}{dt} = - D\left( t \right) = - \frac{{rt^{{\left( {1 - n} \right)/n}} }}{{nT^{{\left( {1 - n} \right)/n}} }},\quad t^{{\prime }} \le t \le T $$
(2)

With regard to boundary conditions \( I\left( 0 \right) = I\left( T \right) = s \), the above differential equations are solved and the solutions are as follows:

$$ I\left( t \right) = s + \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)rT\left( {\frac{t}{T}} \right)^{1/n} ,\quad 0 \le t \le t^{{\prime }} $$
(3)
$$ I\left( t \right) = s + rT - rT\left( {\frac{t}{T}} \right)^{1/n} ,\quad t^{{\prime }} \le t \le T $$
(4)

The net inventory level at \( t^{{\prime }} \), \( I\left( {t^{{\prime }} } \right) \), specified by both Eqs. (3) and (4) must be equal. So that \( t^{{\prime }} \) will be found:

$$ t^{\prime } = \frac{T}{{\left( {1 - \lambda } \right)^{n} \alpha^{n} }} $$
(5)

When \( \lambda = 0 \), Eq. (5) reduces to \( t^{\prime } = \frac{T}{{\alpha^{n} }} \) (given in [24]), that is less than \( t^{\prime } = \frac{T}{{\left( {1 - \lambda } \right)^{n} \alpha^{n} }} \). It is correct because when defective items are produced, system needs more production time to meet the demand. Therefore, function I(t) is increasing on \( \left[ {0,t^{{\prime }} } \right) \) and decreasing on (\( t^{{\prime }} ,T] \). Also I(t) is a continuous and T-periodic function on interval \( \left[ {0,\infty } \right) \). The total demand on interval \( \left[ {0,T} \right) \) is computed by:

$$ \mathop \int \limits_{0}^{T} D\left( t \right)dt = \mathop \int \limits_{0}^{T} \frac{r}{n}\left( {\frac{t}{T}} \right)^{{\frac{1}{n} - 1}} dt = rT $$
(6)

A production size \( Q \) must be added to stock at the end of each cycle as follows:

$$ Q = \mathop \int \limits_{0}^{{t^{\prime } }} P\left( t \right)dt = \alpha \mathop \int \limits_{0}^{{t^{\prime } }} \frac{r}{n}\left( {\frac{t}{T}} \right)^{{\frac{1}{n} - 1}} dt = \frac{rT}{1 - \lambda } $$
(7)

When the system does not consist of defective items \( (\lambda = 0) \), the replenishment size is less than the situation with defective items and it needs to produce more items to meet the demand.

Since total demand is rT by producing \( \frac{rT}{1 - \lambda } \) units in production time, fraction \( \lambda \) of this lot size, given by \( \frac{\lambda rT}{1 - \lambda } \), are defective items and fraction \( 1 - \lambda \), given by rT, are non-defective items. Therefore, rT units of the lot size are of good quality and it can totally fill the demand of the cycle.

When the production quantity is entirely added to stock, the maximum stock level is obtained and calculated by:

$$ I\left( {t^{{\prime }} } \right) = s + \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)rT\left( {\frac{{t^{{\prime }} }}{T}} \right)^{1/n} = s + \frac{{\left( {1 - \lambda } \right)\alpha - 1}}{{\left( {1 - \lambda } \right)\alpha }}rT $$
(8)

3.1 The average inventory level and the average shortage

With regard to the reorder point s and the maximum inventory level given in Eq. (8), three different behaviors of system may occur.

  1. (1)

    If \( s \ge 0 \), there are no shortages and the system only includes inventories.

  2. (2)

    If (\( I(t^{{\prime }} ) \ge 0 \) and \( s \le 0 \)) or \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \), the system includes some inventories and some shortages too.

  3. (3)

    If \( I\left( {t^{{\prime }} } \right) \le 0 \) or \( s \le \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \), only shortages occur.

If \( s \ge 0 \), then only inventories are contained. The average quantity of inventory is as follows:

$$ I_{h} \left( {s,T} \right) = \frac{1}{T}\mathop \int \limits_{0}^{{t^{{\prime }} }} \left[ {s + \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)\frac{rT}{{T^{1/n} }}t^{1/n} } \right]dt + \frac{1}{T}\mathop \int \limits_{{t^{\prime}}}^{T} \left[ {s + rT - \frac{rT}{{T^{1/n} }}t^{1/n} } \right]dt = s + \frac{{\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - 1} \right)rT}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} $$
(9)

Also, there are no shortages here, \( I_{w} \left( {s,T} \right) = 0 \).

If \( s \le \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \), only shortages exist. The average quantity of shortage:

$$ I_{b} \left( {s,T} \right) = \frac{ - 1}{T}\mathop \int \limits_{0}^{{t^{{\prime }} }} \left[ {s + \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)\frac{rT}{{T^{1/n} }}t^{1/n} } \right]dt - \frac{1}{T}\mathop \int \limits_{{t^{\prime}}}^{T} \left[ {s + rT - \frac{rT}{{T^{1/n} }}t^{1/n} } \right]dt = \frac{{\left( {1 - \left( {1 - \lambda } \right)^{n} \alpha^{n} } \right)rT}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - s $$
(10)

And there are no inventories carried, \( I_{h} \left( {s,T} \right) = 0 \).

Eventually, if \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \), both backorders and inventories occur. Suppose that at times \( t_{1} \) and \( t_{2} \) within the production period and the period without production, respectively, the stock level reaches zero. Since \( I\left( {t_{1} } \right) = I\left( {t_{2} } \right) = 0 \), from Eqs. (3) and (4) we obtain \( t_{1} \) and \( t_{2} \) according to decision variables s and T:

$$ t_{1} = \frac{{\left( { - s} \right)^{n} T}}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }} $$
(11)
$$ t_{2} = \frac{{\left( {s + rT} \right)^{n} T}}{{r^{n} T^{n} }} $$
(12)

In this situation, the average inventory level is as follows:

$$ \begin{aligned} I_{h} \left( {s,T} \right) & = \frac{1}{T}\mathop \int \limits_{{t_{1} }}^{{t^{{\prime }} }} \left[ {s + \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)\frac{rT}{{T^{1/n} }}t^{1/n} } \right]dt + \frac{1}{T}\mathop \int \limits_{{t^{\prime}}}^{{t_{2} }} \left[ {s + rT - \frac{rT}{{T^{1/n} }}t^{1/n} } \right]dt \\ & = \frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }} \\ \end{aligned} $$
(13)

And the average shortage is:

$$ \begin{aligned} I_{b} \left( {s,T} \right) & = \frac{1}{T}\mathop \int \limits_{0}^{{t_{1} }} \left[ {s + \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)\frac{rT}{{T^{1/n} }}t^{1/n} } \right]dt + \frac{1}{T}\mathop \int \limits_{{t_{2} }}^{T} \left[ {s + rT - \frac{rT}{{T^{1/n} }}t^{1/n} } \right]dt \\ & = \frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)}} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }} - s \\ \end{aligned} $$
(14)

Also, the average number of production runs is \( \frac{1}{T}. \)

3.2 Costs and optimal inventory policies

We consider three different cases of inventory systems and find the optimal inventory policy for them.

Case I

In this situation, at the time when a defective item is recognized, it may be sold with a discount or may be scrapped. These defective items are not assumed to be in inventory (see figure 2). Now, we model the elements of cost function in the proposed model. Notice that the unit of time can be for example “year”. The production cost is as follows:

$$ CP\left( T \right) = C_{p} \frac{Q}{T} = C_{p} \frac{r}{1 - \lambda } $$
(15)

The inspection cost is:

$$ CI\left( T \right) = C_{i} \frac{Q}{T} = C_{i} \frac{r}{1 - \lambda } $$
(16)

The set-up cost is:

$$ CO\left( T \right) = C_{o} \left( {\frac{1}{T}} \right) = \frac{{C_{o} }}{T} $$
(17)
Figure 2
figure 2

Net inventory level for the EPQ model with a power demand rate dependent production rate and defective items (case I).

Full size image

The holding cost is given by \( CH\left( {s,T} \right) = C_{h} I_{h} \left( {s,T} \right) \). With regard to three situations mentioned before, three holding costs may occur. First if\( s \ge 0 \), from Eq. (9) the holding cost is as follows:

$$ CH\left( {s,T} \right) = C_{h} \left[ {s + \frac{{\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - 1} \right)rT}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }}} \right] $$
(18)

If \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \), from Eq. (13) we have:

$$ CH\left( {s,T} \right) = C_{h} \left[ {\frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }}} \right] $$
(19)

And if \( s \le \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \), we have \( CH\left( {s,T} \right) = 0 \), because there are no inventories in the system. Finally, the shortage cost is calculated by \( CB\left( {s,T} \right) = C_{b} I_{b} \left( {s,T} \right) \). If \( s \ge 0 \), \( CB\left( {s,T} \right) = 0 \), because there are no shortages. For \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \), from Eq. (14) the shortage cost is as follows:

$$ CB\left( {s,T} \right) = C_{b} \left[ {\frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)}} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }} - s} \right] $$
(20)

Finally, if \( s \le \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \), from Eq. (10), the shortage cost is given by

$$ CB\left( {s,T} \right) = C_{b} \left[ {\frac{{\left( {1 - \left( {1 - \lambda } \right)^{n} \alpha^{n} } \right)rT}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - s} \right] $$
(21)

The total cost is the sum of all five costs. That is:

$$ TC_{I} \left( {s,T} \right) = CP\left( T \right) + CI\left( T \right) + CO\left( T \right) + CH\left( {s,T} \right) + CB\left( {s,T} \right) $$
(22)

Therefore, the total cost in three possible situations can be found. First if \( s \ge 0 \), the total cost per unit time is given by:

$$ TC_{I} \left( {s,T} \right) = C_{p} \frac{r}{1 - \lambda } + C_{i} \frac{r}{1 - \lambda } + \frac{{C_{o} }}{T} + C_{h} \left[ {s + \frac{{\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - 1} \right)rT}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }}} \right] $$
(23)

If \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \), the total cost is calculated by:

$$ \begin{aligned} TC_{I} \left( {s,T} \right) & = C_{p} \frac{r}{1 - \lambda } + C_{i} \frac{r}{1 - \lambda } + \frac{{C_{o} }}{T} \\ & \quad + C_{h} \left[ {\frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }}} \right] \\ & \quad + C_{b} \left[ {\frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)}} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }} - s} \right] \\ \end{aligned} $$
(24)

And for \( s \le \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \), the total cost is as follows:

$$ TC_{I} \left( {s,T} \right) = C_{p} \frac{r}{1 - \lambda } + C_{i} \frac{r}{1 - \lambda } + \frac{{C_{o} }}{T} + C_{b} \left[ {\frac{{\left( {1 - \left( {1 - \lambda } \right)^{n} \alpha^{n} } \right)rT}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - s} \right] $$
(25)

To find the minimum of the function \( TC_{I} \left( {s,T} \right) \), we consider three different regions of s. As the cost \( TC_{I} \left( {0,T} \right) \) is always less than the cost \( TC_{I} \left( {s,T} \right) \), the minimum cost cannot be in the region \( s \ge 0 \). Also, since\( TC_{I} \left( {s,T} \right) \) is always greater than\( TC_{I} \left( {\frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT,T} \right) \), then minimum cost cannot be at \( s \le \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \). So that, the optimal cost can be found at \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \). From partial derivatives of objective function (22) with respect to decision variables, we have:

$$ \frac{{\partial TC_{I} \left( {s,T} \right)}}{\partial s} = \left( {C_{h} + C_{b} } \right)\left[ {\frac{{\left( {s + rT} \right)^{n} }}{{r^{n} T^{n} }} - \frac{{\left( { - s} \right)^{n} }}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }}} \right] - C_{b} $$
(26)
$$ \frac{{\partial TC_{I} \left( {s,T} \right)}}{\partial T} = \left( {C_{h} + C_{b} } \right)\left[ {\frac{{\left( {s + rT} \right)^{n} \left( {rT - ns} \right)}}{{\left( {n + 1} \right)r^{n} T^{n + 1} }} - \frac{{n\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n + 1} }}} \right] - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} $$
(27)

Equaling these derivatives to zero the optimal solution \( (s^{*} ,T^{*} ) \) can be calculated. Thus, we have:

$$ \left( {C_{h} + C_{b} } \right)\left[ {\frac{{\left( {s + rT} \right)^{n} }}{{r^{n} T^{n} }} - \frac{{\left( { - s} \right)^{n} }}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }}} \right] - C_{b} = 0 $$
(28)
$$ \left( {C_{h} + C_{b} } \right)\left[ {\frac{{\left( {s + rT} \right)^{n} \left( {rT - ns} \right)}}{{\left( {n + 1} \right)r^{n} T^{n + 1} }} - \frac{{n\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n + 1} }}} \right] - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} = 0 $$
(29)

Let x be a new variable defined by \( x = \frac{ - s}{rT} \). Then the region \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \) is equivalent to \( 0 \le x \le \frac{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }} \). Also, Eqs. (28) and (29) are respectively equivalent to:

$$ \left( {1 - x} \right)^{n} - \frac{{x^{n} }}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} }} - \frac{{C_{b} }}{{C_{h} + C_{b} }} = 0 $$
(30)
$$ \frac{{\left( {C_{h} + C_{b} } \right)\left( {1 - x} \right)^{n} \left( {1 + nx} \right)r}}{{\left( {n + 1} \right)}} - \frac{{n\left( {C_{h} + C_{b} } \right)rx^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} }} - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} = 0 $$
(31)

Proposition 1

Equal \( \left( {1 - x} \right)^{n} - \frac{{x^{n} }}{{\left( {\left( {1 -\uplambda} \right)\alpha - 1} \right)^{n} }} - \frac{{C_{b} }}{{C_{b} + C_{h} }} = 0 \) has a unique solution \( x^{*} \)on the interval \( \left( {0,\frac{{\left( {\left( {1 -\uplambda} \right)\alpha - 1} \right)}}{{\left( {1 -\uplambda} \right)\alpha }}} \right) \).

Proof

Please see “Appendix A”.

Use one of the numerical methods (e.g., Newton–Raphson) to find the solution \( x^{*} \) (see, i.e., [50]). From Eq. (30), we have:

$$ \frac{{x^{n} }}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} }} = \left( {1 - x} \right)^{n} - \frac{{C_{b} }}{{C_{h} + C_{b} }} $$
(32)

Now, by replacement of Eq. (32) in Eq. (31), we have:

$$ \frac{{\left( {C_{h} + C_{b} } \right)\left( {1 - x} \right)^{n} r}}{{\left( {n + 1} \right)}} + \frac{{nC_{b} rx}}{{\left( {n + 1} \right)}} - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} = 0 $$
(33)

Finally, we can obtain the best inventory cycle length \( T^{*} \), by replacement the optimal solution of Eq. (30) in Eq. (33). That cycle length is calculated by:

$$ T^{*} = \sqrt {\frac{{C_{o} }}{{r\left[ {\frac{{\left( {C_{h} + C_{b} } \right)\left( {1 - x^{*} } \right)^{n} }}{{\left( {n + 1} \right)}} + \frac{{nC_{b} x^{*} }}{{\left( {n + 1} \right)}} - \frac{{C_{h} }}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} }}{{\left( {n + 1} \right)}}} \right]}}} $$
(34)

The optimal shortage level is \( s^{*} = - x^{*} rT^{*} \). Also as \( Q = \frac{rT}{1 - \lambda } \) then the economic production quantity \( Q^{*} \) is as follows:

$$ Q^{*} = \frac{1}{1 - \lambda }\sqrt {\frac{{C_{o} r}}{{\left[ {\frac{{\left( {C_{h} + C_{b} } \right)\left( {1 - x^{*} } \right)^{n} }}{{\left( {n + 1} \right)}} + \frac{{nC_{b} x^{*} }}{{\left( {n + 1} \right)}} - \frac{{C_{h} }}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} }}{{\left( {n + 1} \right)}}} \right]}}} $$
(35)

Proposition 2

The total cost function \( TC_{I} \left( {s,T} \right) \) is strictly convex.

Proof

See “Appendix A”.

Case II

In this case, the items with imperfect quality are preserved in inventory and sold in each cycle, when the replenishment period is finished (see figure 3).

Figure 3
figure 3

Net inventory level for the EPQ with a power demand rate dependent production rate and defective items (Case II).

Full size image

The difference between Case I and Case II is that in situation II all of the imperfect products are held in inventory until finishing the replenishment cycle. In addition to five different costs explained in the previous situation, Case II consists of the holding cost of defective items. In this situation during the period \( \left[ {0,t^{{\prime }} } \right] \), inventory of defective items would have risen at a rate \( \lambda P\left( t \right) \). So that, the differential equation is given by:

$$ \frac{dID\left( t \right)}{dt} = \lambda P\left( t \right) = \lambda \alpha D\left( t \right) = \frac{{\lambda \alpha rt^{{\left( {1 - n} \right)/n}} }}{{nT^{{\left( {1 - n} \right)/n}} }},\quad 0 \le t \le t^{{\prime }} $$
(36)

When \( ID\left( t \right) \) is the inventory level of defective items and \( ID\left( 0 \right) = 0 \). The solution of the above differential equation is:

$$ ID\left( t \right) = \lambda \alpha rT\left( {\frac{t}{T}} \right)^{1/n} ,\quad 0 \le t \le t^{{\prime }} $$
(37)

Suppose that \( I_{d} \left( T \right) \) be the average amount of defective items carried in inventory. It can be calculated by:

$$ I_{d} \left( T \right) = \frac{1}{T}\mathop \int \limits_{0}^{{t^{{\prime }} }} \left[ {\frac{\lambda \alpha rT}{{T^{1/n} }}t^{1/n} } \right]dt = \frac{\lambda nrT}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }} $$
(38)

And, the cost of carrying defective items is:

$$ CD\left( T \right) = C_{h} I_{d} \left( T \right) = \frac{{C_{h} \lambda nrT}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }} $$
(39)

By adding \( CD\left( T \right) \) to the total cost of the previous case, the total cost of this situation will be found by:

$$ TC_{II} \left( {s,T} \right) = TC_{I} \left( {s,T} \right) + CD\left( T \right) $$
(40)

Similar to Case I, the minimum inventory cost, can be found in the region \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \). So, we have:

$$ \begin{aligned} TC_{II} \left( {s,T} \right) & = C_{p} \frac{r}{1 - \lambda } + C_{i} \frac{r}{1 - \lambda } + \frac{{C_{o} }}{T} \\ & \quad + C_{h} \left[ {\frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }}} \right] \\ & \quad + C_{b} \left[ {\frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)}} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }} - s} \right] + \frac{{C_{h} \lambda nrT}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }} \\ \end{aligned} $$
(41)

Equaling partial derivatives of the total cost function (41) to zero, we have:

$$ \frac{{\partial TC_{II} \left( {s,T} \right)}}{\partial s} = \left( {C_{h} + C_{b} } \right)\left[ {\frac{{\left( {s + rT} \right)^{n} }}{{r^{n} T^{n} }} - \frac{{\left( { - s} \right)^{n} }}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }}} \right] - C_{b} = 0 $$
(42)
$$ \begin{aligned} \frac{{\partial TC_{II} \left( {s,T} \right)}}{\partial T} & = \left( {C_{h} + C_{b} } \right)\left[ {\frac{{\left( {s + rT} \right)^{n} \left( {rT - ns} \right)}}{{\left( {n + 1} \right)r^{n} T^{n + 1} }} - \frac{{n\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n + 1} }}} \right] \\ & \quad - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} + \frac{{C_{h} \lambda nr}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }} = 0 \\ \end{aligned} $$
(43)

Defining \( x = \frac{ - s}{rT} \), the region \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \) is equivalent to \( 0 \le x \le \frac{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }} \). Also, Eqs. (42) and (43) are respectively equivalent to:

$$ \left( {1 - x} \right)^{n} - \frac{{x^{n} }}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} }} - \frac{{C_{b} }}{{C_{b} + C_{h} }} = 0 $$
(44)
$$ \frac{{\left( {C_{h} + C_{b} } \right)\left( {1 - x} \right)^{n} \left( {1 + nx} \right)}}{{\left( {n + 1} \right)}} - \frac{{n\left( {C_{h} + C_{b} } \right)rx^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} }} - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} + \frac{{C_{h} \lambda nr}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }} = 0 $$
(45)

Equation (44) is exactly same as Eq. (30). So solution \( x^{*} \) within \( \left( {0,\frac{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}} \right) \) is unique. Now, by replacement of Eq. (32) in Eq. (45), we have:

$$ \frac{{\left( {C_{h} + C_{b} } \right)r\left( {1 - x} \right)^{n} }}{{\left( {n + 1} \right)}} + \frac{{nC_{b} rx}}{{\left( {n + 1} \right)}} - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b } r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} + \frac{{C_{h} \lambda nr}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }} = 0 $$
(46)

Finally, we can obtain the optimal inventory policy \( (s^{*} ,T^{*} ) \), by replacement the optimal solution of Eq. (44) in Eq. (46). The optimal scheduling period is calculated by:

$$ T^{*} = \sqrt {\frac{{C_{o } }}{{r\left[ {\frac{{\left( {C_{h} + C_{b } } \right)\left( {1 - x^{*} } \right)^{n} }}{{\left( {n + 1} \right)}} + \frac{{nC_{b } x^{*} }}{{\left( {n + 1} \right)}} - \frac{{C_{h} }}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b } }}{{\left( {n + 1} \right)}} + \frac{{C_{h} \lambda n}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}} \right]}}} $$
(47)

The optimal shortage level is \( s^{*} = - x^{*} rT^{*} \). Also, \( Q^{*} \) is as follows:

$$ Q^{*} = \frac{1}{1 - \lambda }\sqrt {\frac{{C_{o} r}}{{\left[ {\frac{{\left( {C_{h} + C_{b} } \right)\left( {1 - x^{*} } \right)^{n} }}{{\left( {n + 1} \right)}} + \frac{{nC_{b} x^{*} }}{{\left( {n + 1} \right)}} - \frac{{C_{h} }}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} }}{{\left( {n + 1} \right)}} + \frac{{C_{h} \lambda n}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}} \right]}}} $$
(48)

Using the second order derivatives of \( TC_{II} \left( {s,T} \right) \) respect to s and T, we have the same formula and Hessian as in case I. Thus, \( TC_{II} \left( {s,T} \right) \) is strictly convex (see proposition 2).

Case III

The behavior of this inventory system is similar to Case II, the only difference is that the imperfect products are sold when each inventory cycle is finished (see figure 4). In this situation, producing defective items starts just after \( t = 0 \) and continues up to \( t = t^{{\prime }} \), when the inventory level of defective items attains a maximum level \( ID\left( {t^{{\prime }} } \right) \). With respect to that the fraction \( \lambda \) of all \( Q = \frac{rT}{1 - \lambda } \) produced items are defective, the total number of defective items is as follows:

$$ ID\left( {t^{{\prime }} } \right) = \frac{\lambda rT}{1 - \lambda } $$
(49)

And after reaching that, this value doesn’t change until T. So, \( I_{d} \left( T \right) \) is given by:

$$ \begin{aligned} I_{d} \left( T \right) & = \frac{1}{T}\left( {\mathop \int \limits_{0}^{{t^{\prime } }} \left[ {\frac{\lambda \alpha rT}{{T^{1/n} }}t^{1/n} } \right]dt + \frac{\lambda rT}{1 - \lambda }\left( {T - t^{\prime } } \right)} \right) = \frac{\lambda nrT}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }} + \frac{\lambda rT}{1 - \lambda }\left( {T - \frac{T}{{\left( {1 - \lambda } \right)^{n} \alpha^{n} }}} \right) \\ & = \frac{\lambda rT}{{\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - \frac{1}{n + 1}} \right) \\ \end{aligned} $$
(50)

And, the cost of inventory of defective items is:

$$ CD\left( T \right) = C_{h} I_{d} \left( T \right) = \frac{{C_{h} \lambda rT}}{{\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - \frac{1}{n + 1}} \right) $$
(51)

By adding \( CD\left( T \right) \) to the total cost of the previous case, the total cost of this situation will be found by:

$$ TC_{III} \left( {s,T} \right) = TC_{I} \left( {s,T} \right) + CD\left( T \right) $$
(52)

So that, we have:

$$ \begin{aligned} TC_{III} \left( {s,T} \right) & = C_{p} \frac{r}{1 - \lambda } + C_{i} \frac{r}{1 - \lambda } + \frac{{C_{o} }}{T} \\ & \quad + C_{h} \left[ {\frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }}} \right] \\ & \quad + C_{b} \left[ {\frac{{\left( {s + rT} \right)^{n + 1} }}{{\left( {n + 1} \right)r^{n} T^{n} }} - \frac{rT}{{\left( {n + 1} \right)}} + \frac{{\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }} - s} \right] \\ & \quad + \frac{{C_{h} \lambda rT}}{{\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - \frac{1}{n + 1}} \right) \\ \end{aligned} $$
(53)

Equaling partial derivatives of the total cost function (52) to zero, we have:

$$ \frac{{\partial TC_{III} \left( {s,T} \right)}}{\partial s} = \left( {C_{h} + C_{b} } \right)\left[ {\frac{{\left( {s + rT} \right)^{n} }}{{r^{n} T^{n} }} - \frac{{\left( { - s} \right)^{n} }}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n} }}} \right] - C_{b} = 0 $$
(54)
$$ \begin{aligned} \frac{{\partial TC_{III} \left( {s,T} \right)}}{\partial T} & = \left( {C_{h} + C_{b} } \right)\left[ {\frac{{\left( {s + rT} \right)^{n} \left( {rT - ns} \right)}}{{\left( {n + 1} \right)r^{n} T^{n + 1} }} - \frac{{n\left( { - s} \right)^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} r^{n} T^{n + 1} }}} \right] \\ & \quad - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} \\ & \quad + \frac{{C_{h} \lambda r}}{{\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - \frac{1}{n + 1}} \right) = 0 \\ \end{aligned} $$
(55)
Figure 4
figure 4

Net inventory level for the EPQ with a power demand rate dependent production rate and defective items (Case III).

Full size image

Again defining \( x = \frac{ - s}{rT} \), the region \( \frac{{ - \left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }}rT \le s \le 0 \) is equivalent to \( 0 \le x \le \frac{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }} \). Also, Eqs. (54) and (55) are respectively equivalent to:

$$ \left( {1 - x} \right)^{n} - \frac{{x^{n} }}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} }} - \frac{{C_{b} }}{{C_{b} + C_{h} }} = 0 $$
(56)
$$ \frac{{\left( {C_{h} + C_{b} } \right)\left( {1 - x} \right)^{n} \left( {1 + nx} \right)}}{{\left( {n + 1} \right)}} - \frac{{n\left( {C_{h} + C_{b} } \right)rx^{n + 1} }}{{\left( {n + 1} \right)\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} }} - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} + \frac{{C_{h} \lambda r}}{{\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - \frac{1}{n + 1}} \right) = 0 $$
(57)

Now, by replacement of Eq. (32) in Eq. (57), we have:

$$ \frac{{\left( {C_{h} + C_{b} } \right)r\left( {1 - x} \right)^{n} }}{{\left( {n + 1} \right)}} + \frac{{nC_{b} rx}}{{\left( {n + 1} \right)}} - \frac{{C_{h} r}}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} r}}{{\left( {n + 1} \right)}} - \frac{{C_{o} }}{{T^{2} }} + \frac{{C_{h} \lambda r}}{{\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - \frac{1}{n + 1}} \right) = 0 $$
(58)

Finally, like the previous cases, we have:

$$ T^{*} = \sqrt {\frac{{C_{o} }}{{r\left[ {\frac{{\left( {C_{h} + C_{b} } \right)\left( {1 - x^{*} } \right)^{n} }}{{\left( {n + 1} \right)}} + \frac{{nC_{b} x^{*} }}{{\left( {n + 1} \right)}} - \frac{{C_{h} }}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} }}{{\left( {n + 1} \right)}} + \frac{{C_{h} \lambda }}{{\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - \frac{1}{n + 1}} \right)} \right]}}} $$
(59)

The optimal shortage level is \( s^{*} = - x^{*} rT^{*} \). Also, \( Q^{*} \) is as follows:

$$ Q^{*} = \frac{1}{1 - \lambda }\sqrt {\frac{{C_{o} r}}{{\left[ {\frac{{\left( {C_{h} + C_{b} } \right)\left( {1 - x^{*} } \right)^{n} }}{{\left( {n + 1} \right)}} + \frac{{nC_{b} x^{*} }}{{\left( {n + 1} \right)}} - \frac{{C_{h} }}{{\left( {n + 1} \right)\left( {1 - \lambda } \right)^{n} \alpha^{n} }} - \frac{{C_{b} }}{{\left( {n + 1} \right)}} + \frac{{C_{h} \lambda }}{{\left( {1 - \lambda } \right)^{n + 1} \alpha^{n} }}\left( {\left( {1 - \lambda } \right)^{n} \alpha^{n} - \frac{1}{n + 1}} \right)} \right]}}} $$
(60)

By taking the second order derivatives of \( TC_{III} \left( {s,T} \right) \) with respect to s and T, we have the same formula and Hessian as in case I. Thus, the function \( TC_{III} \left( {s,T} \right) \) is strictly convex (see proposition 2).

4 Procedure for determining the optimal values

A brief procedure is explained to obtain the optimum values for all the three proposed cases. Notice that optimal value of variable x is obtained by Eq. (30), or (44) or (56), that are the same for all three cases.

  • Step 1 Enter the values of parameters.

  • Step 2 Obtain \( x^{*} \) of equation \( \left( {1 - x} \right)^{n} - \frac{{x^{n} }}{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)^{n} }} - \frac{{C_{b} }}{{C_{b} + C_{h} }} = 0 \), using a numerical method.

  • Step 3 Specify \( T^{*} \), using Eq. (34) for Case I, Eq. (47) for Case II or Eq. (59) for case III. Use \( s^{*} = - x^{*} rT^{*} \) to calculate optimal reorder point.

  • Step 4 Determine optimal lot size \( Q^{*} \) given by formula (35) for Case I, (48) for Case II or (60) for Case III.

  • Step 5 Calculate the minimum cost \( TC_{I}^{*} \) for Case I using Eq. (24), \( TC_{II}^{*} \) for Case II using Eq. (41) and \( TC_{III}^{*} \) for Case III using Eq. (53).

5 Numerical example

In order to provide input data, we consider an inventory system, in which the parametric values are defined as \( C_{h} \) = $4 per unit and year, \( C_{b} \) = $5 per unit, \( C_{o} \) = $100 per replenishment, \( C_{i} \) = $2 per unit, \( C_{p} \) = $6 per unit, r = 1200 units per year, \( \alpha \) = 1.4, \( \lambda \) = 0.2 and n = 2. Using Eq. (30), the following equation must be solved.

$$ \left( {1 - x} \right)^{2} - \frac{{x^{2} }}{{0.12^{2} }} = \frac{5}{9} $$
(61)

There is a unique solution for this equation inside the interval \( \left( {0,\frac{{\left( {\left( {1 - \lambda } \right)\alpha - 1} \right)}}{{\left( {1 - \lambda } \right)\alpha }} = 0.107143} \right) \), that is \( x^{*} = 0.067286 \). Now for three different cases, we have following optimal values:

Case I

Using Eq. (34), the optimal cycle length is \( T^{*} = 0.8927\,{\text{year}} = 325.8355\,{\text{days}} \). From Eq. (35) the economic lot size is \( Q^{*} = 1339.1 \) units. Using formula \( s^{*} = - x^{*} rT^{*} \), the optimal reorder point is \( s^{*} = - 72.0826 \) units. From Eq. (24), the optimal cost is \( TC_{I}^{*} = \) $12224 per year.

Case II

Using Eq. (47), the optimal cycle length is \( T^{*} = 0.3620 \,{\text{year}} = 132.13 \,{\text{days}} \). From Eq. (48) the economic lot size is \( Q^{*} = 542.9552 \) units. Using formula \( s^{*} = - x^{*} rT^{*} \), the optimal reorder point is \( s^{*} = - 29.2266 \) units. From Eq. (41), the optimal cost is \( TC_{II}^{*} = \) $12553 per year.

Case III

Using Eq. (59), the optimal cycle length is \( T^{*} = 0.2466 \,{\text{year}} = 90.009\,{\text{days}} \). From Eq. (60) the economic lot size is \( Q^{*} = 369.9083 \) units. Using formula \( s^{*} = - x^{*} rT^{*} \), the optimal reorder point is \( s^{*} = - 19.9117 \) units. From Eq. (53), the optimal cost is \( TC_{III}^{*} = \) $12654 per year.

Figures 5, 6 and 7 show the total cost as a function of two variables T and s for Cases I, II and III by using the above example’s input parameters, respectively.

Figure 5
figure 5

Total cost for Case I.

Full size image
Figure 6
figure 6

Total cost for Case II.

Full size image
Figure 7
figure 7

Total cost for Case III.

Full size image

6 Numerical analyses and insights

Some numerical analyses are done to discover the effect of changes in parameters on the results. Basically, the impacts of the production rate \( \alpha \), the defective rate \( \lambda \) and the power demand index n on the variables and the total cost of the system are analyzed in this section. Some extra examples are reported in tables 3 and 4 using the input data taken from [24]. According to the following values of parameters, table 3 is provided: n = 3, \( C_{o} \) = 100, r = 1200, \( C_{h} \) = 4, \( C_{b} \) = 5, \( C_{i} \) = 0 and \( C_{p} \) = 0. Optimal policies of inventory systems considering several combinations of parameters \( \alpha \) and \( \lambda \) are shown in table 3.

Table 3 Numerical analysis of production rate \( \upalpha \) and defective rate \( \uplambda \).
Full size table
Table 4 Numerical analysis of the power demand index n and defective rate \( \uplambda \).
Full size table

Also, the following values are used in table 4: r = 1200, \( C_{o} \) = 100, \( C_{h} \) = 4, \( C_{b} \) = 5, \( C_{i} \) = 2, \( C_{p} \) = 6 and \( \alpha = 1.5 \). The optimal solutions for various values of n and \( \lambda \) are calculated in table 4.

The graph of the minimum cost and lot size changes versus the defective rate changes for Case I is shown in figures 8 and 9, using table 4. In each figure, four different values of n (0.5, 1, 1.5 and 2) are considered.

Figure 8
figure 8

Changes of the total cost value with respect to the changes of the defective rate for Case I, using table 4.

Full size image
Figure 9
figure 9

Changes of the lot size value with respect to the changes of the defective rate for Case I, using table 4.

Full size image

Figures 10 and 11 show the total cost and the cycle length as functions of the defective rate for Case I, when input parameters are used from table 3. In each figure different values of \( \alpha \) are considered (\( \alpha = 1.1, 1.3, 1.5, 1.9 \)).

Figure 10
figure 10

Changes of the total cost value with respect to the changes of the defective rate for Case I, using table 3.

Full size image
Figure 11
figure 11

Changes of the cycle length value with respect to the changes of the defective rate for Case I, using table 3.

Full size image

Figures 12 and 13 show changes of the total cost respect to the changes of the production rate for Cases I and II, respectively, using table 3. In each figure, four different values of \( \lambda \) are assumed (\( \lambda = 0.02, 0.05, 0.2, 0.5 \)).

Figure 12
figure 12

Changes of the total cost value with respect to the changes of the production rate for Case I, using table 3.

Full size image
Figure 13
figure 13

Changes of the total cost value with respect to the changes of the production rate for Case II, using table 3.

Full size image

Figures 14 and 15 show changes of total cost and reorder point respect to the changes of the power demand index for Case I, using table 3. In each figure, four different values of \( \lambda \) are assumed (\( \lambda = 0.02, 0.05, 0.2, 0.5 \)).

Figure 14
figure 14

Changes of the total cost value with respect to the changes in the power demand index for Case I, using table 4.

Full size image
Figure 15
figure 15

Changes of the reorder point value with respect to the changes in the power demand index for Case I, using table 4.

Full size image

Some sensitivity analyses can be expressed as follows.

  • From table 3, we can observe that fixed the production rate parameter \( \alpha \) and considering Case I, the value \( x^{*} \), the total amount of backorders \( - s^{*} \) and the minimum cost \( TC^{*} \) decrease as the defective rate \( \lambda \) increases. However, the optimal cycle length \( T^{*} \) and the economic lot size \( Q^{*} \) increase as the defective rate \( \lambda \) increases. In the same situation, but considering Case II, the minimum cost \( TC^{*} \) increases as the defective rate \( \lambda \) increases. The reason is that in Case I we did not consider the holding cost of defective items; however, in Case 2 we consider it and because of that the results of Case II are more reasonable. Therefore, Case II can show the real world situations much better (in both cases, we do not have inspection and production costs (\( C_{i} \) = \( C_{p} \) = 0)). Also, fixed the defective rate \( \lambda \) and considering Case I, if the production rate \( \alpha \) increases then the value \( x^{*} \) and the minimum cost \( TC^{*} \) increase. However, the optimal cycle length \( T^{*} \)and the economic lot size \( Q^{*} \) decrease as the production rate \( \alpha \) increases.

  • In the same table 3, fixed the production parameter \( \alpha \) and the defective rate \( \lambda \), we can observe that the optimal cycle length \( T^{*} \) and the economic lot size \( Q^{*} \) decrease from case I to case III. However, \( TC^{ *} \) increases in this situation.

  • In table 4, by fixing the power demand index n and considering Case I, if the defective rate \( \lambda \) increases then the cycle length \( T^{ *} \), the optimum lot size \( Q^{ *} \) and the minimum cost \( TC^{ *} \) increase. However, the total omount of backorders \( - s^{*} \) and the value \( x^{ *} \) decrease as the defective rate \( \lambda \) increases. Also, fixed the defective rate \( \lambda \) and considering Case I, if n increases then the value \( x^{ *} \) increases. However, for other inventory policies, we can not find a standard pattern.

  • In the same table 4, by fixing the power demand index n and the defective rate \( \lambda \), we can observe that the optimal cycle length \( T^{*} \)and the optimum production quantity \( Q^{*} \) and the total amount of backorders \( - s^{*} \) decrease from Case I to case III. However, \( TC^{ *} \) increases in this situation.

  • Comparing tables 3 and 4, we can see that if production and inspection costs are involved in the proposed model (in table 4, \( C_{i} \) = 2 $/unit and \( C_{p} \) = 6 $/unit) then fixed the other parameters the optimum cost \( TC^{ *} \) increases as the defective rate \( \lambda \) increases. However, if production and inspection costs are not considered in the proposed model (in table 3, \( C_{i} \) = 0 $/unit and \( C_{p} \) = 0 $/unit), then fixed other parameters the optimal cost \( TC^{ *} \) decreases as the defective rate \( \lambda \) increases. Additionally, it shows considering these costs can help modeling the real world situations much better. When production costs or holding cost of imperfect products are not involved, the obtained results are not reliable enough.

This research offers several managerial insights: all previous related works have focused on the EPQ model in which demand follows a power pattern without considering imperfect items or imperfect items are involved but demand is uniformly distributed. None of those models are applicable enough to be used in the real world situations. Another important feature of our models is considering the time when those defective items are removed from the inventory. One of the most valuable managerial insights of our study is that when production cost and inspection cost as well as holding cost of defective items are equal to zero the results can not be same as the real world situations, as it can be seen that in such cases when defective rate increases the optimal cost decreases (instead of increasing). But when one of production and inspection costs or holding cost of imperfect items are involved the results can model the real system accurately. Another managerial insight is that as the defective rate increases optimum cycle length, best lot quantity and total cost increase. Also case I can be suitable for very small factories that remove the imperfect items when they are discovered or the firms that produce medical items and have to remove defective products as soon as possible. Many other firms can not do the same thing and are forced to keep those items until the end of the production cycle to be reworked or the end of the inventory cycle to be scrapped or sold with a lower price.

7 Conclusions and future directions of research

In this research, we proposed EPQ models with a power demand rate dependent production rate, allowing for shortages completely backordered and defective items. Three cases are considered for the inventory system regarding to the date that defective items are drawn from inventory. In the first case, we suppose that a defective item is eliminated from inventory at the time when it is recognized. In the second and third situations, it is assumed that the items with imperfect quality are kept in stock and sold in each cycle, after ending the replenishment and the inventory cycles respectively. The optimum solutions obtained by the mathematical models are unique and easily calculated by the proposed algorithm. When imperfect items, the holding cost of defective items, inspection and production costs are not considered, the optimal inventory policies consist of the formulate obtained by [24]. One possible extension to the current paper can be considered for rework process in the inventory system. Moreover, a deterioration rate can be considered in the model. Another research can study inventory systems with assuming that shortages are lost sales or partially backorderd. Finally, one can also consider the situation where demand depends on the price of the products. Also we suggest to incorporate the concept of this work as potentials extension to the problems or models suggested by other researchers [51,52,53].