A Production: Inventory Model for Defective Items with Shortages Incorporating Inflation and Time Value of Money

Abstract

This paper develops a production-inventory model of a single product with imperfect production process in which inflation and time value of money are considered under shortages. Demand rate has been considered to be a function of quadratic decreasing and exponential decreasing of selling price. The selling price of a unit is determined by a mark-up over the production cost. Unit production cost is considered incorporating several features like energy and labour cost, raw material cost, replenishment rate and other factors of the manufacturing system. The defective items which is a certain fraction of the total production or a random number are either reworked or refunded if those reach to the customer. Two scenarios have been considered in which defective items are refunded from the customer with penalty in scenario (a) and the defective items are repaired and sold to the customer as good items in scenario (b). Based on these two scenarios, three models have been developed in which defective items are certain fraction of the produced quantity in Model-I, a random number in Model-II, and are dependent in reliability parameter and time in Model-III. Considering all these phenomena optimum production of the product has been evaluated to have maximum profit. Finally, numerical examples are given to illustrate the results along with graphical analysis. Sensitivity analysis has also been carried out for different values of the parameter.

Introduction

In the manufacturing system, a production process is not always completely perfect and as a result of which some defective items may be produced from the very beginning of the production. In that case defective items are certain fraction of the total production. Again on the other hand, all the produced items may be non-defective at the beginning of the production process but as long as the production continues, the production process deteriorates with time. In that case, defective items are random number. These defective items are either repaired or refunded if they reach to the customer. Lee and Park [1], Urban [2], Lin [3], Rosenblatt and Lee [4], Lee and Rosenblatt [5] developed an EPL model of this type of production process. Sana et al. [6, 7] developed an EMQ model in an imperfect production system in which defective items are sold at a reduced price. Then several research works have been done on imperfect production process and defective items [8–11].

Recently, Mondal et al. [12] developed an inventory model for defective items with variable production cost. But in this paper shortages and time-value of money were not taken into account. So, in this paper we have developed an EPL model of defective items considering shortages, inflation and time-value of money (Table 1).

Table 1 Brief literature review

In this model demand has been considered as quadratic and exponential decreasing function of selling price. The selling price of a product is one of the important factors in the present competitive market situation. It has been seen in case of defective goods whose demand is mainly price dependent that higher selling price negates the demand whereas lower selling price has a reverse effect. Whitin [13] first considered the effect of price dependent demand in an inventory model. Then many researchers have worked in this area [14–17]. Recently, Maiti et al. [18] developed a production-inventory with stochastic lead-time where price dependent demand was considered. Different types of demand like stock dependent and time varying demand have also been considered in several research work [19–23].

Again many EOQ models do not take into account the effects of inflation and time-value of money. So the time-value of money which plays an important role, can not be ignored in the present economic situation. Buzacott [24] was the first who had included the idea of inflation in inventory literature. Misra [25], Van Hees and Monhemius [26], Bierman and Thomas [27], Sarkar and Pan [28] also have worked in this direction. Other notable paper in this direction are Hariga [29], Cheung [30], Chung, Liu and Tsai [31].

Again, in the present economic situation, shortage of the items takes an important role. Chandra and Bahner [32] established an inventory model for deteriorating items with shortages and linear time-dependent demand in which time-value of money was considered. Again several research work in the direction of probabilistic deterioration have been done by many researcher [33, 34]. Bose, Goswami and Chaudhuri [35], Dohi, Kaio and Osaki [36], Chen [37], Wee and Law [38] also developed the inventory model in which shortages were taken into consideration. Datta and Pal [39], Bose et al. [40] developed inventory model considering effect of inflation and shortages. Roy and Chaudhuri [41] analysed a finite time-horizon deterministic EOQ model with stock dependent demand and effect of inflation and allowing shortages in all cycles. Sarkar et al. [42] developed an inventory model with finite replenishment rate where price discount offer was considered. Some recent works in this area are given by [43–50] (Table 2).

Table 2 Some recent works in the area of defective items and imperfect production

Notations and Assumptions

This paper is developed with the following Notations and Assumptions.

• Notations:

p::

Selling price per unit item.

D(p)::

Demand rate which is a function of selling price.

P::

Production rate (a decision variable).

f(P)::

Unit production cost.

A::

Advertisement cost per unit item.

$c_{r}$::

Raw material cost.

L::

Labour charges.

S::

Maximum stock level.

$S_{1}$::

Maximum shortage.

$c_{h}$::

Inventory carrying cost per unit quantity per unit time.

$c_{0}$::

Set up cost which is known and constant.

q(t)::

Stock level at time t.

Q::

Number of produced units(a decision variable).

M(Q, P)::

Average profit per unit time for a cycle.

$P_{1}$::

Total number of defective items.

$\mu$::

Scaling parameter for defective items.

$\frac{1}{m}$::

Mean of exponential distribution.

$t_{1}$::

Time upto which the production is made i.e. after $t=t_{1}$ the production is discontinued.

$t_{2}$::

Time at which stock level falls to zero due to demand.

$t_{3}$::

Time at which shortages reach to the level $S_{1}$.

T::

Time at which stock level is again zero i.e. one cycle time.

$\gamma$::

r-i, r is the interest rate per unit currency and i is the inflation rate per unit currency.

$\psi$::

Product reliability parameter.

• Assumptions:

• (a) The demand rate D(p) is deterministic function of selling price p. It is either quadratic decreasing or exponential decreasing function of selling price p. $D(p)=a-bp-cp^{2}$, where $a,b,c>0$ and $D(p)=d \times p^{-k}$, $d,k>0$.

• (b) The unit production cost $f(P)=c_{r}+A+\frac{L}{P^{\alpha }}+KP^{\beta }$, where K is a positive constant and $\alpha ,\beta$ are chosen to provide the feasible solution of the model.

• (c) The defective items are fraction of the produced items in first and third model and a random number for the second model.

• (d) Selling price p is determined by a mark-up over the unit production cost f(P). i.e. $p= {\uplambda }f(P)$, ${\uplambda }>1$ where ${\uplambda }$ is the mark-up.

• (e) Lead time is assumed to be zero.

Development of the Model and Analysis

The defective items are either reworked or refunded if those are sold to the customer. Under these circumstances, we investigate the following two scenarios:

Scenario (a): Q units are to be produced. All produced items including the defective items are sold to the customers at the rate of D units as good units and later $P_{1}$ defective items are refunded from the customer with penalty at a cost of $c_{v}$ per unit.

Scenario (b): Q units are produced and $P_{1}$ defective items are spotted just after the production. Those are repaired against the cost of $c_{\theta }$ per unit and sold as good items to the customer.

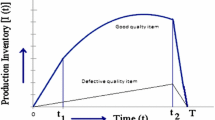
At $t=0$, the stock level is zero and then the variable production starts to produce items at a rate P units per unit time. The production stops at $t=t_{1}$. As the production rate is greater than demand rate, some units are accumulated during the interval $0 \le t \le t_{1}$. At $t=t_{1}$, the inventory level reaches to the maximum stock level S. After $t=t_{1}$, the stock level decreases due to demand only and at $t=t_{2}$ it falls to zero. Then shortages start and are accumulated to the level $S_{1}$ at $t=t_{3}$. After $t=t_{3}$ the production starts again. Fresh production and supply to the consumers occur simultaneously during the interval $t_{3} \le t \le t_{4}$. The whole backlog is cleared by the time $t=t_{4}$ and the stock level is again zero at $t=t_{4}$. The graphical representation of the model is given by Fig. 1.

Fig. 1

Graphical representation of Model

Hence under the above assumptions, the differential equation satisfied by q(t) at time t can be represented as:

$$\begin{aligned} \frac{dq(t)}{dt}= & {} P-D ,\quad 0 \le t \le t_{1} \end{aligned}$$

(1)

$$\begin{aligned} \frac{dq(t)}{dt}= & {} - D ,\quad t_{1} \le t \le t_{2} \end{aligned}$$

(2)

$$\begin{aligned} \frac{dq(t)}{dt}= & {} - D ,\quad t_{2} \le t \le t_{3} \end{aligned}$$

(3)

$$\begin{aligned} \frac{dq(t)}{dt}= & {} P-D ,\quad t_{3} \le t \le T \end{aligned}$$

(4)

with initial and boundary condition

$$\begin{aligned} q(0)=q(t_{2})=q(T)=0 ,\quad q(t_{1})= S ,\quad q(t_{3})= -S_{1}. \end{aligned}$$

(5)

From (1) and (2), we have

$$\begin{aligned} S=Q-D\frac{Q}{P}\quad \left[ since\quad t_{1}=\frac{Q}{P}\right] \end{aligned}$$

(6)

and

$$\begin{aligned} t_{2}=\frac{Q}{D} \end{aligned}$$

(7)

From (3) and (4), we have

$$\begin{aligned} S_{1}=Q-D\frac{Q}{P}\quad [since\quad t_{3}=T-t_{1}] \end{aligned}$$

(8)

and

$$\begin{aligned} T=2\frac{Q}{D} \end{aligned}$$

(9)

The present-value of total revenue is

$$\begin{aligned} C_{REV}= & {} \int _{0}^{T}pDe^{-\gamma t}dt\nonumber \\= & {} \frac{1}{\gamma }pD(1-e^{-\gamma T}) \end{aligned}$$

(10)

The present-value of production cost is

$$\begin{aligned} C_{PRO}= & {} \int _{0}^{T}f(P)De^{-\gamma t}dt\nonumber \\= & {} \frac{f(P)D}{\gamma }(1-e^{-\gamma T}) \end{aligned}$$

(11)

The present-value of holding cost is

$$\begin{aligned} C_{HOL}= & {} \frac{1}{2}\int _{0}^{t_{2}}c_{h}Se^{-\gamma t}dt\nonumber \\= & {} \frac{c_{h}S}{2 \gamma }(1-e^{-\gamma t_{2}}) \end{aligned}$$

(12)

The present-value of set-up cost is

$$\begin{aligned} C_{SET}= & {} \int _{0}^{T}\frac{c_{0}D}{Q}e^{-\gamma t}dt\nonumber \\= & {} \frac{c_{0}D}{\gamma Q}(1-e^{-\gamma T}) \end{aligned}$$

(13)

The present-value of shortage cost is

$$\begin{aligned} C_{SHO}= & {} \frac{1}{2}\int _{0}^{T-t_{2}}c_{s}(-S_{1})e^{-\gamma t}dt\nonumber \\= & {} -\frac{c_{s}S_{1}}{2 \gamma }(1-e^{-\gamma (T-t_{2})}) \end{aligned}$$

(14)

The present-value of refund cost is

$$\begin{aligned} C_{REF}= & {} \int _{0}^{T}c_{v} \mu P^{\delta -1}De^{-\gamma t}dt\nonumber \\= & {} \frac{c_{v} \mu P^{\delta -1}D}{\gamma }(1-e^{-\gamma T}) \end{aligned}$$

(15)

The present-value of rework cost is

$$\begin{aligned} C_{REW}= & {} \int _{0}^{T}c_{\theta } \mu P^{\delta -1}De^{-\gamma t}dt\nonumber \\= & {} \frac{c_{\theta } \mu P^{\delta -1}D}{\gamma }(1-e^{-\gamma T}) \end{aligned}$$

(16)

Model-I : Defective items are a certain fraction of the produced quantity:

Scenario (a): The total profit incorporating inflation and time-value of money is given by

$$\begin{aligned} M\left( Q, P\right)= & {} \frac{1}{\gamma } \left( pD-f\left( P\right) D-c_{0}\frac{D}{Q}- \mu c_{v}P^{\delta -1}D\right) \left( 1-e^{-\gamma T}\right) -\frac{1}{2 \gamma }c_{h}Q\nonumber \\&\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma t_{2}}\right) +\frac{1}{2 \gamma }c_{s}Q\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma \left( T-t_{2}\right) }\right) \end{aligned}$$

(17)

Scenario (b): The total profit incorporating inflation and time-value of money is given by

$$\begin{aligned} M\left( Q, P\right)= & {} \frac{1}{\gamma } \left( pD-f\left( P\right) D-c_{0}\frac{D}{Q}- \mu c_{\theta }P^{\delta -1}D\right) \left( 1-e^{-\gamma T}\right) -\frac{1}{2 \gamma }c_{h}Q\nonumber \\&\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma t_{2}}\right) +\frac{1}{2 \gamma }c_{s}Q\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma \left( T-t_{2}\right) }\right) \end{aligned}$$

(18)

Model-II : Number of defective items is random:

Let the time $\tau$ at which in-control state changes to a out-control state is a random variable and follows exponential distribution with mean $\frac{1}{m}$. So the number of defective items is a random variable and is given by

$$\begin{aligned} X(t_{1})= & {} 0\quad if\quad \tau \ge t_{1}\nonumber \\= & {} \alpha _{1}P(t_{1}-\tau )\quad if\quad \tau <t_{1} \end{aligned}$$

(19)

So the expected number of total defective item is given by

$$\begin{aligned} P_{1}= & {} E[X(t_{1})]\nonumber \\= & {} \alpha _{1}P\left\{ \left( t_{1}+\frac{1}{m}e^{-mt_{1}}\right) -\frac{1}{m}\right\} , t_{1}=\frac{Q}{P} \end{aligned}$$

(20)

Scenario (a): The expected average profit M(Q, P) is given by

$$\begin{aligned} M\left( Q, P\right)= & {} \frac{1}{\gamma } \left[ pD-f\left( P\right) D-c_{0}\frac{D}{Q}-c_{v}\left\{ \alpha _{1}P\left( \frac{Q}{P}+\frac{1}{m}e^{-\frac{mQ}{P}}-\frac{1}{m}\right) D\right\} /Q\right] \nonumber \\&\left( 1-e^{-\gamma T}\right) -\frac{1}{2 \gamma }c_{h}Q\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma t_{2}}\right) +\frac{1}{2 \gamma }c_{s}Q\left( 1-\frac{D}{P}\right) \nonumber \\&\left( 1-e^{-\gamma \left( T-t_{2}\right) }\right) \end{aligned}$$

(21)

Scenario (b): The expected average profit M(Q, P) is given by

$$\begin{aligned} M\left( Q, P\right)= & {} \frac{1}{\gamma } \left[ pD-f\left( P\right) D-c_{0}\frac{D}{Q}-c_{\theta }\left\{ \alpha _{1}P\left( \frac{Q}{P}+\frac{1}{m}e^{-\frac{mQ}{P}}-\frac{1}{m}\right) D\right\} /Q\right] \nonumber \\&\left( 1-e^{-\gamma T}\right) -\frac{1}{2 \gamma }c_{h}Q\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma t_{2}}\right) +\frac{1}{2 \gamma }c_{s}Q\left( 1-\frac{D}{P}\right) \nonumber \\&\left( 1-e^{-\gamma \left( T-t_{2}\right) }\right) \end{aligned}$$

(22)

Model-III : Defective items are dependent on reliability parameter $\psi$ and time t:

The amount of defective items produced at time t is $\eta e^{\psi t }P$ where $\eta e^{\psi t}<1$. Since the fraction $\eta e^{\psi t}$ increases with time t and $\psi$ simultaneously, so in this system the production of defective items increase with increase of time. It has been seen, after a certain time almost all manufacturing system undergoes unsatisfactory performance. So, in long production run process, the system shifts in-control state to a out-control state during malfunctioning. As a result percent of defective items increase with time t. Again, lower value of $\psi$ decrease the percent of defective items. For that reason, the defective items at time t has been considered as $\eta e^{\psi t}P$.

Therefore, the present-value of refund cost is

$$\begin{aligned} C_{REF}= & {} \int _{0}^{T}c_{v} \eta e^{\psi t}De^{-\gamma t}dt\nonumber \\= & {} \frac{c_{v}\eta D}{\gamma -\psi }(1-e^{(\psi -\gamma ) T}) \end{aligned}$$

(23)

Therefore, the present-value of rework cost is

$$\begin{aligned} C_{REF}= & {} \int _{0}^{T}c_{\theta } \eta e^{\psi t}De^{-\gamma t}dt\nonumber \\= & {} \frac{c_{\theta }\eta D}{\gamma -\psi }(1-e^{(\psi -\gamma ) T}) \end{aligned}$$

(24)

Scenario (a): The total profit M(Q, P) is given by

$$\begin{aligned} M\left( Q, P\right)= & {} \frac{1}{\gamma } \left[ pD-f\left( P\right) D-c_{0}\frac{D}{Q}\right] \left( 1-e^{-\gamma T }\right) -\frac{1}{2 \gamma }c_{h}Q\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma t_{2}}\right) \nonumber \\&+\frac{1}{2 \gamma }c_{s}Q\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma \left( T-t_{2}\right) }\right) -\frac{c_{v}\eta D}{\gamma -\psi }\left( 1-e^{\left( \psi -\gamma \right) T}\right) \end{aligned}$$

(25)

Scenario (b): The total profit M(Q, P) is given by

$$\begin{aligned} M\left( Q, P\right)= & {} \frac{1}{\gamma } \left[ pD-f\left( P\right) D-c_{0}\frac{D}{Q}\right] \left( 1-e^{-\gamma T }\right) -\frac{1}{2 \gamma }c_{h}Q\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma t_{2}}\right) \nonumber \\&+\frac{1}{2 \gamma }c_{s}Q\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma \left( T-t_{2}\right) }\right) -\frac{c_{\theta }\eta D}{\gamma -\psi }\left( 1-e^{\left( \psi -\gamma \right) T}\right) \end{aligned}$$

(26)

Numerical Examples

To illustrate the proposed model-1, model-2 and model-3 we consider the following examples given below.

Example-1 of model-1: Let us take $D(p)= a-bp-cp^{2}$ and the parameter values in the inventory system are $c_{0} = \$100$, $c_{h}= \$3$, $c_{s} = \$2$, $c_{r}= \$50$, $a =100$, $b=$ 0.3 $\alpha = 0.7$, $\beta \,=$  1.5, $c_{v} \,=$  200, ${\uplambda }\,=\,$ 1.2, $A \,=$  $50, $\mu \,=$  0.08, $\gamma \,=$  0.02, $L\,=$  $1500, $K\,=$  0.01, $\delta \,=$  0.8, $c\,=$  0.001, in appropriate units. The optimal solution is $P^{*}\,=$  159.811, $Q^{*}\,=\, 80.2984$, and maximum expected average profit is $M\,=\,1637.74$ (Fig. 2).

Fig. 2

Maximum total profit M(Q, P) versus Q and P of Example-1(Model-1)

Example-2 of model-1: Let us take $D(p)\,=\, d\times p^{-k}$ and the parameter values in the inventory system are $c_{0} \,=$ $100, $c_{h} \,=$  $3, $c_{s} \,=$  $2, $c_{r} \,=$  $50, $d \,=$  20000,$k\,=$  1.6 $\alpha \,=$  0.7, $\beta \,=$  1.5, $c_{v} \,=$  200, ${\uplambda }\,=$  1.2, $A \,=$  $50, $\mu \,=$  0.08, $\gamma \,=$  0.02, $L\,=$  $1500, $K\,=$  0.01, $\delta \,=$  0.8, in appropriate units. The optimal solution is $P^{*}\,=$  478.359, $Q^{*}\,=\, 88.9129$, and maximum expected average profit is $M\,=\,2678.58$ (Fig. 3).

Fig. 3

Maximum total profit M(Q, P) versus Q and P of Example-2(Model-1)

Example-1 of model-2: Let us take $D(p)\,=\, a-bp-cp^{2}$ and the parameter values in the inventory system are $c_{0} \,=$  $100, $c_{h} \,=$  $3, $c_{s} \,=$  $2, $c_{r} \,=$  $50, $a \,=$  200,$b\,=$   0.7 $\alpha \,=$  0.7, $m\,=$  0.08, $\alpha _{1} \,=$  0.001, $\beta \,=$  1.5, $c_{v} \,=$  200, ${\uplambda }\,=$  1.2, $A \,=$  $50, $\gamma \,=$  0.01, $L\,=$  $1500, $K\,=$  0.01, $\delta \,=$  0.8, $c\,=$  0.001, in appropriate units. The optimal solution is $P^{*}\,=$  154.575, $Q^{*}\,=$  1081.71, and maximum expected average profit is $M\,=\,30469.9$ (Fig. 4).

Fig. 4

Maximum expected average profit M(Q, P) versus Q and P of Example-1(Model-2)

Example-2 of model-2: Let us take $D(p)= d\times p^{-k}$ and the parameter values in the inventory system are $c_{0} = \$100$, $c_{h} = \$3$, $c_{s} = \$2$, $c_{r} = \$50$, $d = 20000,k= 1.6$, $\alpha = 0.7$, $m= 0.08$, $\alpha _{1} = 0.001$, $\beta = 1.5$, $c_{v} = 200$, ${\uplambda }= 1.2$, $A = \$50$, $\gamma =0.01$, $L=\$1500$, $K=0.01$, in appropriate units. The optimal solution is $P^{*}= 64.704$, $Q^{*}= 156.406$, and maximum expected average profit is $M= 4879.64$ (Fig. 5).

Fig. 5

Maximum expected average profit M(Q, P) versus Q and P of Example-2 (Model-2)

Example-1 of model-3: Let us take $D(p)= a-bp-cp^{2}$ and the parameter values in the inventory system are $c_{0} = \$100$, $c_{h} = \$3$, $c_{s} = \$2$, $c_{r} = \$50$, $a = 200$,$b= 0.7$, $\alpha = 0.7$, $\beta = 1.5$, $c_{v} = 200$, ${\uplambda }= 1.2$, $A = \$50$, $\eta =0.09$, $\psi =0.05$, $\gamma =0.01$, $L=\$1500$, $K=0.01$, $c=0.001$, in appropriate units. The optimal solution is $P^{*}= 159.276$, $Q^{*}= 57.6545$, and maximum expected average profit is $M= 1608.07$ (Fig. 6).

Fig. 6

Maximum total profit M(Q, P) versus Q and P of Example-1(Model-3)

Discussion

In scenario (a) and scenario (b) of model-1, the system with free from defective items ($\mu =0$) gives more profit than the system with defective items ($\mu \ne 0$). Again in defective production system, the amount of profit decreases as $\delta$ changes from 0.8 to 1.0 (Table 3)

Table 3 The optimal solution of model-1 for different values of $\mu$ and $\delta$ in Example-1 and Example-2

In case of model-2 with random defective items, for all scenarios, profit is less when mean of the exponential distribution is less i.e. profit with $m=0.08$ is more than the profit with $m=0.4$. But the change in profit with mean is very slow (Table 4).

Table 4 The optimal solution of model-2 for different values of m in Example-1 and Example-2

In case of model-3 for all scenarios the profit decreases as the reliability parameter $\eta$ changes from 0.05 to 0.08. Therefore lower value of $\eta$ gives more profit (Table 5).

Table 5 The optimal solution of model-3 for different values of $\eta$ and $\psi$ in Example-1

Sensitivity Analysis

The sensitivity of the maximum total profit is examined due to changes in production rate and price mark-up. To illustrate the result, it has been shown only for Model-1 (Example-1), scenario-(a).

Figure 7 shows that total profit increases with the production rate P and it attains maximum value $1637.74 at $P=159.811$ when $Q=80.3$.

Fig. 7

Maximum total profit M versus production rate P

From Fig. 8 it is observed that unit production cost is minimum i.e. Rs. $163.212 at production rate $P= 159.337$. It is interesting to note that at $P=159.811$ unit production cost is not minimum.

Fig. 8

Unit production cost f versus production rate P

Figure 9 represents maximum total profit versus price mark-up ${\uplambda }$. Normally, profit increases with the increase of price mark-up. From Fig. 9, it is observed that the profit is maximum when the price mark-up is 1.17 and the profit decreases as price mark-up is more than 1.17 because demand decreases with increase of selling price. Again sensitivity to the different changes of parameters are observed in Table 6.

Fig. 9

Maximum total profit M versus price mark-up

Table 6 Effects of $c_0 , c_h , c_s ,\gamma$ and L on profit in Example-1 (Model-I)

Conclusions

In this paper, we have extended Mondal et al. [7] EPL model for defective items considering shortages, inflation and time-value of money. Again, in this model different types of demand like quadratic decreasing and exponential decreasing function of selling price have been considered.

This model could be extended in fuzzy and fuzzy-stochastic environment taking demand, defective items and other inventory parameters to be imprecise.

Appendix

Theorem: The profit function M(Q, P) possess a maximum solution.

Proof:

$$\begin{aligned} M\left( Q, P\right)= & {} \frac{1}{\gamma } \left( pD-f\left( P\right) D-c_{0}\frac{D}{Q}- \mu c_{v}P^{\delta -1}D\right) \left( 1-e^{-\gamma T}\right) -\frac{1}{\gamma }c_{h}Q\nonumber \\&\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma t_{2}}\right) +\frac{1}{\gamma }c_{s}Q\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma \left( T-t_{2}\right) }\right) \nonumber \\ \frac{\partial M\left( Q, P\right) }{\partial Q}= & {} \frac{c_{0}D}{\gamma Q^{2}}\left( 1-e^{-\gamma T}\right) +\left( pD-f\left( P\right) D-c_{0}\frac{D}{Q}- \mu c_{v}P^{\delta -1}D\right) \frac{2e^{-\gamma T}}{D}\nonumber \\&-\frac{1}{\gamma }c_{h}\left( 1-\frac{D}{P}\right) \left( 1-e^{-\gamma t_{2}}\right) -\frac{1}{D}c_{h}Q\left( 1-\frac{D}{P}\right) e^{-\gamma t_{2}}+\frac{1}{\gamma }c_{s}\left( 1-\frac{D}{P}\right) \nonumber \\&\left( 1-e^{-\gamma \left( T-t_{2}\right) }\right) + \frac{1}{D}c_{s}Q\left( 1-\frac{D}{P}\right) e^{-\gamma \left( T-t_{2}\right) }=0 \end{aligned}$$

(27)

We first obtain second order derivative of M(Q, P) and using (36) we have

$$\begin{aligned} \frac{\partial ^{2} M\left( Q, P\right) }{\partial Q^{2}}= & {} -2\frac{c_{0}D}{\gamma Q^{3}}\left( 1-e^{-\gamma T}\right) +\frac{4c_{0}}{Q^{2}}e^{-\gamma T}-\frac{4 \gamma e^{-\gamma T}}{D^{2}}\left( pD-f\left( P\right) D-c_{0}\frac{D}{Q}\right. \\&\left. - \mu c_{v}P^{\delta -1}D\right) -\frac{2c_{h}}{D}\left( 1-\frac{D}{P}\right) e^{-\gamma t_{2}}+\frac{\gamma c_{h}Q}{D^{2}}\\&\left. \left( 1-\frac{D}{P}\right) e^{-\gamma t_{2}}+\frac{3c_{s}}{D}\left( 1-\frac{D}{P}\right) e^{-\gamma \left( T-t_{2}\right) }\right) - \frac{\gamma c_{s}Q}{D^{2}}\left( 1-\frac{D}{P}\right) e^{-\gamma \left( T-t_{2}\right) }\\= & {} -\frac{2c_{0}}{Q^{2}}\left( \frac{D}{\gamma Q}-\frac{D}{\gamma Q}e^{-\gamma T}-e^{-\gamma T}\right) -\frac{1}{D}\left( 1-\frac{D}{P}\right) \left( 2c_{h}+\frac{\gamma c_{h}Q}{D}e^{-\gamma t_{2}}-\right. \\&\left. c_{s}\left( 2+e^{-\gamma t_{2}}\right) -\frac{\gamma c_{s}Q}{D}e^{-\gamma \left( T-t_{2}\right) }-\frac{2c_{0}D}{Q^{2}\left( 1-\frac{D}{P}\right) }\right) \\= & {} -\frac{2c_{0}}{Q^{2}}X-\frac{1}{D}\left( 1-\frac{D}{P}\right) Y<0 \end{aligned}$$

provided $X=(\frac{D}{\gamma Q}-\frac{D}{\gamma Q}e^{-\gamma T}-e^{-\gamma T})>0$ and $Y=(2c_{h}+\frac{\gamma c_{h}Q}{D}e^{-\gamma t_{2}}-c_{s}(2+e^{-\gamma t_{2}})-\frac{\gamma c_{s}Q}{D}e^{-\gamma (T-t_{2})}-\frac{2c_{0}D}{Q^{2}(1-\frac{D}{P})})>0$

$$\begin{aligned} \frac{\partial M\left( Q, P\right) }{\partial P}= & {} \frac{1}{\gamma }\left( -\frac{\alpha LD}{P^{\alpha +1}}+K \beta D P^{\beta -1}-\mu c_{v}\left( \delta -1\right) P^{\delta -2}D\right) \left( 1-e^{-\gamma T}\right) \nonumber \\&-\frac{c_{h}QD}{\gamma P^{2}}\left( 1-e^{-\gamma t_{2}}\right) +\frac{1}{\gamma }\frac{c_{s}QD}{P^{2}}\left( 1-e^{-\gamma \left( T-t_{2}\right) }=0\right) \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial ^{2} M(Q, P)}{\partial P^{2}}= & {} \frac{1}{\gamma }\left( -\frac{\alpha (\alpha +1) LD}{P^{\alpha +2}}-K \beta (\beta -1) D P^{\beta -2}-\mu c_{v}(\delta -1)(\delta -2)\right. \\&\left. P^{\delta -3}D\right) (1-e^{-\gamma T})-\frac{2c_{h}QD}{\gamma P^{3}}(1-e^{-\gamma t_{2}})-\frac{2c_{s}QD}{\gamma P^{3}}(1-e^{-\gamma (T-t_{2})})\\= & {} -\frac{1}{\gamma }K \beta (\beta -1) D P^{\beta -2}(1-e^{-\gamma T})-\frac{1}{\gamma }\mu c_{v}(\delta -1)(\delta -2)P^{\delta -3}D\\&(1-e^{-\gamma T})-\frac{2c_{s}QD}{\gamma P^{3}}(1-e^{-\gamma (T-t_{2})})-\frac{D}{\gamma P^{3}}\left\{ \frac{\alpha (\alpha +1)L}{P^{\alpha -1}}-\right. \\&\left. 2c_{h}Q(1-e^{-\gamma t_{2}})\right\} <0 \end{aligned}$$

provided $B= \frac{\alpha (\alpha +1)L}{P^{\alpha -1}}-2c_{h}Q(1-e^{-\gamma t_{2}})>0$

$$\begin{aligned} \frac{\partial ^{2} M(Q, P)}{\partial Q\partial P}= & {} -\frac{D}{\gamma P^{2}}\left\{ c_{h}(1-e^{-\gamma t_{2}})-c_{s}(1-e^{-\gamma (T-t_{2})})\right\} <0 \end{aligned}$$

provided $C=c_{h}(1-e^{-\gamma t_{2}})-c_{s}(1-e^{-\gamma (T-t_{2})})>0$

Hence M(Q, P) has a maximum with respect to Q and P if $\frac{\partial ^{2} M(Q, P)}{\partial Q^{2}}<0$ and $\frac{\partial ^{2} M(Q, P)}{\partial Q^{2}}\frac{\partial ^{2} M(Q, P)}{\partial P^{2}}-\frac{\partial ^{2} M(Q, P)}{\partial Q \partial P}>0$

For our numerical data the above conditions are satisfied and therefore the profit function has a maximum solution.