Optimal production run time for an imperfect production inventory system with rework, random breakdowns and inspection costs

Abstract

In real-life manufacturing systems, the presence of defective products in a lot is inevitable. While these products may be just scrapped in the food industry, in high-tech industries where the final product is very expensive, they may be reworked at a cost. A common assumption in the literature is that the inspection time needed to identify defective items is completed when the production process ends. However, the assumption of continuous inspection during production complicates the analysis, making it impractical for most production systems, especially when the production rate is high, and the proportion of defective items is low, making continuous inspection during production very expensive. In addition, such factors as process deterioration or other uncontrollable factors in the production process may interrupt the production of the lot. To address these practical issues, this paper integrates inspection time and the failure of production facilities into an imperfect production inventory model with rework, where the production run time is a decision variable and an inspection process continues even after a production run; the paper demonstrates significant effects on the optimal solutions, with shortages not allowed. Under these assumptions, a mathematical model is derived, and the concavity of the expected total profit function is proved. Optimal policy is obtained by applying the analytic method. Special cases of the model are studied and a numerical example with sensitivity analysis is provided to draw insights. Moreover, this numerical example is used to compare general and special cases.

1 Introduction

Increasing the efficiency of production, meeting customers’ expectations, and minimizing total costs are some of manufacturers’ principal targets. To meet these targets, each business adopts its own policy for inventory control, depending on its field of activity. The economic production quantity (EPQ) model is one of the commonly used inventory control techniques investigated and developed by many researchers. The classical EPQ model was developed under several assumptions, some of which are rarely met. This model is used when the production process operates perfectly during a production run; hence, the possibility of defective products or failure in the production facilities is excluded from the model. Delivering high-quality products and good customer service can always attract customers and ensure repeat business but, unfortunately, in most manufacturing systems, the production process is rarely perfect. In practice, the production process moves between ‘in-control’ (zero-defect) and ‘out-of-control’ states at random times, for various unpredictable reasons, such as inadequate maintenance, and ineffective production control, leading to creation of occasional defective products which need to be separated through an inspection process. Thus, for a realistic production model, it is necessary to consider what Tai (2013) refers to as ‘imperfect production’.

Recently, many researchers have investigated the effects of the presence of defective products on inventory models. The first model for defective products, developed by Shih (1980), included an additional issue of possible stock-out due to excess demands and defective products. Gupta and Chakraborty (1984) developed a production-inventory model to obtain the optimal batch quantity, in which recycling takes place only from the last stage to the first stage. Porteus (1986) showed that a production process could go out-of-control with a given probability each time it produces defective items and investigated different options of investing in quality improvement and setup cost reduction. Zhang and Gerchak (1990) also studied the impact of inspection costs on the lot size in an EOQ model, in which a random proportion of items are defective. Rosenblatt and Lee (1986) analysed an imperfect production system in which the system deteriorates during the production process and produces some defective items. Having assumed an exponential process shift, they found that the optimal production quantity is smaller than that for the classical EPQ problem. Liu and Yang (1996) studied a lot-sizing problem in a single-stage imperfect production system. They assumed that the production system would generate two types of defective items; namely, reworkable products and non-reworkable products. They further assumed that each lot is subject to a fully automated inspection where inspection times are negligible. Other studies investigating optimal production/ordering lot sizing with a random processing rate include Salameh and Jaber (2000), Chung and Hou (2003), Maddah et al. (2009) and Hsu and Hsu (2015). An excellent review of research areas was given by Khan et al. (2011). More recently, Mokhtari (2018) devised an EPQ model for determining the optimal duration of a production run and the most efficient lot size for a batch-produced item in an imperfect production system.

Inspection is an essential tool for ensuring the quality of items ordered or produced. It is defined as ‘‘the process of measuring, examining, testing, or otherwise comparing the unit to applicable requirements” (Suntag 1993). However, previous studies of imperfect production inventory usually assume that inspection takes place during production (Chiu 2003; Li et al. 2015). Such continuous inspection during production, however, is not achievable in most production systems, especially with a low proportion of defective items and a high rate of production; in-production inspection in such circumstances would be very expensive. The decision to implement an inspection procedure and when to do so is a key part of any production process, together with the decision of how to deal with defective items—by reworking or discarding, for example. All of these decisions affect inventory calculations, making it essential to understand the interrelationship of production, inventory and inspection for the successful management of production and inventory systems (Lee and Rosenblatt 1987; Giri and Dohi 2006; Lin and Lin 2007; Chakraborty and Giri 2014; Wee et al. 2014).

Ma et al. (2010) suggested three models to handle decisions of whether and when to implement a screening process, assuming negligible restoration time and cost. They based their proposal on adapting the classical EMQ model to accommodate imperfect production process. Their models considered three common inspection strategies; namely, no screening, after-production screening, and in-production screening. In the first model, no inspection is carried out. If any defective items are found, they are scrapped immediately. In the second model, all items are checked immediately after a production run, assuming that items can be screened faster than they are produced. Defective items are retained and scrapped together at the end of the screening process. In the third model, a full inspection is carried out during the production run time. Any defective items which are found are retained till the end of the run and then scrapped as a batch. From their numerical results, they deduced that the first model, i.e., with no screening, offered the lowest cost provided that the defective products were a small proportion of the lot. The second most cost-effective method was the in-production method, but with screening continuing after the completion of the run. These results show that continuous inspection during production is not always the best approach to reduce the total cost.

Moussawi-Haidar et al. (2016) considered a manufacturing system with random supply process and an inspection process performed during and after a production run. The inspection process starts with the production and it continues after production, as it is assumed that only good items meet the demand; in other words, the inspection rate in-production equals the demand rate. Furthermore, the after-production inspection process must be shorter than the time required to consume good-quality products: thus, the after-production inspection rate is always higher than the demand rate. Two production inventory models are developed for defective items. In the first model, defective items are salvaged at a discounted price at the end of the inspection process. In the second model, these defective items are reworked at a cost at the end of the inspection process. In line with the work of Ma et al. (2010), each inspection process was associated with a different unit inspection cost, on the basis that in-production inspection involves higher unit inspection costs. However, there was a flaw in the work of Moussawi-Haidar et al. (2016) in relation to their model with reworking of defective items; Öztürk (2017) corrected this flaw and identified the conditions needed for an optimal solution.

The overwhelming majority of manufacturing companies face ever-increasing pressures to produce high-quality products at low costs. Nevertheless, it is inevitable that defective items are occasionally produced, which need to be reworked, scrapped or offered for sale at reduced prices. In practice, these defective items can sometimes be reworked to become serviceable items instead of being scrapped for economic reasons, as is the case in the semiconductor, glass and steel industries, thereby reducing the overall production costs significantly. For example, Hayek and Salameh (2001) analysed the case where the production system deteriorates during production and produces a random proportion of defective items; they considered reworking these defective items. The study by Chan et al. (2003) focused on providing a framework to integrate lower pricing, rework and reject situations into an EPQ model without shortages. Flapper et al. (2002) performed a review of the rework process in process industries. Flapper and Teunter (2004) considered a production system for a single product in which produced lots contain non-defective, reworkable defective or non-reworkable defective items, and in which reworkable defective items deteriorate as they are stored to be reworked, which affects the rework time and the rework cost. Optimal production lot size in a single-stage production inventory model is derived for two rework policies in the study of Jamal et al. (2004). Optimal batch size for a two-stage production system is determined in Inderfurth et al. (2006). The assumption in the first stage is that all items in a batch are produced, and good items populate the inventory to satisfy the demand, while, in the second stage, some of the defective items from the same batch are reworked. However, they deteriorate over time. Kontantaras et al. (2007) studied a production inventory system where each lot received contains some defective items. They investigated two options for the defective items: sell them to a secondary market as a single batch at a lower price or rework them at a cost to restore them to acceptable quality. Liu et al. (2009) developed mathematical models to determine the optimal number of production and rework setups in a cycle, and the optimal production quantity of each setup. Tsao et al. (2011) built on the classical EPQ model with the addition of reworking and trade credit assumptions. Wee et al. (2013) followed up the work of Cárdenas-Barrón (2009), replacing order size with production run time and backorder level with time to eliminate backorder as decision variables and analysing optimal policies under three conditions. Other studies investigating optimal lot sizing with rework include Glock and Jaber (2013a, b), Sarkar et al. (2014), Taleizadeh et al. (2017) and Nobil et al. (2018).

The classical EPQ problem has been investigated in recent years, and an increasing number of researchers analyse the effect of machine breakdowns on production inventory problems. In real industry, to minimize the negative effects of issues such as raw material shortages, quality defects or productivity losses on production line reliability, companies are strongly incentivized to invest in high-quality machines, highly skilled workers, and advanced maintenance technologies. Consequently, assumptions of reworking and disposal may be highly disruptive in a highly automated system. With this in mind, Bielecki and Kumar (1988) examined the conditions under which a zero-inventory policy is actually optimal for an unreliable manufacturing system. Although the machine’s operating time and repair time were random and had exponential distributions, they had different means. A similar manufacturing system in which the production operates under an (s, S) policy was explored by Sharafali (1984).

Groenevelt et al. (1992) investigated the effects of machine breakdowns and corrective maintenance on economic lot sizing decisions, and derived total cost function expressions for both a general failure distribution and the common case of exponential failures. Two production inventory control policies were proposed to deal with machine breakdown. The first of these assumes depletion of the on-hand inventory before the next cycle, instead of continued production of interrupted lots in case of a breakdown. This assumption was called ‘no-resumption (NR)’ policy. The second policy assumes immediate resumption of the production of interrupted lots in case of an on-hand inventory level below a specified threshold: this assumption was called ‘abort/resume (AR)’ policy. Note that these models did not consider setup and corrective maintenance as time-consuming operations.

Berg et al. (1994) studied a production system in which a number of machines needed to be repaired to become operational and which were prone to failure. Although the producing machines operated continuously, the production was stopped due to various factors, including costs, maintenance procedures, inventory capacity limit. Chung (1997) derived the upper and lower bounds for production lot size in the EPQ model proposed by Groenevelt et al. (1992).

Moinzadeh and Aggarwal (1997) studied an inventory system for an unreliable production setup subject to random disruptions, with constant production and demand rates. They assumed constant restoration times, exponential time between breakdowns, and allowed shortages. Abboud (1997) examined the ways machine breakdowns affect the classical EPQ model. The number of failures per production run is assumed to be Poisson distributed, while repair times are random, and shortages are not allowed. Liu and Cao (1999) considered a single-product production inventory system in which demand has a Poisson distribution and machine breakdown is possible. The model discussed in their paper was a type of fluid flow model. Boone et al. (2000) investigated the interaction between lot-sizing and imperfections in the production process, which involves process deterioration and a breakdown of the production process. Abboud (2001) analyzed an inventory model for a single machine that produces a single item, with production and demand rates that are known and constant. The machine is susceptible to random failures in operation, and repair times are also random. Chung (2003) showed that the average cost function per unit of time in the long-run, for exponential failure in the EPQ model with machine breakdown, is unimodal and that it is neither concave nor convex. They also derived a better lower bound for the optimal production lot size and the optimal safety stocks than those obtained in Chung (1997). Lin and Kroll (2006) investigated the effect of an imperfect production process subject to random breakdowns on the classical EPQ model. It is assumed that the elapsed time until breakdown is a random variable with exponential distribution. Chiu et al. (2007) determined the optimal production run time based on an EPQ model subject to stochastic machine breakdown with scrap and rework. It is assumed that a percentage of defective items are scrap, while the others are reworkable. The total cost functions were derived for both EPQ models with breakdown and without breakdown. Glock (2013) urged the researchers to assess their models more comprehensively instead of misleading operators with very restrictive assumptions designed for the model; and suggested an economically rational approach instead of using limited concepts of technical effectiveness.

In the case of machine failures during production, several works exist in the literature, including Chiu et al. (2011), Widyadana and Wee (2011), Chiu et al. (2013), Taleizadeh et al. (2014), and Chiu et al. (2015). Wee and Widyadana (2013) devised a production model covering deteriorating items, assuming stochastic preventive maintenance time and reworking defective items under first-in-first-out (FIFO) rule. Two case examples are applied, using uniform and exponential distribution of preventive maintenance time. Liao (2016) developed an EPQ model to determine optimal production run times, also investigating the effect of maintenance activities, such as restoration and occasional imperfect preventive maintenance, on a production system whose condition is deteriorating. The numerical analysis shows that enhancing maintenance and production capability increases product reliability, thus reducing the costs of production and warranties. The EPQ problem studied by Huang et al. (2017) concerned a production process subject to shifting states, producing defective goods at random intervals, and with a low production rate after state-shifting. They made the assumption that expected shifting time is a variable that can be controlled by investment in assets and technology. They investigated three scenarios for the mathematical model: no shift; shift with no shortages; shift with shortages. They also investigated product deterioration and its effect on the optimal policy, assuming that, because interruption of the production process leads to deterioration costs, repairing time is negligible and the production process cannot be stopped for repair or restoration during a production run.

Table 1 lists some key papers on the topic of inventory problems, together with their assumptions regarding machine breakdown, production policy, and inspection time. Whereas these previous models assume an imperfect process and random machine breakdowns, our model assumes scrappage of a percentage of defective items, uniform distribution of the time to machine breakdown, and a planned inspection policy in-production and post-production. We evaluate an Abort/Resume (AR) inventory control policy which permits the development of closed-form solutions. What is the basis for deciding to scrap items? Usually, when an inspection determines that the cost of repair is below a set threshold, the item is repaired; if the repair cost exceeds the threshold, it is scrapped. Nowadays, manufacturers extract value from scrap. If the scrap is metal, it is sold by the ton; if it is a product, it can be dismantled to obtain value from any functional components that can be reused in the production process.

Table 1 Literature review

In many real-world manufacturing processes, it is inevitable that products will be manufactured with imperfect quality. Often, however, defective items include valuable materials and there are, therefore, economic incentives to rework them. The decision whether to rework or scrap such substandard products is a recurring issue in different industries. Clearly, it is important to set a suitable inspection policy for products and/or machines in order to minimize the cost created by producing defective products. However, it is important to note that, in many industries, continuous inspection during production is impossible, or unrealistically expensive. Furthermore, most inventory models previously developed by researchers recommend that continuous inspection should be performed during every production run in every cycle.

Our key objections to previous literature are shown in Table 1. As the table shows, no study addressed the problem of EPQ inventory where scrap, rework, machine breakdown and inspection policy are all considered, with the inspection process performed during production and continuing at the end of runtime. Thus, this paper examines the optimal policy on replenishment for the EPQ model, incorporating scrap, rework, random machine failures and both in-production and after-production inspection. Our study is motivated by this gap in the literature. Since there are two stages of the inspection process, the proposed model permits the in-production inspection cost to be lower than the after-production inspection cost. Three conditions are analyzed for the optimal policy. Our objective is to optimize the production run time variable in order to maximize the total expected profit per unit time.

This paper adds to the study by Moussawi-Haidar et al. (2016) in two ways. The first is the assumption of random breakdowns in the production system. This is accomplished by a random variable (time-to-breakdown) following a uniform probability distribution, representing elapsed time until breakdown. An AR inventory control policy is adopted, with production being resumed after each machine breakdown. Corrective maintenance is performed following a breakdown in the course of a production run. This extension brings the model closer to real-world conditions, although it increases the mathematical complexity. The other extension of Moussawi-Haidar et al.’s work is the assumption that the defective items include a percentage that cannot be reworked or repaired, and must, therefore, be scrapped at an additional cost. In addition, we will analyse different examples of in-production and after-production inspection costs. Under these assumptions, a mathematical model is derived, and the concavity of the expected total profit function is proved. This study provides a numerical example to illustrate the application of the proposed model, followed by sensitivity analyses performed on optimal solutions with respect to the demand rate, the production rate, the rework rate and the proportions of defective items and scrap items.

This study is organized as follows. The introduction explains the motivation for the study and reviews existing literature. Section 2 offers a description of the production inventory system and the assumptions and notations involved. Section 3 focuses on the mathematical model developed for the inventory problem. Section 4 presents the numerical solution of the developed model and gives managerial insights on optimal decisions. Finally, a summary of the paper and some concluding remarks are given in Sect. 5.

2 Problem definition

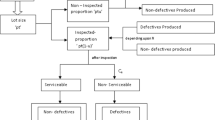
We consider a production process that produces one type of product. During the production process, a proportion $q$ of defective items is produced at a rate $d$. Let $d$ be the production rate of defective items during the regular production process; then, it can be expressed as the product of the production rate $P$ and the proportion of defective items $q$. That is $d = Pq$. The proportion $q$ of defective items is a random variable with a known probability density function. Since demand is only met from good items, it requires the inspection of units produced before they are sold to customers. During this process, if an item is found to be defective, it is replaced with a good item. All items produced are tested to see whether they meet certain quality requirements, and different inspection costs are considered for in-production, $d_{1}$, and after-production, $d_{2}$, where $d_{1} > d_{2}$. Such a relationship has an implication for the analysis of two different situations with regards to the inspection costs, namely, $d_{1} = d_{2}$ and $d_{1} < d_{2}$. The effects of the conditions in question on the optimal solution will be further explored using numerical analysis. The inspection test results are 100% reliable, i.e. no Type I or Type II inspection errors occur. Moreover, when the regular production process ends, inspection of the remaining units of the produced lot is performed at a rate per unit time of $x$, $x > D$. Further, it is assumed that the defective items consist of scrap and reworkable items. While a random proportion $\theta$ of the defective items is just subtracted from inventory with unit cost $C_{s}$ at the end of the inspection process, the others with the proportion of $1 - \theta$ are reworked with unit cost $C_{R}$ and a constant rework rate $P_{1}$, $P_{1} > D$. Futhermore, among the other realistic assumptions, a machine breakdown may occur randomly, and an AR inventory control policy is adopted.

Considering the situation when a breakdown occurs during a production run time, the machine is repaired immediately, with a constant repair time $t_{r}$ and fixed repairing cost $M$, and the interrupted lot will be resumed as soon as the machine is repaired or restored. However, any breakdown during the rework process is not considered. The assumption of constant repair/restoration time aligns with the repair process for modern manufacturing equipment, which often features a modular design, so that the repair process simply involves replacing the faulty unit or module with a new one. Flexible production systems often permit repair of a failed unit “off line”, without affecting production.

This model assumes a constant repair time and uniform distribution of the time to breakdown. Examples of situations which have constant repair times and distribution times with uniform probability of breakdown can be found in Moinzadeh and Aggarwal (1997), Lin and Gong (2006), and Widyadana and Wee (2012).

The following notations are used in this study to develop the mathematical model:

$P$:

The production rate in units per unit time.

$P_{1}$:

The rework rate in units per unit time.

$Q$:

Production lot size per cycle.

$D$:

The demand rate in units per unit time, where demand is constant and continuous.

$d$:

The production rate of defective items in units per unit time.

$x$:

Inspection rate in units per unit time.

$d_{1}$:

The inspection cost during the production.

$d_{2}$:

The inspection cost after the production.

$q$:

The proportion of defective items produced, a random variable.

$\theta$:

The proportion of scrap items in defective items, a random variable.

$T$:

The cycle length when a breakdown occurs.

$T^{\prime}$:

The cycle length when a breakdown does not occur.

$\varvec{T}$:

The cycle length whether a breakdown occurs or not.

$T_{1}$:

The production run time, i.e. the production uptime.

$t$:

The time-to-breakdown, a random variable.

$t_{r}$:

The constant repair/restoration time.

$t_{2}$:

The time required to inspect the items produced.

$t_{3}$:

The time required to rework the reworkable items.

$t_{4}$:

The time required to consume all on-hand inventory.

$TC_{1} \left( {T_{1} } \right)$:

The total cost per cycle where a breakdown occurs in the production run time.

$TC_{2} \left( {T_{1} } \right)$:

The total cost per cycle where a breakdown does not occur in the production run time.

$TP_{1} \left( {T_{1} } \right)$:

The total profit per cycle where a breakdown occurs in the production run time.

$TP_{2} \left( {T_{1} } \right)$:

The total profit per cycle where a breakdown does not occur in the production run time.

$E\left( {TPU\left( {T_{1} } \right)} \right)$:

The expected total profit per unit time whether machine breakdowns occur or not.

$f_{1} \left( . \right)$:

The probability density function of $q$.

$f_{2} \left( . \right)$:

The probability density function of $\theta$.

$f_{3} \left( . \right)$:

The probability density function of $t$.

$S$:

Unit selling price of a good item.

$K$:

The setup cost for each production.

$M$:

Fixed machine repair cost.

$C$:

The production cost per unit ($/unit).

$C_{S}$:

The disposal cost per unit of scrap items ($/unit).

$C_{R}$:

The reworking cost for each reworkable items ($/unit).

$h$:

The holding cost per unit per unit time ($/unit/unit time).

$h_{1}$:

The holding cost for each reworkable items per unit time ($/unit/unit time).

$*$:

The superscript representing optimal value.

3 Mathematical model

Briefly, this paper aims to determine the optimal production run time to maximize the overall total expected profit. An EPQ model with defective items, rework and random machine breakdowns is constructed. A random proportion of defective items is assumed to be scrap, while the remainder are assumed to be reworkable, and these items are reworked at a cost at the end of the inspection process. Production is carried out during time period $T_{1}$. $t$ represents time-to-breakdown during a production run. A breakdown may occur in two possible scenarios. First, the breakdown may occur during the production run time, i.e., $t \in \left[ {0,T_{1} } \right]$. Alternatively, the breakdown may occur after the run time, i.e., $t \in \left[ {T_{1} ,\infty } \right]$. In the latter scenario, the repair is completed before the production cycle ends. Further, repair activity has a fixed duration, $t_{r}$, i.e., $t_{r} = g$, and is not included in the production run time $T_{1}$; however, it is included in the production cycle time $T$.

Figure 1 depicts the on-hand inventory level of non-defective items when a random breakdown occurs during the production uptime, and reworkable items are reworked at a rate $P_{1}$ after the inspection of all items. The total cost per cycle comprises the production setup cost, the machine repair cost, the production cost, the inspection cost during and after production, the disposal cost, the reworking cost and the holding cost. The time duration of a cycle, $T$, is the sum of the production run time, the inspection time, the reworking time, the production downtime and the machine repair time. That is,

$$T = T_{1} + t_{2} + t_{3} + t_{4} + t_{r}.$$

(1)

It is assumed that the production rate is higher than the rate of demand and that good quality items are manufactured during production run time. In case of a machine breakdown, on the other hand, it can be assumed that the time required for repair/restoration activities is negligible. Thus, good quality products may be used to meet the demand accumulated during the production run time and repair time. This approach carries the implication that all the defective items cannot be found until the end of the production run time. Since in-production demand and the demand during machine repair time can only be satisfied with good items, it is assumed that some items are inspected in the pre-sales period and that such inspection is completed before the inventory is depleted. Once the defective product is discovered, it is replaced with a good product and the defective product is stored until the stocks are depleted. In order to be able to meet the demand solely with good items, the number of items to be inspected must be more than the demand. That is, the number of products screened at the time, $T_{1}$, must be higher than the demand, $DT_{1}$, and the number of products screened at the time $t_{r}$, must be higher than the demand, $Dt_{r}$. In other words, the number of products screened must be more than the demand, in order to obtain good quality products to meet the repair time demand under the following conditions: the production process is imperfect, a number of defective products are manufactured, demand can only be satisfied with good quality products, and a decision is made about these products at the end of the inspection time.

Fig. 1

On-hand inventory level of non-defective items

Rezaei (2016) calculated the total number of returned products using a geometric series in an inventory problem with a constant percentage of defective products in a batch delivered to the customer, with these defective products returned to the supplier and replaced with the same quantity of products, also including the same percentage of defective products.

For $0 < q < 1$, the number of items inspected during the production run time, $T_{1}$, can be calculated as

$${\text{Number}}\;{\text{of}}\;{\text{items}}\;{\text{inspected}}\;{\text{during}}\;{\text{the}}\;{\text{production}}\;{\text{run}}\;{\text{time}}\;T_{1} = \left( {D + Dq + Dq^{2} + \cdots } \right)T_{1}$$

(2)

Inside the bracket is the sum of a geometric series (Wazwaz 2011), for which we have

$$D + Dq + Dq^{2} + \cdots = \mathop {\lim }\limits_{n \to \infty } \left( {D + Dq + Dq^{2} + \cdots Dq^{n} } \right) = \frac{D}{1 - q}$$

This means that

$${\text{Number}}\;{\text{of}}\;{\text{items}}\;{\text{inspected}}\;{\text{during}}\;{\text{the}}\;{\text{production}}\;{\text{run}}\;{\text{time}}\;T_{1} = \frac{{DT_{1} }}{1 - q}$$

(3)

and the number of items inspected during the machine repair time $t_{r}$ can be calculated as

$${\text{Number}}\;{\text{of}}\;{\text{items}}\;{\text{inspected}}\;{\text{during}}\;{\text{the}}\;{\text{machine}}\;{\text{repair}}\;{\text{time}}\;t_{r} = \left( {D + Dq + Dq^{2} + \cdots } \right)t_{r} = \frac{{Dt_{r} }}{1 - q}$$

(4)

Then, the total number of items inspected at the end of production is

$$\frac{{DT_{1} }}{1 - q} + \frac{{Dt_{r} }}{1 - q} = \frac{{DT_{1} + Dg}}{1 - q},$$

(5)

where $t_{r} = g$.

The number of defective items identified at the end of $T_{1}$ is the total number of items inspected during the production and machine repair time, as given by Eq. (6), less the demand during these periods. That is

$$\frac{{DT_{1} + Dg}}{1 - q} - \left( {DT_{1} + Dg} \right) = \frac{{\left( {DT_{1} + Dg} \right)q}}{1 - q}$$

(6)

The on-hand inventory not inspected at the end of $T_{1}$ is equal to the maximum inventory level, $\left( {P - D} \right)T_{1} - Dg$, less the number of defective items identified at the end of production, as given by Eq. (7). That is

$$\left( {P - D} \right)T_{1} - Dg - \frac{{\left( {DT_{1} + Dg} \right)q}}{1 - q} = PT_{1} - \frac{{DT_{1} + Dg}}{1 - q}.$$

(7)

Then, the time $t_{2}$ needed to inspect the on-hand inventory not inspected at the end of $T_{1}$ is

$$t_{2} = \frac{{PT_{1} - \frac{{DT_{1} + Dg}}{1 - q}}}{x} = \frac{{T_{1} }}{x}\left( {P - \frac{D}{{\left( {1 - q} \right)}}} \right) - \frac{Dg}{{\left( {1 - q} \right)x}}.$$

(8)

According to Fig. 1, the time required to rework the reworkable items, $t_{3}$, the time to deplete the on-hand inventory of good items after the rework, $t_{4}$, the level of on-hand inventory when machine breakdown occurs, $H_{1}$, the level of inventory when the machine is repaired, $H_{2}$, and the production run time $T_{1}$ are shown in the following equations:

$$t_{3} = \frac{{\left( {1 - \theta } \right)qQ}}{{P_{1} }} = \frac{{\left( {1 - \theta } \right)qPT_{1} }}{{P_{1} }},$$

(9)

$$t_{4} = \frac{{H_{5} }}{D},$$

(10)

$$H_{1} = \left( {P - d - D} \right)t,$$

(11)

$$H_{2} = H_{1} - Dt_{r} = \left( {P - d - D} \right)t - Dg,$$

(12)

$$T_{1} = \frac{Q}{P};\quad \therefore Q = PT_{1} .$$

(13)

The maximum inventory level of good items at the end of the production process, $H_{3}$, is found as follows

$$\begin{aligned} H_{3} & = H_{2} + \left( {P - d - D} \right)\left( {T_{1} - t} \right) \\ & = \left( {P - d - D} \right)t - Dg + \left( {P - d - D} \right)\left( {T_{1} - t} \right) \\ & = \left( {P - d - D} \right)T_{1} - Dg. \\ \end{aligned}$$

(14)

The inventory level of good items at the end of the inspection process, $H_{4}$, is found as follows

$$\begin{aligned} H_{4} & = H_{3} - Dt_{2} \\ & = \left( {P - d - D} \right)T_{1} - Dg - Dt_{2} \\ & = \left( {\left( {P - d - D} \right)T_{1} - Dg} \right) - D\left( {\frac{{T_{1} }}{x}\left( {P - \frac{D}{1 - q}} \right) - \frac{Dg}{{\left( {1 - q} \right)x}}} \right). \\ \end{aligned}$$

(15)

The inventory level of good items at the end of the rework process, $H_{5}$, is found as follows

$$\begin{aligned} H_{5} & = H_{4} + \left( {P_{1} - D} \right)t_{3} = \left( {\left( {P - d - D} \right)T_{1} - Dg} \right) \\ & \quad - D\left( {\frac{{T_{1} }}{x}\left( {P - \frac{D}{1 - q}} \right) - \frac{Dg}{{\left( {1 - q} \right)x}}} \right) + \frac{{\left( {P_{1} - D} \right)PT_{1} \left( {1 - \theta } \right)q}}{{P_{1} }}. \\ \end{aligned}$$

(16)

Referring to Figs. 2 and 3, the total number of defective items produced during the regular production run time, and the number of imperfect quality items to be reworked in the time duration of $t_{3}$ are computed as in Eqs. (17) and (18), respectively:

$$dT_{1} = qPT_{1} = qQ,$$

(17)

$$P_{1} t_{3} = \left( {1 - \theta } \right)\left( {dT_{1} } \right) = \left( {1 - \theta } \right)qPT_{1} .$$

(18)

Fig. 2

On-hand inventory level of defective items

Fig. 3

On-hand inventory level of scrap items

From the above equations, the time duration of a cycle, $T$, can be calculated as

$$T = \frac{{\left( {1 - \theta q} \right)PT_{1} }}{D} .$$

(19)

As a result, the total inventory cost function can be expressed as

$$\begin{aligned} & TC_{1} \left( {T_{1} } \right) = K + M + C\left( {PT_{1} } \right) + C_{s} \theta \left( {qPT_{1} } \right) + d_{1} \left( {\frac{{DT_{1} + Dg}}{1 - q}} \right) \\ & \quad + d_{2} \left( {PT_{1} - \frac{{DT_{1} + Dg}}{1 - q}} \right) + C_{R} \left( {1 - \theta } \right)\left( {qPT_{1} } \right) \\ & \quad + h\left( {\frac{{H_{1} \left( t \right)}}{2} + \frac{{\left( {H_{1} + H_{2} } \right)\left( {t_{r} } \right)}}{2} + \frac{{\left( {H_{2} + H_{3} } \right)\left( {T_{1} - t} \right)}}{2} + \frac{{\left( {H_{3} + H_{4} } \right)\left( {t_{2} } \right)}}{2} + \frac{{\left( {H_{4} + H_{5} } \right)\left( {t_{3} } \right)}}{2} + \frac{{H_{5} \left( {t_{4} } \right)}}{2}} \right) \\ & \quad + h\left( {\frac{{\left( {dt} \right)\left( t \right)}}{2} + \left( {dt} \right)\left( {t_{r} } \right) + \frac{{\left( {dt + dT_{1} } \right)\left( {T_{1} - t} \right)}}{2} + \left( {dT_{1} } \right)\left( {t_{2} } \right)} \right) \\ & \quad + h_{1} \left( {\frac{{\left( {\left( {1 - \theta } \right)dT_{1} } \right)\left( {t_{3} } \right)}}{2}} \right). \\ \end{aligned}$$

(20)

According to “Appendix”, the above equation can be simplified as

$$\begin{aligned} & TC_{1} \left( {T_{1} } \right) = K + M + \left( {C + d_{2} } \right)PT_{1} + C_{s} PT_{1} \left( {\theta q} \right) + + C_{R} PT_{1} \left( {1 - \theta } \right)q \\ & \quad + \left( {d_{1} - d_{2} } \right)DT_{1} \left( {\frac{1}{1 - q}} \right) + \left( {d_{1} - d_{2} } \right)Dg\left( {\frac{1}{1 - q}} \right) \\ & \quad + h\left\{ {P^{2} T_{1}^{2} \left( {\frac{{\left( {1 - \theta } \right)q\left( {1 - q - \frac{D}{P}} \right)}}{D} + \frac{\theta q}{x}\left( {1 - \frac{D}{{\left( {1 - q} \right)P}}} \right) + \frac{{\left( {P_{1} - D} \right)\left( {1 - \theta } \right)^{2} q^{2} }}{{2DP_{1} }} + \frac{q}{2P} + \frac{{\left( {1 - q} \right)\left( {1 - q - \frac{D}{P}} \right)}}{2D}} \right)} \right. \\ & \quad \left. { + PgT_{1} \left( {\theta q - 1 - \frac{D\theta }{x}\left( {\frac{q}{1 - q}} \right)} \right)} \right\} + hPgt + \frac{{h_{1} P^{2} T_{1}^{2} \left( {1 - \theta } \right)^{2} q^{2} }}{{2P_{1} }}. \\ \end{aligned}$$

(21)

The total profit per cycle is as follows

$$\begin{aligned} & TP_{1} \left( {T_{1} } \right) = SPT_{1} \left( {1 - \theta q} \right) \\ & \quad - \left( {K + M + \left( {C + d_{2} } \right)PT_{1} + C_{s} PT_{1} \left( {\theta q} \right) + C_{R} PT_{1} \left( {1 - \theta } \right)q + \left( {d_{1} - d_{2} } \right)DT_{1} \left( {\frac{1}{1 - q}} \right)} \right. \\ & \quad \left. { + \left( {d_{1} - d_{2} } \right)Dg\left( {\frac{1}{1 - q}} \right)} \right) \\ & \quad - h\left\{ {P^{2} T_{1}^{2} \left( {\frac{{\left( {1 - \theta } \right)q\left( {1 - q - \frac{D}{P}} \right)}}{D} + \frac{\theta q}{x}\left( {1 - \frac{D}{{\left( {1 - q} \right)P}}} \right) + \frac{{\left( {P_{1} - D} \right)\left( {1 - \theta } \right)^{2} q^{2} }}{{2DP_{1} }} + \frac{q}{2P} + \frac{{\left( {1 - q} \right)\left( {1 - q - \frac{D}{P}} \right)}}{2D}} \right)} \right. \\ & \quad \left. { + PgT_{1} \left( {\theta q - 1 - \frac{D\theta }{x}\left( {\frac{q}{1 - q}} \right)} \right)} \right\} - hPgt - \frac{{h_{1} P^{2} T_{1}^{2} \left( {1 - \theta } \right)^{2} q^{2} }}{{2P_{1} }}. \\ \end{aligned}$$

(22)

A similar approach can be used to derive the total cost per cycle in case $t \ge T_{1}$. In this case, the total cost per cycle is expressed as:

$$\begin{aligned} & TC_{2} \left( {T_{1} } \right) = K + M + \left( {C + d_{2} } \right)PT_{1} + C_{s} PT_{1} \left( {\theta q} \right) + + C_{R} PT_{1} \left( {1 - \theta } \right)q + \left( {d_{1} - d_{2} } \right)DT_{1} \left( {\frac{1}{1 - q}} \right) \\ & \quad + h\left\{ {P^{2} T_{1}^{2} \left( {\frac{{\left( {1 - \theta } \right)q\left( {1 - q - \frac{D}{P}} \right)}}{D} + \frac{\theta q}{x}\left( {1 - \frac{D}{{\left( {1 - q} \right)P}}} \right) + \frac{{\left( {P_{1} - D} \right)\left( {1 - \theta } \right)^{2} q^{2} }}{{2DP_{1} }} + \frac{q}{2P} + \frac{{\left( {1 - q} \right)\left( {1 - q - \frac{D}{P}} \right)}}{2D}} \right)} \right\} \\ & \quad + \frac{{h_{1} P^{2} T_{1}^{2} \left( {1 - \theta } \right)^{2} q^{2} }}{{2P_{1} }}. \\ \end{aligned}$$

(23)

The total profit per cycle is given by

$$\begin{aligned} & TP_{2} \left( {T_{1} } \right) = SPT_{1} \left( {1 - \theta q} \right) - \left( {K + \left( {C + d_{2} } \right)PT_{1} + C_{s} PT_{1} \left( {\theta q} \right) + + C_{R} PT_{1} \left( {1 - \theta } \right)q + \left( {d_{1} - d_{2} } \right)DT_{1} \left( {\frac{1}{1 - q}} \right)} \right) \\ & \quad - h\left\{ {P^{2} T_{1}^{2} \left( {\frac{{\left( {1 - \theta } \right)q\left( {1 - q - \frac{D}{P}} \right)}}{D} + \frac{\theta q}{x}\left( {1 - \frac{D}{{\left( {1 - q} \right)P}}} \right) + \frac{{\left( {P_{1} - D} \right)\left( {1 - \theta } \right)^{2} q^{2} }}{{2DP_{1} }} + \frac{q}{2P} + \frac{{\left( {1 - q} \right)\left( {1 - q - \frac{D}{P}} \right)}}{2D}} \right)} \right\} \\ & \quad - \frac{{h_{1} P^{2} T_{1}^{2} \left( {1 - \theta } \right)^{2} q^{2} }}{{2P_{1} }}. \\ \end{aligned}$$

(24)

The length of the cycle is the sum of the production run time, the inspection time, the production downtime and the reworking time. It can be expressed as

$$T^{\prime} = T_{1} + t_{2} + t_{3} + t_{4} = \frac{{\left( {1 - \theta q} \right)PT_{1} }}{D}.$$

(25)

The expected total profit per cycle, with or without random breakdowns, is calculated from the probability distribution of the time of the breakdown as follows:

$$E\left( {TP\left( {T_{1} } \right)} \right) = E\left( {\mathop \int \limits_{0}^{{T_{1} }} TP_{1} \left( {T_{1} } \right)f\left( t \right)dt + \mathop \int \limits_{{T_{1} }}^{\infty } TP_{2} \left( {T_{1} } \right)f\left( t \right)dt} \right),$$

(26)

where $TP_{1} \left( {T_{1} } \right)$ and $TP_{2} \left( {T_{1} } \right)$ are given by Eqs. (22) and (24), respectively.

Moreover, the expected cycle length $E\left( \varvec{T} \right)$, is given by

$$E\left( \varvec{T} \right) = E\left( {\mathop \int \limits_{0}^{{T_{1} }} Tf\left( t \right)dt + \mathop \int \limits_{{T_{1} }}^{\infty } T^{\prime}f\left( t \right)dt} \right),$$

(27)

where $T$ and $T^{\prime}$ are given by Eqs. (19) and (25), respectively.

Finally, using the renewal reward theorem, the expected total profit per unit time $E\left( {TPU\left( {T_{1} } \right)} \right)$, is

$$E\left( {TPU\left( {T_{1} } \right)} \right) = \frac{{E\left( {TP\left( {T_{1} } \right)} \right)}}{{E\left( \varvec{T} \right)}} = \frac{{E\left( {\mathop \int \nolimits_{0}^{{T_{1} }} TP_{1} \left( {T_{1} } \right)f\left( t \right)dt + \mathop \int \nolimits_{{T_{1} }}^{\infty } TP_{2} \left( {T_{1} } \right)f\left( t \right)dt} \right)}}{{E\left( {\mathop \int \nolimits_{0}^{{T_{1} }} Tf\left( t \right)dt + \mathop \int \nolimits_{{T_{1} }}^{\infty } T^{\prime}f\left( t \right)dt} \right)}}.$$

(28)

It is assumed that the proportion, $q$, of defective items, the proportion $\theta$ of scrap items and the time to breakdown, $t$, are random variables with known probability density functions. These random variables may be correlated to or independent from each other. Following the studies of Lin and Kroll (2006), Yoo et al. (2009), Khan et al. (2011) and Hsu and Hsu (2013), it is assumed in this model that these variables are independent.

This model treats the time-to breakdown, $t$, as a random variable which is uniformly distributed across the interval $\left[ {0, aT_{1} } \right]$, where $a > 1$. The probability density function $f_{3} \left( t \right)$ is given as:

$$f_{3} \left( t \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{{aT_{1} }}, } & { 0 \le t \le aT_{1} } \\ {0,} & {otherwise.} \\ \end{array} } \right.$$

(29)

To allow realistic practical conditions representing machine breakdown, production run time, $T_{1}$, must be lower than $aT_{1}$; if this is not the case, machine breakdown will not occur when production is finished. Without this condition, the problem would be only the same as the machine breakdown problem considered in studies by Chiu et al. (2007) and Ting et al. (2011).

Substituting the uniform probability density function into Eq. (28), we have

$$\begin{aligned} & E\left( {TPU\left( {T_{1} } \right)} \right) = \frac{{\mathop \int \nolimits_{0}^{{T_{1} }} E\left( {TP_{1} \left( {T_{1} } \right)} \right)f\left( t \right)dt + \mathop \int \nolimits_{{T_{1} }}^{\infty } E\left( {TP_{2} \left( {T_{1} } \right)} \right)f\left( t \right)dt}}{{\mathop \int \nolimits_{0}^{{T_{1} }} E\left( T \right)f\left( t \right)dt + \mathop \int \nolimits_{{T_{1} }}^{\infty } E\left( {T^{\prime}} \right)f\left( t \right)dt}} \\ & \quad = \frac{{\begin{array}{*{20}l} {\mathop \int \limits_{0}^{{T_{1} }} \left\{ {\begin{array}{*{20}l} {SPT_{1} \left( {1 - E\left( \theta \right)E\left( q \right)} \right) - \left( {K + M + \left( {C + d_{2} } \right)PT_{1} + C_{s} PT_{1} E\left( \theta \right)E\left( q \right) + C_{R} PT_{1} \left( {1 - E\left( \theta \right)} \right)E\left( q \right) + \left( {d_{1} - d_{2} } \right)DT_{1} E\left( {\frac{1}{1 - q}} \right) + \left( {d_{1} - d_{2} } \right)DgE\left( {\frac{1}{1 - q}} \right)} \right)} \hfill \\ {\quad - h\left[ {P^{2} T_{1}^{2} \left( {\frac{{\left( {1 - E\left( \theta \right)} \right)E\left( q \right)\left( {1 - E\left( q \right) - \frac{D}{P}} \right)}}{D} + \frac{E\left( \theta \right)E\left( q \right)}{x}\left( {1 - \frac{D}{{\left( {1 - q} \right)P}}} \right) + \frac{{\left( {P_{1} - D} \right)E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{2DP_{1} }} + \frac{E\left( q \right)}{2P} + \frac{{\left( {1 - E\left( q \right)} \right)\left( {1 - E\left( q \right) - \frac{D}{P}} \right)}}{2D}} \right)} \right.} \hfill \\ {\left. {\quad + PgT_{1} \left( {E\left( \theta \right)E\left( q \right) - 1 - \frac{DE\left( \theta \right)}{x}E\left( {\frac{q}{1 - q}} \right)} \right)} \right] - hPgt - \frac{{h_{1} P^{2} T_{1}^{2} E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{2P_{1} }}} \hfill \\ \end{array} } \right\}\frac{1}{{aT_{1} }}dt} \hfill \\ {\quad + \mathop \int \limits_{{T_{1} }}^{\infty } \left\{ {\begin{array}{*{20}l} {SPT_{1} \left( {1 - E\left( \theta \right)E\left( q \right)} \right) - \left( {K + \left( {C + d_{2} } \right)PT_{1} + C_{s} PT_{1} E\left( \theta \right)E\left( q \right) + + C_{R} PT_{1} \left( {1 - E\left( \theta \right)} \right)E\left( q \right) + \left( {d_{1} - d_{2} } \right)DT_{1} E\left( {\frac{1}{1 - q}} \right)} \right)} \hfill \\ {\quad - h\left[ {P^{2} T_{1}^{2} \left( {\frac{{\left( {1 - E\left( \theta \right)} \right)E\left( q \right)\left( {1 - q - \frac{D}{P}} \right)}}{D} + \frac{E\left( \theta \right)E\left( q \right)}{x}\left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right) + \frac{{\left( {P_{1} - D} \right)E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{2DP_{1} }} + \frac{E\left( q \right)}{2P} + \frac{{\left( {1 - E\left( q \right)} \right)\left( {1 - E\left( q \right) - \frac{D}{P}} \right)}}{2D}} \right)} \right]} \hfill \\ {\quad - \frac{{h_{1} P^{2} T_{1}^{2} E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{2P_{1} }}} \hfill \\ \end{array} } \right\}\frac{1}{{aT_{1} }}dt} \hfill \\ \end{array} }}{{\mathop \int \limits_{0}^{{T_{1} }} \left( {\frac{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)PT_{1} }}{D}} \right)\frac{1}{{aT_{1} }}dt + \mathop \int \limits_{{T_{1} }}^{\infty } \left( {\frac{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)PT_{1} }}{D}} \right)\frac{1}{{aT_{1} }}dt}} \\ & \quad = \frac{{\begin{array}{*{20}l} {SPT_{1} \left( {1 - E\left( \theta \right)E\left( q \right)} \right) - \left( {K + \left( {C + d_{2} } \right)PT_{1} + C_{s} PT_{1} E\left( \theta \right)E\left( q \right) + C_{R} PT_{1} \left( {1 - E\left( \theta \right)} \right)E\left( q \right) + \left( {d_{1} - d_{2} } \right)DT_{1} E\left( {\frac{1}{1 - q}} \right)} \right)} \hfill \\ {\quad - h\left[ {P^{2} T_{1}^{2} \left( {\frac{{\left( {1 - E\left( \theta \right)} \right)E\left( q \right)\left( {1 - E\left( q \right) - \frac{D}{P}} \right)}}{D} + \frac{E\left( \theta \right)E\left( q \right)}{x}\left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right) + \frac{{\left( {P_{1} - D} \right)E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{2DP_{1} }} + \frac{E\left( q \right)}{2P} + \frac{{\left( {1 - E\left( q \right)} \right)\left( {1 - E\left( q \right) - \frac{D}{P}} \right)}}{2D}} \right)} \right]} \hfill \\ {\quad - \frac{{h_{1} P^{2} T_{1}^{2} E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{2P_{1} }} - \frac{1}{a}\left[ {M + \left( {d_{1} - d_{2} } \right)DgE\left( {\frac{1}{1 - q}} \right) + hPgT_{1} \left( {E\left( \theta \right)E\left( q \right) - 1 - \frac{DE\left( \theta \right)}{x}E\left( {\frac{q}{1 - q}} \right)} \right)} \right] - \frac{hPg}{{aT_{1} }}\mathop \int \limits_{0}^{{T_{1} }} tdt} \hfill \\ \end{array} }}{{\frac{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)PT_{1} }}{D}}} \\ \end{aligned}$$

(30)

After some manipulation, we have

$$\begin{aligned} & E\left( {TPU\left( {T_{1} } \right)} \right) = SD - \frac{KD}{{PT_{1} }}\frac{1}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} - \left( {C + d_{2} } \right)D\frac{1}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} \\ & \quad - C_{s} D\frac{E\left( \theta \right)E\left( q \right)}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} - C_{R} D\frac{{\left( {1 - E\left( \theta \right)} \right)E\left( q \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} \\ & \quad - \frac{{\left( {d_{1} - d_{2} } \right)D^{2} }}{P}\frac{{E\left( {\frac{1}{1 - q}} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} - \frac{{\left( {d_{1} - d_{2} } \right)D^{2} g}}{{aPT_{1} }}\frac{{E\left( {\frac{1}{1 - q}} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} \\ & \quad - hT_{1} P\left[ {\frac{{E\left( q \right)\left( {1 - E\left( q \right) - {\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D P}}\right.\kern-0pt} \!\lower0.7ex\hbox{$P$}}} \right)\left( {1 - E\left( \theta \right)} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} + \left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right)\frac{D}{x}\frac{E\left( \theta \right)E\left( q \right)}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}} \right. \\ & \quad \left. { + \frac{{\left( {P_{1} - D} \right)}}{{2P_{1} }}\frac{{E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} + \frac{D}{2P}\frac{E\left( q \right)}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} + \frac{{\left( {1 - E\left( q \right) - {\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D P}}\right.\kern-0pt} \!\lower0.7ex\hbox{$P$}}} \right)\left( {1 - E\left( q \right)} \right)}}{{2\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}} \right] - \frac{DM}{{aPT_{1} }}\frac{1}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} \\ & \quad - \frac{hDg}{a}\left[ {\frac{E\left( \theta \right)E\left( q \right)}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} - \frac{1}{{2\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} - \frac{D}{x}\frac{{E\left( \theta \right)E\left( {\frac{q}{1 - q}} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}} \right] - \frac{{h_{1} DT_{1} P}}{{2P_{1} }}\frac{{E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}. \\ \end{aligned}$$

(31)

Let $E_{1} = \frac{1}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}$, $E_{2} = \frac{E\left( \theta \right)E\left( q \right)}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}$, $E_{3} = \frac{{\left( {1 - E\left( \theta \right)} \right)E\left( q \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}$, $E_{4} = \frac{{E\left( {\frac{1}{1 - q}} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}$, $E_{5} = \frac{{E\left( q \right)\left( {1 - E\left( q \right) - {\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D P}}\right.\kern-0pt} \!\lower0.7ex\hbox{$P$}}} \right)\left( {1 - E\left( \theta \right)} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}$, $E_{6} = \frac{{E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}$, $E_{7} = \frac{E\left( q \right)}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}$, $E_{8} = \frac{{\left( {1 - E\left( q \right) - {\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D P}}\right.\kern-0pt} \!\lower0.7ex\hbox{$P$}}} \right)\left( {1 - E\left( q \right)} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}$, $E_{9} = \frac{{E\left( \theta \right)E\left( {\frac{q}{1 - q}} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}}.$

Then, Eq. (31) becomes

$$\begin{aligned} E\left( {TPU\left( {T_{1} } \right)} \right)& = SD - \frac{{KDE_{1} }}{{PT_{1} }} - \left( {C + d_{2} } \right)DE_{1} {-}C_{s} DE_{2} - C_{R} DE_{3} - \frac{{\left( {d_{1} - d_{2} } \right)D^{2} E_{4} }}{P} - \frac{{\left( {d_{1} - d_{2} } \right)D^{2} gE_{4} }}{{aPT_{1} }} \\ & \quad - hT_{1} P\left[ {E_{5} + \left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right)\frac{{DE_{2} }}{x} + \frac{{\left( {P_{1} - D} \right)E_{6} }}{{2P_{1} }} + \frac{{DE_{7} }}{2P} + \frac{{E_{8} }}{2}} \right] \\ & \quad - \frac{{DME_{1} }}{{aPT_{1} }} - \frac{hDg}{a}\left( {E_{2} - \frac{{E_{1} }}{2} - \frac{{DE_{9} }}{x}} \right) - \frac{{h_{1} DT_{1} PE_{6} }}{{2P_{1} }}. \\ \end{aligned}$$

(32)

Note that the expected total profit per unit time function $E\left( {TPU\left( {T_{1} } \right)} \right)$ in Eq. (32) is strictly concave for all positive $T_{1}$. Hence, it follows that, to find the optimal production run time $T_{1}^{*}$, one can partially differentiate $E\left( {TPU\left( {T_{1} } \right)} \right)$ with respect to $T_{1}$, and then set the result equal to zero, i.e.:

The first-order derivative of $E\left( {TPU\left( {T_{1} } \right)} \right)$ is

$$\begin{aligned} & \frac{{\partial E\left( {TPU\left( {T_{1} } \right)} \right)}}{{\partial T_{1} }} = \frac{{KDE_{1} }}{{PT_{1}^{2} }} + \frac{{\left( {d_{1} - d_{2} } \right)D^{2} gE_{4} }}{{aPT_{1}^{2} }} \\ & \quad - hP\left( {E_{5} + \left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right)\frac{{DE_{2} }}{x} + \frac{{\left( {P_{1} - D} \right)E_{6} }}{{2P_{1} }} + \frac{{DE_{7} }}{2P} + \frac{{E_{8} }}{2}} \right) \\ & \quad + \frac{{DME_{1} }}{{aPT_{1}^{2} }} - \frac{{h_{1} DPE_{6} }}{{2P_{1} }} = 0, \\ \end{aligned}$$

(33)

and the second-order derivative of $E\left( {TPU\left( {T_{1} } \right)} \right)$ with respect to $T_{1}$ is

$$\frac{{\partial^{2} E\left( {TPU\left( {T_{1} } \right)} \right)}}{{\partial T_{1}^{2} }} = - \frac{{2DE_{1} \left( {K + \frac{M}{a}} \right)}}{{PT_{1}^{3} }} - \frac{{2\left( {d_{1} - d_{2} } \right)D^{2} gE_{4} }}{{aPT_{1}^{3} }}$$

(34)

Since the parameters $K, D,P, M$ and $g$ are positive, $a > 1$, $E_{1} > 0$ and $E_{4} > 0$, we have $\frac{{\partial^{2} E\left( {TPU\left( {T_{1} } \right)} \right)}}{{\partial T_{1}^{2} }} < 0$ for all positive $T_{1}$, which implies that there exists a unique value $T_{1}^{*}$ which is given as

$$T_{1}^{*} = \frac{1}{P}\sqrt {\frac{{2DE_{1} \left( {K + \frac{M}{a}} \right) + \frac{{2\left( {d_{1} - d_{2} } \right)D^{2} gE_{4} }}{a}}}{{h\left[ {2E_{5} + \left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right)\frac{{2DE_{2} }}{x} + \frac{{\left( {P_{1} - D} \right)E_{6} }}{{P_{1} }} + \frac{{DE_{7} }}{P} + E_{8} } \right] + \frac{{h_{1} DE_{6} }}{{P_{1} }}}}} .$$

(35)

From Eq. (35), the optimal production lot size $Q^{*}$ can be obtained as follows:

$$Q^{*} = \sqrt {\frac{{2DE_{1} \left( {K + \frac{M}{a}} \right) + \frac{{2\left( {d_{1} - d_{2} } \right)D^{2} gE_{4} }}{a}}}{{h\left[ {2E_{5} + \left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right)\frac{{2DE_{2} }}{x} + \frac{{\left( {P_{1} - D} \right)E_{6} }}{{P_{1} }} + \frac{{DE_{7} }}{P} + E_{8} } \right] + \frac{{h_{1} DE_{6} }}{{P_{1} }}}}} .$$

(36)

To avoid shortages, the following two assumptions are made:

• 1. The number of good items produced must always be equal to or greater than the demand during production and machine repair time, i.e.

$$Q - qQ \ge DT_{1} + Dg\;\;{\text{or}}\;\;q \le 1 - \frac{D}{P}\left( {1 - \frac{g}{{T_{1} }}} \right).$$

(37)

• 2. The time required to inspect the on-hand inventory not inspected at the end of production, $t_{2}$, is finished before the end of the cycle. That is,

$$\begin{aligned} & t_{2} < t_{3} + t_{4} \;\;{\text{or}} \\ & x > \frac{{2\left( {T_{1} \left( {P - \frac{D}{1 - q}} \right) - \frac{Dg}{1 - q}} \right)}}{{T_{1} \left( {\frac{{\left( {1 - \theta q} \right)P}}{D} - 1} \right) - g}}. \\ \end{aligned}$$

(38)

Special cases of machine breakdown, scrapped product ratio and uniform distribution parameter will be considered to develop the expected total profit in the next section.

Special cases:

If machine breakdown occurs only during production, then the uniform distribution parameter $a$ is equal to 1. Thus, the expected total profit per unit time, $E\left( {TPU\left( {T_{1} } \right)} \right)$, can be expressed, as follows:

$$\begin{aligned} & E\left( {TPU\left( {T_{1} } \right)} \right) = \frac{{E\left( {\mathop \int \nolimits_{0}^{{T_{1} }} TP\left( {T_{1} } \right)f\left( t \right)dt} \right)}}{E\left( T \right)} = \frac{{E\left( {\mathop \int \nolimits_{0}^{{T_{1} }} TP\left( {T_{1} } \right)\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {T_{1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T_{1} }$}}} \right)dt} \right)}}{{{\raise0.7ex\hbox{${\left( {1 - E\left( \theta \right)E\left( q \right)} \right)PT_{1} }$} \!\mathord{\left/ {\vphantom {{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)PT_{1} } D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}}}} \\ & \quad = SD - \frac{{\left( {K + M} \right)DE_{1} }}{{PT_{1} }} - \left( {C + d_{2} } \right)DE_{1} - C_{s} DE_{2} - C_{R} DE_{3} - \frac{{\left( {d_{1} - d_{2} } \right)D^{2} E_{4} }}{P} - \frac{{\left( {d_{1} - d_{2} } \right)D^{2} gE_{4} }}{{PT_{1} }} \\ & \quad - hT_{1} P\left[ {E_{5} + \left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right)\frac{{DE_{2} }}{x} + \frac{{\left( {P_{1} - D} \right)E_{6} }}{{2P_{1} }} + \frac{{DE_{7} }}{2P} + \frac{{E_{8} }}{2}} \right] \\ & \quad - hDg\left( {E_{2} - \frac{{E_{1} }}{2} - \frac{{DE_{9} }}{x}} \right) - \frac{{h_{1} DT_{1} PE_{6} }}{{2P_{1} }}. \\ \end{aligned}$$

(39)

The optimal production run time $T_{1}^{*}$, and the optimal production lot size $Q^{*}$ can be obtained as follows:

$$T_{1}^{*} = \frac{1}{P}\sqrt {\frac{{2\left( {K + M} \right)DE_{1} + 2\left( {d_{1} - d_{2} } \right)D^{2} gE_{4} }}{{h\left( {2E_{5} + \left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right)\frac{{2DE_{2} }}{x} + \frac{{\left( {P_{1} - D} \right)E_{6} }}{{P_{1} }} + \frac{{DE_{7} }}{P} + E_{8} } \right) + \frac{{h_{1} DE_{6} }}{{P_{1} }}}}} ,$$

(40)

$$Q^{*} = \sqrt {\frac{{2\left( {K + M} \right)DE_{1} + 2\left( {d_{1} - d_{2} } \right)D^{2} gE_{4} }}{{h\left( {2E_{5} + \left( {1 - \frac{D}{P}E\left( {\frac{1}{1 - q}} \right)} \right)\frac{{2DE_{2} }}{x} + \frac{{\left( {P_{1} - D} \right)E_{6} }}{{P_{1} }} + \frac{{DE_{7} }}{P} + E_{8} } \right) + \frac{{h_{1} DE_{6} }}{{P_{1} }}}}} .$$

(41)

When the proposed model does not consider the assumptions of machine breakdowns and the presence of scrap items among the defective items, i.e. $M = 0$, $g = 0$, and $\theta = 0$, then one can derive the same equation as obtained by Öztürk (2017), only if the following equation holds:

$$\left( {1 - \frac{D}{P} - \frac{Dq}{{P\left( {1 - q} \right)}}} \right) = \left( {1 - \frac{D}{P}\left( {1 + \frac{q}{1 - q}} \right)} \right) = \left( {1 - \frac{D}{P}\left( {\frac{1}{1 - q}} \right)} \right).$$

(42)

Furthermore, in the case of a perfect production process, no defective items are produced, in which case we have $q = 0$, $d_{1} = d_{2} = 0$ and $P_{1} \to \infty .$ Then, Eq. (33) reduces to the following equation, as given by the traditional EPQ model:

$$Q^{*} = \sqrt {\frac{2KD}{{h\left( {1 - \frac{D}{P}} \right)}}} .$$

(43)

4 Numerical example

In this section, as an illustration of the proposed model in this paper, we consider an inventory situation similar to those in Hayek and Salameh (2001), and Moussawi-Haidar et al. (2016): the demand rate $D = 1200$ units/year, the production rate $P = 1600$ units/year, the rework rate $P_{1} = 1300$ units/year, the selling price of good items $S = \$ 200$/unit, the production setup cost $K = \$ 1500$, the disposal cost $C_{s} = \$ 6$/unit, the rework cost $C_{R} = \$ 8$/unit, the production cost $C = \$ 104$/unit, the inspection rate x = 175,200 units/year, the inspection cost during production $d_{1} = \$ 0.6$/unit, the inspection cost after production $d_{2} = \$ 0.5$/unit, the holding cost $h = \$ 20$/unit/year, the holding cost of reworkable items $h_{1} = \$ 22$/unit/year.

The proportion $q$ of defective items and the proportion $\theta$ of scrap items are uniformly distributed over the intervals $\left[ {0, 0.1} \right]$ and $\left[ {0, 0.2} \right]$, with the probability density functions $f_{1} \left( q \right)$ and $f_{2} \left( \theta \right)$, respectively, as follows:

$$f_{1} \left( q \right) = \left\{ {\begin{array}{*{20}c} {10, } & {0 \le q \le 0.1} \\ {0,} & {otherwise} \\ \end{array} } \right.\;{\text{and}}\;f_{2} \left( \theta \right) = \left\{ {\begin{array}{*{20}c} {20,} & {0 \le \theta \le 0.2, } \\ {0,} & {otherwise} \\ \end{array} } \right..$$

Moreover, the other related parameters are taken as follows: the repair cost for each breakdown $M = \$ 2000,$ the duration to repair the machine $g = 0.018$ years. The time-to breakdown, $t$, is a random variable with probability density function $f_{3} \left( t \right)$. Unlike other studies (Chung 2003; Chiu et al. 2007; Wee and Widyadana 2013), the time of the breakdown $t$ follows a uniform distribution. The probability density function is

$$f_{3} \left( t \right) = \left\{ {\begin{array}{*{20}l} {\frac{1}{{1.1T_{1} }},} \hfill &\quad {for\; 0 \le t \le 1.1T_{1} } \hfill \\ {0,} \hfill &\quad { otherwise.} \hfill \\ \end{array} } \right.$$

Using the above probability density functions, one can compute the following expected value expressions:

$E_{1} = \frac{1}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} = 1.005025$, $E_{2} = \frac{E\left( \theta \right)E\left( q \right)}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} = 0.005025$, $E_{3} = \frac{{\left( {1 - E\left( \theta \right)} \right)E\left( q \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} = 0.045226$, $E_{4} = \frac{{E\left( {\frac{1}{1 - q}} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} = 1.0589$, $E_{5} = \frac{{E\left( q \right)\left( {1 - E\left( q \right) - {\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D P}}\right.\kern-0pt} \!\lower0.7ex\hbox{$P$}}} \right)\left( {1 - E\left( \theta \right)} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} = 0.009045$, $E_{6} = \frac{{E\left( {\left( {1 - \theta } \right)^{2} } \right)E\left( {q^{2} } \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} = 0.002725$, $E_{7} = \frac{E\left( q \right)}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} = 0.050251$, $E_{8} = \frac{{\left( {1 - E\left( q \right) - {\raise0.7ex\hbox{$D$} \!\mathord{\left/ {\vphantom {D P}}\right.\kern-0pt} \!\lower0.7ex\hbox{$P$}}} \right)\left( {1 - E\left( q \right)} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} = 0.190955$ and $E_{9} = \frac{{E\left( \theta \right)E\left( {\frac{q}{1 - q}} \right)}}{{\left( {1 - E\left( \theta \right)E\left( q \right)} \right)}} = 0.005387.$

Applying Eqs. (35) and (36), one can obtain the optimal production run time $T_{1}^{*} = 0.791433$ years; the optimal production lot size $Q^{*} = 1266.29$ units; and the expected total profit per unit time is obtained as $E\left( {TPU\left( {T_{1}^{*} } \right)} \right) = \$ 107{,}275.11$. Table 2 shows that the optimal production policy depends on the uniform distribution parameter $a$. The optimal production run time $T_{1}^{*}$ decreases and the expected total profit $E\left( {TPU\left( {T_{1}^{*} } \right)} \right)$ increases as $a$ increases. Furthermore, Fig. 4 pictures the concavity of the expected total profit function for $a = 1.1, 1.3, 1.5$ values. For higher $a$ values, the optimal value of the production run time slightly converges to the left, and the expected total profit slightly increases when $a$ is increased. This results from the assumption that $a > 1$. Changing this value causes the behaviour of the model to reverse. If the value of the uniform distribution parameter $a$ is high, a breakdown is less likely to occur before the production run ends.

Table 2 Effect of changes in the uniform distribution parameter $a$ on optimal solution

Fig. 4

The behaviour of total profit versus the production run time for different uniform distribution parameter values

The results obtained for special cases using the proposed model are as follows:

Assuming that the uniform distribution parameter $a$ equals 1, i.e., $a = 1$, and using Eqs. (40), (41), and (39), the optimal production run time, $T_{1}^{*}$, the optimal production lot size, $Q^{*}$, and the expected total profit per unit time, $E\left( {TPU\left( {T_{1}^{*} } \right)} \right)$, would give the following results: $T_{1}^{*} = 0.812838$ years, $Q^{*} = 1300.54$ units, and $E\left( {TPU\left( {T_{1}^{*} } \right)} \right) = \$ 107{,}123.60$. This results in a 2.70% increase in the optimal production run time and − 0.14% decrease in the maximum total profit when compared to the optimal policy for the model when $a = 1.1$. Thus, as might be expected, a reduction in machine reliability, the optimal production run time increases to compensate for time lost as a result of machine breakdowns, and the maximum total profit falls accordingly.

When the proposed model does not allow the assumption of machine breakdown, one can obtain the optimal production run time $T_{1}^{*} = 0.531954$ years, the optimal production lot size $Q^{*} = 851.13$ units and $E\left( {TPU\left( {T_{1}^{*} } \right)} \right) = \$ 109{,}153.25$. This results in a 48.79% increase in the optimal production run time and − 1.28% decrease in the expected total profit when compared to the optimal policy for the model without random breakdowns.

When all the defective items are reworkable, i.e. $\theta = 0$, one can obtain the optimal production run time $T_{1}^{*} = 0.787222$ years, the optimal production lot size $Q^{*} = 1259.56$ units and the expected total profit $E\left( {TPU\left( {T_{1}^{*} } \right)} \right) = \$ 107{,}895.02$.

When there is no machine breakdown and if all the defective items are reworkable, i.e. $M = 0$, $g = 0$, and $\theta = 0$, one can obtain the optimal production run time, $T_{1}^{*} = 0.529124$ years, the optimal production lot size, $Q^{*} = 846.60$ units, and $E\left( {TPU\left( {T_{1}^{*} } \right)} \right) = \$ 109{,}772.86$.

Table 3 shows the results obtained from the relevant special cases. As seen in Table 3, the proposed model gives a higher optimal production run time than the model which does not include random breakdowns. Groenevelt et al. (1992) demonstrated the need for the optimal production lot to be greater than shown by the model without random breakdowns so as to compensate for lost production resulting from machine breakdowns; our results match the findings of Groenevelt et al. (1992). However, our results are not consistent with those of Chakraborty et al. (2008), who determined that both the optimal production lot and production run time would be smaller than in the model without random breakdowns. From the results, it is also observed that the reworking of reworkable items decreases the optimal production run time, while increasing the total profit. In addition, one should decide whether these items are scrapped or reworked to increase the total profit.

Table 3 The results for special cases

The aim of this study was to analyse the effects of both machine breakdown and inspection time on the results of the optimal solution. In this context, one of the most important assumptions made in the inventory question at hand was that the inspection continues even after the production is completed. This, in turn, makes it possible for different inspection costs to be used for in-production and after-production inspection processes. Therefore, it becomes necessary to analyse the effect of inspection cost on the results of the optimal solution.

For this purpose, let’s assume that the in-production inspection cost equals the after-production inspection cost, i.e. $d_{1} = d_{2} = 0.5$. The results of the solution obtained are as follows: The optimal production run time, $T_{1}^{*} = 0.791186$ years, the optimal production lot size, $Q^{*} = 1265.90$ units, and the expected total profit per unit time, $E\left( {TPU\left( {T_{1}^{*} } \right)} \right) = \$ 107{,}372.38$. Now, let’s assume that the in-production inspection cost is lower than that of the after-production inspection cost, i.e., $d_{1} < d_{2} = 0.7$. This solution produces results as follows: The optimal production run time, $T_{1}^{*} = 0.79094$ years, the optimal production lot size, $Q^{*} = 1265.50$ units, and the expected total profit per unit time, $E\left( {TPU\left( {T_{1}^{*} } \right)} \right) = \$ 107{,}228.44$.

These results, with the assumption that inspection continues after production, imply that the total profit is best when the inspection costs are equal to each other. Figure 5 pictures a graphical illustration of the change in the expected total profit and optimal run time with respect to inspection costs.

Fig. 5

The behaviour of total profit versus the production run time for different inspection cost values

We also investigated the effects of differences in the expected percentage of defective items on the optimal production run time and on total profit, including the above-mentioned screening costs, i.e., $d_{1} > d_{2}$, $d_{1} = d_{2}$, $d_{1} < d_{2}$. The first case ($d_{1} > d_{2}$) represents an in-production inspection cost which is higher than the after-production inspection cost, as was assumed by Moussawi-Haidar et al. (2016). In the second case ($d_{1} = d_{2}$), the costs of inspection in-production and after-production are the same. The third case ($d_{1} < d_{2}$) shows in-production inspection costs lower than after-production inspection costs. This indicates whether there is any benefit in conducting in-production inspection rather than after-production inspection. Graphical representations for different values of the expected percentage of defective items are shown in Figs. 6 and 7. All other parameters are unchanged. Increasing values of $E\left( q \right)$ imply production of more defective items, thus more items to inspect, meaning higher inspection cost and lower total profit.

Fig. 6

Total profit in relation to the expected proportion of defective items $E\left( q \right)$

Fig. 7

The production run time in relation to the expected proportion of defective items $E\left( q \right)$

One can see from the results shown in Fig. 6 that a bigger expected defective rate $E\left( q \right)$ leads to greater differences between the three conditions. It is also evident from the same figure that higher expected proportions of defective items make the second case ($d_{1} = d_{2} = 0.5$) increasingly advantageous in terms of profit. Furthermore, in the case of increasing numbers of defective products, though it varies with costs, the third case becomes more profitable than the first, indicating that after-production inspection is less costly than in-production inspection.

Figure 7 shows the optimal production run time for different values of the expected defective rate $E\left( q \right)$. The three curves shown on Fig. 7 illustrate the results for three different combinations of inspection costs. Other parameters are unchanged. It can be observed that the optimal production run time decreases as the expected defective rate $E\left( q \right)$ rises. Also, with higher in-production inspection costs, the optimal production run time is reduced.

Now, sensitivity analysis of the model is conducted to study the effects of changes in the different parameters $D, P$ and $P_{1}$ on the optimal values of the production run time $T_{1}^{*}$ and total profit $E\left( {TPU\left( {T_{1}^{*} } \right)} \right)$ by changing each of the parameters in the range −50% to +50%, focusing on one parameter at a time and keeping the remaining parameters unchanged. It may be interesting to explore the effects of rework rates higher and lower than the rate of demand on the optimal solution.

The results are presented in Table 4. Note that, it is important to verify that the conditions in Eqs. (37) and (38) are satisfied. The table gives the right-hand side (RHS) of Eqs. (37) and (38), calculated for eleven percentage changes in parameters $D, P$ and $P_{1}$. It is interesting to note that, if $D$ is increased from 40 to 50%, and $P$ is increased from − 50 to − 30%, this numerical example cannot be solved optimally. The reason behind this is the fact that the assumptions made about the parameters of $D$ and $P$ would not satisfy $\left( {P > D} \right),$ which will make it impossible to obtain the optimal production run time, $T_{1}^{*}$; therefore, the conditions of Eqs. (37) and (38) cannot be explored. The following observations can be made:

Table 4 Effect of percentage parameter changes in demand rate, production rate and rework rate on optimal solution

The optimal production run time is highly sensitive to changes in the demand rate and the production rate, and slightly sensitive to change in the rework rate. The optimal production run time increases with the increase in the value of the parameters $D$ and $P_{1}$, and decreases in the value of the parameter $P$. This is because of the fact that, the higher the demand, the longer the production run time required. This would require reworking of a higher number of defective items during a production run.

The total profit is significantly affected by the demand rate, moderately affected by the production rate, and slightly affected by the rework rate. The total profit decreases when the production rate increases, and increases when the demand rate and the rework rate increase. The results indicate that, if there is no constraint on the production run time, the higher the rework rates, the higher the total profit.

Table 5 shows the effects of expected defective rate, $E\left( q \right)$, and expected scrap rate, $E\left( \theta \right)$, on the optimal solution, as revealed using sensitivity analyses. The RHS of Eqs. (37) and (38) are calculated for eleven different values of the expected proportion of defective items $E\left( q \right)$ and the expected proportion of scrap items $E\left( \theta \right)$. The following observations can be made:

Table 5 Effect of changes in the expected defective rate and the expected scrap rate on optimal solution

The optimal production run time $T_{1}^{ *}$ is moderately sensitive to changes in the expected defective rate $E\left( q \right)$, and slightly sensitive to change in the expected scrap rate $E\left( \theta \right)$. The optimal production run time decreases when $E\left( q \right)$ increases, and increases when $E\left( \theta \right)$ increases. By reducing the production run time, one can cut the total number of defective items and minimize rework cost. This is because the reworked items are used to satisfy demand, which in turn allows for a decrease in the production run time. Producing a higher proportion of defective items increases production run times, as well as the optimal production lot size, to compensate for the cost of scrap items that are not used to satisfy demand.

The total profit is significantly affected by the expected defective rate $E\left( q \right)$, and slightly affected by the expected scrap rate $E\left( \theta \right)$. The total profit decreases when the expected defective rate $E\left( q \right)$ and the expected scrap rate $E\left( \theta \right)$ increase. Increasing the value of $E\left( q \right)$ involves higher rework cost and reduces total profit. Thus, rework cost can be reduced by decreasing defective items. Figures 8 and 9 illustrate these changes graphically.

Fig. 8

Sensitivity analysis of the production run time

Fig. 9

Sensitivity analysis of the total profit

5 Conclusion

This paper investigated the effects of an imperfect production process, subject to random breakdowns and inspection policy, on a production inventory system with rework. It was designed to give a more realistic analysis than the traditional EPQ model, by allowing for defective products, both for rework and for scrap. The time to machine breakdowns is assumed to follow a uniform distribution; repair or maintenance time of machinery is held constant; and the unit inspection costs for in-production and after-production inspections are different. Total cost functions have options to allow for and not allow for machine breakdown. The total profit per unit time is then calculated. The concavity of the expected total profit function is proved, and optimal policies are obtained. Optimal policy was found with the assumption of in-production inspection cost being higher than after-production inspection cost. However, analyses also incorporated the cases where both costs are equal and in-production inspection cost is lower than the after-production inspection cost.

Results of the numerical analysis showed that the total profit is the highest when in-production inspection cost equals the after-production inspection cost. The results also showed that the model with random breakdowns has higher production run times when compared to the model without random breakdowns, and the expected total profit is lower than in the model without random breakdowns. Groenevelt et al. (1992) demonstrated the need for the optimal production lot to be greater than shown by the model without random breakdowns so as to compensate for lost production resulting from machine breakdowns; our results match the findings of Groenevelt et al. (1992). However, our results are not consistent with those of Chakraborty et al. (2008), who determined that both the optimal production lot and production run time would be smaller than in the model without random breakdowns. Furthermore, the optimal production run time and the expected total profit are highly sensitive to changes in the values of the production rate and demand rate, with the demand rate being the parameter with the highest sensitivity to the maximum total profit. This study contributes to the literature by exploring scenarios such as in-production and after-production inspection, reworking or repairing defective items after inspection, different unit costs for inspection at different stages, and production machinery failure, all of which play an important role in managerial decisions.

The model developed in this study can be extended in a number of ways. In this study, it was assumed that only a percentage of the defective items are scrapped. On the other hand, a more realistic approach would be to assume that a percentage of reworked items are also scrapped before being introduced to the market. Another approach could be to explore this model as a preventive maintenance problem (Taleizadeh et al. 2014) for multiple items with backordering, in which the production process is interrupted more than one time in a production run time in order to restore the process to an in-control state. A failed machine may not be operational for a random period of time, which may result in shortages. The analysis of the model proposed in this study within the framework of an inventory control policy where exponentially distributed time-to-breakdown, exponentially and/or uniformly distributed repair/restoration time, and lost sales and backorder cases are considered, will also be a significant contribution in the future.

Appendix: Derivation of the mathematical equations

The total cost per cycle in (20) includes the production setup cost, the production cost, machine repair cost, inspection cost during and after production, disposal cost, reworking cost and holding cost, which is given as:

$$\begin{aligned} & TC_{1} \left( {T_{1} } \right) = K + M + C\left( {PT_{1} } \right) + C_{s} \theta q\left( {PT_{1} } \right) + d_{1} \left( {\frac{{DT_{1} + Dg}}{1 - q}} \right) + d_{2} \left( {PT_{1} - \frac{{DT_{1} + Dg}}{1 - q}} \right) \\ & \quad + C_{R} \left( {1 - \theta } \right)\left( {qPT_{1} } \right) \\ & \quad + h\left( {\frac{{H_{1} \left( t \right)}}{2} + \frac{{\left( {H_{1} + H_{2} } \right)\left( {t_{r} } \right)}}{2} + \frac{{\left( {H_{2} + H_{3} } \right)\left( {T_{1} - t} \right)}}{2} + \frac{{\left( {H_{3} + H_{4} } \right)\left( {t_{2} } \right)}}{2} + \frac{{\left( {H_{4} + H_{5} } \right)\left( {t_{3} } \right)}}{2} + \frac{{H_{5} \left( {t_{4} } \right)}}{2}} \right) \\ & \quad + h\left( {\frac{{\left( {dt} \right)\left( t \right)}}{2} + \left( {dt} \right)\left( {t_{r} } \right) + \frac{{\left( {dt + dT_{1} } \right)\left( {T_{1} - t} \right)}}{2} + \left( {dT_{1} } \right)\left( {t_{2} } \right)} \right) + h_{1} \left( {\frac{{\left( {\left( {1 - \theta } \right)dT_{1} } \right)\left( {t_{3} } \right)}}{2}} \right). \\ \end{aligned}$$

(44)

Then the first, second, third, fourth, fifth and sixth parts of the eighth term of $TC_{1} \left( {T_{1} } \right)$ become the following equations, respectively:

$$\frac{{H_{1} \left( t \right)}}{2} = \frac{{\left( {P - d - D} \right)t}}{2}t = \frac{{\left( {P - d - D} \right)t^{2} }}{2},$$

(45)

$$\frac{{\left( {H_{1} + H_{2} } \right)\left( {t_{r} } \right)}}{2} = \frac{{\left( {\left( {P - d - D} \right)t + \left( {P - d - D} \right)t - Dg} \right)g}}{2} = \left( {P - d - D} \right)gt - \frac{{Dg^{2} }}{2},$$

(46)

$$\begin{aligned} \frac{{\left( {H_{2} + H_{3} } \right)\left( {T_{1} - t} \right)}}{2} & = \frac{{\left( {\left( {P - d - D} \right)t - Dg + \left( {P - d - D} \right)t - Dg + \left( {P - d - D} \right)\left( {T_{1} - t} \right)} \right)\left( {T_{1} - t} \right)}}{2} \\ & = \left( {\left( {P - d - D} \right)t - Dg} \right)\left( {T_{1} - t} \right) + \frac{{\left( {P - d - D} \right)\left( {T_{1} - t} \right)^{2} }}{2}, \\ \end{aligned}$$

(47)

$$\frac{{\left( {H_{3} + H_{4} } \right)\left( {t_{2} } \right)}}{2} = \frac{{\left( {\left( {P - d - D} \right)t - Dg + \left( {P - d - D} \right)\left( {T_{1} - t} \right) + \left( {P - d - D} \right)t - Dg + \left( {P - d - D} \right)\left( {T_{1} - t} \right) - D\left( {\frac{{PT_{1} }}{x} - \frac{{DT_{1} + Dg}}{{\left( {1 - q} \right)x}}} \right)} \right)\left( {\frac{{PT_{1} }}{x} - \frac{{DT_{1} + Dg}}{{\left( {1 - q} \right)x}}} \right)}}{2}$$

(48)

$$\begin{aligned} \frac{{\left( {H_{4} + H_{5} } \right)\left( {t_{3} } \right)}}{2} & = \frac{{\left( {1 - \theta } \right)qPT_{1} }}{{P_{1} }}\left( {\left( {P - d - D} \right)t - Dg} \right) + \frac{{\left( {1 - \theta } \right)qPT_{1} }}{{P_{1} }}\left( {P - d - D} \right)\left( {T_{1} - t} \right) \\ & \quad - \frac{{\left( {1 - \theta } \right)qPT_{1} D}}{{P_{1} }}\left( {\frac{{PT_{1} }}{x} - \frac{{DT_{1} + Dg}}{{\left( {1 - q} \right)x}}} \right) + \frac{{\left( {P_{1} - D} \right)\left( {1 - \theta } \right)^{2} q^{2} P^{2} T_{1}^{2} }}{{2P_{1}^{2} }}, \\ \end{aligned}$$

(49)

$$\begin{aligned} \frac{{H_{5} \left( {t_{4} } \right)}}{2} & = \frac{{H_{5}^{2} }}{2D} = \frac{1}{2D}\left( {H_{4} + \left( {P_{1} - D} \right)t_{3} } \right)^{2} \\ & = \frac{1}{2D}\left( {\left( {P - d - D} \right)T_{1} - Dg - D\left( {\frac{{PT_{1} }}{x} - \frac{{DT_{1} + Dg}}{{\left( {1 - q} \right)x}}} \right) + \left( {P_{1} - D} \right)\frac{{\left( {1 - \theta } \right)qPT_{1} }}{{P_{1} }}} \right)^{2} . \\ \end{aligned}$$

(50)

In addition, the ninth and tenth terms of $TC\left( {T_{1} } \right)$ become the following equations, respectively:

$$\frac{{\left( {dt} \right)\left( t \right)}}{2} + \left( {dt} \right)\left( {t_{r} } \right) + \frac{{\left( {dt + dT_{1} } \right)\left( {T_{1} - t} \right)}}{2} + \left( {dT_{1} } \right)\left( {t_{2} } \right) = \frac{{Pqt^{2} }}{2} + Pqgt + \frac{{PqT_{1}^{2} }}{2} - \frac{{Pqt^{2} }}{2} + PqT_{1} \left( {\frac{{PT_{1} }}{x} - \frac{{DT_{1} + Dg}}{{\left( {1 - q} \right)x}}} \right),$$

(51)

$$h_{1} \left( {\frac{{\left( {\left( {1 - \theta } \right)dT_{1} } \right)\left( {t_{3} } \right)}}{2}} \right) = \frac{{h_{1} \left( {1 - \theta } \right)^{2} q^{2} P^{2} T_{1}^{2} }}{{2P_{1} }}.$$

(52)

Substituting these equations in (44), we have total inventory cost per cycle as

$$\begin{aligned} & TC_{1} \left( {T_{1} } \right) = K + M + \left( {C + d_{2} } \right)PT_{1} + C_{s} PT_{1} \left( {\theta q} \right) + + C_{R} PT_{1} \left( {1 - \theta } \right)q \\ & \quad + \left( {d_{1} - d_{2} } \right)DT_{1} \left( {\frac{1}{1 - q}} \right) + \left( {d_{1} - d_{2} } \right)Dg\left( {\frac{1}{1 - q}} \right) \\ & \quad + h\left\{ {P^{2} T_{1}^{2} \left( {\frac{{\left( {1 - \theta } \right)q\left( {1 - q - \frac{D}{P}} \right)}}{D} + \frac{\theta q}{x}\left( {1 - \frac{D}{{\left( {1 - q} \right)P}}} \right) + \frac{{\left( {P_{1} - D} \right)\left( {1 - \theta } \right)^{2} q^{2} }}{{2DP_{1} }} + \frac{q}{2P} + \frac{{\left( {1 - q} \right)\left( {1 - q - \frac{D}{P}} \right)}}{2D}} \right)} \right. \\ & \quad \left. { + PgT_{1} \left( {\theta q - 1 - \frac{D\theta }{x}\left( {\frac{q}{1 - q}} \right)} \right)} \right\} \\ & \quad + hPgt + \frac{{h_{1} P^{2} T_{1}^{2} \left( {1 - \theta } \right)^{2} q^{2} }}{{2P_{1} }}. \\ \end{aligned}$$

(53)