Introduction

Additive manufacturing (AM) is a transformative technology that offers great design freedom and environmental/ecological advantages, especially in fabricating components with intricate geometries,1,2 including components made from metals with high melting points. However, since metallic AM is a complicated process with various sources of uncertainty, the quality of the resulting products often shows significant variations,3 which becomes a major issue for the general adoption of metallic AM. A typical source of uncertainty during metallic AM is the fluctuating power absorption. The efficiency of the laser/electron beam power depends strongly on the absorbing surface and is associated with the powder packing4 and/or melt pool dynamics or flow behavior.5,6 Both the powder packing and melt flow inherently show random or unstable nature.7 Thus, uncertainty arises in the power absorption and propagates to the quality of the final product, together with other sources of uncertainty, such as fluctuations of AM machine parameters around their nominal settings, natural variability in temperature boundaries, etc.; For instance, Ma et al.8 clearly pointed out that the quality and properties of AM deposits can vary greatly even when the same materials, processing parameters, and type of AM machine are used. This largely prevents production of AM components with high and guaranteed quality.

To achieve quality control of AM processes, a good understanding of the sources of uncertainty and their effects on product quality through uncertainty quantification (UQ) is needed.9 However, systematic UQ based on extensive experiments to observe the variation of quantities of interest (QoIs) is usually prohibitively expensive. It becomes even more challenging when considering uncertainty management (UM) through robust design,10 where UQ must be repeated under numerous manufacturing conditions.11 This imposes significant technical difficulties on process optimization due to uncertainty. On the other hand, computer simulations based on sound physical principles can provide a cost-effective alternative, allowing UQ by performing virtual experiments in a time- and cost-saving manner. In fact, such model-based UQ has been widely adopted in practical engineering.12,13 Nevertheless, current UQ analysis for AM process is still at its infancy, since most investigations to date have simply focused on one part of the whole AM process, such as the variability in the melt pool geometry caused by uncertainty sources.14,15,16 In other words, the quantity of primary interest is usually not the quality of AM products. Therefore, detailed understanding of the propagation of uncertainty from the process to the microstructure structure and, eventually, to the properties of the product is still lacking.

In this paper, a generic UQ framework is proposed, aiming to enable efficient investigation of uncertainty propagation from process parameters to material microstructure, then to macro-level mechanical properties in the metallic AM process. It takes advantage of extensive multiscale multiphysics AM simulation data, limited experimental data, and surrogate modeling techniques. One specific example, viz. uncertainty quantification of the mechanical behavior of Ti-6Al-4V alloy fabricated by selective electron beam melting (SEBM), is used to illustrate the proposed framework. Six uncertainty sources arising from the melting and solidification processes in AM are investigated. Variance-based global sensitivity analysis is also conducted for comprehensive UQ study.

A Generic Computational Framework for UQ of AM

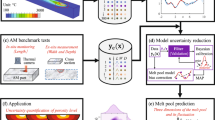
Figure 1 shows the generic procedure of the proposed computational framework for comprehensive UQ study of AM. The whole UQ process contains three steps:

Fig. 1
figure 1

Schematic of proposed UQ framework for the metal-based AM process. Here, a specific three-level UQ is used as an example to illustrate the proposed UQ framework

Full size image

  • Step 1 A specific multiscale physics-based model with experimental validation is selected depending on the involved sources of uncertainty and the product quality of interest (e.g., geometrical accuracy, surface roughness, porosity, strength, etc.). Based on the selected model, a large yet acceptable number of multiscale physics-based simulations are performed to generate training data for the construction of computationally inexpensive surrogate models. Note that the earlier trained lower-level surrogate model can replace the corresponding physical model, to accelerate multiscale simulations and thus generation of data to train a higher-level surrogate model.

  • Step 2 The surrogate models at different levels are trained, followed by cross-validations to test their effectiveness in replacing corresponding physical models. The multiple surrogate models enable uncertainty quantification of corresponding QoIs, thus providing clear insight into the entire process of uncertainty propagation. After construction of the surrogate model, experimental data are used to correct the model and calibrate the unknown model parameters.

  • Step 3 The corrected surrogate models with calibrated unknown model parameters are used to study uncertainty propagation for the entire AM process. Finally, sensitivity analysis is performed to reveal the contribution of each uncertainty source to the variability in product quality.

Taking uncertainty quantification of SEBM-fabricated Ti-6Al-4V components as an example, each step and their substeps are further described in the following sections.

Multiscale Multiphysics AM Simulation Model

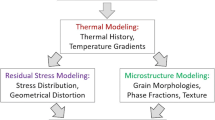
Multiscale multiphysics simulation models are used to predict the product quality under specific AM process parameters. The product quality of interest in the example case is the mechanical behavior of as-built components. Therefore, the multiscale simulation model selected combines a finite-element-based thermal model, grain growth phase-field model, and fast Fourier transform-based crystal elastoviscoplastic model (Fig. 2). Based on the selected model, here we mainly present how to utilize physical models, which usually come with rather complex outputs, to train useful surrogate models for UQ analysis. Regarding the selected multiscale model itself, refer to Refs. 17,18,19,20 for more details.

Fig. 2
figure 2

Schematic of selected multiscale AM simulation model that links process to structure and then properties

Full size image

Finite-Element-Based Thermal Model

In this multiscale model, a finite-element-based heat transfer model incorporating a moving heat source17 is utilized to predict the temperature field development. In the metallic AM process, high-power energy sources, such as a laser or electron beam, are usually applied. This results in a highly nonuniform temperature field within and around the melt pool that governs the formation of the final microstructure of the as-built component.

The current thermal simulation is performed to provide data for only the steady temperature field developed during AM, although it predicts the instantaneous temperature field for the whole AM process. This is primarily due to three reasons. Firstly, incorporation of the full-process thermal information into a grain growth model would be computationally prohibitive. Secondly, the microstructure of interest in grain growth simulation is the prior β-grain structure, which evolves only as the high-temperature field (above the β-transus temperature, Tβ-transus) sweeps through. During most of the process, the high-temperature field remains in a relatively steady state, and even shows a similar shape for different layers.21 As such, the full thermal process can be seen approximately as the steady high-temperature field moving back and forth with the heat source. Thirdly and most importantly, in light of this, a surrogate thermal model, which is able to predict the corresponding steady temperature field, can be trained for a fast approximation of the full thermal process, thus technically facilitating the training of a useful thermal surrogate model.

Grain Growth Phase-Field Model

The phase-field method has been widely adopted for simulating microstructural evolution. In particular, it offers advantages for complicated microstructures by avoiding explicit tracking of the evolving interface/boundary.22,23 Multiple physical phenomena and AM process features are taken into account in our custom phase-field model, including the temperature effect on grain-boundary mobility, undercooling-controlled grain nucleation at the top of the melt pool, a layer-by-layer incremental computational domain, etc.18,24

The grain growth phase-field model enables us to obtain the specific microstructure developed for an input temperature field. In this study, we select the mean and variance of the grain aspect ratio A, viz. μ(A) and σ2(A), as microstructure descriptors for training the surrogate model, rather than directly recognizing the microstructure image. Specifically, small μ(A) and σ2(A) correspond to uniform and equiaxed grain structures, which are favorable. The μ(A) and σ2(A) information is extracted from the phase-field simulation results then used to train a microstructure-prediction surrogate model that can quickly predict the distribution of grain aspect ratios and thus the approximate grain structure.

Fast Fourier Transform-Based Crystal Plasticity Model

A fast Fourier transform (FFT)-based crystal elastoviscoplasticity model is used to predict the local mechanical behavior of polycrystals deforming in the elastoviscoplastic regime. The effective mechanical properties of the polycrystal system can then be predicted by averaging the mechanical fields. The microstructure obtained from the grain growth phase-field simulations is the prior β-grain structure, which would transform to lamellar α + β structure at room temperature. In the current model, material parameters, including hardening and elastic parameters, adopt their volume-weighted average values. A volume fraction of α-phase of 88% is assumed based on experimental observations.25 The model itself just follows the original one for the single phase.19 Note that a more rigorous treatment for mechanical property predictions could use a two-phase model, after simulating the β → α phase transformation of as-received prior β-grains using phase-field models,26 which we leave for future work.

The mechanical behavior of each microstructure is predicted by applying a total tensile strain of 0.06, at a rate of 1.0 s−1, in the Z-direction perpendicular to the building base (along the long columnar grains). The output is the stress–strain curve of the overall polycrystal. The data underlying the stress–strain curve are essentially the effective stress responses at different deformation stages or strains. The current study trains a surrogate model that predicts \( \bar{\sigma } \) every \( \Delta \varepsilon \, = \,0.001 \). This size of Δε is small enough to render stress–strain curves with full details.

Data-Driven Surrogate Modeling of the AM Process

Principles of Surrogate Models

Surrogate models are constructed based on the extensive simulation data obtained from AM simulations. The surrogate model basically constructs the response or QoI as a function of various process variables, thus allowing fast prediction of responses at any given prediction point. Note that the response in practical engineering problems could be high dimensional, e.g., the temperature field and stepwise stress–strain relationship over time in the current case.

Existing methods for constructing computationally cheap surrogates include the classic response surface method,27 polynomial chaos expansion,28 Gaussian process model,29 regression tree,14,30 as well as the emerging artificial neural network.31 In this illustrative case, the Kriging surrogate modeling method (i.e., Gaussian process model)32 is employed to build the surrogate models, since Kriging can effectively capture the nonlinearity of the underlying models and can accommodate the noise in the data. To tackle the high-dimensional response issue, we adopt a singular value decomposition (SVD)-based Kriging surrogate modeling method.3 SVD provides a low-dimensional approximation of the original high-dimensional response in the latent space. This is done by representing the original high-dimensional data using truncated important features.33 In this regard, one actually carries out the surrogate modeling with respect to the low-rank approximations in the latent space. Thus, upon prediction, the as-obtained results are further reconstructed as high-dimensional data for practical use. Note that the framework presented herein is not limited to Kriging surrogate models but is also applicable to other surrogate model techniques.

Figure 3 shows the procedure for training each surrogate model from the melt pool simulation to the grain growth model, then to the elastoviscoplastic model. Note that, here, the response is built as a function of both control variables d (manufacturing settings) and random variables ω (uncertainty sources), thus enabling UQ under different manufacturing conditions and future process optimization under uncertainty. Taking the melt pool surrogate model as an example, next, we explain the training procedure with some mathematical detail. The training of the other two surrogate models (i.e., the microstructure and mechanical property surrogate models) should follow a similar or simpler procedure. After obtaining training data, T (x(i), s), i = 1, 2, …, N, where s represents all the spatial coordinates of the nodes, the original high-dimensional data are first approximated using SVD as follows:

$$ T\left( {\varvec{x}^{\left( i \right)} ,\varvec{s}} \right) \approx \sum\limits_{j = 1}^{m} {\gamma_{j} \left( i \right){\varvec{\upeta}}_{j} \left( \varvec{s} \right)} ,\quad \forall i = 1,2, \ldots ,N, $$
(1)

where γj(i), i = 1, 2, …, N; j = 1, 2, …, m are the responses in the latent space, m is the number of important features used in SVD, and ηj(s), j = 1, 2, …, m are the temperature features over space obtained through singular value decomposition.34 Equation 1 is a reduced-order model of the original temperature field response. We then build surrogate models in the latent space using a Kriging surrogate model or another type of surrogate model as3

$$ \gamma_{j} = \hat{g}_{j} (\varvec{x}),\quad j = 1,\;2, \ldots ,\;m. . $$
(2)
Fig. 3
figure 3

Schematic illustration of the training of surrogate models

Full size image

For any new prediction point x, we predict in the latent space, \( \gamma_{j} (i) \approx \hat{g}_{j} (\varvec{x}^{(i)} ) \). Thus, the high-dimensional response at the new prediction point is reconstructed as3

$$ T\left( {\varvec{x},\;\varvec{s}} \right) \approx \sum\limits_{j = 1}^{m} {\mu_{{\hat{g}_{j} }} (\varvec{x}){\varvec{\upeta}}_{j} (\varvec{s})} , $$
(3)

where \( \mu_{{\hat{g}_{j} }} (\varvec{x}) \) is the mean prediction of the jth latent-space surrogate model.

Replacing the Physics Models

The surrogate models at different levels are trained, followed by cross-validations to test their effectiveness in replacing corresponding physics models. For the surrogate model to accurately capture the relationship between the respective response and multiple inputs, a total of 280 thermal simulations, 150 grain growth simulations, and 150 EVP-FFT simulations are performed at specific training points by the Latin hypercube sampling method.35 The quality of the surrogate models can be quantified using leave-one-out cross-validation or other validation methods. Of all the simulation-obtained data, 20 temperature profiles, 5 microstructures, and 5 stress–strain curves are set aside for cross-validation, while the remainder are used for training. The thermal surrogate model is rather difficult to train compared with the other two because of the extremely high-dimensional responses, i.e., temperatures at 18,746 nodes based on the current adaptive meshing. Figure 4a compares the predicted temperature field (sectional view) between the finite-element simulation and surrogate model prediction. It clearly shows that they predict almost the same steady temperature field, developed by electron beam scanning in the direction from the upper right to bottom left. To present the difference between these predictions in a more straightforward way, Fig. 4b quantitatively compares the temperature predicted at each node of the full field. The minor deviation of all points from the y = x line further demonstrates the small difference between the finite element simulation and surrogate model predictions. For strict validation, the prediction difference is examined at a total of 20 arbitrary prediction points, four of which are shown in Fig. 4b–e due to figure size limit. All of them show similar distribution behaviors of simulation/prediction data points closely attached to the y = x line. More specifically, the average prediction error in terms of all nodes is respectively 0.15%, 0.15%, 0.17%, and 0.18% as compared with finite-element simulations. These comparisons confirm that the constructed surrogate model can be generalized to any prediction point within the practical range and can thus fully replace the original physical model.

Fig. 4
figure 4

(a) Qualitative comparison of temperature fields developed under test condition 1 through the physical simulation and surrogate model prediction; quantitative comparisons of nodal temperatures of temperature fields developed under (b) test condition 1, (c) test condition 2, (d) test condition 3 and (e) test condition 4

Full size image

Experimental Calibration

In the proposed UQ framework, the limited experimental data are used to calibrate and validate the prediction models and unknown parameters, which are specifically reflected in two aspects: (1) experimental validation of physics models and (2) correction and parameter calibration of surrogate models, as shown in Fig. 1. While the experimental validation of simulation models is quite common, in the following, we just provide details about the experimental calibration.

It is known that the original physical models are usually not perfect, due to either simplifications made or imperfect understanding of the AM process. Model discrepancy (i.e., difference between prediction and reality) can be induced and inherited by corresponding surrogate models. There are also other contributing factors to model discrepancy, such as the approximate solution methods in the simulation model, or the surrogate model itself being an approximation to the original model.9 In addition to model discrepancy, there are some unknown model parameters (due to lack of knowledge) in the AM simulation model. To improve confidence in our AM prediction model, the experimental data can be employed to correct the prediction model and calibrate the unknown model parameters simultaneously. Following the framework developed by Kennedy and O’Hagan (commonly referred to as the KOH framework),36 we have the following surrogate model with experimental calibration:

$$ \varvec{y} = G\left( {\varvec{x,\theta }} \right) + \delta \left( {\varvec{x,\theta }} \right) + \varepsilon_{FEA} \left( {\varvec{x,\theta }} \right) + \varepsilon_{obs} , $$
(4)

where y represents the experimental value, G(x, θ) is the prediction through as-obtained Kriging surrogates for given inputs of x and θ, δ accounts for model discrepancy due to model inadequacy, εFEA is the numerical discretization error while solving the simulation model, and εobs is the observation error. θ is a vector of parameters that need to be calibrated; these parameters can have physical meanings, or simply be some tunable parameters to improve the accuracy of predictions.37δ and εFEA are modeled using the as-mentioned SVD-based Kriging model in the case of high-dimensional responses, while εobs is often treated as a simple zero-mean Gaussian random variable. The discretization error εFEA can be directly quantified through simulations with distinct mesh sizes using the Richardson extrapolation method.33 The model discrepancy δ and unknown parameters θ are calibrated simultaneously using Bayesian analysis, in which the posterior density of the calibration parameters can be explored via the Markov chain Monte Carlo (MCMC) method.38 The final surrogate model with experimental calibration, Eq. 4, can be utilized for more practical predictions. Detailed investigations on such experimental calibration are still underway and will be reported in subsequent papers.

Uncertainty Quantification and Sensitivity Analysis

Uncertainty Sources

Many sources of uncertainty are involved in the complex AM process. AM process variables identified as uncertainty sources in previous AM UQ studies can be found in Refs. 8,15,16,39,40,41. As shown in Fig. 5, the uncertainty sources of interest in this illustrative study mainly include thermally related parameters (i.e., fluctuating power absorption efficiency, η, thermal conductivity, k, specific heat capacity, cp, and density, ρ) and grain growth-related parameters (i.e., grain boundary energy, σgb, and thermal activation energy of grain growth, Q). The uncertainty sources selected can directly cause uncertainty in either the temperature field development during melting or the microstructure evolution during solidification, ultimately leading to variability in mechanical properties. The reasonable distribution range of these random variables can be determined by observing the different values for them adopted in previous studies (summarized in Ref. 11). All of the referred studies are based on the same Ti-6Al-4V material and SEBM process. For the sake of illustration, the type of distribution for the random variables is assumed to be either Gaussian or lognormal.

Fig. 5
figure 5

Schematic illustration of uncertainty sources introduced at different levels and uncertainty propagation

Full size image

Uncertainty Quantification

Using the brute-force Monte Carlo (MC) approach,42 uncertainty quantification of a property of the product can be achieved through massive predictions (here 1000 realizations) with the computationally cheap surrogate model. The manufacturing condition is Tpre = 950 K, P = 400 W, and v = 0.40 m/s, based on an Arcam® S12 AM machine in practice. Figure 6a shows the uncertainty of the mechanical properties characterized by the fluctuating stress–strain curves induced by the multiple uncertainty sources mentioned above. The fluctuation is quite clear due to the great variability in these uncertainty sources and their effective propagation to the property; For example, the energy absorption efficiency varies in a wide range of 0.6–0.9 based on practical AM43,44 (both using Ti-6Al-4V material and Arcam® S12 AM machine). These uncertainties propagate first to the microstructure of the material, causing high variability in the microstructure within as-built AM components, as examined and shown in Fig. 6b. The mean prediction indicates that the most likely outcome is to obtain columnar grain structures featuring some equiaxed grains at the top [mean of grain aspect ratio: μ(A) ≈ 2.25, variance of grain aspect ratio: σ2(A) ≈ 2.60]. However, the potential microstructure could be fully columnar [μ(A) ≈ 6.63, σ2(A) ≈ 3.13] or equiaxed [μ(A) ≈ 1.01, σ2(A) ≈ 0.07] in extreme cases. Such large uncertainty in the microstructure would ultimately lead to great variability in the mechanical properties, as reflected by, for example, the significantly higher strength of the equiaxed structure than the columnar structure. In this regard, clear variability in the mechanical properties of AM products has also been found practically.45 Based on the UQ carried out here, as well as previous experimental findings, future work could involve uncertainty management through robust design,10 i.e., intelligently manipulating controllable operating parameters to minimize the variability in product properties caused by uncertainty sources.

Fig. 6
figure 6

(a) Uncertainty quantification of the mechanical properties; (b) uncertainties in process variables first propagate to the microstructure obtained, causing clear uncertainty in the microstructure of the material that ultimately leads to great variability in the mechanical properties of as-built AM products. The probability density function [inset in (a)], clearly shows the likelihood of obtaining different microstructures characterized by different mechanical responses

Full size image

Global Sensitivity Analysis

Global sensitivity analysis46 is also carried out to investigate the contribution of each source of uncertainty to the variability in products. Here, we analyze the individual contribution of the studied uncertainty sources to the variability in the microstructure within as-built products, characterized by the mean and variance of the grain aspect ratio in this study. Figure 7 shows the different effects of each source of uncertainty on these two quantities, based on calculations of their corresponding first-order Sobol index. It is found that the mean aspect ratio of grains is most sensitive to the density and grain boundary energy, while the variance of the aspect ratios of the grains is greatly influenced by the heat capacity and grain growth activation energy. Reducing the uncertainty in these influential uncertainty sources would be more effective to obtain AM products with consistent microstructure and properties.

Fig. 7
figure 7

Sensitivity of microstructure to various uncertainty sources: (a) mean of grain aspect ratio and (b) variance of grain aspect ratio

Full size image

Conclusion

This paper presents a generic UQ framework to systematically study the propagation of uncertainties from the process to the structure and on to the properties in metal-based additive manufacturing, through cooperation between advanced multiscale multiphysics AM simulation and data-driven surrogate modeling. The framework is applied for comprehensive UQ study of SEBM of Ti-6Al-4V alloy. Based on the proposed framework, uncertainty quantification is carried out to reveal the clear variability in the product properties induced by various sources of uncertainty. Global sensitivity analysis is also performed, revealing the high sensitivity of the microstructure to uncertainty sources including the material density, grain boundary energy, heat capacity, and grain growth activation energy.

Following the overall UQ framework proposed, future work will include model correction and parameter calibration of the constructed surrogate models with the availability of experimental data, thus allowing for more reliable UQ analysis. After that, robust design or reliability-based design optimization could be performed to determine the optimal manufacturing condition that enables production of AM components with consistent properties. The proposed model-based UQ framework should be generally applicable to comprehensive UQ study of various product qualities, depending on the physical model selected. Besides the physical model adopted for illustration in this study, there are also other kinds of AM simulation model, which permit linking the process variables to various quality metrics such as porosity,47 surface structure,7,48 residual stress,49,50 mechanical properties,51 and fatigue life.52 As the current model-based UQ of the AM process is still at an early stage, especially in terms of the uncertainty propagation from the process to structure and then properties, the presented UQ framework provides a promising starting point for future research on systematic uncertainty quantification and management of the AM process.