1 Introduction

An electron beam is a widely applied tool in welding technology, surface treatment (e.g., surfi-sculpt [1]) and recently additive manufacturing (e.g., Electron beam selective melting [2]). The major advantages of using an electron beam as a heat source include: (1) high coefficient of energy absorption by materials, especially compared with laser heat sources, (2) high energy density, and (3) a vacuum environment preventing oxidation or other contaminations. These advantages make the electron beam an extremely valuable manufacturing tool but there are many challenges which need to be addressed in order for full maturity of the processing technique to be achieved. For instance, the temperature history and distribution are very complex, including ultrahigh heating/cooling rates (up to \(10^{8}\,\hbox {K/s}\)) and temperature gradients (on the order of \(10^{8}\,\hbox {K/m}\) [3]), resulting from the extremely localized high intensity heat input from the electron beam; distortion, residual stresses and even cracks in the final products are often observed as a direct result. There have been numerous investigations focused on the thermal distribution, the microstructures and mechanical properties, and thermal and thermo-mechanical modeling.

The heat source model is the basis of the thermal simulations, directly determining the accuracy of the entire prediction. The first heat source model can be traced back to the point and line models by Rosenthal [4] in 1946, which were simplified for analytical analyses. The representative Gaussian-distributed heat source model was proposed by Pavelic [5] in 1969, which overcame the limitations of the infinite point model and the line model. Based on Pavelic’s ‘disc’ model, some authors suggested the use of distributed heat throughout the molten zone in order to reflect the penetration of the heat source [6]. Another popular distribution model based on the shape of molten pool is the double ellipsoidal geometry proposed by Goldak in 1984 [7]. In fact, the Gaussian distribution models can be considered special cases of the Goldak model. The Gaussian distribution heat source model remains the most popular model to date [8, 9]. However, the physical basis of these distribution models is quite weak, most being simply based on assumptions according to experimental observations of the molten pool shape. In the electron beam manufacturing processes, the molten pool shape is not only decided by energy distribution of the heat source, but is also strongly influenced by the liquid metal flow driven by a variety of forces such as surface tension and gravity. In other words, the traditional models (as shown in Fig. 1) are effective combinations of many influencing factors but not the actual input energy distributions. Considering that the traditional models are based on the shape of molten pool, the predicted molten pool shape and temperature field outside the molten pool should necessarily be similar to the experiments. However, it is worth noting that the actual development of the molten pool, the temperature field in the molten pool, and the heat affected zone (HAZ), which are typically of primary concern, cannot be predicted accurately. In order to investigate the complex phenomena taking place in the molten pool (e.g., temperature field), it is essential to utilize a realistic heat source model which incorporates the experimentally observed influencing factors along with the energy input distribution.

Fig. 1
figure 1

Traditional heat source models. a Surface Gaussian model [8], b double ellipsoidal model [7] and c rotatory Gaussian body model [9]

Full size image

In this investigation, a new electron beam heat source model was established based on a Monte Carlo simulation of the interaction of the electron beam and a solid substrate, and the general formula of the new heat source model was given. The detailed modeling procedures will be described in the next section. The new heat source model was implemented in the finite element analysis software, ABAQUS, for comparison with the traditional surface flux model and the volumetric flux model through numerical simulation, as shown in Sect. 3.1. A static electron beam heating a substrate was simulated with the new heat source model to illustrate the realistic primary formation process of the molten pool, as described in Sect. 3.2. The general conclusions of the work will be discussed in Sect. 4.

2 New heat source model based on electron-atom interactions

2.1 Monte Carlo simulation of electron-substrate interactions

2.1.1 Basic principles

The process of the electron beam heating a substrate is in essence the result of interaction between electrons and atoms. Numerous electrons impinge the material and then collide elastically or inelastically with the material atoms, resulting in energy transfer from the electrons to the material.

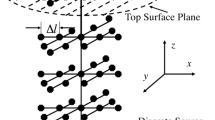
The underlying methodology applied in the Monte Carlo simulation of the electron-material interaction is schematically shown in Fig. 2. First, electrons impinging the material at each position are generated within an assumed Gaussian-distributed electron beam with a preset total number of electrons [10]. The initial kinetic energy of every electron was 60 keV, meaning that the acceleration voltage was 60 kV. Each individual electron trajectory was traced, as depicted in Fig. 2(b). As Fig. 2(b) shows, there are three types of atoms (A, B,C) of different sizes in the substrate, representing three element types. The electron collides with an initial atom followed by an alteration in the speed and direction of the electron while the kinetic energy of the electron is partially transferred to the atom. Essentially, the thermal energy of an object is the summation of the kinetic energy of all the atoms in it. Thus the mechanism of electron beam heating is the collisions between electrons and atoms. In the simulation, the direction change is determined by a random collision angle which represents the random distribution of atoms in the substrate while the energy transfer is taken into account by the mean energy loss model as follows [11]:

$$\begin{aligned} E_{j+1}= & {} E_j +\frac{dE}{dS}\cdot L \nonumber \\ \frac{dE}{dS}= & {} \frac{-7.8\times 10^{-3}\rho }{E_j }{\times }\sum _{i=1}^n {\frac{C_i Z_i }{F_i }} {\ln } \left( 1.116\left( \frac{E_j }{J_i}{+}K_i\right) \right) \nonumber \\&\times \,[KV/nm], \end{aligned}$$
(1)

where E refers to the kinetic energy of an electron, the subscript j is the jth collision, L is the distance between two elastic collisions, and \(C_{i},\, Z_{i},\, J_{i}\) and \(K_{i}\) are the mass fraction, atomic number, mean ionization potential, and a constant of element i, respectively.

Fig. 2
figure 2

Schematic of electron-material interaction methodology. a Simulation flowchart and b electron penetration trajectories

Full size image

The collision and energy transfer are repeated until the electron escapes from the material (see trajectory 2 in Fig. 2(b)) or gets trapped once the kinetic energy falls below the threshold value of 50 eV (see trajectory 1 in Fig. 2(b)). Finally, the input heat distribution could be established by summing the energy transfer between each individual electron and the material in the electron pass-by regions, where the electron penetrated through.

2.1.2 Model setup

The substrate material used in the Monte Carlo simulation for this work was TC4 and the main chemical compositions were used as inputs to the model, as shown in Table 1 (WT % means weight percentage). The trace elements were ignored for the present study. The simulations were performed employing open-source code CASINO [10].

Table 1 Input chemical composition of TC4
Full size table

The electron beam parameters used for the present study are listed in Table 2.

2.1.3 Results

Table 2 Electron beam parameters
Full size table

The simulated electron trajectories are shown in Fig. 3. The blue trajectories mean the electrons got trapped, while the red trajectories imply escape of the electrons. The maximum penetration depth of electrons into the TC4 substrate is about \(15\,\upmu \hbox {m}\), ignoring a minor amount of electrons that penetrate deeper. As shown in Fig. 3, the maximum penetration depth appears in the center of the beam, this is due to a higher number density of electrons at the center than at the perimeter. Naturally, more electrons at a given location will allow for higher probability of reaching larger penetration depths; that is why the penetration depth decreases far from the center.

Fig. 3
figure 3

Simulated electron trajectories

Full size image

2.2 Power density distribution function

The absorbed energy distribution in the TC4 substrate was obtained as shown in Fig. 4. In the XZ plane (y = 0), the highest energy density appears at about 4400 nm underneath the surface, instead of residing on the top surface. The intensity distributions along the transverse and in-plane directions are illustrated in Fig. 5a,b, respectively. A simple curve fit was performed to establish the following energy intensity distribution function as illustrated in Fig. 5. The red line in Fig. 5 is the Gaussian-shaped fitting curve.

$$\begin{aligned} \text{ Intensity(z) }=1.542\,\times \exp \left( -\frac{({\hbox {z-}}4397) ^{{2}}}{{5}712^{{2}}}\right) . \end{aligned}$$
(2)
$$\begin{aligned} \hbox {Intensity(r)}=2.008\,\times \exp \left( -\frac{\hbox {(r{-}1450)}^{{2}}}{22{,}870^{{2}}}\right) . \end{aligned}$$
(3)

According to the definition,

$$\begin{aligned} \hbox {(Intensity(z))}\,\% =\int _{\mathrm{z}-\frac{1}{2}\Delta \hbox {z}}^{\mathrm{z}+\frac{1}{2}\Delta \hbox {z}} {\hbox {f}(\xi )\hbox {d}\xi }. \end{aligned}$$
(4)

\(\Delta \hbox {z}\) is one division depth and \(\hbox {f}(\xi )\) is the energy density distribution as a function of depth.

Fig. 4
figure 4

Absorbed energy intensity distribution in the XZ plane

Full size image
Fig. 5
figure 5

Energy intensity distribution in the transverse and in-plane directions. a Intensity distribution in the transverse direction (Z) and b intensity distribution in the in-plane direction (r)

Full size image

Since \(\Delta \hbox {z}=\hbox {134.7\,nm}\) is small enough compared to the maximum penetration depth of \(15\,\upmu \hbox {m}\),

$$\begin{aligned} \hbox {(Intensity(z))}\%= & {} \text {f}(z)\Delta \hbox {z}. \end{aligned}$$
(5)
$$\begin{aligned} \hbox {f}(z)= & {} \frac{\hbox {(Intensity(z))}\%}{\Delta \hbox {z}}=0.000114\nonumber \\&{\times }\,\exp \left( -\frac{\hbox {(z\,-\,4397)}^{{2}}}{{5}712^{{2}}}\right) (1/\text {nm}). \end{aligned}$$
(6)

Similarly in the radial in-plane direction, with an electron beam radius \(R_{b}=50\,\upmu \hbox {m}\) and \(\Delta \hbox {r}={3}80.5\,\hbox {nm}\), the intensity function becomes

$$\begin{aligned} \hbox {g}(r)=\frac{\hbox {(Intensity(r))}\%}{\Delta \hbox {r}}= & {} 0.000053\,\nonumber \\&{\times }\exp \left( -\frac{\hbox {(r-1450)} ^{{2}}}{22870^{{2}}}\right) (1/\hbox {nm}),\nonumber \\ \end{aligned}$$
(7)

where r and z in the above equation are in nm.

The energy distribution in the transverse direction is determined by the initial kinetic energy of electrons. On the other hand, the energy distribution in the in-plane direction (r direction) is determined by the electron distribution in the cross section of the beam. It should be noted that the distribution of electrons is assumed to have a Gaussian distribution which may require even further scientific validation. This assumption is the reason that the energy density function in the in-plane direction appears to be a Gaussian distribution. However, as the number of electrons at a given location was randomly generated in the simulation, fluctuations exist in the intensity(r), as shown in Fig. 5(b). Therefore, \(\hbox {g}(r)\) has a slight offset from the expected ideal Gaussian shape.

In summary, based on the Monte Carlo simulation of electron-material interactions, the general form of the electron beam heat source model should be:

$$\begin{aligned} q(x,y,z)= & {} Q{\times }\left[ {\frac{{1}}{\delta \!\cdot \! \displaystyle \int _{{-}\frac{\hbox {z}_0 }{\delta }}^{+\infty } {\exp (-\hbox {t}^{{2}})\hbox {dt}} }\exp \left( \!-\!\frac{({z\!-\!z}_0 )^{{2}}}{\delta ^{{2}}}\right) } \right] \nonumber \\&{\times }\left[ \frac{N}{\pi R_b ^{2}}\exp \left( \!-\!N\!\cdot \! \frac{({x\!-\!x}_{\mathrm{s}})^{{2}}\!+\!({y\!-\!y}_{\mathrm{s}} )^{{2}}}{R_b^{{2}}}\right) \right] ,\nonumber \\ \end{aligned}$$
(8)

where Q represents the beam power, the first square bracketed term represents the distribution in transverse direction \((\hbox {f}(z)\) in Eq. (6)), \(\hbox {z}_0\) and \(\delta \) are the location with the highest energy density and the characteristic depth, respectively, as decided by the acceleration voltage only, and the second square bracketed term represents the distribution through the cross section of the beam \((\hbox {g}(r)\) in Eq. (7)), where N represents the concentration coefficient of the electron beam, \(R_{b}\) is the beam radius, and \(x_{s}\) and \(y_{s}\) are the coordinates of the center of the beam. The Monte Carlo simulation results match Eq. (8) almost perfectly when the coordinate variables are transferred from (r, z) in Eqs. (6) and (7) to (x, y, z) in Eq. (8).

For the case of powder bed additive manufacturing, the input energy distribution in the cross section remains the same, while the distribution in the depth direction should also consider the impinging angles at different locations within the powder. Since most electrons will be absorbed by the powder, multi-deflection can be ignored, which is different from the interaction observed between a laser beam and powder bed.

3 Thermal simulations of electron beam heating substrate

In order to evaluate the potential impact of this new heat source model, two thermal processes were simulated. The first process is that of a moving electron beam heating a solid substrate. For comparison, three different heat source models were employed: (1) the surface heat flux model, (2) the traditional volumetric heat flux model and (3) the new model. The second process is that of a static electron beam heating a small solid domain to investigate the formation of the molten pool using the new heat source model. It should be noted that these two processes are general processes and could take place in the electron beam welding, electron beam additive manufacturing and electron beam surface treatment processes.

3.1 Moving electron beam heating substrate

As shown in Fig. 6, the solid substrate of Ti-6Al-4V (TC4) was \(1.2\,\mathrm{{mm}}\times 0.8\,\mathrm{{mm}}\times 0.4\,\mathrm{{mm}}\), while the applied electron beam had a radius of 0.2 mm and was moving at a velocity of 200 mm/s. The main purpose of this section is to investigate the differences between the new heat source model and traditional models when implemented into general thermal simulations without considering molten pool flow or evaporation. The electron beam employed has a concentration coefficient (N) of 3. The new heat source model is as follows (Note that the coordinates were in mm in thermal models).

$$\begin{aligned} q(x,y,z)= & {} Q\times \frac{3}{\pi R^{2}}\exp \left( {-3\cdot \frac{(x-x_s )^{2}+(y-y_s )^{2}}{R^{2}}} \right) \nonumber \\&\times \, 114\, \hbox {exp}\left( {-\frac{\hbox {(z-0.004)}^{2}}{{0.005}^{2}}} \right) . \end{aligned}$$
(9)

The surface flux model, which only takes into account the in-plane distribution, is defined as

$$\begin{aligned} q(x,y,z)=Q\times \frac{3}{\pi R^{2}}\exp \left( {\!-\!3\cdot \frac{(x\!-\!x_s )^{2}+(y-y_s )^{2}}{R^{2}}} \right) .\nonumber \\ \end{aligned}$$
(10)

The traditional volumetric flux model considers the approximated depth of the molten pool as the penetration depth, as illustrated in the following Eq. [12].

$$\begin{aligned} q(x,y,z)= & {} Q\times \frac{3}{\pi R^{2}}\exp \left( {-3\cdot \frac{(x-x_s )^{2}+(y-y_s )^{2}}{R^{2}}} \right) \nonumber \\&\times \frac{2}{h}\left( {1-\frac{z}{h}} \right) , \end{aligned}$$
(11)

where h refers to the approximated depth of molten pool of about 0.1 mm.

Fig. 6
figure 6

schematic of a moving electron beam heating a solid substrate

Full size image

3.1.1 Initial and boundary conditions

A uniform preheated temperature of 900 K was applied to the domain as the initial condition.

Since the process took place in vacuum environment, heat convection was assumed to be negligible and was not considered in the analysis. The thermal conduction through the boundary was also neglected, as insulation often exists, e.g., insulation provided by the powder bed in additive manufacturing. The heat loss by the radiation at the top surface was taken into account as follows:

$$\begin{aligned} q_R =-A\cdot \sigma \cdot \varepsilon \left( T^{4}-T_a ^{4}\right) , \end{aligned}$$
(12)

where A refers to the area of the top surface, \(\sigma =5.67\times 10^{-8}\, (W/(m^{2}\cdot K^{4}))\) is the Stefan–Boltzmann constant, \(\varepsilon =0.2\) is the emissivity coefficient and \(T_a =300\,K\) is the ambient temperature.

3.1.2 Material properties

The material properties were assumed constant for simplification, ignoring temperature dependence. Latent heat was taken into consideration. The material parameters are listed in Table 3.

Table 3 Properties of TC4 [13]
Full size table

3.1.3 Results

The simulated temperature fields by ABAQUS are shown in Fig. 7. It should be noted that the contour legends are the same for ease of comparison. Since the three heat source models differ only by their distributions in the depth direction and thermal conduction can easily compensate some differences, the temperature fields are quite similar. In particular, outside the molten pool, where thermocouples could be set in experiments, the temperature fields are nearly indistinguishable. This could be the reason that publications utilizing different heat source models declare accurate temperature predictions without rigorously determined physics-based heat source models. However, the worth-noting difference is that the peak temperature with surface flux model was above both peak temperatures predicted by the other two heat source models. The peak temperature for the surface flux model, the traditional volumetric model and the new model are 4090, 2774 and 3670 K, respectively. Even though the effective penetration depth of the 60 keV electron beam is only \(15\,\upmu \hbox {m}\), the new heat source model, which considers the penetration depth, leads to quite a different peak temperature (900 K higher than that obtained with the traditional volumetric flux model and 420 K lower than that predicted with the surface heat flux model).

Fig. 7
figure 7

Temperature field obtained for each heat source model (one half cut by plane Y = 0). a Temperature field using the new model, b temperature field using the volumetric flux model and c temperature field using the surface flux model

Full size image

The recoil pressure is the dominant driving force of molten pool dynamics [14] and analysis of this metric requires an accurate prediction of the location and timing of the peak temperature. The actual temperature distribution and the shapes of the molten pool and the HAZ should be a result of the combination of input heat and molten pool dynamics, which all depend heavily on the heat source model. While traditional heat source models were employed as effective combinations of input heat and molten pool dynamics, more investigations should be focused on implementing realistic heat source models and considering the induced molten pool dynamics in order to thoroughly and accurately understand and characterize these processes.

In this paper, Since this work is focused on the realistic heat source model instead of coupled thermo-fluid simulations, evaporation and molten pool flow are not considered. However, when the simulated peak temperatures are equal to or higher than boiling temperature, it could be implied that serious evaporations would occur, causing recoil pressure. In future works, the recoil pressure could be estimated based on the simulated temperature field and then applied in a sequential coupled molten pool flow model to further illustrate the influence of heat source models.

The molten pool is assumed to occur in the region corresponding to temperatures higher than 1900 K, while the HAZ is characterized by temperatures higher than 1250 K. As shown in Fig. 8, the molten pool and HAZ with the three different heat source models are similar in shape. The molten pool sizes with the surface flux model, the new model and the traditional volumetric flux model slightly decrease, while the HAZ sizes are nearly the same, as listed in Table 4 (Note: HAZ width/depth = molten pool width/depth + increment, HAZ length = increment (behind) + molten pool length + increment (front)). The bold underline terms for HAZ represent the sizes of molten pools while other terms represent the increments.

Fig. 8
figure 8

Molten pool (T > 1900 K) and HAZ (1900K>T>1250K). a Molten pool with new model, b molten pool with volumetric flux model, c molten pool with surface flux model, d HAZ with new model, e HAZ with volumetric flux model and f HAZ with surface flux model

Full size image
Table 4 Outline sizes of molten pool and HAZ
Full size table

Therefore, while the molten pool shapes with the three selected models were similar, the major difference that was provided by the new heat source model was the predicted temperature field in the molten pool, particularly the peak temperature, which will influence the evaporation, recoil pressure, molten pool dynamics and thermal convection.

3.2 Primary formation of molten pool

Section 3.1 illustrated that the major difference with the selected models was the temperature field in the molten pool. In order to demonstrate the impact of this difference, the process of a static electron beam heating a small domain was simulated with the new heat source model.

3.2.1 Model setup

As shown in Fig. 9, the solid domain of Ti–6Al–4V (TC4) was \(0.1\,\mathrm{{mm}}\times 0.1\,\mathrm{{mm}}\times 0.03\,\mathrm{{mm}}\), while the diameter of the electron beam was selected to be 0.1 mm. The input heat source model was exactly the aforementioned result of the Monte Carlo simulation. The implemented input heat source model was as follows:

$$\begin{aligned} q(x,y,z)= & {} Q\times \frac{4.8}{\pi R^{2}}\exp \left( -4.8\cdot \frac{x^{2}+y^{2}}{R^{2}}\right) \nonumber \\&\times \, 114\exp \left( -\frac{\hbox {(z-0.0044)}^{2}}{{0.0057}^{2}}\right) . \end{aligned}$$
(13)
Fig. 9
figure 9

Schematic of static electron beam heating a substrate

Full size image

The boundary conditions and material properties were the same as those used in Sect. 3.1 except that the initial temperature of the substrate was 300 K. Preheating was not performed in order to reveal the temperature rising process and primary molten pool formation process more clearly.

3.2.2 Results

Considering the penetration of electrons, the location of the highest temperature underneath the surface of the substrate should correspond to the location of the highest energy density provided by the heat source model. As shown in Fig. 10, the highest temperature appears at about \(4.5\,\upmu \hbox {m}\) underneath the top surface, exactly the \(\hbox {z}_0\) position, which is the location with the highest energy density. In Fig. 10, the red region represents temperatures above 1878 K (the melting point), and the purple region represents temperatures above 3900 K. At \(\hbox {t}=1.45\,\upmu \hbox {s}\), a small red spot appeared at a depth of \(\hbox {z}_0\), representing the first melting position. Then, the molten pool developed and the top surface was not melted until \(\hbox {t}=1.68\,\upmu \hbox {s}\). The thermal distributions in the first three time instances shown demonstrate that the primary formation of the molten pool is driven by the input energy distribution and the thermal conduction inside the domain before evaporation happens. Therefore, there is significant benefit in utilizing a realistic heat source model. It is worth noting that after \(\hbox {t}=4.04\,\upmu \hbox {s}\), the peak temperature rises to a level somewhere in the range of 3900–6000 K. Once the temperature rises to above 3900 K (near the boiling temperature), evaporation may take place and will become the dominant driving force in the development/evolution of the molten pool.

Fig. 10
figure 10

Primary formation of the molten pool. a t\(\,=\,\)0.40 \({\upmu }\)s, b t\(\,=\,\)1.45 \({\upmu }\)s, c t\(\,=\,\)1.61 \({\upmu }\)s, d t\(\,=\,\)1.68 \({\upmu }\)s, e t\(\,=\,\)2.93 \({\upmu }\)s, f t\(\,=\,\)4.04 \({\upmu }\)s and g t\(\,=\,\)4.88 \({\upmu }\)s

Full size image

It is possible that with higher acceleration voltages and higher beam current the penetration depth could get larger and the peak temperature could become high enough that evaporation would take place underneath the surface before the top surface has had time to melt. The explosion or eruption schematically shown in Fig. 11 could then occur. The explosion-eruption phenomena can be explained only by the new heat source model. More detailed investigations will be conducted in future work.

Fig. 11
figure 11

Schematic of explosion and eruption and experimental observations. a Explosion, b eruption and c experimental observations [15]

Full size image

4 Conclusion

In order to overcome the lack of physical basis of traditional surface and volumetric heat flux models of the electron beam, Monte Carlo simulations were performed to describe the penetration trajectories of electrons and the absorbed energy distribution corresponding to an electron beam applied to a solid substrate. A new general form of an electron beam heat source model was obtained, as shown in Eq. (8), which has a much stronger physical relevance than its predecessors.

Thermal simulations of a moving electron beam heating a solid substrate were conducted with different heat source models. It was demonstrated that the new heat source model results in a noticeably different temperature distribution than that obtained with traditional models, while the sizes of the molten pool and the HAZ were similar. On the other hand, the simulation of a static electron beam heating a solid domain employing the new heat source revealed that the molten pool formation started underneath the top surface, overturning traditional knowledge. Some specific phenomena, i.e., eruption and explosion, in electron beam manufacturing can be scientifically explained by the new heat source model while traditional models are found to be lacking in this ability.

On the basis of this work, evaporation should be investigated, especially because of the vacuum environment. The recoil pressure and molten pool dynamics should be considered based on the implementation of the realistic heat source model, to deeply and accurately understand what is going on in the processes.

In future work, laser beam manufacturing, another widely used manufacturing technology, will be investigated. The heat source models for the laser beam should be different from those used for electron beam due to differing physics. One of the primary differences between the interaction of a laser beam applied to a substrate material and its electron beam counterpart is that most of the photons are deflected rather than absorbed into the material. However, for powder-based additive manufacturing methods, such as selective laser melting (SLM), photons could reach deep into the powder bed because of multi-deflection between particles. Therefore, similar Monte Carlo simulations could be performed to investigate the SLM process from the viewpoint of the particle scale.