Controlling Biological Invasions: A Stochastic Host–Generalist Parasitoid Model

Abstract

On a global scale, biological invasions are seriously destroying the stability of ecosystem, sharply decreasing biodiversity and even endangering human health and causing huge economic losses. However, there exist few effective measures controlling biological invasions. To more accurately examine the prevention and control effects of biological control on biological invasions in real environments of random fluctuations, we construct a stochastic host–generalist parasitoid model. We first establish, respectively, the sufficient conditions for the persistence and extinction of invasive hosts and generalist parasitoids, including (1) only the intrusive hosts go extinct; (2) only the generalist parasitoids are extinct, and (3) the intrusive hosts and generalist parasitoids are both extinct or persistent. Then, we perform a series of numerical simulations to verify the validity of the theoretical results obtained, based on which we further discuss the impacts of stochastic environmental fluctuations on the control of intrusive hosts, especially the possible changes of qualitative behavior caused by environmental noises in the bistable scenario. Our theoretical and numerical results indicate that compared with the invasive hosts, the generalist parasitoids are more vulnerable to environmental noises, and the prevention and control effects of biological control on invasive hosts are closely dependent to the initial population sizes. Thus, improving the ability of early detection of ecosystems, including the initial densities of biological populations and their dynamic characteristics, will provide effective predictive guidance for the prevention and control of alien host invasions.

1 Introduction

Biological invasion is the geographical expansion of a species into a region that it has not previously occupied (Ehler 1998). In the context of applied entomology, the invasion process is relevant to both the unintentional introduction of exotic pests and the intentional introduction (i.e., planned invasion) of natural enemies (Ehler 1998). With the rapid development of world trade globalization, people are increasingly aware that biological invasion not only leads to the transformation and reconstruction of ecosystem components, but also changes the basic functions and features of ecosystem, which eventually leads to the extinction of local species and the decline of biodiversity as well as the seriously damages social and economic construction (Mack et al. 2000). In order to mitigate the damage of biological invasion, various control techniques have been developed and applied, including mechanical and physical techniques (such as hand destruction and barriers (Simberloff 2003), chemical pesticide (Hall et al. 2004) and biological control (such as natural enemies and bio-pesticides (Barratt et al. 2018). Mechanical and physical techniques are simple and safe but requires lots of manpower. Chemical pesticide is effective, however it will cause the alien invasive species resistance and resurgence (Yuan et al. 2021). Biological control, the science and technology of controlling pests using natural enemies, has had several recent successes (Strong and Pemberton 2000). In contrast, biological control is the one of the most promising solutions (Moffat et al. 2013; Li et al. 2014; Madec et al. 2017).

In (Owen and Lewis 2001), Owen and Lewis pointed out that when the invasive populations have strong Allee effect, the specialist predators can effectively prevent or even reverse their invasion processes; however, when they have only weak Allee effect, the specialist predators can slow down but cannot reverse the invasion process of alien species. In (Ehler 1998; Owen and Lewis 2001), the authors pointed out that no matter whether the invasive populations have Allee effect or not, the generalist predators can more easily reverse prey invasions than the specialist predators. Since generalist predators do not need to consider the special dynamic properties of focus prey in terms of controlling alien biological invasions, generalist predators can more extensively characterize the scenarios of biological control. Especially, based on a real case that the invasion of leaf-mining microlepidopteron attacking horse chestnut trees in Europe, Magal et al. (Magal et al. 2008) constructed a host–generalist parasitoid model. In the specific model, the parasitoid is a generalist that is already established in a region where the leafminers have been introduced and may spread. Since parasitoid survives on other food resources in the absence of the leafminers, its population dynamics in the absence of the leafminers is described by a logistic equation with a positive growth rate. On the other hand, based on (Owen and Lewis 2001; Fagan et al. 2002), when the leafminers began to invade European horse chestnut trees in 1985, leafminers also followed a logistic growth. Meanwhile, since the introduction of leafminers provided a new food source for the parasitoid, it was supposed that predation by the generalist parasitoid on the leafminers satisfies the Holling II functional response. The biological control system of invading leafminers they proposed takes the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\textrm{d}u}{\textrm{d}\tau }=r_{1}u\big (1-\frac{u}{K_{1}}\big )-\frac{\xi uv}{1+\xi hu},\\ \frac{\textrm{d}v}{\textrm{d}\tau }=r_{2}v\big (1-\frac{v}{K_{2}}\big )+\frac{\gamma \xi uv}{1+\xi hu}, \end{array}\right. } \end{aligned}$$

(1)

where $u(\tau )$ and $v(\tau )$ are, respectively, the population densities of invading hosts (leafminers) and generalist parasitoids at time $\tau \ge 0$. All the parameters in model (1) are positive constants: $r_{1}$ and $K_{1}$ are, respectively, the intrinsic rate of natural increase and the environment carrying capacity for invading hosts; $r_{2}$ and $K_{2}$ are the intrinsic rate of natural increase and the environment carrying capacity for generalist parasitoids in absence of focal hosts; $\xi$ denotes the capture rate of invading hosts by generalist parasitoids; h is the handling time; $\gamma$ is the conversion rate of generalist parasitoids feeding on invading hosts. By performing rigorous some mathematical analyses and a series of numerical simulations, the authors mainly explored effective biological control strategies of the generalist parasitoids and established the sufficient conditions for the extinction of intrusive leafminers in European forest ecosystems.

In a recent paper (Xiang et al. 2020), Xiang et al. have nondimensionalized model (1) as:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\textrm{d}x}{\textrm{d}t}=x(1-x)-\frac{bxy}{a+x},\\ \frac{\textrm{d}y}{\textrm{d}t}=y(\delta -y)+\frac{cxy}{a+x}, \end{array}\right. } \end{aligned}$$

(2)

where $x=\frac{u}{K_{1}}$, $y=\frac{r_{2}v}{r_{1}K_{2}}$, $t=r_{1}\tau$, $a=\frac{1}{K_{1}\xi h}$, $b=\frac{K_{2}}{r_{2}K_{1}h}$, $\delta =\frac{r_{2}}{r_{1}}$ and $c=\frac{\gamma }{r_{1}h}$. Their results showed that there exists a threshold value $K^{*}$ for the environment carrying capacity of generalist parasitoids: When $K_{2}<K^{*}$, the invading hosts survive, which implies that the generalist parasitoids cannot prevent the invasion of hosts; when $K_{2}>K^{*}$, the invading hosts may survive or may die out, which closely depends on the levels of initial populations. Notice that in both scenarios, the generalist parasitoids are always persistent.

However, in nature ecosystems, environmental fluctuations are always everywhere, which affects the survival status of biological populations at all times. May (May 2001) once clearly pointed out that in the real world, various attribute parameters of biological populations, such as the birth rate, mortality, capture rate and transmission coefficient, will inevitably be influenced by random environmental fluctuations to a larger or smaller extent. To this end, many researchers (Neubert et al. 2000; Petrovskii et al. 2005; O’Malley et al. 2009; Schreiber and Ryan 2011; Parsons 2018; Billiard and Smadi 2020) have applied stochastic mathematical models to investigate the control problem of biological invasion. For example, Petrovskii et al. (Petrovskii et al. 2005) considered the patchy spread patterns of models on biological invasions and biological control in deterministic and stochastic environments. Their findings indicated that the tiny fluctuations of controlling parameters could bring the alien populations either to extinction or to restoration of its invasion. Parsons (Parsons 2018) investigated a class of discrete stochastic process population model with density-limited growth, and showed that the population size exists a maximum value and greatly exceeds carrying capacity at arbitrary times with high probability before population extinction.

Motivated by above, it seems more proper to consider the influence of environmental fluctuations in deterministic model (2). Applying standard method to include environmental noises (Evans et al. 2013; Hening et al. 2018; Feng et al. 2021), we can derive the following stochastic differential equations model:

$$\begin{aligned} {\left\{ \begin{array}{ll} \textrm{d}x=\big (x(1-x)-\frac{bxy}{a+x}\big )\textrm{d}t+\sigma _{1}x\textrm{d}B_{1}(t),\\ \textrm{d}y=\big (y(\delta -y)+\frac{cxy}{a+x}\big )\textrm{d}t+\sigma _{2}y\textrm{d}B_{2}(t), \end{array}\right. } \end{aligned}$$

(3)

where $\sigma _{1}^{2}$ and $\sigma _{2}^{2}$ are the intensities of environmental interferences, $B_{1}(t)$ and $B_{2}(t)$ are the mutually independent standard Brownian motions defined on a complete probability space $(\Omega ,\mathcal {F},\{\mathcal {F}_{t}\}_{t\ge 0},\mathbb {P})$ with a filtration $\{\mathcal {F}_{t}\}_{t\ge 0}$ satisfying the usual conditions. The main purpose of this paper is to explore how environmental fluctuations affect the controlling strategies of biological invasions. Our findings indicate that compared with the invasive hosts, generalist parasitoids are more vulnerable to environmental noises, and the prevention and control effects of biological control on invasive hosts are closely related to the initial population sizes. Thus, improving the ability of early detection of ecosystems, including the initial densities of biological populations and their dynamic characteristics, will provide effective predictive guidance for the prevention and control of alien host invasions.

The organization of this paper is as follows: In Sect. 2, we first establish sufficient conditions, respectively, for the persistence and extinction of the stochastic intrusive host–generalist parasitoid model (3), which include (1) only the intrusive hosts go extinct; (2) only the generalist parasitoids are extinct; (3) the entire stochastic model (3) is extinct; and (4) both the intrusive hosts and generalist parasitoids are persistent. Then, in Sect. 3, we perform a series of numerical simulations to verify the validity of the theoretical results obtained, based on which we further discuss the impacts of stochastic environmental fluctuations on the control of intrusive hosts, especially the possible changes of qualitative behavior caused by environmental noises in the bistable scenario. Finally, a brief discussion is presented in Sect. 4.

2 Main Results

2.1 Some Preliminaries

In order to analyze the survival of intrusive hosts and generalist parasitoids theoretically, respectively, further to explore the roles of random interferences on controlling biological invasions of hosts, we first investigate some basis mathematical properties of stochastic model (3), which include the existence, uniqueness and boundedness of the positive solution. We will make use of some correlation theories of stochastic differential equations (see Mao 1997; Klebaner 2005; Khasminskii 2012) to obtain the desired conclusions. Since x(t) and y(t) are, respectively, the population densities of intrusive hosts and generalist parasitoids, they exist biological significances only when both $x(t)\ge 0$ and $y(t)\ge 0$. Thus, we need first to verify the existence and uniqueness of global positive solution for stochastic model (3).

Theorem 1

For any given positive initial value $(x(0),y(0))\in \mathbb {R}_{+}^{2}$, stochastic model (3) has a unique global positive solution (x(t), y(t)) for all $t\ge 0$ almost surely (a.s.).

Proof

See Appendix 1. $\square$

Then, we verify the boundedness for the solution of stochastic model (3), which indicates that the densities of biological populations are bounded.

Theorem 2

The solution (x(t), y(t)) of stochastic model (3) established by Theorem 1 is bounded, that is

$$\begin{aligned} \limsup _{t\rightarrow +\infty }(cx(t)+by(t))<+\infty ~a.s. \end{aligned}$$

Proof

See Appendix 1. $\square$

2.2 Extinction of the Invading Hosts

The research focus of the paper is to explore the important effects of random environmental noises on controlling the invasion of hosts. In this subsection we establish the sufficiently conditions under which the intrusive hosts are extinct, while the generalist parasitoids are persistent. Before that we first present a useful lemma.

Lemma 1

For one-dimensional stochastic differential equation:

$$\begin{aligned} \textrm{d}z=z(\Lambda -z)\textrm{d}t+\sigma z\textrm{d}B(t), \end{aligned}$$

(4)

where B(t) is standard Brownian motion, when $\frac{\sigma ^{2}}{2}<\Lambda$, Eq. (4) exists a unique ergodic stationary distribution with the corresponding invariant density

$$\begin{aligned} \pi (\zeta )=\left( \frac{\sigma ^{2}}{2}\right) ^{1-\frac{2\Lambda }{\sigma ^{2}}}\Gamma ^{-1} \left( \frac{2\Lambda }{\sigma ^{2}}-1\right) e^{-\frac{2\zeta }{\sigma ^{2}}}\zeta ^{\frac{2\Lambda }{\sigma ^{2}}-2},~\mathrm{for~all~}\zeta >0, \end{aligned}$$

(5)

satisfying that for any integrable function $h(\cdot )$,

$$\begin{aligned} \mathbb {P}\Big \{\lim _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}h(z(s))\textrm{d}s=\int _{\mathbb {R}_{+}}h(\zeta )\pi (\zeta )\textrm{d}\zeta \Big \}=1. \end{aligned}$$

(6)

Proof

See Appendix 2. $\square$

Theorem 3

Let (x(t), y(t)) be the nonnegative solution of stochastic model (3) derived in Theorem 1. When $\frac{\sigma _{1}^{2}}{2}>1$, the invading hosts x(t) will go to extinction almost surely, i.e., $\lim _{t\rightarrow +\infty }x(t)=0$ a.s.; Further when $\frac{\sigma _{2}^{2}}{2}<\delta$, the generalist parasitoids y(t) are persistent, there exists a unique ergodic stationary distribution with the corresponding invariant density

$$\begin{aligned} \pi (\zeta )=\left( \frac{\sigma _{2}^{2}}{2}\right) ^{1-\frac{2\delta }{\sigma _{2}^{2}}}\Gamma ^{-1} \left( \frac{2\delta }{\sigma _{2}^{2}}-1\right) e^{-\frac{2\zeta }{\sigma _{2}^{2}}}\zeta ^{\frac{2\delta }{\sigma _{2}^{2}}-2},~\mathrm{for~all~}\zeta >0, \end{aligned}$$

(7)

satisfying that for any integrable function $h(\cdot )$,

$$\begin{aligned} \mathbb {P}\Big \{\lim _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}h(y(s))\textrm{d}s=\int _{\mathbb {R}_{+}}h(\zeta )\pi (\zeta )\textrm{d}\zeta \Big \}=1. \end{aligned}$$

(8)

In addition, the average persistence level of generalist parasitoids is $\int _{0}^{+\infty }\zeta \pi (\zeta )\textrm{d}\zeta =\delta -\frac{\sigma _{2}^{2}}{2}.$

Proof

First, under the condition $\frac{\sigma _{1}^{2}}{2}>1$, we justify the extinction of invading hosts. Applying Itô’s formula to $\ln x(t)$, we have

$$\begin{aligned} \textrm{d}\ln x(t)=&\frac{1}{x}\left( \left( x(1-x)-\frac{bxy}{a+x}\right) \textrm{d}t+\sigma _{1}x\textrm{d} B_{1}(t)\right) +\frac{1}{2}\left( -\frac{1}{x^{2}}\right) \sigma _{1}^{2}x^{2}\textrm{d}t\\ =&\left( 1-x-\frac{by}{a+x}-\frac{1}{2}\sigma _{1}^{2}\right) \textrm{d}t+\sigma _{1}\textrm{d}B_{1}(t)\\ \le&\left( 1-\frac{1}{2}\sigma _{1}^{2}\right) \textrm{d}t+\sigma _{1}\textrm{d}B_{1}(t). \end{aligned}$$

Integrating from 0 to t and dividing by t on both sides of the above equation and then taking limit $t\rightarrow +\infty$, we yield

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{\ln x(t)}{t}\le \lim _{t\rightarrow +\infty }\frac{\ln x(0)}{t}+1-\frac{1}{2}\sigma _{1}^{2}+\lim _{t\rightarrow +\infty } \frac{\mathcal {M}_{1}(t)}{t}, \end{aligned}$$

(9)

where $\mathcal {M}_{1}(t)=\int _{0}^{t}\sigma _{1}\textrm{d}B_{1}(s)$ is a local and continuous martingale satisfying $\mathcal {M}_{1}(0)=0$. By simple computations we have the corresponding quadratic variation $\langle \mathcal {M}_{1},\mathcal {M}_{1}\rangle _{t}=\int _{0}^{t}\sigma _{1}^{2}\textrm{d}s=\sigma _{1}^{2}t$, and $\limsup _{t\rightarrow +\infty }\frac{\langle \mathcal {M}_{1},\mathcal {M}_{1}\rangle _{t}}{t}=\sigma _{1}^{2}<+\infty$ a.s. Then with the help of the strong law of large numbers in (Mao 1997), we can obtain that $\lim _{t\rightarrow +\infty }\frac{\mathcal {M}_{1}(t)}{t}=0$ a.s. It then follows from (9) that

$$\begin{aligned} \lim _{t\rightarrow +\infty }\frac{\ln x(t)}{t}\le 1-\frac{1}{2} \sigma _{1}^{2}<0~~a.s., \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{t\rightarrow +\infty }x(t)=0~~a.s. \end{aligned}$$

Next, on the premise of the extinction of invading hosts, we further consider the limit system of the generalist parasitoids as follows:

$$\begin{aligned} \textrm{d}y=y(\delta -y)\textrm{d}t+\sigma _{2}y\textrm{d}B_{2}(t). \end{aligned}$$

(10)

It follows from Lemma 1 that when $\frac{\sigma _{2}^{2}}{2}<\delta$, system (10) possesses the conclusions (7) and (8).

Finally, combining conclusions (7) and (8), we can further calculate the average persistence level of generalist parasitoids y(t) on the premise of the extinction of invading hosts x(t) . That is,

$$\begin{aligned} \int _{0}^{+\infty }\zeta \pi (\zeta )\textrm{d}\zeta =&\int _{0}^{+\infty }\zeta \left( \frac{\sigma _{2}^{2}}{2}\right) ^{1-\frac{2\delta }{\sigma _{2}^{2}}}\Gamma ^{-1}\left( \frac{2\delta }{\sigma _{2}^{2}}-1\right) e^{-\frac{2\zeta }{\sigma _{2}^{2}}}\zeta ^{\frac{2\delta }{\sigma _{2}^{2}}-2}\textrm{d}\zeta \\ =&\left( \frac{\sigma _{2}^{2}}{2}\right) ^{1-\frac{2\delta }{\sigma _{2}^{2}}} \Gamma ^{-1}\left( \frac{2\delta }{\sigma _{2}^{2}}-1\right) \int _{0}^{+\infty }e^{-\frac{2\zeta }{\sigma _{2}^{2}}}\zeta ^{\frac{2\delta }{\sigma _{2}^{2}}-1}\textrm{d}\zeta \\ =&\left( \frac{\sigma _{2}^{2}}{2}\right) ^{1-\frac{2\delta }{\sigma _{2}^{2}}} \Gamma ^{-1}\left( \frac{2\delta }{\sigma _{2}^{2}}-1\right) \int _{0}^{+\infty }e^{-\theta } \left( \frac{\sigma _{2}^{2}}{2}\theta \right) ^{\frac{2\delta }{\sigma _{2}^{2}}-1} \frac{\sigma _{2}^{2}}{2}\textrm{d}\theta \\ =&\frac{\sigma _{2}^{2}}{2}\Gamma ^{-1}\left( \frac{2\delta }{\sigma _{2}^{2}}-1\right) \int _{0}^{+\infty }e^{-\theta }\theta ^{\frac{2\delta }{\sigma _{2}^{2}}-1}\textrm{d}\theta \\ =&\delta -\frac{\sigma _{2}^{2}}{2}. \end{aligned}$$

This completes the proof of Theorem 3. $\square$

Remark 1

From Theorem 3 we know that when the influences of the environmental interferences acting on the invading hosts population x(t) are larger $\left( \textrm{namely}, \frac{\sigma _{1}^{2}}{2}>1 \right)$, the invading hosts will go to extinction. That is to say, large noise is conducive to the control of invasive species as well as the maintaining stability of ecosystem, which are in accord with the conclusions in (Davis et al. 2000; Davis and Pelsor 2001) and (Wang et al. 2021). Moreover, when the intensities of random environmental noises are smaller than the recruitment rate for the generalist parasitoids y(t) (namely, $\frac{\sigma _{2}^{2}}{2}<\delta$), we can know that the generalist parasitoids population is persistent with the average level $\delta -\frac{\sigma _{2}^{2}}{2}$ in the absence of invading hosts.

2.3 Extinction of the Generalist Parasitoids

Notice that all living populations in nature are inevitably affected by environmental noises. In this subsection we consider the situation when the intensity of environmental fluctuations suffered by the generalist parasitoids is large, while that of the invading hosts is small. The detailed conclusions are as follows:

Theorem 4

Denote by (x(t), y(t)) the solution of stochastic model (3) established by Theorem 1. When $\frac{\sigma _{1}^{2}}{2}<1$ and $\frac{\sigma _{2}^{2}}{2}>\delta +\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}$, the generalist parasitoids y(t) are extinct, namely, $\lim _{t\rightarrow +\infty }y(t)=0$ a.s.; while the invading hosts x(t) are persistent, there exists a unique ergodic stationary distribution with the corresponding invariant density

$$\begin{aligned} \mu (\zeta )=\left( \frac{\sigma _{1}^{2}}{2}\right) ^{1-\frac{2}{\sigma _{1}^{2}}}\Gamma ^{-1} \left( \frac{2}{\sigma _{1}^{2}}-1\right) e^{-\frac{2\zeta }{\sigma _{1}^{2}}}\zeta ^{\frac{2}{\sigma _{1}^{2}}-2},~\mathrm{for~all~}\zeta >0, \end{aligned}$$

(11)

satisfying that for any integrable function $h(\cdot )$,

$$\begin{aligned} \mathbb {P}\Big \{\lim _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}h(x(s))\textrm{d}s=\int _{\mathbb {R}_{+}}h(\zeta )\mu (\zeta )\textrm{d}\zeta \Big \}=1. \end{aligned}$$

(12)

In addition, the average persistence level of intrusive hosts is $\int _{0}^{+\infty }\zeta \mu (\zeta )\textrm{d}\zeta =1-\frac{\sigma _{1}^{2}}{2}.$

Proof

Considering the first equation of stochastic model (3), further with the help of the comparison theorem for stochastic differential equations, we can obtain the following 1-dimensional auxiliary stochastic differential equation

$$\begin{aligned} \textrm{d}X(t)=X(1-X)\textrm{d}t+\sigma _{1}X\textrm{d}B_{1}(t) \end{aligned}$$

(13)

with the initial value $X(0)=x(0)>0$. Obviously $X(t)\ge x(t)$ a.s. It follows from Lemma 1 that when $\frac{\sigma _{1}^{2}}{2}<1$, it is easy to acquire that the Eq. (13) possesses a unique stationary density

$$\begin{aligned} \mu (\zeta )=\left( \frac{\sigma _{1}^{2}}{2}\right) ^{1-\frac{2}{\sigma _{1}^{2}}}\Gamma ^{-1} \left( \frac{2}{\sigma _{1}^{2}}-1\right) e^{-\frac{2\zeta }{\sigma _{1}^{2}}}\zeta ^{\frac{2}{\sigma _{1}^{2}}-2},~\mathrm{for~all~}\zeta >0, \end{aligned}$$

(14)

and the ergodic stationary distribution satisfies

$$\begin{aligned} \mathbb {P}\Big \{\lim _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}h(X(s))\textrm{d}s=\int _{\mathbb {R}_{+}}h(\zeta )\mu (\zeta )\textrm{d}\zeta \Big \}=1. \end{aligned}$$

(15)

Furthermore, we can compute the average persistent level of system (13) as follows:

$$\begin{aligned} \int _{0}^{+\infty }\zeta \mu (\zeta )\textrm{d}\zeta =&\int _{0}^{+\infty }\zeta \left( \frac{\sigma _{1}^{2}}{2}\right) ^{1-\frac{2}{\sigma _{1}^{2}}}\Gamma ^{-1}\left( \frac{2}{\sigma _{1}^{2}}-1\right) e^{-\frac{2\zeta }{\sigma _{1}^{2}}}\zeta ^{\frac{2}{\sigma _{1}^{2}}-2}\textrm{d}\zeta \\ =&\left( \frac{\sigma _{1}^{2}}{2}\right) ^{1-\frac{2}{\sigma _{1}^{2}}} \Gamma ^{-1}\left( \frac{2}{\sigma _{1}^{2}}-1\right) \int _{0}^{+\infty }e^{-\frac{2\zeta }{\sigma _{1}^{2}}}\zeta ^{\frac{2}{\sigma _{1}^{2}}-1}\textrm{d}\zeta . \end{aligned}$$

Applying variable substitution $t=\frac{2\zeta }{\sigma _{1}^{2}}$, the above equation becomes

$$\begin{aligned} \int _{0}^{+\infty }\zeta \mu (\zeta )\textrm{d}\zeta =&\left( \frac{\sigma _{1}^{2}}{2}\right) ^{1-\frac{2}{\sigma _{1}^{2}}} \Gamma ^{-1}\left( \frac{2}{\sigma _{1}^{2}}-1\right) \int _{0}^{+\infty }e^{-t} \left( \frac{\sigma _{1}^{2}}{2}t\right) ^{\frac{2}{\sigma _{1}^{2}}-1} \frac{\sigma _{1}^{2}}{2}\textrm{d}t\\ =&\frac{\sigma _{1}^{2}}{2}\Gamma ^{-1}\left( \frac{2}{\sigma _{1}^{2}}-1\right) \int _{0}^{+\infty }e^{-t}t^{\frac{2}{\sigma _{1}^{2}}-1}\textrm{d}t\\ =&\frac{\sigma _{1}^{2}}{2}\Gamma ^{-1}\left( \frac{2}{\sigma _{1}^{2}}-1\right) \Gamma \left( \frac{2}{\sigma _{1}^{2}}\right) =\frac{\sigma _{1}^{2}}{2}\left( \frac{2}{\sigma _{1}^{2}}-1\right) \\ =&1-\frac{\sigma _{1}^{2}}{2}. \end{aligned}$$

Next, we analyze that under what conditions the generalist parasitoids of stochastic model (3) die out. Making use of Itô’s formula to $\ln y(t)$, we have

$$\begin{aligned} \textrm{d}\ln y(t)=&\frac{1}{y}\left( \left( y(\delta -y)+\frac{cxy}{a+x}\right) \textrm{d}t+\sigma _{2}y\textrm{d}B_{2}(t)\right) +\frac{1}{2} \left( -\frac{1}{y^{2}}\right) \sigma _{2}^{2}y^{2}\textrm{d}t\nonumber \\ =&\left( \delta -y+\frac{cx}{a+x}-\frac{1}{2}\sigma _{2}^{2}\right) \textrm{d}t+\sigma _{2}\textrm{d}B_{2}(t)\nonumber \\ \le&\left( \delta +\frac{cX}{a+X}-\frac{1}{2}\sigma _{2}^{2}\right) \textrm{d}t+\sigma _{2}\textrm{d}B_{2}(t), \end{aligned}$$

(16)

where the inequality sign of Eq. (16) mainly relies on the conclusion of random comparison theorem $X(t)\ge x(t)$ a.s. Then integrating on the both sides of (16) from 0 to t, and dividing by t and simultaneously taking $t\rightarrow +\infty$, we gain that

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{\ln y(t)}{t}\le \delta -\frac{1}{2}\sigma _{2}^{2} +\lim _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}\frac{cX(s)}{a+X(s)}\textrm{d}s +\lim _{t\rightarrow +\infty }\frac{\mathcal {M}_{2}(t)}{t}, \end{aligned}$$

where $\mathcal {M}_{2}(t)=\int _{0}^{t}\sigma _{2}\textrm{d}B_{2}(s)$ denote a locally continuous martingale with $\mathcal {M}_{2}(0)=0$. Further computing $\langle \mathcal {M}_{2},\mathcal {M}_{2}\rangle _{t}=\int _{0}^{t}\sigma _{2}^{2}\textrm{d}s=\sigma _{2}^{2}t$, which shows $\lim _{t\rightarrow +\infty }\frac{\langle \mathcal {M}_{2},\mathcal {M}_{2}\rangle _{t}}{t}$ $=\sigma _{2}^{2}<+\infty$ a.s. So then it follows from the strong law of large numbers that $\lim _{t\rightarrow +\infty }\frac{\mathcal {M}_{2}(t)}{t}=0$ a.s. Further using the Jensen’s inequality to the above equation, we yield

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{\ln y(t)}{t}\le&\delta -\frac{1}{2}\sigma _{2}^{2} +\frac{c\cdot \lim _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}X(s)\textrm{d}s}{a+\lim _{t\rightarrow +\infty }\frac{1}{t}\int _{0}^{t}X(s)\textrm{d}s}\\ =&\delta -\frac{1}{2}\sigma _{2}^{2}+\frac{c\big (1-\frac{\sigma _{1}^{2}}{2}\big )}{a+1-\frac{\sigma _{1}^{2}}{2}}. \end{aligned}$$

Hence, under the conditions $\frac{\sigma _{1}^{2}}{2}<1$ and $\frac{\sigma _{2}^{2}}{2} >\delta +\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}$, we have

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{\ln y(t)}{t}<0~a.s., \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{t\rightarrow +\infty }y(t)=0~a.s. \end{aligned}$$

On the premise of the extinction of the generalist parasitoids y(t), we further consider the following limit system of the intrusive hosts:

$$\begin{aligned} \textrm{d}x(t)=x(1-x)\textrm{d}t+\sigma _{1}x\textrm{d}B_{1}(t). \end{aligned}$$

(17)

Notice that the limit system (17) and the auxiliary system (13) are in complete agreement. It then follows from (14), (15) and the average persistence level $1-\frac{\sigma _{1}^{2}}{2}$ of system (13) that for limit system (17), we have (11) and (12), as well as the average persistence level $1-\frac{\sigma _{1}^{2}}{2}$ for the intrusive hosts. The proof of Theorem 4 is completed. $\square$

Remark 2

Theorem 4 indicates that when the intensity of environmental fluctuations acting on the intrusive hosts is small enough such that $\frac{\sigma _{1}^{2}}{2}<1$, and at the same time when the intensity of environmental fluctuations acting on the generalist parasitoids is sufficiently large such that $\frac{\sigma _{2}^{2}}{2}>\delta +\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}$, then the generalist parasitoids go to extinction, while the invading hosts are stochastically weakly persistent with average level $1-\frac{\sigma _{1}^{2}}{2}$. That is to say, using generalist parasitoids cannot succeed in the control of invasive hosts in this situation.

Recall also that the generalist parasitoids are always persistent in the deterministic model (1) or (2) (Magal et al. 2008; Xiang et al. 2020). This means that using the deterministic model may lead to incorrect predictions on the dynamics of populations living in an environment of random fluctuation, and therefore, it is necessary to consider the effect of environmental fluctuations on the populations when using biological control strategies to prevent the invasion of the exotic species (Petrovskii et al. 2005; Perrings 2005; Schreiber and Lloyd-Smith 2009; Kadoya and Washitani 2010; Chalak et al. 2017).

2.4 Total Extinction of Stochastic Model (3)

The following theorem indicates that both the intrusive hosts and generalist parasitoids will go to extinction when the intensities of environmental noises are large enough.

Theorem 5

Let (x(t), y(t)) be the solution of stochastic model (3) established by Theorem 1. When $\frac{\sigma _{1}^{2}}{2}>1$, the intrusive hosts are extinct, that is, $\lim _{t\rightarrow +\infty }x(t)=0$ a.s.; Further when $\frac{\sigma _{2}^{2}}{2}>\delta$, the generalist parasitoids also die out, namely, $\lim _{t\rightarrow +\infty }y(t)=0$ a.s.

Proof

Similar to the proof of Theorem 3, under the condition $\frac{1}{2}\sigma _{1}^{2}>1$ we have $\lim _{t\rightarrow +\infty }x(t)$ $=0$ a.s. Hence, when the intrusive hosts x(t) are extinct, we can easily see that there are a pair of factors: a time $T>0$ and a set $\Omega _{\epsilon }\subset \Omega$ such that $\mathbb {P}(\Omega _{\epsilon })>1-\epsilon$ and $\frac{cx}{a+x}\le \frac{c\epsilon }{a}$ for all $t\ge T$ and $\omega \in \Omega _{\epsilon }$. In what follows, we further prove the extinction of the generalist parasitoids. Applying Itô’s formula to $\ln y(t)$, we have

$$\begin{aligned} \textrm{d}\ln y(t)=&\frac{1}{y}\left( \left( y(\delta -y)+\frac{cxy}{a+x}\right) \textrm{d}t+\sigma _{2}y\textrm{d}B_{2}(t)\right) +\frac{1}{2} \left( -\frac{1}{y^{2}}\right) \sigma _{2}^{2}y^{2}\textrm{d}t\nonumber \\ =&\left( \delta -y+\frac{cx}{a+x}-\frac{1}{2}\sigma _{2}^{2}\right) \textrm{d}t+\sigma _{2}\textrm{d}B_{2}(t)\nonumber \\ \le&\Big (\delta +\frac{c\epsilon }{a}-\frac{1}{2}\sigma _{2}^{2}\Big )\textrm{d}t+\sigma _{2}\textrm{d}B_{2}(t). \end{aligned}$$

(18)

Integrating on both sides of Eq. (18) from 0 to t, dividing by t, and then taking limit $t\rightarrow +\infty$, we can obtain

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{\ln y(t)}{t}\le&\lim _{t\rightarrow +\infty }\frac{\ln y(0)}{t}+\delta +\frac{c\epsilon }{a}-\frac{1}{2}\sigma _{2}^{2}+\lim _{t\rightarrow +\infty } \frac{\mathcal {M}_{2}(t)}{t}, \end{aligned}$$

where $\mathcal {M}_{2}(t)=\int _{0}^{t}\sigma _{2}\textrm{d}B_{2}(t)$, then $\lim _{t\rightarrow +\infty }\frac{\mathcal {M}_{2}(t)}{t}=0$ a.s. Further based on the condition $\frac{1}{2}\sigma _{2}^{2}>\delta$, the bounded of the initial value $y(0)>0$ and taking $\epsilon \rightarrow 0$, we yield

$$\begin{aligned} \limsup _{t\rightarrow +\infty }\frac{\ln y(t)}{t}\le \delta -\frac{1}{2}\sigma _{2}^{2}<0~ a.s., \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{t\rightarrow +\infty }y(t)=0~a.s. \end{aligned}$$

In summary, under the two conditions of Theorem 5 the whole invading hosts-generalist parasitoids model (3) goes to extinction. $\square$

Remark 3

From Theorem 5 we know that when the negative effects of external environmental interferences acting on the intrusive hosts and generalist parasitoids are both large enough such that $\frac{1}{2}\sigma _{1}^{2}>1$ and $\frac{1}{2}\sigma _{2}^{2}>\delta$, then the two biological populations will go to extinction. This is clearly contrasted with the dynamics of the corresponding deterministic model (2), where $E_{0}(0,0)$ is a unstable node, implying that both the invading hosts and generalist parasitoids will not go to extinction. That is to say, the stochastic fluctuations of external environments can significantly influence the ultimate survivability of the two biological populations, and therefore, it is necessary to consider the impact of stochastic environmental disturbances on the dynamics of biological populations (Liu and Ma 2021; Chang et al. 2019; Liu and Bai 2020; Zhang and Wang 2020; Song et al. 2020; Wang et al. 2020; Guo et al. 2021; Zhang et al. 2022).

2.5 Permanence of Stochastic Model (3)

In this subsection, we will discuss the sufficient conditions for the persistent coexistence of both the invading hosts and generalist parasitoids under the influences of external environmental interferences. For convenience, for any integrable function $g(t),~t\ge 0$, define

$$\begin{aligned} \langle g\rangle (t):=\frac{1}{t}\int _{0}^{t}g(s)\textrm{d}s,~~ g_{*}:=\liminf _{t\rightarrow +\infty }g(t)~~\textrm{and}~~ g^{*}:=\limsup _{t\rightarrow +\infty }g(t). \end{aligned}$$

We have the following result.

Theorem 6

Stochastic model (3) is persistent in the mean provided that

$$\begin{aligned} \max \left\{ \frac{\sigma _{1}^{2}}{2},~\frac{\sigma _{2}^{2}}{2\delta },~ \frac{\sigma _{1}^{2}}{2}+\frac{b}{a}\left( \delta -\frac{\sigma _{2}^{2}}{2}+\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}\right) \right\} <1. \end{aligned}$$

(19)

More precisely,

$$\begin{aligned}{} & {} 1-\frac{\sigma _{1}^{2}}{2}\ge \langle x\rangle ^{*}\ge \langle x\rangle _{*}>1-\frac{\sigma _{1}^{2}}{2}-\frac{b}{a}\left( \delta -\frac{\sigma _{2}^{2}}{2}+\frac{c(1-{\sigma _{1}^{2}} /{2})}{a+1-{\sigma _{1}^{2}}/{2}}\right) ~~a.s., \end{aligned}$$

(20)

$$\begin{aligned}{} & {} \delta -\frac{\sigma _{2}^{2}}{2}+\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}\ge \langle y\rangle ^{*}\ge \langle y\rangle _{*}\ge \delta -\frac{\sigma _{2}^{2}}{2}~~a.s. \end{aligned}$$

(21)

Proof

From stochastic model (3) we have that

$$\begin{aligned} \textrm{d}x\le x(1-x)\textrm{d}t+\sigma _{1}x\textrm{d}B_{1}(t),\\ \textrm{d}y\ge y(\delta -y)\textrm{d}t+\sigma _{2}y\textrm{d}B_{2}(t). \end{aligned}$$

It then follows from the stochastic comparison theorem that

$$\begin{aligned} x(t)\le X(t), ~y(t)\ge Y(t)~~a.s., \end{aligned}$$

where X(t) and Y(t) are, respectively, the solutions of Eq. (13) with initial value $X(0)=x(0)$ and equation

$$\begin{aligned} \textrm{d}Y=Y(\delta -Y)\textrm{d}t+\sigma _{2}Y\textrm{d}B_{2}(t) \end{aligned}$$

with initial value $Y(0)=y(0)$. Thus, we have from Theorems 3 and 4 that

$$\begin{aligned} \langle x\rangle ^{*}\le&\int _{0}^{+\infty }X\mu (X)\textrm{d}X=1-\frac{\sigma _{1}^{2}}{2}~a.s. \end{aligned}$$

(22)

and

$$\begin{aligned} \langle y\rangle _{*}\ge \int _{0}^{+\infty }Y\nu (Y)\textrm{d}Y=\delta -\frac{\sigma _{2}^{2}}{2}~a.s. \end{aligned}$$

(23)

Now making use of the Itô’s formula to $\ln y(t)$, we have from the second equation of stochastic model (3) that

$$\begin{aligned} \textrm{d}\big (\ln y(t)\big )=\left( \delta -y+\frac{cx}{a+x}-\frac{1}{2} \sigma _{2}^{2}\right) \textrm{d}t+\sigma _{2}\textrm{d}B_{2}(t). \end{aligned}$$

(24)

Integrating from 0 to t and then dividing by t on the two sides of Eq. (24), we obtain that

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{y(t)}{y(0)}=&\Big (\delta -\frac{1}{2} \sigma _{2}^{2}\Big )+\frac{1}{t}\int _0^t\frac{cx(s)}{a+x(s)}\textrm{d}s -\frac{1}{t}\int _0^t y(s)\textrm{d}s+\frac{\mathcal {M}_{2}(t)}{t}\\ \le&\Big (\delta -\frac{1}{2} \sigma _{2}^{2}\Big )+\frac{c\langle x(t)\rangle }{a+\langle x(t)\rangle } -\langle y\rangle (t)+\frac{\mathcal {M}_{2}(t)}{t}, \end{aligned} \end{aligned}$$

(25)

where $\mathcal {M}_{2}(t)=\int _{0}^{t}\sigma _{2}\textrm{d}B_{2}(s)$ and we have used the Jensen’s inequality in the last step. Notice from (22) that for any $\varepsilon >0$, there is a $T=T(\varepsilon )>0$ such that when $t>T$, we have $\langle x\rangle (t)<1-\frac{\sigma _{1}^{2}}{2}+\varepsilon$. It then follows from (25) that

$$\begin{aligned} \frac{1}{t}\ln \frac{y(t)}{y(0)}\le \delta -\frac{1}{2} \sigma _{2}^{2}+\frac{c(1-{\sigma _{1}^{2}}/{2}+\varepsilon )}{a+1-{\sigma _{1}^{2}}/{2}+\varepsilon } -\langle y\rangle (t)+\frac{\mathcal {M}_{2}(t)}{t}. \end{aligned}$$

(26)

Notice the arbitrariness of $\varepsilon$. Applying the first conclusion in (Liu et al. 2011, Lemma 4), we have from (26) that

$$\begin{aligned} \langle y\rangle ^{*}\le \delta -\frac{1}{2}\sigma _{2}^{2} +\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}~~a.s. \end{aligned}$$

(27)

Now applying Itô’s formula to $\ln x(t)$, we have from the first equation of stochastic model (3) that

$$\begin{aligned} \textrm{d}\big (\ln x(t)\big )=\left( 1-\frac{1}{2}\sigma _{1}^{2}-x-\frac{by}{a+x}\right) \textrm{d}t+\sigma _{1}\textrm{d}B_{1}(t). \end{aligned}$$

(28)

Proceeding similarly as for (24), we have from (28) that

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{x(t)}{x(0)}=&\Big (1-\frac{1}{2}\sigma _{1}^{2}\Big )-\frac{1}{t}\int _{0}^{t}x(s)\textrm{d}s-\frac{1}{t}\int _{0}^{t}\frac{by(s)}{a+x(s)}\textrm{d}s+\frac{\mathcal {M}_{1}(t)}{t}\\ \ge&\Big (1-\frac{1}{2}\sigma _{1}^{2}\Big )-\frac{1}{t}\int _{0}^{t}x(s)\textrm{d}s-\frac{b}{a}\frac{1}{t}\int _{0}^{t}y(s)\textrm{d}s+\frac{\mathcal {M}_{1}(t)}{t}\\ \end{aligned} \end{aligned}$$

(29)

where $\mathcal {M}_{1}(t)=\int _{0}^{t}\sigma _{1}\textrm{d}B_{1}(s)$. Notice from (27) that for any $\epsilon >0$, there exists a $T_1=T_1(\epsilon )>0$ such that when $t>T_1$, we have $\langle y\rangle (t)\le \delta -\frac{\sigma _{2}^{2}}{2} +\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}+\epsilon$ a.s. It then follows from (29) that when $t>T_1$,

$$\begin{aligned} \begin{aligned} \frac{1}{t}\ln \frac{x(t)}{x(0)}\ge&1-\frac{\sigma _{1}^{2}}{2}-\frac{1}{t}\int _{0}^{t}x(s)\textrm{d}s-\frac{b}{a}\left( \delta -\frac{\sigma _{2}^{2}}{2}+\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}+\epsilon \right) +\frac{\mathcal {M}_{1}(t)}{t}~~a.s.\\ \end{aligned} \end{aligned}$$

(30)

Applying the second conclusion provided in (Liu et al. 2011, Lemma 4), we obtain from (30) that

$$\begin{aligned} \langle x\rangle _{*}\ge 1-\frac{\sigma _{1}^{2}}{2}-\frac{b}{a}\left( \delta -\frac{\sigma _{2}^{2}}{2}+\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}\right) ~~a.s. \end{aligned}$$

(31)

Combining (22), (23), (27) and (31), it then follows form (19) that (20) and (21) hold. The proof is thus completed. $\square$

Remark 4

Theorem 6 indicates that when the effect of environmental fluctuations is not too large such that (19) holds, then the invading hosts and generalist parasitoids can coexist in an natural environment of random fluctuations. This implies that in this situation the generalist parasitoids cannot effectively control the invasion of alien hosts, and consequently may lead to the destruction of original ecosystem stability.

3 Numerical Simulations

In (Xiang et al. 2020), authors have made a detailed mathematical analysis of deterministic model (2), and their results indicate that the model can exhibit complex dynamics, including various bifurcations and bistability phenomena, and therefore, its dynamics is sensitive to and easily affected by the fluctuations of environment. In order to comprehensively explore the effects of environmental stochasticity on biological control of alien invasive species, based on the different attributes of deterministic population dynamics, we use different simulation analysis methods to fully reflect the influences of environmental white noises on the complex dynamics of the population model, and then propose effective measures to reasonably control biological invasions.

More specifically, in the first case, under the premise of fixing a set of parameters to ensure that the deterministic model (2) possesses a unique globally asymptotically stable positive equilibrium, we apply the Milstein’s higher order method proposed by Higham in (Higham 2001) to verify the correctness of the theoretical results obtained by this paper, and further analyze the effects of environmental noises on biological control of alien invasive species; in the second case, under the premise of fixing a set of parameters to ensure that the deterministic model (2) possesses bistability phenomena, we use the method of probability statistics to investigate the qualitative impact of environmental noises on the dynamical behaviors of stochastic model (3) with different initial sizes. The numerical simulations in each case are described as follows:

3.1 The Effects of Environmental Noises on the Persistence of Stochastic Model (3)

In view of the Milstein’s higher-order method, we first discretize the stochastic model (3) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{k+1}=x_{k}+\big (x_{k}(1-x_{k})-\frac{bx_{k}y_{k}}{a+x_{k}}\big )\Delta t+\sigma _{1} x_{k}\sqrt{\Delta t}W_{1k}+\frac{1}{2}\sigma _{1}^{2}x_{k}(W_{1k}^{2}-1)\Delta t,\\ y_{k+1}=y_{k}+\big (y_{k}(\delta -y_{k})+\frac{cx_{k}y_{k}}{a+x_{k}}\big )\Delta t+ \sigma _{2}y_{k}\sqrt{\Delta t}W_{2k}+\frac{1}{2}\sigma _{2}^{2}y_{k}(W_{2k}^{2}-1)\Delta t, \end{array}\right. } \end{aligned}$$

where $\Delta t>0$ denotes the enough small time increment, $W_{ik},~i=1,2$ denote the independent Gaussian random variables with standard normal distribution $\mathcal {N}(0,1)$. Then, we fix the partial parameters of stochastic model (3) from (Xiang et al. 2020):

$$\begin{aligned} a=5/27,~b=32/27,~c=32/135,~\delta =2/15. \end{aligned}$$

(32)

Further choose the initial value $x(0)=0.15$ and $y(0)=0.30$. By simple computations, we can obtain that the corresponding deterministic model (2) has two positive equilibria: An unstable cusp $E_{1}(1/9,2/9)$ and a globally asymptotically stable focus $E_{2}(11/27,8/27)$, see Fig. 1a. In what follows, with the help of numerical simulations we examine the correctness of the obtained theoretical results, and further discuss the significant changes in the persistence and extinction of biological populations under the influences of environmental noises with varying degrees. More specifically, on the premise of fixed parameters (32), we apply four sets of different noise intensities to investigate the corresponding dynamics changes of stochastic host–generalist parasitoid model (3). The specific contents are as follows:

Example 1

Taking $\sigma _{1}=1.45$ and $\sigma _{2}=0.02$. By simple computations, we obtain that $\frac{\sigma _{1}^{2}}{2}=1.05125>1$ and $\frac{\sigma _{2}^{2}}{2}=0.0002<\frac{2}{15}=\delta$. The two conditions of Theorem 3 are satisfied. It then follows from Theorem 3 that the invading hosts x(t) die out exponentially (see Fig. 1b), while the generalist parasitoids y(t) are persistent and exist a unique ergodic stationary distribution with average persistence level $\delta -\frac{\sigma _{2}^{2}}{2}\approx 0.1331$, which are consistent with Fig. 1c and d. This demonstrates that when the influence of the environmental fluctuations on the invasive hosts is large enough (such that $\sigma _{1}^{2}/{2}>1$) but it is not too significant on the generalist parasitoids (i.e., $\sigma _{2}^{2}/{2}<\delta$), then the invasive hosts will go extinct while the generalist parasitoids will persist in the ecosystem. In other words, the hosts cannot successfully invade the system, which is mainly due the existence of environmental fluctuations, independent of the predation by generalist parasitoids. Of course, in this situation the generalist parasitoids will persist with a lower average level compared with the corresponding deterministic model (2) due to the lack of extra food provided by invading hosts.

Fig. 1

a is the time series diagrams of the invading hosts x(t) and generalist parasitoids y(t) for deterministic model (2); b and c are, respectively, the time series diagrams of the invading hosts x(t) and generalist parasitoids y(t) for stochastic model (3), and d is the density function of generalist parasitoids y(t)

From Example 1 we can clearly see that deterministic model (2) predicts that an alien species can successfully invade a new ecosystem but it fails to invade for the corresponding stochastic model (3). This indicates that using the deterministic model (2) to predict the invasion of an alien species may lead to an inconsistent conclusion with real ecosystems.

Example 2

Let $\sigma _{1}=0.02$ and $\sigma _{2}=0.82$. It is easy to check that $\frac{\sigma _{1}^{2}}{2}=0.0002<1$ and $\frac{\sigma _{2}^{2}}{2}=0.3362>\delta +\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}\approx 0.3333$, which show that the two conditions of Theorem 4 hold. Hence, by Theorem 4 we can know that the generalist parasitoids y(t) go to extinction exponentially (see Fig. 2c), but the invading hosts x(t) are persistent and exist the unique ergodic stationary distribution with the average persistence level $1-\frac{\sigma _{1}^{2}}{2}=0.9998$, which are consistent with Fig. 2a and b. This demonstrates that when the impact of noises on the invading hosts is not too significant (i.e., $\sigma _{1}^{2}/{2}<1$) but it is large enough $\left( \mathrm{such~that} \frac{\sigma _{2}^{2}}{2}>\delta +\frac{c(1-{\sigma _{1}^{2}}/{2})}{a+1-{\sigma _{1}^{2}}/{2}}\right)$, then the invading hosts will be persistent but the generalist parasitoids will go to extinction. This is clearly contrasted with the prediction by the corresponding deterministic model (2) that the generalist parasitoids are predicted to be always persistent.

Fig. 2

a and c are, respectively, diagrams of time series for the invading hosts x(t) and generalist parasitoids y(t), and b is the density function of the invading hosts x(t) for stochastic model (3) with $\sigma _{1}=0.02$ and $\sigma _{2}=0.82$

Example 3

Choose $\sigma _{1}=1.45$ and $\sigma _{2}=0.54$. It is easy to compute that $\frac{\sigma _{1}^{2}}{2}=1.05125>1$ and $\frac{\sigma _{2}^{2}}{2}=0.1458>\delta =\frac{2}{15}$, then two conditions of Theorem 5 hold. It follows from Theorem 5 that both the invading hosts x(t) and generalist parasitoids y(t) are extinct exponentially, which are confirmed by the observations in Fig. 3a and b. That is to say, the large environmental noises could lead to the extinction of both the invading hosts x(t) and generalist parasitoids y(t).

Fig. 3

a and b are, respectively, diagrams of time series for the invading hosts x(t) and generalist parasitoids y(t) for stochastic model (3) with $\sigma _{1}=1.45$ and $\sigma _{2}=0.54$

Example 4

Let $\sigma _{1}=0.02$ and $\sigma _{2}=0.02$. It is easy to check that the condition of Theorem 6 is satisfied. It thus follows from Theorem 6 that both the invading hosts x(t) and generalist parasitoids y(t) are persistent, which are consistent with the observations in Fig. 4a and b. This indicates that when the environmental noises are small, then the stochastic model (3) can have the same predictions as deterministic model (2), i.e., both the invading hosts x(t) and the generalist parasitoids y(t) can persist in the ecosystem considered. That is to say, in this situation the alien hosts can successfully invade the ecosystem. From the viewpoint of biological control, the generalist parasitoids y(t) cannot successfully control the invasion of the alien hosts in a small fluctuating environment.

Fig. 4

a and b are, respectively, diagrams of time series for the invading hosts x(t) and generalist parasitoids y(t) for stochastic model (3) with $\sigma _{1}=\sigma _{2}=0.02$

In summary, as a natural factor that cannot be ignored, environmental noise may have profound impacts on the dynamics of biological populations in the real ecosystem. Thus, it is more reasonable to explore the prevention and control of invasive species as well as the protection of biodiversity by stochastic differential equation models, which can more realistically and comprehensively characterize the evolution of ecological populations dynamics in real ecosystems.

3.2 The Effects of Environmental Noises on Invasive Hosts with Different Initial Values

Notice that deterministic model (2) can exhibit complex dynamics, including bistability and multiple types of bifurcations. This means that the dynamics of the model is sensitive to the fluctuations of the external environment, that is small environmental fluctuations may significantly change the dynamics of the original model. For fixed parameter values

$$\begin{aligned} a=1/4,~b=1,~c=1/60,~\delta =1/3, \end{aligned}$$

(33)

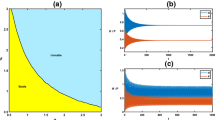
it is shown in (Xiang et al. 2020) that model (2) exists three boundary equilibria: $A_{1}=(0,\frac{1}{3})$ (a stable node), $A_{2}=(0,0)$ (an unstable node) and $A_{3}=(1,0)$ (a saddle); and two positive equilibria: $E_{2}=(0.14902,0.33956)$ (a saddle) and $E_{3}=(0.58853,0.34503)$ (a stable focus). Figure 5 comprehensively describes the vector field of deterministic model (2). The separatrix $\Gamma$ (red solid line), consisting of the two stable manifolds of equilibrium $E_{2}$, divides the positive quadrant into two parts: any trajectory originated from the initial point on the left of the separatrix $\Gamma$ will tend to the invading hosts extinction equilibrium $A_{1}$, meaning that the generalist parasitoids can successfully prevent the invasion of alien hosts; and that on the right of the separatrix $\Gamma$ will tend to the coexistence equilibrium $E_{3}$, meaning that the generalist parasitoids cannot effectively prevent the invasion of alien hosts.

Fig. 5

The vector field of deterministic model (2) with parameters (33)

From above we know that for deterministic model (2) having bistability, whether the alien hosts can successfully invade an ecosystem is completely determined by its initial state. As we have argued above, the environmental noise may have profound impacts on the dynamics of biological populations in the real ecosystems. A natural question is how the fluctuations of environment affect the invasion of the alien hosts and its relative biological control using generalist parasitoids. Under the premise of parameter values fixed in (33), in the following, we will use the corresponding stochastic model (3) to address this problem for four different types of initial values based on the vector field in Fig. 5 of deterministic model (2):

$\bullet$:

The initial values in the neighborhood of coexistence equilibrium $E_{3}$;

$\bullet$:

The initial values in the right neighborhood of separatrix $\Gamma$;

$\bullet$:

The initial values in the left neighborhood of separatrix $\Gamma$;

$\bullet$:

The initial values in the right neighborhood of invading hosts extinction equilibrium $A_{1}$.

For convenience, in the following numerical simulations we always assume that $\sigma _{1}=\sigma _{2}=\sigma$. Meanwhile, we fix the initial value of generalist parasitoids as $y(0)=0.33$ and let the initial value of invading hosts x(0) vary to comprehensively analyze the influence of environmental interferences on the biological control of intrusive hosts for different scenarios of initial values.

3.3 Type 1. The Initial Values in the Neighborhood of Coexistence Equilibrium $E_{3}$

Suppose that the initial population size of the invading hosts is $x(0)=0.55$. It then follows from the vector field in Fig. 5 that the trajectory of deterministic model (2) starting from the initial point $(x(0), y(0))=(0.55, 0.33)$ will tend asymptotically to the coexistence equilibrium $E_{3}$, which implies that the alien hosts can successfully invade the ecosystem. Now we consider the effect of environmental noises on the dynamics of the two populations. We first take two small noise intensity values $\sigma =0.02$ and 0.2, and obtain the corresponding time series shown, respectively, in Fig. 6a and b, from which we can see that both the alien hosts and the generalist parasitoids are persistent, and the fluctuation ranges of population densities increase with the intensities of environmental noises. This indicates that the mild environmental noises cannot lead to the extinction of the two populations. Now we increase the intensity value to $\sigma =0.82$ (see Fig. 6c), we observe that the generalist parasitoids y(t) will go extinct, but the invasive hosts x(t) remain persistent and have a large range of population density fluctuations. This further indicates that compared with the invading hosts x(t), the generalist parasitoids y(t) are more vulnerable to the influences of environmental interferences.

Fig. 6

Time series diagrams of the invading hosts x(t) and generalist parasitoids y(t) for stochastic model (3) with parameters (33) and the initial value (0.55, 0.33)

3.4 Type 2. The Initial Values in the Right Neighborhood of the Separatrix $\Gamma$

Now we take the initial population size of the invading hosts $x(0)=0.16$, then the initial point $(x(0), y(0))=(0.16, 0.33)$ lies in the right neighborhood of the separatrix $\Gamma$. It then follows from the vector field in Fig. 5 that the corresponding trajectory of deterministic model (2) tends asymptotically to the coexistence equilibrium $E_{3}$, meaning that the alien hosts can successfully invade the ecosystem.

Next, we explore the impact of environmental noises on the dynamics of the two species. We take three different intensities of environmental noises: $\sigma =0.02$, $\sigma =0.11$, $\sigma =0.2$, and run, respectively, 3000 numerical simulations in the same length period of time to obtaining the corresponding Fig. 7a, b and c. Since the generalist parasitoids y(t) are always persistent, their time series diagrams are not drawn in the figure. By counting we can know that within the 3000 sample paths of the invasive hosts x(t), in Fig. 7a there are 0 sample paths going to extinction, that is to say, the invading hosts go to extinction with a proportion of $0\%$; in Fig. 7b, there are 325 sample paths going to extinction with a proportion of $10.83\%$; and in Fig. 7c, there are 418 sample paths going to extinction with a proportion of $13.93\%$. This to some extent demonstrates that for this scenario, the existence of environmental noises may be helpful to the control of the invasive hosts.

Fig. 7

a, b and c are the time series diagrams of the invading hosts x(t) with parameters (33) and the initial value (0.16, 0.33), respectively

3.5 Type 3. The Initial Values in Left Neighborhood of the Separatrix $\Gamma$

For this scenario, we take $x(0)=0.14$. It then follows from the vector field in Fig. 5 that the trajectory of deterministic model (2) with initial point $(x(0), y(0))=(0.14, 0.33)$ will tend asymptotically to the invading hosts extinction equilibrium $A_{1}$, that is, the alien hosts cannot successfully invade the ecosystem.

Analyzing as in Type 2, we take three different intensities of environmental noises: $\sigma =0.02$, $\sigma =0.11$, $\sigma =0.2$, and run, respectively, 3000 numerical simulations to obtaining the corresponding Fig. 8a, b and c, where for the same reason as in Type 2, we only draw the time series diagrams of x(t). Among the 3000 sample paths, by counting we know that in Fig. 8a there are 2091 sample paths going to extinction with a proportion of $69.7\%$; in Fig. 8b there are 1289 sample paths going to extinction with a proportion of $42.97\%$; and in Fig. 8c there are 958 sample paths going to extinction with a proportion of $31.93\%$. This to some extent demonstrates that for this scenario, the existence of environmental noises may be unconducive to the control of the invasive hosts, which is clearly contrasted with the observations in Type 2.

Fig. 8

a, b and c are the time series diagrams of the invading hosts x(t) with parameters (33) and the initial value (0.14, 0.33), respectively

4 Type 4. The Initial Values in Right Neighborhood of Invading Hosts Extinction Equilibrium $A_{1}$

Assume that the initial population size of invading hosts is $x(0)=0.01$, by the vector field Fig. 5, it is easy see that the trajectory of deterministic model (2) with initial value $(x(0),y(0))=(0.01,0.33)$ will tend asymptotically to the invading hosts extinction equilibrium $A_{1}$, which implies that the alien hosts cannot successfully invade the ecosystem.

Similarly, we carry out 3000 numerical simulations to obtain the corresponding Figure 9a, b and c, respectively, for three different intensities of environmental noises: $\sigma =0.2, 0.5$ and 0.82. Notice that when $\sigma =0.2$ and $\sigma =0.5$, the generalist parasitoids y(t) are persistent, here we omit verification by drawing. However when $\sigma =0.82$, the generalist parasitoids y(t) are extinct, see Fig. 9d. Among the 3000 sample paths, by counting we know that in Fig. 9a there are 2995 sample paths going to extinction with a proportion of $99.83\%$; in Fig. 9b there are 221 sample paths going to extinction with a proportion of $7.37\%$; in Fig. 9c there are 0 sample paths going to extinction. This to some extent demonstrates that for this scenario, the existence of environmental noises may be unconducive to the control of the invasive hosts.

Fig. 9

a, b and c are the time series diagrams of the invading hosts x(t) with parameters (33) and the initial value (0.01, 0.33), respectively; d is the time series diagrams of invading hosts x(t) and generalist parasitoids y(t) for stochastic model (3) with the same parameters as (c)

To summarize, when the deterministic invading hosts-generalist parasitoids model (2) has bistability, whether the alien hosts can successfully invade a system is completely determined by the initial population sizes. On the premise of fixed model parameters, we carry out a series of numerical simulations, and discuss the influence of environmental interferences on the biological control of intrusive hosts under different initial values. Through comparative analysis, we can find that:

• (1) The generalist parasitoids y(t) are more vulnerable to the influences of environmental interferences than invading hosts x(t);

• (2) When the initial population sizes are different, the effects of environmental stochastic fluctuations on the dynamics of the invasive host–generalist parasitoid model may be opposite. Thus, improving the ability of early detection of ecosystems, including initial densities of biological populations and corresponding properties of population dynamics, will provide effective predictive guidance for the prevention and control of alien host invasions.

5 Conclusion

In order to explore the influence of environmental interferences on the biological control of intrusive hosts, we construct the stochastic host–generalist parasitoid model (3) based on the deterministic model (2). We first perform the persistence and extinction analysis of the model, then through a series of numerical simulations we not only validate the correctness of the theoretical results but also more comprehensively discuss the significant roles of random environmental noises in terms of generalist parasitoids controlling intrusive hosts. It is demonstrated that large environmental fluctuations may seriously threaten the sustainable survival of biological populations, and when the environmental fluctuations are mild and the deterministic model (2) exhibits bistability between the invading hosts extinction equilibrium and a coexistence equilibrium, the effects of environmental noises on the biological control of the invading hosts becomes complex, which is closely related to the initial population sizes. To be specific,

• (1) When the deterministic model (2) has a unique globally stable coexistence equilibrium, relatively mild environmental fluctuations cannot significantly change the survival states of invasive hosts and generalist parasitoids. In this situation, the predictions made by stochastic model are the same as those by the deterministic one: the generalist parasitoids cannot effectively control the invasion of external hosts.

• (2) For the situation when deterministic model (2) exhibits bistability between the invading hosts extinction equilibrium and a coexistence equilibrium, the environmental fluctuations can significantly affect the survival states of populations:

  • When the initial value is seated in the attraction domain of the invasive hosts extinction equilibrium $A_{1}$ (namely, on the left of the separatrix $\Gamma$), the probability of successful invasion of the alien hosts increases with the intensity of environmental fluctuations. That is to say, the existence of environmental white noise is conducive to the successful invasion of foreign hosts. In this scenario, using the deterministic model to predict the invasion of an alien species may lead to an inconsistent conclusion with real ecosystems.

  • When the initial value is seated in the attraction domain of the coexistence equilibrium $E_{3}$ (namely, on the right of separatrix $\Gamma$), we note that generalist parasitoids are more vulnerable to the effects of random environmental fluctuations than the invasive hosts, and the probability of successful invasion of alien hosts may significantly decrease with the increase of the intensity of environmental fluctuations.

  By comparing above, we can know that improving the ability of early detection of ecosystems has important guiding significance for biological control of alien host invasions.

To summarize, the theoretical and numerical results obtained in this paper not only enrich the dynamic research of the host–generalist parasitoid model, but also provide guidance in considering the biological control for alien invasive species using generalist predators in the sense of random environmental fluctuations. However, it is worth noting that spatial dispersal is also an important factor affecting biological control of invasive species. Therefore, applying stochastic partial differential equations to explore the dynamic relationship between invasive hosts and generalist parasitoids will be one of our further research directions.

Appendices

Appendix

1.1 A Proof of Theorem 1

Proof

In order to verify the existence and uniqueness of global positive solution, we divide two steps to prove the conclusion.

Step 1 The proof of the existence and uniqueness for local positive solution. In order to obtain this conclusion, we generally need to test the linear growth conditions and local Lipschitz conditions of model (3) (see (Mao 1997; Hu et al. 2008; Wang 2010)). However it is easy to see that neither of these two criteria of model (3) holds. Hence, to prove the existence and uniqueness of local positive solution, when $t\ge 0$ we let $X_{1}(t)=\ln x(t)$ and $X_{2}(t)=\ln y(t)$. Then for any given positive initial value $(x(0),y(0))\in \mathbb {R}_+^2$, we can obtain the following stochastic differential equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \textrm{d}X_{1}=\left( 1-e^{X_{1}}-\frac{be^{X_{2}}}{a+e^{X_{1}}} -\frac{\sigma _{1}^{2}}{2}\right) \textrm{d}t+\sigma _{1}\textrm{d}B_{1}(t),\\ \textrm{d}X_{2}=\left( \delta -e^{X_{2}}+\frac{ce^{X_{1}}}{a+e^{X_{1}}} -\frac{\sigma _{2}^{2}}{2}\right) \textrm{d}t+\sigma _{2}\textrm{d}B_{2}(t), \end{array}\right. } \end{aligned}$$

(34)

with initial value $X_{1}(0)=\ln x(0)$, $X_{2}(0)=\ln y(0)$. It is easy to check that system (34) satisfies the linear growth conditions and local Lipschitz conditions, which imply the system (34) exists a unique local solution $(X_{1}(t),X_{2}(t))$ for any time $t\in [0,\tau _{e})$ (Mao 1997), where $\tau _{e}$ is the explosion time. It then follows from Itô’s formula that $x(t)=e^{X_{1}(t)}$ and $y(t)=e^{X_{2}(t)}$ are the solution of model (3) with any given initial values $x(0)>0$ and $y(0)>0$. Thus, it proves the existence and uniqueness of local positive solution (x(t), y(t)) of model (3) for all $t\in [0,\tau _{e})$.

Step 2 The proof of global property. In order to testify the global property of the solution (x(t), y(t)) for model (3), we only need to prove $\tau _{e}=+\infty$. To this end, we let $n_{0}>1$ be a sufficiently large constant such that the initial values both $x(0)>0$ and $y(0)>0$ lying in $[\frac{1}{n_{0}},n_{0}]$. Thus, for each positive integer $n>n_{0}$, we define the following stopping time:

$$\begin{aligned} \tau _{n}=\inf \left\{ t\in [0,\tau _{e})\big |\min \{x(t),y(t)\}\le \frac{1}{n} ~\textrm{or}~\max \{x(t),y(t)\}\ge n\right\} . \end{aligned}$$

Obviously, $\tau _{n}$ is monotonic increase as $n\rightarrow +\infty$. We further define $\tau _{\infty }=\lim _{n\rightarrow +\infty }\tau _{n}$, then $\tau _{\infty }\le \tau _{e}$ a.s. Next, we only need to prove $\tau _{\infty }=+\infty$. By proof of contradiction, if $\tau _{\infty }<+\infty$, which implies that there are a pair of constants $T>0$ and $\varepsilon \in (0,1)$ satisfying $\mathbb {P}\{\tau _{\infty }\le T\}>\varepsilon$. Thus, there exists the positive integer $n_{1}\ge n_{0}$ such that

$$\begin{aligned} \mathbb {P}\{\tau _{n}\le T\}\ge \varepsilon ,~n\ge n_{1}. \end{aligned}$$

(35)

We further construct a $\textbf{C}^{2}$ function $V(x,y)=(x-1-\ln x)+\frac{b}{c}(y-1-\ln y)$, by Itô’s formulate one yields

$$\begin{aligned} \textrm{d}V(x,y)=\mathcal {L}V(x,y)\textrm{d}t+\sigma _{1}(x-1)\textrm{d}B_{1}(t)+\frac{b\sigma _{2}}{c}(y-1)\textrm{d}B_{2}(t), \end{aligned}$$

where $\mathcal {L}$ denotes the operator of stochastic differential equation defined by Mao in (Mao 1997). Then

$$\begin{aligned} \mathcal {L}V(x,y)=&\big (1-\frac{1}{x}\big )\left[ x(1-x)-\frac{bxy}{a+x}\right] +\frac{\sigma _{1}^{2}}{2} +\frac{b}{c}\big (1-\frac{1}{y}\big )\left[ y(\delta -y)+\frac{cxy}{a+x}\right] +\frac{b\sigma _{2}^{2}}{2c}\\ =&-(x-1)^{2}+\frac{by}{a+x}+\frac{\sigma _{1}^{2}}{2}+\frac{b\delta y}{c} -\frac{by^{2}}{c}-\frac{b\delta }{c}+\frac{by}{c}-\frac{bx}{a+x} +\frac{b\sigma _{2}^{2}}{2c}\\ \le&-\frac{by^{2}}{c}+\frac{by}{c}(\delta +1)+\frac{by}{a}-\frac{b\delta }{c} +\frac{\sigma _{1}^{2}}{2}+\frac{b\sigma _{2}^{2}}{2c}\\ \le&\frac{b[a(1+\delta )+c]^{2}}{4a^{2}c}-\frac{b\delta }{c} +\frac{\sigma _{1}^{2}}{2}+\frac{b\sigma _{2}^{2}}{2c}\\ :=&C_{3}, \end{aligned}$$

where $C_{3}$ denotes the bounded positive constant. Hence, we can obtain

$$\begin{aligned} \textrm{d}V(x,y)\le C_{3}\textrm{d}t+\sigma _{1}(x-1)\textrm{d}B_{1}(t)+\frac{b\sigma _{2}}{c}(y-1)\textrm{d}B_{2}(t). \end{aligned}$$

(36)

Integrating from 0 to $\tau _{n}\wedge T:=\min \{\tau _{n},T\}$, then taking expectation on both two sides of (36), we can get

$$\begin{aligned} \mathbb {E}V(x(\tau _{n}\wedge T),y(\tau _{n}\wedge T))\le V(x(0),y(0))+C_{3}T. \end{aligned}$$

(37)

Let $\Omega _{n}=\{\tau _{n}\le T\}$, it then follows from (35) that $\mathbb {P}(\Omega _{n})\ge \varepsilon$. By the definition of stopping time, we can know when $t=\tau _{n}$ and for any $\omega \in \Omega _{n}$, at least one of between x(t) and y(t) either is equal to $\frac{1}{n}$ or is equal to n. Thus, we can derive that $V(x(\tau _{n},\omega ),y(\tau _{n},\omega ))$ is not less than

$$\begin{aligned} (n-1-\ln n)\wedge \left( \frac{1}{n}-1+\ln n\right) \wedge \frac{b}{c}(n-1-\ln n)\wedge \frac{b}{c}\left( \frac{1}{n}-1+\ln n\right) . \end{aligned}$$

Further combining with the above conclusion and (37), we have

$$\begin{aligned} V(x(0),y(0))+C_{3}T\ge&\mathbb {E}[\textbf{1}_{\Omega _{n}}V(x(\tau _{n}\wedge T),y(\tau _{n}\wedge T))]\\ \ge&\varepsilon \big [(n-1-\ln n)\wedge \big (\frac{1}{n}-1+\ln n\big )\\&\wedge \frac{b}{c}(n-1-\ln n)\wedge \frac{b}{c}\big (\frac{1}{n}-1+\ln n\big )\big ], \end{aligned}$$

where $\textbf{1}_{\Omega _{n}}$ is the indicator function of $\Omega _{n}$. When $n\rightarrow +\infty$, one can have

$$\begin{aligned} +\infty >V(x(0),y(0))+C_{3}T=+\infty , \end{aligned}$$

which is obviously contradictory. This completes the proof of global property.

In summary, we derive the conclusion of Theorem 1. $\square$

Proof of Theorem 2

Proof

Let $Z(t)=cx(t)+by(t)$, then by simple computations we can yield

$$\begin{aligned} \textrm{d}Z(t)=&c\textrm{d}x(t)+b\textrm{d}y(t)\\ =&[cx(1-x)+by(\delta -y)]\textrm{d}t+c\sigma _{1}x\textrm{d}B_{1}(t)+b\sigma _{2}y\textrm{d}B_{2}(t)\\ =&(2cx-cx^{2}-cx+b\delta y-by^{2}+by-by)\textrm{d}t+c\sigma _{1}x\textrm{d}B_{1}(t)+b\sigma _{2}y\textrm{d}B_{2}(t)\\ \le&\left( c+\frac{(1+\delta )^{2}}{4}-Z(t)\right) \textrm{d}t+c\sigma _{1}x\textrm{d}B_{1}(t)+b\sigma _{2}y\textrm{d}B_{2}(t). \end{aligned}$$

Let N(t) be the solution of the following stochastic differential equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \textrm{d}N(t)=\left( c+\frac{(1+\delta )^{2}}{4}-N(t)\right) \textrm{d}t+c\sigma _{1}x\textrm{d}B_{1}(t)+b\sigma _{2}y\textrm{d}B_{2}(t),\\ N(0)=Z(0)=cx(0)+by(0). \end{array}\right. } \end{aligned}$$

Then we can derive the following formal solution:

$$\begin{aligned} N(t)=\left( c+\frac{(1+\delta )^{2}}{4}\right) +e^{-t}\left( N(0)-c-\frac{(1+\delta )^{2}}{4}\right) +\mathcal {M}(t), \end{aligned}$$

(38)

where $\mathcal {M}(t)=\int _{0}^{t}e^{-(t-\theta )}[c\sigma _{1}x(\theta )\textrm{d}B_{1}(\theta )+b\sigma _{2}y(\theta )\textrm{d}B_{2}(\theta )]$ is a locally continuous martingale satisfying $\mathcal {M}(0)=0$. Further, Eq. (38) can be rewritten as

$$\begin{aligned} N(t)=N(0)+A(t)-U(t)+\mathcal {M}(t), \end{aligned}$$

where $A(t)=\left( c+\frac{(1+\delta )^{2}}{4}\right) (1-e^{-t})$ and $U(t)=N(0)(1-e^{-t})$. It is obvious that A(t) and U(t) are bounded and are two continuous adapted increasing processes with $A(0)=U(0)=0$ for all $t\ge 0$. It then follows from (Mao 1997, Theorem 1.3.9) that $\lim _{t\rightarrow +\infty }N(t)$ exists and is finite. With the help of stochastic comparison theorem, we have $\lim _{t\rightarrow +\infty }Z(t)\le \lim _{t\rightarrow +\infty }N(t)<+\infty ,$ a.s. This completes the proof of the Theorem 2. $\square$

Proof of Lemma 1

Proof

With the help of Fokker-Plank equation as well as the ergodic stationary distribution, we investigate the main conclusions of (4). Let

$$\begin{aligned} f(\zeta )=\zeta (\Lambda -\zeta ),~g(\zeta )=\sigma \zeta ,~\mathrm{for~all}~\zeta >0. \end{aligned}$$

By simple computations, we can obtain that

$$\begin{aligned} \int \frac{f(\zeta )}{g^{2}(\zeta )}\textrm{d}\zeta =\int \frac{\zeta (\Lambda -\zeta )}{\sigma ^{2}\zeta ^{2}}\textrm{d}\zeta =&\frac{\Lambda }{\sigma ^{2}}\int \frac{1}{\zeta }\textrm{d}\zeta -\frac{1}{\sigma ^{2}}\int \textrm{d}\zeta =\frac{\Lambda }{\sigma ^{2}}\ln \zeta -\frac{\zeta }{\sigma ^{2}}+C_{1},\\ \int _{0}^{+\infty }\frac{1}{g^{2}(\zeta )}e^{\int _{1}^{\zeta }\frac{2f(s)}{g^{2}(s)} \textrm{d}s}\textrm{d}\zeta =&\frac{1}{\sigma ^{2}}\int _{0}^{+\infty }\zeta ^{\frac{2\Lambda }{\sigma ^{2}}-2} e^{\frac{2}{\sigma ^{2}}(1-\zeta )}\textrm{d}\zeta <+\infty , \end{aligned}$$

where $C_{1}$ denotes any constant. Based on the sufficiently criteria for the existence of invariant density (see Klebaner 2005, PP. 170–171), it then follows from the above computed results that Eq. (4) exists the stationary distribution with the following density

$$\begin{aligned} \pi (\zeta )=\frac{C_{2}}{g^{2}(\zeta )}e^{\int _{1}^{\zeta }\frac{2f(s)}{g^{2}(s)} \textrm{d}s}=\frac{C_{2}}{\sigma ^{2}}\zeta ^{\frac{2\Lambda }{\sigma ^{2}}-2} e^{\frac{2}{\sigma ^{2}}(1-\zeta )},~\zeta >0, \end{aligned}$$

(39)

where $C_{2}$ is a constant such that

$$\begin{aligned} \int _{0}^{+\infty }\pi (\zeta )\textrm{d}\zeta =\int _{0}^{+\infty }\frac{C_{2}}{\sigma ^{2}}\zeta ^{\frac{2\Lambda }{\sigma ^{2}}-2} e^{\frac{2}{\sigma ^{2}}(1-\zeta )}\textrm{d}\zeta =1. \end{aligned}$$

(40)

In order to derive the explicit expression of $\pi (\zeta )$, we use variable substitution $\theta =\frac{2\zeta }{\sigma ^{2}}$ to Eq. (40) getting

$$\begin{aligned} 2^{1-\frac{2\Lambda }{\sigma ^{2}}}C_{2}e^{\frac{2}{\sigma ^{2}}} \sigma ^{\frac{4\Lambda }{\sigma ^{2}}-4}\int _{0}^{+\infty }\theta ^{\frac{2\Lambda }{\sigma ^{2}}-2}e^{-\theta }\textrm{d}\theta =1. \end{aligned}$$

(41)

Considering the definition of Gamma function in one-dimensional real number domain, we can know that only when $\frac{2\Lambda }{\sigma ^{2}}-1>0$, Eq. (41) has practical significance. Further we can obtain $2^{1-\frac{2\Lambda }{\sigma ^{2}}}C_{2}e^{\frac{2}{\sigma ^{2}}} \sigma ^{\frac{4\Lambda }{\sigma ^{2}}-4}\Gamma \big (\frac{2\Lambda }{\sigma ^{2}}-1 \big )=1,$ that is to say,

$$\begin{aligned} \frac{C_{2}}{\sigma ^{2}}e^{\frac{2}{\sigma ^{2}}}= \left( \frac{\sigma ^{2}}{2}\right) ^{1-\frac{2\Lambda }{\sigma ^{2}}}\Gamma ^{-1} \left( \frac{2\Lambda }{\sigma ^{2}}-1\right) . \end{aligned}$$

(42)

Thus, substituting expression (42) into (39), we finally derive the desired result (5).

In what follows, we verify the Markov process z(t) for system (4) admits a unique ergodic stationary distribution with the invariant density (5) when $t>0$, which implies that for any integrable function $h(\cdot )$ possesses the conclusion (6). The specific verification processes are as follows:

With the help of the definition of ergodic stationary distribution in (Khasminskii 2012, Theorems 4.1 and 4.2), it is easy to check that the diffusion matrix of system (4) is non-degenerate for all bounded open set $S=(\frac{1}{n},n)$. Moreover, we need to construct a $\textbf{C}^{2}$ function $V(z):\mathbb {R}_{+}\rightarrow \mathbb {R}_{+}$ satisfying $\mathcal {L}V(z)<0$ for all $z\in \mathbb {R}_{+}\backslash S$. Thus, under the condition $\frac{\sigma ^{2}}{2}<\Lambda$, we define

$$\begin{aligned} \overline{V}(z)=-M\ln z+z, \end{aligned}$$

where $M>0$ is a sufficiently large value such that

$$\begin{aligned} -M\big (\Lambda -\frac{1}{2}\sigma ^{2}\big )+\sup _{z\in \mathbb {R}_{+}}\{-z^{2} +(M+\Lambda )z\}\le -2. \end{aligned}$$

It is easy to see that $\overline{V}(z)$ is a continuous function and $\liminf _{n\rightarrow +\infty ,z\in \mathbb {R}_{+}\backslash S}\overline{V}(z)=+\infty$, which show that when $z\in \mathbb {R}_{+}$, the function $\overline{V}(z)$ can reach the lowest value at a point $\overline{z}$. Hence, we further construct a new $\textbf{C}^{2}$ function $V(z)=\overline{V}(z)-\overline{V}(\overline{z}):\mathbb {R}_{+}\rightarrow \mathbb {R}_{+}$ as follows:

$$\begin{aligned} V(z)=-M\ln z+z-\overline{V}(\overline{z}). \end{aligned}$$

Applying Itô’s formula to V(z) along the sample path of system (4), we have

$$\begin{aligned} \textrm{d}V(z)=\mathcal {L}V(z)\textrm{d}t+(z-M)\sigma _{2}\textrm{d}B_{2}(t), \end{aligned}$$

where

$$\begin{aligned} \mathcal {L}V(z)=&\left( -\frac{M}{z}+1\right) z(\Lambda -z)+\frac{1}{2}\frac{M}{z^{2}} \sigma ^{2}z^{2}\\ =&-M\Lambda +Mz+\Lambda z-z^{2}+\frac{1}{2}M\sigma ^{2}\\ =&-M\left( \Lambda -\frac{1}{2}\sigma ^{2}\right) +\left( -z^{2}+(M+\Lambda )y\right) . \end{aligned}$$

Therefore, we easily know that

$$\begin{aligned} \mathcal {L}V(z)= {\left\{ \begin{array}{ll} \mathcal {L}V(+\infty )\rightarrow -\infty , &{}\textrm{as}~z\rightarrow +\infty ,\\ -M\big (\Lambda -\frac{1}{2}\sigma ^{2}\big )+\sup _{z\in \mathbb {R}_{+}}\{-z^{2} +(M+\Lambda )z\}\le -2, &{}\textrm{as}~z\rightarrow 0^{+}. \end{array}\right. } \end{aligned}$$

In summary, we prove $\mathcal {L}V(z)<0$ for all $z\in \mathbb {R}_{+}\backslash S$. It thus follows from the above two conditions that the system (4) exists a unique ergodic stationary distribution and the conclusion (6) holds. $\square$