1 Introduction

Analysis of mathematical models of the chemostat has attracted attention from both mathematicians and ecologists. See for example, [1,2,3,4,5,6,7,8,9]. The basic model of exploitative competition by multi-species for a single substrate in the chemostat takes the following form:

$$\begin{aligned} \left\{ \begin{aligned} \frac{dS(t)}{dt}&=D(S^{0}-S(t))-\sum _{i=1}^np_i(S(t))x_i(t),\\ \frac{dx_i(t)}{dt}&=-D_ix_i(t)+p_i(S(t))x_i(t),~~i=1,2,\ldots ,n.\\ \end{aligned} \right. \end{aligned}$$
(1.1)

Here S(t) is the concentration of the substrate in the culture system at time t. For each \(i=1,2,\ldots ,n\), \(x_i(t)\) denotes the concentration of the i-th microbial species that feeds on the growth-limiting substrate. \(p_i(S)\) represents the species’ specific nutrient consumption rate. \(S^{0}\) is the input concentration of nutrient flow into the feed bottle; D is the dilution rate of the mixture of nutrient and species. Constants \(D_i\) denotes the removal rate of the i-th microbial species and is usually regarded as \(D+\epsilon _i\), where \(\epsilon _i\) is the natural death rate of microbial species. Parameters \(S^0\), D and \(D_i\) are all positive constants.

The dynamical behavior of model (1.1) has been investigated by many researchers. Butler and Wolkowicz [2] proved that when the removal rates of the species are equal to the dilution rate (\(D_i=D\)) in the case of any monotone response functions, the competitive exclusion principle (CEP, see [10]) holds for model (1.1), stating that when multiple microorganism compete exploitatively for the single substrate S, only the species with the lowest break-even concentration will survive and will drive all other species to extinction. Wolkowicz and Lu [9] relaxed the assumption \(D_i=D\) and utilized Lyapunov stability theory to prove the CEP for a general class of monotone response functions and inhibitory response functions. Butler et al. [11] considered periodic washout rate and proved that although for certain parameters the CEP still holds for a model of competition in a chemostat, there are other choices of the parameters for which oscillatory coexistence can occur. Readers can refer to [12,13,14,15,16,17,18,19] and the references therein for more studies on different forms of chemostat models.

It has long been recognized that there is a delay between the time that nutrient is consumed and it is subsequently converted to viable biomass. This recognition of a time delay in the growth process has led to extensive experimental and theoretical studies. Caperon et al. [20], Thingtad and Langeland [21] introduced a discrete delay into the species growth equation of the chemostat model with Monod functional response to better fit the observed experimental data and to describe the effect of delay. Freedman et al. [22] considered a model of two microbial populations competing for a single nutrient in a chemostat with delay only in the substrate concentration and predicted that oscillatory coexistence is possible. Ellermeyer [23] improved the mathematical model of [22] by incorporating discrete delay into the whole consumption process. Wolkowicz and Xia [24] analyzed the dynamics of this more realistic model with multi-species and proved the CEP still holds and no sustained oscillatory behavior is possible. Wang and Wolkowicz [25] subsequently showed that although the CEP still holds when species specific death rates are included, damped oscillations may occur, as was observed in the experiments in [3].

Besides discrete delay, many scholars also considered chemostat models with distributed delay, e.g., [26, 27]. For other chemostat models involving delay see [28,29,30,31,32,33,34,35,36,37] and the references therein.

The model considered in Wolkowicz and Xia [24] has the following form:

$$\begin{aligned} \left\{ \begin{aligned} \frac{dS(t)}{dt}&=D(S^{0}-S(t))-\sum _{i=1}^np_i(S(t))x_i(t),\\ \frac{dx_i(t)}{dt}&=-Dx_i(t)+e^{-D\tau _i}p_i(S(t-\tau _i))x_i(t-\tau _i), ~~i=1,2,\ldots ,n,\\ \end{aligned} \right. \end{aligned}$$
(1.2)

where the constant \(\tau _i>0\) stands for the time delay in conversion of nutrient to viable biomass by the i-th species. Hence, \(e^{-D\tau _i}x_i(t-\tau _i)\) represents the biomass of the microbial species \(x_i\) that consumes nutrient at time \(t-\tau _i\) and survives so that it can complete the conversion process of the substrate at time t. The death rates are assumed to be negligible and are ignored, i.e., \(D_i=D\) for all i. All of the other variables and parameters have the same interpretation as in model (1.1).

The growth response functions \(p_i\), \(i=1,2,\ldots ,n\) are assumed to satisfy:

$$\begin{aligned} p_i:[0,\infty )\rightarrow [0,\infty )~\text {and}~p_i(0)=0; \end{aligned}$$
(1.3)
$$\begin{aligned} p_i~\text {is locally Lipschitz}; \end{aligned}$$
(1.4)

moreover, for each i there is a unique real number \(0<\lambda _i\le \infty \) such that

$$\begin{aligned} e^{D\tau _i}p_i(s)<D;~\text {if}~s<\lambda _i, \end{aligned}$$
(1.5)
$$\begin{aligned} e^{D\tau _i}p_i(s)>D;~\text {if}~s>\lambda _i. \end{aligned}$$
(1.6)

We refer to \(\lambda _i\) as the break-even concentration of the nutrient for the i-th species and note that it generally depends on delay \(\tau _i\). It plays an important role in determining the surviving ability of each species. Throughout this paper, we use \(\lambda _i\) to mean \(\lambda _i(\tau _i)\). Clearly, system (1.2) always has one washout equilibrium \(E_0=(S^0,0,\ldots ,0)\), and one equilibrium \(E_0^*=(S^*, x^*,0,\ldots ,0)\), where \(S^*=\lambda _1\), \(x^*=\frac{(S^0-\lambda _1)D}{p_1(\lambda _1)}\).

Denote \(r=\max \{\tau _1,\tau _2,\ldots ,\tau _n\}\), and let \(C_+^{n+1}\) be the positive cone of the Banach space \(C^{n+1}=\{\varphi =(\varphi _0,\varphi _1,\ldots ,\varphi _n):[-r,0]\rightarrow {\mathbb {R}}^{n+1}~\hbox {continous}\}\) of continuous functions with the norm \(\Vert \varphi \Vert =\sup _{-r\le \theta \le 0}|\varphi (\theta )|\), i.e., \(C_+^{n+1}=\{\varphi \in C^{n+1}:\varphi _i(\theta )>0~\hbox {for all}~\theta \in [-r,0],~i=0,1,2,\ldots ,n\}\). In [24], the authors indicated that by using the method of steps, for each \(\varphi \in C_+^{n+1}\), there is a unique positive solution \(\pi (\varphi ,t)=(S(\varphi ,t),x_1(\varphi ,t),\ldots ,x_n(\varphi ,t))\in {\mathbb {R}}_+^{n+1}\) of (1.2) and \(\pi (\varphi ;\cdot )|_{[-r,0]}=\varphi \). They also proved that if \(\lambda _i\ge S^0\) for all \(i\in \{1,2,\ldots ,n\}\), then every solution \(\pi (\varphi ;\cdot )\) of (1.2) satisfies

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\pi (\varphi ;t)=(S^0,0,\ldots ,0). \end{aligned}$$

In [24, 31] it is also proved that if \(0<\lambda _1<\lambda _2\le \ldots \le S^0\), the solution satisfies

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\pi (\varphi ;t)=(S^*,x^*,0,\ldots ,0), \end{aligned}$$

i.e., the competition exclusion principle holds for the deterministic delayed chemostat model (1.2). In other words, only the microorganism with the lowest \(\lambda _i\) will survive. It also follows from [24], when \(D_i\ne D\) for all i, that under some additional technical assumptions, the same result holds. For example, they showed that if the differential death rates as well as the time delays are small, the CEP holds and all solutions approach an equilibrium state. More recently, Liu et al. [31] provided alternative technical conditions under which the CEP holds in the case of both discrete and distributed delays.

The chemostat models mentioned in the above literatures are described by (delay) differential equations without noise. This is somewhat unrealistic because real population systems are always exposed to uncertain environmental factors. Environmental noise will perturb the steady-states either by effecting the densities of populations or influencing the natural parameter of bio-systems. Researchers have analyzed different ways to incorporate stochastic perturbations into a biological model. In general, there are parametric white noise perturbations [38, 39], stochastic perturbations around the positive equilibrium of the associated deterministic models [40, 41] and linear system perturbations [42, 43]. In particular, Imhof and Walcher [44] initially established a stochastic model of competition in the chemostat under linear random perturbation (also called demographic stochasticity). They explored the species extinction induced by white noise in some cases in which the deterministic model predicts survival. See also [45] for the necessity and significance on stochastic modelling of the chemostat. Wang and Jiang [46] introduced demographic stochasticity into chemostat model (1.1) in the case of single-species, and investigated the ergodic property of the stochastic chemostat model under regime switching. The authors in [47] further established a stochastic chemostat model with growth response of the Monod form and suppose the maximal growth rate is influenced by Brownian motion, and studied the asymptotic properties of the stochastic system including species death rate.

In view of the significance of incorporating delays as well as random noise in modeling population dynamics, analysis of mathematical models described by stochastic delay differential equations is an increasingly active research field. On the basis of an interacting multi-species Lotka–Volterra model with delay logistic equations, Mao [48] carried over the theory of stochastic differential equations to stochastic functional differential equations, and discussed the different dynamical behaviors of three types of stochastic delay population systems in which the intrinsic growth rate is perturbed by white noise (see also [49]). This kind of random disturbance belongs to the study of “Environmental Stochasticity”. Particularly, Ivanov et al. [50] summarized the recent results on stochastic delay differential equations and discussed the important problems including the existence of the unique solutions of SDDEs, Markov property of solutions, stochastic stability, numerical approximations and applications in predator–prey model and dynamics of stock price. Han et al. [51] analyzed two kinds of delayed stochastic predator–prey systems and explored the permanence property with respect to average over time. Wei and Wang [52] and Xu et al. [53, 54] developed some basic theoretical results for stochastic functional differential equations including time delay. By incorporating delay into stochastic chemostat model, Sun and Zhang [55] proposed a single-species stochastic model with Monod response function. The time delay only appears in the growth function so the authors obtained the conditions for extinction and persistence in the mean for the microorganism population. Later on, Sun and Zhang [56] considered nonmonotone response function in the single-species stochastic chemostat model and the time delay was involved into the whole nutrient conversion process. They analyzed the asymptotic behaviors of the stochastic solution around the equilibria of the associated deterministic system but didn’t discuss the problem about CEP.

Motivated by the research works above, in this paper, we will focus on the asymptotic behaviors of a stochastic version of the multi-species delayed chemostat model (1.2). By means of the approach utilized in [44, 56, 58] to incorporate stochastic perturbations into deterministic chemostat model, we propose the following stochastic chemostat model with general growth response and discrete delays:

$$\begin{aligned} \left\{ \begin{aligned} dS(t)&=\left[ D(S^{0}-S(t))-\sum _{i=1}^np_i(S(t))x_i(t)\right] dt+\sigma _0S(t)dB_0(t),\\ dx_i(t)&=[-D x_i(t)+e^{-D \tau _i}p_i(S(t-\tau _i))x_i(t-\tau _i)]dt+\sigma _ix_i(t)dB_i(t),~~i=1,2,\ldots ,n.\\ \end{aligned} \right. \end{aligned}$$
(1.7)

\(B_i(t)\), \(i=0,1,2,\ldots ,n\) are independent standard Brownian motion defined on the complete probability space \((\Omega ,{\mathcal {F}},\{{\mathcal {F}}_t\}_{t\ge 0},P)\). \(\sigma _i\) (\(\sigma _i>0\)) are the corresponding intensities of Brownian motion.

The global asymptotic behaviors in certain stochastic chemostat models have been proved. For example, Zhang et al. [57] investigated the competitive exclusion principle in a stochastic multi-species chemostat with Holling type II functional response and different removal rates. Xu and Yuan [58] showed that the CEP still holds for the stochastic chemostat model with linear growth functions and equal removal rates. However, the authors did not consider the effect of time delays. Due to the existence of demographic stochasticity, system (1.7) with discrete delays no longer has any equilibrium. Moreover, because of the discrete delays appears in the species population (i.e. the whole consumption process) it would be therefore difficult to rigorously prove the CEP for this SDDE system. Thus it is significant to investigate the dynamical behaviors around the equilibrium \(E_0\) and \(E_0^*\) of the deterministic delayed chemostat model (1.2) to see whether the competition exclusion occur. Assuming the linear growth functions of the microorganism species (see also [59]), we explore that under some restrict conditions for white noise, the expected time average of the distance (or simply the mean distance) between the stochastic solution and the associated equilibrium is eventually small. In other words, we demonstrate that an analogue of the CEP holds for the stochastic delayed chemostat model (1.7).

This paper is organized as follows. In Sect. 2, we prove that the stochastic delayed chemostat model (1.7) has a unique positive solution. In Sect. 3, assuming the growth functions are linear, we discuss the asymptotic behavior of the solutions for the stochastic delayed system, and show respectively that the expected time average of the distance between the stochastic processes and the corresponding steady states \(E_0\), \(E_0^*\) of the deterministic delayed chemostat model are eventually small. Numerical simulations are also presented in Sect. 3 to illustrate our conclusions. A discussion is given in Sect. 4 summarizing our results. Finally, the proofs of the main results are provided in Appendix.

2 Existence and Uniqueness of the Positive Solutions

In general, the solution of a population system is not only positive, but also remains bounded above. Wolkowicz and Xia [24] proved that in the case of the deterministic chemostat model with discrete delays, with initial data satisfying \(\varphi \in C^{n+1}_+\), the solutions of (1.2) remain positive and bounded for all \(t>0\). In order for the stochastic chemostat model we formulate to make sense, we need to show that the solution of the system of stochastic functional differential equations (1.7) remains positive and exists globally, i.e. the solution will neither touch zero nor go to explosion in any finite time.

We consider the stochastic process \(X_t=\{(S(t+\theta ),x_1(t+\theta ),\ldots ,x_n(t+\theta )):~-r\le \theta \le 0\}\) and assume that the initial data satisfies:

$$\begin{aligned} \left\{ \begin{aligned}&X_{0}=(S(\theta ),x_1(\theta ),\ldots ,x_n(\theta ))=\varphi =(\varphi _0(\theta ), \varphi _1(\theta ),\ldots ,\varphi _n(\theta )),\\&X_{0}~\hbox {is a}~{\mathcal {F}}_{0}-\hbox {measurable}~C^{n+1}_+ \hbox {-valued random variable and}~E\Vert \varphi \Vert ^2<\infty . \end{aligned} \right. \end{aligned}$$
(2.1)

Inspired by the method in [38], in this section, our analysis on the existence of the unique global positive solution for Eq. (1.7) involves using a Lyapunov functional approach. First, we need a generic assumption: \(p_i(S)\le cS\), c is a positive constant (see assumption \(A_1\) in [46]) which will be utilized in the following proof.

Theorem 2.1

For any given initial data (2.1), there is a unique solution \(X(t)=(S(t),x_1(t), x_2(t),\ldots ,x_n(t))\) on \(t\ge -r\) for the stochastic system (1.7), and the solution will remain in \({\mathbb {R}}_+^{n+1}\) with probability 1, namely \((S(t),x_1(t),x_2(t),\ldots ,x_n(t))\in {\mathbb {R}}_+^{n+1}\) for all \(t\ge -r\) almost surely. X(t) is a \({\mathbb {R}}_+^{n+1}\)-valued \({\mathcal {F}}_t\)-adapted stochastic process.

Proof

Since the coefficients of system (1.7) are locally Lipschitz continuous for any given initial value, there is a unique local solution \((S(t),x_1(t),x_2(t),\ldots ,x_n(t))\) on \(t\in [-r,\varsigma _{e})\), where \(\varsigma _{e}\) is the blow up time (see more detail in [48], Chapter 5). If we can prove \(\varsigma _{e}=\infty \) a.s., then the solution will be global. Choose \(k_{0}\ge 0\) sufficiently large such that S(0), \(x_i(0)\) lie within the interval \([\frac{1}{k_{0}},k_{0}]\). For each integer \(k\ge k_{0}\), define the stopping time:

$$\begin{aligned} \varsigma _k= & {} inf\{t\in [0,\varsigma _e):\min \{S(t),x_1(t),x_2(t),\ldots ,x_n(t)\}\\\le & {} \frac{1}{k}~\hbox {or}~\max \{S(t),x_1(t),x_2(t),\ldots ,x_n(t)\}\ge k\}. \end{aligned}$$

Throughout this paper, we set \(inf\phi =\infty \) (\(\phi \) denotes the empty set). Clearly, \(\varsigma _k\) is increasing as \(k\rightarrow \infty \). Let \(\varsigma _{\infty }=\lim \nolimits _{k\rightarrow \infty }\varsigma _k\), where \(\varsigma _{\infty }\le \varsigma _e\) a.s. If we prove that \(\varsigma _{\infty }=\infty \) a.s., then \(\varsigma _e=\infty \) a.s and \((S(t),x_1(t),\ldots ,x_n(y))\in {\mathbb {R}}^{n+1}_+\) a.s. for all \(t\ge 0\). In other words, to complete the proof all we need to show is that \(\varsigma _\infty =\infty ~a.s.\) If not, then there will be one pair of constants \(T>0\) and \(\varepsilon \in (0,1)\) such that

$$\begin{aligned} P\{\varsigma _{\infty }\le T\}>\varepsilon . \end{aligned}$$

Hence there exists an integer \(k_{1}\ge k_{0}\) such that

$$\begin{aligned} P\{\varsigma _{k}\le T\}>\varepsilon ,~for~all~k\ge k_1. \end{aligned}$$
(2.2)

Define a \(C^{2}\)-function V: \([0,+\infty )\times {\mathbb {R}}_+^{n+1}\rightarrow {\mathbb {R}}\) by

$$\begin{aligned} V\left( S,x_1,\ldots ,x_n\right)= & {} e^{-D{\hat{\tau }}}\left( S-a-a\log \frac{S}{a}\right) \\&+\sum _{i=1}^n\left( x_i-1-\log x_i\right) +\sum _{i=1}^ne^{-D\tau _i}\int _{t-\tau _i}^tp_i(S)x_idr, \end{aligned}$$

in which \({\hat{\tau }}=\min \{\tau _1,\tau _2,\ldots ,\tau _n\}\) and \(a=\frac{De^{D{\hat{\tau }}}}{c}\) is a positive constant. The nonnegativity of this function can be derived from \(u-1-\ln u\ge 0\) on \(u>0\). Using Itô’s formula, we get

$$\begin{aligned}&dV\left( S,x_1,\ldots ,x_n\right) \\&\quad =e^{-D{\hat{\tau }}}\left( 1-\frac{a}{S} \right) dS+e^{-D{\hat{\tau }}}\frac{1}{2S^2}\left( dS\right) ^2+ \sum _{i=1}^n\left( 1-\frac{1}{x_i}\right) dx_i+\sum \limits _{i=1}^n \frac{1}{2x_i^2}\left( dx_i\right) ^2\nonumber \\&\qquad +\sum \limits _{i=1}^ne^{-D\tau _i}p_i\left( S\right) x_idt-\sum \limits _{i=1}^ne^{-D\tau _i} p_i\left( S\left( t-\tau _i\right) \right) x_i\left( t-\tau _i\right) dt\nonumber \\&\quad =e^{-D{\hat{\tau }}}\left( 1-\frac{a}{S}\right) \left\{ \left[ D\left( S^0-S\right) -\sum \limits _{i=1}^np_i\left( S\right) x_i\right] dt +\sigma _0SdB_0\right\} +e^{-D{\hat{\tau }}}\frac{a}{2}\sigma _0^2dt\nonumber \\&\qquad +\sum \limits _{i=1}^n\left( 1-\frac{1}{x_i}\right) \left\{ \left[ -Dx_i+e^{-D\tau _i}p_i \left( S\left( t-\tau _i\right) \right) x_i \left( t-\tau _i\right) \right] dt+\sigma _ix_idB_i\left( t\right) \right\} \\&\qquad +\sum \limits _{i=1}^n\frac{1}{2}\sigma _i^2dt\nonumber \\&\qquad +\sum \limits _{i=1}^ne^{-D\tau _i}p_i\left( S\right) x_idt-\sum \limits _{i=1}^ne^{-D\tau _i}p_i \left( S\left( t-\tau _i\right) \right) x_i\left( t-\tau _i\right) dt\nonumber \\&\quad ={\mathcal {L}}V\left( S,x_1,\ldots ,x_n\right) dt+ae^{-D{\hat{\tau }}} \sigma _0\left( S-1\right) dB_0\left( t\right) +\sum \limits _{i=1}^n\sigma _i\left( x_i-1\right) dB_i\left( t\right) , \end{aligned}$$

where \({\mathcal {L}}V\) is the generating operator of system (1.7) and

$$\begin{aligned} {\mathcal {L}}V&=e^{-D{\hat{\tau }}}\left( 1-\frac{a}{S}\right) [D\left( S^0-S\right) -\sum \limits _{i=1}^np_i\left( S\right) x_i] +\sum \limits _{i=1}^n\left( 1-\frac{1}{x_i}\right) \\&\quad \left[ -Dx_i+e^{-D\tau _i}p_i\left( S\left( t-\tau _i\right) \right) x_i \left( t-\tau _i\right) \right] \\&\quad +\sum \limits _{i=1}^ne^{-D\tau _i}p_i\left( S\right) x_i-\sum \limits _{i=1}^ne^{-D\tau _i} p_i\left( S\left( t-\tau _i\right) \right) x_i\left( t-\tau _i\right) +e^{-D{\hat{\tau }}}\frac{a}{2}\sigma _0^2+\sum \limits _{i=1}^n\frac{1}{2}\sigma _i^2\\&=e^{-D{\hat{\tau }}}DS^0-e^{-D{\hat{\tau }}}DS -\sum \limits _{i=1}^ne^{-D{\hat{\tau }}}P_i\left( S\right) x_i-e^{-D{\hat{\tau }}}\frac{DaS^0}{S} +e^{-D{\hat{\tau }}}Da +\sum \limits _{i=1}^nae^{-D{\hat{\tau }}}\frac{p_i\left( S\right) }{S}x_i\\&\quad -\sum \limits _{i=1}^nDx_i+\sum \limits _{i=1}^ne^{-D\tau _i}p_i\left( S\left( t-\tau _i\right) \right) x_i \left( t-\tau _i\right) + D-\sum \limits _{i=1}^ne^{-D\tau _i}\frac{p_i\left( S\left( t-\tau _i\right) \right) x_i\left( t-\tau _i\right) }{x_i}\\&\quad +\sum \limits _{i=1}^ne^{-D\tau _i}p_i\left( S\right) x_i-\sum \limits _{i=1}^ne^{-D\tau _i}p_i \left( S\left( t-\tau _i\right) \right) x_i\left( t-\tau _i\right) + e^{-D{\hat{\tau }}}\frac{a}{2}\sigma _0^2+\sum \limits _{i=1}^n\frac{1}{2}\sigma _i^2\\&=-\sum \limits _{i=1}^n\left( e^{-D{\hat{\tau }}}-e^{-D\tau _i}\right) p_i\left( S\right) x_i +\sum \limits _{i=1}^n\left( ae^{-D{\hat{\tau }}}\frac{p_i\left( S\right) }{S}-D\right) x_i -e^{-D{\hat{\tau }}}DS-e^{-D{\hat{\tau }}}\frac{DaS^0}{S}\\&\quad -\sum \limits _{i=1}^ne^{-D\tau _i}\frac{p_i\left( S\left( t-\tau _i\right) \right) x_i\left( t-\tau _i\right) }{x_i} +e^{-D{\hat{\tau }}}\left( S^0+a\right) D+D+e^{-D{\hat{\tau }}}\frac{a}{2}\sigma _0^2+\sum \limits _{i=1}^n\frac{1}{2}\sigma _i^2\\&\le e^{-D{\hat{\tau }}}\left( S^0+a\right) D+D+e^{-D{\hat{\tau }}}\frac{a}{2}\sigma _0^2 +\sum \limits _{i=1}^n\frac{1}{2}\sigma _i^2-e^{-D{\hat{\tau }}}DS-e^{-D{\hat{\tau }}} \frac{DaS^0}{S}\\&\quad -\sum \limits _{i=1}^ne^{-D\tau _i}\frac{p_i\left( S\left( t-\tau _i\right) \right) x_i\left( t-\tau _i\right) }{x_i}\\&\le R, \end{aligned}$$

where constant \(R=e^{-D{\hat{\tau }}}(S^0+a)D+D +e^{-D{\hat{\tau }}}\frac{a}{2}\sigma _0^2+\sum \limits _{i=1}^n\frac{1}{2}\sigma _i^2>0\). Therefore

$$\begin{aligned} dV(S,x_1,\ldots ,x_n)\le Rdt+ae^{-D{\hat{\tau }}}\sigma _0(S-1)dB_0(t)+\sum \limits _{i=1}^n\sigma _i(x_i-1)dB_i(t). \end{aligned}$$
(2.3)

Integrating (2.3) from 0 to \(\varsigma _{k}\wedge T\) (=\(\min \{\varsigma _k,T\}\)) and then taking expectation on both sides imply that

$$\begin{aligned} \begin{array}{ll} &{}EV(S(\varsigma _{k}\wedge T),x_i(\varsigma _{k}\wedge T),\ldots ,x_n(\varsigma _{k}\wedge T))\\ &{}\quad \le V(S(0),x_1(0),\ldots ,x_n(0))+E\int _{0}^{\varsigma _{k}\wedge T}Rdt\\ &{}\quad \le V(S(0),x_1(0),\ldots ,x_n(0))+RT.\end{array} \end{aligned}$$
(2.4)

Set \(\Omega _k=\{\varsigma _{k}\le T\}\) for all \(k\ge k_1\). Then by (2.2) we have \(P(\Omega _k)\ge \varepsilon \). Note that for every \(\omega \in \Omega _k\), there exists at least one \(S(\varsigma _k,\omega )\) or \(x_i(\varsigma _k,\omega )\), \(i=1,\ldots ,n\) that equals either k or \(\frac{1}{k}\), and then \(V(S(\varsigma _k),x_1(\varsigma _k),\ldots ,x_n(\varsigma _k))\) is no less than

$$\begin{aligned} k-1-\log k~~~or~~\frac{1}{k}-1+\log k. \end{aligned}$$

Consequently,

$$\begin{aligned} V(S(\varsigma _k),x_1(\varsigma _k),\ldots ,x_n(\varsigma _k))\ge (k-1-\log k)\wedge \left( \frac{1}{k}-1+\log k\right) . \end{aligned}$$

Then combining (2.2) with (2.4), we obtain

$$\begin{aligned} \begin{array}{ll} V(S(0),x_1(0),\ldots ,x_n(0))+RT&{}\ge E\left[ {\mathbf {1}}_{\Omega _{k}(\omega )}V(S(\varsigma _k),x_1(\varsigma _k), \ldots ,x_n(\varsigma _k))\right] \\ &{}\ge \varepsilon \left[ (k-1-\log k)\wedge \left( \frac{1}{k}-1+\log k\right) \right] ,\end{array} \end{aligned}$$

where \({\mathbf {1}}_{\Omega _k(\omega )}\) is the indicator function of \(\Omega _k\). Letting \(k\rightarrow \infty \) induces the contradiction that \(\infty >V(S(0),x_1(0),\ldots ,x_n(0))+RT=\infty \). Thus we have \(\varsigma _{\infty }=\infty \) a.s. The proof is then complete. \(\square \)

3 An Analogue of Competitive Exclusion Principle of the Stochastic Chemostat Model with Delay

In this section, we will devote our attention on the competitive exclusion principle (CEP) for a multi-species competition model in a chemostat perturbed by demographic stochasticity. We assume that the response functions of the microbial species are linear, i.e., \(p_i(S)=m_iS\), where \(m_i\) is positive constant, then \(p_i(S)\) is the growth rate of microbial species \(x_i\) (or called the consumption rate of nutrient). Therefore the stochastic chemostat model (1.7) with delays becomes

$$\begin{aligned} \left\{ \begin{aligned} dS(t)&{=}\left[ D(S^{0}-S(t))-\sum _{i=1}^nm_iS(t)x_i(t)\right] dt+\sigma _0S(t)dB_0(t),\\ dx(t)&{=}[-Dx_i(t)+e^{-D\tau _i}m_iS(t-\tau _i)x_i(t-\tau _i)]dt +\sigma _ix_i(t)dB_i(t),~~i=1,2,\ldots ,n.\\ \end{aligned} \right. \end{aligned}$$
(3.1)

In model (3.1), when noises are ignored, the delayed break-even concentration for species \(x_i\) is given by \(\lambda _i=\frac{De^{D\tau _i}}{m_i}\). The stochastic chemostat model with time delays (3.1) does not have any equilibria, and due to the delays in the microbial concentrations, restricted by research technique, it is difficult to rigorously prove that the CEP holds for model (3.1). Instead, we will study the asymptotic behaviors of the stochastic solutions around the equilibrium \(E_0\) and \(E_0^*\) to see how the CEP operates. According to Corollary 2.4 in [24], if \(\lambda _i\ge S^0\) for all \(i\in \{1,2,\ldots ,n\}\), then every solution \(\pi (\varphi ,t)\) of the deterministic chemostat system (1.2) satisfies

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\pi (\varphi ;t)=(S^0,0,\ldots ,0), \end{aligned}$$
(3.2)

i.e. \(\lim \limits _{t\rightarrow \infty }S(t)=S^0\), \(\lim \limits _{t\rightarrow \infty }x_i(t)=0\). This means that there is competition-independent extinction for any population \(x_i\) with \(\lambda _i\ge S^0\). Wang and Wolkowicz [25] pointed out that if for some \(i\in \{1,2,\ldots ,n\}\), \(\lambda _i\ge S^0\), then species \(x_i\) is called an inadequate competitor, since it dies out even in the absence of any other species. Sequentially, for the stochastic system (3.1), we have the following conclusion:

Theorem 3.1

Let \((S(t),x_1(t),x_2(t),\ldots ,x_n(t))\) be the solution of the stochastic chemostat (3.1) with initial data satisfying (2.1). If \(\lambda _i\ge S^0\) for all \(i\in \{1,2,\ldots ,n\}\), \(\sigma _0^2<D\), and \(\max \limits _{1\le i\le n}\{\sigma _i\}^2<D\), then

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t(S(r)-S^0)^2dr\le & {} \frac{\sigma _0^2(S^0)^2}{D-\sigma _0^2}, \end{aligned}$$
(3.3)
$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t\sum \limits _{i=1}^nx_i(r)^2dr\le & {} \frac{2e^{-2D{\hat{\tau }}}\sigma _0^2(S^0)^2}{D-\max \limits _{1\le i\le n}\{\sigma _i\}^2}\left( 1+\frac{2\sigma _0^2}{D-\sigma _0^2}\right) , \end{aligned}$$
(3.4)

for all \(i=1,2,\ldots ,n\).

According to Theorem 2.2 in [31], we can derive that if the following generic condition holds,

$$\begin{aligned} 0<\lambda _1<\lambda _2\le \cdots \le S^0, \end{aligned}$$
(3.5)

then \(E_0^*=(S^*,x^*,0,\ldots ,0)\) with \(S^*=\lambda _1\), \(x^*=e^{-D\tau _1}(S^0-\lambda _1)\) is a globally asymptotically stable equilibrium of (1.2), i.e., any solution \(\pi (\varphi ;t)\) of (1.2) with initial data in \(C^{n+1}_+\) satisfies

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\pi (\varphi ;t)=(S^*,x^*,0,\ldots ,0), \end{aligned}$$
(3.6)

where \(\lim \nolimits _{t\rightarrow \infty }S(t)=S^*\), \(\lim \nolimits _{t\rightarrow \infty }x_1(t)=x^*\), \(\lim \nolimits _{t\rightarrow \infty }x_i(t)=0\) for \(i=2,\ldots ,n\). The adequate microbial competitor \(x_1\) survives while the other species will go to extinction due to the interspecific competition, thus the CEP holds for deterministic chemostat model (1.2). Therefore, in what follow we assume that \(\lambda _i< S^0\) for all \(i\in \{1,2,\ldots ,n\}\) and consider the asymptotic behavior of the stochastic solutions of (3.1) around the steady state \(E_0^*\).

Theorem 3.2

   Let \((S(t),x_1(t),x_2(t),\ldots ,x_n(t))\) be the solution of the stochastic chemostat model (3.1) with initial date given in (2.1). Assume that condition (3.5) holds. Denote constants \(A=\frac{m_1S^*x^*}{D(D-\sigma _0^2)}K_1\), \(B=\frac{2K_2}{D-2\sigma _1^2}\), \(C=\frac{2K_3e^{2D(\tau _1-{\hat{\tau }})}}{D-\max \nolimits _{2\le i\le n}\{\sigma _i\}^2}\). If \(\sigma _0^2<D\), \(\sigma _1^2<\frac{D}{2}\), \(\max \nolimits _{2\le i\le n}\{\sigma _i\}^2<D\), and

$$\begin{aligned} \max \{A,B,C\}<d(E_0^*,E_0)=\sqrt{(S^*-S^0)^2+(x^*)^2}, \end{aligned}$$

then

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t(S(r)-S^*)^2dr\le A, \end{aligned}$$
(3.7)
$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}} \int _0^t(x_1(r)-x^*)^2dr\le B, \end{aligned}$$
(3.8)
$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t\sum \limits _{i=2}^nx_i(r)^2dr\le C. \end{aligned}$$
(3.9)

Here, \(E_0^*=(S^*,x^*,0,\ldots ,0)\) is an equilibrium of the associated model (1.2). \(K_1\), \(K_2\), \(K_3\) are all positive constants defined by

$$\begin{aligned} K_1= & {} \frac{\sigma _1^2\left( D+m_1x^*\right) }{2m_1e^{-D\tau _1}}+\frac{1}{2} \sigma _0^2\left( S^*\right) ^2+\frac{D\sigma _0^2S^*}{m_1x^*},\\ K_2= & {} K_1\frac{e^{-2D\tau _1}\left( D+\sigma _0^2\right) m_1S^*x^*}{D\left( D-\sigma _0^2\right) } +e^{-2D\tau _1}\sigma _0^2\left( S^*\right) ^2+\sigma _1^2\left( x^*\right) ^2,\\ K_3= & {} K_1\frac{e^{-2D\tau _1}m_1S^*x^*\left( 5D+\sigma _0^2\right) }{D\left( D-\sigma _0^2\right) } +K_2\frac{7+2\sigma _1^2}{D-2\sigma _1^2}+e^{-2D\tau _1}\sigma _0^2\left( S^*\right) ^2 +\sigma _1^2\left( x^*\right) ^2. \end{aligned}$$

The proofs are deferred in “Appendix A” and “Appendix B”. Theorems 3.1 and 3.2 state that under the same conditions for break-even concentrations, the stochastic delayed competition chemostat model (3.1) behaves similarly to the corresponding deterministic delayed system in the sense of (3.3), (3.4) and (3.7)–(3.9) when the intensities of white noise are relatively small. In other words, the expected time average of the distance between stochastic solution \((S(t),x_1(t),\ldots ,x_n(t))\) and the equilibrium \(E_0\) and \(E_0^*\) will eventually bounded in a small region. Moreover, the mean distance between \((S(t),x_1(t),\ldots ,x_n(t))\) and \(E_0\) (or \(E_0^*\)) depends on noise density. If we converge the intensity \(\sigma _0\) to zero, then we conclude that when \(\lambda _i\ge S^0\) and \(\max \limits _{1\le i\le n}\{\sigma _i\}^2<D\) for all \(i\in \{1,2,\ldots ,n\}\),

$$\begin{aligned} \begin{array}{ll} \limsup \limits _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t(S(r)-S^0)^2dr =0,~~a.s.\\ \limsup \limits _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t\sum \limits _{i=1}^nx_i(r)^2dr=0,~~a.s. \end{array} \end{aligned}$$
(3.10)

Similarly, converge \(\sigma _0\), \(\sigma _1\) to zero, then if \(0<\lambda _1<\lambda _2\le \ldots \le S^0\) and \(\max \nolimits _{2\le i\le n}\{\sigma _i\}^2<D\), we have

$$\begin{aligned} \begin{array}{ll} \limsup \limits _{t\rightarrow \infty }\frac{1}{t} {\mathbb {E}}\int _0^t(S(r)-S^*)^2dr=0,~~a.s.\\ \limsup \limits _{t\rightarrow \infty }\frac{1}{t}{ \mathbb {E}}\int _0^t(x_1(r)-x^*)^2dr=0,~~a.s.\\ \limsup \limits _{t\rightarrow \infty }\frac{1}{t} {\mathbb {E}}\int _0^t\sum \limits _{i=2}^nx_i(r)^2dr=0,~~a.s. \end{array} \end{aligned}$$
(3.11)

Consequently, we deduce an analogue of CEP for stochastic competition delayed chemostat (3.1) in the sense of (3.10) and (3.11), under the same conditions for break-even concentrations of the deterministic system. Therefore, our theoretical results improve the researches about CEP in [24, 58] to a more general case.

Remark 3.1

According to Fubini’s theorem, the order of integral operation and expectation can be exchanged. Taking Theorem 3.1 for example, we can re-write the conclusion as \(\limsup \nolimits _{t\rightarrow \infty }\frac{1}{t}\int _0^t{\mathbb {E}}|S(r)-S^0|^2dr\le \frac{\sigma _0^2(S^0)^2}{D-\sigma _0^2}\). Therefore, we show that the average over time of the second moments of stochastic processes \(\{S(t)-S^0\}_{t\ge 0}\), \(\{x_i(t)\}_{t\ge 0}\) are bounded. This is also an important analytical property of stochastic differential equations (see more detail in Chapter 11, [48]).

Remark 3.2

For deterministic delayed chemostat model (1.2), if \(0<\lambda _2<\lambda _1\le \lambda _3\le \cdots \le \lambda _n\le S^0\), then there will be an asymptotically stable equilibrium \(E_2=(\lambda _2,0,e^{-D\tau _2}(S^0-\lambda _2), 0,\ldots ,0)\), i.e. microbial species \(x_2\) will survive through the competition and drives all the other species to extinction. In this case, equilibrium \(E_0^*\) vanishes. This means only the microbial species with the lowest break-even concentration, i.e. \(\lambda _i<\lambda _j\), \(i\ne j\), will win the competition. Review (1.5) and (1.6), we know that delay can make a difference to the break-even concentrations of the delayed chemostat model (without stochasticity) versus the nondelayed chemostat model (without stochasticity). Therefore one can reverse the outcome of the competition by changing the length of delay. Similar to the discussion in Theorem 3.2, we can also study the asymptotic property of the stochastic solution for system (3.1) around equilibrium \(E_2\). Here we omit the details for this discussion and verify our inference via the simulations in Fig. 3.

To illustrate the theoretical results obtained in this paper, we consider the case of two competing microbial species and do numerical simulations via Matlab. We use the method in [60], to produce numerical solutions of the stochastic delayed chemostat model (3.1). We compare these solutions with the corresponding deterministic solutions of model (1.2). The choices for parameters are referred to [61].

First we verify the asymptotic behavior of the stochastic process given by system (3.1) around the equilibrium \(E^0\) of the deterministic system (1.2). Time is measured in hours. Supposing the micro-organisms follows: dilution rate \(D=1.0~\hbox {h}^{-1}\); growth constants \(m_1=1.2~\hbox {h}^{-1}\), \(m_2=1.4~\hbox {h}^{-1}\). Inflowing substrate concentration is in medium of \(S^0=1.6~\hbox {g}/\hbox {L}\). Setting time delays \(\tau _1=0.8\) h, \(\tau _2=1.0\) h. We assume the initial concentrations are \(\varphi (t)=(S(t),x_1(t),x_2(t))=(0.8~\hbox {g}/\hbox {L}, 1.2~\hbox {g}/\hbox {L}, 1.0~\hbox {g}/\hbox {L})\), \(t\in [-1,0]\). A simple calculation shows that the deterministic break-even concentrations for system (1.2) are:

$$\begin{aligned} \lambda _1=1.8546,~~\lambda _2=1.9416, \end{aligned}$$

so \(\lambda _i>S^0, i=1,2\). Hence both competitors are inadequate competitors. In this case, the solution of the deterministic delayed chemostat satisfies

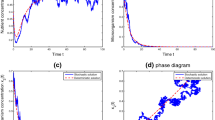
$$\begin{aligned} \lim \limits _{t\rightarrow \infty }(S(t),x_1(t),x_2(t))=(1.6,0,0)\doteq E^0, \end{aligned}$$

i.e., both species are eliminated from the chemostat. We take noise intensities to be \(\sigma _0=0.15\) and \(\sigma _1=\sigma _2=0.1\), so that \(\sigma _0^2<D\) and \(\max \{\sigma _0^2,\sigma _1^2,\sigma _2^2\}=0.0225<D=1\). It then follows from Theorem 3.1 that the stochastic solution fluctuates, but the mean distance between \((S(t),x_1(t),x_2(t))\) and steady state \(E^0\) is eventually small. Simulation outcomes are shown in Fig. 1, where the blue, green and red curves represent the concentrations of the nutrient S, and the microbial species \(x_1\) and \(x_2\), respectively. We note that the two sub-figures both show that the microbial populations die out due to the insufficiency of the input nutrient. In subfigure (b), the density of substrate S(t) in the stochastic model fluctuates at the level of \(1.6~\hbox {g}/\hbox {L}\), while species \(x_1\) and \(x_2\) tend to extinction. As predicted the stochastic model behaves like the deterministic model when the intensities of the noise are relatively small.

Fig. 1
figure 1

a The solution converges to the equilibrium \(E^0\) of the deterministic delayed two-species competition chemostat model (1.2). b The typical sample path of stochastic process \((S(t),x_1(t),x_2(t))\) for the stochastic delayed chemostat model (3.1). Under small noise intensities \(\sigma _0=0.15\) and \(\sigma _1=\sigma _2=0.1\), the stochastic solution fluctuates close to \(E^0\) and both species eventually die out due to the insufficiency of the input nutrient. Time is measured in hours. Input concentration \(S^0=1.6~\hbox {g}/\hbox {L}\), time delays \(\tau _1=0.8\) h, \(\tau _2=1\) h, dilution rate \(D=1.0~\hbox {h}^{-1}\), growth constants \(m_1=1.2~\hbox {h}^{-1}\), \(m_2=1.4~\hbox {h}^{-1}\). Initial biomass \(\varphi (t)=(S(t),x_1(t),x_2(t))=(0.8~\hbox {g}/\hbox {L},1.2~\hbox {g}/\hbox {L}, 1.0~\hbox {g}/\hbox {L}), t\in [-1,0]\) (Color figure online)

Full size image
Fig. 2
figure 2

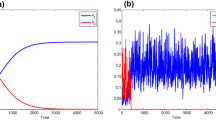
The same parameter values are used as used in Fig. 1 except noise intensity \(\sigma _i=0.1\), \(i=0,1,2\) and the concentration of the input flow is increased to \(S^0=4\hbox {g}/\hbox {L}\). Population \(x_1\) survives and drives population \(x_2\) to extinction for both the deterministic delayed model and the stochastic model. a The solution of the deterministic chemostat model (1.2) converges to \(E_0^*=(1.8546~\hbox {g}/\hbox {L},0.9640~\hbox {g}/\hbox {L}, 0~\hbox {g}/\hbox {L})\). b A typical sample path for the stochastic process \((S(t),x_1(t),x_2(t))\) of the stochastic delayed model (3.1) fluctuates about the steady state \(E_0^*\) (Color figure online)

Full size image

Now we increase the inflowing substrate concentration to medium of \(S^0=4~\hbox {g}/\hbox {L}\), set the noise intensities to \(\sigma _i=0.1\), \(i=0,1,2\), and keep the other growth parameters and time delays unchanged. Initial concentrations for organisms are \(\varphi (t)=(S(t),x_1(t),x_2(t))=(0.8~\hbox {g}/\hbox {L}, 1.2~\hbox {g}/\hbox {L}, 1.0~\hbox {g}/\hbox {L})\), \(t\in [-1,0]\). We compute that in the deterministic delayed chemostat model (1.2), \(\lambda _2<\lambda _1<S^0\), then the solution satisfies

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }(S(t),x_1(t),x_2(t))=(1.8546,0.9640,0)\doteq E_0^*, \end{aligned}$$

i.e., species \(x_1\) survives and will stable at the biomass of \(0.9640~\hbox {g}/\hbox {L}\) while \(x_2\) dies out. In Fig. 2a, it is simulated that the solution trajectories of (1.2) will eventually converges to the equilibrium \(E_0^*\), the competition exclusion occurs. Moreover, the noise intensities satisfy the conditions in Theorem 3.2, system (3.1) predicts that the stochastic process will fluctuate around the equilibrium \(E_0^*\), species \(x_1\) survives (even though oscillating) while drives species \(x_2\) to die out. The simulation result is presented in Fig. 2b. The two delayed competition models behave similarly under small noise intensities. Furthermore, after iterating 10,000 times, our computations show that as time goes,

$$\begin{aligned}&\frac{1}{t}{\mathbb {E}}\int _0^t(S(r)-S^*)^2dr\rightarrow 0.0191~(<A=0.1154), \\&\frac{1}{t}{\mathbb {E}}\int _0^t(x_1(r)-x^*)^2dr\rightarrow 0.0166~(<B=0.0803), \\&\frac{1}{t}{\mathbb {E}}\int _0^tx_2^2(r)dr\rightarrow 0.0014~(<C=0.8439), \end{aligned}$$

through the approximate solutions of the discretization equations in algorithm. This provides a clear illustration of our conclusions in Theorem 3.2.

According to [23], for delayed chemostat model (1.2) with two competitors, when \(0<\lambda _1<\lambda _2<S^0\), then equilibrium \(E_0^*=(\lambda _1, e^{-D\tau _1}(S^0-\lambda _1),0)\) is asymptotically stable, species \(x_1\) is the winner of the competition and drive species \(x_2\) to be extinct; if \(0<\lambda _2<\lambda _1<S^0\), then equilibrium \(E_2=(\lambda _2, 0,e^{-D\tau _2}(S^0-\lambda _2))\) is asymptotically stable, species \(x_2\) is the winning competitor and leads to the extinction of species \(x_1\). Break-even concentrations for deterministic chemostat model (1.2) depend on the time delay, the outcome of the competition can be reversed by changing only the length of the delay for one of the competing species. This should also be true for the corresponding stochastic delayed chemostat model (3.1). Thus in what follows, we make one more simulation in Fig. 3. Increasing the length of delay \(\tau _1\) to 1.2 h, and keeping all the other parametric values and delay \(\tau _2\) unchanged, we obtain

$$\begin{aligned} 1.9416=\lambda _2<\lambda _1=2.7668<S^0. \end{aligned}$$

Consequently, microbial species \(x_2\) wins the competition and the concentration is stable at \(0.7572~\hbox {g}/\hbox {L}\), while \(x_1\) goes to extinction (see Fig. 3a). Under small noise intensities \(\sigma _i=0.1\), \(i=0,1,2\), stochastic process \((S(t), x_1(t), x_2(t))\) will oscillate around \(E_2\), stochastic delayed chemostat model (3.1) exhibits the same outcome of the competition as in model (1.2) (see Fig. 3b).

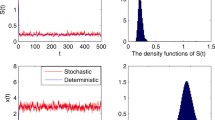
Furthermore, we denote, for example \(\limsup \limits _{t\rightarrow \infty }\frac{1}{t}{\mathbb {E}}\int _0^t(S(r)-S^0)^2dr\), as the ”average difference between S(t) and \(S^0\)”. For better understanding the theoretical results, we make simulations in Fig. 4. It shows that all the curves are approaching to zero, which exhibits that the expected mean distance between stochastic solution \((S(t),x_1(t),x_2(t))\) and \(E_0\) (or \(E_0^*\)) will converge close to zero, the two chemostat systems have similar asymptotical properties. In conclusion, the simulations reveal that an analogue of CEP holds for the stochastic delayed competition chemostat (3.1) in the sense that the expected time average of the distance between stochastic process \((S(t),x_1(t),x_2(t))\) and \(E_0,~E_0^*\) remains bounded.

Fig. 3
figure 3

Increasing the delay \(\tau _1\) to 1.2 h while keeping all of the other parameter values the same as in Fig. 2, there is a reversal of the outcome of the competition. Species \(x_2\) survives and drives species \(x_1\) to extinction for solutions of both the deterministic and stochastic delayed chemostat models (Color figure online)

Full size image
Fig. 4
figure 4

Three curves in (a) are simulations about \(\frac{1}{t}{\mathbb {E}}\int _0^t(S(r)-S^0)^2dr\), \(\frac{1}{t}{\mathbb {E}}\int _0^tx_1^2(r)dr\) and \(\frac{1}{t}{\mathbb {E}}\int _0^tx_2^2(r)dr\), respectively. Three curves in (b) are simulations about \(\frac{1}{t}{\mathbb {E}}\int _0^t(S(r)-S^*)^2dr\), \(\frac{1}{t}{\mathbb {E}}\int _0^t(x_1(r)-x^*)^2dr\) and \(\frac{1}{t}{\mathbb {E}}\int _0^tx_2^2(r)dr\), respectively. Noise intensities \(\sigma _i=0.1\), \(i=0,1,2\) (Color figure online)

Full size image

4 Discussion

In this paper we study a stochastic time delay mathematical model of multi-species competing for a single growth-limiting substrate in a chemostat under demographic stochasticity. With reference to the existing conclusions, our main contributions are:

  1. (1)

    Random noise and discrete delays are initially introduced simultaneously into a multi-species competition model in a chemostat.

  2. (2)

    We prove that the stochastic delayed chemostat model with general response (1.7) has a unique global positive solution, which confirms the rationality of the stochastic population model.

  3. (3)

    In the case of linear growth response functions, we obtain the asymptotic properties of the solutions for stochastic delayed system (3.1) around the equilibrium \(E_0\) and \(E_0^*\) of the corresponding deterministic model, respectively.

  4. (4)

    Our conclusions show that under some restrictions on noise densities, the stochastic solutions will behave similarly to the solutions of the associated deterministic delayed chemostat in the sense that although they fluctuate but the expected time average of the distance between the stochastic solution and the respective equilibria \(E_0\) or \(E_0^*\) will eventually remain small. The mean distances depend on noise densities. The smaller the white noise, the closer the mean distances tending to 0. In other words, an analogue of the competitive exclusion principle holds for the stochastic delayed competition chemostat model.

  5. (5)

    We show numerically that although the solutions of both the delayed deterministic and stochastic models predict that the competitive exclusion principle holds, the values of the delays can influence which species wins the competition and drives the other population to extinction (see Remark 3.2, Figs. 2 and 3).

It should be pointed out that even though we have extended the theorem on the existence of a unique positive solution of the deterministic model (1.2) to the stochastic version (see Theorem 2.1), for technical reasons, we can only obtain the asymptotic behavior of the stochastic delayed chemostat model (3.1) with linear functional response at present. If we introduce environmental noise into the delayed chemostat model established by Freedman et al. in [22], we can try to obtain the competitive exclusion principle according to the research method in [55, 58]. We will defer it for future research.