Turing Pattern Formation in a Semiarid Vegetation Model with Fractional-in-Space Diffusion

Abstract

A fractional power of the Laplacian is introduced to a reaction–diffusion system to describe water’s anomalous diffusion in a semiarid vegetation model. Our linear stability analysis shows that the wavenumber of Turing pattern increases with the superdiffusive exponent. A weakly nonlinear analysis yields a system of amplitude equations, and the analysis of these amplitude equations shows that the spatial patterns are asymptotic stable due to the supercritical Turing bifurcation. Numerical simulations exhibit a bistable regime composed of hexagons and stripes, which confirm our analytical results. Moreover, the characteristic length of the emergent spatial pattern is consistent with the scale of vegetation patterns observed in field studies.

1 Introduction

Vegetation patterns are found in many semiarid regions such as parts of Africa (Worrall 1960; White 1970), Australia (Ludwig and Tongway 1995), and Mexico (Montana et al. 1990). There have been a lot of mathematical models to depict the behavior of the vegetation patterns during the last two decades. They can be classified into three types: The first approach is based on the relationship between the structure of individual plants and the facilitation–competition interactions existing within plant communities (Lefever and Lejeune 1997; Lejeune and Tlidi 1999; Tlidi et al. 2008). The second is based on the reaction–diffusion approach which takes into account the influence of water transport by below-ground diffusion and/or above-ground runoff (Klausmeier 1999). The third approach focuses on the role of environmental randomness as a source of noise-induced symmetry-breaking transitions (Borgogno et al. 2009; Ridif et al. 2011; Couteron et al. 2014; Escaff et al. 2015). In Klausmeier (1999), Klausmeier has proposed a pair of partial differential equations to describe the interaction between plants and water, where the motion of plants obeys a reaction–diffusion equation and that of water obeys an advection equation. By analyzing the Turing instability and obtaining close agreement between the mathematical theory and field observation or numerical experiment, Klausmeier has shown that nonlinear mechanisms are of great importance in determining the spatial structure of plant communities. However, the jump size of water molecule, obeying a heavier-tailed distribution, grows faster than the plant (Benson et al. 2000). In this paper, we introduce the fractional power (more than 1) of the Laplacian to describe the motion of water, when the jump length variance of water molecule possesses a Lévy distribution.

In order to describe the above scenario of vegetation patterns (Worrall 1960; White 1970; Ludwig and Tongway 1995; Montana et al. 1990; Klausmeier 1999), we propose a mathematical model which includes a pair of partial differential equations for water U and plant biomass V. Here, V(x, t) is the density of the vegetation at time t and point x. We define this density as the plant biomass per unit area on the level of individual plant, which is a dominant species accounting for most of the community biomass. Water is supplied uniformly at a rate A and loses at a rate LU due to evaporation. Plants take up water at a rate RG(U)F(V)V, where G(U) is the functional response of plants to water and F(V) is an increasing function which describes how plants increase water infiltration. For simplicity, we use the linear functions $G(U)=U$ and $F(V)=V$, but the results are not sensitive to the exact form of these functions. J is the yield of plant biomass per unit water consumed. Plant biomass is lost only through density-independent mortality and maintenance at a rate MV. Plant dispersal is modeled by a diffusion term with normal diffusion coefficient D. Field observation in Klausmeier (1999) shows that the motions of plants and water are not on similar timescales. The study of Benson et al. (2000) shows that water motion is faster than Gaussian motion. Moreover, the flux of water obeys the Lévy motion. We use the fractional Laplace operator $\nabla ^{\gamma }U$ to describe this process. The mathematical model is written in the form:

$$\begin{aligned}&\frac{\partial U}{\partial t} =A-LU-RUV^2+B\nabla ^{\gamma }U,\nonumber \\&\frac{\partial V}{\partial t} =RJUV^2-MV+D\nabla ^2V, \end{aligned}$$

(1)

where

$$\begin{aligned} \nabla ^{\gamma }U =- \frac{\sec (\pi \gamma /2)}{2\varGamma (2-\gamma )}\frac{d^2}{\mathrm{d} x^2}\int _{-\infty }^{\infty } \frac{U(s)}{|x-s|^{\gamma -1}}\mathrm{d}s. \end{aligned}$$

(2)

In Klausmeier’s semiarid model (Klausmeier 1999), the coefficient B represents the speed of water flow via a form of advection term. From a mathematical point of view, the advection term only considers the locally spatial effect. However, we must introduce a nonlocal fractional Laplacian if we aim to consider the whole spatial effect. Moreover, the nonlocal diffusion has been observed in the movement of real-world river (Benson et al. 2000).

To minimize the number of parameters involved in the model, we introduce dimensionless variables by setting

$$\begin{aligned}&u=R^{1/2}L^{-1/2}JU,~ v=R^{1/2}L^{-1/2}V, ~\tilde{t}= Lt, ~\tilde{x}=L^{1/2}D^{-1/2}x. \end{aligned}$$

(3)

Omitting the tildes, we arrive at a dimensionless fractional reaction–diffusion system:

$$\begin{aligned}&\frac{\partial u}{\partial t} =a-u-uv^2+d\nabla ^{\gamma }u,\nonumber \\&\frac{\partial v}{\partial t} =uv^2-bv+\nabla ^{2}v, \end{aligned}$$

(4)

where

$$\begin{aligned} a=AR^{1/2}L^{-3/2}J, ~ d=BD^{-\gamma /2}L^{(\gamma -2)/2},~ b=M/L. \end{aligned}$$

(5)

The nondimensionalized model (4) has only four parameters: a, measuring water input; b, plant death rate; d, controlling rate at which water flows downhill; $\gamma$, the order of the fractional Laplacian.

The plant density in a spatially heterogeneous environment depends on space, whereas normal diffusive terms are usually introduced to the evolution system (see, e.g., Okubo and Levin (2002)). As is known to all, at molecular level, classical diffusion arises as the result of the standard Brownian motion, and it is typically characterized by the dependence of the mean square displacement of a randomly walking particle on time $\langle (\Delta x)^2 \rangle \sim t$. Apart from classical (or normal) diffusion, molecules may undergo anomalous diffusion effects (Bouchard and Georges 1990; Metzler and Klafter 2000, 2004; Sokolov et al. 2002; Golovin et al. 2008; Gambino et al. 2013), which, in contrast to normal diffusion, need to be characterized by the more general dependence $\langle (\Delta x)^2 \rangle \sim t^{\alpha }$. Here, the exponent $\alpha$ is not necessarily an integer. For $\alpha = 1$, anomalous diffusion reduces to normal diffusion. For $\alpha < 1 (\alpha >1)$, the diffusion process is slower (faster) than normal diffusion, where it is called subdiffusive (resp., superdiffusive). An important limiting case of superdiffusion corresponds to Lévy flights (Metzler and Klafter 2004), which is a phenomenon occurring in systems where there are long jumps of particles, i.e., a jump size distribution with infinite moments. Since in Klausmeier (1999) it is stated that water changes on a much faster timescale than plant biomass does, we incorporate the superdiffusion with Lévy flights to describe the motion of water, and the normal diffusion to the motion of plant. In our model (4), $\langle (\Delta x)^2 \rangle \sim t^{2/\gamma }$ means the superdiffusion.

Pattern formation in reaction–diffusion systems with anomalous diffusion has received considerable attention (Gafiychuk and By 2006; Henry et al. 2005; Weiss et al. 2003; Golovin et al. 2008; Gambino et al. 2013; Zhang and Tian 2014). For instance, the Lévy motion-type superdiffusion is shown to induce the formation of Turing pattern (Golovin et al. 2008). Furthermore, subdiffusion is shown to suppress the formation of Turing pattern (Weiss et al. 2003). In Gambino et al. (2013) and Zhang and Tian (2014), Turing patterns were induced by the anomalous diffusion in both Brusselator chemical system and Boissonade chemical system. Additionally, in systems with Lévy motion, the emergence of spiral waves and chemical turbulence from the nonlinear dynamics of oscillating reaction–diffusion patterns was investigated in Nec et al. (2008). A natural question is how superdiffusion affects the spatial patterns from the mathematical viewpoint. Our aim is to show that the Turing bifurcation causes the spatial regular vegetation.

The remainder of this paper is structured as follows: In Sect. 2, by considering the linear stability of the steady state, we give the Turing parameter space to ensure that Turing bifurcation occurs prior to Hopf bifurcation. In Sect. 3, we present a weakly nonlinear analysis to derive a set of coupled amplitude equations. By analyzing these equations, we show that the regular spatial pattern is asymptotic stable with the slow timescale. In Sect. 4, we present the results of numerical computations, which are in accordance with the field observations. Our paper closes with a brief discussion.

2 Linear Stability Analysis

In this section, we derive the conditions for Turing bifurcation by analyzing the linear stability of the uniform equilibrium to the system (4). This system has three spatially uniform equilibria (a, 0), $\left( \frac{a+\sqrt{a^2-4b^2}}{2},\frac{2b}{a+\sqrt{a^2-4b^2}}\right)$, and $\left( \frac{a-\sqrt{a^2-4b^2}}{2},\frac{2b}{a-\sqrt{a^2-4b^2}}\right)$. The equilibrium consisting of no plants (a, 0) exists and is linearly stable if and only if $a<2b$. But in this case, the coexistent equilibria $\left( \frac{a+\sqrt{a^2-4b^2}}{2},\frac{2b}{a+\sqrt{a^2-4b^2}}\right)$ and $\left( \frac{a-\sqrt{a^2-4b^2}}{2},\frac{2b}{a-\sqrt{a^2-4b^2}}\right)$ do not exist. From the biological perspective, we are interested in studying the stability behavior of the coexistent equilibrium. Therefore, we only consider the case $a>2b$. After the routine linear stability analysis, the equilibrium $\left( \frac{a+\sqrt{a^2-4b^2}}{2},\frac{2b}{a+\sqrt{a^2-4b^2}}\right)$ is always an unstable saddle. In this paper, we only analyze the stability of the third positive equilibrium $(u_s, v_s)\equiv \left( \frac{a-\sqrt{a^2-4b^2}}{2},\frac{2b}{a-\sqrt{a^2-4b^2}}\right)$.

In the absence of water convection, when $a> 2b$, the spatially homogeneous system corresponding to the system (4) exhibits a Hopf bifurcation at $b=1+v_s^2$. The equilibrium $(u_s, v_s)$ is stable to any small spatially homogeneous perturbation for the following hypothesis $(H_1)$:

The linearized system in the neighborhood of $(u_s, v_s)$ is

$$\begin{aligned} \frac{\partial \mathbf {U}}{\partial t}=\mathbf {L} \mathbf {U}+\mathbf {K} \mathbf {U}, ~ \mathbf {U}=\left( \begin{array}{c} u-u_s \\ v-v_s \\ \end{array} \right) , \end{aligned}$$

(6)

where we have defined

$$\begin{aligned} \mathbf {L} =\left( \begin{array}{cc} d \nabla ^{\gamma } &{} 0\\ 0 &{} \nabla ^{2} \end{array} \right) \equiv \mathbf {D}\mathrm{diag}(\nabla ^{\gamma }, \nabla ^{2}),~\mathbf {K} =\left( \begin{array}{cc} -1-v_s^2 &{} -2u_s v_s\\ v_s^2 &{} 2u_s v_s-b \end{array} \right) . \end{aligned}$$

(7)

For the above equations, we seek the general solution

$$\begin{aligned} \mathbf {U}=\left( \begin{array}{c} \rho _1 \\ \rho _2\\ \end{array} \right) \exp (\sigma t+ikx) \end{aligned}$$

(8)

to the linearization of system (4) as a superposition of normal modes. Here, $\sigma$ is the growth rate of the perturbation in time t. i is the imaginary unit and $i^2=-1$, and k is its wavenumber. According to the definition of fractional Laplacian $\nabla ^{\gamma }$, it is easy to verify that the Fourier transform of $\nabla ^{\gamma }v$ satisfies $\mathcal {F}({\nabla ^{\gamma }v})= -|k|^{\gamma }\mathcal {F}(v)$, and $\nabla ^{\gamma }v=-(-\Delta )^{\gamma /2}$. Substituting (8) into the system (6), we obtain the following matrix equation

$$\begin{aligned} \left( \begin{array}{cc} \sigma +1+v_s^2+d k^{\gamma } &{} 2u_s v_s\\ -v_s^2 &{} \sigma +b-2u_s v_s+k^{2} \end{array}\right) \left( \begin{array}{c} \rho _1\\ \rho _2 \end{array}\right) = \left( \begin{array}{c} 0\\ 0 \end{array} \right) . \end{aligned}$$

Therefore, we obtain the dispersion relation

$$\begin{aligned} \sigma ^2+g(k)\sigma +h(k)=0, \end{aligned}$$

(9)

where $g(k)=1+b+v_s^2-2u_sv_s+dk^{\gamma }+k^2$ and $h(k)=(1+v_s^2+dk^{\gamma })(b-2u_sv_s+k^{2})+2u_sv_s^3$.

The equilibrium can lose its stability via both Hopf and Turing bifurcation. Hopf instability occurs when $g(k)=0$ for $k=0$. Then, we can get the critical value of the Hopf bifurcation parameter $b_H$

$$\begin{aligned} b_H=1+v_s^2. \end{aligned}$$

The system (4) undergoes Turing bifurcation if and only if $h(k)=0$. Hence, the neutral instability curve can be written in the form

$$\begin{aligned} b=2u_sv_s-k^{2}-\frac{2u_sv_s^3}{1+v_s^2+dk^{\gamma }}. \end{aligned}$$

(10)

h(k) has a single minimum at $(k_c, b_c)$, where

$$\begin{aligned} \begin{aligned} k_c=x^{\frac{1}{\gamma }},~ b_c=2u_sv_s-x^{2/\gamma }-\frac{2u_sv_s^3}{1+v_s^2+dx}. \end{aligned} \end{aligned}$$

(11)

In conclusion, we obtain the Turing instability threshold $b_c$ and the critical value of the wavenumber $k_c$. Moreover, in order for Turing bifurcation to occur prior to oscillatory instability as a decreases, we need the following parameter space of Turing instability

such that the system is stable to any small spatially homogeneous perturbation.

Fig. 1

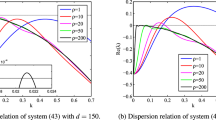
Dispersion relation of the system (4) for three different $\gamma =1,~ 1.5$, and 2, where $\gamma =2$ represents the normal diffusion. Other parameters are $a=2$, $b=0.45$, and $d=242.5$ (Color figure online)

Fig. 2

Turing pattern of the system (4). $\gamma =1.65$ represents the superdiffusion. Other parameter is $d=242.5$

In terms of the disperse relation (9), we illustrate in Fig. 1 the real part of the eigenvalue corresponding to three different sets of parameters as a function of the wavenumber. The superdiffusive exponent $\gamma$ plays an important role in the active wavenumber which increases with $\gamma$. In view of Turing space $(H_2)$, we can depict the parameter spaces where Turing instabilities are expected to appear. In Fig. 2, we illustrate that the behavior of the model (4) is determined by the water input rate a and plant death rate b when water superdiffusion coefficient $d=242.5$. The contours give the dimensional wavelength in meters as determined by the most unstable mode found with linear stability analysis. As water input is decreased or plant loss is increased, the model, to Turing pattern of increasing wavelength, predicts a transition from homogeneous vegetation to no vegetation.

3 Weakly Nonlinear Analysis

In this section, we study the dynamics of Turing pattern by performing a weakly nonlinear analysis of system (4) near the Turing instability threshold. It is convenient to rewrite the system (4) in terms of the deviation of the solution from the positive equilibrium $(u_s, v_s)$ by introducing

$$\begin{aligned} \tilde{u}=u-u_s, \quad \tilde{v}=v-v_s. \end{aligned}$$

Omitting the tildes, we have

$$\begin{aligned}&\frac{\partial u}{\partial t} =(-1-v_s^2)u-2u_sv_sv+d\nabla ^{\gamma }u +(-2v_suv-u_sv^2-uv^2),\nonumber \\&\frac{\partial v}{\partial t} =v_s^2u+(2u_sv_s-b)v+\nabla ^{2}v +(2v_suv+u_sv^2+uv^2). \end{aligned}$$

(12)

By defining

$$\begin{aligned} \mathbf {N}=\left( \begin{array}{c} -2v_suv-u_sv^2-uv^2 \\ 2v_suv+u_sv^2+uv^2 \\ \end{array} \right) , \end{aligned}$$

we have

$$\begin{aligned} \frac{\partial \mathbf {U}}{\partial t}=\mathbf {L} \mathbf {U}+\mathbf {K} \mathbf {U}+\mathbf {N} (\mathbf {U},\mathbf {U}). \end{aligned}$$

(13)

The solution of system (12) is written as a weakly nonlinear expansion in the small control parameter $\varepsilon$, representing the dimensionless distance from the threshold. Here, we let $\varepsilon ^2=\frac{b-b_c}{b_c}$. In the Turing pattern formation, the slow mode is the active mode. We introduce the slow time $T=\varepsilon ^2 t$ and expand both u and v as

$$\begin{aligned} \begin{aligned}&\left( \begin{array}{c} u \\ v\\ \end{array} \right) =\varepsilon \left( \begin{array}{c} u_1 \\ v_1\\ \end{array} \right) +\varepsilon ^2\left( \begin{array}{c} u_2 \\ v_2\\ \end{array} \right) +\varepsilon ^3\left( \begin{array}{c} u_3\\ v_3\\ \end{array} \right) +\cdots .\end{aligned} \end{aligned}$$

(14)

We rewrite the linear operator $\mathbf {L}+\mathbf {K}$ in the following form:

$$\begin{aligned} \mathbf {L}+\mathbf {K}=\mathbf {L_c}-(b-b_c)\mathbf {M}, \end{aligned}$$

(15)

where

$$\begin{aligned} \mathbf {L_c} =\left( \begin{array}{cc} -1-v_s^2+d\nabla ^{\gamma } &{} -2u_s v_s\\ v_s^2 &{} 2u_s v_s-b_c+\nabla ^{2} \end{array} \right) ,~\mathbf {M} =\left( \begin{array}{cc} 0 &{} 0\\ 0 &{} 1 \end{array} \right) \end{aligned}$$

(16)

Substituting Eq. (14) into the system (13) and collecting same powers of $\varepsilon$, we obtain at orders $\varepsilon ^j (j=1,2,3)$ the sequences of equations as follows

$$\begin{aligned} \begin{aligned} O(\varepsilon ):\mathbf {L_c}\left( \begin{array}{c} u_1 \\ v_1\\ \end{array} \right)&=0,\\ O(\varepsilon ^2):\mathbf {L_c}\left( \begin{array}{c} u_2\\ v_2\\ \end{array} \right)&=\left( \begin{array}{c} 2v_su_1v_1+u_sv_1^2\\ -2v_su_1v_1-u_sv_1^2\\ \end{array} \right) , \\O(\varepsilon ^3):\mathbf {L_c}\left( \begin{array}{c} u_3 \\ v_3\\ \end{array} \right)&=\frac{\partial }{\partial T}\left( \begin{array}{c} u_1\\ v_1\\ \end{array} \right) \\ {}&\quad +\left( \begin{array}{c} 2v_su_1v_2+2v_su_2v_1+2u_sv_1v_2+u_1v_1^2\\ -2v_su_1v_2-2v_su_2v_1-2u_sv_1v_2-u_1v_1^2+b_cv_1\\ \end{array} \right) .\end{aligned} \end{aligned}$$

(17)

A denotes the amplitude of the solution to system (13). By solving the above equations (17), we have the amplitude equation

$$\begin{aligned} \frac{\mathrm{d}A}{\mathrm{d}t}=\sigma A-LA^3, \end{aligned}$$

(18)

where

$$\begin{aligned} \sigma= & {} \frac{\rho _2(v_s^2+a+dx)}{u_s^2-v_s^2-1-dx}(b-b_c), \nonumber \\ L= & {} \frac{3}{4}\rho _2^2+2v_s\rho _2w_{20}^1 +(2v_s+2u_s\rho _2)w_{20}^2 +v_s\rho _2w_{22}^1+(v_s+u_s\rho _2)w_{22}^2.\nonumber \\ \end{aligned}$$

(19)

The detailed parameters of $\sigma$ and L are given in “Appendix.”

Since the growth rate coefficient $\sigma$ is always positive, the dynamics of the amplitude Eq. (18), depending on the sign of L, can be divided into two qualitatively different cases: the supercritical case when $L>0$ and the subcritical case when $L<0$.

4 Numerical Results

In this section, we present the results of computational examples using pseudospectral method (Huang and Sloan 1994). The domain of (4) is confined to a two-dimensional domain $[0,L_x]\times [0,L_y]$. The wavenumber for this two-dimensional domain is therefore

$$\begin{aligned} \mathbf {k}=2\pi (m/L_x, n/L_y),~|\mathbf { k}|=2\pi \sqrt{(m/L_x)^2+(n/L_y)^2},~m,n=1, 2,\ldots . \end{aligned}$$

Here, the fractional Laplacian is a symmetry operator written in the following form:

$$\begin{aligned} \nabla ^{\gamma } u(x,y)= & {} - \frac{\sec (\pi \gamma /2)}{2\varGamma (2-\gamma )}\left( \frac{\partial ^2}{\partial x^2}\int _{-\infty }^{\infty } \frac{u(s)}{|x-s|^{\gamma -1}}ds+\frac{\partial ^2}{\partial y^2}\int _{-\infty }^{\infty } \frac{u(s)}{|y-s|^{\gamma -1}}ds\right) .\nonumber \\ \end{aligned}$$

(20)

The model (4) is in agreement with field observation by order of magnitude. Some field data from Africa area are as follows: $a=0.94$ to 2.81, $b=0.45$, and $d=242.5$ (Klausmeier 1999). The exponent of water’s superdiffusion is $\gamma =1.65$ (Benson et al. 2000). Field observations show that grass-striped pattern ranged from 30 to 60 m in wavelength (Fig. 3a, b). In view of the above reality, we choose the parameters as follows:

$$\begin{aligned} a=2,\quad b=0.45,\quad d=242.5, \quad \gamma =1.65. \end{aligned}$$

(21)

Given these parameters, our numerical experiment predicts tree stripes to have wavelengths from 23 to 67 m (seen in Fig. 3c). The wavelength of the real-world semiarid vegetation is similar to the one of the numerical experiment. On the one hand, the real-world semiarid vegetation has two types: spotted pattern (Fig. 3a) and striped pattern (Fig. 3b). The numerical experiment (Fig. 3c) exhibits a mixed state of these two kinds.

Fig. 3

A comparison between real-world semiarid vegetation and the numerical experiment. c is the numerical result with combination of spotted pattern and striped pattern. a and b are grayscale images of semiarid vegetation in Chad and Republic of Niger, captured from Google Earth. Dark shades are inferred vegetation, and white/lighter shades are inferred bare sediment. In each image, north is vertical, and each image covers approximately $300\times 300$ m. From left to right, the image locations are a $11^{\circ }$52’09.52”N, $15^{\circ }$59’42.7”E (Chad); b $13^{\circ }$06’08.29”N, $2^{\circ }$13’19.12”E (Republic of Niger)

Fig. 4

Snapshots of plant densities obtained by model (4) on a 100 by 100 domain (in dimensional terms, 2500 m$^2$). The left figure is the transient at time $t=100$, which is a spotted pattern. The right one is the steady state at time $t=5000$, which is a bistable pattern combined spots and stripes

Moreover, we wish to compare our numerical experiment with the theory of pattern selection for semiarid vegetation model by Lejeune et al. (2004). In Lejeune et al. (2004), the authors found that in many arid regions, the rainfall affects the pattern selection; when the rainfall reduces, patterns constituted of spots of sparser vegetation transform into an alternation of stripes of sparser and thicker vegetation, and they ultimately transform into a pattern of vegetation spots separated by bare ground. As for our numerical experiment, the transient pattern is spot (Fig. 4 left). As time goes on, some spots in the left and bottom part are gradually replaced by stripes. Ultimately, the stripped patterns coexist with the spotted patterns (Fig. 4 right), which exhibits a bistable regime.

5 Discussion

In this paper, we have developed a theoretical framework for studying pattern formation in a two-dimensional fractional reaction–diffusion system. In our semiarid vegetation model, we have shown that the field observation on striped patterns can be mathematically interpreted by the Turing pattern formation. With the application of a weakly nonlinear analysis and suitable numerical simulations, we investigate the Turing parameter space, the Turing bifurcation, and stability of amplitude equations. A threshold of the plants loss rate has been defined to determine the spatial pattern of the vegetation. Numerical studies have been employed to confirm and extend the obtained theoretical results.

In fact, the semiarid vegetation model has been investigated in the previous works (Klausmeier 1999; Sherratt 2005; Kealy and Wollkind 2012). The difference lies on how to describe the effect of water flow. The effect of water flow was described by an advection term in Klausmeier (1999) and Sherratt (2005) as well as a normal diffusion term in Kealy and Wollkind (2012). We compare our theoretical results and numerical results with both theoretical predictions (Kealy and Wollkind 2012) and relevant observational evidence (Sherratt 2005) involving tiger and pearl bush patterns. One main object is the effect of the water flow on the scope of Turing parameter space. In Fig. 5, we find that the advection-type water flow admits the largest Turing parameter space, while the normal-type water flow admits the smallest Turing parameter space. In terms of the superdiffusion’s fractional derivative, when $\gamma =2$, the fractional derivative is reduced to the normal diffusion; when $\gamma =1$, the fractional derivative is reduced to the advection. The biological meaning of the comparison lies when the water flow is faster; the dynamical system composed of water and plant more easily generates plant vegetation.

In conclusion, this fractional Laplacian model for biomass and surface water defined over an semiarid environment provides a new method to describe the motion of water. If motion of water obeys fractional Laplacian, the amount of rainfall causing plant vegetation far exceeds that in normal diffusion and is less than that in advection.

Fig. 5

A comparison of superdiffusion’s neutral stability curve between normal diffusion and advection. The domain below the curve is unstable

Appendix: Derivation of the Amplitude Equation

In this appendix, we sketch a derivation of the amplitude Eq. (18). Note that in Zhang and Tian (2014), the authors study a fractional system with the same fractional order. However, in the system (4), the two fractional orders are different.

Since $\mathbf {L_c}$ is the linear operator of the system at the Turing instability threshold, $(u_1,v_1)^T$ is the eigenvector corresponding to the eigenvalue 0. Therefore, at $O(\varepsilon )$ the solution is given in the form

$$\begin{aligned} (u_1,v_1)^T=\mathbf {\rho }A(T) \cos (k_cx),~\text { with } \mathbf {\rho }\equiv (\rho _1, \rho _2)^T\in Ker\left( \mathbf {L}-\mathbf {D}\mathrm{diag}\left( {k_c}^{\gamma }, {k_c}^2\right) \right) , \end{aligned}$$

where A(T) is the amplitude of the pattern and is still arbitrary at this level. Its form is determined by the perturbational term of the higher order. The vector $\mathbf {\rho }$ is defined up to a constant, and we shall make the normalization in the following way:

$$\begin{aligned} \mathbf {\rho }=(1, \rho _2)^T, \text { with } \rho _2=-(1+v_s^2+dx)/(2u_sv_s). \end{aligned}$$

(22)

Next, we turn to $O(\varepsilon ^2)$. The equation is written in the form

$$\begin{aligned} \mathbf {L_c}\left( \begin{array}{c} u_2\\ v_2\\ \end{array} \right) =A^2(1+\cos (2k_c x))(\rho _2v_s+\rho _2^2u_s/2)\left( \begin{array}{c} 1\\ -1\\ \end{array} \right) . \end{aligned}$$

(23)

Since the right-hand side does not have the resonance, the Fredholm alternative is automatically satisfied. The solution of system (23) is then explicitly computed in terms of the parameters of the full system

$$\begin{aligned} \left( \begin{array}{c} u_2 \\ v_2 \end{array} \right) =A^2\mathbf {(w_{20}}+\mathbf {w_{22}}\cos (2k_cx)), \end{aligned}$$

where $\mathbf {w_{20}}$ and $\mathbf {w_{22}}$ are, respectively, the solutions of the following linear systems

$$\begin{aligned} (\mathbf {L}-\mathbf {D}\mathrm{diag}\left( {0k_c}^{\gamma }, {0k_c}^2\right) )\mathbf {w_{20}}=(\rho _2v_s+\rho _2^2u_s/2)(1, -1)^T, \end{aligned}$$

(24)

$$\begin{aligned} (\mathbf {L}-\mathbf {D}\mathrm{diag}({(2k_c)}^{\gamma }, {(2k_c)}^2))\mathbf {w_{22}}=(\rho _2v_s+\rho _2^2u_s/2)(1, -1)^T. \end{aligned}$$

(25)

Now $O(\varepsilon ^3)$. The equation is written in the form

$$\begin{aligned} \mathbf {L_c}\left( \begin{array}{c} u_3\\ v_3\\ \end{array} \right)= & {} \left( \begin{array}{c} 1\\ -1\\ \end{array} \right) \left[ \cos (k_c x)\left( \frac{\mathrm{d}A}{\mathrm{d} T}+A^3\left( \frac{3}{4}\rho _2^2+2v_s\rho _2w_{20}^1 +(2v_s+2u_s\rho _2)w_{20}^2\right. \right. \right. \nonumber \\&+\,\left. \left. \left. v_s\rho _2w_{22}^1+(v_s+u_s\rho _2)w_{22}^2\right) \right) +\cos (3k_c x)\left( \frac{1}{4}\rho _2^2+v_s\rho _2w_{22}^1\right. \right. \nonumber \\&+\,\left. \left. (v_2+u_s\rho _2)w_{22}^2\right) \right] -\left( \begin{array}{c} 0\\ b_c\rho _2A\cos (k_cx)\\ \end{array} \right) . \end{aligned}$$

(26)

According to the Fredholm solubility condition, the vector function of the right-hand side must be orthogonal with the zero eigenvalues of the operator $\mathbf {L_c^+}$ to ensure the existence of the nontrivial solution to this equation, where $\mathbf {L_c^+}$ is the adjoint operator of $\mathbf {L_c}$. The nontrivial kernel of the operator $\mathbf {L_c^+}$ is

$$\begin{aligned} \left( \begin{array}{c} 1 \\ (v_s^2+1+dx)/u_s^2\\ \end{array} \right) \cos (k_c x). \end{aligned}$$

(27)

In order to ensure the Fredholm solubility condition, we only consider the resonance of the system (26). Thus, we have the amplitude equation

$$\begin{aligned} \frac{dA}{dt}=\sigma A-LA^3, \end{aligned}$$

(28)

where

$$\begin{aligned} \begin{array}{c} \displaystyle \sigma =\frac{\rho _2(v_s^2+a+dx)}{u_s^2-v_s^2-1-dx}(b-b_c), \nonumber \\ \displaystyle L=\frac{3}{4}\rho _2^2+2v_s\rho _2w_{20}^1 +(2v_s+2u_s\rho _2)w_{20}^2 +v_s\rho _2w_{22}^1+(v_s+u_s\rho _2)w_{22}^2.\nonumber \\ \end{array}\\ \end{aligned}$$

(29)